Purpose. Teach children to make geometric shapes from a certain amount of sticks, using the admission of attachment to one figure, taken as the basis, the other. Material. Children's educational games, lessons, crafts
Purpose. Teach children to make up geometric figures From a certain number of sticks, using the admission of attachment to one figure, taken as the basis, the other.
Material: In children at the tables, counting sticks, board, chalk at this and next occupation.
Progress. 1. The tutor offers children to count 5 sticks, check and put them in front of them. Then says: "Tell me how much sticks need to make a triangle, each side of which will be equal to one stick. How many wands need to compile two such triangles? You have only 5 sticks, but you need to make up too 2 equal triangles. Think how it can be done, and make up. "
After most children fulfill the task, the educator asks them to tell, how to make 2 equal triangles of 5 sticks. Draws attention to the guys to perform the task in different ways. Methods of execution must be sketched. With the explanation to use the expression "attached to one triangle another bottom" (left, etc.), and in explaining the solution of the problem to use the expression "attached to one triangle, using only 2 sticks."
2. Make 2 equal squares of 7 sticks (the tutor pre-clarifies which geometric shape can be made up of 4 sticks). It gives a task: count 7 sticks and think about how to make up 2 equal square on the table.
After completing the task, consider different methods Adduction to one square of the other, the teacher sketches them on the board.
Questions for analysis: "How did 2 equal squares of 7 sticks amounted to? What did it first that then? Of how many sticks amounted to 1 square? From how many sticks attached to it the second square? How much did the chopsticks need to compose 2 equal squares?"
2. Example
Purpose. Make figures by attachment. See and show the new, resulting from the compilation of the figure; Use the expression: "attached to one figure another", think about practical actions.
^ Pro progress. The educator invites children to remember which figures they constituted using the admission of attachment. Reports what they will do today - learn to make new, more complex figures. Gives tasks:
After completing the task, the teacher offers all children to make 3 triangles in a row so that the new figure is a quadrangle (Fig. 2). This version of solutions are sketching with chalk on the board. The educator asks to show 3 separate triangles, a quadrangle and a triangle (2 figures), a quadrangle.
Fig. 2 Drawing up figures from triangles
2. Of the 9 sticks to make 4 equal triangles. Think about how it can be done, to tell, then perform the task.
After that, the teacher invites children to draw up the shapes on the blackboard and tell about the setting of the task.
Questions for analysis: "How did 4 equal triangles of 9 sticks amounted to? Which of the triangles was the first? What figures turned out as a result and how much?"
The teacher, specifying the answers of the children, says: "It is possible to start to form a figure from any triangle, and then to it to attach other on the right or left, on top or bottom."
3. Example
Purpose. Exercising children in independent search for ways to make figures based on a preliminary flow of the solution.
^ Pro progress. The tutor sets the children questions: "From how many sticks can be a square, each of the sides of which is equal to one wand? 2 squares? (Out of 8 and 7). How will you be 2 squares of 7 sticks?"
As the teacher is fulfilled, it causes several children to draw them figures on the board and tell the sequence of compilation. It offers all children to make a figure from 3 equal squares located in a row, horizontally. On the board draws the same and says: "Look at the board. It is drawn here how to solve this task in different ways. You can add to one square another, and then the third one. (Shows.) And then you can make a rectangle of 8 sticks, then split it on 3 equal squares with 2 chopsticks. " (Shows.) Then asks questions: "What figures turned out and how much? How many rectangles do it? Find and show them."
2. From 5 sticks to make a square and 2 equal triangles. First tell, and then make up.
When performing this task, children tend to make a mistake: form 2 triangles with an assimilated method - an attachment, resulting in a quadrangle. Therefore, the educator draws the attention of the guys on the condition of the task, the need to compose a square, suggests the leading questions: "How many sticks are needed to compose a square? Because you have chopsticks? Is it possible to draw up 1 triangle to another? How to make it? What kind of figure should be started? " After completing the task, the children explain how they did: it is necessary to make a square and divide it with 1 stick to 2 equal triangles.
4. Example
Purpose. Exercise children in the ability to express an alleged decision to guess.
^ Pro progress. 1. From 9 sticks to make a square and 4 triangles. Think and say how to make up. (Several children express assumptions.)
If children are hampered, the teacher advises: "Remember how the square and 2 triangles were made of 5 sticks. Think and guess how you can perform the task. The one who first decides the task, sacrows the resulting figure on the board."
After performing and sketching a response, the tutor offers all children to make the same figures (Fig. 3).

Fig. 3 Compilation of triangles figures
Questions for analysis: "What geometric shapes turned out? How many triangles, squares, quadrangles? How are you? How comfortable, faster?"
2. From 10 sticks to make 2 squares - small and large.
3. Of the 9 sticks to make 5 triangles.
If necessary, during the execution of the second and third tasks, the educator gives leading questions, tips: "First consider, then make up. Do not repeat the errors, look new move solutions. Is the problem of the size of triangles? These are the tasks of the smelting, it is necessary to figure out, guess how to solve the problem. "
So, in the initial period of children's training for 5 years, solving simple tasks to the smelter they independently, mostly practically acting with chopsticks, are looking for a solution. In order to develop the ability to plan the course of thought should be offered to children to express preliminary reasoning or combine them with practical samples, to explain the way and the path of decision.
There are several types of solutions to the tasks of the first group. Having learned the method of attachment of the figures, subject to the common parties, children are very easily and quickly gives 2-3 solution options. Each figure is different from the previous spatial position. At the same time, children master the method of constructing specified figures by dividing the obtained geometric shape into several (quadrangle or square per triangle, a rectangle - for 3 squares).
Decision with children 5-6 years of more complex tasks for the rebuilding of figures should be started with those in which in order to change the figure, it is necessary to remove a certain amount of sticks and the simplest - to shifting the sticks.
The process of searching for children solving the tasks of the second and third groups is much more complicated than the first group. To do this, you need to remember and comprehend the nature of the transformation and the result (which figures should work out and how much) and constantly during the searches of the decision to relate it to the alleged or already implemented changes. In the process of solving, a visual and mental analysis of the task is necessary, the ability to present possible changes in the figure.
Thus, in the process of solving problems, children must master such mental operational analysis operations, as a result of which mentally different transformations can be represented, check them, then, threading the wrong, search and try new strokes of the solution. Training should be aimed at forming in children the ability to think about the moves mentally, fully or partially solve the task in mind, limit practical samples.
In what sequence should we offer to children 5-6 years of tasks for the second and third groups?
In a figure consisting of 5 squares, remove 4 sticks, leaving one rectangle (Fig. 4).

Fig. four
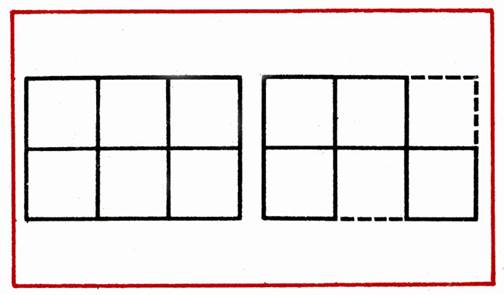
In a figure consisting of 6 squares, remove 2 sticks so that there are 4 equal squares left (Fig. 5).

Fig. five
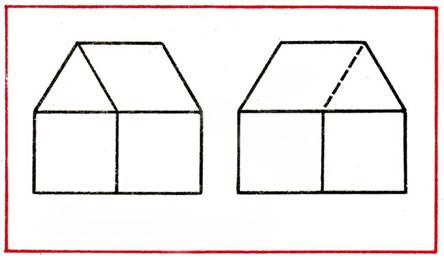
Create a house of 6 sticks, and then shifting 2 sticks so that it turns out the checkbox (Fig. 6).
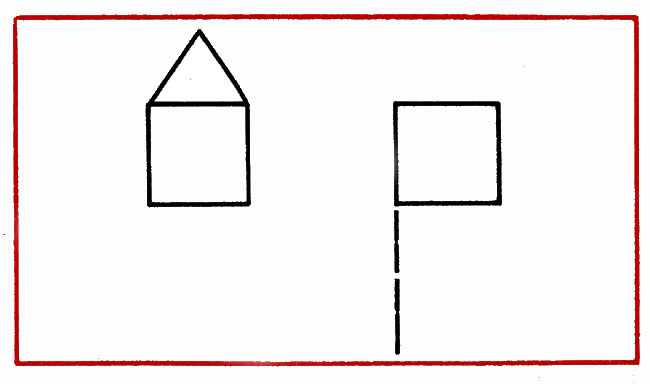
Fig. 6.
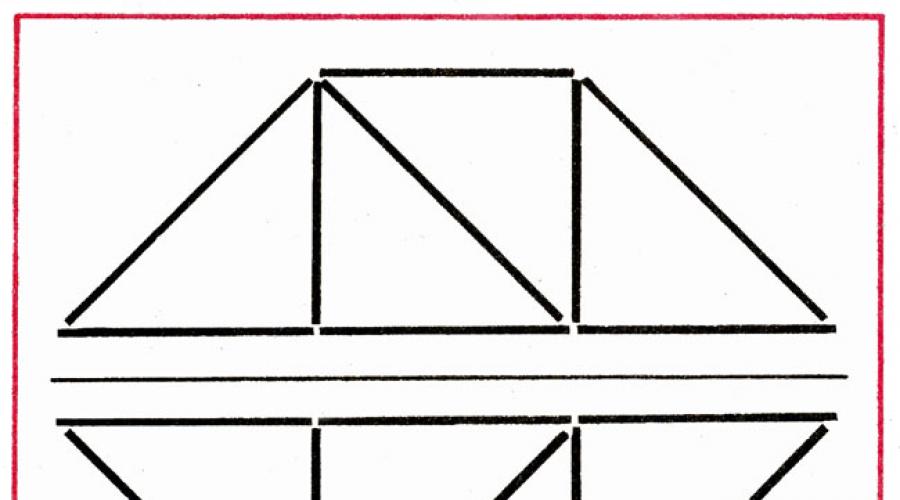
In this figure, shields 2 sticks so that it turned out 3, equal triangles (Fig. 7).
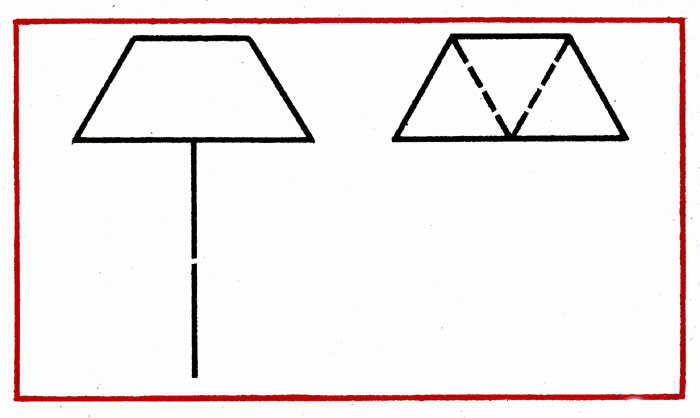
Fig. 7.
In a figure consisting of 5 squares, remove 3 sticks to remain 3 of the same squares (Fig. 8).
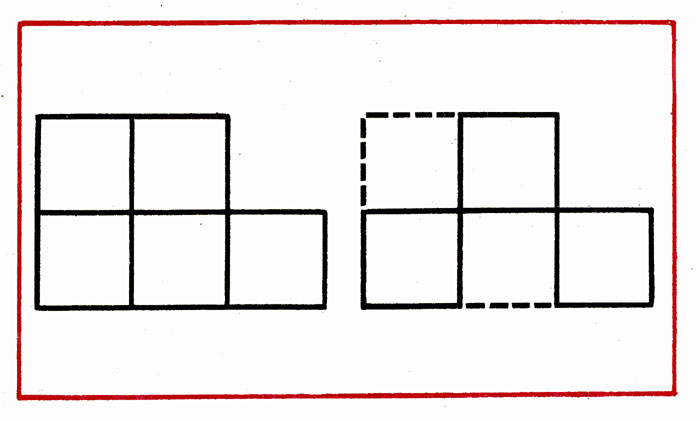
Fig. eight
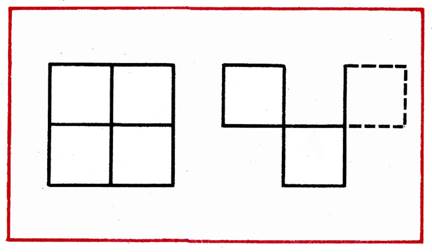
In a figure consisting of 4 squares, remove 2 sticks to remain 2 unequal squares (Fig. 9).

Fig. nine
In the figure of 5 squares, remove 4 sticks so that there are 2 unequal squares (Fig. 10).

Fig. 10
In the figure of 5 squares, remove 4 sticks to remain 3 squares (Fig. 11).
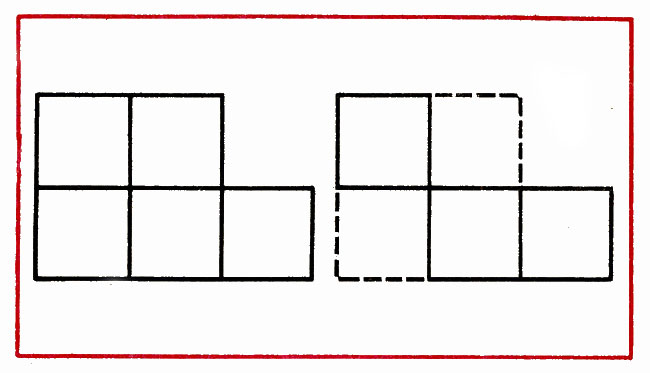
Fig. eleven
In the figure of 4 squares, shifting 2 sticks so that it turned out 5 squares (Fig. 12).
Fig. 12
In the figure of 5 squares, remove 4 sticks so that there are 3 squares left (Fig. 13).
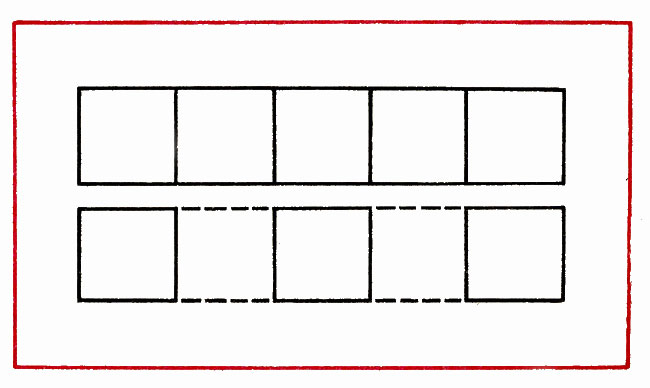
Fig. 13
For these and other similar problems on the smelter, it is characteristic that the transformation required for the solution leads to a change in the number of squares from which a given figure is composed (tasks 2, 5, etc.), a change in their size (task 6, 7), modifying Figures, for example, the conversion of squares into a rectangle in task 1.
During occupations for the purpose of manual search activities Children The educator uses various techniques that contribute to the upbringing of their positive attitude towards a long-term persistent search, but at the same time fast response, refusal from the developed way of searches. The interest of children is supported by the desire to achieve success, for which the asset needs, the work of thought.
^
Transformation of one shape to another. Changing the number of squares in the figure.
1. Example
Purpose. Exercising children in the ability to solve problems by targeted practical samples and thinking about the solution.
Material: Accounting sticks in children, at the educator - depicted graphically tasks (on this and the following classes).
^ Pro progress. 1. The tutor shows the table with the figure depicted on it, proposes the same (Fig. 4) from sticks. Considers it with children, determines the number of squares. Then says: "This is a task. Listen to what to do to solve it. It is necessary to guess which 4 wands to remove the one rectangle. First, think about how it can be done, and then remove the sticks."
After the task is solved, the teacher calls one child to the board, he shows and tells how to solve it. The teacher approves the attempts of children to act independently.
2. Dana figure of 6 squares. It is necessary to remove 2 sticks so that there are 4 of the same square (Fig. 5).
After drawing up children by sample such a figure there is an analysis For questions: "How many squares in the figure? How are you? According to which some of the sticks forming the squares, you need to remove them immediately decreased?"
Children independently solve the task. The educator in case of difficulty helps them, focusing on the search. right ways.
2. Example
Purpose. Exercise children in the ability to carry out targeted samples, limit the number of practical samples by pondering the stroke of the search, guesses.
^ Pro progress. 1. Dana figure out of 5 squares. It is necessary to remove 3 sticks, leaving 3 squares (Fig. 8). The educator sets questions, encourages children to solve the problem: "How many squares in the figure? How much should it remain? How many sticks need to be removed? This task on the smelter should be guessed, what 3 wands need to be removed so that the squares have less - 3?"
Children are embarking. The educator resembles the need to preliminarize the stroke of the solution of the decision. In case of difficulty, it reminds the condition of the task, it proposes not to repeat trial actions that do not lead to the correct solution.
One of the children who solved the task among the first, sketches and explains the decision at the board.
2. Dana figure from 4 equal squares. It is necessary to remove 2 sticks to get 2 unequal squares (Fig. 9).
Questions for analyzing a sample figure: "How many squares? Can you prove that they are equal? \u200b\u200bThink how to solve the task."
At the suggestion of the teacher, one child explains the problem of the task.
3. Example
Purpose. Express the presumptive stroke of the search for solutions, check it through targeted search engines.
^ Course of classes. 1. A figure of 5 equal squares is given; It is necessary to remove 4 sticks to become 3 equal squares (Fig. 13).
The educator, referring to the children, says: "Consider the figure, think how to solve the task, which of the sticks can be removed to change this figure. First, tell me, and then remove the sticks."
The educator asks some children (but so that their stories do not hear other guys), invites everyone to solve the problem on their own. Children explain the solution of the task at the board, so that in the course of the story it was possible to make sketching figures.
2. The figure of 4 squares is given: it is necessary to shift 2 sticks to get 5 equal squares (Fig. 12).
The educator after the formation of the figures and the analysis of the task says to children so that they, before shifting the sticks, thought whether this action leads to an increase in the number of squares, they described how they think to solve the task. During the verification of the decision, the teacher emphasizes that it is possible to solve the problem in different ways.
In the process of studying in classes, children 5-6 years are actively included not only in the practical solution of the solution, but also in mental. This is evidenced by their statements, reasoning about the pathways. So, the children were given a figure of 5 squares; It is necessary to remove 4 sticks so that there are 3 of the same square (Fig. 14). Responding to a teacher's question about how the task will be solved, some answer: "I take these sticks (a, b and k) and this (c). What then it turns out? (Thinking.) No, I do not know how." Others argue: "I think that it is necessary to remove 2 angular sticks (e, g) and somewhere else to see." "I guessed. I looked and guessed: if these to remove (shows on g, d, and, h), then there will be 3 squares: one, two, three."

Fig. fourteen
During the execution of tasks, children master the ability based on the reference of the search process (task analysis) to assume a solution to check it in almost the search for new ways, justify them.
For teaching children to independent analysis of the task, the search for the solution, the ability to guess it is advisable to use various methodical techniques, instructions on the need for a search approach to solving the problem: "First, think about how you decide the task, and tell about it. Check your assumption, shifting the sticks or even touching them. If you think that you should think about how to solve the task of -Other, and not repeat your mistakes. We must carefully consider the figure and guess how to solve the problem. " Evaluation, confirmation of the correctness or error in the course: "You removed this wand correctly, think about how to solve the task" - and the other stimulate the activity of the guys, help them find the right decision.
^ In working with children of the 7th year of life Complete the nature of the tasks for the conversion of figures. They are solved by combining practical and mental samples or only in terms of mental action - in the mind, with a justification, expression in the speech of the decision.
The sequence of the execution of 6-7 years of tasks to convert shapes.
Put 1 wand so that the house is inverted in the other direction (Fig. 15).

Fig. fifteen
In a figure consisting of 9 squares, remove 4 sticks to remain 5 squares (Fig. 16).
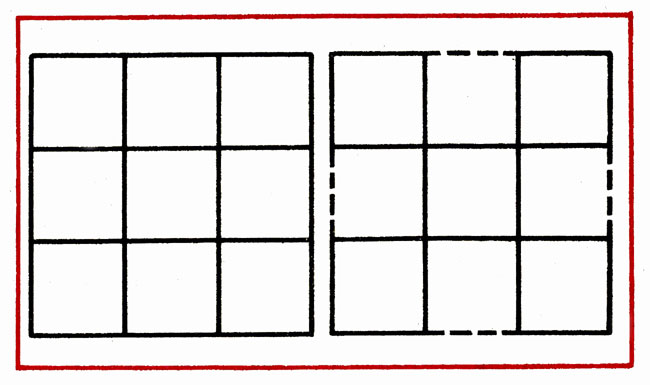
Fig. sixteen
In the figure of 6 squares, remove 3 sticks so that 4 square remains (Fig. 17).
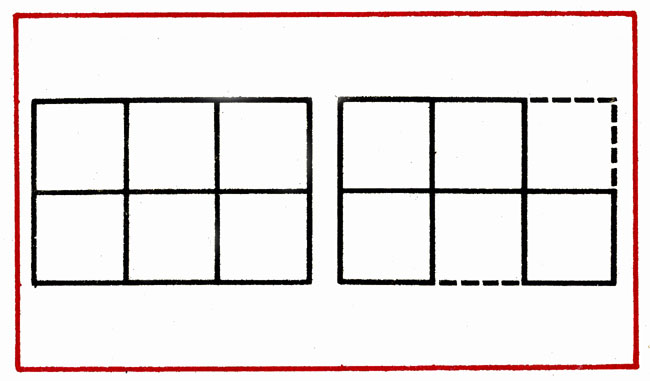
Fig. 17.
In the figure, similar to the key, shifting 4 sticks to get 3 squares (Fig. 18).
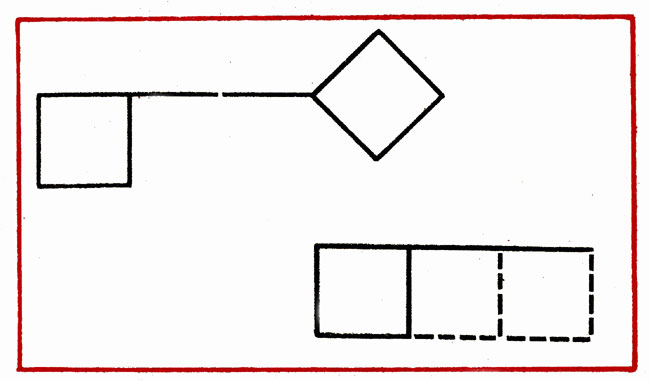
Fig. eighteen
In the figure of 6 squares, remove 2 sticks so that 4 equal square remains (Fig. 19).
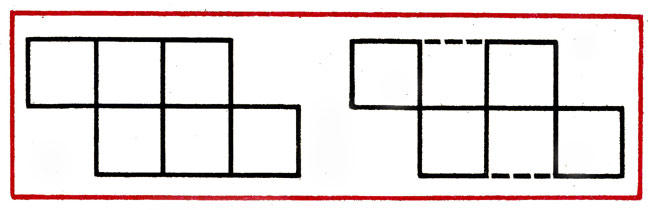
Fig. nineteen
In the figure depicting an arrow, shifting 4 sticks so that 4 triangles are obtained (Fig. 20).

Fig. twenty
In the figure of 5 squares, shifting 3 sticks to become 4 squares (Fig. 21).
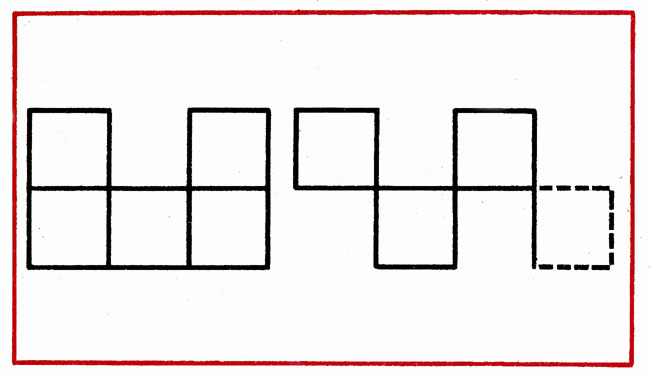
Fig. 21.
In the figure shifting 3 sticks so that 4 equal triangles are obtained (Fig. 22).
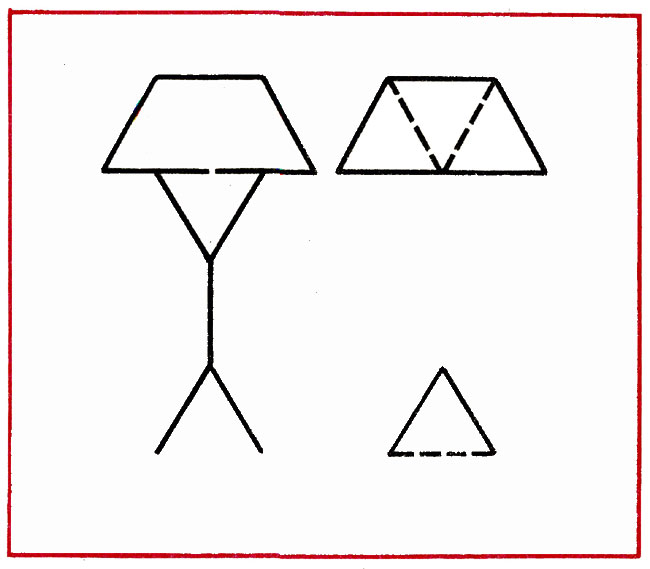
Fig. 22.
In a figure consisting of 4 squares, shifting 3 sticks so that it turned out 3 of the same square (Fig.23).

Fig. 23.
Shut up 4 sticks so that 4 equal triangles are obtained from the ax (Fig. 24).
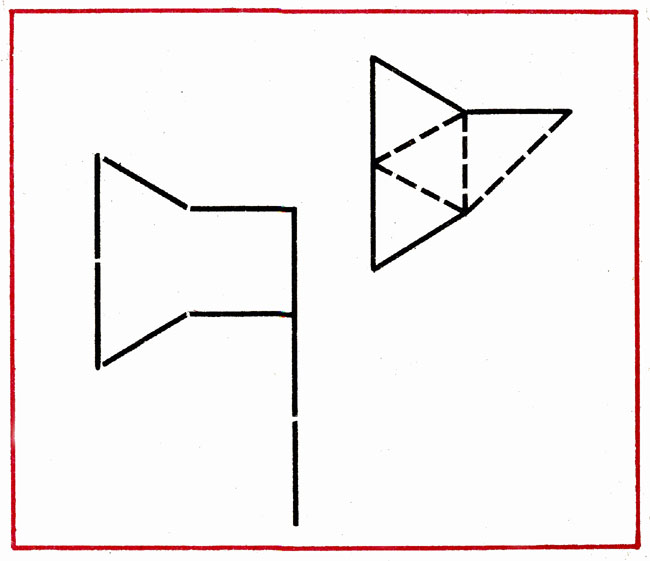
Fig.24
In a figure resembling a lantern, shifting 4 sticks to get a quadrilateral consisting of 4 equal triangles (Fig. 25).

Fig. 25.
Shifting 2 sticks so that the figure; Similar to the cow, looked in the other side (Fig. 26).

Fig. 26.
What the smallest number of sticks should be shifted to remove the garbage from the Sovka? (Fig. 27.)
Fig. 27.
IN  Preparatory for School Group Training Children to solve problems on the smelter contributes to the further development of their mental activity, the ability to plan the progress of searches
Preparatory for School Group Training Children to solve problems on the smelter contributes to the further development of their mental activity, the ability to plan the progress of searches
Chapter 12 already mentioned Polyminino and its creator S. Golombe. After publishing an article about Polymino on the pages of the Journal of Scientific American A957), the game has become an unusually popular mathematical entertainment. Hundreds of new tasks and bizarre configurations of Polymino were discovered. About them and there will be here.
Recall that the figures on chessboard You can cover five adjacent cells forming a connected area, are called Pentamino. There are twelve such figures. If these figures are positioned as shown in Fig. 234, it becomes clear that each figure in shape resembles some Latin letter, so to memorize the shape and names of figures (every figure we will call some letter) is enough to know the end of the Latin alphabet (T, u, V, W, X, Y, Z) and word Filipino.
Fig. 234.
Chapter 12 (see Fig. 71) it was shown that from the twelve elements of pentamino with a total area of \u200b\u200b60 squares, the rectangles of four sizes are added: 3x20, 4x15, 5x12 and 6x10. The same 12 figures can be put on a chessboard size of 8x8, and the square of four extra cells (the board area is 64 squares) can be in any place of the board.
Any element of Pentamino can triple with the help of some nine figures from among the remaining (it is understood that the figure like the chosen one will be folded from these nine pentamino, but three times higher and longer). From twelve pentamino, you can still build two 5x6 rectangles. The last task is called the task of the superposition, because the constructed figures can be applied to each other. Golomba told me five new tasks for the superposition, which are first published in this book. If the reader still does not understand the entire charms of Pentamino, he needs to cut from the cardboard a set of pentamino elements and break her head over some of the tasks below.
In all puzzles, pentamino elements can be put on a plane by any side.
1. Blizzard twelve pentamino into three groups of four elements in each. Then find the figure in 20 squares, which can be folded from elements of each group. One of possible solutions depicted in fig. 235.
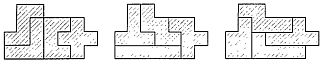
Fig. 235.
2. Break twelve pentamino into three groups of four elements. Each group is divided by half and find such a figure (for each group of its own), which has an area of \u200b\u200b10 squares, which can be folded from both pairs of elements separately.
One solution is shown in Fig. 236. Can you come up with other solutions to at least in one of them figures did not have holes?

Fig. 236.
3. Spice twelve pentamino into three groups of four elements. To each group, add the monomino (one square) and build a 3x7 rectangle. How to do it, shown in Fig. 237.
Fig. 237.
Solution is the only one with one reservation: in the first rectangle, the monomino and element Y. Pentamino can be turned over without changing common form And the area composed of a single-connected figure.
To prove the uniqueness of the solution as follows.
First of all, we note that in fig. 238 Element X should be used as a pair with an element U. Neither the element F nor the W element is suitable in order to complete the construction of the rectangle.

Fig. 238.
If the element x is supplemented by an element U, then in the same 3x7 rectangle, the elements F and W can already be used. Therefore, elements X and U elements will be used from three rectangles in size 3 x 7 in one, the second will contain the element W (but not u ), and the third is an element F (but not u). If you go through everything possible options Rectangles and compare them (it takes away from you quite a lot of time), it turns out that the estimated solution (see Fig. 237) is the only one.
4. Spread twelve pentamino into four groups of three elements in each. Find such a polygon area of \u200b\u200b15 squares, which can be folded from three elements of each group.
The solution of this puzzle is unknown; On the other hand, no one has not yet proven that the task is insoluble.
5. Find the minimum size area on the chessboard on which any of the twelve elements of Pentamino fits.
The minimum area of \u200b\u200bsuch an area is equal to nine squares, and only two of its forms are known (Fig. 239).
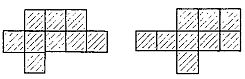
Fig. 239.
Each figure Fig. 239 satisfies the conditions; To prove, it is enough to notice that any element of Pentamino fits on it. The proof that the number of squares cannot be less than nine is carried out as follows.
If a figure was suitable containing less than nine squares, then elements I, X and V could be closed by no more than eight squares. At the same time, elements I and X were three common squares. (Otherwise, it would be necessary for nine squares, or, which would be excessive luxury, the longest direct consisted of six squares.) It can be achieved only in two different ways (Fig. 240), but in the other case you need also the ninth square to fit the element U.
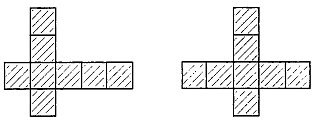
Fig. 240.
Thus, eight squares are missing, while from the above examples it can be seen that nine squares are enough.
With the advent of computers, the task with Pentamino began to explore them. Chapter 12 has already mentioned how the Scott is given with the help of a computer found all the methods of compiling from the twelve elements of pentamino chessboard of 8x8 with a square hole in four cells in the center. 65 fundamentally different solutions were found (two solutions resulting with one of the different turn or reflection are considered the same). K. B. Heiselgrove, Mathematics from the University of Manchester, listed with the help of a computer all possible options for a rectangle with a size of 6x10, folded from twelve pentamino. He found 2389 different solutions, not counting those from each other turns and reflections! In addition, he checked the program drawn up by Scott for a chessboard 8x8.
Fine puzzles are obtained from pentamino. In fig. 241, and depicted a pyramid of 64 cells, which can be folded from twelve elements of pentamino and square tetramino 2x2.
It is unusually difficult to collect from twelve pentamino the cross shown in Fig. 241, b. For a figure shown in fig. 241, in, the decisions have not yet been found (no one has folded it, but also the impossibility of building is also not proven). Even for the case when the hole in the form of monomially carved in another place, the solutions also not found. Fig. 241, g is a figure that is closest in shape to the previous one. Apparently, also unsolvable puzzle of Herbert Taylor, shown in Fig. 241, d; True, so far no one has managed to prove that the solutions do not exist.
Fortunately, not all unresolved tasks are shrouded in darkness of unknown. So, T. M. Robinson proved that, for example, a figure, which is depicted in fig. 241, e, it is impossible to fold from twelve pentamino.

Fig. 241.
From the edges it is limited to 22 squares, and if you carefully examine the elements of pentamino and write down how many squares of each element can be on the edge of the foldable figure, then in the amount for all elements, this number will be equal to 21, that is, one is less than necessary. This method of reasoning is commonly used in puzzles about the folding of zigzag-like storces. (On paper or cardboard, you need to draw a rectangle with a sawdust edge and cut it into pieces of any form. Mix the pieces and try to fold the original rectangle from them.) Typically distinguishes the internal and external parts of the figure and first try to fold the edges of the puzzle.
Polyminino, occupying four squares of a chessboard, are called Tetramino. Unlike pentamino of five of its various elements, a rectangle cannot be folded. To prove to color the rectangles in 20 squares in checkelling order - there are only two of them: 4x5 and 2x10 (Fig. 242).
Fig. 242.
Four of the five elements of Tetramino can be covered with two black and two white squares (Fig. 243), and the fifth, T-shaped element, always covers three squares of the same color and one else.
Fig. 243.
Therefore, all five figures tetramino together occupy an area consisting of an odd number of squares of each color, and both rectangles about which this is speech, contain 10 squares of each color, that is, consist of an even number of squares.
On the other hand, if you take a few different elements Pentamino, then any of them together with five tetramino forms a set from which you can build a square size of 5x5. Two examples of such buildings are shown in Fig. 244.
Fig. 244.
Arises interest Ask: How many different pentamino can be used for this purpose?
Aspirant-mathematician of the Oregon University of R. Joutht proposed the task of domino (Polyminico from two squares), completely unlike the challenges that we still do. Is there such a rectangle folded from domino bones, in which it is impossible to carry out a vertical or horizontal straight, connecting the opposite sides? In the rectangle shown in Fig. 245, for example, such a line is carried out between the upper and lower bases. If you imagine that instead of domino, bricks are taken, the existence of such a line ("seam") will indicate fragile laying.

Fig. 245.
Thus, the task of Jouthata comes down to the question of how to put rectangular bricks so that the construction does not fall apart.
We will continue the corresponding rectangles in the future "durable" rectangles. Many, holding for this task, soon give up, confident that it is insoluble; In fact, there is an infinite set of its solutions.
I suggest the reader to arm a set of domino (more than enough to take an ordinary set of 28 bones) and try to determine the size of the smallest of the "durable" rectangles, which can be folded from them.
Since this chapter appeared in Scientific American, large changes have occurred in the study of polyminino and "durable" rectangles. In 1965, the Book of Golomb "Polyminino" was published, in which a thorough study of the subject was carried out.
It turned out that the puzzle of the city of Taylor (Fig. 241, e) and a toothed square (Fig. 241, c) are insoluble; However, for neither the one for another figure still has not yet been found for a short and elegant proof of the impossibility of building them.
You can add a toothed square, in which the monomino (hole) is on the edge, next to the angle or in the corner. Sixteen different solutions of the last type are found. However, it is not yet known whether to monomically to defend the corner further than one cell.
Patton, many years engaged in "durable" rectangles composed of Domino, sent me new interesting tasks. What are, for example, minimum dimensions "Durable" rectangle, in which the same number of bones of Domino is located vertically and horizontally? Maybe the reader wants to find a solution himself, so I only give the answer: 5x8 rectangle size.
Folding out of the domino "durable" squares, you can come up with a lot of games that, as far as I know, not studied at all.
For example, opponents put in turn of domino on a square chessboard. Wins the one who first build a vertical and horizontal line "loss of strength" or vice versa: the one who first builds such lines loses.
Answers
In fig. 246 and 247 are shown how to fold the pyramid and cross.

Fig. 246. How to fold the pyramid.

Fig. 247. How to lay a cross.
Both solutions are not the only one.
To determine which element pentamino should be added to five tetramino so that the square of all six figures can be constructed the size of 5x5, all the elements of pentamino, except the elements I, T, X and V.
The smallest "durable" rectangle, which can be folded from the domino, has size 5x6. Two fundamentally different solutions are depicted in Fig. 248.
Fig. 248. Answers to the task of "durable" rectangles.
It is easy to show that the minimum width of the "durable" rectangle must be more than four. (Cases when the width of the rectangle is 2, 3 and 4, it is best to consider separately.) Since the square size of 5x5 consists of an odd number of squares, and the area of \u200b\u200bthe area built from the domino is always even, then the minimum dimensions of the rectangle are 5x6.
The 5x6 rectangle can be increased to the sizes of a chessboard (8x8), and it will still be "durable". An example of such a construction is depicted in Fig. 249.

Fig. 249. Durable rectangle on a chessboard of 8x8 cells.
It is not surprising, but there are no "durable" rectangles of 6x6. This fact has wonderful proof.
Imagine that the 6x6 rectangle is entirely covered with Domino. For this you need 18 domino bones (half of the area), and to divide the rectangle on the cells, you will need 10 lines (five vertical and five horizontal). The rectangle will be "durable" if the straight of the forming grid crosses at least one domino.
Starting proof, first of all we will show that in any "durable" rectangle every direct mesh boundaries crosses the even number of domino elements. Consider any vertical direct grid. The area to the left of it is even (that is, it is also expressed by an even number of single squares): 6, 12, 18, 24 or 30. Those domino, which are entirely to the left of this straight, should occupy an even area, since each element domino covers two squares. Domino, which are cut by this straight, also occupy an even area from it, because this area is equal to the difference in two even numbers (the entire area to the left of the straight and the area of \u200b\u200bthe continued domino, which are also on the left). But since the cut domino takes only one square to the left of the selected straight line, the number of domino elements cut direct should be even. The grid in the 6x6 square consists of nine straight lines. For a rectangle to be "durable", each direct should cross at least two dominoes.
No domino can cross more than one line of the mesh, so the grid cuts at least 12 dominoes. And in the square 6x6 only 18 dominoes!
Similarly, it is possible to show that the 6x8 rectangle will be "durable" only if each segment of the mesh boundaries crosses exactly two dominoes. Such a rectangle is depicted in fig. 250.

Fig. 250. Durable rectangle 6x8.
In very general The result can be formulated as follows: from the domino you can fold the "durable" rectangle, if its area is even, and the length and width is more than four; The exception is the square 6x6. In fact, to fold the larger rectangle, you need to apply to the 5x6 and 6x8 rectangles and the length of the length or width into two units.
The easiest way to explain how this is done, with the help of Fig. 251.
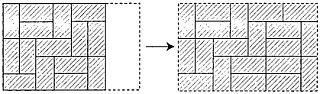
Fig. 251. The general solution to the problem of building a "durable" rectangle.
To lengthen the figure in the horizontal direction, two units must be put on one domino next to each domino, lying horizontally, and all vertical dominoes must be pulled out to new borders, having laid the vacated horizontal domino.
Maybe it will be interesting for the reader to consider the elements of trimino as bricks. In particular, the question arises: what are the smallest dimensions "Durable" rectangle, which can be folded from two or more "Straight trimino" (i.e. rectangles size 1x3)?
Notes:
Kraitchik M. Mathematical Recreations. - 1942, p. 184.
Golomb S. Polyminino. - M.: Mir, 1975.
Psychoanalytic test 6 squares online on the blog of the psychologist of happiness. The most complete and wide psychoanalytic interpretation of your drawings of this test. Dorisinate 6 drawings and get psychological decoding Test.
Psychoanalytic tests
What is the psychoanalytic test of 6 squares different from psychological?
It is practically no different because the practice of psychology is the direct heiress of psychoanalysis.
A decent collection of psychological and psychoanalytic tests online has already been collected on the blog of the psychologist of happiness.
Psychological tests online at www.Syt
Today, the psychologist of happiness will be replenished with a real test based on psychoanalysis.
Psychoanalysis, Psychiatry, Psychology or Psychotherapy?
Consider briefly development psychological testing In the historical sequence of development of the fundamental sciences.
Psychologist, psychoanalyst, psychotherapist and psychiatrist - who choose?
First, psychiatry emerged, then the psychiatrist Sigmund Freud's psychiatrist founded psychiatric psychiatry psychiatric school, then the branch of medical psychology was picked up from psychoanalysis - psychotherapy, and the branch of psychological science.
Psychologist It works with a soul of a man, he does not make diagnoses and does not prescribe drugs, the psychologist works within the spiritual and personal norm. However, it can carry out psychotherapeutic impact and apply psychoanalytic techniques in its work. - not a medical psychologist.
Psychoanalyst psychologist Works by the method of psychoanalysis, he analyzes mental, dream, identity of the client.
Psychoanalyst doctor Maybe add to psychoanalysis medical techniques, hard hypnosis and physical procedures.
Psychotherapist - This is a doctor who has passed psychological or psychoanalytic training.
Psychiatrist - A doctor who works with mentally ill people and customers with various pathologies and personality disorders. It works in nonzero.
Today we will get acquainted with psychoanalytic - and analyze some traits of our personality and attitude to some areas of our life.
Psychoanalytic Test 6 squares online
In front of you in Figure 6 squares, in each of which is an unfinished drawing - and it can be finished by any way.

Before you begin to execute instructions for this test, let's agree on some aspects of interpretation.
Bottom of each square - this is a material plan, and top of Square - This is a spiritual plan of being.
Left third of Square - this past, middle - Present I. right third square - Future.
If you have finished objects in the pictures - for example, an animal, some sign - look in the Internet symbolic meaning These objects.
Name each figure - It will give additional information On the subject of the square, even if the drawing is symbolic - still try to give it a name.
Insofar as the main analysis you will do yourself - This information can give you a lot of nuances.
Questions on test analysis of 6 squares can be asked in the comments to this article.
Instructions for test Psychoanalytic test 6 squares:
Instruction: Dorisite sequentially (right left and top down - starting from the left upper square with a point) Drawing in each of the 6 squares.
Draw quickly, without thinking and not trying to guess what should be drawn and how it will be deciphered.
In psychoanalytic tests there is no prepared interpretation and evaluation of test material.
Decoding test 6 squares
The summary of each of the 6 squares-drawings, which is designed only to push you on your own insight - the discovery of yourself.
Square number 1 goals
The drawing that you typed in this square shows what character have your goals.
If you conducted a line in the center in the center or several lines - see which direction the picture is directed, how many of these lines.
When the point becomes the center of the figure, maybe now you have, which you follow. If the point is an eye of any creature, then you really imagine what you want.
If you draw a lot of other points nearby, then you have a lot of goals and you cannot choose the main one.
Square number 2 conformism
Your drawing in the second square indicates how much you are from other people or other people's ideas.
If you drew another wavy line or more, you are dependent on the opinions of others.
If you have an independent object - a boat, a plane or something else, - you are prone to independent decision making.
By itself, the object in this picture reports how conservative or creative personality.
Square number 3 house
Figure 3 square shows your attitude to the family and to the house.
The small square in the picture shows the family principles, and everything else is the outside world.
Where you have more items, your attention is sent there anymore.
If a small square has become a window, and the rest of the space is a room, it means that the family is for you - everything, and the rest of the world is only a background.
Square number 4 Communicability
Figure 4 square allows you to measure your - the ability to interact and find mutual language with other people.
If you connected two lines - you are a sociable person. If the lines have become a single whole - the river or expensive, it means that communication with people is based on your life.
If new objects appeared in the picture - decrypt their symbolic value - it will give a wider understanding of your abilities to communicate.
Square number 5 thinking
In this picture, we check: concrete or abstract thinking you.
If you drew something real - fruit, man, machine, - you. This means that you are friends with logic and can make successful career Manager or financier.
Drew an incomprehensible pattern of circles, curls and points? You think creative. Painting and theatrical scene are conquered!
Again all attention symbolic values Drawn objects and their location on the square.
Square number 6 love
In this picture you will understand your attitude to the interaction with the opposite sex.
This picture is interpreted almost like dreams. If you combined two lines into something high - you have forbidden thoughts. Torch - you lack passion. Or, for example, a skyscraper with windows - you are in the partner's choice. If these are trees, then you need warmth and romance.
The drawing in 6 square shows your position and or in friendly.
ATTENTION: Tick \u200b\u200bthe square that caused the greatest difficulty or in which it failed to draw anything sensible.
Perhaps during drawing in one of the squares, you experienced some kind of feeling: Health, irritation, passion, tenderness, or something else - write in the comments and I will say how it can be interpret.
Example Decryption Test 6 squares-drawings
Let's briefly go through the decryption of psychoanalytic test, maybe it will make it a little easy to assess and analyze your own drawings.
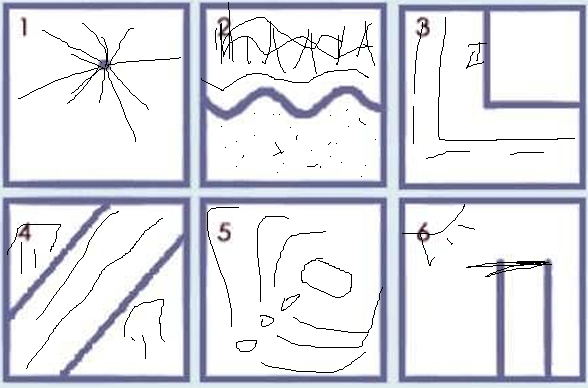
Example of a filled dough 6 squares
Immediately make a reservation - the decoding of the drawings is not complete - since the online format does not allow you to turn around the styre and deep into.
Square number 1. A lot of lines crosses the point in the center - a person may be right now, in the present there are a lot of current and problem tasks that the human energy is shoved as if he fell into a web (the picture resembles a spider). Although, perhaps the man himself would see the cracked land (desert) - then we would talk about his loneliness and devastation, or the sun - the mood is close to apathy and fatigue. And all this concerns the achievement of goals, the fulfillment of the dream and solving everyday tasks.
Square number 2. A person is more dependent, the conform. And B. spiritual Plan He is influenced by several ideas at once and it seems quite confused, but he leaves the soil from under his feet. He sues in the quagmire of routine cases, in which there is also a lot of disadvantage.
Square number 3. Man is just looking for exits to create a family, build own house. Coldness and loneliness. There is an impact from the past, which prevents it from establishing clear boundaries, in addition, in relations with the candidate, it is possible that the conflict of two valuables systems occur.
Square number 4. There are any problems in communication, an attempt to link your past and the future. And there is no clear plan in communication with other people - where the curve will bring out. The behavioral repertoire of narrow - requires further development of communicative skills.
Square number 5. Thinking concrete, although the root creative abilities There are, but they are not fully developed. Again pops up the theme "Spider" - I would recommend to study this symbol in more detail.
It is believed to be spider is an symbol fate of man as well symbol Those who personally create their own destiny.
Spider - Ancient symbol Creation, creativity and hard work.
But with this material it would be fine - for example, to the author of the blog.
Square number 6. A man in the past lack of love, or rather, on the contrary - the memory of the past relationship warms. Currently on love Front Empty. Whether the flag "On Help" is posted, or a person is waiting for a spring swallow, which will bring good news. There is a desire in the near future to combine your heart with another.
Proposal to test 6 squares from a psychologist happiness
I am pleased to answer questions and requests in each comments to this test.
If you want to order full analysis of this testin relation to your current situation or problem - order a service 3-month subscription with a psychologist (with a discount of 950 rubles) and get decoding the test of 6 squares with a bonus - as a gift for this service * .
* number full analyzes Dough is limited because it takes a lot of time!

A psychologist's blog of happiness is a place where your dreams take power.
Psychoanalytic test 6 squares passed? Share its result in the comments - your rating is very interesting.
Of the variety of puzzles, the most acceptable in the older preschool age(5-7 years) puzzles with chopsticks (you can use matches without sulfur). They are called the tasks for the smell geometric characterSince during the solution, as a rule, there is a transfiguration, transformation of some figures to others, and not just a change in their quantity. In preschool age, the simplest puzzles are used. To organize work with children, it is necessary to have sets of conventional counting sticks to compile from them visually represented puzzle tasks. In addition, tables with graphic figures are graphically depicted on them, which are subject to transformation. On the back side The tables are indicated which transformation must be done and which figure should turn out as a result.
Tasks for smelting are different in the degree of complexity, the nature of the conversion (transfiguration). They cannot be solved in any previously learned in the way. During the solution of each new task, the child is included in the active search of the solution path, striving to the ultimate goal required to modify or build a spatial figure.
For children, 5-7 years old, the tasks for the smelting can be combined into 3 groups (according to the method of rebuilding figures, the degree of complexity).
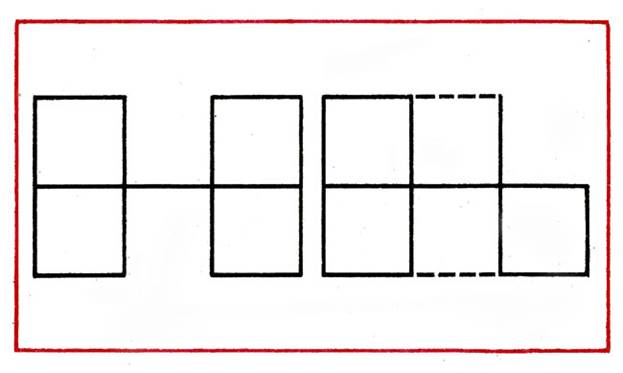
Tasks for the preparation of a given figure from a certain amount of sticks: Make 2 equal squares of 7 sticks, 2 equal triangles of 5 sticks.
Tasks for changing figures to solve which the specified number of sticks should be removed.
The tasks for the smelter, the solution of which consists in shifting the sticks for the purpose of modification, the transformation of the specified figure.
In the course of learning how to solve, the tasks for the mixture are given in the specified sequence, starting with the simpler, so that the skills learned by the children and the skills prepared the guys to more complex actions. By organizing this work, the educator puts the goal - to teach children to accepting self-searching for solving problems, without offering any ready-made techniques, methods, samples of the solution.
To such an independent search for solving the simplest tasks of the first group, children are prepared as a result of everyday work. For this, it is sufficient to further exercise them in the preparation of geometric figures (squares, rectangles, triangles) from the counting sticks.
Drawing up geometric figures
(Preparatory gaming exercises for children 5 years)
Purpose. Exercise children in the preparation of geometric shapes on the plane of the table, analysis and examination by their visual-tactile way.
Material: Counting sticks 5 cm long (15-20 pieces per child), 2 thick threads 25-30 cm long.
Progress. The educator invites children to call the famous geometric shapes. After the listing reports purpose: "We will make shapes on the table and talk about them." Gives tasks:
1. Create a square and triangle of small size.
Questions for analysis: "How many wands needed to compile a square? Triangle? Why? Show the parties, corners, the vertices of the figures."
2. Create a small and large squares.
Questions for analysis: "From how many sticks is made up by each side of a large square? The whole square? Why is the left, right, upper and lower sides of the square are made up of the same amount of sticks?"
You can give a task to the compilation of a large and small triangle. Analysis of the task is carried out similarly.
3. Create a rectangle, the upper and lower sides of which will be equal to 3 wands, and the left and right -2.
After analysis, children are offered to make up any quadrilateral and prove the correctness of the task.
4. Compose from threads consistently figures: a circle and oval, large and small squares, triangles, rectangles and quadrangles. Small figures are made up of threads folded twice.
Analysis of the figures is carried out according to the scheme: "Compare and tell me how they differ than the figures. Prove that the figure is made correct."
Clarifying the ideas of children about geometric figures; Their elementary properties (number of corners and parties), the exercise in the preparation will help the assimilation of the methods of solving the puzzles of the first group. They are offered to children in a certain sequence:
Create 2 equal triangles of 5 sticks.
Create 2 equal squares of 7 sticks.
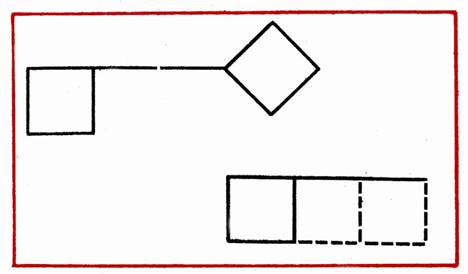
Create 3 equal triangles of 7 sticks.
Make 4 equal triangles of 9 sticks.
Create 3 equal squares of 10 sticks.
Of 5 sticks, make a square and 2 equal triangles.
Of the 9 sticks, make a square and 4 triangles.
From 10 sticks to make 2 squares: a large and small (a small square is made up of 2 sticks inside the large).
Of the 9 sticks, it is 5 triangles (4 small triangles obtained as a result of a building form 1 large).
From 9 sticks to make 2 squares and 4 equal triangles (of 7 sticks are 2 squares and divided into triangles with 2 chopsticks).
In order to solve these tasks, you need to own the method of pre-building, attaching one figure to another. For the first time, receiving such a task, children are trying to make 2 separate triangles, square. After a number of unsuccessful attempts, they recognize the need to attach to one triangle, the square of the other, for which it is enough 2, 3 sticks.
As the experience of experience gained in solving such problems with the "trial and error" by the number of incorrect samples, practical action begins to decline. Based on this, the educator, while maintaining the enormity, the gaming nature of the exercise, sends the guys to targeted samples, which precedes at least elementary thinking of a particular course of the solution. In the process of finding a solution, the guys pay attention to the fact that, before making a response, it is necessary to think about how it can be done. It is enough to hold 3-4 classes, in the process of which children master the ways to attach to one figure another so that one or several sides are common.
Examples (for children 5-6 years)
Drawing up figures from triangles and squares
Purpose. Teach children to make geometric shapes from a certain amount of sticks, using the admission of attachment to one figure, taken as the basis, the other.
Material: children on the tables counting sticks, board, chalk at this and next occupations.
Progress. 1. The tutor offers children to count 5 sticks, check and put them in front of them. Then says: "Tell me how much sticks need to make a triangle, each side of which will be equal to one wand. How many wands need to prepare two such triangles? You have only 5 sticks, but of them need to be 2 equal triangles. Think like 2 This can be done, and make up. "
After most children fulfill the task, the educator asks them to tell, how to make 2 equal triangles of 5 sticks. Draws attention to the guys to perform the task in different ways. Methods of execution must be sketched. With the explanation to use the expression "attached to one triangle another bottom" (left, etc.), and in explaining the solution of the problem to use the expression "attached to one triangle, using only 2 sticks."
2. Make 2 equal squares of 7 sticks (the tutor pre-clarifies which geometric shape can be made up of 4 sticks). It gives a task: count 7 sticks and think about how to make up 2 equal square on the table.
After completing the task, various ways of attachment to one square of the other are considered, the teacher sketches them on the board.
Questions for analysis: "How did 2 equal squares of 7 sticks amounted to? What did it first that then? Of how many sticks amounted to 1 square? From how many sticks attached to it the second square? How much did the chopsticks need to compose 2 equal squares?"
Purpose. Make figures by attachment. See and show the new, resulting from the compilation of the figure; Use the expression: "attached to one figure another", think about practical actions.
Progress. The educator invites children to remember which figures they constituted using the admission of attachment. Reports what they will do today - learn to make new, more complex figures. Gives tasks:
After completing the task, the teacher offers all children to make 3 triangles in a row so that the new figure is a quadrangle (Fig. 2). This version of solutions are sketching with chalk on the board. The educator asks to show 3 separate triangles, a quadrangle and a triangle (2 figures), a quadrangle.
Fig. 2 Drawing up figures from triangles
2. Of the 9 sticks to make 4 equal triangles. Think about how it can be done, to tell, then perform the task.
After that, the teacher invites children to draw up the shapes on the blackboard and tell about the setting of the task.
Questions for analysis: "How did 4 equal triangles of 9 sticks amounted to? Which of the triangles was the first? What figures turned out as a result and how much?"
The teacher, specifying the answers of the children, says: "It is possible to start to form a figure from any triangle, and then to it to attach other on the right or left, on top or bottom."
Purpose. Exercising children in independent search for ways to make figures based on a preliminary flow of the solution.
Progress. The tutor sets the children questions: "From how many sticks can be a square, each of the sides of which is equal to one wand? 2 squares? (Out of 8 and 7). How will you be 2 squares of 7 sticks?"
As the teacher is fulfilled, it causes several children to draw them figures on the board and tell the sequence of compilation. It offers all children to make a figure from 3 equal squares located in a row, horizontally. On the board draws the same and says: "Look at the board. It is drawn here how to solve this task in different ways. You can add to one square another, and then the third one. (Shows.) And then you can make a rectangle of 8 sticks, then split it on 3 equal squares with 2 chopsticks. " (Shows.) Then asks questions: "What figures turned out and how much? How many rectangles do it? Find and show them."
2. From 5 sticks to make a square and 2 equal triangles. First tell, and then make up.
When performing this task, children tend to make a mistake: form 2 triangles with an assimilated method - an attachment, resulting in a quadrangle. Therefore, the educator draws the attention of the guys on the condition of the task, the need to compose a square, suggests the leading questions: "How many sticks are needed to compose a square? Because you have chopsticks? Is it possible to draw up 1 triangle to another? How to make it? What kind of figure should be started? " After completing the task, the children explain how they did: it is necessary to make a square and divide it with 1 stick to 2 equal triangles.
Purpose. Exercise children in the ability to express an alleged decision to guess.
Progress. 1. From 9 sticks to make a square and 4 triangles. Think and say how to make up. (Several children express assumptions.)
If children are hampered, the teacher advises: "Remember how the square and 2 triangles were made of 5 sticks. Think and guess how you can perform the task. The one who first decides the task, sacrows the resulting figure on the board."
After performing and sketching a response, the tutor offers all children to make the same figures (Fig. 3).
Fig. 3 Compilation of triangles figures
Questions for analysis: "What geometric shapes turned out? How many triangles, squares, quadrangles? How are you? How comfortable, faster?"
2. From 10 sticks to make 2 squares - small and large.
3. Of the 9 sticks to make 5 triangles.
If necessary, during the fulfillment of the second and third tasks, the educator gives leading questions, tips: "First think, then make up. Do not repeat the errors, look for a new decision of the solution. Is the problem of the size of the triangles? These are the tasks for the smelting, you need to figure out, guess, How to solve the task. "
So, in the initial period of children's training for 5 years, solving simple tasks to the smelter they independently, mostly practically acting with chopsticks, are looking for a solution. In order to develop the ability to plan the course of thought should be offered to children to express preliminary reasoning or combine them with practical samples, to explain the way and the path of decision.
There are several types of solutions to the tasks of the first group. Having learned the method of attachment of the figures, subject to the common parties, children are very easily and quickly gives 2-3 solution options. Each figure is different from the previous spatial position. At the same time, children master the method of constructing specified figures by dividing the obtained geometric shape into several (quadrangle or square per triangle, a rectangle - for 3 squares).
Decision with children 5-6 years of more complex tasks for the rebuilding of figures should be started with those in which in order to change the figure, it is necessary to remove a certain amount of sticks and the simplest - to shifting the sticks.
The process of searching for children solving the tasks of the second and third groups is much more complicated than the first group. To do this, you need to remember and comprehend the nature of the transformation and the result (which figures should work out and how much) and constantly during the searches of the decision to relate it to the alleged or already implemented changes. In the process of solving, a visual and mental analysis of the task is necessary, the ability to present possible changes in the figure.
Thus, in the process of solving problems, children must master such mental operational analysis operations, as a result of which mentally different transformations can be represented, check them, then, threading the wrong, search and try new strokes of the solution. Training should be aimed at forming in children the ability to think about the moves mentally, fully or partially solve the task in mind, limit practical samples.
In what sequence should we offer to children 5-6 years of tasks for the second and third groups?
In a figure consisting of 5 squares, remove 4 sticks, leaving one rectangle (Fig. 4).
In a figure consisting of 6 squares, remove 2 sticks so that there are 4 equal squares left (Fig. 5).
Create a house of 6 sticks, and then shifting 2 sticks so that it turns out the checkbox (Fig. 6).

In this figure, shields 2 sticks to obtain 3, equal triangles (Fig. 7)
 .
.
In a figure consisting of 5 squares, remove 3 sticks to remain 3 of the same squares (Fig. 8).
In a figure consisting of 4 squares, remove 2 sticks to remain 2 unequal squares (Fig. 9).
In the figure of 5 squares, remove 4 sticks so that there are 2 unequal squares (Fig. 10).
In the figure of 5 squares, remove 4 sticks to remain 3 squares (Fig. 11).

In the figure of 4 squares, shifting 2 sticks so that it turned out 5 squares (Fig. 12).
In the figure of 5 squares, remove 4 sticks so that there are 3 squares left (Fig. 13).
![]()
For these and other similar problems on the smelter, it is characteristic that the transformation required for the solution leads to a change in the number of squares from which a given figure is composed (tasks 2, 5, etc.), a change in their size (task 6, 7), modifying Figures, for example, the conversion of squares into a rectangle in task 1.
During the occupation, with the aim of managing the search activity of children, the educator uses various techniques that contribute to the upbringing of their positive attitude towards a long-term persistent search, but at the same time fast reaction, refusal from the developed search path. The interest of children is supported by the desire to achieve success, for which the asset needs, the work of thought.
Transformation of one shape to another. Changing the number of squares in the figure.
Purpose. Exercising children in the ability to solve problems by targeted practical samples and thinking about the solution.
Material: Accounting sticks in children, at the educator - depicted graphically tasks (on this and the following classes).
Progress. 1. The tutor shows the table with the figure depicted on it, proposes the same (Fig. 4) from sticks. Considers it with children, determines the number of squares. Then says: "This is a task. Listen to what to do to solve it. It is necessary to guess which 4 wands to remove the one rectangle. First, think about how it can be done, and then remove the sticks."
After the task is solved, the teacher calls one child to the board, he shows and tells how to solve it. The teacher approves the attempts of children to act independently.
2. Dana figure of 6 squares. It is necessary to remove 2 sticks so that there are 4 of the same square (Fig. 5).
After creating children on the sample of such a figure, there is an analysis on questions: "How many squares in the figure are there? How are you? According to which some of the sticks forming the squares should be removed to immediately decrease their number?"
Children independently solve the task. The educator in case of difficulty helps them, orienting to find the right ways.
Purpose. Exercise children in the ability to carry out targeted samples, limit the number of practical samples by pondering the stroke of the search, guesses.
Progress. 1. Dana figure out of 5 squares. It is necessary to remove 3 sticks, leaving 3 squares (Fig. 8). The educator sets questions, encourages children to solve the problem: "How many squares in the figure? How much should it remain? How many sticks need to be removed? This task on the smelter should be guessed, what 3 wands need to be removed so that the squares have less - 3?"
Children are embarking. The educator resembles the need to preliminarize the stroke of the solution of the decision. In case of difficulty, it reminds the condition of the task, it proposes not to repeat trial actions that do not lead to the correct solution.
One of the children who solved the task among the first, sketches and explains the decision at the board.
2. Dana figure from 4 equal squares. It is necessary to remove 2 sticks to get 2 unequal squares (Fig. 9).
Questions for analyzing a sample figure: "How many squares? Can you prove that they are equal? \u200b\u200bThink how to solve the task."
At the suggestion of the teacher, one child explains the problem of the task.
Purpose. Express the presumptive stroke of the search for solutions, check it through targeted search engines.
Travel course. 1. A figure of 5 equal squares is given; It is necessary to remove 4 sticks to become 3 equal squares (Fig. 13).
The educator, referring to the children, says: "Consider the figure, think how to solve the task, which of the sticks can be removed to change this figure. First, tell me, and then remove the sticks."
The educator asks some children (but so that their stories do not hear other guys), invites everyone to solve the problem on their own. Children explain the solution of the task at the board, so that in the course of the story it was possible to make sketching figures.
2. The figure of 4 squares is given: it is necessary to shift 2 sticks to get 5 equal squares (Fig. 12).
The educator after the formation of the figures and the analysis of the task says to children so that they, before shifting the sticks, thought whether this action leads to an increase in the number of squares, they described how they think to solve the task. During the verification of the decision, the teacher emphasizes that it is possible to solve the problem in different ways.
In the process of studying in classes, children 5-6 years are actively included not only in the practical solution of the solution, but also in mental. This is evidenced by their statements, reasoning about the pathways. So, the children were given a figure of 5 squares; It is necessary to remove 4 sticks so that there are 3 of the same square (Fig. 14). Responding to a teacher's question about how the task will be solved, some answer: "I take these sticks (a, b and k) and this (c). What then it turns out? (Thinking.) No, I do not know how." Others argue: "I think that it is necessary to remove 2 angular sticks (e, g) and somewhere else to see." "I guessed. I looked and guessed: if these to remove (shows on g, d, and, h), then there will be 3 squares: one, two, three."
During the execution of tasks, children master the ability based on the reference of the search process (task analysis) to assume a solution to check it in almost the search for new ways, justify them.
For learning children to independently analyze the task, finding a solution, the ability to guess the use of various methodological techniques, instructions on the need for a search approach to solving the problem: "First, think about how you decide the task, and tell about it. Check your assumption, shifting sticks or even Not touching them. If you think that it is mistaken, you have to come up with how to solve the problem differently, and not to repeat your mistakes. We must carefully consider the figure and guess how to solve the task. " Evaluation, confirmation of the correctness or error in the course: "You removed this wand correctly, think about how to solve the task" - and the other stimulate the activity of the guys, help them find the right decision.
In working with the children of the 7th year of life, the nature of the tasks for converting figures is complicated. They are solved by combining practical and mental samples or only in terms of mental action - in the mind, with a justification, expression in the speech of the decision.
The sequence of the execution of 6-7 years of tasks to convert shapes.
Put 1 wand so that the house is inverted in the other direction (Fig. 15).
In a figure consisting of 9 squares, remove 4 sticks to remain 5 squares (Fig. 16).
In the figure of 6 squares, remove 3 sticks so that 4 square remains (Fig. 17).
In the figure, similar to the key, shifting 4 sticks to get 3 squares (Fig. 18).
In the figure of 6 squares, remove 2 sticks so that 4 equal square remains (Fig. 19).
In the figure depicting an arrow, shifting 4 sticks so that 4 triangles are obtained (Fig. 20).
In the figure of 5 squares, shifting 3 sticks to become 4 squares (Fig. 21).
Fig. 21 In the figure, shifting 3 sticks so that it turned out 4 equal triangles 
In a figure consisting of 4 squares, shifting 3 sticks so that it turned out 3 of the same square (Fig.23).
Shut up 4 sticks so that 4 equal triangles are obtained from the ax (Fig. 24).
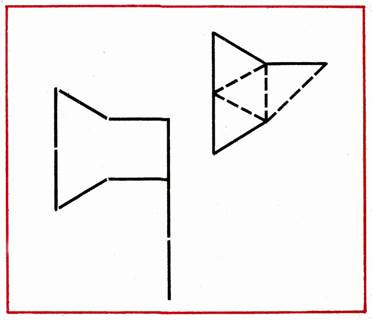
In a figure resembling a lantern, shifting 4 sticks to get a quadrilateral consisting of 4 equal triangles (Fig. 25).
Shifting 2 sticks so that the figure; Similar to the cow, looked in the other side (Fig. 26).
What the smallest number of sticks should be shifted to remove the garbage from the Sovka? (Fig. 27.)

In the group preparatory for school, children's learning to solve the tasks for the mixture contributes to the further development of their mental activity, the ability to plan the course of searches.
Examples (for children 6-7 years)
Converting figures
Purpose. Exercising children in the ability to carry out targeted search actions of a mental and practical plan, a partial mental solution to the problem.
Progress. The educator reports to children: "Today we will solve new, more complex tasks on a mixture. Make out of the sticks here such a figure (shows) and tell me which geometric figures it consists. "
1. Dana figure of 6 squares. It is necessary to remove 2 sticks to remain 4 squares (Fig. 19).
The tutor helps children in finding ways to solve: "Think which wands need to be removed so that the squares have become less. Do not hurry to shift the sticks, first think about how to solve the task. It is possible to remove wands only if the number of squares in the figure is reduced.
The problem is checked at the board.
2. Dana figure similar to the arrow. It is necessary to shift 4 sticks to get 4 triangles (Fig. 20).
After analyzing and clarifying the terms of the task, the educator asks who the children already guessed how to solve it. On the instructions of the educator, some children express an alleged solution so that others do not hear. The educator invites them to check the guesses practically. Encourages actions aimed at mental solving the task, reasoning, emphasizes that this task has several solutions that sketch on the board.
Purpose. Plan in the mind a full or partial decision of the solution, represent changes that will occur in the figure as a result of transformation, suggest suggesting.
Progress. In the figure, similar to the lamp, shifting 3 sticks so that it becomes 4 equal triangles (Fig. 22).
Questions for analysis: "How do you think, what sticks and where to shift? What will change as a result of this?"
The educator invites children to express their assumptions and solve the task.
In the case of an incorrect search of searches (as shown in Fig. 28), the educator explains that when solving some puzzles, geometric shapes (triangles, squares) can be located one of the other.
Purpose. Teach children to solve problems on the basis of mental analysis by nominating the hypothesis (assumptions) and checking it.
Material: magnetic board with a figure made up on it.
Progress. In the Figure of the Lantern, shifting 4 sticks so that a quadrilateer is obtained, consisting of 4 equal triangles (Fig. 24).
The educator says to children: "You solved a lot of tasks to draw up a figure of sticks. This task will not be from sticks. Watch on the board, where this task is drawn, and try to solve it." Then questions the questions: "How many sticks are made up of a flashlight figure? How many sticks need to shield, so that the other figure should be? What kind of figure should it? Consider this quadrangle (shows the top of the figure). What are the figures here? How can you make such a figure?"
Next, children are invited to check the solution on the magnetic board, which they consider faithful. Incorrect paths are not checked in a practical way; In such cases, the educator stimulates the search for a new solution.
In the preparatory for school, many children, subject to systematic learning, purposefully analyze the tasks for the smelter and detect simple rational ways to solve them. Thus, in the conversion task in 4 equal triangles (shown in Fig. 29), children intelligently explain possible transformations. For example, they reason: "I am so broadcasting sticks: this (a) here, this and this (b and c) is also down to get triangles, but this (g) ... I'll think about it, where to put it ... down You can either here, and 4 triangles should get (Fig. 29, b) "," I think so to solve this problem: 3 sticks (s, and, k) put it, on top, it turns out 3 triangles, and this (g) "After all, it's not needed here - I will put on top, it will turn out 4 triangles, we have accounted for" (Fig. 29, c).
In the course of learning, the search for children's solutions to the task is reduced, the character of the samples changes, thinking about the decision begins to occupy an increasing place. Therefore, at a certain stage, the proposed task, the children were able to decide, analyzing it on the basis of only graphic image. Practical compilation and modification of figures served here a means of verification.
As a result of regularly organized by the teacher of classes, exercises to solve puzzle tasks, children acquire the ability to approach each non-standard task Creatively, from the position of finding a new decision of the decision, and not the use of the already known to them. The nature of the search action is gradually changing: from practical ("samples and errors") - to targeted practical actions (for the purpose of the intended transformation), and from them - to mental samples through the prediction of the solution path.
From solving puzzle problems with the help of an educator (based on partial tips, the use of leading issues, confirmation of a partial decision), children are moving to a completely independent rapid solution to the tasks.
Children 6-7 years old can invent elementary tasks for a mixture (puzzles with chopsticks). For this, teacher must be held with children a conversation about how such tasks come up with that they are set (any figure), which transformation is required to be carried out (modify the figure, reduce or increase the number of squares, triangles, rectangles).
Puzzles with chopsticks invented by children:
Shoot 6 sticks so that the tank is from the ship (Fig. 30, a). (Renat M., 6 years 10 months)
In the figure shifting 3 sticks to get a kite (Fig. 30, b). (Lena M., 7 years old.)
Shifting 5 sticks to get a TV (Fig. 30, B) from the vase.
Show 1 wand so that it turned out 5 equal squares (Fig. 30, d).
Transfer 3 sticks so that 4 equal triangles are obtained (Fig. 30, e). (Ilya M., 4 years 7 months).
Puzzles with chopsticks
These tasks are very simple, in each of them you need to transform figures by shifting the sticks. They are invented by children by analogy with those challenges that they were previously resolved, but, of course, are the indicator more high level Development of spatial representation, thinking.
Children are able to present possible spatial, qualitative changes not only during the solution of the task proposed by them, but also in their independently. All this testifies to the development of mixtures and intelligence. In this case, the mixture should be understood as the ability to quickly establish links between the parts of the task, to send the solution to the correct search for it, eliminating the error path, to discard insignificant elements of the task.
Only on the basis of the analysis of the conditions of the problem, independent searches as a result of mastering mental operations (generalization, comparison, analysis, etc.) becomes possible by the manifestation of smelting and independent conclusion.
As children are mastered, the tasks solutions change the ratio of actions and reasoning during their solution. At the beginning of training, children with difficulty justify their to the end unconscious practical actions, therefore the search process is mainly from some practical samples. The verbal expression of the decision is reflected in the comments: "These will take", "here I will put", "so need," and others. Under the influence of exercises, children begin to prevail the reasoning, the actions are becoming more appropriate, their number is reduced. The character and role of reasoning is changing: from reasoning in the process of practical actions - to reasoning, which precedes these actions (nomination of assumptions, the hypothesis of the decision). In addition, the quality of reasoning is changing, which accompany practical actions. Children 6-7 years argued the solution, prove the correctness or error in the course, based on the task and the goal of the transfiguration. They master the ability to assume a solution and check it without practical actions, i.e., in the process of mental action, find the right solution to the problem.
Geometric problems of geometric nature are partially included directly into the content of classes in the formation of elementary mathematical ideas in senior and preparatory to school groups in order to enhance childhood, development logical thinking, Develop the ability to guess, smelting and intelligence, which is important to a person for life, labor activity. At the same time, the strict sequence should be observed in the complication of the tasks themselves, the requirements for the organization of the search for their children. - Analysis of the tasks, the nature of the search operation, the level of manifestation of the independence of thinking and decisions, a combination of actions and reasoning is specified and more complicated.
"Pentamino" is one of the most popular world puzzles, the peak of popularity fell at the end of the 60s. The game itself was described in detail in the magazine "Science and Life". Children and adults can play in this puzzle.
Pantomino patented Solomon Wolf Golomb, a resident of Baltimore, Mathematics and Engineer, University Professor South California. The game consists of flat figuresEach of which consists of five identical squares connected by the parties, hence the name. There are also the version of tetramino puzzles, consisting of four squares, from this game and there was a famous tetris.
Pentamino elements

The game set "Pentamino" consists of 12 figures. Each figure is indicated latin letterwhose shape it reminds. When solving tasks and puzzles, the figures can be twisted and turned over, so when making the game, make elements with your own hands.
Popular puzzles
Pentamino-based games and toys
Now in online stores you can find games and puzzles made on the basis of pentamino elements.
Pentamino do it yourself
We offer to make elements of a game of dense cardboard or plastic and enclose with colored paper or adhesive film. Below is the option of making cardboard.

- We draw each element on solid cardboard or plastic. It is better to draw, each element separately, without folding into a rectangle - it will be easier to cut.
- Cut out the first figure "U", we recheck the dimensions. Next, cut out all other elements, checking that they calmly entered the element "u" with their convex parts. Cut, if you need too much. The photos show the elements with a size of a square module 2.5 x 2.5 centimeters.
- We supply the finished cardboard element on a folded half of the colored paper and cut out two color details at once. Better color items to do a little less than cardboard, and glued better, and the edges will not donate from frequent use.
- Glue colored paper On both sides to the cardboard.
- We find a box for storing parts, where then we will also add schemes and tasks to the game. Schemes can be printed on the site, and you can draw and color on a tetrad sheet into a cell.