Η εφαπτομενική εξίσωση έχει τη μορφή. Η εξίσωση της εφαπτομένης στο γράφημα της συνάρτησης - Υπερμάρκετ Γνώσης

Τύπος εργασίας: 7

Κατάσταση

Η ευθεία y=3x+2 εφάπτεται στη γραφική παράσταση της συνάρτησης y=-12x^2+bx-10. Βρείτε το b , δεδομένου ότι η τετμημένη του σημείου επαφής είναι μικρότερη από το μηδέν.

Απόφαση

Έστω x_0 η τετμημένη του σημείου της γραφικής παράστασης της συνάρτησης y=-12x^2+bx-10 από το οποίο διέρχεται η εφαπτομένη σε αυτή τη γραφική παράσταση.

Η τιμή της παραγώγου στο σημείο x_0 είναι ίση με την κλίση της εφαπτομένης, δηλαδή y"(x_0)=-24x_0+b=3. Από την άλλη πλευρά, το σημείο εφαπτομένης ανήκει τόσο στη γραφική παράσταση της συνάρτησης όσο και στην εφαπτομένη, δηλ. -12x_0^2+bx_0-10= 3x_0 + 2. Παίρνουμε ένα σύστημα εξισώσεων \begin(περιπτώσεις) -24x_0+b=3,\\-12x_0^2+bx_0-10=3x_0+2. \end (περιπτώσεις)

Λύνοντας αυτό το σύστημα, παίρνουμε x_0^2=1, που σημαίνει είτε x_0=-1 είτε x_0=1. Σύμφωνα με την συνθήκη της τετμημένης, τα σημεία επαφής είναι μικρότερα από το μηδέν, επομένως x_0=-1, μετά b=3+24x_0=-21.

Απάντηση

Τύπος εργασίας: 7
Θέμα: Η γεωμετρική σημασία της παραγώγου. Γράφημα εφαπτομένης συνάρτησης

Κατάσταση

Η ευθεία y=-3x+4 είναι παράλληλη στην εφαπτομένη της γραφικής παράστασης της συνάρτησης y=-x^2+5x-7. Βρείτε την τετμημένη του σημείου επαφής.

Απόφαση

Η κλίση της γραμμής στο γράφημα της συνάρτησης y=-x^2+5x-7 σε ένα αυθαίρετο σημείο x_0 είναι y"(x_0). Αλλά y"=-2x+5, άρα y"(x_0)=- 2x_0+5.Γωνιακός ο συντελεστής της ευθείας y=-3x+4 που καθορίζεται στη συνθήκη είναι -3.Οι παράλληλες γραμμές έχουν τις ίδιες κλίσεις.Επομένως, βρίσκουμε μια τέτοια τιμή x_0 που =-2x_0 +5=-3.

Παίρνουμε: x_0 = 4.

Απάντηση

Πηγή: «Μαθηματικά. Προετοιμασία για τις εξετάσεις-2017. επίπεδο προφίλ. Εκδ. F. F. Lysenko, S. Yu. Kulabukhova.

Τύπος εργασίας: 7
Θέμα: Η γεωμετρική σημασία της παραγώγου. Γράφημα εφαπτομένης συνάρτησης

Κατάσταση

Απόφαση

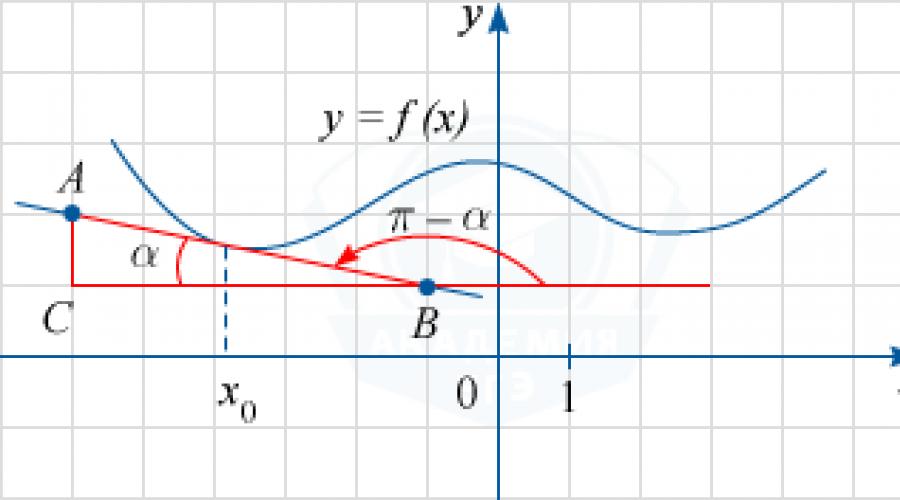
Από το σχήμα, προσδιορίζουμε ότι η εφαπτομένη διέρχεται από τα σημεία A(-6; 2) και B(-1; 1). Σημειώστε με C(-6; 1) το σημείο τομής των ευθειών x=-6 και y=1 και με \άλφα τη γωνία ABC (μπορεί να φανεί στο σχήμα ότι είναι απότομη). Τότε η ευθεία ΑΒ σχηματίζει αμβλεία γωνία \pi -\άλφα με τη θετική φορά του άξονα Ox.

Όπως γνωρίζετε, το tg(\pi -\alpha) θα είναι η τιμή της παραγώγου της συνάρτησης f(x) στο σημείο x_0. σημειώσε ότι tg \άλφα =\frac(AC)(CB)=\frac(2-1)(-1-(-6))=\frac15.Από εδώ, με τους τύπους αναγωγής, παίρνουμε: tg(\pi -\alpha) =-tg \alpha =-\frac15=-0,2.

Απάντηση

Πηγή: «Μαθηματικά. Προετοιμασία για τις εξετάσεις-2017. επίπεδο προφίλ. Εκδ. F. F. Lysenko, S. Yu. Kulabukhova.

Τύπος εργασίας: 7
Θέμα: Η γεωμετρική σημασία της παραγώγου. Γράφημα εφαπτομένης συνάρτησης

Κατάσταση

Η ευθεία y=-2x-4 εφάπτεται στη γραφική παράσταση της συνάρτησης y=16x^2+bx+12. Βρείτε το b , δεδομένου ότι η τετμημένη του σημείου επαφής είναι μεγαλύτερη από το μηδέν.

Απόφαση

Έστω x_0 η τετμημένη του σημείου στη γραφική παράσταση της συνάρτησης y=16x^2+bx+12 μέσω της οποίας

εφάπτεται σε αυτό το γράφημα.

Η τιμή της παραγώγου στο σημείο x_0 είναι ίση με την κλίση της εφαπτομένης, δηλαδή y "(x_0)=32x_0+b=-2. Από την άλλη πλευρά, το σημείο εφαπτομένης ανήκει τόσο στη γραφική παράσταση της συνάρτησης όσο και στην εφαπτομένη, δηλ. 16x_0^2+bx_0+12=- 2x_0-4 Παίρνουμε ένα σύστημα εξισώσεων \begin(περιπτώσεις) 32x_0+b=-2,\\16x_0^2+bx_0+12=-2x_0-4. \end (περιπτώσεις)

Λύνοντας το σύστημα, παίρνουμε x_0^2=1, που σημαίνει είτε x_0=-1 είτε x_0=1. Σύμφωνα με την συνθήκη της τετμημένης, τα σημεία επαφής είναι μεγαλύτερα από το μηδέν, επομένως x_0=1, τότε b=-2-32x_0=-34.

Απάντηση

Πηγή: «Μαθηματικά. Προετοιμασία για τις εξετάσεις-2017. επίπεδο προφίλ. Εκδ. F. F. Lysenko, S. Yu. Kulabukhova.

Τύπος εργασίας: 7
Θέμα: Η γεωμετρική σημασία της παραγώγου. Γράφημα εφαπτομένης συνάρτησης

Κατάσταση

Το σχήμα δείχνει ένα γράφημα της συνάρτησης y=f(x) που ορίζεται στο διάστημα (-2; 8). Να προσδιορίσετε τον αριθμό των σημείων όπου η εφαπτομένη στη γραφική παράσταση της συνάρτησης είναι παράλληλη στην ευθεία y=6.

Απόφαση

Η ευθεία y=6 είναι παράλληλη στον άξονα Ox. Επομένως, βρίσκουμε τέτοια σημεία στα οποία η εφαπτομένη στο γράφημα της συνάρτησης είναι παράλληλη με τον άξονα Ox. Σε αυτό το γράφημα, τέτοια σημεία είναι ακραία σημεία (μέγιστα ή ελάχιστα σημεία). Όπως μπορείτε να δείτε, υπάρχουν 4 ακραία σημεία.

Απάντηση

Πηγή: «Μαθηματικά. Προετοιμασία για τις εξετάσεις-2017. επίπεδο προφίλ. Εκδ. F. F. Lysenko, S. Yu. Kulabukhova.

Τύπος εργασίας: 7
Θέμα: Η γεωμετρική σημασία της παραγώγου. Γράφημα εφαπτομένης συνάρτησης

Κατάσταση

Η ευθεία y=4x-6 είναι παράλληλη στην εφαπτομένη της γραφικής παράστασης της συνάρτησης y=x^2-4x+9. Βρείτε την τετμημένη του σημείου επαφής.

Απόφαση

Η κλίση της εφαπτομένης στη γραφική παράσταση της συνάρτησης y \u003d x ^ 2-4x + 9 σε ένα αυθαίρετο σημείο x_0 είναι y "(x_0). Αλλά y" \u003d 2x-4, που σημαίνει y "(x_0) \ u003d 2x_0-4. Η κλίση της εφαπτομένης y \u003d 4x-7 που καθορίζεται στη συνθήκη είναι ίση με 4. Οι παράλληλες γραμμές έχουν τις ίδιες κλίσεις. Επομένως, βρίσκουμε μια τέτοια τιμή x_0 ώστε 2x_0-4 \u003d 4. Παίρνουμε : x_0 \u003d 4.

Απάντηση

Πηγή: «Μαθηματικά. Προετοιμασία για τις εξετάσεις-2017. επίπεδο προφίλ. Εκδ. F. F. Lysenko, S. Yu. Kulabukhova.

Τύπος εργασίας: 7
Θέμα: Η γεωμετρική σημασία της παραγώγου. Γράφημα εφαπτομένης συνάρτησης

Κατάσταση

Στο σχήμα φαίνεται η γραφική παράσταση της συνάρτησης y=f(x) και η εφαπτομένη σε αυτήν στο σημείο με την τετμημένη x_0. Να βρείτε την τιμή της παραγώγου της συνάρτησης f(x) στο σημείο x_0.

Απόφαση

Από το σχήμα, προσδιορίζουμε ότι η εφαπτομένη διέρχεται από τα σημεία A(1; 1) και B(5; 4). Δηλώστε με C(5; 1) το σημείο τομής των ευθειών x=5 και y=1 και με \άλφα τη γωνία BAC (μπορεί να φανεί στο σχήμα ότι είναι οξεία). Τότε η ευθεία ΑΒ σχηματίζει γωνία \άλφα με τη θετική φορά του άξονα Ox.

Το εκπαιδευτικό βίντεο "Η εξίσωση της εφαπτομένης στο γράφημα μιας συνάρτησης" παρουσιάζει εκπαιδευτικό υλικό για την κατάκτηση του θέματος. Κατά τη διάρκεια του μαθήματος βίντεο, παρουσιάζεται το θεωρητικό υλικό που είναι απαραίτητο για τον σχηματισμό της έννοιας της εξίσωσης της εφαπτομένης στη γραφική παράσταση μιας συνάρτησης σε ένα δεδομένο σημείο, παρουσιάζεται ο αλγόριθμος για την εύρεση μιας τέτοιας εφαπτομένης, παραδείγματα επίλυσης προβλημάτων χρησιμοποιώντας το περιγράφεται το θεωρητικό υλικό που μελετήθηκε.

Το εκπαιδευτικό βίντεο χρησιμοποιεί μεθόδους που βελτιώνουν την ορατότητα του υλικού. Σχέδια, διαγράμματα εισάγονται στην προβολή, δίνονται σημαντικά φωνητικά σχόλια, εφαρμόζονται κινούμενα σχέδια, χρωματική επισήμανση και άλλα εργαλεία.

Το βίντεο μάθημα ξεκινά με την παρουσίαση του θέματος του μαθήματος και την εικόνα μιας εφαπτομένης στη γραφική παράσταση κάποιας συνάρτησης y=f(x) στο σημείο Μ(a;f(a)). Είναι γνωστό ότι η κλίση της εφαπτομένης της γραφικής παράστασης σε ένα δεδομένο σημείο είναι ίση με την παράγωγο της συνάρτησης f΄(a) σε ένα δεδομένο σημείο. Επίσης από την πορεία της άλγεβρας είναι γνωστή η εξίσωση της ευθείας y=kx+m. Παρουσιάζεται σχηματικά η λύση του προβλήματος της εύρεσης της εφαπτομένης εξίσωσης σε ένα σημείο, η οποία ανάγεται στην εύρεση των συντελεστών k, m. Γνωρίζοντας τις συντεταγμένες του σημείου που ανήκει στη γραφική παράσταση της συνάρτησης, μπορούμε να βρούμε m αντικαθιστώντας την τιμή των συντεταγμένων στην εξίσωση της εφαπτομένης f(a)=ka+m. Από αυτό βρίσκουμε m=f(a)-ka. Έτσι, γνωρίζοντας την τιμή της παραγώγου σε ένα δεδομένο σημείο και τις συντεταγμένες του σημείου, μπορούμε να αναπαραστήσουμε την εφαπτομένη εξίσωση με αυτόν τον τρόπο y=f(a)+f΄(a)(x-a).

Το παρακάτω είναι ένα παράδειγμα σύνταξης μιας εφαπτομενικής εξίσωσης, ακολουθώντας το σχήμα. Δίνεται συνάρτηση y=x 2 , x=-2. Έχοντας δεχτεί a=-2, βρίσκουμε την τιμή της συνάρτησης σε αυτό το σημείο f(a)= f(-2)=(-2) 2 =4. Καθορίζουμε την παράγωγο της συνάρτησης f΄(х)=2х. Στο σημείο αυτό, η παράγωγος ισούται με f΄(a)= f΄(-2)=2 (-2)=-4. Για τη σύνταξη της εξίσωσης βρίσκονται όλοι οι συντελεστές a=-2, f(a)=4, f΄(a)=-4, άρα η εφαπτομένη εξίσωση y=4+(-4)(x+2). Απλοποιώντας την εξίσωση, παίρνουμε y \u003d -4-4x.

Στο παρακάτω παράδειγμα, προτείνεται να διατυπωθεί η εξίσωση της εφαπτομένης στην αρχή της γραφικής παράστασης της συνάρτησης y=tgx. Στο σημείο αυτό a=0, f(0)=0, f΄(х)=1/cos 2 x, f΄(0)=1. Άρα η εφαπτομενική εξίσωση μοιάζει με y=x.

Ως γενίκευση, η διαδικασία σύνταξης της εξίσωσης της εφαπτομένης στο γράφημα συνάρτησης σε κάποιο σημείο επισημοποιείται ως αλγόριθμος που αποτελείται από 4 βήματα:

• Εισάγεται ονομασία για την τετμημένη του σημείου επαφής.
• Το f(a) υπολογίζεται.
• Προσδιορίζεται η F΄(х) και υπολογίζεται η f΄(a). Οι τιμές που βρέθηκαν a, f(a), f΄(a) αντικαθίστανται στον τύπο της εφαπτομενικής εξίσωσης y=f(a)+f΄(a)(x-a).

Το Παράδειγμα 1 εξετάζει τη σύνταξη της εξίσωσης της εφαπτομένης στη γραφική παράσταση της συνάρτησης y \u003d 1 / x στο σημείο x \u003d 1. Χρησιμοποιούμε έναν αλγόριθμο για να λύσουμε το πρόβλημα. Για αυτή τη συνάρτηση στο σημείο a=1, η τιμή της συνάρτησης f(a)=-1. Παράγωγος της συνάρτησης f΄(х)=1/х 2 . Στο σημείο a=1, η παράγωγος f΄(a)= f΄(1)=1. Χρησιμοποιώντας τα δεδομένα που ελήφθησαν, συντάσσεται η εξίσωση της εφαπτομένης y \u003d -1 + (x-1), ή y \u003d x-2.

Στο παράδειγμα 2, πρέπει να βρείτε την εξίσωση της εφαπτομένης στο γράφημα της συνάρτησης y \u003d x 3 +3x 2 -2x-2. Η κύρια προϋπόθεση είναι ο παραλληλισμός της εφαπτομένης και της ευθείας y \u003d -2x + 1. Αρχικά, βρίσκουμε την κλίση της εφαπτομένης, ίση με την κλίση της ευθείας y \u003d -2x + 1. Αφού f΄(a)=-2 για αυτή την ευθεία, τότε k=-2 για την επιθυμητή εφαπτομένη. Βρίσκουμε την παράγωγο της συνάρτησης (x 3 + 3x 2 -2x-2) ΄ \u003d 3x 2 + 6x-2. Γνωρίζοντας ότι f΄(a)=-2, βρίσκουμε τις συντεταγμένες του σημείου 3а 2 +6а-2=-2. Λύνοντας την εξίσωση, παίρνουμε 1 \u003d 0 και 2 \u003d -2. Χρησιμοποιώντας τις συντεταγμένες που βρέθηκαν, μπορείτε να βρείτε την εξίσωση εφαπτομένης χρησιμοποιώντας έναν πολύ γνωστό αλγόριθμο. Βρίσκουμε την τιμή της συνάρτησης στα σημεία f(a 1)=-2, f(a 2)=-18. Η τιμή της παραγώγου στο σημείο f΄(а 1)= f΄(а 2)=-2. Αντικαθιστώντας τις τιμές που βρέθηκαν στην εξίσωση εφαπτομένης, λαμβάνουμε για το πρώτο σημείο ένα 1 \u003d 0 y \u003d -2x-2 και για το δεύτερο σημείο a 2 \u003d -2 την εφαπτομένη εξίσωση y \u003d -2x- 22.

Το Παράδειγμα 3 περιγράφει τη διατύπωση της εφαπτομένης εξίσωσης για το σχέδιό της στο σημείο (0;3) στη γραφική παράσταση της συνάρτησης y=√x. Η απόφαση λαμβάνεται σύμφωνα με τον γνωστό αλγόριθμο. Το σημείο επαφής έχει συντεταγμένες x=a, όπου a>0. Η τιμή της συνάρτησης στο σημείο f(a)=√x. Η παράγωγος της συνάρτησης f΄(х)=1/2√х, επομένως, στο δεδομένο σημείο f΄(а)=1/2√а. Αντικαθιστώντας όλες τις λαμβανόμενες τιμές στην εφαπτομενική εξίσωση, παίρνουμε y \u003d √a + (x-a) / 2√a. Μετασχηματίζοντας την εξίσωση, παίρνουμε y=x/2√a+√a/2. Γνωρίζοντας ότι η εφαπτομένη διέρχεται από το σημείο (0; 3), βρίσκουμε την τιμή του a. Βρείτε ένα από 3=√a/2. Άρα √a=6, a=36. Βρίσκουμε την εξίσωση της εφαπτομένης y \u003d x / 12 + 3. Το σχήμα δείχνει τη γραφική παράσταση της συνάρτησης που εξετάζουμε και την κατασκευασμένη επιθυμητή εφαπτομένη.

Υπενθυμίζονται στους μαθητές οι κατά προσέγγιση ισότητες Δy=≈f΄(x)Δxand f(x+Δx)-f(x)≈f΄(x)Δx. Λαμβάνοντας x=a, x+Δx=x, Δx=x-a, παίρνουμε f(x)- f(a)≈f΄(a)(x-a), επομένως f(x)≈f(a)+ f΄( α)(χ-α).

Στο παράδειγμα 4, είναι απαραίτητο να βρεθεί η κατά προσέγγιση τιμή της έκφρασης 2.003 6 . Δεδομένου ότι είναι απαραίτητο να βρούμε την τιμή της συνάρτησης f (x) \u003d x 6 στο σημείο x \u003d 2.003, μπορούμε να χρησιμοποιήσουμε τον γνωστό τύπο, λαμβάνοντας f (x) \u003d x 6, a \u003d 2 , f (a) \u003d f (2) \u003d 64, f ΄(x)=6х 5 . Παράγωγος στο σημείο f΄(2)=192. Επομένως, 2,003 6 ≈65-192 0,003. Αφού υπολογίσουμε την παράσταση, παίρνουμε 2.003 6 ≈64.576.

Το βίντεο μάθημα «Η εξίσωση της εφαπτομένης στη γραφική παράσταση μιας συνάρτησης» προτείνεται για χρήση σε ένα παραδοσιακό μάθημα μαθηματικών στο σχολείο. Για έναν δάσκαλο εξ αποστάσεως εκπαίδευσης, το υλικό βίντεο θα σας βοηθήσει να εξηγήσετε το θέμα με μεγαλύτερη σαφήνεια. Το βίντεο μπορεί να προταθεί για αυτοεξέταση από τους μαθητές εάν είναι απαραίτητο για να εμβαθύνουν την κατανόησή τους για το θέμα.

ΕΡΜΗΝΕΙΑ ΚΕΙΜΕΝΟΥ:

Γνωρίζουμε ότι αν το σημείο M (a; f (a)) (em με συντεταγμένες a και eff από το a) ανήκει στη γραφική παράσταση της συνάρτησης y \u003d f (x) και αν σε αυτό το σημείο μπορεί να σχεδιαστεί μια εφαπτομένη η γραφική παράσταση της συνάρτησης, όχι κάθετη προς την τετμημένη του άξονα, τότε η κλίση της εφαπτομένης είναι f "(a) (εφ διαδρομή από a).

Έστω μια συνάρτηση y = f(x) και ένα σημείο M (a; f(a)), και είναι επίσης γνωστό ότι υπάρχει f´(a). Ας συνθέσουμε την εξίσωση της εφαπτομένης στη γραφική παράσταση μιας δεδομένης συνάρτησης σε ένα δεδομένο σημείο. Αυτή η εξίσωση, όπως η εξίσωση οποιασδήποτε ευθείας γραμμής που δεν είναι παράλληλη με τον άξονα y, έχει τη μορφή y = kx + m (y ισούται με ka x συν em), επομένως η εργασία είναι να βρούμε τις τιμές των συντελεστών κ και μ. (κα και εμ)

Κλίση k \u003d f "(a). Για να υπολογίσουμε την τιμή του m, χρησιμοποιούμε το γεγονός ότι η επιθυμητή ευθεία διέρχεται από το σημείο M (a; f (a)). Αυτό σημαίνει ότι αν αντικαταστήσουμε τις συντεταγμένες του σημείο Μ στην εξίσωση της ευθείας, παίρνουμε τη σωστή ισότητα : f(a) = ka+m, από όπου βρίσκουμε ότι m = f(a) - ka.

Απομένει να αντικαταστήσουμε τις τιμές που βρέθηκαν των συντελεστών ki και m στην εξίσωση μιας ευθείας γραμμής:

y = kx+(f(a)-ka);

y = f(a)+k(x-a);

y= φά(ένα)+ φά"(ένα) (Χ- ένα). (Το Y ισούται με το eff από μια συν ef διαδρομή πολλαπλασιασμένη επί x μείον α).

Έχουμε λάβει την εξίσωση της εφαπτομένης στη γραφική παράσταση της συνάρτησης y = f(x) στο σημείο x=a.

Εάν, ας πούμε, y \u003d x 2 και x \u003d -2 (δηλαδή a \u003d -2), τότε f (a) \u003d f (-2) \u003d (-2) 2 \u003d 4; f´(x) \u003d 2x, άρα f "(a) \u003d f´(-2) \u003d 2 (-2) \u003d -4. (τότε το eff από το a είναι ίσο με τέσσερα, το eff πρώτο από το x είναι ίσο με δύο x, που σημαίνει ef εγκεφαλικό επεισόδιο από ίσο μείον τέσσερα)

Αντικαθιστώντας στην εξίσωση τις τιμές που βρέθηκαν a \u003d -2, f (a) \u003d 4, f "(a) \u003d -4, παίρνουμε: y \u003d 4 + (-4) (x + 2) , δηλαδή y \u003d -4x -4.

(y ισούται με μείον τέσσερα x μείον τέσσερα)

Ας συνθέσουμε την εξίσωση της εφαπτομένης στη γραφική παράσταση της συνάρτησης y \u003d tgx (y ισούται με την εφαπτομένη x) στην αρχή. Έχουμε: a = 0, f(0) = tg0=0;

f"(x)= , άρα f"(0) = l. Αντικαθιστώντας τις τιμές a=0, f(a)=0, f´(a) = 1 στην εξίσωση, παίρνουμε: y=x.

Γενικεύουμε τα βήματά μας για την εύρεση της εξίσωσης της εφαπτομένης στη γραφική παράσταση της συνάρτησης στο σημείο x χρησιμοποιώντας τον αλγόριθμο.

ΑΛΓΟΡΙΘΜΟΣ ΓΙΑ ΤΗ ΣΥΝΘΕΣΗ ΤΗΣ ΕΞΙΣΩΣΗΣ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ που εφάπτεται στο ΓΡΑΦΗΜΑ y \u003d f (x):

1) Να χαρακτηρίσετε την τετμημένη του σημείου επαφής με το γράμμα α.

2) Υπολογίστε τη f(a).

3) Βρείτε το f´(x) και υπολογίστε το f´(a).

4) Αντικαταστήστε τους αριθμούς που βρέθηκαν a, f(a), f´(a) στον τύπο y= φά(ένα)+ φά"(ένα) (Χ- ένα).

Παράδειγμα 1. Γράψτε την εξίσωση της εφαπτομένης στη γραφική παράσταση της συνάρτησης y \u003d - in

σημείο x = 1.

Απόφαση. Ας χρησιμοποιήσουμε τον αλγόριθμο, λαμβάνοντας υπόψη ότι σε αυτό το παράδειγμα

2) f(a)=f(1)=-=-1

3) f´(x)=; f´(a)= f´(1)= =1.

4) Αντικαταστήστε τους τρεις αριθμούς που βρέθηκαν: a \u003d 1, f (a) \u003d -1, f "(a) \u003d 1 στον τύπο. Παίρνουμε: y \u003d -1 + (x-1), y \u003d x-2.

Απάντηση: y = x-2.

Παράδειγμα 2. Δίνεται συνάρτηση y = x 3 +3x 2 -2x-2. Γράψτε την εξίσωση της εφαπτομένης στη γραφική παράσταση της συνάρτησης y \u003d f (x), παράλληλη στην ευθεία y \u003d -2x +1.

Χρησιμοποιώντας τον αλγόριθμο για τη σύνταξη της εφαπτομένης εξίσωσης, λαμβάνουμε υπόψη ότι σε αυτό το παράδειγμα f(x) = x 3 +3x 2 -2x-2, αλλά η τετμημένη του σημείου επαφής δεν προσδιορίζεται εδώ.

Ας αρχίσουμε να μιλάμε έτσι. Η επιθυμητή εφαπτομένη πρέπει να είναι παράλληλη προς την ευθεία y \u003d -2x + 1. Και οι παράλληλες γραμμές έχουν ίσες κλίσεις. Επομένως, η κλίση της εφαπτομένης είναι ίση με την κλίση της δεδομένης ευθείας: k cas. = -2. Hok cas. = f "(a). Έτσι, μπορούμε να βρούμε την τιμή του a από την εξίσωση f ´ (a) \u003d -2.

Ας βρούμε την παράγωγο της συνάρτησης y=φά(Χ):

φά"(Χ) \u003d (x 3 + 3x 2 -2x-2)´ \u003d 3x 2 + 6x-2;φά"(a) \u003d 3a 2 + 6a-2.

Από την εξίσωση f "(a) \u003d -2, δηλ. 3α 2 +6α-2\u003d -2 βρίσκουμε ένα 1 \u003d 0, ένα 2 \u003d -2. Αυτό σημαίνει ότι υπάρχουν δύο εφαπτομένες που ικανοποιούν την συνθήκη του προβλήματος: η μία στο σημείο με την τετμημένη 0, η άλλη στο σημείο με την τετμημένη -2.

Τώρα μπορείτε να ενεργήσετε σύμφωνα με τον αλγόριθμο.

1) ένα 1 \u003d 0 και 2 \u003d -2.

2) f(a 1) = 0 3 +3 0 2 -2∙0-2=-2; f(a2)= (-2) 3 +3 (-2) 2 -2 (-2)-2=6;

3) f "(a 1) = f" (a 2) = -2.

4) Αντικαθιστώντας τις τιμές a 1 = 0, f (a 1) = -2, f "(a 1) = -2 στον τύπο, παίρνουμε:

y=-2-2(x-0), y=-2x-2.

Αντικαθιστώντας τις τιμές a 2 \u003d -2, f (a 2) \u003d 6, f "(a 2) \u003d -2 στον τύπο, παίρνουμε:

y=6-2(x+2), y=-2x+2.

Απάντηση: y=-2x-2, y=-2x+2.

Παράδειγμα 3. Από το σημείο (0; 3) σχεδιάστε μια εφαπτομένη στη γραφική παράσταση της συνάρτησης y \u003d. Απόφαση. Ας χρησιμοποιήσουμε τον αλγόριθμο για τη σύνταξη της εφαπτομένης εξίσωσης, δεδομένου ότι σε αυτό το παράδειγμα f(x) = . Σημειώστε ότι εδώ, όπως στο Παράδειγμα 2, η τετμημένη του σημείου επαφής δεν αναφέρεται ρητά. Ωστόσο, ενεργούμε σύμφωνα με τον αλγόριθμο.

1) Έστω x = a η τετμημένη του σημείου επαφής. είναι σαφές ότι a > 0.

3) f´(x)=()´=; f´(a) =.

4) Αντικατάσταση των τιμών a, f(a) = , f "(a) = στον τύπο

y \u003d f (a) + f "(a) (x-a), παίρνουμε:

Κατά συνθήκη, η εφαπτομένη διέρχεται από το σημείο (0; 3). Αντικαθιστώντας τις τιμές x = 0, y = 3 στην εξίσωση, παίρνουμε: 3 = , και μετά =6, a =36.

Όπως μπορείτε να δείτε, σε αυτό το παράδειγμα, μόνο στο τέταρτο βήμα του αλγορίθμου καταφέραμε να βρούμε την τετμημένη του σημείου επαφής. Αντικαθιστώντας την τιμή a =36 στην εξίσωση, παίρνουμε: y=+3

Στο σχ. Το σχήμα 1 παρουσιάζει μια γεωμετρική απεικόνιση του εξεταζόμενου παραδείγματος: σχεδιάζεται ένα γράφημα της συνάρτησης y \u003d, σχεδιάζεται μια ευθεία γραμμή y \u003d +3.

Απάντηση: y = +3.

Γνωρίζουμε ότι για τη συνάρτηση y = f(x), που έχει παράγωγο στο σημείο x, η κατά προσέγγιση ισότητα είναι αληθής: Δyf´(x)Δx

ή, πιο αναλυτικά, f(x+Δx)-f(x) f´(x) Δx (ef από x συν δέλτα x μείον ef από x είναι περίπου ίσο με το ef πρώτο από x έως δέλτα x).

Για ευκολία περαιτέρω συλλογισμού, αλλάζουμε τον συμβολισμό:

αντί για x θα γράψουμε ένα,

αντί για x + Δx θα γράψουμε x

αντί για Δx θα γράψουμε x-a.

Τότε η κατά προσέγγιση ισότητα που γράφτηκε παραπάνω θα έχει τη μορφή:

f(x)-f(a)f´(a)(x-a)

f(x)f(a)+f´(a)(x-a). (Το ef από το x είναι περίπου ίσο με το eff από ένα συν ef διαδρομή από το a, πολλαπλασιαζόμενο με τη διαφορά μεταξύ x και a).

Παράδειγμα 4. Βρείτε την κατά προσέγγιση τιμή της αριθμητικής παράστασης 2.003 6 .

Απόφαση. Μιλάμε για την εύρεση της τιμής της συνάρτησης y \u003d x 6 στο σημείο x \u003d 2.003. Ας χρησιμοποιήσουμε τον τύπο f(x)f(a)+f´(a)(x-a), θεωρώντας ότι σε αυτό το παράδειγμα f(x)=x 6 , a = 2,f(a) = f(2) = 2 6 =64; x \u003d 2,003, f "(x) \u003d 6x 5 και, επομένως, f" (a) \u003d f "(2) \u003d 6 2 5 \u003d 192.

Ως αποτέλεσμα, παίρνουμε:

2.003 6 64+192 0.003, δηλ. 2.003 6 = 64.576.

Αν χρησιμοποιήσουμε μια αριθμομηχανή, παίρνουμε:

2,003 6 = 64,5781643...

Όπως μπορείτε να δείτε, η ακρίβεια προσέγγισης είναι αρκετά αποδεκτή.

Σκεφτείτε το ακόλουθο σχήμα:

Δείχνει κάποια συνάρτηση y = f(x) που είναι διαφορίσιμη στο σημείο α. Σημειώθηκε το σημείο Μ με συντεταγμένες (a; f(a)). Μέσα από ένα αυθαίρετο σημείο P(a + ∆x; f(a + ∆x)) του γραφήματος, σχεδιάζεται ένα τέμνον MP.

Εάν τώρα το σημείο P μετατοπιστεί κατά μήκος της γραφικής παράστασης στο σημείο M, τότε η ευθεία γραμμή MP θα περιστραφεί γύρω από το σημείο M. Στην περίπτωση αυτή, το Δx θα τείνει στο μηδέν. Από εδώ μπορούμε να διατυπώσουμε τον ορισμό της εφαπτομένης στη γραφική παράσταση μιας συνάρτησης.

Γράφημα εφαπτομένης συνάρτησης

Η εφαπτομένη στο γράφημα της συνάρτησης είναι η οριακή θέση της τομής όταν η αύξηση του ορίσματος τείνει στο μηδέν. Θα πρέπει να γίνει κατανοητό ότι η ύπαρξη της παραγώγου της συνάρτησης f στο σημείο x0 σημαίνει ότι σε αυτό το σημείο της γραφικής παράστασης υπάρχει εφαπτομένοςσε αυτόν.

Στην περίπτωση αυτή, η κλίση της εφαπτομένης θα είναι ίση με την παράγωγο αυτής της συνάρτησης σε αυτό το σημείο f’(x0). Αυτή είναι η γεωμετρική σημασία της παραγώγου. Η εφαπτομένη στη γραφική παράσταση της διαφοροποιήσιμης συνάρτησης f στο σημείο x0 είναι κάποια ευθεία που διέρχεται από το σημείο (x0;f(x0)) και έχει κλίση f’(x0).

Εξίσωση εφαπτομένης

Ας προσπαθήσουμε να πάρουμε την εξίσωση της εφαπτομένης στη γραφική παράσταση κάποιας συνάρτησης f στο σημείο A(x0; f(x0)). Η εξίσωση ευθείας με κλίση k έχει την εξής μορφή:

Αφού η κλίση μας είναι ίση με την παράγωγο f'(x0), τότε η εξίσωση θα πάρει την ακόλουθη μορφή: y = f'(x0)*x + β.

Τώρα ας υπολογίσουμε την τιμή του b. Για να γίνει αυτό, χρησιμοποιούμε το γεγονός ότι η συνάρτηση διέρχεται από το σημείο Α.

f(x0) = f’(x0)*x0 + b, από εδώ εκφράζουμε b και παίρνουμε b = f(x0) - f’(x0)*x0.

Αντικαθιστούμε την τιμή που προκύπτει στην εφαπτομενική εξίσωση:

y = f'(x0)*x + b = f'(x0)*x + f(x0) - f'(x0)*x0 = f(x0) + f'(x0)*(x - x0).

y = f(x0) + f'(x0)*(x - x0).

Εξετάστε το ακόλουθο παράδειγμα: βρείτε την εξίσωση της εφαπτομένης στη γραφική παράσταση της συνάρτησης f (x) \u003d x 3 - 2 * x 2 + 1 στο σημείο x \u003d 2.

2. f(x0) = f(2) = 2 2 - 2*2 2 + 1 = 1.

3. f'(x) = 3*x 2 - 4*x.

4. f'(x0) = f'(2) = 3*2 2 - 4*2 = 4.

5. Αντικαταστήστε τις λαμβανόμενες τιμές στον εφαπτομενικό τύπο, παίρνουμε: y = 1 + 4*(x - 2). Ανοίγοντας τις αγκύλες και φέρνοντας παρόμοιους όρους, παίρνουμε: y = 4*x - 7.

Απάντηση: y = 4*x - 7.

Γενικό σχήμα για τη σύνταξη της εφαπτομένης εξίσωσηςστη γραφική παράσταση της συνάρτησης y = f(x):

1. Προσδιορίστε το x0.

2. Υπολογίστε την f(x0).

3. Υπολογίστε το f'(x)

Εφαπτομένοςείναι μια ευθεία που διέρχεται από ένα σημείο της καμπύλης και συμπίπτει με αυτό σε αυτό το σημείο μέχρι την πρώτη τάξη (Εικ. 1).

Άλλος ορισμός: αυτή είναι η οριακή θέση του τμήματος στο Δ Χ→0.

Εξήγηση: Πάρτε μια ευθεία που τέμνει την καμπύλη σε δύο σημεία: ΑΛΛΑκαι σι(βλέπε εικόνα). Αυτό είναι ένα τμήμα. Θα το περιστρέψουμε δεξιόστροφα μέχρι να έχει μόνο ένα κοινό σημείο με την καμπύλη. Έτσι παίρνουμε μια εφαπτομένη.

Αυστηρός ορισμός εφαπτομένης:

Γράφημα εφαπτομένης συνάρτησης φά, διαφοροποιήσιμο σε ένα σημείο Χσχετικά με, είναι μια ευθεία που διέρχεται από το σημείο ( Χσχετικά με; φά(Χσχετικά με)) και έχοντας κλίση φά′( Χσχετικά με).

Η κλίση έχει ευθεία γραμμή y=kx +σι. Συντελεστής κκαι είναι συντελεστής κλίσηςαυτή η ευθεία γραμμή.

Ο γωνιακός συντελεστής είναι ίσος με την εφαπτομένη της οξείας γωνίας που σχηματίζεται από αυτή την ευθεία με τον άξονα x:

Εδώ η γωνία α είναι η γωνία μεταξύ της ευθείας y=kx +σικαι τη θετική (δηλαδή αριστερόστροφη) φορά του άξονα x. Ονομάζεται γωνία κλίσης ευθεία(Εικ.1 και 2).

Αν η γωνία κλίσης είναι ευθεία y=kx +σιοξεία, τότε η κλίση είναι θετικός αριθμός. Το γράφημα αυξάνεται (Εικ. 1).

Αν η γωνία κλίσης είναι ευθεία y=kx +σιαμβλεία, τότε η κλίση είναι αρνητικός αριθμός. Το γράφημα μειώνεται (Εικ. 2).

Αν η ευθεία είναι παράλληλη προς τον άξονα x, τότε η κλίση της ευθείας είναι μηδέν. Σε αυτή την περίπτωση, η κλίση της ευθείας είναι επίσης μηδέν (αφού η εφαπτομένη του μηδέν είναι μηδέν). Η ευθύγραμμη εξίσωση θα μοιάζει με y = b (Εικ. 3).

Αν η γωνία κλίσης μιας ευθείας είναι 90º (π/2), δηλαδή είναι κάθετη στον άξονα x, τότε η ευθεία δίνεται από την ισότητα x=ντο, που ντο- κάποιο πραγματικό αριθμό (Εικ. 4).

Η εξίσωση της εφαπτομένης στη γραφική παράσταση της συνάρτησηςy = φά(Χ) στο σημείο Χσχετικά με:

Παράδειγμα : Ας βρούμε την εξίσωση της εφαπτομένης στη γραφική παράσταση της συνάρτησης φά(Χ) = Χ 3 – 2Χ 2 + 1 στο σημείο με τετμημένη 2.

Απόφαση.

Ακολουθούμε τον αλγόριθμο.

1) Σημείο αφής Χσχετικά μεισούται με 2. Υπολογίστε φά(Χσχετικά με):

φά(Χσχετικά με) = φά(2) = 2 3 – 2 ∙ 2 2 + 1 = 8 – 8 + 1 = 1

2) Βρείτε φά′( Χ). Για να γίνει αυτό, χρησιμοποιούμε τους τύπους διαφοροποίησης που περιγράφονται στην προηγούμενη ενότητα. Σύμφωνα με αυτούς τους τύπους, Χ 2 = 2Χ, ένα Χ 3 = 3Χ 2. Που σημαίνει:

φά′( Χ) = 3Χ 2 – 2 ∙ 2Χ = 3Χ 2 – 4Χ.

Τώρα, χρησιμοποιώντας την τιμή που προκύπτει φά′( Χ), υπολογίστε φά′( Χσχετικά με):

φά′( Χσχετικά με) = φά′(2) = 3 ∙ 2 2 – 4 ∙ 2 = 12 – 8 = 4.

3) Έχουμε λοιπόν όλα τα απαραίτητα δεδομένα: Χσχετικά με = 2, φά(Χσχετικά με) = 1, φά ′( Χσχετικά με) = 4. Αντικαθιστούμε αυτούς τους αριθμούς στην εφαπτομενική εξίσωση και βρίσκουμε την τελική λύση:

y= φά(Χσχετικά με) + φά′( Χσχετικά με) (x – x o) \u003d 1 + 4 ∙ (x - 2) \u003d 1 + 4x - 8 \u003d -7 + 4x \u003d 4x - 7.

Απάντηση: y \u003d 4x - 7.

Παράδειγμα 1Δίνεται μια λειτουργία φά(Χ) = 3Χ 2 + 4Χ– 5. Ας γράψουμε την εξίσωση της εφαπτομένης στη γραφική παράσταση της συνάρτησης φά(Χ) στο σημείο της γραφικής παράστασης με την τετμημένη Χ 0 = 1.

Απόφαση.Παράγωγος συνάρτησης φά(Χ) υπάρχει για οποιοδήποτε x R . Ας το βρούμε:

= (3Χ 2 + 4Χ– 5)′ = 6 Χ + 4.

Τότε φά(Χ 0) = φά(1) = 2; (Χ 0) = = 10. Η εφαπτομενική εξίσωση έχει τη μορφή:

y = (Χ 0) (Χ – Χ 0) + φά(Χ 0),

y = 10(Χ – 1) + 2,

y = 10Χ – 8.

Απάντηση. y = 10Χ – 8.

Παράδειγμα 2Δίνεται μια λειτουργία φά(Χ) = Χ 3 – 3Χ 2 + 2Χ+ 5. Ας γράψουμε την εξίσωση της εφαπτομένης στη γραφική παράσταση της συνάρτησης φά(Χ), παράλληλα με τη γραμμή y = 2Χ – 11.

Απόφαση.Παράγωγος συνάρτησης φά(Χ) υπάρχει για οποιοδήποτε x R . Ας το βρούμε:

= (Χ 3 – 3Χ 2 + 2Χ+ 5)′ = 3 Χ 2 – 6Χ + 2.

Αφού η εφαπτομένη στη γραφική παράσταση της συνάρτησης φά(Χ) στο σημείο με την τετμημένη ΧΤο 0 είναι παράλληλο στην ευθεία y = 2Χ– 11, τότε η κλίση του είναι 2, δηλ. ( Χ 0) = 2. Βρείτε αυτήν την τετμημένη από την συνθήκη ότι 3 Χ– 6Χ 0 + 2 = 2. Αυτή η ισότητα ισχύει μόνο για Χ 0 = 0 και Χ 0 = 2. Αφού και στις δύο περιπτώσεις φά(Χ 0) = 5, μετά η ευθεία γραμμή y = 2Χ + σιαγγίζει τη γραφική παράσταση της συνάρτησης είτε στο σημείο (0; 5) είτε στο σημείο (2; 5).

Στην πρώτη περίπτωση, η αριθμητική ισότητα είναι αληθής 5 = 2×0 + σι, που σι= 5, και στη δεύτερη περίπτωση, η αριθμητική ισότητα είναι αληθής 5 = 2 × 2 + σι, που σι = 1.

Άρα υπάρχουν δύο εφαπτομένες y = 2Χ+ 5 και y = 2Χ+ 1 στη γραφική παράσταση της συνάρτησης φά(Χ) παράλληλα με τη γραμμή y = 2Χ – 11.

Απάντηση. y = 2Χ + 5, y = 2Χ + 1.

Παράδειγμα 3Δίνεται μια λειτουργία φά(Χ) = Χ 2 – 6Χ+ 7. Ας γράψουμε την εξίσωση της εφαπτομένης στη γραφική παράσταση της συνάρτησης φά(Χ) περνώντας από το σημείο ΕΝΑ (2; –5).

Απόφαση.Οπως και φά(2) –5, μετά το σημείο ΕΝΑδεν ανήκει στο γράφημα της συνάρτησης φά(Χ). Ας είναι Χ 0 - τετμημένη του σημείου επαφής.

Παράγωγος συνάρτησης φά(Χ) υπάρχει για οποιοδήποτε x R . Ας το βρούμε:

= (Χ 2 – 6Χ+ 1)′ = 2 Χ – 6.

Τότε φά(Χ 0) = Χ– 6Χ 0 + 7; (Χ 0) = 2Χ 0 - 6. Η εφαπτομενική εξίσωση έχει τη μορφή:

y = (2Χ 0 – 6)(Χ – Χ 0) + Χ– 6Χ+ 7,

y = (2Χ 0 – 6)Χ– Χ+ 7.

Από το σημείο ΕΝΑανήκει στην εφαπτομένη, τότε η αριθμητική ισότητα είναι αληθής

–5 = (2Χ 0 – 6)×2– Χ+ 7,

που Χ 0 = 0 ή Χ 0 = 4. Αυτό σημαίνει ότι μέσα από το σημείο ΕΝΑείναι δυνατόν να σχεδιάσουμε δύο εφαπτόμενες στη γραφική παράσταση της συνάρτησης φά(Χ).

Αν ένα Χ 0 = 0, τότε η εφαπτομενική εξίσωση έχει τη μορφή y = –6Χ+ 7. Αν Χ 0 = 4, τότε η εφαπτομενική εξίσωση έχει τη μορφή y = 2Χ – 9.

Απάντηση. y = –6Χ + 7, y = 2Χ – 9.

Παράδειγμα 4Δεδομένες λειτουργίες φά(Χ) = Χ 2 – 2Χ+ 2 και σολ(Χ) = –Χ 2 - 3. Ας γράψουμε την εξίσωση της κοινής εφαπτομένης στις γραφικές παραστάσεις αυτών των συναρτήσεων.

Απόφαση.Ας είναι Χ 1 - τετμημένη του σημείου επαφής της επιθυμητής γραμμής με το γράφημα της συνάρτησης φά(Χ), ένα Χ 2 - τετμημένη του σημείου επαφής της ίδιας ευθείας με τη γραφική παράσταση της συνάρτησης σολ(Χ).

Παράγωγος συνάρτησης φά(Χ) υπάρχει για οποιοδήποτε x R . Ας το βρούμε:

= (Χ 2 – 2Χ+ 2)′ = 2 Χ – 2.

Τότε φά(Χ 1) = Χ– 2Χ 1 + 2; (Χ 1) = 2Χ 1 - 2. Η εφαπτομενική εξίσωση έχει τη μορφή:

y = (2Χ 1 – 2)(Χ – Χ 1) + Χ– 2Χ 1 + 2,

y = (2Χ 1 – 2)Χ – Χ+ 2. (1)

Ας βρούμε την παράγωγο της συνάρτησης σολ(Χ):

= (–Χ 2 – 3)′ = –2 Χ.