Aritmetik ilerlemenin ilk 15 sayısının toplamı. Örneklerle aritmetik ilerleme
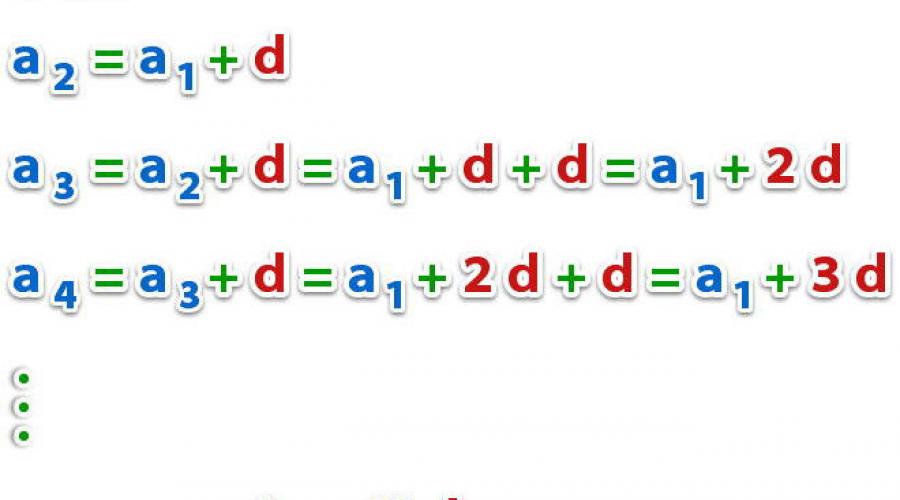
Ayrıca okuyun
Veya aritmetik, özellikleri okul cebir dersinde incelenen bir tür sıralı sayısal dizidir. Bu makale, bir aritmetik ilerlemenin toplamının nasıl bulunacağı sorusunu ayrıntılı olarak tartışmaktadır.
Bu ilerleme nedir?
Soruyu (bir aritmetik ilerlemenin toplamı nasıl bulunur) düşünmeye geçmeden önce, neyin tartışılacağını anlamaya değer.
Her bir önceki sayıdan bir değer ekleyerek (çıkararak) elde edilen herhangi bir gerçek sayı dizisine cebirsel (aritmetik) ilerleme denir. Matematik diline çevrilen bu tanım şu şekli alır:
Burada i, a i satırının elemanının sıra sayısıdır. Böylece, sadece bir tohum bilerek, tüm seriyi kolayca yeniden oluşturabilirsiniz. Formüldeki d parametresine ilerleme farkı denir.
Söz konusu sayı dizisi için aşağıdaki eşitliğin geçerli olduğu kolayca gösterilebilir:
bir n = bir 1 + d * (n - 1).
Yani, n'inci elemanın değerini sırayla bulmak için, d farkını ilk elemana 1 n-1 kez ekleyin.

Aritmetik bir ilerlemenin toplamı nedir: formül
Belirtilen miktar için bir formül vermeden önce, basit bir özel durumu düşünmeye değer. 1'den 10'a kadar bir doğal sayılar dizisi verildiğinde, toplamlarını bulmanız gerekir. Progresyonda (10) üye sayısı az olduğu için problemi baştan çözmek, yani tüm öğeleri sırayla toplamak mümkündür.
S 10 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55.
İlginç bir şeyi dikkate almakta fayda var: her terim bir sonrakinden aynı d = 1 değeriyle farklı olduğundan, o zaman birincinin onuncu, ikincinin dokuzuncu vb. ikili toplamı aynı sonucu verecektir. Yok canım:
11 = 1+10 = 2+9 = 3+8 = 4+7 = 5+6.
Gördüğünüz gibi, bu toplamlardan sadece 5 tanesi var, yani dizideki eleman sayısından tam olarak iki kat daha az. Daha sonra toplam sayısını (5) her toplamın (11) sonucu ile çarparak ilk örnekte elde edilen sonuca ulaşacaksınız.
Bu akıl yürütmeyi genelleştirirsek, aşağıdaki ifadeyi yazabiliriz:
S n = n * (a 1 + bir n) / 2.
Bu ifade, tüm öğeleri arka arkaya toplamanın hiç gerekli olmadığını, ilk a 1 ve son a n'nin değerini ve toplam n terim sayısını bilmek yeterlidir.
Gauss'un bu eşitliği ilk olarak öğretmeni tarafından belirlenen bir probleme çözüm ararken düşündüğüne inanılıyor: İlk 100 tamsayıyı toplayın.

m'den n'ye kadar olan elementlerin toplamı: formül
Önceki paragrafta verilen formül, bir aritmetik ilerlemenin (ilk elemanlar) toplamının nasıl bulunacağı sorusuna bir cevap verir, ancak çoğu zaman problemlerde, ilerlemenin ortasındaki bir dizi sayıyı toplamak gerekir. Nasıl yapılır?
Bu soruyu yanıtlamanın en kolay yolu şu örneği dikkate almaktır: m-th'den n-th'e kadar olan terimlerin toplamını bulmamız gereksin. Sorunu çözmek için, ilerlemenin m'den n'ye belirli bir segmenti yeni bir sayısal dizi şeklinde sunulmalıdır. Bu gösterimde, birinci terim a m olacak ve a n, n- (m-1) olacaktır. Bu durumda, toplam için standart formülü uygulayarak aşağıdaki ifadeyi alırsınız:
S m n = (n - m + 1) * (bir m + bir n) / 2.
Formül kullanma örneği
Aritmetik bir ilerlemenin toplamının nasıl bulunacağını bilmek, verilen formülleri kullanmanın basit bir örneğini düşünmeye değer.
Aşağıda sayısal bir dizi var, 5. ile başlayan ve 12. ile biten üyelerinin toplamını bulmalısınız:
Verilen sayılar, d farkının 3'e eşit olduğunu göstermektedir. n'inci eleman için ifadeyi kullanarak, ilerlemenin 5. ve 12. terimlerinin değerlerini bulabilirsiniz. Çıkıyor:
a 5 = a 1 + d * 4 = -4 + 3 * 4 = 8;
a 12 = a 1 + d * 11 = -4 + 3 * 11 = 29.
Dikkate alınan cebirsel ilerlemenin sonundaki sayıların değerlerini bilmek ve ayrıca satırdaki hangi sayıları işgal ettiklerini bilmek, önceki paragrafta elde edilen toplam formülü kullanabilirsiniz. Ortaya çıkacak:
S 5 12 = (12 - 5 + 1) * (8 + 29) / 2 = 148.
Bu değerin farklı şekilde elde edilebileceğini belirtmekte fayda var: önce standart formülü kullanarak ilk 12 öğenin toplamını bulun, ardından aynı formülü kullanarak ilk 4 öğenin toplamını hesaplayın, ardından ikinciyi ilk toplamdan çıkarın.
Genel bir eğitim okulunda (9. sınıf) cebir okurken, önemli konulardan biri, ilerlemeleri - geometrik ve aritmetik içeren sayısal dizilerin incelenmesidir. Bu yazıda aritmetik ilerlemeyi ve çözümlü örnekleri ele alacağız.
aritmetik ilerleme nedir?
Bunu anlamak için, düşünülen ilerlemenin bir tanımını vermek ve ayrıca problemlerin çözümünde daha fazla kullanılacak temel formülleri vermek gerekir.
Bazı cebirsel dizilerde 1. terimin 6'ya ve 7. terimin 18'e eşit olduğu bilinmektedir. Farkı bulmak ve bu diziyi 7. terime geri yüklemek gerekir.
Bilinmeyen terimi belirlemek için formülü kullanalım: a n = (n - 1) * d + a 1. İçinde koşuldan bilinen verileri, yani a 1 ve 7 sayılarını değiştiririz, elimizde: 18 = 6 + 6 * d. Bu ifadeden farkı kolayca hesaplayabilirsiniz: d = (18 - 6) / 6 = 2. Böylece problemin ilk kısmını cevaplamış olduk.
7 terime kadar bir diziyi geri yüklemek için, cebirsel bir ilerlemenin tanımını kullanmalısınız, yani a 2 = a 1 + d, a 3 = a 2 + d, vb. Sonuç olarak, tüm diziyi geri yükleriz: a 1 = 6, a 2 = 6 + 2 = 8, a 3 = 8 + 2 = 10, a 4 = 10 + 2 = 12, a 5 = 12 + 2 = 14 , 6 = 14 + 2 = 16, 7 = 18.
Örnek # 3: ilerleme yapmak

Sorunun durumunu daha da karmaşıklaştıralım. Şimdi aritmetik ilerlemenin nasıl bulunacağı sorusuna cevap vermek gerekiyor. Aşağıdaki örneği verebilirsiniz: iki sayı verilmiş, örneğin - 4 ve 5. Cebirsel bir dizileme yapmak gerekir, böylece bunların arasına üç terim daha sığar.
Bu problemi çözmeye başlamadan önce, verilen sayıların gelecekteki ilerlemede hangi yeri işgal edeceğini anlamak gerekir. Aralarında üç terim daha olacağı için 1 = -4 ve 5 = 5. Bunu belirledikten sonra, öncekine benzer olan probleme geçiyoruz. Yine, n'inci terim için şu formülü kullanırız: a 5 = a 1 + 4 * d. Nereden: d = (a 5 - a 1) / 4 = (5 - (-4)) / 4 = 2.25. Burada farkın tamsayı değerini almadık, ancak bu bir rasyonel sayıdır, bu nedenle cebirsel ilerleme formülleri aynı kalır.
Şimdi bulunan farkı 1'e ekleyin ve ilerlemenin eksik üyelerini geri yükleyin. Şunu elde ederiz: a 1 = - 4, a 2 = - 4 + 2.25 = - 1.75, a 3 = -1.75 + 2.25 = 0.5, a 4 = 0.5 + 2.25 = 2.75, a 5 = 2.75 + 2.25 = 5 Sorunun durumu ile.
Örnek # 4: ilerlemenin ilk terimi

Çözümlü aritmetik ilerleme örnekleri vermeye devam edelim. Önceki tüm problemlerde, cebirsel ilerlemenin ilk sayısı biliniyordu. Şimdi farklı türde bir problem düşünün: 15 = 50 ve 43 = 37 olmak üzere iki sayı verilsin. Bu dizinin başladığı sayıyı bulmak gerekir.
Şimdiye kadar kullanılan formüller, a 1 ve d bilgisini varsayar. Sorun bildiriminde bu sayılar hakkında hiçbir şey bilinmiyor. Yine de, hakkında bilgi bulunan her üye için ifadeler yazıyoruz: a 15 = a 1 + 14 * d ve a 43 = a 1 + 42 * d. 2 bilinmeyen niceliğin (a 1 ve d) olduğu iki denklem alındı. Bu, problemin bir lineer denklem sistemini çözmeye indirgendiği anlamına gelir.
Bu sistemi çözmenin en kolay yolu, her denklemde bir 1 ifade etmek ve ardından elde edilen ifadeleri karşılaştırmaktır. İlk denklem: a 1 = 15 - 14 * d = 50 - 14 * d; ikinci denklem: a 1 = a 43 - 42 * d = 37 - 42 * d. Bu ifadeleri eşitleyerek, şunu elde ederiz: 50 - 14 * d = 37 - 42 * d, bu nedenle fark d = (37 - 50) / (42 - 14) = - 0.464 (sadece 3 ondalık basamak verilir).
d'yi bilerek, 1 için yukarıdaki 2 ifadeden herhangi birini kullanabilirsiniz. Örneğin, birincisi: a 1 = 50 - 14 * d = 50 - 14 * (- 0.464) = 56.496.
Sonuç hakkında şüpheniz varsa, kontrol edebilirsiniz, örneğin, koşulda belirtilen ilerlemenin 43 terimini belirleyin. Şunu elde ederiz: a 43 = a 1 + 42 * d = 56.496 + 42 * (- 0.464) = 37.008. Küçük bir hata, hesaplamaların binde birine yuvarlama kullanması gerçeğinden kaynaklanmaktadır.
Örnek # 5: miktar
Şimdi aritmetik bir ilerlemenin toplamı için çözümler içeren bazı örneklere bakalım.
Aşağıdaki formun sayısal bir dizisi verilsin: 1, 2, 3, 4, ...,. Bu 100 sayının toplamını nasıl hesaplarsınız?
Bilgisayar teknolojisinin gelişmesi sayesinde, bu sorunu çözmek, yani bir kişi Enter tuşuna basar basmaz bilgisayarın yapacağı tüm sayıları sırayla toplamak mümkündür. Ancak, sunulan sayı dizisinin cebirsel bir ilerleme olduğuna ve farkının 1 olduğuna dikkat edersek, sorun akılda çözülebilir. Toplam için formülü uygularsak, şunu elde ederiz: S n = n * (a 1 + bir) / 2 = 100 * (1 + 100) / 2 = 5050.
Bu sorunun "Gauss" olarak adlandırılması ilginçtir, çünkü 18. yüzyılın başında ünlü Alman, henüz 10 yaşında olmasına rağmen, birkaç saniye içinde kafasında çözebildi. Çocuk bir cebirsel ilerlemenin toplamının formülünü bilmiyordu, ancak dizinin kenarlarındaki sayıları çiftler halinde toplarsanız, her zaman bir sonuç elde ettiğinizi fark etti, yani 1 + 100 = 2 + 99 = 3 + 98 = ... ve bu miktarların tam olarak 50 (100/2) olacağı için, doğru cevabı almak için 50 ile 101'i çarpmak yeterlidir.

Örnek # 6: n'den m'ye kadar olan üyelerin toplamı
Bir aritmetik ilerlemenin toplamının bir başka tipik örneği şudur: bir dizi sayı verildiğinde: 3, 7, 11, 15, ..., 8'den 14'e kadar olan üyelerinin toplamının neye eşit olacağını bulmanız gerekir.
Problem iki şekilde çözülür. Bunlardan ilki, 8'den 14'e kadar bilinmeyen terimleri bulmayı ve ardından bunların sıralı toplamını içerir. Birkaç terim olduğu için bu yöntem yeterince zahmetli değildir. Bununla birlikte, bu sorunun daha evrensel olan ikinci yöntemle çözülmesi önerilmektedir.
Buradaki fikir, n> m'nin tamsayı olduğu m ve n terimleri arasındaki cebirsel ilerlemenin toplamı için bir formül elde etmektir. Her iki durum için de toplam için iki ifade yazalım:
- S m = m * (bir m + bir 1) / 2.
- S n = n * (bir n + bir 1) / 2.
n> m olduğundan, 2 toplamının birinciyi içerdiği açıktır. Son sonuç, bu toplamlar arasındaki farkı alıp buna a m terimini eklersek (fark alınması durumunda S n toplamından çıkarılır), o zaman soruna gerekli cevabı aldığımız anlamına gelir. Şunlara sahibiz: S mn = S n - S m + am = n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am = a 1 * (n - m) / 2 + an * n / 2 + am * (1- m / 2). Bu ifadede, formülleri n ve a m'nin yerine koymak gerekir. Sonra şunu elde ederiz: S mn = a 1 * (n - m) / 2 + n * (a 1 + (n - 1) * d) / 2 + (a 1 + (m - 1) * d) * (1 - m / 2) = 1 * (n - m + 1) + d * n * (n - 1) / 2 + d * (3 * m - m 2 - 2) / 2.
Ortaya çıkan formül biraz zahmetlidir; bununla birlikte, S mn'nin toplamı yalnızca n, m, a 1 ve d'ye bağlıdır. Bizim durumumuzda a 1 = 3, d = 4, n = 14, m = 8. Bu sayıları değiştirerek şunu elde ederiz: S mn = 301.

Verilen çözümlerden de anlaşılacağı gibi, tüm problemler n'inci terim için ifade ve birinci terimler kümesinin toplamı için formül bilgisine dayanmaktadır. Bu sorunlardan herhangi birinin çözümüne geçmeden önce, durumu dikkatlice okumanız, neyin bulunması gerektiğini açıkça anlamanız ve ancak bundan sonra çözüme geçmeniz önerilir.
Diğer bir ipucu ise basitlik için çabalamaktır, yani bir soruyu karmaşık matematiksel hesaplamalar kullanmadan cevaplayabiliyorsanız, o zaman tam olarak bunu yapmanız gerekir, çünkü bu durumda hata yapma olasılığı daha azdır. Örneğin, çözüm # 6 ile bir aritmetik ilerleme örneğinde, S mn = n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am formülünde durabilir ve ara verebilir genel sorunu ayrı alt görevlere ayırın (bu durumda, önce üyeleri bir ve am olarak bulun).
Elde edilen sonuç hakkında şüphe varsa, verilen bazı örneklerde olduğu gibi kontrol edilmesi önerilir. Aritmetik ilerlemeyi nasıl bulacağımızı bulduk. Bunu anlarsan, o kadar da zor değil.
Karar vermeye başlamadan önce aritmetik ilerleme problemleri, bir sayı dizisinin ne olduğunu düşünün, çünkü aritmetik bir ilerleme, bir sayı dizisinin özel bir durumudur.
Sayısal dizi, her elemanın kendi sıra numarasına sahip olduğu sayısal bir dizidir.... Bu kümenin elemanları dizinin elemanları olarak adlandırılır. Dizi öğesinin sıra numarası, dizinle gösterilir:
Dizinin ilk elemanı;
Dizinin beşinci elemanı;
- dizinin "n'inci" öğesi, yani. "sıradaki" öğe
Bir dizi öğesinin değeri ile sıra sayısı arasında bir ilişki vardır. Bu nedenle, bir diziyi, argümanı dizinin bir öğesinin sıra sayısı olan bir fonksiyon olarak düşünebiliriz. Başka bir deyişle, diyebiliriz ki bir dizi, doğal bir argümanın bir işlevidir:
Sıra üç şekilde ayarlanabilir:
1 . Sıra bir tablo kullanılarak ayarlanabilir. Bu durumda, dizinin her bir üyesinin değerini ayarladık.
Örneğin, Birisi kişisel zaman yönetimi yapmaya karar verdi ve başlamak için hafta boyunca VKontakte'de ne kadar zaman harcadığını hesaplayın. Tablodaki zamanı yazarken, yedi elementten oluşan bir dizi alacaktır:

Tablonun ilk satırı haftanın gün sayısını, ikincisi - dakika cinsinden zamanı içerir. Görüyoruz ki, Pazartesi günü Birisi VKontakte'de 125 dakika, yani Perşembe - 248 dakika ve yani Cuma günü sadece 15 dakika geçirdi.
2 . Dizi, n'inci terim formülü kullanılarak belirtilebilir.
Bu durumda, dizi elemanının değerinin sayısına bağımlılığı, doğrudan bir formül şeklinde ifade edilir.
Örneğin, eğer öyleyse
![]()
![]()
Belirli bir sayıya sahip bir dizinin bir elemanının değerini bulmak için, eleman numarasını n'inci terimin formülünde yerine koyarız.
Argümanın değeri biliniyorsa, bir fonksiyonun değerini bulmamız gerekirse de aynısını yaparız. Argümanın değerini fonksiyonun denkleminde yerine koyarız:
Örneğin, ![]() , sonra
, sonra
Bir kez daha, bir dizide, rastgele bir sayısal işlevin aksine, yalnızca bir doğal sayının bir argüman olabileceğini not ediyorum.
3 ... Bir dizi, numaralandırılmış dizi üyesinin değerinin önceki üyelerin değerine bağımlılığını ifade eden bir formül kullanılarak belirtilebilir. Bu durumda değerini bulmak için sadece dizi elemanının numarasını bilmek bizim için yeterli değildir. Dizinin ilk üyesini veya ilk birkaç üyesini belirtmemiz gerekiyor.
Örneğin, sırayı düşünün ![]() ,
, ![]()
Dizinin üyelerinin değerlerini bulabiliriz sıraylaüçüncüden başlayarak:
Yani dizinin n'inci üyesinin değerini her seferinde bulmak için önceki ikisine geri dönüyoruz. Bu sıralama yöntemine denir tekrarlayan, Latince kelimeden tekrar eden- geri gel.
Şimdi aritmetik bir ilerleme tanımlayabiliriz. Aritmetik ilerleme, bir sayı dizisinin basit bir özel durumudur.
Aritmetik ilerleme her bir üyesi ikinciden başlayarak bir öncekine eşit olan ve aynı sayıya eklenen sayısal bir dizidir.

numara aranır aritmetik ilerleme farkı... Aritmetik ilerlemedeki fark pozitif, negatif veya sıfır olabilir.
Eğer başlık = "(! DİL: d> 0">, то каждый член арифметической прогрессии больше предыдущего, и прогрессия является !} artan.
Örneğin, 2; 5; sekiz; on bir;...
Eğer aritmetik ilerlemenin her bir üyesi bir öncekinden küçükse ve ilerleme azalan.
Örneğin, 2; -1; -4; -7; ...
Eğer, o zaman dizinin tüm üyeleri aynı sayıya eşitse ve dizi şu şekildedir: sabit.
Örneğin, 2; 2; 2; 2; ...
Aritmetik ilerlemenin ana özelliği:
Resime bakalım.
bunu görüyoruz
![]() , ve aynı zamanda
, ve aynı zamanda
![]()
Bu iki eşitliği toplayarak şunu elde ederiz:
![]() .
.
Eşitliğin her iki tarafını da 2'ye bölün:

Böylece, ikinciden başlayarak aritmetik ilerlemenin her bir üyesi, iki komşu olanın aritmetik ortalamasına eşittir:

Ayrıca, beri
![]() , ve aynı zamanda
, ve aynı zamanda
![]() , sonra
, sonra
![]() , ve bu nedenle
, ve bu nedenle
 Başlık = "(! LANG: k> l ile başlayan aritmetik dizinin her bir üyesi">, равен среднему арифметическому двух равноотстоящих.
!}
Başlık = "(! LANG: k> l ile başlayan aritmetik dizinin her bir üyesi">, равен среднему арифметическому двух равноотстоящих.
!}
inci üyenin formülü.
Aritmetik ilerlemenin üyeleri için aşağıdaki ilişkilerin geçerli olduğunu görüyoruz:
![]()
![]()
ve sonunda
Aldık n'inci terimin formülü.
![]()
ÖNEMLİ! Aritmetik ilerlemenin herhangi bir üyesi ve cinsinden ifade edilebilir. İlk terimi ve aritmetik ilerlemenin farkını bilerek, terimlerinden herhangi birini bulabilirsiniz.
Bir aritmetik ilerlemenin n üyesinin toplamı.
Keyfi bir aritmetik dizide, uç noktadan eşit uzaklıkta bulunan üyelerin toplamları birbirine eşittir:
n terimli bir aritmetik ilerleme düşünün. Bu ilerlemenin n üyesinin toplamı olsun.
Dizinin üyelerini önce sayıların artan sırasına, sonra da azalan sıraya göre düzenleyelim:

Çiftler halinde ekleyelim:
Her parantez içindeki toplam eşittir, çift sayısı n'dir.
Alırız:
![]()

Yani, bir aritmetik ilerlemenin n üyesinin toplamı şu formüllerle bulunabilir:
Düşünmek aritmetik ilerleme için problem çözme.
1 . Dizi, n'inci terim formülüyle verilir: . Bu dizinin aritmetik bir ilerleme olduğunu kanıtlayın.
Dizinin iki komşu elemanı arasındaki farkın aynı sayıya eşit olduğunu ispatlayalım.
Dizinin iki komşu üyesi arasındaki farkın sayılarına bağlı olmadığını ve sabit olduğunu anladık. Bu nedenle, tanım gereği, bu dizi aritmetik bir ilerlemedir.
2 . Size aritmetik bir ilerleme verilir -31; -27; ...
a) İlerlemenin 31 üyesini bulun.
b) 41 sayısının bu diziye dahil olup olmadığını belirleyin.
a) Bunu görüyoruz;
İlerlememiz için n'inci terimin formülünü yazalım.
Genel olarak ![]()
bizim durumumuzda ![]() , Öyleyse
, Öyleyse ![]()
Alırız:
B) 41'in dizinin bir üyesi olduğunu varsayalım. Numarasını bulalım. Bunu yapmak için denklemi çözüyoruz:
![]()
n'nin doğal değerini aldık, bu nedenle, evet, 41 sayısı ilerlemenin bir üyesidir. n'nin bulunan değeri bir doğal sayı olmasaydı, 41 sayısının dizinin bir üyesi OLMADIĞINI söylerdik.
3 ... a) 2 ve 8 sayıları arasına, verilen sayılarla birlikte aritmetik bir ilerleme yapacak şekilde 4 sayı girin.
b) Ortaya çıkan ilerlemenin üyelerinin toplamını bulun.
a) 2 ve 8 sayıları arasına dört sayı girin:

6 üye ile aritmetik bir ilerleme elde ettik. ![]()
Bu ilerlemenin farkını bulalım. Bunu yapmak için, n'inci terim için formülü kullanacağız:
![]()
Artık sayıların değerlerini bulmak çok kolay:
3,2; 4,4; 5,6; 6,8
B) 
Cevap: a) evet; b) 30
4. Kamyon, 240 ton ağırlığındaki bir yığın kırma taşı taşıyor ve taşıma oranını aynı ton kadar artırıyor. İlk gün 2 ton kırmataş taşındığı biliniyor. Tüm işler 15 günde tamamlanırsa, on ikinci günde kaç ton moloz taşındığını belirleyin.
Sorunun durumuna göre kamyonun taşıdığı moloz miktarı her gün aynı sayıda artıyor. Bu nedenle, aritmetik bir ilerleme ile uğraşıyoruz.
Bu sorunu aritmetik bir ilerleme açısından formüle edelim.
İlk gün 2 ton kırma taş taşındı: a_1 = 2.
Tüm işler 15 gün içinde yapıldı:.
Kamyon, 240 ton ağırlığında bir yığın kırma taş taşıyor:
Bulmalıyız.
İlk olarak, ilerlemedeki farkı bulun. İlerlemenin n teriminin toplamı için formülü kullanalım.

Bizim durumumuzda:
![]()
![]()
 Evet, evet: aritmetik ilerleme sizin için bir oyuncak değil :)
Evet, evet: aritmetik ilerleme sizin için bir oyuncak değil :) Pekala, arkadaşlar, eğer bu metni okuyorsanız, o zaman dahili kap-kanıtlar bana aritmetik ilerlemenin ne olduğunu henüz bilmediğinizi söylüyor, ama gerçekten (hayır, bunun gibi: ÇOoooooo!) Bilmek istiyorsunuz. Bu nedenle uzun tanıtımlarla sizi üzmeyeceğim ve hemen işe koyulacağım.
Birkaç örnekle başlayalım. Birkaç sayı kümesi düşünün:
- 1; 2; 3; 4; ...
- 15; 20; 25; 30; ...
- $ \ kare (2); \ 2 \ kare (2); \ 3 \ kare (2); ... $
Tüm bu setlerin ortak noktası nedir? İlk bakışta, hiçbir şey. Ama aslında bir şey var. Yani: sonraki her eleman bir öncekinden aynı sayıda farklıdır.
Kendin için yargıla. İlk küme, her biri bir öncekinden daha fazla olan ardışık sayılardır. İkinci durumda, bitişik sayılar arasındaki fark zaten beşe eşittir, ancak bu fark hala sabittir. Üçüncü durumda, genel olarak kökler. Ancak, $ 2 \ sqrt (2) = \ sqrt (2) + \ sqrt (2) $ ve $ 3 \ sqrt (2) = 2 \ sqrt (2) + \ sqrt (2) $, yani. ve bu durumda, sonraki her öğe $ \ sqrt (2) $ ile artar (ve bu sayının irrasyonel olduğundan korkmayın).
Yani: tüm bu dizilere aritmetik ilerlemeler denir. Kesin bir tanım yapalım:
Tanım. Bir sonrakinin bir öncekinden tam olarak aynı miktarda farklı olduğu bir sayı dizisine aritmetik ilerleme denir. Sayıların farklılık gösterdiği miktara ilerleme farkı denir ve çoğunlukla $ d $ harfi ile gösterilir.
Tanımlama: $ \ sol (((a) _ (n)) \ sağ) $ - ilerlemenin kendisi, $ d $ - farkı.
Ve sadece birkaç önemli açıklama. İlk olarak, sadece düzenli sayı dizisi: kesinlikle yazıldığı sıraya göre okunmalarına izin verilir - başka bir şey değil. Numaraları yeniden düzenleyemez veya değiştiremezsiniz.
İkincisi, dizinin kendisi ya sonlu ya da sonsuz olabilir. Örneğin, (1; 2; 3) kümesi açıkça sonlu bir aritmetik ilerlemedir. Ancak ruhta bir şeyler yazarsanız (1; 2; 3; 4; ...) - bu zaten sonsuz bir ilerlemedir. Dördünden sonraki üç nokta, olduğu gibi, hala birkaç sayı olduğunu ima ediyor. Sonsuz sayıda, örneğin. :)
İlerlemelerin arttığını ve azaldığını da belirtmek isterim. Artanları zaten gördük - aynı küme (1; 2; 3; 4; ...). Ve işte azalan ilerleme örnekleri:
- 49; 41; 33; 25; 17; ...
- 17,5; 12; 6,5; 1; −4,5; −10; ...
- $ \ kare (5); \ \ kare (5) -1; \ \ kare (5) -2; \ \ kare (5) -3; ... $
Tamam, tamam: Bu son örnek fazla karmaşık görünebilir. Ama gerisini, anladığınızı düşünüyorum. Bu nedenle, yeni tanımlar sunacağız:
Tanım. Bir aritmetik ilerleme denir:
- sonraki her öğe bir öncekinden daha büyükse artan;
- aksine, sonraki her öğe bir öncekinden daha azsa azalır.
Ek olarak, "durağan" diziler vardır - bunlar aynı tekrar eden sayıdan oluşur. Örneğin, (3; 3; 3; ...).
Geriye tek bir soru kalıyor: Artan bir ilerlemeyi azalan bir ilerlemeden nasıl ayırt edebiliriz? Neyse ki, hepsi $ d $ sayısının işaretine bağlıdır, yani. fark ilerlemesi:
- $ d \ gt 0 $ ise, ilerleme artıyor;
- $ d \ lt 0 $ ise, ilerleme açıkça azalmaktadır;
- Son olarak, $ d = 0 $ durumu vardır - bu durumda tüm ilerleme, aynı sayıların sabit bir dizisine indirgenir: (1; 1; 1; 1; ...), vb.
Yukarıda verilen üç azalan ilerleme için $ d $ farkını hesaplamaya çalışalım. Bunu yapmak için, herhangi iki bitişik öğeyi (örneğin, birinci ve ikinci) almak ve soldaki sayıyı sağdaki sayıdan çıkarmak yeterlidir. Bunun gibi görünecek:
- 41−49=−8;
- 12−17,5=−5,5;
- $ \ kare (5) -1- \ kare (5) = - 1 $.
Gördüğünüz gibi, her üç durumda da fark gerçekten negatif çıktı. Artık tanımları az çok çözdüğümüze göre, ilerlemelerin nasıl tanımlandığını ve özelliklerinin neler olduğunu çözmenin zamanı geldi.
İlerleme üyeleri ve tekrarlayan formül
Dizilerimizin elemanları değiştirilemeyeceği için numaralandırılabilirler:
\ [\ sol (((a) _ (n)) \ sağ) = \ sol \ (((a) _ (1)), \ ((a) _ (2)), ((a) _ (3 )), ... \ sağ \) \]
Bu kümenin bireysel öğelerine ilerlemenin üyeleri denir. Bir sayı ile gösterilirler: birinci terim, ikinci terim, vb.
Ek olarak, zaten bildiğimiz gibi, ilerlemenin komşu üyeleri şu formülle ilişkilendirilir:
\ [((a) _ (n)) - ((a) _ (n-1)) = d \ Sağ Ok ((a) _ (n)) = ((a) _ (n-1)) + d \]
Kısacası, dizideki $ n $ th terimini bulmak için $ n-1 $ th terimini ve $ d $ farkını bilmeniz gerekir. Böyle bir formüle tekrarlayan denir, çünkü onun yardımı ile sadece bir öncekini (ve aslında - öncekilerin hepsini) bilerek herhangi bir sayı bulabilirsiniz. Bu çok elverişsizdir, bu nedenle herhangi bir hesaplamayı ilk terime ve farka indirgeyen daha zor bir formül vardır:
\ [((a) _ (n)) = ((a) _ (1)) + \ sol (n-1 \ sağ) d \]
Elbette bu formülle zaten tanışmışsınızdır. Her türlü referans kitabında ve reshebnik'te vermeyi severler. Ve matematikle ilgili herhangi bir mantıklı ders kitabında, ilklerden birine gider.
Yine de, biraz pratik yapmamızı öneririm.
Sorun numarası 1. $ \ left (((a) _ (n)) \ sağ) $ aritmetik ilerlemesinin ilk üç terimini yazın, eğer $ ((a) _ (1)) = 8, d = -5 $.
Çözüm. Böylece, $ ((a) _ (1)) = 8 $ ilk terimini ve $ d = -5 $ progresyonunun farkını biliyoruz. Şimdi verilen formülü kullanalım ve $ n = 1 $, $ n = 2 $ ve $ n = 3 $ yerine koyalım:
\ [\ başla (hizala) & ((a) _ (n)) = ((a) _ (1)) + \ sol (n-1 \ sağ) d; \\ & ((a) _ (1)) = ((a) _ (1)) + \ sol (1-1 \ sağ) d = ((a) _ (1)) = 8; \\ & ((a) _ (2)) = ((a) _ (1)) + \ sol (2-1 \ sağ) d = ((a) _ (1)) + d = 8-5 = 3; \\ & ((a) _ (3)) = ((a) _ (1)) + \ sol (3-1 \ sağ) d = ((a) _ (1)) + 2d = 8-10 = -2. \\ \ bitiş (hizalama) \]
Cevap: (8; 3; -2)
Bu kadar! Lütfen dikkat: ilerlememiz azalıyor.
Tabii ki, $ n = 1 $ ikame edilemezdi - ilk terim zaten bizim tarafımızdan biliniyor. Ancak yerine bir tane koyarak formülümüzün birinci terim için bile işe yaramasını sağladık. Diğer durumlarda, hepsi önemsiz aritmetiklere indirgendi.
Sorun numarası 2. Yedinci terimi -40 ve on yedinci terimi -50 ise aritmetik ilerlemenin ilk üç terimini yazın.
Çözüm. Sorunun durumunu olağan terimlerle yazalım:
\ [((a) _ (7)) = - 40; \ dörtlü ((a) _ (17)) = - 50. \]
\ [\ sol \ (\ başla (hizala) & ((a) _ (7)) = ((a) _ (1)) + 6d \\ & ((a) _ (17)) = ((a) _ (1)) + 16d \\ \ bitiş (hizalama) \ sağa. \]
\ [\ sol \ (\ başlangıç (hizalama) & ((a) _ (1)) + 6d = -40 \\ & ((a) _ (1)) + 16d = -50 \\ \ bitiş (hizalama) \ sağ. \]
Sistemin işaretini koydum çünkü bu gereksinimlerin aynı anda yerine getirilmesi gerekiyor. Ve şimdi, birinciyi ikinci denklemden çıkarırsak (bir sistemimiz olduğu için bunu yapma hakkımız var), şunu elde ederiz:
\ [\ başla (hizala) & ((a) _ (1)) + 16d- \ sol (((a) _ (1)) + 6d \ sağ) = - 50- \ sol (-40 \ sağ); \\ & ((a) _ (1)) + 16d - ((a) _ (1)) - 6d = -50 + 40; \\ & 10d = -10; \\ & d = -1. \\ \ bitiş (hizalama) \]
İlerlemedeki farkı bu kadar kolay bulduk! Bulunan sayıyı sistemin denklemlerinden herhangi birine yerleştirmek için kalır. Örneğin, ilkinde:
\ [\ başlangıç (matris) ((a) _ (1)) + 6d = -40; \ dörtlü d = -1 \\ \ Downarrow \\ ((a) _ (1)) - 6 = -40; \\ ((a) _ (1)) = - 40 + 6 = -34. \\ \ bitiş (matris) \]
Şimdi, birinci terimi ve farkı bilerek, ikinci ve üçüncü terimleri bulmak için kalır:
\ [\ başla (hizala) & ((a) _ (2)) = ((a) _ (1)) + d = -34-1 = -35; \\ & ((a) _ (3)) = ((a) _ (1)) + 2d = -34-2 = -36. \\ \ bitiş (hizalama) \]
Hazır! Problem çözüldü.
Cevap: (-34; -35; -36)
İlerlemenin keşfettiğimiz ilginç bir özelliğine dikkat edin: $ n $ th ve $ m $ th terimlerini alıp birbirinden çıkarırsak, ilerlemenin farkını $ n-m $ sayısıyla çarparak elde ederiz:
\ [((a) _ (n)) - ((a) _ (m)) = d \ cdot \ sol (n-m \ sağ) \]
Kesinlikle bilmeniz gereken basit ama çok kullanışlı bir özellik - onun yardımıyla, ilerlemelerdeki birçok sorunun çözümünü önemli ölçüde hızlandırabilirsiniz. İşte en önemli örnek:
Sorun numarası 3. Aritmetik dizinin beşinci terimi 8.4'tür ve onuncu terimi 14.4'tür. Bu ilerlemenin on beşinci terimini bulun.
Çözüm. $ ((a) _ (5)) = 8.4 $, $ ((a) _ (10)) = 14,4 $ olduğundan ve $ ((a) _ (15)) $ bulmanız gerekiyor, o zaman şunu not ediyoruz :
\ [\ başla (hizala) & ((a) _ (15)) - ((a) _ (10)) = 5d; \\ & ((a) _ (10)) - ((a) _ (5)) = 5d. \\ \ bitiş (hizalama) \]
Ancak $ ((a) _ (10)) - ((a) _ (5)) = 14.4-8.4 = 6 $, dolayısıyla 5d $ = 6 $ koşuluna göre, buradan:
\ [\ başla (hizala) & ((a) _ (15)) - 14.4 = 6; \\ & ((a) _ (15)) = 6 + 14.4 = 20.4. \\ \ bitiş (hizalama) \]
Cevap: 20.4
Bu kadar! Bazı denklem sistemleri oluşturmamıza ve ilk terimi ve farkı hesaplamamıza gerek yoktu - her şey sadece birkaç satırda çözüldü.
Şimdi başka bir görev türünü ele alalım - ilerlemenin olumsuz ve olumlu üyelerini bulmak. İlerleme artarsa, ilk terim olumsuz iken, er ya da geç olumlu terimlerin içinde ortaya çıkacağı bir sır değildir. Ve tam tersine: azalan ilerlemenin üyeleri er ya da geç negatif olacaklardır.
Aynı zamanda, bu anı sırayla elementlerden geçerek "kafaya" el yordamıyla elde etmek her zaman mümkün değildir. Çoğu zaman problemler, formülleri bilmeden hesaplamaların birkaç sayfa alacağı şekilde tasarlanır - cevabı bulduğumuzda uykuya dalardık. Bu nedenle, bu sorunları daha hızlı bir şekilde çözmeye çalışacağız.
Sorun numarası 4. Aritmetik dizide kaç tane olumsuz terim var -38.5; -35.8; ...?
Çözüm. Yani, $ ((a) _ (1)) = - 38.5 $, $ ((a) _ (2)) = - 35.8 $, farkı hemen bulduğumuz yerden:
Farkın pozitif olduğunu, dolayısıyla ilerlemenin arttığını unutmayın. İlk terim negatiftir, bu nedenle bir noktada gerçekten pozitif sayılara rastlayacağız. Tek soru ne zaman olacağı.
Şunu bulmaya çalışalım: terimlerin olumsuzluğu ne kadar süreyle (yani hangi doğal sayıya kadar $ n $) korunur:
\ [\ başla (hizala) & ((a) _ (n)) \ lt 0 \ Sağ Ok ((a) _ (1)) + \ sol (n-1 \ sağ) d \ lt 0; \\ & -38.5+ \ sol (n-1 \ sağ) \ cdot 2.7 \ lt 0; \ dörtlü \ sol | \ cdot 10 \ sağ. \\ & -385 + 27 \ cdot \ sol (n-1 \ sağ) \ lt 0; \\ & -385 + 27n-27 \ lt 0; \\ & 27n \ lt 412; \\ & n \ lt 15 \ frak (7) (27) \ Sağ Ok ((n) _ (\ maks)) = 15. \\ \ bitiş (hizalama) \]
Son satır açıklama gerektiriyor. Yani, $ n \ lt 15 \ frac (7) (27) $ olduğunu biliyoruz. Öte yandan, sayının yalnızca tamsayı değerlerinden memnun olacağız (ayrıca: $ n \ in \ mathbb (N) $), bu nedenle izin verilen en büyük sayı tam olarak $ n = 15 $ ve hiçbir şekilde 16.
Sorun numarası 5. Aritmetik ilerlemede $ (() _ (5)) = - 150, (() _ (6)) = - 147 $. Bu ilerlemenin ilk pozitif teriminin sayısını bulun.
Bir öncekiyle tamamen aynı problem olurdu, ancak $ ((a) _ (1)) $'ı bilmiyoruz. Ancak komşu terimler bilinmektedir: $ ((a) _ (5)) $ ve $ ((a) _ (6)) $, böylece ilerleme farkını kolayca bulabiliriz:
Ayrıca, standart formüle göre birinci ve fark açısından beşinci terimi ifade etmeye çalışacağız:
\ [\ başla (hizala) & ((a) _ (n)) = ((a) _ (1)) + \ sol (n-1 \ sağ) \ cdot d; \\ & ((a) _ (5)) = ((a) _ (1)) + 4d; \\ & -150 = ((a) _ (1)) + 4 \ cdot 3; \\ & ((a) _ (1)) = - 150-12 = -162. \\ \ bitiş (hizalama) \]
Şimdi önceki göreve benzeterek ilerliyoruz. Dizimizin hangi noktasında pozitif sayılar olacağını öğreniyoruz:
\ [\ başla (hizala) & ((a) _ (n)) = - 162+ \ sol (n-1 \ sağ) \ cdot 3 \ gt 0; \\ & -162 + 3n-3 \ gt 0; \\ & 3n \ gt 165; \\ & n \ gt 55 \ Sağ Ok ((n) _ (\ dak)) = 56. \\ \ bitiş (hizalama) \]
Bu eşitsizliğin en küçük tamsayı çözümü 56'dır.
Lütfen dikkat: son görevde her şey katı bir eşitsizliğe indirildi, bu nedenle $ n = 55 $ seçeneği bize uymayacak.
Şimdi basit problemleri nasıl çözeceğimizi öğrendiğimize göre, daha karmaşık olanlara geçelim. Ama önce, gelecekte bize çok zaman kazandıracak ve eşit olmayan hücrelerden tasarruf sağlayacak olan aritmetik ilerlemelerin çok yararlı bir başka özelliğini inceleyelim. :)
Aritmetik ortalama ve eşit girintiler
Artan $ \ left (((a) _ (n)) \ right) $ aritmetik ilerlemesinin birkaç ardışık üyesini düşünün. Onları sayı satırında işaretlemeye çalışalım:
Sayı doğrusunda aritmetik bir ilerlemenin üyeleri$ ((a) _ (n-3)), ..., ((a) _ (n + 3)) $, herhangi bir $ ((a) _ (1)), \ ( değil, rastgele terimleri özellikle kaydettim. (a) _ (2)), \ ((a) _ (3)) $, vb. Çünkü şimdi bahsedeceğim kural her "segment" için aynı şekilde çalışır.
Ve kural çok basit. Tekrarlama formülünü hatırlayalım ve işaretlenen tüm üyeler için yazalım:
\ [\ başla (hizala) & ((a) _ (n-2)) = ((a) _ (n-3)) + d; \\ & ((a) _ (n-1)) = ((a) _ (n-2)) + d; \\ & ((a) _ (n)) = ((a) _ (n-1)) + d; \\ & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n + 1)) + d; \\ \ bitiş (hizalama) \]
Ancak, bu eşitlikler farklı şekilde yeniden yazılabilir:
\ [\ başla (hizala) & ((a) _ (n-1)) = ((a) _ (n)) - d; \\ & ((a) _ (n-2)) = ((a) _ (n)) - 2d; \\ & ((a) _ (n-3)) = ((a) _ (n)) - 3d; \\ & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n)) + 2d; \\ & ((a) _ (n + 3)) = ((a) _ (n)) + 3d; \\ \ bitiş (hizalama) \]
Peki ne olmuş? Ve $ ((a) _ (n-1)) $ ve $ ((a) _ (n + 1)) $ terimlerinin $ ((a) _ (n)) $'dan aynı uzaklıkta olduğu gerçeği . Ve bu mesafe $ d $'a eşittir. Aynısı $ ((a) _ (n-2)) $ ve $ ((a) _ (n + 2)) $ üyeleri için de söylenebilir - bunlar da $ ((a) _ (n)'den çıkarılır ) $ aynı mesafe $ 2d $'a eşittir. Süresiz olarak devam edebilirsiniz, ancak anlam resim tarafından iyi gösterilmiştir.
 İlerlemenin üyeleri merkezden aynı uzaklıkta uzanır.
İlerlemenin üyeleri merkezden aynı uzaklıkta uzanır. Bu bizim için ne anlama geliyor? Bu, komşu sayılar biliniyorsa $ ((a) _ (n)) $ öğesini bulabileceğiniz anlamına gelir:
\ [((a) _ (n)) = \ frac (((a) _ (n-1)) + ((a) _ (n + 1))) (2) \]
Harika bir ifade bulduk: aritmetik dizinin her üyesi komşu terimlerin aritmetik ortalamasına eşittir! Ayrıca: $ ((a) _ (n)) $ sol ve sağ adımlarımızdan bir adım değil, $ k $ adımlarımızdan sapabiliriz - ve yine de formül doğru olacaktır:
\ [((a) _ (n)) = \ frac (((a) _ (n-k)) + ((a) _ (n + k))) (2) \]
Onlar. $ ((a) _ (100)) $ ve $ ((a) _ (200)) $ biliyorsak, $ ((a) _ (150))) $'ı kolayca bulabiliriz, çünkü $ (( a) _ (150)) = \ frac (((a) _ (100)) + ((a) _ (200))) (2) $. İlk bakışta, bu gerçeğin bize yararlı bir şey vermediği görünebilir. Bununla birlikte, pratikte, birçok problem aritmetik ortalamanın kullanımı için özel olarak "keskinleştirilmiştir". Bir göz at:
Sorun numarası 6. $ -6 ((x) ^ (2)) $, $ x + 1 $ ve $ 14 + 4 ((x) ^ (2)) $ sayılarının ardışık üye olduğu tüm $ x $ değerlerini bulun aritmetik ilerlemenin (sırasıyla).
Çözüm. Belirtilen sayılar ilerlemenin üyeleri olduğundan, aritmetik ortalamanın koşulu onlar için sağlanır: merkezi öğe $ x + 1 $, bitişik öğeler cinsinden ifade edilebilir:
\ [\ start (hizalama) & x + 1 = \ frac (-6 ((x) ^ (2)) + 14 + 4 ((x) ^ (2))) (2); \\ & x + 1 = \ frak (14-2 ((x) ^ (2))) (2); \\ & x + 1 = 7 - ((x) ^ (2)); \\ & ((x) ^ (2)) + x-6 = 0. \\ \ bitiş (hizalama) \]
Sonuç klasik bir ikinci dereceden denklemdir. Kökleri: $ x = 2 $ ve $ x = -3 $ - cevaplar bunlar.
Cevap: -3; 2.
Sorun numarası 7. $ -1; 4-3; (() ^ (2)) + 1 $ sayılarının aritmetik bir ilerleme yaptığı $$ değerlerini bulun (bu sırayla).
Çözüm. Yine orta terimi, komşu terimlerin aritmetik ortalaması cinsinden ifade ediyoruz:
\ [\ başla (hizala) & 4x-3 = \ frac (x-1 + ((x) ^ (2)) + 1) (2); \\ & 4x-3 = \ frak (((x) ^ (2)) + x) (2); \ dörtlü \ sol | \ cdot 2 \ sağ .; \\ & 8x-6 = ((x) ^ (2)) + x; \\ & ((x) ^ (2)) - 7x + 6 = 0. \\ \ bitiş (hizalama) \]
Yine ikinci dereceden denklem. Ve yine iki kök var: $ x = 6 $ ve $ x = 1 $.
Cevap 1; 6.
Bir problemi çözme sürecinde bazı acımasız sayılar çıkarırsanız veya bulunan cevapların doğruluğundan tam olarak emin değilseniz, kontrol etmenize izin veren harika bir teknik var: sorunu doğru çözdük mü?
Örneğin 6. problemde -3 ve 2 cevaplarını aldık. Bu cevapların doğru olup olmadığı nasıl kontrol edilir? Bunları başlangıç durumuna bağlayalım ve ne olduğunu görelim. Bir aritmetik dizi oluşturması gereken üç sayı ($ -6 (() ^ (2)) $, $ + 1 $ ve $ 14 + 4 (() ^ (2)) $) olduğunu hatırlatmama izin verin. İkame $ x = -3 $:
\ [\ başla (hizala) & x = -3 \ Sağ Ok \\ & -6 ((x) ^ (2)) = - 54; \\ & x + 1 = -2; \\ & 14 + 4 ((x) ^ (2)) = 50. \ bitiş (hizalama) \]
Alınan numaralar -54; -2; 52 ile farklılık gösteren 50, şüphesiz aritmetik bir ilerlemedir. Aynı şey $ x = 2 $ için de olur:
\ [\ start (align) & x = 2 \ Rightarrow \\ & -6 ((x) ^ (2)) = - 24; \\ & x + 1 = 3; \\ & 14 + 4 ((x) ^ (2)) = 30. \ bitiş (hizalama) \]
Yine bir ilerleme, ancak 27'lik bir farkla. Böylece sorun doğru bir şekilde çözüldü. İlgilenenler ikinci sorunu kendi başlarına kontrol edebilirler, ancak hemen söyleyeceğim: orada da her şey doğru.
Genel olarak, son problemleri çözerken, hatırlanması gereken başka bir ilginç gerçekle karşılaştık:
Üç sayı, ikincisi birincinin ve sonun aritmetik ortalaması olacak şekilde ise, bu sayılar bir aritmetik ilerleme oluşturur.
Gelecekte, bu ifadeyi anlamak, sorunun durumuna göre gerekli ilerlemeleri kelimenin tam anlamıyla "inşa etmemize" izin verecektir. Ancak böyle bir "yapıya" geçmeden önce, daha önce düşünülmüş olandan doğrudan çıkan bir gerçeğe daha dikkat etmeliyiz.
Elemanların gruplandırılması ve toplamı
Tekrar sayı eksenine dönelim. Orada, belki de aralarında ilerlemenin birkaç üyesini not edelim. diğer birçok üye var:
Sayı doğrusunda işaretlenmiş 6 eleman vardır."Sol kuyruğu" $ ((a) _ (n)) $ ve $ d $ cinsinden, "sağ kuyruk"u ise $ ((a) _ (k)) $ ve $ d $ cinsinden ifade etmeye çalışalım. . Çok basit:
\ [\ başla (hizala) & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n)) + 2d; \\ & ((a) _ (k-1)) = ((a) _ (k)) - d; \\ & ((a) _ (k-2)) = ((a) _ (k)) - 2d. \\ \ bitiş (hizalama) \]
Şimdi, aşağıdaki toplamların eşit olduğuna dikkat edin:
\ [\ başla (hizala) & ((a) _ (n)) + ((a) _ (k)) = S; \\ & ((a) _ (n + 1)) + ((a) _ (k-1)) = ((a) _ (n)) + d + ((a) _ (k)) - d = S; \\ & ((a) _ (n + 2)) + ((a) _ (k-2)) = ((a) _ (n)) + 2d + ((a) _ (k)) - 2d = S. \ bitiş (hizalama) \]
Basitçe söylemek gerekirse, toplamda bir miktar $ S $ sayısına eşit olan ilerlemenin iki öğesini bir başlangıç olarak kabul edersek ve sonra bu öğelerden zıt yönlerde yürümeye başlarsak (birbirine doğru veya tam tersi uzaklaşmak için), sonra rastlayacağımız elementlerin toplamı da eşit olacaktır.$ S $. Bu en açık şekilde grafiksel olarak gösterilebilir:
 Eşit girinti eşit miktarlar verir
Eşit girinti eşit miktarlar verir Bu gerçeği anlamak, yukarıda düşündüklerimizden temelde daha yüksek bir karmaşıklık düzeyindeki sorunları çözmemize izin verecektir. Örneğin:
Sorun numarası 8. Birinci terimin 66 olduğu ve ikinci ve on ikinci terimlerin çarpımının mümkün olan en küçük olduğu aritmetik ilerlemenin farkını belirleyin.
Çözüm. Bildiğimiz her şeyi yazalım:
\ [\ başla (hizala) & ((a) _ (1)) = 66; \\ & d =? \\ & ((a) _ (2)) \ cdot ((a) _ (12)) = \ min. \ bitiş (hizalama) \]
Yani, $ d $ ilerlemesinin farkını bilmiyoruz. Aslında, tüm çözüm fark etrafında inşa edilecektir, çünkü $ ((a) _ (2)) \ cdot ((a) _ (12)) $ ürünü aşağıdaki gibi yeniden yazılabilir:
\ [\ başla (hizala) & ((a) _ (2)) = ((a) _ (1)) + d = 66 + d; \\ & ((a) _ (12)) = ((a) _ (1)) + 11d = 66 + 11d; \\ & ((a) _ (2)) \ cdot ((a) _ (12)) = \ sol (66 + d \ sağ) \ cdot \ sol (66 + 11d \ sağ) = \\ & = 11 \ cdot \ sol (d + 66 \ sağ) \ cdot \ sol (d + 6 \ sağ). \ bitiş (hizalama) \]
Tanktakiler için: İkinci parantezden 11'in ortak çarpanını çıkardım. Böylece, aranan ürün $d $ değişkenine göre ikinci dereceden bir fonksiyondur. Bu nedenle, $ f \ left (d \ right) = 11 \ left (d + 66 \ right) \ left (d + 6 \ sağ) $ işlevini düşünün - grafiği, dalları yukarı doğru olan bir parabol olacaktır, çünkü parantezleri genişletirsek, şunu elde ederiz:
\ [\ başla (hizala) & f \ sol (d \ sağ) = 11 \ sol (((d) ^ (2)) + 66d + 6d + 66 \ cdot 6 \ sağ) = \\ & = 11 (( d) ^ (2)) + 11 \ cdot 72d + 11 \ cdot 66 \ cdot 6 \ bitiş (hizalama) \]
Gördüğünüz gibi, baştaki terimdeki katsayı 11'dir - bu pozitif bir sayıdır, yani gerçekten dalları yukarıda olan bir parabol ile uğraşıyoruz:
ikinci dereceden fonksiyon grafiği - parabol
Lütfen dikkat: bu parabol minimum değerini tepe noktasında apsis $ ((d) _ (0)) $ ile alır. Tabii ki, bu apsisi standart şemaya göre hesaplayabiliriz (ayrıca $ ((d) _ (0)) = (- b) / (2a) \; $ formülü de vardır), ancak çok daha mantıklı olurdu İstenen tepe noktasının parabolün eksen simetrisi üzerinde olduğunu fark etmek için $ ((d) _ (0)) $ noktası $ f \ left (d \ right) = 0 $ denkleminin köklerinden eşit uzaklıktadır:
\ [\ başla (hizala) & f \ sol (d \ sağ) = 0; \\ & 11 \ cdot \ sol (d + 66 \ sağ) \ cdot \ sol (d + 6 \ sağ) = 0; \\ & ((d) _ (1)) = - 66; \ dörtlü ((d) _ (2)) = - 6. \\ \ bitiş (hizalama) \]
Bu yüzden parantezleri açmak için acelem yoktu: orijinal formda kökleri bulmak çok, çok kolaydı. Bu nedenle, apsis, −66 ve −6 sayılarının aritmetik ortalamasına eşittir:
\ [((d) _ (0)) = \ frak (-66-6) (2) = - 36 \]
Keşfedilen sayı bize ne veriyor? Bununla, gerekli ürün en küçük değeri alır (bu arada, $ ((y) _ (\ min)) $ saymadık - buna ihtiyacımız yok). Aynı zamanda, bu sayı orijinal ilerleme, yani. cevabı bulduk. :)
Cevap: -36
Sorun numarası 9. $ - \ frac (1) (2) $ ve $ - \ frac (1) (6) $ sayıları arasına, verilen sayılarla birlikte aritmetik bir ilerleme oluşturacak şekilde üç sayı yerleştirin.
Çözüm. Temel olarak, ilk ve son sayılar zaten bilinen beş sayıdan oluşan bir dizi yapmamız gerekiyor. Eksik sayıları $ x $, $ y $ ve $ z $ değişkenleriyle gösterelim:
\ [\ sol ((a) _ (n)) \ sağ) = \ sol \ (- \ frak (1) (2); x; y; z; - \ frak (1) (6) \ sağ \ ) \]
$ y $ sayısının dizimizin "ortası" olduğuna dikkat edin - hem $ x $ hem de $ z $ sayılarından ve $ - \ frac (1) (2) $ ve $ - \ sayılarından eşit uzaklıktadır. frak (1) ( 6) $. Ve şu anda $ x $ ve $ z $ sayılarından $ y $ alamıyorsak, o zaman ilerlemenin uçlarında durum farklıdır. Aritmetik ortalamayı hatırlamak:
Şimdi $ y $ bilerek kalan sayıları bulacağız. $ x $'ın $ - \ frac (1) (2) $ sayıları ile az önce bulunan $ y = - \ frac (1) (3) $ sayıları arasında olduğuna dikkat edin. Bu yüzden
Benzer şekilde akıl yürüterek, kalan sayıyı buluruz:
Hazır! Üç sayıyı da bulduk. Bunları orijinal sayılar arasına yerleştirilmesi gereken sırayla cevaba yazalım.
Cevap: $ - \ frak (5) (12); \ - \ frak (1) (3); \ - \ frak (1) (4) $
Sorun numarası 10. Girilen sayıların birinci, ikinci ve sonunun toplamının 56 olduğunu biliyorsanız, bu sayılarla birlikte aritmetik bir ilerleme oluşturan 2 ve 42 sayıları arasına birkaç sayı girin.
Çözüm. Bununla birlikte, öncekilerle aynı şemaya göre - aritmetik ortalama aracılığıyla çözülen daha da zor bir görev. Sorun şu ki, tam olarak kaç tane sayı ekleyeceğimizi bilmiyoruz. Bu nedenle, kesinlik için, her şeyi ekledikten sonra tam olarak $ n $ sayıları olacağını ve bunlardan ilkinin 2 ve sonunun 42 olduğunu varsayalım. Bu durumda, aranan aritmetik ilerleme şu şekilde temsil edilebilir:
\ [\ sol (((a) _ (n)) \ sağ) = \ sol \ (2; ((a) _ (2)); ((a) _ (3)); ...; (( a) _ (n-1)); 42 \ sağ \) \]
\ [((a) _ (2)) + ((a) _ (3)) + ((a) _ (n-1)) = 56 \]
Ancak, $ ((a) _ (2)) $ ve $ ((a) _ (n-1)) $ sayılarının kenarlardaki 2 ve 42 sayılarından birbirine doğru birer adım ile elde edildiğine dikkat ediniz, yani... sıranın ortasına. Bunun anlamı şudur ki
\ [((a) _ (2)) + ((a) _ (n-1)) = 2 + 42 = 44 \]
Ancak daha sonra yukarıda yazılan ifade aşağıdaki gibi yeniden yazılabilir:
\ [\ başla (hizala) & ((a) _ (2)) + ((a) _ (3)) + ((a) _ (n-1)) = 56; \\ & \ sol (((a) _ (2)) + ((a) _ (n-1)) \ sağ) + ((a) _ (3)) = 56; \\ & 44 + ((a) _ (3)) = 56; \\ & ((a) _ (3)) = 56-44 = 12. \\ \ bitiş (hizalama) \]
$ ((a) _ (3)) $ ve $ ((a) _ (1)) $ bilerek, ilerlemenin farkını kolayca bulabiliriz:
\ [\ başla (hizala) & ((a) _ (3)) - ((a) _ (1)) = 12 - 2 = 10; \\ & ((a) _ (3)) - ((a) _ (1)) = \ sol (3-1 \ sağ) \ cdot d = 2d; \\ & 2d = 10 \ Sağ ok d = 5. \\ \ bitiş (hizalama) \]
Sadece üyelerin geri kalanını bulmak için kalır:
\ [\ başla (hizala) & ((a) _ (1)) = 2; \\ & ((a) _ (2)) = 2 + 5 = 7; \\ & ((a) _ (3)) = 12; \\ & ((a) _ (4)) = 2 + 3 \ cdot 5 = 17; \\ & ((a) _ (5)) = 2 + 4 \ cdot 5 = 22; \\ & ((a) _ (6)) = 2 + 5 \ cdot 5 = 27; \\ & ((a) _ (7)) = 2 + 6 \ cdot 5 = 32; \\ & ((a) _ (8)) = 2 + 7 \ cdot 5 = 37; \\ & ((a) _ (9))) = 2 + 8 \ cdot 5 = 42; \\ \ bitiş (hizalama) \]
Böylece, zaten 9. adımda dizinin sol ucuna geleceğiz - 42 sayısı. Toplamda sadece 7 sayı eklemek gerekiyordu: 7; 12; 17; 22; 27; 32; 37.
Cevap: 7; 12; 17; 22; 27; 32; 37
İlerlemelerle ilgili kelime sorunları
Sonuç olarak, birkaç nispeten basit görevi düşünmek istiyorum. Pekala, ne kadar basit: okulda matematik okuyan ve yukarıda yazılanları okumamış çoğu öğrenci için bu görevler bir teneke gibi görünebilir. Yine de, matematikte OGE ve USE'de karşılaşılan tam da bu tür problemlerdir, bu yüzden onlara aşina olmanızı tavsiye ederim.
Sorun numarası 11. Tugay Ocak ayında 62 parça üretti ve sonraki her ay bir öncekinden 14 parça daha üretti. Takım Kasım ayında kaç bölüm yaptı?
Çözüm. Açıkçası, aya göre planlanan parça sayısı artan bir aritmetik ilerlemeyi temsil edecektir. Dahası:
\ [\ başla (hizala) & ((a) _ (1)) = 62; \ dörtlü d = 14; \\ & ((a) _ (n)) = 62+ \ sol (n-1 \ sağ) \ cdot 14. \\ \ bitiş (hizalama) \]
Kasım yılın 11. ayıdır, bu yüzden $ ((a) _ (11)) $ bulmamız gerekiyor:
\ [((a) _ (11))) = 62 + 10 \ cdot 14 = 202 \]
Sonuç olarak, Kasım ayında 202 parça üretilecek.
Sorun numarası 12. Cilt atölyesi Ocak ayında 216 kitap bağladı ve her ay bir öncekinden 4 kitap daha ciltledi. Çalıştay Aralık ayında kaç kitap bağladı?
Çözüm. Hepsi aynı:
$ \ başla (hizala) & ((a) _ (1)) = 216; \ dörtlü d = 4; \\ & ((a) _ (n)) = 216+ \ sol (n-1 \ sağ) \ cdot 4. \\ \ bitiş (hizalama) $
Aralık, yılın son 12. ayıdır, bu nedenle $ ((a) _ (12)) $ arıyoruz:
\ [((a) _ (12)) = 216 + 11 \ cdot 4 = 260 \]
Cevap bu - Aralık'ta 260 kitap ciltlenecek.
Pekala, buraya kadar okuduysanız, sizi tebrik etmek için acele ediyorum: aritmetik ilerlemelerdeki "genç dövüş kursunu" başarıyla geçtiniz. Bir ilerlemenin toplamının formülünü ve bundan önemli ve çok faydalı sonuçları inceleyeceğimiz bir sonraki derse güvenle ilerleyebilirsiniz.
İlk seviye
Aritmetik ilerleme. Örneklerle ayrıntılı teori (2019)
sayı dizisi
O halde oturalım ve bazı sayıları yazmaya başlayalım. Örneğin:
Herhangi bir sayı yazabilirsiniz ve istediğiniz kadar olabilir (bizim durumumuzda, onlar). Ne kadar sayı yazarsak yazalım, hangisinin birinci, hangisinin ikinci olduğunu her zaman söyleyebiliriz, yani sonuncuya kadar, yani onları numaralandırabiliriz. Bu bir sayı dizisi örneğidir:
sayı dizisi
Örneğin dizimiz için:
Atanan numara, dizideki yalnızca bir numaraya özeldir. Başka bir deyişle, dizide üç saniyelik sayı yoktur. İkinci sayı (-inci sayı gibi) her zaman birdir.
Numaralı sayı, dizinin inci üyesi olarak adlandırılır.
Genellikle tüm diziye bir harf (örneğin) deriz ve bu dizinin her üyesi, bu üyenin numarasına eşit bir indekse sahip aynı harftir:.
Bizim durumumuzda: 
Diyelim ki bitişik sayılar arasındaki farkın aynı ve eşit olduğu bir sayısal dizimiz var.
Örneğin: 
vesaire.
Bu sayı dizisine aritmetik ilerleme denir.
"İlerleme" terimi, 6. yüzyılda Romalı yazar Boethius tarafından tanıtıldı ve daha geniş anlamda sonsuz bir sayı dizisi olarak anlaşıldı. "Aritmetik" adı, eski Yunanlılar tarafından işgal edilen sürekli oranlar teorisinden alınmıştır.
Bu, her bir üyesi bir öncekine eşit olan ve aynı sayıya eklenen sayısal bir dizidir. Bu sayıya aritmetik ilerlemenin farkı denir ve ile gösterilir.
Hangi sayı dizilerinin aritmetik ilerleme olduğunu ve hangilerinin olmadığını belirlemeye çalışın:
a)
B)
C)
NS)
Anlaşıldı? Cevaplarımızı karşılaştıralım:
Bir aritmetik ilerleme - b, c.
Değil aritmetik ilerleme - a, d.
Verilen ilerlemeye () geri dönelim ve onun inci üyesinin değerini bulmaya çalışalım. var 2 onu bulmanın yolu.
1. Yöntem
Dizinin üçüncü terimine gelene kadar dizi sayısının bir önceki değerine ekleyebiliriz. Özetleyecek fazla bir şeyimiz olmaması iyi - sadece üç değer:
Yani, açıklanan aritmetik ilerlemenin inci üyesi eşittir.
2. Yöntem
İlerlemede inci terimin değerini bulmamız gerekirse ne olur? Toplama işlemi bir saatten fazla zamanımızı alacaktı ve sayıları eklerken yanılmayacağımız bir gerçek değil.
Elbette matematikçiler, aritmetik ilerlemenin farkını önceki değere eklemenize gerek olmayan bir yol bulmuşlardır. Çizilen resme daha yakından bakın ... Elbette zaten belirli bir desen fark etmişsinizdir, yani:
Örneğin, bu aritmetik ilerlemenin inci üyesinin değerinin nasıl eklendiğini görelim: 
Diğer bir deyişle:
Belirli bir aritmetik ilerlemenin bir üyesinin değerini bu şekilde kendiniz bulmaya çalışın.
Hesaplanmış mı? Notlarınızı cevapla karşılaştırın:
Aritmetik ilerlemenin üyelerini önceki değere art arda eklediğimizde, önceki yöntemle tam olarak aynı sayıyı elde ettiğinizi lütfen unutmayın.
Bu formülü "personalize etmeye" çalışalım - onu genel forma getireceğiz ve şunu elde edeceğiz:
|
Aritmetik ilerleme denklemi. |
Aritmetik ilerlemeler artıyor ve bazen azalıyor.
artan- üyelerin sonraki her değerinin bir öncekinden daha büyük olduğu ilerlemeler.
Örneğin:
azalan- üyelerin sonraki her değerinin bir öncekinden daha az olduğu ilerlemeler.
Örneğin:
Elde edilen formül, aritmetik bir ilerlemenin hem artan hem de azalan terimlerinin hesaplanmasında kullanılır.
Pratikte kontrol edelim.
Bize aşağıdaki sayılardan oluşan bir aritmetik dizi veriliyor: Bunu hesaplamak için formülümüzü kullanırsak, bu aritmetik dizinin inci sayısının ne olacağını kontrol edelim:

O zamandan beri:
Böylece formülün hem azalan hem de artan aritmetik ilerlemede çalışmasını sağladık.
Bu aritmetik ilerlemenin inci ve inci terimlerini kendi başınıza bulmaya çalışın.
Elde edilen sonuçları karşılaştıralım:
Aritmetik ilerleme özelliği
Görevi karmaşıklaştıralım - aritmetik ilerlemenin özelliğini türeteceğiz.
Diyelim ki bize aşağıdaki koşul verildi:
- aritmetik ilerleme, değeri bulun.
Kolay, diyorsun ve zaten bildiğin formüle göre saymaya başlıyorsun:
A, diyelim, o zaman:
Kesinlikle doğru. İlk önce bulduğumuz, ardından ilk sayıya eklediğimiz ve aradığımızı elde ettiğimiz ortaya çıktı. İlerleme küçük değerlerle temsil ediliyorsa, bunda karmaşık bir şey yoktur, ancak durumda bize sayılar verilirse? Kabul edin, hesaplamalarda hata yapma şansınız var.
Şimdi düşünün, bu sorunu herhangi bir formül kullanarak tek bir eylemde çözmek mümkün mü? Tabii ki, evet ve şimdi geri çekilmeye çalışacağımız kişi o.
Aritmetik ilerlemenin gerekli terimini, onu bulma formülünü bildiğimiz gibi gösterelim - bu, başlangıçta elde ettiğimiz formülün aynısıdır:
, sonra:
- ilerlemenin önceki üyesi:
- ilerlemenin bir sonraki üyesi:
İlerlemenin önceki ve sonraki üyelerini özetleyelim:
Dizinin önceki ve sonraki üyelerinin toplamının, aralarında bulunan ilerlemenin üyesinin iki katı değeri olduğu ortaya çıktı. Başka bir deyişle, bilinen önceki ve ardışık değerlere sahip bir dizinin bir üyesinin değerini bulmak için, bunları toplayıp bölmek gerekir.
Doğru, aynı numarayı aldık. Malzemeyi düzeltelim. İlerlemenin değerini kendiniz hesaplayın, çünkü hiç de zor değil.
Tebrikler! İlerleme hakkında neredeyse her şeyi biliyorsun! Efsaneye göre, tüm zamanların en büyük matematikçilerinden biri olan "matematikçilerin kralı" - Karl Gauss tarafından kolayca çıkarsanan öğrenilecek tek bir formül kaldı ...
Karl Gauss 9 yaşındayken, diğer sınıflardaki öğrencilerin çalışmalarını kontrol etmekle meşgul olan bir öğretmen derste şu görevi sordu: "Tüm doğal sayıların toplamını (diğer kaynaklara göre) dahil olmak üzere hesaplayın." Cesaretin sınıf arkadaşlarının çoğu, uzun hesaplamalardan sonra yanlış sonuç alırken, öğrencilerinden biri (Karl Gauss'du) bir dakika içinde probleme doğru cevabı verdiğinde öğretmenin şaşkınlığını hayal edin ...
Genç Karl Gauss, kolayca fark edebileceğiniz belirli bir model fark etti.
Diyelim ki -th üyelerinden oluşan bir aritmetik dizimiz var: Aritmetik dizinin verilen üyelerinin toplamını bulmamız gerekiyor. Tabii ki, tüm değerleri manuel olarak toplayabiliriz, ancak ya görevde Gauss'un aradığı gibi üyelerinin toplamını bulmak gerekirse?
Verilen bir ilerlemeyi çizelim. Vurgulanan sayılara yakından bakın ve onlarla çeşitli matematiksel işlemler yapmaya çalışın. 
Bunu denediniz mi? Ne fark ettin? Doğru! Toplamları eşittir

Şimdi söyle bana, verilen ilerlemede böyle kaç çift var? Tabii ki, tüm sayıların tam yarısı, yani.
Bir aritmetik ilerlemenin iki üyesinin toplamının ve benzer eşit çiftlerin toplamının eşit olduğu gerçeğine dayanarak, toplam toplamın şu olduğunu elde ederiz:
.
Böylece, herhangi bir aritmetik ilerlemenin ilk terimlerinin toplamı için formül aşağıdaki gibi olacaktır:
Bazı problemlerde th terimini bilmiyoruz ama progresyondaki farkı biliyoruz. Toplamın formülünde, inci terimin formülünü değiştirmeye çalışın.
Ne yaptın?
Tebrikler! Şimdi Karl Gauss'a sorulan probleme dönelim: -th'den başlayan sayıların toplamının ve -th'den başlayan sayıların toplamının ne olduğunu kendiniz hesaplayın.
Ne kadar aldın?
Gauss, üyelerin toplamının ve üyelerin toplamının eşit olduğunu buldu. Böyle mi karar verdin?
Aslında, bir aritmetik ilerlemenin üyelerinin toplamı için formül, eski Yunan bilim adamı Diophantus tarafından 3. yüzyılda kanıtlandı ve bu süre boyunca, esprili insanlar aritmetik bir ilerlemenin özelliklerini kudret ve ana ile kullanıyorlardı.
Örneğin, Eski Mısır'ı ve o zamanın en iddialı şantiyesini hayal edin - piramidin inşası ... Resim bunun bir tarafını gösteriyor. 
Buradaki ilerleme nerede diyorsunuz? Yakından bakın ve piramit duvarının her satırındaki kum bloklarının sayısında bir desen bulun. 
Bu aritmetik bir ilerleme değil mi? Tabana blok tuğlalar yerleştirilmişse, bir duvar inşa etmek için kaç blok gerektiğini hesaplayın. Umarım parmağınızı monitörde gezdirerek saymazsınız, son formülü ve aritmetik ilerleme hakkında söylediğimiz her şeyi hatırlıyor musunuz?
Bu durumda, ilerleme şöyle görünür:.
Aritmetik ilerleme farkı.
Aritmetik ilerlemenin üye sayısı.
Verilerimizi son formüllerle değiştirelim (blok sayısını 2 şekilde sayacağız).
Yöntem 1.
Yöntem 2.
Ve şimdi monitörde hesaplayabilirsiniz: elde edilen değerleri piramidimizdeki blok sayısıyla karşılaştırın. Bir araya geldi mi? Tebrikler, aritmetik ilerleme terimlerinin toplamında ustalaştınız.
Tabii ki, tabandaki bloklardan bir piramit inşa edemezsiniz, ama ? Bu koşulla bir duvar inşa etmek için kaç tane kum tuğlası gerektiğini hesaplamaya çalışın.
Becerebildin mi?
Doğru cevap bloklardır:
Egzersiz yapmak
Görevler:
- Masha yaza kadar şekilleniyor. Her gün squat sayısını artırıyor. İlk antrenmanda ağız kavgası yaptıysa, Masha haftalar içinde kaç kez çömelir.
- İçinde bulunan tek sayıların toplamı kaçtır?
- Günlükleri saklarken, oduncular bunları her üst katman bir öncekinden bir kütük daha az içerecek şekilde istifler. Bir duvarda kaç tane kütük var, eğer kütükler duvarın temeli olarak hizmet ediyorsa.
Yanıtlar:
- Aritmetik ilerlemenin parametrelerini tanımlayalım. Bu durumda
(haftalar = günler).Cevap:İki hafta sonra Masha günde bir kez çömelir.
- İlk tek sayı, son sayı.
Aritmetik ilerleme farkı.
Tek sayıların sayısı yarıdır, ancak, aritmetik bir ilerlemenin -th terimini bulmak için formülü kullanarak bu gerçeği kontrol edeceğiz:Sayılar tek sayılar içerir.
Mevcut verileri formülde değiştirin:Cevap:İçindeki tüm tek sayıların toplamı eşittir.
- Piramit problemini hatırlayalım. Bizim durumumuz için a, her bir üst katman bir log azaltıldığından, o zaman sadece bir grup katmanda, yani.
Verileri formülde yerine koyalım:Cevap: Duvarda kütükler var.
özetleyelim
- - bitişik sayılar arasındaki farkın aynı ve eşit olduğu sayısal bir dizi. Artan ve azalan olabilir.
- formül bulma Aritmetik dizinin -inci üyesi - formülüyle yazılır, dizideki sayıların sayısı nerede.
- Bir aritmetik ilerlemenin üyelerinin özelliği- - ilerlemedeki sayıların sayısı nerede.
- Bir aritmetik ilerlemenin üyelerinin toplamı iki şekilde bulunabilir:
, değerlerin sayısı nerede.
ARİTMETİK İLERLEME. ORTALAMA SEVİYE
sayı dizisi
Oturup birkaç rakam yazmaya başlayalım. Örneğin:
Herhangi bir sayı yazabilirsiniz ve istediğiniz kadar olabilir. Ama hangisinin birinci, hangisinin ikinci olduğunu her zaman söyleyebilirsiniz, yani onları numaralandırabiliriz. Bu bir sayı dizisi örneğidir.
sayı dizisi her birine benzersiz bir numara atanabilen bir dizi sayıdır.
Başka bir deyişle, her sayı belirli bir doğal sayı ve tek sayı ile ilişkilendirilebilir. Ve bu numarayı bu setten başka bir numaraya atamayacağız.
Numaralı sayı, dizinin inci üyesi olarak adlandırılır.
Genellikle tüm diziye bir harf (örneğin) deriz ve bu dizinin her üyesi, bu üyenin numarasına eşit bir indekse sahip aynı harftir:.
Dizinin inci teriminin bir formülle belirtilebilmesi çok uygundur. Örneğin, formül
sırayı belirtir:
Ve formül aşağıdaki sıradır:
Örneğin, bir aritmetik ilerleme bir dizidir (buradaki ilk terim eşittir ve farktır). Veya (, fark).
N. terim formülü
inci üyeyi bulmak için tekrarlayan bir formül diyoruz, önceki veya birkaç öncekini bilmeniz gerekir:
Örneğin, böyle bir formül kullanarak ilerlemenin inci terimini bulmak için, önceki dokuzu hesaplamamız gerekecek. Örneğin, izin verin. Sonra:
Peki, şimdi formül ne?
Her satırda bir sayı ile çarparak ekliyoruz. Ne için? Çok basit: bu, mevcut üye eksi sayısıdır:
Artık çok daha uygun, değil mi? Kontrol ediyoruz:
Kendin için karar ver:
Aritmetik bir ilerlemede, n'inci terimin formülünü bulun ve yüzüncü terimi bulun.
Çözüm:
İlk terim eşittir. Fark ne? Ve işte ne:
(bunun nedeni, ilerlemenin ardışık üyelerinin farkına eşit olan fark olarak adlandırılmasıdır).
Yani formül:
O halde yüzüncü terim:
ile arasındaki tüm doğal sayıların toplamı kaçtır?
Efsaneye göre, 9 yaşındaki büyük matematikçi Karl Gauss, bu miktarı birkaç dakika içinde hesapladı. İlk ve son sayıların toplamının eşit olduğunu, ikinci ve sonuncunun toplamının aynı olduğunu, sondan üçüncü ve üçüncünün toplamının aynı olduğunu vb. fark etti. Böyle kaç çift olacak? Bu doğru, tüm sayıların tam olarak yarısı, yani. Yani,
Herhangi bir aritmetik ilerlemenin ilk üyelerinin toplamı için genel formül şöyle olacaktır:
Örnek:
Tüm iki basamaklı katların toplamını bulun.
Çözüm:
Bu tür ilk sayı. Her sonraki, bir önceki sayıya eklenerek elde edilir. Böylece ilgilendiğimiz sayılar birinci terim ve fark ile aritmetik bir dizi oluşturur.
Bu ilerleme için üçüncü terim formülü:
Hepsinin çift haneli olması gerekiyorsa, ilerlemede kaç üye var?
Çok kolay: .
İlerlemedeki son terim eşit olacaktır. Sonra toplamı:
Cevap: .
Şimdi kendiniz karar verin:
- Sporcu her gün bir önceki günden daha fazla m koşar. İlk gün km m koşarsa haftalar içinde kaç kilometre koşar?
- Bir bisikletçi her gün bir öncekinden daha fazla kilometre yapar. İlk gün km sürdü. Km'yi kat etmek için kaç gün seyahat etmesi gerekiyor? Yolculuğun son gününde kaç kilometre yol gidecek?
- Bir mağazadaki buzdolabının fiyatı her yıl aynı oranda düşmektedir. Buzdolabının fiyatının her yıl ne kadar düştüğünü belirleyin, eğer ruble için satışa çıkarsa, altı yıl sonra ruble için satıldıysa.
Yanıtlar:
- Buradaki en önemli şey, aritmetik ilerlemeyi tanımak ve parametrelerini belirlemektir. Bu durumda, (hafta = gün). Bu ilerlemenin ilk üyelerinin toplamını belirlemeniz gerekir:
.
Cevap: - Burada verilmiştir: bulmak gereklidir.
Açıkçası, önceki problemdekiyle aynı toplam formülünü kullanmanız gerekir:
.
Değerleri değiştirin:Kök açıkça uymuyor, bu yüzden cevap.
Son gün için kat edilen mesafeyi inci terim formülünü kullanarak hesaplayalım:
(km).
Cevap: - Verilen:. Bulmak: .
Daha kolay olamazdı:
(ovmak).
Cevap:
ARİTMETİK İLERLEME. KISACA ANA HAKKINDA
Bu, bitişik sayılar arasındaki farkın aynı ve eşit olduğu sayısal bir dizidir.
Aritmetik ilerleme artan () ve azalan () olabilir.
Örneğin:
Bir aritmetik ilerlemenin n'inci terimini bulma formülü
formül ile yazılır, ilerlemedeki sayıların sayısı nerede.
Bir aritmetik ilerlemenin üyelerinin özelliği
Komşu üyeleri biliniyorsa, ilerlemenin bir üyesini kolayca bulmanızı sağlar - ilerlemedeki sayıların sayısı nerede.
Bir aritmetik ilerlemenin üyelerinin toplamı
Tutarı bulmanın iki yolu vardır:
Değerlerin sayısı nerede.
Değerlerin sayısı nerede.
Neyse konu kapandı. Bu satırları okuyorsanız çok iyisiniz demektir.
Çünkü insanların sadece %5'i kendi başlarına bir konuda ustalaşabiliyor. Ve sonuna kadar okursanız, o zaman o %5'in içindesiniz!
Şimdi en önemli şey geliyor.
Bu konudaki teoriyi anladınız. Ve yine, bu ... bu sadece süper! Zaten yaşıtlarının büyük çoğunluğundan daha iyisin.
Sorun şu ki, bu yeterli olmayabilir ...
Ne için?
Sınavı başarıyla geçmek, enstitüye bütçeden kabul edilmek ve EN ÖNEMLİ ömür boyu.
Seni hiçbir şeye ikna etmeyeceğim, sadece bir şey söyleyeceğim ...
İyi bir eğitim almış insanlar, almayanlara göre çok daha fazla kazanırlar. Bunlar istatistik.
Ama bu da ana şey değil.
Ana şey, DAHA MUTLU olmalarıdır (böyle çalışmalar var). Belki de onlar için çok daha fazla fırsat olduğu ve hayat daha parlak hale geldiği için? Bilmemek...
Ama kendin düşün...
Sınavda diğerlerinden kesinlikle daha iyi olmak ve nihayetinde ... daha mutlu olmak için ne gerekiyor?
BU KONUDA ELLE ÇÖZME SORUNLARI ALIN.
Sınavda sizden teori istenmeyecek.
İhtiyacın olacak sorunları bir süreliğine çözmek.
Ve eğer onları çözmediyseniz (ÇOK!), Aptalca bir yere gideceğinizden emin olabilirsiniz ya da sadece zamanında olmayacaksınız.
Sporda olduğu gibi - kesin olarak kazanmak için defalarca tekrarlamanız gerekir.
İstediğiniz yerde bir koleksiyon bulun, mutlaka çözümlerle, detaylı analizlerle ve karar ver, karar ver, karar ver!
Görevlerimizi kullanabilirsiniz (isteğe bağlı) ve elbette bunları tavsiye ederiz.
Görevlerimizin yardımıyla elinizi doldurmak için, şu anda okumakta olduğunuz YouClever ders kitabının ömrünü uzatmaya yardımcı olmanız gerekiyor.
Nasıl? İki seçenek var:
- Bu makaledeki tüm gizli görevleri paylaşın - 299 saat
- Eğiticinin 99 makalesinin tümünde tüm gizli görevlere erişimin kilidini açın - 999 RUB
Evet, ders kitabımızda bu tür 99 makale var ve tüm görevlere ve içindeki tüm gizli metinlere erişim bir kerede açılabilir.
ikinci durumda sana vereceğiz simülatör "Her konu için, tüm karmaşıklık seviyeleri için çözümler ve cevaplar içeren 6000 problem." Herhangi bir konudaki problemlerin çözümüne hakim olmak kesinlikle yeterli olacaktır.
Aslında, bu sadece bir simülatörden çok daha fazlasıdır - bütün bir eğitim programı. Gerekirse ÜCRETSİZ olarak da kullanabilirsiniz.
Sitenin tüm kullanım ömrü boyunca tüm metinlere ve programlara erişim sağlanır.
Sonuç olarak...
Görevlerimizi beğenmiyorsanız, başkalarını bulun. Sadece teori üzerinde durmayın.
“Anladım” ve “Çözebiliyorum” tamamen farklı becerilerdir. İkisine de ihtiyacın var.
Sorunları bulun ve çözün!