Zbroj prvih 15 brojeva aritmetičke progresije. Aritmetička progresija na primjerima
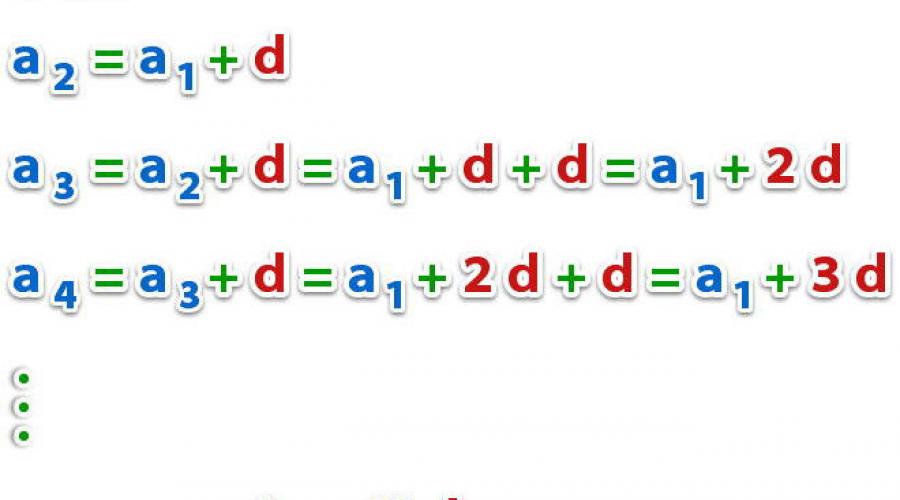
Pročitajte također
Ili je aritmetika vrsta uređenog numeričkog niza čija se svojstva proučavaju u kolegiju školske algebre. Ovaj članak detaljno razmatra pitanje kako pronaći zbroj aritmetičke progresije.
Što je to napredovanje?
Prije nego što nastavimo razmatrati pitanje (kako pronaći zbroj aritmetičke progresije), vrijedi razumjeti o čemu će biti riječi.
Svaki niz realnih brojeva koji se dobije zbrajanjem (oduzimanjem) neke vrijednosti od svakog prethodnog broja naziva se algebarska (aritmetička) progresija. Ova definicija, prevedena na jezik matematike, ima oblik:
Ovdje je i redni broj elementa reda a i. Dakle, poznavajući samo jedno sjeme, lako možete rekonstruirati cijeli niz. Parametar d u formuli naziva se razlika progresije.
Lako se može pokazati da za niz brojeva koji se razmatra vrijedi sljedeća jednakost:
a n = a 1 + d * (n - 1).
To jest, da biste pronašli vrijednost n-tog elementa u redoslijedu, dodajte razliku d prvom elementu a 1 n-1 puta.

Koliki je zbroj aritmetičke progresije: formula
Prije nego što date formulu za navedeni iznos, vrijedi razmotriti jednostavan poseban slučaj. S obzirom na napredak prirodnih brojeva od 1 do 10, morate pronaći njihov zbroj. Budući da je u napredovanju malo članova (10), moguće je problem riješiti izravno, odnosno zbrojiti sve elemente po redu.
S 10 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55.
Vrijedi razmotriti jednu zanimljivost: budući da se svaki pojam razlikuje od sljedećeg po istoj vrijednosti d = 1, tada će zbrajanje u paru prvog s desetim, drugog s devetim itd. Dati isti rezultat. Stvarno:
11 = 1+10 = 2+9 = 3+8 = 4+7 = 5+6.
Kao što vidite, postoji samo 5 ovih zbroja, odnosno točno dva puta manje od broja elemenata u nizu. Zatim množenjem zbroja (5) s rezultatom svakog zbroja (11) doći ćete do rezultata dobivenog u prvom primjeru.
Ako generaliziramo ovo zaključivanje, tada možemo napisati sljedeći izraz:
S n = n * (a 1 + a n) / 2.
Ovaj izraz pokazuje da uopće nije potrebno zbrajati sve elemente u nizu, dovoljno je znati vrijednost prvog a 1 i posljednjeg a n, kao i ukupan broj pojmova n.
Vjeruje se da je Gauss prvi put pomislio na ovu jednakost kada je tražio rješenje problema koji je postavio njegov školski učitelj: zbrojiti prvih 100 cijelih brojeva.

Zbroj elemenata od m do n: formula
Formula dana u prethodnom odlomku daje odgovor na pitanje kako pronaći zbroj aritmetičke progresije (prvi elementi), no često je u problemima potrebno zbrojiti niz brojeva u sredini progresije. Kako to učiniti?
Najlakši način za odgovor na ovo pitanje je razmotriti sljedeći primjer: neka je potrebno pronaći zbroj pojmova od m-tog do n-og. Kako bi se riješio problem, zadani segment od m do n progresije trebao bi biti predstavljen u obliku novog numeričkog niza. U ovom prikazu, m-ti pojam a m bit će prvi, a a n će biti n- (m-1). U ovom slučaju, primjenom standardne formule za zbroj, dobivate sljedeći izraz:
S m n = (n - m + 1) * (a m + a n) / 2.
Primjer korištenja formula
Znajući kako pronaći zbroj aritmetičke progresije, vrijedi razmotriti jednostavan primjer korištenja navedenih formula.
Ispod je numerički niz, trebali biste pronaći zbroj njegovih članova, počevši od 5. do 12.:
Navedeni brojevi ukazuju da je razlika d jednaka 3. Koristeći izraz za n -ti element, možete pronaći vrijednosti 5. i 12. člana progresije. Ispada:
a 5 = a 1 + d * 4 = -4 + 3 * 4 = 8;
a 12 = a 1 + d * 11 = -4 + 3 * 11 = 29.
Poznavajući vrijednosti brojeva na krajevima razmatrane algebarske progresije, a također i znajući koje brojeve u retku zauzimaju, možete upotrijebiti formulu za zbroj dobiven u prethodnom odlomku. Pokazat će se:
S 5 12 = (12 - 5 + 1) * (8 + 29) / 2 = 148.
Vrijedi napomenuti da se ta vrijednost može dobiti drugačije: prvo pronađite zbroj prvih 12 elemenata pomoću standardne formule, zatim izračunajte zbroj prva 4 elementa pomoću iste formule, a zatim od prvog zbroja oduzmite drugi.
Prilikom proučavanja algebre u općeobrazovnoj školi (9. razred) jedna od važnih tema je proučavanje numeričkih nizova koji uključuju progresije - geometrijske i aritmetičke. U ovom ćemo članku razmotriti aritmetičku progresiju i primjere s rješenjima.
Što je aritmetička progresija?
Da bismo to razumjeli, potrebno je dati definiciju razmatrane progresije, kao i dati osnovne formule koje će se dalje koristiti u rješavanju problema.
Poznato je da je u nekoj algebarskoj progresiji prvi član jednak 6, a sedmi član jednak 18. Potrebno je pronaći razliku i vratiti ovaj niz u 7. član.
Pomoću formule odredimo nepoznati pojam: a n = (n - 1) * d + a 1. Zamjenjujemo u njemu poznate podatke iz uvjeta, odnosno brojeve a 1 i 7, imamo: 18 = 6 + 6 * d. Iz ovog izraza možete lako izračunati razliku: d = (18 - 6) / 6 = 2. Tako smo odgovorili na prvi dio zadatka.
Da biste vratili niz do 7 pojmova, trebali biste koristiti definiciju algebarske progresije, to jest a 2 = a 1 + d, a 3 = a 2 + d, itd. Kao rezultat toga, vraćamo cijeli niz: a 1 = 6, a 2 = 6 + 2 = 8, a 3 = 8 + 2 = 10, a 4 = 10 + 2 = 12, a 5 = 12 + 2 = 14 , a 6 = 14 + 2 = 16, a 7 = 18.
Primjer 3: napredovanje

Još više zakomplicirajmo stanje problema. Sada je potrebno odgovoriti na pitanje kako pronaći aritmetičku progresiju. Možete navesti sljedeći primjer: s obzirom na dva broja, na primjer - 4 i 5. Potrebno je napraviti algebarsku progresiju tako da između njih stanu još tri pojma.
Prije nego što počnemo rješavati ovaj problem, potrebno je razumjeti koje će mjesto dati brojevi zauzeti u budućoj progresiji. Budući da će između njih biti još tri pojma, tada je 1 = -4 i 5 = 5. Nakon što smo to utvrdili, prelazimo na problem koji je sličan prethodnom. Opet, za n -ti pojam, koristimo formulu, dobivamo: a 5 = a 1 + 4 * d. Odakle je: d = (a 5 - a 1) / 4 = (5 - (-4)) / 4 = 2,25. Ovdje nismo dobili cijelu vrijednost razlike, već je to racionalan broj, pa formule za algebarsku progresiju ostaju iste.
Sada dodajte pronađenu razliku u 1 i vratite nedostajuće članove progresije. Dobivamo: a 1 = - 4, a 2 = - 4 + 2,25 = - 1,75, a 3 = -1,75 + 2,25 = 0,5, a 4 = 0,5 + 2,25 = 2,75, a 5 = 2,75 + 2,25 = 5, što se poklopilo sa stanjem problema.
Primjer # 4: prvi član progresije

Nastavimo s davanjem primjera aritmetičke progresije s rješenjem. U svim prethodnim problemima bio je poznat prvi broj algebarske progresije. Razmotrimo sada problem druge vrste: neka su zadana dva broja, gdje je 15 = 50 i 43 = 37. Potrebno je pronaći broj od kojeg počinje ovaj niz.
Do sada korištene formule pretpostavljaju poznavanje 1 i d. U izjavi o problemu ništa se ne zna o tim brojevima. Ipak, za svaki član ispisujemo izraze o kojima postoje informacije: a 15 = a 1 + 14 * d i 43 = a 1 + 42 * d. Primljene dvije jednadžbe, u kojima 2 nepoznate veličine (a 1 i d). To znači da se problem svodi na rješavanje sustava linearnih jednadžbi.
Najjednostavniji način rješavanja ovog sustava je izraziti 1 u svakoj jednadžbi, a zatim usporediti dobivene izraze. Prva jednadžba: a 1 = a 15 - 14 * d = 50 - 14 * d; druga jednadžba: a 1 = a 43 - 42 * d = 37 - 42 * d. Izjednačavanjem ovih izraza dobivamo: 50 - 14 * d = 37 - 42 * d, odakle je razlika d = (37 - 50) / (42 - 14) = - 0,464 (navedena su samo 3 decimalna mjesta).
Poznavajući d, možete koristiti bilo koji od 2 gornja izraza za 1. Na primjer, prvi: a 1 = 50 - 14 * d = 50 - 14 * ( - 0.464) = 56.496.
Ako sumnjate u rezultat, možete ga provjeriti, na primjer, odrediti 43 pojava progresije, koji je naveden u uvjetu. Dobivamo: a 43 = a 1 + 42 * d = 56,496 + 42 * (- 0,464) = 37,008. Mala pogreška nastaje zbog činjenice da su izračuni upotrijebili zaokruživanje na tisućinke.
Primjer # 5: iznos
Pogledajmo sada neke primjere s rješenjima za zbroj aritmetičke progresije.
Neka je dana numerička progresija sljedećeg oblika: 1, 2, 3, 4, ...,. Kako izračunati zbroj ovih 100 brojeva?
Zahvaljujući razvoju računalne tehnologije moguće je riješiti ovaj problem, odnosno zbrojiti sve brojeve uzastopno, što će računalo učiniti čim osoba pritisne tipku Enter. Međutim, problem se može riješiti u umu, ako obratimo pažnju da je predstavljeni niz brojeva algebarska progresija, a njegova razlika je 1. Primjenom formule za zbroj dobivamo: S n = n * (a 1 + an) / 2 = 100 * (1 + 100) / 2 = 5050.
Zanimljivo je primijetiti da se ovaj problem naziva "gaussovskim", jer je početkom 18. stoljeća slavni Nijemac, dok je još imao samo 10 godina, uspio riješiti to u svojoj glavi u nekoliko sekundi. Dječak nije znao formulu za zbroj algebarske progresije, ali je primijetio da ako zbrojite u parovima brojeve na rubovima niza, uvijek dobijete jedan rezultat, to jest 1 + 100 = 2 + 99 = 3 + 98 = ..., a budući da će od ovih iznosa biti točno 50 (100/2), tada je za točan odgovor dovoljno pomnožiti 50 sa 101.

Primjer # 6: zbroj članova od n do m
Drugi tipičan primjer zbroja aritmetičke progresije je sljedeći: s obzirom na niz brojeva: 3, 7, 11, 15, ..., morate pronaći koliko će biti zbroj njegovih članova od 8 do 14.
Problem se rješava na dva načina. Prvi od njih uključuje pronalaženje nepoznatih pojmova od 8 do 14, a zatim njihovo uzastopno dodavanje. Budući da postoji nekoliko termina, ova metoda nije dovoljno naporna. Ipak, predlaže se rješavanje ovog problema drugom metodom, koja je univerzalnija.
Ideja je dobiti formulu za zbroj algebarske progresije između pojmova m i n, gdje su n> m cijeli brojevi. Napišimo dva izraza za zbir u oba slučaja:
- S m = m * (a m + a 1) / 2.
- S n = n * (a n + a 1) / 2.
Budući da je n> m, očito je da 2 zbroja uključuje prvu. Posljednji zaključak znači da ako uzmemo razliku između ovih zbroja, i tome dodamo izraz a m (u slučaju uzimanja razlike, oduzima se od zbroja S n), tada dobivamo potreban odgovor na problem. Imamo: S mn = S n - S m + am = n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am = a 1 * (n - m) / 2 + an * n / 2 + am * (1- m / 2). U ovom izrazu potrebno je zamijeniti formule za a n i a m. Tada dobivamo: S mn = a 1 * (n - m) / 2 + n * (a 1 + (n - 1) * d) / 2 + (a 1 + (m - 1) * d) * (1 - m / 2) = a 1 * (n - m + 1) + d * n * (n - 1) / 2 + d * (3 * m - m 2 - 2) / 2.
Dobivena formula donekle je nezgrapna; ipak, zbroj S mn ovisi samo o n, m, a 1 i d. U našem slučaju, a 1 = 3, d = 4, n = 14, m = 8. Zamjenom ovih brojeva dobivamo: S mn = 301.

Kao što se može vidjeti iz danih rješenja, svi se problemi temelje na poznavanju izraza za n -ti član i formule za zbroj skupa prvih članova. Prije nego što nastavite s rješavanjem bilo kojeg od ovih problema, preporuča se pažljivo pročitati uvjet, jasno razumjeti što je potrebno pronaći i tek onda pristupiti rješenju.
Još jedan savjet je težiti jednostavnosti, odnosno ako možete odgovoriti na pitanje bez korištenja složenih matematičkih izračuna, tada morate učiniti upravo to, jer je u ovom slučaju vjerojatnost pogreške manja. Na primjer, u primjeru aritmetičke progresije s rješenjem # 6, moglo bi se zaustaviti na formuli S mn = n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am, i prekinuti opći problem u zasebne podzadaće (u ovom slučaju prvo pronađite članove an i am).
Ako postoje sumnje u dobiveni rezultat, preporučuje se da ga provjerite, kao što je to učinjeno u nekim od navedenih primjera. Smislili smo kako pronaći aritmetičku progresiju. Ako to shvatite, nije tako teško.
Prije nego što počnemo odlučivati aritmetički problemi progresije, razmotrimo što je to brojčani niz, budući da je aritmetička progresija poseban slučaj nizova brojeva.
Numerički niz je brojčani skup, čiji svaki element ima svoj redni broj... Elementi ovog skupa nazivaju se članovi niza. Redni broj elementa niza označen je indeksom:
Prvi element niza;
Peti element niza;
- "nth" element niza, tj. stavka "u redu" n.
Postoji odnos između vrijednosti elementa niza i njegovog rednog broja. Stoga niz možemo smatrati funkcijom čiji je argument redni broj elementa niza. Drugim riječima, to možemo reći niz je funkcija prirodnog argumenta:
Slijed se može postaviti na tri načina:
1 . Slijed se može postaviti pomoću tablice. U ovom slučaju jednostavno postavljamo vrijednost svakog člana niza.
Na primjer, Netko je odlučio preuzeti osobno upravljanje vremenom i za početak izračunati koliko vremena provodi na VKontakteu tijekom tjedna. Zapisujući vrijeme u tablicu, primit će niz koji se sastoji od sedam elemenata:

Prvi redak tablice sadrži broj dana u tjednu, drugi - vrijeme u minutama. Vidimo da je, dakle, u ponedjeljak Netko proveo 125 minuta na VKontakteu, odnosno u četvrtak - 248 minuta, a, odnosno u petak, samo 15.
2 . Slijed se može odrediti pomoću formule n -tog pojma.
U ovom slučaju, ovisnost vrijednosti elementa niza o njegovu broju izražava se izravno u obliku formule.
Na primjer, ako, onda
![]()
![]()
Da bismo pronašli vrijednost elementa niza s zadanim brojem, zamjenjujemo broj elementa u formulu n -tog člana.
Isto činimo ako trebamo pronaći vrijednost funkcije ako je vrijednost argumenta poznata. Vrijednost argumenta zamjenjujemo jednadžbom funkcije:
Ako npr. ![]() , tada
, tada
Još jednom napominjem da u nizu, za razliku od proizvoljne numeričke funkcije, samo prirodni broj može biti argument.
3 ... Slijed se može specificirati pomoću formule koja izražava ovisnost vrijednosti člana niza numeriranog o vrijednosti prethodnih članova. U ovom slučaju nije nam dovoljno znati samo broj člana niza kako bismo pronašli njegovu vrijednost. Moramo navesti prvog člana ili prvih nekoliko članova niza.
Na primjer, razmotrite slijed ![]() ,
, ![]()
Možemo pronaći vrijednosti članova niza u nizu počevši od trećeg:
Odnosno, svaki put da bismo pronašli vrijednost n-tog člana niza, vraćamo se na prethodna dva. Ovaj način sekvenciranja naziva se ponavljajući, od latinske riječi recurro- vrati se.
Sada možemo definirati aritmetičku progresiju. Aritmetička progresija jednostavan je poseban slučaj nizova brojeva.
Aritmetička progresija je numerički niz, čiji je svaki član, počevši od drugog, jednak prethodnom, dodan istom broju.

Broj se zove razlika aritmetičke progresije... Razlika u aritmetičkoj progresiji može biti pozitivna, negativna ili nula.
Ako je naslov = "(! LANG: d> 0">, то каждый член арифметической прогрессии больше предыдущего, и прогрессия является !} povećavajući.
Na primjer, 2; 5; osam; jedanaest;...
Ako je tada svaki član aritmetičke progresije manji od prethodnog, a progresija je umanjujući se.
Na primjer, 2; -1; -4; -7; ...
Ako su tada svi članovi progresije jednaki istom broju, a progresija je stacionarna.
Na primjer, 2; 2; 2; 2; ...
Glavno svojstvo aritmetičke progresije:
Pogledajmo sliku.
To vidimo
![]() , i u isto vrijeme
, i u isto vrijeme
![]()
Sabiranjem ove dvije jednakosti dobivamo:
![]() .
.
Podijelite obje strane jednakosti na 2:

Dakle, svaki član aritmetičke progresije, počevši od drugog, jednak je aritmetičkoj sredini dvaju susjednih:

Štoviše, od
![]() , i u isto vrijeme
, i u isto vrijeme
![]() , tada
, tada
![]() , i stoga
, i stoga
 Svaki član aritmetičke progresije koji počinje s title = "(! LANG: k> l">, равен среднему арифметическому двух равноотстоящих.
!}
Svaki član aritmetičke progresije koji počinje s title = "(! LANG: k> l">, равен среднему арифметическому двух равноотстоящих.
!}
Formula tog člana.
Vidimo da su za članove aritmetičke progresije ispunjeni sljedeći odnosi:
![]()
![]()
i konačno
Dobili smo formula n -tog pojma.
![]()
VAŽNO! Svaki član aritmetičke progresije može se izraziti pomoću i. Poznavajući prvi pojam i razliku aritmetičke progresije, možete pronaći bilo koji njegov izraz.
Zbroj n članova aritmetičke progresije.
U proizvoljnoj aritmetičkoj progresiji zbrojevi članova jednako udaljenih od krajnosti jednaki su međusobno:
Razmotrimo aritmetičku progresiju s n članova. Neka zbroj n članova ove progresije bude.
Posložimo članove progresije najprije uzlaznim brojevima, a zatim silaznim:

Dodajmo u parovima:
Zbroj u svakoj zagradi jednak je, broj parova je n.
Dobivamo:
![]()

Tako, zbroj n članova aritmetičke progresije može se pronaći po formulama:
Smatrati rješavanje zadataka za aritmetičku progresiju.
1 . Slijed je dat formulom n -tog pojma: . Dokažite da je ovaj niz aritmetička progresija.
Dokažimo da je razlika između dva susjedna člana niza jednaka istom broju.
Dobili smo da razlika između dva susjedna člana niza ne ovisi o njihovom broju i konstantna je. Stoga je po definiciji ovaj niz aritmetička progresija.
2 . Daje vam se aritmetička progresija -31; -27; ...
a) Pronađi 31 člana progresije.
b) Odredite je li broj 41 uključen u ovu progresiju.
a) To vidimo;
Napišimo formulu za n -ti izraz za našu progresiju.
Općenito ![]()
U našem slučaju ![]() , dakle
, dakle ![]()
Dobivamo:
b) Pretpostavimo da je 41 član niza. Pronađimo njegov broj. Da bismo to učinili, rješavamo jednadžbu:
![]()
Dobili smo prirodnu vrijednost n, stoga je, da, broj 41 član progresije. Da pronađena vrijednost n nije prirodan broj, tada bismo odgovorili da broj 41 NIJE član progresije.
3 ... a) Između brojeva 2 i 8 umetnite 4 broja tako da zajedno s danim brojevima naprave aritmetičku progresiju.
b) Pronađite zbroj članova rezultirajuće progresije.
a) Umetnite četiri broja između brojeva 2 i 8:

Dobili smo aritmetičku progresiju sa 6 članova. ![]()
Pronađimo razliku u ovoj progresiji. Da bismo to učinili, upotrijebit ćemo formulu za n -ti pojam:
![]()
Sada je lako pronaći vrijednosti brojeva:
3,2; 4,4; 5,6; 6,8
b) 
Odgovor: a) da; b) 30
4. Kamion prevozi šaržu drobljenog kamena tešku 240 tona, povećavajući dnevno stopu transporta za isti broj tona. Poznato je da su tijekom prvog dana prevezene 2 tone drobljenog kamena. Odredite koliko je tona šuta prevezeno dvanaestog dana ako su svi radovi završeni u 15 dana.
Prema stanju problema, količina ruševina koje kamion prevozi povećava se svaki dan za isti broj. Stoga imamo posla s aritmetičkom progresijom.
Formulirajmo ovaj problem u smislu aritmetičke progresije.
Tijekom prvog dana prevezene su 2 tone drobljenog kamena: a_1 = 2.
Sav posao je obavljen u 15 dana :.
Kamion prevozi šaržu drobljenog kamena tešku 240 tona:
Moramo pronaći.
Prvo pronađite razliku u napredovanju. Upotrijebimo formulu za zbroj n članova progresije.

U našem slučaju:
![]()
![]()
 Da, da: napredak aritmetike nije igračka za vas :)
Da, da: napredak aritmetike nije igračka za vas :) Pa, prijatelji, ako čitate ovaj tekst, onda mi interni dokazi govore da još ne znate što je aritmetička progresija, ali zaista (ne, ovako: SOOOOO!) Želite znati. Stoga vas neću mučiti dugim uvodima i prijeći na stvar.
Počnimo s nekoliko primjera. Razmotrimo nekoliko skupova brojeva:
- 1; 2; 3; 4; ...
- 15; 20; 25; 30; ...
- $ \ sqrt (2); \ 2 \ sqrt (2); \ 3 \ sqrt (2); ... $
Što je zajedničko svim tim skupovima? Na prvi pogled ništa. Ali zapravo postoji nešto. Naime: svaki sljedeći element razlikuje se od prethodnog istim brojem.
Prosudite sami. Prvi skup su jednostavno uzastopni brojevi, svaki sljedeći više od prethodnog. U drugom slučaju, razlika između susjednih brojeva već je jednaka pet, ali je ta razlika i dalje konstantna. U trećem slučaju, korijeni općenito. Međutim, $ 2 \ sqrt (2) = \ sqrt (2) + \ sqrt (2) $, a $ 3 \ sqrt (2) = 2 \ sqrt (2) + \ sqrt (2) $, tj. iu ovom slučaju svaki sljedeći element jednostavno se povećava za $ \ sqrt (2) $ (i nemojte se bojati da je ovaj broj iracionalan).
Dakle: svi se takvi nizovi nazivaju aritmetičkim progresijama. Dajmo strogu definiciju:
Definicija. Niz brojeva u kojima se svaki sljedeći razlikuje od prethodnog za potpuno isti iznos naziva se aritmetička progresija. Sam iznos po kojem se brojevi razlikuju naziva se razlika progresije i najčešće se označava slovom $ d $.
Oznaka: $ \ left (((a) _ (n)) \ right) $ - sama progresija, $ d $ - njezina razlika.
I samo par važnih napomena. Prvo, samo uredno redoslijed brojeva: dopušteno ih je čitati strogo redoslijedom kojim su napisani - i ništa drugo. Ne možete preurediti ili zamijeniti brojeve.
Drugo, sam niz može biti konačan ili beskonačan. Na primjer, skup (1; 2; 3) je očito konačna aritmetička progresija. Ali ako napišete nešto u duhu (1; 2; 3; 4; ...) - ovo je već beskrajan napredak. Elipsa nakon četiri, takoreći, nagovještava da se još uvijek događa podosta brojeva. Beskonačno mnogo, na primjer. :)
Također želim napomenuti da se progresije povećavaju i smanjuju. Već smo vidjeli sve veće - isti skup (1; 2; 3; 4; ...). I evo primjera smanjenja progresije:
- 49; 41; 33; 25; 17; ...
- 17,5; 12; 6,5; 1; −4,5; −10; ...
- $ \ sqrt (5); \ \ sqrt (5) -1; \ \ sqrt (5) -2; \ \ sqrt (5) -3; ... $
U redu, u redu: ovaj posljednji primjer mogao bi izgledati previše kompliciran. Ali ostalo, mislim da razumijete. Stoga ćemo uvesti nove definicije:
Definicija. Aritmetička progresija naziva se:
- povećanje ako je svaki sljedeći element veći od prethodnog;
- smanjuje se ako je, naprotiv, svaki sljedeći element manji od prethodnog.
Osim toga, postoje takozvani "stacionarni" nizovi - sastoje se od istog ponavljajućeg broja. Na primjer, (3; 3; 3; ...).
Ostaje samo jedno pitanje: kako razlikovati rastuću progresiju od opadajuće? Srećom, sve ovisi o predznaku broja $ d $, tj. progresija razlike:
- Ako je $ d \ gt 0 $, tada se progresija povećava;
- Ako je $ d \ lt 0 $, tada se napredovanje očito smanjuje;
- Konačno, postoji slučaj $ d = 0 $ - u ovom slučaju cijela se progresija svodi na stacionarni niz identičnih brojeva: (1; 1; 1; 1; ...) itd.
Pokušajmo izračunati razliku $ d $ za tri gore navedene rastuće progresije. Da biste to učinili, dovoljno je uzeti bilo koja dva susjedna elementa (na primjer, prvi i drugi) i oduzeti broj s lijeve strane od broja s desne strane. To će izgledati ovako:
- 41−49=−8;
- 12−17,5=−5,5;
- $ \ sqrt (5) -1- \ sqrt (5) = - 1 $.
Kao što vidite, u sva tri slučaja razlika se doista pokazala negativnom. A sada kada smo manje -više shvatili definicije, vrijeme je da shvatimo kako su progresije opisane i koja su njihova svojstva.
Članovi progresije i ponavljajuća formula
Budući da se elementi naših nizova ne mogu zamijeniti, mogu se numerirati:
\ [\ lijevo (((a) _ (n)) \ desno) = \ lijevo \ (((a) _ (1)), \ ((a) _ (2)), ((a) _ (3 )), ... \ udesno \) \]
Pojedini elementi ovog skupa nazivaju se članovi progresije. Označeni su brojem: prvi pojam, drugi pojam itd.
Osim toga, kao što već znamo, susjedni članovi progresije povezani su formulom:
\ [((a) _ (n))-((a) _ (n-1)) = d \ Desna strelica ((a) _ (n)) = ((a) _ (n-1)) + d \]
Ukratko, da biste pronašli $ n $ -ti pojam u progresiji, morate znati $ n-1 $ -ti pojam i $ d $ razliku. Takva se formula naziva ponavljajućom, jer uz njenu pomoć možete pronaći bilo koji broj, samo poznavajući prethodni (a zapravo - sve prethodne). To je vrlo nezgodno pa postoji složenija formula koja sve izračune svodi na prvi član i razliku:
\ [((a) _ (n)) = ((a) _ (1)) + \ lijevo (n-1 \ desno) d \]
Sigurno ste već upoznali ovu formulu. Obožavaju ga davati u svim vrstama priručnika i reshebnika. I u svakom razumnom udžbeniku iz matematike, ona je jedna od prvih.
Ipak, predlažem da malo vježbamo.
Problem broj 1. Zapišite prva tri člana aritmetičke progresije $ \ left (((a) _ (n)) \ right) $ if $ ((a) _ (1)) = 8, d = -5 $.
Riješenje. Dakle, znamo da je prvi izraz $ ((a) _ (1)) = 8 $ i razlika progresije $ d = -5 $. Upotrijebimo formulu koju smo upravo dali i zamijenimo $ n = 1 $, $ n = 2 $ i $ n = 3 $:
\ [\ begin (align) & ((a) _ (n)) = ((a) _ (1)) + \ lijevo (n-1 \ desno) d; \\ & ((a) _ (1)) = ((a) _ (1)) + \ lijevo (1-1 \ desno) d = ((a) _ (1)) = 8; \\ & ((a) _ (2)) = ((a) _ (1)) + \ lijevo (2-1 \ desno) d = ((a) _ (1)) + d = 8-5 = 3; \\ & ((a) _ (3)) = ((a) _ (1)) + \ lijevo (3-1 \ desno) d = ((a) _ (1)) + 2d = 8-10 = -2. \\ \ završi (poravnaj) \]
Odgovor: (8; 3; −2)
To je sve! Imajte na umu: naš napredak se smanjuje.
Naravno, $ n = 1 $ nije se moglo zamijeniti - prvi izraz nam je već poznat. Međutim, zamijenivši jedan, pobrinuli smo se da naša formula djeluje čak i za prvi mandat. U drugim slučajevima sve se svelo na trivijalnu aritmetiku.
Problem broj 2. Ispišite prva tri člana aritmetičke progresije ako je njegov sedmi član −40, a sedamnaesti −50.
Riješenje. Zapisimo stanje problema uobičajenim izrazima:
\ [((a) _ (7)) = - 40; \ quad ((a) _ (17)) = - 50. \]
\ [\ left \ (\ begin (align) & ((a) _ (7)) = ((a) _ (1)) + 6d \\ & ((a) _ (17)) = ((a) _ (1)) + 16d \\ \ završi (poravnaj) \ udesno. \]
\ [\ left \ (\ start (align) & ((a) _ (1)) + 6d = -40 \\ & ((a) _ (1)) + 16d = -50 \\ \ end (align) \ u redu. \]
Stavila sam znak sustava jer se ti zahtjevi moraju istovremeno ispuniti. I sada primijetite da ako oduzmemo prvu od druge jednadžbe (imamo pravo na to, budući da imamo sustav), dobivamo ovo:
\ [\ begin (align) & ((a) _ (1)) + 16d- \ left (((a) _ (1)) + 6d \ right) =- 50- \ left (-40 \ right); \\ & ((a) _ (1)) + 16d - ((a) _ (1)) - 6d = -50 + 40; \\ & 10d = -10; \\ & d = -1. \\ \ završi (poravnaj) \]
Tako smo lako pronašli razliku u napredovanju! Ostaje zamijeniti pronađeni broj u bilo kojoj od jednadžbi sustava. Na primjer, u prvom:
\ [\ begin (matrica) ((a) _ (1)) + 6d = -40; \ quad d = -1 \\ \ Downarrow \\ ((a) _ (1)) -6 = -40; \\ ((a) _ (1)) = - 40 + 6 = -34. \\ \ kraj (matrica) \]
Sada, znajući prvi pojam i razliku, ostaje pronaći drugi i treći član:
\ [\ begin (align) & ((a) _ (2)) = ((a) _ (1)) + d = -34-1 = -35; \\ & ((a) _ (3)) = ((a) _ (1)) + 2d = -34-2 = -36. \\ \ završi (poravnaj) \]
Spreman! Problem je riješen.
Odgovor: (-34; -35; -36)
Obratite pozornost na jedno zanimljivo svojstvo progresije koje smo otkrili: ako uzmemo $ n $ th i $ m $ th izraze i oduzmemo ih jedan od drugog, dobit ćemo razliku progresije pomnoženu s brojem $ n-m $:
\ [((a) _ (n)) - ((a) _ (m)) = d \ cdot \ lijevo (n -m \ desno) \]
Jednostavno, ali vrlo korisno svojstvo koje biste svakako trebali znati - uz njegovu pomoć možete značajno ubrzati rješavanje mnogih problema u progresiji. Evo vrhunskog primjera:
Problem broj 3. Peti član aritmetičke progresije je 8,4, a deseti 14,4. Pronađi petnaesti član ove progresije.
Riješenje. Budući da je $ ((a) _ (5)) = 8,4 $, $ ((a) _ (10)) = 14,4 $, a vi morate pronaći $ ((a) _ (15)) $, tada bilježimo sljedeće :
\ [\ begin (align) & ((a) _ (15)) - ((a) _ (10)) = 5d; \\ & ((a) _ (10)) - ((a) _ (5)) = 5d. \\ \ završi (poravnaj) \]
Ali prema uvjetu $ ((a) _ (10)) - ((a) _ (5)) = 14,4-8,4 = 6 USD, dakle 5d = 6 USD, odakle imamo:
\ [\ begin (align) & ((a) _ (15)) - 14.4 = 6; \\ & ((a) _ (15)) = 6 + 14,4 = 20,4. \\ \ završi (poravnaj) \]
Odgovor: 20.4
To je sve! Nismo morali sastaviti neke sustave jednadžbi i izračunati prvi član i razliku - sve je riješeno u samo nekoliko redaka.
Razmotrimo sada drugu vrstu zadataka - pronaći negativne i pozitivne članove progresije. Nije tajna da ako se progresija poveća, dok je prvi pojam negativan, u njemu će se prije ili kasnije pojaviti pozitivni termini. I naprotiv: članovi opadajuće progresije prije ili kasnije postat će negativni.
Istodobno, daleko je od toga da je ovaj trenutak moguće "opipati", uzastopno prolazeći kroz elemente. Često su problemi osmišljeni na takav način da bi bez poznavanja formula izračuni trajali nekoliko listova - samo bismo zaspali dok smo pronašli odgovor. Stoga ćemo te probleme pokušati riješiti na brži način.
Problem broj 4. Koliko negativnih članova ima u aritmetičkoj progresiji -38,5; −35,8; ...?
Riješenje. Dakle, $ ((a) _ (1)) = - 38,5 $, $ ((a) _ (2)) = - 35,8 $, odakle odmah nalazimo razliku:
Imajte na umu da je razlika pozitivna, pa se progresija povećava. Prvi izraz je negativan, pa ćemo u jednom trenutku zaista naići na pozitivne brojeve. Pitanje je samo kada će se to dogoditi.
Pokušajmo saznati: koliko dugo (tj. Do kojeg prirodnog broja $ n $) se čuva negativnost pojmova:
\ [\ begin (align) & ((a) _ (n)) \ lt 0 \ Desna strelica ((a) _ (1)) + \ lijevo (n-1 \ desno) d \ lt 0; \\ & -38,5+ \ lijevo (n -1 \ desno) \ cdot 2,7 \ lt 0; \ quad \ lijevo | \ cdot 10 \ udesno. \\ & -385 + 27 \ cdot \ lijevo (n -1 \ desno) \ lt 0; \\ & -385 + 27n -27 \ lt 0; \\ & 27n \ lt 412; \\ & n \ lt 15 \ frac (7) (27) \ Rightarrow ((n) _ (\ max)) = 15. \\ \ završi (poravnaj) \]
Zadnji redak zahtijeva pojašnjenje. Dakle, znamo da je $ n \ lt 15 \ frac (7) (27) $. S druge strane, zadovoljit ćemo se samo cijelim vrijednostima broja (štoviše: $ n \ in \ mathbb (N) $), pa je najveći dopušteni broj točno $ n = 15 $, i nikako 16.
Problem broj 5. U aritmetičkoj progresiji $ (() _ (5)) = - 150, (() _ (6)) = - 147 $. Pronađi broj prvog pozitivnog člana ove progresije.
To bi bio potpuno isti problem kao i prethodni, ali ne znamo $ ((a) _ (1)) $. No, poznati su susjedni pojmovi: $ ((a) _ (5)) $ i $ ((a) _ (6)) $, pa lako možemo pronaći razliku progresije:
Osim toga, pokušat ćemo peti izraz izraziti u smislu prvog i razlike prema standardnoj formuli:
\ [\ begin (align) & ((a) _ (n)) = ((a) _ (1)) + \ left (n-1 \ right) \ cdot d; \\ & ((a) _ (5)) = ((a) _ (1)) + 4d; \\ & -150 = ((a) _ (1)) + 4 \ cdot 3; \\ & ((a) _ (1)) = -150-12 = -162. \\ \ završi (poravnaj) \]
Sada nastavljamo analogno s prethodnim zadatkom. Doznajemo u kojem će trenutku našeg slijeda biti pozitivnih brojeva:
\ [\ begin (align) & ((a) _ (n)) = - 162+ \ lijevo (n -1 \ desno) \ cdot 3 \ gt 0; \\ & -162 + 3n -3 \ gt 0; \\ & 3n \ gt 165; \\ & n \ gt 55 \ Desna strelica ((n) _ (\ min)) = 56. \\ \ završi (poravnaj) \]
Najmanji cijeli broj ove nejednakosti je 56.
Napomena: u zadnjem zadatku sve se svelo na strogu nejednakost, pa nam opcija $ n = 55 $ neće odgovarati.
Sada kada smo naučili rješavati jednostavne probleme, prijeđimo na složenije. No, prvo, proučimo još jedno vrlo korisno svojstvo aritmetičkih progresija, koje će nam u budućnosti uštedjeti mnogo vremena i nejednakih ćelija. :)
Aritmetička sredina i jednake alineje
Razmotrimo nekoliko uzastopnih članova rastuće aritmetičke progresije $ \ left (((a) _ (n)) \ right) $. Pokušajmo ih označiti na brojčanoj liniji:
Članovi aritmetičke progresije na brojevnoj pravojPosebno sam naveo proizvoljne članove $ ((a) _ (n-3)), ..., ((a) _ (n + 3)) $, a ne bilo koje $ ((a) _ (1)), \ ( (a) _ (2)), \ ((a) _ (3)) $ itd. Budući da pravilo, o kojem ću sada govoriti, djeluje isto za sve "segmente".
A pravilo je vrlo jednostavno. Sjetimo se formule ponavljanja i zapišite je za sve označene članove:
\ [\ begin (align) & ((a) _ (n-2)) = ((a) _ (n-3)) + d; \\ & ((a) _ (n-1)) = ((a) _ (n-2)) + d; \\ & ((a) _ (n)) = ((a) _ (n-1)) + d; \\ & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n + 1)) + d; \\ \ završi (poravnaj) \]
Međutim, te se jednakosti mogu drugačije prepisati:
\ [\ begin (align) & ((a) _ (n -1)) = ((a) _ (n)) - d; \\ & ((a) _ (n -2)) = ((a) _ (n)) - 2d; \\ & ((a) _ (n -3)) = ((a) _ (n)) - 3d; \\ & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n)) + 2d; \\ & ((a) _ (n + 3)) = ((a) _ (n)) + 3d; \\ \ završi (poravnaj) \]
Pa, pa što? A činjenica da izrazi $ ((a) _ (n-1)) $ i $ ((a) _ (n + 1)) $ leže na istoj udaljenosti od $ ((a) _ (n)) $ . I ta je udaljenost jednaka $ d $. Isto se može reći za članove $ ((a) _ (n -2)) $ i $ ((a) _ (n + 2)) $ - oni se također uklanjaju iz $ ((a) _ (n) ) $ ista udaljenost jednaka 2d $. Možete nastaviti u nedogled, ali značenje je dobro ilustrirano slikom.
 Članovi progresije leže na istoj udaljenosti od središta
Članovi progresije leže na istoj udaljenosti od središta Što to za nas znači? To znači da možete pronaći $ ((a) _ (n)) $ ako su poznati susjedni brojevi:
\ [((a) _ (n)) = \ frac (((a) _ (n-1)) + ((a) _ (n + 1))) (2) \]
Došli smo do izvrsne izjave: svaki član aritmetičke progresije jednak je aritmetičkoj sredini susjednih pojmova! Štoviše: možemo odstupiti od naših $ ((a) _ (n)) $ lijevo i desno ne jedan korak, već $ k $ koraka - i dalje će formula biti točna:
\ [((a) _ (n)) = \ frac (((a) _ (n-k)) + ((a) _ (n + k))) (2) \]
Oni. lako možemo pronaći neke $ ((a) _ (150)) $ ako znamo $ ((a) _ (100)) $ i $ ((a) _ (200)) $, jer $ ((a) _ (150)) = \ frac (((a) _ (100)) + ((a) _ (200))) (2) $. Na prvi pogled može se činiti da nam ta činjenica ne daje ništa korisno. Međutim, u praksi se mnogi problemi posebno "izoštravaju" za korištenje aritmetičke sredine. Pogledaj:
Problem broj 6. Pronađite sve vrijednosti $ x $ za koje su brojevi $ -6 ((x) ^ (2)) $, $ x + 1 $ i $ 14 + 4 ((x) ^ (2)) $ uzastopni članovi aritmetičke progresije (redom).
Riješenje. Budući da su navedeni brojevi članovi progresije, uvjet aritmetičke sredine za njih je zadovoljen: središnji element $ x + 1 $ može se izraziti u smislu susjednih elemenata:
\ [\ begin (align) & x + 1 = \ frac (-6 ((x) ^ (2)) + 14 + 4 ((x) ^ (2))) (2); \\ & x + 1 = \ frac (14-2 ((x) ^ (2))) (2); \\ & x + 1 = 7 - ((x) ^ (2)); \\ & ((x) ^ (2)) + x-6 = 0. \\ \ završi (poravnaj) \]
Rezultat je klasična kvadratna jednadžba. Njegovi korijeni: $ x = 2 $ i $ x = -3 $ - ovo su odgovori.
Odgovor: −3; 2.
Problem broj 7. Pronađite vrijednosti $$ za koje brojevi $ -1; 4-3; (() ^ (2)) + 1 $ čine aritmetičku progresiju (tim redoslijedom).
Riješenje. Opet, izražavamo srednji pojam u smislu aritmetičke sredine susjednih pojmova:
\ [\ begin (align) & 4x-3 = \ frac (x-1 + ((x) ^ (2)) + 1) (2); \\ & 4x-3 = \ frac (((x) ^ (2)) + x) (2); \ quad \ left | \ cdot 2 \ desno.; \\ & 8x-6 = ((x) ^ (2)) + x; \\ & ((x) ^ (2)) - 7x + 6 = 0. \\ \ završi (poravnaj) \]
Opet kvadratna jednadžba. I opet postoje dva korijena: $ x = 6 $ i $ x = 1 $.
Odgovor: 1; 6.
Ako u procesu rješavanja problema dobijete neke brutalne brojeve ili niste potpuno sigurni u točnost pronađenih odgovora, postoji prekrasna tehnika koja vam omogućuje da provjerite: jesmo li problem riješili ispravno?
Na primjer, u zadatku broj 6 dobili smo odgovore -3 i 2. Kako provjeriti jesu li ti odgovori točni? Uključimo ih samo u početno stanje i vidimo što će se dogoditi. Dopustite mi da vas podsjetim da imamo tri broja ($ -6 (() ^ (2)) $, $ + 1 $ i $ 14 + 4 (() ^ (2)) $). Zamjena $ x = -3 $:
\ [\ begin (align) & x = -3 \ Rightarrow \\ & -6 ((x) ^ (2)) = -54; \\ & x + 1 = -2; \\ & 14 + 4 ((x) ^ (2)) = 50. \ end (poravnaj) \]
Primljeni brojevi -54; −2; 50, koji se razlikuju po 52, nesumnjivo je aritmetička progresija. Ista se stvar događa za $ x = 2 $:
\ [\ begin (align) & x = 2 \ Rightarrow \\ & -6 ((x) ^ (2)) = - 24; \\ & x + 1 = 3; \\ & 14 + 4 ((x) ^ (2)) = 30. \ end (poravnaj) \]
Opet napredovanje, ali s razlikom od 27. Dakle, problem je ispravno riješen. Zainteresirani mogu sami provjeriti drugi problem, ali odmah ću reći: i tu je sve točno.
Općenito, rješavajući posljednje probleme, naišli smo na još jednu zanimljivu činjenicu, koju također treba zapamtiti:
Ako su tri broja takva da je drugi aritmetička sredina prvog i posljednjeg, tada ti brojevi tvore aritmetičku progresiju.
U budućnosti će nam razumijevanje ove izjave doslovno "konstruirati" potrebne progresije, na temelju stanja problema. No, prije nego što prijeđemo na takvu "izgradnju", trebali bismo obratiti pozornost na još jednu činjenicu, koja izravno proizlazi iz već razmatranog.
Grupiranje i zbroj elemenata
Vratimo se opet na osi brojeva. Zabilježimo tamo nekoliko članova progresije, između kojih je možda. ima puno drugih članova:
Brojčana linija ima 6 označenih elemenataPokušajmo izraziti "lijevi rep" u smislu $ ((a) _ (n)) $ i $ d $, a "desni rep" u smislu $ ((a) _ (k)) $ i $ d $ . Vrlo je jednostavno:
\ [\ begin (align) & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n)) + 2d; \\ & ((a) _ (k -1)) = ((a) _ (k)) - d; \\ & ((a) _ (k -2)) = ((a) _ (k)) - 2d. \\ \ završi (poravnaj) \]
Sada imajte na umu da su sljedeće sume jednake:
\ [\ begin (align) & ((a) _ (n)) + ((a) _ (k)) = S; \\ & ((a) _ (n + 1)) + ((a) _ (k -1)) = ((a) _ (n)) + d + ((a) _ (k)) - d = S; \\ & ((a) _ (n + 2)) + ((a) _ (k -2)) = ((a) _ (n)) + 2d + ((a) _ (k)) - 2d = S. \ end (poravnaj) \]
Jednostavno rečeno, ako za početak uzmemo u obzir dva elementa progresije, koji su ukupno jednaki nekom broju $ S $, a zatim krećemo od tih elemenata u suprotnim smjerovima (jedan prema drugom ili obrnuto da se odmaknemo), zatim zbroji elemenata na koje ćemo se spotaknuti također će biti jednaki$ S $. To se najjasnije može grafički prikazati:
 Jednako uvlačenje daje jednake količine
Jednako uvlačenje daje jednake količine Razumijevanje ove činjenice omogućit će nam rješavanje problema fundamentalno veće razine složenosti od onih koje smo gore razmatrali. Na primjer, takve:
Problem broj 8. Odredite razliku aritmetičke progresije u kojoj je prvi član 66, a umnožak drugog i dvanaestog člana najmanji mogući.
Riješenje. Zapišimo sve što znamo:
\ [\ begin (align) & ((a) _ (1)) = 66; \\ & d =? \\ & ((a) _ (2)) \ cdot ((a) _ (12)) = \ min. \ end (poravnaj) \]
Dakle, ne znamo razliku u napredovanju $ d $. Zapravo, cijelo rješenje bit će izgrađeno oko razlike, budući da se proizvod $ ((a) _ (2)) \ cdot ((a) _ (12)) $ može prepisati na sljedeći način:
\ [\ begin (align) & ((a) _ (2)) = ((a) _ (1)) + d = 66 + d; \\ & ((a) _ (12)) = ((a) _ (1)) + 11d = 66 + 11d; \\ & ((a) _ (2)) \ cdot ((a) _ (12)) = \ lijevo (66 + d \ desno) \ cdot \ lijevo (66 + 11d \ desno) = \\ & = 11 \ cdot \ lijevo (d + 66 \ desno) \ cdot \ lijevo (d + 6 \ desno). \ end (poravnaj) \]
Za one u spremniku: izvadio sam zajednički faktor 11 iz druge zagrade. Dakle, traženi proizvod je kvadratna funkcija s obzirom na varijablu $ d $. Stoga razmotrimo funkciju $ f \ left (d \ right) = 11 \ left (d + 66 \ right) \ left (d + 6 \ right) $ - njezin će graf biti parabola s granama prema gore, budući da proširimo li zagrade, dobivamo:
\ [\ begin (align) & f \ left (d \ right) = 11 \ left (((d) ^ (2)) + 66d + 6d + 66 \ cdot 6 \ right) = \\ & = 11 (( d) ^ (2)) + 11 \ cdot 72d + 11 \ cdot 66 \ cdot 6 \ end (poravnaj) \]
Kao što vidite, koeficijent na vodećem terminu je 11 - ovo je pozitivan broj, pa se zaista bavimo parabolom s granama prema gore:
kvadratni grafikon funkcija - parabola
Napomena: ova parabola uzima svoju minimalnu vrijednost na svom vrhu s apscisom $ ((d) _ (0)) $. Naravno, ovu apscisu možemo izračunati prema standardnoj shemi (postoji i formula $ ((d) _ (0)) = (- b) / (2a) \; $), ali bilo bi mnogo razumnije primijetiti da željeni vrh leži na osi simetrije parabole, pa je točka $ ((d) _ (0)) $ jednako udaljena od korijena jednadžbe $ f \ lijevo (d \ desno) = 0 $:
\ [\ begin (align) & f \ left (d \ right) = 0; \\ & 11 \ cdot \ lijevo (d + 66 \ desno) \ cdot \ lijevo (d + 6 \ desno) = 0; \\ & ((d) _ (1)) = - 66; \ quad ((d) _ (2)) = - 6. \\ \ završi (poravnaj) \]
Zato nisam žurio s otvaranjem zagrada: u izvornom obliku korijenje je bilo vrlo, vrlo lako pronaći. Stoga je apscisa jednaka aritmetičkoj sredini brojeva −66 i −6:
\ [((d) _ (0)) = \ frac (-66-6) (2) =-36 \]
Što nam otkriveni broj daje? S njim traženi proizvod poprima najmanju vrijednost (usput, nismo brojali $ ((y) _ (\ min)) $ - ovo nam ne treba). Istodobno, ovaj broj je razlika između izvorne progresije, tj. odgovor smo pronašli. :)
Odgovor: −36
Problem broj 9. Umetnite tri broja između brojeva $ - \ frac (1) (2) $ i $ - \ frac (1) (6) $ tako da zajedno s danim brojevima tvore aritmetičku progresiju.
Riješenje. U osnovi, moramo napraviti niz od pet brojeva, s tim da su prvi i zadnji broj već poznati. Označimo nedostajuće brojeve varijablama $ x $, $ y $ i $ z $:
\ [\ lijevo (((a) _ (n)) \ desno) = \ lijevo \ ( - \ frac (1) (2); x; y; z; - \ frac (1) (6) \ right \ ) \]
Imajte na umu da je broj $ y $ "sredina" našeg niza - jednako je udaljen i od brojeva $ x $ i $ z $, i od brojeva $ - \ frac (1) (2) $ i $ - \ razlomak (1) (6) $. A ako trenutno ne možemo dobiti $ y $ iz brojeva $ x $ i $ z $, onda je situacija drugačija s krajevima progresije. Zapamtite aritmetičku sredinu:
Sada ćemo, znajući $ y $, pronaći preostale brojeve. Imajte na umu da se $ x $ nalazi između brojeva $ - \ frac (1) (2) $ i upravo pronađenih $ y = - \ frac (1) (3) $. Zato
Slično obrazloženju, nalazimo preostali broj:
Spreman! Pronašli smo sva tri broja. Zapišite ih u odgovor redoslijedom kojim ih treba umetnuti između izvornih brojeva.
Odgovor: $ - \ frac (5) (12); \ - \ frac (1) (3); \ - \ frac (1) (4) $
Problem broj 10. Umetnite nekoliko brojeva između brojeva 2 i 42, koji zajedno s tim brojevima tvore aritmetičku progresiju, ako znate da je zbroj prvog, drugog i posljednjeg od umetnutih brojeva 56.
Riješenje. Još teži zadatak, koji se, međutim, rješava po istoj shemi kao i prethodni - kroz aritmetičku sredinu. Problem je u tome što ne znamo točno koliko brojeva umetnuti. Stoga, radi definitivnosti, pretpostavimo da će nakon umetanja svega biti točno $ n $ brojeva, a prvi od njih je 2, a posljednji 42. U tom se slučaju željena aritmetička progresija može predstaviti kao:
\ [\ lijevo (((a) _ (n)) \ desno) = \ lijevo \ (2; ((a) _ (2)); ((a) _ (3)); ...; (( a) _ (n-1)); 42 \ udesno \) \]
\ [((a) _ (2)) + ((a) _ (3)) + ((a) _ (n-1)) = 56 \]
Imajte na umu, međutim, da se brojevi $ ((a) _ (2)) $ i $ ((a) _ (n-1)) $ dobivaju iz brojeva 2 i 42 na rubovima za jedan korak jedan prema drugom, tj ... do središta niza. Ovo znači to
\ [((a) _ (2)) + ((a) _ (n-1)) = 2 + 42 = 44 \]
No tada se gore napisani izraz može prepisati na sljedeći način:
\ [\ begin (align) & ((a) _ (2)) + ((a) _ (3)) + ((a) _ (n-1)) = 56; \\ & \ lijevo (((a) _ (2)) + ((a) _ (n-1)) \ desno) + ((a) _ (3)) = 56; \\ & 44 + ((a) _ (3)) = 56; \\ & ((a) _ (3)) = 56-44 = 12. \\ \ završi (poravnaj) \]
Poznavajući $ ((a) _ (3)) $ i $ ((a) _ (1)) $, lako možemo pronaći razliku progresije:
\ [\ begin (align) & ((a) _ (3)) - ((a) _ (1)) = 12 - 2 = 10; \\ & ((a) _ (3)) - ((a) _ (1)) = \ lijevo (3-1 \ desno) \ cdot d = 2d; \\ & 2d = 10 \ Desna strelica d = 5. \\ \ završi (poravnaj) \]
Ostaje samo pronaći ostale članove:
\ [\ begin (align) & ((a) _ (1)) = 2; \\ & ((a) _ (2)) = 2 + 5 = 7; \\ & ((a) _ (3)) = 12; \\ & ((a) _ (4)) = 2 + 3 \ cdot 5 = 17; \\ & ((a) _ (5)) = 2 + 4 \ cdot 5 = 22; \\ & ((a) _ (6)) = 2 + 5 \ cdot 5 = 27; \\ & ((a) _ (7)) = 2 + 6 \ cdot 5 = 32; \\ & ((a) _ (8)) = 2 + 7 \ cdot 5 = 37; \\ & ((a) _ (9)) = 2 + 8 \ cdot 5 = 42; \\ \ završi (poravnaj) \]
Tako ćemo već u 9. koraku doći do lijevog kraja niza - broja 42. Ukupno je bilo potrebno umetnuti samo 7 brojeva: 7; 12; 17; 22; 27; 32; 37.
Odgovor: 7; 12; 17; 22; 27; 32; 37
Riječi problemi s progresijama
Zaključno, htio bih razmotriti nekoliko relativno jednostavnih zadataka. Pa, kako jednostavno: većini učenika koji proučavaju matematiku u školi i nisu pročitali gore napisano, ti se zadaci mogu činiti kao lim. Ipak, upravo se takvi problemi pojavljuju u OGE -u i USE -u u matematici, pa vam preporučujem da se s njima upoznate.
Problem broj 11. Brigada je u siječnju proizvela 62 dijela, a u svakom sljedećem mjesecu proizvodila je 14 dijelova više nego u prethodnom. Koliko je dijelova tim napravio u studenom?
Riješenje. Očito će broj dijelova, raspoređenih po mjesecima, predstavljati sve veću aritmetičku progresiju. Štoviše:
\ [\ begin (align) & ((a) _ (1)) = 62; \ quad d = 14; \\ & ((a) _ (n)) = 62+ \ lijevo (n-1 \ desno) \ cdot 14. \\ \ kraj (poravnanje) \]
Studeni je 11. mjesec u godini, pa moramo pronaći $ ((a) _ (11)) $:
\ [((a) _ (11)) = 62 + 10 \ cdot 14 = 202 \]
Slijedom toga, 202 dijela bit će proizvedena u studenom.
Problem broj 12. Radionica uveza uvezala je 216 knjiga u siječnju, a svaki sljedeći mjesec uvezivala je 4 knjige više od prethodnog. Koliko je knjiga uvezala radionica u prosincu?
Riješenje. Sve isto:
$ \ begin (align) & ((a) _ (1)) = 216; \ quad d = 4; \\ & ((a) _ (n)) = 216+ \ lijevo (n-1 \ desno) \ cdot 4. \\ \ end (align) $
Prosinac je posljednji, 12. mjesec u godini, pa tražimo $ ((a) _ (12)) $:
\ [((a) _ (12)) = 216 + 11 \ cdot 4 = 260 \]
Ovo je odgovor - u prosincu će biti uvezano 260 knjiga.
Pa, ako ste do sada čitali, žurim vam čestitati: uspješno ste prošli "tečaj mladih boraca" u aritmetičkim progresijama. Možete sigurno prijeći na sljedeću lekciju, gdje ćemo proučiti formulu za zbroj progresije, kao i važne i vrlo korisne posljedice iz nje.
Prva razina
Aritmetička progresija. Detaljna teorija s primjerima (2019)
Numerički niz
Pa sjednimo i počnimo pisati neke brojeve. Na primjer:
Možete napisati bilo koje brojeve, a može ih biti koliko god želite (u našem slučaju njih). Bez obzira koliko brojeva napisali, uvijek možemo reći koji je prvi, koji drugi, pa tako i do posljednjeg, odnosno možemo ih numerirati. Ovo je primjer niza brojeva:
Numerički niz
Na primjer, za naš niz:
Dodijeljeni broj specifičan je samo za jedan broj u nizu. Drugim riječima, u nizu ne postoje tri druga broja. Drugi broj (poput -tog broja) uvijek je jedan.
Broj s brojem naziva se th član niza.
Obično cijeli niz nazivamo nekim slovom (na primjer,), a svaki član ovog niza isto je slovo s indeksom jednakim broju ovog člana :.
U našem slučaju: 
Recimo da imamo numerički niz u kojem je razlika među susjednim brojevima jednaka i jednaka.
Na primjer: 
itd.
Ovaj niz brojeva naziva se aritmetička progresija.
Izraz "progresija" uveo je rimski autor Boethius u 6. stoljeću i shvaćen je u širem smislu kao beskonačni broj niza. Naziv "aritmetika" prenijet je iz teorije kontinuiranih proporcija koju su zauzimali stari Grci.
Ovo je numerički niz, čiji je svaki član jednak prethodnom, dodan istom broju. Taj se broj naziva razlika aritmetičke progresije i označava se sa.
Pokušajte odrediti koji su nizovi brojeva aritmetička progresija, a koji nisu:
a)
b)
c)
d)
Razumijete? Usporedimo naše odgovore:
Je aritmetička progresija - b, c.
Nije aritmetička progresija - a, d.
Vratimo se zadanoj progresiji () i pokušajmo pronaći vrijednost njezinog člana. Postoji dva način da ga pronađete.
1. Metoda
Prethodnoj vrijednosti broja progresije možemo dodavati sve dok ne dođemo do tog termina progresije. Dobro je što nemamo puno za sažeti - samo tri vrijednosti:
Dakle, th član opisane aritmetičke progresije jednak je.
2. Metoda
Što ako bismo morali pronaći vrijednost tog izraza u progresiji? Zbrajanje bi nam oduzelo više od jednog sata, a nije činjenica da ne bismo pogriješili pri zbrajanju brojeva.
Naravno, matematičari su smislili način na koji ne morate dodati razliku aritmetičke progresije prethodnoj vrijednosti. Pomnije pogledajte nacrtanu sliku ... Sigurno ste već primijetili određeni uzorak, naime:
Na primjer, pogledajmo kako se dodaje vrijednost tog člana ove aritmetičke progresije: 
Drugim riječima:
Pokušajte na ovaj način samostalno pronaći vrijednost člana zadane aritmetičke progresije.
Izračunato? Usporedite svoje bilješke s odgovorom:
Imajte na umu da ste dobili potpuno isti broj kao u prethodnoj metodi, kada smo sukcesivno dodavali članove aritmetičke progresije prethodnoj vrijednosti.
Pokušajmo "depersonalizirati" ovu formulu - dovest ćemo je u opći oblik i dobiti:
|
Jednadžba aritmetičke progresije. |
Aritmetičke progresije rastu, a ponekad se smanjuju.
Uzlazni- progresije u kojima je svaka sljedeća vrijednost članova veća od prethodne.
Na primjer:
Smanjuje se- progresije u kojima je svaka sljedeća vrijednost članova manja od prethodne.
Na primjer:
Izvedena formula koristi se za izračunavanje pojmova u rastućim i opadajućim člancima aritmetičke progresije.
Provjerimo to u praksi.
Dobili smo aritmetičku progresiju koja se sastoji od sljedećih brojeva: Provjerimo koliki će biti taj broj ove aritmetičke progresije ako za izračun upotrijebimo našu formulu:

Od tad:
Tako smo se pobrinuli da formula djeluje u opadajućoj i rastućoj aritmetičkoj progresiji.
Pokušajte sami pronaći th i th izraze ove aritmetičke progresije.
Usporedimo dobivene rezultate:
Svojstvo aritmetičke progresije
Komplicirajmo zadatak - izvest ćemo svojstvo aritmetičke progresije.
Recimo da imamo sljedeći uvjet:
- aritmetička progresija, pronađite vrijednost.
Lako, reci i počni brojati prema formuli koju već znaš:
Neka je, a, tada:
Apsolutno u pravu. Ispada da prvo pronađemo, pa ga dodamo prvom broju i dobijemo ono što tražimo. Ako je progresija predstavljena malim vrijednostima, onda u tome nema ništa komplicirano, ali ako nam se u uvjetu daju brojevi? Priznajte, postoji mogućnost da pogriješite u izračunima.
Sada razmislite, je li moguće riješiti ovaj problem u jednoj radnji pomoću bilo koje formule? Naravno, da, i upravo nju ćemo se sada pokušati povući.
Označimo traženi izraz aritmetičke progresije kao, znamo formulu za njegovo pronalaženje - to je ista formula koju smo izveli na početku:
, zatim:
- prethodni član progresije je:
- sljedeći član progresije je:
Sažmimo prethodne i sljedeće članove napredovanja:
Ispada da je zbroj prethodnih i sljedećih članova progresije udvostručena vrijednost člana progresije koji se nalazi između njih. Drugim riječima, kako bi se pronašla vrijednost člana progresije s poznatim prethodnim i uzastopnim vrijednostima, potrebno ih je zbrojiti i podijeliti s.
Tako je, imamo isti broj. Popravimo materijal. Sami izračunajte vrijednost progresije, jer to uopće nije teško.
Dobro napravljeno! Znate gotovo sve o progresiji! Ostaje samo jedna formula za naučiti, koju je, prema legendi, lako zaključio jedan od najvećih matematičara svih vremena, "kralj matematičara" - Karl Gauss ...
Kad je Karl Gauss imao 9 godina, učitelj koji se bavio provjerom rada učenika drugih razreda postavio je na satu sljedeći problem: "Izračunajte zbroj svih prirodnih brojeva od do (uključujući i druge izvore do) uključivo." Zamislite učiteljevo iznenađenje kada je jedan od njegovih učenika (to je bio Karl Gauss) u minuti dao točan odgovor na problem, dok je većina hrabrih kolega nakon dugih kalkulacija dobila pogrešan rezultat ...
Mladi Karl Gauss primijetio je određeni obrazac koji lako možete primijetiti.
Recimo da imamo aritmetičku progresiju koja se sastoji od -tih članova: Moramo pronaći zbroj zadanih članova aritmetičke progresije. Naravno, možemo ručno zbrojiti sve vrijednosti, ali što ako je u zadatku potrebno pronaći zbroj njegovih članova, kako je Gauss tražio?
Prikažimo zadanu progresiju. Pažljivo pogledajte označene brojeve i pokušajte s njima izvesti razne matematičke operacije. 
Jeste li probali? Što ste primijetili? Pravo! Njihovi su iznosi jednaki

Reci mi sada, koliko takvih parova postoji u datoj progresiji? Naravno, točno polovica svih brojeva, tj.
Na temelju činjenice da je zbroj dva člana aritmetičke progresije jednak i sličnih jednakih parova, dobivamo da je ukupni zbroj:
.
Dakle, formula za zbroj prvih članova bilo koje aritmetičke progresije bit će sljedeća:
U nekim problemima ne znamo taj pojam, ali znamo razliku u progresiji. Pokušajte u formuli zamijeniti zbroj, formulu tog pojma.
Što si učinio?
Dobro napravljeno! Vratimo se sada problemu koji je dobio Karl Gauss: sami izračunajte koliki je zbroj brojeva koji počinju od -tog, a zbroj brojeva koji počinju od -th.
Koliko ste dobili?
Gauss je otkrio da je zbroj članova jednak, a zbroj članova. Jeste li tako odlučili?
Zapravo, formulu za zbroj članova aritmetičke progresije dokazao je starogrčki znanstvenik Diofant još u 3. stoljeću, a sve to vrijeme duhoviti ljudi su se snagom i silom koristili svojstvima aritmetičke progresije.
Na primjer, zamislite Stari Egipat i najambicioznije gradilište tog doba - gradnju piramide ... Na slici je prikazana jedna njena strana. 
Gdje kažete napredak ovdje? Pomno pogledajte i pronađite uzorak u broju pješčanih blokova u svakom redu zida piramide. 
Nije li to aritmetička progresija? Izračunajte koliko je blokova potrebno za izgradnju jednog zida ako su blokovi postavljeni u podnožje. Nadam se da nećete računati prelazeći prstom preko monitora, sjećate li se posljednje formule i svega što smo rekli o aritmetičkoj progresiji?
U ovom slučaju napredovanje izgleda ovako :.
Razlika aritmetičke progresije.
Broj članova aritmetičke progresije.
Zamijenimo naše podatke u posljednje formule (broj blokova brojat ćemo na dva načina).
Metoda 1.
Metoda 2.
A sada možete izračunati na monitoru: usporedite dobivene vrijednosti s brojem blokova koji se nalaze u našoj piramidi. Je li se to spojilo? Bravo, savladali ste zbroj članova aritmetičke progresije.
Naravno, ne možete izgraditi piramidu od blokova u bazi, ali od? Pokušajte izračunati koliko je cigli od pijeska potrebno za izgradnju zida s ovim uvjetom.
Jeste li se snašli?
Točan odgovor su blokovi:
Vježbati
Zadaci:
- Maša se do ljeta dovodi u formu. Svaki dan povećava broj čučnjeva za. Koliko će puta Maša čučati u tjednima, ako je na prvom treningu radila čučnjeve.
- Koliki je zbroj svih neparnih brojeva sadržanih u.
- Prilikom skladištenja trupaca drvosječe ih slažu na takav način da svaki gornji sloj sadrži jedan trupac manje od prethodnog. Koliko trupaca ima u jednom zidanju, ako trupci služe kao osnova zida.
Odgovori:
- Definirajmo parametre aritmetičke progresije. U ovom slučaju
(tjedni = dani).Odgovor: Nakon dva tjedna, Maša bi trebala čučati jednom dnevno.
- Prvi neparan broj, posljednji broj.
Razlika aritmetičke progresije.
Broj neparnih brojeva u pola je, međutim, provjerit ćemo ovu činjenicu pomoću formule za pronalaženje -tog člana aritmetičke progresije:Brojevi sadrže neparne brojeve.
Zamijenite dostupne podatke formulom:Odgovor: Zbroj svih neparnih brojeva sadržanih u jednak je.
- Sjetimo se problema s piramidama. Za naš slučaj, a, budući da je svaki gornji sloj smanjen za jedan dnevnik, tada samo u hrpi slojeva, tj.
Zamijenimo podatke u formulu:Odgovor: U zidanju ima balvana.
Ukratko rezimirajmo
- - numerički niz u kojem je razlika među susjednim brojevima jednaka i jednaka. Može biti uzlazno i opadajuće.
- Traženje formule-ti član aritmetičke progresije zapisuje se formulom -, gdje je broj brojeva u progresiji.
- Svojstvo članova aritmetičke progresije- - gdje je broj brojeva u progresiji.
- Zbroj članova aritmetičke progresije može se pronaći na dva načina:
, gdje je broj vrijednosti.
Aritmetička progresija. PROSJEČNA RAZINA
Numerički niz
Sjednimo i počnimo pisati neke brojeve. Na primjer:
Možete pisati bilo koje brojeve, a može ih biti koliko god želite. Ali uvijek možete reći koji je prvi, koji drugi, i tako dalje, odnosno možemo ih numerirati. Ovo je primjer niza brojeva.
Numerički niz je skup brojeva, od kojih se svakom može dodijeliti jedinstveni broj.
Drugim riječima, svaki se broj može povezati s određenim prirodnim brojem i jedinim. I ovaj broj nećemo dodijeliti nijednom drugom broju iz ovog skupa.
Broj s brojem naziva se th član niza.
Obično cijeli niz nazivamo nekim slovom (na primjer,), a svaki član ovog niza isto je slovo s indeksom jednakim broju ovog člana :.
Vrlo je prikladno ako se taj izraz niza može odrediti nekom formulom. Na primjer, formula
postavlja niz:
A formula je sljedeći slijed:
Na primjer, aritmetička progresija je niz (prvi izraz ovdje je jednak, a razlika). Ili (, razlika).
Formula n -tog pojma
Rekurentnim nazivamo formulu u kojoj za otkrivanje tog člana morate znati prethodni ili nekoliko prethodnih:
Da bismo, na primjer, pronašli th pojam progresije pomoću takve formule, morat ćemo izračunati prethodnih devet. Na primjer, neka. Zatim:
Pa, koja je sad formula?
U svakom retku dodamo, pomnoženo s nekim brojem. Za što? Vrlo jednostavno: ovo je broj trenutnog člana minus:
Sada je mnogo prikladnije, zar ne? Provjeravamo:
Odlučite sami:
U aritmetičkoj progresiji pronađite formulu za n -ti pojam i pronađite stoti član.
Riješenje:
Prvi član je jednak. Koja je razlika? A evo što:
(to je zato što se naziva razlika, koja je jednaka razlici uzastopnih članova progresije).
Dakle, formula je:
Tada je stoti pojam:
Koliki je zbroj svih prirodnih brojeva od do?
Prema legendi, veliki matematičar Karl Gauss, kao devetogodišnji dječak, izračunao je ovaj iznos u nekoliko minuta. Primijetio je da je zbroj prvog i posljednjeg broja jednak, zbroj drugog i posljednjeg, ali jednog jednak, zbroj trećeg i trećeg s kraja isti, itd. Koliko će biti takvih parova? Tako je, točno polovica broja svih brojeva, tj. Tako,
Opća formula za zbroj prvih članova bilo koje aritmetičke progresije bila bi:
Primjer:
Nađi zbroj svih dvoznamenkastih višekratnika.
Riješenje:
Prvi takav broj je. Svaki sljedeći dobiva se zbrajanjem prethodnog broja. Dakle, brojevi koji nas zanimaju tvore aritmetičku progresiju s prvim članom i razlikom.
Formula tog pojma za ovaj napredak je:
Koliko je članova u progresiji ako svi moraju biti dvoznamenkasti?
Vrlo jednostavno: .
Zadnji član u progresiji bit će jednak. Zatim zbroj:
Odgovor:.
Sada odlučite sami:
- Svaki dan sportaš trči više od prethodnog dana. Koliko će kilometara pretrčati u tjednima ako je prvog dana pretrčao km m?
- Biciklist svaki dan vozi više kilometara od prethodnog. Prvog dana vozio je km. Koliko mu je dana potrebno da prijeđe kilometar? Koliko će kilometara prijeći u posljednjem danu putovanja?
- Cijena hladnjaka u trgovini svake godine pada za istu količinu. Odredite koliko se cijena hladnjaka smanjivala svake godine, ako je, stavljena na prodaju za rublje, šest godina kasnije prodana za rublje.
Odgovori:
- Ovdje je najvažnije prepoznati aritmetičku progresiju i odrediti njezine parametre. U ovom slučaju, (tjedni = dani). Morate odrediti zbroj prvih članova ove progresije:
.
Odgovor: - Ovdje je navedeno :, potrebno je pronaći.
Očigledno, morate koristiti istu formulu zbroja kao u prethodnom problemu:
.
Zamijenite vrijednosti:Korijen se očito ne uklapa pa je odgovor.
Izračunajmo prijeđenu udaljenost za posljednji dan koristeći formulu tog pojma:
(km).
Odgovor: - S obzirom :. Pronaći: .
Ne može biti lakše:
(trljati).
Odgovor:
Aritmetička progresija. KRATKO O GLAVNOM
Ovo je numerički niz u kojem je razlika među susjednim brojevima jednaka i jednaka.
Aritmetička progresija može biti uzlazna () i opadajuća ().
Na primjer:
Formula za pronalaženje n-tog člana aritmetičke progresije
zapisano formulom, gdje je broj brojeva u progresiji.
Svojstvo članova aritmetičke progresije
Omogućuje vam jednostavno pronalaženje člana progresije ako su poznati njezini susjedni članovi - gdje je broj brojeva u progresiji.
Zbroj članova aritmetičke progresije
Postoje dva načina za pronalaženje iznosa:
Gdje je broj vrijednosti.
Gdje je broj vrijednosti.
Pa tema je gotova. Ako čitate ove retke, onda ste jako cool.
Zato što samo 5% ljudi može samostalno savladati nešto. A ako pročitate do kraja, onda ste u tih 5%!
Sada ono najvažnije.
Shvatio si teoriju o ovoj temi. I, opet, ovo je ... jednostavno je super! Već ste bolji od velike većine svojih vršnjaka.
Problem je u tome što to možda neće biti dovoljno ...
Za što?
Za uspješan polaganje ispita, za upis na institut iz proračuna i, NAJVAŽNIJE, doživotno.
Neću vas ništa uvjeravati, reći ću samo jedno ...
Ljudi koji su stekli dobro obrazovanje zarađuju mnogo više od onih koji ga nisu stekli. Ovo su statistike.
Ali ni ovo nije glavno.
Glavna stvar je da su VIŠE SREĆNI (postoje takve studije). Možda zato što im postoji toliko više mogućnosti i život postaje svjetliji? Ne znam...
Ali razmislite sami ...
Što je potrebno da biste na ispitu bili sigurno bolji od drugih i na kraju bili ... sretniji?
RECITE RJEŠAVANJE PROBLEMA NA OVU TEMU.
Na ispitu se od vas neće tražiti teorija.
Trebat će vam rješavati zadatke neko vrijeme.
A, ako ih niste riješili (MNOGO!), Sigurno ćete negdje glupo pogriješiti ili jednostavno nećete stići na vrijeme.
To je kao u sportu - morate to ponavljati uvijek iznova da biste pobijedili.
Pronađite zbirku gdje želite, nužno s rješenjima, detaljnom analizom i odluči, odluči, odluči!
Možete koristiti naše zadatke (izborno) i mi ih, naravno, preporučujemo.
Kako biste ispunili svoju ruku uz pomoć naših zadataka, trebate pomoći produžiti vijek trajanja udžbenika YouClever koji trenutno čitate.
Kako? Postoje dvije mogućnosti:
- Podijelite sve skrivene zadatke u ovom članku - 299 r
- Otključajte pristup svim skrivenim zadacima u svih 99 članaka vodiča - 999 RUB
Da, u našem udžbeniku imamo 99 takvih članaka, a pristup svim zadacima i svim skrivenim tekstovima u njima može se otvoriti odjednom.
U drugom slučaju mi ćemo vam dati simulator "6000 problema s rješenjima i odgovorima, za svaku temu, za sve razine složenosti." Svakako će biti dovoljno da se pozabavite rješavanjem problema o bilo kojoj temi.
Zapravo, ovo je mnogo više od simulatora - cijeli program obuke. Ako je potrebno, možete ga koristiti i BESPLATNO.
Pristup svim tekstovima i programima omogućen je tijekom cijelog vijeka trajanja stranice.
U zaključku...
Ako vam se ne sviđaju naši zadaci, pronađite druge. Samo se nemojte zadržavati na teoriji.
"Razumijem" i "Ja sam u stanju riješiti" potpuno su različite vještine. Trebate oboje.
Pronađite probleme i riješite ih!