Task B7 - transformation of logarithmic and indicative expressions. Logarithmic expressions
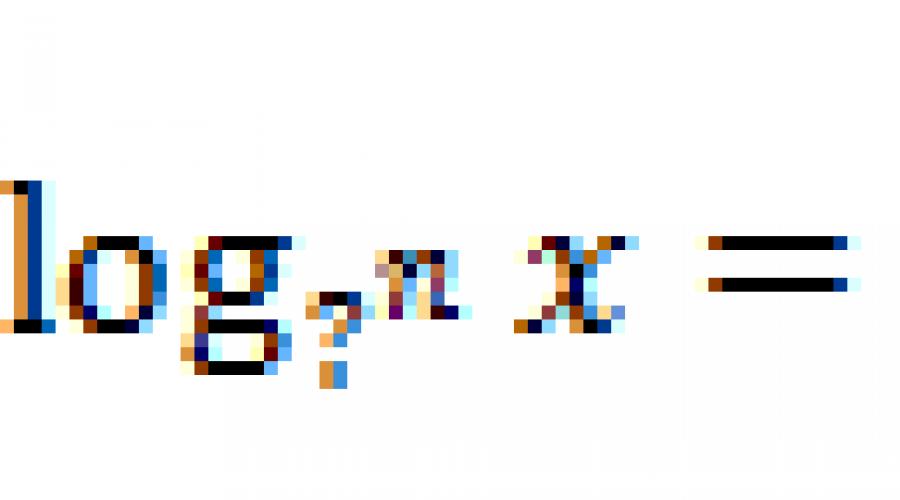
Type of lesson: Lesson of generalization and systematization of knowledge
Objectives:
- to actualize the knowledge of students about logarithms and their properties within the framework of a generalizing repetition and preparation for the USE;
- promote the development of the mental activity of students, the skills of applying theoretical knowledge when performing exercises;
- promote the development of personal qualities of students, self-control skills and self-assessment of their activities; Educate hard work, patient, persistence, independence.
Equipment:computer, projector, presentation (Attachment 1), Cards with a homework (you can attach a file with a task in an electronic diary).
During the classes
I. Organizational moment. Greeting, mood to lesson.
II. Discussion homework.
III. Message themes and objectives of the lesson. Motivation.(Slide 1) Presentation.
We continue to generalize the repetition of the mathematics course in preparation for the exam. And today in the lesson we will talk about logarithms and their properties.
Tasks for the calculation of logarithms and the transformation of logarithmic expressions are necessarily present in control and measurement materials of both basic and profile levels. Therefore, the purpose of our lesson is to restore the ideas about the meaning of the concept of "logarithm" and to update the skills to transform logarithmic expressions. Write down the subject of the lesson in notebooks.
IV. Actualization of knowledge.
1. / oral /To begin with, remember what is called logarithm. (Slide 2)
(The logarithm of the positive number B for the base A (where a\u003e 0, ah? 1) is called an indicator of the degree in which the number A should be taken to get the number B)
Log A B \u003d N<-> A n \u003d b, (a\u003e 0, and 1, b\u003e 0)
So, "logarithm" is the "indicator of the degree"!
(Slide 3) then A n \u003d b can be rewritten as \u003d B is the main logarithmic identity.
If the base is \u003d 10, then the logarithm is called decimal and denoted LGB.
If A \u003d E, then the logarithm is called natural and denote LNB.
2. / Written / (Slide 4)Fill in the skips to get faithful equality:
LOG? x + log a? \u003d LOG? (? y)
Log a? - LOG? Y \u003d Log? (X /?)
Log A x? \u003d Plog? (?)
Check:
one; one; a, y, x; x, a, a, y; p, a, x.
These are the properties of logarithms. And also a group of properties: (Slide 5)
Check:
a, 1, n, x; n, x, p, a; x, b, a, y; a, x, b; A, 1, B.
V. Oral work
(Slide 6) №1. Calculate:
a B C D) ; e).
Answers : a) 4; b) - 2; at 2; d) 7; e) 27.
(Slide 7) №2. Find x:
but) ; b) (Answers: a) 1/4; b) 9).
Number 3. Does it make sense to consider such a logarithm:
but) ; b); in) ? (Not)
Vi. Independent work in groups, strong disciples - consultants. (Slide 8)
# 1. Calculate: 
.
No. 2. Simplify:
# 3. Find the value of the expression if
№ 4. Simplify the expression: 
№ 5. Calculate:
№ 6. Calculate:№ 7. Calculate:
No. 8. Calculate:
After execution - checking and discussion on the harvested solution or using the document - cameras.
VII. Solution of the task of increased complexity(A strong student on the board, the rest - in notebooks) (Slide 9)
Find the value of the expression:
VIII. Homework (on cards) differentiated.(Slide 10)
№1. Calculate: 
Listed equality in converting expressions with logarithms are used both to the right left and left to right.
It is worth noting that to memorize the effects from the properties is optional: when carrying out transformations, it is possible to do with the main properties of logarithms and other facts (for example, in that with b≥0), of which the corresponding consequences flow. The "side effect" of this approach is only manifested that the decision will be slightly longer. For example, to do without the investigation, which is expressed by the formula 
And repelly only from the main properties of logarithms, you will have to carry out a chain of transformations of the following type: 
.
The same can be said about the last property from the above list, which corresponds to the formula 
Since it also follows from the main properties of logarithms. The main thing to understand that there is always the possibility of a positive number with a logarithm in the indicator to change the foundation of the degree and the number under the logarithm sign. For the sake of justice, we note that examples that imply the implementation of transformations of such a kind are rare in practice. We give a few examples below the text.
Transformation of numerical expressions with logarithms
The properties of logarithms remembered, now it's time to learn to apply them in practice to convert expressions. Naturally start with the transformation of numerical expressions, and not expressions with variables, as they are more convenient and easier to know the basics. So we will do, and start with very simple examples to learn how to choose the desired property of the logarithm, but we will gradually complicate examples, up to the moment when you need to use several properties in a row to get the final result.
Selection of the desired properties of logarithms
The properties of logarithms are not so little, and it is clear that you need to be able to choose from them the appropriate, which in this particular case will lead to the desired result. It is usually difficult to do this, comparing the type of transformed logarithm or expression with the views of the left and right parts of the formulas expressing the properties of logarithms. If the left or right side of one of the formulas coincides with a given logarithm or expression, then most likely it is this property that needs to be applied when converting. The following examples are clearly demonstrated.
Let's start with examples of converting expressions using the definition of a logarithm that corresponds to the formula A Log A B \u003d B, A\u003e 0, A ≠ 1, B\u003e \u200b\u200b0.
Example.
Calculate if possible: a) 5 log 5 4, b) 10 lg (1 + 2 · π), B) 
, d) 2 log 2 (-7), e).
Decision.
In the example, under the letter a), the structure A Log A b is clearly visible, where a \u003d 5, b \u003d 4. These numbers satisfy the conditions a\u003e 0, a ≠ 1, b\u003e 0, so you can use the equality a Log A b \u003d b. We have 5 log 5 4 \u003d 4.
b) here a \u003d 10, b \u003d 1 + 2 · π, conditions a\u003e 0, a ≠ 1, b\u003e 0 are made. In this case, there is an equality of 10 lg (1 + 2 · π) \u003d 1 + 2 · π.
c) and in this example we are dealing with a degree of type A log a b, where and b \u003d ln15. So 
.
Despite the belonging to the same type of A Log A B (here a \u003d 2, b \u003d -7), the expression under the letter d) cannot be converted by the formula A Log A B \u003d B. The reason is that it does not make sense, as it contains a negative number under the sign of the logarithm. Moreover, the number B \u003d -7 does not satisfy the condition B\u003e 0, which does not allow to resort to the formula A log a B \u003d B, since it requires the fulfillment of the conditions a\u003e 0, a ≠ 1, b\u003e 0. So, it is impossible to talk about the calculation of the value of 2 log 2 (-7). In this case, recording 2 log 2 (-7) \u003d -7 will be an error.
Similarly, in the example under the letter D), the solution cannot be brought 
Since the initial expression does not make sense.
Answer:
a) 5 log 5 4 \u003d 4, b) 10 lg (1 + 2 · π) \u003d 1 + 2 · π, c) , d), e) expressions do not make sense.
It is often useful for the conversion at which a positive number is presented in the form of a degree of any positive and different number with a logarithm in the indicator. It is based on the same definition of logarithm a log a b \u003d b, a\u003e 0, a ≠ 1, b\u003e 0, but the formula is applied to the right left, that is, in the form B \u003d a log a b. For example, 3 \u003d E ln3 or 5 \u003d 5 log 5 5.
Go to the application of the properties of logarithms to convert expressions.
Example.
Find the value of the expression: a) log -2 1, b) log 1 1, c) log 0 1, d) log 7 1, e) ln1, e) lg1, g) log 3,75, s) log 5 · π 7 1.
Decision.
In the examples under the letters a), b) and c) the expressions of Log -2 1, Log 1 1, log 0 1, which does not make sense, because at the base of the logarithm should not be a negative number, zero or unit, because we determined Logarithm only for positive and different from the base unit. Therefore, in examples a) - c) there can be no question of finding the expression value.
In all other tasks, it is obvious that there are positive and different numbers from the unit 7, E, 10, 3.75 and 5 · π 7, respectively, and under the signs of logarithms everywhere there are units. And we know the property of the logarithm unit: Log A 1 \u003d 0 for any A\u003e 0, A ≠ 1. Thus, the values \u200b\u200bof expressions b) - e) are equal to zero.
Answer:
a), b), c) expressions do not make sense, d) log 7 1 \u003d 0, d) ln1 \u003d 0, e) lg1 \u003d 0, g) log 3,75 1 \u003d 0, h) log 5 · E 7 1 \u003d 0.
Example.
Calculate: a), b) lne, c) LG10, D) log 5 · π 3 -2 (5 · π 3 -2), e) log -3 (-3), e) log 1 1.
Decision.
It is clear that we have to take advantage of the property of the logarithm of the base, which corresponds to the formula Log A A \u003d 1 at a\u003e 0, a ≠ 1. Indeed, in the tasks under all the letters, the number under the sign of the logarithm coincides with its basis. Thus, I want to immediately say that the meaning of each of the specified expressions is 1. However, it is not necessary to hurry with the conclusions: in the tasks under the letters a) - d) the values \u200b\u200bof expressions are truly equal to one, and in the tasks D) and E) the initial expressions do not make sense, therefore it cannot be said that the values \u200b\u200bof these expressions are 1.
Answer:
a), b) lne \u003d 1, c) lg10 \u003d 1, d) log 5 · π 3 -2 (5 · π 3 -2) \u003d 1, D), e) expressions do not make sense.
Example.
Find a value: a) log 3 3 11, b) 
, c), d) log -10 (-10) 6.
Decision.
Obviously, under the signs of logarithms there are some degrees of foundation. Based on this, we understand that it is useful to us here the degree of the foundation: Log A A P \u003d P, where a\u003e 0, a ≠ 1 and p is any valid number. Given this, we have the following results: a) Log 3 3 11 \u003d 11, b) 
, in) 
. Is it possible to record similar equality for the example under the letter d) of the type of log -10 (-10) 6 \u003d 6? No, it is impossible, since the expression Log -10 (-10) 6 does not make sense.
Answer:
a) log 3 3 11 \u003d 11, b) , in) , d) the expression does not make sense.
Example.
Imagine an expression in the form of a sum or the difference of logarithms on the same basis: a) 
, b), c) lg ((- 5) · (-12)).
Decision.
a) under the sign of the logarithm is a work, and we know the logarithm property of the work of Log A (x · y) \u003d log a x + log a y, a\u003e 0, a ≠ 1, x\u003e 0, y\u003e 0. In our case, the number at the base of the logarithm and the number in the work is positive, that is, satisfy the conditions of the selected property, so we can calmly apply it: 
.
b) Here we use the property of the logarithm of the private, where a\u003e 0, a ≠ 1, x\u003e 0, y\u003e 0. In our case, the base of the logarithm is a positive number E, the numerator and denominator π are positive, which means that the conditions of the property are satisfying, so we have the right to use the chosen formula: 
.
c) First, we note that the expression Lg ((- 5) · (-12)) makes sense. But at the same time, for him, we do not have the right to apply the logarithm formula of the work of Log A (x · y) \u003d log a x + log ay, a\u003e 0, a ≠ 1, x\u003e 0, y\u003e 0, since the numbers -5 and -12 - negative and do not satisfy the conditions x\u003e 0, y\u003e 0. That is, it is impossible to conduct such a conversion: lG ((- 5) · (-12)) \u003d lg (-5) + lg (-12). And what to do? In such cases, the initial expression needs a preliminary transformation that allows you to get away from negative numbers. We will talk about such cases of transformation of expressions with negative numbers under the sign of logarithm in detail in one of the following examples, which is understandable, and without explanation: lG ((- 5) · (-12)) \u003d lg (5 · 12) \u003d LG5 + LG12.
Answer:
but) b) , c) lg ((- 5) · (-12)) \u003d LG5 + LG12.
Example.
Simplify the expression: a) log 3 0.25 + log 3 16 + log 3 0.5, b).
Decision.
Here we will help all the same properties of the logarithm of the work and logarithm of the private, which we used in previous examples, only now we will apply them to right to left. That is, the amount of logarithms is transforming into the logarithm of the work, and the difference between logarithms - in the logarithm of private. Have
but) log 3 0.25 + log 3 16 + log 3 0.5 \u003d log 3 (0.25 · 16 · 0.5) \u003d log 3 2.
b) 
.
Answer:
but) log 3 0.25 + log 3 16 + Log 3 0.5 \u003d log 3 2b) 
.
Example.
Get rid of the extent under the sign of the logarithm: a) log 0.7 5 11, b) 
, c) log 3 (-5) 6.
Decision.
It is easy to see that we are dealing with expressions of the Log A B p. The corresponding property of the logarithm has the kind of log a B p \u003d p · log a b, where a\u003e 0, a ≠ 1, b\u003e 0, p is any valid number. That is, when performing conditions a\u003e 0, a ≠ 1, b\u003e 0 from the logarithm of the degree of log a b p, we can move to the product P · Log A B. We will conduct this conversion with specified expressions.
a) In this case, a \u003d 0.7, b \u003d 5 and p \u003d 11. So log 0.7 5 11 \u003d 11 · Log 0.7 5.
b) Here, conditions a\u003e 0, a ≠ 1, b\u003e 0 are performed. therefore 
c) The expression Log 3 (-5) 6 has the same structure log a b p, a \u003d 3, b \u003d -5, p \u003d 6. But for B, the condition b\u003e 0 is not satisfied, which makes it impossible to use the Log A B P \u003d P · Log A B. So, it is impossible to cope with the task? It is possible, but a pre-converting expression is required, we will talk about in detail below in the heading point. The decision will be: log 3 (-5) 6 \u003d log 3 5 6 \u003d 6 · LOG 3 5.
Answer:
a) log 0.7 5 11 \u003d 11 · log 0.7 5,
b)
c) Log 3 (-5) 6 \u003d 6 · Log 3 5.
Quite often, the logarithm formula of the degree during transformation is necessary to apply right to left as p · log a b \u003d log a b p (this requires the performance of the same conditions for A, B and P). For example, 3 · ln5 \u003d ln5 3 and lg2 · log 2 3 \u003d log 2 3 LG2.
Example.
a) Calculate the value of Log 2 5, if it is known that LG2≈0,3010 and LG5≈0,6990. b) Present a fraction in the form of a logarithm based on 3.
Decision.
a) The formula for the transition to a new base of the logarithm allows this logarithm to represent in the form of a ratio of decimal logarithms, whose values \u200b\u200bare known to us :. It remains only to carry out calculations, we have 
.
b) here it is enough to take advantage of the transition to a new base, and apply it to the right left, that is, in the form of 
. Receive 
.
Answer:
a) log 2 5≈2,3223, b) .
At this stage, we sufficiently scrupulously considered the conversion of the most simple expressions using the main properties of logarithms and the definition of logarithm. In these examples, we had to apply some kind of property and nothing more. Now with a calm conscience, you can move to examples, the transformation of which requires the use of several properties of logarithms and other additional transformations. We will go in the next paragraph. But before that, in short, we will briefly focus on the examples of the consequences of the main properties of logarithms.
Example.
a) Get rid of the root under the sign of the logarithm. b) Convert fraction in the logarithm on the base 5. c) Frequently from the degrees under the logarithm sign and in its foundation. d) Calculate the value of the expression 
. e) replace the expression of the degree with the base 3.
Decision.
a) if you remember about the consequence of the property of the logarithm 
You can immediately answer: 
.
b) we use the formula 
right to left we have 
.
c) In this case, the result leads the formula . Receive 
.
d) and here it is enough to apply a consequence that the formula is responsible 
. So 
.
e) property logarithm Allows us to achieve the desired result: 
.
Answer:
but) . b) . in) 
. d) 
. e) .
Sequential use of several properties
Real tasks for the transformation of expressions using the properties of logarithms are usually more complicated by those we engaged in the previous paragraph. In them, as a rule, the result is not one step, and the solution is already in the consistent application of one property after another, along with additional identity transformations, such as disclosure of brackets, bringing similar terms, reduction of fractions, etc. So let's get closer to such examples. There is nothing difficult in this, the main thing is to act neatly and consistently, observing the procedure for performing actions.
Example.
Calculate the value of the expression (Log 3 15-Log 3 5) · 7 log 7 5.
Decision.
The difference of logarithms in brackets for the property of the logarithm of a private can be replaced with logarithm Log 3 (15: 5), and further calculate its value log 3 (15: 5) \u003d log 3 3 \u003d 1. And the value of expression 7 log 7 5 by definition of logarithm is equal to 5. Substitute these results in the original expression, we get (log 3 15-Log 3 5) · 7 log 7 5 \u003d 1 · 5 \u003d 5.
Let us give a solution without explanation:
(Log 3 15-log 3 5) · 7 log 7 5 \u003d log 3 (15: 5) · 5 \u003d
\u003d log 3 3 · 5 \u003d 1 · 5 \u003d 5.
Answer:
(log 3 15-Log 3 5) · 7 log 7 5 \u003d 5.
Example.
What is the value of the numerical expression log 3 log 2 2 3 -1?
Decision.
We first transform the logarithm, which is located under the sign of the logarithm, according to the logarithm formula: Log 2 2 3 \u003d 3. Thus, log 3 log 2 2 3 \u003d Log 3 3 and further log 3 3 \u003d 1. So log 3 log 2 2 3 -1 \u003d 1-1 \u003d 0.
Answer:
log 3 log 2 2 3 -1 \u003d 0.
Example.
Simplify the expression.
Decision.
The transition formula to the new base of the logarithm allows the relationship of logarithms to one base to be represented as Log 3 5. In this case, the initial expression will take the form. By definition of logarithm 3 Log 3 5 \u003d 5, that is 
, And the value of the expression obtained, due to the same definition of the logarithm, is two.
Here is a brief version of the solution that is usually given: 
.
Answer:
.
For a smooth transition to the following item information, let's take a look at the expressions 5 2 + LOG 5 3, and LG0.01. Their structure is not suitable for any of the properties of logarithms. So what happens, they cannot be converted using the properties of logarithms? It is possible if you can conduct preliminary transformations that prepare these expressions to the application of the properties of logarithms. So 5 2 + LOG 5 3 \u003d 5 2 · 5 log 5 3 \u003d 25 · 3 \u003d 75, 
and LG0.01 \u003d LG10 -2 \u003d -2. Then we will understand in detail how such training of expressions is carried out.
Preparation of expressions to the application of the properties of logarithms
Logarithms in the composition of the transformed expression very often differ from the left and right parts of the formulas corresponding to the properties of logarithms. But no less often the transformation of these expressions implies the use of the properties of logarithms: to use them only requires preliminary preparation. And this preparation is in carrying out certain identical transformations leading logarithms to the form, convenient to apply properties.
For fairness, we note that almost any transformations of expressions can act as preliminary transformations, from the banal actuator of such terms to the use of trigonometric formulas. This is understandable, since the transformed expressions may contain any mathematical objects: brackets, modules, fractions, roots, degrees, etc. Thus, you need to be ready to perform any needed conversion to further be able to use the properties of logarithms.
Immediately, let's say that in this point we do not set ourselves the task to classify and disassemble all imaginable preliminary transformations, which further apply the properties of logarithms or the definition of logarithm. Here we will dwell only on four of them, which are most characteristic and most often found in practice.
And now in detail about each of them, after which, as part of our topic, it will only remain to deal with the transformation of expressions with variables under the signs of logarithms.
Selection of degrees under the sign of logarithm and in its foundation
Let's start immediately from the example. Let us be logarithm. Obviously, in this form, its structure does not have to use the properties of logarithms. Is it possible to somehow convert this expression to simplify it, and even better calculate its value? To answer this question, let's look carefully in numbers 81 and 1/9 in the context of our example. It is easy to notic here that these numbers allow the representation of the degree of number 3, indeed, 81 \u003d 3 4 and 1/9 \u003d 3 -2. In this case, the initial logarithm is presented in the form and the possibility of applying the formula . So, 
.
An analysis of the disassembled example creates the following thought: If possible, you can try to highlight the degree under the sign of the logarithm and in its foundation to apply the property of the logarithm or its consequence. It remains only to find out how to allocate these degrees. Let's give some recommendations on this issue.
Sometimes it is rather obvious that the number under the sign of the logarithm and / or in its foundation is some of the whole degree as in the example above. Practically constantly have to deal with detects of twos, which were well thought away: 4 \u003d 2 2, 8 \u003d 2 3, 16 \u003d 2 4, 32 \u003d 2 5, 64 \u003d 2 6, 128 \u003d 2 7, 256 \u003d 2 8, 512 \u003d 2 9, 1024 \u003d 2 10. This can be said about the degree of triple: 9 \u003d 3 2, 27 \u003d 3 3, 81 \u003d 3 4, 243 \u003d 3 5, ... in general, it does not hurt if it will be before our eyes table of degrees of natural numbers within a dozen. It is also not difficult to work with integer degrees of ten, hundred, thousands, etc.
Example.
Calculate the value or simplify the expression: a) log 6 216, b), c) log 0.000001 0.001.
Decision.
a) It is obvious that 216 \u003d 6 3, therefore Log 6 216 \u003d log 6 6 3 \u003d 3.
b) Table of degrees of natural numbers allows you to present numbers 343 and 1/243 in the form of degrees 7 3 and 3 -4, respectively. Therefore, it is possible to follow the following transformation of a given logarithm: 
c) as 0.000001 \u003d 10 -6 and 0.001 \u003d 10 -3, then lOG 0.000001 0.001 \u003d log 10 -6 10 -3 \u003d (- 3) / (- 6) \u003d 1/2.
Answer:
a) log 6 216 \u003d 3, b) 
, c) log 0.000001 0.001 \u003d 1/2.
In more complex cases, to highlight the degrees of numbers have to resort to.
Example.
Convert the expression to a simpler type of Log 3 648 · Log 2 3.
Decision.
Let's see what is a decomposition of a number of 648 per simple factors:
That is, 648 \u003d 2 3 · 3 4. In this way, log 3 648 · Log 2 3 \u003d log 3 (2 3 · 3 4) · log 2 3.
Now the logarithm of works is transforming in the amount of logarithms, after which the properties of the logarithm of the degree are applicable:
log 3 (2 3 · 3 4) · log 2 3 \u003d (log 3 2 3 + log 3 3 4) · log 2 3 \u003d
\u003d (3 · Log 3 2 + 4) · Log 2 3.
Due to the investigation from the property of the logarithm to which the formula is responsible The product log32 · log23 is a work, and it is known to be one. Considering it, we get 3 · log 3 2 · log 2 3 + 4 · log 2 3 \u003d 3 · 1 + 4 · log 2 3 \u003d 3 + 4 · LOG 2 3.
Answer:
log 3 648 · Log 2 3 \u003d 3 + 4 · Log 2 3.
Quite often, expressions under the logarithm sign and in its foundation are works or ratios of roots and / or degrees of some numbers, for example,. Such expressions can be represented as a degree. For this, the transition from roots to degrees, and applied. These conversions allow you to highlight degrees under the logarithm sign and in its base, after which you apply the properties of logarithms.
Example.
Calculate: a) 
, b).
Decision.
a) the expression at the base of the logarithm is the product of degrees with the same bases, according to the appropriate property of degrees, we have 5 2 · 5 -0,5 · 5 -1 \u003d 5 2-0.5-1 \u003d 5 0.5.
Now we transform the fraction under the sign of the logarithm: we turn from the root to the degree, after which we will use the property of degrees with the same grounds: 
.
It remains to substitute the results obtained into the initial expression, use the formula and finish transformations: 
b) Since 729 \u003d 3 6, and 1/9 \u003d 3 -2, then the initial expression can be rewritten in the form.
Next, apply the property of the root from the degree, we carry out the transition from the root to the degree and use the degree ratio property to convert the logarithm to the degree: 
.
Considering the last result, we have 
.
Answer:
but) 
, b).
It is clear that in general, to obtain degrees under the sign of the logarithm and, in its foundation, various transformations of various expressions may be required. We give a couple of examples.
Example.
What is the value of the expression: a) 
b) 
.
Decision.
Therefore, we note that the specified expression has the form of Log A B P, where a \u003d 2, b \u003d x + 1 and p \u003d 4. Numeric expressions of such kind We were converted by the property of the logarithm of the extent Log A B P \u003d p · Log A B, therefore, with a given expression, I want to do the same as, and from Log 2 (X + 1) 4 go to 4 · log 2 (x + 1). And now let's calculate the value of the initial expression and the expression obtained after the transformation, for example, with x \u003d -2. Have log 2 (-2 + 1) 4 \u003d log 2 1 \u003d 0, and 4 · Log 2 (-2 + 1) \u003d 4 · log 2 (-1) - Not meaning expression. This causes a natural question: "What did we do wrong"?
And the reason is as follows: we performed the transformation log 2 (x + 1) 4 \u003d 4 · log 2 (x + 1), based on the formula Log ABP \u003d P · Log AB, but we have the right to apply this formula only when condition A \u003e 0, a ≠ 1, b\u003e 0, p - any valid number. That is, the conversion done by us takes place if X + 1\u003e 0, which is the same x\u003e -1 (for A and P - the conditions are made). However, in our case, the OTZ variable x for the initial expression consists not only from the interval x\u003e -1, but also from the period x<−1 . Но для x<−1 мы не имели права осуществлять преобразование по выбранной формуле.
The need to take into account ...
We will continue to disassemble the transformation of the Log 2 (X + 1) 4 selected expressions by us, and now let's see what happens with OTZ when moving to expression 4 · log 2 (x + 1). In the previous paragraph, we found even the source expression - this is a set (-∞, -1) ∪ (-1, + ∞). Now we find the area of \u200b\u200bpermissible values \u200b\u200bof the variable x for expression 4 · log 2 (x + 1). It is determined by the condition X + 1\u003e 0, which corresponds to the set (-1, + ∞). Obviously, when moving from Log 2 (X + 1) 4 to 4 · Log 2 (X + 1), the area of \u200b\u200bvalid values \u200b\u200boccurs. And we agreed to avoid transformations leading to the narrowing of OTZ, as this can lead to various negative consequences.
It is worth noting here for yourself that it is useful to control the OTZ at every step of the transformation and prevent its narrowing. And if suddenly, at some stage of the transformation, there was a narrowing of OST, then it is worth looking very carefully, and whether this transformation is permissible and whether we have the right to carry out it.
For example, let's say that in practice, it is usually necessary to work with expressions, whose OTZ variables are such that, when carrying out transformations, use the properties of logarithms without restrictions in the form already known to us, and both from left to right and right to left. You quickly get used to it, and you begin to carry out transformations mechanically, without thinking, and whether it was possible to conduct them. And at such moments, as discharged, slipper more complex examples in which the inaccient use of the properties of logarithms leads to errors. So you need to always be on a check, and follow that there is no narrowing of OTZ.
It does not hurt separately select the main transformations based on the properties of logarithms that need to be carried out very carefully, which can lead to a narrowing of OTZ, and as a result - to errors:
Some transformations of expressions according to the properties of logarithms can lead to the inverse - expansion of OTZ. For example, the transition from 4 · log 2 (x + 1) to Log 2 (X + 1) 4 expands odd from the set (-1, + ∞) to (-∞, -1) ∪ (-1, + ∞). Such transformations occur if remain within the ODZD for the initial expression. So the only mentioned conversion 4 · log 2 (x + 1) \u003d log 2 (x + 1) 4 takes place on the OTZ variable x for the original expression 4 · log 2 (x + 1), that is, with x + 1\u003e 0, which is the same (-1, + ∞).
Now that we discussed the nuances for which you need to pay attention to when converting expressions with variables using the properties of logarithms, it remains to figure out how correctly these transformations need to be carried out.
X + 2\u003e 0. Does it work in our case? To answer this question, take a look at the OTZ variable x. It is determined by the inequality system 
which is equivalent to the condition x + 2\u003e 0 (if necessary, see the article solving systems of inequality). Thus, we can calmly apply the logarithm property.
Have
3 · lg (x + 2) 7 -lg (x + 2) -5 · lg (x + 2) 4 \u003d
\u003d 3 · 7 · lg (x + 2) -lg (x + 2) -5 · 4 · lg (x + 2) \u003d
\u003d 21 · lg (x + 2) -lg (x + 2) -20 · lg (x + 2) \u003d
\u003d (21-1-20) · Lg (x + 2) \u003d 0.
You can act and otherwise, the benefit of OTZ allows it to do, for example: 
Answer:
3 · lg (x + 2) 7 -lg (x + 2) -5 · lg (x + 2) 4 \u003d 0.
And what to do when the conditions for the accompanying properties of logarithms are not satisfied? We will deal with this on the examples.
Suppose from us to simplify the expression Lg (x + 2) 4 -lg (x + 2) 2. The transformation of this expression, in contrast to the expression from the previous example, does not allow the log of the logarithm degree. Why? OTZ variable x in this case is a combination of two gaps x\u003e -2 and x<−2 . При x>-2 We can calmly apply the logarithm property and act as disassembled above: lg (x + 2) 4 -lg (x + 2) 2 \u003d 4 · lg (x + 2) -2 · lg (x + 2) \u003d 2 · lg (x + 2). But OTZ contains another period of X + 2<0 , для которого последнее преобразование будет некорректно. Что же делать при x+2<0 ? В подобных случаях на помощь приходит . Определение модуля позволяет выражение x+2 при x+2<0 представить как −|x+2| . Тогда при x+2<0 от lg(x+2) 4 −lg(x+2) 2 переходим к lG (- | x + 2 |) 4 -LG (- | x + 2 |) 2 And further by force of degree properties to LG | X + 2 | 4 -LG | X + 2 | 2. The resulting expression can be converted by the logarithm property, since | x + 2 |\u003e 0 for any values \u200b\u200bof the variable. Have lG | X + 2 | 4 -LG | X + 2 | 2 \u003d 4 · lg | x + 2 | -2 · lg | x + 2 | \u003d 2 · lg | x + 2 |. Now you can free yourself from the module, as he did his job. Since we are conducting conversion at x + 2<0 , то 2·lg|x+2|=2·lg(−(x+2)) . Итак, можно считать, что мы справились с поставленной задачей. Ответ: . Полученный результат можно записать компактно с использованием модуля как .
Consider another example so that work with modules has become familiar. Let we have conceived from the expression 
Go to the sum and difference between the logarithms of linear bounces X-1, X-2 and X-3. First we find ... 
At the interval (3, + ∞) the values \u200b\u200bof expressions X-1, X-2 and X-3 are positive, so we calmly apply the properties of the logarithm of sums and differences: 
And on the interval (1, 2), the values \u200b\u200bof the expression X-1 are positive, and the values \u200b\u200bof expressions X-2 and X-3 are negative. Therefore, in the interval under consideration, we present X-2 and X-3 using the module as - | x-2 | and - | x-3 | respectively. Wherein 
Now you can apply the properties of the logarithm of the work and private, as it is on the interval (1, 2) the values \u200b\u200bof expressions X-1, | x-2 | and | x-3 | - Positive.
Have 
The results can be combined:
In general, similar arguments allow the logarithm formulas on the basis of the logarithm, relationships and degrees to obtain three practically useful results, which are quite convenient to use:
- The logarithm works of two arbitrary expressions X and Y of the type of log a (x · y) can be replaced with the summable logarithms log a | x | + log a | y | , A\u003e 0, A ≠ 1.
- Logarithm Private Log A (X: Y) Can be replaced with the difference between logarithms Log A | X | -Log A | Y | , a\u003e 0, a ≠ 1, x and y - arbitrary expressions.
- From the logarithm of some expression B in an even degree p of the Log A B P form you can go to the expression P · log a | b | , where a\u003e 0, a ≠ 1, p is an even number and b - an arbitrary expression.
Similar results are given, for example, in instructions to solve indicative and logarithmic equations in the collection of problems in mathematics for applicants to universities under the editors of M. I. Scanavi.
Example.
Simplify expression 
.
Decision.
It would be good to apply the properties of the logarithm, amounts and differences. But can we do it here? To answer this question, we need to know OTZ.
We define it: 
It is rather obvious that the expressions X + 4, X-2 and (X + 4) 13 on the values \u200b\u200bof the permissible values \u200b\u200bof the variable x can take both positive and negative values. Therefore, we will have to act through modules. 
The properties of the module allow you to rewrite as, therefore 
Also nothing prevents from the property of the logarithm degree, then bring similar terms to: 
The other sequence of transformations leads to the same result: 
and since the expression X-2 can take both positive and negative values, then when submitting an even degree rate of 14
Tasks whose solution lies in transformation of logarithmic expressions, quite often meet on the exam.
To successfully cope with them at minimal time except the main logarithmic identities, you need to know and correctly use some formulas.
This is: a log a b \u003d b, where a, b\u003e 0, and ≠ 1 (it follows directly from the definition of the logarithm).
log a b \u003d log with b / log with a or log a b \u003d 1 / log b a
where a, b, c\u003e 0; A, C ≠ 1.
log a m b n \u003d (m / n) log | a | | b |
where a, b\u003e 0, a ≠ 1, m, n є r, n ≠ 0.
and log with b \u003d b log with a
where a, b, c\u003e 0 and a, b, s ≠ 1
To show the fairness of the fourth equality, prologate the left and the right-hand side of the A. We get Log A (and log with b) \u003d log A (b log with a) or log with B \u003d log with a · log a b; log with b \u003d log with a · (log with b / log with a); Log with B \u003d log with b.
We have proven equality of logarithms, which means equal to the expressions under logarithms. Formula 4 is proved.
Example 1.
Calculate 81 LOG 27 5 LOG 5 4.
Decision.
81 = 3 4 , 27 = 3 3 .
log 27 5 \u003d 1/3 log 3 5, log 5 4 \u003d log 3 4 / LOG 3 5. Consequently,
log 27 5 · log 5 4 \u003d 1/3 log 3 5 · (Log 3 4 / Log 3 5) \u003d 1/3 log 3 4.
Then 81 log 27 5 Log 5 4 \u003d (3 4) 1/3 log 3 4 \u003d (3 log 3 4) 4/3 \u003d (4) 4/3 \u003d 4 3 √4.
You can independently perform the following task.
Calculate (8 log 2 3 + 3 1 / Log 2 3) - log 0.2 5.
As a tip 0.2 \u003d 1/5 \u003d 5 -1; Log 0.2 5 \u003d -1.
Answer: 5.
Example 2.
Calculate (√11) log. √3 9- log 121 81.
Decision.
Perform the replacement of expressions: 9 \u003d 3 2, √3 \u003d 3 1/2, Log √3 9 \u003d 4,
121 \u003d 11 2, 81 \u003d 3 4, Log 121 81 \u003d 2 log 11 3 (Formula 3 was used).
Then (√11) Log √3 9- log 121 81 \u003d (11 1/2) 4-2 log 11 3 \u003d (11) 2- log 11 3 \u003d 11 2 / (11) Log 11 3 \u003d 11 2 / ( 11 LOG 11 3) \u003d 121/3.
Example 3.
Calculate Log 2 24 / Log 96 2- log 2 192 / log 12 2.
Decision.
Logarithms contained in the example, replace logarithms with a base 2.
log 96 2 \u003d 1 / log 2 96 \u003d 1 / log 2 (2 5 · 3) \u003d 1 / (Log 2 2 5 + log 2 3) \u003d 1 / (5 + log 2 3);
log 2 192 \u003d log 2 (2 6 · 3) \u003d (log 2 2 6 + log 2 3) \u003d (6 + log 2 3);
log 2 24 \u003d log 2 (2 3 · 3) \u003d (log 2 2 3 + log 2 3) \u003d (3 + LOG 2 3);
log 12 2 \u003d 1 / log 2 12 \u003d 1 / log 2 (2 2 · 3) \u003d 1 / (Log 2 2 2 + log 2 3) \u003d 1 / (2 + log 2 3).
Then log 2 24 / log 96 2 - log 2 192 / log 12 2 \u003d (3 + log 2 3) / (1 / (5 + log 2 3)) - ((6 + LOG 2 3) / (1 / ( 2 + log 2 3)) \u003d
\u003d (3 + Log 2 3) · (5 + log 2 3) - (6 + log 2 3) (2 + Log 2 3).
After disclosing brackets and bringing similar terms, we obtain the number 3. (with a simplification of the expression, Log 2 3 can designate via n and simplify expression
(3 + n) · (5 + n) - (6 + n) (2 + n)).
Answer: 3.
You can independently perform the following task:
Calculate (log 3 4 + log 4 3 + 2) · Log 3 16 · log 2 144 3.
Here it is necessary to make a transition to logarithms based on 3 and decomposition on simple multipliers of large numbers.
Answer: 1/2.
Example 4.
Three numbers a \u003d 1 / (log 3 0.5), B \u003d 1 / (log 0.5 3), C \u003d log 0.5 12 - log 0.5 3. Place them in ascending order.
Decision.
We transform the numbers a \u003d 1 / (log 3 0.5) \u003d log 0.5 3; C \u003d LOG 0.5 12 - log 0.5 3 \u003d log 0.5 12/3 \u003d log 0.5 4 \u003d -2.
Compare them
log 0.5 3\u003e log 0.5 4 \u003d -2 and log 0.5 3< -1 = log 0,5 2, так как функция у = log 0,5 х – убывающая.
Or 2< log 0,5 3 < -1. Тогда -1 < 1/(log 0,5 3) < -1/2.
Answer. Consequently, the procedure for placing numbers: C; BUT; IN.
Example 5.
How many integers are located on the interval (Log 3 1/16; log 2 6 48).
Decision.
We define between what degrees of the number 3 is the number 1/16. We get 1/27< 1 / 16 < 1 / 9 .
Since the function y \u003d log 3 x is increasing, then log 3 (1/2 27)< log 3 (1 / 16) < log 3 (1 / 9); -3 < log 3 (1 / 16) < -2.
log 6 48 \u003d log 6 (36 · 4/3) \u003d log 6 36 + log 6 (4/3) \u003d 2 + log 6 (4/3). Compare Log 6 (4/3) and 1/5. And for this, compare numbers 4/3 and 6 1/5. Erected both numbers in 5 degree. We obtain (4/3) 5 \u003d 1024/243 \u003d 4 52/243< 6. Следовательно,
log 6 (4/3)< 1 / 5 . 2 < log 6 48 < 2 1 / 5 . Числа, входящие в двойное неравенство, положительные. Их можно возводить в квадрат. Знаки неравенства при этом не изменятся. Тогда 4 < log 6 2 48 < 4 21 / 25.
Consequently, the interval (log 3 1/16; log 6 48) includes the interval [-2; 4] and the integers are placed on it; -one; 0; one; 2; 3; four.
Answer: 7 integers.
Example 6.
Calculate 3 LGLG 2 / LG 3 - LG20.
Decision.
3 LG LG 2 / LG 3 \u003d (3 1 / LG3) LG LG 2 \u003d (3 Lo G 3 10) LG LG 2 \u003d 10 LG LG 2 \u003d LG2.
Then 3 lglg2 / lg3 - lg 20 \u003d lg 2 - lg 20 \u003d lg 0.1 \u003d -1.
Answer: -1.
Example 7.
It is known that Log 2 (√3 + 1) + log 2 (√6 - 2) \u003d A. Find Log 2 (√3 -1) + log 2 (√6 + 2).
Decision.
Numbers (√3 + 1) and (√3 - 1); (√6 - 2) and (√6 + 2) - conjugate.
We will conduct the following transformation of expressions
√3 - 1 \u003d (√3 - 1) · (√3 + 1)) / (√3 + 1) \u003d 2 / (√3 + 1);
√6 + 2 \u003d (√6 + 2) · (√6 - 2)) / (√6 - 2) \u003d 2 / (√6 - 2).
Then log 2 (√3 - 1) + Log 2 (√6 + 2) \u003d log 2 (2 / (√3 + 1)) + log 2 (2 / (√6 - 2)) \u003d
Log 2 2 - log 2 (√3 + 1) + log 2 2 - log 2 (√6 - 2) \u003d 1 - log 2 (√3 + 1) + 1 - Log 2 (√6 - 2) \u003d
2 - log 2 (√3 + 1) - Log 2 (√6 - 2) \u003d 2 - A.
Answer: 2 - A.
Example 8..
Simplify and find the approximate value of the expression (log 3 2 · log 4 3 · Log 5 4 · Log 6 5 · ... · log 10 9.
Decision.
All logarithms we give to the total base 10.
(log 3 2 · log 4 3 · log 5 4 · log 6 5 · ... · log 10 9 \u003d (LG 2 / LG 3) · (LG 3 / LG 4) · (LG 4 / LG 5) · (LG 5 / LG 6) · ... · (LG 8 / LG 9) · LG 9 \u003d LG 2 ≈ 0.3010. (The approximate LG 2 value can be found using a table, a logarithmic line or a calculator).
Answer: 0,3010.
Example 9..
Calculate Log A 2 B 3 √ (A 11 B -3) if log √ A B 3 \u003d 1. (In this example, and 2 B 3 is the base of the logarithm).
Decision.
If log √ a b 3 \u003d 1, then 3 / (0.5 log a b \u003d 1. and log a B \u003d 1/6.
Then log a 2 B 3√ (A 11 b -3) \u003d 1/2 Log A 2 B 3 (A 11 b -3) \u003d Log A (A 11 B -3) / (2log A (A 2 B 3) ) \u003d (log A A 11 + Log A B -3) / (2 (log a A A 2 + LOG A B 3)) \u003d (11 - 3Log A B) / (2 (2 + 3Log A B)) Considering that that log a B \u003d 1/6 is obtained (11 - 3 · 1/6) / (2 (2 + 3 · 1/6)) \u003d 10.5 / 5 \u003d 2.1.
Answer: 2.1.
You can independently perform the following task:
Calculate Log √3 6 √2.1 if log 0.7 27 \u003d a.
Answer: (3 + a) / (3a).
Example 10.
Calculate 6.5 4 / LOG 3 169 · 3 1 / LOG 4 13 + LOG125.
Decision.
6.5 4 / Log 3 169 · 3 1 / log 4 13 + log 125 \u003d (13/2) 4/2 Log 3 13 · 3 2 / log 2 13 + 2Log 5 5 3 \u003d (13/2) 2 log 13 3 · 3 2 log 13 2 + 6 \u003d (13 log 13 3/2 Log 13 3) 2 · (3 log 13 2) 2 + 6 \u003d (3/2 log 13 3) 2 · (3 log 13 2) 2 + 6 \u003d (3 2 / (2 log 13 3) 2) · (2 \u200b\u200bLog 13 3) 2 + 6.
(2 Log 13 3 \u003d 3 log 13 2 (Formula 4))
We obtain 9 + 6 \u003d 15.
Answer: 15.
Have questions? Do not know how to find the value of the logarithmic expression?
To get a tutor help - register.
The first lesson is free!
the site, with full or partial copying of the material reference to the original source is required.
Logarithmic expressions, solving examples. In this article, we will consider the tasks associated with the solution of logarithms. The tasks raises the question of finding the expression value. It should be noted that the concept of logarithm is used in many tasks and understand its meaning is extremely important. As for the USE, the logarithm is used in solving equations, in applied tasks, also in the tasks associated with the study of functions.
We give examples to understand the sense of logarithm:
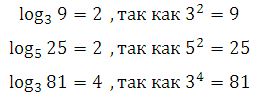
Basic logarithmic identity:
The properties of the logarithms that must always be remembered:
* The logarithm of the work is equal to the sum of the logarithms of the factors.
* * *
* Private logarithm (fraction) is equal to the difference in the logarithms of the factors.
* * *
* The logarithm is equal to the product of the degree in the logarithm of its base.
* * *
* Transition to a new base
* * *
More properties:
* * *
The calculation of logarithms is closely related to the use of the properties of the degree indicators.
List some of them:
The essence of this property is that when transferring the numerator to the denominator, and on the contrary, the indicator sign changes to the opposite. For example:
Consequence of this property:
* * *
When erecting a degree to a degree, the foundation remains the same, and the indicators are variable.
* * *
How did you see the very concept of logarithm simple. The main thing is that good practice is needed, which gives a certain skill. Of course, knowledge of the formulas must. If the skill in the conversion of elementary logarithms is not formed, then when solving simple tasks, you can easily allow an error.
Practice, decide first the simplest examples from the course of mathematics, then go to more complex. In the future, I will definitely show how "terrible" logarithms are solved, there will be no such ones on the exam, but they are of interest, do not miss!
That's all! Success to you!
Sincerely, Alexander Krutitsky
P.S: I will be grateful if you tell about the site on social networks.
Logarithms, like any numbers, can be folded, deduct and convert. But since logarithms are not quite ordinary numbers, there are its own rules that are called basic properties.
These rules must necessarily know - no serious logarithmic task is solved without them. In addition, they are quite a bit - everything can be learned in one day. So, proceed.
Addition and subtraction of logarithms
Consider two logarithm with the same bases: Log a. x. and log. a. y.. Then they can be folded and deducted, and:
- log. a. x. + Log. a. y. \u003d Log. a. (x. · y.);
- log. a. x. - Log. a. y. \u003d Log. a. (x. : y.).
So, the amount of logarithms is equal to the logarithm of the work, and the difference is the logarithm of private. Please note: the key point here is same grounds. If the foundations are different, these rules do not work!
These formulas will help calculate the logarithmic expression even when individual parts are not considered (see the lesson "What is logarithm"). Take a look at the examples - and make sure:
Log 6 4 + Log 6 9.
Since the bases in logarithms are the same, we use the sum of the sum:
log 6 4 + Log 6 9 \u003d Log 6 (4 · 9) \u003d log 6 36 \u003d 2.
A task. Find the value of the expression: Log 2 48 - Log 2 3.
The foundations are the same, using the difference formula:
log 2 48 - Log 2 3 \u003d Log 2 (48: 3) \u003d log 2 16 \u003d 4.
A task. Find the value of the expression: Log 3 135 - Log 3 5.
Again the foundations are the same, so we have:
log 3 135 - Log 3 5 \u003d log 3 (135: 5) \u003d log 3 27 \u003d 3.
As you can see, the initial expressions are made up of "bad" logarithms, which are not separately considered separately. But after transformation, quite normal numbers are obtained. In this fact, many test work are built. But what is the control - such expressions are in full (sometimes - almost unchanged) are offered on the exam.
Executive degree from logarithm
Now a little complicate the task. What if at the base or argument of logarithm costs a degree? Then the indicator of this extent can be taken out of the logarithm sign according to the following rules:
It is easy to see that the last rule follows their first two. But it is better to remember it, in some cases it will significantly reduce the amount of calculations.
Of course, all these rules make sense if compliance with the OTZ Logarithm: a. > 0, a. ≠ 1, x. \u003e 0. And also: learn to apply all formulas not only from left to right, but on the contrary, i.e. You can make numbers facing the logarithm, to the logarithm itself. That is most often required.
A task. Find the value of the expression: log 7 49 6.
Get rid of the extent in the argument on the first formula:
log 7 49 6 \u003d 6 · Log 7 49 \u003d 6 · 2 \u003d 12
A task. Find the value of the expression:
[Signature to Figure]
Note that in the denominator there is a logarithm, the base and the argument of which are accurate degrees: 16 \u003d 2 4; 49 \u003d 7 2. We have:
[Signature to Figure] I think the latest example requires explanation. Where did the logarithms disappeared? Until the last moment, we only work with the denominator. They presented the basis and argument of a logarithm there in the form of degrees and carried out indicators - received a "three-story" fraction.
Now let's look at the basic fraction. The number in the numerator and the denominator is the same number: log 2 7. Since log 2 7 ≠ 0, we can reduce the fraction - 2/4 will remain in the denominator. According to the rules of arithmetic, the four can be transferred to the numerator, which was done. The result was the answer: 2.
Transition to a new base
Speaking about the rules for the addition and subtraction of logarithms, I specifically emphasized that they work only with the same bases. And what if the foundations are different? What if they are not accurate degrees of the same number?
Formulas for the transition to a new base come to the rescue. We formulate them in the form of theorem:
Let Logarithm Log a. x.. Then for any number c. such that c. \u003e 0 I. c. ≠ 1, true equality:
[Signature to Figure]
In particular, if you put c. = x.We will get:
[Signature to Figure]
From the second formula it follows that the base and argument of the logarithm can be changed in places, but at the same time the expression "turns over", i.e. Logarithm turns out to be in the denominator.
These formulas are rare in conventional numerical expressions. Assessing how convenient they are, it is possible only when solving logarithmic equations and inequalities.
However, there are tasks that are generally not solved anywhere as a transition to a new base. Consider a couple of such:
A task. Find the value of the expression: Log 5 16 · Log 2 25.
Note that the arguments of both logarithms are accurate degrees. I will summarize: log 5 16 \u003d log 5 2 4 \u003d 4Log 5 2; Log 2 25 \u003d log 2 5 2 \u003d 2Log 2 5;
And now "invert" the second logarithm:
[Signature to Figure]Since the work does not change from the rearrangement of multipliers, we calmly changed the four and a two, and then sorted out with logarithms.
A task. Find the value of the expression: Log 9 100 · LG 3.
The basis and argument of the first logarithm - accurate degrees. We write it and get rid of the indicators:
[Signature to Figure]Now get rid of the decimal logarithm, by turning to the new base:
[Signature to Figure]Basic logarithmic identity
Often, the solution is required to submit a number as a logarithm for a specified base. In this case, formulas will help us:
In the first case n. It becomes an indicator of the extent in the argument. Number n. It can be absolutely anyone, because it is just a logarithm value.
The second formula is actually a paraphrassed definition. It is called: the main logarithmic identity.
In fact, what will happen if the number b. build in such a degree that the number b. to this extent gives the number a.? Correctly: this is the most a.. Carefully read this paragraph again - many "hang" on it.
Like the transition formulas to a new base, the main logarithmic identity is sometimes the only possible solution.
A task. Find the value of the expression:
[Signature to Figure]
Note that log 25 64 \u003d log 5 8 - just made a square from the base and the argument of the logarithm. Given the rules for multiplication of degrees with the same base, we get:
[Signature to Figure]If someone is not aware, it was a real task of ege :)
Logarithmic unit and logarithmic zero
In conclusion, I will give two identities that it is difficult to name the properties - rather, this is the consequence of the definition of logarithm. They are constantly found in tasks and, which is surprising, create problems even for "advanced" students.
- log. a. a. \u003d 1 is a logarithmic unit. Record once and forever: logarithm on any basis a. From the very base is equal to one.
- log. a. 1 \u003d 0 is a logarithmic zero. Base a. Maybe somehow, but if the argument is a unit - logarithm is zero! Because a. 0 \u003d 1 is a direct consequence of the definition.
That's all properties. Be sure to practice apply them in practice! Download the crib at the beginning of the lesson, print it - and solve the tasks.