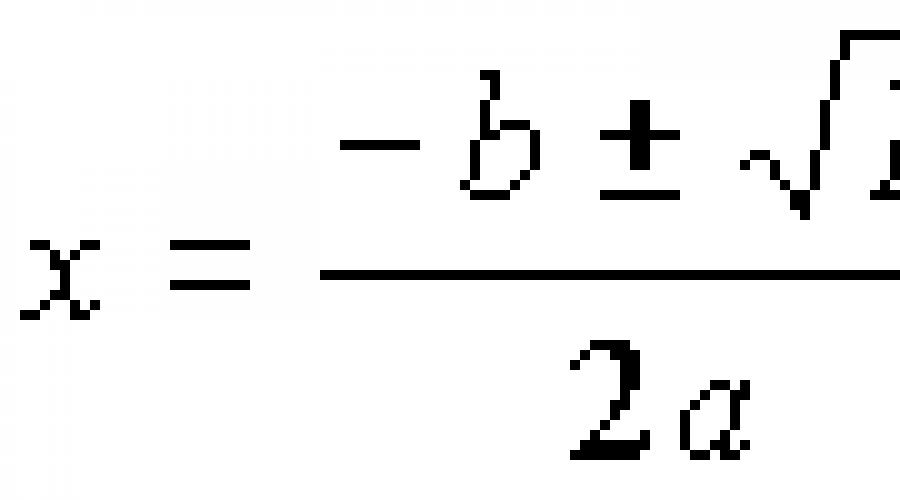
Square equations are studied in grade 8, so there is nothing difficult here. The ability to solve them is absolutely necessary.

The square equation is the equation of the form AX 2 + BX + C \u003d 0, where the coefficients A, B and C are arbitrary numbers, and a ≠ 0.

Before studying specific decision methods, we note that all square equations can be divided into three classes:

1. Do not have roots;
2. Have exactly one root;
3. Have two different roots.

This is an important difference between square equations from linear, where the root always exists and is unique. How to determine how many roots have an equation? For this there is a wonderful thing - discriminant.

Discriminant

Let the square equation AX 2 + BX + C \u003d 0. Then the discriminant is just the number d \u003d b 2 - 4ac.

This formula must be known by heart. Where she takes - now it does not matter. Other It is important: the discriminant sign can be determined how many roots has a square equation. Namely:

1. If D< 0, корней нет;
2. If D \u003d 0, there is exactly one root;
3. If D\u003e 0, there will be two roots.

Please note: the discriminant indicates the number of roots, and not at all on their signs, as for some reason, many consider. Take a look at the examples - and you will understand everything:

A task. How many roots are square equations:

1. x 2 - 8x + 12 \u003d 0;
2. 5x 2 + 3x + 7 \u003d 0;
3. x 2 - 6x + 9 \u003d 0.

We repel the coefficients for the first equation and find the discriminant:
a \u003d 1, b \u003d -8, c \u003d 12;
D \u003d (-8) 2 - 4 · 1 · 12 \u003d 64 - 48 \u003d 16

So, the discriminant is positive, so the equation has two different roots. Similarly, disassemble the second equation:
a \u003d 5; b \u003d 3; C \u003d 7;
D \u003d 3 2 - 4 · 5 · 7 \u003d 9 - 140 \u003d -131.

The discriminant is negative, no roots. The last equation remains:
a \u003d 1; b \u003d -6; C \u003d 9;
D \u003d (-6) 2 - 4 · 1 · 9 \u003d 36 - 36 \u003d 0.

The discriminant is zero - the root will be one.

Please note that for each equation the coefficients were discharged. Yes, it's a long time, yes, it's a tedious - but you will not confuse the coefficients and do not allow stupid mistakes. Choose yourself: speed or quality.

By the way, if you "fill the hand", after a while no longer need to write all the coefficients. Such operations you will be performed in your head. Most people begin to do so somewhere after 50-70 solved equations - in general, not so much.

Roots square equation

We now turn, actually, to the decision. If discriminant D\u003e 0, roots can be found by formulas:

The basic formula of the roots of the square equation

When D \u003d 0, you can use any of these formulas - it will be the same number that will be the answer. Finally, if D< 0, корней нет — ничего считать не надо.

1. x 2 - 2x - 3 \u003d 0;
2. 15 - 2x - x 2 \u003d 0;
3. x 2 + 12x + 36 \u003d 0.

First equation:
x 2 - 2x - 3 \u003d 0 ⇒ a \u003d 1; b \u003d -2; C \u003d -3;
D \u003d (-2) 2 - 4 · 1 · (-3) \u003d 16.

D\u003e 0 ⇒ The equation has two roots. Find them:

Second equation:
15 - 2x - x 2 \u003d 0 ⇒ a \u003d -1; b \u003d -2; C \u003d 15;
D \u003d (-2) 2 - 4 · (-1) · 15 \u003d 64.

D\u003e 0 ⇒ The equation again has two roots. We find them

\\ [\\ begin (Align) & ((x) _ (1)) \u003d \\ FRAC (2+ \\ SQRT (64)) (2 \\ Cdot \\ left (-1 \\ right)) \u003d - 5; \\\\ & ((x) _ (2)) \u003d \\ FRAC (2- \\ SQRT (64)) (2 \\ Cdot \\ left (-1 \\ right)) \u003d 3. \\\\ \\ END (ALIGN) \\]

Finally, the third equation:
x 2 + 12x + 36 \u003d 0 ⇒ a \u003d 1; b \u003d 12; C \u003d 36;
D \u003d 12 2 - 4 · 1 · 36 \u003d 0.

D \u003d 0 ⇒ The equation has one root. You can use any formula. For example, the first:

As can be seen from examples, everything is very simple. If you know the formula and be able to consider, there will be no problems. Most often, errors occur during substitution in the formula of negative coefficients. Here, again, the reception described above will help: look at the formula literally, paint every step - and very soon get rid of errors.

Incomplete square equations

It happens that the square equation is somewhat different from what is given in the definition. For example:

1. x 2 + 9x \u003d 0;
2. x 2 - 16 \u003d 0.

It is easy to see that in these equations there is no one of the terms. Such square equations are even easier than standard: they do not even need to consider discriminant. So, we introduce a new concept:

The AX 2 + BX + C \u003d 0 equation is called an incomplete square equation if B \u003d 0 or C \u003d 0, i.e. The coefficient with a variable x or the free element is zero.

Of course, a completely difficult case is possible when both of these coefficients are zero: b \u003d c \u003d 0. In this case, the equation takes the form AX 2 \u003d 0. Obviously, such an equation has a single root: x \u003d 0.

Consider the remaining cases. Let b \u003d 0 be 0, then we obtain an incomplete square equation of the form AX 2 + C \u003d 0. We convert it a little:

Since the arithmetic square root exists only from a non-negative number, the latter equality makes sense exclusively at (-C / a) ≥ 0. Conclusion:

1. If in an incomplete square equation of the form AX 2 + C \u003d 0, inequality (-C / a) is performed ≥ 0, there will be two roots. The formula is given above;
2. If (-c / a)< 0, корней нет.

As you can see, the discriminant did not need - in incomplete square equations there are no complex computing. In fact, even it is not necessary to remember the inequality (-c / a) ≥ 0. It is enough to express the value of X 2 and see what stands on the other side of the equality sign. If there is a positive number - the roots will be two. If negative - the roots will not be at all.

Now we will understand with the equations of the form AX 2 + BX \u003d 0, in which the free element is zero. Everything is simple here: the roots will always be two. It is enough to decompose a polynomial to multipliers:

Multiplier for bracket

The work is zero, when at least one of the multipliers is zero. From here there are roots. In conclusion, we will analyze several such equations:

A task. Square square equations:

1. x 2 - 7x \u003d 0;
2. 5x 2 + 30 \u003d 0;
3. 4x 2 - 9 \u003d 0.

x 2 - 7x \u003d 0 ⇒ x · (x - 7) \u003d 0 ⇒ x 1 \u003d 0; x 2 \u003d - (- 7) / 1 \u003d 7.

5x 2 + 30 \u003d 0 ⇒ 5x 2 \u003d -30 ⇒ x 2 \u003d -6. No roots, because Square cannot be equal to a negative number.

4x 2 - 9 \u003d 0 ⇒ 4x 2 \u003d 9 ⇒ x 2 \u003d 9/4 ⇒ x 1 \u003d 3/2 \u003d 1.5; x 2 \u003d -1.5.

View equation

Expression D. \u003d B. 2 - 4 AC. Call discriminant square equation. If a D. \u003d 0, the equation has one valid root; If D \u003e 0, the equation has two valid roots.
In the case when D. = 0 Sometimes they say that the square equation has two identical root.
Using the designation D. \u003d B. 2 - 4 AC. , you can rewrite formula (2) as

If a B. \u003d 2 K. The formula (2) takes the form:

where K. \u003d B. / 2 .
The last formula is especially convenient in cases where B. / 2 - integer, i.e. coefficient B. - even number.
Example 1: Solve equation 2 X. 2 - 5 X. + 2 = 0 . Here a \u003d 2, b \u003d -5, c \u003d 2. Have D. \u003d B. 2 - 4 AC. = (-5) 2- 4*2*2 = 9 . As D. > 0 , the equation has two roots. Find them by formula (2)

so X. 1 \u003d (5 + 3) / 4 \u003d 2, x 2 =(5 - 3) / 4 = 1 / 2 ,
i.e X. 1 = 2 and X. 2 = 1 / 2 - The roots of the specified equation.
Example 2: Solve equation 2 X. 2 - 3 X. + 5 = 0 . Here a \u003d 2, b \u003d -3, c \u003d 5. We find discriminant D. \u003d B. 2 - 4 AC. = (-3) 2- 4*2*5 = -31 . As D. 0 The equation does not have valid roots.

Incomplete square equations. If in the square equation AX. 2 + BX. + C. =0 The second coefficient B. or free dick C. equal to zero, then the square equation is called incomplete. Incomplete equations are isolated because to find their roots, it is possible not to use the root formula of the square equation - it is easier to solve the equation by the method of decomposition of its left part of the factors.
Example 1: Solve equation 2 X. 2 - 5 X. = 0 .
Have X. (2 X. - 5) = 0 . So either X. = 0 either 2 X. - 5 = 0 , i.e X. = 2.5 . So the equation has two roots: 0 and 2.5
Example 2: Solve equation 3 X. 2 - 27 = 0 .
Have 3 X. 2 = 27 . Consequently, the roots of this equation - 3 and -3 .

Vieta theorem. If the reduced square equation X. 2 + px. + Q. =0 has valid roots, then their amount is equal - P. , and the work is equal Q. , i.e

x 1 + x 2 \u003d -p,
x 1 x 2 \u003d Q

(The sum of the roots of the given square equation is equal to the second coefficient taken with the opposite sign, and the product of the roots is equal to a free member).

With this mathematical program you can solve square equation.

The program not only gives the answer task, but also displays the solution process in two ways:
- with the help of discriminant
- Using the Vieta Theorem (if possible).

Moreover, the answer is output accurate, not approximate.
For example, for the equation \\ (81x ^ 2-16x-1 \u003d 0 \\), the answer is output in this form:

$$ x_1 \u003d \\ FRAC (8+ \\ SQRT (145)) (81), \\ quad x_2 \u003d \\ FRAC (8-1 \\ SQRT (145)) (81) $$ and not in this: \\ (x_1 \u003d 0.247; \\ quad x_2 \u003d -0.05 \\)

This program may be useful to students of high schools of general education schools when preparing for tests and exams, when checking knowledge before the exam, parents for monitoring the solution of many problems in mathematics and algebra. Or maybe you are too expensive to hire a tutor or buy new textbooks? Or you just want to make your homework in mathematics or algebra as possible? In this case, you can also use our programs with a detailed solution.

Thus, you can conduct your own training and / or training of your younger brothers or sisters, while the level of education in the field of solved tasks increases.

If you are not familiar with the rules of entering a square polynomial, we recommend familiarizing yourself with them.

Square polynomial input rules

As a variable can be any Latin Letter.
For example: \\ (x, y, z, a, b, c, o, p, q \\), etc.

Numbers can enter whole or fractional.
Moreover, fractional numbers can be administered not only in the form of a decimal, but also in the form of an ordinary fraction.

The rules for entering decimal fractions.
In decimal fractions, the fractional part of the whole can be separated as a point and the comma.
For example, you can enter decimal fractions like this: 2.5x - 3.5x ^ 2

Rules for entering ordinary fractions.
Only an integer can act as a numerator, denominator and a whole part of the fraction.

The denominator cannot be negative.

When entering a numeric fraction, the numerator separated from the denominator to the fission mark: /
The whole part is separated from the fraraty ampersand sign: &
Input: 3 & 1/3 - 5 & 6 / 5z + 1 / 7z ^ 2
Result: \\ (3 \\ FRAC (1) (3) - 5 \\ FRAC (6) (5) Z + \\ FRAC (1) (7) z ^ 2 \\)

When entering the expression you can use brackets. In this case, when solving the square equation, the entered expression is first simplified.
For example: 1/2 (Y - 1) (Y + 1) - (5Y-10 & 1/2)

=0

Decide

It is found that some scripts required to solve this task are not loaded, and the program may not work.
You may have adblock included.
In this case, disconnect it and update the page.

You have javascript execution in your browser.
To make the solution appear, you need to enable JavaScript.
Here are the instructions, how to enable JavaScript in your browser.

Because Wishing to solve the task is very much, your request is in line.
After a few seconds, the solution will appear below.
Please wait sec ...

If you noticed a mistake in solvingYou can write about it in the feedback form.
Do not forget specify what task You decide and what enter in the field.

Our games, puzzles, emulators:

A bit of theory.

Square equation and its roots. Incomplete square equations

Each of the equations
\\ (- x ^ 2 + 6x + 1,4 \u003d 0, \\ quad 8x ^ 2-7x \u003d 0, \\ quad x ^ 2- \\ FRAC (4) (9) \u003d 0 \\)
Has appearance
\\ (AX ^ 2 + BX + C \u003d 0, \\)
where X is variable, A, B and C - numbers.
In the first equation a \u003d -1, b \u003d 6 and c \u003d 1.4, in the second a \u003d 8, b \u003d -7 and c \u003d 0, in the third a \u003d 1, b \u003d 0 and c \u003d 4/9. Such equations are called square equations.

Definition.
Square equation The equation of the form AX 2 + BX + C \u003d 0, where X is the variable, A, B and C are some numbers, and \\ (A \\ NEQ 0 \\).

The numbers A, B and C are the coefficients of the square equation. The number A is called the first coefficient, the number B is the second coefficient and the number C - a free member.

In each of the equations of the form AX 2 + BX + C \u003d 0, where \\ (A \\ NEQ 0 \\), the greatest degree of variable x - square. Hence the name: Square equation.

Note that the square equation is also called the equation of the second degree, since its left part has a second degree polynomial.

Square equation in which the coefficient at x 2 is 1, called given square equation. For example, given square equations are equations
\\ (x ^ 2-11x + 30 \u003d 0, \\ quad x ^ 2-6x \u003d 0, \\ quad x ^ 2-8 \u003d 0 \\)

If in the square equation AX 2 + BX + C \u003d 0, at least one of the coefficients B or C is zero, then such an equation is called incomplete square equation. So, the equations -2x 2 + 7 \u003d 0, 3x 2 -10x \u003d 0, -4x 2 \u003d 0 are incomplete square equations. In the first of them b \u003d 0, in the second C \u003d 0, in the third b \u003d 0 and c \u003d 0.

Incomplete square equations are three species:
1) AX 2 + C \u003d 0, where \\ (C \\ NEQ 0 \\);
2) AX 2 + BX \u003d 0, where \\ (B \\ NEQ 0 \\);
3) AX 2 \u003d 0.

Consider the solution of the equations of each of these species.

To solve an incomplete square equation of the form AX 2 + C \u003d 0, with \\ (C \\ NEQ 0 \\), it is transferred to its free member into the right-hand side and make both parts of the equation on A:
\\ (x ^ 2 \u003d - \\ FRAC (C) (a) \\ rightarrow x_ (1,2) \u003d \\ pm \\ sqrt (- \\ FRAC (C) (A)) \\)

Since \\ (C \\ NEQ 0 \\), then \\ (- \\ FRAC (C) (A) \\ NEQ 0 \\)

If \\ (- \\ FRAC (C) (A)\u003e 0 \\), the equation has two roots.

If \\ (- \\ FRAC (C) (a), to solve an incomplete square equation of the form AX 2 + BX \u003d 0, with \\ (B \\ NEQ 0 \\), they decline its left part to multipliers and get the equation
\\ (X (AX + B) \u003d 0 \\ RIGHTARROW \\ LEFT \\ (\\ Begin (Array) (L) x \u003d 0 \\\\ Ax + B \u003d 0 \\ END (Array) \\ Right. \\ Rightarrow \\ Left \\ (\\ Begin (Array) (L) X \u003d 0 \\\\ X \u003d - \\ FRAC (B) (A) \\ END (Array) \\ Right. \\)

So, an incomplete square equation of the form AX 2 + BX \u003d 0 with \\ (B \\ NEQ 0 \\) always has two roots.

An incomplete square equation of the form AX 2 \u003d 0 is equivalent to equation x 2 \u003d 0 and therefore has the only root 0.

Square equation root formula

Consider now how the square equations solve in which both coefficients with unknown and free member are different from zero.

Spest square equation in general and as a result we obtain the root formula. Then this formula can be used when solving any square equation.

Resister Square equation AX 2 + BX + C \u003d 0

Separating both parts of it on A, we obtain the equivalent of the presented square equation
\\ (x ^ 2 + \\ FRAC (B) (A) X + \\ FRAC (C) (A) \u003d 0 \\)

We transform this equation, highlighting the square of the bounced:
\\ (x ^ 2 + 2x \\ Cdot \\ FRAC (B) (2a) + \\ left (\\ FRAC (B) (2a) \\ Right) ^ 2- \\ LEFT (\\ FRAC (B) (2a) \\ Right) ^ 2 + \\ FRAC (C) (A) \u003d 0 \\ RIGHTARROW \\)

\\ (x ^ 2 + 2x \\ Cdot \\ FRAC (B) (2a) + \\ left (\\ FRAC (B) (2a) \\ Right) ^ 2 \u003d \\ left (\\ FRAC (B) (2A) \\ Right) ^ 2 - \\ FRAC (C) (A) \\ RIGHTARROW \\) \\ (\\ Left (X + \\ FRAC (B) (2a) \\ Right) ^ 2 \u003d \\ FRAC (B ^ 2) (4a ^ 2) - \\ FRAC ( c) (a) \\ rightarrow \\ left (x + \\ frac (b) (2a) \\ right) ^ 2 \u003d \\ FRAC (B ^ 2-4ac) (4a ^ 2) \\ Rightarrow \\) \\ (x + \\ FRAC (B ) (2a) \u003d \\ pm \\ sqrt (\\ FRAC (B ^ 2-4ac) (4a ^ 2)) \\ Rightarrow x \u003d - \\ FRAC (b) (2a) + \\ FRAC (\\ pm \\ sqrt (b ^ 2 -4AC)) (2a) \\ Rightarrow \\) \\ (x \u003d \\ FRAC (-b \\ pm \\ sqrt (b ^ 2-4ac)) (2a) \\)

The guided expression is called discriminant square equation AX 2 + BX + C \u003d 0 ("discriminant" in Latin is a distinctor). It is denoted by the letter D, i.e.
\\ (D \u003d b ^ 2-4ac \\)

Now, using the designation of the discriminant, rewrite the formula for the roots of the square equation:
\\ (X_ (1,2) \u003d \\ FRAC (-b \\ pm \\ sqrt (d)) (2a) \\), where \\ (d \u003d b ^ 2-4ac \\)

It's obvious that:
1) If D\u003e 0, the square equation has two roots.
2) If D \u003d 0, the square equation has one root \\ (x \u003d - \\ FRAC (B) (2a) \\).
3) if D is thus, depending on the discriminant value, the square equation may have two roots (with D\u003e 0), one root (at d \u003d 0) or not to have roots (with D, when solving the square equation for this formula, it is advisable to apply to the following way:
1) calculate the discriminant and compare it with zero;
2) If the discriminant is positive or equal to zero, then use the root formula, if the discriminant is negative, then write down the roots.

Vieta theorem

The presented square equation AX 2 -7x + 10 \u003d 0 has roots 2 and 5. The amount of the roots is 7, and the product is 10. We see that the amount of the roots is equal to the second coefficient taken with the opposite sign, and the product of the roots is equal to a free member. Such property has any given square equation having a root.

The sum of the roots of the presented square equation is equal to the second coefficient taken with the opposite sign, and the product of the roots is equal to a free member.

Those. The Vieta Theorem argues that the roots of the X 1 and X 2 of the given square equation x 2 + px + q \u003d 0 have a property:
\\ (\\ left \\ (\\ begin (array) (L) x_1 + x_2 \u003d -p \\\\ x_1 \\ cdot x_2 \u003d q \\ end (array) \\ right. \\)

I hope that studying this article, you will learn to find the roots of a complete square equation.

With the help of discriminant, only complete square equations are solved, for solve square equations, other methods that you find in the article "Decision of incomplete square equations" are used.

What square equations are called full? it equations of the form ah 2 + b x + c \u003d 0where the coefficients a, b and are not equal to zero. So, to solve a complete square equation, it is necessary to calculate the discriminant D.

D \u003d b 2 - 4As.

Depending on what kind of importance is discriminant, we will write the answer.

If discriminant is a negative number (D< 0),то корней нет.

If the discriminant is zero, x \u003d (-b) / 2a. When the discriminant is a positive number (D\u003e 0),

then x 1 \u003d (-b - √d) / 2a, and x 2 \u003d (-b + √d) / 2a.

For example. Solve equation x 2 - 4x + 4 \u003d 0.

D \u003d 4 2 - 4 · 4 \u003d 0

x \u003d (- (-4)) / 2 \u003d 2

Answer: 2

Solve equation 2. x 2 + x + 3 \u003d 0.

D \u003d 1 2 - 4 · 2 · 3 \u003d - 23

Answer: No roots.

Solve equation 2. x 2 + 5x - 7 \u003d 0.

D \u003d 5 2 - 4 · 2 · (-7) \u003d 81

x 1 \u003d (-5 - √81) / (2 · 2) \u003d (-5 - 9) / 4 \u003d - 3.5

x 2 \u003d (-5 + √81) / (2 · 2) \u003d (-5 + 9) / 4 \u003d 1

Answer: - 3.5; one.

So let's imagine the solution of complete square equations by the scheme in Figure1.

According to these formulas, you can solve any complete square equation. You only need to carefully monitor the equation was recorded by a polynomial of a standard type.

but x 2 + BX + C, Otherwise you can make an error. For example, in the record of the equation x + 3 + 2x 2 \u003d 0, it is erroneously can be solved that

a \u003d 1, b \u003d 3 and c \u003d 2. then

D \u003d 3 2 - 4 · 1 · 2 \u003d 1 and then the equation has two roots. And this is incorrect. (See the solution of Example 2 above).

Therefore, if the equation is not written not to a polynomial of a standard species, at first a complete square equation should be recorded by a polynomial of a standard species (in the first place should be unrocked with the greatest indicator, that is but x 2 then with smaller – bX.and then free dick from.

When solving a given square equation and a square equation with an even coefficient, with the second term, other formulas can be used. Let's get acquainted with these formulas. If in a complete square equation in the second term, the coefficient will be even (b \u003d 2k), then the equation according to the formulas in the figure 2 can be solved.

The full square equation is called the above, if the coefficient is x 2 equal to one and the equation will take the form x 2 + px + q \u003d 0. Such an equation can be given to solve, or is obtained by dividing all coefficients to the coefficient equation butstanding for x 2 .

Figure 3 shows the scheme of solving the above square
equations. Consider on the example the application of the formulas considered in this article.

Example. Solve equation

3x 2 + 6x - 6 \u003d 0.

Let's decide this equation using the formulas shown in the Figure 1 scheme.

D \u003d 6 2 - 4 · 3 · (- 6) \u003d 36 + 72 \u003d 108

√D \u003d √108 \u003d √ (36 · 3) \u003d 6√3

x 1 \u003d (-6 - 6√3) / (2 · 3) \u003d (6 (-1- √ (3))) / 6 \u003d -1 - √3

x 2 \u003d (-6 + 6√3) / (2 · 3) \u003d (6 (-1+ √ (3))) / 6 \u003d -1 + √3

Answer: -1 - √3; -1 + √3

It can be seen that the coefficient at x in this equation is an even number, that is, b \u003d 6 or b \u003d 2k, from where k \u003d 3. Then we try to solve the equation according to the formulas shown in the diagram D 1 \u003d 3 2 - 3 · (- 6 ) \u003d 9 + 18 \u003d 27

√ (D 1) \u003d √27 \u003d √ (9 · 3) \u003d 3√3

x 1 \u003d (-3 - 3√3) / 3 \u003d (3 (-1 - √ (3))) / 3 \u003d - 1 - √3

x 2 \u003d (-3 + 3√3) / 3 \u003d (3 (-1 + √ (3))) / 3 \u003d - 1 + √3

Answer: -1 - √3; -1 + √3. Noticed that all coefficients in this square equation are divided into 3 and by performing division, we obtain the reduced square equation x 2 + 2x - 2 \u003d 0 by solving this equation using formulas for the specified square
equations Figure 3.

D 2 \u003d 2 2 - 4 · (- 2) \u003d 4 + 8 \u003d 12

√ (D 2) \u003d √12 \u003d √ (4 · 3) \u003d 2√3

x 1 \u003d (-2 - 2√3) / 2 \u003d (2 (-1 - √ (3))) / 2 \u003d - 1 - √3

x 2 \u003d (-2 + 2√3) / 2 \u003d (2 (-1+ √ (3))) / 2 \u003d - 1 + √3

Answer: -1 - √3; -1 + √3.

As we see, when solving this equation on various formulas, we received the same answer. Therefore, it is well aware of the formulas shown in the Figure 1 scheme, you can always solve any complete square equation.

the site, with full or partial copying of the material reference to the original source is required.

In continuation of the topic "Decision of equations", the material of this article will introduce you to square equations.

Consider everything in detail: the essence and record of the square equation, set the accompanying terms, we will analyze the scheme for the solution of incomplete and complete equations, get acquainted with the formula of roots and discriminant, establish links between roots and coefficients, and of course we give a visual solution of practical examples.

Yandex.rtb R-A-339285-1

Square equation, its types

Definition 1.

Quadratic equation - This is the equation recorded as a · x 2 + b · x + c \u003d 0where X. - variable, a, b and C. - Some numbers, while a.no zero.

Often, square equations are also called the name of the second degree equations, since in essence the square equation is the algebraic equation of the second degree.

We give an example to illustrate a given definition: 9 · x 2 + 16 · x + 2 \u003d 0; 7, 5 · x 2 + 3, 1 · x + 0, 11 \u003d 0, etc. - These are square equations.

Definition 2.

Numbers a, b and C. - these are the coefficients of the square equation a · x 2 + b · x + c \u003d 0, with the coefficient A. It is called the first, or older, or the coefficient at x 2, b - the second coefficient, or the coefficient when X., but C. Call free member.

For example, in a square equation 6 · x 2 - 2 · x - 11 \u003d 0 Senior coefficient is 6, the second coefficient is − 2 and free member is equal − 11 . Pay attention to the fact that when the coefficients B.and / or C are negative, then a brief form of a view recording is used. 6 · x 2 - 2 · x - 11 \u003d 0, but not 6 · x 2 + (- 2) · x + (- 11) \u003d 0.

We also clarify this aspect: if the coefficients A. and / or B. equal 1 or − 1 , then explicit participation in the recording of the square equation, they may not be taken, which is explained by the features of the record of these numeric coefficients. For example, in a square equation Y 2 - Y + 7 \u003d 0 Senior coefficient is 1, and the second coefficient is − 1 .

Specified and unmarried square equations

By the value of the first coefficient, the square equations are divided into the above and unpaid.

Definition 3.

The reduced square equation - This is a square equation where the older coefficient is equal to 1. For other values \u200b\u200bof the older coefficient, the square equation is non-invalid.

We give examples: square equations x 2 - 4 · x + 3 \u003d 0, x 2 - x - 4 5 \u003d 0 are presented in each of which the older coefficient is 1.

9 · x 2 - x - 2 \u003d 0 - an integral square equation, where the first coefficient is different from 1 .

Any unpassed square equation is possible to convert into a given equation if it is divided from both parts to the first coefficient (equivalent transformation). The transformed equation will have the same roots as the specified intelligent equation or not to have roots at all.

Consideration of a specific example will allow us to clearly demonstrate the transition from an integral square equation to the given one.

Example 1.

The equation is set 6 · x 2 + 18 · x - 7 \u003d 0 . It is necessary to convert the initial equation in the above form.

Decision

The scheme of the specified above is separated by both parts of the initial equation on the senior coefficient 6. Then we get: (6 · x 2 + 18 · x - 7): 3 \u003d 0: 3And this is the same as: (6 · x 2): 3 + (18 · x): 3 - 7: 3 \u003d 0 And further: (6: 6) · x 2 + (18: 6) · x - 7: 6 \u003d 0. From here: x 2 + 3 · x - 1 1 6 \u003d 0. Thus, an equation is considered to be specified.

Answer: x 2 + 3 · x - 1 1 6 \u003d 0.

Full and incomplete square equations

Turn to the definition of the square equation. In it we clarified that A ≠ 0. Such a condition is necessary to equation a · x 2 + b · x + c \u003d 0 it was exactly square because a \u003d 0 It is essentially converted into linear equation b · x + c \u003d 0.

In the case when the coefficients B. and C.equal to zero (which is possible, both individually and together), the square equation is called incomplete.

Definition 4.

Incomplete square equation - such a square equation a · x 2 + b · x + c \u003d 0,where at least one of the coefficients B.and C.(or both) is zero.

Full square equation - a square equation in which all numeric coefficients are not zero.

We indulge in why the types of square equations are given exactly the names.

For b \u003d 0 square equation takes the form A · x 2 + 0 · X + C \u003d 0that the same thing is that a · x 2 + c \u003d 0. For C \u003d 0. Square equation is recorded as a · x 2 + b · x + 0 \u003d 0That is equivalent a · x 2 + b · x \u003d 0. For B \u003d 0. and C \u003d 0. The equation will take the view a · x 2 \u003d 0. The equations that we have received are different from the full square equation in that their left parts are not contained either a component from the X variable or a free member or both at once. Actually, this fact was asked the name of such a type of equations - incomplete.

For example, x 2 + 3 · x + 4 \u003d 0 and - 7 · x 2 - 2 · x + 1, 3 \u003d 0 are complete square equations; x 2 \u003d 0, - 5 · x 2 \u003d 0; 11 · x 2 + 2 \u003d 0, - x 2 - 6 · x \u003d 0 - incomplete square equations.

Decision of incomplete square equations

The above definition makes it possible to distinguish the following types of incomplete square equations:

• a · x 2 \u003d 0, this equation corresponds to the coefficients B \u003d 0. and c \u003d 0;
• a · x 2 + c \u003d 0 for b \u003d 0;
• a · x 2 + b · x \u003d 0 at c \u003d 0.

Consider the decision of each type of incomplete square equation.

Solution of the equation A · x 2 \u003d 0

As mentioned above, the equation corresponds to the coefficients B. and C.equal to zero. The equation a · x 2 \u003d 0 It is possible to convert equation to equivalent to it x 2 \u003d 0which we get, sharing both parts of the source equation for the number A.not equal to zero. Obvious fact that the root of the equation x 2 \u003d 0 this is zero because 0 2 = 0 . Other roots, this equation has no, which is explained by the properties of the degree: for any number p,not equal to zero, faithful inequality P 2\u003e 0what follows that when P ≠ 0 equality P 2 \u003d 0will never be achieved.

Definition 5.

Thus, for an incomplete square equation A · x 2 \u003d 0 there is the only root x \u003d 0..

Example 2.

For example, we solve an incomplete square equation - 3 · x 2 \u003d 0. It is equivalent to the equation x 2 \u003d 0, his only root is x \u003d 0., Then the initial equation has the only root - zero.

Briefly the decision is made up so:

- 3 · x 2 \u003d 0, x 2 \u003d 0, x \u003d 0.

Solution of the equation A · x 2 + c \u003d 0

On the queue - the solution of incomplete square equations, where B \u003d 0, C ≠ 0, that is, the equations of the form a · x 2 + c \u003d 0. We transform this equation carried out the term from one part of the equation to another, changing the sign to the opposite and dividing both parts of the equation to the number, not equal to zero:

• transfer C. in the right part, which gives the equation A · x 2 \u003d - C;
• we divide both parts of the equation on A., I get in the end x \u003d - c a.

Our transformations are equivalent, respectively, the resulting equation is also equivalent to the source, and this fact makes it possible to conclude the roots of the equation. From what is the meanings A. and C.the value of the expression depends - C A: it may have a minus sign (let's say if a \u003d 1. and C \u003d 2., then - c a \u003d - 2 1 \u003d - 2) or a plus sign (for example, if A \u003d - 2 and C \u003d 6., then - C a \u003d - 6 - 2 \u003d 3); it is not zero because C ≠ 0.. Let us dwell in more detail in situations when - C a< 0 и - c a > 0 .

In the case when - C A< 0 , уравнение x 2 = - c a не будет иметь корней. Утверждая это, мы опираемся на то, что квадратом любого числа является число неотрицательное. Из сказанного следует, что при - c a < 0 ни для какого числа P. Equality P 2 \u003d - C A cannot be true.

All otherwise, when - C a\u003e 0: Recall the square root, and it will be obvious that the equation x 2 \u003d - C A will be the number - C A, since - C a 2 \u003d - C a. It is not difficult to understand that the number is - C A is also the root of the equation x 2 \u003d - C a: indeed, - - C a 2 \u003d - C a.

Other roots equation will not have. We can demonstrate it using the nasty method. To begin with, set the designations found above the roots as x 1 and - X 1.. I will suggest that equation x 2 \u003d - C A is also root x 2which differs from the roots x 1 and - X 1.. We know that, substituting into the equation instead X. Its roots, we transform the equation into a fair numerical equality.

For x 1 and - X 1. We write: x 1 2 \u003d - C A, and for x 2 - x 2 2 \u003d - C a. Relying on the properties of numerical equalities, replete one right equality from another, which will give us: x 1 2 - x 2 2 \u003d 0. Use the properties of actions with numbers to rewrite the latest equality as (x 1 - x 2) · (x 1 + x 2) \u003d 0. It is known that the work of two numbers is zero then and only if at least one of the numbers is zero. From said it follows that x 1 - x 2 \u003d 0 and / or x 1 + x 2 \u003d 0that the same thing x 2 \u003d x 1 and / or x 2 \u003d - x 1. There was an obvious contradiction, because at first it was agreed that the root of the equation x 2 differs from x 1 and - X 1.. So, we proved that the equation does not have other roots, except x \u003d - c a and x \u003d - - c a.

We summarize all reasoning above.

Definition 6.

Incomplete square equation a · x 2 + c \u003d 0 equivalent to equation x 2 \u003d - c a, which:

• will not have roots when - c a< 0 ;
• there will be two roots X \u003d - C A and X \u003d - - C A with - C a\u003e 0.

We give examples of solving equations a · x 2 + c \u003d 0.

Example 3.

The square equation is specified 9 · x 2 + 7 \u003d 0.It is necessary to find his decision.

Decision

We transfer a free member to the right-hand part of the equation, then the equation will take the form 9 · x 2 \u003d - 7.
We divide both parts of the obtained equation on 9 , come to x 2 \u003d - 7 9. In the right part, we see a number with a minus sign, which means: the specified equation has no roots. Then the original incomplete square equation 9 · x 2 + 7 \u003d 0 Will not have roots.

Answer: the equation 9 · x 2 + 7 \u003d 0it does not have roots.

Example 4.

It is necessary to solve the equation - x 2 + 36 \u003d 0.

Decision

We move 36 to the right side: - x 2 \u003d - 36.
We split both parts on − 1 , get x 2 \u003d 36. In the right part - a positive number, from here we can conclude that x \u003d 36 or X \u003d - 36.
Remove the root and write down the final result: an incomplete square equation - x 2 + 36 \u003d 0 It has two roots x \u003d 6. or x \u003d - 6.

Answer: x \u003d 6. or x \u003d - 6.

Solution of the equation A · x 2 + b · x \u003d 0

We will examine the third type of incomplete square equations when C \u003d 0.. To find a decision of an incomplete square equation a · x 2 + b · x \u003d 0, We use the method of decomposition on multipliers. Spread on multipliers of the polynomial, which is in the left part of the equation, by making a general multiplier for brackets X.. This step will provide an opportunity to convert the original incomplete square equation to the equivalent x · (a · x + b) \u003d 0. And this equation, in turn, is equivalent to the totality of equations x \u003d 0. and A · X + B \u003d 0. The equation A · X + B \u003d 0 Linear, and its root: x \u003d - b a.

Definition 7.

Thus, an incomplete square equation a · x 2 + b · x \u003d 0 will have two roots x \u003d 0. and x \u003d - b a.

Fasten the material by an example.

Example 5.

It is necessary to find the solution of the equation 2 3 · x 2 - 2 2 7 · x \u003d 0.

Decision

Let's lead X. For brackets and obtain equation x · 2 3 · x - 2 2 7 \u003d 0. This equation is equivalent to equations x \u003d 0. and 2 3 · x - 2 2 7 \u003d 0. Now it is necessary to solve the resulting linear equation: 2 3 · x \u003d 2 2 7, x \u003d 2 2 7 2 3.

Briefly solving the equation to write this way:

2 3 · x 2 - 2 2 7 · x \u003d 0 x · 2 3 · x - 2 2 7 \u003d 0

x \u003d 0 or 2 3 · x - 2 2 7 \u003d 0

x \u003d 0 or x \u003d 3 3 7

Answer: x \u003d 0, x \u003d 3 3 7.

Discriminant, the roots formula of the square equation

To find a solution of square equations, there is a formula for roots:

Definition 8.

x \u003d - b ± d 2 · a where D \u003d b 2 - 4 · a · c - the so-called discriminant of a square equation.

Recording X \u003d - B ± D 2 · A in essence means that x 1 \u003d - b + d 2 · a, x 2 \u003d - b - d 2 · a.

It will be useful to understand how the specified formula was derived and how to apply it.

The output of the roots of the square equation

Let us be challenged to solve the square equation a · x 2 + b · x + c \u003d 0. Perform a number of equivalent transformations:

• we split both parts of the equation for the number a.other than zero, we obtain the reduced square equation: x 2 + b a · x + c a \u003d 0;
• we highlight the full square in the left side of the received equation:
  x 2 + ba · x + ca \u003d x 2 + 2 · b 2 · a · x + b 2 · a 2 - b 2 · a 2 + ca \u003d x + b 2 · a 2 - b 2 · a 2 + CA.
  After that, the equation will take the form: X + B 2 · A 2 - B 2 · A 2 + C a \u003d 0;
• now it is possible to make the transfer of the last two terms into the right-hand side, changing the sign to the opposite, after which we obtain: x + b 2 · a 2 \u003d b 2 · a 2 - C a;
• finally, we transform the expression recorded on the right side of the last equality:
  B 2 · A 2 - C a \u003d b 2 4 · a 2 - C a \u003d b 2 4 · a 2 - 4 · A · C 4 · A 2 \u003d B 2 - 4 · A · C 4 · A 2.

Thus, we came to the equation X + B 2 · a 2 \u003d B 2 - 4 · A · C 4 · A 2, equivalent source equation a · x 2 + b · x + c \u003d 0.

We understood the solution of such equations in previous paragraphs (decision of incomplete square equations). The experience gained makes it possible to conclude regarding the roots of the equation X + B 2 · A 2 \u003d B 2 - 4 · A · C 4 · A 2:

• at B 2 - 4 · A · C 4 · A 2< 0 уравнение не имеет действительных решений;
• for B 2 - 4 · A · C 4 · A 2 \u003d 0, the equation has the form x + b 2 · a 2 \u003d 0, then x + b 2 · a \u003d 0.

Hence the only root X \u003d - B 2 · A is obvious;

• for b 2 - 4 · a · C 4 · A 2\u003e 0, it will be correct: X + B 2 · A \u003d B 2 - 4 · A · C 4 · A 2 or X \u003d B 2 · A - B 2 - 4 · a · C 4 · a 2, which is the same as X + - B 2 · A \u003d B 2 - 4 · A · C 4 · A 2 or X \u003d - B 2 · A - B 2 - 4 · A · C 4 · A 2, i.e. The equation has two roots.

It is possible to conclude that the presence or absence of the roots of the equation X + B 2 · A 2 \u003d B 2 - 4 · A · C 4 · A 2 (and hence the initial equation) depends on the sign of expression B 2 - 4 · A · C 4 · A 2, recorded on the right side. And the sign of this expression is set by the number of the numerator, (denominator 4 · a 2 will always be positive), that is, a sign of expression B 2 - 4 · A · C. This expression B 2 - 4 · A · C The name is the discriminant of a square evacuation and is defined as its designation of the letter D. Here you can record the essence of the discriminant - by its value and the sign are concluded whether the square equation will have valid roots, and if it is, what is the number of roots - one or two.

Returning to the equation X + B 2 · A 2 \u003d B 2 - 4 · A · C 4 · A 2. I rewrite it using the discriminant designation: X + B 2 · a 2 \u003d D 4 · A 2.

We will formulate conclusions again:

Definition 9.

• for D.< 0 The equation has no valid roots;
• for D \u003d 0. The equation has the only root X \u003d - B 2 · A;
• for D\u003e 0 The equation has two roots: x \u003d - b 2 · a + d 4 · a 2 or x \u003d - b 2 · a - d 4 · a 2. These roots based on the properties of the radicals can be written in the form: x \u003d - b 2 · a + d 2 · a or - b 2 · a - d 2 · a. And when we reveal the modules and give the fractions to the common denominator, we obtain: x \u003d - b + d 2 · a, x \u003d - b - d 2 · a.

Thus, the result of our reasoning was the removal of the formula of the roots of the square equation:

x \u003d - b + d 2 · a, x \u003d - b - d 2 · a, discriminant D. Calculated by formula D \u003d b 2 - 4 · a · c.

These formulas make it possible when discriminated is larger to determine both valid roots. When the discriminant is zero, the use of both formulas will give the same root as the sole solution of the square equation. In the case when the discriminant is negative, trying to use the root formula of the square equation, we will face the need to remove the square root from the negative number, which will lead us beyond the actual numbers. With a negative discriminant, the square equation will not be valid roots, but a pair of comprehensively conjugate roots, determined by the same root formulas obtained by us are possible.

Algorithm for solving square equations on root formulas

It is possible to solve the square equation, immediately cycling the formula of the roots, but basically they do, if necessary, find complex roots.

In the main mass of cases, it is usually implied for the search for non-complex, but valid roots of the square equation. Then optimally before using the formulas of the roots of the square equation, first determine the discriminant and make sure it is not negative (otherwise we conclude that the equation has no valid roots), and then proceed to calculate the roots value.

The arguments above provide the ability to formulate an algorithm for solving a square equation.

Definition 10.

To solve a square equation a · x 2 + b · x + c \u003d 0, it is necessary:

• according to the formula D \u003d b 2 - 4 · a · c find the value of the discriminant;
• with D.< 0 сделать вывод об отсутствии у квадратного уравнения действительных корней;
• at d \u003d 0 find the only root of the equation according to the formula X \u003d - B 2 · A;
• for d\u003e 0, determine the two valid roots of the square equation according to the formula x \u003d - b ± d 2 · a.

Note that when the discriminant is zero, you can use the formula x \u003d - b ± d 2 · a, it will give the same result as the formula X \u003d - B 2 · a.

Consider examples.

Examples of solutions of square equations

We present the solution of examples at different values \u200b\u200bof the discriminant.

Example 6.

It is necessary to find the roots of the equation x 2 + 2 · x - 6 \u003d 0.

Decision

We write the number coefficients of the square equation: a \u003d 1, b \u003d 2 and C \u003d - 6. Next, we act on the algorithm, i.e. We will proceed to calculate the discriminant, for which we will substitute the coefficients A, B and C. In the formula of the discriminant: D \u003d B 2 - 4 · A · C \u003d 2 2 - 4 · 1 · (- 6) \u003d 4 + 24 \u003d 28.

So, we obtained D\u003e 0, and this means that the initial equation will have two valid roots.
To find them, we use the root formula x \u003d - b ± d 2 · a and, substituting the corresponding values, we obtain: x \u003d - 2 ± 28 2 · 1. We simplify the resulting expression, making a multiplier for the root sign, followed by the cutting of the fraction:

x \u003d - 2 ± 2 · 7 2

x \u003d - 2 + 2 · 7 2 or x \u003d - 2 - 2 · 7 2

x \u003d - 1 + 7 or x \u003d - 1 - 7

Answer: X \u003d - 1 + 7, x \u003d - 1 - 7.

Example 7.

It is necessary to solve the square equation - 4 · x 2 + 28 · x - 49 \u003d 0.

Decision

Determine the discriminant: D \u003d 28 2 - 4 · (- 4) · (- 49) \u003d 784 - 784 \u003d 0. With this discriminant value, the initial equation will have only one root defined by the formula X \u003d - B 2 · a.

x \u003d - 28 2 · (- 4) x \u003d 3, 5

Answer: x \u003d 3, 5.

Example 8.

It is necessary to solve the equation 5 · Y 2 + 6 · Y + 2 \u003d 0

Decision

The numeric coefficients of this equation will be: a \u003d 5, b \u003d 6 and c \u003d 2. We use these values \u200b\u200bto find a discriminant: d \u003d b 2 - 4 · a · C \u003d 6 2 - 4 · 5 · 2 \u003d 36 - 40 \u003d - 4. The calculated discriminant is negative, thus, the initial square equation does not have valid roots.

In the case when the task is to specify complex roots, apply the root formula, performing actions with complex numbers:

x \u003d - 6 ± - 4 2 · 5,

x \u003d - 6 + 2 · i 10 or x \u003d - 6 - 2 · i 10,

x \u003d - 3 5 + 1 5 · i or x \u003d - 3 5 - 1 5 · i.

Answer: There are no valid roots; Complex roots are as follows: - 3 5 + 1 5 · I, - 3 5 - 1 5 · I.

In the school program, there is still no requirement to look for complex roots, so if during the solution discriminant is defined as a negative, the answer is immediately recorded that there are no valid roots.

Formula roots for even second coefficients

The formula of the roots x \u003d - b ± d 2 · a (d \u003d b 2 - 4 · a · c) makes it possible to obtain another formula, more compact, allowing to find solutions of square equations with an even coefficient at x (or with a type 2 coefficient · n, for example, 2 · 3 or 14 · ln 5 \u003d 2 · 7 · ln 5). We show how this formula is displayed.

Let us be the task of finding the solution of the square equation A · x 2 + 2 · n · x + c \u003d 0. We act on the algorithm: Determine the discriminant d \u003d (2 · n) 2 - 4 · a · c \u003d 4 · n 2 - 4 · a · c \u003d 4 · (n 2 - a · c), and then use the root formula:

x \u003d - 2 · n ± d 2 · a, x \u003d - 2 · n ± 4 · n 2 - a · C 2 · a, x \u003d - 2 · n ± 2 n 2 - a · C 2 · a, x \u003d - n ± N 2 - A · Ca.

Let the expression N 2 - A · C be indicated as D 1 (sometimes D "). Then the formula of the roots of the square equation under consideration with the second coefficient 2 · n will take the form:

x \u003d - n ± d 1 A, where d 1 \u003d n 2 - a · c.

It is easy to see that that d \u003d 4 · d 1, or d 1 \u003d d 4. In other words, D 1 is a quarter of the discriminant. It is obvious that the sign D 1 is the same as the sign D, which means the sign D 1 can also serve as an indicator of the presence or absence of the roots of the square equation.

Definition 11.

Thus, to find the solution of the square equation with the second coefficient 2 · n, it is necessary:

• find D 1 \u003d N 2 - A · C;
• with D 1.< 0 сделать вывод, что действительных корней нет;
• for d 1 \u003d 0, determine the only root of the equation according to the formula X \u003d - N A;
• for d 1\u003e 0, determine the two valid roots according to the formula x \u003d - n ± d 1 a.

Example 9.

It is necessary to solve the square equation 5 · x 2 - 6 · x - 32 \u003d 0.

Decision

The second coefficient of the specified equation can be represented as 2 · (- 3). Then rewrite the specified square equation as 5 · x 2 + 2 · (- 3) · x - 32 \u003d 0, where a \u003d 5, n \u003d - 3 and c \u003d - 32.

We calculate the fourth part of the discriminant: D 1 \u003d N 2 - A · C \u003d (- 3) 2 - 5 · (- 32) \u003d 9 + 160 \u003d 169. The value obtained positively, this means that the equation has two valid roots. We define them according to the corresponding root formula:

x \u003d - n ± d 1 a, x \u003d - - 3 ± 169 5, x \u003d 3 ± 13 5,

x \u003d 3 + 13 5 or x \u003d 3 - 13 5

x \u003d 3 1 5 or x \u003d - 2

It would be possible to make calculations and by the usual formula of the roots of the square equation, but in this case the solution would be more cumbersome.

Answer: x \u003d 3 1 5 or x \u003d - 2.

Simplification of the species of square equations

Sometimes it is possible to optimize the type of source equation, which will simplify the process of calculating the roots.

For example, a square equation 12 · x 2 - 4 · X - 7 \u003d 0 is clearly more convenient for solving than 1200 · x 2 - 400 · x - 700 \u003d 0.

More often simplification of the species of the square equation is performed by the multiplication or division of its both parts into a kind of number. For example, we showed a simplified record of the equation 1200 · x 2 - 400 · x - 700 \u003d 0, obtained by dividing both parts by 100.

Such a conversion is possible when the coefficients of the square equation are not mutually simple numbers. Then there are usually dividing both parts of the equation to the largest common divisor of absolute values \u200b\u200bof its coefficients.

As an example, use a square equation 12 · x 2 - 42 · x + 48 \u003d 0. We define the node of absolute values \u200b\u200bof its coefficients: nodes (12, 42, 48) \u003d node (node \u200b\u200b(12, 42), 48) \u003d node (6, 48) \u003d 6. We will divide the two parts of the original square equation to 6 and we obtain the equivalent square equation 2 · x 2 - 7 · x + 8 \u003d 0.

The multiplication of both parts of the square equation is usually get rid of fractional coefficients. At the same time multiplied by the smallest general multiple denominator of its coefficients. For example, if each part of the square equation is 1 6 · x 2 + 2 3 · x - 3 \u003d 0 multiply from the NOC (6, 3, 1) \u003d 6, then it will become recorded in a simpler form x 2 + 4 · X - 18 \u003d 0.

Finally, we note that almost always get rid of the minus at the first coefficient of the square equation, changing the signs of each member of the equation, which is achieved by multiplying (or divisions) of both parts of 1. For example, from a square equation - 2 · x 2 - 3 · x + 7 \u003d 0, you can go to its simplified version 2 · x 2 + 3 · x - 7 \u003d 0.

Communication between roots and coefficients

The formula of the roots of square equations x \u003d - b ± d 2 · A already known to us expresses the roots of the equation through its numerical coefficients. Relying on this formula, we have the opportunity to set other dependencies between the roots and coefficients.

The most famous and applicable are the formulas of the Vieta theorem:

x 1 + x 2 \u003d - b a and x 2 \u003d c a.

In particular, for the reduced square equation, the amount of the roots is the second coefficient with the opposite sign, and the product of the roots is free of charge. For example, according to the species of the square equation 3 · x 2 - 7 · x + 22 \u003d 0, it is possible to immediately determine that the sum of its roots is 7 3, and the product of the roots is 22 3.

You can also find a number of other links between the roots and coefficients of the square equation. For example, the sum of squares of the roots of the square equation can be expressed through the coefficients:

x 1 2 + x 2 2 \u003d (x 1 + x 2) 2 - 2 · x 1 · x 2 \u003d - Ba 2 - 2 · Ca \u003d B 2 A 2 - 2 · Ca \u003d B 2 - 2 · A · Ca 2.

If you notice a mistake in the text, please select it and press Ctrl + Enter