Μετατροπή έκφρασης. Λεπτομερής Θεωρία (2020)
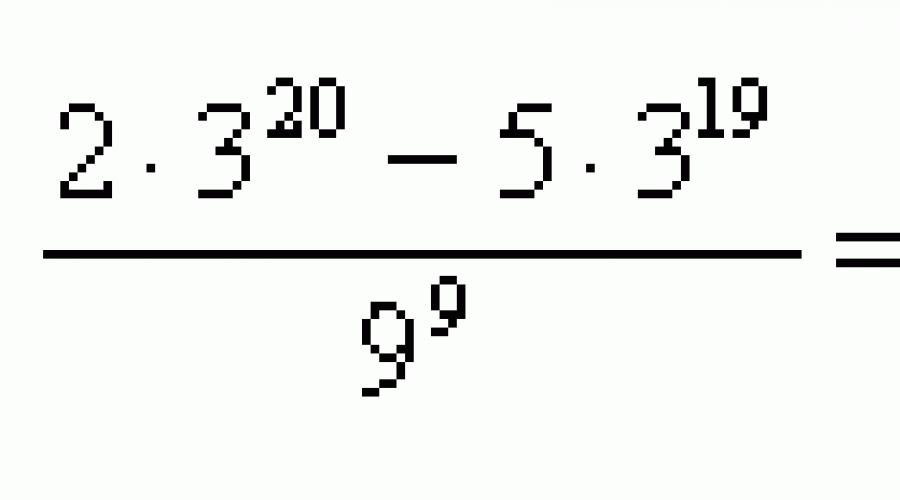
Διαβάστε επίσης
Ενότητες: Μαθηματικά
Τάξη: 9
ΣΚΟΠΟΣ: Η εδραίωση και η βελτίωση των δεξιοτήτων εφαρμογής των ιδιοτήτων ενός πτυχίου με ορθολογικό δείκτη. να αναπτύξουν τις δεξιότητες να εκτελούν απλούς μετασχηματισμούς παραστάσεων που περιέχουν βαθμούς με κλασματικό εκθέτη.
ΤΥΠΟΣ ΜΑΘΗΜΑΤΟΣ: μάθημα για την εμπέδωση και την εφαρμογή γνώσεων σε ένα δεδομένο θέμα.
ΣΧΟΛΙΚΟ ΒΙΒΛΙΟ: Άλγεβρα 9 έκδ. ΑΝΩΝΥΜΗ ΕΤΑΙΡΙΑ. Ο Τελιακόφσκι.
ΚΑΤΑ ΤΑ ΜΑΘΗΜΑΤΑ
Εισαγωγική ομιλία του δασκάλου
"Οι άνθρωποι που δεν είναι εξοικειωμένοι με την άλγεβρα δεν μπορούν να φανταστούν τα καταπληκτικά πράγματα που μπορούν να επιτευχθούν ... με τη βοήθεια της εν λόγω επιστήμης." G.V. Leibniz
Η Άλγεβρα μας ανοίγει τις πόρτες στο εργαστηριακό συγκρότημα «Πτυχίο με ορθολογικό εκθέτη».
1. Μετωπική έρευνα
1) Να ορίσετε το βαθμό με κλασματικό εκθέτη.
2) Για ποιον κλασματικό εκθέτη ορίζεται ο βαθμός με βάση ίση με μηδέν;
3) Θα προσδιοριστεί ο βαθμός με κλασματικό εκθέτη για αρνητική βάση;
Εργασία: Γράψτε τον αριθμό 64 ως δύναμη με βάση - 2; 2; οκτώ.
Ποιος κύβος είναι το 64;
Υπάρχει κάποιος άλλος τρόπος να αναπαραστήσουμε τον αριθμό 64 ως δύναμη με λογικό εκθέτη;
2. Εργαστείτε σε ομάδες
1 ομάδα. Να αποδείξετε ότι οι εκφράσεις (-2) 3/4 ; Το 0-2 δεν έχει νόημα.
2 ομάδα. Αντιπροσωπεύστε τον βαθμό με κλασματικό εκθέτη ως ρίζα: 2 2/3; 3 -1|3 ; -σε 1,5; 5α 1/2; (x-y) 2/3 .
3η ομάδα. Εκφράστε ως βαθμό με κλασματικό εκθέτη: v3; 8 va 4; 3v2 -2 ; v(x+y) 2/3 ; vvv.
3. Ας πάμε στο εργαστήριο "Δράση στις δυνάμεις"
Συχνοί επισκέπτες του εργαστηρίου είναι αστρονόμοι. Φέρνουν τους «αστρονομικούς αριθμούς» τους, τους υποβάλλουν σε αλγεβρική επεξεργασία και παίρνουν χρήσιμα αποτελέσματα.
Για παράδειγμα, η απόσταση από τη Γη στο νεφέλωμα της Ανδρομέδας εκφράζεται με τον αριθμό
95000000000000000000 = 95 10 18 km;
λέγεται πεντακισεκατομμύριον.
Η μάζα του ήλιου σε γραμμάρια εκφράζεται με τον αριθμό 1983 10 30 gr - μη αλιόν.
Επιπλέον, άλλα σοβαρά καθήκοντα εμπίπτουν στο εργαστήριο. Για παράδειγμα, υπάρχει συχνά ένα πρόβλημα αξιολόγησης εκφράσεων της φόρμας:
ένα) ; β) ; σε) .
Το προσωπικό του εργαστηρίου εκτελεί τέτοιους υπολογισμούς με τον πιο βολικό τρόπο.
Μπορείτε να συνδεθείτε στην εργασία. Για να γίνει αυτό, επαναλαμβάνουμε τις ιδιότητες των μοιρών με λογικούς εκθέτες:
Τώρα υπολογίστε ή απλοποιήστε την έκφραση εφαρμόζοντας τις ιδιότητες των εκθετών με ορθολογικούς εκθέτες:
1 ομάδα:
2 ομάδα:
3η ομάδα:
Έλεγχος: ένα άτομο από την ομάδα στον πίνακα.
4. Εργασία για σύγκριση
Πώς, χρησιμοποιώντας τις ιδιότητες των μοιρών, να συγκρίνουμε τις εκφράσεις 2 100 και 10 30 ;
Απάντηση:
2 100 =(2 10) 10 =1024 10 .
10 30 =(10 3) 10 =1000 10
1024 10 >1000 10
2 100 >10 30
5. Και τώρα σας προσκαλώ στο εργαστήριο «Έρευνα Πτυχίων».
Τι μετασχηματισμούς μπορούμε να κάνουμε στις δυνάμεις;
1) Εκφράστε τον αριθμό 3 ως δύναμη με εκθέτη 2. 3; -ένας.
2) Με ποιον τρόπο μπορούν να συνυπολογιστούν οι εκφράσεις a-b; σε + σε 1/2; α-2α 1/2; 2 το 2?
3) Μειώστε το κλάσμα με επακόλουθη αμοιβαία επαλήθευση:
4) Εξηγήστε τους μετασχηματισμούς που πραγματοποιήθηκαν και βρείτε την τιμή της παράστασης:

6. Εργαστείτε με το σχολικό βιβλίο.Νο. 611 (d, e, f).
Ομάδα 1: (δ).
Ομάδα 2: (ε).
Ομάδα 3: (ε).
Νο. 629 (α, β).
Αμοιβαία επαλήθευση.
7. Πραγματοποιούμε συνεργείο (ανεξάρτητη εργασία).
Δοσμένες εκφράσεις:

Κατά την αναγωγή ποιων κλασμάτων χρησιμοποιούνται οι τύποι συντετμημένου πολλαπλασιασμού και αγκύλωσης του κοινού παράγοντα;
1 γκρουπ: Νο. 1, 2, 3.
Ομάδα 2: Νο. 4, 5, 6.
Ομάδα 3: Νο. 7, 8, 9.
Όταν ολοκληρώνετε την εργασία, μπορείτε να χρησιμοποιήσετε τις συστάσεις.
- Αν υπάρχουν και οι δύο εκθέτες με λογικό εκθέτη και nοη ρίζες στην εγγραφή του παραδείγματος, τότε γράψτε τις ν η ρίζες ως εκθέτες με ορθολογικό εκθέτη.
- Προσπαθήστε να απλοποιήσετε την έκφραση στην οποία εκτελούνται οι ενέργειες: ανοίγοντας τις αγκύλες, εφαρμόζοντας τον τύπο μειωμένου πολλαπλασιασμού, μετακίνηση από έναν αρνητικό εκθέτη σε μια έκφραση που περιέχει θετικούς εκθέτες.
- Προσδιορίστε τη σειρά με την οποία πρέπει να εκτελεστούν οι ενέργειες.
- Εκτελέστε τα βήματα με τη σειρά που εκτελούνται.
Αξιολογεί τον δάσκαλο συλλέγοντας τετράδια.
8. Εργασία για το σπίτι: Αρ. 624, 623.
Δημοτικό κρατικό εκπαιδευτικό ίδρυμα
βασικό γενικό σχολείο Νο 25
Μάθημα Άλγεβρας
Θέμα:
« Μετατροπή παραστάσεων που περιέχουν βαθμούς με κλασματικούς εκθέτες»
Αναπτύχθηκε από:
,
καθηγητής μαθηματικών
υψηλότερο kκατηγορίας προσόντων
οζώδης
2013
Θέμα μαθήματος: Μετατροπή παραστάσεων που περιέχουν δυνάμεις με κλασματικούς εκθέτες
Ο σκοπός του μαθήματος:
1. Περαιτέρω σχηματισμός δεξιοτήτων, γνώσεων, δεξιοτήτων για μετασχηματισμό εκφράσεων που περιέχουν βαθμούς με κλασματικούς δείκτες
2. Ανάπτυξη της ικανότητας εύρεσης λαθών, ανάπτυξη της σκέψης, της δημιουργικότητας, του λόγου, των υπολογιστικών δεξιοτήτων
3. Εκπαίδευση ανεξαρτησίας, ενδιαφέρον για το θέμα, προσοχή, ακρίβεια.
ΔΣΜ:μαγνητικός πίνακας, κάρτες ελέγχου, πίνακες, ατομικές κάρτες, οι μαθητές έχουν κενά υπογεγραμμένα φύλλα για ατομική εργασία στο τραπέζι, ένα σταυρόλεξο, πίνακες για μαθηματική προθέρμανση, έναν προβολέα πολυμέσων.
Τύπος μαθήματος: κούμπωμα ZUN.
Σχέδιο μαθήματος έγκαιρα
1. Οργανωτικές στιγμές (2 λεπτά)
2. Έλεγχος της εργασίας (5 λεπτά)
3. Σταυρόλεξο (3 λεπτά)
4. Μαθηματική προθέρμανση (5 λεπτά)
5. Επίλυση ασκήσεων για τη στερέωση του μπροστινού μέρους (7 λεπτά)
6. Ατομική εργασία (10 λεπτά)
7. Λύση επαναληπτικών ασκήσεων (5 λεπτά)
8. Περίληψη του μαθήματος (2 λεπτά)
9. Εργασία για το σπίτι (1 λεπτό)
Κατά τη διάρκεια των μαθημάτων
1) Έλεγχος της εργασίας με τη μορφή αξιολόγησης από ομοτίμους . Οι καλοί μαθητές ελέγχουν τα τετράδια των αδύναμων παιδιών. Και οι αδύνατοι τσεκάρουν με τους δυνατούς σύμφωνα με το μοντέλο της κάρτας ελέγχου. Οι εργασίες για το σπίτι δίνονται σε δύο εκδοχές.
Εγώ εύκολη επιλογή εργασίας
II επιλογή δύσκολης εργασίας
Ως αποτέλεσμα του ελέγχου, τα παιδιά υπογραμμίζουν τα λάθη με ένα απλό μολύβι και βάζουν ένα σημάδι. Τέλος, ελέγχω την εργασία αφού τα παιδιά βάλουν τα τετράδια τους μετά το μάθημα. Ζητώ από τα παιδιά τα αποτελέσματα της δοκιμής τους και βάζω βαθμούς για αυτό το είδος εργασίας στον συνοπτικό μου πίνακα.
2) Προσφέρεται σταυρόλεξο για τη δοκιμή της θεωρητικής ύλης..
Κάθετα:
1. Ιδιότητα πολλαπλασιασμού που χρησιμοποιείται κατά τον πολλαπλασιασμό ενός μονωνύμου με ένα πολυώνυμο;
2. Η επίδραση των εκθετών κατά την αύξηση ενός βαθμού σε μια ισχύ;
3. Ένας βαθμός με μηδενικό εκθέτη;
4. Ένα προϊόν που αποτελείται από τους ίδιους παράγοντες;
Οριζόντια:
5. Ρίζα n - ο βαθμός από μη αρνητικό αριθμό;
6. Πώς λειτουργούν οι εκθέτες κατά τον πολλαπλασιασμό των εκθετών;
7. Η δράση των εκθετών στη διαίρεση των βαθμών;
8. Ο αριθμός όλων των ίδιων παραγόντων;
3) Μαθηματική προθέρμανση
α) εκτελέστε τον υπολογισμό και χρησιμοποιήστε την κρυπτογράφηση για να διαβάσετε τη λέξη που κρύβεται στο πρόβλημα.
Υπάρχει ένα τραπέζι στον πίνακα μπροστά σας. Ο πίνακας στη στήλη 1 περιέχει παραδείγματα που πρέπει να υπολογιστούν.
Κλειδί για το τραπέζι
491/2 | ||
27-1/3 | ||
4*81/3 | ||
5*25-1/2 | ||
7*82/3 | ||
(49/144)1/2 | 7/12 | |
(27*64)1/3 |
7/12 |
Και γράψτε την απάντηση στη στήλη II, και στη στήλη III βάλτε το γράμμα που αντιστοιχεί σε αυτή την απάντηση.
Δάσκαλος: Άρα, η κρυπτογραφημένη λέξη είναι "πτυχίο". Στην επόμενη εργασία, δουλεύουμε με τον 2ο και τον 3ο βαθμό
β) Το παιχνίδι "Κοίτα, μην κάνεις λάθος"
Αντικαταστήστε τις τελείες με έναν αριθμό
α) x \u003d (x ...) 2; β) a3/2 = (a1/2)…; γ) a=(a1/3)…; δ) 5… = (51/4)2; ε) 34/3=(34/9)…; στ) 74/5 = (7…)2; ζ) x1/2=(x…)2; η) y1/2=(y…)2
Ας βρούμε το σφάλμα:
А1/4 – 2а1/2 + 1 = (а1/
Λοιπόν, παιδιά, τι έπρεπε να κάνετε για να ολοκληρώσετε αυτήν την εργασία:
Η ιδιότητα των μοιρών: κατά την αύξηση ενός βαθμού σε μια ισχύ, οι δείκτες πολλαπλασιάζονται.
4) Τώρα ας πάμε στο μπροστινό έργο. χρησιμοποιώντας τα αποτελέσματα προηγούμενων εργασιών. Τα ανοιχτά τετράδια γράφουν τον αριθμό, το θέμα του μαθήματος.
№ 000
α) a - c \u003d (a1/2) 2 - (b1/2) 2 \u003d (a1/2 - c1/2) * (a1/2 + c1/2)
β) a - c \u003d (a1/3) 3 - (c1/3) 3 \u003d (a1/3 - c1/3) * (a2/3 + a1/3 c1/3 + c2/3)
Νο. 000 (a, c, d, e)
ένα ) m2 – 5 = m2 – (m1/2)2 = (m – 51/2)*(m+51/2)
γ) a3 - 4 = (a3/2)2 - 22 = (a3/2 - 2)*(a3/2 +2)
δ) x2/5 – y4/5 = (x1/5)2 – (y2/5)2 = (x1/5 – y2/5)*(x1/5 + y2/5)
ε) 4 – a = 22 – (a1/2)2 = (2 – a1/2)*(2+a1/2)
Αρ. 000 (α, δ, ε)
α) x3 - 2 = x3 - (21/3)3 = (x - 21/3)*(x2 + 21/3 x + 22/3)
δ) a6/5 + 27 = (a2/5)3 + 33 = (a2/5 + 3)*(a4/3 - 3 a2/5 + 9)
στ) 4 + y = (41/3)3 + (y1/3)3 = (41/3 + y1/3)*(42/3 + 41/3 y1/3 + y2/3)
Βαθμός
5) Εργαστείτε σε μεμονωμένες κάρτες σύμφωνα με τέσσερις επιλογές σε ξεχωριστά φύλλα
Εργασίες με διάφορους βαθμούς δυσκολίας ολοκληρώνονται χωρίς καμία προτροπή από τον δάσκαλο.
Ελέγχω αμέσως το έργο και βάζω σημάδια στο τραπέζι μου και στα φύλλα των τύπων.
Νο. 000 (a, c, e, h)
α) 4*31/2/(31/2 - 3) = 4*31/2 /31/2*(1 - 31/2) = 4 / (1 - 31/2)
γ) x + x1/2 /2x = x1/2*(x1/2+1)/ 2*(x1/2)2 = (x1/2+1)/ 2x1/2
ε) (α2/3 – v2/3)/(а1/3 + в1/3) = (а1/3)2 – (в1/3)2/(а1/3 + в1/3) = (α1/3 + v1/3)*(а1/3 – v1/3)/(а1/3 + v1/3) = a1/3 – v1/3
η) (x2/3 - x1/3 y1/3 + y2/3)/(x + y) = ((x1/3)2 - x1/3 y1/3 + (y1/3)2)/(( x1/3)3 + (y1/3)3) = ((x1/3)2 – x1/3 y1/3 + (y1/3)2)/(x1/3 + y1/3)*((x1 /3)2 – x1/3 y1/3 + (y1/3)2) = 1/ (x1/3 + y1/3)
7) Εργαστείτε σε μεμονωμένες κάρτες με διάφορους βαθμούς πολυπλοκότητας. Σε ορισμένες ασκήσεις υπάρχουν συστάσεις από τον δάσκαλο, καθώς το υλικό είναι περίπλοκο και είναι δύσκολο για τα αδύναμα παιδιά να αντεπεξέλθουν στην εργασία
Υπάρχουν επίσης τέσσερις διαθέσιμες επιλογές. Η αξιολόγηση γίνεται αμέσως. Εισάγω όλες τις βαθμολογίες σε ένα υπολογιστικό φύλλο.
Πρόβλημα № από τη συλλογή
Ο δάσκαλος κάνει ερωτήσεις:
1. Τι πρέπει να βρεθεί στο πρόβλημα;
2. Τι πρέπει να γνωρίζετε για αυτό;
3. Πώς εκφράζεται η ώρα 1 πεζού και 2 πεζού;
4. Συγκρίνετε τον χρόνο 1 και 2 πεζών ανάλογα με την συνθήκη του προβλήματος και φτιάξτε μια εξίσωση.
Η λύση του προβλήματος:
Έστω x (km/h) η ταχύτητα 1 πεζού
X +1 (km/h) – ταχύτητα 2 πεζοί
4/х (η) – χρόνος περπατήματος
4 / (x +1) (η) - ώρα του δεύτερου πεζού
Με την προϋπόθεση του προβλήματος 4/х >4/ (х +1) για 12 λεπτά
12 λεπτά = 12/60 h = 1/5 h
Κάνουμε μια εξίσωση
X / 4 - 4 / (x + 1) \u003d 1/5
NOZ: 5x(x +1) ≠ 0
5*4*(x+1) – 5*4x = x*(x+1)
20x + 20 - 20x - x2 - x = 0
X2 + x -20 = 0
D \u003d 1 - 4 * (-20) \u003d 81, 81> 0, 2 k
x1 \u003d (-1 -√81) / (-2) \u003d 5 km / h - η ταχύτητα 1 πεζού
x2 = (-1 + √81)/(-2) = 4 - δεν ταιριάζει με το νόημα της εργασίας, αφού x>0
Απάντηση: 5 km / h - η ταχύτητα 2 πεζών
9) Περίληψη μαθήματος: Λοιπόν, παιδιά, σήμερα στο μάθημα εμπεδώσαμε τις γνώσεις, τις δεξιότητες, τις δεξιότητες μετασχηματισμού εκφράσεων που περιέχουν βαθμούς, εφαρμόσαμε τους τύπους του συντετμημένου πολλαπλασιασμού, βγάζοντας τον κοινό παράγοντα από αγκύλες, επαναλάβαμε την ύλη που καλύφθηκε. Επισημαίνω τα πλεονεκτήματα και τα μειονεκτήματα.
Συνοψίζοντας το μάθημα στον πίνακα.
Σταυρόλεξο | Χαλάκι. ζέσταμα | Εμπρός. Δουλειά | Ind. εργασία Κ-1 | Ind. εργασία Κ-2 | ||||
10) Ανακοινώνω τις βαθμολογίες. Εργασία για το σπίτι
Ατομικά φύλλα Κ - 1 και Κ - 2
Αλλάζω Β - 1 και Β - 2. Β - 3 και Β - 4, αφού είναι ισοδύναμα
Αιτήσεις για το μάθημα.
1) Κάρτες εργασίας
1. απλοποιώ
α) (x1/2 - y1/2)2 + 2x1/2 y1/2
β) (a3/2 + 5a1\2)2 - 10a2
2. παρουσιάζουν ως άθροισμα
α) a1/3 c1\4*(b2/3 + c3/4)
β) (a1/2 - c1/2)*(a + a1/2 c1\2 + c)
3. βγάλτε τον κοινό παράγοντα
γ) 151/3 +201/3
1. απλοποιώ
α) √m + √n – (m1/4 – n1/4)2
β) (а1/4 + в1/4)*(α1/8 + β1/8)*(α1\8 - β1/8)
2. παρουσιάζουν ως άθροισμα
α) x0,5 y0,5*(x-0,5 – y1,5)
β) (x1/3 + y1/3)*(x2\3 - x1/3 y1\3 + y2/3)
3. Βγάλτε τον κοινό παράγοντα από αγκύλες
β) c1\3 - γ
γ) (2α)1/3 - (5α)1\3
2) κάρτα ελέγχου για B - 2
α) √m + √n – (m 1|4 – n 1|4)2 = m 1|2 + n 1|2 – ((m 1|2)2 – 2 m 1/4 n 1/4 + (n 1/2)2) = m 1/2 + n 1/2 - m 1/2 + 2 m 1/4 n 1/4 - n 1/2 = 2 m 1/4 n 1/4
β) (а1/4 + в1/4)*(а1/8 + в1/8)*(α1/8 - β1/8) = (α1/4 + β1/4)*(α1/8)2 - ( в1/8)2 = (а1/4 + в1/4)*(а1/4 - в1/4) = (а1/4)2 - (в1/4)2 = a1/2 - в1/2
α) x0,5 y0,5* (x-0,5- y1,5) = x0,5 y0,5 x-0,5 – x0,5 y0,5y1,5 = x0 y0,5 – x0,5 y2 = y0. 5 – x0,5 y2
β) (x1/3 + y1/3)*(x2/3 - x1/3 y1\3 + y2/3) = (x1\3 + y1/3)*((x1/3)2 - x1/3 y1\3 + (y1/3)2) = (x1/3)2 + (y1/3)2 = x + y
α) 3 - 31/2 = 31/2 * (31/2 - 1)
β) c1/3 - c \u003d c1/3 * (1 - c2/3)
γ) (2a)1/3 - (5a)1/3 = a1/3*(21/3 - 51/3)
3) Κάρτες για την πρώτη ατομική εργασία
α) a - y, x ≥ 0, y ≥ 0
β) a – i, a ≥ 0
1. Παραγοντοποιήστε παρουσιάζοντας ως διαφορά τετραγώνων
α) α1/2 - β1/2
2. Παραγοντοποιήστε παρουσιάζοντας ως διαφορά ή άθροισμα κύβων
α) c1/3 + d1/3
1. Παραγοντοποιήστε παρουσιάζοντας ως διαφορά τετραγώνων
α) Χ1/2 + Υ1/2
β) Χ1/4 - Υ1/4
2. Παραγοντοποιήστε παρουσιάζοντας ως διαφορά ή άθροισμα κύβων
4) κάρτες για τη δεύτερη ατομική εργασία
α) (x - x1/2) / (x1/2 - 1)
Υπόδειξη: x1/2 αγκύλες τους αριθμητές
β) (α - γ) / (α1/2 - γ1/2)
Σημείωση: a - b = (a1/2)2 - (b1/2)2
Μειώστε το κλάσμα
α) (21/4 - 2) / 5*21/4
Υπόδειξη: βραχίονας 21/4
β) (α - γ) / (5a1/2 - 5v1/2)
Σημείωση: a - b = (a1/2)2 - (b1/2)2
Επιλογή 3
1. Μειώστε το κλάσμα
α) (x1/2 - x1/4)/x3/4
Οδηγία: βραχίονας x1/4
β) (а1/2 - β1/2) / (4α1/4 - 4χ1/4)
Επιλογή 4
Μειώστε το κλάσμα
α) 10/ (10 - 101/2)
β) (α - γ) / (a2/3 + a1 \ 3b1 / 3 + B 1/3)
Η αριθμητική πράξη που εκτελείται τελευταία κατά τον υπολογισμό της τιμής της παράστασης είναι η "κύρια".
Δηλαδή, αν αντικαταστήσετε κάποιους (οποιονδήποτε) αριθμούς αντί για γράμματα και προσπαθήσετε να υπολογίσετε την τιμή της παράστασης, τότε εάν η τελευταία ενέργεια είναι πολλαπλασιασμός, τότε έχουμε ένα γινόμενο (η παράσταση αποσυντίθεται σε παράγοντες).
Εάν η τελευταία ενέργεια είναι πρόσθεση ή αφαίρεση, αυτό σημαίνει ότι η έκφραση δεν συνυπολογίζεται (και επομένως δεν μπορεί να μειωθεί).
Για να το διορθώσετε μόνοι σας, μερικά παραδείγματα:
Παραδείγματα:
Λύσεις:
1. Ελπίζω να μην βιάσατε αμέσως να κόψετε και; Δεν ήταν ακόμα αρκετό να «μειωθούν» μονάδες όπως αυτό:
Το πρώτο βήμα πρέπει να είναι η παραγοντοποίηση:
4. Πρόσθεση και αφαίρεση κλασμάτων. Φέρνοντας τα κλάσματα σε κοινό παρονομαστή.
Η πρόσθεση και η αφαίρεση συνηθισμένων κλασμάτων είναι μια πολύ γνωστή πράξη: αναζητούμε έναν κοινό παρονομαστή, πολλαπλασιάζουμε κάθε κλάσμα με τον παράγοντα που λείπει και προσθέτουμε/αφαιρούμε τους αριθμητές.
Ας θυμηθούμε:
Απαντήσεις:
1. Οι παρονομαστές και είναι συμπρωτογενείς, δηλαδή δεν έχουν κοινούς παράγοντες. Επομένως, το LCM αυτών των αριθμών είναι ίσο με το γινόμενο τους. Αυτός θα είναι ο κοινός παρονομαστής:
2. Εδώ ο κοινός παρονομαστής είναι:
3. Εδώ, πρώτα απ 'όλα, μετατρέπουμε τα μικτά κλάσματα σε ακατάλληλα και στη συνέχεια - σύμφωνα με το συνηθισμένο σχήμα:
Είναι εντελώς άλλο θέμα εάν τα κλάσματα περιέχουν γράμματα, για παράδειγμα:
Ας ξεκινήσουμε απλά:
α) Οι παρονομαστές δεν περιέχουν γράμματα
Εδώ όλα είναι ίδια με τα συνηθισμένα αριθμητικά κλάσματα: βρίσκουμε έναν κοινό παρονομαστή, πολλαπλασιάζουμε κάθε κλάσμα με τον παράγοντα που λείπει και προσθέτουμε / αφαιρούμε τους αριθμητές:
τώρα στον αριθμητή μπορείτε να φέρετε παρόμοια, εάν υπάρχουν, και να τα συνυπολογίσετε:
Δοκιμάστε το μόνοι σας:
Απαντήσεις:
β) Οι παρονομαστές περιέχουν γράμματα
Ας θυμηθούμε την αρχή της εύρεσης κοινού παρονομαστή χωρίς γράμματα:
Πρώτα απ 'όλα, προσδιορίζουμε τους κοινούς παράγοντες.
Στη συνέχεια, γράφουμε όλους τους κοινούς παράγοντες μία φορά.
και πολλαπλασιάστε τους με όλους τους άλλους παράγοντες, όχι με τους κοινούς.
Για να προσδιορίσουμε τους κοινούς παράγοντες των παρονομαστών, πρώτα τους αναλύουμε σε απλούς παράγοντες:
Τονίζουμε τους κοινούς παράγοντες:
Τώρα γράφουμε τους κοινούς παράγοντες μία φορά και προσθέτουμε σε αυτούς όλους τους μη κοινούς (όχι υπογραμμισμένους) παράγοντες:
Αυτός είναι ο κοινός παρονομαστής.
Ας επιστρέψουμε στα γράμματα. Οι παρονομαστές δίνονται με τον ίδιο ακριβώς τρόπο:
Αποσυνθέτουμε τους παρονομαστές σε παράγοντες.
προσδιορίζει κοινούς (πανομοιότυπους) πολλαπλασιαστές.
γράψτε όλους τους κοινούς παράγοντες μία φορά.
Τους πολλαπλασιάζουμε με όλους τους άλλους παράγοντες, όχι με τους κοινούς.
Λοιπόν, με τη σειρά:
1) διασπάστε τους παρονομαστές σε παράγοντες:
2) προσδιορίστε τους κοινούς (πανομοιότυπους) παράγοντες:
3) Καταγράψτε όλους τους κοινούς παράγοντες μία φορά και πολλαπλασιάστε τους με όλους τους άλλους (όχι υπογραμμισμένους) παράγοντες:
Ο κοινός παρονομαστής λοιπόν είναι εδώ. Το πρώτο κλάσμα πρέπει να πολλαπλασιαστεί με, το δεύτερο - με:
Παρεμπιπτόντως, υπάρχει ένα κόλπο:
Για παράδειγμα: .
Βλέπουμε τους ίδιους παράγοντες στους παρονομαστές, μόνο όλοι με διαφορετικούς δείκτες. Ο κοινός παρονομαστής θα είναι:
στο βαθμό
στο βαθμό
στο βαθμό
σε βαθμό.
Ας περιπλέκουμε το έργο:
Πώς να κάνετε τα κλάσματα να έχουν τον ίδιο παρονομαστή;
Ας θυμηθούμε τη βασική ιδιότητα ενός κλάσματος:
Πουθενά δεν λέγεται ότι ο ίδιος αριθμός μπορεί να αφαιρεθεί (ή να προστεθεί) από τον αριθμητή και τον παρονομαστή ενός κλάσματος. Γιατί δεν είναι αλήθεια!
Δείτε μόνοι σας: πάρτε οποιοδήποτε κλάσμα, για παράδειγμα, και προσθέστε κάποιον αριθμό στον αριθμητή και στον παρονομαστή, για παράδειγμα, . Τι έχει μάθει;
Λοιπόν, ένας άλλος ακλόνητος κανόνας:
Όταν φέρνετε κλάσματα σε κοινό παρονομαστή, χρησιμοποιήστε μόνο την πράξη πολλαπλασιασμού!
Τι χρειάζεται όμως να πολλαπλασιάσετε για να πάρετε;
Εδώ και πολλαπλασιάστε. Και πολλαπλασιάστε με:
Οι εκφράσεις που δεν μπορούν να παραγοντοποιηθούν θα ονομάζονται «στοιχειώδεις παράγοντες».
Για παράδειγμα, είναι ένας στοιχειώδης παράγοντας. - πολύ. Αλλά - όχι: αποσυντίθεται σε παράγοντες.
Τι γίνεται με την έκφραση; Είναι στοιχειώδες;
Όχι, γιατί μπορεί να παραγοντοποιηθεί:
(διάβασες ήδη για παραγοντοποίηση στο θέμα "").
Έτσι, οι στοιχειώδεις παράγοντες στους οποίους αποσυνθέτεις μια έκφραση με γράμματα είναι ανάλογοι των απλών παραγόντων στους οποίους αποσυνθέτεις τους αριθμούς. Και με αυτούς θα κάνουμε το ίδιο.
Βλέπουμε ότι και οι δύο παρονομαστές έχουν έναν παράγοντα. Θα πάει στον κοινό παρονομαστή στην εξουσία (θυμάστε γιατί;).
Ο πολλαπλασιαστής είναι στοιχειώδης και δεν τον έχουν κοινό, πράγμα που σημαίνει ότι το πρώτο κλάσμα θα πρέπει απλώς να πολλαπλασιαστεί με αυτό:
Ενα άλλο παράδειγμα:
Λύση:
Πριν πολλαπλασιάσετε αυτούς τους παρονομαστές σε έναν πανικό, πρέπει να σκεφτείτε πώς να τους συνυπολογίσετε; Και οι δύο αντιπροσωπεύουν:
Εξοχος! Επειτα:
Ενα άλλο παράδειγμα:
Λύση:
Ως συνήθως, παραγοντοποιούμε τους παρονομαστές. Στον πρώτο παρονομαστή, το βάζουμε απλά εκτός παρενθέσεων. στο δεύτερο - η διαφορά των τετραγώνων:
Φαίνεται ότι δεν υπάρχουν κοινοί παράγοντες. Αλλά αν κοιτάξετε προσεκτικά, μοιάζουν ήδη τόσο πολύ... Και η αλήθεια είναι:
Ας γράψουμε λοιπόν:
Δηλαδή, έγινε έτσι: μέσα στην αγκύλη, αλλάξαμε τους όρους και ταυτόχρονα, το πρόσημο μπροστά από το κλάσμα άλλαξε στο αντίθετο. Λάβετε υπόψη σας, θα πρέπει να το κάνετε συχνά.
Τώρα φέρνουμε σε έναν κοινό παρονομαστή:
Το έπιασα? Τώρα ας ελέγξουμε.
Εργασίες για ανεξάρτητη λύση:
Απαντήσεις:
Εδώ πρέπει να θυμηθούμε ένα ακόμη πράγμα - τη διαφορά των κύβων:
Σημειώστε ότι ο παρονομαστής του δεύτερου κλάσματος δεν περιέχει τον τύπο "τετράγωνο του αθροίσματος"! Το τετράγωνο του αθροίσματος θα μοιάζει με αυτό:
Το Α είναι το λεγόμενο ατελές τετράγωνο του αθροίσματος: ο δεύτερος όρος σε αυτό είναι το γινόμενο του πρώτου και του τελευταίου, και όχι το διπλασιασμένο γινόμενο τους. Το ημιτελές τετράγωνο του αθροίσματος είναι ένας από τους παράγοντες για την επέκταση της διαφοράς των κύβων:
Τι γίνεται αν υπάρχουν ήδη τρία κλάσματα;
Ναι, το ίδιο! Πρώτα απ 'όλα, θα βεβαιωθούμε ότι ο μέγιστος αριθμός παραγόντων στους παρονομαστές είναι ο ίδιος:
Προσοχή: αν αλλάξετε τα σημάδια μέσα σε μία αγκύλη, το πρόσημο μπροστά από το κλάσμα αλλάζει στο αντίθετο. Όταν αλλάξουμε τα σημάδια στη δεύτερη αγκύλη, το πρόσημο μπροστά από το κλάσμα αντιστρέφεται ξανά. Ως αποτέλεσμα, αυτός (το πρόσημο μπροστά από το κλάσμα) δεν έχει αλλάξει.
Γράφουμε τον πρώτο παρονομαστή πλήρως στον κοινό παρονομαστή και μετά προσθέτουμε σε αυτόν όλους τους παράγοντες που δεν έχουν γραφτεί ακόμη, από τον δεύτερο και μετά από τον τρίτο (και ούτω καθεξής, αν υπάρχουν περισσότερα κλάσματα). Δηλαδή, πάει ως εξής:
Χμ... Με τα κλάσματα, είναι ξεκάθαρο τι πρέπει να κάνουμε. Τι γίνεται όμως με τα δύο;
Είναι απλό: ξέρεις πώς να προσθέτεις κλάσματα, σωστά; Άρα, πρέπει να βεβαιωθείτε ότι το δίδυμο γίνεται κλάσμα! Θυμηθείτε: ένα κλάσμα είναι μια πράξη διαίρεσης (ο αριθμητής διαιρείται με τον παρονομαστή, σε περίπτωση που το ξεχάσατε ξαφνικά). Και δεν υπάρχει τίποτα πιο εύκολο από τη διαίρεση ενός αριθμού με. Σε αυτή την περίπτωση, ο ίδιος ο αριθμός δεν θα αλλάξει, αλλά θα μετατραπεί σε κλάσμα:
Ακριβώς ότι χρειάζεται!
5. Πολλαπλασιασμός και διαίρεση κλασμάτων.
Λοιπόν, το πιο δύσκολο κομμάτι έχει τελειώσει. Και μπροστά μας είναι το πιο απλό, αλλά ταυτόχρονα το πιο σημαντικό:
Διαδικασία
Ποια είναι η διαδικασία για τον υπολογισμό μιας αριθμητικής παράστασης; Θυμηθείτε, λαμβάνοντας υπόψη την αξία μιας τέτοιας έκφρασης:
μετρήσατε;
Θα πρέπει να λειτουργήσει.
Σας θυμίζω λοιπόν.
Το πρώτο βήμα είναι ο υπολογισμός του πτυχίου.
Το δεύτερο είναι ο πολλαπλασιασμός και η διαίρεση. Εάν υπάρχουν πολλοί πολλαπλασιασμοί και διαιρέσεις ταυτόχρονα, μπορείτε να τους κάνετε με οποιαδήποτε σειρά.
Και τέλος, κάνουμε πρόσθεση και αφαίρεση. Και πάλι, με οποιαδήποτε σειρά.
Αλλά: η έκφραση σε παρένθεση αξιολογείται εκτός σειράς!
Εάν πολλαπλασιαστούν ή διαιρεθούν πολλές αγκύλες η μία με την άλλη, πρώτα αξιολογούμε την έκφραση σε κάθε μία από τις αγκύλες και στη συνέχεια τις πολλαπλασιάζουμε ή τις διαιρούμε.
Τι γίνεται αν υπάρχουν άλλες παρενθέσεις μέσα στις αγκύλες; Λοιπόν, ας σκεφτούμε: κάποια έκφραση είναι γραμμένη μέσα στις αγκύλες. Ποιο είναι το πρώτο πράγμα που πρέπει να κάνετε κατά την αξιολόγηση μιας έκφρασης; Σωστά, υπολογίστε αγκύλες. Λοιπόν, το καταλάβαμε: πρώτα υπολογίζουμε τις εσωτερικές αγκύλες και μετά όλα τα άλλα.
Έτσι, η σειρά των ενεργειών για την παραπάνω έκφραση είναι η εξής (η τρέχουσα ενέργεια επισημαίνεται με κόκκινο, δηλαδή η ενέργεια που εκτελώ αυτήν τη στιγμή):
Εντάξει, όλα είναι απλά.
Αλλά αυτό δεν είναι το ίδιο με μια έκφραση με γράμματα, έτσι δεν είναι;
Όχι, το ίδιο είναι! Μόνο αντί για αριθμητικές πράξεις είναι απαραίτητο να γίνουν αλγεβρικές πράξεις, δηλαδή οι πράξεις που περιγράφονται στην προηγούμενη ενότητα: φέρνοντας παρόμοια, προσθήκη κλασμάτων, μείωση κλασμάτων κ.ο.κ. Η μόνη διαφορά θα είναι η δράση της παραγοντοποίησης πολυωνύμων (το χρησιμοποιούμε συχνά όταν εργαζόμαστε με κλάσματα). Τις περισσότερες φορές, για παραγοντοποίηση, πρέπει να χρησιμοποιήσετε το i ή απλώς να αφαιρέσετε τον κοινό παράγοντα εκτός παρενθέσεων.
Συνήθως ο στόχος μας είναι να αναπαραστήσουμε μια έκφραση ως προϊόν ή πηλίκο.
Για παράδειγμα:
Ας απλοποιήσουμε την έκφραση.
1) Αρχικά απλοποιούμε την έκφραση σε αγκύλες. Εκεί έχουμε τη διαφορά των κλασμάτων, και στόχος μας είναι να την παραστήσουμε ως γινόμενο ή πηλίκο. Έτσι, φέρνουμε τα κλάσματα σε έναν κοινό παρονομαστή και προσθέτουμε:
Είναι αδύνατο να απλοποιηθεί περαιτέρω αυτή η έκφραση, όλοι οι παράγοντες εδώ είναι στοιχειώδεις (θυμάστε ακόμα τι σημαίνει αυτό;).
2) Παίρνουμε:
Πολλαπλασιασμός κλασμάτων: τι θα μπορούσε να είναι ευκολότερο.
3) Τώρα μπορείτε να συντομεύσετε:
Εντάξει όλα τελείωσαν τώρα. Τίποτα περίπλοκο, σωστά;
Ενα άλλο παράδειγμα:
Απλοποιήστε την έκφραση.
Πρώτα, προσπαθήστε να το λύσετε μόνοι σας και μόνο μετά δείτε τη λύση.
Λύση:
Πρώτα απ 'όλα, ας ορίσουμε τη διαδικασία.
Αρχικά, ας προσθέσουμε τα κλάσματα σε αγκύλες, αντί για δύο κλάσματα, θα βγει ένα.
Στη συνέχεια θα κάνουμε τη διαίρεση των κλασμάτων. Λοιπόν, προσθέτουμε το αποτέλεσμα με το τελευταίο κλάσμα.
Θα αριθμήσω σχηματικά τα βήματα:
Τώρα θα δείξω όλη τη διαδικασία, χρωματίζοντας την τρέχουσα ενέργεια με κόκκινο:
1. Εάν υπάρχουν παρόμοια, πρέπει να προσκομιστούν άμεσα. Όποια στιγμή κι αν έχουμε παρόμοια, καλό είναι να τα φέρουμε άμεσα.
2. Το ίδιο ισχύει και για τα αναγωγικά κλάσματα: μόλις παρουσιαστεί ευκαιρία για μείωση, πρέπει να χρησιμοποιηθεί. Η εξαίρεση είναι τα κλάσματα που προσθέτετε ή αφαιρείτε: εάν τώρα έχουν τους ίδιους παρονομαστές, τότε η αναγωγή θα πρέπει να αφεθεί για αργότερα.
Ακολουθούν ορισμένες εργασίες που πρέπει να επιλύσετε μόνοι σας:
Και υποσχέθηκε στην αρχή:
Απαντήσεις:
Λύσεις (σύντομη):
Εάν αντιμετωπίσατε τουλάχιστον τα τρία πρώτα παραδείγματα, τότε σκεφτείτε ότι έχετε κατακτήσει το θέμα.
Τώρα στη μάθηση!
ΜΕΤΑΤΡΟΠΗ ΕΚΦΡΑΣΗΣ. ΣΥΝΟΨΗ ΚΑΙ ΒΑΣΙΚΟΣ ΤΥΠΟΣ
Βασικές λειτουργίες απλοποίησης:
- Φέρνοντας παρόμοια: για να προσθέσετε (μειώσετε) όρους όπως, πρέπει να προσθέσετε τους συντελεστές τους και να αντιστοιχίσετε το τμήμα γράμματος.
- Παραγοντοποίηση:βγάζοντας τον κοινό παράγοντα εκτός παρένθεσης, εφαρμόζοντας κ.λπ.
- Αναγωγή κλασμάτων: ο αριθμητής και ο παρονομαστής ενός κλάσματος μπορούν να πολλαπλασιαστούν ή να διαιρεθούν με τον ίδιο μη μηδενικό αριθμό, από τον οποίο η τιμή του κλάσματος δεν αλλάζει.
1) αριθμητής και παρονομαστής παραγοντοποιώ
2) εάν υπάρχουν κοινοί παράγοντες στον αριθμητή και στον παρονομαστή, μπορούν να διαγραφούν.ΣΗΜΑΝΤΙΚΟ: μόνο οι πολλαπλασιαστές μπορούν να μειωθούν!
- Πρόσθεση και αφαίρεση κλασμάτων:
; - Πολλαπλασιασμός και διαίρεση κλασμάτων:
;
Μια έκφραση της μορφής a (m/n), όπου n είναι κάποιος φυσικός αριθμός, m είναι κάποιος ακέραιος και η βάση του βαθμού a είναι μεγαλύτερη από το μηδέν, ονομάζεται βαθμός με κλασματικό εκθέτη.Επιπλέον, ισχύει η ακόλουθη ισότητα. n√(a m) = a (m/n) .
Όπως ήδη γνωρίζουμε, οι αριθμοί της μορφής m/n, όπου n είναι κάποιος φυσικός αριθμός και m είναι κάποιος ακέραιος, ονομάζονται κλασματικοί ή ρητικοί αριθμοί. Από τα παραπάνω, παίρνουμε ότι ο βαθμός ορίζεται, για κάθε λογικό εκθέτη και κάθε θετική βάση του βαθμού.
Για οποιουσδήποτε ρητούς αριθμούς p,q και οποιονδήποτε a>0 και b>0, ισχύουν οι ακόλουθες ισότητες:
- 1. (a p)*(a q) = a (p+q)
- 2. (a p): (b q) = a (p-q)
- 3. (a p) q = a (p*q)
- 4. (a*b) p = (a p)*(b p)
- 5. (a/b) p = (a p)/(b p)
Αυτές οι ιδιότητες χρησιμοποιούνται ευρέως κατά τη μετατροπή διαφόρων εκφράσεων που περιέχουν βαθμούς με κλασματικούς εκθέτες.
Παραδείγματα μετασχηματισμών παραστάσεων που περιέχουν βαθμό με κλασματικό εκθέτη
Ας δούμε μερικά παραδείγματα που δείχνουν πώς αυτές οι ιδιότητες μπορούν να χρησιμοποιηθούν για να μετασχηματίσουν εκφράσεις.
1. Υπολογίστε 7 (1/4) * 7 (3/4) .
- 7 (1/4) * 7 (3/4) = z (1/4 + 3/4) = 7.
2. Υπολογίστε 9 (2/3) : 9 (1/6) .
- 9 (2/3) : 9 (1/6) = 9 (2/3 - 1/6) = 9 (1/2) = √9 = 3.
3. Υπολογίστε (16 (1/3)) (9/4) .
- (16 (1/3)) (9/4) = 16 ((1/3)*(9/4)) =16 (3/4) = (2 4) (3/4) = 2 (4*3/4) = 2 3 = 8.
4. Υπολογίστε 24 (2/3) .
- 24 (2/3) = ((2 3)*3) (2/3) = (2 (2*2/3))*3 (2/3) = 4*3√(3 2)=4*3√9.
5. Υπολογίστε (8/27) (1/3) .
- (8/27) (1/3) = (8 (1/3))/(27 (1/3)) = ((2 3) (1/3))/((3 3) (1/3))= 2/3.
6. Απλοποιήστε την παράσταση ((a (4/3))*b + a*b (4/3))/(3√a + 3√b)
- ((a (4/3))*b + a*b (4/3))/(3√a + 3√b) = (a*b*(a (1/3) + b (1/3 )))/(1/3) + b (1/3)) = a*b.
7. Υπολογίστε (25 (1/5))*(125 (1/5)).
- (25 (1/5))*(125 (1/5)) =(25*125) (1/5) = (5 5) (1/5) = 5.
8. Απλοποιήστε την έκφραση
- (α (1/3) - α (7/3))/(α (1/3) - α (4/3)) - (α (-1/3) - α (5/3))/( α(2/3) + α(-1/3)).
- (α (1/3) - α (7/3))/(α (1/3) - α (4/3)) - (α (-1/3) - α (5/3))/( α(2/3) + α(-1/3)) =
- = ((a (1/3))*(1-a 2))/((a (1/3))*(1-a)) - ((a (-1/3))*(1- a 2))/ ((a (-1/3))*(1+a)) =
- = 1 + a - (1-a) = 2*a.
Όπως μπορείτε να δείτε, χρησιμοποιώντας αυτές τις ιδιότητες, μπορείτε να απλοποιήσετε πολύ ορισμένες εκφράσεις που περιέχουν βαθμούς με κλασματικούς εκθέτες.