Στο Είναι πολύ σημαντικό να έχουμε μια καλή ιδέα για το αν η πιθανότητα () εμφάνισης ενός γεγονότος που μας ενδιαφέρει εξαρτάται από τον τρόπο με τον οποίο εξελίσσονται άλλα γεγονότα.

Στην περίπτωση του κλασικού σχήματος, όταν όλα τα αποτελέσματα είναι εξίσου πιθανά, μπορούμε ήδη να εκτιμήσουμε τις τιμές της πιθανότητας του συγκεκριμένου γεγονότος που μας ενδιαφέρει ανεξάρτητα. Μπορούμε να το κάνουμε αυτό ακόμη και αν το συμβάν είναι μια σύνθετη συλλογή από πολλά στοιχειώδη αποτελέσματα. Τι θα συμβεί αν συμβούν πολλά τυχαία γεγονότα ταυτόχρονα ή διαδοχικά; Πώς επηρεάζει αυτό την πιθανότητα εκδήλωσης που μας ενδιαφέρει;

Αν ρίξω ένα ζάρι αρκετές φορές και θέλω να έρθει ένα εξάρι, αλλά δεν είμαι τυχερός όλη την ώρα, αυτό σημαίνει ότι πρέπει να αυξήσω το στοίχημα, επειδή, σύμφωνα με τη θεωρία της πιθανότητας, πρόκειται να πάρω τυχερός? Αλίμονο, η θεωρία της πιθανότητας δεν δηλώνει τίποτα από το είδος. Ούτε κόκαλο, ούτε κάρτα, ούτε νόμισμα δεν ξέρω πώς να απομνημονεύσω, τι μας έδειξαν την προηγούμενη φορά. Δεν τους ενδιαφέρει καθόλου αν για πρώτη φορά ή για δέκατη φορά σήμερα δοκιμάζω τη μοίρα μου. Κάθε φορά που επαναλαμβάνω τη ρίψη, ξέρω μόνο ένα πράγμα: και αυτή τη φορά η πιθανότητα να πάρετε έξι είναι πάλι ίση με το ένα έκτο. Φυσικά, αυτό δεν σημαίνει ότι ο αριθμός που χρειάζομαι δεν θα πέσει ποτέ. Σημαίνει μόνο ότι η απώλεια μου μετά την πρώτη ρίψη και μετά από οποιαδήποτε άλλη ρίψη είναι ανεξάρτητα γεγονότα.

Τα γεγονότα Α και Β ονομάζονται ανεξάρτητοςεάν η εφαρμογή ενός από αυτά δεν επηρεάζει με κανένα τρόπο την πιθανότητα ενός άλλου συμβάντος. Για παράδειγμα, οι πιθανότητες να χτυπήσετε έναν στόχο με το πρώτο από τα δύο όπλα δεν εξαρτώνται από το αν ο στόχος χτυπήθηκε από άλλο όπλο, οπότε τα γεγονότα "το πρώτο όπλο χτύπησε τον στόχο" και "το δεύτερο όπλο χτύπησε τον στόχο" είναι ανεξάρτητα Το

Εάν δύο γεγονότα Α και Β είναι ανεξάρτητα και η πιθανότητα καθενός από αυτά είναι γνωστή, τότε η πιθανότητα ταυτόχρονης εμφάνισης τόσο του γεγονότος Α όσο και του γεγονότος Β (συμβολίζεται με ΑΒ) μπορεί να υπολογιστεί χρησιμοποιώντας το ακόλουθο θεώρημα.

Θεώρημα πολλαπλασιασμού για πιθανότητες για ανεξάρτητα γεγονότα

P (AB) = P (A) * P (B)- πιθανότητα ταυτόχρονοςδύο ανεξάρτητοςγεγονότα ίσα προϊόντις πιθανότητες αυτών των γεγονότων.

Παράδειγμα.Οι πιθανότητες χτυπήματος στο στόχο κατά την εκτόξευση του πρώτου και του δεύτερου πυροβόλου είναι αντίστοιχα ίσες: p 1 = 0,7. ρ 2 = 0,8. Βρείτε την πιθανότητα να χτυπήσετε με ένα βόλεϊ και με τα δύο όπλα ταυτόχρονα.

Λύση:όπως έχουμε ήδη δει τα γεγονότα Α (χτυπήθηκε από το πρώτο όπλο) και Β (χτυπήθηκε από το δεύτερο όπλο) είναι ανεξάρτητα, δηλ. P (AB) = P (A) * P (B) = p 1 * p 2 = 0,56.

Τι συμβαίνει με τις εκτιμήσεις μας εάν τα εκδηλώσεις έναρξης δεν είναι ανεξάρτητες; Ας τροποποιήσουμε λίγο το προηγούμενο παράδειγμα.

Παράδειγμα.Δύο σκοπευτές στον διαγωνισμό πυροβολούν σε στόχους, και αν ένας από αυτούς σουτάρει με ακρίβεια, ο αντίπαλος γίνεται νευρικός και τα αποτελέσματά του επιδεινώνονται. Πώς να μετατρέψετε αυτήν την καθημερινή κατάσταση σε μαθηματικό πρόβλημα και να σκιαγραφήσετε τρόπους επίλυσής του; Είναι διαισθητικά σαφές ότι είναι απαραίτητο να χωριστούν με κάποιο τρόπο τα δύο σενάρια για την εξέλιξη των γεγονότων, να καταρτιστούν ουσιαστικά δύο σενάρια, δύο διαφορετικά καθήκοντα. Στην πρώτη περίπτωση, αν ο αντίπαλος χάσει, το σενάριο θα είναι ευνοϊκό για τον νευρικό αθλητή και η ακρίβειά του θα είναι μεγαλύτερη. Στη δεύτερη περίπτωση, αν ο αντίπαλος έχει αξιοποιήσει αξιοπρεπώς την ευκαιρία του, μειώνεται η πιθανότητα να χτυπήσει τον στόχο για τον δεύτερο αθλητή.

Για να διαχωρίσουμε πιθανά σενάρια (συχνά ονομάζονται υποθέσεις) γεγονότων, θα χρησιμοποιήσουμε συχνά ένα σχήμα "δέντρου πιθανοτήτων". Αυτό το σχήμα είναι παρόμοιο ως προς το δέντρο αποφάσεων, με το οποίο πιθανότατα είχατε ήδη να αντιμετωπίσετε. Κάθε κλάδος αντιπροσωπεύει ένα ξεχωριστό σενάριο εξέλιξης των γεγονότων, μόνο που τώρα έχει τη δική του σημασία του λεγόμενου υποθετικόςπιθανότητες (q 1, q 2, q 1 -1, q 2 -1).

Αυτό το σχήμα είναι πολύ βολικό για την ανάλυση διαδοχικών τυχαίων συμβάντων.

Μένει να διευκρινίσουμε ένα ακόμη σημαντικό ερώτημα: πού βρίσκονται οι αρχικές τιμές των πιθανοτήτων πραγματικές καταστάσεις ; Τελικά, η θεωρία της πιθανότητας δεν λειτουργεί με τα ίδια νομίσματα και ζάρια; Συνήθως αυτές οι εκτιμήσεις λαμβάνονται από στατιστικά στοιχεία και όταν τα στατιστικά δεν είναι διαθέσιμα, διεξάγουμε τη δική μας έρευνα. Και συχνά πρέπει να το ξεκινήσουμε όχι με τη συλλογή δεδομένων, αλλά με το ερώτημα τι πληροφορίες χρειαζόμαστε γενικά.

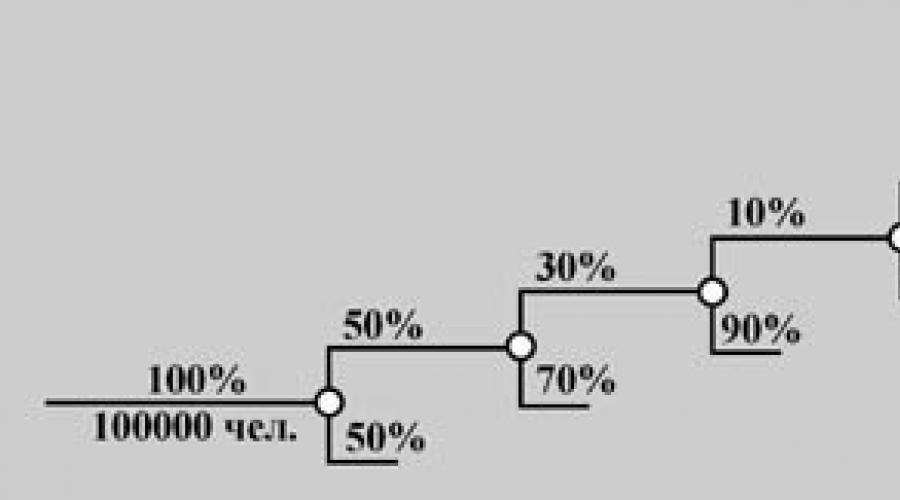
Παράδειγμα.Ας πούμε ότι πρέπει να εκτιμήσουμε το μέγεθος της αγοράς σε μια πόλη με πληθυσμό εκατό χιλιάδων κατοίκων για ένα νέο προϊόν που δεν είναι απαραίτητο, για παράδειγμα, για ένα βάλσαμο για τη φροντίδα των βαμμένων μαλλιών. Εξετάστε ένα σχήμα "δέντρου πιθανότητας". Σε αυτή την περίπτωση, πρέπει να εκτιμήσουμε περίπου την τιμή της πιθανότητας σε κάθε "κλάδο". Έτσι, οι εκτιμήσεις μας για το μέγεθος της αγοράς:

1) Το 50% όλων των κατοίκων της πόλης είναι γυναίκες,

2) από όλες τις γυναίκες, μόνο το 30% βάφει τα μαλλιά τους συχνά,

3) μόνο το 10% αυτών χρησιμοποιεί βάλσαμα για βαμμένα μαλλιά,

4) από αυτά, μόνο το 10% μπορεί να έχει το θάρρος να δοκιμάσει ένα νέο προϊόν,

5) Το 70% αυτών αγοράζουν συνήθως τα πάντα όχι από εμάς, αλλά από τους ανταγωνιστές μας.

Λύση:Σύμφωνα με το νόμο του πολλαπλασιασμού των πιθανοτήτων, καθορίζουμε την πιθανότητα του γεγονότος που μας ενδιαφέρει Α = (ένας κάτοικος της πόλης αγοράζει αυτό το νέο βάλσαμο από εμάς) = 0.00045.

Ας πολλαπλασιάσουμε αυτήν την τιμή της πιθανότητας με τον αριθμό των κατοίκων της πόλης. Ως αποτέλεσμα, έχουμε μόνο 45 δυνητικούς πελάτες και αν λάβουμε υπόψη ότι μια φούσκα από αυτά τα χρήματα είναι αρκετή για αρκετούς μήνες, το εμπόριο δεν είναι πολύ ζωντανό.

Ωστόσο, υπάρχει κάποιο όφελος από τις εκτιμήσεις μας.

Πρώτον, μπορούμε να συγκρίνουμε τις προβλέψεις διαφορετικών επιχειρηματικών ιδεών, θα έχουν διαφορετικά «πιρούνια» στα διαγράμματα και, φυσικά, οι τιμές πιθανότητας θα είναι επίσης διαφορετικές.

Δεύτερον, όπως έχουμε ήδη πει, μια τυχαία μεταβλητή δεν ονομάζεται τυχαία επειδή δεν εξαρτάται από τίποτα. Μόνο εκείνη ακριβήςη τιμή δεν είναι γνωστή εκ των προτέρων. Γνωρίζουμε ότι ο μέσος αριθμός αγοραστών μπορεί να αυξηθεί (για παράδειγμα, με τη διαφήμιση ενός νέου προϊόντος). Είναι λοιπόν λογικό να επικεντρώσουμε τις προσπάθειές μας σε εκείνα τα «πιρούνια» όπου η κατανομή πιθανότητας δεν μας ταιριάζει ιδιαίτερα, σε εκείνους τους παράγοντες που μπορούμε να επηρεάσουμε.

Εξετάστε ένα άλλο ποσοτικό παράδειγμα έρευνας συμπεριφοράς αγορών.

Παράδειγμα.Κατά μέσο όρο, 10.000 άτομα επισκέπτονται την αγορά τροφίμων την ημέρα. Η πιθανότητα ένας επισκέπτης της αγοράς να μπει σε ένα περίπτερο γαλακτοκομικών είναι 1/2. Είναι γνωστό ότι σε αυτό το περίπτερο, κατά μέσο όρο, πωλούνται 500 κιλά διάφορα προϊόντα την ημέρα.

Μπορούμε να πούμε ότι η μέση αγορά σε ένα περίπτερο ζυγίζει μόνο 100 g;

Συζήτηση.Φυσικά και όχι. Είναι σαφές ότι δεν κατέληξαν όλοι όσοι μπήκαν στο περίπτερο να αγοράσουν κάτι εκεί.

Όπως φαίνεται στο διάγραμμα, για να απαντήσουμε στην ερώτηση σχετικά με το μέσο βάρος αγοράς, πρέπει να βρούμε την απάντηση στην ερώτηση, ποια είναι η πιθανότητα ένα άτομο που μπαίνει στο περίπτερο να αγοράσει κάτι εκεί. Εάν δεν έχουμε τέτοια δεδομένα στη διάθεσή μας, αλλά τα χρειαζόμαστε, θα πρέπει να τα αποκτήσουμε μόνοι μας, αφού παρατηρήσουμε τους επισκέπτες του περιπτέρου για κάποιο χρονικό διάστημα. Ας πούμε ότι οι παρατηρήσεις μας έδειξαν ότι μόνο το ένα πέμπτο των επισκεπτών του περιπτέρου αγοράζουν κάτι.

Μόλις λάβουμε αυτές τις εκτιμήσεις, το έργο γίνεται ήδη απλό. Από τα 10.000 άτομα που έρχονται στην αγορά, 5.000 θα εισέλθουν στο περίπτερο των γαλακτοκομικών προϊόντων και θα υπάρχουν μόνο 1.000 αγορές.Το μέσο βάρος αγοράς είναι 500 γραμμάρια. Είναι ενδιαφέρον να σημειωθεί ότι για να δημιουργηθεί μια πλήρης εικόνα του τι συμβαίνει, η λογική της «διακλάδωσης» υπό όρους πρέπει να ορίζεται σε κάθε στάδιο του συλλογισμού μας σαφώς σαν να δουλεύουμε με μια «συγκεκριμένη» κατάσταση και όχι με πιθανότητες.

Εργασίες αυτοέλεγχου

1. Αφήστε να υπάρχει ένα ηλεκτρικό κύκλωμα που αποτελείται από n στοιχεία συνδεδεμένα σε σειρά, καθένα από τα οποία λειτουργεί ανεξάρτητα από τα άλλα.

Η πιθανότητα p αποτυχίας κάθε στοιχείου είναι γνωστή. Προσδιορίστε την πιθανότητα σωστής λειτουργίας ολόκληρου του τμήματος της αλυσίδας (συμβάν Α).

2. Ο μαθητής γνωρίζει 20 από τις 25 ερωτήσεις των εξετάσεων. Βρείτε την πιθανότητα ο μαθητής να γνωρίζει τις τρεις ερωτήσεις που προτείνει ο εξεταστής.

3. Η παραγωγή αποτελείται από τέσσερα διαδοχικά στάδια, σε καθένα από τα οποία λειτουργεί εξοπλισμός, για τα οποία οι πιθανότητες αστοχίας εντός του επόμενου μήνα είναι ίσες με p 1, p 2, p 3 και p 4, αντίστοιχα. Βρείτε την πιθανότητα να μην υπάρξει διακοπή παραγωγής λόγω βλάβης εξοπλισμού σε ένα μήνα.

Τα γεγονότα που συμβαίνουν στην πραγματικότητα ή στη φαντασία μας μπορούν να χωριστούν σε 3 ομάδες. Αυτά είναι αξιόπιστα γεγονότα που σίγουρα θα συμβούν, αδύνατα γεγονότα και τυχαία γεγονότα. Η θεωρία πιθανοτήτων μελετά τυχαία γεγονότα, δηλ. γεγονότα που μπορεί να συμβούν ή όχι. Αυτό το άρθρο θα παρουσιάσει εν συντομία τη θεωρία της πιθανότητας του τύπου και παραδείγματα επίλυσης προβλημάτων στη θεωρία πιθανοτήτων, η οποία θα είναι στην 4η εργασία των εξετάσεων στα μαθηματικά (επίπεδο προφίλ).

Γιατί χρειάζεται η θεωρία της πιθανότητας

Ιστορικά, η ανάγκη μελέτης αυτών των προβλημάτων προέκυψε τον 17ο αιώνα σε σχέση με την ανάπτυξη και τον επαγγελματισμό των τυχερών παιχνιδιών και την εμφάνιση των καζίνο. Αυτό ήταν ένα πραγματικό φαινόμενο που απαιτούσε μελέτη και έρευνα.

Παιχνίδια, craps, ρουλέτα δημιούργησαν καταστάσεις όπου θα μπορούσε να συμβεί οποιοδήποτε από έναν πεπερασμένο αριθμό εξίσου δυνατών γεγονότων. Προέκυψε η ανάγκη να δοθούν αριθμητικές εκτιμήσεις για την πιθανότητα να συμβεί ένα συγκεκριμένο συμβάν.

Στον 20ό αιώνα, έγινε σαφές ότι αυτή η φαινομενικά επιπόλαιη επιστήμη παίζει σημαντικό ρόλο στην κατανόηση των θεμελιωδών διαδικασιών που λαμβάνουν χώρα στον μικρόκοσμο. Δημιουργήθηκε η σύγχρονη θεωρία πιθανοτήτων.

Βασικές έννοιες της θεωρίας πιθανοτήτων

Το αντικείμενο μελέτης της θεωρίας των πιθανοτήτων είναι τα γεγονότα και οι πιθανότητες τους. Εάν το γεγονός είναι περίπλοκο, τότε μπορεί να αναλυθεί σε απλά συστατικά, οι πιθανότητες των οποίων είναι εύκολο να βρεθούν.

Το άθροισμα των γεγονότων Α και Β ονομάζεται γεγονός Γ, το οποίο συνίσταται στο γεγονός ότι είτε το συμβάν Α, είτε το συμβάν Β, είτε τα γεγονότα Α και Β συνέβησαν ταυτόχρονα.

Το γινόμενο των γεγονότων Α και Β ονομάζεται συμβάν Γ, το οποίο συνίσταται στο γεγονός ότι έχουν συμβεί τόσο το συμβάν Α όσο και το συμβάν Β.

Τα γεγονότα Α και Β ονομάζονται ασυνεπή εάν δεν μπορούν να συμβούν ταυτόχρονα.

Το συμβάν Α λέγεται αδύνατο αν δεν μπορεί να συμβεί. Ένα τέτοιο συμβάν υποδηλώνεται με ένα σύμβολο.

Το συμβάν Α ονομάζεται αξιόπιστο εάν αναγκαστικά θα συμβεί. Ένα τέτοιο συμβάν υποδηλώνεται με ένα σύμβολο.

Αφήστε κάθε συμβάν Α να συσχετιστεί με τον αριθμό Ρ (Α). Αυτός ο αριθμός P (A) ονομάζεται πιθανότητα συμβάντος A εάν πληρούνται οι ακόλουθες προϋποθέσεις για αυτήν την αντιστοιχία.

Μια σημαντική ειδική περίπτωση είναι η κατάσταση όταν υπάρχουν ισοδύναμα στοιχειώδη αποτελέσματα και αυθαίρετα από αυτά τα αποτελέσματα σχηματίζουν γεγονότα Α. Σε αυτή την περίπτωση, η πιθανότητα μπορεί να εισαχθεί χρησιμοποιώντας τον τύπο. Η πιθανότητα που εισάγεται με αυτόν τον τρόπο ονομάζεται κλασική πιθανότητα. Μπορεί να αποδειχθεί ότι σε αυτή την περίπτωση ικανοποιούνται οι ιδιότητες 1-4.

Τα προβλήματα στη θεωρία πιθανοτήτων που συναντώνται κατά την εξέταση στα μαθηματικά σχετίζονται κυρίως με την κλασική πιθανότητα. Τέτοιες εργασίες μπορεί να είναι πολύ απλές. Τα προβλήματα θεωρίας πιθανοτήτων σε δοκιμαστικές εκδόσεις είναι ιδιαίτερα απλά. Είναι εύκολο να υπολογιστεί ο αριθμός των ευνοϊκών αποτελεσμάτων, ο αριθμός όλων των αποτελεσμάτων γράφεται ακριβώς στην κατάσταση.

Παίρνουμε την απάντηση με τον τύπο.

Ένα παράδειγμα προβλήματος από τις εξετάσεις στα μαθηματικά για τον προσδιορισμό της πιθανότητας

Υπάρχουν 20 πίτες στο τραπέζι - 5 με λάχανο, 7 με μήλα και 8 με ρύζι. Η Μαρίνα θέλει να πάρει μια πίτα. Ποια είναι η πιθανότητα να πάρει την ρυζόπιτα;

Λύση.

Υπάρχουν συνολικά 20 ισοδύναμα στοιχειώδη αποτελέσματα, δηλαδή η Μαρίνα μπορεί να πάρει οποιαδήποτε από τις 20 πίτες. Πρέπει όμως να εκτιμήσουμε την πιθανότητα η Μαρίνα να πάρει πίτα με ρύζι, δηλαδή όπου Α είναι η επιλογή πίτας με ρύζι. Έτσι έχουμε τον αριθμό των ευνοϊκών αποτελεσμάτων (επιλογές πίτας με ρύζι) μόνο 8. Τότε η πιθανότητα θα καθοριστεί από τον τύπο:

Ανεξάρτητα, αντίθετα και αυθαίρετα γεγονότα

Ωστόσο, πιο περίπλοκες εργασίες άρχισαν να εμφανίζονται στην ανοιχτή τράπεζα εργασιών. Επομένως, ας επιστήσουμε την προσοχή του αναγνώστη σε άλλα θέματα που μελετώνται στη θεωρία της πιθανότητας.

Τα γεγονότα Α και Β ονομάζονται ανεξάρτητα εάν η πιθανότητα καθενός από αυτά δεν εξαρτάται από το αν έχει συμβεί άλλο γεγονός.

Το συμβάν Β σημαίνει ότι το συμβάν Α δεν συνέβη, δηλ. το γεγονός Β είναι αντίθετο με το γεγονός Α. Η πιθανότητα του αντίθετου γεγονότος είναι ίση με ένα μείον την πιθανότητα του άμεσου γεγονότος, δηλ. ...

Θεωρήματα προσθήκης και πολλαπλασιασμού για πιθανότητες, τύποι

Για αυθαίρετα γεγονότα Α και Β, η πιθανότητα του αθροίσματος αυτών των γεγονότων είναι ίση με το άθροισμα των πιθανοτήτων τους χωρίς την πιθανότητα του κοινού τους γεγονότος, δηλ. ...

Για ανεξάρτητα γεγονότα Α και Β, η πιθανότητα του γινομένου αυτών των γεγονότων είναι ίση με το γινόμενο των πιθανοτήτων τους, δηλ. σε αυτήν την περίπτωση .

Οι 2 τελευταίες προτάσεις ονομάζονται θεωρήματα προσθήκης και πολλαπλασιασμού πιθανοτήτων.

Ο υπολογισμός του αριθμού των αποτελεσμάτων δεν είναι πάντα τόσο εύκολος. Σε ορισμένες περιπτώσεις, είναι απαραίτητο να χρησιμοποιήσετε συνδυαστικούς τύπους. Σε αυτή την περίπτωση, το πιο σημαντικό είναι να μετρήσετε τον αριθμό των συμβάντων που πληρούν ορισμένες προϋποθέσεις. Μερικές φορές αυτού του είδους οι υπολογισμοί μπορούν να γίνουν ανεξάρτητες εργασίες.

Με πόσους τρόπους μπορούν να καθίσουν 6 μαθητές σε 6 κενές θέσεις; Ο πρώτος μαθητής θα πάρει οποιαδήποτε από τις 6 θέσεις. Κάθε μία από αυτές τις επιλογές αντιστοιχεί σε 5 τρόπους για να πάρει τη θέση του δεύτερου μαθητή. Για τον τρίτο μαθητή υπάρχουν 4 ελεύθερες θέσεις, για τον τέταρτο - 3, για τον πέμπτο - 2, ο έκτος θα πάρει τη μόνη εναπομείναντα θέση. Για να βρείτε τον αριθμό όλων των επιλογών, πρέπει να βρείτε το προϊόν, το οποίο συμβολίζεται με το σύμβολο 6! και γράφει "six factorial".

Στη γενική περίπτωση, η απάντηση σε αυτήν την ερώτηση δίνεται από τον τύπο για τον αριθμό των μεταθέσεων n στοιχείων Στην περίπτωσή μας.

Εξετάστε τώρα μια άλλη περίπτωση με τους μαθητές μας. Με πόσους τρόπους μπορούν να καθίσουν 2 μαθητές για 6 κενές θέσεις; Ο πρώτος μαθητής θα πάρει οποιαδήποτε από τις 6 θέσεις. Κάθε μία από αυτές τις επιλογές αντιστοιχεί σε 5 τρόπους για να πάρει τη θέση του δεύτερου μαθητή. Για να βρείτε τον αριθμό όλων των επιλογών, πρέπει να βρείτε το προϊόν.

Στη γενική περίπτωση, η απάντηση σε αυτήν την ερώτηση δίνεται από τον τύπο για τον αριθμό των τοποθετήσεων n στοιχείων για k στοιχεία

Στην περίπτωσή μας .

Και η τελευταία περίπτωση αυτής της σειράς. Πόσοι τρόποι υπάρχουν για να επιλέξετε τρεις μαθητές από τους 6; Ο πρώτος μαθητής μπορεί να επιλεγεί με 6 τρόπους, ο δεύτερος με 5 τρόπους, ο τρίτος με τέσσερις. Αλλά μεταξύ αυτών των επιλογών, οι ίδιοι τρεις μαθητές συναντώνται 6 φορές. Για να βρείτε τον αριθμό όλων των επιλογών, πρέπει να υπολογίσετε την τιμή :. Σε γενικές γραμμές, η απάντηση σε αυτήν την ερώτηση δίνεται από τον τύπο για τον αριθμό των συνδυασμών στοιχείων ανά στοιχεία:

Στην περίπτωσή μας .

Παραδείγματα επίλυσης προβλημάτων από τις εξετάσεις στα μαθηματικά για τον προσδιορισμό της πιθανότητας

Πρόβλημα 1. Από τη συλλογή, εκδ. Γιαστσένκο.

Υπάρχουν 30 πίτες στο πιάτο: 3 με κρέας, 18 με λάχανο και 9 με κεράσια. Η Σάσα επιλέγει τυχαία μία πίτα. Βρείτε την πιθανότητα να καταλήξει με κεράσι.

.

Απάντηση: 0.3.

Πρόβλημα 2. Από τη συλλογή, εκδ. Γιαστσένκο.

Κάθε παρτίδα 1000 λαμπτήρων περιέχει κατά μέσο όρο 20 ελαττωματικούς λαμπτήρες. Βρείτε την πιθανότητα να λειτουργήσει ένας τυχαίος λαμπτήρας από μια παρτίδα.

Λύση: Ο αριθμός των λαμπτήρων που μπορούν να επισκευαστούν είναι 1000-20 = 980. Τότε η πιθανότητα ένας λαμπτήρας που έχει ληφθεί τυχαία από τη παρτίδα να είναι λειτουργικός:

Απάντηση: 0,98.

Η πιθανότητα ο μαθητής U. να λύσει σωστά περισσότερα από 9 προβλήματα στο μαθηματικό τεστ είναι 0,67. Η πιθανότητα ότι η U. θα λύσει σωστά περισσότερα από 8 προβλήματα είναι 0,73. Βρείτε την πιθανότητα ότι το U θα λύσει ακριβώς 9 προβλήματα σωστά.

Αν φανταστούμε μια αριθμητική γραμμή και σημειώσουμε τα σημεία 8 και 9 πάνω της, τότε θα δούμε ότι η συνθήκη «Υ. θα λύσει σωστά ακριβώς 9 προβλήματα "περιλαμβάνεται στη συνθήκη" U. θα λύσει σωστά περισσότερα από 8 προβλήματα ", αλλά δεν ισχύει για τον όρο" W. θα λύσει σωστά περισσότερα από 9 προβλήματα ».

Ωστόσο, η συνθήκη «W. θα λύσει σωστά περισσότερα από 9 προβλήματα "περιέχεται στη συνθήκη" W. θα λύσει σωστά περισσότερα από 8 προβλήματα ». Έτσι, αν ορίσουμε εκδηλώσεις: «W. θα λύσει σωστά ακριβώς 9 προβλήματα "- μέσω Α," Υ. θα λύσει σωστά περισσότερα από 8 προβλήματα "- μέσω Β," U. θα λύσει σωστά περισσότερα από 9 προβλήματα "μέσω C. Αυτή η λύση θα μοιάζει με αυτό:

Απάντηση: 0,06.

Στην εξέταση γεωμετρίας, ο μαθητής απαντά σε μία ερώτηση από τη λίστα των ερωτήσεων των εξετάσεων. Η πιθανότητα να πρόκειται για ερώτηση τριγωνομετρίας είναι 0,2. Η πιθανότητα να πρόκειται για ερώτηση εκτός γωνίας είναι 0,15. Δεν υπάρχουν ερωτήσεις που να σχετίζονται ταυτόχρονα με αυτά τα δύο θέματα. Βρείτε την πιθανότητα ένας μαθητής να πάρει μια ερώτηση για ένα από αυτά τα δύο θέματα στην εξέταση.

Ας σκεφτούμε τι είδους εκδηλώσεις έχουμε. Μας δίνονται δύο ασυμβίβαστα γεγονότα. Δηλαδή, είτε η ερώτηση θα αφορά το θέμα «Τριγωνομετρία», είτε το θέμα «Εξωτερικές γωνίες». Σύμφωνα με το θεώρημα πιθανότητας, η πιθανότητα ασυνεπών γεγονότων είναι ίση με το άθροισμα των πιθανοτήτων κάθε γεγονότος, πρέπει να βρούμε το άθροισμα των πιθανοτήτων αυτών των γεγονότων, δηλαδή:

Απάντηση: 0,35.

Το δωμάτιο φωτίζεται από ένα φανάρι με τρεις λάμπες. Η πιθανότητα να καεί ένας λαμπτήρας σε ένα έτος είναι 0,29. Βρείτε την πιθανότητα τουλάχιστον ένας λαμπτήρας να μην καεί μέσα σε ένα χρόνο.

Ας εξετάσουμε πιθανά γεγονότα. Έχουμε τρεις λαμπτήρες, καθένας από τους οποίους μπορεί να καεί ή όχι ανεξάρτητα από οποιονδήποτε άλλο λαμπτήρα. Αυτά είναι ανεξάρτητα γεγονότα.

Στη συνέχεια, θα υποδείξουμε τις επιλογές για τέτοιες εκδηλώσεις. Ας πάρουμε τον ακόλουθο συμβολισμό: - το φως είναι αναμμένο, - το φως έχει καεί. Και ακριβώς δίπλα του υπολογίζουμε την πιθανότητα του συμβάντος. Για παράδειγμα, προέκυψε η πιθανότητα ενός συμβάντος στο οποίο τρία ανεξάρτητα συμβάντα "ο λαμπτήρας κάηκε", "ο λαμπτήρας είναι αναμμένος", "ο λαμπτήρας είναι αναμμένος" προέκυψε: ...

Σημειώστε ότι υπάρχουν μόνο 7 ασυνεπή γεγονότα ευνοϊκά για εμάς. Η πιθανότητα τέτοιων γεγονότων είναι ίση με το άθροισμα των πιθανοτήτων καθενός από τα γεγονότα :.

Απάντηση: 0,975608.

Μπορείτε να δείτε ένα ακόμη πρόβλημα στην εικόνα:

Έτσι, εσείς και εγώ καταλάβαμε ποια είναι η θεωρία πιθανοτήτων του τύπου και παραδείγματα επίλυσης προβλημάτων στα οποία μπορείτε να συναντήσετε στην έκδοση της εξέτασης.

Τι είναι πιθανότητα;

Αντιμετωπίζοντας αυτόν τον όρο για πρώτη φορά, δεν θα καταλάβαινα τι είναι. Ως εκ τούτου, θα προσπαθήσω να το εξηγήσω με προσιτό τρόπο.

Η πιθανότητα είναι η πιθανότητα να συμβεί το γεγονός που χρειαζόμαστε.

Για παράδειγμα, αποφασίσατε να επισκεφθείτε έναν φίλο, να θυμηθείτε την είσοδο και ακόμη και το πάτωμα στο οποίο ζει. Αλλά ξέχασα τον αριθμό και τη θέση του διαμερίσματος. Και εδώ στέκεστε στη σκάλα, και μπροστά σας είναι οι πόρτες για να διαλέξετε.

Ποια είναι η πιθανότητα (πιθανότητα) ότι αν χτυπήσετε την πρώτη πόρτα, ο φίλος σας θα σας ανοίξει; Ολόκληρο το διαμέρισμα, και ο φίλος ζει μόνο για έναν από αυτούς. Μπορούμε να επιλέξουμε οποιαδήποτε πόρτα με ίσες πιθανότητες.

Ποια είναι όμως αυτή η ευκαιρία;

Πόρτες, η σωστή πόρτα. Πιθανότητα εικασίας χτυπώντας την πρώτη πόρτα :. Δηλαδή, μία φορά στις τρεις θα μαντέψετε σίγουρα.

Θέλουμε να μάθουμε τηλεφωνώντας μία φορά, πόσο συχνά θα μαντέψουμε την πόρτα; Ας εξετάσουμε όλες τις επιλογές:

1. Πήρες τηλέφωνο 1ημια πόρτα
2. Πήρες τηλέφωνο 2ημια πόρτα
3. Πήρες τηλέφωνο 3ημια πόρτα

Τώρα ας δούμε όλες τις επιλογές όπου μπορεί να είναι ένας φίλος:

ένα. Ανά 1ηαπό την πόρτα
σι. Ανά 2ηαπό την πόρτα
v. Ανά 3ηαπό την πόρτα

Ας συγκρίνουμε όλες τις επιλογές με τη μορφή πίνακα. Ένα τικ σημειώνει τις επιλογές όταν η επιλογή σας συμπίπτει με τη θέση ενός φίλου, ένα σταυρό - όταν δεν ταιριάζει.

Πώς τα βλέπεις όλα Μπορεί επιλογέςη τοποθεσία του φίλου και η επιλογή σας ποια πόρτα θα χτυπήσετε.

ΕΝΑ ευνοϊκά αποτελέσματα όλων . Δηλαδή, θα μαντέψετε μια φορά έξω χτυπώντας μια φορά το κουδούνι της πόρτας, δηλ. ...

Αυτή είναι η πιθανότητα - ο λόγος ενός ευνοϊκού αποτελέσματος (όταν η επιλογή σας συνέπεσε με την τοποθεσία ενός φίλου) προς τον αριθμό των πιθανών συμβάντων.

Ο ορισμός είναι ένας τύπος. Η πιθανότητα συνήθως συμβολίζεται p, επομένως:

Δεν είναι πολύ βολικό να γράψουμε έναν τέτοιο τύπο, επομένως θα λάβουμε υπόψη - τον αριθμό των ευνοϊκών αποτελεσμάτων και - τον συνολικό αριθμό των αποτελεσμάτων.

Η πιθανότητα μπορεί να γραφτεί ως ποσοστό, γι 'αυτό πρέπει να πολλαπλασιάσετε το αποτέλεσμα που προκύπτει με:

Πιθανώς η λέξη "αποτελέσματα" να τραβήξει το μάτι σας. Δεδομένου ότι οι μαθηματικοί ονομάζουν διάφορες ενέργειες (στην περίπτωσή μας, μια τέτοια ενέργεια είναι ένα κουδούνισμα στην πόρτα) πειράματα, το αποτέλεσμα τέτοιων πειραμάτων συνήθως ονομάζεται αποτέλεσμα.

Λοιπόν, τα αποτελέσματα είναι ευνοϊκά και δυσμενή.

Ας επιστρέψουμε στο παράδειγμά μας. Ας πούμε ότι χτυπήσαμε μία από τις πόρτες, αλλά μας την άνοιξε ένας άγνωστος. Δεν μαντέψαμε. Ποια είναι η πιθανότητα αν χτυπήσουμε μια από τις υπόλοιπες πόρτες, να μας ανοίξει ο φίλος μας;

Αν το σκεφτήκατε, τότε αυτό είναι λάθος. Ας το καταλάβουμε.

Μας έχουν μείνει δύο πόρτες. Έτσι, έχουμε πιθανά βήματα:

1) Καλέστε 1ημια πόρτα
2) Καλέστε 2ημια πόρτα

Ένας φίλος, με όλα αυτά, είναι σίγουρα πίσω από έναν από αυτούς (άλλωστε, δεν ήταν πίσω από αυτόν που καλέσαμε):

α) Φίλος για 1ηαπό την πόρτα
β) Φίλος για 2ηαπό την πόρτα

Ας σχεδιάσουμε ξανά τον πίνακα:

Όπως μπορείτε να δείτε, υπάρχουν όλες οι επιλογές, εκ των οποίων είναι ευνοϊκές. Δηλαδή, η πιθανότητα είναι ίση.

Γιατί όχι?

Η κατάσταση που εξετάσαμε - παράδειγμα εξαρτημένων γεγονότων.Το πρώτο συμβάν είναι το πρώτο κουδούνι της πόρτας, το δεύτερο συμβάν είναι το δεύτερο κουδούνι.

Και ονομάζονται εξαρτημένοι επειδή επηρεάζουν τις ακόλουθες ενέργειες. Τελικά, αν ένας φίλος μας άνοιγε την πόρτα μετά το πρώτο κουδούνισμα, ποια θα ήταν η πιθανότητα να βρίσκεται πίσω από ένα από τα άλλα δύο; Σωστά, .

Αν όμως υπάρχουν εξαρτώμενα γεγονότα, τότε πρέπει να υπάρχουν ανεξάρτητος; Αλήθεια, υπάρχουν.

Ένα παράδειγμα σχολικού βιβλίου πετάει ένα νόμισμα.

1. Ρίξτε ένα νόμισμα μια φορά. Ποια είναι η πιθανότητα, για παράδειγμα, να βγουν κεφάλια; Αυτό είναι σωστό - επειδή οι επιλογές για τα πάντα (είτε κεφαλές είτε ουρές, παραμελούμε την πιθανότητα ενός νομίσματος να σταθεί στην άκρη), αλλά μας ταιριάζει μόνο.
2. Αλλά ήταν ουρές. Εντάξει, ας το ρίξουμε άλλη μια φορά. Ποια είναι η πιθανότητα να πάρεις κεφάλια τώρα; Τίποτα δεν έχει αλλάξει, όλα είναι ίδια. Πόσες επιλογές; Δύο. Και πόσο μας ταιριάζει; Ενας.

Και ας βγει ουρές χίλιες συνεχόμενες φορές. Η πιθανότητα να πάρετε κεφάλια ταυτόχρονα θα είναι η ίδια. Υπάρχουν πάντα επιλογές, αλλά ευνοϊκές.

Είναι εύκολο να διακρίνουμε εξαρτώμενα γεγονότα από ανεξάρτητα:

1. Εάν το πείραμα πραγματοποιηθεί μία φορά (μόλις ρίξουν ένα νόμισμα, χτυπήσουν το κουδούνι μία φορά κ.λπ.), τότε τα γεγονότα είναι πάντα ανεξάρτητα.
2. Εάν το πείραμα πραγματοποιείται αρκετές φορές (ένα νόμισμα ρίχνεται μία φορά, το κουδούνι χτυπά πολλές φορές), τότε το πρώτο συμβάν είναι πάντα ανεξάρτητο. Και στη συνέχεια, εάν ο αριθμός των ευνοϊκών ή ο αριθμός όλων των αποτελεσμάτων αλλάξει, τότε τα γεγονότα εξαρτώνται, και αν όχι, είναι ανεξάρτητα.

Ας εξασκηθούμε στον προσδιορισμό της πιθανότητας λίγο.

Παράδειγμα 1.

Το νόμισμα ρίχνεται δύο φορές. Ποια είναι η πιθανότητα να χτυπήσει κεφάλι δύο φορές στη σειρά;

Λύση:

Ας εξετάσουμε όλες τις πιθανές επιλογές:

1. Αετός-αετός
2. Κεφαλές-ουρές
3. Κεφαλές-ουρές
4. Ουρές-ουρές

Όπως μπορείτε να δείτε, ολόκληρη η επιλογή. Από αυτά, μόνο μας ταιριάζει. Δηλαδή, η πιθανότητα:

Εάν η συνθήκη απλά ζητηθεί να βρεθεί η πιθανότητα, τότε η απάντηση πρέπει να δοθεί με τη μορφή δεκαδικού κλάσματος. Αν υποδεικνυόταν ότι η απάντηση πρέπει να δοθεί ως ποσοστό, τότε θα πολλαπλασιαζόμασταν με.

Απάντηση:

Παράδειγμα 2.

Στο κουτί σοκολάτες, όλες οι σοκολάτες συσκευάζονται στο ίδιο περιτύλιγμα. Ωστόσο, από γλυκά - με ξηρούς καρπούς, με κονιάκ, με κεράσια, με καραμέλα και με μαντολάτο.

Ποια είναι η πιθανότητα, παίρνοντας μια καραμέλα, να πάρετε μια καραμέλα με ξηρούς καρπούς. Δώστε την απάντησή σας ως ποσοστό.

Λύση:

Πόσα πιθανά αποτελέσματα υπάρχουν; ...

Δηλαδή, παίρνοντας μια καραμέλα, θα είναι μία από αυτές στο κουτί.

Πόσα ευνοϊκά αποτελέσματα;

Γιατί το κουτί περιέχει μόνο σοκολάτες με ξηρούς καρπούς.

Απάντηση:

Παράδειγμα 3.

Σε ένα κουτί με μπάλες. από αυτά λευκά, - μαύρα.

1. Ποια είναι η πιθανότητα να τραβήξει τη λευκή μπάλα;
2. Προσθέσαμε περισσότερες μαύρες μπάλες στο κουτί. Ποια είναι τώρα η πιθανότητα να τραβήξει τη λευκή μπάλα;

Λύση:

α) Υπάρχουν όλες οι μπάλες στο κουτί. Από αυτά, λευκό.

Η πιθανότητα είναι ίση με:

β) Τώρα υπάρχουν μπάλες στο κουτί. Και ο ίδιος αριθμός λευκών παρέμεινε -.

Απάντηση:

Πλήρης πιθανότητα

Η πιθανότητα όλων των πιθανών γεγονότων είναι ().

Ας πούμε σε ένα κουτί κόκκινες και πράσινες μπάλες. Ποια είναι η πιθανότητα να τραβήξει την κόκκινη μπάλα; Πράσινη μπάλα; Κόκκινη ή πράσινη μπάλα;

Δυνατότητα τραβήγματος κόκκινης μπάλας

Πράσινη μπάλα:

Κόκκινη ή πράσινη μπάλα:

Όπως μπορείτε να δείτε, το άθροισμα όλων των πιθανών γεγονότων είναι (). Η κατανόηση αυτής της στιγμής θα σας βοηθήσει να λύσετε πολλά προβλήματα.

Παράδειγμα 4.

Το κουτί περιέχει δείκτες: πράσινο, κόκκινο, μπλε, κίτρινο, μαύρο.

Ποια είναι η πιθανότητα να τραβήξετε ένα ΔΕΝ κόκκινο μαρκαδόρο;

Λύση:

Ας μετρήσουμε το ποσό ευνοϊκά αποτελέσματα.

ΟΧΙ κόκκινος δείκτης, σημαίνει πράσινο, μπλε, κίτρινο ή μαύρο.

Η πιθανότητα να μην συμβεί το συμβάν είναι ίση με την πιθανότητα να συμβεί.

Ο κανόνας για τον πολλαπλασιασμό των πιθανοτήτων ανεξάρτητων γεγονότων

Γνωρίζετε ήδη τι είναι ανεξάρτητες εκδηλώσεις.

Τι γίνεται αν πρέπει να βρείτε την πιθανότητα να συμβούν δύο (ή περισσότερα) ανεξάρτητα γεγονότα στη σειρά;

Ας υποθέσουμε ότι θέλουμε να μάθουμε ποια είναι η πιθανότητα όταν γυρίσουμε ένα νόμισμα μία φορά, να δούμε έναν αετό δύο φορές;

Έχουμε ήδη μετρήσει -.

Και αν γυρίσουμε ένα νόμισμα μια φορά; Ποια είναι η πιθανότητα να δούμε έναν αετό στη σειρά;

Όλες οι πιθανές επιλογές:

1. Αετός-αετός-αετός
2. Κεφάλια-κεφάλια-ουρές
3. Κεφάλια-ουρές-κεφάλια
4. Κεφαλές-ουρές-ουρές
5. Ουρές-κεφάλια-κεφάλια
6. Ουρές-κεφάλια-ουρές
7. Ουρές-ουρές-κεφάλια
8. Ουρές-Ουρές-Ουρές

Δεν ξέρω για εσάς, αλλά έκανα ένα λάθος μία φορά όταν έκανα αυτήν τη λίστα. Ουάου! Και μόνο η επιλογή (πρώτη) μας ταιριάζει.

Για 5 ρίψεις, μπορείτε να φτιάξετε μόνοι σας μια λίστα με πιθανά αποτελέσματα. Αλλά οι μαθηματικοί δεν είναι τόσο εργατικοί όσο εσείς.

Ως εκ τούτου, πρώτα παρατήρησαν και στη συνέχεια απέδειξαν ότι η πιθανότητα μιας συγκεκριμένης ακολουθίας ανεξάρτητων γεγονότων μειώνεται κάθε φορά από την πιθανότητα ενός γεγονότος.

Με άλλα λόγια,

Εξετάστε το παράδειγμα του ίδιου ατυχούς νομίσματος.

Η πιθανότητα να μπουν τα κεφάλια σε μια πρόκληση; ... Τώρα γυρίζουμε ένα νόμισμα μια φορά.

Ποια είναι η πιθανότητα να χτυπήσετε κεφάλια μία φορά στη σειρά;

Αυτός ο κανόνας λειτουργεί όχι μόνο εάν μας ζητηθεί να βρούμε την πιθανότητα να συμβεί το ίδιο γεγονός πολλές φορές στη σειρά.

Αν θέλαμε να βρούμε την ακολουθία GRIP-EAGLE-GRILLE για ρίψεις στη σειρά, θα κάναμε το ίδιο.

Η πιθανότητα πτώσης κεφαλών είναι -, κεφάλια -.

Πιθανότητα πτώσης από την ακολουθία GRILLE-EAGLE-GRILLE-GRILLE:

Μπορείτε να το ελέγξετε μόνοι σας φτιάχνοντας ένα τραπέζι.

Ο κανόνας για την προσθήκη των πιθανοτήτων ασυνεπών γεγονότων.

Σταμάτα λοιπόν! Νέος ορισμός.

Ας το καταλάβουμε. Πάρτε το φθαρμένο μας νόμισμα και ρίξτε το μια φορά.
Πιθανές επιλογές:

1. Αετός-αετός-αετός
2. Κεφάλια-κεφάλια-ουρές
3. Κεφάλια-ουρές-κεφάλια
4. Κεφαλές-ουρές-ουρές
5. Ουρές-κεφάλια-κεφάλια
6. Ουρές-κεφάλια-ουρές
7. Ουρές-ουρές-κεφάλια
8. Ουρές-Ουρές-Ουρές

Έτσι, τα ασύμβατα γεγονότα είναι μια ορισμένη, προκαθορισμένη ακολουθία γεγονότων. είναι ασυμβίβαστα γεγονότα.

Αν θέλουμε να καθορίσουμε ποια είναι η πιθανότητα δύο (ή περισσοτέρων) ασυμβίβαστων γεγονότων, τότε προσθέτουμε τις πιθανότητες αυτών των γεγονότων.

Πρέπει να καταλάβετε ότι η πτώση κεφαλιών ή ουρών είναι δύο ανεξάρτητα γεγονότα.

Αν θέλουμε να καθορίσουμε ποια είναι η πιθανότητα μιας ακολουθίας) (ή οποιασδήποτε άλλης), τότε χρησιμοποιούμε τον κανόνα του πολλαπλασιασμού των πιθανοτήτων.
Ποια είναι η πιθανότητα να πάρεις κεφάλια στην πρώτη ρίψη, και στο δεύτερο και τρίτο κεφάλι;

Αλλά αν θέλουμε να μάθουμε ποια είναι η πιθανότητα να έχουμε μία από τις πολλές ακολουθίες, για παράδειγμα, όταν τα κεφάλια πέσουν ακριβώς μία φορά, δηλ. επιλογές και, στη συνέχεια, πρέπει να προσθέσουμε τις πιθανότητες αυτών των ακολουθιών.

Όλες οι επιλογές είναι κατάλληλες για εμάς.

Μπορούμε να πάρουμε το ίδιο πράγμα προσθέτοντας τις πιθανότητες κάθε ακολουθίας:

Έτσι, προσθέτουμε πιθανότητες όταν θέλουμε να προσδιορίσουμε τις πιθανότητες κάποιων ασυνεπών ακολουθιών γεγονότων.

Υπάρχει ένας μεγάλος βασικός κανόνας που θα σας βοηθήσει να αποφύγετε τη σύγχυση πότε να πολλαπλασιάσετε και πότε να προσθέσετε:

Ας επιστρέψουμε στο παράδειγμα όταν γυρίσαμε ένα νόμισμα μία φορά και θέλουμε να μάθουμε την πιθανότητα να δούμε κεφάλια μία φορά.
Τι πρόκειται να συμβεί?

Πρέπει να πέσει:
(κεφάλια ΚΑΙ ουρές ΚΑΙ ουρές) (ουρές ΚΑΙ κεφαλές ΚΑΙ ουρές) (ουρές ΚΑΙ ουρές ΚΑΙ κεφάλια).
Αποδεικνύεται λοιπόν:

Ας δούμε μερικά παραδείγματα.

Παράδειγμα 5.

Το κουτί περιέχει μολύβια. κόκκινα, πράσινα, πορτοκάλια και κίτρινα και μαύρα. Ποια είναι η πιθανότητα να βγάλουμε κόκκινα ή πράσινα μολύβια;

Λύση:

Παράδειγμα 6.

Τα ζάρια ρίχνονται δύο φορές, ποια είναι η πιθανότητα συνολικά 8 πόντων;

Λύση.

Πώς μπορούμε να πάρουμε πόντους;

(και) ή (και) ή (και) ή (και) ή (και).

Η πιθανότητα πτώσης από ένα (οποιοδήποτε) πρόσωπο -.

Υπολογίζουμε την πιθανότητα:

Προπόνηση.

Νομίζω ότι τώρα σας έγινε σαφές πότε να μετρήσετε τις πιθανότητες, πότε να τις προσθέσετε και πότε να τις πολλαπλασιάσετε. Δεν είναι? Ας εξασκηθούμε λίγο.

Καθήκοντα:

Ας πάρουμε μια τράπουλα καρτών, στην οποία κάρτες, συμπεριλαμβανομένων φτυάρι, καρδιών, 13 κλαμπ και 13 διαμαντιών. Από τον άσο του κάθε κοστουμιού.

1. Ποια είναι η πιθανότητα να σχεδιάσουμε κλαμπ στη σειρά (βάζουμε το πρώτο τραβηγμένο φύλλο πίσω στο κατάστρωμα και το ανακατεύουμε);
2. Ποια είναι η πιθανότητα να τραβήξετε μια μαύρη κάρτα (φτυάρι ή μπαστούνια);
3. Ποια είναι η πιθανότητα να τραβήξετε μια εικόνα (γρύλος, βασίλισσα, βασιλιάς ή άσος);
4. Ποια είναι η πιθανότητα να σχεδιάσουμε δύο εικόνες στη σειρά (αφαιρούμε το πρώτο τραβηγμένο φύλλο από το κατάστρωμα);
5. Ποια είναι η πιθανότητα, αφού έχετε πάρει δύο φύλλα, να συλλέξετε έναν συνδυασμό - (jack, queen ή king) και έναν άσο Η σειρά στην οποία θα τραβηχτούν τα φύλλα δεν έχει σημασία.

Απαντήσεις:

Εάν καταφέρατε να λύσετε όλα τα προβλήματα μόνοι σας, τότε είστε εξαιρετικός συνεργάτης! Τώρα θα κάνετε κλικ στις πιθανότητες στην Ενιαία Εξέταση Κράτους!

ΘΕΩΡΙΑ ΠΙΘΑΝΟΤΗΤΩΝ. ΜΕΣΟ ΕΠΙΠΕΔΟ

Ας δούμε ένα παράδειγμα. Ας πούμε ότι ρίχνουμε μια μήτρα. Τι κόκκαλο είναι αυτό, ξέρεις; Αυτό είναι το όνομα ενός κύβου με αριθμούς στις άκρες. Πόσα πρόσωπα, τόσοι αριθμοί: από έως πόσους; Πριν.

Έτσι, τυλίγουμε τη μήτρα και θέλουμε να κυλήσουμε ή. Και μας πέφτει.

Η πιθανότητα λέει τι συνέβη ευνοϊκό γεγονός(μην το συγχέετε με τους εύπορους).

Αν έπεφτε, το γεγονός θα ήταν επίσης ευνοϊκό. Συνολικά, μπορούν να συμβούν μόνο δύο ευνοϊκά γεγονότα.

Και πόσες είναι δυσμενείς; Δεδομένου ότι υπάρχουν όλα τα πιθανά γεγονότα, σημαίνει ότι τα δυσμενή γεγονότα είναι μεταξύ αυτών (αυτό συμβαίνει εάν πέσει έξω ή).

Ορισμός:

Πιθανότητα είναι ο λόγος του αριθμού των ευνοϊκών γεγονότων προς τον αριθμό όλων των πιθανών γεγονότων... Δηλαδή, η πιθανότητα δείχνει ποια αναλογία όλων των πιθανών γεγονότων είναι ευνοϊκή.

Η πιθανότητα συμβολίζεται με το λατινικό γράμμα (προφανώς, από την αγγλική λέξη πιθανότητα).

Είναι συνηθισμένο να μετράμε την πιθανότητα ως ποσοστό (βλέπε θέμα,). Για να γίνει αυτό, η τιμή πιθανότητας πρέπει να πολλαπλασιαστεί με. Στο παράδειγμα των ζαριών, η πιθανότητα.

Και ως ποσοστό :.

Παραδείγματα (αποφασίστε μόνοι σας):

1. Ποια είναι η πιθανότητα να πάρεις κεφάλια όταν αναποδογυρίσεις ένα νόμισμα; Ποια είναι η πιθανότητα να πάρετε ουρές;
2. Ποια είναι η πιθανότητα να έρθει ένας ζυγός αριθμός σε μια ζαριά; Και με ποιο - περίεργο;
3. Σε ένα κουτί μολύβια, μπλε και κόκκινο. Σχεδιάστε ένα μολύβι τυχαία. Ποια είναι η πιθανότητα να βγάλουμε ένα απλό;

Λύσεις:

1. Πόσες επιλογές υπάρχουν; Τα κεφάλια και οι ουρές είναι μόνο δύο. Πόσες από αυτές είναι ευνοϊκές; Μόνο ένας είναι αετός. Εξ ου και η πιθανότητα

   Είναι το ίδιο με τις ουρές :.

2. Συνολικές επιλογές: (πόσες πλευρές έχει ο κύβος, τόσες πολλές διαφορετικές επιλογές). Ευνοϊκά: (όλα αυτά είναι άρτιοι αριθμοί :).
   Πιθανότητα. Με το περίεργο, φυσικά, το ίδιο πράγμα.
3. Σύνολο: . Ευνοϊκός:. Πιθανότητα:.

Πλήρης πιθανότητα

Όλα τα μολύβια στο συρτάρι είναι πράσινα. Ποια είναι η πιθανότητα να βγάλουμε ένα κόκκινο μολύβι; Δεν υπάρχει πιθανότητα: πιθανότητα (εξάλλου, ευνοϊκά γεγονότα -).

Ένα τέτοιο γεγονός ονομάζεται αδύνατο.

Ποια είναι η πιθανότητα να βγάλουμε ένα πράσινο μολύβι; Υπάρχουν ακριβώς ο ίδιος αριθμός ευνοϊκών γεγονότων με τα συνολικά γεγονότα (όλα τα γεγονότα είναι ευνοϊκά). Ως εκ τούτου, η πιθανότητα είναι ίση με ή.

Ένα τέτοιο γεγονός ονομάζεται αξιόπιστο.

Εάν υπάρχουν πράσινα και κόκκινα μολύβια στο κουτί, ποια είναι η πιθανότητα να τραβήξετε το πράσινο ή το κόκκινο; Για άλλη μία φορά. Σημειώστε αυτό το πράγμα: η πιθανότητα να τραβήξετε το πράσινο είναι ίση και το κόκκινο είναι.

Συνολικά, αυτές οι πιθανότητες είναι ακριβώς ίσες. Αυτό είναι, το άθροισμα των πιθανοτήτων όλων των πιθανών γεγονότων είναι ίσο με ή.

Παράδειγμα:

Σε ένα κουτί μολύβια, ανάμεσά τους μπλε, κόκκινο, πράσινο, απλό, κίτρινο και τα υπόλοιπα είναι πορτοκαλί. Ποια είναι η πιθανότητα να μην τραβήξει πράσινο;

Λύση:

Θυμηθείτε ότι όλες οι πιθανότητες αθροίζονται. Και η πιθανότητα να τραβήξει πράσινο είναι ίση. Αυτό σημαίνει ότι η πιθανότητα να μην τραβήξει πράσινο είναι ίση με.

Θυμηθείτε αυτό το κόλπο:η πιθανότητα να μην συμβεί το συμβάν είναι ίση με μείον την πιθανότητα να συμβεί.

Ανεξάρτητα γεγονότα και κανόνας πολλαπλασιασμού

Γυρίζετε ένα νόμισμα μία φορά και θέλετε να πέσουν τα κεφάλια και τις δύο φορές. Ποια είναι η πιθανότητα να συμβεί αυτό;

Ας εξετάσουμε όλες τις πιθανές επιλογές και να καθορίσουμε πόσες είναι:

Κεφάλια-Κεφάλια, Κεφάλια-Κεφάλια, Κεφάλια-Κεφάλια, Κεφάλια-Κεφάλια. Τι άλλο?

Ολόκληρη η επιλογή. Από αυτά, μόνο ένα είναι κατάλληλο για εμάς: Eagle-Eagle. Συνολικά, η πιθανότητα είναι.

Καλός. Και τώρα ρίχνουμε ένα νόμισμα μια φορά. Μετρήστε το μόνοι σας. Έγινε; (απάντηση).

Mayσως έχετε παρατηρήσει ότι με την προσθήκη κάθε επόμενης ρίψης, η πιθανότητα μειώνεται κατά καιρούς. Ο γενικός κανόνας ονομάζεται κανόνας πολλαπλασιασμού:

Οι πιθανότητες ανεξάρτητων γεγονότων αλλάζουν.

Τι είναι οι ανεξάρτητες εκδηλώσεις; Όλα είναι λογικά: αυτά είναι αυτά που δεν εξαρτώνται το ένα από το άλλο. Για παράδειγμα, όταν πετάμε ένα νόμισμα αρκετές φορές, κάθε φορά γίνεται μια νέα ρίψη, το αποτέλεσμα της οποίας δεν εξαρτάται από όλες τις προηγούμενες ρίψεις. Μπορούμε να αναποδογυρίσουμε δύο διαφορετικά νομίσματα ταυτόχρονα.

Περισσότερα παραδείγματα:

1. Τα ζάρια ρίχνονται δύο φορές. Ποια είναι η πιθανότητα να κυλήσουν και οι δύο φορές;
2. Το νόμισμα πετάγεται μία φορά. Ποια είναι η πιθανότητα να προσγειωθεί αρχικά και μετά να πέσει δύο φορές;
3. Ο παίκτης ρίχνει δύο ζάρια. Ποια είναι η πιθανότητα το άθροισμα των αριθμών πάνω τους να είναι ίσο;

Απαντήσεις:

1. Τα γεγονότα είναι ανεξάρτητα, πράγμα που σημαίνει ότι ο κανόνας πολλαπλασιασμού λειτουργεί :.
2. Η πιθανότητα ενός αετού είναι. Η πιθανότητα εμφάνισης ουρών είναι επίσης. Πολλαπλασιάζουμε:
3. 12 μπορεί να ληφθεί μόνο εάν τυλιχτούν δύο -ki :.

Μη συμβατά συμβάντα και κανόνας προσθήκης

Ασυμβίβαστα γεγονότα ονομάζονται γεγονότα που αλληλοσυμπληρώνονται με πλήρη πιθανότητα. Όπως υποδηλώνει το όνομα, δεν μπορούν να συμβούν ταυτόχρονα. Για παράδειγμα, αν αναποδογυρίσουμε ένα νόμισμα, μπορεί να βγει είτε κεφαλές είτε ουρές.

Παράδειγμα.

Σε ένα κουτί μολύβια, ανάμεσά τους μπλε, κόκκινο, πράσινο, απλό, κίτρινο και τα υπόλοιπα είναι πορτοκαλί. Ποια είναι η πιθανότητα να τραβήξει πράσινο ή κόκκινο;

Λύση .

Η πιθανότητα να τραβήξετε ένα πράσινο μολύβι είναι. Το κόκκινο - .

Συνολικά ευοίωνες εκδηλώσεις: πράσινο + κόκκινο. Αυτό σημαίνει ότι η πιθανότητα να τραβήξει πράσινο ή κόκκινο είναι ίση με.

Η ίδια πιθανότητα μπορεί να αναπαρασταθεί ως εξής :.

Αυτός είναι ο κανόνας προσθήκης:οι πιθανότητες ασυνεπών γεγονότων αθροίζονται.

Μικτά προβλήματα

Παράδειγμα.

Το νόμισμα ρίχνεται δύο φορές. Ποια είναι η πιθανότητα το αποτέλεσμα των ρίψεων να είναι διαφορετικό;

Λύση .

Αυτό σημαίνει ότι εάν το πρώτο χτύπημα είναι κεφαλές, το δεύτερο θα πρέπει να είναι ουρές και αντίστροφα. Αποδεικνύεται ότι υπάρχουν δύο ζεύγη ανεξάρτητων γεγονότων και αυτά τα ζεύγη είναι ασυμβίβαστα μεταξύ τους. Πώς να μην μπερδευτείτε, πού να πολλαπλασιαστείτε και πού να προσθέσετε.

Υπάρχει ένας απλός βασικός κανόνας για αυτές τις καταστάσεις. Προσπαθήστε να περιγράψετε τι πρόκειται να συμβεί συνδέοντας τα γεγονότα με AND ή OR. Για παράδειγμα, σε αυτήν την περίπτωση:

Θα πρέπει να ανέβει (κεφάλια και ουρές) ή (ουρές και κεφάλια).

Όπου υπάρχει σύνδεσμος "και", θα υπάρχει πολλαπλασιασμός και όπου "ή" - πρόσθεση:

Δοκιμάστε το μόνοι σας:

1. Ποια είναι η πιθανότητα η ίδια πλευρά να πέσει σε δύο ρίψεις ενός νομίσματος και τις δύο φορές;
2. Τα ζάρια ρίχνονται δύο φορές. Ποια είναι η πιθανότητα το σύνολο να είναι πόντοι;

Λύσεις:

Ενα άλλο παράδειγμα:

Πετάμε ένα νόμισμα μια φορά. Ποια είναι η πιθανότητα να βγουν κεφάλια τουλάχιστον μία φορά;

Λύση:

ΘΕΩΡΙΑ ΠΙΘΑΝΟΤΗΤΩΝ. ΣΥΝΤΟΜΗ ΓΙΑ ΤΟ ΚΥΡΙΟ

Πιθανότητα είναι ο λόγος του αριθμού των ευνοϊκών γεγονότων προς τον αριθμό όλων των πιθανών γεγονότων.

Ανεξάρτητες εκδηλώσεις

Δύο γεγονότα είναι ανεξάρτητα εάν κατά την εμφάνιση του ενός η πιθανότητα εμφάνισης του άλλου δεν αλλάζει.

Πλήρης πιθανότητα

Η πιθανότητα όλων των πιθανών γεγονότων είναι ().

Η πιθανότητα να μην συμβεί το συμβάν είναι ίση με την πιθανότητα να συμβεί.

Ο κανόνας για τον πολλαπλασιασμό των πιθανοτήτων ανεξάρτητων γεγονότων

Η πιθανότητα μιας συγκεκριμένης ακολουθίας ανεξάρτητων γεγονότων είναι ίση με το γινόμενο των πιθανοτήτων καθενός από τα γεγονότα

Ασυμβίβαστα συμβάντα

Τα ασυμβίβαστα συμβάντα ονομάζονται γεγονότα που δεν μπορούν να συμβούν ταυτόχρονα ως αποτέλεσμα ενός πειράματος. Μια σειρά ασυνεπών γεγονότων αποτελούν μια πλήρη ομάδα γεγονότων.

Οι πιθανότητες ασυνεπών γεγονότων αθροίζονται.

Έχοντας περιγράψει τι πρέπει να συμβεί, χρησιμοποιώντας τους συνδέσμους "ΚΑΙ" ή "OR", αντί για "ΚΑΙ" βάζουμε το σύμβολο του πολλαπλασιασμού και αντί του "OR" - προσθήκη.

Λοιπόν, το θέμα τελείωσε. Αν διαβάζετε αυτές τις γραμμές, τότε είστε πολύ κουλ.

Γιατί μόνο το 5% των ανθρώπων είναι σε θέση να κατακτήσουν κάτι μόνοι τους. Και αν διαβάζετε μέχρι το τέλος, τότε είστε σε αυτό το 5%!

Τώρα έρχεται το πιο σημαντικό πράγμα.

Καταλάβατε τη θεωρία για αυτό το θέμα. Και, πάλι, αυτό είναι ... είναι απλά σούπερ! Είστε ήδη καλύτεροι από τη συντριπτική πλειοψηφία των συνομηλίκων σας.

Το πρόβλημα είναι ότι αυτό μπορεί να μην είναι αρκετό ...

Για τι?

Για την επιτυχή επιτυχία των εξετάσεων, για την εισαγωγή στο ινστιτούτο με προϋπολογισμό και, ΠΙΟ ΣΗΜΑΝΤΙΚΟ, για μια ζωή.

Δεν θα σας πείσω για τίποτα, θα πω μόνο ένα πράγμα ...

Τα άτομα που έχουν λάβει μια καλή εκπαίδευση κερδίζουν πολύ περισσότερα από εκείνα που δεν έχουν λάβει. Αυτά είναι στατιστικά.

Αλλά ούτε αυτό είναι το κύριο.

Το κυριότερο είναι ότι είναι ΠΕΡΙΣΣΟΤΕΡΑ (υπάρχουν τέτοιες μελέτες). Becauseσως επειδή υπάρχουν τόσες περισσότερες ευκαιρίες γι 'αυτούς και η ζωή γίνεται πιο φωτεινή; Δεν ξέρω...

Σκέψου όμως μόνος σου ...

Τι χρειάζεται για να είσαι σίγουρα καλύτερος από τους άλλους στις εξετάσεις και τελικά να είσαι ... πιο ευτυχισμένος;

ΛΑΜΒΑΝΤΕ ΕΝΑ ΧΕΙΡΟΛΥΓΜΑ ΠΡΟΒΛΗΜΑΤΑ ΣΕ ΑΥΤΟ ΤΟ ΘΕΜΑ.

Στην εξέταση, δεν θα σας ζητηθεί θεωρία.

Θα χρειαστείτε λύσει τα καθήκοντα για λίγο.

Και, αν δεν τα λύσατε (ΠΟΛΛΑ!), Σίγουρα θα πάτε κάπου με ηλίθιο λάθος ή απλά δεν θα είναι εγκαίρως.

Είναι όπως στον αθλητισμό - πρέπει να το επαναλαμβάνεις ξανά και ξανά για να κερδίσεις σίγουρα.

Βρείτε μια συλλογή όπου θέλετε, απαραίτητα με λύσεις, λεπτομερή ανάλυσηκαι αποφάσισε, αποφάσισε, αποφάσισε!

Μπορείτε να χρησιμοποιήσετε τις εργασίες μας (προαιρετικά) και εμείς, φυσικά, τις προτείνουμε.

Για να γεμίσετε το χέρι σας με τις εργασίες μας, πρέπει να βοηθήσετε στην παράταση της ζωής του σχολικού βιβλίου YouClever που διαβάζετε αυτήν τη στιγμή.

Πως? Υπάρχουν δύο επιλογές:

1. Μοιραστείτε όλες τις κρυφές εργασίες σε αυτό το άρθρο - 299 r
2. Ξεκλειδώστε την πρόσβαση σε όλες τις κρυφές εργασίες και στα 99 άρθρα του σεμιναρίου - 499 ρούβλια

Ναι, έχουμε 99 τέτοια άρθρα στο σχολικό μας βιβλίο και η πρόσβαση για όλες τις εργασίες και όλα τα κρυμμένα κείμενα σε αυτά μπορεί να ανοίξει ταυτόχρονα.

Παρέχεται πρόσβαση σε όλες τις κρυφές εργασίες για όλη τη διάρκεια ζωής του ιστότοπου.

Συμπερασματικά...

Αν δεν σας αρέσουν τα καθήκοντά μας, βρείτε άλλα. Απλώς μην ασχολείστε με τη θεωρία.

"Κατανοητό" και "Είμαι σε θέση να λύσω" είναι τελείως διαφορετικές δεξιότητες. Χρειάζεστε και τα δύο.

Βρες προβλήματα και λύσε!

Ενότητα 1. Τυχαία γεγονότα (50 ώρες)

Θεματικό σχέδιο του κλάδου για φοιτητές μερικής φοίτησης

Θεματικό σχέδιο του κλάδου για μαθητές αλληλογραφίας

2.3. Δομικό και λογικό σχήμα της πειθαρχίας

Μαθηματικά μέρος 2ο. Θεωρία πιθανοτήτων και στοιχεία της θεωρίας των μαθηματικών στατιστικών

Ενότητα 1 Τυχαία γεγονότα

Ενότητα 3 Στοιχεία Μαθηματικών Στατιστικών

Ενότητα 2 Τυχαίες μεταβλητές

2.5. Πρακτικό μπλοκ

2.6. Σύστημα βαθμολόγησης

Πληροφοριακοί πόροι του κλάδου

Βιβλιογραφική λίστα Κύρια:

3.2. Βασική σύνοψη για το μάθημα «Μαθηματικά, μέρος 2. Θεωρία πιθανοτήτων και στοιχεία μαθηματικών στατιστικών »εισαγωγή

Ενότητα 1. Τυχαία γεγονότα

1.1. Η έννοια ενός τυχαίου γεγονότος

1.1.1. Πληροφορίες από τη θεωρία συνόλων

1.1.2. Χώρος στοιχειωδών γεγονότων

1.1.3. Ταξινόμηση συμβάντων

1.1.4. Άθροισμα και προϊόν γεγονότων

1.2. Οι πιθανότητες τυχαίων γεγονότων.

1.2.1. Σχετική συχνότητα ενός γεγονότος, αξιώματα θεωρίας πιθανοτήτων. Κλασικός ορισμός της πιθανότητας

1.2.2. Γεωμετρικός ορισμός της πιθανότητας

Υπολογισμός της πιθανότητας ενός συμβάντος μέσω των στοιχείων της συνδυαστικής ανάλυσης

1.2.4. Ιδιότητες πιθανοτήτων συμβάντων

1.2.5. Ανεξάρτητες εκδηλώσεις

1.2.6. Υπολογισμός της πιθανότητας λειτουργίας χωρίς βλάβη της συσκευής

Τύποι για τον υπολογισμό της πιθανότητας γεγονότων

1.3.1. Ακολουθία ανεξάρτητων δοκιμών (σχέδιο Bernoulli)

1.3.2. Υπό όρους πιθανότητα ενός συμβάντος

1.3.4. Τύπος συνολικής πιθανότητας και τύπος Bayes

Ενότητα 2. Τυχαίες μεταβλητές

2.1. Περιγραφή τυχαίων μεταβλητών

2.1.1. Ορισμός και μέθοδοι εκχώρησης μιας τυχαίας μεταβλητής Μια από τις βασικές έννοιες της θεωρίας της πιθανότητας είναι η έννοια μιας τυχαίας μεταβλητής. Ας δούμε μερικά παραδείγματα τυχαίων μεταβλητών:

Για να ορίσετε μια τυχαία μεταβλητή, πρέπει να υποδείξετε τον νόμο διανομής της. Οι τυχαίες μεταβλητές συμβολίζονται συνήθως με ελληνικά γράμματα ,, , και οι πιθανές τιμές τους συμβολίζονται με λατινικά γράμματα με δείκτες xi, yi, zi.

2.1.2. Διακριτές τυχαίες μεταβλητές

Εξετάστε τα γεγονότα Ai που περιέχουν όλα τα στοιχειώδη γεγονότα  που οδηγούν στην τιμή XI:

Αφήστε το p να υποδηλώσει την πιθανότητα του γεγονότος Ai:

2.1.3. Συνεχείς τυχαίες μεταβλητές

2.1.4. Η συνάρτηση διανομής και οι ιδιότητές της

2.1.5. Πυκνότητα κατανομής πιθανοτήτων και οι ιδιότητές της

2.2. Αριθμητικά χαρακτηριστικά τυχαίων μεταβλητών

2.2.1. Η μαθηματική προσδοκία μιας τυχαίας μεταβλητής

2.2.2. Διακύμανση τυχαίας μεταβλητής

2.2.3. Κανονική κατανομή μιας τυχαίας μεταβλητής

2.2.4. Διωνυμική κατανομή

2.2.5. Διανομή Poisson

Ενότητα 3. Στοιχεία μαθηματικών στατιστικών

3.1. Βασικοί ορισμοί

ραβδόγραμμα

3.3. Σημειακές εκτιμήσεις των παραμέτρων κατανομής

ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ

Σημειακές εκτιμήσεις μαθηματικής προσδοκίας και διακύμανσης

3.4. Διαστημικές εκτιμήσεις

Έννοια εκτίμησης διαστήματος

Εκτιμήσεις διαστήματος κτιρίου

Βασικές στατιστικές κατανομές

Διαστημικές εκτιμήσεις της μαθηματικής προσδοκίας μιας κανονικής κατανομής

Μεσοδιάστημα εκτίμηση της διακύμανσης της κανονικής κατανομής

συμπέρασμα

Γλωσσάριο

4. Μεθοδικές οδηγίες για εργαστηριακές εργασίες

Βιβλιογραφικός κατάλογος

Εργαστηριακή εργασία 1 περιγραφή τυχαίων μεταβλητών. Αριθμητικά χαρακτηριστικά

Παραγγελία εργαστηριακών εργασιών

Εργαστηριακή εργασία 2 Βασικοί ορισμοί. Συστηματοποίηση του δείγματος. Σημειακές εκτιμήσεις των παραμέτρων κατανομής. Διαστημικές εκτιμήσεις.

Η έννοια μιας στατιστικής υπόθεσης σχετικά με το είδος της κατανομής

Παραγγελία εργαστηριακών εργασιών

Αξία κυψέλης Αξία κυψέλης

5. Μεθοδικές οδηγίες για την εκτέλεση της δοκιμαστικής εργασίας Εργασία για τη δοκιμή

Μεθοδολογικές οδηγίες για την εκτέλεση εργασιών ελέγχου Γεγονότα και πιθανότητες

Τυχαίες μεταβλητές

Τυπική απόκλιση

Στοιχεία μαθηματικών στατιστικών

6. Μπλοκ ελέγχου της απόκτησης της πειθαρχίας

Ερωτήσεις για τις εξετάσεις για το μάθημα «Μαθηματικά, μέρος 2. Θεωρία πιθανοτήτων και στοιχεία μαθηματικών στατιστικών "

Συνέχεια του πίνακα στο

Τέλος του πίνακα μέσα

Ομοιόμορφα κατανεμημένοι τυχαίοι αριθμοί

Περιεχόμενο

Ενότητα 1. Τυχαία γεγονότα ………………………………………. δεκαοχτώ

Τομέας 2. Τυχαίες μεταβλητές .. …………………………… .. 41

Ενότητα 3. Στοιχεία μαθηματικών στατιστικών ................ 64

4. Μεθοδικές οδηγίες για την εκτέλεση εργαστηρίου

5. Μεθοδολογικές οδηγίες για την εφαρμογή του ελέγχου

1. Τύποι για τον υπολογισμό της πιθανότητας γεγονότων

1.3.1. Ακολουθία ανεξάρτητων δοκιμών (σχέδιο Bernoulli)

Ας υποθέσουμε ότι ένα συγκεκριμένο πείραμα μπορεί να πραγματοποιηθεί επανειλημμένα υπό τις ίδιες συνθήκες. Ας γίνει αυτή η εμπειρία νφορές, δηλαδή μια ακολουθία νδοκιμές.

Ορισμός. Ακολουθία ν ονομάζονται δοκιμές αμοιβαία ανεξάρτητη εάν οποιοδήποτε συμβάν που σχετίζεται με αυτό το τεστ είναι ανεξάρτητο από τυχόν γεγονότα που σχετίζονται με τα υπόλοιπα τεστ.

Ας υποθέσουμε ότι κάποιο γεγονός ΕΝΑμπορεί να συμβεί με πιθανότητα Πως αποτέλεσμα μιας δοκιμής ή δεν συμβαίνει με πιθανότητα q= 1- Π.

Ορισμός . Ακολουθία του νη δοκιμή σχηματίζει ένα σχέδιο Bernoulli εάν πληρούνται οι ακόλουθες προϋποθέσεις:

ακολουθία νοι δοκιμές είναι αμοιβαία ανεξάρτητες,

2) η πιθανότητα ενός γεγονότος ΕΝΑδεν αλλάζει από δοκιμή σε δοκιμή και δεν εξαρτάται από το αποτέλεσμα σε άλλες δοκιμές.

Εκδήλωση ΕΝΑονομάζεται «επιτυχία» της δίκης και το αντίθετο γεγονός ονομάζεται «αποτυχία». Σκεφτείτε ένα γεγονός

= (σε νοι δοκιμές έγιναν ακριβώς Μ"Επιτυχία").

Για τον υπολογισμό της πιθανότητας αυτού του γεγονότος, ισχύει ο τύπος Bernoulli

Π() =
, Μ = 1, 2, …, ν , (1.6)

όπου - ο αριθμός των συνδυασμών των νστοιχεία από Μ :

=
=
.

Παράδειγμα 1.16. Η μήτρα τυλίγεται τρεις φορές. Εύρημα:

α) η πιθανότητα 6 πόντων να πέσουν δύο φορές ·

β) η πιθανότητα ο αριθμός των έξι να μην εμφανίζεται περισσότερες από δύο φορές.

Λύση . Η "επιτυχία" της δοκιμής θα θεωρηθεί ως το αποτέλεσμα στον κύβο του προσώπου με την εικόνα των 6 πόντων.

α) Ο συνολικός αριθμός των δοκιμών - ν= 3, ο αριθμός των "επιτυχιών" - Μ = 2. Η πιθανότητα "επιτυχίας" - Π=, και η πιθανότητα «αποτυχίας» είναι q= 1 - =. Στη συνέχεια, σύμφωνα με τον τύπο του Μπερνούλι, η πιθανότητα ότι η πλευρά με έξι πόντους θα πέσει δύο φορές ως αποτέλεσμα της ρίψης των ζαριών τρεις φορές θα είναι ίση με

.

β) Δηλώστε με ΕΝΑένα γεγονός, το οποίο συνίσταται στο γεγονός ότι η όψη με τον αριθμό των σημείων 6 εμφανίζεται όχι περισσότερο από δύο φορές. Τότε το συμβάν μπορεί να αναπαρασταθεί ως το άθροισμα των τριών ασυμβίβαστωνγεγονότα Α =
,

όπου V 3 0 - ένα γεγονός όταν το πρόσωπο του ενδιαφέροντος δεν εμφανίζεται ποτέ,

V 3 1 - συμβάν όταν το πρόσωπο ενδιαφέροντος εμφανιστεί μία φορά,

V 3 2 - ένα συμβάν όταν εμφανίζεται δύο φορές ένα πρόσωπο ενδιαφέροντος.

Με τον τύπο του Bernoulli (1,6), βρίσκουμε

Π(ΕΝΑ) = p (
) = Π(
)=
+
+
=

=
.

1.3.2. Υπό όρους πιθανότητα ενός συμβάντος

Η υπό όρους πιθανότητα αντικατοπτρίζει την επίδραση ενός γεγονότος στην πιθανότητα ενός άλλου. Η αλλαγή των συνθηκών στις οποίες διεξάγεται το πείραμα επηρεάζει επίσης

σχετικά με την πιθανότητα εμφάνισης του γεγονότος που μας ενδιαφέρει.

Ορισμός. Ας είναι ΕΝΑ και σι- ορισμένα γεγονότα και η πιθανότητα Π(σι)> 0.

Υπό όρους πιθανότηταεξελίξεις ΕΝΑμε την προϋπόθεση ότι «το γεγονός σιήδησυνέβη »είναι ο λόγος της πιθανότητας παραγωγής αυτών των γεγονότων προς την πιθανότητα ενός γεγονότος που συνέβη νωρίτερα από το συμβάν, η πιθανότητα του οποίου πρέπει να βρεθεί. Η πιθανότητα υπό όρους συμβολίζεται ως Π(ΕΝΑ σι). Στη συνέχεια εξ ορισμού

Π (ΕΝΑ  σι) =
. (1.7)

Παράδειγμα 1.17. Ρίξτε δύο ζάρια. Ο χώρος των στοιχειωδών γεγονότων αποτελείται από διατεταγμένα ζεύγη αριθμών

(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)

(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)

(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)

(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6).

Στο Παράδειγμα 1.16, διαπιστώθηκε ότι το συμβάν ΕΝΑ= (αριθμός πόντων στην πρώτη μήτρα> 4) και συμβάν ντο= (το άθροισμα των πόντων είναι ίσο με 8) εξαρτώνται. Ας συνθέσουμε τη σχέση

.

Αυτή η σχέση μπορεί να ερμηνευθεί ως εξής. Ας υποθέσουμε ότι το αποτέλεσμα του πρώτου ρολού είναι γνωστό ότι ο αριθμός των πόντων στην πρώτη μήτρα είναι> 4. Ακολουθεί ότι το ρολό της δεύτερης μήτρας μπορεί να οδηγήσει σε ένα από τα 12 αποτελέσματα που συνθέτουν το γεγονός ΕΝΑ:

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6) .

Στην εκδήλωση αυτή ντομόνο δύο από αυτά μπορούν να ταιριάξουν (5,3) (6,2). Σε αυτή την περίπτωση, η πιθανότητα του γεγονότος ντο θα είναι ίση
... Έτσι, πληροφορίες σχετικά με την εμφάνιση ενός συμβάντος ΕΝΑεπηρέασε την πιθανότητα ενός γεγονότος ντο.

Πιθανότητα εμφάνισης γεγονότων

Θεώρημα πολλαπλασιασμού

Πιθανότητα εμφάνισης γεγονότωνΕΝΑ 1 ΕΝΑ 2  ΕΝΑ ν ορίζεται από τον τύπο

Π(ΕΝΑ 1 ΕΝΑ 2  ΕΝΑ ν)= σελ(ΕΝΑ 1)Π(ΕΝΑ 2  ΕΝΑ 1)) Π(ΕΝΑ ν  ΕΝΑ 1 ΕΝΑ 2  ΕΝΑ n- 1). (1.8)

Για την παραγωγή δύο εκδηλώσεων, από αυτό προκύπτει ότι

Π(ΑΒ)= σελ(ΕΝΑ Β) σελ{σι)= σελ(σι ΕΝΑ)Π{ΕΝΑ). (1.9)

Παράδειγμα 1.18. Μια παρτίδα 25 αντικειμένων περιέχει 5 ελαττωματικά αντικείμενα. Επιλέξτε διαδοχικά 3 προϊόντα τυχαία. Καθορίστε την πιθανότητα όλα τα επιλεγμένα στοιχεία να είναι ελαττωματικά.

Λύση. Ας ορίσουμε εκδηλώσεις:

ΕΝΑ 1 = (το πρώτο προϊόν είναι ελαττωματικό),

ΕΝΑ 2 = (το δεύτερο προϊόν είναι ελαττωματικό),

ΕΝΑ 3 = (το τρίτο προϊόν είναι ελαττωματικό),

ΕΝΑ = (όλα τα προϊόντα είναι ελαττωματικά).

Εκδήλωση ΕΝΑ υπάρχει προϊόν τριών εκδηλώσεων ΕΝΑ = ΕΝΑ 1 ΕΝΑ 2 ΕΝΑ 3 .

Από το θεώρημα πολλαπλασιασμού (1.6) παίρνω

Π(ΕΝΑ)= p ( ΕΝΑ 1 ΕΝΑ 2 ΕΝΑ 3 ) = Π(ΕΝΑ 1) Π(ΕΝΑ 2  ΕΝΑ 1))Π(ΕΝΑ 3  ΕΝΑ 1 ΕΝΑ 2).

Ο κλασικός ορισμός της πιθανότητας επιτρέπει σε κάποιον να βρει Π(ΕΝΑ 1) είναι ο λόγος του αριθμού των ελαττωματικών προϊόντων προς το συνολικό αριθμό των προϊόντων:

Π(ΕΝΑ 1)= ;

Π(ΕΝΑ 2) – αυτό είναι ο λόγος του αριθμού των ελαττωματικών προϊόντων που απομένουν μετά την απόσυρση ενός προς το συνολικό αριθμό των υπολειπόμενων προϊόντων:

Π(ΕΝΑ 2  ΕΝΑ 1))= ;

Π(ΕΝΑ 3) είναι ο λόγος του αριθμού των ελαττωματικών προϊόντων που απομένουν μετά την κατάσχεση δύο ελαττωματικών προϊόντων προς το συνολικό αριθμό των υπολειπόμενων προϊόντων:

Π(ΕΝΑ 3  ΕΝΑ 1 ΕΝΑ 2)=.

Στη συνέχεια, η πιθανότητα του γεγονότος ΕΝΑ θα είναι ίση

Π(ΕΝΑ) ==
.

Πολλοί, όταν έρχονται αντιμέτωποι με την έννοια της «θεωρίας πιθανοτήτων», φοβούνται, νομίζοντας ότι αυτό είναι κάτι το συντριπτικό, πολύ δύσκολο. Αλλά στην πραγματικότητα όλα δεν είναι τόσο τραγικά. Σήμερα θα εξετάσουμε τη βασική έννοια και θα μάθουμε πώς να λύνουμε προβλήματα χρησιμοποιώντας συγκεκριμένα παραδείγματα.

Η επιστήμη

Τι μελετά ένας κλάδος των μαθηματικών όπως η «θεωρία πιθανοτήτων»; Σημειώνει μοτίβα και ποσότητες. Για πρώτη φορά, οι επιστήμονες ενδιαφέρθηκαν για αυτό το ζήτημα τον δέκατο όγδοο αιώνα, όταν σπούδασαν τον τζόγο. Η βασική έννοια της θεωρίας της πιθανότητας είναι ένα γεγονός. Αυτό είναι κάθε γεγονός που διαπιστώνεται με εμπειρία ή παρατήρηση. Τι είναι όμως η εμπειρία; Μια άλλη βασική έννοια της θεωρίας των πιθανοτήτων. Αυτό σημαίνει ότι αυτό το σύνολο συνθηκών δεν δημιουργήθηκε τυχαία, αλλά για συγκεκριμένο σκοπό. Όσο για την παρατήρηση, εδώ ο ίδιος ο ερευνητής δεν συμμετέχει στο πείραμα, αλλά είναι απλώς μάρτυρας αυτών των γεγονότων, δεν επηρεάζει σε καμία περίπτωση αυτό που συμβαίνει.

Εξελίξεις

Μάθαμε ότι η βασική έννοια της θεωρίας πιθανοτήτων είναι ένα γεγονός, αλλά δεν εξετάσαμε την ταξινόμηση. Όλες εμπίπτουν στις ακόλουθες κατηγορίες:

• Αξιόπιστος.
• Αδύνατο.
• Τυχαίος.

Ανεξάρτητα από το είδος των γεγονότων που παρατηρούνται ή δημιουργούνται κατά τη διάρκεια του πειράματος, όλα υπόκεινται σε αυτήν την ταξινόμηση. Σας προσκαλούμε να εξοικειωθείτε με καθένα από τα είδη ξεχωριστά.

Αξιόπιστο γεγονός

Πρόκειται για μια τέτοια περίσταση, μπροστά στην οποία έχει ληφθεί το απαραίτητο σύμπλεγμα μέτρων. Για να κατανοήσουμε καλύτερα την ουσία, είναι καλύτερα να δώσουμε μερικά παραδείγματα. Η φυσική, η χημεία, τα οικονομικά και τα ανώτερα μαθηματικά υπόκεινται σε αυτόν τον νόμο. Η θεωρία πιθανοτήτων περιλαμβάνει μια τόσο σημαντική έννοια όπως ένα αξιόπιστο γεγονός. Ορίστε μερικά παραδείγματα:

• Δουλεύουμε και λαμβάνουμε αμοιβές με τη μορφή μισθών.
• Περάσαμε καλά τις εξετάσεις, περάσαμε τον διαγωνισμό, για τον οποίο λαμβάνουμε ανταμοιβή με τη μορφή εισαγωγής σε εκπαιδευτικό ίδρυμα.
• Έχουμε επενδύσει χρήματα στην τράπεζα, αν χρειαστεί, θα τα πάρουμε πίσω.

Τέτοια γεγονότα είναι αξιόπιστα. Εάν έχουμε εκπληρώσει όλες τις απαραίτητες προϋποθέσεις, τότε σίγουρα θα έχουμε το αναμενόμενο αποτέλεσμα.

Αδύνατα γεγονότα

Τώρα εξετάζουμε τα στοιχεία της θεωρίας της πιθανότητας. Προτείνουμε να προχωρήσουμε σε μια εξήγηση του επόμενου τύπου γεγονότος, δηλαδή του αδύνατου. Αρχικά, ας ορίσουμε τον πιο σημαντικό κανόνα - η πιθανότητα ενός αδύνατου γεγονότος είναι μηδενική.

Δεν μπορεί κανείς να παρεκκλίνει από αυτήν τη διατύπωση κατά την επίλυση προβλημάτων. Για διευκρινίσεις, εδώ είναι παραδείγματα τέτοιων γεγονότων:

• Το νερό πάγωσε σε θερμοκρασία συν δέκα (αυτό είναι αδύνατο).
• Η έλλειψη ηλεκτρικής ενέργειας δεν επηρεάζει την παραγωγή με κανέναν τρόπο (εξίσου αδύνατο όπως στο προηγούμενο παράδειγμα).

Δεν αξίζει να δώσουμε περισσότερα παραδείγματα, αφού αυτά που περιγράφονται παραπάνω αντικατοπτρίζουν πολύ καθαρά την ουσία αυτής της κατηγορίας. Ένα αδύνατο γεγονός δεν θα συμβεί ποτέ κατά τη διάρκεια μιας εμπειρίας υπό οποιεσδήποτε συνθήκες.

Τυχαία γεγονότα

Μελετώντας τα στοιχεία της θεωρίας της πιθανότητας, πρέπει να δοθεί ιδιαίτερη προσοχή σε αυτό το συγκεκριμένο είδος γεγονότων. Είναι αυτοί που μελετά αυτή η επιστήμη. Ως αποτέλεσμα της εμπειρίας, κάτι μπορεί να συμβεί ή όχι. Επιπλέον, η δοκιμή μπορεί να πραγματοποιηθεί απεριόριστα πολλές φορές. Εντυπωσιακά παραδείγματα είναι:

• Η ρίψη ενός νομίσματος είναι μια εμπειρία ή μια δοκιμή · η πτώση ενός κεφαλιού είναι ένα γεγονός.
• Το να βγάζετε τυφλά μια μπάλα από την τσάντα είναι μια δοκιμή, μια κόκκινη μπάλα πιάνεται - αυτό είναι ένα γεγονός και ούτω καθεξής.

Μπορεί να υπάρχουν απεριόριστοι αριθμοί τέτοιων παραδειγμάτων, αλλά, σε γενικές γραμμές, η ουσία πρέπει να είναι σαφής. Για να συνοψίσουμε και να συστηματοποιήσουμε τις γνώσεις που αποκτήθηκαν για τα γεγονότα, δίνεται ένας πίνακας. Η θεωρία πιθανοτήτων μελετά μόνο το τελευταίο είδος από όλα τα παρουσιαζόμενα.

τίτλος	ορισμός
Αξιόπιστος	Εκδηλώσεις που λαμβάνουν χώρα με εγγύηση 100% υπό ορισμένες προϋποθέσεις.	Είσοδος σε εκπαιδευτικό ίδρυμα με καλή επιτυχία στις εισαγωγικές εξετάσεις.
Αδύνατο	Γεγονότα που δεν θα συμβούν ποτέ σε καμία περίπτωση.	Χιονίζει σε θερμοκρασία αέρα συν τριάντα βαθμούς Κελσίου.
Τυχαίος	Ένα συμβάν που μπορεί να συμβεί ή όχι κατά τη διάρκεια του πειράματος / δοκιμής.	Χτύπημα ή έλλειψη όταν ρίχνετε μπάσκετ στο καλάθι.

Οι νόμοι

Η θεωρία πιθανοτήτων είναι μια επιστήμη που μελετά την πιθανότητα να συμβεί ένα συμβάν. Όπως και άλλοι, έχει κάποιους κανόνες. Υπάρχουν οι ακόλουθοι νόμοι της θεωρίας της πιθανότητας:

• Σύγκλιση ακολουθιών τυχαίων μεταβλητών.
• Ο νόμος των μεγάλων αριθμών.

Κατά τον υπολογισμό της πιθανότητας ενός συγκροτήματος, μπορείτε να χρησιμοποιήσετε ένα σύνολο απλών συμβάντων για να επιτύχετε ένα αποτέλεσμα με ευκολότερο και γρηγορότερο τρόπο. Σημειώστε ότι οι νόμοι της θεωρίας πιθανοτήτων αποδεικνύονται εύκολα χρησιμοποιώντας κάποια θεωρήματα. Σας προτείνουμε να εξοικειωθείτε πρώτα με τον πρώτο νόμο.

Σύγκλιση ακολουθιών τυχαίων μεταβλητών

Σημειώστε ότι υπάρχουν διάφοροι τύποι σύγκλισης:

• Μια ακολουθία τυχαίων μεταβλητών συγκλίνει σε πιθανότητα.
• Σχεδόν αδύνατον.
• Σύγκλιση ρίζας-μέσου-τετραγώνου.
• Σύγκλιση κατανομής.

Έτσι, εν κινήσει, είναι πολύ δύσκολο να κατανοήσουμε την ουσία. Ακολουθούν ορισμοί που θα σας βοηθήσουν να κατανοήσετε αυτό το θέμα. Για αρχή, η πρώτη προβολή. Η ακολουθία λέγεται συγκλίνουν στην πιθανότητα, εάν πληρούται η ακόλουθη συνθήκη: το n τείνει στο άπειρο, ο αριθμός στον οποίο τείνει η ακολουθία είναι μεγαλύτερος από μηδέν και είναι κοντά στο ένα.

Ας περάσουμε στην επόμενη φόρμα, σχεδόν σίγουρα... Η ακολουθία λέγεται ότι συγκλίνει σχεδόν σίγουρασε μια τυχαία μεταβλητή καθώς το n τείνει στο άπειρο και το P τείνει σε μια τιμή κοντά στην ενότητα.

Ο επόμενος τύπος είναι Σύγκλιση RMS... Όταν χρησιμοποιείται SK-σύγκλιση, η μελέτη των διανυσματικών στοχαστικών διαδικασιών μειώνεται στη μελέτη των συντεταγμένων στοχαστικών διαδικασιών τους.

Ο τελευταίος τύπος παραμένει, ας τον αναλύσουμε εν συντομία για να προχωρήσουμε άμεσα στην επίλυση προβλημάτων. Η σύγκλιση στη διανομή έχει ένα ακόμη όνομα - "αδύναμο", παρακάτω θα εξηγήσουμε γιατί. Αδύναμη σύγκλισηΕίναι η σύγκλιση των συναρτήσεων διανομής σε όλα τα σημεία συνέχειας της περιοριστικής συνάρτησης κατανομής.

Σίγουρα θα τηρήσουμε την υπόσχεσή μας: η ασθενής σύγκλιση διαφέρει από όλα τα παραπάνω στο ότι η τυχαία μεταβλητή δεν ορίζεται στο χώρο πιθανότητας. Αυτό είναι δυνατό επειδή η συνθήκη σχηματίζεται αποκλειστικά χρησιμοποιώντας συναρτήσεις διανομής.

Ο νόμος των μεγάλων αριθμών

Θεωρήματα της θεωρίας πιθανοτήτων, όπως:

• Η ανισότητα του Τσεμπίσεφ.
• Θεώρημα του Τσεμπίσεφ.
• Γενικευμένο θεώρημα Chebyshev.
• Θεώρημα Μάρκοφ.

Εάν λάβουμε υπόψη όλα αυτά τα θεωρήματα, τότε αυτή η ερώτηση μπορεί να παραταθεί για αρκετές δεκάδες σελίδες. Το κύριο καθήκον μας είναι να εφαρμόσουμε την θεωρία της πιθανότητας στην πράξη. Σας προτείνουμε να το κάνετε τώρα και να το κάνετε. Αλλά πριν από αυτό, ας εξετάσουμε τα αξιώματα της θεωρίας πιθανοτήτων, θα είναι οι κύριοι βοηθοί στην επίλυση προβλημάτων.

Αξιώματα

Συναντήσαμε ήδη τον πρώτο όταν μιλήσαμε για ένα αδύνατο γεγονός. Ας θυμηθούμε: η πιθανότητα ενός αδύνατου γεγονότος είναι μηδενική. Δώσαμε ένα πολύ ζωντανό και αξέχαστο παράδειγμα: χιόνισε σε θερμοκρασία αέρα τριάντα βαθμών Κελσίου.

Το δεύτερο έχει ως εξής: συμβαίνει ένα αξιόπιστο γεγονός με πιθανότητα ίση με μία. Τώρα θα δείξουμε πώς να το γράψουμε χρησιμοποιώντας μαθηματική γλώσσα: P (B) = 1.

Τρίτον: Ένα τυχαίο γεγονός μπορεί να συμβεί ή όχι, αλλά η πιθανότητα κυμαίνεται πάντα από μηδέν σε ένα. Όσο πιο κοντά είναι η τιμή στο ένα, τόσο μεγαλύτερες είναι οι πιθανότητες. αν η τιμή πλησιάσει το μηδέν, η πιθανότητα είναι πολύ μικρή. Ας το γράψουμε σε μαθηματική γλώσσα: 0<Р(С)<1.

Εξετάστε το τελευταίο, τέταρτο αξίωμα, που ακούγεται ως εξής: η πιθανότητα του αθροίσματος δύο γεγονότων είναι ίση με το άθροισμα των πιθανοτήτων τους. Γράφουμε σε μαθηματική γλώσσα: P (A + B) = P (A) + P (B).

Τα αξιώματα της θεωρίας πιθανοτήτων είναι οι απλούστεροι κανόνες που δεν θα είναι δύσκολο να θυμηθούμε. Ας προσπαθήσουμε να λύσουμε κάποια προβλήματα, στηριζόμενοι στις ήδη αποκτηθείσες γνώσεις.

Λαχείο

Ας ξεκινήσουμε εξετάζοντας το πιο απλό παράδειγμα - μια κλήρωση. Φανταστείτε ότι αγοράσατε ένα λαχείο για καλή τύχη. Ποια είναι η πιθανότητα να κερδίσετε τουλάχιστον είκοσι ρούβλια; Συνολικά, χίλια εισιτήρια συμμετέχουν στην κλήρωση, ένα από τα οποία έχει έπαθλο πεντακόσια ρούβλια, δέκα για εκατό ρούβλια, πενήντα για είκοσι ρούβλια και εκατό για πέντε. Τα προβλήματα πιθανότητας βασίζονται στην εύρεση της ευκαιρίας για τύχη. Τώρα θα αναλύσουμε μαζί τη λύση της παραπάνω εργασίας.

Εάν δηλώσουμε μια νίκη πεντακοσίων ρούβλια με το γράμμα Α, τότε η πιθανότητα να πάρει το Α θα είναι 0,001. Πώς το πήραμε; Απλώς πρέπει να διαιρέσετε τον αριθμό των «τυχερών» εισιτηρίων με το συνολικό αριθμό τους (στην περίπτωση αυτή: 1/1000).

Το Β είναι μια νίκη εκατό ρούβλια, η πιθανότητα θα είναι 0,01. Τώρα ενεργήσαμε με την ίδια αρχή όπως και στην προηγούμενη δράση (10/1000)

С - τα κέρδη είναι ίσα με είκοσι ρούβλια. Βρίσκουμε την πιθανότητα, είναι ίση με 0,05.

Τα υπόλοιπα εισιτήρια δεν μας ενδιαφέρουν, καθώς το ταμείο τους είναι μικρότερο από αυτό που καθορίζεται στην κατάσταση. Ας εφαρμόσουμε το τέταρτο αξίωμα: Η πιθανότητα να κερδίσετε τουλάχιστον είκοσι ρούβλια είναι P (A) + P (B) + P (C). Το γράμμα P υποδηλώνει την πιθανότητα εμφάνισης αυτού του γεγονότος, τα έχουμε ήδη βρει σε προηγούμενες ενέργειες. Απομένει μόνο να προσθέσουμε τα απαραίτητα δεδομένα, στην απάντηση παίρνουμε 0.061. Αυτός ο αριθμός θα είναι η απάντηση στην ερώτηση εργασίας.

Κατάστρωμα καρτών

Τα προβλήματα θεωρίας πιθανοτήτων είναι επίσης πιο πολύπλοκα, για παράδειγμα, ας αναλάβουμε την ακόλουθη εργασία. Εδώ είναι μια τράπουλα με τριάντα έξι κάρτες. Ο στόχος σας είναι να τραβήξετε δύο φύλλα στη σειρά χωρίς να αναμίξετε το σωρό, το πρώτο και το δεύτερο φύλλο πρέπει να είναι άσοι, το κοστούμι δεν έχει σημασία.

Αρχικά, ας βρούμε την πιθανότητα ότι το πρώτο φύλλο θα είναι άσος, γι 'αυτό διαιρούμε το τέσσερα με τριάντα έξι. Το αφήσαμε στην άκρη. Βγάζουμε το δεύτερο φύλλο, θα είναι άσος με πιθανότητα τρία τριάντα πέμπτα. Η πιθανότητα ενός δεύτερου γεγονότος εξαρτάται από το φύλλο που τραβάμε πρώτο, αναρωτιόμαστε αν ήταν άσος ή όχι. Από αυτό προκύπτει ότι το γεγονός Β εξαρτάται από το γεγονός Α.

Το επόμενο βήμα είναι να βρούμε την πιθανότητα ταυτόχρονης εμφάνισης, δηλαδή πολλαπλασιάζουμε τα Α και Β. Το γινόμενό τους βρίσκεται ως εξής: η πιθανότητα ενός γεγονότος πολλαπλασιάζεται με την υπό όρους πιθανότητα ενός άλλου, την οποία υπολογίζουμε, υποθέτοντας ότι το πρώτο συνέβη το γεγονός, δηλαδή τραβήξαμε έναν άσο με το πρώτο φύλλο.

Για να γίνουν όλα σαφή, θα δώσουμε έναν χαρακτηρισμό σε ένα τέτοιο στοιχείο όπως τα γεγονότα. Υπολογίζεται, υποθέτοντας ότι έχει συμβεί το συμβάν Α. Υπολογίζεται ως εξής: P (B / A).

Ας συνεχίσουμε να λύνουμε το πρόβλημά μας: P (A * B) = P (A) * P (B / A) ή P (A * B) = P (B) * P (A / B). Η πιθανότητα είναι (4/36) * ((3/35)/(4/36). Υπολογίστε, στρογγυλοποιώντας το πλησιέστερο εκατοστό. Έχουμε: 0,11 * (0,09/0,11) = 0,11 * 0, 82 = 0,09 Η πιθανότητα ότι θα σχεδιάσουμε δύο άσσους στη σειρά είναι ίσο με εννιακόσια Η τιμή είναι πολύ μικρή, πράγμα που σημαίνει ότι η πιθανότητα εμφάνισης του γεγονότος είναι εξαιρετικά μικρή.

Ξεχασμένος αριθμός

Προτείνουμε να αναλύσουμε μερικές ακόμη επιλογές για εργασίες που μελετά η θεωρία των πιθανοτήτων. Έχετε ήδη δει παραδείγματα επίλυσης ορισμένων από αυτά σε αυτό το άρθρο, ας προσπαθήσουμε να λύσουμε το ακόλουθο πρόβλημα: το αγόρι ξέχασε το τελευταίο ψηφίο του αριθμού τηλεφώνου του φίλου του, αλλά επειδή η κλήση ήταν πολύ σημαντική, άρχισε να καλεί τα πάντα με τη σειρά του. Πρέπει να υπολογίσουμε την πιθανότητα να καλέσει όχι περισσότερες από τρεις φορές. Η λύση στο πρόβλημα είναι η απλούστερη εάν είναι γνωστοί οι κανόνες, οι νόμοι και τα αξιώματα της θεωρίας πιθανοτήτων.

Πριν εξετάσετε τη λύση, προσπαθήστε να τη λύσετε μόνοι σας. Γνωρίζουμε ότι το τελευταίο ψηφίο μπορεί να είναι από μηδέν έως εννέα, δηλαδή υπάρχουν μόνο δέκα τιμές. Η πιθανότητα απόκτησης του απαιτούμενου είναι 1/10.

Στη συνέχεια, πρέπει να εξετάσουμε τις επιλογές για την προέλευση του γεγονότος, ας υποθέσουμε ότι το αγόρι μάντεψε σωστά και πληκτρολόγησε αμέσως το επιθυμητό, ​​η πιθανότητα ενός τέτοιου γεγονότος είναι 1/10. Η δεύτερη επιλογή: η πρώτη κλήση είναι χαμένη και η δεύτερη στο στόχο. Ας υπολογίσουμε την πιθανότητα ενός τέτοιου γεγονότος: πολλαπλασιάστε το 9/10 με 1/9, στο τέλος παίρνουμε επίσης το 1/10. Η τρίτη επιλογή: η πρώτη και η δεύτερη κλήση ήταν σε λάθος διεύθυνση, μόνο από την τρίτη το αγόρι έφτασε όπου ήθελε. Υπολογίζουμε την πιθανότητα ενός τέτοιου γεγονότος: πολλαπλασιάστε το 9/10 με 8/9 και με το 1/8, παίρνουμε το 1/10 ως αποτέλεσμα. Δεν μας ενδιαφέρουν άλλες επιλογές ανάλογα με την κατάσταση του προβλήματος, οπότε μένει να προσθέσουμε τα αποτελέσματα που έχουμε, στο τέλος έχουμε 3/10. Απάντηση: Η πιθανότητα ένα αγόρι να καλέσει όχι περισσότερο από τρεις φορές είναι 0,3.

Κάρτες αριθμών

Υπάρχουν εννέα κάρτες μπροστά σας, καθένα από τα οποία έχει έναν αριθμό από ένα έως εννέα γραμμένους, οι αριθμοί δεν επαναλαμβάνονται. Τα έβαλαν σε ένα κουτί και αναμίχθηκαν καλά. Πρέπει να υπολογίσετε την πιθανότητα

• θα πέσει ένας ζυγός αριθμός.
• διψήφιο.

Πριν προχωρήσουμε στη λύση, ας ορίσουμε ότι m είναι ο αριθμός επιτυχημένων περιπτώσεων και n είναι ο συνολικός αριθμός επιλογών. Ας βρούμε την πιθανότητα ο αριθμός να είναι άρτιος. Δεν θα είναι δύσκολο να υπολογίσουμε ότι υπάρχουν τέσσερις ζυγοί αριθμοί, αυτό θα είναι το m μας, συνολικά υπάρχουν εννέα επιλογές, δηλαδή m = 9. Τότε η πιθανότητα είναι 0,44 ή 4/9.

Εξετάστε τη δεύτερη περίπτωση: ο αριθμός των επιλογών είναι εννέα, αλλά δεν μπορεί να υπάρξουν καθόλου επιτυχημένα αποτελέσματα, δηλαδή το m ισούται με μηδέν. Η πιθανότητα η τραβηγμένη κάρτα να περιέχει διψήφιο αριθμό είναι επίσης μηδενική.