Tangento lygtis turi formą. Funkcijos grafiko liestinės lygtis - Žinių hipermarketas
Taip pat skaitykite
Darbo tipas: 7
Būklė
Tiesė y = 3x + 2 yra funkcijos y = -12x ^ 2 + bx-10 grafiko liestinė. Raskite b, atsižvelgiant į tai, kad lietimo taško abscisė yra mažesnė už nulį.
Rodyti sprendimąSprendimas
Tegu x_0 yra funkcijos y = -12x ^ 2 + bx-10 grafiko taško, per kurį eina šio grafiko liestinė, abscisė.
Išvestinės reikšmė taške x_0 yra lygi liestinės nuolydžiui, tai yra, y "(x_0) = - 24x_0 + b = 3. Kita vertus, liestinės taškas priklauso abiem funkcijos grafikui ir liestinė, tai yra -12x_0 ^ 2 + bx_0-10 = 3x_0 + 2. Gauname lygčių sistemą \ pradžia (atvejai) -24x_0 + b = 3, \\ - 12x_0 ^ 2 + bx_0-10 = 3x_0 + 2. \ pabaiga (atvejai)
Išspręsdami šią sistemą, gauname x_0 ^ 2 = 1, o tai reiškia arba x_0 = -1, arba x_0 = 1. Pagal sąlygą prisilietimo taško abscisė yra mažesnė už nulį, todėl x_0 = -1, tada b = 3 + 24x_0 = -21.
Atsakymas
Darbo tipas: 7
Tema: Geometrinė vedinio reikšmė. Funkcijos grafiko liestinė
Būklė
Tiesė y = -3x + 4 yra lygiagreti funkcijos y = -x ^ 2 + 5x-7 grafiko liestinei. Raskite lietimo taško abscisę.
Rodyti sprendimąSprendimas
Funkcijos y = -x ^ 2 + 5x-7 grafiko tiesės nuolydis savavališkame taške x_0 yra lygus y "(x_0). Bet y" = - 2x + 5, taigi y "(x_0) ) = - 2x_0 + 5. Kampinis sąlygoje nurodytos tiesės y = -3x + 4 koeficientas lygus -3. Lygiagrečių linijų nuolydis yra toks pat.Todėl reikšmę x_0 randame tokią, kad = -2x_0 + 5 = -3.
Gauname: x_0 = 4.
Atsakymas
Šaltinis: „Matematika. Pasiruošimas egzaminui-2017 m. Profilio lygis“. Red. FF Lysenko, S. Yu. Kulabukhova.
Darbo tipas: 7
Tema: Geometrinė vedinio reikšmė. Funkcijos grafiko liestinė
Būklė
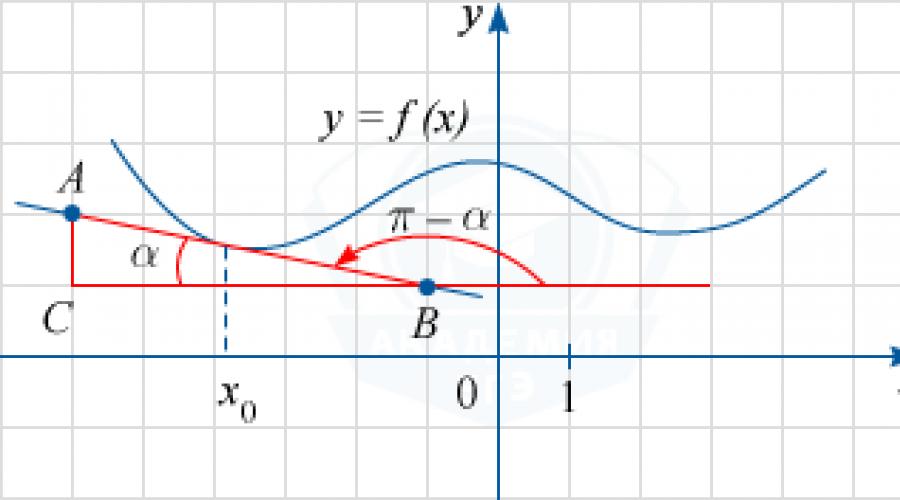
Rodyti sprendimąSprendimas
Iš paveikslo nustatome, kad liestinė eina per taškus A (-6; 2) ir B (-1; 1). C (-6; 1) pažymime tiesių x = -6 ir y = 1 susikirtimo tašką, o \ alfa – kampą ABC (paveiksle matote, kad jis smailus). Tada tiesė AB sudaro bukąjį kampą \ pi - \ alfa su teigiama Ox ašies kryptimi.

Kaip žinote, tg (\ pi - \ alfa) bus funkcijos f (x) išvestinės reikšmė taške x_0. pastebėti, kad tg \ alfa = \ frac (AC) (CB) = \ frac (2-1) (- 1 - (- 6)) = \ frac15. Iš čia, naudodami redukcijos formules, gauname: tg (\ pi - \ alfa) = -tg \ alfa = - \ frac15 = -0,2.
Atsakymas
Šaltinis: „Matematika. Pasiruošimas egzaminui-2017 m. Profilio lygis“. Red. FF Lysenko, S. Yu. Kulabukhova.
Darbo tipas: 7
Tema: Geometrinė vedinio reikšmė. Funkcijos grafiko liestinė
Būklė
Tiesė y = -2x-4 yra funkcijos y = 16x ^ 2 + bx + 12 grafiko liestinė. Raskite b, atsižvelgiant į tai, kad prisilietimo taško abscisė yra didesnė už nulį.
Rodyti sprendimąSprendimas
Tegu x_0 yra funkcijos y = 16x ^ 2 + bx + 12 grafiko taško abscisė, per kurią
yra šio grafiko liestinė.
Išvestinės reikšmė taške x_0 yra lygi liestinės nuolydžiui, tai yra, y "(x_0) = 32x_0 + b = -2. Kita vertus, liestinės taškas priklauso abiem funkcijos grafikui ir liestinė, tai yra 16x_0 ^ 2 + bx_0 + 12 = - 2x_0-4. Gauname lygčių sistemą \ pradėti (atvejai) 32x_0 + b = -2, \\ 16x_0 ^ 2 + bx_0 + 12 = -2x_0-4. \ pabaiga (atvejai)
Išspręsdami sistemą, gauname x_0 ^ 2 = 1, o tai reiškia arba x_0 = -1, arba x_0 = 1. Pagal sąlygą prisilietimo taško abscisė yra didesnė už nulį, todėl x_0 = 1, tada b = -2-32x_0 = -34.
Atsakymas
Šaltinis: „Matematika. Pasiruošimas egzaminui-2017 m. Profilio lygis“. Red. FF Lysenko, S. Yu. Kulabukhova.
Darbo tipas: 7
Tema: Geometrinė vedinio reikšmė. Funkcijos grafiko liestinė
Būklė
Paveikslėlyje parodytas funkcijos y = f (x), apibrėžtos intervale (-2; 8), grafikas. Nustatykite taškų, kuriuose funkcijos grafiko liestinė yra lygiagreti tiesei y = 6, skaičių.

Sprendimas
Tiesė y = 6 yra lygiagreti Ox ašiai. Todėl randame taškus, kuriuose funkcijos grafiko liestinė yra lygiagreti Ox ašiai. Šioje diagramoje tokie taškai yra kraštutiniai taškai (maksimalaus arba minimumo taškai). Kaip matote, yra 4 ekstremalūs taškai.
Atsakymas
Šaltinis: „Matematika. Pasiruošimas egzaminui-2017 m. Profilio lygis“. Red. FF Lysenko, S. Yu. Kulabukhova.
Darbo tipas: 7
Tema: Geometrinė vedinio reikšmė. Funkcijos grafiko liestinė
Būklė
Tiesė y = 4x-6 yra lygiagreti funkcijos y = x ^ 2-4x + 9 grafiko liestinei. Raskite lietimo taško abscisę.
Rodyti sprendimąSprendimas
Funkcijos y = x ^ 2-4x + 9 grafiko liestinės nuolydis savavališkame taške x_0 yra lygus y "(x_0). Bet y" = 2x-4, taigi y "(x_0) = 2x_0 -4.Sąlygoje nurodytos liestinės y = 4x-7 nuolydis lygus 4. Lygiagrečios tiesės turi tokį patį nuolydį.Todėl reikšmę x_0 randame tokią, kad 2x_0-4 = 4. Gauname: x_0 = 4 .
Atsakymas
Šaltinis: „Matematika. Pasiruošimas egzaminui-2017 m. Profilio lygis“. Red. FF Lysenko, S. Yu. Kulabukhova.
Darbo tipas: 7
Tema: Geometrinė vedinio reikšmė. Funkcijos grafiko liestinė
Būklė
Paveiksle pavaizduotas funkcijos y = f (x) grafikas ir jos liestinė taške su abscise x_0. Raskite funkcijos f (x) išvestinės reikšmę taške x_0.

Sprendimas
Iš paveikslo nustatome, kad liestinė eina per taškus A (1; 1) ir B (5; 4). C (5; 1) pažymime tiesių x = 5 ir y = 1 susikirtimo tašką, o \ alfa – kampą BAC (paveiksle matote, kad jis smailus). Tada tiesė AB sudaro kampą \ alfa su teigiama Ox ašies kryptimi.
Vaizdo pamokoje „Funkcijos grafiko liestinės lygtis“ demonstruojama mokomoji medžiaga temos įsisavinimui. Vaizdo pamokos metu pateikiama teorinė medžiaga, reikalinga suformuoti funkcijos grafiko liestinės konkrečiame taške lygties sampratą, tokios liestinės suradimo algoritmas, uždavinių sprendimo pavyzdžiai naudojant studijuojamą. aprašyta teorinė medžiaga.
Vaizdo pamokoje naudojami metodai, kurie pagerina medžiagos aiškumą. Pristatyme įterpiami paveikslėliai, diagramos, pateikiami svarbūs balso komentarai, taikoma animacija, paryškinimas spalvomis ir kitomis priemonėmis.
Video pamoka prasideda pamokos temos pristatymu ir kokios nors funkcijos y = f (x) grafiko liestinės taške M (a; f (a)) vaizdiniu. Yra žinoma, kad grafiko liestinės linijos nuolydis tam tikrame taške yra lygus funkcijos f΄ (a) išvestinei tam tikrame taške. Taip pat iš algebros eigos žinoma tiesės y = kx + m lygtis. Schemiškai pateiktas liestinės taške lygties radimo problemos sprendimas, kuris redukuojamas iki koeficientų k, m suradimo. Žinodami funkcijos grafikui priklausančio taško koordinates, galime rasti m, pakeitę koordinačių reikšmę tangentinėje lygtyje f (a) = ka + m. Iš jo randame m = f (a) -ka. Taigi, žinodami išvestinės reikšmę duotame taške ir taško koordinates, liestinės lygtį galime pavaizduoti taip y = f (a) + f΄ (a) (x-a).
Toliau pateikiamas liestinės lygties sudarymo pagal schemą pavyzdys. Funkcijai duota y = x 2, x = -2. Paėmę a = -2, randame funkcijos reikšmę šiame taške f (a) = f (-2) = (- 2) 2 = 4. Nustatykite funkcijos f΄ (x) = 2x išvestinę. Šiuo metu išvestinė yra f΄ (a) = f΄ (-2) = 2 · (-2) = -4. Norėdami sudaryti lygtį, visi koeficientai randami a = -2, f (a) = 4, f΄ (a) = - 4, todėl liestinės lygtis y = 4 + (- 4) (x + 2). Supaprastinus lygtį, gauname y = -4-4x.
Toliau pateiktame pavyzdyje siūloma įrašyti funkcijos y = tgx grafiko liestinės lygtį. Šiuo metu a = 0, f (0) = 0, f΄ (x) = 1 / cos 2 x, f΄ (0) = 1. Taigi liestinės lygtis atrodo taip, kad y = x.
Apibendrinant, funkcijos grafiko liestinės lygties sudarymo procesas tam tikru momentu formalizuojamas algoritmo, susidedančio iš 4 žingsnių, forma:
- Įvedamas lietimo taško abscisių žymėjimas a;
- F (a) apskaičiuojamas;
- Nustatomas F (x) ir apskaičiuojamas f΄ (a). Rastos reikšmės a, f (a), f΄ (a) pakeičiamos į liestinės lygties formulę y = f (a) + f΄ (a) (x-a).
1 pavyzdyje nagrinėjama funkcijos y = 1 / x grafiko liestinės lygties sudarymas taške x = 1. Norėdami išspręsti problemą, naudojame algoritmą. Tam tikrai funkcijai taške a = 1, funkcijos f (a) reikšmė = - 1. Funkcijos f΄ (x) išvestinė = 1 / x 2. Taške a = 1, išvestinė f΄ (a) = f΄ (1) = 1. Naudojant gautus duomenis, sudaroma liestinės y = -1 + (x-1) arba y = x-2 lygtis.
2 pavyzdyje reikia rasti funkcijos y = x 3 + 3x 2 -2x-2 grafiko liestinės lygtį. Pagrindinė sąlyga yra liestinės ir tiesės y = -2x + 1 lygiagretumas. Pirmiausia randame liestinės nuolydį, lygų tiesės y = -2x + 1 nuolydžiui. Kadangi f΄ (a) = - 2 tam tikrai tiesei, tai k = -2 norimai liestine. Raskite funkcijos (x 3 + 3x 2 -2x-2) ΄ = 3x 2 + 6x-2 išvestinę. Žinodami, kad f΄ (a) = - 2, randame taško 3a 2 + 6a-2 = -2 koordinates. Išspręsdami lygtį, gauname a 1 = 0 ir 2 = -2. Naudodami rastas koordinates, galite rasti liestinės lygtį naudodami gerai žinomą algoritmą. Raskite funkcijos reikšmę taškuose f (a 1) = - 2, f (a 2) = - 18. Išvestinės reikšmė taške f΄ (a 1) = f΄ (a 2) = - 2. Rastas reikšmes pakeisdami į liestinės lygtį, pirmajam taškui gauname a 1 = 0 y = -2x-2, o antrojo taško a 2 = -2 liestinės lygtį y = -2x-22.
3 pavyzdyje aprašomas liestinės linijos lygties sudarymas, kad ji būtų nubrėžta funkcijos y = √x grafiko taške (0; 3). Sprendimas pagamintas pagal gerai žinomą algoritmą. Liestinės taško koordinatės x = a, kur a> 0. Funkcijos reikšmė taške f (a) = √x. Funkcijos f΄ (x) išvestinė = 1 / 2√x, todėl šiame taške f΄ (a) = 1 / 2√a. Pakeitę visas gautas reikšmes į liestinės lygtį, gauname y = √a + (x-a) / 2√a. Transformuodami lygtį, gauname y = x / 2√a + √a / 2. Žinodami, kad liestinė eina per tašką (0; 3), randame a reikšmę. Raskite a nuo 3 = √a / 2. Taigi √a = 6, a = 36. Raskite liestinės tiesės y = x / 12 + 3 lygtį. Paveiksle parodytas nagrinėjamos funkcijos grafikas ir sukonstruota norima liestinės linija.
Mokiniams primenamos apytikslės lygybės Δy = ≈f΄ (x) Δx ir f (x + Δx) -f (x) ≈f΄ (x) Δx. Imant x = a, x + Δx = x, Δx = x-a, gauname f (x) - f (a) ≈f΄ (a) (x-a), taigi f (x) ≈f (a) + f΄ ( a) (xa).
4 pavyzdyje reikia rasti apytikslę išraiškos reikšmę 2.003 6. Kadangi taške x = 2,003 reikia rasti funkcijos f (x) = x 6 reikšmę, galime naudoti gerai žinomą formulę, imant f (x) = x 6, a = 2, f (a ) = f (2) = 64, f ΄ (x) = 6x 5. Išvestinė taške f΄ (2) = 192. Todėl 2,003 6 ≈65-192 0,003. Apskaičiavę išraišką, gauname 2,003 6 ≈64,576.
Vaizdo pamoką „Funkcijos grafiko liestinės lygtis“ rekomenduojama naudoti tradicinėje matematikos pamokoje mokykloje. E-mokymosi mokytojui vaizdo įrašas padės aiškiau paaiškinti temą. Vaizdo įrašą studentai gali rekomenduoti savarankiškai peržiūrėti, jei reikia, kad jie galėtų giliau suprasti dalyką.
TEKSTO KODAS:
Žinome, kad jei taškas M (a; f (a)) (em su koordinatėmis a ir ff iš a) priklauso funkcijos y = f (x) grafikui ir jei šiame taške galima nubrėžti liestinę funkcijos grafikas, kuris nėra statmenas abscisių ašiai, tada liestinės nuolydis yra lygus f "(a) (eff pirminis iš a).
Tarkime, kad duota funkcija y = f (x) ir taškas M (a; f (a)), ir taip pat žinoma, kad egzistuoja f´ (a). Sudarykime tam tikros funkcijos grafiko liestinės lygtį duotame taške. Ši lygtis, kaip ir bet kurios tiesės, kuri nėra lygiagreti ordinačių ašiai, lygtis yra y = kx + m (žaidimas lygus ka x plius em), todėl užduotis yra rasti koeficientų reikšmes. k ir m. (Ka ir em)
Nuolydis k = f "(a). Norėdami apskaičiuoti m reikšmę, mes naudojame tai, kad norima tiesė eina per tašką M (a; f (a)). Tai reiškia, kad jei pakeisime taško koordinates M į tiesės lygtį gauname teisingą lygybę : f (a) = ka + m, iš kur randame, kad m = f (a) - ka.
Belieka rastąsias koeficientų k ir m vertes pakeisti tiesės lygtimi:
y = kx + (f (a) -ka);
y = f (a) + k (x-a);
y= f(a)+ f"(a) (x- a). ( reikšmė yra lygi eff nuo plius eff brūkšnio iš a, padauginta iš x atėmus a).

Gavome funkcijos y = f (x) grafiko liestinės lygtį taške x = a.
Jei, tarkime, y = x 2 ir x = -2 (t. y. a = -2), tai f (a) = f (-2) = (-2) 2 = 4; f´ (x) = 2x, o tai reiškia f "(a) = f´ (-2) = 2 · (-2) = -4. ef eiga iš a yra lygi minus keturi)
Rastas reikšmes a = -2, f (a) = 4, f "(a) = -4 pakeisdami į lygtį, gauname: y = 4 + (- 4) (x + 2), ty y = -4x -4.
(y lygus minus keturi x minus keturi)
Sudarykime funkcijos y = tgx (y lygi x liestinės) grafiko liestinės lygtį ištakoje. Turime: a = 0, f (0) = tg0 = 0;
f "(x) =, taigi f" (0) = l. Rastas reikšmes a = 0, f (a) = 0, f´ (a) = 1 pakeitę į lygtį, gauname: y = x.
Apibendrinkime veiksmus, kaip rasti funkcijos grafiko liestinės lygtį taške x, naudodami algoritmą.
GRAFIKOS FUNKCIJOS LIETTINĖS LYGTYBĖS SUDARYMO ALGORITMAS у = f (x):
1) Lietimo taško abscisę pažymėkite raide a.
2) Apskaičiuokite f (a).
3) Raskite f´ (x) ir apskaičiuokite f´ (a).
4) Rastus skaičius a, f (a), f´ (a) pakeiskite į formulę y= f(a)+ f"(a) (x- a).
1 pavyzdys. Nubraižykite funkcijos y = - grafiko liestinės lygtį
taškas x = 1.
Sprendimas. Šiame pavyzdyje mes naudosime algoritmą, atsižvelgdami į tai
2) f (a) = f (1) = - = -1
3) f' (x) =; f´ (a) = f´ (1) = = 1.
4) Formulėje pakeiskite rastus tris skaičius: a = 1, f (a) = -1, f "(a) = 1. Gauname: y = -1+ (x-1), y = x-2 .
Atsakymas: y = x-2.
2 pavyzdys. Duota funkcija y = x 3 + 3x 2 -2x-2... Parašykite funkcijos y = f (x) grafiko liestinės lygtį, lygiagrečią tiesei y = -2x +1.
Naudodami tangentinės lygties sudarymo algoritmą, atsižvelgiame į tai, kad šiame pavyzdyje f (x) = x 3 + 3x 2 -2x-2, bet liestinės taško abscisė čia nenurodyta.
Pradėkime taip galvoti. Norima liestinė turi būti lygiagreti tiesei y = -2x + 1. O lygiagrečios linijos turi vienodus nuolydžius. Tai reiškia, kad liestinės nuolydis lygus duotosios tiesės nuolydžiui: k cas. = -2. Hok cas. = f "(a). Taigi a reikšmę galime rasti iš lygties f ´ (a) = -2.
Raskite funkcijos išvestinę y =f(x):
f"(x) = (x 3 + 3x 2 -2x-2) ´ = 3x 2 + 6x-2;f"(a) = 3a 2 + 6a-2.
Iš lygties f "(a) = -2, t.y. 3a 2 + 6a-2= -2 randame a 1 = 0, a 2 = -2. Vadinasi, yra dvi liestinės, kurios tenkina uždavinio sąlygą: viena taške, kurio abscisė yra 0, kita taške, kurio abscisė yra -2.
Dabar galite sekti algoritmą.
1) a 1 = 0 ir 2 = -2.
2) f (a 1) = 0 3 + 3 0 2 -2 ∙ 0-2 = -2; f (a 2) = (-2) 3 + 3 (-2) 2 -2 (-2) -2 = 6;
3) f "(a 1) = f" (a 2) = -2.
4) Formulėje pakeitę reikšmes a 1 = 0, f (a 1) = -2, f "(a 1) = -2, gauname:
y = -2-2 (x-0), y = -2x-2.

Formulėje pakeitę reikšmes a 2 = -2, f (a 2) = 6, f "(a 2) = -2, gauname:
y = 6-2 (x + 2), y = -2x + 2.
Atsakymas: y = -2x-2, y = -2x + 2.
3 pavyzdys. Iš taško (0; 3) nubrėžkite funkcijos y = grafiko liestinę. Sprendimas. Naudokime tangentinės lygties sudarymo algoritmą, atsižvelgdami į tai, kad šiame pavyzdyje f (x) =. Atkreipkite dėmesį, kad čia, kaip ir 2 pavyzdyje, liestinės taško abscisė nėra aiškiai nurodyta. Nepaisant to, mes veikiame pagal algoritmą.
1) Tegul x = a yra lietimo taško abscisė; aišku, kad a> 0.
3) f´ (x) = () ´ =; f' (a) =.
4) reikšmių a, f (a) =, f "(a) = pakeitimas į formulę
y = f (a) + f "(a) (x-a), mes gauname:
Darant prielaidą, liestinė eina per tašką (0; 3). Pakeitę reikšmes x = 0, y = 3 į lygtį, gauname: 3 =, o toliau = 6, a = 36.
Kaip matote, šiame pavyzdyje tik ketvirtame algoritmo žingsnyje pavyko rasti liesties taško abscisę. Pakeitę reikšmę a = 36 į lygtį, gauname: y = + 3
Fig. 1 parodyta nagrinėjamo pavyzdžio geometrinė iliustracija: nubraižytas funkcijos y = grafikas, nubrėžta tiesė y = +3.
Atsakymas: y = +3.
Žinome, kad funkcijai y = f (x), kuri turi išvestinę taške x, galioja apytikslė lygybė: Δyf´ (x) Δx (delta y yra apytiksliai lygi x pirminiam eff, padaugintam iš delta x)
arba, tiksliau, f (x + Δx) -f (x) f´ (x) Δx (eff iš x plius delta x atėmus eff iš x yra maždaug lygus eff nuo x iki delta x).
Tolesnio samprotavimo patogumui keičiame žymėjimą:
vietoj x rašysime a,
vietoj x + Δx rašome x
vietoj Δx rašysime x-a.
Tada aukščiau parašyta apytikslė lygybė bus tokia:
f (x) -f (a) f' (a) (x-a)
f (x) f (a) + f´ (a) (x-a). (ff iš x yra apytiksliai lygus ff iš plius ef pirminis iš a, padaugintas iš skirtumo tarp x ir a).

4 pavyzdys. Raskite apytikslę skaitinės išraiškos reikšmę 2,003 6.
Sprendimas. Kalbame apie funkcijos y = x 6 reikšmės radimą taške x = 2,003. Naudokime formulę f (x) f (a) + f´ (a) (xa), atsižvelgdami į tai, kad šiame pavyzdyje f (x) = x 6, a = 2, f (a) = f (2) = 2 6 = 64; x = 2,003, f "(x) = 6x 5 ir todėl f" (a) = f "(2) = 6 · 2 5 = 192.
Dėl to gauname:
2,003 6 64 + 192 0,003, t.y. 2,003 6 = 64,576.
Jei naudosime skaičiuotuvą, gausime:
2,003 6 = 64,5781643...
Kaip matote, aproksimacijos tikslumas yra gana priimtinas.
Apsvarstykite šį paveikslą:
Jame pavaizduota funkcija y = f (x), kuri yra diferencijuojama taške a. Pažymėtas taškas M koordinatėmis (a; f (a)). Per savavališką grafiko tašką P (a + ∆x; f (a + ∆x)) nubrėžiamas sekantinis MR.
Jeigu dabar taškas P pagal grafiką perkeliamas į tašką M, tai tiesė MR suksis aplink tašką M. Šiuo atveju ∆x bus linkęs į nulį. Taigi galime suformuluoti funkcijos grafiko liestinės apibrėžimą.
Funkcijos grafiko liestinė
Funkcijos grafiko liestinė yra sekanto ribinė padėtis, kai argumento prieaugis linkęs į nulį. Reikėtų suprasti, kad funkcijos f išvestinės egzistavimas taške x0 reiškia, kad šiame grafiko taške egzistuoja liestinė jam.
Šiuo atveju liestinės nuolydis bus lygus šios funkcijos išvestinei šiame taške f '(x0). Tai geometrinė išvestinės reikšmė. Funkcijos f, kuri skiriasi taške x0, grafiko liestinė yra tiesė, einanti per tašką (x0; f (x0)) ir kurios nuolydis f '(x0).
Tangento lygtis
Pabandykime gauti kokios nors funkcijos f grafiko liestinės lygtį taške A (x0; f (x0)). Tiesios linijos su nuolydžiu k lygtis yra tokia:
Kadangi mūsų nuolydis lygus išvestinei f '(x0), tada lygtis įgauna tokią formą: y = f '(x0)*x + b.
Dabar apskaičiuokime b reikšmę. Norėdami tai padaryti, naudojame faktą, kad funkcija eina per tašką A.
f (x0) = f ’(x0) * x0 + b, iš čia išreiškiame b ir gauname b = f (x0) - f’ (x0) * x0.
Pakeiskite gautą reikšmę į liestinės lygtį:
y = f '(x0) * x + b = f' (x0) * x + f (x0) - f '(x0) * x0 = f (x0) + f' (x0) * (x - x0).
y = f (x0) + f ’(x0) * (x - x0).
Apsvarstykite tokį pavyzdį: raskite funkcijos f (x) = x 3 - 2 * x 2 + 1 grafiko liestinės lygtį taške x = 2.
2.f (x0) = f (2) = 2 2 - 2 * 2 2 + 1 = 1.
3.f '(x) = 3 * x 2 - 4 * x.
4.f '(x0) = f' (2) = 3 * 2 2 - 4 * 2 = 4.
5. Pakeiskite gautas reikšmes liestinės formulėje, gausime: y = 1 + 4 * (x - 2). Išplėsdami skliaustus ir suteikdami panašius terminus, gauname: y = 4 * x - 7.
Atsakymas: y = 4 * x - 7.
Bendroji liestinės lygties sudarymo schemaį funkcijos y = f (x) grafiką:
1. Nustatykite x0.
2. Apskaičiuokite f (x0).
3. Apskaičiuokite f '(x)
Tangentas Ar tiesi linija, einanti per kreivės tašką ir sutampanti su juo šiame taške iki pirmos eilės (1 pav.).
Kitas apibrėžimas: tai sekanto ribinė padėtis ties Δ x→0.
Paaiškinimas: Paimkite tiesią liniją, kuri kerta kreivę dviejuose taškuose: A ir b(žr. pav.). Tai sekantas. Suksime jį pagal laikrodžio rodyklę, kol jis ras tik vieną bendrą tašką su kreive. Tai suteiks mums liestinės liniją.
Griežtas liestinės apibrėžimas:
Funkcijos grafiko liestinė f taške skiriasi xO, yra tiesi linija, einanti per tašką ( xO; f(xO)) ir turintis nuolydį f′( xO).
Šlaitas turi tiesią formos liniją y =kx +b... Koeficientas k ir yra nuolydisši tiesi linija.
Nuolydis yra lygus smailaus kampo, kurį sudaro ši tiesi linija su abscisių ašimi, liestei:
|
Čia kampas α yra kampas tarp tiesės y =kx +b ir teigiama (ty prieš laikrodžio rodyklę) abscisės kryptį. Tai vadinama tiesios linijos pasvirimo kampas(1 ir 2 pav.).  Jei pasvirimo kampas tiesus y =kx +būminis, tada nuolydis yra teigiamas skaičius. Grafikas didėja (1 pav.).
Jei pasvirimo kampas tiesus y =kx +būminis, tada nuolydis yra teigiamas skaičius. Grafikas didėja (1 pav.).
Jei pasvirimo kampas tiesus y =kx +b bukas, tada nuolydis yra neigiamas. Grafikas mažėja (2 pav.).
Jei tiesė lygiagreti abscisių ašiai, tai tiesės pasvirimo kampas lygus nuliui. Šiuo atveju tiesės nuolydis taip pat lygus nuliui (nes nulio liestinė lygi nuliui). Tiesios lygties forma bus y = b (3 pav.).
Jei tiesės polinkio kampas yra 90º (π / 2), tai yra, jis yra statmenas abscisių ašiai, tada tiesioji linija nurodoma lygybe x =c, kur c- kažkoks tikrasis skaičius (4 pav.).
Funkcijos grafiko liestinės lygtisy = f(x) taške xO:
Pavyzdys: Raskite funkcijos grafiko liestinės lygtį f(x) = x 3 – 2x 2 + 1 taške su abscise 2.
Sprendimas.
Mes laikomės algoritmo.
1) Lietimo taškas xO yra lygus 2. Apskaičiuokite f(xO):
f(xO) = f(2) = 2 3 – 2 ∙ 2 2 + 1 = 8 – 8 + 1 = 1
2) Rasti f′( x). Norėdami tai padaryti, taikome ankstesniame skyriuje nurodytas diferenciacijos formules. Pagal šias formules, NS 2 = 2NS, a NS 3 = 3NS 2. Priemonės:
f′( x) = 3NS 2 – 2 ∙ 2NS = 3NS 2 – 4NS.
Dabar naudokite gautą vertę f′( x), apskaičiuojame f′( xO):
f′( xO) = f′ (2) = 3 ∙ 2 2 - 4 ∙ 2 = 12 - 8 = 4.
3) Taigi, mes turime visus reikiamus duomenis: xO = 2, f(xO) = 1, f ′( xO) = 4. Pakeiskite šiuos skaičius į liestinės lygtį ir raskite galutinį sprendimą:
y = f(xO) + f′( xO) (x - x о) = 1 + 4 ∙ (x - 2) = 1 + 4x - 8 = -7 + 4x = 4x - 7.
Atsakymas: y = 4x - 7.
1 pavyzdys. Funkcija duota f(x) = 3x 2 + 4x- 5. Parašykite funkcijos grafiko liestinės lygtį f(x) grafiko taške su abscisėmis x 0 = 1.
Sprendimas. Funkcijos išvestinė f(x) egzistuoja bet kuriam x R ... Suraskime:
= (3x 2 + 4x– 5) ′ = 6 x + 4.
Tada f(x 0) = f(1) = 2; (x 0) = = 10. Tangentinė lygtis yra tokia:
y = (x 0) (x – x 0) + f(x 0),
y = 10(x – 1) + 2,
y = 10x – 8.
Atsakymas. y = 10x – 8.
2 pavyzdys. Funkcija duota f(x) = x 3 – 3x 2 + 2x+ 5. Parašykite funkcijos grafiko liestinės lygtį f(x) lygiagrečiai tiesei y = 2x – 11.
Sprendimas. Funkcijos išvestinė f(x) egzistuoja bet kuriam x R ... Suraskime:
= (x 3 – 3x 2 + 2x+ 5) ′ = 3 x 2 – 6x + 2.
Kadangi funkcijos grafiko liestinė f(x) taške su abscise x 0 lygiagrečiai tiesei y = 2x- 11, tada jo nuolydis yra 2, t.y. ( x 0) = 2. Raskime šią abscisę iš sąlygos, kad 3 x– 6x 0 + 2 = 2. Ši lygybė galioja tik x 0 = 0 ir už x 0 = 2. Kadangi abiem atvejais f(x 0) = 5, tada tiesi linija y = 2x + b paliečia funkcijos grafiką taške (0; 5) arba taške (2; 5).
Pirmuoju atveju skaitinė lygybė yra teisinga 5 = 2 × 0 + b, kur b= 5, o antruoju atveju skaitinė lygybė yra teisinga 5 = 2 × 2 + b, kur b = 1.
Taigi yra dvi liestinės y = 2x+ 5 ir y = 2x+ 1 funkcijos grafikui f(x) lygiagrečiai tiesei y = 2x – 11.
Atsakymas. y = 2x + 5, y = 2x + 1.
3 pavyzdys. Funkcija duota f(x) = x 2 – 6x+ 7. Parašykite funkcijos grafiko liestinės lygtį f(x) einantis per tašką A (2; –5).
Sprendimas. Nes f(2) –5, tada taškas A nepriklauso funkcijų grafikui f(x). Leisti būti x 0 – lietimo taško abscisė.
Funkcijos išvestinė f(x) egzistuoja bet kuriam x R ... Suraskime:
= (x 2 – 6x+ 1) ′ = 2 x – 6.
Tada f(x 0) = x– 6x 0 + 7; (x 0) = 2x 0 - 6. Tangento lygtis yra tokia:
y = (2x 0 – 6)(x – x 0) + x– 6x+ 7,
y = (2x 0 – 6)x– x+ 7.
Nuo taško A priklauso liestinės tiesei, tada skaitinei lygybei
–5 = (2x 0–6) × 2– x+ 7,
kur x 0 = 0 arba x 0 = 4. Tai reiškia, kad per tašką A galite nubrėžti dvi funkcijos grafiko liestines f(x).
Jeigu x 0 = 0, tada liestinės lygtis turi formą y = –6x+ 7. Jei x 0 = 4, tada liestinės lygtis turi formą y = 2x – 9.
Atsakymas. y = –6x + 7, y = 2x – 9.
4 pavyzdys. Suteiktos funkcijos f(x) = x 2 – 2x+ 2 ir g(x) = –x 2 - 3. Į šių funkcijų grafikus užrašykime bendrosios liestinės tiesės lygtį.
Sprendimas. Leisti būti x 1 - norimos tiesės liesties taško su funkcijos grafiku abscisė f(x), a x 2 - tos pačios tiesės ir funkcijos grafiku lietimo taško abscisė g(x).
Funkcijos išvestinė f(x) egzistuoja bet kuriam x R ... Suraskime:
= (x 2 – 2x+ 2) ′ = 2 x – 2.
Tada f(x 1) = x– 2x 1 + 2; (x 1) = 2x 1 - 2. Tangento lygtis yra tokia:
y = (2x 1 – 2)(x – x 1) + x– 2x 1 + 2,
y = (2x 1 – 2)x – x+ 2. (1)
Raskite funkcijos išvestinę g(x):
= (–x 2–3) ′ = –2 x.