L'equazione tangente ha la forma. L'equazione della tangente al grafico della funzione - Ipermercato della conoscenza

Tipo di lavoro: 7

Condizione

La retta y=3x+2 è tangente al grafico della funzione y=-12x^2+bx-10. Trova b , dato che l'ascissa del punto di contatto è minore di zero.

Soluzione

Sia x_0 l'ascissa del punto sul grafico della funzione y=-12x^2+bx-10 attraverso la quale passa la tangente a questo grafico.

Il valore della derivata nel punto x_0 è uguale alla pendenza della tangente, cioè y"(x_0)=-24x_0+b=3. D'altra parte, il punto tangente appartiene sia al grafico della funzione che al tangente, cioè -12x_0^2+bx_0-10= 3x_0 + 2. Otteniamo un sistema di equazioni \begin(casi) -24x_0+b=3,\\-12x_0^2+bx_0-10=3x_0+2. \fine(casi)

Risolvendo questo sistema, otteniamo x_0^2=1, che significa x_0=-1 o x_0=1. Secondo la condizione dell'ascissa, i punti di contatto sono minori di zero, quindi x_0=-1, quindi b=3+24x_0=-21.

Risposta

Tipo di lavoro: 7
Argomento: Il significato geometrico della derivata. Tangente al grafico della funzione

Condizione

La retta y=-3x+4 è parallela alla tangente al grafico della funzione y=-x^2+5x-7. Trova l'ascissa del punto di contatto.

Soluzione

La pendenza della retta rispetto al grafico della funzione y=-x^2+5x-7 in un punto arbitrario x_0 è y"(x_0). Ma y"=-2x+5, quindi y"(x_0)=- 2x_0+5 Angolare il coefficiente della retta y=-3x+4 specificato nella condizione è -3.Le rette parallele hanno gli stessi coefficienti di pendenza.Pertanto, troviamo un valore tale x_0 che =-2x_0 +5=-3.

Otteniamo: x_0 = 4.

Risposta

Fonte: "Matematica. Preparazione all'esame-2017. livello di profilo. ed. FF Lysenko, S. Yu Kulabukhova.

Tipo di lavoro: 7
Argomento: Il significato geometrico della derivata. Tangente al grafico della funzione

Condizione

Soluzione

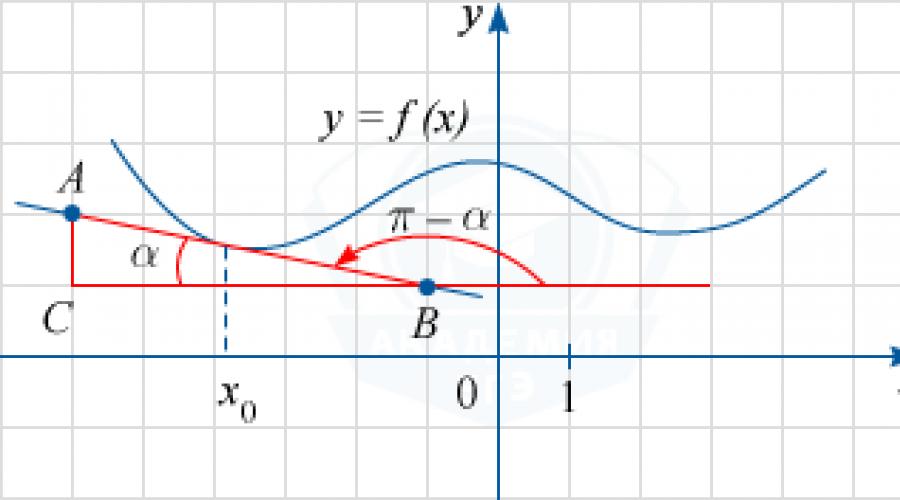
Dalla figura determiniamo che la tangente passa per i punti A(-6; 2) e B(-1; 1). Indichiamo con C(-6; 1) il punto di intersezione delle rette x=-6 e y=1, e con \alpha l'angolo ABC (si vede nella figura che è acuto). Quindi la linea AB forma un angolo ottuso \pi -\alpha con la direzione positiva dell'asse Ox.

Come sapete, tg(\pi -\alpha) sarà il valore della derivata della funzione f(x) nel punto x_0. notare che tg \alpha =\frac(AC)(CB)=\frac(2-1)(-1-(-6))=\frac15. Da qui, con le formule di riduzione, otteniamo: tg(\pi -\alpha) =-tg \alpha =-\frac15=-0.2.

Risposta

Fonte: "Matematica. Preparazione all'esame-2017. livello di profilo. ed. FF Lysenko, S. Yu Kulabukhova.

Tipo di lavoro: 7
Argomento: Il significato geometrico della derivata. Tangente al grafico della funzione

Condizione

La retta y=-2x-4 è tangente al grafico della funzione y=16x^2+bx+12. Trova b , dato che l'ascissa del punto di contatto è maggiore di zero.

Soluzione

Sia x_0 l'ascissa del punto sul grafico della funzione y=16x^2+bx+12 attraverso la quale

è tangente a questo grafico.

Il valore della derivata nel punto x_0 è uguale alla pendenza della tangente, cioè y "(x_0)=32x_0+b=-2. D'altra parte, il punto tangente appartiene sia al grafico della funzione che al tangente, cioè 16x_0^2+bx_0+12=- 2x_0-4 Otteniamo un sistema di equazioni \begin(casi) 32x_0+b=-2,\\16x_0^2+bx_0+12=-2x_0-4. \fine(casi)

Risolvendo il sistema, otteniamo x_0^2=1, che significa x_0=-1 o x_0=1. Secondo la condizione dell'ascissa, i punti di contatto sono maggiori di zero, quindi x_0=1, quindi b=-2-32x_0=-34.

Risposta

Fonte: "Matematica. Preparazione all'esame-2017. livello di profilo. ed. FF Lysenko, S. Yu Kulabukhova.

Tipo di lavoro: 7
Argomento: Il significato geometrico della derivata. Tangente al grafico della funzione

Condizione

La figura mostra un grafico della funzione y=f(x) definita sull'intervallo (-2; 8). Determina il numero di punti in cui la tangente al grafico della funzione è parallela alla retta y=6.

Soluzione

La retta y=6 è parallela all'asse Ox. Pertanto, troviamo tali punti in cui la tangente al grafico della funzione è parallela all'asse Ox. In questo grafico, tali punti sono punti estremi (punti massimi o minimi). Come puoi vedere, ci sono 4 punti estremi.

Risposta

Fonte: "Matematica. Preparazione all'esame-2017. livello di profilo. ed. FF Lysenko, S. Yu Kulabukhova.

Tipo di lavoro: 7
Argomento: Il significato geometrico della derivata. Tangente al grafico della funzione

Condizione

La retta y=4x-6 è parallela alla tangente al grafico della funzione y=x^2-4x+9. Trova l'ascissa del punto di contatto.

Soluzione

La pendenza della tangente al grafico della funzione y \u003d x ^ 2-4x + 9 in un punto arbitrario x_0 è y "(x_0). Ma y" \u003d 2x-4, che significa y "(x_0) \ u003d 2x_0-4. La pendenza della tangente y \u003d 4x-7 specificata nella condizione è uguale a 4. Le linee parallele hanno le stesse pendenze. Pertanto, troviamo un valore tale x_0 che 2x_0-4 \u003d 4. Otteniamo : x_0 \u003d 4.

Risposta

Fonte: "Matematica. Preparazione all'esame-2017. livello di profilo. ed. FF Lysenko, S. Yu Kulabukhova.

Tipo di lavoro: 7
Argomento: Il significato geometrico della derivata. Tangente al grafico della funzione

Condizione

La figura mostra il grafico della funzione y=f(x) e la tangente ad essa nel punto con l'ascissa x_0. Trova il valore della derivata della funzione f(x) nel punto x_0.

Soluzione

Dalla figura determiniamo che la tangente passa per i punti A(1; 1) e B(5; 4). Indichiamo con C(5; 1) il punto di intersezione delle rette x=5 e y=1, e con \alpha l'angolo BAC (si vede nella figura che è acuto). Quindi la linea AB forma un angolo \alfa con la direzione positiva dell'asse Ox.

Il video tutorial "L'equazione della tangente al grafico di una funzione" mostra materiale didattico per padroneggiare l'argomento. Durante la videolezione viene presentato il materiale teorico necessario per la formazione del concetto dell'equazione della tangente al grafico di una funzione in un dato punto, l'algoritmo per trovare tale tangente, esempi di risoluzione dei problemi utilizzando il teorico studiato materiale sono descritti.

Il video tutorial utilizza metodi che migliorano la visibilità del materiale. Disegni, diagrammi vengono inseriti nella vista, vengono forniti importanti commenti vocali, vengono applicati animazioni, evidenziazioni a colori e altri strumenti.

La videolezione inizia con la presentazione dell'argomento della lezione e l'immagine di una tangente al grafico di una qualche funzione y=f(x) nel punto M(a;f(a)). È noto che la pendenza della tangente tracciata al grafico in un dato punto è uguale alla derivata della funzione f΄(a) in un dato punto. Anche dal corso dell'algebra è nota l'equazione della retta y=kx+m. Viene schematicamente presentata la soluzione del problema di trovare l'equazione tangente in un punto, che si riduce a trovare i coefficienti k, m. Conoscendo le coordinate del punto appartenente al grafico della funzione, possiamo trovare m sostituendo il valore delle coordinate nell'equazione della tangente f(a)=ka+m. Da esso troviamo m=f(a)-ka. Quindi, conoscendo il valore della derivata in un dato punto e le coordinate del punto, possiamo rappresentare l'equazione tangente in questo modo y=f(a)+f΄(a)(x-a).

Quello che segue è un esempio di elaborazione di un'equazione tangente, seguendo lo schema. Data una funzione y=x 2 , x=-2. Accettato a=-2, troviamo il valore della funzione a questo punto f(a)= f(-2)=(-2) 2 =4. Determiniamo la derivata della funzione f΄(х)=2х. A questo punto la derivata è uguale a f΄(a)= f΄(-2)=2 (-2)=-4. Per compilare l'equazione, si trovano tutti i coefficienti a=-2, f(a)=4, f΄(a)=-4, quindi l'equazione tangente y=4+(-4)(x+2). Semplificando l'equazione, otteniamo y \u003d -4-4x.

Nell'esempio seguente si propone di formulare l'equazione della tangente all'origine del grafico della funzione y=tgx. A questo punto a=0, f(0)=0, f΄(х)=1/cos 2 x, f΄(0)=1. Quindi l'equazione tangente appare come y=x.

In generale, il processo di compilazione dell'equazione della tangente al grafico della funzione a un certo punto viene formalizzato come un algoritmo composto da 4 passaggi:

• Viene introdotta una designazione per l'ascissa del punto di contatto;
• f(a) è calcolato;
• Si determina F΄(х) e si calcola f΄(a). I valori trovati a, f(a), f΄(a) sono sostituiti nella formula dell'equazione tangente y=f(a)+f΄(a)(x-a).

L'esempio 1 considera la compilazione dell'equazione della tangente al grafico della funzione y \u003d 1 / x nel punto x \u003d 1. Usiamo un algoritmo per risolvere il problema. Per questa funzione nel punto a=1, il valore della funzione f(a)=-1. Derivata della funzione f΄(х)=1/х 2 . Nel punto a=1, la derivata f΄(a)= f΄(1)=1. Utilizzando i dati ottenuti, viene compilata l'equazione della tangente y \u003d -1 + (x-1) o y \u003d x-2.

Nell'esempio 2, devi trovare l'equazione della tangente al grafico della funzione y \u003d x 3 +3x 2 -2x-2. La condizione principale è il parallelismo della tangente e della retta y \u003d -2x + 1. Innanzitutto, troviamo la pendenza della tangente, uguale alla pendenza della retta y \u003d -2x + 1. Poiché f΄(a)=-2 per questa retta, allora k=-2 per la tangente desiderata. Troviamo la derivata della funzione (x 3 + 3x 2 -2x-2) ΄ \u003d 3x 2 + 6x-2. Sapendo che f΄(a)=-2, troviamo le coordinate del punto 3а 2 +6а-2=-2. Risolvendo l'equazione, otteniamo 1 \u003d 0 e 2 \u003d -2. Usando le coordinate trovate, puoi trovare l'equazione tangente usando un noto algoritmo. Troviamo il valore della funzione nei punti f(a 1)=-2, f(a 2)=-18. Il valore della derivata nel punto f΄(а 1)= f΄(а 2)=-2. Sostituendo i valori trovati nell'equazione tangente, otteniamo per il primo punto a 1 \u003d 0 y \u003d -2x-2 e per il secondo punto a 2 \u003d -2 l'equazione tangente y \u003d -2x- 22.

L'esempio 3 descrive la formulazione dell'equazione tangente per il suo disegno nel punto (0;3) del grafico della funzione y=√x. La decisione viene presa secondo l'algoritmo noto. Il punto di contatto ha coordinate x=a, dove a>0. Il valore della funzione nel punto f(a)=√x. La derivata della funzione f΄(х)=1/2√х, quindi, nel punto dato f΄(а)=1/2√а. Sostituendo tutti i valori ottenuti nell'equazione tangente, otteniamo y \u003d √a + (x-a) / 2√a. Trasformando l'equazione, otteniamo y=x/2√a+√a/2. Sapendo che la tangente passa per il punto (0; 3), troviamo il valore di a. Trova a da 3=√a/2. Quindi √a=6, a=36. Troviamo l'equazione della tangente y \u003d x / 12 + 3. La figura mostra il grafico della funzione in esame e la tangente desiderata costruita.

Si ricordano agli studenti le uguaglianze approssimative Δy=≈f΄(x)Δxe f(x+Δx)-f(x)≈f΄(x)Δx. Prendendo x=a, x+Δx=x, Δx=x-a, otteniamo f(x)- f(a)≈f΄(a)(x-a), quindi f(x)≈f(a)+ f΄( a)(x-a).

Nell'esempio 4 è necessario trovare il valore approssimativo dell'espressione 2.003 6 . Poiché è necessario trovare il valore della funzione f (x) \u003d x 6 nel punto x \u003d 2.003, possiamo utilizzare la nota formula, prendendo f (x) \u003d x 6, a \u003d 2 , f (a) \u003d f (2) \u003d 64, f ΄(x)=6х 5 . Derivata al punto f΄(2)=192. Pertanto, 2,003 6 ≈65-192 0,003. Dopo aver calcolato l'espressione, otteniamo 2.003 6 ≈64.576.

La lezione video "L'equazione della tangente al grafico di una funzione" è consigliata per l'uso in una lezione di matematica tradizionale a scuola. Per un insegnante di formazione a distanza, il materiale video aiuterà a spiegare l'argomento in modo più chiaro. Il video può essere consigliato agli studenti per l'autoconsiderazione, se necessario, per approfondire la loro comprensione dell'argomento.

INTERPRETAZIONE DEL TESTO:

Sappiamo che se il punto M (a; f (a)) (em con coordinate a ed eff da a) appartiene al grafico della funzione y \u003d f (x) e se a questo punto si può tracciare una tangente a il grafico della funzione, non perpendicolare all'asse delle ascisse, allora la pendenza della tangente è f "(a) (ef corsa da a).

Sia data una funzione y = f(x) e un punto M (a; f(a)), ed è anche noto che f´(a) esiste. Componiamo l'equazione della tangente al grafico di una data funzione in un dato punto. Questa equazione, come l'equazione di qualsiasi retta non parallela all'asse y, ha la forma y = kx + m (y è uguale a ka x più em), quindi il compito è trovare i valori dei coefficienti k e m. (ka ed em)

Pendenza k \u003d f "(a). Per calcolare il valore di m, utilizziamo il fatto che la retta desiderata passa per il punto M (a; f (a)). Ciò significa che se sostituiamo le coordinate del punto M nell'equazione della retta, otteniamo la corretta uguaglianza : f(a) = ka+m, da cui troviamo che m = f(a) - ka.

Resta da sostituire i valori trovati dei coefficienti ki e m nell'equazione di una retta:

y = kx+(f(a)-ka);

y = f(a)+k(x-a);

y= f(un)+ f"(un) (X- un). ( Y è uguale a eff da un tratto più ef da a moltiplicato per x meno a).

Abbiamo ottenuto l'equazione della tangente al grafico della funzione y = f(x) nel punto x=a.

Se, diciamo, y \u003d x 2 e x \u003d -2 (cioè a \u003d -2), allora f (a) \u003d f (-2) \u003d (-2) 2 \u003d 4; f´(x) \u003d 2x, quindi f "(a) \u003d f´(-2) \u003d 2 (-2) \u003d -4. (quindi eff da a è uguale a quattro, eff primo da x è uguale a due x, che significa ef corsa da a uguale a meno quattro)

Sostituendo nell'equazione i valori trovati a \u003d -2, f (a) \u003d 4, f "(a) \u003d -4, otteniamo: y \u003d 4 + (-4) (x + 2) , ovvero y \u003d -4x -quattro.

(y è uguale a meno quattro x meno quattro)

Componiamo l'equazione della tangente al grafico della funzione y \u003d tgx (y è uguale a tangente x) all'origine. Abbiamo: a = 0, f(0) = tg0=0;

f"(x)= , quindi f"(0) = l. Sostituendo i valori trovati a=0, f(a)=0, f´(a) = 1 nell'equazione, otteniamo: y=x.

Generalizziamo i nostri passaggi per trovare l'equazione della tangente al grafico della funzione nel punto x usando l'algoritmo.

ALGORITMO PER LA COMPOSIZIONE DELL'EQUAZIONE DELLA FUNZIONE tangente al GRAFICO y \u003d f (x):

1) Designare l'ascissa del punto di contatto con la lettera a.

2) Calcola f(a).

3) Trova f´(x) e calcola f´(a).

4) Sostituisci i numeri trovati a, f(a), f´(a) nella formula y= f(un)+ f"(un) (X- un).

Esempio 1. Scrivi l'equazione della tangente al grafico della funzione y \u003d - in

punto x = 1.

Soluzione. Usiamo l'algoritmo, considerando che in questo esempio

2) f(a)=f(1)=-=-1

3) f´(x)=; f´(a)= f´(1)= =1.

4) Sostituisci i tre numeri trovati: a \u003d 1, f (a) \u003d -1, f "(a) \u003d 1 nella formula. Otteniamo: y \u003d -1 + (x-1), y \u003d x-2.

Risposta: y = x-2.

Esempio 2. Data una funzione y = x 3 +3x 2 -2x-2. Scrivi l'equazione della tangente al grafico della funzione y \u003d f (x), parallela alla retta y \u003d -2x +1.

Utilizzando l'algoritmo per compilare l'equazione tangente, teniamo conto che in questo esempio f(x) = x 3 +3x 2 -2x-2, ma qui non è specificata l'ascissa del punto di contatto.

Iniziamo a parlare così. La tangente desiderata deve essere parallela alla retta y \u003d -2x + 1. E le rette parallele hanno pendenze uguali. Quindi la pendenza della tangente è uguale alla pendenza della retta data: k cas. = -2. Hok ca. = f "(a). Pertanto, possiamo trovare il valore di a dall'equazione f ´ (a) \u003d -2.

Troviamo la derivata della funzione y=f(X):

f"(X) \u003d (x 3 + 3x 2 -2x-2)´ \u003d 3x 2 + 6x-2;f"(a) \u003d 3a 2 + 6a-2.

Dall'equazione f "(a) \u003d -2, cioè 3à 2 +6à-2\u003d -2 troviamo un 1 \u003d 0, un 2 \u003d -2. Ciò significa che esistono due tangenti che soddisfano le condizioni del problema: una in un punto con ascissa 0, l'altra in un punto con ascissa -2.

Ora puoi agire secondo l'algoritmo.

1) a 1 \u003d 0 e 2 \u003d -2.

2) f(a 1) = 0 3 +3 0 2 -2∙0-2=-2; f(a2)= (-2) 3 +3 (-2) 2 -2 (-2)-2=6;

3) f "(a 1) = f" (a 2) = -2.

4) Sostituendo i valori a 1 = 0, f (a 1) = -2, f "(a 1) = -2 nella formula, otteniamo:

y=-2-2(x-0), y=-2x-2.

Sostituendo i valori a 2 \u003d -2, f (a 2) \u003d 6, f "(a 2) \u003d -2 nella formula, otteniamo:

y=6-2(x+2), y=-2x+2.

Risposta: y=-2x-2, y=-2x+2.

Esempio 3. Dal punto (0; 3) traccia una tangente al grafico della funzione y \u003d. Soluzione. Usiamo l'algoritmo per compilare l'equazione tangente, dato che in questo esempio f(x) = . Si noti che qui, come nell'Esempio 2, l'ascissa del punto di contatto non è esplicitamente indicata. Tuttavia, agiamo secondo l'algoritmo.

1) Sia x = a l'ascissa del punto di contatto; è chiaro che a > 0.

3) f´(x)=()´=; f´(a) =.

4) Sostituendo i valori a, f(a) = , f "(a) = nella formula

y \u003d f (a) + f "(a) (x-a), noi abbiamo:

Per condizione, la tangente passa per il punto (0; 3). Sostituendo i valori x = 0, y = 3 nell'equazione, otteniamo: 3 = , e quindi =6, a =36.

Come puoi vedere, in questo esempio, solo al quarto passaggio dell'algoritmo siamo riusciti a trovare l'ascissa del punto di contatto. Sostituendo il valore a =36 nell'equazione, otteniamo: y=+3

Sulla fig. La figura 1 presenta un'illustrazione geometrica dell'esempio considerato: viene tracciato un grafico della funzione y \u003d, viene tracciata una linea retta y \u003d +3.

Risposta: y = +3.

Sappiamo che per la funzione y = f(x), che ha una derivata nel punto x, vale l'uguaglianza approssimativa: Δyf´(x)Δx

o, più in dettaglio, f(x+Δx)-f(x) f´(x) Δx (ef da x più delta x meno ef da x è approssimativamente uguale a ef primo da x a delta x).

Per comodità di ulteriore ragionamento, cambiamo la notazione:

invece di x scriveremo un,

invece di x + Δx scriveremo x

invece di Δx scriveremo x-a.

Quindi l'uguaglianza approssimativa scritta sopra assumerà la forma:

f(x)-f(a)f´(a)(x-a)

f(x)f(a)+f´(a)(x-a). (ef da x è approssimativamente uguale a eff da un più ef tratto da a, moltiplicato per la differenza tra x e a).

Esempio 4. Trova il valore approssimativo dell'espressione numerica 2.003 6 .

Soluzione. Stiamo parlando di trovare il valore della funzione y \u003d x 6 nel punto x \u003d 2.003. Usiamo la formula f(x)f(a)+f´(a)(x-a), considerando che in questo esempio f(x)=x 6 , a = 2,f(a) = f(2) = 2 6 = 64; x \u003d 2.003, f "(x) \u003d 6x 5 e, quindi, f" (a) \u003d f "(2) \u003d 6 2 5 \u003d 192.

Di conseguenza, otteniamo:

2.003 6 64+192 0.003, cioè 2.003 6 = 64.576.

Se utilizziamo una calcolatrice, otteniamo:

2,003 6 = 64,5781643...

Come puoi vedere, l'accuratezza dell'approssimazione è abbastanza accettabile.

Considera la figura seguente:

Mostra una funzione y = f(x) derivabile nel punto a. Punto M segnato con le coordinate (a; f(a)). Attraverso un punto arbitrario P(a + ∆x; f(a + ∆x)) del grafico, viene tracciata una secante MP.

Se ora il punto P viene spostato lungo il grafico fino al punto M, la retta MP ruoterà attorno al punto M. In questo caso, ∆x tenderà a zero. Da qui possiamo formulare la definizione di tangente al grafico di una funzione.

Tangente al grafico della funzione

La tangente al grafico della funzione è la posizione limite della secante quando l'incremento dell'argomento tende a zero. Va inteso che l'esistenza della derivata della funzione f nel punto x0 significa che a questo punto del grafico c'è tangente a lui.

In questo caso, la pendenza della tangente sarà uguale alla derivata di questa funzione in questo punto f'(x0). Questo è il significato geometrico della derivata. La tangente al grafico della funzione f derivabile nel punto x0 è una retta passante per il punto (x0;f(x0)) e avente pendenza f'(x0).

Equazione tangente

Proviamo a ottenere l'equazione della tangente al grafico di qualche funzione f nel punto A(x0; f(x0)). L'equazione di una retta con pendenza k ha la forma seguente:

Poiché la nostra pendenza è uguale alla derivata f'(x0), allora l'equazione assumerà la seguente forma: y = f'(x0)*x + b.

Calcoliamo ora il valore di b. Per fare ciò, utilizziamo il fatto che la funzione passa per il punto A.

f(x0) = f'(x0)*x0 + b, da qui esprimiamo b e otteniamo b = f(x0) - f'(x0)*x0.

Sostituiamo il valore risultante nell'equazione tangente:

y = f'(x0)*x + b = f'(x0)*x + f(x0) - f'(x0)*x0 = f(x0) + f'(x0)*(x - x0).

y = f(x0) + f'(x0)*(x - x0).

Considera il seguente esempio: trova l'equazione della tangente al grafico della funzione f (x) \u003d x 3 - 2 * x 2 + 1 nel punto x \u003d 2.

2. f(x0) = f(2) = 2 2 - 2*2 2 + 1 = 1.

3. f'(x) = 3*x 2 - 4*x.

4. f'(x0) = f'(2) = 3*2 2 - 4*2 = 4.

5. Sostituisci i valori ottenuti nella formula tangente, otteniamo: y = 1 + 4*(x - 2). Aprendo le parentesi e portando termini simili, otteniamo: y = 4*x - 7.

Risposta: y = 4*x - 7.

Schema generale per la compilazione dell'equazione tangente al grafico della funzione y = f(x):

1. Determina x0.

2. Calcola f(x0).

3. Calcola f'(x)

Tangenteè una retta passante per un punto della curva e coincidente con esso in questo punto fino al primo ordine (Fig. 1).

Altra definizione: questa è la posizione limite della secante a Δ X→0.

Spiegazione: prendi una linea che interseca la curva in due punti: MA e b(Guarda l'immagine). Questa è una secante. Lo ruoteremo in senso orario finché non avrà un solo punto in comune con la curva. Quindi prendiamo una tangente.

Definizione rigorosa di tangente:

Tangente al grafico della funzione f, differenziabile in un punto Xdi, è una retta passante per il punto ( Xdi; f(Xdi)) e avendo una pendenza f′( Xdi).

La pendenza ha una linea retta y=kx +b. Coefficiente K ed è fattore di pendenza questa linea retta.

Il coefficiente angolare è uguale alla tangente dell'angolo acuto formato da questa retta con l'asse x:

Qui l'angolo α è l'angolo tra la linea y=kx +b e la direzione positiva (cioè antioraria) dell'asse x. È chiamato angolo di inclinazione diritto(Fig.1 e 2).

Se l'angolo di inclinazione è diritto y=kx +b acuto, allora la pendenza è un numero positivo. Il grafico aumenta (Fig. 1).

Se l'angolo di inclinazione è diritto y=kx +b ottuso, allora la pendenza è un numero negativo. Il grafico è in diminuzione (Fig. 2).

Se la linea è parallela all'asse x, la pendenza della linea è zero. In questo caso, anche la pendenza della retta è zero (poiché la tangente di zero è zero). L'equazione della retta apparirà come y = b (Fig. 3).

Se l'angolo di inclinazione di una retta è 90º (π/2), cioè è perpendicolare all'asse x, allora la retta è data dall'uguaglianza x=c, dove c- qualche numero reale (Fig. 4).

L'equazione della tangente al grafico della funzioney = f(X) al punto Xdi:

Esempio : Troviamo l'equazione della tangente al grafico della funzione f(X) = X 3 – 2X 2 + 1 al punto con ascissa 2.

Soluzione.

Seguiamo l'algoritmo.

1) Punto di contatto Xdiè uguale a 2. Calcola f(Xdi):

f(Xdi) = f(2) = 2 3 – 2 ∙ 2 2 + 1 = 8 – 8 + 1 = 1

2) Trova f′( X). Per fare ciò, utilizziamo le formule di differenziazione delineate nella sezione precedente. Secondo queste formule, X 2 = 2X, un X 3 = 3X 2. Significa:

f′( X) = 3X 2 – 2 ∙ 2X = 3X 2 – 4X.

Ora, usando il valore risultante f′( X), calcola f′( Xdi):

f′( Xdi) = f′(2) = 3 ∙ 2 2 – 4 ∙ 2 = 12 – 8 = 4.

3) Quindi, abbiamo tutti i dati necessari: Xdi = 2, f(Xdi) = 1, f ′( Xdi) = 4. Sostituiamo questi numeri nell'equazione tangente e troviamo la soluzione finale:

y= f(Xdi) + f′( Xdi) (x – x o) \u003d 1 + 4 ∙ (x - 2) \u003d 1 + 4x - 8 \u003d -7 + 4x \u003d 4x - 7.

Risposta: y \u003d 4x - 7.

Esempio 1 Data una funzione f(X) = 3X 2 + 4X– 5. Scriviamo l'equazione della tangente al grafico della funzione f(X) nel punto del grafico con l'ascissa X 0 = 1.

Soluzione. Derivata di funzione f(X) esiste per ogni x R . Troviamolo:

= (3X 2 + 4X– 5)′ = 6 X + 4.

Quindi f(X 0) = f(1) = 2; (X 0) = = 10. L'equazione tangente ha la forma:

y = (X 0) (X – X 0) + f(X 0),

y = 10(X – 1) + 2,

y = 10X – 8.

Risposta. y = 10X – 8.

Esempio 2 Data una funzione f(X) = X 3 – 3X 2 + 2X+ 5. Scriviamo l'equazione della tangente al grafico della funzione f(X), parallela alla linea y = 2X – 11.

Soluzione. Derivata di funzione f(X) esiste per ogni x R . Troviamolo:

= (X 3 – 3X 2 + 2X+ 5)′ = 3 X 2 – 6X + 2.

Poiché la tangente al grafico della funzione f(X) nel punto con l'ascissa X 0 è parallelo alla retta y = 2X– 11, allora la sua pendenza è 2, cioè ( X 0) = 2. Trova questa ascissa dalla condizione che 3 X– 6X 0 + 2 = 2. Questa uguaglianza è valida solo per X 0 = 0 e X 0 = 2. Poiché in entrambi i casi f(X 0) = 5, quindi la retta y = 2X + b tocca il grafico della funzione nel punto (0; 5) o nel punto (2; 5).

Nel primo caso, l'uguaglianza numerica è vera 5 = 2×0 + b, dove b= 5, e nel secondo caso, l'uguaglianza numerica è vera 5 = 2 × 2 + b, dove b = 1.

Quindi ci sono due tangenti y = 2X+ 5 e y = 2X+ 1 al grafico della funzione f(X) parallela alla linea y = 2X – 11.

Risposta. y = 2X + 5, y = 2X + 1.

Esempio 3 Data una funzione f(X) = X 2 – 6X+ 7. Scriviamo l'equazione della tangente al grafico della funzione f(X) passante per il punto UN (2; –5).

Soluzione. Perché f(2) –5, quindi il punto UN non appartiene al grafico della funzione f(X). Permettere X 0 - ascissa del punto di contatto.

Derivata di funzione f(X) esiste per ogni x R . Troviamolo:

= (X 2 – 6X+ 1)′ = 2 X – 6.

Quindi f(X 0) = X– 6X 0 + 7; (X 0) = 2X 0 - 6. L'equazione tangente ha la forma:

y = (2X 0 – 6)(X – X 0) + X– 6X+ 7,

y = (2X 0 – 6)X– X+ 7.

Dal momento che il punto UN appartiene alla tangente, allora l'uguaglianza numerica è vera

–5 = (2X 0 – 6)×2– X+ 7,

dove X 0 = 0 o X 0 = 4. Ciò significa che attraverso il punto UNè possibile disegnare due tangenti al grafico della funzione f(X).

Se una X 0 = 0, allora l'equazione tangente ha la forma y = –6X+ 7. Se X 0 = 4, allora l'equazione tangente ha la forma y = 2X – 9.

Risposta. y = –6X + 7, y = 2X – 9.

Esempio 4 Funzioni date f(X) = X 2 – 2X+ 2 e g(X) = –X 2 - 3. Scriviamo l'equazione della tangente comune ai grafici di queste funzioni.

Soluzione. Permettere X 1 - ascissa del punto di contatto della linea desiderata con il grafico della funzione f(X), un X 2 - ascissa del punto di contatto della stessa linea con il grafico della funzione g(X).

Derivata di funzione f(X) esiste per ogni x R . Troviamolo:

= (X 2 – 2X+ 2)′ = 2 X – 2.

Quindi f(X 1) = X– 2X 1 + 2; (X 1) = 2X 1 - 2. L'equazione tangente ha la forma:

y = (2X 1 – 2)(X – X 1) + X– 2X 1 + 2,

y = (2X 1 – 2)X – X+ 2. (1)

Troviamo la derivata della funzione g(X):

= (–X 2 – 3)′ = –2 X.