Classic probability. The probability of a random event
At It is very important to have a good idea of whether the probability () of the occurrence of an event of interest to us depends on how other events develop.
In the case of the classical scheme, when all outcomes are equally probable, we can already estimate the values of the probability of the particular event of interest to us independently. We can do this even if the event is a complex collection of several elementary outcomes. What if several random events occur simultaneously or sequentially? How does this affect the likelihood of the event of interest to us?
If I roll a dice several times and want a six to come up, but I’m not lucky all the time, does that mean I need to increase the bet, because, according to the theory of probability, I’m about to get lucky? Alas, the theory of probability does not say anything like that. No bone, no card, no coin do not know how to memorize, what they showed us last time. It doesn't matter to them at all whether for the first time or for the tenth time today I am testing my fate. Every time I repeat the throw, I only know one thing: and this time the probability of getting a six is again equal to one-sixth. Of course, this does not mean that the number I need will never fall out. It only means that my loss after the first throw and after any other throw are independent events.
Events A and B are called independent if the implementation of one of them does not affect the probability of another event in any way. For example, the probabilities of hitting a target with the first of two guns do not depend on whether the target was hit by another gun, so the events "the first gun hit the target" and "the second gun hit the target" are independent.
If two events A and B are independent, and the probability of each of them is known, then the probability of simultaneous occurrence of both event A and event B (denoted by AB) can be calculated using the following theorem.
Multiplication theorem for probabilities for independent events
P (AB) = P (A) * P (B)- probability simultaneous two independent events equals product the probabilities of these events.Example.The probabilities of hitting the target when firing the first and second guns are respectively equal: p 1 = 0.7; p 2 = 0.8. Find the probability of hitting with one volley with both guns simultaneously.
Solution: as we have already seen events A (hit by the first gun) and B (hit by the second gun) are independent, i.e. P (AB) = P (A) * P (B) = p 1 * p 2 = 0.56.
What happens to our estimates if the initiating events are not independent? Let's modify the previous example a bit.
Example.Two shooters in the competition shoot at targets, and if one of them shoots accurately, the opponent becomes nervous and his results deteriorate. How to turn this everyday situation into a mathematical problem and outline ways to solve it? It is intuitively clear that it is necessary to somehow separate the two scenarios for the development of events, to draw up essentially two scenarios, two different tasks. In the first case, if the opponent misses, the scenario will be favorable for the nervous athlete and his accuracy will be higher. In the second case, if the opponent has decently realized his chance, the probability of hitting the target for the second athlete is reduced.
To separate possible scenarios (often called hypotheses) of events, we will often use a "probability tree" scheme. This scheme is similar in meaning to the decision tree, with which you probably already had to deal with. Each branch represents a separate scenario for the development of events, only now it has its own meaning of the so-called conditional probabilities (q 1, q 2, q 1 -1, q 2 -1).
This scheme is very convenient for analyzing sequential random events.
It remains to clarify one more important question: where do the initial values of the probabilities in real situations ? After all, the theory of probability works not with the same coins and dice? Usually these estimates are taken from statistics, and when statistics are not available, we conduct our own research. And we often have to start it not with collecting data, but with the question of what information we generally need.
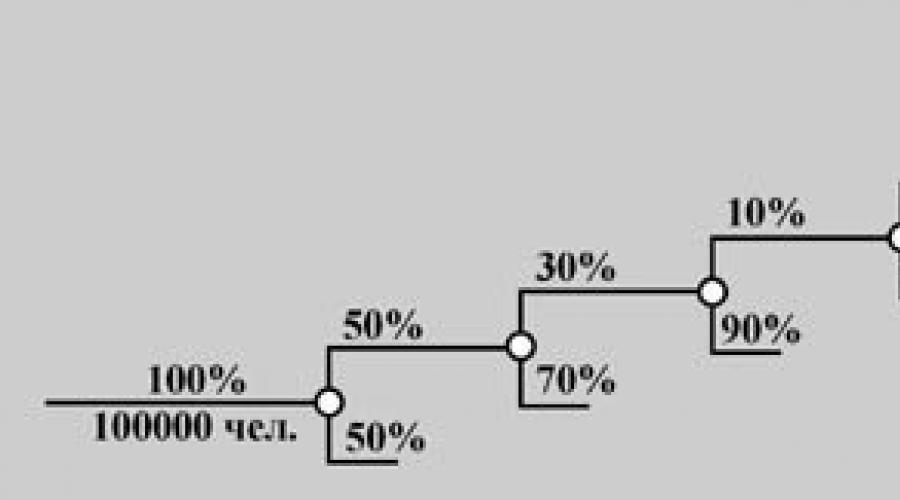
Example.Let's say we need to estimate the market size in a city with a population of one hundred thousand inhabitants for a new product that is not an essential item, for example, for a balm for the care of colored hair. Consider a "probability tree" scheme. In this case, the value of the probability on each "branch" we need to approximately estimate. So, our estimates of the market capacity:
1) 50% of all residents of the city are women,
2) of all women, only 30% dye their hair often,
3) only 10% of them use balms for colored hair,
4) of these, only 10% can get up the courage to try a new product,
5) 70% of them usually buy everything not from us, but from our competitors.

Solution: According to the law of multiplication of probabilities, we determine the probability of the event of interest to us A = (a resident of the city buys this new balm from us) = 0.00045.
Let's multiply this value of probability by the number of inhabitants of the city. As a result, we have only 45 potential customers, and if we consider that one bubble of this money is enough for several months, the trade is not very lively.
Still, there is some benefit from our assessments.
Firstly, we can compare forecasts of different business ideas, they will have different “forks” on the diagrams, and, of course, the probability values will also be different.
Secondly, as we have already said, a random variable is not called random because it does not depend on anything at all. Just her precise the value is not known in advance. We know that the average number of buyers can be increased (for example, by advertising a new product). So it makes sense to focus our efforts on those “forks” where the probability distribution does not particularly suit us, on those factors that we are able to influence.
Consider another quantitative example of shopping behavior research.
Example. On average, 10,000 people visit the food market per day. The probability that a market visitor enters a dairy pavilion is 1/2. It is known that in this pavilion, on average, 500 kg of various products are sold per day.
Can we say that the average purchase in a pavilion weighs only 100 g?
Discussion. Of course not. It is clear that not everyone who entered the pavilion ended up buying something there.

As shown in the diagram, in order to answer the question about the average purchase weight, we must find the answer to the question, what is the probability that a person who enters the pavilion will buy something there. If we do not have such data at our disposal, but we need them, we will have to obtain them ourselves, after observing the pavilion visitors for some time. Let's say our observations have shown that only a fifth of the pavilion's visitors buy something.
As soon as we have received these estimates, the task becomes already simple. Out of 10,000 people who come to the market, 5,000 will enter the pavilion of dairy products, and there will be only 1,000 purchases. The average purchase weight is 500 grams. It is interesting to note that to build a complete picture of what is happening, the logic of conditional "branching" must be defined at each stage of our reasoning as clearly as if we were working with a "specific" situation, and not with probabilities.
Self-test tasks
1. Let there be an electrical circuit consisting of n series-connected elements, each of which works independently of the others.

The probability p of failure of each element is known. Determine the probability of correct operation of the entire section of the chain (event A).
2. The student knows 20 of the 25 exam questions. Find the probability that the student knows the three questions suggested by the examiner.
3. Production consists of four successive stages, at each of which the equipment operates, for which the probabilities of failure within the next month are equal to p 1, p 2, p 3 and p 4, respectively. Find the probability that there will be no production interruption due to equipment failure in a month.
Events that happen in reality or in our imagination can be divided into 3 groups. These are reliable events that will definitely happen, impossible events and random events. Probability theory studies random events, i.e. events that may or may not happen. This article will briefly present the theory of probability of the formula and examples of solving problems in probability theory, which will be in the 4th task of the exam in mathematics (profile level).
Why the theory of probability is needed
Historically, the need to study these problems arose in the 17th century in connection with the development and professionalization of gambling and the emergence of casinos. This was a real phenomenon that required study and research.
Playing cards, craps, roulette created situations when any of a finite number of equally possible events could occur. The need arose to give numerical estimates of the possibility of a particular event occurring.
In the XX century, it became clear that this seemingly frivolous science plays an important role in understanding the fundamental processes taking place in the microcosm. The modern theory of probability was created.
Basic concepts of probability theory
The object of study of the theory of probability is events and their probabilities. If the event is complex, then it can be broken down into simple components, the probabilities of which are easy to find.
The sum of events A and B is called event C, which consists in the fact that either event A, or event B, or events A and B occurred simultaneously.
The product of events A and B is called event C, which consists in the fact that both event A and event B have occurred.
Events A and B are called inconsistent if they cannot happen at the same time.
Event A is called impossible if it cannot happen. Such an event is indicated by a symbol.
Event A is called credible if it will necessarily happen. Such an event is indicated by a symbol.
Let each event A be associated with the number P (A). This number P (A) is called the probability of event A if the following conditions are fulfilled for this correspondence.
An important special case is the situation when there are equiprobable elementary outcomes, and arbitrary of these outcomes form events A. In this case, the probability can be entered using the formula. The probability introduced in this way is called the classical probability. It can be proved that in this case properties 1-4 are satisfied.
Problems in probability theory that are encountered on the exam in mathematics are mainly related to classical probability. Such tasks can be very simple. Probability theory problems in demo versions are especially simple. It is easy to calculate the number of favorable outcomes, the number of all outcomes is written right in the condition.

We get the answer by the formula.
An example of a problem from the exam in mathematics to determine probability
There are 20 pies on the table - 5 with cabbage, 7 with apples and 8 with rice. Marina wants to take a pie. What is the likelihood that she will take the rice pie?
Solution.
There are 20 equiprobable elementary outcomes in total, that is, Marina can take any of 20 pies. But we need to estimate the likelihood that Marina will take a pie with rice, that is, where A is the choice of a pie with rice. So we have the number of favorable outcomes (choices of pies with rice) only 8. Then the probability will be determined by the formula:
![]()
Independent, opposite and arbitrary events
However, more complex tasks began to appear in the open bank of tasks. Therefore, let us draw the reader's attention to other issues studied in the theory of probability.
Events A and B are called independent if the probability of each of them does not depend on whether another event has occurred.
Event B means that event A did not happen, i.e. event B is opposite to event A. The probability of the opposite event is equal to one minus the probability of a direct event, i.e. ...
Addition and multiplication theorems for probabilities, formulas
For arbitrary events A and B, the probability of the sum of these events is equal to the sum of their probabilities without the probability of their joint event, i.e. ...
For independent events A and B, the probability of the product of these events is equal to the product of their probabilities, i.e. in this case .
The last 2 statements are called the theorems of addition and multiplication of probabilities.
Counting the number of outcomes is not always so easy. In some cases, it is necessary to use combinatorial formulas. In this case, the most important thing is to count the number of events that meet certain conditions. Sometimes this kind of calculations can become independent tasks.
In how many ways can 6 students be seated for 6 vacant seats? The first student will take any of the 6 seats. Each of these options corresponds to 5 ways to take the place of the second student. For the third student there are 4 free places, for the fourth - 3, for the fifth - 2, the sixth will take the only remaining place. To find the number of all options, you need to find the product, which is denoted by the symbol 6! and it reads "six factorial".
In the general case, the answer to this question is given by the formula for the number of permutations of n elements In our case.
Consider now another case with our students. In how many ways can 2 students be seated for 6 vacant seats? The first student will take any of the 6 seats. Each of these options corresponds to 5 ways to take the place of the second student. To find the number of all options, you need to find the product.
In the general case, the answer to this question is given by the formula for the number of placements of n elements for k elements
In our case .
And the last case in this series. How many ways are there to choose three students out of 6? The first student can be selected in 6 ways, the second - in 5 ways, the third - in four ways. But among these options, the same three students are encountered 6 times. To find the number of all options, you need to calculate the value:. In the general case, the answer to this question is given by the formula for the number of combinations of elements by elements:
In our case .
Examples of solving problems from the exam in mathematics to determine probability
Problem 1. From the collection, ed. Yashchenko.
There are 30 pies on the plate: 3 with meat, 18 with cabbage and 9 with cherries. Sasha chooses one pie at random. Find the probability that he ends up with a cherry.
![]() .
.
Answer: 0.3.
Problem 2. From the collection, ed. Yashchenko.
Each batch of 1000 bulbs contains an average of 20 defective bulbs. Find the probability that a light bulb taken at random from a batch will be working properly.
Solution: The number of serviceable bulbs is 1000-20 = 980. Then the probability that the light bulb taken at random from the batch will be serviceable:
![]()
Answer: 0.98.
The probability that student U. will correctly solve more than 9 problems on the math test is 0.67. The probability that U. will correctly solve more than 8 problems is 0.73. Find the probability that U will solve exactly 9 problems correctly.
If we imagine a number line and mark points 8 and 9 on it, then we will see that the condition “Y. will correctly solve exactly 9 problems "is included in the condition" U. will correctly solve more than 8 problems ", but does not apply to the condition" W. will solve more than 9 problems correctly ”.
However, the condition “W. will correctly solve more than 9 problems "is contained in the condition" W. will solve more than 8 problems correctly ”. Thus, if we designate events: “W. will correctly solve exactly 9 problems "- through A," Y. will solve more than 8 problems correctly "- through B," U. will correctly solve more than 9 problems "through C. That solution will look like this:
Answer: 0.06.
In the geometry exam, the student answers one question from the list of exam questions. The probability that this is a Trigonometry question is 0.2. The probability that this is an Outside Angles question is 0.15. There are no questions that simultaneously relate to these two topics. Find the probability that a student will get a question on one of these two topics on the exam.
Let's think about what kind of events we have. We are given two incompatible events. That is, either the question will relate to the topic "Trigonometry", or to the topic "Outside angles". According to the probability theorem, the probability of inconsistent events is equal to the sum of the probabilities of each event, we must find the sum of the probabilities of these events, that is:
Answer: 0.35.
The room is illuminated by a lantern with three lamps. The probability of one lamp burning out in a year is 0.29. Find the probability that at least one lamp will not burn out within a year.
Let's consider possible events. We have three bulbs, each of which may or may not burn out independently of any other bulb. These are independent events.
Then we will indicate the options for such events. Let us take the following notation: - the light is on, - the light is burnt out. And right next to it we will calculate the probability of the event. For example, the probability of an event in which three independent events “the light bulb burned out”, “the light bulb is on”, “the light bulb is on” occurred: ...
Note that there are only 7 inconsistent events favorable to us. The probability of such events is equal to the sum of the probabilities of each of the events:.
Answer: 0.975608.
You can see one more problem in the picture:

Thus, you and I understood what the probability theory of the formula and examples of solving problems on which you can meet in the version of the exam are.
What is probability?
Faced with this term for the first time, I would not understand what it is. Therefore, I will try to explain it in an accessible way.
Probability is the chance that the event we need will happen.
For example, you decided to visit a friend, remember the entrance and even the floor on which he lives. But I forgot the number and location of the apartment. And here you are standing on the staircase, and in front of you are the doors to choose from.
What is the chance (probability) that if you ring the first door, your friend will open for you? The whole apartment, and the friend lives only for one of them. We can choose any door with an equal chance.
But what is this chance?
Doors, the right door. Probability of guessing by ringing the first door:. That is, one time out of three you will guess for sure.
We want to know by calling once, how often will we guess the door? Let's consider all the options:
- You called in 1st Door
- You called in 2nd Door
- You called in 3rd Door
Now let's look at all the options where a friend may be:
but. Per 1st by the door
b. Per 2nd by the door
in. Per 3rd by the door
Let's compare all the options in the form of a table. A tick marks the options when your choice coincides with the location of a friend, a cross - when it does not match.
How do you see everything Maybe options the friend's location and your choice of which door to ring.
BUT favorable outcomes of all . That is, you will guess from time to time by ringing the doorbell, i.e. ...
This is probability - the ratio of a favorable outcome (when your choice coincided with the location of a friend) to the number of possible events.
Definition is a formula. The probability is usually denoted p, therefore:
It is not very convenient to write such a formula, therefore we will take for - the number of favorable outcomes, and for - the total number of outcomes.
The probability can be written as a percentage, for this you need to multiply the resulting result by:
Probably the word "outcomes" caught your eye. Since mathematicians call various actions (in our case, such an action is a ringing at the door) experiments, the result of such experiments is usually called the outcome.
Well, the outcomes are favorable and unfavorable.
Let's go back to our example. Let's say we rang one of the doors, but a stranger opened it to us. We didn't guess. What is the probability that if we ring one of the remaining doors, our friend will open for us?
If you thought that, then this is a mistake. Let's figure it out.
We have two doors left. Thus, we have possible steps:
1) Call in 1st Door
2) Call in 2nd Door
A friend, with all this, is definitely behind one of them (after all, he was not behind the one we called):
a) Friend for 1st by the door
b) Friend for 2nd by the door
Let's draw the table again:

As you can see, there are all options, of which are favorable. That is, the probability is equal.
Why not?
The situation we have considered - example of dependent events. The first event is the first doorbell, the second event is the second doorbell.
And they are called dependent because they affect the following actions. After all, if after the first ring of the door a friend opened the door for us, then what would be the probability that he is behind one of the other two? Right, .
But if there are dependent events, then there must be independent? True, there are.
A textbook example is tossing a coin.
- Throw a coin once. What is the probability that, for example, heads will come out? That's right - because the options for everything (either heads or tails, we neglect the probability of a coin to stand on the edge), but only suits us.
- But it was tails. Okay, let's throw it one more time. What is the probability of getting heads now? Nothing has changed, everything is the same. How many options? Two. And how much suits us? One.
And let it come up tails a thousand times in a row. The probability of getting heads at one time will be the same. There are always options, but favorable ones.
It is easy to distinguish dependent events from independent ones:
- If the experiment is carried out once (once they throw a coin, ring the doorbell once, etc.), then the events are always independent.
- If the experiment is carried out several times (a coin is thrown once, the doorbell rings several times), then the first event is always independent. And then, if the number of favorable or the number of all outcomes changes, then the events are dependent, and if not, they are independent.
Let's practice determining the probability a little.
Example 1.
The coin is thrown twice. What is the probability of hitting heads twice in a row?
Solution:
Let's consider all possible options:
- Eagle-eagle
- Heads-tails
- Heads-tails
- Tails-tails
As you can see, the whole option. Of these, only suits us. That is, the probability:
If the condition is asked to simply find the probability, then the answer must be given in the form of a decimal fraction. If it were indicated that the answer should be given as a percentage, then we would multiply by.
Answer:
Example 2.
In the box of chocolates, all the chocolates are packed in the same wrapper. However, from sweets - with nuts, with cognac, with cherries, with caramel and nougat.
What is the probability, taking one candy, to get a candy with nuts. Give your answer as a percentage.
Solution:
How many possible outcomes are there? ...
That is, taking one candy, it will be one of the ones in the box.
How many favorable outcomes?
Because the box contains only chocolates with nuts.
Answer:
Example 3.
In a box of balls. of them white, - black.
- What is the probability of pulling out the white ball?
- We've added more black balls to the box. What is now the probability of pulling out the white ball?
Solution:
a) There are all balls in the box. Of these, white.
The probability is equal to:
b) Now there are balls in the box. And the same number of whites remained -.
Answer:
Full probability
| The probability of all possible events is (). |
Let's say in a box of red and green balls. What is the probability of pulling out the red ball? Green ball? Red or green ball?
Possibility of pulling a red ball
Green ball:
Red or green ball:
As you can see, the sum of all possible events is (). Understanding this moment will help you solve many problems.
Example 4.
The box contains markers: green, red, blue, yellow, black.
What is the chance of pulling out a NOT red felt-tip pen?
Solution:
Let's count the amount favorable outcomes.
NOT a red marker, it means green, blue, yellow or black.
| The probability that the event will not occur is equal to minus the probability that the event will occur. |
The rule for multiplying the probabilities of independent events
You already know what independent events are.
What if you need to find the probability that two (or more) independent events will occur in a row?
Let's say we want to know what is the probability that when we flip a coin once, we will see an eagle twice?
We have already counted -.
And if we flip a coin once? What is the probability of seeing an eagle in a row?
All possible options:
- Eagle-eagle-eagle
- Heads-heads-tails
- Heads-tails-heads
- Heads-tails-tails
- Tails-heads-heads
- Tails-heads-tails
- Tails-Tails-Heads
- Tails-Tails-Tails
I don’t know about you, but I made a mistake once when making this list. Wow! And only option (first) suits us.
For 5 throws, you can make a list of possible outcomes yourself. But mathematicians are not as hardworking as you are.
Therefore, they first noticed and then proved that the probability of a certain sequence of independent events decreases each time by the probability of one event.
In other words,
Consider the example of the same unfortunate coin.
The likelihood of getting heads in a challenge? ... Now we flip a coin once.
What is the probability of hitting heads once in a row?
This rule works not only if we are asked to find the probability that the same event will occur several times in a row.
If we wanted to find the GRIP-EAGLE-GRILLE sequence for throws in a row, we would do the same.
The probability of falling heads is -, heads -.
Probability of falling out of the sequence GRILLE-EAGLE-GRILLE-GRILLE:
You can check it yourself by making a table.
The rule for adding the probabilities of inconsistent events.
So stop! New definition.
Let's figure it out. Take our worn out coin and toss it once.
Possible options:
- Eagle-eagle-eagle
- Heads-heads-tails
- Heads-tails-heads
- Heads-tails-tails
- Tails-heads-heads
- Tails-heads-tails
- Tails-Tails-Heads
- Tails-Tails-Tails
So incompatible events are a definite, predetermined sequence of events. are incompatible events.
If we want to determine what the probability of two (or more) incompatible events is, then we add the probabilities of these events.
You need to understand that falling heads or tails are two independent events.
If we want to determine what is the probability of a sequence) (or any other), then we use the rule of multiplication of probabilities.
What is the probability of getting heads on the first throw, and on the second and third heads?
But if we want to know what is the probability of getting one of several sequences, for example, when heads fall out exactly once, i.e. options and, then we have to add the probabilities of these sequences.
All options are suitable for us.
We can get the same thing by adding the probabilities of each sequence:
Thus, we add probabilities when we want to determine the probabilities of some inconsistent sequences of events.
There is a great rule of thumb to help you avoid confusion when to multiply and when to add:
Let's go back to the example when we flipped a coin once, and we want to know the probability of seeing heads once.
What is going to happen?
Should drop out:
(heads AND tails AND tails) OR (tails AND heads AND tails) OR (tails AND tails AND heads).
So it turns out:
Let's look at a few examples.
Example 5.
The box contains pencils. reds, greens, oranges and yellows and blacks. What is the likelihood of pulling out red or green pencils?
Solution:
Example 6.
The dice are rolled twice, what is the probability of a total of 8 points?
Solution.
How can we get points?
(and) or (and) or (and) or (and) or (and).
The probability of falling out of one (any) face -.
We calculate the probability:
Workout.
I think now it became clear to you when to calculate the probabilities, when to add them, and when to multiply them. Is not it? Let's practice a little.
Tasks:
Let's take a card deck, in which cards, including spades, hearts, 13 clubs and 13 diamonds. From to ace of each suit.
- What is the probability of drawing clubs in a row (we put the first drawn card back into the deck and shuffle it)?
- What is the probability of drawing a black card (spades or clubs)?
- What is the probability of pulling a picture (jack, queen, king or ace)?
- What is the probability of drawing two pictures in a row (we remove the first drawn card from the deck)?
- What is the probability, taking two cards, to collect a combination - (jack, queen or king) and ace The sequence in which the cards will be drawn does not matter.
Answers:
If you were able to solve all the problems yourself, then you are a great fellow! Now you will be clicking on probabilities in the Unified State Exam!
THEORY OF PROBABILITIES. AVERAGE LEVEL
Let's look at an example. Let's say we roll a die. What kind of bone is this, you know? This is the name of a cube with numbers on the edges. How many faces, so many numbers: from to how many? Before.
So, we roll the die and want to roll or. And it falls to us.
Probability says what happened favorable event(not to be confused with the prosperous).
If it fell out, the event would also be favorable. In total, only two favorable events can occur.
And how many are unfavorable? Since there are all possible events, it means that unfavorable events are among them (this is if it falls out or).
Definition:
Probability is the ratio of the number of favorable events to the number of all possible events... That is, the probability shows what proportion of all possible events are favorable.
The probability is denoted by the Latin letter (apparently, from the English word probability).
It is customary to measure the probability as a percentage (see topic,). To do this, the value of the probability must be multiplied by. In the dice example, the probability.
And as a percentage:.
Examples (decide for yourself):
- What is the probability of getting heads when flipping a coin? What is the probability of getting tails?
- What is the likelihood of an even number coming up on a dice roll? And with which - odd?
- In a box of pencils, blue and red. Draw one pencil at random. What is the probability of pulling out a simple one?
Solutions:
- How many options are there? Heads and tails are just two. How many of them are favorable? Only one is an eagle. So the probability
It's the same with tails:.
- Total options: (how many sides the cube has, so many different options). Favorable ones: (these are all even numbers :).
Probability. With odd, of course, the same thing. - Total: . Favorable:. Probability: .
Full probability
All pencils in the drawer are green. What is the probability of pulling out a red pencil? There is no chance: probability (after all, favorable events -).
Such an event is called impossible.
What is the probability of pulling out a green pencil? There are exactly the same number of favorable events as there are total events (all events are favorable). Hence, the probability is equal to or.
Such an event is called reliable.
If there are green and red pencils in a box, what is the probability of pulling out a green or red one? Yet again. Note this thing: the probability of pulling green is equal, and red is.
In sum, these probabilities are exactly equal. I.e, the sum of the probabilities of all possible events is equal to or.
Example:
In a box of pencils, among them blue, red, green, plain, yellow, and the rest are orange. What is the probability of not pulling green?
Solution:
Remember that all probabilities add up. And the probability of pulling green is equal. This means that the probability of not pulling out green is equal to.
Remember this trick: the probability that the event will not occur is equal to minus the probability that the event will occur.
Independent events and the multiplication rule
You flip a coin once, and you want heads to fall both times. What is the likelihood of this happening?
Let's go over all the possible options and determine how many there are:
Heads-Heads, Heads-Heads, Heads-Heads, Heads-Heads. What else?
The whole option. Of these, only one is suitable for us: Eagle-Eagle. Total, the probability is.
Good. And now we throw a coin once. Count it yourself. Happened? (answer).
You may have noticed that with the addition of each next throw, the probability decreases by times. The general rule is called multiplication rule:
The probabilities of independent events change.
What are independent events? Everything is logical: these are those that do not depend on each other. For example, when we toss a coin several times, a new toss is made each time, the result of which does not depend on all previous tosses. We can just as well flip two different coins at the same time.
More examples:
- The dice are rolled twice. What is the probability that both times will be rolled?
- The coin is thrown once. What is the likelihood that it will land heads first and then tails twice?
- The player rolls two dice. What is the probability that the sum of the numbers on them will be equal?
Answers:
- The events are independent, which means that the multiplication rule works:.
- The probability of an eagle is. The likelihood of tails is also. We multiply:
- 12 can only be obtained if two -ki are rolled:.
Incompatible events and the addition rule
Events that complement each other up to full probability are called inconsistent. As the name suggests, they cannot happen at the same time. For example, if we flip a coin, it can come up either heads or tails.
Example.
In a box of pencils, among them blue, red, green, plain, yellow, and the rest are orange. What is the probability of pulling green or red?
Solution .
The probability of pulling out a green pencil is. Red - .
Auspicious events in total: green + red. This means that the probability of pulling out green or red is equal to.
The same probability can be represented as follows:.
This is the addition rule: the probabilities of inconsistent events add up.
Mixed problems
Example.
The coin is thrown twice. What is the likelihood that the result of the throws will be different?
Solution .
This means that if the first hit is heads, the second should be tails, and vice versa. It turns out that there are two pairs of independent events, and these pairs are incompatible with each other. How not to get confused, where to multiply, and where to add.
There is a simple rule of thumb for these situations. Try to describe what is going to happen by connecting the events with AND or OR. For example, in this case:
Should come up (heads and tails) or (tails and heads).
Where there is a conjunction "and", there will be multiplication, and where "or" - addition:
Try it yourself:
- What is the likelihood that the same side will land on two tosses of a coin both times?
- The dice are rolled twice. What is the probability that the total will be points?
Solutions:
Another example:
We toss a coin once. What is the probability that heads will come out at least once?
Solution:
THEORY OF PROBABILITIES. BRIEFLY ABOUT THE MAIN
Probability is the ratio of the number of favorable events to the number of all possible events.
Independent events
Two events are independent if at the occurrence of one the probability of the occurrence of the other does not change.
Full probability
The probability of all possible events is ().
The probability that the event will not occur is equal to minus the probability that the event will occur.
The rule for multiplying the probabilities of independent events
The probability of a certain sequence of independent events is equal to the product of the probabilities of each of the events
Incompatible events
Incompatible events are called events that cannot happen simultaneously as a result of an experiment. A number of incompatible events form a complete group of events.
The probabilities of inconsistent events add up.
Having described what should happen, using the conjunctions "AND" or "OR", instead of "AND" we put the sign of multiplication, and instead of "OR" - addition.
Well, the topic is over. If you are reading these lines, then you are very cool.
Because only 5% of people are able to master something on their own. And if you read to the end, then you are in that 5%!
Now comes the most important thing.
You figured out the theory on this topic. And, again, this is ... it's just super! You are already better than the vast majority of your peers.
The problem is that this may not be enough ...
For what?
For the successful passing of the exam, for admission to the institute on a budget and, MOST IMPORTANT, for life.
I will not convince you of anything, I will just say one thing ...
People who have received a good education earn much more than those who have not received it. These are statistics.
But this is not the main thing either.
The main thing is that they are MORE HAPPY (there are such studies). Perhaps because there are so many more opportunities open up before them and life becomes brighter? Do not know...
But think for yourself ...
What does it take to be for sure better than others on the exam and be ultimately ... more happy?
GET A HAND SOLVING PROBLEMS ON THIS TOPIC.
On the exam, you will not be asked for theory.
You will need solve problems for a while.
And if you didn’t solve them (A LOT!), You are sure to go somewhere stupidly mistaken or simply will not have time.
It's like in sports - you have to repeat it over and over to win for sure.
Find a collection where you want, necessarily with solutions, detailed analysis and decide, decide, decide!
You can use our tasks (optional) and we, of course, recommend them.
In order to fill your hand with the help of our tasks, you need to help extend the life of the YouClever textbook that you are currently reading.
How? There are two options:
- Share all hidden tasks in this article - 299 r
- Unlock access to all hidden tasks in all 99 articles of the tutorial - RUB 499
Yes, we have 99 such articles in our textbook, and access for all tasks and all hidden texts in them can be opened at once.
Access to all hidden tasks is provided for the entire lifetime of the site.
In conclusion...
If you don't like our tasks, find others. Just don't dwell on theory.
“Understood” and “I am able to solve” are completely different skills. You need both.
Find problems and solve!
Formulas for calculating the probability of events
1.3.1. Sequence of independent tests (Bernoulli scheme)
Suppose that a certain experiment can be performed repeatedly under the same conditions. Let this experience be made n times, i.e., a sequence of n tests.
Definition. Subsequence n tests are called mutually independent if any event associated with this test is independent of any events related to the remaining tests.
Suppose that some event A can happen with probability p as a result of one test or not happen with probability q= 1- p.
Definition . Sequence of n test forms a Bernoulli scheme if the following conditions are met:
subsequence n tests are mutually independent,
2) the likelihood of an event A does not change from test to test and does not depend on the result in other tests.
Event A is called the "success" of the test, and the opposite event is called "failure." Consider an event
 = (in n tests happened exactly m"Success").
= (in n tests happened exactly m"Success").
To calculate the probability of this event, the Bernoulli formula is valid
p( )
=
)
=
 , m
= 1, 2, …, n
, (1.6)
, m
= 1, 2, …, n
, (1.6)
where  - the number of combinations of n elements by m
:
- the number of combinations of n elements by m
:
 =
=
 =
= .
.
Example 1.16. The die is rolled three times. To find:
a) the probability that 6 points will be dropped twice;
b) the probability that the number of sixes does not appear more than two times.
Solution . The "success" of the test will be considered the fallout on the cube of the face with the image of 6 points.
a) The total number of tests - n= 3, the number of "successes" - m
= 2. The probability of "success" - p= ,
and the probability of “failure” is q= 1 - =. Then, according to Bernoulli's formula, the probability that the side with six points will fall out twice as a result of throwing the dice three times will be equal to
,
and the probability of “failure” is q= 1 - =. Then, according to Bernoulli's formula, the probability that the side with six points will fall out twice as a result of throwing the dice three times will be equal to
 .
.
b) Denote by BUT an event, which consists in the fact that the face with the number of points 6 appears no more than two times. Then the event can be represented as the sum of the three incompatible events A =
 ,
,
where IN 3 0 - an event when the face of interest never appears,
IN 3 1 - event when the face of interest appears once,
IN 3 2 - an event when a face of interest appears twice.
By Bernoulli's formula (1.6), we find
p(BUT)
= p ( )
=
p(
)
=
p( )=
)=
 +
+ +
+ =
=
=
 .
.
1.3.2. Conditional probability of an event
Conditional probability reflects the effect of one event on the likelihood of another. Changing the conditions in which the experiment is carried out also affects
on the probability of occurrence of the event of interest.
Definition. Let be A and B- some events, and the probability p(B)> 0.
Conditional probability developments A provided that “event Balready happened ”is the ratio of the probability of the production of these events to the probability of an event that occurred earlier than the event, the probability of which is to be found. The conditional probability is denoted as p(A B). Then by definition
p
(A
B)
=
 .
(1.7)
.
(1.7)
Example 1.17. Throw in two dice. The space of elementary events consists of ordered pairs of numbers
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6).
In Example 1.16, it was established that the event A= (number of points on the first die> 4) and event C= (the sum of points is equal to 8) are dependent. Let's compose the relation
 .
.
This relationship can be interpreted as follows. Let us assume that the result of the first roll is known that the number of points on the first die is> 4. It follows that the roll of the second die can lead to one of the 12 outcomes that make up the event A:
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6) .
At this event C only two of them can match (5,3) (6,2). In this case, the probability of the event C
will be equal  ... Thus, information about the occurrence of an event A influenced the likelihood of an event C.
... Thus, information about the occurrence of an event A influenced the likelihood of an event C.
Probability of the occurrence of events
Multiplication theorem
Probability of the occurrence of eventsA 1 A 2 A n is defined by the formula
p(A 1 A 2 A n)= p(A 1)p(A 2 A 1)) p(A n A 1 A 2 A n- 1). (1.8)
For the production of two events, it follows from this that
p(AB)= p(A B) p{B)= p(B A)p{A). (1.9)
Example 1.18. A batch of 25 items contains 5 defective items. Sequentially select 3 products at random. Determine the likelihood that all selected items are defective.
Solution. Let's designate events:
A 1 = (the first product is defective),
A 2 = (second product is defective),
A 3 = (the third product is defective),
A = (all products are defective).
Event BUT there is a product of three events A = A 1 A 2 A 3 .
From the multiplication theorem (1.6) get
p(A)= p ( A 1 A 2 A 3 ) = p(A 1) p(A 2 A 1))p(A 3 A 1 A 2).
The classical definition of probability allows one to find p(A 1) is the ratio of the number of defective products to the total number of products:
p(A 1)=
 ;
;
p(A 2) – This the ratio of the number of defective products remaining after the seizure of one to the total number of remaining products:
p(A 2
A 1))=
 ;
;
p(A 3) is the ratio of the number of defective products remaining after the seizure of two defective products to the total number of remaining products:
p(A 3
A 1 A 2)= .
.
Then the probability of the event A will be equal
p(A)
=

 =
= .
.
Many, when faced with the concept of "probability theory", get scared, thinking that this is something overwhelming, very difficult. But everything is actually not so tragic. Today we will consider the basic concept and learn how to solve problems using specific examples.
The science
What does such a branch of mathematics as "probability theory" study? She notes patterns and quantities. For the first time, scientists became interested in this issue back in the eighteenth century, when they studied gambling. The basic concept of the theory of probability is an event. This is any fact that is ascertained by experience or observation. But what is experience? Another basic concept of the theory of probability. It means that this set of circumstances was not created by chance, but for a specific purpose. As for observation, here the researcher himself does not participate in the experiment, but simply witnesses these events, he does not in any way affect what is happening.
Developments
We learned that the basic concept of probability theory is an event, but we did not consider classification. They all fall into the following categories:
- Credible.
- Impossible.
- Random.
Regardless of what kind of events are observed or created in the course of the experiment, they are all subject to this classification. We invite you to get acquainted with each of the types separately.
Credible event

This is such a circumstance, in front of which the necessary set of measures was taken. In order to better understand the essence, it is better to give a few examples. Physics, chemistry, economics, and higher mathematics are subject to this law. Probability theory includes such an important concept as a reliable event. Here are some examples:
- We work and receive remuneration in the form of wages.
- We passed the exams well, passed the competition, for which we receive a reward in the form of admission to an educational institution.
- We have invested money in the bank, if necessary, we will get it back.
Such events are credible. If we have fulfilled all the necessary conditions, then we will definitely get the expected result.
Impossible events
We are now looking at the elements of the theory of probability. We propose to move on to an explanation of the next type of event, namely, the impossible. To begin with, let's stipulate the most important rule - the probability of an impossible event is zero.
One cannot deviate from this formulation when solving problems. For clarification, here are examples of such events:
- The water froze at a temperature of plus ten (this is impossible).
- The lack of electricity does not affect production in any way (just as impossible as in the previous example).
It is not worth giving more examples, since the ones described above very clearly reflect the essence of this category. An impossible event will never happen during an experience under any circumstances.
Random events

Studying the elements of the theory of probability, special attention should be paid to this particular type of event. It is them that this science studies. As a result of the experience, something can happen or not. In addition, the test can be carried out an unlimited number of times. Striking examples are:
- The toss of a coin is an experience, or a test, the falling of a head is an event.
- Pulling a ball out of the bag blindly is a test, a red ball is caught - this is an event, and so on.
There can be an unlimited number of such examples, but, in general, the essence should be clear. To summarize and systematize the knowledge gained about events, a table is given. Probability theory studies only the last species of all presented.
title | definition | |
Credible | Events occurring with a 100% guarantee subject to certain conditions. | Admission to an educational institution with a good passing of the entrance exam. |
Impossible | Events that will never happen under any circumstances. | It is snowing at an air temperature of plus thirty degrees Celsius. |
Random | An event that may or may not occur during the experiment / test. | Hitting or missing when throwing a basketball into the basket. |
The laws
Probability theory is a science that studies the possibility of an event occurring. Like others, it has some rules. There are the following laws of the theory of probability:
- Convergence of sequences of random variables.
- The law of large numbers.
When calculating the possibility of a complex, you can use a set of simple events to achieve a result in an easier and faster way. Note that the laws of probability theory are easily proved using some theorems. We suggest that you first get acquainted with the first law.
Convergence of sequences of random variables

Note that there are several types of convergence:
- A sequence of random variables converges in probability.
- Almost impossible.
- Root-mean-square convergence.
- Distribution convergence.
So, on the fly, it is very difficult to grasp the essence. Here are some definitions that will help you understand this topic. For starters, the first view. The sequence is called converging in probability, if the following condition is met: n tends to infinity, the number to which the sequence tends is greater than zero and is close to one.
Let's move on to the next form, almost surely... The sequence is said to converge almost surely to a random variable as n tends to infinity, and P tends to a value close to unity.
The next type is RMS convergence... When using SK-convergence, the study of vector stochastic processes is reduced to the study of their coordinate stochastic processes.
The last type remains, let's briefly analyze it in order to proceed directly to solving problems. The convergence in distribution has one more name - “weak”, below we will explain why. Weak convergence Is the convergence of distribution functions at all points of continuity of the limiting distribution function.
We will definitely keep our promise: weak convergence differs from all of the above in that the random variable is not defined in the probability space. This is possible because the condition is formed exclusively using distribution functions.
The law of large numbers
Theorems of probability theory, such as:
- Chebyshev's inequality.
- Chebyshev's theorem.
- Generalized Chebyshev's theorem.
- Markov's theorem.
If we consider all these theorems, then this question can drag on for several tens of pages. Our main task is to apply the theory of probability in practice. We suggest you do this right now and do it. But before that, let's consider the axioms of probability theory, they will be the main helpers in solving problems.
Axioms

We already met the first when we talked about an impossible event. Let's remember: the probability of an impossible event is zero. We gave a very vivid and memorable example: it snowed at an air temperature of thirty degrees Celsius.
The second is as follows: a reliable event occurs with a probability equal to one. Now we will show how to write this using mathematical language: P (B) = 1.
Third: A random event may or may not happen, but the possibility always varies from zero to one. The closer the value is to one, the greater the chances; if the value approaches zero, the probability is very small. Let's write it in mathematical language: 0<Р(С)<1.
Consider the last, fourth axiom, which sounds like this: the probability of the sum of two events is equal to the sum of their probabilities. We write in mathematical language: P (A + B) = P (A) + P (B).
The axioms of probability theory are the simplest rules that will not be difficult to remember. Let's try to solve some problems based on the knowledge we have already acquired.
Lottery ticket

Let's start by looking at the simplest example - a lottery. Imagine you bought one lottery ticket for good luck. What is the probability that you will win at least twenty rubles? In total, a thousand tickets participate in the draw, one of which has a prize of five hundred rubles, ten for one hundred rubles, fifty for twenty rubles, and one hundred for five. Probability problems are based on finding the opportunity for luck. Now we will analyze the solution of the above presented task together.
If we denote a win of five hundred rubles with the letter A, then the probability of getting A will be 0.001. How did we get it? You just need to divide the number of "lucky" tickets by their total number (in this case: 1/1000).
B is a win of one hundred rubles, the probability will be 0.01. Now we acted on the same principle as in the previous action (10/1000)
С - the winnings are equal to twenty rubles. We find the probability, it is equal to 0.05.
The rest of the tickets are not of interest to us, since their prize fund is less than the one specified in the condition. Let's apply the fourth axiom: The probability of winning at least twenty rubles is P (A) + P (B) + P (C). The letter P denotes the probability of the occurrence of this event, we have already found them in previous actions. It remains only to add the necessary data, in the answer we get 0.061. This number will be the answer to the task question.
Card deck
Probability theory problems are also more complex, for example, let's take the following task. Here is a deck of thirty-six cards. Your task is to draw two cards in a row without mixing the pile, the first and second cards must be aces, the suit does not matter.
First, let's find the probability that the first card will be an ace, for this we divide four by thirty-six. We put it aside. We take out the second card, it will be an ace with a probability of three thirty-fifths. The probability of a second event depends on which card we draw first, we wonder if it was an ace or not. It follows from this that event B depends on event A.
The next step is to find the probability of simultaneous occurrence, that is, we multiply A and B. Their product is found as follows: the probability of one event is multiplied by the conditional probability of another, which we calculate, assuming that the first event happened, that is, we drew an ace with the first card.
In order to make everything clear, we will give a designation to such an element as events. It is calculated, assuming that event A has occurred. Calculated as follows: P (B / A).
Let's continue solving our problem: P (A * B) = P (A) * P (B / A) or P (A * B) = P (B) * P (A / B). The probability is (4/36) * ((3/35) / (4/36). Calculate, rounding to the nearest hundredth. We have: 0.11 * (0.09 / 0.11) = 0.11 * 0, 82 = 0.09 The probability that we will draw two aces in a row is equal to nine hundredths The value is very small, which means that the probability of the event occurring is extremely small.
Forgotten number
We propose to analyze a few more options for tasks that the theory of probability studies. You have already seen examples of solving some of them in this article, let's try to solve the following problem: the boy forgot the last digit of his friend's phone number, but since the call was very important, he began to dial everything in turn. We need to calculate the probability that he will call no more than three times. The solution to the problem is the simplest if the rules, laws and axioms of the theory of probability are known.
Before looking at the solution, try to solve it yourself. We know that the last digit can be from zero to nine, that is, there are only ten values. The probability of getting the required one is 1/10.
Next, we need to consider the options for the origin of the event, suppose that the boy guessed right and immediately typed the desired one, the probability of such an event is 1/10. The second option: the first call is a miss, and the second on target Let's calculate the probability of such an event: multiply 9/10 by 1/9, in the end we also get 1/10. The third option: the first and second calls were at the wrong address, only from the third the boy got where he wanted. We calculate the probability of such an event: multiply 9/10 by 8/9 and by 1/8, we get 1/10 as a result. We are not interested in other options according to the condition of the problem, so it remains for us to add up the results obtained, in the end we have 3/10. Answer: The probability that a boy will call no more than three times is 0.3.
Number cards

There are nine cards in front of you, each of which has a number from one to nine written, the numbers are not repeated. They were put in a box and mixed thoroughly. You need to calculate the probability that
- an even number will be dropped;
- two-digit.
Before proceeding to the solution, let us stipulate that m is the number of successful cases, and n is the total number of options. Let's find the probability that the number will be even. It will not be difficult to calculate that there are four even numbers, this will be our m, in total there are nine options, that is, m = 9. Then the probability is 0.44 or 4/9.
Consider the second case: the number of options is nine, but there can be no successful outcomes at all, that is, m equals zero. The probability that the drawn card will contain a two-digit number is also zero.