Ποια είναι η αρχή του Huygens; Η αρχή του Huygens

Η αρχή του Huygens

Τεκμηριώνοντας την κυματική θεωρία του φωτός, ο Huygens πρότεινε μια αρχή που κατέστησε δυνατή την οπτική επίλυση ορισμένων προβλημάτων διάδοσης και διάθλασης του φωτός. Η σημασία του είναι ότι: Εάν σε οποιαδήποτε χρονική στιγμή το μέτωπο του φωτεινού κύματος είναι γνωστό, τότε για να προσδιοριστεί η θέση του μετά από ένα ορισμένο χρονικό διάστημα ίσο με $\\τρίγωνο t$, τότε κάθε σημείο του μετώπου θα πρέπει να θεωρηθεί ως πηγή ενός σφαιρικού κύματος, κατασκευάστε μια σφαίρα γύρω από μια τέτοια δευτερεύουσα πηγή κύματος με ακτίνα $c\τρίγωνο t$, όπου $c$ είναι η ταχύτητα του φωτός στο κενό. Σε αυτήν την περίπτωση, η επιφάνεια που κάμπτεται γύρω από τα δευτερεύοντα σφαιρικά κύματα θα είναι το μπροστινό μέρος του αρχικού κύματος μετά από ένα δεδομένο χρονικό διάστημα $\τρίγωνο t$.

Όσον αφορά το φυσικό περιεχόμενο, η αρχή του Huygens εκφράζει την άποψη για το φως ως μια συνεχή διαδικασία στο χώρο. Χρησιμοποιώντας την αρχή του Huygens, μπορεί να εξηγηθεί γιατί τα κύματα φωτός πέφτουν στη γεωμετρική περιοχή σκιάς.

Το κύριο πρόβλημα με την αρχή του Huygens είναι ότι δεν λαμβάνει υπόψη το φαινόμενο της παρεμβολής φωτός. Αυτή η αρχή δεν παρέχει πληροφορίες σχετικά με το πλάτος και την ένταση των κυμάτων.

Η αρχή Huygens-Fresnel, η αναλυτική της έκφραση

Ορισμός 1

Ο Fresnel ανέπτυξε την αρχή του Huygens και αυτή η θέση άρχισε να διατυπώνεται ως εξής: Κάθε σημείο που ανήκει στο μέτωπο κύματος μετατρέπεται σε πηγή δευτερευόντων κυμάτων (αυτό είναι από την αρχή του Huygens), ενώ οι δευτερεύουσες πηγές είναι συνεπείς μεταξύ τους και τα δευτερεύοντα κύματα που εκπέμπονται από αυτά παρεμβαίνουν. Για μια επιφάνεια που συμπίπτει με την επιφάνεια του κύματος, οι δυνάμεις της δευτερογενούς ακτινοβολίας ίσων περιοχών είναι οι ίδιες. Επιπλέον, το φως που διαδίδεται από κάθε δευτερεύουσα πηγή πηγαίνει προς την κατεύθυνση του εξωτερικού κανονικού.

Ο Rayleigh συνόψισε την παραπάνω αρχή:

Ας περιβάλουμε όλα τα $S_1,S_2,S_3,\dots $ με μια κλειστή επιφάνεια $(F)$ αυθαίρετου σχήματος. Σε αυτή την περίπτωση, οποιοδήποτε σημείο στην επιφάνεια $F$ μπορεί να θεωρηθεί δευτερεύουσα πηγή κυμάτων που διαδίδονται προς όλες τις κατευθύνσεις. Αυτά τα κύματα είναι συνεκτικά, αφού διεγείρονται από τις ίδιες πρωτογενείς πηγές. Το φωτεινό πεδίο που εμφανίζεται ως αποτέλεσμα της χωρικής τους παρεμβολής έξω από την επιφάνεια $F$ συμπίπτει με το πεδίο των πραγματικών πηγών φωτός.

Έτσι, οι πραγματικές πηγές φωτός μπορούν να αντικατασταθούν από μια φωτεινή επιφάνεια που τις περιβάλλει. Επιπλέον, συνεκτικές δευτερεύουσες πηγές κυμάτων φωτός φαίνεται να κατανέμονται συνεχώς σε όλη αυτή την επιφάνεια. Η διαφορά με αυτή την υποθετική επιφάνεια είναι ότι είναι διαφανής σε οποιαδήποτε ακτινοβολία.

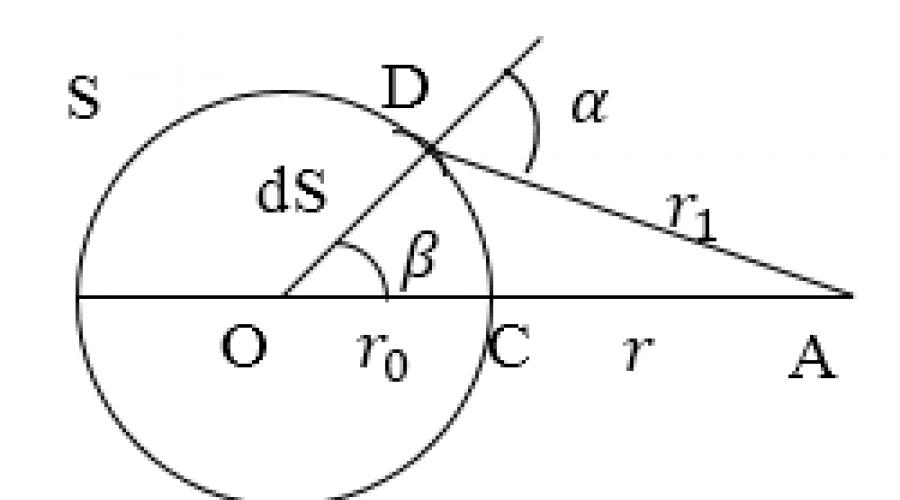
Ας υποθέσουμε ότι η πηγή φωτός είναι μονόχρωμη και το μέσο είναι ομοιογενές και ισότροπο. Έτσι, σύμφωνα με τη διορθωμένη αρχή, κάθε στοιχείο της επιφάνειας κύματος $S$ (Εικ. 1) είναι μια πηγή ενός δευτερεύοντος σφαιρικού κύματος, το οποίο έχει ένα πλάτος ανάλογο με το μέγεθος αυτού του στοιχείου ($dS$).

Εικόνα 1.

Από οποιοδήποτε τμήμα $dS$ της επιφάνειας του κύματος, μια ταλάντωση έρχεται στο σημείο $A$ (Εικ. 1), το οποίο βρίσκεται μπροστά από την επιφάνεια $S$, το οποίο μπορεί να περιγραφεί από την ακόλουθη εξίσωση:

όπου $\left(\omega t+(\alpha)_0\right)$ είναι η φάση ταλάντωσης στη θέση της επιφάνειας $S$, $k$ είναι ο αριθμός κύματος, $r$ είναι η απόσταση από το στοιχείο επιφάνειας ( $dS)$ στο σημείο $A$, $a_0$ - πλάτος δόνησης φωτός στη θέση του στοιχείου $dS$. Το $K$ είναι ένας συντελεστής που εξαρτάται από τη γωνία $\varphi $ μεταξύ του κανονικού $\overrightarrow(n)$ στην περιοχή $dS$ και της κατεύθυνσης από αυτό στο σημείο $4A$. Αν $\varphi =0,\ $τότε έχουμε $K=K_(max)$, με $\ \ \varphi =\frac(\pi )(2)$ $K=0.$

Η συνολική ταλάντωση στο σημείο Α βρίσκεται ως υπέρθεση ταλαντώσεων που λαμβάνονται για ολόκληρη την επιφάνεια κύματος $S$, δηλαδή:

Ο τύπος (2) είναι μια ολοκληρωμένη διατύπωση της αρχής Huygens-Fresnel.

Ερμηνεία της αρχής Huygens-Fresnel

Ο Fresnel αντικατέστησε την τεχνητή υπόθεση του Huygens σχετικά με το περίβλημα των δευτερογενών κυμάτων με μια σαφή φυσική θέση κατά μήκος της οποίας τα δευτερεύοντα κύματα, όταν προστίθενται, παρεμβαίνουν. Σε αυτή την περίπτωση, το φως είναι ορατό στα μέγιστα παρεμβολές όπου τα κύματα αλληλοεξουδετερώνονται, υπάρχει σκοτάδι. Έτσι, εξηγείται η φυσική έννοια του φακέλου. Τα δευτερεύοντα κύματα πλησιάζουν το περίβλημα στις ίδιες φάσεις, επομένως η παρεμβολή προκαλεί μεγαλύτερη ένταση φωτός. Η αρχή Huygens-Fresnel εξηγεί την απουσία οπισθοδρομικού κύματος. Τα δευτερεύοντα κύματα, τα οποία διαδίδονται προς τα εμπρός από το μέτωπο του κύματος, πηγαίνουν σε ένα χώρο χωρίς ενόχληση. Ταυτόχρονα, παρεμβαίνουν μόνο μεταξύ τους. Τα δευτερεύοντα κύματα που πηγαίνουν προς τα πίσω πέφτουν στο διάστημα όπου υπάρχει ήδη ένα άμεσο κύμα, επομένως τα δευτερεύοντα κύματα αποσβένουν το άμεσο κύμα, επομένως, αφού περάσει το κύμα, ο χώρος πάνω του δεν έχει καμία διαταραχή.

Στη διατύπωση του Rayleigh, η εν λόγω αρχή σημαίνει ότι ένα κύμα, το οποίο έχει διαχωριστεί από την πηγή του, τότε υπάρχει αυτόνομα, ανεξάρτητα από την παρουσία πηγών.

Η αρχή Huygens-Fresnel μας επιτρέπει να εξηγήσουμε το φαινόμενο της περίθλασης.

Παράδειγμα 1

Ασκηση:Γράψτε μια έκφραση για την ένταση του ηλεκτρικού πεδίου ($E$) στο κύμα, αν υποθέσουμε ότι το κύμα είναι σφαιρικό και διαδίδεται ελεύθερα.

Λύση:

Σχήμα 2.

Ας εξετάσουμε την ελεύθερη διάδοση ενός σφαιρικού κύματος σε ένα ομοιογενές μέσο (Εικ. 2), μπορεί να περιγραφεί χρησιμοποιώντας την εξίσωση:

Η βοηθητική επιφάνεια κύματος στην περίπτωσή μας είναι η επιφάνεια S, η οποία έχει ακτίνα $r_0$. Σύμφωνα με τον Fresnel, κάθε στοιχείο αυτής της επιφάνειας ($dS$) εκπέμπει ένα δευτερεύον σφαιρικό κύμα. Σε αυτήν την περίπτωση, βρίσκουμε το πεδίο κύματος που εκπέμπεται από το στοιχείο $dS$ στο σημείο $A$ ως:

Χρησιμοποιώντας την υπόθεση Fresnel έχουμε:

όπου $K\left(\alpha \right)$ είναι μια συνάρτηση που εξαρτάται από το μήκος κύματος και τη γωνία μεταξύ του κανονικού προς το μέτωπο του κύματος και της κατεύθυνσης διάδοσης του δευτερεύοντος κύματος (Εικ. 2).

Ας αναπαραστήσουμε το συνολικό πεδίο κυμάτων στο σημείο $A$ με το ολοκλήρωμα:

Ας πάρουμε ως στοιχείο $dS$ την περιοχή του δακτυλίου, που κόβεται από το μέτωπο του κύματος από δύο απείρως κοντινές ομόκεντρες σφαίρες των οποίων τα κέντρα βρίσκονται στο σημείο $A$ (Εικ. 2). Σε αυτή την περίπτωση, μπορούμε να γράψουμε ότι:

Λαμβάνουμε την απόσταση $r_1.$ ως μεταβλητή ολοκλήρωσης Θεωρούμε τις ποσότητες $r_0$ και $r$ σταθερές. Από το τρίγωνο $DOA$ βρίσκουμε:

\[(r_1)^2=(r_0)^2+(\left(r_0+r\right))^2-2r_0\left(r_0+r\right)cos\beta \left(1.6\right).\ ]

Ας διαφοροποιήσουμε την έκφραση (1.6), έχουμε:

Αντικαθιστώντας την έκφραση (1.7) για $dS$ στον τύπο (1.4), λαμβάνουμε:

όπου η συνάρτηση $K\left(\alpha \right)\ \consider\ as$ συνάρτηση $r_1$. Σε αυτήν την περίπτωση $r_(max)=r+2r_0.$

Απάντηση:$E=\frac(2\pi A_0)(\left(r_0+r\right))e^(i\left(\omega t-kr_0\right))\int\limits^(r_(max))_r (K\left(r_1\right)e^(-ikr_1))dr_1.$

Παράδειγμα 2

Ασκηση:Πώς να χρησιμοποιήσετε την αρχή Huygens-Fresnel για να εξηγήσετε το φαινόμενο της περίθλασης;

Λύση:

Ας υποθέσουμε ότι ένα επίπεδο κύμα προσπίπτει στην οθόνη κάθετα προς την οπή σε αυτό. Σύμφωνα με την αρχή Huygens-Fresnel, κάθε σημείο του τμήματος του μετώπου κύματος, το οποίο απομονώνεται από μια τρύπα στην οθόνη, γίνεται πηγή δευτερογενών κυμάτων. Εάν το μέσο είναι ομοιογενές και ισότροπο, τα δευτερεύοντα κύματα είναι σφαιρικά. Κατά την κατασκευή του περιβλήματος των δευτερευόντων κυμάτων για μια σταθερή χρονική στιγμή, αποδεικνύεται ότι το μπροστινό μέρος του κύματος εισέρχεται στην περιοχή της γεωμετρικής σκιάς, πράγμα που σημαίνει ότι το κύμα κάμπτεται γύρω από την τρύπα.

Τα φαινόμενα της παρεμβολής φωτός σε όλη τους την ποικιλομορφία χρησιμεύουν ως η πιο πειστική απόδειξη της κυματικής φύσης των διεργασιών φωτός. Ωστόσο, η τελική νίκη των κυματικών εννοιών ήταν αδύνατη χωρίς ερμηνεία από την κυματική άποψη του θεμελιώδους και καλά επιβεβαιωμένου από την εμπειρία νόμου της ευθύγραμμης διάδοσης του φωτός.

Οι κυματικές έννοιες στην αρχική μορφή με την οποία τις ανέπτυξε ο Huygens (Treatise on Light, 1690) δεν μπορούσαν να δώσουν μια ικανοποιητική απάντηση στο ερώτημα που τέθηκε. Το δόγμα του Huygens για τη διάδοση του φωτός βασίζεται στην αρχή που φέρει το όνομά του. Σύμφωνα με τις ιδέες του Huygens, το φως, κατ' αναλογία με τον ήχο, είναι κύματα που διαδίδονται σε ένα ειδικό μέσο - τον αιθέρα, ο οποίος καταλαμβάνει όλο το χώρο, ιδίως γεμίζοντας τα κενά μεταξύ των σωματιδίων οποιασδήποτε ουσίας, τα οποία, όπως λέγαμε, βυθίζονται στον ωκεανό. του αιθέρα. Από αυτή την άποψη, ήταν φυσικό να υποθέσουμε ότι η δονητική κίνηση των σωματιδίων του αιθέρα μεταδίδεται όχι μόνο στο σωματίδιο που βρίσκεται στο «μονοπάτι» της δέσμης φωτός, δηλαδή στην ευθεία γραμμή που συνδέει την πηγή φωτός μεγάλο, (Εικ. 1.1) με το επίμαχο σημείο ΕΝΑ, αλλά σε όλα τα σωματίδια που γειτνιάζουν με ΕΝΑ, δηλαδή το φωτεινό κύμα διαδίδεται από ΕΝΑπρος όλες τις κατευθύνσεις, σαν ένα σημείο ΕΝΑχρησίμευε ως πηγή φωτός. Η επιφάνεια που κάμπτεται γύρω από αυτά τα δευτερεύοντα κύματα είναι η επιφάνεια του μετώπου του κύματος. Για την περίπτωση που φαίνεται στο Σχ. 1.1, αυτός ο φάκελος (παχύ τόξο) θα αναπαρασταθεί ως μέρος μιας σφαιρικής επιφάνειας με κέντρο στο μεγάλο, που οριοθετείται από έναν κώνο που οδηγεί στις άκρες μιας κυκλικής οπής στην οθόνη MN. Η αρχή του Huygens κατέστησε δυνατή την αποσαφήνιση των ζητημάτων της ανάκλασης και της διάθλασης του φωτός, συμπεριλαμβανομένου του πολύπλοκου προβλήματος της διπλής διάθλασης. αλλά το πρόβλημα της ευθύγραμμης διάδοσης του φωτός δεν λύθηκε ουσιαστικά, γιατί δεν τέθηκε σε σύνδεση με τα φαινόμενα της απόκλισης από την ευθύγραμμη, δηλ. με τα φαινόμενα της περίθλασης.

Ο λόγος έγκειται στο γεγονός ότι η αρχή του Huygens στην αρχική της μορφή ήταν μια αρχή της οποίας το πεδίο εφαρμογής ήταν το πεδίο της γεωμετρικής οπτικής. Στη γλώσσα της κυματικής οπτικής, αναφερόταν σε περιπτώσεις όπου το μήκος κύματος μπορούσε να θεωρηθεί απειροελάχιστο σε σύγκριση με το μέγεθος του μετώπου κύματος. Ως εκ τούτου, κατέστησε δυνατή την επίλυση μόνο προβλημάτων σχετικά με την κατεύθυνση διάδοσης του μετώπου φωτός και δεν έθιξε ουσιαστικά το ζήτημα της έντασης των κυμάτων που ταξιδεύουν σε διαφορετικές κατευθύνσεις. Αυτή η έλλειψη αναπληρώνεται
Neil Fresnel, ο οποίος έβαλε ένα φυσικό νόημα στην αρχή του Huygens, συμπληρώνοντάς το με την ιδέα της παρεμβολής κυμάτων. Χάρη σε αυτό, η επιφάνεια περιβλήματος των στοιχειωδών κυμάτων, που εισήχθη από τον Huygens καθαρά τυπικά, απέκτησε ένα σαφές φυσικό περιεχόμενο ως επιφάνεια όπου, λόγω της αμοιβαίας παρεμβολής των στοιχειωδών κυμάτων, το κύμα που προκύπτει έχει μια αξιοσημείωτη ένταση.

Η αρχή Huygens-Fresnel που τροποποιήθηκε με αυτόν τον τρόπο γίνεται η βασική αρχή της οπτικής κυμάτων και καθιστά δυνατή τη μελέτη ερωτήσεων που σχετίζονται με την ένταση του προκύπτοντος κύματος σε διαφορετικές κατευθύνσεις, δηλαδή την επίλυση προβλημάτων σχετικά με τη διάθλαση του φωτός (βλ. παρακάτω). Σύμφωνα με αυτό, επιλύθηκε το ζήτημα των ορίων εφαρμογής του νόμου της ευθύγραμμης διάδοσης του φωτός και η αρχή Huygens-Fresnel αποδείχθηκε ότι ήταν εφαρμόσιμη για την αποσαφήνιση του νόμου της διάδοσης κυμάτων οποιουδήποτε μήκους.

Για να βρεθεί η ένταση (πλάτος) του κύματος που προκύπτει, είναι απαραίτητο, σύμφωνα με τον Fresnel, να διατυπωθεί η αρχή του Huygens ως εξής.

Ας περικυκλώσουμε την πηγή μεγάλονοητή κλειστή επιφάνεια μικρόοποιοδήποτε σχήμα (Εικ. 1.2). Η σωστή τιμή της έντασης (πλάτους) της διαταραχής σε οποιοδήποτε σημείο ΣΕεξω απο μικρόμπορεί να ληφθεί ως εξής: εξάλειψη μεγάλο, και την επιφάνεια μικρόθα το θεωρήσουμε ως μια φωτεινή επιφάνεια, η ακτινοβολία επιμέρους στοιχείων της οποίας, φθάνοντας στο ΣΕ, καθορίζει από την ολότητά του τη δράση σε αυτό το σημείο. Ακτινοβολία κάθε στοιχείου dsεπιφάνειες μικρόπρέπει να το φανταστεί κανείς ως ένα σφαιρικό κύμα (δευτερογενές κύμα), που φέρνει σε ένα σημείο ΣΕκούνια:

,

Οπου ένα 0καθορίζεται από το πλάτος, και φ - η φάση της πραγματικής ταλάντωσης που προήλθε μεγάλοσε στοιχείο dsπου βρίσκεται σε απόσταση rαπό σημείο ΣΕ. Σε αυτή την περίπτωση, οι διαστάσεις του στοιχείου dsυποτίθεται ότι είναι τόσο μικρά που φ Και rγια οποιοδήποτε μέρος μπορεί να θεωρηθεί ότι έχει τις ίδιες έννοιες. Με άλλα λόγια, κάθε στοιχείο dsθεωρείται ως κάποια βοηθητική πηγή, άρα το πλάτος ένα 0, ανάλογο του εμβαδού ds.

Το αξίωμα του Fresnel, το οποίο μας επιτρέπει να προσδιορίσουμε ένα 0Και φ μέσα από το πλάτος και τη φάση αυτού που έχει φτάσει dsΟι διακυμάνσεις αντιπροσωπεύουν μια συγκεκριμένη υπόθεση, η καταλληλότητα της οποίας μπορεί να διαπιστωθεί συγκρίνοντας τα συμπεράσματα που εξάγονται με τη βοήθειά της με τα αποτελέσματα του πειράματος.

Δεδομένου ότι οι φάσεις όλων των βοηθητικών πηγών καθορίζονται από τη διαταραχή που προέρχεται από μεγάλο, τότε είναι αυστηρά συνεπείς μεταξύ τους, και, ως εκ τούτου, βοηθητικές πηγές συναφής. Επομένως, τα δευτερεύοντα κύματα που προέρχονται από αυτά θα παρεμβαίνουν μεταξύ τους. Η συνδυασμένη δράση τους σε κάθε σημείο μπορεί να οριστεί ως αποτέλεσμα παρεμβολής, και επομένως, η ιδέα του Huygens για τον ειδικό ρόλο του φακέλου παύει να είναι υπόθεση, αλλά θα πρέπει να είναι μόνο συνέπεια των νόμων της παρεμβολής. Σύμφωνα με το παραπάνω αξίωμα του Fresnel, το ζήτημα της αντικατάστασης των βοηθητικών πηγών μεγάλο, λύνεται μοναδικά μόλις επιλεγεί η βοηθητική επιφάνεια ΜΙΚΡΟ.Η επιλογή αυτής της επιφάνειας είναι εντελώς αυθαίρετη. Επομένως, για κάθε συγκεκριμένο πρόβλημα, θα πρέπει να επιλέγεται με τον πιο συμφέροντα τρόπο επίλυσής του. Εάν η βοηθητική επιφάνεια μικρόσυμπίπτει με το μέτωπο του κύματος που προέρχεται από μεγάλο. (αντιπροσωπεύει μια σφαίρα με κέντρο στο μικρό), τότε όλες οι βοηθητικές πηγές θα έχουν την ίδια φάση. Αν η επιλογή μικρόγίνεται διαφορετικά, οι φάσεις των βοηθητικών πηγών δεν είναι ίδιες, αλλά οι πηγές, φυσικά, παραμένουν συνεκτικές.

Στην περίπτωση που μεταξύ πηγών μεγάλοκαι το σημείο παρατήρησης υπάρχουν αδιαφανείς οθόνες με τρύπες, το αποτέλεσμα αυτών των οθονών μπορεί να ληφθεί υπόψη ως εξής. Επιλέγουμε την επιφάνεια μικρόώστε να συμπίπτει με την επιφάνεια των σήτων παντού, και να σφίγγει τις τρύπες σε αυτές με αυθαίρετο τρόπο, που επιλέγεται ανάλογα με το πρόβλημα που αναλύεται. Στην επιφάνεια των αδιαφανών οθονών, τα πλάτη των βοηθητικών πηγών πρέπει να θεωρούνται ίσα με μηδέν. στην επιφάνεια που διέρχεται από τις οπές των οθονών, τα πλάτη επιλέγονται σύμφωνα με το αξίωμα του Fresnel, δηλαδή σαν να απουσίαζε η οθόνη. Έτσι, θεωρείται ότι το υλικό της οθόνης δεν παίζει ρόλο εκτός εάν η οθόνη είναι διαφανής.

Υπολογίζοντας τα αποτελέσματα της παρεμβολής στοιχειωδών κυμάτων που αποστέλλονται από βοηθητικές πηγές, φτάνουμε στην τιμή του πλάτους (έντασης) σε οποιοδήποτε σημείο ΣΕ, δηλαδή καθορίζουμε το σχέδιο διάδοσης του φωτός. Τα αποτελέσματα αυτών των υπολογισμών επιβεβαιώνονται από πειραματικά δεδομένα. Έτσι, χρησιμοποιώντας τη μέθοδο Huygens-Fresnel, είναι δυνατό να ληφθεί μια σωστή λύση στο ζήτημα της κατανομής της έντασης φωτός τόσο στην περίπτωση της ελεύθερης διάδοσης των κυμάτων φωτός (ευθύγραμμη διάδοση) όσο και στην παρουσία οθονών αποκλεισμού (διάθλαση). .

Το πρώτο πρόβλημα που έπρεπε να εξετάσει ο Fresnel, προτείνοντας μια νέα διατύπωση της αρχής του Huygens, ήταν το πρόβλημα της ευθύγραμμης διάδοσης του φωτός. Ο Fresnel το έλυσε εξετάζοντας την αμοιβαία παρεμβολή δευτερευόντων κυμάτων, χρησιμοποιώντας μια εξαιρετικά οπτική τεχνική που αντικαθιστά πολύπλοκους υπολογισμούς και είναι γενικής σημασίας για την ανάλυση προβλημάτων διάδοσης κυμάτων. Αυτή η μέθοδος ονομάζεται μέθοδος Ζώνες Fresnel.

Εξετάστε τη δράση ενός φωτεινού κύματος που εκπέμπεται από ένα σημείο ΕΝΑ, σε οποιοδήποτε σημείο παρατήρησης ΣΕ. Σύμφωνα με την αρχή Huygens-Fresnel, αντικαθιστούμε τη δράση της πηγής ΕΝΑμε τη δράση φανταστικών πηγών που βρίσκονται στη βοηθητική επιφάνεια μικρό.

Ως τέτοια βοηθητική επιφάνεια μικρόας επιλέξουμε την επιφάνεια του μετώπου κύματος από την οποία προέρχεται ΕΝΑ(επιφάνεια σφαίρας με κέντρο ΕΝΑ, Εικ. 1.3). Ο υπολογισμός του αποτελέσματος της παρεμβολής των δευτερευόντων κυμάτων απλοποιείται πολύ αν εφαρμόσουμε την ακόλουθη τεχνική που υποδεικνύει ο Fresnel: να υπολογίσουμε τη δράση σε ένα σημείο ΣΕσυνδέω-συωδεομαι ΕΝΑΜε ΣΕκαι σπάστε την επιφάνεια μικρόσε ζώνες τέτοιου μεγέθους που οι αποστάσεις από τα άκρα της ζώνης στο Β διαφέρουν κατά λ /2 δηλ.

M 1 B – M 0 B = M 2 B – M 1 B =M 3 B – M 2 B =…= λ/2

(βλ. Εικ. 1.3). Δεν είναι δύσκολο να υπολογιστούν τα μεγέθη των ζωνών που λαμβάνονται με αυτόν τον τρόπο. Από το Σχ. 1,4 παίρνουμε για την πρώτη ζώνη

r 2 =a 2 – (a – x) 2 = (b+ λ/2) 2 – (b+x) 2

Επειδή λ πολύ λίγο σε σύγκριση με ΕΝΑή σι, Οτι

,

και επομένως η περιοχή του σφαιρικού τμήματος που αντιπροσωπεύει την πρώτη ή την κεντρική ζώνη είναι:

Για την περιοχή του τμήματος που αντιπροσωπεύει τις δύο πρώτες ζώνες, βρίσκουμε την τιμή , δηλ. η περιοχή της δεύτερης ζώνης είναι επίσης ίση . Κάθε μία από όλες τις επόμενες ζώνες θα έχει σχεδόν την ίδια περιοχή. Έτσι, η κατασκευή Fresnel διαιρεί την επιφάνεια ενός σφαιρικού κύματος σε ίσες ζώνες, καθεμία από τις οποίες έχει ένα εμβαδόν

Για περαιτέρω υπολογισμούς, χρειάζεται μόνο να λάβετε υπόψη ότι η δράση μεμονωμένων ζωνών σε ένα σημείο ΣΕόσο μικρότερη τόσο μεγαλύτερη είναι η γωνία φ μεταξύ της κανονικής προς την επιφάνεια της ζώνης και της κατεύθυνσης προς ΣΕ. Έτσι, η επίδραση των ζωνών σταδιακά μειώνεται από την κεντρική ζώνη (περίπου Μ 0) σε περιφερειακό. Η αυθαίρετη εισαγωγή αυτού του βοηθητικού παράγοντα εξασθένησης είναι ένα από τα μειονεκτήματα της μεθόδου Fresnel.

Για να ληφθεί το τελικό αποτέλεσμα, μπορεί κανείς να συλλογιστεί ως εξής: αφήστε τη δράση της κεντρικής ζώνης στο σημείο ΣΕεκφράζεται με τη διέγερση δονήσεων με πλάτος s 1, η δράση της γειτονικής ζώνης είναι μια ταλάντωση με πλάτος s 2, το επόμενο - με πλάτος s 3κλπ. Όπως υποδεικνύεται, η επίδραση των ζωνών σταδιακά (αν και αργά) μειώνεται από το κέντρο προς την περιφέρεια, έτσι ώστε s 1> s 2 > s 3 > s 4και τα λοιπά.; δράση Πη ζώνη s nμπορεί να είναι πολύ μικρό αν Παρκετά μεγάλο. Επιπλέον, χάρη στην επιλεγμένη μέθοδο διαχωρισμού σε ζώνες, είναι εύκολο να διαπιστωθεί ότι οι ενέργειες των γειτονικών ζωνών εξασθενούν η μία την άλλη. Πράγματι, από τότε

M 1 B – M 0 B=λ/2Και M 2 B – M 1 B=λ/2

τότε οι φανταστικές πηγές της ζώνης M 0 M 1βρίσκεται ½ λ πιο κοντά στο ΣΕαπό τις αντίστοιχες πηγές ζώνης Μ 1 Μ 2, ώστε οι δονήσεις που αποστέλλονται να φτάνουν ΣΕσε αντίθετες φάσεις. Έτσι, για την ουσία ΣΕη δράση της κεντρικής ζώνης θα αποδυναμωθεί από τη δράση της γειτονικής ζώνης κ.λπ. Συνεχίζοντας αυτά τα επιχειρήματα, βρίσκουμε ότι η τελική τιμή πλάτηταλαντώσεις διεγερμένες σε ένα σημείο ΣΕολόκληρο το σύνολο των ζωνών, δηλαδή ολόκληρο το φωτεινό κύμα, θα είναι ίσο με:

s=s 1 – s 2 + s 3 – s 4 + s 5 – s 6 +…=s 1 – (s 2 - s 3) – (s 4 – s 5) – (s 6 – s 7) – …(1.1)

Από την κατάσταση s 1> s 2 > s 3 > s 4...συνεπάγεται ότι όλες οι εκφράσεις σε παρένθεση είναι θετικές, άρα μικρό<s1.Φωτισμός μιστο σημείο παρατήρησης ΣΕείναι ανάλογο με το τετράγωνο του προκύπτοντος πλάτους δόνησης. Ως εκ τούτου, μι ~ s 2 < s 1 2|.

Άρα το πλάτος μικρόη προκύπτουσα δόνηση που προκύπτει από την αμοιβαία παρεμβολή του φωτός που ταξιδεύει σε ένα σημείο ΣΕαπό διαφορετικά μέρη του σφαιρικού μας κύματος, είναι μικρότερο από το πλάτος που δημιουργείται από τη δράση μιας κεντρικής ζώνης. Έτσι, η δράση ολόκληρου του κύματος σε ένα σημείο ΣΕανάγεται στη δράση του μικρού τμήματός του, μικρότερου από την κεντρική ζώνη με εμβαδόν . Μήκος κύματος φωτός λ πολύ μικρό (για πράσινο φως λ = 5 10 -4 mm). Επομένως, ακόμη και σε απόσταση ΕΝΑΚαι σιτης τάξης του 1 m, η περιοχή του ενεργού τμήματος του κύματος είναι μικρότερη από 1 mm 2. Επομένως, η διάδοση του φωτός από ΕΝΑΠρος την ΣΕΣυμβαίνει πραγματικά σαν η φωτεινή ροή να πήγαινε μέσα σε ένα πολύ στενό κανάλι κατά μήκος ΑΒ, δηλαδή ευθύγραμμα.

Αυτό δεν σημαίνει, ωστόσο, ότι αν τοποθετήσουμε στη γραμμή ΑΒοποιαδήποτε μικρή αδιαφανή οθόνη, μετά στο σημείο ΣΕτο φως δεν θα φτάσει? Άλλωστε, η εισαγωγή μιας οθόνης που θα κάλυπτε, για παράδειγμα, την πρώτη ζώνη, θα παραβίαζε την ορθότητα του συλλογισμού μας. Σε αυτήν την περίπτωση, ο πρώτος όρος της εναλλασσόμενης σειράς (1.1) θα πέσει έξω και τώρα αποδεικνύεται ότι μικρό < |s 2| κλπ., δηλ. μικρόλιγότερη ενότητα s m, Οπου Τ- αριθμός της πρώτης ζώνης που ανοίγει στην άκρη της οθόνης. Αν Τόχι υπέροχο, για παράδειγμα Τ < 10, то освещенность в точке наблюдения ΣΕστον άξονα της οθόνης θα παραμείνει σχεδόν ίδια με την απουσία του. Αλλά εάν μια μικρή οθόνη έχει ανομοιόμορφες άκρες με οδοντωτές άκρες συγκρίσιμες με το πλάτος της ζώνης Fresnel κατά μήκος της οποίας περνά αυτή η άκρη, τότε μειώνει σημαντικά την ένταση στο σημείο παρατήρησης ΣΕ.

Διάλεξη 21. Περίθλαση φωτός.

Αρχή Huygens-Fresnel. Μέθοδος ζώνης Fresnel. Διανυσματικό διάγραμμα. Περίθλαση από κυκλική οπή και κυκλικό δίσκο. Περίθλαση Fraunhofer από σχισμή. Η απόλυτη μετάβαση από την κυματική οπτική στη γεωμετρική οπτική.

Περίθλαση- αυτό είναι το φαινόμενο της απόκλισης από την ευθύγραμμη διάδοση του φωτός, εάν δεν μπορεί να είναι συνέπεια ανάκλασης, διάθλασης ή κάμψης των ακτίνων φωτός που προκαλείται από χωρική αλλαγή του δείκτη διάθλασης. Σε αυτή την περίπτωση, όσο μικρότερο είναι το μήκος κύματος του φωτός, τόσο μικρότερη είναι η απόκλιση από τους νόμους της γεωμετρικής οπτικής.

Σχόλιο. Δεν υπάρχει θεμελιώδης διαφορά μεταξύ της περίθλασης και της παρεμβολής. Και τα δύο φαινόμενα συνοδεύονται από μια ανακατανομή της φωτεινής ροής ως αποτέλεσμα της υπέρθεσης κυμάτων.

Ένα παράδειγμα περίθλασης είναι το φαινόμενο όταν το φως πέφτει σε ένα αδιαφανές διαμέρισμα με μια τρύπα. Σε αυτή την περίπτωση, παρατηρείται ένα μοτίβο περίθλασης στην οθόνη πίσω από το διαμέρισμα στην περιοχή του ορίου της γεωμετρικής σκιάς.

Είναι σύνηθες να γίνεται διάκριση μεταξύ δύο τύπων περίθλασης. Στην περίπτωση που ένα κύμα που προσπίπτει σε ένα διαμέρισμα μπορεί να περιγραφεί από ένα σύστημα ακτίνων παράλληλων μεταξύ τους (για παράδειγμα, όταν η πηγή φωτός είναι αρκετά μακριά), τότε μιλάμε για Περίθλαση Fraunhoferή περίθλαση σε παράλληλες ακτίνες. Σε άλλες περιπτώσεις μιλάνε για Περίθλαση Fresnelή περίθλαση σε αποκλίνουσες ακτίνες.

Κατά την περιγραφή των φαινομένων περίθλασης, είναι απαραίτητο να λυθεί το σύστημα των εξισώσεων Maxwell με τις αντίστοιχες οριακές και αρχικές συνθήκες. Ωστόσο, η εύρεση μιας ακριβούς λύσης στις περισσότερες περιπτώσεις είναι πολύ δύσκολη. Ως εκ τούτου, στην οπτική, χρησιμοποιούνται συχνά κατά προσέγγιση μέθοδοι που βασίζονται στην αρχή του Huygens στη γενικευμένη σύνθεση του Fresnel ή του Kirchhoff.

Αρχή του Huygens.

Διατύπωση της αρχής του Huygens. Κάθε σημείο του περιβάλλοντος, στο οποίο κάποια στιγμή tΗ κίνηση του κύματος έφτασε, χρησιμεύει ως πηγή δευτερεύοντα σφαιρικά κύματα. Το περίβλημα αυτών των κυμάτων δίνει τη θέση του μετώπου κύματος την επόμενη χρονική στιγμή κλεισίματος t+dt. Οι ακτίνες των δευτερευόντων κυμάτων είναι ίσες με το γινόμενο της ταχύτητας φάσης του φωτός και του χρονικού διαστήματος
.

Μια απεικόνιση αυτής της αρχής χρησιμοποιώντας το παράδειγμα ενός κύματος που προσπίπτει σε ένα αδιαφανές διαμέρισμα με μια τρύπα δείχνει ότι το κύμα διεισδύει στην περιοχή της γεωμετρικής σκιάς. Αυτή είναι μια εκδήλωση περίθλασης.

Ωστόσο, η αρχή του Huygens δεν παρέχει εκτιμήσεις για την ένταση των κυμάτων που διαδίδονται σε διαφορετικές κατευθύνσεις.

Αρχή Huygens-Fresnel.

Ο Fresnel συμπλήρωσε την αρχή του Huygens με την ιδέα της παρεμβολής δευτερευόντων κυμάτων. Από τα πλάτη των δευτερευόντων κυμάτων, λαμβάνοντας υπόψη τις φάσεις τους, μπορεί κανείς να βρει το πλάτος του κύματος που προκύπτει σε οποιοδήποτε σημείο του χώρου.

Κάθε μικρό στοιχείο της επιφάνειας του κύματος είναι μια πηγή ενός δευτερεύοντος σφαιρικού κύματος, το πλάτος του οποίου είναι ανάλογο με το μέγεθος του στοιχείου dSκαι του οποίου η εξίσωση κατά μήκος της ακτίνας έχει τη μορφή

η εδώ ένα 0 - συντελεστής ανάλογος με το πλάτος των ταλαντώσεων των σημείων στην επιφάνεια του κύματος dS,
- συντελεστής ανάλογα με τη γωνία μεταξύ της ακτίνας και του διανύσματος
, και τέτοια ώστε στο
παίρνει τη μέγιστη τιμή και πότε
- ελάχιστο (κοντά στο μηδέν).

Το πλάτος της προκύπτουσας ταλάντωσης σε κάποιο σημείο παρατήρησης Rκαθορίζεται από την αναλυτική έκφραση της αρχής Huygens-Fresnel, η οποία προέκυψε Kirchhoff:

Το ολοκλήρωμα λαμβάνεται πάνω από την επιφάνεια κύματος που καταγράφεται σε κάποια χρονική στιγμή. Για ένα κύμα που διαδίδεται ελεύθερα, η τιμή του ολοκληρώματος δεν εξαρτάται από την επιλογή της επιφάνειας ολοκλήρωσης μικρό.

Σαφής υπολογισμός του πλάτους της προκύπτουσας ταλάντωσης χρησιμοποιώντας τον τύπο Kirchhoffμια μάλλον εντατική διαδικασία, οπότε στην πράξη χρησιμοποιούν κατά προσέγγιση μέθοδοιβρίσκοντας την τιμή αυτού του ολοκληρώματος.

Να βρείτε το πλάτος των ταλαντώσεων στο σημείο παρατήρησης Πολόκληρη την επιφάνεια του κύματος μικρόχωρισμένο σε τμήματα ( Ζώνες Fresnel). Ας υποθέσουμε ότι παρατηρούμε περίθλαση σε αποκλίνουσες ακτίνες (διάθλαση Fresnel), δηλ. θεωρούμε ένα σφαιρικό που διαδίδεται από κάποια σημειακή πηγή μεγάλο. Το κύμα διαδίδεται στο κενό.

Ας διορθώσουμε την επιφάνεια του κύματος σε κάποια χρονική στιγμή t. Έστω η ακτίνα αυτής της επιφάνειας ένα. Γραμμή LPτέμνει την επιφάνεια του κύματος στο σημείο Ο. Ας υποθέσουμε ότι η απόσταση μεταξύ των σημείων ΣΧΕΤΙΚΑ ΜΕΚαι Rισοδυναμεί σι. Από σημείο Rσχεδιάστε διαδοχικά σφαίρες των οποίων οι ακτίνες
. Δύο γειτονικές σφαίρες «έκοψαν» τμήματα δακτυλίου στην επιφάνεια του κύματος, που ονομάζονται Ζώνες Fresnel. (Όπως είναι γνωστό, δύο σφαίρες τέμνονται κατά μήκος ενός κύκλου που βρίσκεται σε ένα επίπεδο κάθετο στην ευθεία γραμμή στην οποία βρίσκονται τα κέντρα αυτών των σφαιρών). Ας βρούμε την απόσταση από το σημείο Ο έως το όριο του αριθμού ζώνης Μ. Έστω η ακτίνα του εξωτερικού ορίου της ζώνης Fresnel ίση με r Μ. Επειδή η ακτίνα της επιφάνειας του κύματος είναι ένα, Οτι .

Εν,

Να γιατί
, που
.

Για ορατά μήκη κύματος και όχι πολύ μεγάλες τιμές αριθμού Μμπορούμε να παραμελήσουμε τον όρο
σε σύγκριση με το Μ. Επομένως, στην προκειμένη περίπτωση
και για την τετραγωνική ακτίνα παίρνουμε την έκφραση
, στην οποία η τελευταία θητεία μπορεί και πάλι να παραμεληθεί. Στη συνέχεια η ακτίνα Μη ζώνη Fresnel (για περίθλαση σε αποκλίνουσες ακτίνες)

.

Συνέπεια. Για την περίθλαση σε παράλληλες ακτίνες (διάθλαση Fraunhofer), η ακτίνα των ζωνών Fresnel προκύπτει περνώντας στο όριο ένα:

.

Τώρα ας συγκρίνουμε τις περιοχές των ζωνών Fresnel. Περιοχή ενός τμήματος μιας σφαιρικής επιφάνειας που βρίσκεται μέσα Μη ζώνη, όπως είναι γνωστό, είναι ίση με
. Ζώνη με αριθμό Μπερικλείεται μεταξύ των ορίων ζωνών με αριθμούς ΜΚαι Μ-1. Επομένως το εμβαδόν του είναι ίσο

.

Μετά τους μετασχηματισμούς, η έκφραση θα πάρει τη μορφή
.

Αν παραμελήσουμε την αξία
, τότε από την έκφραση
συνεπάγεται ότι για μικρούς αριθμούς η περιοχή των ζωνών δεν εξαρτάται από τον αριθμό Μ.

Εύρεση του πλάτους που προκύπτει στο σημείο παρατήρησης Rγίνεται ως εξής. Επειδή τα εκπεμπόμενα δευτερεύοντα κύματα είναι συνεκτικά και οι αποστάσεις από τα παρακείμενα όρια στο σημείο Rδιαφέρουν κατά το ήμισυ του μήκους κύματος, τότε η διαφορά φάσης των ταλαντώσεων από δευτερεύουσες πηγές σε αυτά τα όρια που φτάνουν στο σημείο R, ισούται με  (όπως λένε, οι ταλαντώσεις έρχονται σε αντιφάση). Ομοίως, για οποιοδήποτε σημείο σε οποιαδήποτε ζώνη, είναι βέβαιο ότι υπάρχει ένα σημείο στη γειτονική ζώνη, οι ταλαντώσεις από το οποίο προέρχονται Rσε αντιφάση. Το πλάτος του διανύσματος κύματος είναι ανάλογο με το εμβαδόν της ζώνης
. Αλλά οι περιοχές των ζωνών είναι οι ίδιες, και όσο αυξάνεται ο αριθμός Μη γωνία  αυξάνεται, άρα η τιμή
μειώνεται. Επομένως, μπορεί να γραφτεί μια διατεταγμένη ακολουθία πλάτους. Στο διάγραμμα πλάτους-διανύσματος, λαμβάνοντας υπόψη τη διαφορά φάσης, αυτή η ακολουθία απεικονίζεται από αντίθετα κατευθυνόμενα διανύσματα, επομένως

Ας χωρίσουμε την πρώτη ζώνη σε μεγάλο αριθμό Νεσωτερικές ζώνες με τον ίδιο τρόπο όπως παραπάνω, αλλά τώρα οι αποστάσεις από τα όρια δύο παρακείμενων εσωτερικών ζωνών στο σημείο Rθα διαφέρει κατά ένα μικρό ποσό
. Επομένως, η διαφορά φάσης μεταξύ των κυμάτων που φτάνουν σε ένα σημείο Rθα ισούται με μια μικρή τιμή
. Στο διάγραμμα πλάτους-διανύσματος, το διάνυσμα πλάτους από καθεμία από τις εσωτερικές ζώνες θα περιστραφεί κατά μια μικρή γωνία σε σχέση με την προηγούμενη, επομένως το πλάτος της συνολικής ταλάντωσης από τις πρώτες εσωτερικές ζώνες θα αντιστοιχεί στο διάνυσμα
που συνδέει την αρχή και το τέλος μιας διακεκομμένης γραμμής. Όσο αυξάνεται ο αριθμός της εσωτερικής ζώνης, η συνολική διαφορά φάσης θα αυξάνεται και στο όριο της πρώτης ζώνης θα γίνεται ίση με. Αυτό σημαίνει το διάνυσμα πλάτους από την τελευταία εσωτερική ζώνη
που κατευθύνεται απέναντι από το διάνυσμα πλάτους από την πρώτη εσωτερική ζώνη
. Στο όριο ενός απείρως μεγάλου αριθμού εσωτερικών ζωνών, αυτή η διακεκομμένη γραμμή θα μετατραπεί σε μέρος της σπείρας.

ΕΝΑ το πλάτος των ταλαντώσεων από την πρώτη ζώνη Fresnel θα αντιστοιχεί τότε στο διάνυσμα , από δύο ζώνες - και τα λοιπά. Σε περίπτωση μεταξύ του σημείου Rκαι δεν υπάρχουν εμπόδια με την πηγή φωτός, ένας άπειρος αριθμός ζωνών θα είναι ορατός από το σημείο παρατήρησης, έτσι η σπείρα θα τυλιχτεί γύρω από το εστιακό σημείο φά. Επομένως, ένα ελεύθερο κύμα με ένταση ΕγώΤο 0 αντιστοιχεί στο διάνυσμα πλάτους , κατευθυνόμενη σε ένα σημείο φά.

Από το σχήμα φαίνεται ότι για το πλάτος από την πρώτη ζώνη μπορεί κανείς να λάβει την εκτίμηση
, άρα η ένταση από την πρώτη ζώνη
- 4 φορές την ένταση του προσπίπτοντος κύματος. Ισότητα
μπορεί να ερμηνευθεί με άλλο τρόπο. Αν για άπειρο αριθμό ανοιχτών ζωνών το συνολικό πλάτος γράφεται στη μορφή

(Μείναι ζυγός αριθμός), μετά από
ακολουθεί αξιολόγηση
.

Σχόλιο. Αν με κάποιο τρόπο αλλάξεις τις φάσεις των ταλαντώσεων στο σημείο Rαπό ζυγές ή περιττές ζώνες κατά , ή για να κλείσουμε ζώνες άρτιες ή περιττές, τότε το συνολικό πλάτος θα αυξηθεί σε σύγκριση με το πλάτος του ανοιχτού κύματος. Έχει αυτή την ιδιοκτησία πλάκα ζώνης- μια επίπεδη-παράλληλη γυάλινη πλάκα με εγχάρακτους ομόκεντρους κύκλους, η ακτίνα της οποίας συμπίπτει με τις ακτίνες των ζωνών Fresnel. Η πλάκα ζώνης «απενεργοποιεί» ζώνες Fresnel άρτιες ή περιττές, γεγονός που οδηγεί σε αύξηση της έντασης φωτός στο σημείο παρατήρησης.

Περίθλαση από στρογγυλή οπή.

Ο συλλογισμός που δόθηκε παραπάνω μας επιτρέπει να συμπεράνουμε ότι το πλάτος της ταλάντωσης στο σημείο Rεξαρτάται από τον αριθμό των ζωνών Fresnel. Εάν ένας περιττός αριθμός ζωνών Fresnel είναι ανοιχτός για ένα σημείο παρατήρησης, τότε σε αυτό το σημείο θα υπάρχει μια μέγιστη ένταση. Εάν ένας άρτιος αριθμός ζωνών είναι ανοιχτός, τότε ο ελάχιστος.

Το σχέδιο περίθλασης από μια στρογγυλή τρύπα μοιάζει με εναλλασσόμενους φωτεινούς και σκοτεινούς δακτυλίους. Καθώς η ακτίνα της οπής αυξάνεται (και ο αριθμός των ζωνών Fresnel αυξάνεται), η εναλλαγή των σκοτεινών και φωτεινών δακτυλίων θα παρατηρείται μόνο κοντά στο όριο της γεωμετρικής σκιάς και ο φωτισμός στο εσωτερικό θα παραμείνει ουσιαστικά αμετάβλητος.

Διατυπώστε την αρχή Huygens-Fresnel. 1. Όλες οι δευτερεύουσες πηγές του μετώπου κύματος που προέρχονται από μία πηγή είναι συνεπείς μεταξύ τους. 2. Για δευτερεύουσες πηγές ισχύει η αρχή της υπέρθεσης. 3. Ίσες περιοχές της επιφάνειας του κύματος εκπέμπουν ίσες εντάσεις κατά τον υπολογισμό του πλάτους των ταλαντώσεων φωτός που διεγείρονται από την πηγή S 0 σε ένα αυθαίρετο σημείο M, η πηγή S 0 μπορεί να αντικατασταθεί από ένα ισοδύναμο σύστημα δευτερευουσών πηγών - μικρά τμήματα dS οποιουδήποτε κλειστή βοηθητική επιφάνεια S, σχεδιασμένη έτσι ώστε να καλύπτει την πηγή S 0 και να μην καλύπτει το υπό εξέταση σημείο M

1. Οι δευτερεύουσες πηγές είναι συνεκτικές S 0 μεταξύ τους, επομένως τα δευτερεύοντα κύματα που διεγείρονται από αυτές παρεμβάλλονται όταν υπερτίθενται

   Το πλάτος dA των ταλαντώσεων που διεγείρονται στο σημείο M από μια δευτερεύουσα πηγή είναι ανάλογο με το λόγο της περιοχής dS του αντίστοιχου τμήματος του επιφανειακού κύματος S προς την απόσταση r από αυτό στο σημείο M και εξαρτάται από τη γωνία μεταξύ της εξωτερικής κανονικής προς την επιφάνεια του κύματος και την κατεύθυνση από το στοιχείο dS στο σημείο Μ.

   Εάν μέρος της επιφάνειας S καταλαμβάνεται από αδιαφανή οθόνες, τότε οι αντίστοιχες δευτερεύουσες πηγές δεν εκπέμπουν, και οι υπόλοιπες εκπέμπουν το ίδιο όπως και στην απουσία οθονών.

Αρχή Huygens-Fresnel. Η ουσία του είναι η εξής: για κάθε συγκεκριμένη εργασία, το μέτωπο κύματος θα πρέπει να χωρίζεται με συγκεκριμένο τρόπο σε τμήματα (ζώνες Fresnel), τα οποία θεωρούνται ως ανεξάρτητες πανομοιότυπες πηγές κυμάτων. το πλάτος (και η ένταση) του κύματος στο σημείο παρατήρησης καθορίζεται ως αποτέλεσμα παρεμβολής από κύματα που υποτίθεται ότι δημιουργούνται από μεμονωμένες ζώνες.

Εξηγήστε την είσοδο του φωτός στην περιοχή μιας γεωμετρικής σκιάς χρησιμοποιώντας την αρχή του Huygens. Κάθε σημείο του τμήματος μετώπου κύματος που απομονώνεται από την οπή χρησιμεύει ως πηγή δευτερευόντων κυμάτων που κάμπτονται γύρω από τις άκρες της οπής. τρύπα.

Τι είναι η περίθλαση; Το φαινόμενο των κυμάτων φωτός που εκτρέπονται από την ευθεία διάδοση όταν περνούν μέσα από τρύπες και κοντά στα άκρα των οθονών ονομάζεται περίθλαση (η κάμψη του φωτός γύρω από τα επερχόμενα εμπόδια). Το φαινόμενο της απόκλισης των κυμάτων φωτός από την ευθύγραμμη διάδοση κατά τη διέλευση από τρύπες και κοντά στα άκρα των οθονών ονομάζεται περίθλαση (κάμψη φωτός γύρω από επερχόμενα εμπόδια που παρατηρούνται κατά τη διάδοση του φωτός σε ένα μέσο με έντονες ανομοιογένειες, τις διαστάσεις). των οποίων είναι συγκρίσιμα με το μήκος κύματος και σχετίζονται με αποκλίσεις από τους νόμους της γεωμετρικής οπτικής

Ορίστε την περίθλαση Fresnel και την περίθλαση Fraunhofer.εάν το σχήμα περίθλασης παρατηρείται σε πεπερασμένη απόσταση από το αντικείμενο που προκαλεί περίθλαση και πρέπει να ληφθεί υπόψη η καμπυλότητα του μετώπου κύματος, τότε μιλάμε για Περίθλαση Fresnel. Με την περίθλαση Fresnel, μια εικόνα περίθλασης ενός εμποδίου παρατηρείται στην οθόνη.

εάν τα μέτωπα των κυμάτων είναι επίπεδα (οι ακτίνες είναι παράλληλες) και το μοτίβο περίθλασης παρατηρείται σε απείρως μεγάλη απόσταση (για αυτό χρησιμοποιούνται φακοί), τότε μιλάμε για Περίθλαση Fraunhofer.

Τι είναι η μέθοδος ζώνης Fresnel; Η διαίρεση της επιφάνειας κύματος S σε ζώνες, τα όρια της πρώτης (κεντρικής) ζώνης είναι τα σημεία της επιφάνειας S που βρίσκονται σε απόσταση l+λ\2 από το σημείο Μ. Τα σημεία της σφαίρας βρίσκονται σε απόσταση l+2λ\2, l+3λ\2 από το σημείο Μ, εικόνα ζώνες Fresnel. Όταν αυτές οι ταλαντώσεις υπερτίθενται, εξασθενούν αμοιβαία η μία την άλλη A=A 1 -A 2 +A 3 -A 4 …+A i Με την αύξηση του αριθμού της ζώνης, μειώνοντας την ένταση ακτινοβολίας της ζώνης προς την κατεύθυνση t.M, δηλαδή μειώνοντας A i A 1 > A i >A 3 …>A i

Γιατί στη μέθοδο της ζώνης Fresnel επιλέγονται με τέτοιο τρόπο ώστε οι αποστάσεις από τις γειτονικές ζώνες να διαφέρουν κατά /2; /2 είναι η διαφορά διαδρομής. Οι ταλαντώσεις που διεγείρονται στο σημείο P, μεταξύ δύο γειτονικών ζωνών, είναι αντίθετες σε φάση

A m = (A m-1 + A m+1)/2; Α=Α 1/2

Τι είναι ένα πλέγμα περίθλασης; Το πλέγμα περίθλασης είναι μια οπτική συσκευή που λειτουργεί με βάση την αρχή της περίθλασης του φωτός και είναι μια συλλογή από μεγάλο αριθμό γραμμών σε τακτική απόσταση (σχισμές, προεξοχές) που εφαρμόζονται σε μια συγκεκριμένη επιφάνεια. Η πρώτη περιγραφή του φαινομένου έγινε από τον James Gregory, ο οποίος χρησιμοποίησε φτερά πουλιών ως πλέγμα.

Ποια είναι η περίοδος ενός πλέγματος περίθλασης; Η απόσταση μέσω της οποίας επαναλαμβάνονται οι γραμμές στο πλέγμα ονομάζεται περίοδος του πλέγματος περίθλασης. Συμβολίζεται με το γράμμα δ. Εάν ο αριθμός των κτυπημάτων είναι γνωστός ( Ν), ανά 1 mm τρίψιμο, τότε η περίοδος τριψίματος βρίσκεται χρησιμοποιώντας τον τύπο: 0,001 / Ν

Γιατί το φυσικό φως χωρίζεται σε ένα φάσμα όταν το φως διέρχεται από ένα πλέγμα περίθλασης; Η θέση των κύριων μεγίστων εξαρτάται από το μήκος κύματος λ, επομένως, όταν το λευκό φως διέρχεται από το πλέγμα, όλα τα μέγιστα εκτός από το κεντρικό (m = 0) θα αποσυντεθούν σε ένα φάσμα, η ιώδης περιοχή του οποίου θα είναι στραμμένη προς το κέντρο του σχεδίου περίθλασης, η κόκκινη περιοχή προς τα έξω.

Ποια είναι η ανάλυση ενός πλέγματος περίθλασης; Η ανάλυση του πλέγματος αποδεικνύεται ίση με R = mN. Έτσι, η ανάλυση του πλέγματος εξαρτάται από τη σειρά m του φάσματος και από τον συνολικό αριθμό N γραμμών του λειτουργικού τμήματος του πλέγματος, δηλ. εκείνο το τμήμα από το οποίο διέρχεται η υπό μελέτη ακτινοβολία και από το οποίο εξαρτάται το μοτίβο περίθλασης που προκύπτει. Η ανάλυση / ενός πλέγματος περίθλασης χαρακτηρίζει την ικανότητα του πλέγματος να διαχωρίζει τα μέγιστα φωτισμού για δύο μήκη κύματος  1 και  2 κοντά το ένα στο άλλο σε ένα δεδομένο φάσμα. Εδώ   2 – 1 . Αν /kN, τότε τα μέγιστα φωτισμού για  1 και  2 δεν επιλύονται στο φάσμα kth τάξης.

Τι είναι η περίθλαση φωτός

Η περίθλαση είναι ένα σύνολο φαινομένων που παρατηρούνται κατά τη διάδοση του φωτός σε ένα μέσο με έντονες ανομοιογένειες και σχετίζονται με αποκλίσεις από τους νόμους της γεωμετρικής οπτικής.

Η περίθλαση των κυμάτων φωτός καθορίζει την ποιότητα των οπτικών συσκευών, ιδιαίτερα την ανάλυσή τους.

Η κάμψη των ηχητικών κυμάτων γύρω από τα εμπόδια (δηλαδή η περίθλαση των ηχητικών κυμάτων) παρατηρείται συνεχώς στην καθημερινή ζωή. Για την παρατήρηση της περίθλασης των κυμάτων φωτός, είναι απαραίτητο να δημιουργηθούν ειδικές συνθήκες. Αυτό οφείλεται στα μικρά μήκη κύματος του φωτός. Γνωρίζουμε ότι στο όριο στο l→ 0 οι νόμοι της κυματικής οπτικής μετατρέπονται σε νόμους της γεωμετρικής οπτικής. Κατά συνέπεια, οι αποκλίσεις από τους νόμους της γεωμετρικής οπτικής, ενώ άλλα πράγματα είναι ίσα, αποδεικνύονται μικρότερες, όσο μικρότερο είναι το μήκος κύματος.

Αρχή Huygens Fresnel.

Η διείσδυση των κυμάτων φωτός στην περιοχή μιας γεωμετρικής σκιάς μπορεί να εξηγηθεί χρησιμοποιώντας την αρχή του Huygens. Ωστόσο, αυτή η αρχή δεν παρέχει πληροφορίες σχετικά με το πλάτος, και επομένως την ένταση, των κυμάτων που διαδίδονται σε διαφορετικές κατευθύνσεις. Ο Fresnel συμπλήρωσε την αρχή του Huygens με την ιδέα της παρεμβολής δευτερευόντων κυμάτων, δηλαδή, σύμφωνα με τον Fresnel, όλες οι δευτερεύουσες πηγές είναι συνεπείς μεταξύ τους. Λαμβάνοντας υπόψη τα πλάτη και τις φάσεις των δευτερευόντων κυμάτων μας επιτρέπει να βρούμε το πλάτος του προκύπτοντος κύματος

Εικ.8.3

σε οποιοδήποτε σημείο του χώρου. Η αρχή Huygens που αναπτύχθηκε με αυτόν τον τρόπο ονομάζεται αρχή Huygens-Fresnel.

Σύμφωνα με την αρχή Huygens-Fresnel, κάθε στοιχείο της επιφάνειας κύματος S (Εικ. 8.3) χρησιμεύει ως πηγή ενός δευτερεύοντος σφαιρικού κύματος, το πλάτος του οποίου είναι ανάλογο με την τιμή του στοιχείου dS. Το πλάτος ενός σφαιρικού κύματος μειώνεται με την απόσταση r από την πηγή σύμφωνα με το νόμο 1/r (Συνεπώς, από κάθε τμήμα dS της επιφάνειας κύματος, μια ταλάντωση έρχεται στο σημείο P που βρίσκεται μπροστά από αυτήν την επιφάνεια

Σε αυτήν την έκφραση, η φάση της ταλάντωσης στη θέση της επιφάνειας κύματος S, k είναι ο αριθμός κύματος, r είναι η απόσταση από το επιφανειακό στοιχείο dS στο σημείο P. Ο πολλαπλασιαστής καθορίζεται από το πλάτος της ταλάντωσης φωτός στη θέση dS. Ο συντελεστής K εξαρτάται από τη γωνία j μεταξύ του κανονικού n προς τη θέση dS και της κατεύθυνσης από dS προς το σημείο P. Στο j =0 αυτός ο συντελεστής είναι μέγιστος, στο j =p/2 πηγαίνει στο μηδέν.

Η προκύπτουσα ταλάντωση στο σημείο P είναι μια υπέρθεση ταλαντώσεων που λαμβάνονται για ολόκληρη την επιφάνεια κύματος S:

Αυτός ο τύπος είναι μια αναλυτική έκφραση της αρχής Huygens-Fresnel.

Αυτό σημαίνει ότι κατά τον υπολογισμό του πλάτους της ταλάντωσης που δημιουργείται στο σημείο P από ένα κύμα φωτός που διαδίδεται από μια πραγματική πηγή, είναι δυνατό να αντικατασταθεί αυτή η πηγή με ένα σύνολο δευτερευουσών πηγών που βρίσκονται κατά μήκος της επιφάνειας του κύματος. Και αυτή είναι η ουσία της αρχής Huygens-Fresnel.

Δεδομένου ότι οι δευτερεύουσες πηγές είναι συνεκτικές μεταξύ τους, το σχέδιο περίθλασης θα αντιπροσωπεύει μια ανακατανομή της έντασης της φωτεινής ροής. Δεν υπάρχει σημαντική φυσική διαφορά μεταξύ παρεμβολής και περίθλασης. Και τα δύο φαινόμενα περιλαμβάνουν την ανακατανομή της φωτεινής ροής ως αποτέλεσμα της υπέρθεσης κυμάτων. Για ιστορικούς λόγους, η ανακατανομή της έντασης που προκύπτει από την υπέρθεση κυμάτων που διεγείρονται από έναν πεπερασμένο αριθμό διακριτών συνεκτικών πηγών ονομάζεται συνήθως κυματική παρεμβολή. Η ανακατανομή της έντασης που συμβαίνει ως αποτέλεσμα της υπέρθεσης κυμάτων που διεγείρονται από συνεκτικές πηγές που βρίσκονται συνεχώς ονομάζεται συνήθως περίθλαση κυμάτων. Η παρατήρηση περίθλασης πραγματοποιείται συνήθως σύμφωνα με το ακόλουθο σχήμα. Στη διαδρομή ενός φωτεινού κύματος που διαδίδεται από μια συγκεκριμένη πηγή, τοποθετείται ένα αδιαφανές φράγμα που καλύπτει μέρος της επιφάνειας κύματος του φωτεινού κύματος. Πίσω από το φράγμα υπάρχει μια οθόνη στην οποία εμφανίζεται ένα μοτίβο περίθλασης.

Υπάρχουν δύο είδη φαινομένων περίθλασης ανάλογα με την απόσταση του σημείου παρατήρησης από το εμπόδιο ή την ανομοιογένεια, καθώς και με τον τύπο του μετώπου κύματος στο σημείο παρατήρησης. Εάν το σημείο παρατήρησης βρίσκεται αρκετά μακριά από το εμπόδιο και ένα επίπεδο κύμα φτάσει στο σημείο παρατήρησης αφού αλληλεπιδράσει με την ανομοιογένεια, τότε μιλάμε για περίθλαση Fraunhofer. Σε άλλες περιπτώσεις μιλάμε για περίθλαση Fresnel.

Ως παράδειγμα, εξετάστε την αλληλεπίδραση μιας φωτεινής ροής από μια πηγή με ένα αδιαφανές επίπεδο φράγμα στο οποίο κόβεται μια τρύπα αυθαίρετου σχήματος. Στην περίθλαση Fresnel (Εικ. 8.4a), τα σφαιρικά κύματα φτάνουν στο σημείο παρατήρησης που βρίσκεται στην οθόνη σε μια πεπερασμένη απόσταση από το εμπόδιο από μια πηγή που βρίσκεται σε μια πεπερασμένη απόσταση από το εμπόδιο και από σημεία του περιγράμματος που περιορίζουν την τρύπα. Κατά τη διάρκεια της περίθλασης Fraunhofer (Εικ. 8.4β) ενός φωτεινού κύματος από μια πηγή απείρως μακριά από το εμπόδιο, επίπεδα κύματα φτάνουν στο σημείο παρατήρησης, επίσης απείρως μακριά από το εμπόδιο.

Εικ.8.4

Από αυτό προκύπτει ότι η περίθλαση Fresnel εκδηλώνεται με τη μορφή παρεμβολής σφαιρικών (κυλινδρικών) κυμάτων που φτάνουν στο σημείο παρατήρησης από την ανομοιογένεια με την οποία αλληλεπιδρά το ηλεκτρομαγνητικό κύμα (φως). Η παρεμβολή των κυλινδρικών κυμάτων, που είναι ειδική περίπτωση της παρεμβολής των σφαιρικών κυμάτων, συμβαίνει στην περίπτωση που τόσο το κύμα φωτός όσο και η ανομοιογένεια του μέσου διάδοσης έχουν κοινό άξονα συμμετρίας, λόγω του οποίου το κυματικό πεδίο και η ανομοιογένεια οι παράμετροι είναι ίδιες σε κάθε τμήμα που είναι κάθετο στον άξονα συμμετρίας.

Η περίθλαση Fraunhofer προκαλείται από την παρεμβολή παράλληλων, επίπεδων κυμάτων (ακτίνων) που φτάνουν στο σημείο παρατήρησης από μια ανομοιογένεια με την οποία αλληλεπιδρά ένα ηλεκτρομαγνητικό κύμα (φως). Χρήση φακού 2 (Εικ. 8.5)

Εικ.8.5

Η περίθλαση Fraunhofer μπορεί να παρατηρηθεί σε μια οθόνη που βρίσκεται σε πεπερασμένη απόσταση από το εμπόδιο με το οποίο αλληλεπιδρά το φως (ένα ηλεκτρομαγνητικό κύμα). Ο φακός 1 (Εικ. 8.6), στην εστία του οποίου βρίσκεται η πηγή, χρησιμοποιείται για να φωτίσει μια τρύπα στο στόχο με ένα επίπεδο κύμα.

Ζώνες Fresnel

Όπως προκύπτει από την αρχή Huygens-Fresnel, το πλάτος του κύματος στο σημείο παρατήρησης (Εικ. 8.3), που δημιουργήθηκε από την πηγή ενός μονοχρωματικού ηλεκτρομαγνητικού κύματος στο σημείο, μπορεί να βρεθεί ως υπέρθεση των πλατών των σφαιρικών κυμάτων που εκπέμπονται από δευτερεύουσες πηγές σε αυθαίρετη κλειστή επιφάνεια που καλύπτει το σημείο σύμφωνα με την έκφραση ( 8.2).

Οι υπολογισμοί με χρήση του τύπου (8.2) είναι, γενικά, πολύ δύσκολο έργο. Ωστόσο, όπως έδειξε ο Fresnel, σε περιπτώσεις που χαρακτηρίζονται από συμμετρία, το πλάτος της δόνησης που προκύπτει μπορεί να βρεθεί με απλή αλγεβρική ή γεωμετρική άθροιση.

Για να κατανοήσουμε την ουσία της μεθόδου που ανέπτυξε ο Fresnel, το πλάτος της δόνησης φωτός που διεγείρεται στο σημείο P από ένα σφαιρικό κύμα που διαδίδεται σε ένα ισότροπο, ομοιογενές μέσο από μια σημειακή πηγή S (Εικ. 8.6). Οι επιφάνειες κύματος ενός τέτοιου φωτεινού κύματος είναι συμμετρικές σε σχέση με την ευθεία γραμμή SP. Εκμεταλλευόμενοι αυτό, χωρίζουμε την επιφάνεια κύματος που φαίνεται στο σχήμα σε ζώνες δακτυλίου, κατασκευασμένες έτσι ώστε οι αποστάσεις από τις άκρες κάθε ζώνης έως το σημείο P να διαφέρουν κατά l/2. Οι ζώνες με αυτή την ιδιότητα ονομάζονται ζώνες Fresnel.

Εικ.8.6

Από το Σχ. 8.6 είναι σαφές ότι η απόσταση b m από το εξωτερικό άκρο του mth είναι ίση με

(8.3)

(b είναι η απόσταση από την κορυφή της επιφάνειας κύματος O έως το σημείο P). Οι ταλαντώσεις που έρχονται στο σημείο P από παρόμοια σημεία δύο γειτονικών ζωνών (δηλαδή, από σημεία που βρίσκονται στο μέσο των ζωνών, ή στα εξωτερικά άκρα των ζωνών κ.λπ.) βρίσκονται σε αντιφάση. Επομένως, οι προκύπτουσες ταλαντώσεις που δημιουργούνται από καθεμία από τις ζώνες ως σύνολο θα διαφέρουν σε φάση κατά p για γειτονικές ζώνες.

Ας υπολογίσουμε την ακτίνα των ζωνών Fresnel. Έτσι, το όριο της ζώνης Fresnel () διαχωρίζεται από την ευθεία γραμμή (Εικ. 8.6) σε μια απόσταση που ονομάζεται ακτίνα της ζώνης Fresnel. Ας βρούμε την ακτίνα της ζώνης Fresnel. Όπως προκύπτει από γεωμετρικές εκτιμήσεις (Εικ. 8.7):

πού είναι η απόσταση κατά μήκος μιας ευθείας γραμμής από την πηγή έως το κέντρο του μετώπου του κύματος. - απόσταση κατά μήκος μιας ευθείας γραμμής από το κέντρο του μετώπου του κύματος μέχρι το σημείο παρατήρησης.

Από το 8.4, παραμελώντας , για όχι πολύ μεγάλο βρίσκουμε:

(8.5)

Χρησιμοποιώντας αυτή τη σχέση από το (8.4) βρίσκουμε

(8.6)

Εικ8.7

Στη συγκεκριμένη περίπτωση μιας πηγής απείρως μακριά από το σημείο παρατήρησης (), το μέτωπο κύματος είναι ένα επίπεδο και η ακτίνα της m-ης ζώνης Fresnel καθορίζεται από τον τύπο

Λαμβάνοντας υπόψη (Εικ. 8.5), βρίσκουμε το εμβαδόν ενός σφαιρικού τμήματος ακτίνας και ύψους

και βρίσκουμε ότι η περιοχή της ζώνης Fresnel είναι:

Δεν εξαρτάται από το .

Έτσι, οι περιοχές των ζωνών Fresnel είναι περίπου οι ίδιες. Η απόσταση b m από τη ζώνη στο σημείο P αυξάνεται αργά με τον αριθμό της ζώνης m. Η γωνία j μεταξύ των κανονικών στοιχείων της ζώνης και της κατεύθυνσης προς το σημείο P αυξάνεται επίσης με το m. Όλα αυτά οδηγούν στο γεγονός ότι το πλάτος E m της ταλάντωσης που διεγείρεται από την m-η ζώνη στο σημείο P μειώνεται μονότονα με την αύξηση του m. Έτσι, τα πλάτη των ταλαντώσεων που διεγείρονται στο σημείο P από τις ζώνες Fresnel σχηματίζουν μια μονότονα φθίνουσα ακολουθία:

E 1 >E 2 >E 3 > E m >E m + n

Οι φάσεις των ταλαντώσεων που διεγείρονται από γειτονικές ζώνες διαφέρουν κατά p.

Πράγματι, έστω τα πλάτη που δημιουργούνται από το πρώτο, το δεύτερο κ.λπ. Ζώνες Fresnel. Τότε το απαιτούμενο πλάτος στο σημείο , που δημιουργήθηκε από όλες τις ζώνες Fresnel στο σημείο παρατήρησης, είναι ίσο με

Τότε από την έκφραση (8.10) παίρνουμε:

Έτσι, το πλάτος της προκύπτουσας ταλάντωσης που προκύπτει από την αμοιβαία παρεμβολή του φωτός που έρχεται στο σημείο P από διαφορετικά μέρη του σφαιρικού κύματος είναι μικρότερο από το πλάτος της πρώτης ζώνης Fresnel. Δεδομένου ότι σε ένα ομοιογενές ισότροπο μέσο η ένταση του φωτός που διαδίδεται καθορίζεται μόνο από το πλάτος της πρώτης ζώνης Fresnel, μπορούμε να εκτιμήσουμε την ακτίνα του κυλινδρικού καναλιού μέσω του οποίου διαδίδεται το φως: έστω a = b = 1 m, l = 0,5 μm, μετά r 1 = 0,5 mm . Κατά συνέπεια, η διάδοση του φωτός από το σημείο S στο σημείο P συμβαίνει σε ένα στενό κανάλι, δηλ. ευθύγραμμα, που αντιστοιχεί στους νόμους της γεωμετρικής οπτικής. Έτσι, η θεωρία των ζωνών Fresnel δεν έρχεται σε αντίθεση με τους νόμους της γεωμετρικής οπτικής.

Λαμβάνοντας υπόψη ότι η ένταση του κύματος είναι ανάλογη με το τετράγωνο του συντελεστή των ηλεκτρομαγνητικών διανυσμάτων, μπορούμε να συμπεράνουμε ότι η ένταση του πεδίου που δημιουργείται από την πρώτη ζώνη Fresnel είναι τέσσερις φορές μεγαλύτερη από την ένταση του κύματος πηγής στο σημείο παρατήρησης που δημιουργούνται από όλες τις δευτερεύουσες πηγές στην επιφάνεια:

Πινακίδες ζώνης.

Βρήκαμε μια έκφραση για τις ακτίνες των ζωνών Fresnel των σφαιρικών κυμάτων φωτός

(8.13)

Χρησιμοποιώντας αυτήν την έκφραση, είναι δυνατό να παρασκευαστεί μια οθόνη που αποτελείται από διαδοχικά εναλλασσόμενους διαφανείς και αδιαφανείς δακτυλίους, οι ακτίνες των οποίων ικανοποιούν την προϋπόθεση 8.13 για δεδομένες τιμές των a, b και l. Η πλάκα που παρασκευάζεται με αυτόν τον τρόπο ονομάζεται πλάκα ζώνης πλάτους. Οι ταλαντώσεις από άρτιες και περιττές ζώνες Fresnel βρίσκονται σε αντιφάση και, ως εκ τούτου, αμοιβαία αποδυναμώνουν η μία την άλλη. Εάν τοποθετήσετε μια προετοιμασμένη πλάκα στη διαδρομή του φωτεινού κύματος, η οποία θα κάλυπτε όλες τις ζυγές ή περιττές ζώνες, τότε η ένταση του φωτός στο σημείο P αυξάνεται απότομα. Μια τέτοια πλάκα λειτουργεί σαν συγκλίνοντας φακός.

Εικ.8.8

Στο Σχ. Το 8.8 δείχνει μια πλάκα που καλύπτει ζυγές ζώνες.

Ένα ακόμη μεγαλύτερο αποτέλεσμα μπορεί να επιτευχθεί χωρίς να επικαλύπτονται ζυγές (ή περιττές) ζώνες, αλλά αλλάζοντας τη φάση των ταλαντώσεων τους κατά p. Αυτό μπορεί να γίνει με βοήθεια

μια διαφανή πλάκα, το πάχος της οποίας σε σημεία που αντιστοιχούν σε ζυγές ή περιττές ζώνες διαφέρει κατά μια σωστά επιλεγμένη ποσότητα. Μια τέτοια πλάκα ονομάζεται πλάκα ζώνης φάσης. Σε σύγκριση με την πλάκα ζώνης πλάτους που επικαλύπτει τη ζώνη, η πλάκα φάσης παρέχει πρόσθετη αύξηση στο πλάτος κατά δύο φορές και την ένταση φωτός κατά τέσσερις φορές.

Για μια πλάκα φάσης, το προκύπτον πλάτος του διανύσματος φωτός μπορεί να γραφτεί ως εξής.