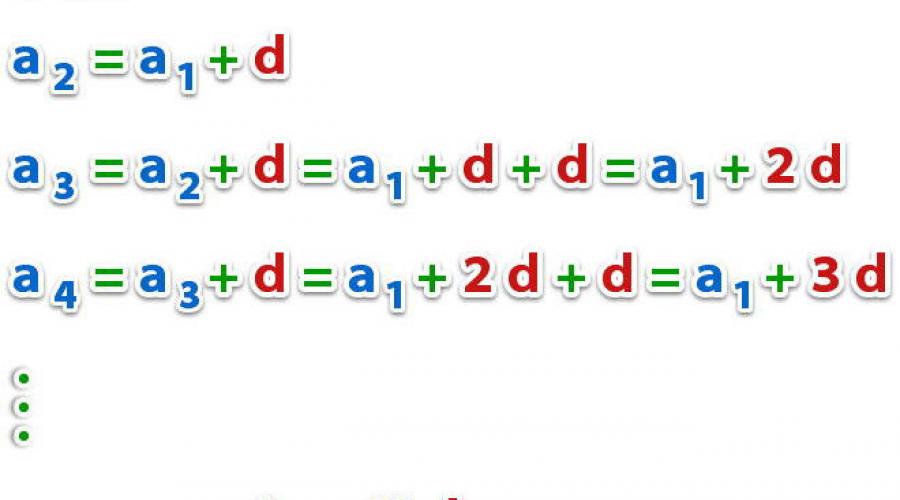
Or αριθμητική είναι ένας τύπος ταξινομημένης αριθμητικής ακολουθίας, οι ιδιότητες της οποίας μελετώνται σε ένα σχολικό μάθημα άλγεβρας. Αυτό το άρθρο συζητά λεπτομερώς το ερώτημα πώς να βρείτε το άθροισμα μιας αριθμητικής προόδου.

Ποια είναι αυτή η εξέλιξη;

Πριν προχωρήσετε στην εξέταση της ερώτησης (πώς να βρείτε το άθροισμα μιας αριθμητικής προόδου), αξίζει να καταλάβετε τι θα συζητηθεί.

Οποιαδήποτε ακολουθία πραγματικών αριθμών που λαμβάνεται προσθέτοντας (αφαιρώντας) κάποια τιμή από κάθε προηγούμενο αριθμό ονομάζεται αλγεβρική (αριθμητική) πρόοδος. Αυτός ο ορισμός, μεταφρασμένος στη γλώσσα των μαθηματικών, έχει τη μορφή:

Εδώ i είναι ο κανονικός αριθμός του στοιχείου της σειράς a i. Έτσι, γνωρίζοντας μόνο έναν σπόρο, μπορείτε εύκολα να ανακατασκευάσετε ολόκληρη τη σειρά. Η παράμετρος d στον τύπο ονομάζεται διαφορά της προόδου.

Μπορεί εύκολα να αποδειχθεί ότι ισχύει η ακόλουθη ισότητα για τη σειρά αριθμών που εξετάζονται:

a n = a 1 + d * (n - 1).

Δηλαδή, για να βρείτε την τιμή του n-ου στοιχείου στη σειρά, προσθέστε τη διαφορά d στο πρώτο στοιχείο 1 n-1 φορές.

Ποιο είναι το άθροισμα μιας αριθμητικής προόδου: τύπος

Πριν δώσετε έναν τύπο για το αναφερόμενο ποσό, αξίζει να εξετάσετε μια απλή ειδική περίπτωση. Δεδομένης της εξέλιξης των φυσικών αριθμών από το 1 στο 10, πρέπει να βρείτε το άθροισμά τους. Δεδομένου ότι υπάρχουν λίγα μέλη στην εξέλιξη (10), είναι δυνατό να επιλυθεί το πρόβλημα κατά μέτωπο, δηλαδή να αθροίσουμε όλα τα στοιχεία με τη σειρά.

S 10 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55.

Αξίζει να εξεταστεί ένα ενδιαφέρον πράγμα: δεδομένου ότι κάθε όρος διαφέρει από τον επόμενο με την ίδια τιμή d = 1, τότε το άθροισμα ζεύγος του πρώτου με το δέκατο, του δεύτερου με το ένατο και ούτω καθεξής θα δώσει το ίδιο αποτέλεσμα. Πραγματικά:

11 = 1+10 = 2+9 = 3+8 = 4+7 = 5+6.

Όπως μπορείτε να δείτε, υπάρχουν μόνο 5 από αυτά τα ποσά, δηλαδή δύο φορές λιγότερο από τον αριθμό των στοιχείων της σειράς. Στη συνέχεια, πολλαπλασιάζοντας τον αριθμό των αθροισμάτων (5) με το αποτέλεσμα κάθε αθροίσματος (11), θα φτάσετε στο αποτέλεσμα που ελήφθη στο πρώτο παράδειγμα.

Αν γενικεύσουμε αυτό το σκεπτικό, τότε μπορούμε να γράψουμε την ακόλουθη έκφραση:

S n = n * (a 1 + a n) / 2.

Αυτή η έκφραση δείχνει ότι δεν είναι καθόλου απαραίτητο να συνοψίσουμε όλα τα στοιχεία σε μια σειρά, αρκεί να γνωρίζουμε την τιμή του πρώτου a 1 και του τελευταίου a n, καθώς και του συνολικού αριθμού των όρων n.

Πιστεύεται ότι ο Gauss σκέφτηκε για πρώτη φορά αυτή την ισότητα όταν έψαχνε μια λύση σε ένα πρόβλημα που έθεσε ο δάσκαλός του στο σχολείο: αθροίστε τους πρώτους 100 ακέραιους.

Άθροισμα στοιχείων από m έως n: τύπος

Ο τύπος που δόθηκε στην προηγούμενη παράγραφο δίνει μια απάντηση στο ερώτημα πώς να βρούμε το άθροισμα μιας αριθμητικής προόδου (πρώτα στοιχεία), αλλά συχνά σε προβλήματα είναι απαραίτητο να συνοψίσουμε μια σειρά αριθμών στη μέση της προόδου. Πως να το κάνεις?

Ο ευκολότερος τρόπος για να απαντήσετε σε αυτήν την ερώτηση είναι εξετάζοντας το ακόλουθο παράδειγμα: ας είναι απαραίτητο να βρεθεί το άθροισμα των όρων από m-th έως n-th. Για να λυθεί το πρόβλημα, ένα δεδομένο τμήμα από m έως n της προόδου πρέπει να παρουσιαστεί με τη μορφή μιας νέας αριθμητικής σειράς. Σε αυτήν την αναπαράσταση, ο mth όρος a m θα είναι ο πρώτος και ο n θα είναι n- (m-1). Σε αυτήν την περίπτωση, εφαρμόζοντας τον τυποποιημένο τύπο για το άθροισμα, λαμβάνετε την ακόλουθη έκφραση:

S m n = (n - m + 1) * (a m + a n) / 2.

Παράδειγμα χρήσης τύπων

Γνωρίζοντας πώς να βρείτε το άθροισμα μιας αριθμητικής προόδου, αξίζει να εξετάσετε ένα απλό παράδειγμα χρήσης των τύπων που δίνονται.

Παρακάτω είναι μια αριθμητική ακολουθία, θα πρέπει να βρείτε το άθροισμα των μελών της, ξεκινώντας από το 5ο και τελειώνοντας με το 12ο:

Οι αριθμοί που δίνονται υποδεικνύουν ότι η διαφορά d είναι ίση με 3. Χρησιμοποιώντας την έκφραση για το ένατο στοιχείο, μπορείτε να βρείτε τις τιμές του 5ου και 12ου όρου της προόδου. Αποδεικνύεται:

a 5 = a 1 + d * 4 = -4 + 3 * 4 = 8;

a 12 = a 1 + d * 11 = -4 + 3 * 11 = 29.

Γνωρίζοντας τις τιμές των αριθμών στα άκρα της εξεταζόμενης αλγεβρικής προόδου, και επίσης γνωρίζοντας ποιοι αριθμοί στη σειρά καταλαμβάνουν, μπορείτε να χρησιμοποιήσετε τον τύπο για το άθροισμα που ελήφθη στην προηγούμενη παράγραφο. Θα αποδειχθεί:

S 5 12 = (12 - 5 + 1) * (8 + 29) / 2 = 148.

Αξίζει να σημειωθεί ότι αυτή η τιμή θα μπορούσε να ληφθεί διαφορετικά: πρώτα, βρείτε το άθροισμα των πρώτων 12 στοιχείων χρησιμοποιώντας τον τυπικό τύπο, στη συνέχεια υπολογίστε το άθροισμα των πρώτων 4 στοιχείων χρησιμοποιώντας τον ίδιο τύπο και, στη συνέχεια, αφαιρέστε το δεύτερο από το πρώτο άθροισμα.

Κατά τη μελέτη της άλγεβρας σε σχολείο γενικής εκπαίδευσης (τάξη 9), ένα από τα σημαντικά θέματα είναι η μελέτη αριθμητικών ακολουθιών, οι οποίες περιλαμβάνουν προόδους - γεωμετρικές και αριθμητικές. Σε αυτό το άρθρο, θα εξετάσουμε την αριθμητική πρόοδο και παραδείγματα με λύσεις.

Τι είναι η αριθμητική πρόοδος;

Για να γίνει κατανοητό αυτό, είναι απαραίτητο να δοθεί ένας ορισμός της εξεταζόμενης εξέλιξης, καθώς και να δοθούν οι βασικοί τύποι που θα χρησιμοποιηθούν περαιτέρω για την επίλυση προβλημάτων.

Είναι γνωστό ότι σε κάποια αλγεβρική εξέλιξη ο 1ος όρος ισούται με 6 και ο 7ος όρος είναι με 18. Είναι απαραίτητο να βρεθεί η διαφορά και να αποκατασταθεί αυτή η ακολουθία στον 7ο όρο.

Ας χρησιμοποιήσουμε τον τύπο για να προσδιορίσουμε τον άγνωστο όρο: a n = (n - 1) * d + a 1. Αντικαθιστούμε σε αυτό τα γνωστά δεδομένα από την συνθήκη, δηλαδή τους αριθμούς a 1 και a 7, έχουμε: 18 = 6 + 6 * d. Από αυτήν την έκφραση, μπορείτε εύκολα να υπολογίσετε τη διαφορά: d = (18 - 6) / 6 = 2. Έτσι, έχουμε απαντήσει στο πρώτο μέρος του προβλήματος.

Για να επαναφέρετε μια ακολουθία έως 7 όρους, θα πρέπει να χρησιμοποιήσετε τον ορισμό μιας αλγεβρικής προόδου, δηλαδή a 2 = a 1 + d, a 3 = a 2 + d κ.ο.κ. Ως αποτέλεσμα, αποκαθιστούμε ολόκληρη την ακολουθία: a 1 = 6, a 2 = 6 + 2 = 8, a 3 = 8 + 2 = 10, a 4 = 10 + 2 = 12, a 5 = 12 + 2 = 14 , a 6 = 14 + 2 = 16, a 7 = 18.

Παράδειγμα # 3: πραγματοποίηση προόδου

Ας περιπλέξουμε ακόμα περισσότερο την κατάσταση του προβλήματος. Τώρα είναι απαραίτητο να απαντήσουμε στο ερώτημα πώς να βρούμε την αριθμητική πρόοδο. Μπορείτε να δώσετε το ακόλουθο παράδειγμα: δίνοντας δύο αριθμούς, για παράδειγμα - 4 και 5. Είναι απαραίτητο να κάνετε μια αλγεβρική πρόοδο έτσι ώστε να ταιριάζουν τρεις ακόμη όροι μεταξύ αυτών.

Πριν ξεκινήσετε την επίλυση αυτού του προβλήματος, είναι απαραίτητο να καταλάβετε ποια θέση θα καταλάβουν οι δεδομένοι αριθμοί στη μελλοντική πρόοδο. Δεδομένου ότι θα υπάρχουν τρεις ακόμη όροι μεταξύ τους, τότε 1 = -4 και 5 = 5. Αφού το καθορίσουμε αυτό, προχωρούμε στο πρόβλημα, το οποίο είναι παρόμοιο με το προηγούμενο. Και πάλι, για τον ένατο όρο, χρησιμοποιούμε τον τύπο, παίρνουμε: a 5 = a 1 + 4 * d. Από πού: d = (a 5 - a 1) / 4 = (5 - (-4)) / 4 = 2.25. Εδώ δεν λάβαμε μια ακέραια τιμή της διαφοράς, αλλά είναι ένας λογικός αριθμός, οπότε οι τύποι για την αλγεβρική πρόοδο παραμένουν οι ίδιοι.

Τώρα προσθέστε τη διαφορά που βρέθηκε στο 1 και επαναφέρετε τα μέλη που λείπουν από την πρόοδο. Παίρνουμε: a 1 = - 4, a 2 = - 4 + 2.25 = - 1.75, a 3 = -1.75 + 2.25 = 0.5, a 4 = 0.5 + 2.25 = 2.75, a 5 = 2.75 + 2.25 = 5, που συνέπεσε με την κατάσταση του προβλήματος.

Παράδειγμα # 4: ο πρώτος όρος της προόδου

Ας συνεχίσουμε να δίνουμε παραδείγματα αριθμητικής προόδου με λύση. Σε όλα τα προηγούμενα προβλήματα, ο πρώτος αριθμός της αλγεβρικής προόδου ήταν γνωστός. Τώρα εξετάστε ένα πρόβλημα διαφορετικού τύπου: ας δοθούν δύο αριθμοί, όπου ένα 15 = 50 και ένα 43 = 37. Είναι απαραίτητο να βρείτε τον αριθμό από τον οποίο ξεκινά αυτή η ακολουθία.

Οι τύποι που χρησιμοποιήθηκαν μέχρι τώρα υποθέτουν τη γνώση των 1 και d. Τίποτα δεν είναι γνωστό για αυτούς τους αριθμούς στη δήλωση προβλήματος. Παρ 'όλα αυτά, γράφουμε εκφράσεις για κάθε μέλος για τις οποίες υπάρχουν πληροφορίες: a 15 = a 1 + 14 * d και 43 = a 1 + 42 * d. Έλαβε δύο εξισώσεις, στις οποίες 2 άγνωστες ποσότητες (α 1 και δ). Αυτό σημαίνει ότι το πρόβλημα μειώνεται στην επίλυση ενός συστήματος γραμμικών εξισώσεων.

Ο ευκολότερος τρόπος για να λύσετε αυτό το σύστημα είναι να εκφράσετε ένα 1 σε κάθε εξίσωση και στη συνέχεια να συγκρίνετε τις εκφράσεις που προκύπτουν. Η πρώτη εξίσωση: a 1 = a 15 - 14 * d = 50 - 14 * d; δεύτερη εξίσωση: a 1 = a 43 - 42 * d = 37 - 42 * d. Εξισώνοντας αυτές τις εκφράσεις, παίρνουμε: 50 - 14 * d = 37 - 42 * d, από όπου η διαφορά d = (37 - 50) / (42 - 14) = - 0.464 (δίνονται μόνο 3 δεκαδικά ψηφία).

Γνωρίζοντας το d, μπορείτε να χρησιμοποιήσετε οποιαδήποτε από τις 2 παραπάνω εκφράσεις για το 1. Για παράδειγμα, το πρώτο: a 1 = 50 - 14 * d = 50 - 14 * ( - 0.464) = 56.496.

Εάν έχετε αμφιβολίες για το αποτέλεσμα, μπορείτε να το ελέγξετε, για παράδειγμα, να προσδιορίσετε τον όρο 43 της προόδου, ο οποίος καθορίζεται στην κατάσταση. Παίρνουμε: a 43 = a 1 + 42 * d = 56,496 + 42 * (- 0,464) = 37,008. Ένα μικρό σφάλμα οφείλεται στο γεγονός ότι οι υπολογισμοί χρησιμοποίησαν στρογγυλοποίηση στα χιλιοστά.

Παράδειγμα # 5: ποσό

Τώρα ας δούμε μερικά παραδείγματα με λύσεις για το άθροισμα μιας αριθμητικής προόδου.

Ας δοθεί μια αριθμητική πρόοδος της ακόλουθης μορφής: 1, 2, 3, 4, ...,. Πώς υπολογίζετε το άθροισμα αυτών των 100 αριθμών;

Χάρη στην ανάπτυξη της τεχνολογίας των υπολογιστών, είναι δυνατό να επιλυθεί αυτό το πρόβλημα, δηλαδή να προστεθούν διαδοχικά όλοι οι αριθμοί, τους οποίους ο υπολογιστής θα κάνει μόλις ένα άτομο πατήσει το πλήκτρο Enter. Ωστόσο, το πρόβλημα μπορεί να λυθεί στο μυαλό, αν προσέξουμε ότι η σειρά αριθμών που παρουσιάζεται είναι αλγεβρική εξέλιξη και η διαφορά του είναι 1. Εφαρμόζοντας τον τύπο για το άθροισμα, παίρνουμε: S n = n * (a 1 + αν) / 2 = 100 * (1 + 100) / 2 = 5050.

Είναι περίεργο να σημειωθεί ότι αυτό το πρόβλημα ονομάζεται "Gaussian", επειδή στις αρχές του 18ου αιώνα ο διάσημος Γερμανός, ενώ ήταν ακόμα μόλις 10 ετών, μπόρεσε να το λύσει στο κεφάλι του σε λίγα δευτερόλεπτα. Το αγόρι δεν γνώριζε τον τύπο για το άθροισμα μιας αλγεβρικής προόδου, αλλά παρατήρησε ότι αν προσθέσετε σε ζεύγη τους αριθμούς στις άκρες της ακολουθίας, έχετε πάντα ένα αποτέλεσμα, δηλαδή 1 + 100 = 2 + 99 = 3 + 98 = ..., και αφού από αυτά τα ποσά θα είναι ακριβώς 50 (100/2), τότε για να πάρετε τη σωστή απάντηση, αρκεί να πολλαπλασιάσετε το 50 επί 101.

Παράδειγμα # 6: άθροισμα μελών από n έως m

Ένα άλλο τυπικό παράδειγμα του αθροίσματος μιας αριθμητικής προόδου είναι το ακόλουθο: δεδομένης μιας σειράς αριθμών: 3, 7, 11, 15, ..., πρέπει να βρείτε τι θα ισούται με το άθροισμα των μελών του από 8 έως 14.

Το πρόβλημα λύνεται με δύο τρόπους. Το πρώτο από αυτά περιλαμβάνει την εύρεση άγνωστων όρων από το 8 έως το 14 και στη συνέχεια την προσθήκη τους διαδοχικά. Δεδομένου ότι υπάρχουν λίγοι όροι, αυτή η μέθοδος δεν είναι αρκετά επίπονη. Ωστόσο, προτείνεται η επίλυση αυτού του προβλήματος με τη δεύτερη μέθοδο, η οποία είναι πιο καθολική.

Η ιδέα είναι να ληφθεί ένας τύπος για το άθροισμα της αλγεβρικής προόδου μεταξύ των όρων m και n, όπου n> m είναι ακέραιοι. Ας γράψουμε δύο εκφράσεις για το άθροισμα και για τις δύο περιπτώσεις:

1. S m = m * (a m + a 1) / 2.
2. S n = n * (a n + a 1) / 2.

Δεδομένου ότι n> m, είναι προφανές ότι το άθροισμα 2 περιλαμβάνει το πρώτο. Το τελευταίο συμπέρασμα σημαίνει ότι αν πάρουμε τη διαφορά μεταξύ αυτών των αθροισμάτων και προσθέσουμε σε αυτόν τον όρο a m (στην περίπτωση που λαμβάνεται η διαφορά, αφαιρείται από το άθροισμα S n), τότε παίρνουμε την απαραίτητη απάντηση στο πρόβλημα. Έχουμε: S mn = S n - S m + am = n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am = a 1 * (n - m) / 2 + an * n / 2 + am * (1- m / 2). Σε αυτή την έκφραση είναι απαραίτητο να αντικατασταθούν οι τύποι με ένα n και ένα m. Στη συνέχεια παίρνουμε: S mn = a 1 * (n - m) / 2 + n * (a 1 + (n - 1) * d) / 2 + (a 1 + (m - 1) * d) * (1 - m / 2) = a 1 * (n - m + 1) + d * n * (n - 1) / 2 + d * (3 * m - m 2 - 2) / 2.

Ο τύπος που προκύπτει είναι κάπως δυσκίνητος · ωστόσο, το άθροισμα του S mn εξαρτάται μόνο από τα n, m, a 1 και d. Στην περίπτωσή μας, a 1 = 3, d = 4, n = 14, m = 8. Αντικαθιστώντας αυτούς τους αριθμούς, παίρνουμε: S mn = 301.

Όπως φαίνεται από τις λύσεις που δόθηκαν, όλα τα προβλήματα βασίζονται στη γνώση της έκφρασης για τον ένατο όρο και στον τύπο για το άθροισμα του συνόλου των πρώτων όρων. Πριν προχωρήσετε στη λύση οποιουδήποτε από αυτά τα προβλήματα, συνιστάται να διαβάσετε προσεκτικά την κατάσταση, να κατανοήσετε σαφώς τι απαιτείται για να βρεθεί και μόνο στη συνέχεια να προχωρήσετε στη λύση.

Μια άλλη συμβουλή είναι να προσπαθήσετε για απλότητα, δηλαδή, εάν μπορείτε να απαντήσετε σε μια ερώτηση χωρίς να χρησιμοποιήσετε περίπλοκους μαθηματικούς υπολογισμούς, τότε πρέπει να κάνετε ακριβώς αυτό, αφού σε αυτή την περίπτωση η πιθανότητα να κάνετε λάθος είναι μικρότερη. Για παράδειγμα, σε ένα παράδειγμα αριθμητικής προόδου με λύση # 6, θα μπορούσε κανείς να σταματήσει στον τύπο S mn = n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am, και να σπάσει το γενικό πρόβλημα σε ξεχωριστές δευτερεύουσες εργασίες (σε αυτήν την περίπτωση, βρείτε πρώτα τα μέλη a και am).

Εάν υπάρχουν αμφιβολίες για το αποτέλεσμα, συνιστάται να το ελέγξετε, όπως έγινε σε μερικά από τα παραδείγματα που δόθηκαν. Καταλάβαμε πώς να βρούμε την αριθμητική πρόοδο. Αν το καταλάβετε, δεν είναι τόσο δύσκολο.

Πριν αρχίσουμε να αποφασίζουμε προβλήματα αριθμητικής εξέλιξης, εξετάστε τι είναι μια ακολουθία αριθμών, αφού μια αριθμητική πρόοδος είναι μια ειδική περίπτωση μιας ακολουθίας αριθμών.

Μια αριθμητική ακολουθία είναι ένα αριθμητικό σύνολο, κάθε στοιχείο του οποίου έχει τον δικό του κανονικό αριθμό... Τα στοιχεία αυτού του συνόλου ονομάζονται μέλη της ακολουθίας. Ο κανονικός αριθμός του στοιχείου ακολουθίας υποδεικνύεται από τον δείκτη:

Το πρώτο στοιχείο της ακολουθίας.

Πέμπτο στοιχείο της ακολουθίας.

- "n" στοιχείο της ακολουθίας, δηλ. το στοιχείο "στην ουρά" n.

Υπάρχει σχέση μεταξύ της τιμής ενός στοιχείου ακολουθίας και του κανονικού αριθμού του. Επομένως, μπορούμε να σκεφτούμε μια ακολουθία ως μια συνάρτηση της οποίας το όρισμα είναι ο κανονικός αριθμός ενός στοιχείου της ακολουθίας. Με άλλα λόγια, μπορούμε να το πούμε μια ακολουθία είναι συνάρτηση ενός φυσικού επιχειρήματος:

Η ακολουθία μπορεί να ρυθμιστεί με τρεις τρόπους:

1 . Η ακολουθία μπορεί να ρυθμιστεί χρησιμοποιώντας έναν πίνακα.Σε αυτή την περίπτωση, απλώς ορίζουμε την τιμή κάθε μέλους της ακολουθίας.

Για παράδειγμα, κάποιος αποφάσισε να αναλάβει προσωπική διαχείριση χρόνου και, αρχικά, να υπολογίσει πόσο χρόνο ξοδεύει στο VKontakte κατά τη διάρκεια της εβδομάδας. Γράφοντας την ώρα στον πίνακα, θα λάβει μια ακολουθία που αποτελείται από επτά στοιχεία:

Η πρώτη γραμμή του πίνακα περιέχει τον αριθμό της ημέρας της εβδομάδας, η δεύτερη - την ώρα σε λεπτά. Βλέπουμε ότι, δηλαδή τη Δευτέρα, Κάποιος πέρασε 125 λεπτά στο VKontakte, δηλαδή την Πέμπτη - 248 λεπτά και, δηλαδή, την Παρασκευή, μόνο 15.

2 . Η ακολουθία μπορεί να καθοριστεί χρησιμοποιώντας τον τύπο του όγδοου όρου.

Σε αυτή την περίπτωση, η εξάρτηση της τιμής του στοιχείου ακολουθίας από τον αριθμό του εκφράζεται απευθείας με τη μορφή ενός τύπου.

Για παράδειγμα, αν, τότε

Για να βρούμε την τιμή ενός στοιχείου μιας ακολουθίας με έναν δεδομένο αριθμό, αντικαθιστούμε τον αριθμό του στοιχείου στον τύπο του ένατου όρου.

Κάνουμε το ίδιο εάν χρειαστεί να βρούμε την τιμή μιας συνάρτησης εάν η τιμή του ορίσματος είναι γνωστή. Αντικαθιστούμε την τιμή του ορίσματος στην εξίσωση της συνάρτησης:

Εάν, για παράδειγμα, , τότε

Για άλλη μια φορά, σημειώνω ότι σε μια ακολουθία, σε αντίθεση με μια αυθαίρετη αριθμητική συνάρτηση, μόνο ένας φυσικός αριθμός μπορεί να είναι όρισμα.

3 ... Μια ακολουθία μπορεί να καθοριστεί χρησιμοποιώντας έναν τύπο που εκφράζει την εξάρτηση της τιμής του αριθμού μέλους ακολουθίας που αριθμείται από την τιμή των προηγούμενων μελών. Σε αυτή την περίπτωση, δεν αρκεί να γνωρίζουμε μόνο τον αριθμό του μέλους της ακολουθίας για να βρούμε την τιμή του. Πρέπει να καθορίσουμε το πρώτο μέλος ή τα πρώτα μέλη της ακολουθίας.

Για παράδειγμα, λάβετε υπόψη την ακολουθία ,

Μπορούμε να βρούμε τις τιμές των μελών της ακολουθίας σε ακολουθίαξεκινώντας από το τρίτο:

Δηλαδή, κάθε φορά, για να βρούμε την τιμή του n-ου μέλους της ακολουθίας, επιστρέφουμε στα δύο προηγούμενα. Αυτός ο τρόπος αλληλουχίας ονομάζεται επαναλαμβανόμενος, από τη λατινική λέξη επαναλαμβανόμενος- ελα πισω.

Τώρα μπορούμε να ορίσουμε μια αριθμητική πρόοδο. Η αριθμητική πρόοδος είναι μια απλή ειδική περίπτωση μιας ακολουθίας αριθμών.

Αριθμητική πρόοδος είναι μια αριθμητική ακολουθία, κάθε μέλος της οποίας, ξεκινώντας από το δεύτερο, είναι ίσο με το προηγούμενο, που προστίθεται στον ίδιο αριθμό.

Ο αριθμός καλείται διαφορά αριθμητικής προόδου... Η διαφορά στην αριθμητική πρόοδο μπορεί να είναι θετική, αρνητική ή μηδενική.

Εάν ο τίτλος = "(! LANG: d> 0">, то каждый член арифметической прогрессии больше предыдущего, и прогрессия является !} αυξανόμενη.

Για παράδειγμα, 2? 5; οκτώ; έντεκα;...

Εάν, τότε κάθε μέλος της αριθμητικής προόδου είναι μικρότερο από το προηγούμενο, και η πρόοδος είναι μειώνεται.

Για παράδειγμα, 2? -1; -4; -7; ...

Εάν, τότε όλα τα μέλη της προόδου είναι ίσα με τον ίδιο αριθμό, και η πρόοδος είναι ακίνητος.

Για παράδειγμα, 2; 2; 2; 2; ...

Η κύρια ιδιότητα της αριθμητικής προόδου:

Ας δούμε την εικόνα.

Το βλέπουμε

, και ταυτόχρονα

Προσθέτοντας αυτές τις δύο ισότητες, παίρνουμε:

.

Χωρίστε και τις δύο πλευρές της ισότητας με 2:

Έτσι, κάθε μέλος της αριθμητικής προόδου, ξεκινώντας από το δεύτερο, είναι ίσο με τον αριθμητικό μέσο δύο γειτονικών:

Επιπλέον, από τότε

, και ταυτόχρονα

, τότε

, και ως εκ τούτου

Κάθε μέλος της αριθμητικής προόδου ξεκινά με τον τίτλο = "(! LANG: k> l">, равен среднему арифметическому двух равноотстоящих. !}

Τύπος του ου μέλους.

Βλέπουμε ότι για τα μέλη της αριθμητικής προόδου, πληρούνται οι ακόλουθες σχέσεις:

και τελικά

Πήραμε ο τύπος του ένατου όρου.

ΣΠΟΥΔΑΙΟΣ!Οποιοδήποτε μέλος της αριθμητικής προόδου μπορεί να εκφραστεί με όρους και. Γνωρίζοντας τον πρώτο όρο και τη διαφορά της αριθμητικής προόδου, μπορείτε να βρείτε οποιονδήποτε από τους όρους του.

Το άθροισμα των n μελών μιας αριθμητικής προόδου.

Σε μια αυθαίρετη αριθμητική πρόοδο, τα ποσά των μελών που ισαπέχουν από το άκρο είναι ίσα μεταξύ τους:

Εξετάστε μια αριθμητική πρόοδο με n όρους. Ας είναι το άθροισμα των n μελών αυτής της προόδου.

Ας τακτοποιήσουμε τα μέλη της εξέλιξης πρώτα σε αύξουσα σειρά αριθμών και μετά σε φθίνουσα σειρά:

Ας προσθέσουμε ανά δύο:

Το άθροισμα σε κάθε παρένθεση είναι ίσο, ο αριθμός των ζευγαριών είναι n.

Παίρνουμε:

Ετσι, το άθροισμα των n μελών μιας αριθμητικής προόδου μπορεί να βρεθεί με τους τύπους:

Σκεφτείτε επίλυση προβλημάτων για αριθμητική πρόοδο.

1 . Η ακολουθία δίνεται από τον τύπο του όγδοου όρου: . Αποδείξτε ότι αυτή η ακολουθία είναι μια αριθμητική πρόοδος.

Ας αποδείξουμε ότι η διαφορά μεταξύ δύο γειτονικών μελών της ακολουθίας είναι ίση με τον ίδιο αριθμό.

Πήραμε ότι η διαφορά μεταξύ δύο παρακείμενων μελών της ακολουθίας δεν εξαρτάται από τον αριθμό τους και είναι σταθερή. Επομένως, εξ ορισμού, αυτή η ακολουθία είναι μια αριθμητική πρόοδος.

2 . Σας δίνεται μια αριθμητική πρόοδος -31. -27; ...

α) Βρείτε 31 μέλη της προόδου.

β) Καθορίστε εάν ο αριθμός 41 περιλαμβάνεται σε αυτήν την πρόοδο.

ένα)Το βλέπουμε?

Ας γράψουμε τον τύπο του ένατου όρου για την πρόοδό μας.

Γενικά

Στην περίπτωσή μας , επομένως

Παίρνουμε:

σι)Ας υποθέσουμε ότι το 41 είναι μέλος μιας ακολουθίας. Ας βρούμε τον αριθμό του. Για να γίνει αυτό, λύνουμε την εξίσωση:

Πήραμε τη φυσική τιμή του n, επομένως, ναι, ο αριθμός 41 είναι μέλος της προόδου. Εάν η τιμή που βρέθηκε το n δεν ήταν φυσικός αριθμός, τότε θα απαντούσαμε ότι ο αριθμός 41 ΔΕΝ είναι μέλος της εξέλιξης.

3 ... α) Μεταξύ των αριθμών 2 και 8, εισαγάγετε 4 αριθμούς, ώστε αυτοί, μαζί με τους αριθμούς που έχουν δοθεί, να κάνουν αριθμητική πρόοδο.

β) Να βρείτε το άθροισμα των μελών της προκύπτουσας προόδου.

ένα)Εισάγετε τέσσερις αριθμούς μεταξύ των αριθμών 2 και 8:

Πήραμε μια αριθμητική πρόοδο με 6 μέλη.

Ας βρούμε τη διαφορά αυτής της εξέλιξης. Για να γίνει αυτό, θα χρησιμοποιήσουμε τον τύπο για τον ένατο όρο:

Τώρα είναι εύκολο να βρείτε τις τιμές των αριθμών:

3,2; 4,4; 5,6; 6,8

σι)

Απάντηση: α) ναι β) 30

4. Το φορτηγό μεταφέρει μια παρτίδα θρυμματισμένης πέτρας βάρους 240 τόνων, αυξάνοντας καθημερινά το ποσοστό μεταφοράς κατά τον ίδιο αριθμό τόνων. Είναι γνωστό ότι κατά την πρώτη ημέρα μεταφέρθηκαν 2 τόνοι θρυμματισμένης πέτρας. Καθορίστε πόσους τόνους ερείπια μεταφέρθηκαν τη δωδέκατη ημέρα εάν όλη η εργασία είχε ολοκληρωθεί σε 15 ημέρες.

Ανάλογα με την κατάσταση του προβλήματος, η ποσότητα των μπάζων που μεταφέρονται από το φορτηγό αυξάνεται κατά τον ίδιο αριθμό κάθε μέρα. Επομένως, έχουμε να κάνουμε με μια αριθμητική πρόοδο.

Ας διατυπώσουμε αυτό το πρόβλημα με όρους αριθμητικής προόδου.

Κατά την πρώτη ημέρα, μεταφέρθηκαν 2 τόνοι θρυμματισμένης πέτρας: a_1 = 2.

Όλες οι εργασίες ολοκληρώθηκαν σε 15 ημέρες :.

Το φορτηγό μεταφέρει μια παρτίδα θρυμματισμένης πέτρας βάρους 240 τόνων:

Πρέπει να βρούμε.

Πρώτον, βρείτε τη διαφορά στην εξέλιξη. Ας χρησιμοποιήσουμε τον τύπο για το άθροισμα των n όρων της προόδου.

Στην περίπτωσή μας:

Ναι, ναι: η αριθμητική εξέλιξη δεν είναι παιχνίδι για εσάς :)

Λοιπόν, φίλοι, αν διαβάζετε αυτό το κείμενο, τότε το εσωτερικό καπάκι-προφανές μου λέει ότι δεν γνωρίζετε ακόμα τι είναι η αριθμητική εξέλιξη, αλλά πραγματικά (όχι, έτσι: SOOOOO!) Θέλετε να μάθετε. Επομένως, δεν θα σας βασανίσω με μακρές εισαγωγές και θα μπω αμέσως στην επιχείρηση.

Ας ξεκινήσουμε με μερικά παραδείγματα. Εξετάστε διάφορα σύνολα αριθμών:

• 1; 2; 3; 4; ...
• 15; 20; 25; 30; ...
• $ \ sqrt (2); \ 2 \ sqrt (2); \ 3 \ sqrt (2); ... $

Τι κοινό έχουν όλα αυτά τα σύνολα; Με την πρώτη ματιά, τίποτα. Αλλά στην πραγματικότητα υπάρχει κάτι. Και συγκεκριμένα: κάθε επόμενο στοιχείο διαφέρει από το προηγούμενο με τον ίδιο αριθμό.

Κρίνετε μόνοι σας. Το πρώτο σετ είναι απλώς διαδοχικοί αριθμοί, ο καθένας επόμενος περισσότερο από τον προηγούμενο. Στη δεύτερη περίπτωση, η διαφορά μεταξύ των παρακείμενων αριθμών είναι ήδη ίση με πέντε, αλλά αυτή η διαφορά είναι ακόμα σταθερή. Στην τρίτη περίπτωση, οι ρίζες γενικά. Ωστόσο, $ 2 \ sqrt (2) = \ sqrt (2) + \ sqrt (2) $, και $ 3 \ sqrt (2) = 2 \ sqrt (2) + \ sqrt (2) $, δηλ. και σε αυτήν την περίπτωση, κάθε επόμενο στοιχείο απλώς αυξάνεται κατά $ \ sqrt (2) $ (και μην φοβάστε ότι αυτός ο αριθμός είναι παράλογος).

Άρα: όλες αυτές οι ακολουθίες ονομάζονται αριθμητικές προόδους. Ας δώσουμε έναν αυστηρό ορισμό:

Ορισμός. Μια ακολουθία αριθμών στους οποίους κάθε επόμενος διαφέρει από τον προηγούμενο με την ίδια ακριβώς ποσότητα ονομάζεται αριθμητική πρόοδος. Το ίδιο το ποσό με το οποίο διαφέρουν οι αριθμοί ονομάζεται διαφορά της προόδου και τις περισσότερες φορές συμβολίζεται με το γράμμα $ d $.

Ορισμός: $ \ left (((a) _ (n)) \ right) $ - η ίδια η εξέλιξη, $ d $ - η διαφορά της.

Και μερικές σημαντικές παρατηρήσεις. Πρώτον, μόνο τακτικόςακολουθία αριθμών: επιτρέπεται να διαβάζονται αυστηρά με τη σειρά με την οποία γράφονται - και τίποτα άλλο. Δεν μπορείτε να αναδιατάξετε ή να ανταλλάξετε αριθμούς.

Δεύτερον, η ίδια η ακολουθία μπορεί να είναι πεπερασμένη ή άπειρη. Για παράδειγμα, το σύνολο (1; 2; 3) είναι προφανώς μια πεπερασμένη αριθμητική εξέλιξη. Αλλά αν γράψετε κάτι στο πνεύμα (1; 2; 3; 4; ...) - αυτό είναι ήδη μια ατελείωτη εξέλιξη. Η έλλειψη μετά τα τέσσερα, όπως ήταν, υπονοεί ότι υπάρχουν ακόμα αρκετοί αριθμοί σε εξέλιξη. Άπειρα πολλά, για παράδειγμα. :)

Θα ήθελα επίσης να σημειώσω ότι οι προόδους αυξάνονται και μειώνονται. Έχουμε ήδη δει τα αυξανόμενα - το ίδιο σετ (1; 2; 3; 4; ...). Και εδώ είναι παραδείγματα μειωμένων προόδων:

• 49; 41; 33; 25; 17; ...
• 17,5; 12; 6,5; 1; −4,5; −10; ...
• $ \ sqrt (5); \ \ sqrt (5) -1; \ \ sqrt (5) -2; \ \ sqrt (5) -3; ... $

Εντάξει, εντάξει: αυτό το τελευταίο παράδειγμα μπορεί να φαίνεται υπερβολικά περίπλοκο. Αλλά τα υπόλοιπα, νομίζω ότι τα καταλαβαίνετε. Επομένως, θα εισαγάγουμε νέους ορισμούς:

Ορισμός. Μια αριθμητική πρόοδος ονομάζεται:

1. αυξάνεται εάν κάθε επόμενο στοιχείο είναι μεγαλύτερο από το προηγούμενο.
2. μειώνεται εάν, αντίθετα, κάθε επόμενο στοιχείο είναι μικρότερο από το προηγούμενο.

Επιπλέον, υπάρχουν οι λεγόμενες "στάσιμες" ακολουθίες - αποτελούνται από τον ίδιο επαναλαμβανόμενο αριθμό. Για παράδειγμα, (3; 3; 3; ...).

Παραμένει μόνο ένα ερώτημα: πώς να διακρίνουμε μια αυξανόμενη εξέλιξη από μια φθίνουσα; Ευτυχώς, όλα εξαρτώνται από το πρόσημο του αριθμού $ d $, δηλ. διαφορά εξέλιξης:

1. Εάν $ d \ gt 0 $, τότε η πρόοδος αυξάνεται.
2. Εάν $ d \ lt 0 $, τότε η πρόοδος μειώνεται προφανώς.
3. Τέλος, υπάρχει η περίπτωση $ d = 0 $ - σε αυτή την περίπτωση ολόκληρη η εξέλιξη μειώνεται σε μια σταθερή ακολουθία πανομοιότυπων αριθμών: (1; 1; 1; 1; ...), κ.λπ.

Ας προσπαθήσουμε να υπολογίσουμε τη διαφορά $ d $ για τις τρεις μειούμενες προόδους που δίνονται παραπάνω. Για να γίνει αυτό, αρκεί να πάρετε δύο παρακείμενα στοιχεία (για παράδειγμα, το πρώτο και το δεύτερο) και να αφαιρέσετε τον αριθμό στα αριστερά από τον αριθμό στα δεξιά. Θα μοιάζει με αυτό:

• 41−49=−8;
• 12−17,5=−5,5;
• $ \ sqrt (5) -1- \ sqrt (5) = - 1 $.

Όπως μπορείτε να δείτε, και στις τρεις περιπτώσεις η διαφορά αποδείχθηκε πραγματικά αρνητική. Και τώρα που καταλάβαμε λίγο πολύ τους ορισμούς, ήρθε η ώρα να καταλάβουμε πώς περιγράφονται οι προόδους και ποιες είναι οι ιδιότητές τους.

Μέλη προόδου και επαναλαμβανόμενος τύπος

Δεδομένου ότι τα στοιχεία των ακολουθιών μας δεν μπορούν να ανταλλαχθούν, μπορούν να αριθμηθούν:

\ [\ αριστερά (((α) _ (n)) \ δεξιά = \ αριστερά \ (((a) _ (1)), \ ((a) _ (2)), ((a) _ (3 )), ... \ σωστά \) \]

Τα επιμέρους στοιχεία αυτού του συνόλου ονομάζονται μέλη της προόδου. Υποδεικνύονται με έναν αριθμό: τον πρώτο όρο, τον δεύτερο όρο κ.λπ.

Επιπλέον, όπως ήδη γνωρίζουμε, τα παρακείμενα μέλη της εξέλιξης σχετίζονται με τον τύπο:

\ [((a) _ (n))-((a) _ (n-1)) = d \ Rightarrow ((a) _ (n)) = ((a) _ (n-1)) + d \]

Εν ολίγοις, για να βρείτε τον όρο $ n $ th στην εξέλιξη, πρέπει να γνωρίζετε τον όρο $ n-1 $ th και τη διαφορά $ d $. Ένας τέτοιος τύπος ονομάζεται επαναλαμβανόμενος, αφού με τη βοήθειά του μπορείτε να βρείτε οποιονδήποτε αριθμό, γνωρίζοντας μόνο τον προηγούμενο (και στην πραγματικότητα - όλους τους προηγούμενους). Αυτό είναι πολύ ενοχλητικό, οπότε υπάρχει ένας πιο περίπλοκος τύπος που μειώνει τυχόν υπολογισμούς στον πρώτο όρο και τη διαφορά:

\ [((a) _ (n)) = ((a) _ (1)) + \ αριστερά (n-1 \ δεξιά) d \]

Σίγουρα έχετε ήδη συναντήσει αυτόν τον τύπο. Τους αρέσει να το δίνουν σε κάθε λογής βιβλία αναφοράς και ρεσεμπνίκ. Και σε οποιοδήποτε λογικό εγχειρίδιο μαθηματικών, πηγαίνει ένα από τα πρώτα.

Ωστόσο, προτείνω να εξασκηθούμε λίγο.

Πρόβλημα νούμερο 1. Γράψτε τους τρεις πρώτους όρους της αριθμητικής προόδου $ \ αριστερά (((a) _ (n)) \ δεξιά) $, αν $ ((a) _ (1)) = 8, d = -5 $.

Λύση. Έτσι, γνωρίζουμε τον πρώτο όρο $ ((a) _ (1)) = 8 $ και τη διαφορά της προόδου $ d = -5 $. Ας χρησιμοποιήσουμε τον τύπο που μόλις δόθηκε και αντικαταστήστε $ n = 1 $, $ n = 2 $ και $ n = 3 $:

\ [\ ξεκινά (στοίχιση) & ((a) _ (n)) = ((a) _ (1)) + \ αριστερά (n-1 \ δεξιά) d; \\ & ((a) _ (1)) = ((a) _ (1)) + \ αριστερά (1-1 \ δεξιά) d = ((a) _ (1)) = 8; \\ & ((a) _ (2)) = ((a) _ (1)) + \ αριστερά (2-1 \ δεξιά) d = ((a) _ (1)) + d = 8-5 = 3; \\ & ((a) _ (3)) = ((a) _ (1)) + \ αριστερά (3-1 \ δεξιά) d = ((a) _ (1)) + 2d = 8-10 = -2. \\ \ τέλος (στοίχιση) \]

Απάντηση: (8; 3; −2)

Αυτό είναι όλο! Λάβετε υπόψη: η πρόοδος μας μειώνεται.

Φυσικά, $ n = 1 $ δεν θα μπορούσε να έχει αντικατασταθεί - ο πρώτος όρος είναι ήδη γνωστός σε εμάς. Ωστόσο, αντικαθιστώντας ένα, βεβαιωθήκαμε ότι ο τύπος μας λειτουργεί ακόμη και για τον πρώτο όρο. Σε άλλες περιπτώσεις, όλα κατέληξαν σε ασήμαντη αριθμητική.

Πρόβλημα νούμερο 2. Γράψτε τους πρώτους τρεις όρους της αριθμητικής προόδου αν ο έβδομος όρος του είναι −40 και ο δέκατος έβδομος όρος είναι −50.

Λύση. Ας γράψουμε την κατάσταση του προβλήματος με τους συνήθεις όρους:

\ [((a) _ (7)) = - 40; \ quad ((a) _ (17)) = - 50. \]

\ [\ αριστερά \ (\ έναρξη (στοίχιση) & ((α) _ (7)) = ((α) _ (1)) + 6δ \\ & ((α) _ (17)) = ((α) _ (1)) + 16d \\ \ τέλος (στοίχιση) \ δεξιά. \]

\ [\ αριστερά \ (\ έναρξη (στοίχιση) & ((α) _ (1)) + 6d = -40 \\ & ((α) _ (1)) + 16d = -50 \\ \ τέλος (στοίχιση) \ σωστά. \]

Βάζω το σύμβολο του συστήματος γιατί αυτές οι απαιτήσεις πρέπει να πληρούνται ταυτόχρονα. Και τώρα σημειώστε ότι αν αφαιρέσουμε το πρώτο από τη δεύτερη εξίσωση (έχουμε το δικαίωμα να το κάνουμε αυτό, αφού έχουμε σύστημα), παίρνουμε αυτό:

\ [\ ξεκινά (στοίχιση) & ((α) _ (1)) + 16d- \ αριστερά (((α) _ (1)) + 6δ \ δεξιά) =- 50- \ αριστερά (-40 \ δεξιά); \\ & ((α) _ (1)) + 16d - ((a) _ (1)) - 6d = -50 + 40; \\ & 10d = -10; \\ & d = -1. \\ \ τέλος (στοίχιση) \]

Έτσι βρήκαμε τη διαφορά στην εξέλιξη! Απομένει να αντικαταστήσουμε τον αριθμό που βρέθηκε σε οποιαδήποτε από τις εξισώσεις του συστήματος. Για παράδειγμα, στο πρώτο:

\ [\ begin (matrix) ((a) _ (1)) + 6d = -40; \ quad d = -1 \\ \ Downarrow \\ ((a) _ (1)) -6 = -40; \\ ((α) _ (1)) = - 40 + 6 = -34. \\ \ τέλος (μήτρα) \]

Τώρα, γνωρίζοντας τον πρώτο όρο και τη διαφορά, μένει να βρούμε τον δεύτερο και τον τρίτο όρο:

\ [\ ξεκινά (στοίχιση) & ((α) _ (2)) = ((α) _ (1)) + d = -34-1 = -35; \\ & ((α) _ (3)) = ((α) _ (1)) + 2d = -34-2 = -36. \\ \ τέλος (στοίχιση) \]

Ετοιμος! Το πρόβλημα λύθηκε.

Απάντηση: (-34; -35; -36)

Δώστε προσοχή σε μια ενδιαφέρουσα ιδιότητα της προόδου που ανακαλύψαμε: αν πάρουμε τους όρους $ n $ th και $ m $ th και τους αφαιρέσουμε ο ένας από τον άλλο, έχουμε τη διαφορά της προόδου πολλαπλασιασμένη με τον αριθμό $ n-m $:

\ [((a) _ (n)) - ((a) _ (m)) = d \ cdot \ αριστερά (n -m \ δεξιά) \]

Μια απλή αλλά πολύ χρήσιμη ιδιότητα που πρέπει οπωσδήποτε να γνωρίζετε - με τη βοήθειά της, μπορείτε να επιταχύνετε σημαντικά την επίλυση πολλών προβλημάτων σταδιακά. Εδώ είναι ένα εξαιρετικό παράδειγμα:

Πρόβλημα αριθμός 3. Ο πέμπτος όρος της αριθμητικής προόδου είναι 8,4 και ο δέκατος όρος είναι 14,4. Βρείτε τον δέκατο πέμπτο όρο αυτής της προόδου.

Λύση. Δεδομένου ότι $ ((a) _ (5)) = 8,4 $, $ ((a) _ (10)) = 14,4 $, και πρέπει να βρείτε $ ((a) _ (15)) $, τότε σημειώνουμε τα ακόλουθα :

\ [\ ξεκινά (στοίχιση) & ((α) _ (15)) - ((α) _ (10)) = 5δ; \\ & ((α) _ (10)) - ((α) _ (5)) = 5δ. \\ \ τέλος (στοίχιση) \]

Αλλά υπό τον όρο $ ((a) _ (10)) - ((a) _ (5)) = 14,4-8,4 = 6 $, άρα $ 5d = 6 $, από όπου έχουμε:

\ [\ ξεκινά (στοίχιση) & ((α) _ (15)) - 14,4 = 6; \\ & ((α) _ (15)) = 6 + 14,4 = 20,4. \\ \ τέλος (στοίχιση) \]

Απάντηση: 20.4

Αυτό είναι όλο! Δεν χρειαζόταν να συνθέσουμε κάποια συστήματα εξισώσεων και να υπολογίσουμε τον πρώτο όρο και τη διαφορά - όλα λύθηκαν σε μερικές γραμμές.

Τώρα ας εξετάσουμε έναν άλλο τύπο εργασιών - να βρούμε αρνητικά και θετικά μέλη της εξέλιξης. Δεν είναι μυστικό ότι εάν η πρόοδος αυξηθεί, ενώ ο πρώτος όρος είναι αρνητικός, τότε αργά ή γρήγορα θα εμφανιστούν θετικοί όροι σε αυτόν. Και αντίθετα: τα μέλη της φθίνουσας προόδου αργά ή γρήγορα θα γίνουν αρνητικά.

Ταυτόχρονα, είναι πολύ μακριά από πάντα δυνατό να δούμε αυτήν τη στιγμή "κατά μέτωπο", διαδοχικά περνώντας από τα στοιχεία. Συχνά, τα προβλήματα σχεδιάζονται με τέτοιο τρόπο ώστε χωρίς να γνωρίζουμε τους τύπους, οι υπολογισμοί θα έπαιρναν πολλά φύλλα - απλώς θα αποκοιμιόμασταν ενώ βρήκαμε την απάντηση. Επομένως, θα προσπαθήσουμε να λύσουμε αυτά τα προβλήματα με ταχύτερο τρόπο.

Πρόβλημα αριθμός 4. Πόσοι αρνητικοί όροι υπάρχουν στην αριθμητική πρόοδο -38,5; .835,8; ...?

Λύση. Έτσι, $ ((a) _ (1)) = - 38,5 $, $ ((a) _ (2)) = - 35,8 $, από τα οποία βρίσκουμε αμέσως τη διαφορά:

Σημειώστε ότι η διαφορά είναι θετική, επομένως η πρόοδος αυξάνεται. Ο πρώτος όρος είναι αρνητικός, οπότε κάποια στιγμή θα πέσουμε πάνω σε θετικούς αριθμούς. Το μόνο ερώτημα είναι πότε θα συμβεί.

Ας προσπαθήσουμε να μάθουμε: πόσο καιρό (δηλαδή μέχρι ποιος φυσικός αριθμός $ n $) διατηρείται η αρνητικότητα των όρων:

\ [\ ξεκινά (στοίχιση) & ((a) _ (n)) \ lt 0 \ Rightarrow ((a) _ (1)) + \ left (n-1 \ right) d \ lt 0; \\ & -38.5+ \ αριστερά (n -1 \ δεξιά) \ cdot 2.7 \ lt 0; \ quad \ αριστερά | \ cdot 10 \ δεξιά. \\ & -385 + 27 \ cdot \ αριστερά (n -1 \ δεξιά) \ lt 0; \\ & -385 + 27n -27 \ lt 0; \\ & 27n \ lt 412; \\ & n \ lt 15 \ frac (7) (27) \ Rightarrow ((n) _ (\ max)) = 15. \\ \ τέλος (στοίχιση) \]

Η τελευταία γραμμή χρειάζεται κάποια εξήγηση. Έτσι, γνωρίζουμε ότι $ n \ lt 15 \ frac (7) (27) $. Από την άλλη πλευρά, θα είμαστε ικανοποιημένοι μόνο με ακέραιες τιμές του αριθμού (επιπλέον: $ n \ in \ mathbb (N) $), οπότε ο μεγαλύτερος επιτρεπόμενος αριθμός είναι ακριβώς $ n = 15 $, και σε καμία περίπτωση είναι 16.

Πρόβλημα αριθμός 5. Σε αριθμητική πρόοδο $ (() _ (5)) = - 150, (() _ (6)) = - 147 $. Βρείτε τον αριθμό του πρώτου θετικού όρου αυτής της εξέλιξης.

Θα ήταν ακριβώς το ίδιο πρόβλημα με το προηγούμενο, αλλά δεν γνωρίζουμε $ ((a) _ (1)) $. Αλλά οι γειτονικοί όροι είναι γνωστοί: $ ((a) _ (5)) $ και $ ((a) _ (6)) $, έτσι μπορούμε εύκολα να βρούμε τη διαφορά της προόδου:

Επιπλέον, θα προσπαθήσουμε να εκφράσουμε τον πέμπτο όρο ως προς τον πρώτο και τη διαφορά σύμφωνα με τον τυποποιημένο τύπο:

\ [\ ξεκινά (στοίχιση) & ((a) _ (n)) = ((a) _ (1)) + \ αριστερά (n-1 \ δεξιά) \ cdot d; \\ & ((α) _ (5)) = ((α) _ (1)) + 4d; \\ & -150 = ((α) _ (1)) + 4 \ cdot 3; \\ & ((α) _ (1)) = -150-12 = -162. \\ \ τέλος (στοίχιση) \]

Τώρα προχωρούμε κατ 'αναλογία με την προηγούμενη εργασία. Ανακαλύπτουμε σε ποιο σημείο της ακολουθίας μας θα υπάρχουν θετικοί αριθμοί:

\ [\ ξεκινά (στοίχιση) & ((α) _ (n)) = - 162+ \ αριστερά (n -1 \ δεξιά) \ cdot 3 \ gt 0; \\ & -162 + 3n -3 \ gt 0; \\ & 3n \ gt 165; \\ & n \ gt 55 \ Rightarrow ((n) _ (\ min)) = 56. \\ \ τέλος (στοίχιση) \]

Η μικρότερη ακέραιη λύση σε αυτήν την ανισότητα είναι 56.

Λάβετε υπόψη: στην τελευταία εργασία, όλα μειώθηκαν σε μια αυστηρή ανισότητα, οπότε η επιλογή $ n = 55 $ δεν θα μας ταιριάζει.

Τώρα που μάθαμε πώς να λύνουμε απλά προβλήματα, ας προχωρήσουμε σε πιο πολύπλοκα. Αλλά πρώτα, ας μελετήσουμε μια άλλη πολύ χρήσιμη ιδιότητα αριθμητικών προόδων, η οποία θα μας εξοικονομήσει πολύ χρόνο και άνισα κελιά στο μέλλον. :)

Αριθμητική μέση τιμή και ίσες εσοχές

Εξετάστε αρκετά διαδοχικά μέλη της αυξανόμενης αριθμητικής προόδου $ \ left (((a) _ (n)) \ right) $. Ας προσπαθήσουμε να τα σημειώσουμε στην αριθμητική γραμμή:

Μέλη μιας αριθμητικής προόδου σε μια αριθμητική γραμμή

Σημείωσα συγκεκριμένα αυθαίρετους όρους $ ((a) _ (n-3)), ..., ((a) _ (n + 3)) $, όχι κανένα $ ((a) _ (1)), \ ( (α) _ (2)), \ ((α) _ (3)) $, κ.λπ. Γιατί ο κανόνας, για τον οποίο θα μιλήσω τώρα, λειτουργεί το ίδιο για τυχόν «τμήματα».

Και ο κανόνας είναι πολύ απλός. Ας θυμηθούμε τον τύπο επανάληψης και να τον γράψουμε για όλα τα επισημασμένα μέλη:

\ [\ ξεκινά (στοίχιση) & ((a) _ (n-2)) = ((a) _ (n-3)) + d; \\ & ((a) _ (n-1)) = ((a) _ (n-2)) + d; \\ & ((a) _ (n)) = ((a) _ (n-1)) + d; \\ & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n + 1)) + d; \\ \ τέλος (στοίχιση) \]

Ωστόσο, αυτές οι ισότητες μπορούν να ξαναγραφούν διαφορετικά:

\ [\ ξεκινά (στοίχιση) & ((a) _ (n -1)) = ((a) _ (n)) - d; \\ & ((a) _ (n -2)) = ((a) _ (n)) - 2d; \\ & ((a) _ (n -3)) = ((a) _ (n)) - 3d; \\ & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n)) + 2d; \\ & ((a) _ (n + 3)) = ((a) _ (n)) + 3d; \\ \ τέλος (στοίχιση) \]

Λοιπόν, τι; Και το γεγονός ότι οι όροι $ ((a) _ (n-1)) $ και $ ((a) _ (n + 1)) $ βρίσκονται στην ίδια απόσταση από $ ((a) _ (n)) $ Το Και αυτή η απόσταση είναι ίση με $ d $. Το ίδιο μπορεί να ειπωθεί για τα μέλη $ ((a) _ (n -2)) $ και $ ((a) _ (n + 2)) $ - αφαιρούνται επίσης από το $ ((a) _ (n) ) $ ίδια απόσταση ίση με $ 2d $. Μπορείτε να συνεχίσετε επ 'αόριστον, αλλά το νόημα απεικονίζεται καλά από την εικόνα.

Τα μέλη της εξέλιξης βρίσκονται στην ίδια απόσταση από το κέντρο

Τι σημαίνει αυτό για εμάς; Αυτό σημαίνει ότι μπορείτε να βρείτε $ ((a) _ (n)) $ εάν είναι γνωστοί οι γειτονικοί αριθμοί:

\ [((a) _ (n)) = \ frac (((a) _ (n-1)) + ((a) _ (n + 1))) (2) \]

Καταλήξαμε σε μια εξαιρετική δήλωση: κάθε μέλος της αριθμητικής προόδου είναι ίσο με τον αριθμητικό μέσο των γειτονικών όρων! Επιπλέον: μπορούμε να αποκλίνουμε από το $ ((a) _ (n)) $ αριστερά και δεξιά μας όχι ένα βήμα, αλλά $ k $ βήματα - και παρόλα αυτά ο τύπος θα είναι σωστός:

\ [((a) _ (n)) = \ frac (((a) _ (n-k)) + ((a) _ (n + k))) (2) \]

Εκείνοι. μπορούμε εύκολα να βρούμε κάποια $ ((a) _ (150)) $ αν γνωρίζουμε $ ((a) _ (100)) $ και $ ((a) _ (200)) $, επειδή $ ((a) _ (150)) = \ frac (((a) _ (100)) + ((a) _ (200))) (2) $. Με την πρώτη ματιά, μπορεί να φαίνεται ότι αυτό το γεγονός δεν μας δίνει τίποτα χρήσιμο. Ωστόσο, στην πράξη, πολλά προβλήματα «ακονίζονται» ειδικά για τη χρήση του αριθμητικού μέσου όρου. Ρίξε μια ματιά:

Πρόβλημα αριθμός 6. Βρείτε όλες τις τιμές των $ x $ για τις οποίες οι αριθμοί $ -6 ((x) ^ (2)) $, $ x + 1 $ και $ 14 + 4 ((x) ^ (2)) $ είναι διαδοχικά μέλη της αριθμητικής προόδου (κατά σειρά).

Λύση. Δεδομένου ότι οι αριθμοί που υποδεικνύονται είναι μέλη της προόδου, η συνθήκη του αριθμητικού μέσου πληρούται γι 'αυτούς: το κεντρικό στοιχείο $ x + 1 $ μπορεί να εκφραστεί με όρους παρακείμενων στοιχείων:

\ [\ ξεκινά (στοίχιση) & x + 1 = \ frac (-6 ((x) ^ (2)) + 14 + 4 ((x) ^ (2))) (2); \\ & x + 1 = \ frac (14-2 ((x) ^ (2))) (2); \\ & x + 1 = 7 - ((x) ^ (2)); \\ & ((x) ^ (2)) + x-6 = 0. \\ \ τέλος (στοίχιση) \]

Το αποτέλεσμα είναι μια κλασική τετραγωνική εξίσωση. Οι ρίζες του: $ x = 2 $ και $ x = -3 $ - αυτές είναι οι απαντήσεις.

Απάντηση: −3; 2

Πρόβλημα αριθμός 7. Βρείτε τις τιμές $ $ για τις οποίες οι αριθμοί $ -1; 4-3; (() ^ (2)) + 1 $ κάνουν αριθμητική πρόοδο (με αυτή τη σειρά).

Λύση. Και πάλι, εκφράζουμε τον μεσαίο όρο ως προς τον αριθμητικό μέσο των γειτονικών όρων:

\ [\ ξεκινά (στοίχιση) & 4x-3 = \ frac (x-1 + ((x) ^ (2)) + 1) (2); \\ & 4x-3 = \ frac (((x) ^ (2)) + x) (2); \ quad \ left | \ cdot 2 \ δεξιά.; \\ & 8x-6 = ((x) ^ (2)) + x; \\ & ((x) ^ (2)) - 7x + 6 = 0. \\ \ τέλος (στοίχιση) \]

Και πάλι η τετραγωνική εξίσωση. Και πάλι υπάρχουν δύο ρίζες: $ x = 6 $ και $ x = 1 $.

Απάντηση: 1? 6

Εάν κατά τη διαδικασία επίλυσης ενός προβλήματος βγάζετε κάποιους βάναυσους αριθμούς ή δεν είστε απόλυτα σίγουροι για την ορθότητα των απαντήσεων που βρέθηκαν, τότε υπάρχει μια υπέροχη τεχνική που σας επιτρέπει να ελέγξετε: λύσαμε σωστά το πρόβλημα;

Για παράδειγμα, στο πρόβλημα αρ. 6 λάβαμε απαντήσεις -3 και 2. Πώς να ελέγξουμε ότι αυτές οι απαντήσεις είναι σωστές; Ας τα συνδέσουμε στην αρχική κατάσταση και να δούμε τι θα συμβεί. Επιτρέψτε μου να σας υπενθυμίσω ότι έχουμε τρεις αριθμούς ($ -6 (() ^ (2)) $, $ + 1 $ και $ 14 + 4 (() ^ (2)) $), οι οποίοι πρέπει να σχηματίζουν αριθμητική πρόοδο. Αντικατάσταση $ x = -3 $:

\ [\ ξεκινά (στοίχιση) & x = -3 \ Rightarrow \\ & -6 ((x) ^ (2)) = -54; \\ & x + 1 = -2; \\ & 14 + 4 ((x) ^ (2)) = 50. \ τέλος (στοίχιση) \]

Λήφθηκαν οι αριθμοί -54. ;2; 50, που διαφέρουν κατά 52, είναι αναμφίβολα μια αριθμητική πρόοδος. Το ίδιο συμβαίνει για $ x = 2 $:

\ [\ ξεκινήσει (στοίχιση) & x = 2 \ Rightarrow \\ & -6 ((x) ^ (2)) = - 24; \\ & x + 1 = 3; \\ & 14 + 4 ((x) ^ (2)) = 30. \ τέλος (στοίχιση) \]

Και πάλι μια εξέλιξη, αλλά με διαφορά 27. Έτσι, το πρόβλημα λύνεται σωστά. Οι ενδιαφερόμενοι μπορούν να ελέγξουν μόνοι τους το δεύτερο πρόβλημα, αλλά θα πω αμέσως: όλα είναι σωστά και εκεί.

Σε γενικές γραμμές, κατά την επίλυση των τελευταίων προβλημάτων, συναντήσαμε ένα άλλο ενδιαφέρον γεγονός, το οποίο πρέπει επίσης να θυμόμαστε:

Εάν τρεις αριθμοί είναι τέτοιοι ώστε ο δεύτερος να είναι ο αριθμητικός μέσος όρος του πρώτου και του τελευταίου, τότε αυτοί οι αριθμοί σχηματίζουν μια αριθμητική πρόοδο.

Στο μέλλον, η κατανόηση αυτής της δήλωσης θα μας επιτρέψει να "κατασκευάσουμε" κυριολεκτικά τις απαραίτητες προόδους, με βάση την κατάσταση του προβλήματος. Αλλά πριν φτάσουμε σε μια τέτοια "κατασκευή", θα πρέπει να δώσουμε προσοχή σε ένα ακόμη γεγονός, το οποίο προκύπτει άμεσα από όσα έχουν ήδη εξεταστεί.

Ομαδοποίηση και άθροισμα στοιχείων

Ας επιστρέψουμε ξανά στον αριθμητικό άξονα. Ας σημειώσουμε εκεί αρκετά μέλη της εξέλιξης, μεταξύ των οποίων, ίσως. υπάρχουν πολλά άλλα μέλη:

Η αριθμητική γραμμή έχει 6 στοιχεία επισημασμένα

Ας προσπαθήσουμε να εκφράσουμε την "αριστερή ουρά" σε $ ((a) _ (n)) $ και $ d $ και "δεξιά ουρά" σε $ ((a) _ (k)) $ και $ d $ Το Είναι πολύ απλό:

\ [\ ξεκινά (στοίχιση) & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n)) + 2d; \\ & ((a) _ (k -1)) = ((a) _ (k)) - d; \\ & ((a) _ (k -2)) = ((a) _ (k)) - 2d. \\ \ τέλος (στοίχιση) \]

Τώρα, σημειώστε ότι τα ακόλουθα ποσά είναι ίσα:

\ [\ ξεκινά (στοίχιση) & ((a) _ (n)) + ((a) _ (k)) = S; \\ & ((a) _ (n + 1)) + ((a) _ (k -1)) = ((a) _ (n)) + d + ((a) _ (k)) - d = S; \\ & ((a) _ (n + 2)) + ((a) _ (k -2)) = ((a) _ (n)) + 2d + ((a) _ (k)) - 2d = Σ. \ τέλος (στοίχιση) \]

Με απλά λόγια, αν λάβουμε υπόψη ως αρχή δύο στοιχεία της προόδου, τα οποία είναι συνολικά ίσα με κάποιον αριθμό $ S $, και τότε αρχίζουμε να περπατάμε από αυτά τα στοιχεία σε αντίθετες κατευθύνσεις (το ένα προς το άλλο ή αντίστροφα για να απομακρυνθούμε) , τότε τα ποσά των στοιχείων στα οποία θα πέσουμε θα είναι επίσης ίσα$ S $. Αυτό μπορεί να αναπαρασταθεί σαφέστερα γραφικά:

Η ίση εσοχή δίνει ίσα ποσά

Η κατανόηση αυτού του γεγονότος θα μας επιτρέψει να λύσουμε προβλήματα ενός βασικά υψηλότερου επιπέδου πολυπλοκότητας από αυτά που θεωρήσαμε παραπάνω. Για παράδειγμα, τέτοια:

Πρόβλημα νούμερο 8. Προσδιορίστε τη διαφορά της αριθμητικής προόδου στην οποία ο πρώτος όρος είναι 66 και το γινόμενο του δεύτερου και δωδέκατου όρου είναι το μικρότερο δυνατό.

Λύση. Ας γράψουμε όλα όσα γνωρίζουμε:

\ [\ ξεκινά (στοίχιση) & ((α) _ (1)) = 66; \\ & d =? \\ & ((a) _ (2)) \ cdot ((a) _ (12)) = \ min \ τέλος (στοίχιση) \]

Έτσι, δεν γνωρίζουμε τη διαφορά της προόδου $ d $. Στην πραγματικότητα, ολόκληρη η λύση θα βασιστεί στη διαφορά, αφού το προϊόν $ ((a) _ (2)) \ cdot ((a) _ (12)) $ μπορεί να ξαναγραφεί ως εξής:

\ [\ ξεκινά (στοίχιση) & ((α) _ (2)) = ((α) _ (1)) + d = 66 + d; \\ & ((α) _ (12)) = ((α) _ (1)) + 11d = 66 + 11d; \\ & ((a) _ (2)) \ cdot ((a) _ (12)) = \ left (66 + d \ right) \ cdot \ left (66 + 11d \ right) = \\ & = 11 \ cdot \ αριστερά (d + 66 \ δεξιά) \ cdot \ αριστερά (d + 6 \ δεξιά). \ τέλος (στοίχιση) \]

Για όσους βρίσκονται στη δεξαμενή: Έβγαλα τον κοινό συντελεστή 11 από τη δεύτερη παρένθεση. Έτσι, το προϊόν που αναζητείται είναι μια τετραγωνική συνάρτηση σε σχέση με τη μεταβλητή $ d $. Επομένως, σκεφτείτε τη συνάρτηση $ f \ left (d \ right) = 11 \ left (d + 66 \ right) \ left (d + 6 \ right) $ - το γράφημα της θα είναι μια παραβολή με διακλαδώσεις προς τα πάνω, αφού αν επεκτείνουμε τις αγκύλες, τότε έχουμε:

\ [\ ξεκινά (στοίχιση) & f \ αριστερά (d \ δεξιά) = 11 \ αριστερά (((δ) ^ (2)) + 66d + 6d + 66 \ cdot 6 \ δεξιά) = \\ & = 11 (( δ) ^ (2)) + 11 \ cdot 72d + 11 \ cdot 66 \ cdot 6 \ τέλος (στοίχιση) \]

Όπως μπορείτε να δείτε, ο συντελεστής στον κύριο όρο είναι 11 - αυτός είναι ένας θετικός αριθμός, οπότε πραγματικά έχουμε να κάνουμε με μια παραβολή με διακλαδώσεις προς τα πάνω:

τετράγωνη γραφική παράσταση - παραβολή

Λάβετε υπόψη: αυτή η παραβολή παίρνει την ελάχιστη τιμή της στην κορυφή της με την περίληψη $ ((d) _ (0)) $. Φυσικά, μπορούμε να υπολογίσουμε αυτήν την τετμημένη σύμφωνα με το τυπικό σχήμα (υπάρχει επίσης ο τύπος $ ((d) _ (0)) = (- b) / (2a) \; $), αλλά θα ήταν πολύ πιο λογικό για να παρατηρήσετε ότι η επιθυμητή κορυφή βρίσκεται στη συμμετρία άξονα της παραβολής, οπότε το σημείο $ ((d) _ (0)) $ βρίσκεται σε ίση απόσταση από τις ρίζες της εξίσωσης $ f \ αριστερά (d \ δεξιά) = 0 $:

\ [\ ξεκινά (στοίχιση) & f \ αριστερά (d \ δεξιά) = 0; \\ & 11 \ cdot \ αριστερά (d + 66 \ δεξιά) \ cdot \ αριστερά (d + 6 \ δεξιά) = 0; \\ & ((d) _ (1)) = - 66; \ quad ((d) _ (2)) = - 6. \\ \ τέλος (στοίχιση) \]

Αυτός είναι ο λόγος για τον οποίο δεν βιαζόμουν να ανοίξω τις αγκύλες: στην αρχική μορφή, οι ρίζες ήταν πολύ, πολύ εύκολο να βρεθούν. Επομένως, η τετμημένη είναι ίση με τον αριθμητικό μέσο όρο των αριθμών −66 και −6:

\ [((d) _ (0)) = \ frac (-66-6) (2) =-36 \]

Τι μας δίνει ο ανακαλυφθείς αριθμός; Με αυτό, το απαιτούμενο προϊόν παίρνει τη μικρότερη τιμή (παρεμπιπτόντως, δεν έχουμε μετρήσει $ ((y) _ (\ min)) $ - δεν το χρειαζόμαστε). Ταυτόχρονα, αυτός ο αριθμός είναι η διαφορά μεταξύ της αρχικής προόδου, δηλ. βρήκαμε την απάντηση. :)

Απάντηση: −36

Πρόβλημα νούμερο 9. Εισάγετε τρεις αριθμούς μεταξύ των αριθμών $ - \ frac (1) (2) $ και $ - \ frac (1) (6) $ έτσι ώστε μαζί με τους δεδομένους αριθμούς να σχηματίσουν αριθμητική πρόοδο.

Λύση. Βασικά, πρέπει να δημιουργήσουμε μια ακολουθία πέντε αριθμών, με τον πρώτο και τον τελευταίο αριθμό να είναι ήδη γνωστοί. Ας υποδείξουμε τους αριθμούς που λείπουν με τις μεταβλητές $ x $, $ y $ και $ z $:

\ [\ left (((a) _ (n)) \ right) = \ left \ ( - \ frac (1) (2); x; y; z; - \ frac (1) (6) \ right \ ) \]

Σημειώστε ότι ο αριθμός $ y $ είναι το "μέσο" της ακολουθίας μας - είναι ισαπέχοντας τόσο από τους αριθμούς $ x $ και $ z $, όσο και από τους αριθμούς $ - \ frac (1) (2) $ και $ - \ frac (1) (6) $. Και αν αυτή τη στιγμή δεν μπορούμε να πάρουμε $ y $ από τους αριθμούς $ x $ και $ z $, τότε η κατάσταση είναι διαφορετική με τα άκρα της εξέλιξης. Θυμηθείτε τον αριθμητικό μέσο όρο:

Τώρα, γνωρίζοντας $ y $, θα βρούμε τους υπόλοιπους αριθμούς. Σημειώστε ότι $ x $ βρίσκεται μεταξύ των αριθμών $ - \ frac (1) (2) $ και του $ y = - \ frac (1) (3) $ που μόλις βρέθηκε. Να γιατί

Ομοίως, βρίσκουμε τον υπόλοιπο αριθμό:

Ετοιμος! Βρήκαμε και τους τρεις αριθμούς. Ας τα γράψουμε στην απάντηση με τη σειρά με την οποία πρέπει να εισαχθούν μεταξύ των αρχικών αριθμών.

Απάντηση: $ - \ frac (5) (12); \ - \ frac (1) (3); \ - \ frac (1) (4) $

Πρόβλημα αριθμός 10. Εισάγετε πολλούς αριθμούς μεταξύ των αριθμών 2 και 42, οι οποίοι μαζί με αυτούς τους αριθμούς σχηματίζουν μια αριθμητική πρόοδο, αν γνωρίζετε ότι το άθροισμα του πρώτου, δεύτερου και τελευταίου αριθμού που έχει εισαχθεί είναι 56.

Λύση. Ένα ακόμη πιο δύσκολο έργο, το οποίο, ωστόσο, επιλύεται σύμφωνα με το ίδιο σχήμα με τα προηγούμενα - μέσω του αριθμητικού μέσου όρου. Το πρόβλημα είναι ότι δεν γνωρίζουμε πόσους αριθμούς πρέπει να εισαγάγουμε. Επομένως, για οριστικότητα, ας υποθέσουμε ότι μετά την εισαγωγή όλων θα υπάρχουν ακριβώς $ n $ αριθμοί, και ο πρώτος από αυτούς είναι 2 και ο τελευταίος είναι 42. Σε αυτή την περίπτωση, η αναζητούμενη αριθμητική εξέλιξη μπορεί να αναπαρασταθεί ως:

\ [\ αριστερά (((α) _ (n)) \ δεξιά = \ αριστερά \ (2; ((a) _ (2)); ((a) _ (3)); ...; (( α) _ (n-1)); 42 \ δεξιά \) \]

\ [((α) _ (2)) + ((α) _ (3)) + ((α) _ (n-1)) = 56 \]

Σημειώστε, ωστόσο, ότι οι αριθμοί $ ((a) _ (2)) $ και $ ((a) _ (n-1)) $ λαμβάνονται από τους αριθμούς 2 και 42 στις άκρες κατά ένα βήμα ο ένας προς τον άλλον, δηλ ... στο κέντρο της ακολουθίας. Αυτό σημαίνει ότι

\ [((α) _ (2)) + ((α) _ (n-1)) = 2 + 42 = 44 \]

Αλλά τότε η έκφραση που γράφτηκε παραπάνω μπορεί να ξαναγραφεί ως εξής:

\ [\ ξεκινά (στοίχιση) & ((a) _ (2)) + ((a) _ (3)) + ((a) _ (n-1)) = 56; \\ & \ αριστερά (((α) _ (2)) + ((α) _ (n-1)) \ δεξιά) + ((α) _ (3)) = 56; \\ & 44 + ((α) _ (3)) = 56; \\ & ((α) _ (3)) = 56-44 = 12. \\ \ τέλος (στοίχιση) \]

Γνωρίζοντας $ ((a) _ (3)) $ και $ ((a) _ (1)) $, μπορούμε εύκολα να βρούμε τη διαφορά της προόδου:

\ [\ ξεκινά (στοίχιση) & ((α) _ (3)) - ((α) _ (1)) = 12 - 2 = 10; \\ & ((a) _ (3)) - ((a) _ (1)) = \ αριστερά (3-1 \ δεξιά) \ cdot d = 2d; \\ & 2d = 10 \ Rightarrow d = 5. \\ \ τέλος (στοίχιση) \]

Απομένει μόνο να βρούμε τα υπόλοιπα μέλη:

\ [\ ξεκινά (στοίχιση) & ((α) _ (1)) = 2; \\ & ((α) _ (2)) = 2 + 5 = 7; \\ & ((α) _ (3)) = 12; \\ & ((α) _ (4)) = 2 + 3 \ cdot 5 = 17; \\ & ((α) _ (5)) = 2 + 4 \ cdot 5 = 22; \\ & ((α) _ (6)) = 2 + 5 \ cdot 5 = 27; \\ & ((α) _ (7)) = 2 + 6 \ cdot 5 = 32; \\ & ((α) _ (8)) = 2 + 7 \ cdot 5 = 37; \\ & ((α) _ (9)) = 2 + 8 \ cdot 5 = 42; \\ \ τέλος (στοίχιση) \]

Έτσι, ήδη στο 9ο βήμα θα φτάσουμε στο αριστερό άκρο της ακολουθίας - τον αριθμό 42. Συνολικά, ήταν απαραίτητο να εισαγάγουμε μόνο 7 αριθμούς: 7; 12; 17; 22; 27; 32; 37

Απάντηση: 7? 12; 17; 22; 27; 32; 37

Προβλήματα λέξεων με προοδεύσεις

Εν κατακλείδι, θα ήθελα να εξετάσω μερικές σχετικά απλές εργασίες. Λοιπόν, πόσο απλό: για τους περισσότερους μαθητές που σπουδάζουν μαθηματικά στο σχολείο και δεν έχουν διαβάσει όσα γράφονται παραπάνω, αυτές οι εργασίες μπορεί να φαίνονται σαν τενεκέ. Παρ 'όλα αυτά, είναι ακριβώς τέτοια προβλήματα που συναντώνται στην OGE και στη ΧΡΗΣΗ στα μαθηματικά, γι' αυτό σας συνιστώ να εξοικειωθείτε με αυτά.

Πρόβλημα αριθμός 11. Η ταξιαρχία παρήγαγε 62 μέρη τον Ιανουάριο και κάθε επόμενο μήνα παρήγαγε 14 περισσότερα μέρη από ό, τι τον προηγούμενο. Πόσα κομμάτια έκανε η ομάδα τον Νοέμβριο;

Λύση. Προφανώς, ο αριθμός των τμημάτων, προγραμματισμένο ανά μήνα, θα αντιπροσωπεύει μια αυξανόμενη αριθμητική πρόοδο. Εξάλλου:

\ [\ ξεκινά (στοίχιση) & ((a) _ (1)) = 62; \ quad d = 14; \\ & ((a) _ (n)) = 62+ \ αριστερά (n-1 \ δεξιά) \ cdot 14. \\ \ τέλος (στοίχιση) \]

Ο Νοέμβριος είναι ο 11ος μήνας του έτους, οπότε πρέπει να βρούμε $ ((a) _ (11)) $:

\ [((α) _ (11)) = 62 + 10 \ cdot 14 = 202 \]

Κατά συνέπεια, 202 ανταλλακτικά θα κατασκευαστούν τον Νοέμβριο.

Πρόβλημα αριθμός 12. Το εργαστήριο βιβλιοδεσίας δέσμευσε 216 βιβλία τον Ιανουάριο και κάθε επόμενο μήνα δέσμευε 4 περισσότερα βιβλία από το προηγούμενο. Πόσα βιβλία δέσμευσε το εργαστήριο τον Δεκέμβριο;

Λύση. Ολα τα ίδια:

$ \ begin (στοίχιση) & ((a) _ (1)) = 216; \ quad d = 4; \\ & ((a) _ (n)) = 216+ \ αριστερά (n-1 \ δεξιά) \ cdot 4. \\ \ τέλος (στοίχιση) $

Ο Δεκέμβριος είναι ο τελευταίος, 12ος μήνας του έτους, οπότε αναζητούμε $ ((a) _ (12)) $:

\ [((α) _ (12)) = 216 + 11 \ cdot 4 = 260 \]

Αυτή είναι η απάντηση - 260 βιβλία θα κυκλοφορήσουν τον Δεκέμβριο.

Λοιπόν, αν έχετε διαβάσει μέχρι τώρα, σπεύδω να σας συγχαρώ: περάσατε με επιτυχία την "πορεία των νέων μαχητών" σε αριθμητικές προόδους. Μπορείτε να προχωρήσετε με ασφάλεια στο επόμενο μάθημα, όπου θα μελετήσουμε τον τύπο για το άθροισμα μιας προόδου, καθώς και σημαντικές και πολύ χρήσιμες συνέπειες από αυτό.

Πρώτο επίπεδο

Αριθμητική πρόοδος. Αναλυτική θεωρία με παραδείγματα (2019)

Ακολουθία αριθμών

Ας καθίσουμε λοιπόν να αρχίσουμε να γράφουμε μερικούς αριθμούς. Για παράδειγμα:
Μπορείτε να γράψετε οποιονδήποτε αριθμό και μπορεί να υπάρχουν όσοι θέλετε (στην περίπτωσή μας, αυτοί). Ανεξάρτητα από το πόσους αριθμούς γράφουμε, μπορούμε πάντα να πούμε ποιος είναι ο πρώτος, ποιος ο δεύτερος και ούτω καθεξής μέχρι τον τελευταίο, δηλαδή μπορούμε να τους αριθμήσουμε. Αυτό είναι ένα παράδειγμα ακολουθίας αριθμών:

Ακολουθία αριθμών
Για παράδειγμα, για την ακολουθία μας:

Ο αριθμός που έχει εκχωρηθεί είναι συγκεκριμένος μόνο για έναν αριθμό στην ακολουθία. Με άλλα λόγια, δεν υπάρχουν αριθμοί τριών δευτερολέπτων στην ακολουθία. Ο δεύτερος αριθμός (όπως ο -ος αριθμός) είναι πάντα ένας.
Ο αριθμός με τον αριθμό καλείται το ου μέλος της ακολουθίας.

Συνήθως ονομάζουμε ολόκληρη την ακολουθία με κάποιο γράμμα (για παράδειγμα,) και κάθε μέλος αυτής της ακολουθίας είναι το ίδιο γράμμα με ευρετήριο ίσο με τον αριθμό αυτού του μέλους :.

Στην περίπτωσή μας:

Ας πούμε ότι έχουμε μια αριθμητική ακολουθία στην οποία η διαφορά μεταξύ παρακείμενων αριθμών είναι η ίδια και η ίδια.
Για παράδειγμα:

και τα λοιπά.
Αυτή η ακολουθία αριθμών ονομάζεται αριθμητική πρόοδος.
Ο όρος «πρόοδος» εισήχθη από τον Ρωμαίο συγγραφέα Boethius τον 6ο αιώνα και έγινε κατανοητός με μια ευρύτερη έννοια ως ατελείωτη ακολουθία αριθμών. Το όνομα "αριθμητική" μεταφέρθηκε από τη θεωρία των συνεχών αναλογιών, την οποία κατέλαβαν οι αρχαίοι Έλληνες.

Αυτή είναι μια αριθμητική ακολουθία, κάθε μέλος της οποίας είναι ίσο με το προηγούμενο, που προστίθεται στον ίδιο αριθμό. Αυτός ο αριθμός ονομάζεται διαφορά της αριθμητικής προόδου και συμβολίζεται με.

Προσπαθήστε να προσδιορίσετε ποιες ακολουθίες αριθμών είναι αριθμητική πρόοδο και ποιες όχι:

ένα)
σι)
ντο)
ρε)

Κατάλαβες; Ας συγκρίνουμε τις απαντήσεις μας:
Είναι ένααριθμητική πρόοδο - β, γ.
Δεν είναιαριθμητική πρόοδος - α, δ.

Ας επιστρέψουμε στη δεδομένη εξέλιξη () και προσπαθήσουμε να βρούμε την τιμή του μέλους του. Υπάρχει δύοο τρόπος να το βρεις.

1. Μέθοδος

Μπορούμε να προσθέσουμε στην προηγούμενη τιμή τον αριθμό της προόδου μέχρι να φτάσουμε στον πέμπτο όρο της προόδου. Είναι καλό που δεν έχουμε πολλά να συνοψίσουμε - μόνο τρεις τιμές:

Έτσι, το ου μέλος της περιγραφόμενης αριθμητικής προόδου είναι ίσο με.

2. Μέθοδος

Τι θα γινόταν αν χρειαζόταν να βρούμε την τιμή του ου όρου της προόδου; Η άθροιση θα μας πάρει περισσότερο από μία ώρα και δεν είναι γεγονός ότι δεν θα κάνουμε λάθος όταν προσθέτουμε αριθμούς.
Φυσικά, οι μαθηματικοί έχουν βρει έναν τρόπο με τον οποίο δεν χρειάζεται να προσθέσετε τη διαφορά της αριθμητικής προόδου στην προηγούμενη τιμή. Ρίξτε μια πιο προσεκτική ματιά στην τραβηγμένη εικόνα ... Σίγουρα έχετε ήδη παρατηρήσει ένα συγκεκριμένο μοτίβο, δηλαδή:

Για παράδειγμα, ας δούμε πώς προστίθεται η τιμή του μέλους αυτής της αριθμητικής προόδου:


Με άλλα λόγια:

Προσπαθήστε να βρείτε μόνοι σας με αυτόν τον τρόπο την αξία ενός μέλους μιας δεδομένης αριθμητικής προόδου.

Υπολογίστηκε; Συγκρίνετε τις σημειώσεις σας με την απάντηση:

Λάβετε υπόψη ότι έχετε τον ίδιο ακριβώς αριθμό με την προηγούμενη μέθοδο, όταν προσθέσαμε διαδοχικά τα μέλη της αριθμητικής προόδου στην προηγούμενη τιμή.
Ας προσπαθήσουμε να "αποπροσωποποιήσουμε" αυτόν τον τύπο - θα τον φέρουμε σε γενική μορφή και θα πάρουμε:

Αριθμητική εξίσωση προόδου.

Οι αριθμητικές εξελίξεις αυξάνονται και μερικές φορές μειώνονται.

Ανεβαίνοντας- προόδους στις οποίες κάθε επόμενη τιμή των μελών είναι μεγαλύτερη από την προηγούμενη.
Για παράδειγμα:

Μειώνεται- προόδους στις οποίες κάθε επόμενη τιμή των μελών είναι μικρότερη από την προηγούμενη.
Για παράδειγμα:

Ο παραγόμενος τύπος χρησιμοποιείται για τον υπολογισμό των όρων τόσο σε αυξανόμενους όσο και σε μειωτικούς όρους μιας αριθμητικής προόδου.
Ας το ελέγξουμε στην πράξη.
Μας δίνεται μια αριθμητική πρόοδος που αποτελείται από τους ακόλουθους αριθμούς: Ας ελέγξουμε ποιος θα είναι ο αριθμός th αυτής της αριθμητικής εξέλιξης εάν χρησιμοποιήσουμε τον τύπο μας για να τον υπολογίσουμε:

Από τότε:

Έτσι, βεβαιωθήκαμε ότι ο τύπος λειτουργεί τόσο στη μείωση όσο και στην αύξηση της αριθμητικής προόδου.
Προσπαθήστε να βρείτε μόνοι σας τον ου και τον όρο αυτής της αριθμητικής εξέλιξης.

Ας συγκρίνουμε τα αποτελέσματα που προκύπτουν:

Αριθμητική ιδιότητα προόδου

Ας περιπλέξουμε το έργο - θα αντλήσουμε την ιδιότητα της αριθμητικής προόδου.
Ας υποθέσουμε ότι μας δίνεται η ακόλουθη προϋπόθεση:
- αριθμητική πρόοδο, βρείτε την τιμή.
Εύκολα, λέτε και αρχίζετε να μετράτε σύμφωνα με τον τύπο που ήδη γνωρίζετε:

Αφήστε, α, τότε:

Απόλυτο δίκιο. Αποδεικνύεται ότι πρώτα το βρίσκουμε, μετά το προσθέτουμε στον πρώτο αριθμό και παίρνουμε αυτό που ψάχνουμε. Εάν η πρόοδος αντιπροσωπεύεται από μικρές τιμές, τότε δεν υπάρχει τίποτα περίπλοκο σε αυτήν, αλλά αν μας δοθούν αριθμοί στην κατάσταση; Παραδεχτείτε το, υπάρχει πιθανότητα να κάνετε λάθος στους υπολογισμούς.
Τώρα σκεφτείτε, είναι δυνατόν να επιλυθεί αυτό το πρόβλημα με μία ενέργεια χρησιμοποιώντας οποιονδήποτε τύπο; Φυσικά, ναι, και αυτή θα προσπαθήσουμε να αποσυρθούμε τώρα.

Ας υποδείξουμε τον απαιτούμενο όρο της αριθμητικής προόδου, καθώς γνωρίζουμε τον τύπο για τον εντοπισμό του - αυτός είναι ο ίδιος τύπος που βγάλαμε στην αρχή:
, τότε:

• το προηγούμενο μέλος της εξέλιξης είναι:
• το επόμενο μέλος της εξέλιξης είναι:

Ας συνοψίσουμε τα προηγούμενα και τα επόμενα μέλη της εξέλιξης:

Αποδεικνύεται ότι το άθροισμα των προηγούμενων και επόμενων μελών της προόδου είναι η διπλή τιμή του μέλους της προόδου που βρίσκεται μεταξύ τους. Με άλλα λόγια, για να βρούμε την τιμή ενός μέλους της προόδου με γνωστές προηγούμενες και διαδοχικές τιμές, είναι απαραίτητο να τις προσθέσουμε και να τις διαιρέσουμε.

Σωστά, έχουμε τον ίδιο αριθμό. Ας διορθώσουμε το υλικό. Υπολογίστε μόνοι σας την τιμή για την εξέλιξη, γιατί δεν είναι καθόλου δύσκολο.

Μπράβο! Γνωρίζετε σχεδόν τα πάντα για την εξέλιξη! Απομένει μόνο ένας τύπος για να μάθουμε, ο οποίος, σύμφωνα με τον μύθο, συμπέρανε εύκολα για τον εαυτό του έναν από τους μεγαλύτερους μαθηματικούς όλων των εποχών, τον "βασιλιά των μαθηματικών" - τον Καρλ Γκάους ...

Όταν ο Karl Gauss ήταν 9 ετών, ένας δάσκαλος που ασχολούνταν με τον έλεγχο της εργασίας των μαθητών σε άλλες τάξεις έθεσε την ακόλουθη εργασία στο μάθημα: "Υπολογίστε το άθροισμα όλων των φυσικών αριθμών από έως και (σύμφωνα με άλλες πηγές έως) συμπεριλαμβανομένου." Φανταστείτε την έκπληξη του δασκάλου όταν ένας από τους μαθητές του (ήταν ο Karl Gauss) έδωσε τη σωστή απάντηση στο πρόβλημα σε ένα λεπτό, ενώ οι περισσότεροι από τους συμμαθητές του daredevil, μετά από μακρούς υπολογισμούς, έλαβαν το λάθος αποτέλεσμα ...

Ο νεαρός Karl Gauss παρατήρησε ένα συγκεκριμένο μοτίβο που μπορείτε εύκολα να παρατηρήσετε.
Ας υποθέσουμε ότι έχουμε μια αριθμητική πρόοδο που αποτελείται από -ό μέλη: Πρέπει να βρούμε το άθροισμα των δοθέντων μελών της αριθμητικής προόδου. Φυσικά, μπορούμε να αθροίσουμε χειροκίνητα όλες τις τιμές, αλλά τι γίνεται αν στην εργασία είναι απαραίτητο να βρούμε το άθροισμα των μελών του, όπως έψαχνε ο Γκάους;

Ας σχεδιάσουμε μια δεδομένη εξέλιξη. Κοιτάξτε προσεκτικά τους επισημασμένους αριθμούς και προσπαθήστε να εκτελέσετε διάφορες μαθηματικές πράξεις με αυτούς.


Το έχεις δοκιμάσει? Τι έχετε παρατηρήσει; Σωστά! Τα ποσά τους είναι ίσα

Τώρα πείτε μου, πόσα τέτοια ζεύγη υπάρχουν στη δεδομένη εξέλιξη; Φυσικά, ακριβώς το ήμισυ όλων των αριθμών, δηλαδή.
Με βάση το γεγονός ότι το άθροισμα δύο μελών μιας αριθμητικής προόδου είναι ίσο και παρόμοια ίσα ζεύγη, παίρνουμε ότι το συνολικό άθροισμα είναι:
.
Έτσι, ο τύπος για το άθροισμα των πρώτων όρων οποιασδήποτε αριθμητικής προόδου θα είναι ο εξής:

Σε ορισμένα προβλήματα, δεν γνωρίζουμε τον όρο ου, αλλά γνωρίζουμε τη διαφορά στην εξέλιξη. Προσπαθήστε να αντικαταστήσετε στον τύπο το άθροισμα, τον τύπο του ου όρου.
Τι έκανες;

Μπράβο! Τώρα ας επιστρέψουμε στο πρόβλημα που τέθηκε στον Karl Gauss: υπολογίστε μόνοι σας ποιο είναι το άθροισμα των αριθμών που ξεκινούν από το -th και το άθροισμα των αριθμών που ξεκινούν από το -th.

Πόσα πήρες;
Ο Gauss διαπίστωσε ότι το άθροισμα των μελών είναι ίσο και το άθροισμα των μελών. Έτσι αποφασίσατε;

Στην πραγματικότητα, ο τύπος για το άθροισμα των μελών μιας αριθμητικής προόδου αποδείχθηκε από τον αρχαίο Έλληνα επιστήμονα Διόφαντο τον 3ο αιώνα, και καθ 'όλη τη διάρκεια αυτής της περιόδου, οι πνευματώδεις άνθρωποι χρησιμοποιούσαν στο μέγιστο βαθμό τις ιδιότητες μιας αριθμητικής προόδου.
Για παράδειγμα, φανταστείτε την Αρχαία Αίγυπτο και το πιο φιλόδοξο εργοτάξιο εκείνης της εποχής - την κατασκευή της πυραμίδας ... Η εικόνα δείχνει τη μία πλευρά της.

Πού είναι η εξέλιξη εδώ λέτε; Κοιτάξτε προσεκτικά και βρείτε ένα μοτίβο στον αριθμό των μπλοκ άμμου σε κάθε σειρά του πυραμιδικού τοίχου.


Δεν είναι αριθμητική εξέλιξη; Υπολογίστε πόσα μπλοκ χρειάζονται για την κατασκευή ενός τοίχου εάν τοποθετηθούν τούβλα μπλοκ στη βάση. Ελπίζω να μην μετράτε περνώντας το δάχτυλό σας στην οθόνη, θυμάστε τον τελευταίο τύπο και όλα όσα είπαμε για την αριθμητική πρόοδο;

Σε αυτήν την περίπτωση, η εξέλιξη μοιάζει με αυτήν :.
Διαφορά αριθμητικής προόδου.
Ο αριθμός των μελών της αριθμητικής προόδου.
Ας αντικαταστήσουμε τα δεδομένα μας στους τελευταίους τύπους (ας μετρήσουμε τον αριθμό των μπλοκ με 2 τρόπους).

Μέθοδος 1.

Μέθοδος 2.

Και τώρα μπορείτε να υπολογίσετε στην οθόνη: συγκρίνετε τις ληφθείσες τιμές με τον αριθμό των μπλοκ που βρίσκονται στην πυραμίδα μας. Συνενώθηκε; Μπράβο, έχετε κατακτήσει το άθροισμα των όρων της αριθμητικής προόδου.
Φυσικά, δεν μπορείτε να χτίσετε μια πυραμίδα από μπλοκ στη βάση, αλλά από; Προσπαθήστε να υπολογίσετε πόσα τούβλα άμμου χρειάζονται για να χτίσετε έναν τοίχο με αυτήν την κατάσταση.
Κατάφερες?
Η σωστή απάντηση είναι τα μπλοκ:

Προπόνηση

Καθήκοντα:

1. Η Μάσα μπαίνει σε φόρμα μέχρι το καλοκαίρι. Κάθε μέρα αυξάνει τον αριθμό των καταλήψεων κατά. Πόσες φορές θα κάτσει η Μάσα σε εβδομάδες, αν στην πρώτη προπόνηση έκανε καταλήψεις.
2. Ποιο είναι το άθροισμα όλων των περιττών αριθμών που περιέχονται.
3. Κατά την αποθήκευση των κορμών, οι ξυλοκόποι τα στοιβάζουν με τέτοιο τρόπο ώστε κάθε επάνω στρώμα να περιέχει ένα ημερολόγιο λιγότερο από το προηγούμενο. Πόσα κούτσουρα υπάρχουν σε μια τοιχοποιία, εάν τα κούτσουρα χρησιμεύουν ως βάση της τοιχοποιίας.

Απαντήσεις:

1. Ας ορίσουμε τις παραμέτρους της αριθμητικής προόδου. Σε αυτήν την περίπτωση
   (εβδομάδες = ημέρες).

   Απάντηση:Μετά από δύο εβδομάδες, η Masha πρέπει να κάνει οκλαδόν μία φορά την ημέρα.

2. Πρώτος μονός αριθμός, τελευταίος αριθμός.
   Διαφορά αριθμητικής προόδου.
   Ο αριθμός των περιττών αριθμών είναι στο μισό, ωστόσο, θα ελέγξουμε αυτό το γεγονός χρησιμοποιώντας τον τύπο για να βρούμε τον -ό όρο μιας αριθμητικής προόδου:

   Οι αριθμοί περιέχουν περιττούς αριθμούς.
   Αντικαταστήστε τα διαθέσιμα δεδομένα στον τύπο:

   Απάντηση:Το άθροισμα όλων των περιττών αριθμών που περιέχονται είναι ίσο με.

3. Ας θυμηθούμε το πρόβλημα της πυραμίδας. Για την περίπτωσή μας, a, αφού κάθε επάνω στρώμα μειώνεται κατά ένα ημερολόγιο, τότε μόνο σε μια δέσμη επιπέδων, δηλαδή.
   Ας αντικαταστήσουμε τα δεδομένα στον τύπο:

   Απάντηση:Υπάρχουν κούτσουρα στην τοιχοποιία.

Ας συνοψίσουμε

1. - μια αριθμητική ακολουθία στην οποία η διαφορά μεταξύ παρακείμενων αριθμών είναι ίδια και ίση. Μπορεί να είναι ανοδική και φθίνουσα.
2. Εύρεση τύπου-ο μέλος της αριθμητικής προόδου γράφεται με τον τύπο -, όπου είναι ο αριθμός των αριθμών στην πρόοδο.
3. Ιδιότητα μελών μιας αριθμητικής προόδου- - πού είναι ο αριθμός των αριθμών στην εξέλιξη.
4. Το άθροισμα των μελών μιας αριθμητικής προόδουμπορεί να βρεθεί με δύο τρόπους:
   
   , πού είναι ο αριθμός των τιμών.

ΑΡΙΘΜΕΤΙΚΗ ΠΡΟΟΔΟΣ. ΜΕΣΟ ΕΠΙΠΕΔΟ

Ακολουθία αριθμών

Ας καθίσουμε να αρχίσουμε να γράφουμε μερικούς αριθμούς. Για παράδειγμα:

Μπορείτε να γράψετε οποιονδήποτε αριθμό και μπορεί να υπάρχουν όσοι θέλετε. Αλλά μπορείτε πάντα να πείτε ποια είναι η πρώτη, ποια η δεύτερη και ούτω καθεξής, δηλαδή μπορούμε να τα αριθμήσουμε. Αυτό είναι ένα παράδειγμα ακολουθίας αριθμών.

Ακολουθία αριθμώνείναι ένα σύνολο αριθμών, καθένας από τους οποίους μπορεί να εκχωρήσει έναν μοναδικό αριθμό.

Με άλλα λόγια, κάθε αριθμός μπορεί να συσχετιστεί με έναν συγκεκριμένο φυσικό αριθμό και τον μοναδικό. Και δεν θα εκχωρήσουμε αυτόν τον αριθμό σε κανένα άλλο αριθμό από αυτό το σύνολο.

Ο αριθμός με τον αριθμό καλείται το ου μέλος της ακολουθίας.

Συνήθως ονομάζουμε ολόκληρη την ακολουθία με κάποιο γράμμα (για παράδειγμα,) και κάθε μέλος αυτής της ακολουθίας είναι το ίδιο γράμμα με ευρετήριο ίσο με τον αριθμό αυτού του μέλους :.

Είναι πολύ βολικό αν ο όρος της ακολουθίας μπορεί να καθοριστεί με κάποιον τύπο. Για παράδειγμα, ο τύπος

ορίζει την ακολουθία:

Και ο τύπος είναι η ακόλουθη ακολουθία:

Για παράδειγμα, μια αριθμητική πρόοδος είναι μια ακολουθία (ο πρώτος όρος εδώ είναι ίσος και η διαφορά). Or (, διαφορά).

Τύπος ένατου όρου

Καλούμε τον επαναλαμβανόμενο τύπο στον οποίο για να μάθετε το th μέλος, πρέπει να γνωρίζετε το προηγούμενο ή πολλά προηγούμενα:

Για να βρούμε, για παράδειγμα, τον όρο της εξέλιξης χρησιμοποιώντας έναν τέτοιο τύπο, θα πρέπει να υπολογίσουμε τους προηγούμενους εννέα. Για παράδειγμα, ας. Τότε:

Λοιπόν, ποιος είναι ο τύπος τώρα;

Σε κάθε γραμμή που προσθέτουμε, πολλαπλασιάζεται με κάποιο αριθμό. Για τι? Πολύ απλό: αυτός είναι ο αριθμός του τρέχοντος μέλους μείον:

Πολύ πιο βολικό τώρα, σωστά; Ελέγχουμε:

Αποφασίστε μόνοι σας:

Σε μια αριθμητική πρόοδο, βρείτε τον τύπο για τον ένατο όρο και βρείτε τον εκατό όρο.

Λύση:

Ο πρώτος όρος είναι ίσος. Ποιά είναι η διαφορά? Και ιδού τι:

(είναι επειδή ονομάζεται η διαφορά, η οποία ισούται με τη διαφορά των διαδοχικών μελών της προόδου).

Ο τύπος λοιπόν είναι:

Τότε η εκατοστή θητεία είναι:

Ποιο είναι το άθροισμα όλων των φυσικών αριθμών από έως;

Σύμφωνα με τον μύθο, ο μεγάλος μαθηματικός Καρλ Γκάους, όντας ένα 9χρονο αγόρι, υπολόγισε αυτό το ποσό σε λίγα λεπτά. Παρατήρησε ότι το άθροισμα του πρώτου και του τελευταίου αριθμού είναι ίσο, το άθροισμα του δεύτερου και του τελευταίου αλλά ενός είναι το ίδιο, το άθροισμα του τρίτου και του τρίτου από το τέλος είναι το ίδιο και ούτω καθεξής. Πόσα τέτοια ζευγάρια θα υπάρχουν; Σωστά, ακριβώς το ήμισυ του αριθμού όλων των αριθμών, δηλαδή. Ετσι,

Ο γενικός τύπος για το άθροισμα των πρώτων μελών οποιασδήποτε αριθμητικής προόδου θα είναι:

Παράδειγμα:
Βρείτε το άθροισμα όλων των διψήφιων πολλαπλών.

Λύση:

Ο πρώτος τέτοιος αριθμός είναι. Κάθε επόμενο λαμβάνεται με την προσθήκη στον προηγούμενο αριθμό. Έτσι, οι αριθμοί που μας ενδιαφέρουν σχηματίζουν μια αριθμητική πρόοδο με τον πρώτο όρο και τη διαφορά.

Ο τύπος του όρου όρου για αυτήν την εξέλιξη είναι:

Πόσα μέλη βρίσκονται σε εξέλιξη εάν όλα πρέπει να είναι διψήφια;

Πολύ εύκολο: .

Ο τελευταίος όρος στην εξέλιξη θα είναι ίσος. Στη συνέχεια, το άθροισμα:

Απάντηση:.

Τώρα αποφασίστε μόνοι σας:

1. Κάθε μέρα, ο αθλητής τρέχει περισσότερο m από την προηγούμενη ημέρα. Πόσα χιλιόμετρα θα τρέξει σε εβδομάδες αν έτρεξε χιλιόμετρα την πρώτη μέρα;
2. Ένας ποδηλάτης οδηγεί περισσότερα χιλιόμετρα κάθε μέρα από την προηγούμενη. Την πρώτη μέρα, οδήγησε χιλιόμετρα. Πόσες μέρες χρειάζεται να διανύσει για να διανύσει το χλμ; Πόσα χιλιόμετρα θα διανύσει την τελευταία μέρα του ταξιδιού;
3. Η τιμή ενός ψυγείου σε ένα κατάστημα μειώνεται κατά το ίδιο ποσό κάθε χρόνο. Καθορίστε πόσο μειώθηκε η τιμή ενός ψυγείου κάθε χρόνο εάν, πουλήθηκε προς πώληση για ρούβλια, έξι χρόνια αργότερα πωλήθηκε για ρούβλια.

Απαντήσεις:

1. Το πιο σημαντικό πράγμα εδώ είναι να αναγνωρίσουμε την αριθμητική πρόοδο και να καθορίσουμε τις παραμέτρους της. Στην περίπτωση αυτή, (εβδομάδες = ημέρες). Πρέπει να καθορίσετε το άθροισμα των πρώτων μελών αυτής της προόδου:
   .
   Απάντηση:
2. Δίνεται εδώ :, είναι απαραίτητο να βρεθεί.
   Προφανώς, πρέπει να χρησιμοποιήσετε τον ίδιο τύπο αθροίσματος όπως στο προηγούμενο πρόβλημα:
   .
   Αντικαταστήστε τις τιμές:

   Η ρίζα προφανώς δεν ταιριάζει, οπότε η απάντηση είναι.
   Ας υπολογίσουμε την απόσταση που διανύθηκε για την τελευταία ημέρα χρησιμοποιώντας τον τύπο του όρου:
   (χλμ.)
   Απάντηση:

3. Δεδομένος:. Εύρημα: .
   Δεν θα μπορούσε να είναι πιο εύκολο:
   (τρίψιμο).
   Απάντηση:

ΑΡΙΘΜΕΤΙΚΗ ΠΡΟΟΔΟΣ. ΣΥΝΤΟΜΗ ΓΙΑ ΤΟ ΚΥΡΙΟ

Πρόκειται για μια αριθμητική ακολουθία στην οποία η διαφορά μεταξύ παρακείμενων αριθμών είναι η ίδια και η ίδια.

Η αριθμητική πρόοδος μπορεί να είναι αύξουσα () και φθίνουσα ().

Για παράδειγμα:

Ο τύπος για την εύρεση του n-ου όρου μιας αριθμητικής προόδου

γραμμένο με τον τύπο, όπου είναι ο αριθμός των αριθμών στην εξέλιξη.

Ιδιότητα μελών μιας αριθμητικής προόδου

Σας επιτρέπει να βρείτε εύκολα ένα μέλος της προόδου εάν είναι γνωστά τα γειτονικά μέλη του - πού βρίσκεται ο αριθμός των αριθμών στην εξέλιξη.

Το άθροισμα των μελών μιας αριθμητικής προόδου

Υπάρχουν δύο τρόποι για να βρείτε το ποσό:

Πού είναι ο αριθμός των τιμών.

Πού είναι ο αριθμός των τιμών.

Λοιπόν, το θέμα τελείωσε. Αν διαβάζετε αυτές τις γραμμές, τότε είστε πολύ κουλ.

Γιατί μόνο το 5% των ανθρώπων είναι σε θέση να κατακτήσουν κάτι μόνοι τους. Και αν διαβάζετε μέχρι το τέλος, τότε είστε σε αυτό το 5%!

Τώρα έρχεται το πιο σημαντικό πράγμα.

Καταλάβατε τη θεωρία για αυτό το θέμα. Και, πάλι, αυτό είναι ... είναι απλά σούπερ! Είστε ήδη καλύτεροι από τη συντριπτική πλειοψηφία των συνομηλίκων σας.

Το πρόβλημα είναι ότι αυτό μπορεί να μην είναι αρκετό ...

Για τι?

Για την επιτυχή επιτυχία των εξετάσεων, για την εισαγωγή στο ινστιτούτο με προϋπολογισμό και, ΠΙΟ ΣΗΜΑΝΤΙΚΟ, για μια ζωή.

Δεν θα σας πείσω για τίποτα, θα πω μόνο ένα πράγμα ...

Τα άτομα που έχουν λάβει μια καλή εκπαίδευση κερδίζουν πολύ περισσότερα από εκείνα που δεν έχουν λάβει. Αυτά είναι στατιστικά.

Αλλά ούτε αυτό είναι το κύριο.

Το κυριότερο είναι ότι είναι ΠΕΡΙΣΣΟΤΕΡΑ (υπάρχουν τέτοιες μελέτες). Becauseσως επειδή υπάρχουν τόσες περισσότερες ευκαιρίες γι 'αυτούς και η ζωή γίνεται πιο φωτεινή; Δεν ξέρω...

Σκέψου όμως μόνος σου ...

Τι χρειάζεται για να είσαι σίγουρα καλύτερος από τους άλλους στις εξετάσεις και τελικά να είσαι ... πιο ευτυχισμένος;

ΛΑΜΒΑΝΤΕ ΕΝΑ ΧΕΙΡΟΛΥΓΜΑ ΠΡΟΒΛΗΜΑΤΑ ΣΕ ΑΥΤΟ ΤΟ ΘΕΜΑ.

Στην εξέταση, δεν θα σας ζητηθεί θεωρία.

Θα χρειαστείτε λύσει τα προβλήματα για λίγο.

Και, αν δεν τα λύσατε (ΠΟΛΛΑ!), Σίγουρα θα πάτε κάπου με ηλίθιο λάθος ή απλά δεν θα είναι εγκαίρως.

Είναι όπως στον αθλητισμό - πρέπει να το επαναλαμβάνεις ξανά και ξανά για να κερδίσεις σίγουρα.

Βρείτε μια συλλογή όπου θέλετε, απαραίτητα με λύσεις, λεπτομερή ανάλυσηκαι αποφάσισε, αποφάσισε, αποφάσισε!

Μπορείτε να χρησιμοποιήσετε τις εργασίες μας (προαιρετικά) και εμείς, φυσικά, τις προτείνουμε.

Για να γεμίσετε το χέρι σας με τη βοήθεια των εργασιών μας, πρέπει να βοηθήσετε στην παράταση της ζωής του σχολικού βιβλίου YouClever που διαβάζετε αυτήν τη στιγμή.

Πως? Υπάρχουν δύο επιλογές:

1. Μοιραστείτε όλες τις κρυφές εργασίες σε αυτό το άρθρο - 299 r
2. Ξεκλειδώστε την πρόσβαση σε όλες τις κρυφές εργασίες και στα 99 άρθρα του σεμιναρίου - 999 ρούβλια

Ναι, έχουμε 99 τέτοια άρθρα στο σχολικό μας βιβλίο και η πρόσβαση για όλες τις εργασίες και όλα τα κρυμμένα κείμενα σε αυτά μπορεί να ανοίξει ταυτόχρονα.

Στη δεύτερη περίπτωση θα σας δώσουμεπροσομοιωτής "6000 προβλήματα με λύσεις και απαντήσεις, για κάθε θέμα, για όλα τα επίπεδα πολυπλοκότητας." Σίγουρα θα είναι αρκετό για να επιλύσετε προβλήματα σε οποιοδήποτε θέμα.

Στην πραγματικότητα, αυτό είναι πολύ περισσότερο από έναν προσομοιωτή - ένα ολόκληρο εκπαιδευτικό πρόγραμμα. Εάν χρειάζεται, μπορείτε επίσης να το χρησιμοποιήσετε ΔΩΡΕΑΝ.

Η πρόσβαση σε όλα τα κείμενα και προγράμματα παρέχεται για όλη τη διάρκεια ζωής του ιστότοπου.

Συμπερασματικά...

Αν δεν σας αρέσουν τα καθήκοντά μας, βρείτε άλλα. Απλώς μην ασχολείστε με τη θεωρία.

"Κατανοητό" και "Είμαι σε θέση να λύσω" είναι τελείως διαφορετικές δεξιότητες. Χρειάζεστε και τα δύο.

Βρες προβλήματα και λύσε!