Arifmetik progressiyaning dastlabki 15 sonining yig'indisi. Misollar yordamida arifmetik progressiya
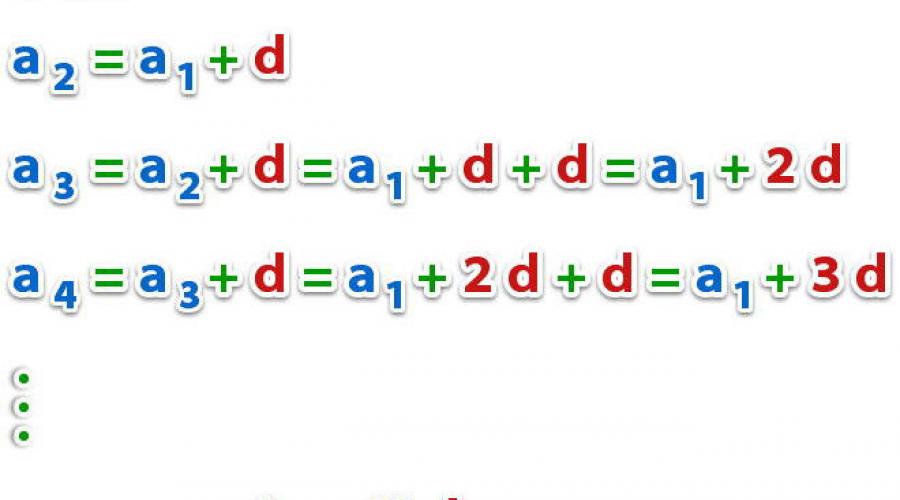
Shuningdek o'qing
Yoki arifmetika bu tartibli sonli ketma -ketlikning bir turi bo'lib, uning xususiyatlari maktab algebra kursida o'rganiladi. Ushbu maqolada arifmetik progressiyaning yig'indisini qanday topish mumkinligi haqidagi savol batafsil muhokama qilinadi.
Bu qanday rivojlanish?
Savolni ko'rib chiqishdan oldin (arifmetik progressiyaning yig'indisini qanday topish mumkin), nima muhokama qilinishini tushunishga arziydi.
Har bir oldingi sondan ba'zi qiymatlarni qo'shish (ayirish) natijasida olingan haqiqiy sonlarning har qanday ketma -ketligi algebraik (arifmetik) progressiya deb ataladi. Matematika tiliga tarjima qilingan bu ta'rif quyidagi shaklni oladi:
Bu erda i - a i qator elementining tartib raqami. Shunday qilib, bitta urug'ni bilib, siz butun seriyani osongina tiklashingiz mumkin. Formuladagi d parametri progressiyaning farqi deyiladi.
Ko'rib chiqilayotgan raqamlar qatori uchun quyidagi tenglik to'g'ri ekanligini osongina ko'rsatish mumkin:
a n = a 1 + d * (n - 1).
Ya'ni, tartibda n-chi elementning qiymatini topish uchun birinchi elementga d farqini 1 n-1 marta qo'shing.

Arifmetik progressiyaning yig'indisi nima: formula
Ko'rsatilgan miqdor uchun formulani berishdan oldin, oddiy alohida holatni ko'rib chiqishga arziydi. Tabiiy sonlarning 1 dan 10 gacha o'zgarishini hisobga olib, ularning yig'indisini topish kerak. Progressiyada a'zolar kam bo'lgani uchun (10), masalani bosh bilan hal qilish mumkin, ya'ni hamma elementlarni tartibda yig'ish mumkin.
S 10 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55.
Bir qiziq narsani o'ylab ko'rishga arziydi: har bir atama keyingi davrdan bir xil qiymat bilan farq qiladi d = 1, keyin birinchisini o'ninchi bilan, ikkinchisini to'qqizinchi bilan va boshqalar shunga o'xshash natija beradi. Haqiqatan ham:
11 = 1+10 = 2+9 = 3+8 = 4+7 = 5+6.
Ko'rib turganingizdek, bu summaning atigi 5 tasi bor, ya'ni seriyadagi elementlar sonidan ikki baravar kam. Keyin (5) summa sonini har bir summaning (11) natijasiga ko'paytirib, siz birinchi misolda olingan natijaga kelasiz.
Agar biz bu fikrni umumlashtirsak, quyidagi ifodani yozishimiz mumkin:
S n = n * (a 1 + a n) / 2.
Bu ifoda shuni ko'rsatadiki, barcha elementlarni ketma -ket yig'ish shart emas, birinchisining qiymatini bilish kifoya a 1 va oxirgisi a n, shuningdek n sonining umumiy sonini bilish kifoya.
Gauss bu tenglik haqida birinchi marta maktab o'qituvchisi qo'ygan muammoning echimini izlaganida o'ylagan: birinchi 100 ta butun sonni jamlang.

M dan n gacha elementlarning yig'indisi: formula
Oldingi paragrafda keltirilgan formulada arifmetik progressiyaning yig'indisini qanday topish mumkinligi haqidagi savolga javob berilgan (birinchi elementlar), lekin ko'pincha masalalarda progressiyaning o'rtasida bir qator sonlarni yig'ish kerak bo'ladi. Buni qanday qilish kerak?
Bu savolga javob berishning eng oson yo'li quyidagi misolni ko'rib chiqishdir: m-th dan n-th gacha bo'lgan atamalar yig'indisini topish kerak. Muammoni hal qilish uchun progressiyaning m dan n gacha berilgan segmenti yangi sonli qator ko'rinishida taqdim etilishi kerak. Bu tasvirda m-chi a muddat birinchi bo'ladi va a n n- (m-1) bo'ladi. Bunday holda, summaning standart formulasini qo'llagan holda, siz quyidagi ifodani olasiz:
S m n = (n - m + 1) * (a m + a n) / 2.
Formulalarni ishlatishga misol
Arifmetik progressiyaning yig'indisini qanday topishni bilgan holda, berilgan formulalarni ishlatishning oddiy misolini ko'rib chiqishga arziydi.
Quyida raqamli ketma -ketlik bor, siz uning a'zolarining yig'indisini topishingiz kerak, 5 -dan boshlab 12 -chi bilan tugaydi:
Berilgan raqamlar d farqi 3 ga teng ekanligini bildiradi. N -element uchun ifoda yordamida siz progressiyaning 5- va 12 -chi shartlarining qiymatlarini topishingiz mumkin. Ma'lum bo'lishicha:
a 5 = a 1 + d * 4 = -4 + 3 * 4 = 8;
a 12 = a 1 + d * 11 = -4 + 3 * 11 = 29.
Ko'rib chiqilgan algebraik progressiyaning oxiridagi sonlarning qiymatlarini bilish, shuningdek qatorda qaysi raqamlar joylashganligini bilish uchun siz oldingi paragrafda olingan summaning formulasidan foydalanishingiz mumkin. Bu shunday bo'ladi:
S 5 12 = (12 - 5 + 1) * (8 + 29) / 2 = 148.
Shuni ta'kidlash joizki, bu qiymatni boshqacha olish mumkin edi: birinchi navbatda, standart formuladan foydalanib, birinchi 12 elementning yig'indisini toping, so'ngra o'sha formuladan foydalanib, birinchi 4 elementning yig'indisini hisoblang, so'ngra birinchi yig'indidan ikkinchisini olib tashlang.
Umumta'lim maktabida (9 -sinf) algebrani o'qiyotganda, muhim mavzulardan biri progressiyalar - geometrik va arifmetikani o'z ichiga olgan sonli ketma -ketlikni o'rganishdir. Ushbu maqolada biz arifmetik progressiya va yechimlari bo'lgan misollarni ko'rib chiqamiz.
Arifmetik progressiya nima?
Buni tushunish uchun ko'rib chiqilayotgan progressiyaning ta'rifini berish, shuningdek, muammolarni hal qilishda qo'llaniladigan asosiy formulalarni berish kerak.
Ma'lumki, ba'zi algebraik progressiyada 1 -chi birlik 6 ga, 7 -chi a'zo 18 ga teng. Farqni topib, bu ketma -ketlikni 7 -chi a'zoga qaytarish kerak.
Noma'lum atamani aniqlash uchun formuladan foydalanamiz: a n = (n - 1) * d + a 1. Biz unga ma'lum bo'lgan ma'lumotlarni, ya'ni a va 7 raqamlarini almashtiramiz, bizda: 18 = 6 + 6 * d. Bu ifodadan farqni osongina hisoblashingiz mumkin: d = (18 - 6) / 6 = 2. Shunday qilib, biz masalaning birinchi qismiga javob berdik.
7 atamaga qadar ketma -ketlikni tiklash uchun siz algebraik progressiyaning ta'rifini ishlatishingiz kerak, ya'ni 2 = a 1 + d, 3 = a 2 + d va boshqalar. Natijada biz butun ketma -ketlikni tiklaymiz: a 1 = 6, 2 = 6 + 2 = 8, 3 = 8 + 2 = 10, 4 = 10 + 2 = 12, a 5 = 12 + 2 = 14 a 6 = 14 + 2 = 16, 7 = 18.
3 -misol: oldinga siljish

Keling, muammoning holatini yanada murakkablashtiraylik. Endi arifmetik progressiyani qanday topish mumkinligi haqidagi savolga javob berish kerak. Siz quyidagi misolni keltira olasiz: ikkita raqam berilgan, masalan - 4 va 5. Bular orasiga yana uchta atama to'g'ri kelishi uchun algebraik progressiya qilish kerak.
Bu muammoni hal qilishni boshlashdan oldin, berilgan sonlar kelajakda qanday o'rinni egallashini tushunish kerak. Ular o'rtasida yana uchta atama bo'lishi uchun 1 = -4 va 5 = 5 bo'ladi. Buni aniqlab, biz avvalgisiga o'xshash masalaga o'tamiz. Shunga qaramay, n -chi davr uchun biz formuladan foydalanamiz, biz olamiz: a 5 = a 1 + 4 * d. Qayerdan: d = (a 5 - a 1) / 4 = (5 - (-4)) / 4 = 2.25. Bu erda biz farqning butun sonini olmadik, lekin bu ratsional son, shuning uchun algebraik progressiyaning formulalari o'zgarishsiz qoladi.
Endi topilgan farqni 1 ga qo'shing va progressiyaning yo'qolgan a'zolarini tiklang. Biz olamiz: a 1 = - 4, a 2 = - 4 + 2,25 = - 1,75, 3 = -1,75 + 2,25 = 0,5, 4 = 0,5 + 2,25 = 2,75, 5 = 2,75 + 2,25 = 5 muammoning sharti bilan.
4 -misol: progressiyaning birinchi davri

Keling, yechim bilan arifmetik progressiyaga misollar berishni davom ettiraylik. Oldingi barcha muammolarda algebraik progressiyaning birinchi soni ma'lum bo'lgan. Endi boshqa turdagi masalani ko'rib chiqaylik: ikkita raqam berilsin, bu erda 15 = 50 va 43 = 37. Bu ketma -ketlik boshlanadigan raqamni topish kerak.
Hozirgacha ishlatilgan formulalar 1 va d dagi bilimlarni nazarda tutadi. Muammo bayonotida bu raqamlar haqida hech narsa ma'lum emas. Shunga qaramay, biz har bir a'zo uchun ma'lumot mavjud bo'lgan iboralarni yozamiz: a 15 = a 1 + 14 * d va 43 = a 1 + 42 * d. 2 ta noma'lum miqdor (a 1 va d) bo'lgan ikkita tenglama olindi. Bu shuni anglatadiki, muammo chiziqli tenglamalar tizimini echishga kamayadi.
Bu tizimni hal qilishning eng oson yo'li - har bir tenglamada 1 ni ifodalash, so'ngra olingan ifodalarni solishtirish. Birinchi tenglama: a 1 = a 15 - 14 * d = 50 - 14 * d; ikkinchi tenglama: a 1 = a 43 - 42 * d = 37 - 42 * d. Bu ifodalarni tenglashtirib, biz olamiz: 50 - 14 * d = 37 - 42 * d, bu erda farq d = (37 - 50) / (42 - 14) = - 0,464 (faqat 3 ta kasrli joy berilgan).
D ni bilsangiz, yuqoridagi 2 ta ifodadan birini 1 uchun ishlatishingiz mumkin. Masalan, birinchisi: a 1 = 50 - 14 * d = 50 - 14 * ( - 0,464) = 56,496.
Agar siz natijaga shubha qilsangiz, uni tekshirishingiz mumkin, masalan, shartda ko'rsatilgan progressiyaning 43 muddatini aniqlang. Biz olamiz: a 43 = a 1 + 42 * d = 56.496 + 42 * (- 0.464) = 37.008. Kichkina xato, hisob -kitoblarning mingdan bir qismigacha yaxlitlash ishlatilganligi bilan bog'liq.
5 -misol: miqdor
Keling, arifmetik progressiyaning yig'indisiga yechimlari bo'lgan ba'zi misollarni ko'rib chiqaylik.
Quyidagi shakldagi sonli progressiya berilsin: 1, 2, 3, 4, ...,. Bu 100 ta raqamning yig'indisini qanday hisoblaysiz?
Kompyuter texnologiyalarining rivojlanishi tufayli, bu muammoni hal qilish mumkin, ya'ni ketma -ket barcha raqamlarni qo'shish mumkin, bu kompyuter Enter tugmachasini bosishi bilan kompyuter bajaradi. Ammo, masalani ongda hal qilish mumkin, agar biz berilgan raqamlar qatori algebraik progressiya ekanligiga va uning farqi 1 ga tengligiga e'tibor bersak, yig'indining formulasini qo'llaymiz: S n = n * (a 1) + an) / 2 = 100 * (1 + 100) / 2 = 5050.
Qizig'i shundaki, bu muammo "Gauss" deb nomlangan, chunki 18 -asrning boshlarida mashhur nemis hali 10 yoshda bo'lsa ham, uni bir necha soniya ichida boshida hal qila olgan. Bola algebraik progressiyaning yig'indisining formulasini bilmas edi, lekin agar siz ketma -ketlikdagi sonlarni juft -juft qilib qo'shsangiz, har doim bitta natijaga erishasiz, ya'ni 1 + 100 = 2 + 99 = 3 + 98 = ..., va bu miqdorlarning aynan 50 (100/2) bo'lishi uchun to'g'ri javobni olish uchun 50 ni 101 ga ko'paytirish kifoya.

6 -misol: n dan m gacha a'zolar yig'indisi
Arifmetik progressiya yig'indisining yana bir tipik misoli quyidagicha: bir qator sonlar berilgan: 3, 7, 11, 15, ..., siz uning 8 dan 14 gacha a'zolarining yig'indisi nimaga teng bo'lishini topishingiz kerak.
Muammo ikki yo'l bilan hal qilinadi. Ulardan birinchisi 8 dan 14 gacha noma'lum atamalarni topishni, so'ngra ularning ketma -ket yig'ilishini o'z ichiga oladi. Terminalar kam bo'lgani uchun, bu usul etarli darajada mehnat talab qilmaydi. Shunga qaramay, bu muammoni yanada universal bo'lgan ikkinchi usul bilan hal qilish taklif etiladi.
Fikr m va n atamalari orasidagi algebraik progressiyaning yig'indisi uchun formulani olishdir, bu erda n> m butun sonlardir. Keling, har ikkala holat uchun ham ikkita ifodani yozamiz:
- S m = m * (a m + a 1) / 2.
- S n = n * (a n + a 1) / 2.
N> m bo'lgani uchun, aniqki, 2 sum birinchi summani o'z ichiga oladi. Oxirgi xulosa shuni anglatadiki, agar biz bu summalar orasidagi farqni olsak va unga a m atamasini qo'shsak (farqni olgan holda, u S n yig'indisidan chiqariladi), keyin biz masalaning kerakli javobini olamiz. Bizda: S mn = S n - S m + am = n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am = a 1 * (n - m) / 2 + an * n / 2 + am * (1- m / 2). Bu ifodada n va m uchun formulalarni almashtirish kerak. Keyin biz: S mn = a 1 * (n - m) / 2 + n * (a 1 + (n - 1) * d) / 2 + (a 1 + (m - 1) * d) * (1 - m / 2) = a 1 * (n - m + 1) + d * n * (n - 1) / 2 + d * (3 * m - m 2 - 2) / 2.
Olingan formula biroz og'ir; shunga qaramay, S mn yig'indisi faqat n, m, a 1 va d ga bog'liq. Bizning holda, a 1 = 3, d = 4, n = 14, m = 8. Bu sonlarni almashtirib, biz: S mn = 301.

Berilgan echimlardan ko'rinib turibdiki, barcha masalalar n -chi davr ifodasi va birinchi atamalar to'plamining yig'indisi formulasini bilishga asoslangan. Ushbu muammolarning birortasini hal qilishni davom ettirishdan oldin, shartni diqqat bilan o'qib chiqish, nima topish kerakligini aniq tushunish va shundan keyingina echimga o'tish tavsiya etiladi.
Yana bir maslahat - soddalikka intilish, ya'ni murakkab matematik hisob -kitoblarsiz savolga javob bera olsangiz, aynan shunday qilish kerak, chunki bu holda xato qilish ehtimoli kamroq. Masalan, 6 -sonli arifmetik progressiya misolida, S mn = n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am formulasida to'xtab, sindirish mumkin. umumiy muammoni alohida vazifalarga ajratish (bu holda, avval a va am a'zolarini toping).
Olingan natijaga shubha tug'ilsa, ba'zi misollarda bo'lgani kabi, uni tekshirish tavsiya etiladi. Biz arifmetik progressiyani qanday topish kerakligini aniqladik. Agar tushunsangiz, bu unchalik qiyin emas.
Biz qaror qabul qilishni boshlashdan oldin arifmetik progressiya muammolari, sonlar ketma -ketligi nima ekanligini ko'rib chiqing, chunki arifmetik progressiya - bu sonlar ketma -ketligining alohida holati.
Raqamli ketma -ketlik - bu har bir elementning o'z tartib raqami bo'lgan raqamlar to'plami... Bu to`plam elementlari ketma -ketlik a'zolari deyiladi. Tartib elementining tartib raqami indeks bilan ko'rsatilgan:
Ketma -ketlikning birinchi elementi;
Ketma -ketlikning beshinchi elementi;
- ketma -ketlikning "n -chi" elementi, ya'ni. "navbatda" bandi n.
Tartib elementining qiymati va uning tartib raqami o'rtasida bog'liqlik mavjud. Shunday qilib, biz ketma -ketlikni element elementining tartib raqami bo'lgan funktsiya deb hisoblashimiz mumkin. Boshqacha aytganda, buni aytishimiz mumkin ketma -ketlik tabiiy argument funktsiyasidir:
Tartibni uchta usulda o'rnatish mumkin:
1 . Jadval yordamida ketma -ketlikni sozlash mumkin. Bunday holda, biz ketma -ketlikning har bir a'zosining qiymatini belgilaymiz.
Misol uchun, kimdir shaxsiy vaqtni boshqarishni o'z zimmasiga olishga qaror qildi va avvaliga hafta davomida VKontakte -da qancha vaqt o'tkazishini hisoblab chiqdi. Vaqtni jadvalga yozib, u etti elementdan iborat ketma -ketlikni oladi:

Jadvalning birinchi qatorida haftaning kun raqami, ikkinchisida - daqiqalar vaqti ko'rsatilgan. Ko'ryapmizki, ya'ni dushanba kuni kimdir "VKontakte" da 125 daqiqa, ya'ni payshanba kuni - 248 daqiqa, yoki juma kuni atigi 15 daqiqa sarflagan.
2 . N ketma -ketlik formulasi yordamida ketma -ketlikni ko'rsatish mumkin.
Bunda ketma -ket element qiymatining uning soniga bog'liqligi to'g'ridan -to'g'ri formulada ifodalanadi.
Masalan, agar, keyin
![]()
![]()
Berilgan sonli ketma -ketlik elementining qiymatini topish uchun biz element sonini n -chi sonli formulaga almashtiramiz.
Agar biz argumentning qiymati ma'lum bo'lsa, funktsiyaning qiymatini topishimiz kerak bo'lsa, biz ham shunday qilamiz. Biz argument qiymatini funktsiya tenglamasiga almashtiramiz:
Agar, masalan, ![]() , keyin
, keyin
Yana bir bor ta'kidlayman, ketma -ketlikda, ixtiyoriy sonli funktsiyadan farqli o'laroq, faqat natural son argument bo'lishi mumkin.
3 ... Ketma -ketlik a'zosi qiymatining oldingi a'zolar qiymatiga bog'liqligini ifodalovchi formula yordamida ketma -ketlikni ko'rsatish mumkin. Bunday holda, uning qiymatini topish uchun bizga faqat ketma -ket a'zo sonini bilish etarli emas. Biz ketma -ketlikning birinchi a'zosini yoki birinchi bir nechta a'zolarini ko'rsatishimiz kerak.
Masalan, ketma -ketlikni ko'rib chiqing ![]() ,
, ![]()
Biz ketma -ketlik a'zolarining qiymatlarini topa olamiz ketma -ketlikda uchinchisidan boshlab:
Ya'ni, har safar ketma-ketlikning n-chi a'zosining qiymatini topish uchun biz avvalgi ikkisiga qaytamiz. Bu tartiblash tartibi deyiladi takroriy, Lotin so'zidan takroriy- qaytib kelmoq.
Endi biz arifmetik progressiyani aniqlay olamiz. Arifmetik progressiya - bu raqamlar ketma -ketligining oddiy maxsus holati.
Arifmetik progressiya sonli ketma -ketlikdir, uning har bir a'zosi ikkinchisidan boshlab, avvalgisiga teng bo'lib, bir xil songa qo'shiladi.

Raqam chaqiriladi arifmetik progressiyaning farqi... Arifmetik progressiyaning farqi ijobiy, manfiy yoki nol bo'lishi mumkin.
Agar sarlavha = "(! LANG: d> 0">, то каждый член арифметической прогрессии больше предыдущего, и прогрессия является !} ortib bormoqda.
Masalan, 2; 5; sakkiz; o'n bir; ...
Agar, u holda arifmetik progressiyaning har bir a'zosi oldingisidan kam bo'lsa, progressiya esa kamayib borayotgan.
Masalan, 2; -1; -4; -7; ...
Agar shunday bo'lsa, progressiyaning barcha a'zolari bir xil songa teng, va progressiya harakatsiz.
Masalan, 2; 2; 2; 2; ...
Arifmetik progressiyaning asosiy xususiyati:
Keling, rasmga qaraylik.
Biz buni ko'ramiz
![]() , va shu bilan birga
, va shu bilan birga
![]()
Ushbu ikkita tenglikni qo'shib, biz olamiz:
![]() .
.
Tenglikning ikkala tomonini ikkiga bo'ling:

Shunday qilib, arifmetik progressiyaning har bir a'zosi, ikkinchisidan boshlab, ikkita qo'shnining arifmetik o'rtacha qiymatiga teng:

Bundan tashqari, beri
![]() , va shu bilan birga
, va shu bilan birga
![]() , keyin
, keyin
![]() va shuning uchun
va shuning uchun
 Title = "(! LANG: k> l) bilan boshlanadigan arifmetik progressiyaning har bir a'zosi">, равен среднему арифметическому двух равноотстоящих.
!}
Title = "(! LANG: k> l) bilan boshlanadigan arifmetik progressiyaning har bir a'zosi">, равен среднему арифметическому двух равноотстоящих.
!}
Uchinchi a'zoning formulasi.
Ko'ramizki, arifmetik progressiyaning a'zolari uchun quyidagi munosabatlar mavjud:
![]()
![]()
va nihoyat,
Bizda bor n -chi davrning formulasi.
![]()
MUHIM! Arifmetik progressiyaning har qanday a'zosi va bilan ifodalanishi mumkin. Birinchi atama va arifmetik progressiyaning farqini bilib, siz uning istalgan shartlarini topishingiz mumkin.
Arifmetik progressiyaning n a'zosi yig'indisi.
O'zboshimchalik bilan arifmetik progressiyada, ekstremaldan teng masofada joylashgan a'zolar yig'indisi bir -biriga teng:
N atamali arifmetik progressiyani ko'rib chiqing. Bu progressiyaning n a'zosi yig'indisi bo'lsin.
Keling, progressiya a'zolarini birinchi navbatda sonlarning o'sish tartibida, so'ngra kamayish tartibida tartibga solaylik:

Keling, juftlik bilan qo'shamiz:
Har bir qavs ichidagi summa teng, juftlar soni n.
Biz olamiz:
![]()

Shunday qilib, arifmetik progressiyaning n a'zosi yig'indisini quyidagi formulalar orqali topish mumkin:
O'ylab ko'ring arifmetik progressiya masalalarini hal qilish.
1 . N ketma -ketlik formulasi bilan berilgan ketma -ketlik: . Bu ketma -ketlik arifmetik progressiya ekanligini isbotlang.
Keling, ketma -ketlikning ikkita qo'shni a'zosi orasidagi farq bir xil songa teng ekanligini isbotlaylik.
Biz ketma -ketlikning ikkita qo'shni a'zosi o'rtasidagi farq ularning soniga bog'liq emasligini va doimiy ekanligini aniqladik. Shuning uchun, ta'rifga ko'ra, bu ketma -ketlik arifmetik progressiya hisoblanadi.
2 . Sizga arifmetik progressiya beriladi -31; -27; ...
a) Progressiyaning 31 a'zosini toping.
b) 41 -son bu progressiyaga kiradimi -yo'qligini aniqlang.
a) Biz buni ko'ramiz;
Keling, rivojlanishimizning n -chi davrining formulasini yozaylik.
Umuman ![]()
Bizning holatda ![]() , shuning uchun
, shuning uchun ![]()
Biz olamiz:
b) Faraz qilaylik, 41 ketma -ketlik a'zosi. Keling, uning raqamini topaylik. Buning uchun biz tenglamani yechamiz:
![]()
Biz n ning tabiiy qiymatini oldik, shuning uchun ha, 41 raqami progressiyaning a'zosi. Agar topilgan n qiymati natural son bo'lmasa, biz 41 raqami progressiyaning a'zosi emas deb javob beramiz.
3 ... a) 2 va 8 raqamlari orasiga 4 ta raqamni kiriting, shunda ular berilgan sonlar bilan birgalikda arifmetik progressiya qiladi.
b) Olingan progressiya a'zolarining yig'indisini toping.
a) 2 va 8 raqamlari orasiga to'rtta raqamni kiriting:

Biz 6 a'zodan iborat arifmetik progressiyani oldik. ![]()
Keling, bu progressiyaning farqini topaylik. Buning uchun biz n -chi davr uchun formuladan foydalanamiz:
![]()
Endi raqamlarning qiymatlarini topish oson:
3,2; 4,4; 5,6; 6,8
b) 
Javob: a) ha; b) 30
4. Yuk mashinasi og'irligi 240 tonna bo'lgan ezilgan toshlarni tashiydi, bu esa har kuni bir xil tonnaga yuk tashish tezligini oshiradi. Ma'lumki, birinchi kun davomida 2 tonna ezilgan tosh tashilgan. Agar barcha ishlar 15 kunda bajarilgan bo'lsa, o'n ikkinchi kuni qancha tonna moloz tashilganligini aniqlang.
Muammoning shartiga ko'ra, yuk mashinasi tashadigan xarobalar miqdori har kuni o'sha miqdorda ko'payadi. Shuning uchun biz arifmetik progressiya bilan shug'ullanmoqdamiz.
Keling, bu muammoni arifmetik progressiya nuqtai nazaridan shakllantiraylik.
Birinchi kun davomida 2 tonna ezilgan tosh tashildi: a_1 = 2.
Barcha ishlar 15 kun ichida bajarildi :.
Yuk mashinasi og'irligi 240 tonna bo'lgan ezilgan toshni tashiydi:
Biz topishimiz kerak.
Birinchidan, rivojlanishdagi farqni toping. Progressiyaning n atamasi yig'indisi uchun formuladan foydalanaylik.

Bizning holatda:
![]()
![]()
 Ha, ha: arifmetik progressiya siz uchun o'yinchoq emas :)
Ha, ha: arifmetik progressiya siz uchun o'yinchoq emas :) Xo'sh, do'stlar, agar siz bu matnni o'qiyotgan bo'lsangiz, ichki dalillar sizga arifmetik progressiya nima ekanligini hali bilmasligingizni aytadi, lekin siz haqiqatan ham (yo'q, bu kabi: SOOOOO!) Bilishni xohlaysiz. Shuning uchun, men sizni uzoq tanishtirishlar bilan qiynamayman va darhol ishga kirishaman.
Keling, bir nechta misollardan boshlaylik. Bir nechta raqamlar to'plamini ko'rib chiqing:
- 1; 2; 3; 4; ...
- 15; 20; 25; 30; ...
- $ \ sqrt (2); \ 2 \ sqrt (2); \ 3 \ sqrt (2); ... $
Bu to'plamlarning umumiyligi nimada? Bir qarashda, hech narsa. Lekin aslida nimadir bor. Aynan: har bir keyingi element avvalgisidan bir xil raqam bilan farq qiladi.
O'zingiz hukm qiling. Birinchi to'plam - bu ketma -ket raqamlar, ularning har biri oldingi raqamdan ko'p. Ikkinchi holda, qo'shni raqamlar orasidagi farq allaqachon beshga teng, lekin bu farq hali ham o'zgarmaydi. Uchinchi holatda, umuman ildizlar. Biroq, $ 2 \ sqrt (2) = \ sqrt (2) + \ sqrt (2) $ va $ 3 \ sqrt (2) = 2 \ sqrt (2) + \ sqrt (2) $, ya'ni. va bu holda, har bir keyingi element $ \ sqrt (2) $ ga ko'payadi (va bu raqam mantiqsiz deb qo'rqmang).
Shunday qilib: barcha bunday ketma -ketliklar arifmetik progressiyalar deb ataladi. Keling, aniq ta'rif beraylik:
Ta'rif. Har bir keyingi qismi avvalgisidan aynan bir xil miqdorda farq qiladigan sonlar ketma -ketligiga arifmetik progressiya deyiladi. Raqamlar farq qiladigan miqdor progressiyaning farqi deb ataladi va ko'pincha $ d $ harfi bilan belgilanadi.
Belgilanish: $ \ chap (((a) _ (n)) \ o'ng) $ - progressiyaning o'zi, $ d $ - uning farqi.
Va faqat bir nechta muhim izohlar. Birinchidan, faqat tartibli raqamlar ketma -ketligi: ularni yozilish tartibida o'qishga ruxsat beriladi - boshqa hech narsa emas. Siz raqamlarni o'zgartira olmaysiz yoki o'zgartira olmaysiz.
Ikkinchidan, ketma -ketlikning o'zi cheklangan yoki cheksiz bo'lishi mumkin. Masalan, (1; 2; 3) to'plam aniq cheklangan arifmetik progressiya. Ammo agar siz ruhda biror narsa yozsangiz (1; 2; 3; 4; ...) - bu allaqachon cheksiz taraqqiyot. To'rtlikdan keyingi ellips, go'yoki, hali ham juda ko'p sonlar borligini ko'rsatadi. Masalan, cheksiz ko'p. :)
Shuni ham ta'kidlashni istardimki, taraqqiyot o'sib bormoqda va kamaymoqda. Biz o'sib borayotganlarni ko'rdik - xuddi shu to'plam (1; 2; 3; 4; ...). Va bu erda rivojlanishning pasayishiga misollar:
- 49; 41; 33; 25; 17; ...
- 17,5; 12; 6,5; 1; −4,5; −10; ...
- $ \ sqrt (5); \ \ sqrt (5) -1; \ \ sqrt (5) -2; \ \ sqrt (5) -3; ... $
Yaxshi, mayli: bu oxirgi misol juda murakkab ko'rinishi mumkin. Ammo qolganlari, menimcha, sizga tushunarli. Shuning uchun biz yangi ta'riflarni kiritamiz:
Ta'rif. Arifmetik progressiya deyiladi:
- har bir keyingi element avvalgisidan kattaroq bo'lsa, ortadi;
- kamayadi, aksincha, har bir keyingi element avvalgisidan kam bo'lsa.
Bundan tashqari, "statsionar" deb nomlangan ketma -ketliklar mavjud - ular bir xil takrorlanadigan sondan iborat. Masalan, (3; 3; 3; ...).
Faqat bitta savol qolmoqda: ortib borayotgan progressiyani kamayayotganidan qanday ajratish mumkin? Yaxshiyamki, barchasi $ d $ raqamining belgisiga bog'liq, ya'ni. farqning rivojlanishi:
- Agar $ d \ gt 0 $ bo'lsa, u holda rivojlanish kuchayadi;
- Agar $ d \ lt 0 $ bo'lsa, demak, taraqqiyot kamaymoqda;
- Nihoyat, $ d = 0 $ holati mavjud - bu holda butun progress bir xil sonlarning statsionar ketma -ketligiga kamayadi: (1; 1; 1; 1; ...) va boshqalar.
Keling, yuqoridagi uchta kamayayotgan progressiya uchun $ d $ farqini hisoblab ko'rishga harakat qilaylik. Buning uchun ikkita qo'shni elementni (masalan, birinchi va ikkinchi) olish va o'ngdagi raqamdan chapdagi raqamni olib tashlash kifoya. Bu shunday ko'rinadi:
- 41−49=−8;
- 12−17,5=−5,5;
- $ \ sqrt (5) -1- \ sqrt (5) = - 1 $.
Ko'rib turganingizdek, har uch holatda ham farq haqiqatan ham salbiy bo'lib chiqdi. Va endi biz ta'riflarni ozmi -ko'pmi aniqladik, progressiyalar qanday tasvirlanganligini va ularning xususiyatlari nimada ekanligini aniqlash vaqti keldi.
Progressiya a'zolari va takrorlanuvchi formula
Bizning ketma -ketlik elementlarini almashtirish mumkin emasligi uchun ularni raqamlash mumkin:
\ [\ chap (((a) _ (n)) \ o'ng) = \ chap \ (((a) _ (1)), \ ((a) _ (2)), ((a) _ (3) )), ... \ o'ng \) \]
Ushbu to'plamning alohida elementlari progressiyaning a'zolari deb ataladi. Ular raqam bilan ko'rsatilgan: birinchi davr, ikkinchi davr va boshqalar.
Bundan tashqari, biz bilganimizdek, progressiyaning qo'shni a'zolari quyidagi formula bilan bog'liq.
\ [((a) _ (n))-((a) _ (n-1)) = d \ O'ng o'q ((a) _ (n)) = ((a) _ (n-1)) + d \]
Qisqacha aytganda, $ n $ th muddatini topish uchun $ n-1 $ th muddatini va $ d $ farqini bilish kerak. Bunday formulani takroriy deb atashadi, chunki uning yordami bilan har qanday raqamni topish mumkin, faqat avvalgisini bilish (va aslida - avvalgilarining hammasi). Bu juda noqulay, shuning uchun har qanday hisob -kitoblarni birinchi davrgacha va farqni kamaytiradigan murakkabroq formula mavjud:
\ [((a) _ (n)) = ((a) _ (1)) + \ chap (n-1 \ o'ng) d \]
Shubhasiz, siz allaqachon ushbu formulaga erishgansiz. Ular buni har xil ma'lumotnomalarda va reshebniklarda berishni yaxshi ko'radilar. Matematika bo'yicha har qanday oqilona darslikda u birinchilardan bo'lib ketadi.
Shunga qaramay, men biroz mashq qilishni taklif qilaman.
Muammo raqami 1. $ \ Chap (((a) _ (n)) \ o'ng) $ arifmetik progressiyaning birinchi uchta shartini yozing, agar $ ((a) _ (1)) = 8 bo'lsa, d = -5 $.
Yechim. Shunday qilib, biz $ ((a) _ (1)) = 8 $ birinchi davrini va $ d = -5 $ progressining farqini bilamiz. Keling, berilgan formuladan foydalanamiz va $ n = 1 $, $ n = 2 $ va $ n = 3 $ ni almashtiramiz:
\ [\ boshlash (tekislash) va ((a) _ (n)) = ((a) _ (1)) + \ chap (n-1 \ o'ng) d; \\ & ((a) _ (1)) = ((a) _ (1)) + \ chap (1-1 \ o'ng) d = ((a) _ (1)) = 8; \\ & ((a) _ (2)) = ((a) _ (1)) + \ chap (2-1 \ o'ng) d = ((a) _ (1)) + d = 8-5 = 3; \\ & ((a) _ (3)) = ((a) _ (1)) + \ chap (3-1 \ o'ng) d = ((a) _ (1)) + 2d = 8-10 = -2. \\ \ end (tekislash) \]
Javob: (8; 3; -2)
Hammasi shu! E'tibor bering: bizning harakatimiz pasaymoqda.
Albatta, $ n = 1 $ ni almashtirish mumkin emas edi - birinchi atama bizga allaqachon ma'lum. Ammo, birini almashtirib, biz formulamiz birinchi davrada ham ishlashiga ishonch hosil qildik. Boshqa hollarda, hammasi arifmetikaga aylandi.
Muammo raqami 2. Arifmetik progressiyaning dastlabki uchta shartini yozing, agar uning ettinchi a'zosi -40, o'n ettinchi qismi -50 bo'lsa.
Yechim. Keling, muammoning shartini odatiy so'zlar bilan yozaylik:
\ [((a) _ (7)) = - 40; \ quad ((a) _ (17)) = - 50. \]
\ [\ chap \ (\ boshlash (tekislash) va ((a) _ (7)) = ((a) _ (1)) + 6d \\ & ((a) _ (17)) = ((a) _ (1)) + 16d \\ \ end (tekislash) \ o'ng. \]
\ [\ chap \ (\ boshlash (tekislash) va ((a) _ (1)) + 6d = -40 \\ & ((a) _ (1)) + 16d = -50 \\ \ tugatish (tekislash) \ o'ng. \]
Men tizim belgisini qo'ydim, chunki bu talablar bir vaqtning o'zida bajarilishi kerak. Va shuni esda tutingki, agar biz ikkinchi tenglamadan birinchisini olib tashlasak (bizda tizim mavjud bo'lgani uchun buni qilish huquqiga egamiz), biz buni olamiz:
\ [\ boshlash (tekislash) & ((a) _ (1)) + 16d- \ chap (((a) _ (1)) + 6d \ o'ng) =- 50- \ chap (-40 \ o'ng); \\ & ((a) _ (1)) + 16d - ((a) _ (1)) - 6d = -50 + 40; \\ & 10d = -10; \\ & d = -1. \\ \ end (tekislash) \]
Mana, biz rivojlanishning farqini qanchalik oson topdik! Topilgan sonni tizimning har qanday tenglamasiga almashtirish qoladi. Masalan, birinchisida:
\ [\ boshlanish (matritsa) ((a) _ (1)) + 6d = -40; \ quad d = -1 \\ \ Downarrow \\ ((a) _ (1)) -6 = -40; \\ ((a) _ (1)) = - 40 + 6 = -34. \\ \ end (matritsa) \]
Endi, birinchi atama va farqni bilib, ikkinchi va uchinchi shartlarni topish qoladi:
\ [\ boshlash (tekislash) & ((a) _ (2)) = ((a) _ (1)) + d = -34-1 = -35; \\ & ((a) _ (3)) = ((a) _ (1)) + 2d = -34-2 = -36. \\ \ end (tekislash) \]
Tayyor! Muammo hal qilindi.
Javob: (-34; -35; -36)
Biz kashf etgan progressning qiziqarli xususiyatiga e'tibor bering: agar biz $ n $ th va $ m $ th shartlarini olsak va ularni bir-biridan ayirsak, biz $ n-m $ soniga ko'paytirilgan farqni olamiz:
\ [((a) _ (n)) - ((a) _ (m)) = d \ cdot \ chap (n -m \ o'ng) \]
Siz bilishingiz kerak bo'lgan oddiy, lekin juda foydali xususiyat - uning yordami bilan siz ko'p muammolarni bosqichma -bosqich hal qilishni sezilarli darajada tezlashtirasiz. Mana eng yaxshi misol:
Muammo raqami 3. Arifmetik progressiyaning beshinchi muddati - 8,4, uning o'ninchi qismi - 14,4. Bu progressiyaning o'n beshinchi muddatini toping.
Yechim. $ ((A) _ (5)) = 8.4 $, $ ((a) _ (10)) = 14.4 $ bo'lgani uchun siz $ ((a) _ (15)) $ ni topishingiz kerak bo'lsa, biz quyidagilarni e'tiborga olamiz. :
\ [\ boshlash (tekislash) & ((a) _ (15)) - ((a) _ (10)) = 5d; \\ & ((a) _ (10)) - ((a) _ (5)) = 5d. \\ \ end (tekislash) \]
Lekin $ ((a) _ (10)) - ((a) _ (5)) = 14.4-8.4 = 6 $ sharti bilan, shuning uchun $ 5d = $ 6, bizda:
\ [\ boshlash (tekislash) & ((a) _ (15)) - 14.4 = 6; \\ & ((a) _ (15)) = 6 + 14.4 = 20.4. \\ \ end (tekislash) \]
Javob: 20.4
Hammasi shu! Bizga ba'zi tenglamalar tizimini tuzish va birinchi atama va farqni hisoblash shart emas edi - hamma narsa bir necha satrda hal qilingan.
Keling, boshqa turdagi vazifalarni ko'rib chiqaylik - progressiyaning salbiy va ijobiy a'zolarini topish. Hech kimga sir emaski, agar progressiya oshsa, birinchi atama manfiy bo'lsa, unda ertami -kechmi ijobiy atamalar paydo bo'ladi. Va aksincha: kamayib borayotgan progressiya a'zolari ertami kechmi salbiy bo'lib qoladi.
Shu bilan birga, elementlarni ketma-ket o'tib, bu lahzani "bosh bilan" ko'rib chiqish har doim ham mumkin emas. Ko'pincha muammolar shunday tuzilganki, formulalarni bilmasdan, hisob -kitoblar bir necha varaqdan iborat bo'ladi - biz javob topganimizda uxlab qolamiz. Shuning uchun biz bu muammolarni tezroq hal qilishga harakat qilamiz.
Muammo raqami 4. Arifmetik progressiyada nechta manfiy atama bor -38,5; -35.8; ...?
Yechim. Shunday qilib, $ ((a) _ (1)) = - 38,5 $, $ ((a) _ (2)) = - 35,8 $, bu erda biz darhol farqni topamiz:
E'tibor bering, farq ijobiydir, shuning uchun rivojlanish kuchayadi. Birinchi atama manfiy, shuning uchun bir paytlar biz haqiqatan ham ijobiy raqamlarga qoqilamiz. Bitta savol - bu qachon sodir bo'ladi.
Keling, aniqlashga harakat qilaylik: qancha vaqt (ya'ni $ n $ tabiiy soniga qadar) atamalarning salbiyligi saqlanib qoladi:
\ [\ boshlash (tekislash) va ((a) _ (n)) \ lt 0 \ O'ng o'q ((a) _ (1)) + \ chap (n-1 \ o'ng) d \ lt 0; \\ & -38.5+ \ chap (n -1 \ o'ng) \ cdot 2.7 \ lt 0; \ to'rt \ chap | \ cdot 10 \ o'ng. \\ & -385 + 27 \ cdot \ chap (n -1 \ o'ng) \ lt 0; \\ & -385 + 27n -27 \ lt 0; \\ & 27n \ lt 412; \\ & n \ lt 15 \ frac (7) (27) \ O'ng o'q ((n) _ (\ max)) = 15. \\ \ end (tekislash) \]
Oxirgi qator tushuntirishni talab qiladi. Shunday qilib, $ n \ lt 15 \ frac (7) (27) $ ekanligini bilamiz. Boshqa tomondan, biz faqat sonning tamsayı qiymatlaridan mamnun bo'lamiz (bundan tashqari, $ n \ in \ mathbb (N) $), shuning uchun ruxsat etilgan eng katta raqam aynan $ n = 15 $ va hech qanday holatda 16.
Muammo raqami 5. Arifmetik progressiyada $ (() _ (5)) = - 150, (() _ (6)) = - 147 $. Bu progressiyaning birinchi musbat sonining sonini toping.
Bu avvalgisiga o'xshash muammo bo'lar edi, lekin biz $ ((a) _ (1)) $ ni bilmaymiz. Lekin qo'shni atamalar ma'lum: $ ((a) _ (5)) $ va $ ((a) _ (6)) $, shuning uchun biz progressiyaning farqini osongina topishimiz mumkin:
Bundan tashqari, biz beshinchi atamani birinchisi va standart formulaga muvofiq farq bilan ifodalashga harakat qilamiz:
\ [\ boshlash (tekislash) va ((a) _ (n)) = ((a) _ (1)) + \ chap (n-1 \ o'ng) \ cdot d; \\ & ((a) _ (5)) = ((a) _ (1)) + 4d; \\ & -150 = ((a) _ (1)) + 4 \ cdot 3; \\ & ((a) _ (1)) = -150-12 = -162. \\ \ end (tekislash) \]
Endi biz oldingi vazifaga o'xshab harakat qilamiz. Biz ketma -ketlikning qaysi nuqtasida ijobiy raqamlar bo'lishini bilib olamiz:
\ [\ begin (align) & ((a) _ (n)) = - 162+ \ chap (n -1 \ o'ng) \ cdot 3 \ gt 0; \\ & -162 + 3n -3 \ gt 0; \\ & 3n \ gt 165; \\ & n \ gt 55 \ O'ng o'q ((n) _ (\ min)) = 56. \\ \ end (tekislash) \]
Bu tengsizlikning eng kichik sonli yechimi 56 ga teng.
E'tibor bering: oxirgi vazifada hamma narsa qat'iy tengsizlikka tushirildi, shuning uchun $ n = 55 $ varianti bizga mos kelmaydi.
Endi biz oddiy muammolarni qanday hal qilishni o'rgandik, keling murakkabroq masalalarga o'tamiz. Birinchidan, keling, bizga ko'p vaqt va teng bo'lmagan hujayralarni tejaydigan arifmetik progressiyaning yana bir foydali xususiyatini o'rganaylik. :)
O'rtacha arifmetik va teng chiziqlar
$ \ Chap (((a) _ (n)) \ o'ng) $ ortib borayotgan arifmetik progressiyaning ketma -ket a'zolarini ko'rib chiqing. Keling, ularni raqamlar qatorida belgilashga harakat qilaylik:
Raqamlar qatoridagi arifmetik progressiyaning a'zolariMen $ ((a) _ (n-3)), ..., ((a) _ (n + 3)) $ emas, balki $ ((a) _ (1)), \ ( (a) _ (2)), \ ((a) _ (3)) $ va boshqalar. Chunki men hozir gaplashadigan qoida har qanday "segmentlar" uchun bir xil ishlaydi.
Va qoida juda oddiy. Keling, rekursiya formulasini eslaylik va uni belgilangan barcha a'zolar uchun yozamiz:
\ [\ boshlash (tekislash) va ((a) _ (n-2)) = ((a) _ (n-3)) + d; \\ & ((a) _ (n-1)) = ((a) _ (n-2)) + d; \\ & ((a) _ (n)) = ((a) _ (n-1)) + d; \\ & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n + 1)) + d; \\ \ end (tekislash) \]
Biroq, bu tengliklarni boshqacha yozish mumkin:
\ [\ boshlash (tekislash) va ((a) _ (n -1)) = ((a) _ (n)) - d; \\ & ((a) _ (n -2)) = ((a) _ (n)) - 2d; \\ & ((a) _ (n -3)) = ((a) _ (n)) - 3d; \\ & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n)) + 2d; \\ & ((a) _ (n + 3)) = ((a) _ (n)) + 3d; \\ \ end (tekislash) \]
Xo'sh, nima? $ ((A) _ (n-1)) $ va $ ((a) _ (n + 1)) $ shartlari $ ((a) _ (n)) $ dan bir xil masofada yotadi. . Va bu masofa $ d $ ga teng. $ ((A) _ (n -2)) $ va $ ((a) _ (n + 2)) $ a'zolari haqida ham shunday deyish mumkin - ular ham $ ((a) _ (n) dan chiqariladi. ) $ bir xil masofa $ 2d $ ga teng. Siz cheksiz davom ettirishingiz mumkin, lekin uning ma'nosi rasmda yaxshi tasvirlangan.
 Progressiya a'zolari markazdan bir xil masofada yotadi
Progressiya a'zolari markazdan bir xil masofada yotadi Bu biz uchun nimani anglatadi? Bu shuni anglatadiki, agar qo'shni raqamlar ma'lum bo'lsa, $ ((a) _ (n)) $ ni topishingiz mumkin:
\ [((a) _ (n)) = \ frac (((a) _ (n-1)) + ((a) _ (n + 1))) (2) \]
Biz ajoyib bayonot bilan chiqdik: arifmetik progressiyaning har bir a'zosi qo'shni atamalarning o'rtacha arifmetikasiga teng! Bundan tashqari, biz $ ((a) _ (n)) $ dan chapga va o'ngga bir qadam emas, balki $ k $ qadamlarini chetlab o'tishimiz mumkin - va shunga qaramay, formula to'g'ri bo'ladi:
\ [((a) _ (n)) = \ frac (((a) _ (n-k)) + ((a) _ (n + k))) (2) \]
Bular. $ ((a) _ (100)) $ va $ ((a) _ (200)) $ bilsak, biz $ ((a) _ (150)) $ ni osongina topa olamiz, chunki $ ((a) _ (150)) = \ frac (((a) _ (100)) + ((a) _ (200))) (2) $. Bir qarashda, bu fakt bizga hech qanday foydali narsa bermayotganga o'xshaydi. Biroq, amalda, ko'plab masalalar o'rtacha arifmetikani ishlatish uchun maxsus "keskinlashadi". Qarab qo'ymoq:
Muammo raqami 6. $ -6 ((x) ^ (2)) $, $ x + 1 $ va $ 14 + 4 ((x) ^ (2)) $ raqamlari ketma -ket a'zo bo'lgan $ x $ qiymatlarini toping. arifmetik progressiya (tartibda).
Yechim. Ko'rsatilgan raqamlar progressiyaning a'zolari bo'lgani uchun, ular uchun o'rtacha arifmetik shart bajariladi: $ x + 1 $ markaziy elementi qo'shni elementlar bilan ifodalanishi mumkin:
\ [\ begin (align) & x + 1 = \ frac (-6 ((x) ^ (2)) + 14 + 4 ((x) ^ (2))) (2); \\ & x + 1 = \ frac (14-2 ((x) ^ (2))) (2); \\ & x + 1 = 7 - ((x) ^ (2)); \\ & ((x) ^ (2)) + x-6 = 0. \\ \ end (tekislash) \]
Natijada klassik kvadratik tenglama olinadi. Uning ildizlari: $ x = 2 $ va $ x = -3 $ - bu javoblar.
Javob: -3; 2018-05-01 xoxlasa buladi 121 2.
Muammo raqami 7. $$ qiymatlarini toping, ular uchun $ -1; 4-3; (() ^ (2)) + 1 $ raqamlari arifmetik progressiya qiladi (shu tartibda).
Yechim. Shunga qaramay, biz o'rta muddatni qo'shni atamalarning o'rtacha arifmetik nuqtai nazaridan ifodalaymiz:
\ [\ begin (align) & 4x-3 = \ frac (x-1 + ((x) ^ (2)) + 1) (2); \\ & 4x-3 = \ frac (((x) ^ (2)) + x) (2); \ quad \ chap | \ cdot 2 \ o'ng.; \\ & 8x-6 = ((x) ^ (2)) + x; \\ & ((x) ^ (2)) - 7x + 6 = 0. \\ \ end (tekislash) \]
Yana kvadrat tenglama. Va yana ikkita ildiz bor: $ x = 6 $ va $ x = 1 $.
Javob: 1; 6.
Agar muammoni hal qilish jarayonida siz shafqatsiz raqamlarni topsangiz yoki topilgan javoblarning to'g'riligiga to'liq ishonchingiz komil bo'lmasa, tekshirishga imkon beradigan ajoyib usul mavjud: biz muammoni to'g'ri hal qildikmi?
Masalan, 6 -sonli masalada biz -3 va 2. javoblarni oldik. Bu javoblarning to'g'riligini qanday tekshirish mumkin? Keling, ularni ulab, nima bo'lishini ko'rib chiqaylik. Eslatib o'taman, bizda uchta raqam bor ($ -6 (() ^ (2)) $, $ + 1 $ va $ 14 + 4 (() ^ (2)) $), ular arifmetik progressiyani hosil qilishi kerak. $ X = -3 $ ni almashtiring:
\ [\ boshlash (tekislash) & x = -3 \ O'ng o'q \\ & -6 ((x) ^ (2)) = -54; \\ & x + 1 = -2; \\ & 14 + 4 ((x) ^ (2)) = 50. \ tugatish (tekislash) \]
Qabul qilingan raqamlar -54; -2; 52, 52 bilan farq qiladigan, shubhasiz, arifmetik progressiya. Xuddi shu narsa $ x = 2 $ uchun sodir bo'ladi:
\ [\ boshlash (tekislash) & x = 2 \ O'ng o'q \\ & -6 ((x) ^ (2)) = - 24; \\ & x + 1 = 3; \\ & 14 + 4 ((x) ^ (2)) = 30. \ tugatish (tekislash) \]
Yana progressiya, lekin farq 27 bilan. Shunday qilib, muammo to'g'ri hal qilingan. Qiziquvchilar ikkinchi muammoni mustaqil hal qilishlari mumkin, lekin men darhol aytaman: u erda ham hamma narsa to'g'ri.
Umuman olganda, oxirgi muammolarni hal qilishda biz yana bir qiziq faktga duch keldik, uni ham eslash kerak:
Agar uchta raqam shunday bo'lsa, ikkinchisi birinchi va oxirgi arifmetik o'rtacha bo'lsa, bu raqamlar arifmetik progressiyani hosil qiladi.
Kelgusida, bu bayonotni tushunish bizga muammoning shartidan kelib chiqib, kerakli taraqqiyotni tom ma'noda "qurish" imkonini beradi. Ammo bunday "qurilish" ga o'tishdan oldin, biz ko'rib chiqilgan narsadan bevosita kelib chiqadigan yana bir faktga e'tibor qaratishimiz kerak.
Elementlarning guruhlanishi va yig'indisi
Yana raqamlar o'qiga qaytamiz. Keling, progressning bir nechta a'zolarini ta'kidlaylik, ular orasida, ehtimol. boshqa ko'plab a'zolar bor:
Raqam chizig'ida 6 ta element belgilanganKeling, "chap quyruq" ni $ ((a) _ (n)) $ va $ d $, "o'ng quyruq" ni $ ((a) _ (k)) $ va $ d $ bilan ifodalashga harakat qilaylik. . Bu juda oddiy:
\ [\ boshlash (tekislash) va ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n)) + 2d; \\ & ((a) _ (k -1)) = ((a) _ (k)) - d; \\ & ((a) _ (k -2)) = ((a) _ (k)) - 2d. \\ \ end (tekislash) \]
E'tibor bering, quyidagi summalar teng:
\ [\ boshlash (tekislash) & ((a) _ (n)) + ((a) _ (k)) = S; \\ & (a) _ (n + 1)) + ((a) _ (k -1)) = ((a) _ (n)) + d + ((a) _ (k)) - d = S; \\ & (a) _ (n + 2)) + ((a) _ (k -2)) = ((a) _ (n)) + 2d + ((a) _ (k)) - 2d = S. \ tugatish (tekislash) \]
Oddiy qilib aytganda, agar biz boshlang'ich sifatida ikkita $ S $ raqamiga teng keladigan ikkita elementni ko'rib chiqsak va keyin biz bu elementlardan qarama -qarshi yo'nalishda (bir -birimizga yoki aksincha uzoqlashish uchun) yurishni boshlasak, keyin biz qoqinadigan elementlarning yig'indisi ham teng bo'ladi$ S $. Buni grafikada eng aniq ifodalash mumkin:
 Teng girinti teng miqdorlarni beradi
Teng girinti teng miqdorlarni beradi Bu haqiqatni tushunish bizga yuqorida ko'rib chiqilganlarga qaraganda ancha murakkablikdagi muammolarni hal qilishga imkon beradi. Masalan, bunday:
Muammo raqami 8. Arifmetik progressiyaning farqini aniqlang, bunda birinchi atama 66, ikkinchi va o'n ikkinchi a'zolar hosilasi mumkin bo'lgan eng kichikdir.
Yechim. Keling, bilgan hamma narsani yozaylik:
\ [\ boshlash (tekislash) & ((a) _ (1)) = 66; \\ & d =? \\ & ((a) _ (2)) \ cdot ((a) _ (12)) = \ min. \ tugatish (tekislash) \]
Shunday qilib, biz $ d $ progressining farqini bilmaymiz. Aslida, butun yechim farqga asoslanadi, chunki $ ((a) _ (2)) \ cdot ((a) _ (12)) $ mahsulotini quyidagicha qayta yozish mumkin:
\ [\ boshlash (tekislash) & ((a) _ (2)) = ((a) _ (1)) + d = 66 + d; \\ & ((a) _ (12)) = ((a) _ (1)) + 11d = 66 + 11d; \\ & ((a) _ (2)) \ cdot ((a) _ (12)) = \ chap (66 + d \ o'ng) \ cdot \ chap (66 + 11d \ o'ng) = \\ & = 11 \ cdot \ chap (d + 66 \ o'ng) \ cdot \ chap (d + 6 \ o'ng). \ tugatish (tekislash) \]
Tankda bo'lganlar uchun: Men ikkinchi qavsdan umumiy 11 faktorini oldim. Shunday qilib, qidirilayotgan mahsulot $ d $ o'zgaruvchiga nisbatan kvadratik funktsiyadir. Shuning uchun $ f \ chap (d \ o'ng) = 11 \ chap (d + 66 \ o'ng) \ chap (d + 6 \ o'ng) $ funktsiyasini ko'rib chiqing - uning grafigi shoxlari parabola bo'ladi, chunki Agar biz qavslarni kengaytirsak, biz quyidagilarni olamiz:
\ [\ boshlash (tekislash) va f \ chap (d \ o'ng) = 11 \ chap (((d) ^ (2)) + 66d + 6d + 66 \ cdot 6 \ o'ng) = \\ & = 11 (( d) ^ (2)) + 11 \ cdot 72d + 11 \ cdot 66 \ cdot 6 \ end (align) \]
Ko'rib turganingizdek, etakchi davrda koeffitsient 11 ga teng - bu ijobiy raqam, shuning uchun biz chindan ham shoxlari parabola bilan ishlaymiz:
kvadrat funktsiya grafigi - parabola
Iltimos, diqqat qiling: bu parabola o'zining minimal qiymatini o'z tepasida $ abscissa $ ((d) _ (0)) $ bilan oladi. Albatta, biz bu abscissani standart sxema bo'yicha hisoblashimiz mumkin ($ ((d) _ (0)) = (- b) / (2a) \; $ formulasi ham mavjud), lekin bu ancha oqilona bo'lardi $ \ (d) _ (0)) $ nuqtasi $ f \ chap (d \ o'ng) = 0 $ tenglamasining ildizlaridan bir xil masofada joylashgan:
\ [\ boshlash (tekislash) va f \ chap (d \ o'ng) = 0; \\ & 11 \ cdot \ chap (d + 66 \ o'ng) \ cdot \ chap (d + 6 \ o'ng) = 0; \\ & ((d) _ (1)) = - 66; \ quad ((d) _ (2)) = - 6. \\ \ end (tekislash) \]
Shuning uchun men qavslarni ochishga shoshilmadim: asl shaklida ildizlarni topish juda oson edi. Shuning uchun, abssissa -66 va -6 sonlarining arifmetik o'rtacha qiymatiga teng:
\ [((d) _ (0)) = \ frac (-66-6) (2) =-36 \]
Kashf etilgan raqam bizga nima beradi? U bilan kerakli mahsulot eng kichik qiymatni oladi (aytmoqchi, biz $ ((y) _ (\ min)) $ ni hisoblamadik - bu bizdan talab qilinmaydi). Shu bilan birga, bu raqam boshlang'ich progressiya o'rtasidagi farq, ya'ni. javobni topdik. :)
Javob: -36
Muammo raqami 9. $ - \ frac (1) (2) $ va $ - \ frac (1) (6) $ raqamlari orasiga uchta raqamni kiriting, shunda ular berilgan raqamlar bilan birgalikda arifmetik progressiyani hosil qiladi.
Yechim. Asosan, biz besh raqamli ketma -ketlikni tuzishimiz kerak, birinchi va oxirgi raqamlar allaqachon ma'lum. Yo'qotilgan raqamlarni $ x $, $ y $ va $ z $ o'zgaruvchilari bilan belgilaylik:
\ [\ chap (((a) _ (n)) \ o'ng) = \ chap \ ( - \ frac (1) (2); x; y; z; - \ frac (1) (6) \ o'ng \ )]]
E'tibor bering, $ y $ raqami bizning ketma -ketligimizning "o'rtasi" dir - u $ x $ va $ z $ raqamlaridan, $ - \ frac (1) (2) $ va $ - \ raqamlaridan teng masofada joylashgan. frac (1) (6) $. Va agar biz hozirda $ x $ va $ z $ raqamlaridan $ y $ ololmasak, u holda rivojlanishning oxiri bilan vaziyat boshqacha. O'rtacha arifmetikani eslang:
Endi $ y $ ni bilib, qolgan raqamlarni topamiz. E'tibor bering, $ x $ $ - \ frac (1) (2) $ va $ y = - \ frac (1) (3) $ raqamlari orasida joylashgan. Shunung uchun
Xuddi shunday fikr yuritib, qolgan raqamni topamiz:
Tayyor! Biz uchta raqamni topdik. Keling, ularni asl raqamlar orasiga qo'yilishi kerak bo'lgan tartibda javobga yozib qo'yaylik.
Javob: $ - \ frac (5) (12); \ - \ frac (1) (3); \ - \ frac (1) (4) $
Muammo raqami 10. Agar siz kiritilgan raqamlarning birinchi, ikkinchi va oxirgi yig'indisi 56 ekanligini bilsangiz, bu raqamlar bilan birgalikda arifmetik progressiyani tashkil etuvchi 2 va 42 raqamlari orasiga bir nechta sonlarni kiriting.
Yechim. Bundan ham murakkab vazifa, ammo avvalgilariga o'xshash sxema bo'yicha - o'rtacha arifmetik orqali hal qilinadi. Muammo shundaki, biz qancha raqam kiritish kerakligini aniq bilmaymiz. Shuning uchun, aniqlik uchun, hamma narsani kiritgandan so'ng, aynan $ n $ sonlari bo'ladi, deb hisoblaymiz va ularning birinchisi 2, oxirgi 42 bo'ladi. Bunday holda, izlanayotgan arifmetik progressiya quyidagicha ifodalanishi mumkin:
\ [\ chap (((a) _ (n)) \ o'ng) = \ chap \ (2; ((a) _ (2)); ((a) _ (3)); ...; (( a) _ (n-1)); 42 \ o'ng \) \]
\ [((a) _ (2)) + ((a) _ (3)) + ((a) _ (n-1)) = 56 \]
Shunga qaramay, $ ((a) _ (2)) $ va $ ((a) _ (n-1)) $ raqamlari 2 va 42 sonlardan bir-biriga bir qadam narida olinganligini, ya'ni ... ketma -ketlikning markaziga. Bu shuni anglatadiki
\ [((a) _ (2)) + ((a) _ (n-1)) = 2 + 42 = 44 \]
Ammo keyin yuqorida yozilgan iborani quyidagicha qayta yozish mumkin:
\ [\ boshlash (tekislash) & ((a) _ (2)) + ((a) _ (3)) + ((a) _ (n-1)) = 56; \\ & \ chap (((a) _ (2)) + ((a) _ (n-1)) \ o'ng) + ((a) _ (3)) = 56; \\ & 44 + ((a) _ (3)) = 56; \\ & ((a) _ (3)) = 56-44 = 12. \\ \ end (tekislash) \]
$ ((A) _ (3)) $ va $ ((a) _ (1)) $ ni bilgan holda, biz jarayonning farqini osongina topamiz:
\ [\ boshlash (tekislash) va ((a) _ (3)) - ((a) _ (1)) = 12 - 2 = 10; \\ & ((a) _ (3)) - ((a) _ (1)) = \ chap (3-1 \ o'ng) \ cdot d = 2d; \\ & 2d = 10 \ O'ng o'q d = 5. \\ \ end (tekislash) \]
Qolgan a'zolarni topishgina qoladi:
\ [\ boshlash (tekislash) & ((a) _ (1)) = 2; \\ & ((a) _ (2)) = 2 + 5 = 7; \\ & ((a) _ (3)) = 12; \\ & ((a) _ (4)) = 2 + 3 \ cdot 5 = 17; \\ & ((a) _ (5)) = 2 + 4 \ cdot 5 = 22; \\ & ((a) _ (6)) = 2 + 5 \ cdot 5 = 27; \\ & ((a) _ (7)) = 2 + 6 \ cdot 5 = 32; \\ & ((a) _ (8)) = 2 + 7 \ cdot 5 = 37; \\ & ((a) _ (9)) = 2 + 8 \ cdot 5 = 42; \\ \ end (tekislash) \]
Shunday qilib, allaqachon 9 -qadamda biz ketma -ketlikning chap uchiga - 42 -raqamga kelamiz. Hammasi bo'lib, faqat 7 ta raqamni kiritish kerak edi: 7; 12; 17; 22; 27; 32; 37.
Javob: 7; 12; 17; 22; 27; 32; 37
Progressiya bilan so'z muammolari
Xulosa qilib aytganda, men bir nechta oddiy vazifalarni ko'rib chiqmoqchiman. Xo'sh, qanchalik sodda: maktabda matematikani o'qiyotgan va yuqorida yozilganlarni o'qimagan ko'pchilik o'quvchilar uchun bu vazifalar qalay bo'lib tuyulishi mumkin. Shunga qaramay, aynan mana shunday muammolar matematikada OGE va USE da uchraydi, shuning uchun ular bilan tanishishingizni maslahat beraman.
Muammo raqami 11. Brigada yanvar oyida 62 dona ishlab chiqargan, har oyda esa avvalgisiga qaraganda 14 tadan ko'proq. Noyabr oyida jamoa nechta qismdan iborat bo'ldi?
Yechim. Shubhasiz, oylar bo'yicha rejalashtirilgan tafsilotlar soni ortib borayotgan arifmetik progressiyani ifodalaydi. Bundan tashqari:
\ [\ boshlash (tekislash) & ((a) _ (1)) = 62; \ to'rtlik d = 14; \\ & ((a) _ (n)) = 62+ \ chap (n-1 \ o'ng) \ cdot 14. \\ \ end (tekislash) \]
Noyabr - yilning 11 -oyi, shuning uchun $ ((a) _ (11)) $ topishimiz kerak:
\ [((a) _ (11)) = 62 + 10 \ cdot 14 = 202 \]
Shunday qilib, noyabr oyida 202 ta ehtiyot qism ishlab chiqariladi.
Muammo raqami 12. Kitob bog‘lash ustaxonasi yanvar oyida 216 ta kitobni, har oyda esa avvalgisidan 4 tadan ko‘p kitobni bog‘ladi. Seminar dekabr oyida nechta kitobni bog'lab qo'ydi?
Yechim. Hammasi bir xil:
$ \ begin (align) & ((a) _ (1)) = 216; \ quad d = 4; \\ & ((a) _ (n)) = 216+ \ chap (n-1 \ o'ng) \ cdot 4. \\ \ end (align) $
Dekabr - yilning oxirgi, 12 -oyi, shuning uchun biz $ ((a) _ (12)) $ qidiramiz:
\ [((a) _ (12)) = 216 + 11 \ cdot 4 = 260 \]
Bu javob - dekabr oyida 260 ta kitob nashr qilinadi.
Xo'sh, agar siz hozirgacha o'qigan bo'lsangiz, men sizni tabriklashga shoshaman: siz "yosh jangchi kursini" arifmetik progressiyada muvaffaqiyatli o'tdingiz. Siz bemalol keyingi darsga o'tishingiz mumkin, u erda biz progressiya yig'indisi formulasini, shuningdek, uning muhim va juda foydali oqibatlarini o'rganamiz.
Birinchi daraja
Arifmetik progressiya. Misollar bilan batafsil nazariya (2019)
Raqamlar ketma -ketligi
Keling, o'tirib, ba'zi raqamlarni yozishni boshlaylik. Masalan:
Siz har qanday raqamlarni yozishingiz mumkin va siz xohlaganingizcha bo'lishi mumkin (bizning holatda ular). Qancha raqamlar yozmasligimizdan qat'i nazar, biz har doim qaysi biri birinchi, ikkinchisi va hokazolarni oxirigacha aytishimiz mumkin, ya'ni ularni sanashimiz mumkin. Bu raqamlar ketma -ketligiga misol:
Raqamlar ketma -ketligi
Masalan, bizning ketma -ketligimiz uchun:
Belgilangan raqam ketma -ketlikdagi bitta raqamga xosdir. Boshqacha qilib aytganda, ketma -ketlikda uch soniyali raqamlar yo'q. Ikkinchi raqam ( -son kabi) har doim bitta.
Raqamli son ketma -ketlikning uchinchi a'zosi deb nomlanadi.
Biz odatda butun ketma -ketlikni ba'zi harflar deb ataymiz (masalan,) va bu ketma -ketlikning har bir a'zosi xuddi shu harf bo'lib, uning a'zosi soniga teng :.
Bizning holatda: 
Aytaylik, bizda qo'shni sonlar orasidagi farq bir xil va teng bo'lgan sonli ketma -ketlik bor.
Masalan: 
va hokazo.
Bu sonlar ketma -ketligiga arifmetik progressiya deyiladi.
"Progressiya" atamasi 6 -asrda rim muallifi Boetsiy tomonidan kiritilgan va keng ma'noda cheksiz sonlar ketma -ketligi sifatida tushunilgan. "Arifmetika" nomi qadimgi yunonlar egallagan uzluksiz nisbatlar nazariyasidan olingan.
Bu raqamli ketma -ketlik, uning har bir a'zosi avvalgisiga teng, bir xil songa qo'shilgan. Bu raqam arifmetik progressiyaning farqi deb ataladi va u bilan belgilanadi.
Qaysi sonlar ketma -ketligi arifmetik progressiya va qaysi biri emasligini aniqlashga harakat qiling.
a)
b)
v)
d)
Tushundingizmi? Keling, javoblarimizni solishtiraylik:
Bu arifmetik progressiya - b, v.
Emas arifmetik progressiya - a, d.
Keling, berilgan progressiyaga () qaytaylik va uning uchinchi a'zosining qiymatini topishga harakat qilaylik. Mavjud ikkita uni topish usuli.
1. Usul
Biz progressiyaning uchinchi davriga etib borgunimizcha, progressiya sonining oldingi qiymatiga qo'shishimiz mumkin. Yaxshisi, bizda ko'p narsa qolmaydi - faqat uchta qiymat:
Shunday qilib, ta'riflangan arifmetik progressiyaning uchinchi a'zosi tengdir.
2. Usul
Agar biz uchinchi davrning qiymatini bosqichma -bosqich topishimiz kerak bo'lsa -chi? Yig'ish bir soatdan ko'proq vaqtni oladi va biz raqamlarni qo'shishda adashmagan bo'lamiz.
Albatta, matematiklar avvalgi qiymatga arifmetik progressiyaning farqini qo'shishning hojati yo'q usulni o'ylab topdilar. Chizilgan rasmga diqqat bilan qarang ... Albatta siz allaqachon ma'lum bir naqshni payqadingiz, ya'ni:
Masalan, bu arifmetik progressiyaning uchinchi a'zosining qiymati qanday qo'shilganini ko'rib chiqaylik: 
Boshqa so'zlar bilan aytganda:
Berilgan arifmetik progressiya a'zosining qiymatini shu tarzda mustaqil ravishda topishga harakat qiling.
Hisoblanganmi? Izohlaringizni javob bilan solishtiring:
E'tibor bering, siz arifmetik progressiyaning a'zolarini ketma -ket oldingi qiymatga qo'shganimizda, siz avvalgi usulda bo'lgani kabi bir xil raqamni oldingiz.
Keling, ushbu formulani "shaxssizlashtirish" ga harakat qilaylik - biz uni umumiy shaklga keltiramiz va olamiz:
|
Arifmetik progressiya tenglamasi. |
Arifmetik progressiyalar ko'tariladi va ba'zida kamayadi.
Ko'tarilish- a'zolarning har bir keyingi qiymati avvalgisidan kattaroq bo'lgan progressiyalar.
Masalan:
Kamaymoqda- a'zolarning har bir keyingi qiymati avvalgisidan past bo'lgan progressiyalar.
Masalan:
Olingan formulalar arifmetik progressiyaning ortish va kamayish shartlarini hisoblashda ishlatiladi.
Keling, buni amalda tekshirib ko'ramiz.
Bizga quyidagi raqamlardan tashkil topgan arifmetik progressiya berilgan: Keling, agar hisoblash uchun formulamizdan foydalansak, bu arifmetik progressiyaning uchinchi soni qanday bo'lishini tekshirib ko'ramiz:

O'shandan beri:
Shunday qilib, biz formulaning arifmetik progressiyani kamaytirishda ham, oshirishda ham ishlashiga ishonch hosil qildik.
Ushbu arifmetik progressiyaning uchinchi va uchinchi shartlarini o'zingiz topishga harakat qiling.
Keling, olingan natijalarni taqqoslaylik:
Arifmetik progressiya xususiyati
Keling, vazifani murakkablashtiraylik - biz arifmetik progressiyaning xususiyatini olamiz.
Aytaylik, bizga quyidagi shart berilgan:
- arifmetik progressiya, qiymatini toping.
Oson, siz aytganingizdek va o'zingiz bilgan formulaga muvofiq hisoblashni boshlang:
Keling, a:
Mutlaqo to'g'ri. Ma'lum bo'lishicha, biz avval topamiz, keyin uni birinchi raqamga qo'shamiz va qidirayotganimizni olamiz. Agar progressiya kichik qiymatlar bilan ifodalangan bo'lsa, unda murakkab narsa yo'q, lekin agar bizga shartlar bo'yicha raqamlar berilgan bo'lsa? Tan oling, hisob -kitoblarda xato qilish ehtimoli bor.
Endi o'ylab ko'ring, har qanday formuladan foydalanib, bu muammoni bitta harakatda hal qilish mumkinmi? Albatta, ha, va aynan u biz hozir chekinishga harakat qilamiz.
Keling, arifmetik progressiyaning kerakli muddatini belgilaymiz, chunki biz uni topish formulasini bilamiz - bu biz boshida chiqargan formula.
, keyin:
- progressiyaning oldingi a'zosi:
- progressiyaning keyingi a'zosi:
Keling, progressiyaning oldingi va keyingi a'zolarini sarhisob qilaylik:
Ma'lum bo'lishicha, progressiyaning oldingi va keyingi a'zolarining yig'indisi ularning o'rtasida joylashgan progressiya a'zosining ikki barobar qiymatidir. Boshqacha qilib aytganda, ma'lum bo'lgan oldingi va ketma -ket qiymatlarga ega bo'lgan progressiya a'zosining qiymatini topish uchun ularni qo'shish va bo'lish kerak.
To'g'ri, biz bir xil raqamni oldik. Keling, materialni tuzataylik. Progressning qiymatini o'zingiz hisoblang, chunki bu umuman qiyin emas.
Juda qoyil! Siz progress haqida deyarli hamma narsani bilasiz! O'rganish uchun faqat bitta formula qoldi, afsonaga ko'ra, uni hamma zamonning eng buyuk matematiklaridan biri, "matematiklar qiroli" - Karl Gauss osonlikcha o'ylab topgan ...
Karl Gauss 9 yoshida, boshqa sinf o'quvchilarining ishini tekshirish bilan shug'ullanuvchi o'qituvchi darsda quyidagi vazifani so'radi: "Inklyuzivdan (boshqa manbalarga ko'ra) gacha bo'lgan barcha natural sonlarning yig'indisini hisoblang". O'qituvchining ajablanishini tasavvur qiling -a, shogirdlaridan biri (bu Karl Gauss edi) bir daqiqada muammoning to'g'ri javobini berdi, jasoratli sinfdoshlarining ko'plari uzoq hisob -kitoblardan so'ng noto'g'ri natija olishdi ...
Yosh Karl Gauss siz sezishingiz mumkin bo'lgan ma'lum bir naqshni payqadi.
Aytaylik, bizda -chi a'zolardan iborat arifmetik progressiya bor: Biz arifmetik progressiyaning berilgan a'zolari yig'indisini topishimiz kerak. Albatta, biz qo'lda barcha qiymatlarni yig'a olamiz, lekin agar vazifada Gauss izlaganidek uning a'zolarining yig'indisini topish kerak bo'lsa -chi?
Keling, berilgan progressiyani chizamiz. Belgilangan raqamlarga diqqat bilan qarang va ular bilan turli matematik amallarni bajarishga harakat qiling. 
Siz sinab ko'rdingizmi? Siz nimani payqadingiz? To'g'ri! Ularning summasi teng

Ayting -chi, berilgan progressiyada nechta shunday juftlik bor? Albatta, barcha raqamlarning aniq yarmi, ya'ni.
Arifmetik progressiyaning ikkita a'zosining yig'indisi teng va shunga o'xshash teng juftliklarga asoslanib, biz umumiy yig'indini olamiz:
.
Shunday qilib, har qanday arifmetik progressiyaning birinchi a'zolari yig'indisining formulasi quyidagicha bo'ladi:
Ba'zi muammolarda biz uchinchi davrni bilmaymiz, lekin biz rivojlanishning farqini bilamiz. Uchinchi davrning yig'indisi formulasini almashtirishga harakat qiling.
Nima qildingiz?
Juda qoyil! Keling, Karl Gaussga berilgan muammoga qaytaylik: o'zingizni hisoblang -sonidan boshlab sonining yig'indisi nima, va sonidan boshlab sonining yig'indisi.
Qancha oldingiz?
Gauss a'zolar yig'indisi va a'zolar yig'indisi teng ekanligini aniqladi. Siz shunday qaror qildingizmi?
Aslida, arifmetik progressiya a'zolarining yig'indisining formulasini III asrda qadimgi yunon olimi Diofant isbotlagan va shu vaqt mobaynida aqlli odamlar arifmetik progressiyaning xususiyatlaridan qudrat va asosiy bilan foydalanganlar.
Masalan, Qadimgi Misrni va o'sha davrning eng shuhratparast qurilish maydonini tasavvur qiling - piramidaning qurilishi ... Rasmda uning bir tomoni ko'rsatilgan. 
Bu erda taraqqiyot qayerda? Yaxshilab qarang va piramida devorining har bir qatorida qum bloklari sonini aniqlang. 
Bu arifmetik progressiya emasmi? Agar bazaga blokli g'isht qo'yilsa, bitta devorni qurish uchun qancha blok kerakligini hisoblang. Umid qilamanki, siz barmog'ingizni monitor bo'ylab o'tkazib hisoblamaysiz, siz oxirgi formulani va arifmetik progress haqida aytganlarimizni eslaysizmi?
Bunday holda, rivojlanish quyidagicha ko'rinadi.
Arifmetik progressiyaning farqi.
Arifmetik progressiya a'zolari soni.
Ma'lumotlarimizni oxirgi formulalarga almashtiraylik (bloklar sonini 2 usulda hisoblaymiz).
1 -usul.
2 -usul.
Va endi siz monitorda hisoblashingiz mumkin: olingan qiymatlarni bizning piramidadagi bloklar soni bilan solishtiring. Birga keldimi? Yaxshi, siz arifmetik progressiyaning shartlari yig'indisini o'zlashtirdingiz.
Albatta, siz bazadagi bloklardan piramida qura olmaysiz, lekin? Bu shart bilan devor qurish uchun qancha qumli g'isht kerakligini hisoblab ko'ring.
Siz muvaffaq bo'ldingizmi?
To'g'ri javob bloklar:
Tayyorlamoq
Vazifalar:
- Masha yozda shaklini oladi. Har kuni u chayqalishlar sonini ko'paytiradi. Masha haftada necha marta cho'kadi, agar u birinchi mashg'ulotda cho'kib o'tirgan bo'lsa.
- Undagi barcha toq sonlarning yig'indisi nima?
- Kundaliklarni saqlashda, o'rmonchilar ularni shunday yig'adilarki, har bir yuqori qatlamda oldingisiga qaraganda bitta jurnal kamroq bo'ladi. Bir toshda qancha loglar bor, agar yog'ochdan yasalgan toshlar poydevor bo'lib xizmat qilsa.
Javoblar:
- Arifmetik progressiyaning parametrlarini aniqlaylik. Ushbu holatda
(hafta = kun).Javob: Ikki haftadan so'ng, Masha kuniga bir marta cho'kishi kerak.
- Birinchi toq son, oxirgi raqam.
Arifmetik progressiyaning farqi.
G'alati sonlar soni yarmiga teng, ammo biz bu faktni arifmetik progressiyaning -tinchi sonini topish formulasi yordamida tekshiramiz:Raqamlar g'alati raqamlarni o'z ichiga oladi.
Mavjud ma'lumotlarni formulaga almashtiring:Javob: Barcha toq sonlarning yig'indisi tengdir.
- Keling, piramida muammosini eslaylik. Bizning holatimizda, a, chunki har bir yuqori qatlam bitta jurnalga kamayadi, keyin faqat bir guruh qatlamlarda, ya'ni.
Ma'lumotni formulaga almashtiramiz:Javob: Masonlukta jurnallar bor.
Xulosa qilaylik
- - qo'shni sonlar orasidagi farq bir xil va teng bo'lgan sonli ketma -ketlik. Bu ko'tarilish va kamayish bo'lishi mumkin.
- Formulani topish-arifmetik progressiyaning uchinchi a'zosi -formulasi bilan yoziladi, bu erda progressiyada sonlar soni.
- Arifmetik progressiya a'zolarining mulki- - progressiyada raqamlar soni qayerda.
- Arifmetik progressiya a'zolarining yig'indisi ikki usulda topish mumkin:
, bu erda qiymatlar soni.
ARITMETIKA ISHLAB CHIQISH. O'RTACHA DARAJASI
Raqamlar ketma -ketligi
Keling, o'tirib, ba'zi raqamlarni yozishni boshlaylik. Masalan:
Siz har qanday raqamni yozishingiz mumkin va siz xohlaganingizcha bo'lishi mumkin. Lekin siz har doim ayting: qaysi biri birinchi, ikkinchisi va hokazo, ya'ni biz ularni sanashimiz mumkin. Bu raqamlar ketma -ketligiga misol.
Raqamlar ketma -ketligi raqamlar to'plami bo'lib, ularning har biriga o'ziga xos raqam berilishi mumkin.
Boshqacha qilib aytganda, har bir raqam ma'lum bir natural son bilan bog'lanishi mumkin va yagona. Va biz bu raqamni ushbu to'plamdan boshqa raqamlarga bermaymiz.
Raqamli son ketma -ketlikning uchinchi a'zosi deb nomlanadi.
Biz odatda butun ketma -ketlikni ba'zi harflar deb ataymiz (masalan,) va bu ketma -ketlikning har bir a'zosi xuddi shu harf bo'lib, uning a'zosi soniga teng :.
Agar ketma -ketlikning uchinchi muddatini biron bir formula bilan ko'rsatish mumkin bo'lsa, bu juda qulay. Masalan, formula
ketma -ketlikni o'rnatadi:
Va formula quyidagi ketma -ketlikda:
Masalan, arifmetik progressiya ketma -ketlikdir (bu erda birinchi atama teng va farq). Yoki (, farq).
To'rtinchi davr formulasi
Biz takroriy formulani chaqiramiz, unda uchinchi a'zoni bilish uchun siz avvalgi yoki bir nechta oldingi a'zolarni bilishingiz kerak:
Masalan, bunday formuladan foydalanib, progressiyaning uchinchi davrini topish uchun biz oldingi to'qqiztasini hisoblashimiz kerak bo'ladi. Masalan, ruxsat bering. Keyin:
Xo'sh, hozir qanday formula bor?
Biz qo'shadigan har bir satrda, ba'zi raqamlarga ko'paytiriladi. Nima uchun? Juda oddiy: bu joriy a'zolar soni minus:
Hozir ancha qulayroq, to'g'rimi? Biz tekshiramiz:
O'zingiz qaror qiling:
Arifmetik progressiyada n -chi sonning formulasini va yuzinchi sonini toping.
Yechim:
Birinchi atama teng. Farqi nima? Va bu erda:
(chunki bu farq deyiladi, bu progressiyaning ketma -ket a'zolari farqiga teng).
Shunday qilib, formula:
Keyin yuzinchi atama:
Dan to gacha bo'lgan barcha natural sonlarning yig'indisi nima?
Afsonaga ko'ra, buyuk matematik Karl Gauss 9 yoshli bola bo'lib, bu miqdorni bir necha daqiqada hisoblab chiqqan. U birinchi va oxirgi sonlarning yig'indisi teng ekanligini, ikkinchisining va oxirgi sonining yig'indisi bir xilligini, oxiridan uchinchi va uchinchi yig'indisi bir xilligini va boshqalarni payqadi. Bunday juftliklar nechta bo'ladi? To'g'ri, barcha raqamlar sonining yarmi, ya'ni. Shunday qilib,
Har qanday arifmetik progressiyaning birinchi a'zolari yig'indisining umumiy formulasi quyidagicha bo'ladi:
Misol:
Ikki xonali ko'pliklarning yig'indisini toping.
Yechim:
Birinchi bunday raqam. Har bir keyingi raqam oldingi raqamni qo'shish orqali olinadi. Shunday qilib, bizni qiziqtirgan raqamlar birinchi atama va farq bilan arifmetik progressiyani hosil qiladi.
Bu rivojlanishning uchinchi davr formulasi:
Hamma ikki raqamli bo'lishi kerak bo'lsa, qancha a'zo davom etmoqda?
Juda oson: .
Progressdagi oxirgi muddat teng bo'ladi. Keyin summa:
Javob:.
Endi o'zingiz qaror qiling:
- Har kuni sportchi oldingi kunga qaraganda ko'proq m yuguradi. Agar u birinchi kuni km m yugursa, u necha hafta ichida necha kilometr yuguradi?
- Velosipedchi har kuni oldingisiga qaraganda ko'proq kilometr yuradi. Birinchi kuni u km masofani bosib o'tdi. Kmni bosib o'tish uchun u necha kun yo'l bosishi kerak? U sayohatning oxirgi kunida necha kilometr yo'l bosadi?
- Do'konda muzlatgich narxi har yili bir xil miqdorda pasayadi. Agar muzlatgich rublga sotilgan bo'lsa, olti yildan keyin u rublga sotilgan bo'lsa, muzlatgich har yili qancha pasayganini aniqlang.
Javoblar:
- Bu erda eng muhim narsa - arifmetik progressiyani tan olish va uning parametrlarini aniqlash. Bunday holda, (hafta = kun). Siz ushbu progressiyaning birinchi a'zolarining yig'indisini aniqlashingiz kerak:
.
Javob: - Bu erda berilgan :, topish kerak.
Shubhasiz, siz avvalgi muammo bilan bir xil formuladan foydalanishingiz kerak:
.
Qiymatlarni almashtiring:Shubhasiz, ildiz mos emas, shuning uchun javob.
Keling, oxirgi kun uchun bosib o'tgan masofani uchinchi davr formulasidan foydalanib hisoblaymiz:
(km).
Javob: - Berilgan :. Toping:.
Buni osonroq qilish mumkin emas edi:
(silamoq).
Javob:
ARITMETIKA ISHLAB CHIQISH. ASOSIY HAQIDA QISQA
Bu raqamli ketma -ketlik bo'lib, unda qo'shni raqamlar orasidagi farq bir xil va tengdir.
Arifmetik progressiya ko'tarilish () va kamayish () bo'lishi mumkin.
Masalan:
Arifmetik progressiyaning n-chi sonini topish formulasi
formulada yozilgan, bu erda progressdagi sonlar soni.
Arifmetik progressiya a'zolarining mulki
Agar siz uning qo'shni a'zolari ma'lum bo'lsa, progressiya a'zosini osongina topishingiz mumkin - bu progressiyaning sonlari soni.
Arifmetik progressiya a'zolarining yig'indisi
Miqdorni topishning ikki yo'li mavjud:
Qiymatlar soni qayerda.
Qiymatlar soni qayerda.
Xo'sh, mavzu tugadi. Agar siz bu satrlarni o'qiyotgan bo'lsangiz, demak siz juda zo'rsiz.
Chunki odamlarning atigi 5 foizi biror narsani mustaqil ravishda o'zlashtira oladi. Va agar siz oxirigacha o'qigan bo'lsangiz, demak siz o'sha 5%!
Endi eng muhim narsa keladi.
Siz ushbu mavzu bo'yicha nazariyani bilib oldingiz. Va yana, bu ... bu shunchaki super! Siz allaqachon tengdoshlaringizning ko'pchiligidan yaxshiroqsiz.
Muammo shundaki, bu etarli bo'lmasligi mumkin ...
Sabab?
Imtihonni muvaffaqiyatli topshirganingiz uchun, byudjetga institutga qabul qilinganingiz uchun va eng muhimi, umr bo'yi.
Men sizni hech narsaga ishontirmayman, faqat bitta narsani aytaman ...
Yaxshi ta'lim olganlar, olmaganlarga qaraganda ancha ko'p maosh oladilar. Bu statistika.
Lekin bu ham asosiy narsa emas.
Asosiysi, ular KO'PROQ BAXTLI (bunday tadqiqotlar bor). Balki ular uchun imkoniyatlar ko'p bo'lgani va hayot yanada yorqinroq bo'lgani uchunmi? Bilmayman...
Lekin o'zingiz o'ylab ko'ring ...
Imtihonda boshqalardan ko'ra yaxshiroq bo'lish va oxir -oqibat ... ko'proq baxtli bo'lish uchun nima kerak?
BU MAVZUDA QO'L QILISh MUAMMOLARINI OLING.
Imtihonda sizdan nazariya so'ralmaydi.
Sizga kerak bo'ladi muammolarni bir muncha vaqt hal qiling.
Va agar siz ularni hal qilmagan bo'lsangiz (KO'P!), Siz adashib adashgan joyga borasiz, yoki o'z vaqtida bo'lmaydi.
Bu xuddi sportdagi kabi - aniq g'alaba qozonish uchun uni qayta -qayta takrorlash kerak.
Istalgan joydan kollektsiyani toping, albatta echimlar, batafsil tahlil bilan va qaror, qaror, qaror!
Siz bizning vazifalarimizdan foydalanishingiz mumkin (ixtiyoriy) va biz, albatta, ularni tavsiya qilamiz.
Qo'lingizni vazifalarimiz yordamida to'ldirish uchun siz hozir o'qiyotgan YouClever darsligining umrini uzaytirishga yordam berishingiz kerak.
Qanaqasiga? Ikkita variant bor:
- Ushbu maqoladagi barcha yashirin vazifalarni baham ko'ring - 299 r
- O'quv qo'llanmaning 99 ta maqolasida barcha yashirin vazifalarga kirishni oching. 999 rubl
Ha, bizning darsligimizda shunday 99 ta maqola bor va barcha vazifalar va ulardagi barcha yashirin matnlarga kirish birdaniga ochilishi mumkin.
Ikkinchi holatda biz sizga beramiz simulyator "Har bir mavzu uchun, murakkablikning barcha darajalari uchun echimlari va javoblari bilan 6000 ta muammo". Bu, albatta, har qanday mavzu bo'yicha muammolarni hal qilish uchun etarli bo'ladi.
Aslida, bu simulyatordan ham ko'proq - butun o'quv dasturi. Agar kerak bo'lsa, uni BEPUL ishlatishingiz mumkin.
Barcha matnlar va dasturlarga kirish saytning butun faoliyati davomida ta'minlanadi.
Xulosa...
Agar sizga bizning vazifalarimiz yoqmasa, boshqalarini toping. Faqat nazariya ustida to'xtamang.
"Tushundim" va "men hal qila olaman" - bu mutlaqo boshqacha ko'nikmalar. Sizga ikkalasi ham kerak.
Muammolarni toping va hal qiling!