Úloha B7 - Transformácia logaritmických a orientačných výrazov. Logaritmické výrazy
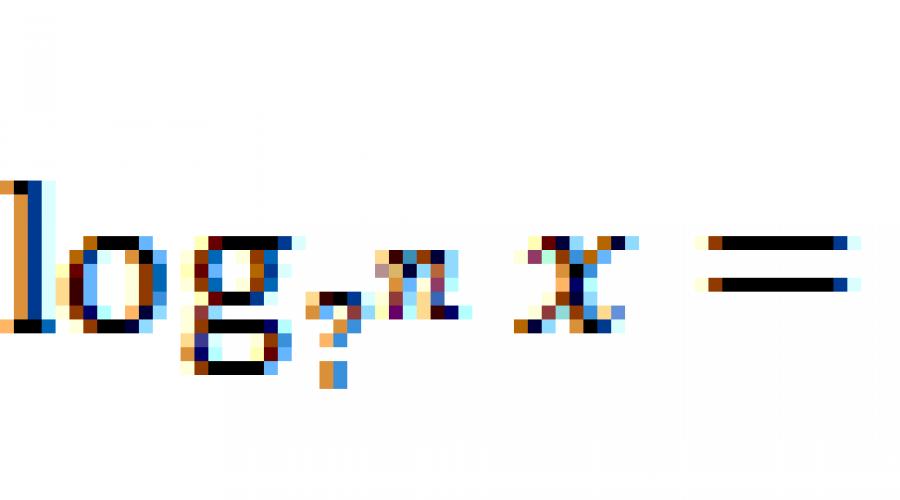
Typ lekcie: Lekcia zovšeobecnenia a systematizácie vedomostí
Ciele:
- aktualizovať znalosti študentov o logaritmoch a ich vlastnostiach v rámci všeobecného opakovania a prípravy na použitie;
- podporovať rozvoj mentálnej aktivity študentov, zručnosti uplatňovania teoretických poznatkov pri vykonávaní cvičení;
- podporovať rozvoj osobných kvalít študentov, sebakontrolu zručností a sebahodnotenia ich činností; Vzdelávajte tvrdú prácu, pacienta, vytrvalosť, nezávislosť.
Vybavenie:počítač, projektor, prezentácia (Príloha 1), Karty s domácimi úlohami (môžete pripojiť súbor s úlohou v elektronickom denníku).
Počas tried
I. Organizačný moment. Pozdrav, nálada na lekciu.
II. Diskusia domáca úloha.
III. Posolstvo tém a ciele lekcie. Motivácia.(Slide 1) Prezentácia.
Pokračujeme v zovšeobecnení opakovanie kurzu matematiky v príprave na skúšku. A dnes v lekcii budeme hovoriť o logaritmoch a ich vlastnostiach.
Úlohy pre výpočet logaritmov a transformácia logaritmických výrazov sú nevyhnutne prítomné v kontrolných a meracích materiáloch základných a úrovní profilu. Účelom našej lekcie je preto obnoviť myšlienky o zmysle konceptu "logaritmu" a aktualizovať zručnosti na transformáciu logaritmických výrazov. Zapíšte si predmet lekcie v notebookoch.
IV. Aktualizáciu poznatkov.
1. / ORAL /Začať, pamätajte, čo sa nazýva logaritmus. (Slide 2)
(Logaritmus pozitívneho čísla B pre základňu A (kde A\u003e 0, AH? 1) sa nazýva indikátor stupňa, v ktorom je potrebné získať číslo A na získanie čísla B)
Log a b \u003d n<-> N \u003d b, (a\u003e 0, a 1, b\u003e 0)
Takže "LOGARITHM" je "indikátorom titulu"!
(Snímka 3) Potom je možné prepísať n \u003d b \u003d B je hlavnou logaritmickou identitou.
Ak je základňa \u003d 10, potom sa logaritmus nazýva desatinné a označované LGB.
Ak A \u003d E, potom sa logaritmus nazýva prirodzený a označuje LNB.
2. / písomné / (Slide 4)Vyplňte preskoky, aby ste získali vernú rovnosť:
Log? X + LOG A? \u003d Log? (? Y)
Log a? - log? Y \u003d log? (X /?)
Log a x? \u003d Plog? (?)
Skontrolujte:
jeden; jeden; A, Y, X; x, a, a, y; p, a, x.
Toto sú vlastnosti logaritmov. A tiež skupina vlastností: (Slide 5)
Skontrolujte:
a, 1, N, X; n, x, p, a; X, B, A, Y; A, X, B; A, 1, B.
V. Orálna práca
(Slide 6) №1. Vypočítajte:
a B C d) ; e).
Odpovede : A) 4; b) - 2; na 2; d) 7; e) 27.
(Slide 7) №2. Nájsť X:
ale) ; b) (odpovede: a) 1/4; b) 9).
Číslo 3. Má zmysel zvážiť takýto logaritmus:
ale) ; b); in)? (Nie)
Vi. Nezávislá práca v skupinách, silní učeníci - konzultanti. (Slide 8)
# 1. Vypočítajte: 
.
Č. 2. Zjednodušte:
# 3. Nájdite hodnotu výrazu, ak
№ 4. Zjednodušiť výraz: 
№ 5. Vypočítajte:
№ 6. Vypočítajte:№ 7. vypočítať:
8. Vypočítajte:
Po vykonaní - Kontrola a diskusiu o zbernom riešení alebo pomocou dokumentu - kamery.
VII. Riešenie úlohy zvýšenej zložitosti(Silný študent na palube, zvyšok - v notebookoch) (Slide 9)
Nájdite hodnotu výrazu:
VIII. Domáca úloha (na kartách) diferencovaných.(Slide 10)
№1. Vypočítajte: 
Uvedená rovnosť pri konverziách výrazov s logaritmmi sa používajú ako vpravo doľava a doľava doprava.
Stojí za zmienku, že zapamätať si účinky z vlastností je nepovinné: Pri vykonávaní transformácií je možné dosiahnuť s hlavnými vlastnosťami logaritmov a iných faktov (napríklad v tom, že s B \u003e0), z ktorých zodpovedajúca následky tok. "Bočný účinok" tohto prístupu sa prejavuje len na to, že rozhodnutie bude o niečo dlhšie. Napríklad bez vyšetrovania, ktorý je vyjadrený vzorcom 
A odpudzuje len z hlavných vlastností logaritmov, budete musieť vykonať reťazec transformácií nasledujúceho typu: 
.
To isté možno povedať o poslednej vlastnosti z vyššie uvedeného zoznamu, ktorý zodpovedá vzorec 
Pretože z hlavných vlastností logaritmov. Hlavná vec pochopiť, že vždy existuje možnosť pozitívneho čísla s logaritmom v indikátore na zmenu základu titulu a čísla pod znakom logaritmu. V záujme spravodlivosti sme všimli, že príklady, ktoré znamenajú implementáciu transformácií takéhoto druhu, sú v praxi zriedkavé. Dávame niekoľko príkladov pod textom.
Transformácia numerických výrazov s logaritmmi
Vlastnosti logaritmov si spomenuli, teraz je čas naučiť sa ich aplikovať v praxi, aby sa konvertovali výrazy. Prirodzene začať s transformáciou numerických výrazov, a nie výrazné s premennými, pretože sú pohodlnejšie a ľahšie poznať základy. Takže budeme robiť, a začať s veľmi jednoduchými príkladmi, aby sme sa naučili, ako si vybrať požadovanú vlastnosť logaritmu, ale budeme postupne komplikovať príklady, až do okamihu, keď potrebujete použiť niekoľko vlastností v rade, aby ste získali konečný výsledok.
Výber požadovaných vlastností logaritmov
Vlastnosti logaritmov nie sú také malé, a je jasné, že musíte vybrať z nich vhodné, ktoré v tomto konkrétnom prípade povedie k požadovanému výsledku. Zvyčajne je to ťažké, porovnávať typ transformovaného logaritmu alebo expresie s pohľady ľavého a pravého častí vzorcov, ktoré vyjadrujú vlastnosti logaritmov. Ak je ľavá alebo pravá strana jedného zo vzorcov zhoduje s daným logaritmom alebo výrazom, potom s najväčšou pravdepodobnosťou je to táto vlastnosť, ktorá je potrebné aplikovať pri konverzii. Nasledujúce príklady sú jasne preukázané.
Začnite s príkladmi konverzie výrazov pomocou definície logaritmu, ktorý zodpovedá vzorcu A Log A B \u003d B, A\u003e 0, A ≠ 1, B\u003e \u200b\u200b0.
Príklad.
Vypočítať, ak je to možné: a) 5 log 5 4, b) 10 lg (1 + 2 · π), b) 
, d) 2 log 2 (-7), e).
Rozhodnutie.
V príklade, pod písmenom A), štruktúra A BEB je jasne viditeľný, kde A \u003d 5, B \u003d 4. Tieto čísla spĺňajú podmienky A\u003e 0, A ≠ 1, B\u003e \u200b\u200b0, takže môžete použiť rovnosť a log a b \u003d b. Máme 5 log 5 4 \u003d 4.
b) tu A \u003d 10, B \u003d 1 + 2 · π, podmienky A\u003e 0, A ≠ 1, B\u003e \u200b\u200b0. V tomto prípade existuje rovnosť 10 LG (1 + 2 · π) \u003d 1 + 2 · π.
c) A v tomto príklade sa zaoberáme stupňom typu A Log A B, kde a B \u003d LN15. Tak 
.
Napriek patriacemu k rovnakému typu loga A B (tu A \u003d 2, B \u003d -7), expresia pod písmenom d) nie je možné konvertovať vzorcom A Log A B \u003d B. Dôvodom je, že nedáva zmysel, pretože obsahuje záporné číslo pod označením logaritmu. Okrem toho číslo B \u003d -7 nespĺňa podmienku B\u003e 0, ktorá neumožňuje uchýliť sa k vzorec A log A B \u003d B, pretože vyžaduje splnenie podmienok A\u003e 0, A ≠ 1, B \u003e 0. Takže nie je možné hovoriť o výpočte hodnoty 2 log 2 (-7). V tomto prípade bude nahrávanie 2 log 2 (-7) \u003d -7 chyba.
Podobne, v príklade podľa písmena d), nie je možné priviesť riešenie 
Od počiatočného výrazu nedáva zmysel.
Odpoveď:
a) 5 log 5 4 \u003d 4, b) 10 lg (1 + 2 · π) \u003d 1 + 2 · π, c) , d), e) výrazy nedávajú zmysel.
Často je užitočné pre konverziu, na ktorej je kladné číslo prezentované vo forme stupňa akéhokoľvek pozitívneho a odlišného čísla s logaritmom v indikátore. Je založený na rovnakej definícii logaritmu log a b \u003d b, a\u003e 0, a ≠ 1, b\u003e 0, ale vzorec sa aplikuje vpravo doľava, to znamená vo forme B \u003d log A B. Napríklad 3 \u003d E LN3 alebo 5 \u003d 5 LOG 5 5.
Previesť výrazy vlastností logaritmov na aplikáciu vlastností logaritmov.
Príklad.
Nájdite hodnotu výrazu: a) log -2 1, b) log 1, c) log 0 1, d) log 7 1, e) ln1, e) lg1, g) log 3,75, s) log 5 π 7 1.
Rozhodnutie.
V príkladoch pod písmenami a), b) a c) výrazy log -2 1, log 1 1, log 0 1, ktorý nemá zmysel, pretože na základni logaritmu by nemali byť záporné číslo, nula alebo jednotka, pretože sme určili logaritmus len pre pozitívne a odlišné od základnej jednotky. Preto v príkladoch A) - C) nie je možné nájsť hodnotu výrazu.
Vo všetkých ostatných úlohách je zrejmé, že existujú pozitívne a rôzne čísla z jednotky 7, E, 10, 3,75 a 5 π 7, a pod znakmi logaritmov všade sú jednotky. A poznáme vlastnosť jednotky logaritmu: Log A 1 \u003d 0 pre ľubovoľnú A\u003e 0, A ≠ 1. Hodnoty výrazov b) - e) sú teda rovné nule.
Odpoveď:
a), b), c) výrazy nemajú zmysel, d) log 7 1 \u003d 0, d) ln1 \u003d 0, e) lg1 \u003d 0, g) log 3,75 1 \u003d 0, h) log 5 · e 7 1 \u003d 0.
Príklad.
Vypočítať: a), b) lne, c) lg10, d) lOG 5 · 3 -2 (5 · 3 -2)e) log -3 (-3), e) log 1 1.
Rozhodnutie.
Je jasné, že musíme využiť vlastnosť logaritmu základne, ktorý zodpovedá protokolu vzorca A \u003d 1 pri A\u003e 0, A ≠ 1. V skutočnosti, v úlohách podľa všetkých písmen, číslo pod označením logaritmu sa zhoduje so svojím základom. Chcem teda okamžite povedať, že význam každej zo špecifikovaných výrazov je 1. Nie je však potrebné ponáhľať sa so závermi: v úlohách podľa písmen a) - d) hodnoty výrazov sú skutočne rovné jednej a v úlohách d) a e) počiatočné výrazy nerobia Zmysel, preto nemožno povedať, že hodnoty týchto výrazov sú 1.
Odpoveď:
a), b) lne \u003d 1, c) lg10 \u003d 1, d) log 5 π 3 -2 (5 · π 3 -2) \u003d 1, D), e) výrazy nedávajú zmysel.
Príklad.
Nájdite hodnotu: a) LOG 3 3 11, B) 
, c), d) log -10 (-10) 6.
Rozhodnutie.
Samozrejme, že pod známkami logaritmov sú niektoré stupne nadácie. Na základe toho chápeme, že je pre nás užitočný stupeň nadácie: log a p \u003d p, kde a\u003e 0, a ≠ 1 a p je akékoľvek platné číslo. Vzhľadom na to máme nasledovné výsledky: a) log 3 3 11 \u003d 11, b) 
v) 
. Je možné zaznamenať podobnú rovnosť pre príklad v písmene d) typu LOG \u200b\u200b-10 (-10) 6 \u003d 6? Nie, je to nemožné, pretože záznam expresie -10 (-10) 6 nedáva zmysel.
Odpoveď:
a) log 3 3 11 \u003d 11, b) v) , d) výraz nedáva zmysel.
Príklad.
Predstavte si výraz vo forme sumy alebo rozdielu logaritmov na rovnakom základe: a) 
, b), c) lg ((- 5) · (-12)).
Rozhodnutie.
a) Pod znalosťou logaritmu je práca, a poznáme vlastnosť logaritmu práce loga A (X · Y) \u003d log AX + LOG AY, A\u003e 0, A ≠ 1, X\u003e 0, Y\u003e 0. V našom prípade je číslo na základni logaritmu a číslo v práci pozitívne, to znamená, že spĺňa podmienky vybraného majetku, takže ho môžeme pokojne použiť: 
.
b) Tu používame majetok logaritmu súkromného, \u200b\u200bkde A\u003e 0, A ≠ 1, X\u003e 0, Y\u003e 0. V našom prípade je základom logaritmu kladným číslom E, čitateľ a menovateľ π sú pozitívne, čo znamená, že podmienky nehnuteľnosti spĺňajú, takže máme právo používať zvolený vzorec: 
.
c) Po prvé, všimneme si, že výraz LG ((- 5) · (-12)) dáva zmysel. Ale zároveň, pre neho nemáme právo aplikovať logaritmus vzorec práce protokolu A (x · y) \u003d log AX + LOG AY, A\u003e 0, A ≠ 1, X\u003e 0, Y\u003e 0, pretože čísla -5 a -12 - negatívne a nespĺňajú podmienky X\u003e 0, Y\u003e 0. To znamená, že takáto konverzia nie je možné vykonať: lG ((- 5) · (-12)) \u003d LG (-5) + LG (-12). A čo robiť? V takýchto prípadoch počiatočný výraz potrebuje predbežnú transformáciu, ktorá vám umožní dostať sa od negatívnych čísel. Budeme hovoriť o takýchto prípadoch transformácie výrazov s negatívnymi číslami pod znakom logaritmu podrobne v jednom z nasledujúcich príkladov, čo je zrozumiteľné a bez vysvetlenia: lG ((- 5) · (-12)) \u003d LG (5 · 12) \u003d LG5 + LG12.
Odpoveď:
ale) b) , c) lg ((- 5) · (-12)) \u003d LG5 + LG12.
Príklad.
Zjednodušte výraz: a) LOG 3 0,25 + LOG 3 16 + LOG 3 0,5, B).
Rozhodnutie.
Tu pomôžeme všetkým rovnakým vlastnostiam logaritmu práce a logaritmu súkromného, \u200b\u200bktoré sme použili v predchádzajúcich príkladoch, len teraz ich aplikujeme doprava doľava. To znamená, že množstvo logaritmov sa transformuje na logaritmus práce a rozdiel medzi logaritmmi - v logaritme súkromného. Mať
ale) lOG 3 0,25 + LOG 3 16 + LOG 3 0.5 \u003d LOG 3 (0,25 · 16 · 0,5) \u003d log 3 2.
b) 
.
Odpoveď:
ale) lOG 3 0.25 + LOG 3 16 + LOG 3 0.5 \u003d LOG 3 2b) 
.
Príklad.
Zbavte sa v rozsahu pod označením logaritmu: a) log 0,7 5 11, b) 
, c) log 3 (-5) 6.
Rozhodnutie.
Je ľahké vidieť, že sa zaoberáme výrazmi protokolu A B p. Zodpovedajúca vlastnosť logaritmu má druh log A B P \u003d P · Log A B, kde A\u003e 0, A ≠ 1, B\u003e \u200b\u200b0, P je akékoľvek platné číslo. To znamená, že pri vykonávaní podmienok A\u003e 0, A ≠ 1, B\u003e \u200b\u200b0 z logaritmu stupňa loga A B P, môžeme presunúť na produkt P · Log A B. Túto konverziu vykonáme so špecifikovanými výrazmi.
a) V tomto prípade A \u003d 0,7, B \u200b\u200b\u003d 5 a p \u003d 11. Takže log 0,7 5 11 \u003d 11 · log 0,7 5.
b) Uskutočňujú sa tu podmienky A\u003e 0, A ≠ 1, B\u003e \u200b\u200b0. teda 
c) Protokol expresie 3 (-5) 6 má rovnakú štruktúru log A B p, a \u003d 3, b \u003d -5, p \u003d 6. Ale pre B, stav B\u003e 0 nie je spokojný, čo znemožňuje používať log A B P \u003d P · Log A B. Takže nie je možné vyrovnať sa s úlohou? Je to možné, ale vyžaduje sa predbežná konverzia, budeme podrobne hovoriť nižšie v bode nadpisu. Rozhodnutie bude: log 3 (-5) 6 \u003d log 3 5 6 \u003d 6 · log 3 5.
Odpoveď:
a) log 0,7 5 11 \u003d 11 · log 0,7 5,
b)
c) log 3 (-5) 6 \u003d 6 · log 3 5.
Pomerne často, logaritmus vzorec stupňa počas transformácie je potrebné aplikovať právo naľavo ako p · log A B \u003d log A B P (to vyžaduje výkon rovnakých podmienok pre A, B a P). Napríklad 3 · LN5 \u003d LN5 3 a LG2 · LOG 2 3 \u003d LOG 2 3 LG2.
Príklad.
a) Vypočítajte hodnotu protokolu 2 5, ak je známe, že LG2≈0,3010 a LG5≈0,6990. b) Predložte frakciu vo forme logaritmu na základe 3.
Rozhodnutie.
a) Vzorec pre prechod na novú základňu logaritmu umožňuje tomuto logaritmu reprezentovať vo forme pomeru desatinných logaritmov, ktorých hodnoty sú pre nás známe :. Zostáva len na vykonávanie výpočtov, máme 
.
b) Tu stačí využiť prechod na novú základňu, a aplikovať ju na pravú ľavú, to znamená vo forme 
. Prijať 
.
Odpoveď:
a) log 2 5≈2,3223, B) .
V tomto štádiu sme dostatočne dôrazne považovali za konverziu najjednoduchších výrazov pomocou hlavných vlastností logaritmov a definíciu logaritmu. V týchto príkladoch sme museli použiť nejaký druh nehnuteľností a nič viac. Teraz s pokojným svedomím, môžete sa presunúť na príklady, ktorých transformácia vyžaduje použitie niekoľkých vlastností logaritmov a ďalších ďalších transformácií. Pôjdeme v nasledujúcom odseku. Ale predtým, že krátko sa stručne zameriame na príklady dôsledkov hlavných vlastností logaritmov.
Príklad.
a) zbaviť sa koreňa pod znakom logaritmu. b) Konvertovať frakciu v logaritme na základni 5. c) často od stupňov pod znakom logaritmu a vo svojom nadácii. d) Vypočítajte hodnotu výrazu 
. e) Vymeňte výraz titulu so základňou 3.
Rozhodnutie.
a) Ak si spomeniete na dôsledok majetku logaritmu 
Môžete okamžite odpovedať: 
.
b) Používame vzorec 
Práve vľavo 
.
c) V tomto prípade vedie výsledok vzorec . Prijať 
.
d) A tu stačí použiť preto, že vzorec je zodpovedný 
. Tak 
.
e) Logaritmus nehnuteľností Umožňuje nám dosiahnuť požadovaný výsledok: 
.
Odpoveď:
ale) . b) . v) 
. d) 
. e) .
Sekvenčné použitie viacerých vlastností
Skutočné úlohy pre transformáciu výrazov pomocou vlastností logaritmov sú zvyčajne komplikovanejšie tým, že sme zapojení do predchádzajúceho odseku. V ich pravidle nie je výsledok jedným krokom a riešenie je už v konzistentnom uplatňovaní jedného majetku po druhom, spolu s ďalšími transformáciami totožnosti, ako je napríklad zverejnenie zátvoriek, ktoré prinášajú podobné výrazy, zníženie frakcií atď. . Poďme sa bližšie k takýmto príkladom. V tom nie je nič ťažké, hlavná vec je konať úhľadne a dôsledne, dodržiavanie postupu vykonávania činností.
Príklad.
Vypočítajte hodnotu výrazu (Log 3 15-log 3 5) · 7 log 7 5.
Rozhodnutie.
Rozdiel logaritmov v zátvorkách pre majetok logaritmu súkromného môže byť nahradený logaritmovým logom 3 (15: 5), a ďalej vypočítať svoj log 3 (15: 5) \u003d log 3 \u003d 1. A hodnota expresie 7 log 7 5 podľa definície logaritmu sa rovná 5. Nahradiť tieto výsledky v pôvodnom výraze, dostaneme (log 3 15-log 3 5) · 7 log 7 5 \u003d 1 · 5 \u003d 5.
Uveďte riešenie bez vysvetlenia:
(Log 3 15-log 3 5) · 7 log 7 5 \u003d log 3 (15: 5) · 5 \u003d
\u003d log 3 3 · 5 \u003d 1 · 5 \u003d 5.
Odpoveď:
(log 3 15-log 3 5) · 7 log 7 5 \u003d 5.
Príklad.
Aká je hodnota numerického záznamu výrazu 3 log 2 2 3 -1?
Rozhodnutie.
Najprv transformujeme logaritmus, ktorý sa nachádza pod znakom logaritmu podľa logaritmu vzorec: log 2 2 3 \u003d 3. Tak, log 3 log 2 2 3 \u003d log 3 3 a ďalší protokol 3 \u003d 1. Takže log 3 log 2 2 -1 \u003d 1-1 \u003d 0.
Odpoveď:
log 3 log 2 2 3 -1 \u003d 0.
Príklad.
Zjednodušte výraz.
Rozhodnutie.
Prechodný vzorec na novú základňu logaritmu umožňuje vzťahu logaritmov na jednu základňu reprezentovať ako protokol 3 5. V tomto prípade bude počiatočný výraz tvoriť formulár. Podľa definície logaritmu 3 log 3 5 \u003d 5, to je 
A hodnota získanej expresie, vzhľadom na rovnakú definíciu logaritmu, je dva.
Tu je krátka verzia riešenia, ktorá je zvyčajne daná: 
.
Odpoveď:
.
Pre hladký prechod na nasledujúce informácie o položke sa pozrime na výrazy 5 2 + log 5 3 a LG0.01. Ich štruktúra nie je vhodná pre žiadne vlastnosti logaritmov. Takže čo sa stane, nemôžu byť prevedené pomocou vlastností logaritmov? Je možné, ak môžete vykonať predbežné transformácie, ktoré pripravujú tieto výrazy na aplikáciu vlastností logaritmov. Tak 5 2 + log 5 3 \u003d 5 2 · 5 log 5 3 \u003d 25 · 3 \u003d 75, 
a LG0.01 \u003d LG10 -2 \u003d -2. Potom budeme podrobne pochopiť, ako sa takéto školenie prejaví.
Príprava výrazov na aplikáciu vlastností logaritmov
Logaritmy v zložení transformovanej expresie sa veľmi často líšia od ľavej a pravej časti vzorcov zodpovedajúcich vlastnostiam logaritmov. Ale nie menej často transformácia týchto výrazov znamená použitie vlastností logaritmov: použiť ich len vyžadovať predbežnú prípravu. A tento prípravok je pri vykonávaní určitých rovnakých transformácií, ktoré vedú logaritmy k forme, vhodné na použitie vlastností.
V prípade spravodlivosti sme všimli, že takmer akékoľvek transformácie výrazov môžu pôsobiť ako predbežné transformácie, z banálneho pohonu takýchto podmienok na použitie trigonometrických vzorcov. Je to pochopiteľné, pretože transformované výrazy môžu obsahovať akékoľvek matematické objekty: konzol, moduly, frakcie, korene, stupne atď. Takže musíte byť pripravení vykonať akúkoľvek potrebnú konverziu, aby ste mohli používať vlastnosti logaritmov.
Poďme okamžite povedzme, že v tomto bode nestanovujeme úlohu na klasifikáciu a demontáž všetkých predstaviteľných predbežných transformácií, ktoré ďalej uplatňujú vlastnosti logaritmov alebo definíciu logaritmu. Tu budeme bývať len na štyroch z nich, ktoré sú najviac charakteristické a najčastejšie sa nachádza v praxi.
A teraz podrobne o každom z nich, potom, čo, ako súčasť našej témy, bude len zostať riešiť transformáciu výrazov s premennými pod znakmi logaritmov.
Výber stupňov pod znakom logaritmu a vo svojom nadácii
Začnime okamžite z príkladu. Buďme logaritmom. Je zrejmé, že v tomto podobe, jej štruktúra nemusí používať vlastnosti logaritmov. Je možné nejakým spôsobom previesť tento výraz na zjednodušenie, a ešte lepšie vypočítať jeho hodnotu? Ak chcete odpovedať na túto otázku, pozrime pozorne v číslach 81 a 1/9 v kontexte nášho príkladu. Je ľahké tu, aby tieto čísla umožňovali reprezentáciu stupňa čísla 3, skutočne 81 \u003d 3 4 a 1/9 \u003d 3 -2. V tomto prípade je počiatočný logaritmus prezentovaný vo forme a možnosť použitia vzorec . Tak, 
.
Analýza demontovaného príkladu vytvára nasledujúcu myšlienku: Ak je to možné, môžete sa pokúsiť zdôrazniť titul pod označením logaritmu a vo svojom nadácii uplatniť majetok logaritmu alebo jeho dôsledkom. Zostáva len zistiť, ako prideliť tieto stupne. Uveďte niekoľko odporúčaní k tejto otázke.
Niekedy je skôr zrejmé, že číslo pod označením logaritmu a / alebo vo svojom nadácii je niektoré z celého stupňa, ako je napríklad v tomto príklade. Prakticky sa neustále musí riešiť detekciou twos, ktoré boli dobre premyslené preč: 4 \u003d 2 2, 8 \u003d 2 3, 16 \u003d 2 4, 32 \u003d 2 5, 64 \u003d 2 6, 128 \u003d 2 7, 256 \u003d 2 8 , 512 \u003d 2 9, 1024 \u003d 2 10. To možno povedať o stupni trojitého: 9 \u003d 3 2, 27 \u003d 3 3, 81 \u003d 3 4, 243 \u003d 3 5, ... Všeobecne sa to neublíži, ak to bude pred našimi očami tabuľky prirodzených čísel v tucte. Nie je tiež ťažké pracovať s integrovanými stupňami desiatich, sto, tisíce atď.
Príklad.
Vypočítajte hodnotu alebo zjednodušiť výraz: a) log 616, b), c) log 0,000001 0.001.
Rozhodnutie.
a) Je zrejmé, že 216 \u003d 6 3, preto log 6 216 \u003d log 6 6 3 \u003d 3.
b) Tabuľka stupňov prírodných čísel vám umožňuje prezentovať čísla 343 a 1/243 vo forme stupňov 7 a 3 až 4, resp. Preto je možné sledovať nasledujúcu transformáciu daného logaritmu: 
c) ako 0,000001 \u003d 10-6 a 0,001 \u003d 10 -3, potom lOG 0,000001 0,001 \u003d LOG 10 -6 10 -3 \u003d (- 3) / (- 6) \u003d 1/2.
Odpoveď:
a) log 6 216 \u003d 3, b) 
, c) log 0,000001 0,001 \u003d 1/2.
V zložitejších prípadoch zdôrazniť stupne čísel sa musia uchýliť.
Príklad.
Konvertovať výraz do jednoduchšieho typu log 3 648 · log 2 3.
Rozhodnutie.
Pozrime sa, čo je rozklad čísla 648 na jednoduché faktory:
To znamená 648 \u003d 2 3 · 3 4. Touto cestou, lOG 3 648 · LOG 2 3 \u003d LOG 3 (2 3 · 3 4) · LOG 2 3.
Teraz sa logaritmus diel transformuje do množstva logaritmov, po ktorých sú použiteľné vlastnosti logaritmu stupňa:
lOG 3 (2 3 · 3 4) · LOG 2 3 \u003d (LOG 3 2 3 + LOG 3 3 4) · LOG 2 3 \u003d
\u003d (3 · LOG 3 2 + 4) · LOG 2 3.
Vzhľadom na vyšetrovanie z majetku logaritmu, ku ktorému je vzorec zodpovedný Log32 · Log23 je práca, a je známe, že je jedna. Vzhľadom k tomu, dostaneme 3 · LOG 3 2 · LOG 2 3 + 4 · LOG 2 3 \u003d 3 · 1 + 4 · LOG 2 3 \u003d 3 + 4 · LOG 2 3.
Odpoveď:
lOG 3 648 · LOG 2 3 \u003d 3 + 4 · LOG 2 3.
Pomerne často, výrazy v rámci znamenia logaritmu a vo svojom nadácii sú diela alebo pomery koreňov a / alebo stupňov niektorých čísel, napríklad. Takéto výrazy môžu byť zastúpené ako stupeň. Pre toto, prechod z koreňov do stupňov a aplikovaný. Tieto konverzie vám umožňujú zvýrazniť stupne pod znakom logaritmu av jeho základni, po ktorom aplikujete vlastnosti logaritmov.
Príklad.
Vypočítať: a) 
, b).
Rozhodnutie.
a) Výraz na základni logaritmu je produktom stupňov s rovnakými základňami, podľa príslušnej vlastnosti stupňov, máme 5 2 · 5 -0,5 · 5 -1 \u003d 5 2-0,5-1 \u003d 5 0,5.
Teraz transformujeme frakciu pod znakom logaritmu: Obraciame sa z koreňa do titulu, po ktorom budeme používať majetok stupňov s týmito dôvodmi: 
.
Zostáva nahradiť výsledky získané do počiatočného výrazu, použite vzorec a dokončiť transformácie: 
b) Od 729 \u003d 3 6, 1/9 \u003d 3 -2, potom môže byť počiatočná expresia prepísaná vo forme.
Ďalej aplikujte vlastnosť koreňa zo stupňa, vykonávame prechod z koreňa do titulu a použijeme vlastnosť pomeru stupňa na prevod logaritmu do stupňa: 
.
Vzhľadom na posledný výsledok máme 
.
Odpoveď:
ale) 
, b).
Je jasné, že vo všeobecnosti získať tituly pod znakom logaritmu a vo svojom nadácii môžu byť potrebné rôzne transformácie rôznych výrazov. Dávame niekoľko príkladov.
Príklad.
Aká je hodnota výrazu: a) 
b) 
.
Rozhodnutie.
Preto sme si všimli, že špecifikovaná expresia má formu protokolu A B P, kde A \u003d 2, B \u003d X + 1 a P \u003d 4. Číselné výrazy takého druhu sme boli konvertované vlastnosťou logaritmu rozsahu rozsahu log ABP \u003d P · Log AB, preto, s daným výrazom, chcem urobiť to isté ako, a z log 2 (x + 1) 4 Prejdite na 4 · LOG 2 (X + 1). A teraz vypočítajme hodnotu počiatočného výrazu a expresiu získanú po transformácii, napríklad s X \u003d -2. Majú log 2 (-2 + 1) 4 \u003d log 2 1 \u003d 0, a 4 · LOG 2 (-2 + 1) \u003d 4 · LOG 2 (-1) - neznamená to výraz. To spôsobuje prirodzenú otázku: "Čo sme urobili zle"?
A Dôvod je nasledovný: Vykonali sme transformačný protokol 2 (X + 1) 4 \u003d 4 · Log 2 (X + 1), na základe protokolu vzorca ABP \u003d P · Log AB, ale máme právo aplikovať Vzorec len ak podmienka A\u003e 0, A ≠ 1, B\u003e \u200b\u200b0, P - akékoľvek platné číslo. To znamená, že konverzia vykonaná nami prebieha, ak x + 1\u003e 0, čo je rovnaké x\u003e -1 (pre A a P - sú vyrobené podmienky). V našom prípade však variabilný X pre počiatočnú expresiu pozostáva nielen z intervalu X\u003e -1, ale aj z obdobia X<−1 . Но для x<−1 мы не имели права осуществлять преобразование по выбранной формуле.
Potreba zohľadniť ...
Budeme naďalej rozoberať transformáciu log 2 (X + 1) 4 Vybrané výrazy podľa nás, a teraz sa pozrime, čo sa stane s OTZ pri prechode k výrazu 4 · log 2 (x + 1). V predchádzajúcom odseku sme zistili aj výraz zdroj - toto je set (-∞, -1) ∪ (-1, + ∞). Teraz nájdeme oblasť prípustných hodnôt premennej X pre výraz 4 · log 2 (X + 1). Je určený podmienkou x + 1\u003e 0, čo zodpovedá nastavenej (-1, + ∞). Samozrejme, keď sa pohybuje z log 2 (x + 1) 4 až 4 · log 2 (x + 1), nastáva oblasť platných hodnôt. A súhlasili sme, že sa vyhnú transformáciám, ktoré vedú k zúženiu OTZ, pretože to môže viesť k rôznym negatívnym dôsledkom.
Treba tu zaznamenať, že je užitočné kontrolovať OTZ pri každom kroku transformácie a zabrániť jeho zúženiu. A ak sa náhle, v určitom štádiu transformácie, tam bolo zúženie OST, potom stojí za to vyzerať veľmi opatrne a či je táto transformácia prípustná a či máme právo na jeho vykonanie.
Povedzme napríklad, že v praxi je zvyčajne potrebné pracovať s výrazmi, ktorého premenné OTZ sú také, že pri vykonávaní transformácií používajú vlastnosti logaritmov bez obmedzení vo forme, na ktoré sa s nami, a obaja zľava na vpravo a doprava doľava. Rýchlo si na to zvyknete, a začnete vykonávať transformácie mechanicky, bez myslenia a či je možné ich viesť. A pri takýchto momentoch, ako sú vypúšťané, páčko komplexnejšie príklady, v ktorých sa neprístupné používanie vlastností logaritmov vedie k chybám. Takže musíte byť vždy na kontrole a sledujte, že neexistuje žiadny zúženie OTZ.
To neublíži samostatne vybrať hlavné transformácie na základe vlastností logaritmov, ktoré je potrebné vykonať veľmi opatrne, čo môže viesť k zúženiu OTZ, a ako výsledok - na chyby:
Niektoré transformácie výrazov podľa vlastností logaritmov môžu viesť k inverznému expanzii OTZ. Napríklad prechod od 4 · log 2 (x + 1) na log 2 (x + 1) 4 rozširuje nepárne zo set (-1, + ∞) na (-∞, -1) ∪ (-1, + ∞). Takéto transformácie sa vyskytujú, ak zostanú v rámci ODZD pre počiatočnú expresiu. Takže jediná uvedená konverzia 4 · log 2 (x + 1) \u003d log 2 (x + 1) 4 prebieha na premennej OTZ X pre pôvodný výraz 4 · Log 2 (X + 1), to znamená s X + 1\u003e 0, čo je rovnaké (-1, + ∞).
Teraz, o ktorom sme diskutovali o nuans, pre ktoré potrebujete venovať pozornosť pri konverzii výrazov s premennými pomocou vlastností logaritmov, zostáva zistiť, ako správne tieto transformácie musia vykonať.
X + 2\u003e 0. Pracuje v našom prípade? Ak chcete odpovedať na túto otázku, pozrite sa na premennú OTZ X. Je určený systémom nerovnosti 
ktorý je ekvivalentný stavu x + 2\u003e 0 (ak je to potrebné, pozri článok riešenie systémov nerovnosti). Môžeme teda pokojne aplikovať vlastnosť logarithm.
Mať
3 · LG (X + 2) 7-gg (X + 2) -5 · LG (X + 2) 4 \u003d
\u003d 3,7 · LG (X + 2) -LG (X + 2) -5 · 4 · LG (X + 2) \u003d
\u003d 21 · LG (X + 2) -LG (X + 2) -20 · LG (X + 2) \u003d
\u003d (21-1-20) · LG (x + 2) \u003d 0.
Môžete konať a inak, výhoda OTZ umožňuje, napríklad: 
Odpoveď:
3 · lg (x + 2) 7-gg (x + 2) -5 · lg (x + 2) 4 \u003d 0.
A čo robiť, keď nie sú splnené podmienky pre sprievodné vlastnosti logaritmov? Budeme sa s tým zaoberať príkladmi.
Predpokladajme od nás, aby ste zjednodušili expresiu LG (X + 2) 4-gg (X + 2) 2. Transformácia tohto výrazu, na rozdiel od expresie z predchádzajúceho príkladu, neumožňuje protokolu logaritmu. Prečo? Premenná OTZ X V tomto prípade je kombinácia dvoch medzier x\u003e -2 a x<−2 . При x>-2 Môžeme pokojne aplikovať majetok logaritmu a konať ako rozobraté vyššie: lG (X + 2) 4-grg (X + 2) 2 \u003d 4 · LG (X + 2) -2 · LG (X + 2) \u003d 2 · LG (X + 2). Ale OTZ obsahuje ďalšie obdobie x + 2<0 , для которого последнее преобразование будет некорректно. Что же делать при x+2<0 ? В подобных случаях на помощь приходит . Определение модуля позволяет выражение x+2 при x+2<0 представить как −|x+2| . Тогда при x+2<0 от lg(x+2) 4 −lg(x+2) 2 переходим к lg (- | x + 2 |) 4-gg (- | x + 2 |) 2 A ďalej silou vlastností stupňa LG | X + 2 | 4 -LG | X + 2 | 2. Výsledný výraz môže byť konvertovaný vlastnosťou logaritmu, pretože X + 2 |\u003e 0 pre všetky hodnoty premennej. Mať lg | x + 2 4 -LG | X + 2 | 2 \u003d 4 · LG | X + 2 | -2 · LG | X + 2 | \u003d 2 · LG | X + 2 |. Teraz sa môžete oslobodiť od modulu, ako to urobil svoju prácu. Vzhľadom k tomu, že vykonávame konverziu na x + 2<0 , то 2·lg|x+2|=2·lg(−(x+2)) . Итак, можно считать, что мы справились с поставленной задачей. Ответ: . Полученный результат можно записать компактно с использованием модуля как .
Zvážte ďalší príklad, aby sa práca s modulmi zoznámili. Nechceme počítať od výrazu 
Prejdite na súčet a rozdiel medzi logaritmmi lineárneho bodu X-1, X-2 a X-3. Najprv nájdeme ... 
V intervale (3, + ∞) sú hodnoty výrazov X-1, X-2 a X-3 pozitívne, takže pokojne aplikujeme vlastnosti logaritmu súm a rozdielov: 
A v intervale (1, 2) sú hodnoty expresie X-1 pozitívne a hodnoty výrazov X-2 a X-3 sú negatívne. Preto v posudzovanom intervale predstavujeme X-2 a X-3 pomocou modulu ako - X-2 | a - | X-3 | resp. Kde 
Teraz môžete použiť vlastnosti logaritmu práce a súkromného, \u200b\u200bpretože je na intervale (1, 2) hodnoty výrazov X-1, | X-2 | a | X-3 | - pozitívne.
Mať 
Výsledky môžu byť kombinované:
Všeobecne platí, že podobné argumenty umožňujú logaritmu vzorce na základe logaritmu, vzťahov a stupňov, aby získali tri prakticky užitočné výsledky, ktoré sú pomerne vhodné na použitie:
- Logarithmové diela dvoch ľubovoľných výrazov X a Y typu Log A (X · Y) môžu byť nahradené sodnými logaritms log A | X | + Log A | Y | , A\u003e 0, A ≠ 1.
- Logarithm Private Log A (X: Y) môže byť nahradený rozdielom medzi logaritms log A | X | -log A | Y | ,\u003e 0, A ≠ 1, X a Y - ľubovoľné výrazy.
- Z logaritmu nejakej expresie B v rovnomernom stupni p prihlášku A B P Forma môžete prejsť na výraz p · log A | B | , kde A\u003e 0, A ≠ 1, P je párne číslo a B - ľubovoľný výraz.
Podobné výsledky sú uvedené napríklad v pokynoch na riešenie indikatívnych a logaritmických rovníc v zbierke problémov v matematike pre žiadateľov na univerzity pod editormi M. I. Scaavi.
Príklad.
Zjednodušiť výraz 
.
Rozhodnutie.
Bolo by dobré aplikovať vlastnosti logaritmu, množstva a rozdielov. Ale môžeme to urobiť? Ak chcete odpovedať na túto otázku, potrebujeme vedieť OTZ.
Definujeme ho: 
Je dosť zrejmé, že výrazy x + 4, X-2 a (x + 4) 13 na hodnotách prípustných hodnôt premennej X môžu mať pozitívne aj záporné hodnoty. Preto budeme musieť konať prostredníctvom modulov. 
Vlastnosti modulu vám umožňujú prepísať ako, teda 
Tiež nič nezabraňuje majetku systému logaritmu, potom prinesie podobné výrazy na: 
Druhý postup transformácií vedie k rovnakému výsledku: 
A keďže výraz X-2 môže mať pozitívne aj záporné hodnoty, potom pri odosielaní rovnomernej miery 14
Úlohy, ktorých riešenie leží transformácia logaritmických výrazov, často sa stretávajú na skúške.
Ak chcete úspešne vyrovnať s nimi v minimálnom čase okrem hlavných logaritmických identít, musíte vedieť a správne používať niektoré vzorce.
To je: log A B \u003d B, kde A, B\u003e 0 a ≠ 1 (priamo z definície logaritmu).
log a b \u003d log s b / log s A alebo log a b \u003d 1 / log b a
kde A, B, C\u003e 0; A, C ≠ 1.
log a m b n \u003d (m / n) log | A | | B |
kde A, B\u003e 0, A ≠ 1, M, N є R, N ≠ 0.
a log s b \u003d b logom s a
kde A, B, C\u003e 0 a A, B, S ≠ 1
Ak chcete ukázať spravodlivosť štvrtej rovnosti, prohom doľava a pravej strane A. Dostávame log a (a log s b) \u003d log a (b log s a) alebo log s b \u003d log s · log A B; log s b \u003d log s · (log s b / log s a); Prihláste sa s b \u003d log s b.
Ukázali sme rovnosť logaritmov, čo znamená rovné výrazom v logaritmoch. Ukázalo sa, že vzorec 4.
Príklad 1.
Vypočítajte 81 LOG 27 5 LOG 5 4.
Rozhodnutie.
81 = 3 4 , 27 = 3 3 .
log 27 5 \u003d 1/3 log 3 5, log 5 4 \u003d log 3 4 / log 3 5. V dôsledku toho
lOG 27 5 · LOG 5 4 \u003d 1/3 LOG 3 5 · (log 3 4 / log 3 5) \u003d 1/3 log 3 4.
Potom 81 log 27 5 log 5 4 \u003d (3 4) 1/3 log 3 4 \u003d (3 log 3 4) 4/3 \u003d (4) 4/3 \u003d 4 3 √4.
Môžete nezávisle vykonávať nasledujúcu úlohu.
Vypočítajte (8 log 2 3 + 3 1 / log 2 3) - log 0.2 5.
Ako hrot 0,2 \u003d 1/5 \u003d 5 -1; Log 0,2 5 \u003d -1.
Odpoveď: 5.
Príklad 2.
Vypočítať (√11) log. √3 9- LOG 121 81.
Rozhodnutie.
Vykonajte výmenu výrazov: 9 \u003d 3 2, √3 \u003d 3 1/2, log √3 9 \u003d 4,
121 \u003d 11 2, 81 \u003d 3 4, LOG 121 81 \u003d 2 LOG 11 3 (vzorec 3 bol použitý).
Potom (√11) log √3 9- log 121 81 \u003d (11 1/2) 4-2 LOG 11 3 \u003d (11) 2- LOG 11 3 \u003d 11 2 / (11) LOG 11 3 \u003d 11 2 / ( 11 LOG 11 3) \u003d 121/3.
Príklad 3.
Vypočítať protokol 2 24 / log 96 2- log 2 192 / log 12 2.
Rozhodnutie.
Logaritmy obsiahnuté v príklade, vymeňte logaritmy so základňou 2.
log 96 2 \u003d 1 / log 2 96 \u003d 1 / log 2 (2 5 · 3) \u003d 1 / (log 2 2 5 + log 2 3) \u003d 1 / (5 + log 2 3);
log 2 192 \u003d log 2 (2 6 · 3) \u003d (log 2 2 6 + log 2 3) \u003d (6 + log 2 3);
log 2 24 \u003d log 2 (2 3 · 3) \u003d (log 2 2 3 + log 2 3) \u003d (3 + log 2 3);
lOG 12 2 \u003d 1 / LOG 2 12 \u003d 1 / LOG 2 (2 2 · 3) \u003d 1 / (log 2 2 2 + log 2 3) \u003d 1 / (2 + log 2 3).
Potom log 2 24 / log 96 2 - log 2 192 / log 12 2 \u003d (3 + log 2 3) / (1 / (5 + log 2 3)) - ((6 + log 2 3) / (1 / ( 2 + log 2 3) \u003d
\u003d (3 + log 2 3) · (5 + log 2 3) - (6 + log 2 3) (2 + log 2 3).
Po zverejnení zátvoriek a prinášame podobné výrazy, získame číslo 3. (so zjednodušením výrazu, log 2 3 môže označiť cez N a zjednodušiť výraz
(3 + n) · (5 + n) - (6 + n) (2 + n)).
Odpoveď: 3.
Môžete nezávisle vykonávať nasledujúcu úlohu:
Vypočítajte (log 3 4 + log 4 3 + 2) · LOG 3 16 · LOG 2 144 3.
Tu je potrebné vykonať prechod na logaritmy na základe 3 a rozkladu na jednoduchých multiplikátoroch veľkého počtu.
Odpoveď: 1/2
Príklad 4.
Tri čísla A \u003d 1 / (log 3 0,5), b \u003d 1 / (log 0,5 3), c \u003d log 0,5 12 - log 0,5 3. Umiestnite ich do vzostupného poradia.
Rozhodnutie.
Transformujeme čísla A \u003d 1 / (log 3 0,5) \u003d log 0,5 3; C \u003d log 0,5 12 - log 0,5 3 \u003d log 0,5 12/3 \u003d log 0,5 4 \u003d -2.
Porovnať ich
log 0,5 3\u003e log 0,5 4 \u003d -2 a log 0,5 3< -1 = log 0,5 2, так как функция у = log 0,5 х – убывающая.
Alebo 2< log 0,5 3 < -1. Тогда -1 < 1/(log 0,5 3) < -1/2.
Odpoveď. V dôsledku toho postup uvádzania čísel: c; ALE; V.
Príklad 5.
Koľko celé čísla sa nachádza v intervale (log 3 1/16; log 2 6 48).
Rozhodnutie.
Definujeme medzi akým stupňami čísla 3 je číslo 1/16. Dostaneme 1/27< 1 / 16 < 1 / 9 .
Vzhľadom k tomu, funkcia y \u003d log 3 x sa zvyšuje, potom protokol 3 (1/2 27)< log 3 (1 / 16) < log 3 (1 / 9); -3 < log 3 (1 / 16) < -2.
log 6 48 \u003d log 6 (36 · 4/3) \u003d log 6 36 + log 6 (4/3) \u003d 2 + log 6 (4/3). Porovnať log 6 (4/3) a 1/5. A na to porovnajte čísla 4/3 a 6 1/5. Postavili obe čísla v 5 stupňoch. Získame (4/3) 5 \u003d 1024/243 \u003d 4 52/243< 6. Следовательно,
log 6 (4/3)< 1 / 5 . 2 < log 6 48 < 2 1 / 5 . Числа, входящие в двойное неравенство, положительные. Их можно возводить в квадрат. Знаки неравенства при этом не изменятся. Тогда 4 < log 6 2 48 < 4 21 / 25.
V dôsledku toho interval (log 3 1/16; log 6 48) zahŕňa interval [-2; 4] a celé čísla sú umiestnené na ňom; -Vyberte; 0; jeden; 2; 3; štyri.
Odpoveď: 7 celé čísla.
Príklad 6.
Vypočítajte 3 LGGLG 2 / LG 3 - LG20.
Rozhodnutie.
3 LG LG2 / LG3 \u003d (3 1 / LG3) LG LG2 \u003d (3 LOG 3 10) LG LG2 \u003d 10 LG LG2 \u003d LG2.
Potom 3 LGLG2 / LG3 - LG 20 \u003d LG 2 - LG 20 \u003d LG 0,1 \u003d -1.
Odpoveď: -1.
Príklad 7.
Je známe, že log 2 (√3 + 1) + log 2 (√6 - 2) \u003d A. Nájsť log 2 (√3 -1) + log 2 (√6 + 2).
Rozhodnutie.
Čísla (√3 + 1) a (√3 - 1); (√6 - 2) a (√6 + 2) - konjugát.
Vykonáme nasledujúcu transformáciu výrazov
√3 - 1 \u003d (√3 - 1) · (√3 + 1)) / (√3 + 1) \u003d 2 / (√3 + 1);
√6 + 2 \u003d (√6 + 2) · (√6 - 2)) / (√6 - 2) \u003d 2 / (√6 - 2).
Potom protokol 2 (√3 - 1) + log 2 (√6 + 2) \u003d log 2 (2 / (√3 + 1)) + log 2 (2 / (√6 - 2)) \u003d
Log 2 2 - log 2 (√3 + 1) + log 2 2 - log 2 (√6 - 2) \u003d 1 - log 2 (√3 + 1) + 1 - log 2 (√6 - 2) \u003d
2 - log 2 (√3 + 1) - log 2 (√6 - 2) \u003d 2 - A.
Odpoveď: 2 - A.
Príklad 8..
Zjednodušte a nájdite približnú hodnotu výrazu (log 3 2 · log 4 3 · log 5 4 · log 6 5 · · log 10 9.
Rozhodnutie.
Všetky logaritmy dávame celkovú základňu 10.
(LOG 3 2 · LOG 4 3 · LOG 5 4 · LOG 6 5 · ... · LOG 10 9 \u003d (LG 2 / LG 3) · (LG 3 / LG 4) · (LG 4 / LG 5) · LG 5 / LG 6) · ... · (LG 8 / LG 9) · LG 9 \u003d LG 2 ≈ 0,3010. (Približná hodnota LG 2 možno nájsť pomocou tabuľky, logaritmickej čiary alebo kalkulačky).
Odpoveď: 0,3010.
Príklad 9..
Vypočítajte protokol A 2 B 3 √ (A 11 B -3) Ak Log √ A B3 \u003d 1. (v tomto príklade a 2 B3 je základom logaritmu).
Rozhodnutie.
Ak log √ a b3 \u003d 1, potom 3 / (0,5 log A B \u003d 1. a log A B \u003d 1/6.
Potom sa denník A2 B3√ \u003d 1/2 Log A2 B3 (A 11 B -3) \u003d Log A (A 11 B -3) / (2LOG A (A2 B3) ) \u003d (Log AA 11 + LOG AB -3) / (2 (LOG A AA 2 + LOG AB 3)) \u003d (11 - 3LOG AB) / (2 (2 + 3LOG AB)) Vzhľadom na to, že protokol A B \u003d Získa sa 1/6 (11 - 3 · 1/6) / (2 (2 + 3 · 1/6)) \u003d 10,5 / 5 \u003d 2.1.
Odpoveď: 2.1.
Môžete nezávisle vykonávať nasledujúcu úlohu:
Vypočítajte log √3 6 √2.1 Ak log 0,7 27 \u003d a.
Odpoveď: (3 + A) / (3a).
Príklad 10.
Vypočítajte 6,5 4 / log 3 169 · 3 1 / log 4 13 + log125.
Rozhodnutie.
6.5 4 / log 3 169 · 3 1 / log 4 13 + log 125 \u003d (13/2) 4/2 log 3 13 · 3 2 / log 2 13 + 2log 5 5 3 \u003d (13/2) 2 log 13 3 · 3 2 log 13 2 + 6 \u003d (13 log 13 3/2 log 13 3) 2 · (3 log 13 2) 2 + 6 \u003d (3/2 log 13 3) 2 · (3 log 13 2) 2 + 6 \u003d (3 2 / (2 log 13 3) 2) · (2 \u200b\u200blog 13 3) 2 + 6.
(2 log 13 3 \u003d 3 log 13 2 (vzorca 4))
Získame 9 + 6 \u003d 15.
Odpoveď: 15.
Máte otázky? Neviem, ako nájsť hodnotu logaritmického výrazu?
Ak chcete získať pomocníka - zaregistrujte sa.
Prvá lekcia je zadarmo!
miesto, s plným alebo čiastočným kopírovaním materiálu odkazu na pôvodný zdroj.
Logaritmické výrazy, riešenie príkladov. V tomto článku zvážime úlohy spojené s riešením logaritmov. Úlohy vyvoláva otázku zistenia hodnoty výrazu. Treba poznamenať, že koncepcia logaritmu sa používa v mnohých úlohách a pochopí jeho význam je nesmierne dôležitý. Pokiaľ ide o používanie, logaritmus sa používa pri riešení rovníc v aplikovaných úlohách, a to aj v úlohách spojených so štúdiou funkcií.
Dávame príklady pochopiť zmysel pre logaritmus:
Základná logaritmická identita:
Vlastnosti logaritmov, ktoré sa musia vždy pamätať:
* Logaritmus práce sa rovná súčtu logaritmov faktorov.
* * *
* Súkromný logaritmus (frakcia) sa rovná rozdielu v logaritmoch faktorov.
* * *
* Logaritmus sa rovná produktu stupňa v logaritme jej základne.
* * *
* Prechod na novú základňu
* * *
Viac vlastností:
* * *
Výpočet logaritmov úzko súvisí s používaním vlastností indikátorov stupňa.
Uveďte niektoré z nich:
Podstatou tejto nehnuteľnosti je, že pri prenose čitateľa na denominátor a naopak, indikátor sa zmení na opačnom mieste. Napríklad:
Dôsledkom tejto nehnuteľnosti:
* * *
Pri zostavovaní stupňa do určitej miery zostáva základ rovnaký a indikátory sú variabilné.
* * *
Ako ste videli veľmi koncepciu logaritmu jednoduchého. Hlavná vec je, že je potrebná dobrá prax, ktorá dáva určité zručnosti. Samozrejme, znalosť vzorcov musia. Ak sa zručnosť v konverzii elementárnych logaritmov nie je vytvorená, potom pri riešení jednoduchých úloh môžete ľahko umožniť chybu.
Prax, rozhodnúť o prvé najjednoduchšie príklady z priebehu matematiky, potom ísť do zložitejšieho. V budúcnosti určite ukážem, ako sa vyriešia "hrozné" logaritmy, na skúške nie sú žiadne takéto také, ale sú zaujímavé, nenechajte si ujsť!
To je všetko! Úspech pre vás!
S pozdravom, Alexander Krutitsky
P.S: Budem vďačný, ak hovoríte o stránke o sociálnych sieťach.
Logaritmy, ako všetky čísla, môžu byť zložené, odpočítať a konvertovať. Ale pretože logaritmy nie sú celkom bežné čísla, sú tu vlastné pravidlá, ktoré sa nazývajú základné vlastnosti.
Tieto pravidlá musia nevyhnutne poznať - bez nich sa nevyrieši žiadna vážna logaritmická úloha. Okrem toho sú dosť trochu - všetko sa dá naučiť za jeden deň. Pokračujte.
Pridanie a odčítanie logaritmov
Zvážte dva logaritmus s rovnakými základňami: a. x. a denník. a. y.. Potom môžu byť zložené a odpočítané a:
- log. a. x. + Denník. a. y. \u003d Log. a. (x. · y.);
- log. a. x. - Denník. a. y. \u003d Log. a. (x. : y.).
Množstvo logaritmov je teda rovná logaritmu práce a rozdiel je logaritmom súkromného. Upozornenie: Kľúčový bod tu je rovnaké dôvody. Ak sú základy iné, tieto pravidlá nefungujú!
Tieto vzorce pomôžu vypočítať logaritmický výraz, aj keď nie sú zvažované jednotlivé časti (pozri lekciu "Čo je logaritmus"). Pozrite sa na príklady - a uistite sa, že:
LOG 6 4 + LOG 6 9.
Vzhľadom k tomu, základy v logaritmoch sú rovnaké, používame sumu sumy:
log 6 4 + log 6 9 \u003d log 6 (4 · 9) \u003d log 6 36 \u003d 2.
Úloha. Nájdite hodnotu výrazu: log 2 48 - log 2 3.
Základy sú rovnaké, pomocou rozdielu vzorec:
lOG 2 48 - LOG 2 3 \u003d LOG 2 (48: 3) \u003d LOG 2 16 \u003d 4.
Úloha. Nájdite hodnotu výrazu: log 3 135 - log 3 5.
Opäť základy sú rovnaké, takže máme:
log 3 135 - log 3 5 \u003d log 3 (135: 5) \u003d log 3 27 \u003d 3.
Ako vidíte, počiatočné výrazy sa skladajú z "zlých" logaritmov, ktoré nie sú oddelene považované za samostatne. Ale po transformácii sa získajú celkom normálne čísla. V tejto skutočnosti sú postavené mnoho testovacích prác. Aká je však kontrola - takéto výrazy sú v plnom rozsahu (niekedy - takmer nezmenené) sú ponúkané na skúške.
Výkonný stupeň z logaritmu
Teraz trochu komplikuje úlohu. Čo ak na základni alebo argumenty logaritmu stojí titul? Potom môže byť indikátor tohto rozsahu vyňatý z označenia logaritmu podľa nasledujúcich pravidiel:
Je ľahké vidieť, že posledné pravidlo sleduje ich prvé dve. Je však lepšie si to pamätať, v niektorých prípadoch to výrazne zníži množstvo výpočtov.
Samozrejme, že všetky tieto pravidlá majú zmysel, ak sú zhodné s logaritmom OTZ: a. > 0, a. ≠ 1, x. \u003e 0. A tiež: Naučte sa aplikovať všetky vzorce nielen zľava doprava, ale naopak, t.j. Môžete vytvoriť čísla s logaritmom, na samotný logaritmus. Najčastejšie sa vyžaduje.
Úloha. Nájdite hodnotu výrazu: log 7 49 6.
Zbavte sa v rozsahu v argumente v prvom vzorci:
lOG 7 49 6 \u003d 6 · LOG 7 49 \u003d 6 · 2 \u003d 12
Úloha. Nájdite hodnotu výrazu:
[Podpis na obrázok]
Všimnite si, že v denominátore je logaritmus, základňa a argument, z ktorých sú presné stupne: 16 \u003d 2 4; 49 \u003d 7 2. Máme:
[Podpis na obrázok] Myslím, že posledný príklad si vyžaduje vysvetlenie. Kde sa logaritmy zmizli? Až do posledného momentu pracujeme len s menovateľom. Prezentovali základ a argumenty logaritmu tam vo forme titulov a vykonávali indikátory - dostali "trojposchodovú" frakciu.
Pozrime sa na základnú frakciu. Číslo v čísla a menovateľ je rovnaký počet: log 2 7. Keďže protokol 2 7 ≠ 0, môžeme znížiť frakciu - 2/4 zostane v denominátori. Podľa pravidiel aritmetiky môžu byť štyri prenesené na nuterátor, ktorý bol vykonaný. Výsledkom bola odpoveď: 2.
Prechod na novú základňu
Hovoriť o pravidlách pridávania a odpočítania logaritmov, konkrétne som zdôraznil, že pracujú len s rovnakými základňami. A čo ak sa základy líšia? Čo ak nie sú presné stupne rovnakého čísla?
Formuláry pre prechod na novú základňu prichádzajú na záchranu. Vyvolávame ich vo forme teoremity:
Nechajte logaritmus log a. x.. Potom pre ľubovoľné číslo c. také, že c. \u003e 0 I. c. ≠ 1, skutočná rovnosť:
[Podpis na obrázok]
Najmä, ak ste dali c. = x.Dostaneme:
[Podpis na obrázok]
Z druhého vzorca vyplýva, že základňa a argument logaritmu možno zmeniť na miestach, ale zároveň výraz "otočí", t.j. Logaritmus sa ukáže, že je v denominátori.
Tieto vzorce sú zriedkavé v bežných numerických výrazoch. Posúdenie toho, aké pohodlné sú, je možné len pri riešení logaritmických rovníc a nerovností.
Existujú však úlohy, ktoré sa vo všeobecnosti nevyriešia kdekoľvek ako prechod na novú základňu. Zvážte pár takýchto:
Úloha. Nájdite hodnotu výrazu: log 5 16 · log 2 25.
Upozorňujeme, že argumenty oboch logaritmov sú presné stupne. Budem zhrnúť: log 5 16 \u003d log 5 2 4 \u003d 4LOG 5 2; Log 2 25 \u003d log 2 5 \u003d 2LOG 2 5;
A teraz "invertovať" druhý logaritmus:
[Podpis na obrázok]Vzhľadom k tomu, že práca sa nezmení z preskupenia multiplikátorov, pokojne sme zmenili štyri a dva, a potom sa vyradili s logaritmami.
Úloha. Nájdite hodnotu výrazu: log 9 100 · lg 3.
Základ a argument prvého logaritmu - presné stupne. Píšeme a zbavte sa indikátorov:
[Podpis na obrázok]Teraz sa zbavte desatinného logaritmu, otočením na novú základňu:
[Podpis na obrázok]Základná logaritmická identita
Riešenie je často potrebné na odoslanie čísla ako logaritmus pre určenú základňu. V tomto prípade nám vzory pomôžu:
V prvom prípade n. Stáva sa ukazovateľom rozsahu v argumente. Číslo n. Môže to byť absolútne niekto, pretože je to len logaritmus.
Druhým vzorcom je vlastne parafrázovaná definícia. Nazýva sa: hlavná logaritmická identita.
V skutočnosti, čo sa stane, ak je číslo b. v takomto stupni, že číslo b. v tomto rozsahu dáva číslo a.? Správne: Toto je najviac a.. Opatrne si prečítajte tento odsek - mnoho "visí" na ňom.
Podobne ako prechodné vzorce na novú základňu, hlavná logaritmická identita je niekedy jediným možným riešením.
Úloha. Nájdite hodnotu výrazu:
[Podpis na obrázok]
Všimnite si, že protokol 25 64 \u003d log 5 8 - práve urobil štvorec od základne a argument logaritmu. Vzhľadom na pravidlá množenia stupňov s rovnakou základňou získame:
[Podpis na obrázok]Ak niekto nie je vedomý, bola to skutočná úloha EGE :)
Logaritmická jednotka a logaritmická nula
Na záver, budem dať dve identity, že je ťažké pomenovať vlastnosti - skôr je to dôsledok definície logaritmu. Neustále sa nachádzajú v úlohách a čo je prekvapujúce, vytvárajú problémy aj pre študentov "Advanced".
- log. a. a. \u003d 1 je logaritmická jednotka. Záznam raz a navždy: logaritmus na každom základe a. Od samého základu sa rovná jednej.
- log. a. 1 \u003d 0 je logaritmická nula. Základňa a. Možno nejako, ale ak argument je jednotka - logaritmus je nula! Pretože a. 0 \u003d 1 je priamym dôsledkom definície.
To sú všetky vlastnosti. Uistite sa, že praktizuje ich v praxi! Stiahnite si postieľku na začiatku lekcie, vytlačte ho - a vyriešiť úlohy.