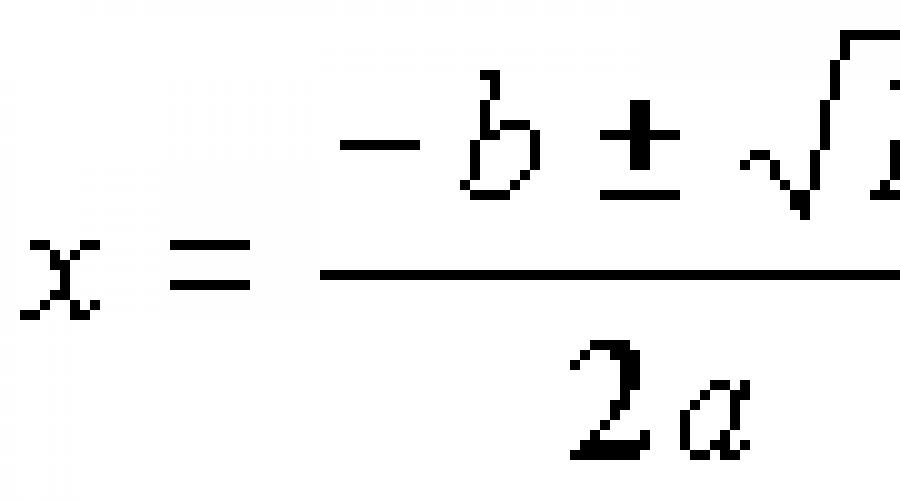
Kvadratinės lygtys yra tiriamos 8 klasėje, todėl čia nėra nieko sunku. Gebėjimas juos išspręsti yra absoliučiai būtina.

Kvadratinė lygtis yra formos AX 2 + BX + C \u003d 0 lygtis, kai koeficientai A, B ir C yra savavališki skaičiai, ir a ≠ 0.

Prieš mokydamiesi konkrečių sprendimų metodų, atkreipiame dėmesį, kad visos kvadratinės lygtys gali būti suskirstytos į tris klases:

1. Neturi šaknų;
2. Turėti tiksliai vieną šaknį;
3. Turėti dvi skirtingas šaknis.

Tai yra svarbus skirtumas tarp kvadratinių lygčių iš linijinių, kur šaknis visada egzistuoja ir yra unikalus. Kaip nustatyti, kiek šaknų turi lygtį? Dėl to yra nuostabus dalykas - diskriminant.

Diskriminant

Leiskite kvadratinės lygties AX 2 + BX + C \u003d 0. Tada diskriminant yra tik numeris D \u003d B 2 - 4AC.

Ši formulė turi būti žinoma pagal širdį. Kur ji trunka - dabar nesvarbu. Kita Svarbu: diskriminuojantis ženklas gali būti nustatomas, kiek šaknų turi kvadratinę lygtį. Būtent:

1. Jei D.< 0, корней нет;
2. Jei d \u003d 0, yra tiksliai vienas šaknis;
3. Jei d\u003e 0, bus dvi šaknys.

Atkreipkite dėmesį: diskriminant rodo šaknų skaičių, o ne visai jų ženkluose, kaip dėl kokių nors priežasčių, daugelis apsvarsto. Pažvelkite į pavyzdžius - ir jūs suprasite viską:

Užduotis. Kiek šaknų yra kvadratinių lygčių:

1. x 2 - 8x + 12 \u003d 0;
2. 5x 2 + 3x + 7 \u003d 0;
3. x 2 - 6x + 9 \u003d 0.

Mes atstumome pirmosios lygties koeficientus ir rasti diskriminant:
a \u003d 1, b \u003d -8, c \u003d 12;
D \u003d (-8) 2 - 4 · 1 · 12 \u003d 64 - 48 \u003d 16

Taigi, diskriminant yra teigiamas, todėl lygtis turi dvi skirtingas šaknis. Panašiai išardyti antrąją lygtį:
a \u003d 5; B \u003d 3; C \u003d 7;
D \u003d 3 2 - 4 · 5 · 7 \u003d 9 - 140 \u003d -131.

Diskriminieriai yra neigiama, nėra šaknų. Paskutinė lygtis išlieka:
a \u003d 1; B \u003d -6; C \u003d 9;
D \u003d (-6) 2 - 4 · 1 · 9 \u003d 36 - 36 \u003d 0.

Diskriminant yra nulis - šaknis bus vienas.

Atkreipkite dėmesį, kad kiekvienai lygtinai koeficientai buvo įvykdyti. Taip, tai ilgas laikas, taip, tai yra nuobodus - bet jūs nesupainiate koeficientų ir neleiskite kvailiems klaidų. Pasirinkite save: greitį ar kokybę.

Beje, jei jūs "užpildysite ranką", po kurio laiko nebereikia parašyti visų koeficientų. Tokios operacijos, kurias bus atliktas jūsų galva. Dauguma žmonių pradeda tai padaryti kažkur po 50-70 išsprestų lygčių - apskritai, ne tiek daug.

Šaknų aikštės lygtis

Dabar mes iš tikrųjų kreipiamės į sprendimą. Jei diskriminant D\u003e 0, šaknys galima rasti formulėse:

Pagrindinė kvadratinių lygčių šaknų formulė

Kai D \u003d 0, galite naudoti bet kurią iš šių formulių - tai bus tas pats numeris, kuris bus atsakymas. Galiausiai, jei d< 0, корней нет — ничего считать не надо.

1. x 2 - 2x - 3 \u003d 0;
2. 15 - 2x - x 2 \u003d 0;
3. x 2 + 12x + 36 \u003d 0.

Pirmoji lygtis:
x 2 - 2x - 3 \u003d 0 ⇒ a \u003d 1; B \u003d -2; C \u003d -3;
D \u003d (-2) 2 - 4 · 1 · (-3) \u003d 16.

D\u003e 0 ⇒ lygtis turi dvi šaknis. Surask juos:

Antroji lygtis:
15 - 2x - x 2 \u003d 0 ⇒ a \u003d -1; B \u003d -2; C \u003d 15;
D \u003d (-2) 2 - 4 · (-1) · 15 \u003d 64.

D\u003e 0 ⇒ lygtis vėl turi dvi šaknis. Mes juos randame

[pradžia (sulygiu) ir ((x) _ (1)) \u003d \\ t frac (2+ (2+) (64)) (2 cdot į kairę (-1 į dešinę)) \u003d - 5; ir (x) _ (2)) \u003d frac (2- \\ t (64)) (2 cdot į kairę (-1 į dešinę)) \u003d 3. Pabaiga (lygi) \\ t

Galiausiai trečioji lygtis:
x 2 + 12x + 36 \u003d 0 ⇒ a \u003d 1; B \u003d 12; C \u003d 36;
D \u003d 12 2 - 4 · 1 · 36 \u003d 0.

D \u003d 0 ⇒ lygtis turi vieną šaknį. Galite naudoti bet kokią formulę. Pavyzdžiui, pirmasis:

Kaip matyti iš pavyzdžių, viskas yra labai paprasta. Jei žinote formulę ir galėsite apsvarstyti, nebus jokių problemų. Dažniausiai klaidos atsiranda pakeitimo metu neigiamų koeficientų formulėje. Čia vėl, pirmiau aprašytas priėmimas padės: pažvelgti į formulę tiesiogine prasme, dažykite kiekvieną žingsnį - ir labai greitai atsikratyti klaidų.

Nebaigtos kvadratinės lygtys

Taip atsitinka, kad kvadratinė lygtis yra šiek tiek skiriasi nuo apibrėžime. Pavyzdžiui:

1. x 2 + 9x \u003d 0;
2. x 2 - 16 \u003d 0.

Tai lengva pamatyti, kad šiose lygtys nėra jokių terminų. Tokios kvadratinės lygtys yra net lengviau nei standartai: jie net nereikia atsižvelgti į diskriminant. Taigi, pristatome naują koncepciją:

AX 2 + BX + C \u003d 0 lygtis vadinama neišsamia kvadratine lygtimi, jei b \u003d 0 arba c \u003d 0, i.e. Koeficientas su kintamu x arba laisvas elementas yra nulis.

Žinoma, visiškai sudėtingas atvejis yra įmanoma, kai abu šie koeficientai yra nulis: b \u003d c \u003d 0. Šiuo atveju lygtis užima formą AX 2 \u003d 0. Akivaizdu, kad tokia lygtis turi vieną šaknį: x \u003d 0 .

Apsvarstykite likusius atvejus. Leiskite b \u003d 0 būti 0, tada mes gauname neišsamią lygtinę formos kirvį 2 + c \u003d 0. Mes šiek tiek konvertuojame:

Kadangi aritmetinis kvadratinė šaknis egzistuoja tik nuo ne neigiamo skaičiaus, pastaroji lygybė yra prasminga tik esant (-C / a) ≥ 0. Išvada:

1. Jei neužbaigta kvadratinių lygčių formos AX 2 + C \u003d 0, nelygybė (-C / A) atliekama ≥ 0, bus dvi šaknys. Formulė pateikiama pirmiau;
2. Jei (-C / a)< 0, корней нет.

Kaip matote, diskriminant nereikėjo - neišsamių kvadratinių lygčių nėra sudėtingų kompiuterių. Tiesą sakant, net nebūtina prisiminti nelygybę (-C / a) ≥ 0. Pakanka išreikšti x 2 vertę ir pamatyti, kas stovi kitoje lygybės ženklo pusėje. Jei yra teigiamas skaičius - šaknys bus du. Jei neigiama - šaknys nebus.

Dabar mes suprasime su formos AX 2 + BX \u003d 0 lygtimis, kuriuose laisvas elementas yra nulis. Viskas yra paprasta čia: šaknys visada bus du. Pakanka suskaidyti polinomo į daugiklius:

"Subliks" daugiklis

Darbas yra nulis, kai bent vienas iš daugiklio yra nulis. Iš čia yra šaknys. Apibendrinant, mes analizuosime keletą tokių lygčių:

Užduotis. Kvadratinės kvadratinės lygtys:

1. x 2 - 7x \u003d 0;
2. 5x 2 + 30 \u003d 0;
3. 4x 2 - 9 \u003d 0.

x 2 - 7x \u003d 0 ⇒ x · (x - 7) \u003d 0 ⇒ x 1 \u003d 0; x 2 \u003d - (- 7) / 1 \u003d 7.

5x 2 + 30 \u003d 0 ⇒ 5x 2 \u003d -30 ⇒ x 2 \u003d -6. Nėra šaknų, nes Kvadratas negali būti lygus neigiamam skaičiui.

4x 2 - 9 \u003d 0 ⇒ 4x 2 \u003d 9 ⇒ x 2 \u003d 9/4 ⇒ x 1 \u003d 3/2 \u003d 1.5; x 2 \u003d -1,5.

Peržiūrėti lygtį

Išraiška D. \u003d B. 2 - 4 AC. Skambinkite diskriminant Kvadratinė lygtis. Jeigu D. \u003d 0, lygtis turi vieną galiojančią šaknį; Jei D. \u003e 0, lygtis turi dvi galiojančias šaknis.
Tuo atveju, kai D. = 0 Kartais jie sako, kad kvadratinė lygtis turi dvi identišką šaknį.
Naudojant žymėjimą D. \u003d B. 2 - 4 AC. , galite perrašyti formulę (2) kaip

Jeigu B. \u003d 2 K. Formulė (2) yra:

kur K. \u003d B. / 2 .
Paskutinė formulė yra ypač patogi tais atvejais, kai B. / 2 - sveikasis skaičius, t.y. koeficientas B. - lyginis skaičius.
1 pavyzdys: Išspręsti lygtį 2 X. 2 - 5 X. + 2 = 0 . Čia a \u003d 2, b \u003d -5, c \u003d 2. Turėti D. \u003d B. 2 - 4 AC. = (-5) 2- 4*2*2 = 9 . Kaip D. > 0 , lygtis turi dvi šaknis. Juos rasti pagal formulę (2)

SO X. 1 \u003d (5 + 3) / 4 \u003d 2, x 2 =(5 - 3) / 4 = 1 / 2 ,
t.y X. 1 = 2 ir. \\ T X. 2 = 1 / 2 - nurodytos lygties šaknys.
2 pavyzdys: Išspręsti lygtį 2 X. 2 - 3 x. + 5 = 0 . Čia a \u003d 2, b \u003d -3, c \u003d 5. Mes rasti diskriminant D. \u003d B. 2 - 4 AC. = (-3) 2- 4*2*5 = -31 . Kaip D. 0 Lygtis neturi galiojančių šaknų.

Nebaigtos kvadratinės lygtys. Jei yra kvadratinėje lygtyje Kirvis. 2 + BX. + C. =0 Antrasis koeficientas B. arba laisvas penis C. lygus nuliui, tada kvadratinė lygtis vadinama nebaigtas. Neišsamos lygtys yra izoliuotos, nes norint rasti savo šaknis, galima nenaudoti kvadratinės lygties šaknų formulės - lengviau išspręsti lygtį pagal jo kairiojo veiksnių dalies skilimo metodą.
1 pavyzdys: Išspręsti lygtį 2 X. 2 - 5 x. = 0 .
Turėti X. (2 x. \\ T - 5) = 0 . Taip arba X. = 0 taip pat 2 X. - 5 = 0 , t.y X. = 2.5 . Taigi lygtis turi dvi šaknis: 0 ir. \\ T 2.5
2 pavyzdys: Išspręsti lygtį 3 X. 2 - 27 = 0 .
Turėti 3 X. 2 = 27 . Todėl šios lygties šaknys - 3 ir. \\ T -3 .

Vieta teorema. Jei sumažinta kvadratinė lygtis X. 2 + PX. + Q. =0 turi galiojančias šaknis, tada jų suma yra lygi - P. ir darbas yra lygus Q. , t.y

x 1 + x 2 \u003d -p,
x 1 x 2 \u003d q

(Šio kvadratinio lygties šaknų suma yra lygi antrajam koeficientui, priimtam su priešingu ženklu, o šaknų produktas yra lygus laisvam nariui).

Su šia matematine programa galite išspręskite kvadratinę lygtį.

Programa ne tik suteikia atsakymo užduotį, bet ir rodo sprendimo procesą dviem būdais:
- su diskriminant
- naudojant Vieta teoremą (jei įmanoma).

Be to, atsakymas yra tiksli, ne apytikslis.
Pavyzdžiui, už lygtį (81x ^ 2-16x-1 \u003d 0), atsakymas yra produkcija šioje formoje:

$$ x_1 \u003d FRAC (8+ SQRT (145)) (81), \\ quad x_2 \u003d frac (8-1 SQRT (145)) (81) $$, o ne tai: \\ (x_1 \u003d 0,247 ; quad x_2 \u003d -0.05 \\ t

Ši programa gali būti naudinga studentams aukštųjų mokyklų bendrojo lavinimo mokyklų rengiant bandymus ir egzaminus, tikrindami žinias prieš egzaminą, tėvai stebėti daugelio problemų matematikos ir algebros sprendimą. O gal esate per brangu samdyti mokytoją ar pirkti naujus vadovėlius? Arba jūs tiesiog norite padaryti savo namų darbus matematikos ar algebros kaip įmanoma? Šiuo atveju taip pat galite naudoti savo programas su išsamiu sprendimu.

Taigi, jūs galite atlikti savo jaunesnių brolių ar seserų mokymą ir (arba) mokymą, o švietimo lygis išspręstų užduočių srityje didėja.

Jei nesate susipažinę su kvadratinio polinomo įvedimo taisyklėmis, rekomenduojame su jais susipažinti su jais.

Kvadratinių polinominių įvesties taisyklių

Kadangi kintamasis gali būti bet koks lotyniškas laiškas.
Pavyzdžiui: (x, y, z, a, b, c, o, p, q) ir kt.

Numeriai gali patekti į visą ar dalinį.
Be to, daliniai numeriai gali būti skiriami ne tik dešimtainio formos, bet ir įprastos frakcijos pavidalu.

Dešimtainių frakcijų įvedimo taisyklės.
Dešimtosios dalies frakcijose visos dalinė dalis gali būti atskirta kaip taškas ir kableliais.
Pavyzdžiui, galite įvesti tokius dešimtainius frakcijas: 2.5x - 3,5x ^ 2

Įprastinių frakcijų įvedimo taisyklės.
Tik sveikasis skaičius gali veikti kaip skaitiklis, vardiklis ir visa dalis frakcijos.

Denominatorius negali būti neigiamas.

Įvedant skaitmeninę frakciją, skaitmuo atskirtas nuo vardiklio į skilimo ženklą: /
Visa dalis yra atskirta nuo fraraty ampersand ženklo: &
Įėjimas: 3 ir 1/3 - 5 ir 6 / 5z + 1 / 7z ^ 2
Rezultatas: (3 frac (1) (3) - 5 frac (6) (5) Z + \\ t (1) (7) Z ^ 2 \\)

Įeinant į išraišką galite naudoti skliaustelius. Šiuo atveju, sprendžiant kvadratinę lygtį, įvesta išraiška pirmą kartą supaprastinta.
Pavyzdžiui: 1/2 (Y - 1) (Y + 1) - (5Y-10 & 1/2)

=0

Nuspręsti

Nustatyta, kad kai kurie scenarijai, reikalingi šiai užduočiai išspręsti, ir programa gali neveikti.
Jūs galite turėti "Adblock".
Tokiu atveju atjunkite ir atnaujinkite puslapį.

Jūsų naršyklėje turite "JavaScript" vykdymą.
Kad būtų rodomas sprendimas, turite įjungti "JavaScript".
Čia yra instrukcijos, kaip įjungti "JavaScript" naršyklėje.

Nes. Norint išspręsti užduotį, yra labai daug, jūsų prašymas yra eilėje.
Po kelių sekundžių sprendimas bus rodomas žemiau.
Prašau palauk ...

Jei tu pastebėjo klaidą sprendžiantJūs galite rašyti apie tai grįžtamojo ryšio forma.
Nepamiršk nurodykite kokią užduotį Jūs nuspręsite ir ką Įveskite lauką.

Mūsų žaidimai, galvosūkiai, emuliatoriai:

Šiek tiek teorijos.

Kvadratinių lygčių ir jos šaknų. Nebaigtos kvadratinės lygtys

Kiekviena lygtis
(- x ^ 2 + 6x + 1,4 \u003d 0, quad 8x ^ 2-7x \u003d 0, quad x ^ 2- \\ frac (4) (9) \u003d 0 \\)
Turi išvaizdą
(AX ^ 2 + BX + C \u003d 0, \\)
kur x yra kintamasis, A, B ir C - numeriai.
Pirmojoje lygtyje A \u003d -1, B \u003d 6 ir C \u003d 1,4, antrajame a \u003d 8, b \u003d -7 ir c \u003d 0, trečiame a \u003d 1, b \u003d 0 ir c \u003d 4/9. Tokios lygtys vadinamos kvadratinės lygtys. \\ T.

Apibrėžimas.
Kvadratinė lygtis Formos AX 2 + BX + C \u003d 0 lygtis, kur X yra kintamasis, A, B ir C yra kai kurie numeriai, ir (a neq 0).

A, B ir C numeriai yra kvadratinės lygties koeficientai. A numeris yra vadinamas pirmuoju koeficientu, skaičius B yra antrasis koeficientas ir numeris C - nemokamai narys.

Kiekvienoje iš formos AX 2 + BX + C \u003d 0 lygtis, kur (a neq 0), didžiausias kintamojo X kvadratas. Taigi pavadinimas: kvadratinė lygtis.

Atkreipkite dėmesį, kad kvadratinė lygtis taip pat vadinama antrojo laipsnio lygtimi, nes jo kairėje dalyje yra antrojo laipsnio polinomo.

Kvadratinė lygtis, kurioje X2 koeficientas yra 1, vadinamas suteikta kvadratinė lygtis. Pavyzdžiui, tam tikros kvadratinės lygtys yra lygtys
x ^ 2-11x + 30 \u003d 0, quad x ^ 2-6x \u003d 0, \\ quad x ^ 2-8 \u003d 0 \\) \\ t

Jei į kvadratinės lygties AX 2 + BX + C \u003d 0, bent vienas iš koeficientų B arba C yra nulis, tada tokia lygtis vadinama nebaigta kvadratinė lygtis. Taigi, lygtys -2x 2 + 7 \u003d 0, 3x 2 -10x \u003d 0, -4x 2 \u003d 0 yra neišsamios lygtys. Pirmoje iš jų B \u003d 0, antrajame C \u003d 0, trečiame B \u003d 0 ir C \u003d 0.

Nebaigtos kvadratinės lygtys yra trys rūšys:
1) AX 2 + C \u003d 0, kur (neq 0);
2) AX 2 + BX \u003d 0, kur (b);
3) AX 2 \u003d 0.

Apsvarstykite kiekvienos iš šių rūšių lygčių sprendimą.

Norėdami išspręsti neišsamią kvadratinę lygtį formos AX 2 + C \u003d 0, su (C), jis perduodamas į savo nemokamą narį į dešinę pusę ir padaryti abi dalis lygtį a:
(x ^ 2 \u003d - frac (c) (a) (a)) x_ (1,2) \u003d pm \\ t \\ t frac (c) (a)) \\) \\ t

Nuo tada, kai 0), tada (- frac (c) (a) neq 0 \\ t

Jei (C) (a)\u003e 0) lygtis turi dvi šaknis.

Jei (C) (c) (a) išspręsti neišsamios formos formos AX 2 + BX \u003d 0, su \\ (b neq 0), jie mažėja savo kairiąją dalį dauginant ir gauti lygtį
X (ax + b) \u003d 0 (pradžia) (pradžia (masyvas) (l) x \u003d 0 cen + b \u003d 0 (masyvas) į dešinę. \\ T (Masyvas) (l) x \u003d 0 (b) (b) (a) pabaiga (masyvas) \\ t

Taigi, nebaigta kvadratinių lygčių formos AX 2 + BX \u003d 0 su \\ (BEQ 0) visada turi dvi šaknis.

Nebaigta kvadratinė lygtinė formos AX 2 \u003d 0 yra lygiavertė x 2 \u003d 0 lygiaverčiai ir todėl turi vienintelę šaknį 0.

Kvadratinės lygties šaknų formulė

Apsvarstykite, kaip kvadratinių lygtis išspręsta, kai abu koeficientai su nežinomu ir nemokamu nariu skiriasi nuo nulio.

SPEST SQUARE lygtis apskritai ir dėl to gauname šaknų formulę. Tada ši formulė gali būti naudojama sprendžiant bet kokią kvadratinę lygtį.

"Resist" kvadratinės lygties AX 2 + BX + C \u003d 0

Abiejų dalių atskyrimas a, mes gauname pateiktos kvadratinės lygties ekvivalentą
x ^ 2 + frac (b) (a) x + frac (c) (a) \u003d 0 \\)

Mes transformuojame šią lygtį, pabrėžiant sugadintos kvadratą:
(x ^ 2 + 2x cbot (b) (2a) + į kairę ((b) (b) (2a) į dešinę) ^ 2- \\ t 2 + frac (c) (a) \u003d 0 \\ t

(x ^ 2 + 2x cbot (b) (2a) + į kairę ((b) (b) (2a)) ^ 2 \u003d kairė (frac (b) (2a) teisinga) ^ 2 - frac (c) (a) (kairėn (x + frac (b) (2a) teisinga) ^ 2 \u003d frac (b ^ 2) (4a ^ 2) - \\ t (C) (a) (a) į kairę (x + (b) (b) (2a)) ^ 2 \u003d frac (b ^ 2-4ac) (4a ^ 2) \\ t- x + \\ t Frac (b) (2a) \u003d pm \\ l pm (b) (b) (b) (b) (b) (2a) + \\ t frac (pm \\ t \\ t \\ t \\ t B ^ 2 -4ac)) (2a) (2) (x \u003d frac (-b) (b ^ 2-4ac)) (2a) \\ t

Vadovaujama išraiška vadinama diskriminavimo aikštės lygtis AX 2 + BX + C \u003d 0 ("diskriminantija" lotynų kalba yra atskira). Tai reiškia raidė d, i.e.
D \u003d b ^ 2-4ac \\ t

Dabar, naudojant diskriminacinį paskyrimą, perrašykite kvadratinės lygties šaknų formulę:
(X_ (1,2) \u003d frac (-b) (d)) (2a) (d \u003d b ^ 2-4ac) \\ t

Akivaizdu, kad:
1) Jei D\u003e 0, kvadratinė lygtis turi dvi šaknis.
2) Jei d \u003d 0, kvadratinė lygtis turi vieną šaknį (x \u003d - frac (b) (2a).).
3) Jei D yra, priklausomai nuo diskriminano vertės, kvadratinė lygtis gali turėti dvi šaknis (su D\u003e 0), vieną šaknį (D \u003d 0) arba neturėti šaknų (su D, sprendžiant kvadratinę lygtį Ši formulė, patartina kreiptis į tokį būdą:
1) Apskaičiuokite diskriminant ir palyginkite jį su nuliu;
2) Jei diskriminantija yra teigiama arba lygi nuliui, tada naudokite šaknų formulę, jei diskidanta yra neigiama, tada užrašykite šaknis.

Vieta teorema

Pateikta kvadratinių lygčių ax 2 -7x + 10 \u003d 0 turi šaknis 2 ir 5. šaknų kiekis yra 7, o produktas yra 10. Matome, kad šaknų kiekis yra lygus antrajam koeficientui, priimtam su priešais ženklas, o šaknų produktas yra lygus laisvam nariui. Tokia nuosavybė turi kokią nors kvadratinę lygtį, turinčią šaknį.

Pateiktos kvadratinės lygties šaknų suma yra lygi antrajam koeficientui, priimtam su priešingu ženklu, o šaknų produktas yra lygus laisvam nariui.

Tie. Vieta teorema teigia, kad X1 ir X 2 iš tam tikros kvadratinio lygties x 2 + PX + Q \u003d 0 turi turtą:
(Pradžios (masyvas) (l) x_1 + x_2 \u003d -p \\\\ X_1 CDOT x_2 \u003d Q pabaiga (masyvas) \\ t

Tikiuosi, kad mokytis šio straipsnio, jūs išmoksite rasti visos kvadratinės lygties šaknis.

Naudojant diskriminant, išspręstos tik visos kvadratinės lygtys, sprendžiami kvadratinėms lygtims, kiti metodai, kuriuos rasite straipsnyje "Nugaliųjų kvadratinių lygčių sprendimas".

Kokios kvadratinės lygtys yra pilnos? IT aH 2 + B X + C \u003d 0 lygtyskai koeficientai A, B ir nėra lygūs nuliui. Taigi, išspręsti visą kvadratinę lygtį, būtina apskaičiuoti diskriminuotoją D.

D \u003d B 2 - 4A.

Priklausomai nuo to, kokios svarbos yra diskriminant, mes parašysime atsakymą.

Jei diskriminant yra neigiamas skaičius (D< 0),то корней нет.

Jei diskriminant yra nulis, x \u003d (-b) / 2a. Kai diskriminant yra teigiamas skaičius (D\u003e 0),

tada x 1 \u003d (-B - √d) / 2a ir x 2 \u003d (-b + √d) / 2a.

Pavyzdžiui. Išspręsti lygtį x 2 - 4x + 4 \u003d 0.

D \u003d 4 2 - 4 · 4 \u003d 0

x \u003d (- (-4)) / 2 \u003d 2

Atsakymas: 2.

Išspręskite 2 lygtį. x 2 + x + 3 \u003d 0.

D \u003d 1 2 - 4 · 2 · 3 \u003d - 23

Atsakymas: Nėra šaknų.

Išspręskite 2 lygtį. x 2 + 5x - 7 \u003d 0.

D \u003d 5 2 - 4 · 2 · (-7) \u003d 81

x 1 \u003d (-5 - √81) / (2 · 2) \u003d (-5 - 9) / 4 \u003d - 3.5

x 2 \u003d (-5 + √81) / (2 · 2) \u003d (-5 + 9) / 4 \u003d 1

Atsakymas: - 3.5; vienas.

Taigi, įsivaizduojame visiškų kvadratinių lygčių sprendimą pagal schemą1.

Pagal šias formules galite išspręsti bet kokią išsamią kvadratinę lygtį. Jums reikia tik atidžiai stebėti lygtis buvo užfiksuota standartinio tipo polinominiu.

bet x 2 + BX + C, Priešingu atveju galite padaryti klaidą. Pavyzdžiui, X + 3 + 2x 2 \u003d 0 lygties įraše, tai klaidingai gali būti išspręsta

a \u003d 1, b \u003d 3 ir c \u003d 2. Tada

D \u003d 3 2 - 4 · 1 · 2 \u003d 1 Ir tada lygtis turi dvi šaknis. Ir tai neteisinga. (Žr. 2 pavyzdžio sprendimą).

Todėl, jei lygtis nėra parašyta ne į standartinės rūšies polinomą, iš pradžių visoje kvadratinėje lygtis turėtų būti užregistruotas standartinių rūšių polinominiu (pirmiausia turėtų būti neatskleista su didžiausiu rodikliu, tai yra bet x 2 Tada su mažesniu – bX.ir tada nemokamai penis nuo.

Sprendžiant tam tikrą kvadratinę lygtį ir kvadratinę lygtį su net koeficientu, su antruoju terminu galima naudoti kitas formules. Susipažinkime su šiomis formulėmis. Jei į visą kvadratinę lygtį antrajame termine, koeficientas bus lygus (b \u003d 2k), tada lygtis pagal formules 2 paveiksle gali būti išspręsta.

Visa kvadratinė lygtis vadinama pirmiau minėtu, jei koeficientas yra x 2 lygus vienai ir lygtis bus formuojama x 2 + px + q \u003d 0. Tokia lygtis gali būti skiriama išspręsti arba gaunama dalijant visus koeficientų koeficiento lygtį betstovėti x 2 .

3 paveiksle parodyta pirmiau minėtos kvadrato sprendimo schema
lygtys. Apsvarstykite pavyzdį šiame straipsnyje nagrinėjamų formulių taikymas.

Pavyzdys. Išspręsti lygtį

3x 2 + 6x - 6 \u003d 0.

Nuspręskime šią lygybę naudodami 1 paveikslo schemoje nurodytus formules.

D \u003d 6 2 - 4 · 3 · (- 6) \u003d 36 + 72 \u003d 108

√D \u003d √108 \u003d √ (36 · 3) \u003d 6√3

x 1 \u003d (-6 - 6√3) / (2 · 3) \u003d (6 (-1- √ (3))) / 6 \u003d -1 - √3

x 2 \u003d (-6 + 6√3) / (2 · 3) \u003d (6 (-1+ √ (3))) / 6 \u003d -1 + √3

Atsakymas: -1 - √3; -1 + √3.

Galima matyti, kad x koeficientas šioje lygtyje yra lygus skaičius, ty B \u003d 6 arba b \u003d 2k, iš kur k \u003d 3. Tada mes stengiamės išspręsti lygtį pagal d diagramoje parodytą formulę 1 \u003d 3 2 - 3 · (- 6) \u003d 9 + 18 \u003d 27

√ (D 1) \u003d √27 \u003d √ (9 · 3) \u003d 3√3

x 1 \u003d (-3 - 33) / 3 \u003d (3 (-1 - √ (3))) / 3 \u003d - 1 - √3

x 2 \u003d (-3 + 3√3) / 3 \u003d (3 (-1 + √ (3))) / 3 \u003d - 1 + √3

Atsakymas: -1 - √3; -1 + √3.. Pastebėjo, kad visi šios kvadratinio lygties koeficientai yra suskirstyti į 3 ir atliekant padalijimą, mes gauname sumažintą kvadratinę lygtį x 2 + 2x - 2 \u003d 0 sprendžiant šią lygtį naudojant formules nurodytam kvadratams
3 lygtis.

D 2 \u003d 2 2 - 4 · (- 2) \u003d 4 + 8 \u003d 12

√ (D 2) \u003d √12 \u003d √ (4 · 3) \u003d 2√3

x 1 \u003d (-2 - 2√3) / 2 \u003d (2 (-1 - √ (3))) / 2 \u003d - 1 - √3

x 2 \u003d (-2 + 2√3) / 2 \u003d (2 (-1+ √ (3))) / 2 \u003d - 1 + √3

Atsakymas: -1 - √3; -1 + √3.

Kaip matome, sprendžiant šią lygtį įvairiomis formulėmis, gavome tą patį atsakymą. Todėl gerai žino apie 1 paveiksle schemoje formules, visada galite išspręsti bet kokią išsamią kvadratinę lygtį.

svetainė, visiškai arba dalinis kopijavimas medžiagos nuoroda į pradinį šaltinį reikalingas.

Tęsiant temą "Sprendimas lygtys", šio straipsnio medžiaga bus supažindinti su kvadratinių lygčių.

Apsvarstykite viską išsamiai: kvadrato lygties esmė ir įrašai, nustatykite pridedamomis sąlygomis, mes analizuosime neišsamių ir išsamių lygčių sprendimo schemą, susipažinsime su šaknų ir diskriminaciniu formule, nustatys ryšius tarp šaknų ir koeficientų, Ir, žinoma, mes pateikiame vizualinį praktinių pavyzdžių sprendimą.

Yandex.rtb r-a-339285-1

Kvadratinė lygtis, jos tipai

Apibrėžimas 1.

Kvadratinė lygtis - tai yra lygtis, užregistruota kaip a · x 2 + b · x + c \u003d 0kur X. - kintamasis, a, b ir C. - kai kurie numeriai, o a.nėra nulio.

Dažnai kvadratinės lygtys taip pat vadinamos antrosios pakopos lygtimi, nes iš esmės kvadratinė lygtis yra antrojo laipsnio algebrinė lygtis.

Pateikiame pavyzdį iliustruoti tam tikrą apibrėžimą: 9 · x 2 + 16 · x + 2 \u003d 0; 7, 5 · x 2 + 3, 1 · x + 0, 11 \u003d 0 ir kt. - Tai yra kvadratinės lygtys.

2 apibrėžimas 2.

A, B ir C. - tai yra kvadratinės lygties koeficientai a · x 2 + b · x + c \u003d 0, su koeficientu A. Jis vadinamas pirmuoju arba vyresniu arba koeficientu x 2, B - antrojo koeficiento ar koeficiento, kai X., bet C. Skambinkite nemokamu nariu.

Pavyzdžiui, kvadratinėje lygtyje 6 · x 2 - 2 · x - 11 \u003d 0 Vyresnysis koeficientas yra 6, antrasis koeficientas yra − 2 ir laisvas narys yra lygus − 11 . Atkreipkite dėmesį į tai, kad kai koeficientai B.ir (arba) C yra neigiami, naudojama trumpa vaizdo įrašymo forma. 6 · x 2 - 2 · x - 11 \u003d 0, bet ne 6 · x 2 + (- 2) · x + (- 11) \u003d 0.

Taip pat paaiškinome šį aspektą: jei koeficientai A. ir /. \\ t B. lygus. \\ T 1 arba. \\ T − 1 , tada aiškiai dalyvauti kvadratinės lygties įrašyme, jie negali būti imtasi, o tai paaiškinama šių skaitmenų koeficientų įrašo savybės. Pavyzdžiui, kvadratinėje lygtyje Y2 - Y + 7 \u003d 0 Vyresnysis koeficientas yra 1, o antrasis koeficientas yra − 1 .

Nurodytos ir nesusituoktos kvadratinės lygtys

Pagal pirmojo koeficiento vertę, kvadratinės lygtys yra suskirstyti į pirmiau minėtą ir neapmokėtą.

3 apibrėžimas.

Sumažinta kvadratinė lygtis - tai yra kvadratinė lygtis, kur vyresnis koeficientas yra lygus 1. Kitoms vyresnio amžiaus koeficiento vertėms kvadratinė lygtis yra neteisinga.

Mes pateikiame pavyzdžius: kvadratinių lygtis x 2 - 4 · x + 3 \u003d 0, x 2 - x - 4 5 \u003d 0 yra pristatyti kiekvienoje iš jų senesnis koeficientas yra 1.

9 · x 2 - x - 2 \u003d 0 - neatskiriama kvadratinės lygties, kur pirmasis koeficientas skiriasi nuo 1 .

Bet kokia štampuota kvadratinė lygtis yra įmanoma konvertuoti į tam tikrą lygtį, jei ji yra padalinta iš abiejų dalių iki pirmojo koeficiento (lygiavertė transformacija). Transformuota lygtis turės tas pačias šaknis kaip nurodyta protinga lygtis arba neturi turėti šaknų.

Svarstymas konkretaus pavyzdžio leis mums aiškiai parodyti perėjimą nuo neatsiejama kvadratinių lygčių į tam tikrą.

1 pavyzdys.

Lygtis yra 6 · x 2 + 18 · x - 7 \u003d 0 . Būtina konvertuoti pradinę lygtį pirmiau minėtoje formoje.

Sprendimas Šis sprendimas

Pirmiau nurodytos nurodytos schemos yra atskirtos abiem pirminės lygties atžvilgiu vyresniuoju koeficientu 6. Tada mes gauname: (6 · x 2 + 18 · x - 7): 3 \u003d 0: 3Ir tai yra tas pats, kaip: (6 · x 2): 3 + (18 · x): 3 - 7: 3 \u003d 0 Ir toliau: (6: 6) · x 2 + (18: 6) · x - 7: 6 \u003d 0. Iš čia: x 2 + 3 · x - 1 1 6 \u003d 0. Taigi, laikoma, kad lygtis yra nurodyta.

Atsakymas: x 2 + 3 · x - 1 1 6 \u003d 0.

Pilnos ir neišsamios kvadratinės lygtys

Pasukite į kvadratinio lygties apibrėžimą. Mes tai paaiškinome A ≠ 0.. Tokia sąlyga yra būtina lygimui a · x 2 + b · x + c \u003d 0 tai buvo tiksliai kvadratinė, nes A \u003d 0. Tai iš esmės konvertuojama į linijinę lygtį b · x + c \u003d 0.

Tuo atveju, kai koeficientai B. ir. \\ T C.lygus nuliui (kuris yra įmanomas tiek individualiai, tiek kartu), kvadratinė lygtis vadinama neišsamia.

Apibrėžimas 4.

Nebaigta kvadratinė lygtis - tokia kvadratinė lygtis a · x 2 + b · x + c \u003d 0,kur bent vienas iš koeficientų B.ir. \\ T C.(arba abu) yra nulis.

Visa kvadratinė lygtis - kvadratinės lygties, kurioje visi skaitmeniniai koeficientai nėra nuliniai.

Mes mėgstame, kodėl kvadratinių lygčių tipai yra tiksliai pavadinimai.

Už b \u003d 0 kvadratinių lygčių A · x 2 + 0 · x + c \u003d 0kad tas pats yra a · x 2 + c \u003d 0. Dėl C \u003d 0. Kvadratinė lygtis įrašoma kaip a · x 2 + b · x + 0 \u003d 0Tai yra lygiavertis a · x 2 + b · x \u003d 0. Dėl B \u003d 0. ir. \\ T C \u003d 0. Lygtis priims nuomonę a · x 2 \u003d 0. Turėjome lygtis skiriasi nuo visos kvadratinės lygties, nes jų kairiosios dalys nėra įtrauktos į X kintamąjį arba nemokamą nario komponentą arba abu vieną kartą. Tiesą sakant, šis faktas buvo paprašyta tokio tipo lygčių tipo - neišsami.

Pavyzdžiui, x 2 + 3 · x + 4 \u003d 0 ir - 7 · x 2 - 2 · x + 1, 3 \u003d 0 yra pilnos kvadratinės lygtys; x 2 \u003d 0, - 5 · x 2 \u003d 0; 11 · x 2 + 2 \u003d 0, - x 2 - 6 · x \u003d 0 - Nebaigtos kvadratinės lygtys.

Nebaigtų kvadratinių lygčių sprendimas

Pirmiau apibrėžtis leidžia atskirti šias neišsamių kvadratinių lygčių rūšis:

• a · x 2 \u003d 0, ši lygtis atitinka koeficientus B \u003d 0. ir c \u003d 0;
• a · x 2 + c \u003d 0 b \u003d 0;
• a · x 2 + b · x \u003d 0 ne c \u003d 0.

Apsvarstykite kiekvieno nebaigtos kvadratinės lygties tipo sprendimą.

A · x 2 \u003d 0 lygties sprendimas

Kaip minėta pirmiau, lygtis atitinka koeficientus B. ir. \\ T C.lygus nuliui. Lygtis. \\ T a · x 2 \u003d 0 Galima konvertuoti lygtį lygiaverčiui x 2 \u003d 0Kuris gauname, dalijamasi abiem šalies lygties dalimis A.nėra lygus nuliui. Akivaizdu, kad lygties šaknis x 2 \u003d 0 Tai yra nulis, nes 0 2 = 0 . Kitos šaknys, ši lygtis neturi, kuri yra paaiškinta pagal laipsnio savybes: bet kokiam skaičiui p,nėra lygus nuliui, ištikimas nelygybė P2\u003e 0Kas tai darau, kai P ≠ 0. lygybė. \\ t P 2 \u003d 0niekada nebus pasiektas.

5 apibrėžimas.

Taigi, neužbaigtos kvadratinės lygties a · x 2 \u003d 0 yra vienintelė šaknis x \u003d 0..

2 pavyzdys.

Pavyzdžiui, mes išsprendžiame neišsamią kvadratinę lygtį - 3 · x 2 \u003d 0. Tai atitinka lygtį x 2 \u003d 0, jo vienintelė šaknis yra x \u003d 0., Tada pradinė lygtis turi vienintelę šaknį - nulį.

Trumpai tariant, sprendimas yra sudarytas taip:

- 3 · x 2 \u003d 0, x 2 \u003d 0, x \u003d 0.

A · x 2 + c \u003d 0 lygties sprendimas

Ant eilės - neišsamių kvadratinių lygčių tirpalas, kur b \u003d 0, c ≠ 0, ty formos lygtys a · x 2 + c \u003d 0. Mes transformuojame šią lygtį atlikdami terminą nuo vienos lygties dalies į kitą, keičiant ženklą į priešingą ir dalijant abiem dalių lygtį į numerį, o ne lygus nuliui:

• perkėlimas. \\ T C. dešinėje pusėje, kuri suteikia lygtį A · x 2 \u003d - c;
• mes padaliame abi lygties dalis A., Aš einu į pabaigą x \u003d - c a.

Mūsų transformacijos yra lygiavertės, atitinkamai, gauta lygtis taip pat yra lygiavertė šaltiniui, ir šis faktas leidžia užbaigti lygties šaknis. Nuo to, kas yra reikšmės A. ir. \\ T C.išraiškos vertė priklauso - C A: jis gali turėti minuso ženklą (tarkim, jei a \u003d 1. ir. \\ T C \u003d 2., tada - c a \u003d - 2 1 \u003d - 2) arba plius ženklas (pavyzdžiui, jei A \u003d - 2 ir. \\ T C \u003d 6., tada - C A \u003d - 6 - 2 \u003d 3); tai nėra nulis, nes C ≠ 0.. Leiskite mums išsamiau išsamiau situacijose, kai - C a< 0 и - c a > 0 .

Tuo atveju, kai - C a< 0 , уравнение x 2 = - c a не будет иметь корней. Утверждая это, мы опираемся на то, что квадратом любого числа является число неотрицательное. Из сказанного следует, что при - c a < 0 ни для какого числа P. Lygybė P 2 \u003d - C negali būti tiesa.

Priešingu atveju, kai - C A\u003e 0: prisiminkite kvadratinę šaknį, ir tai bus akivaizdu, kad x 2 \u003d - C a lygtis bus numeris - C A, nes - C A 2 \u003d - C a. Sunku suprasti, kad numeris yra - C A taip pat yra x 2 \u003d - C A: iš tiesų, - - C A 2 \u003d - C a.

Kita šaknų lygtis nebus. Mes galime tai įrodyti naudojant bjaurus metodą. Pradėti su, nustatykite virš šaknų nurodymus x 1 ir. \\ T - x 1.. Aš siūlau, kad lygtis x 2 \u003d - C A taip pat yra šaknis x 2kuri skiriasi nuo šaknų x 1 ir. \\ T - x 1.. Mes žinome, kad vietoj to pakeisime į lygtį X. Jo šaknys, mes transformuojame lygtį į teisingą skaičių lygybę.

Dėl x 1 ir. \\ T - x 1. Mes rašome: x 1 2 \u003d - C A, ir x 2 - x 2 2 \u003d - C a. Remdamasi skaitinių lygių savybių, pakartokite vieną teisingą lygybę iš kitos, kuri suteiks mums: x 1 2 - x 2 2 \u003d 0. Naudokite veiksmų su numeriais, kad perrašytumėte naujausią lygybę kaip (x 1 - x 2) · (x 1 + x 2) \u003d 0. Yra žinoma, kad dviejų numerių darbas yra nulis, o tik jei bent vienas iš numerių yra nulis. Iš minėtų to taip x 1 - x 2 \u003d 0 ir /. \\ t x 1 + x 2 \u003d 0kad tas pats dalykas x 2 \u003d x 1 ir /. \\ t x 2 \u003d - x 1. Buvo akivaizdus prieštaravimas, nes iš pradžių buvo susitarta, kad lygties šaknis x 2 skiriasi nuo x 1 ir. \\ T - x 1.. Taigi, įrodėme, kad lygtis neturi kitų šaknų, išskyrus X \u003d - C A ir X \u003d - C a.

Apibendriname visus pirmiau nurodytus argumentus.

6 apibrėžimas.

Nebaigta kvadratinė lygtis a · x 2 + c \u003d 0 lygiavertis x 2 lygimui \u003d - C a, kuris:

• neturės šaknų, kai - C a< 0 ;
• bus dvi šaknys x \u003d - C A ir X \u003d - - C A su - C A\u003e 0.

Pateikiame pavyzdžių sprendžiant lygtis a · x 2 + c \u003d 0.

3 pavyzdys.

Nurodoma kvadratinė lygtis 9 · x 2 + 7 \u003d 0.Būtina rasti jo sprendimą.

Sprendimas Šis sprendimas

Mes perkeliame nemokamą narį į dešinę dalį lygties, tada lygtis bus formuojama 9 · x 2 \u003d - 7.
Mes padalijame abi gautos lygties dalis 9 , ateiti į x 2 \u003d - 7 9. Dešinėje dalyje matome numerį su minuso ženklu, o tai reiškia: nurodyta lygtis neturi šaknų. Tada originali neišsamia kvadratinė lygtis 9 · x 2 + 7 \u003d 0 Neturės šaknų.

Atsakymas: lygtis. \\ T 9 · x 2 + 7 \u003d 0jis neturi šaknų.

4 pavyzdys.

Būtina išspręsti lygtį - x 2 + 36 \u003d 0.

Sprendimas Šis sprendimas

Mes perkeliame 36 į dešinę pusę: - x 2 \u003d - 36.
Mes padalijome abi dalis − 1 , gauti x 2 \u003d 36. Dešinėje dalyje - teigiamas skaičius, nuo čia galime daryti išvadą, kad x \u003d 36 arba X \u003d - 36.
Nuimkite šaknį ir užrašykite galutinį rezultatą: neišsami kvadratinių lygčių - x 2 + 36 \u003d 0 Jis turi dvi šaknis x \u003d 6. arba. \\ T x \u003d - 6.

Atsakymas: x \u003d 6. arba. \\ T x \u003d - 6.

Sprendimas a · x 2 + b · x \u003d 0

Apsvarstysime trečią neišsamių kvadratinių lygčių tipą C \u003d 0.. Rasti neišsamios kvadratinės lygties sprendimą a · x 2 + b · x \u003d 0, Mes naudojame skilimo apie daugikles metodą. Papildykite daugiapakopius polinomo, kuris yra kairėje lygties dalyje, padarydami bendrą daugiklį skliausteliams X.. Šis žingsnis suteiks galimybę konvertuoti originalią neišsamią kvadratinę lygtį į ekvivalentą x · (a · x + b) \u003d 0. Ir ši lygtis savo ruožtu yra lygiavertė lygčių visumui x \u003d 0. ir. \\ T A · x + b \u003d 0. Lygtis. \\ T A · x + b \u003d 0 Linijinis ir jo šaknis: x \u003d - b a.

Apibrėžimas 7.

Taigi, nebaigta kvadratinė lygtis a · x 2 + b · x \u003d 0 turės dvi šaknis x \u003d 0. ir. \\ T x \u003d - b a.

Pavyzdžiui pritvirtinkite medžiagą.

5 pavyzdys.

Būtina rasti 2 3 · x 2 - 2 2 7 · x \u003d 0 lygties tirpalą.

Sprendimas Šis sprendimas

Leiskite vadovauti X. Skliausteliuose ir gauti x · 2 3 · x - 2 2 7 \u003d 0. Ši lygtis yra lygiavertė lygtis x \u003d 0. ir 2 3 · x - 2 2 7 \u003d 0. Dabar būtina išspręsti gautą linijinę lygtį: 2 3 · x \u003d 2 2 7, X \u003d 2 2 7 2 3.

Trumpai išspręskite lygtį tokiu būdu parašyti:

2 3 · x 2 - 2 2 7 · x \u003d 0 x · 2 3 · x - 2 2 7 \u003d 0

x \u003d 0 arba 2 3 · x - 2 2 7 \u003d 0

x \u003d 0 arba x \u003d 3 3 7

Atsakymas: x \u003d 0, x \u003d 3 3 7.

Diskriminant, šaknų formulė kvadratinės lygties

Norėdami rasti kvadratinių lygčių sprendimą, yra šaknų formulė:

Apibrėžimas 8.

x \u003d - b ± d 2 · a kur D \u003d B 2 - 4 · a · c - vadinamoji kvadrato lygties diskriminant.

Įrašymas X \u003d - B ± D 2 · A iš esmės reiškia, kad x 1 \u003d - B + D 2 · A, X2 \u003d - B - D 2 · a.

Tai bus naudinga suprasti, kaip buvo gauta nurodyta formulė ir kaip ją taikyti.

Kvadratinės lygties šaknų išėjimas

Būkite iššūkis išspręsti kvadratinę lygtį a · x 2 + b · x + c \u003d 0. Atlikti daug lygiaverčių transformacijų:

• mes padalijome abi dalis lygties a.Išskyrus nulį, mes gauname sumažintą kvadratinę lygtį: x 2 + B a · x + c a \u003d 0;
• pažymėjome visą kvadratą kairėje gautos lygties pusėje:
  x 2 + ba · x + ca \u003d x 2 + 2 · b 2 · A · x + b 2 · A 2 - B 2 · A 2 + Ca \u003d X + B 2 · A 2 - B 2 · A 2 + CA .
  Po to lygtis imsis formą: X + B 2 · A 2 - B 2 · A 2 + C A \u003d 0;
• dabar galima perkelti paskutines dvi sąlygas į dešinę pusę, pakeisdami ženklą į priešingą, po kurio mes gauname: X + B 2 · A 2 \u003d B 2 · A 2 - C A;
• galiausiai, mes paversti įrašytą dešinėje pusėje paskutinio lygybės:
  B 2 · A 2 - C A \u003d B 2 4 · A 2 - C A \u003d B 2 4 · A2 - 4 · A · C4 · A 2 \u003d B 2 - 4 · A · C 4 · A 2.

Taigi, mes atvykome į X + B 2 · A 2 \u003d B 2 - 4 · A · C 4 · A 2, lygiavertė šaltinio lygtis a · x 2 + b · x + c \u003d 0.

Mes supratome tokių lygčių sprendimą ankstesnėse pastraipose (neišsamių kvadratinių lygčių sprendimas). Įgyta patirtis leidžia užbaigti apie X + B 2 · A 2 \u003d B 2 - 4 · A · C 4 · A 2:

• b 2 - 4 · a · c 4 · a 2< 0 уравнение не имеет действительных решений;
• b 2 - 4 · A · C4 · A 2 \u003d 0, lygtis turi formą X + B 2 · A 2 \u003d 0, tada X + B 2 · A \u003d 0.

Taigi vienintelė šaknų x \u003d - B 2 · A yra akivaizdi;

• b 2 - 4 · A · C4 · A 2\u003e 0, jis bus teisingas: X + B 2 · A \u003d B 2 - 4 · A · C4 · A 2 arba X \u003d B 2 · A - B 2 - 4 · A · C4 · A 2, kuris yra toks pat kaip X + - B 2 · A \u003d B 2 - 4 · A · C4 · A 2 arba X \u003d - B 2 · A - B 2 - 4 · A · C 4 · A 2, t.y. Lygtis turi dvi šaknis.

Galima daryti išvadą, kad X + B 2 · A 2 \u003d B 2 - 4 · A · C4 · A 2 (taigi pirminė lygtis) priklauso nuo išraiškos ženklo b 2 - 4 · A · C4 · A 2, įrašyti dešinėje pusėje. Ir šios išraiškos ženklą nustato skaitiklio numeris (vardiklis 4 · A 2 visada bus teigiamas), tai yra išraiškos ženklas B 2 - 4 · a · c. Ši išraiška B 2 - 4 · a · c Pavadinimas yra kvadratinio evakuacijos diskriminacija ir apibrėžiamas kaip raidės paskyrimas D. Čia galite įrašyti diskriminacinį esmę - pagal savo vertę ir žymenis yra baigtas, ar kvadratinė lygtis turės galiojančias šaknis, ir jei tai yra, kas yra šaknų skaičius - vienas ar du.

Grįžimas į X + B 2 · A 2 \u003d B 2 - 4 · A · C4 · A 2. Aš perrašau jį naudojant diskriminacinį pavadinimą: X + B 2 · A 2 \u003d D 4 · A 2.

Dar kartą suformuosime išvadas:

9 apibrėžimas 9.

• dėl D.< 0 Lygtis neturi galiojančių šaknų;
• dėl D \u003d 0. Lygtis turi vienintelę šaknį x \u003d - B 2 · a;
• dėl D\u003e 0. Lygtis turi dvi šaknis: X \u003d - B 2 · A + D 4 · A2 arba X \u003d - B 2 · A - D 4 · A 2. Šios šaknys, pagrįstos radikalų savybėmis, galima parašyti formoje: X \u003d - B 2 · A + D 2 · A arba - B 2 · A - D 2 · a. Ir kai mes atskleidžiame modulius ir suteikiame frakcijas į bendrą vardiklį, mes gauname: x \u003d - B + D 2 · A, X \u003d - B-D 2 · a.

Taigi mūsų argumentų rezultatas buvo kvadratinės lygties šaknų formulės pašalinimas:

x \u003d - B + D 2 · A, X \u003d - B - D 2 · A, Diskriminer D. Apskaičiuojamas pagal formulę. \\ T D \u003d B 2 - 4 · a · c.

Šios formulės leidžia diskriminuoti, kad būtų galima nustatyti galiojančias šaknis. Kai diskriminant yra nulis, abiejų formulių naudojimas suteiks tą patį šaknį kaip vienintelį kvadratinio lygties tirpalą. Jei diskidora yra neigiama, bando naudoti šaknų formulę kvadratinės lygties, mes susidursime su poreikiu pašalinti kvadratinę šaknį nuo neigiamo skaičiaus, kuris veda mus už faktinių skaičių. Su neigiama diskriminant, kvadratinių lygtys nebus galiojančios šaknys, bet visapusiškai konjugatų šaknų pora, nustatoma pagal tas pačias šaknų formules, gautas JAV.

Algoritmas, skirtas išspręsti kvadratinių lygčių šaknų formules

Galima išspręsti kvadratinę lygtį, nedelsiant dviračiu šaknų formulę, bet iš esmės jie, jei reikia, rasti sudėtingų šaknų.

Pagrindiniame atvejų masėje paprastai tai yra ne sudėtingų, bet galiojančių kvadratinių lygčių šaknų paieškai. Tada optimaliai prieš naudojant kvadratinės lygties šaknų formules, pirmiausia nustatykite diskriminant ir įsitikinkite, kad jis nėra neigiamas (kitaip mes darome išvadą, kad lygtis neturi galiojančių šaknų) ir tada pereikite prie šaknų vertės.

Pirmiau pateikti argumentai suteikia galimybę suformuluoti algoritmą kvadratinės lygties sprendimui.

Apibrėžimas 10.

Norėdami išspręsti kvadratinę lygtį a · x 2 + b · x + c \u003d 0, tai būtina:

• pagal formulę D \u003d B 2 - 4 · a · c rasti diskriminant;
• su D.< 0 сделать вывод об отсутствии у квадратного уравнения действительных корней;
• d \u003d 0 rasti vienintelę lygties šaknį pagal formulę X \u003d - B 2 · a;
• d\u003e 0 nustatykite dvi galiojančias kvadratinės lygties šaknis pagal formulę X \u003d - B ± D 2 · a.

Atkreipkite dėmesį, kad kai diskriminant yra nulis, galite naudoti formulę X \u003d - B ± D 2 · A, jis suteiks tą patį rezultatą kaip formulę X \u003d - B 2 · a.

Apsvarstykite pavyzdžius.

Kvadratinių lygčių sprendimų pavyzdžiai

Pateikiame skirtingų diskriminant vertybių pavyzdžių sprendimą.

6 pavyzdys.

Būtina rasti lygties šaknis x 2 + 2 · x - 6 \u003d 0.

Sprendimas Šis sprendimas

Mes parašytume skaičių koeficientus kvadratinės lygties: a \u003d 1, b \u003d 2 ir C \u003d - 6. Be to, mes elgiamės su algoritmu, t.y. Mes eisime apskaičiuoti diskriminacinį, kuriam mes pakeisime koeficientus a, b ir. \\ T C. Diskriminavimo formulėje: D \u003d B 2 - 4 · A · C \u003d 2 2 - 4 · 1 · (- 6) \u003d 4 + 24 \u003d 28.

Taigi, mes gavome D\u003e 0, o tai reiškia, kad pirminė lygtis turės dvi galiojančias šaknis.
Norėdami juos rasti, mes naudojame šaknų formulę x \u003d - B ± D 2 · A ir, pakeičiant atitinkamas vertes, mes gauname: x \u003d - 2 ± 28 2 · 1. Mes supaprastiname gautą išraišką, todėl šaknų ženklo daugiklis, po kurio seka frakcija:

x \u003d - 2 ± 2 · 7 2 2

x \u003d - 2 + 2 · 7 2 arba x \u003d - 2 - 2 · 7 2

x \u003d - 1 + 7 arba x \u003d - 1 - 7

Atsakymas: X \u003d - 1 + 7, x \u003d - 1 - 7.

7 pavyzdys.

Būtina išspręsti kvadratinę lygtį - 4 · x 2 + 28 · x - 49 \u003d 0.

Sprendimas Šis sprendimas

Nustatyti diskriminant: D \u003d 28 2 - 4 · (- 4) · (- 49) \u003d 784 - 784 \u003d 0. Su šia diskriminantija verte pradinė lygtis turės tik vieną šaknį, apibrėžtą formulėje X \u003d - B 2 · a.

x \u003d - 28 2 · (- 4) x \u003d 3, 5

Atsakymas: x \u003d 3, 5.

8 pavyzdys.

Būtina išspręsti lygtį 5 · Y 2 + 6 · Y + 2 \u003d 0

Sprendimas Šis sprendimas

Šios lygties skaitmeniniai koeficientai bus: a \u003d 5, b \u003d 6 ir c \u003d 2. Šias vertybes naudojame diskriminant: D \u003d B 2 - 4 · A · C \u003d 6 2 - 4 · 5 · 2 \u003d 36 - 40 \u003d - 4. Apskaičiuota diskriminant yra neigiama, todėl pradinė kvadratinė lygtis neturi galiojančių šaknų.

Jei užduotis yra nurodyti sudėtingas šaknis, taikyti šaknų formulę, atliekant veiksmus su sudėtingais numeriais:

x \u003d - 6 ± - 4 2 · 5,

x \u003d - 6 + 2 · I 10 arba X \u003d - 6 - 2 · I 10,

x \u003d - 3 5 + 1 5 · I arba X \u003d - 3 5 - 1 5 · I.

Atsakymas: Nėra galiojančių šaknų; Sudėtingos šaknys yra tokios: - 3 5 + 1 5 · I, - 3 5 - 1 5 · I.

Mokyklos programoje vis dar nėra reikalavimo ieškoti sudėtingų šaknų, todėl jei sprendimo metu diskriminant yra apibrėžiamas kaip neigiamas, atsakymas nedelsiant užfiksuotas, kad nėra galiojančių šaknų.

Formulės šaknys net antrajam koeficientams

Šaknų x \u003d - b ± d2 · a (d \u003d B 2 - 4 · a · c) formulė leidžia gauti kitą formulę, kompaktiškiau, leidžiančią rasti kvadratinių lygčių sprendimus su lygiu koeficientu x (arba 2 tipo koeficientas · N, pavyzdžiui, 2 · 3 arba 14 · ln 5 \u003d 2 · 7 · ln 5). Mes parodome, kaip rodoma ši formulė.

Būkite užduotis rasti kvadratinės lygties tirpalą a · x 2 + 2 · n · x + c \u003d 0. Mes veikiame ant algoritmo: nustatyti diskriminer D \u003d (2 · N) 2 - 4 · a · c \u003d 4 · n 2 - 4 · a · c \u003d 4 · (n 2 - a · c), tada naudokite Šaknų formulė:

x \u003d - 2 · N ± D 2 · A, X \u003d - 2 · N ± 4 · N 2 - A · C2 · A, X \u003d - 2 · N ± 2 N 2 - A · C2 · A, X \u003d - N ± N 2 - a · ca.

Leiskite išraiška N 2 - A · C turi būti nurodyta kaip D 1 (kartais D). Tada formulė kvadratinės lygties pagal antrą koeficientą 2 · n formulę formą:

x \u003d - N ± D 1 A, kur D 1 \u003d N 2 - a · c.

Tai lengva matyti, kad D \u003d 4 · D 1 arba D 1 \u003d D 4. Kitaip tariant, D 1 yra diskriminano ketvirtadalis. Akivaizdu, kad ženklas d 1 yra tas pats, kaip ir žymens D, o tai reiškia, kad ženklas d 1 taip pat gali būti kaip kvadratinės lygties šaknų buvimo ar nebuvimo rodiklis.

Apibrėžimas 11.

Taigi, norint rasti kvadratinės lygties sprendimą su antrojo koeficiento 2 · N, būtina:

• rasti D 1 \u003d N 2 - A · C;
• su D 1.< 0 сделать вывод, что действительных корней нет;
• d 1 \u003d 0, nustatykite vienintelę lygties šaknį pagal formulę X \u003d - N a;
• d 1\u003e 0 nustatykite dvi galiojančias šaknis pagal formulę X \u003d - N ± D 1 a.

9 pavyzdys.

Būtina išspręsti kvadratinę 5 · x 2 - 6 · x - 32 \u003d 0.

Sprendimas Šis sprendimas

Antrasis nurodytos lygties koeficientas gali būti sudarytas kaip 2 · (- 3). Tada perrašykite nurodytą kvadratinę lygtį kaip 5 · x 2 + 2 · (- 3) · x - 32 \u003d 0, kur A \u003d 5, N \u003d - 3 ir C \u003d - 32.

Apskaičiuojame ketvirtą diskriminacijos dalį: D 1 \u003d N 2 - A · C \u003d (- 3) 2 - 5 · (- 32) \u003d 9 + 160 \u003d 169. Gauta vertė teigiamai, tai reiškia, kad lygtis turi dvi galiojančias šaknis. Mes juos apibrėžiame pagal atitinkamą šaknų formulę:

x \u003d - N ± D 1 A, X \u003d - - 3 ± 169 5, x \u003d 3 ± 13 5,

x \u003d 3 + 13 5 arba x \u003d 3 - 13 5

x \u003d 3 1 5 arba x \u003d - 2

Būtų galima atlikti skaičiavimus ir įprastą kvadratinės lygties šaknų formulę, tačiau šiuo atveju sprendimas būtų sudėtingesnis.

Atsakymas: x \u003d 3 1 5 arba x \u003d - 2.

Supaprastinimas kvadratinių lygčių rūšių

Kartais galima optimizuoti šaltinio lygties tipą, kuris supaprastins šaknų skaičiavimo procesą.

Pavyzdžiui, kvadratinių lygčių 12 · x 2 - 4 · x - 7 \u003d 0 yra aiškiai patogiau nei 1200 · x 2 - 400 · x - 700 \u003d 0.

Dažniau supaprastinti kvadratinės lygties rūšį atlieka abiejų dalių dauginimas arba padalijimas į tam tikrą skaičių. Pavyzdžiui, parodėme supaprastintą 1200 · x 2 - 400 · x - 700 \u003d 0, gaunamą padalijant abi dalis iki 100.

Toks konversija yra įmanoma, kai kvadratinių lygčių koeficientai nėra tarpusavyje paprasti numeriai. Tada paprastai dalijasi abiem dalimis, lygiaverčiu iki didžiausio bendros absoliučių koeficientų verčių dalių.

Pavyzdžiui, naudokite kvadratinę lygtį 12 · x 2 - 42 · x + 48 \u003d 0. Apibrėžiame absoliutaus koeficientų verčių mazgus: mazgai (12, 42, 48) \u003d mazgas (mazgas (12, 42), 48) \u003d mazgas (6, 48) \u003d 6. Mes padalinsime dvi originalios kvadratinės lygties dalis iki 6 ir mes gauname lygiavertę kvadratinę 2 · x 2 - 7 · x + 8 \u003d 0.

Abiejų kvadratinių lygties dalių dauginimas paprastai atsikratytų dalinių koeficientų. Tuo pačiu metu padaugintas iš mažiausio bendrojo savo koeficientų vardiklio. Pavyzdžiui, jei kiekviena kvadratinio lygties dalis yra 1 6 · x 2 + 2 3 · x - 3 \u003d 0 dauginti nuo NOC (6, 3, 1) \u003d 6, tada jis bus įrašytas į paprastesnę X 2 formą + 4 · x - 18 \u003d 0.

Galiausiai atkreipiame dėmesį, kad beveik visada atsikratykite minuso pirmuoju kvadratinės lygties koeficientu, keičiant kiekvieno lygties nario ženklus, kurie pasiekiami abiejų 1 dalių padauginimu (arba padaliniais). Pavyzdžiui, iš kvadratinės lygties - 2 · x 2 - 3 · x + 7 \u003d 0, galite pereiti prie supaprastintos 2 · x 2 + 3 · x - 7 \u003d 0.

Bendravimas tarp šaknų ir koeficientų

Kvadratinių lygčių šaknų formulė x \u003d - B ± D 2 · A jau žinoma, kad mes išreiškia lygties šaknis per savo skaitmeninius koeficientus. Remdamiesi šioje formulėje, mes turime galimybę nustatyti kitas priklausomybes tarp šaknų ir koeficientų.

Garsiausi ir taikomi yra Vieta teoremo formulės:

x 1 + x 2 \u003d - b a ir x 2 \u003d c a.

Visų pirma dėl sumažintos kvadratinės lygties, šaknų kiekis yra antrasis koeficientas su priešingu ženklu, o šaknų produktas yra nemokamas. Pavyzdžiui, pagal kvadratinės 3 · x 2 - 7 · x + 22 \u003d 0 rūšių, galima nedelsiant nustatyti, kad jos šaknų suma yra 7 3, o šaknų produktas yra 22 3.

Taip pat galite rasti kitų nuorodų tarp šaknų ir koeficientų kvadratinės lygties. Pavyzdžiui, kvadratų lygties šaknų kvadratų suma gali būti išreikšta per koeficientus:

x 1 2 + x 2 2 \u003d (x 1 + x 2) 2 - 2 · x 1 · x 2 \u003d - ba 2 - 2 · ca \u003d b 2 a 2 - 2 · ca \u003d b 2 - 2 · a · ca 2.

Jei pastebėsite klaidą tekste, pasirinkite jį ir paspauskite Ctrl + Enter