Scalar produkto vektoriai

Mes ir toliau kovojame su vektoriais. Pirmojoje pamokoje Vektoriai Mes pažvelgėme į vektoriaus koncepciją, veiksmus su vektoriais, vektoriniais koordinatais ir paprasčiausiomis užduotimis su vektoriais. Jei įvedėte šį puslapį pirmą kartą nuo paieškos sistemos, aš primygtinai rekomenduoju skaityti pirmiau pateiktą įvadą, nes būtina naršyti man, kad manęs, notacijos, turėti pagrindines žinias apie vektorių ir sugebėti išspręsti pagrindines užduotis. Ši pamoka yra logiška tema, ir apie tai nustatysiu tipines užduotis, kuriose naudojamas vektorių skaliaras. Tai labai svarbi profesija.. Stenkitės nepraleisti pavyzdžių, su jais pridedama naudinga premija - praktika padės jums nustatyti perduotą medžiagą ir "užpildyti ranką" sprendžiant bendrus analitinės geometrijos uždavinius.

Vektorių pridėjimas, vektoriniai dauginimas pagal numerį. Būtų naivu manyti, kad matematika neatsirado nieko kito. Be jau peržiūrėtų veiksmų, yra keletas kitų operacijų su vektoriais, būtent: scalar produkto vektoriai, vektoriniai meno kūriniai ir. \\ T mišrios vektoriai. Scalar produktas vektorių yra pažįstamas mums iš mokyklos, du kiti darbai tradiciškai nurodo aukštesnės matematikos kursą. Temos yra paprastos, algoritmas daugeliui knibodančių užduočių ir yra suprantamas. Vienintelis dalykas. Informacija yra padorus, todėl nepageidautina pabandyti įvaldyti viską ir nedelsiant. Tai ypač pasakytina apie arbatą, tiki manimi, autorius nenori jausti chikatilo iš matematikos. Na, ne iš matematikos, žinoma, taip pat \u003d) Daugiau paruošti mokiniai gali naudoti medžiagas selektyviai, tam tikrą prasme ", kad" trūksta žinių, jums bus nekenksmingas grafikas Dracula \u003d)

Galiausiai atidarysime duris ir aistringai pamatyti, kas atsitinka, kai dvi variantai susitinka vienas su kitu.

Vektorių skaliaro apibrėžimas.
Salypų produkto savybės. Tipinės užduotys

Svarstymo darbo sąvoka

Pirmasis Pro Kampas tarp vektorių. Manau, kad kiekvienas yra intuityvus, kad toks kampas tarp vektorių, bet tik šiek tiek daugiau. Apsvarstykite nemokamus nulinio vektorių ir. Jei atidedate šiuos vektorius iš savavališko taško, tada paaiškėja, kad daugelis jau pateikė psichiškai:

Aš prisipažinsiu, čia aš paklausti situaciją tik supratimo lygiu. Jei jums reikia griežtos sąsajos tarp vektorių, kreipkitės į vadovėlį, už praktines užduotis, tai iš esmės nėra nieko. Taip pat aš būsiu vietose, kad galėčiau ignoruoti nulinio vektorių dėl savo mažos praktinės reikšmės. Rezervacija konkrečiai pateikta pažengusiems lankytojams, kurie gali mane paniekinti teoriniu kai kurių vėlesnių pareiškimų nežymiu.

Tai gali užtrukti nuo 0 iki 180 laipsnių (nuo 0 iki radianų) imtinai. Analitiškai šis faktas įrašomas į dvigubo nelygybės forma: arba. \\ T (radianuose).

Literatūroje kampo piktograma dažnai praleidžia ir rašo.

Apibrėžimas: Dviejų vektorių skalarinas produktas vadinamas skaičiumi, lygiais šių vektorių gaminiui tarp jų kampe:

Tai dabar yra gana griežta apibrėžtis.

Mes sutelkiame dėmesį į pagrindinę informaciją:

Paskyrimas: Scalar produktas yra pažymėtas arba tiesiog.

Operacijos rezultatas yra numeris: Vektorius padauginamas iš vektoriaus ir gaunamas skaičius. Iš tiesų, jei vektorių ilgiai yra skaičiai, kampo kosinumas - numeris, tada jų darbas Taip pat bus ir numeris.

Nedelsiant atšilimo pavyzdžių pora:

1 pavyzdys.

Sprendimas: Mes naudojame formulę . Tokiu atveju:

Atsakymas:

Cosine vertes galima rasti trigonometrinė lentelė. Aš rekomenduoju jį išspausdinti - beveik visose bokšto skyriuose bus reikalingas daug kartų.

Tik matematiniu požiūriu Scalar produktas yra nematomas, tai yra rezultatas, šiuo atveju yra tiesiog numeris ir tai yra. Nuo atsižvelgiant į fizikos uždavinių tašką, svarsto produktas visada turi tam tikrą fizinę reikšmę, tai yra po rezultato, turite nurodyti tam tikrą fizinį vienetą. Kanoninis pavyzdys apskaičiuojant jėgos darbą galima rasti bet kuriame vadovėlyje (formulė tiksliai yra skaliaras produktas). Jėgos darbas matuojamas džauliuose, todėl atsakymas bus įrašytas gana konkrečiai, pavyzdžiui.

2 pavyzdys.

Rasti, jei ir tarp vektorių kampas yra lygus.

Tai yra nepriklausomo sprendimo pavyzdys, atsakymas pamokos pabaigoje.

Tarp vektorių ir skalinio produkto vertės

Pavyzdžiui, "Scalar" produktas buvo teigiamas, ir 2 pavyzdyje - neigiamas. Sužinokite, koks priklauso nuo svarsto produkto ženklas. Mes žiūrime į mūsų formulę: . Nonero vektorių ilgiai visada yra teigiami: todėl ženklas gali priklausyti tik nuo kosinijos vertės.

Pastaba: Siekiant geriau suprasti toliau pateiktą informaciją, geriau ištirti kosino grafiką metoduose Funkcijos diagramos ir savybės. Pažiūrėkite, kaip kosinas ant segmento elgiasi.

Kaip jau buvo pažymėta, tarp vektorių kampas gali skirtis Ir šie atvejai yra galimi:

1) Jei kampas tarp vektorių Ūmus: (nuo 0 iki 90 laipsnių), tada , I. scalar produktas bus teigiamas pažintisKampinis tarp jų laikomas nuliu, o skalar produktas taip pat bus teigiamas. Kadangi formulė yra supaprastinta :.

2) Jei kampas tarp vektorių kvailas: (nuo 90 iki 180 laipsnių) ir atitinkamai, skalar produktas neigiamas:. Ypatingas atvejis: jei vektoriai nukreipta priešaisTada laikoma kampe tarp jų išvyko: (180 laipsnių). Salar produktas taip pat yra neigiamas, nes

Sąžiningos ir grąžinimo pareiškimai:

1) Jei kampas tarp vektorių yra aštrus. Alternatyviai, vektoriai yra padengti.

2) Jei kampas tarp duomenų vektorių yra kvailas. Arba vektoriai yra nukreipti priešingai.

Tačiau trečiasis atvejis yra ypač svarbus:

3) Jei kampas tarp vektorių tiesiai: (90 laipsnių), tada scalar produktas yra nulis:. Priešingai taip pat tiesa: jei tada. Kompaktiškas pareiškimas yra suformuluotas taip: Dviejų vektorių skalar produktas yra nulis, jei ir tik jei šie vektoriai yra stačiakampiai. Trumpas matematinis įrašymas:

! Pastaba : Pakartokite matematinės logikos pagrindai: Dvipusis loginės pasekmės piktograma paprastai yra skaitoma "jei ir tik tada", ", ir tik tuo atveju." Kaip matote, rodyklės yra nukreiptos į abi puses - "Tai išplaukia iš to ir atgal - nuo to, tai reiškia." Koks, beje, skirtumas nuo vienašalės šios piktogramos? Piktograma patvirtina tik tai, kadkad "tai išplaukia iš to", o ne tai, kad priešingai yra teisinga. Pavyzdžiui: Bet ne kiekvienas žvėris yra Panther, todėl šiuo atveju neįmanoma naudoti piktogramos. Tuo pačiu metu, vietoj piktogramos gali Naudokite vienpusį piktogramą. Pavyzdžiui, sprendžiant užduotį, mes sužinojome, kad padarėme išvadą, kad vektoriai yra ortogoninis: - toks įrašas bus teisingas ir dar svarbesnis nei .

Trečiasis atvejis turi didelę praktinę reikšmę.Nes tai leidžia jums patikrinti, ortogoniniai vektoriai ar ne. Šią užduotį išsprendžiame antrajame pamokos skyriuje.

Salarinio gabalo savybės

Grįžkime prie situacijos, kai dvi versijos pažintis. Šiuo atveju tarp jų esantis kampas yra nulis, o skalinio produkto formulė yra :.

Ir kas atsitiks, jei vektolis yra padaugintas su savimi? Akivaizdu, kad vektorius yra padengtas savimi, todėl mes naudojame aukščiau supaprastintą formulę:

Numeris vadinamas scalar aikštė Vektorius ir vadinamas.

Šiuo būdu, Vektorius Scalar Square yra lygus šio vektoriaus ilgio kvadrato:

Iš šios lygybės galite gauti formulę, skirtą skaičiuoti vektoriaus ilgį:

Nors atrodo nepertraukiamas, tačiau pamokos užduotys bus išnyks. Norėdami išspręsti problemas, mes taip pat reikės salarinio gabalo savybės.

Savavališkiems vektoriams ir bet kokiam skaičiui, šios savybės galioja:

1) - judėjimas arba vietinis. \\ T Svarstymo įstatymas.

2) - platinimas. \\ T skirstymas. \\ T Svarstymo įstatymas. Tiesiog galite atskleisti skliaustelius.

3) - Kvėpuokite arba asociatyvus. Svarstymo įstatymas. Nuolatinis gali būti išimtas iš skalės produkto.

Dažnai visos savybės (kurios vis dar reikalingos!) Studentai suvokia kaip nereikalingą šiukšles, kuri turi būti siunčiama ir iškart po egzamino saugiai pamiršta. Atrodo, kad čia yra svarbus, viskas ir taip nuo pirmos klasės žino, kad darbas nesikeičia nuo daugiklio Permutimo :. Turi įspėti, aukštesnėje matematikoje su panašiu požiūriu jį lengva blokuoti malkomis. Taigi, pavyzdžiui, pereinamasis turtas nėra teisingas algebriniai matricai. Tai yra neteisinga vektorius meno vektoriai. Todėl bet kokiomis savybėmis, kurias susitiksite aukštesnėje matematikoje, bent jau geriau, kad suprastumėte, ką galite padaryti, bet kodėl tai neįmanoma.

3 pavyzdys.

.

Sprendimas:Pirma, paaiškinkite situaciją su vektoriumi. Kas tai yra? Vektorių suma yra visiškai apibrėžtas vektorius, kuris yra nurodytas. Geometrinio veiksmai su vektoriais galima rasti straipsnyje Vektoriai. Tie patys petražolės su vektoriumi yra vektorių ir. \\ T

Taigi, pagal sąlygą, reikia rasti svarstymo produktą. Teoriškai, jums reikia taikyti darbo formulę Tačiau bėda yra ta, kad mes nežinome vektorių ilgio ir tarp jų. Tačiau sąlyga, atsižvelgiant į panašius dektorių parametrus, todėl eisime skirtingi būdai:

(1) Mes pakeisime vektorių išraišką.

(2) Atskleisti skliausteliuose pagal polinomalių dauginimo taisyklę, galite rasti rašybą straipsnyje. Sudėtingi numeriai arba. \\ T Dalinės racionalios funkcijos integravimas. Aš ne pakartojau \u003d) beje, atskleisti skliaustelius mums visą skalarino produkto paskirstymo turtą. Mes turime teisę.

(3) Pirmajame ir paskutiniame kadencijoje vektorių skalės kvadratai yra kompaktiški: . Antra, mes naudojame "Scalar" produkto pertvarkymą :.

(4) Mes pateikiame panašias sąlygas :.

(5) Pirmuoju laikotarpiu mes naudojame skalar aikštės formulę, kuri buvo paminėta ne taip seniai. Paskutiniu laikotarpiu, atitinkamai, tas pats dalykas veikia :. Antrasis terminas plečiasi pagal standartinę formulę .

(6) Mes pakeisime šias sąlygas ir atidžiai atlikite galutinius skaičiavimus.

Atsakymas:

Neigiama vertė Scalar produkto teigia, kad tarp vektorių kampas yra bukas.

Tipiškas užduotis, čia yra nepriklausomo sprendimo pavyzdys:

4 pavyzdys.

Raskite skalės produktą vektorių ir, jei žinote .

Dabar kita bendra užduotis yra tik nauja vektorinė ilgio formulė. Dalyvavimas čia bus šiek tiek sutampa, todėl aiškumo aš jį perrašysiu su kitu laišku:

5 pavyzdys.

Raskite vektoriaus ilgį, jei .

Sprendimas Šis sprendimas Tai bus tokia:

(1) Mes tiekiame vektoriaus išraišką.

(2) Naudojant ilgio formulę:, kaip vektoriaus "VE", mes turime sveiką skaičių išraišką.

(3) Naudojame vasaros suvestinę suvestinę formulę. Atkreipkite dėmesį, kaip ji čia veikia: "Tiesą sakant, tai yra skirtumo aikštė, ir iš tikrųjų tai yra." Tie, kurie nori, gali pertvarkyti vektorių vietose: - paaiškėjo, kaip ir šarmų tikslumu.

(4) toliau jau yra susipažinę iš dviejų ankstesnių užduočių.

Atsakymas:

Jei kalbate apie ilgį, nepamirškite nurodyti matmenų - "vienetų".

6 pavyzdys.

Raskite vektoriaus ilgį, jei .

Tai yra nepriklausomo sprendimo pavyzdys. Pilnas sprendimas ir atsakymas pamokos pabaigoje.

Mes ir toliau išspausti naudingus dalykus iš skalarinio produkto. Vėl pažvelkime į mūsų formulę . Pasak proporcingos taisyklės, kad būtų galima iš naujo nustatyti vektorių ilgį kairiajame pusėje:

Ir dalys pakeis vietas:

Kokia yra šios formulės reikšmė? Jei yra žinomi dviejų vektorių ir jų skalarino produkto ilgiai, gali būti apskaičiuojamas tarp duomenų vektorių kampas, taigi ir pats kampas.

Scalar produktas yra numeris? Numeris. Vektorinis ilgis - numeriai? Skaičiai. Taigi, frakcija taip pat yra tam tikras skaičius. Ir jei žinoma kampo kosina: , tai lengva rasti pačią kampą, naudojant atvirkštinę funkciją: .

7 pavyzdys.

Raskite kampą tarp vektorių ir, jei tai žinoma.

Sprendimas: Mes naudojame formulę:

Pasibaigus skaičiavimams buvo naudojamas techninis priėmimas - neracionalumo panaikinimas vardiklyje. Norint pašalinti neracionalumą, aš dominuoju NIZER ir vardiklį.

Taigi, jei.. \\ T , tada:

Atvirkštinių trigonometrinių funkcijų vertės gali būti nustatytos trigonometrinė lentelė. Nors tai vyksta retai. Analitinės geometrijos užduotyse atrodo, kad tam tikras neaiški lokys atrodo daug dažniau, o kampo vertė turi rasti maždaug naudojant skaičiuoklę. Tiesą sakant, mes vis dar pakarsime tokį vaizdą.

Atsakymas:

Vėlgi, nepamirškite nurodyti matmens - radians ir laipsnių. Asmeniškai aš būsiu tikri, kad "pašalinti visus klausimus", aš norėčiau nurodyti tiek, kad (jei, be sąlygų, žinoma, tai nėra būtina pateikti atsakymą tik į radianais arba tik laipsniais).

Dabar galite susidoroti su sudėtingesne užduotimi:

7 pavyzdys * *

Danies - vektorių ilgis ir tarp jų esantis kampas. Raskite kampą tarp vektorių.

Užduotis nėra taip sudėtinga kaip daug.
Mes analizuosime tirpalo algoritmą:

1) Pagal sąlygą reikia rasti kampą tarp vektorių ir, todėl jums reikia naudoti formulę .

2) Rasti svarstymo produktą (žr. 3, 4 pavyzdžius).

3) Radome vektoriaus ilgį ir vektoriaus ilgį (žr. 5, 6 pavyzdžius).

4) Sprendimo pabaiga sutampa su pavyzdžiu 7 - mes žinome numerį, todėl yra lengva rasti paties kampo:

Trumpas sprendimas ir atsakymas pamokos pabaigoje.

Antrasis pamokos skyrius yra skirtas to pačiai skalės produktui. Koordinatės. Tai bus dar lengviau nei pirmojoje dalyje.

Scalar produktas vektorių,
paprašė koordinatės orjormaliu pagrindu

Atsakymas:

Ką pasakyti, spręsti koordinates yra daug malonesnis.

14 pavyzdys.

Rasti vektorių skalės produktą ir jei

Tai yra nepriklausomo sprendimo pavyzdys. Čia galite naudoti operacijos asociacijos, tai yra, neskaito, bet nedelsiant atnešti tris viršų už skalar produkto ir atnaujinti į jį paskutinį. Sprendimas ir atsakymas pamokos pabaigoje.

Sudarant pastraipą provokuojantis pavyzdys dėl vektoriaus ilgio skaičiavimo:

15 pavyzdys.

Rasti ilgio vektorių , jeigu

Sprendimas:ankstesnio skyriaus metodas vėl pasirodo: bet yra dar vienas kelias:

Rasti vektorių:

Ir jo ilgis trivialėje formulėje :

Scalar produktas nėra čia.

Ne taip, kaip jis nėra, apskaičiuojant vektoriaus ilgį:
Sustabdyti. Negalima pasinaudoti akivaizdžia vekto ilgio nuosavybe? Ką galima pasakyti apie vektoriaus ilgį? Šis vektorius yra ilgesnis 5 kartus. Kryptis yra priešinga, tačiau ji neatlieka vaidmens, nes kalbėti apie ilgį. Akivaizdu, kad vektoriaus ilgis yra lygus darbui modulis. \\ T Skaičiai už vektoriaus ilgį:
- modulio ženklas "valgo" galimą atėmus numerį.

Šiuo būdu:

Atsakymas:

Cosine formulė tarp vektorių, kuriuos nustato koordinatės

Dabar mes turime išsamią informaciją, kuri anksčiau būtų gauta iš kosino kosinio formulės tarp vektorių per vektorių koordinates:

Kosinio kampas tarp lėktuvų vektorių ir nurodyta orjormaliu pagrindu, formulė išreiškiama:
.

Cosine kampas tarp kosmoso vektorių apibrėžta ortonormaliu pagrindu formulė išreiškiama:

16 pavyzdys.

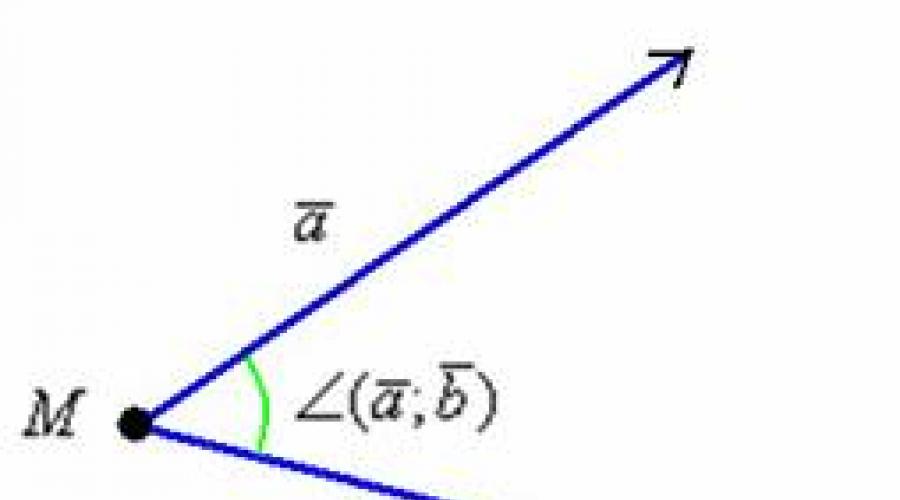
Pateikiami trys trikampio viršūnės. Rasti (kampas viršuje).

Sprendimas:Pagal sąlygą brėžinys nereikalingas, tačiau vis dar:

Norimas kampas pažymėtas žalia lanku. Nedelsiant prisiminkite kampo mokyklos paskyrimą: - ypatingas dėmesys viduryje Laiškas yra jūsų poreikio kampo viršuje. Dėl trumpumo, taip pat buvo galima įrašyti paprasčiausiai.

Iš piešinio, kad trikampio kampas sutampa su tarp vektorių ir, kitaip tariant: .

Analizė pageidautina mokytis atlikti psichiškai.

Ieškoti vektorių:

Apskaičiuojame "Scalar" produktą:

Ir vektorių ilgis:

Cosine Corner:

Būtent ši procedūra atlieka užduotį, kuri rekomenduoja arbatą. Daugiau paruoštų skaitytojų gali įrašyti "vienos eilutės" skaičiavimus:

Čia yra "blogos" kosinos vertės pavyzdys. Gauta vertė nėra galutinis, todėl nėra jokios prasmės atsikratyti neracionalumo vardiklyje.

Raskite pačią kampą:

Jei pažvelgsite į brėžinį, rezultatas yra gana tikėtinas. Norėdami patikrinti kampą, taip pat gali būti matuojamas ir vežėjas. Nepamirškite monitoriaus dangos \u003d)

Atsakymas:

Atsakydamas, nepamirškite to paklausė apie trikampio kampą (o ne apie tarp vektorių kampo), nepamirškite nurodyti tikslaus atsakymo: ir apytikslę kampo vertę: rasti skaičiuokle.

Tie, kurie turėjo procesą, gali apskaičiuoti kampus ir įsitikinkite, kad kanoninės lygybės teisingumas

17 pavyzdys.

Erdvą skiriama jų viršūnių trikampio koordinatės. Rasti kampą tarp šalių ir

Tai yra nepriklausomo sprendimo pavyzdys. Pilnas sprendimas ir atsakymas pamokos pabaigoje

Mažas galutinis skyrius bus skirtos projekcijoms, kuriose "Scalar" produktas taip pat "dalyvauja":

Vektorius projekcija ant vektoriaus. Koordinatės ašių projekcija.
"Cosine Guides Vector"

Apsvarstykite vektorių ir:

"Spogit" vektorius ant vektoriaus, nes tai, iš pradžios ir pabaigos vekto pertgendiculary. ant vektoriaus (žalios linijos). Įsivaizduokite, kad šviesos spinduliai statmenai patenka į vektorių. Tada segmentas (raudona linija) bus "vektoriaus šešėlis". Šiuo atveju vektorinė projekcija ant vektoriaus yra segmento ilgis. Tai yra, projekcija yra numeris.

Šis numeris nurodomas taip: "Didelis vektorius" rodo vektorių Kuris yra. \\ T Projektavimas, "mažas substrato vektorius" nurodo vektorių ANT kuri numatoma.

Pats įrašas yra skaitomas taip: "Vektorinio projekcija" A "ant vektoriaus."

Kas atsitiks, jei vektorius yra "per trumpas"? Mes atliekame tiesią liniją, kurioje yra vektorius. Ir vektorinė "a" bus jau prognozuojama ant vektoriaus krypties "būti"Tiesiog - tiesia linija, kurioje yra vektorius. Tas pats atsitinka, jei karalystės trisdešimtoje dešimtmetyje yra atidėtas vektorinis "A" - jis vis dar lengvai nesuderinamas prie tiesios linijos, kurioje yra vektorinė.

Jei kampas tarp vektorių Ūmus (kaip ir paveiksle), tada

Jei vektoriai ortogoninis, Tada (projekcija yra taškas, kurių matmenys laikomi nuliais).

Jei kampas tarp vektorių kvailas(Paveiksle, protiškai pertvarkykite vektoriaus rodyklę), tada (tas pats ilgis, bet paimtas su minuso ženklu).

Aš atidedu šiuos vektorius iš vieno taško:

Akivaizdu, kad perkeliant vektorių, jo projekcija nekeičia

Užduotys yra nepriklausomo sprendimo, į kurį galite matyti atsakymus.

Jei į užduotį ir ilgį vektorių, ir tarp jų kampas pateikiamas "ant lėkštės su mėlyna diską", tada problemos būklė ir jo sprendimas atrodo taip:

1 pavyzdys.Didžiuliai vektoriai. Raskite vektorių skalarinį produktą, jei jų ilgiai ir kampas tarp jų pateikiamos tokia prasme:

Taip pat apibrėžiamas kitas apibrėžimas, visiškai lygi 1 apibrėžimui 1.

2 apibrėžimas 2.. Vektorių skaliaro produktas vadinamas numeriu (skalaru), lygus šių vektorių ilgio dėl kito vektoriaus, kurį nustato pirmoji iš pirmųjų vektorių, projekcija. Formulė pagal 2 apibrėžimą:

Užduotis naudojant šią formulę yra išspręsta po kito svarbaus teorinio taško.

Vektorių skalavimo produkto nustatymas per koordinates

Tą patį numerį galima gauti, jei kintamieji vektoriai nustato pagal jų koordinates.

3 apibrėžimas. Vektorių skaliaro produktas yra numeris, lygus jų atitinkamų koordinatėms kūrinių sumai.

Ant paviršiaus

Jei dvi versijos ir plokštumoje apibrėžiami jų du carteso stačiakampio koordinatės

Šių vektorių skaliaro produktas yra lygus jų atitinkamų koordinatėms kūrinių sumai:

.

2 pavyzdys.Raskite skaitinį vektoriaus projekcijos dydį ant ašies lygiagrečiai vektoriui.

Sprendimas. Mes randame vektorių skalarinį produktą, sulankstant jų koordinates kūrinius:

Dabar turime prilyginti vektoriaus ilgio vektorinio skalės produktą ant vekto projekcijos ant ašies lygiagrečiai vektoriui (pagal formulę).

Mes randame vektoriaus ilgį kaip kvadratinę šaknį nuo koordinatės kvadratų sumos:

.

Mes kompiliuojame lygtį ir išspręstume:

Atsakymas. Norima skaitmeninė vertė yra minus 8.

Kosmose

Jei dvi versijos ir vietos yra apibrėžtos jų trijų krepšių stačiakampių koordinates

,

Šių vektorių skalarinas produktas taip pat yra lygus jų atitinkamų koordinatėms poravimo darbų sumai, tik koordinatės jau yra trys:

.

Užtikrinti svarstymo produktą su laikomu metodu užduotis - po analizuojant svarsto produkto savybes. Kadangi užduotį reikės nustatyti, kuris kampo formos kintamieji vektoriai.

Vektorių svarstymo produkto savybės

Algebriniai savybės

1. (perkelti turtą: Nuo pokyčių kintamųjų vektorių vietose, jų svarsto produkto dydis nesikeičia).

2. (kovos telefono numeris proport: Scalar produktas vektoriaus padaugintas iš kai kurių daugiklio, o kitas vektorius, lygus skaliarui produktui šių vektorių, padaugintų iš to paties veiksnio).

3. (paskirstymas, palyginti su vektorių turto sumąDviejų vektorių antrinio vektoriaus skalės produktas yra lygus pirmojo vektoriaus skalavimo darbų sumai trečiame vektoriuje ir antrajame vektoriuje trečiame vektoriuje).

4. (scalar Square Vector Daugiau nulio), jei tai yra nulinis vektorius, ir, jei - nulinis vektorius.

Geometrinės savybės

Apibrėžimuose, kad mes jau kalbėjome apie dviejų vektorių kampo sąvoką. Atėjo laikas paaiškinti šią koncepciją.

Pirmiau pateiktame paveikslėlyje rodoma du vektoriai, rodomi bendriems pradžioje. Ir pirmas dalykas atkreipti dėmesį į: tarp šių vektorių yra du kampas - φ 1 ir. \\ T φ 2 . Kuris iš šių kampų atsiranda vektorių skaliaro apibrėžimuose ir savybėmis? Laikomų kampų suma yra lygi 2 π Ir todėl šių kampų kosinimai yra lygūs. Svarstymo produkto apibrėžimas apima tik kampo kosiną, o ne jo išraiškos prasmę. Tačiau savybėms laikoma tik vienas kampas. Ir tai yra vienas iš dviejų kampų, kurie neviršija π , tai yra 180 laipsnių. Paveikslėlyje šis kampas yra nurodytas kaip φ 1 .

1. Du vektoriai skambučiai ortogoninis ir. \\ T kampas tarp šių vektorių - tiesioginis (90 laipsnių arba π / 2) jei Šių vektorių svarsto produktas yra nulis :

.

Ortodalizmas vektoriaus algebra yra dviejų vektorių statmeniškumas.

2. Du ne nulinės vektorinės yra aštrus kampas (nuo 0 iki 90 laipsnių, arba, kuris yra tas pats - mažiau π scalar produktas teigiamai .

3. yra du nulinės vektoriai "Botuse" kampas (nuo 90 iki 180 laipsnių arba tas pats dalykas yra daugiau π / 2) jei ir tik tada, kai jie skalar produktas neigiamas .

3 pavyzdys. Vektoriai pateikiami koordinatėse:

.

Apskaičiuokite visų šių vektorių porų kūrinius. Koks kampas (aštrus, tiesus, kvailas) sudaro šias vektorių poras?

Sprendimas. Apskaičiuokite atitinkamų koordinačių darbus.

Gavo neigiamą skaičių, todėl vektoriai sudaro kvailą kampą.

Gavo teigiamą skaičių, todėl vektoriai sudaro aštrią kampą.

Gauta nulis, todėl vektoriai sudaro tiesinį kampą.

Gavo teigiamą skaičių, todėl vektoriai sudaro aštrią kampą.

.

Gavo teigiamą skaičių, todėl vektoriai sudaro aštrią kampą.

Dėl savikontrolės galite naudoti internetinis skaičiuoklė Scalar produktas vektorių ir kosine kampų tarp jų .

4 pavyzdys. Pateikiami dviejų vektorių ir tarp jų kampo ilgiai:

.

Nustatykite, kokia yra vektorių skaičiaus ir stačiono (statmens) vertė.

Sprendimas. Perkelkite vektorių pagal polinomalių dauginimo taisyklę:

Dabar apskaičiuojame kiekvieną terminą:

.

Padaryti lygtį (lygybė nulio), mes pristatome panašius narius ir sprendžiant lygtį:

Atsakymas: mes turime vertę λ \u003d 1.8, kai vektoriai yra ortogoninė.

5 pavyzdys.Įrodyti, kad vektorius Ortogoninis (statmens) vektorius

Sprendimas. Norėdami patikrinti ortogonalumą, kintamus vektorių ir kaip polinomials, pakeičiant vietoj jos išraiškos, pateiktos TERK sąlyga:

.

Norėdami tai padaryti, kiekvienas pirmųjų polinomų narių narys padaugina kiekvienam antrojo nario nariui ir gauti darbai:

.

Atsižvelgiant į rezultatus, frakcija sumažinama sąnaudomis. Gauta šis rezultatas:

Išvada: Dėl daugybos, nulis, todėl ortogoniškumas (statgoniculy) yra įrodyta.

Išspręskite užduotį patys ir pamatysite sprendimą

6 pavyzdys. Vektorių ilgis yra suteiktas ir, o tarp šių vektorių kampas yra lygus π / keturi. Nustatykite, kokia vertė μ Vektoriai ir abipusiai statmenai.

Dėl savikontrolės galite naudoti internetinis skaičiuoklė Scalar produktas vektorių ir kosine kampų tarp jų .

Matricos atstovavimas skalavimo produkto vektorių ir N-dimensijų vektorių produkto

Kartais laimėjimas dėl aiškumo yra dviejų kintamųjų vektorių atstovavimas matricų pavidalu. Tada pirmasis vektorius yra atstovaujamas kaip matricos eilutė, o antroji - stulpelio matrica:

Tada bus vektorių skalės produktas Šių matricų produktas :

Rezultatas yra toks pat, kaip ir gautas metodas, kurį jau svarstėme. Gavome vieną numerį, o kolonėlės matricos matricos eilutės produktas taip pat yra vienas numeris.

Matricos formoje patogu atstovauti abstrakčių n-dimensijų vektorių produktą. Taigi dviejų keturių dimensijų vektorių produktas bus matricos eilutės produktas su keturiais kolonėlės matrica, taip pat su keturiais elementais, dviejų penkių dimensijų vektorių produktas - matricos eilutės produktas su penkiais elementais Stulpelio matrica taip pat su penkiais elementais ir pan.

7 pavyzdys. Rasti Steam vektorių skalaro kūrinius

,

naudojant matricos vaizdą.

Sprendimas. Pirmoji vektorių pora. Mes pristatome pirmąjį vektorių matricos eilutės forma, o antrasis - stulpelio matricos pavidalu. Mes randame šių vektorių skalarinį produktą kaip matricos eilutės produktą stulpelio matricoje:

Panašiai pristatome antrą porą ir surasime:

Kaip matome, rezultatai pasirodė tokie patys kaip ir tos pačios poros iš 2 pavyzdžio.

Kampas tarp dviejų vektorių

Cosine formulės iš dviejų vektorių produkcija yra labai graži ir trumpai.

Norėdami išreikšti skalarinį vektorių produktą

(1)

koordinatės forma, mes preliminariai surasime "Scalar" produktą ORT. "Scalar" produktas vektoriaus pats pagal apibrėžimą:

Kas yra įrašyta į formulę aukščiau: vektoriaus skalar produktas pats yra lygus jo ilgio kvadratams. Nulio kosinumas yra lygus vienai, todėl kiekvieno ORT aikštė bus lygi vienai:

Nuo vektorių

paprasiai statmenai, tada poros darbai ORTS bus nulis:

Dabar atlikite vektorinių polinomų dauginimą:

Mes pakeisime atitinkamų statinių kūrinių verčių lygybę:

Mes gauname kosinio kampo formulę tarp dviejų vektorių:

8 pavyzdys.Pateikiami trys taškai A.(1;1;1), B.(2;2;1), C.(2;1;2).

Rasti kampą.

Sprendimas. Mes randame vektorių koordinates:

,

.

Pagal kosino formulę, mes gauname:

Taigi,.

Dėl savikontrolės galite naudoti internetinis skaičiuoklė Scalar produktas vektorių ir kosine kampų tarp jų .

9 pavyzdys.Dana du vektoriai

Rasti sumą, skirtumą, ilgį, skalarinį produktą ir kampą tarp jų.

2. Nenaudokite. \\ T

I. Scalar produktas yra nulinės į nulį ir tik tuo atveju, kai bent vienas iš vektorių yra nulis arba jei vektoriai yra statmenai. Tiesą sakant, jei taip pat, ar tai.

Atgal, jei kintamieji vektoriai nėra nuliniai, tada dėl būklės

kai tai yra:

Kadangi nulinio vektoriaus kryptis yra neaiški, nulinis vektorius gali būti laikomas statmenai bet kuriam vektoriui. Todėl, nurodytas skalarino produkto turtas gali būti suformuluotas trumpai: skalar produktas yra nulinė, ir tik tuo atveju, kai vektoriai yra statmenai.

Ii. "Scalar" produktas turi judėjimo savybę:

Šis turtas tiesiogiai išplaukia iš apibrėžimo:

kadangi įvairūs to paties kampo pavadinimai.

III. Paskirstymo įstatymas yra labai svarbus. Jo naudojimas yra toks pat didelis, kaip įprasta aritmetika arba algebra, kur jis yra suformuluotas taip: padauginti sumą, jums reikia dauginti kiekvieną gerai ir sulankstyti gautus darbus, i.e ..

Akivaizdu, kad algebros aritmetiniai ar polinominiai aritmetiniai arba polinomialuose dauginimas yra pagrįstas šiuo dauginamuoju savybe.

Šis įstatymas turi tokią pačią didelę svarbą vektoriaus algebra, nes remiantis ja galime kreiptis į vektorių įprastą daugiapolių polinomalių.

Mes įrodome, kad už tris vektorių A, B, su lygiavertiškumu

Pagal antrąjį svarstymo produkto apibrėžimą, išreikštą formulėje, mes gauname:

Dabar taikant 2 projekcijų turtą iš 5 straipsnio 5, mes randame:

q.E.D.

IV. "Scalar" produktas turi derinio tikslumą, palyginti su skaitmeniniu veiksniu; Šis turtas išreiškiamas taip:

i.E. Norėdami dauginti skalarino produkto vektorių skaičiumi, pakanka dauginti šį numerį vienu iš veiksnių.