Skalarski proizvodi vektori

Nastavljamo se nositi s vektorima. U prvoj lekciji Vektori za čajnike Pogledali smo koncept vektora, akcije s vektorima, koordinate vektora i najjednostavnijim zadacima s vektorima. Ako ste prvi put unijeli ovu stranicu iz tražilice, preporučujem čitanja gore navedenog članka uvod, budući da je potrebno za navigaciju pojmovima koje me koristi, notacija, da imaju osnovno znanje o vektorima i biti u mogućnosti za rješavanje elementarnih zadataka. Ova lekcija je logičan nastavak teme, a na njemu ću definirati tipične zadatke u kojima se koristi skalarni proizvod vektora. Ovo je vrlo važno zanimanje., Pokušajte ne propustiti primjere, koristan bonus je pričvršćen na njih - praksa će vam pomoći da popravite materijal koji je prošao i "ispunite ruku" na rješavanju zajedničkih zadataka analitičke geometrije.

Dodavanje vektora, vektor množenja po broju .... Bilo bi naivno misliti da matematika nije smislila ništa drugo. Osim već pregledanih radnji, postoji niz drugih operacija s vektorima, naime: skalarski proizvodi vektori, vektorski radovi vektori i mješoviti vektori, Skalarni proizvod vektora nam je poznat iz škole, dva druga djela tradicionalno se odnose na tijek veće matematike. Teme su jednostavne, algoritam za rješavanje mnogih zadataka začuvanja i razumljiv. Jedina stvar. Informacije su pristojne, tako da je nepoželjno pokušati svladati sve i odmah. To posebno vrijedi za čajnike, vjerujte mi, autor ne želi osjetiti Chikata iz matematike. Pa, ne iz matematike, naravno, također, previše pripremljenih studenata može koristiti materijale selektivno, u određenom smislu, "da bi dobili" nedostaje znanje, za vas ću biti bezopasan graf Dracula \u003d)

Otvorit ćemo, konačno, vrata i strastveno vidjeti što se događa kada se dvije verzije međusobno upoznaju.

Definicija skalarnog proizvoda vektora.
Svojstva skalarnog proizvoda. Tipični zadaci

Koncept skalarnog rada

Prvi pro Kut između vektora, Mislim da su svi intuitivni da takav kut između vektora, ali samo u slučaju malo više. Razmislite o slobodnim vektorima bez kore i. Ako odgodite ove vektore iz proizvoljne točke, onda ispadne slike koju su mnogi već predstavili mentalno:

Priznajem, ovdje sam prekršio situaciju samo na razini razumijevanja. Ako trebate strogu definiciju kuta između vektora, obratite se udžbeniku, za praktične zadatke, to je u načelu za ništa. U daljnjem tekstu, bit ću na mjestima za ignorirati nulte vektore zbog njihove male praktične značajnosti. Rezervacija je napravljena posebno za napredne posjetitelje koji me mogu prigovoriti u teoretskoj nepotpunosti nekih naknadnih izjava.

Može poduzeti vrijednosti od 0 do 180 stupnjeva (od 0 do radijana) inkluzivno. Analitički se ta činjenica bilježi u obliku dvostruke nejednakosti: ili (u radijanima).

U literaturi je ikona kuta često preskakanje i pisanje jednostavno.

Definicija: Skalarni proizvod dva vektora naziva se broj jednak proizvod ovih vektora na kosinu kutu između njih:

Ovo je sada prilično stroga definicija.

Usredotočeni smo na bitne informacije:

Oznaka: Skalarni proizvod označen je ili jednostavno.

Rezultat operacije je broj: Vektor se umnožava s vektorom, a broj se dobiva. Doista, ako su duljine vektora brojevi, kosinu kut - broj, zatim njihov rad Također će biti i broj.

Odmah nekoliko primjera zagrijavanja:

Primjer 1.

Odluka: Koristimo formulu , U ovom slučaju:

Odgovor:

Vrijednosti kosinusa mogu se naći u trigonometrijski stol, Preporučujem da ga ispis - bit će potrebno u gotovo svim dijelovima tornja i trebat će mnogo puta.

Čisto od matematičkog stajališta Skalarni proizvod je bezdimenzionalno, to jest, rezultat, u ovom slučaju, je jednostavno broj i to je to. Sa stajališta o zadacima fizike, skalarni proizvod uvijek ima određeno fizičko značenje, to jest, nakon rezultata, morate odrediti određenu fizičku jedinicu. Kanonski primjer izračunavanja rada sile može se naći u bilo kojem udžbeniku (formula točno je skalarni proizvod). Rad sile se mjeri u džulama, dakle, odgovor će se zabilježiti sasvim posebno, na primjer.

Primjer 2.

Pronaći ako i kut između vektora je jednak.

To je primjer za samostalnu odluku, odgovor na kraju lekcije.

Kut između vektora i vrijednosti skalarnog proizvoda

U primjeru 1, skalarni proizvod bio je pozitivan, au primjeru 2 - negativan. Saznajte što ovisi znak skalarnog proizvoda. Gledamo našu formulu: , Duljine neezerskih vektora uvijek su pozitivne: stoga znak može ovisiti samo o količini kosine.

Bilješka: Za bolje razumijevanje informacija u nastavku, bolje je istražiti raspored kosine u metodama Grafikoni i svojstva funkcije, Pogledajte kako se kosinus na segmentu ponaša.

Kao što je već navedeno, kut između vektora može varirati unutar I mogući su sljedeći slučajevi:

1) ako kut između vektora akutan: (od 0 do 90 stupnjeva), zatim , I. skalarni proizvod će biti pozitivan sinovenUgao između njih smatra se nulom, a skalarni proizvod će također biti pozitivan. Budući da je formula pojednostavljena :.

2) ako kut između vektora glup: (od 90 do 180 stupnjeva) i na odgovarajući način, skalarni proizvod negativan:. Poseban slučaj: ako vektori usmjeren nasuprotTada se razmatra kutak između njih odstupao: (180 stupnjeva). Skalarni proizvod je također negativan jer

Poštena i povratna izjava:

1) Ako je kut između podataka vektora oštar. Alternativno, vektori su obloženi.

2) Ako je kut između podataka vektora glup. Alternativno, vektori su usmjereni nasuprot.

Ali treći slučaj je od posebnog interesa:

3) ako kut između vektora ravno: (90 stupnjeva), zatim skalarni proizvod je nula:. Također je istina: ako, onda. Kompaktna izjava formulira se na sljedeći način: Skalarni proizvod dva vektora je nula ako i samo ako su ovi vektori ortogonalni, Kratko matematičko snimanje:

! Bilješka : Ponovite osnove matematičke logike: Ikona dvosmjerne logičke posljedice obično se čita "ako i samo tada", "u to i samo u slučaju." Kao što možete vidjeti, strelice su usmjerene na obje strane - "to slijedi iz ovoga, i natrag - od toga, slijedi." Što, usput, razlika od unilateralne ikone? Ikona odobrava samo toTo "to slijedi iz toga", a ne činjenica da je upravo suprotno. Na primjer: ali ne i svaka zvijer je panter, pa u ovom slučaju nemoguće je koristiti ikonu. U isto vrijeme, umjesto ikone limenka Koristite jednosmjernu ikonu. Na primjer, rješavamo zadatak, otkrili smo da smo zaključili da su vektori ortogonalni: - Takav će zapis biti točan, pa čak i više relevantniji od .

Treći slučaj ima veliki praktični značaj.jer vam omogućuje da provjerite, ortogonalni vektori ili ne. Ovaj zadatak riješimo u drugom dijelu lekcije.

Svojstva skalarnog komada

Vratimo se na situaciju kada su dvije verzije sinoven, U tom slučaju, kut između njih je nula, a formula skalarnog proizvoda uzima oblik :.

I što će se dogoditi ako se vektor umnoži s vama? Jasno je da je vektor obložen samim sobom, tako da koristimo gornju pojednostavljenu formulu:

Broj se zove skalar Vektor i naziva se.

Na ovaj način, Vector Scalar Trg jednak je kvadratu duljine ovog vektora:

Iz te jednakosti možete dobiti formulu za izračunavanje duljine vektora:

Iako se čini neprekidnim, ali zadaci lekcije će svi nestati na mjestu. Da bismo riješili probleme, također ćemo trebati svojstva skalarnog komada.

Za proizvoljne vektore i bilo koji broj, sljedeća svojstva važe:

1) - kretanje ili komutativan Zakon skalarnog rada.

2) - distribucija ili distributivni Zakon skalarnog rada. Jednostavno, možete otkriti zagrade.

3) - prozračan ili asocijativan Zakon skalarnog rada. Konstanta se može izvaditi iz skalarnog proizvoda.

Često, sve vrste svojstava (koje su još uvijek potrebne!) Studenti percipiraju kao nepotrebno smeće, koje treba samo poslati i odmah nakon što je ispit sigurno zaboravljen. Čini se da je ovdje važno, sve i tako iz prve klase zna da se rad ne mijenja iz permutacija multiplikatora :. Mora se upozoriti, u većoj matematici sa sličnim pristupom lako je blokirati ogrjev. Dakle, na primjer, imovina prijelaza nije poštena za algebarske matrice, Pogrešno je vektorski umjetnički vektori, Stoga, u bilo kojoj osobinama koje ćete sastajati tijekom veće matematike, barem je bolje da se deneže razumjeti što možete učiniti, ali zašto je nemoguće.

Primjer 3.

.

Odluka:Prvo, razjasnite situaciju s vektorom. Što je uopće? Zbroj vektora je potpuno definiran vektor, koji je označen. Geometrijsko tumačenje aktivnosti s vektorima može se naći u članku Vektori za čajnike, Isti peršina s vektorom je zbroj vektora i.

Dakle, po uvjetima, potrebno je pronaći skalarni proizvod. U teoriji trebate primijeniti radnu formulu Ali problem je da smo nepoznati dužina vektora i kut između njih. No, u stanju dajući slične parametre za vektore, tako ćemo ići na različite načine:

(1) Zamijenimo izraz vektora.

(2) Otkriti zagrade prema pravilu umnožavanja polinoma, možete pronaći čaroliju u članku. Složeni brojevi ili Integriranje frakcijske racionalne funkcije, Neću se ponavljati \u003d) usput, otkriti zagrade za sve raspodjelu svojstva skalarnog proizvoda. Imamo pravo.

(3) U prvom i posljednjem roku, skalarni kvadrati vektora su kompaktni: , U drugom, koristimo preraspodjelu skalarnog proizvoda :.

(4) Dajemo slične uvjete :.

(5) U prvom mandatu koristimo formulu skalarnog trga, koji se spominje ne tako davno. U posljednjem mandatu, u skladu s tim, ista stvar radi :. Drugi izraz se širi prema standardnoj formuli .

(6) Zamijenimo te uvjete i pažljivo provesti konačne izračune.

Odgovor:

Negativna vrijednost skalarnog proizvoda navodi činjenicu da je kut između vektora tupi.

Zadatak tipičan, ovdje je primjer za neovisno rješenje:

Primjer 4.

Pronađite skalarni proizvod vektora i ako to znate .

Sada još jedan zajednički zadatak je samo nova formula duljine vektora. Oznake ovdje bit će pomalo podudaraju, pa ću za jasnoću ponovno napisati s drugim slovom:

Primjer 5.

Pronađite duljinu vektora ako .

Odluka To će biti kako slijedi:

(1) Mi isporučujemo izraz vektora.

(2) Korištenje formule duljine:, dok kao vektor "ve", imamo cijeli broj.

(3) Koristimo ljetnu sažetku sažetak formule. Imajte na umu kako ovdje radi znatiželjno: "Zapravo, to je kvadrat razlike i, zapravo, jest." Oni koji žele mogu preurediti vektore na mjestima: - Isto je ispalo s točnosti alkalisa.

(4) Nadalje je već poznato od dva prethodna zadatka.

Odgovor:

Ako govorite o duljini, ne zaboravite navesti dimenziju - "jedinice".

Primjer 6.

Pronađite duljinu vektora ako .

Ovo je primjer za neovisno rješenje. Kompletno rješenje i odgovor na kraju lekcije.

Nastavljamo stisnuti korisne stvari iz skalarnog proizvoda. Ponovno pogledajmo našu formulu , Prema pravilu proporcije za resetiranje duljine vektora u nazivnicu lijeve strane:

I dijelovi će promijeniti mjesta:

Što je značenje ove formule? Ako su duljine dva vektora i njihov skalarni proizvod, onda se može izračunati kosinu kut između vektora podataka, a time i kut.

Skalarni proizvod je broj? Broj. Duljina vektora - brojevi? Brojevi. Dakle, frakcija je također neki broj. I ako je poznata kosinusna kutak: , lako je pronaći kut koji koristi obrnutu funkciju: .

Primjer 7.

Pronađite kut između vektora i, ako je to poznato.

Odluka: Koristimo formulu:

U završnoj fazi izračuna korištena je tehnički prijem - eliminaciju iracionalnosti u nazivniku. Kako bi se uklonila iracionalnost, domomio sam Nizer i nazivnika.

Dakle, ako , onda:

Vrijednosti inverzne trigonometrijske funkcije mogu se pronaći trigonometrijski stol, Iako se to dogodi rijetko. U zadacima analitičke geometrije čini se da neka vrsta nejasne medvjeda čini se da se pojavljuje mnogo češće, a vrijednost kutne mora pronaći približno korištenjem kalkulatora. Zapravo, još ćemo ponoviti takvu sliku.

Odgovor:

Opet, ne zaboravite navesti dimenziju - radijani i stupnjeve. Osobno ću biti siguran da "ukloniti sva pitanja", radije bih navela da (ako, po uvjetima, naravno, nije potrebno predstaviti odgovor samo na radijanima ili samo u stupnjevima).

Sada možete se nositi sa složenijim zadatkom:

Primjer 7 *

Danies - duljine vektora i kut između njih. Pronađite kut između vektora.

Zadatak nije tako kompliciran kao višestruko.
Analizirat ćemo algoritam rješenja:

1) pod uvjetom je potrebno pronaći kut između vektora i, tako da trebate koristiti formulu .

2) Pronađite skalarni proizvod (vidi primjere broj 3, 4).

3) Nalazimo duljinu vektora i duljine vektora (vidi primjere 5, 6).

4) Završetak odluke podudara se s primjerom 7 - znamo broj i stoga je lako pronaći kut:

Kratko rješenje i odgovor na kraju lekcije.

Drugi dio lekcije posvećen je istom skakaru proizvod. Koordinate. To će biti još lakše nego u prvom dijelu.

Skalarni proizvod vektora,
upita koordinate u ortonormalnoj osnovi

Odgovor:

Što reći, za rješavanje koordinata je mnogo ugodnije.

Primjer 14.

Pronađite skalarni proizvod vektora i ako

Ovo je primjer za neovisno rješenje. Ovdje možete koristiti asocijativnost operacije, to jest, ne računati, ali odmah donijeti prva tri izvan skalarnog proizvoda i unaprijediti na nju. Rješenje i odgovor na kraju lekcije.

U zaključku paragraf provokativnog primjera o izračunavanju duljine vektora:

Primjer 15.

Pronađite duljine vektore , ako a

Odluka:pojavit će se metoda prethodnog dijela: ali postoji još jedan put:

Pronađite vektor:

I njezinu duljinu u trivijalnoj formuli :

Skalarni proizvod nije ovdje uopće.

Ne kao što ne, pri izračunavanju duljine vektora:
Stop. Nemojte iskoristiti očiglednu imovinu vektorske duljine? Što se može reći o duljini vektora? Ovaj vektor je duži vektor 5 puta. Smjer je suprotan, ali ne igra ulogu, jer govori o duljini. Očito je da je duljina vektora jednaka radu modul Brojevi za duljinu vektora:
- Znak modula "jede" mogući minus broj.

Na ovaj način:

Odgovor:

Kosinu formulu kuta između vektora koje su postavljene koordinatom

Sada imamo potpune informacije koje treba prethodno izvesti iz fosinu formule između vektora kroz koordinate vektora:

Kut kosenice između ravnini vektora i navedeno u ortonormalnoj osnovi, formula je izražena:
.

Kut kosinusa između svemirskih vektora definirano u ortonormalnoj osnovi formula je izražena:

Primjer 16.

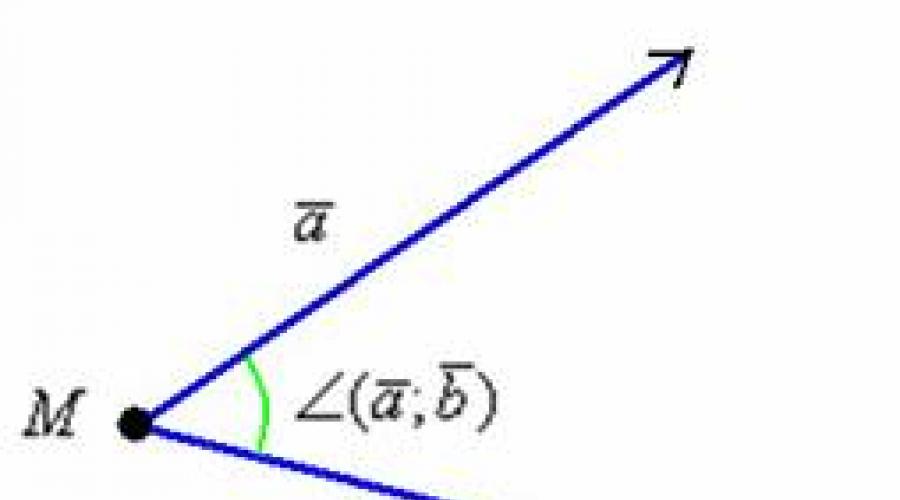
Daje se tri vrha trokuta. Pronađite (kut na vrhu).

Odluka:Pod uvjetom, crtež nije potreban, ali još uvijek:

Željeni kut označen je zelenim lukom. Odmah zapamtite školsku oznaku kutka: - posebnu pozornost na sredina Pismo je vrh ugla koji vam je potreban. Za kratkoću, bilo je moguće jednostavno snimiti.

Iz crteža je jasno da se kut trokuta podudara s kutom između vektora i, drugim riječima: .

Analiza je poželjno učenje da se izvode mentalno.

Pronađite vektore:

Izračunavamo skalarni proizvod:

I duljina vektora:

Cosine corner:

To je ovaj postupak za obavljanje zadatka koji preporučuju čajne. Pripremljeniji čitatelji mogu zabilježiti izračune "jedne linije":

Evo primjera "loše" kosinus. Dobivena vrijednost nije konačna, tako da nema posebnog smisla da biste dobili osloboditi od iracionalnosti u denominatoru.

Pronađite samog kuta:

Ako pogledate crtež, rezultat je prilično uvjerljiv. Za provjeru kuta također se može mjeriti i transporter. Ne oštetite premaz monitora \u003d)

Odgovor:

Kao odgovor, nemojte to zaboraviti upitao o kutu trokuta (i ne o kutu između vektora) ne zaboravite navesti točan odgovor: i približnu vrijednost kuta: pronađeno korištenje kalkulatora.

Oni koji su uživali u procesu mogu izračunati kutove i osigurati pravdu kanonske jednakosti

Primjer 17.

Prostor se daje koordinate trokuta njihovih vrhova. Pronaći kut između stranaka i

Ovo je primjer za neovisno rješenje. Kompletno rješenje i odgovor na kraju lekcije

Mali završni dio bit će posvećen projekcijama u kojima je ikakoran proizvod "uključen":

Vektorska projekcija na vektoru. Projekcija vektora na koordinatne osi.
Vodiči kosinusa

Razmislite o vektorima i:

Sprogitni vektor na vektoru, za to, od početka i kraja vektora izostavljanja permikular na vektoru (zelene isprekidane linije). Zamislite da zrake svjetlosti okomito spadaju u vektor. Tada će segment (crvena linija) biti "sjena" vektora. U tom slučaju, vektor projekcija na vektoru je duljina segmenta. To jest, projekcija je broj.

Ovaj broj je označen na sljedeći način :, "Veliki vektor" označava vektor Koji projekcija, "mali vektor podloge" označava vektor Na koji je projiciran.

Sam zapis čita se ovako: "Projekcija vektora" A "na vektoru."

Što se događa ako je vektor "prekratak"? Provodimo ravnu liniju koja sadrži vektor. I vektor "a" će biti projiciran već u smjeru vektora "Budite"Jednostavno - na ravnoj liniji koja sadrži vektor. Isto se događa ako se vektor "a" odgođen u tridesetim kraljevstvom - to je još uvijek lako diskobran na ravnu liniju koja sadrži vektor.

Ako kut između vektora akutan (kao na slici), onda

Ako vektori ortogonalan, Zatim (projekcija je točka, čiji se dimenzije smatraju nulom).

Ako kut između vektora glup(Na slici, mentalno preurediti strelicu vektora), zatim (ista duljina, ali uzeti s minus znakom).

Odredit ću te vektore s jedne točke:

Očito, kada se pomakne vektor, njegova se projekcija ne mijenja

Bit će zadataka za neovisno rješenje koje možete vidjeti odgovore.

Ako je u zadatku i duljini vektora, a kut između njih prikazan je "na tanjuriću s plavim pogonom", onda je stanje problema i njegovo rješenje izgleda ovako:

Primjer 1.Ogroman vektori. Pronađite skalarni proizvod vektora ako su njihove duljine i kut između njih prikazani u sljedećem značenju:

Još jedna definicija je također definirana, potpuno ekvivalentna definiciji 1.

Definicija 2., Skalarni proizvod vektora naziva se broj (skalar), jednak duljini duljine ovih vektora na projekciji drugog vektora na osi određenoj prvim određenim vektorima. Formula prema definiciji 2:

Zadatak s korištenjem ove formule rješava se nakon sljedeće važne teorijske točke.

Određivanje skalarnog proizvoda vektora kroz koordinate

Isti broj se može dobiti ako su varijabilni vektori postavljeni po njihovim koordinatama.

Definicija 3. Skalarni proizvod vektora je broj jednak zbroju radova njihovih koordinata.

Na površini

Ako su dvije verzije i na ravninu definirane svojim dvoje kartezijanske pravokutne koordinate

skalarni proizvod ovih vektora jednak je zbroju radova njihovih koordinata:

.

Primjer 2.Pronađite numeričku veličinu vektora projekcije na osi paralelno s vektorom.

Odluka. Nalazimo skalarni proizvod vektora, sklopivši radovi njihovih koordinata:

Sada moramo izjednačiti rezultirajući skalarni proizvod vektora vektora dužine vektora na vektorskoj projekciji na osi paralelno s vektorom (u skladu s formulom).

Duljinu vektora nalazimo kao kvadratni korijen iz zbroja kvadrata njegove koordinate:

.

Sastavljamo jednadžbu i riješimo ga:

Odgovor. Željena numerička vrijednost je minus 8.

U svemiru

Ako su dvije verzije i prostor definirane njihovim tri kartezijanske pravokutne koordinate

,

skalarni proizvod ovih vektora također je jednak zbroju radova u parovima njihovih koordinata, samo su koordinate već tri:

.

Zadatak pronalaženja skalarnog proizvoda s razmatranom metodom - nakon što je raščlanjivao svojstva skalarnog proizvoda. Budući da će zadatak morati odrediti koji varijabilni vektori kuta.

Svojstva skalarnog proizvoda vektora

Algebarska svojstva

1. (premjestiti svojstvo: Od promjena na mjestima varijabilnih vektora, veličina njihovog skalarnog proizvoda ne mijenja se).

2. (kombinacija telefonski broj: Skalarni proizvod vektora pomnožen s nekim multiplikator, i drugi vektor, jednak skalarnom produktu tih vektora, pomnožen s istim faktorom).

3. (distribucija u odnosu na iznos imovine vektora: Skalarni proizvod zbroja dva vektora na trećem vektoru jednak je zbroju skalarskih radova prvog vektora na trećem vektoru i drugom vektoru na trećem vektoru).

4. (skalarni trg vektor više nula), ako je to neezer vektor, i, ako - nula vektor.

Geometrijska svojstva

U definicijama omamljenog rada već smo zabrinuti koncept kuta između dva vektora. Vrijeme je da razjasnimo ovaj koncept.

Gore navedene slike prikazuje dva vektor, koji su prikazani općim početkom. I prva stvar koja treba obratiti pozornost na: Postoje dva kuta između tih vektora - φ 1 i φ 2 , Koji se od tih kutova pojavljuje u definicijama i svojstvima skalarnog proizvoda vektora? Iznos razmatranih kutova jednak je 2 π I stoga su kosines tih kutova jednaki. Definicija skalarnog proizvoda uključuje samo kosinu kut, a ne značenje njezina izraza. Ali samo jedan kut se razmatra u svojstvima. I to je jedan od dva kuta koji ne prelazi π , to jest, 180 stupnjeva. Na slici, ovaj kut je označen kao φ 1 .

1. Dva poziva vektora ortogonalan i kut između tih vektora - izravan (90 stupnjeva ili π / 2) ako skalarni proizvod ovih vektora je nula :

.

Pravoslalizam u vektorskoj algebri je okopanost dva vektora.

2. Dva ne-nula vektor čine oštro kut (od 0 do 90 stupnjeva, ili, što je isto - manje π skalarni proizvod pozitivno .

3. Dva ne-nula vektora čine tup kut (od 90 do 180 stupnjeva, ili da je ista stvar više π / 2) ako i samo kada skalarni proizvod negativan .

Primjer 3. Vektori se daju u koordinatama:

.

Izračunajte skalarna djela svih parova tih vektora. Koji kut (oštro, ravan, glupi) oblikuju ove parove vektora?

Odluka. Izračunaj će biti dodatak radova relevantnih koordinata.

Dobio negativan broj, tako da vektori stvaraju glupi kut.

Primio pozitivan broj, tako da vektori formiraju oštar kut.

Primili nulu, tako da vektori formiraju ravni kut.

Primio pozitivan broj, tako da vektori formiraju oštar kut.

.

Primio pozitivan broj, tako da vektori formiraju oštar kut.

Za samopouzdanje možete koristiti online kalkulator skalarni proizvod vektora i kosinus između njih .

Primjer 4. Duljine dva vektora i kut između njih su dani:

.

Odredite, s kakvom vrijednošću broja vektora i ortogonalnih (okomito).

Odluka. Pomaknite vektore u skladu s pravilom umnožavanja polinoma:

Sada izračunavamo svaki izraz:

.

Napravite jednadžbu (jednakost rada nula), predstavljamo slične članove i rješavamo jednadžbu:

Odgovor: Imamo vrijednost λ \u003d 1.8, u kojem su vektori ortogonalni.

Primjer 5.Dokazati taj vektor ortogonalna (okomita) vektor

Odluka. Da biste provjerili ortogonalnost, varijabilne vektore i polinome, zamjenjujući umjesto njezinog izraza dano u terk stanju:

.

Da biste to učinili, svaki član (izraz) prvih polinoma pomnoženi na svaki član drugog i dobivenih radova su presavijeni:

.

U rezultatu koji rezultiraju, frakcija se smanjuje na rashodu. Dobiven je sljedeći rezultat:

Zaključak: Kao rezultat umnožavanja, nula se stoga dokazuje ortogonalnost (okomitost) vektora.

Sami riješite zadatak, a zatim vidite odluku

Primjer 6. Duljine vektora su dane i, a kut između tih vektora je jednak π / četiri. Odredite s kakvom vrijednošću μ Vektori i međusobno okomit.

Za samopouzdanje možete koristiti online kalkulator skalarni proizvod vektora i kosinus između njih .

Matrica zastupljenost skalarnog proizvoda vektora i produkt n-dimenzionalnih vektora

Ponekad je pobjeda za jasnoću predstavljanje dva varijabilni vektora u obliku matrica. Tada je prvi vektor predstavljen kao matrični niz, a drugi - u obliku matrice stupca:

Tada će biti skalarni proizvod vektora proizvod ovih matrica :

Rezultat je isti kao i dobivena metoda koju smo već razmotrili. Dobili smo jedan broj, a proizvod matričnog niza na matrici stupca je također jedan jedan broj.

U matričnom obliku prikladno je predstavljati proizvod apstraktnih n-dimenzionalnih vektora. Prema tome, proizvod od dva četverodimenzionalni vektori će biti proizvod matričnog niza s četiri elementa na matrici stupca također s četiri elementa, proizvod od dva fivezonski vektora - proizvod matričnog niza s pet elemenata na Stupac matrica također s pet elemenata i tako dalje.

Primjer 7. Pronaći skalarna djela pare vektora

,

koristeći prikaz matrice.

Odluka. Prvi par vektora. Predstavljamo prvi vektor u obliku matričnog niza, a drugi - u obliku matrice stupca. Skalarni proizvod ovih vektora nalazimo kao proizvod matričnog niza na matrici stupca:

Slično tome, predstaviti drugi par i pronaći:

Kao što možemo vidjeti, rezultati su ispitani isti kao i isti parovi iz Primjera 2.

Kutak između dva vektora

Izlaz kosinu formule kutka između dva vektora je vrlo lijepa i kratka.

Izraziti skalarni proizvod vektora

(1)

u koordinatnom obliku, preliminarno ćemo pronaći skalarni proizvod Ort. Skalarni proizvod vektora na sebe po definiciji:

Što je zabilježeno u gornjoj formuli: skalarni proizvod vektora na sebi jednak je kvadratu duljine, Kosinu nula jednaka je jednom, pa će kvadrat svakog orkta biti jednak jednom:

Od vektora

paralično okomite, a zatim par Djela Orts će biti nula:

Sada izvršite množenje vektorskih polinula:

Zamijenimo jednakost vrijednosti odgovarajućih skalarskih radova Orthops:

Dobivamo kosinu formulu kuta između dva vektora:

Primjer 8.Dane su tri boda A.(1;1;1), B.(2;2;1), C.(2;1;2).

Pronađite kut.

Odluka. Nalazimo koordinate vektora:

,

.

Prema kosinoj formuli, dobivamo:

Stoga, .

Za samopouzdanje možete koristiti online kalkulator skalarni proizvod vektora i kosinus između njih .

Primjer 9.Dana dva vektora

Pronađite količinu, razliku, duljinu, skalarni proizvod i kut između njih.

2. DRUGA

I. Skalarni proizvod je nacrtana na nulu u to i samo u slučaju kada je barem jedan od vektora nula ili ako su vektori okomita. Zapravo, ako ili, ili to.

Natrag, ako varijabilni vektori nisu nula, onda zbog stanja

kada slijedi:

Budući da je smjer nultog vektora neizvjestan, nulti vektor se može smatrati okomitom na bilo koji vektor. Stoga se određeno svojstvo skalarnog proizvoda može formulirati: Skalarni proizvod je nacrtana na nulu u tome i samo slučaj kada su vektori okomita.

Ii. Skalarni proizvod ima svojstvo kretanja:

Ovo svojstvo izravno slijedi iz definicije:

jer različite oznake istog ugla.

Iii. Distributivni zakon je iznimno važan. Njegova je upotreba velika kao u uobičajenoj aritmetici ili algebri, gdje se formulira kao: da umnožava količinu, morate razmnožiti svaku dobro i presaviti dobivene radove, tj ..

Očito, umnožavanje višestrukih brojeva u aritmetičkim ili polinom u algebri temelji se na ovom svojstvu množenja.

Ovaj zakon ima istu glavnu važnost u vektorskoj algebri, budući da se na temelju toga možemo primijeniti na vektore uobičajene vladati polinomi.

Dokažimo da za bilo koji tri vektora a, b, s jednakošću

Prema drugoj definiciji skalarnog proizvoda, izražena formulom, dobivamo:

Primjena sada imovine 2 projekcije iz § 5, nalazimo:

q.E.D.

Iv. Skalarni proizvod ima točnost kombinacije u odnosu na numerički čimbenik; Ova nekretnina je izražena na sljedeći način:

tj. Zamnožavanje skalarnog proizvoda vektora po broju, dovoljno je umnožiti s tog broja jedan od čimbenika.