Επίλυση εκθετικών τριγωνομετρικών εξισώσεων. Πιο πολύπλοκες τριγωνομετρικές εξισώσεις
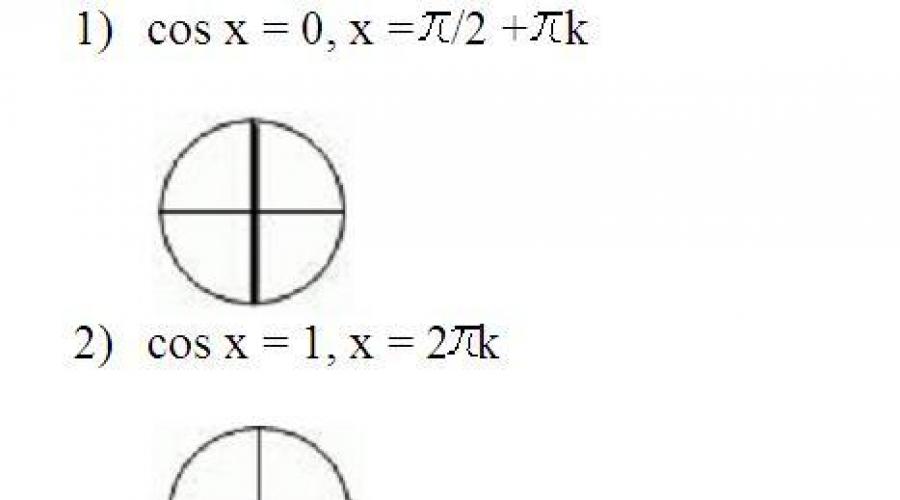
Διαβάστε επίσης
Απαιτεί γνώση των βασικών τύπων της τριγωνομετρίας - το άθροισμα των τετραγώνων του ημιτόνου και του συνημιτόνου, η έκφραση της εφαπτομένης μέσω του ημιτόνου και του συνημιτόνου και άλλα. Για όσους τα έχουν ξεχάσει ή δεν τα γνωρίζουν, συνιστούμε να διαβάσετε το άρθρο "".
Έτσι, γνωρίζουμε τους βασικούς τριγωνομετρικούς τύπους, ήρθε η ώρα να τους χρησιμοποιήσουμε στην πράξη. Επίλυση τριγωνομετρικών εξισώσεωνμε τη σωστή προσέγγιση, είναι μια αρκετά συναρπαστική δραστηριότητα, όπως, για παράδειγμα, η επίλυση ενός κύβου του Ρούμπικ.
Με βάση το ίδιο το όνομα, είναι σαφές ότι μια τριγωνομετρική εξίσωση είναι μια εξίσωση στην οποία ο άγνωστος βρίσκεται κάτω από το πρόσημο της τριγωνομετρικής συνάρτησης.
Υπάρχουν οι λεγόμενες απλούστερες τριγωνομετρικές εξισώσεις. Έτσι φαίνονται: sinx = a, cos x = a, tg x = a. Σκεφτείτε πώς να λύσετε τέτοιες τριγωνομετρικές εξισώσεις, για λόγους σαφήνειας, θα χρησιμοποιήσουμε τον ήδη γνωστό τριγωνομετρικό κύκλο.
sinx = α
cos x = α
tg x = α
κούνια x = α
Οποιαδήποτε τριγωνομετρική εξίσωση λύνεται σε δύο στάδια: φέρνουμε την εξίσωση στην απλούστερη μορφή και στη συνέχεια την λύνουμε ως την απλούστερη τριγωνομετρική εξίσωση.
Υπάρχουν 7 βασικές μέθοδοι με τις οποίες λύνονται οι τριγωνομετρικές εξισώσεις.
Μεταβλητή Αντικατάσταση και Μέθοδος Αντικατάστασης
Επίλυση τριγωνομετρικών εξισώσεων μέσω παραγοντοποίησης
Αναγωγή σε ομοιογενή εξίσωση
Επίλυση εξισώσεων πηγαίνοντας στη μισή γωνία
Εισαγωγή βοηθητικής γωνίας
Λύστε την εξίσωση 2cos 2 (x + / 6) - 3sin (/ 3 - x) +1 = 0
Χρησιμοποιώντας τους τύπους μείωσης, παίρνουμε:
2cos 2 (x + / 6) - 3cos (x + / 6) +1 = 0
Αντικαταστήστε το cos (x + / 6) με το y για απλότητα και λάβετε τη συνηθισμένη τετραγωνική εξίσωση:
2 ετών 2 - 3 ετών + 1 + 0
Των οποίων οι ρίζες y 1 = 1, y 2 = 1/2
Τώρα ας πάμε με την αντίστροφη σειρά
Αντικαθιστούμε τις τιμές y που βρέθηκαν και παίρνουμε δύο απαντήσεις:
Πώς να λύσετε την εξίσωση sin x + cos x = 1;
Μετακινήστε τα πάντα προς τα αριστερά, ώστε το 0 να παραμείνει στα δεξιά:
sin x + cos x - 1 = 0
Θα χρησιμοποιήσουμε τις παραπάνω ταυτότητες για να απλοποιήσουμε την εξίσωση:
αμαρτία x - 2 αμαρτία 2 (x / 2) = 0
Κάνουμε την παραγοντοποίηση:
2 sin (x / 2) * cos (x / 2) - 2 sin 2 (x / 2) = 0
2 sin (x / 2) * = 0
Παίρνουμε δύο εξισώσεις
Μια εξίσωση είναι ομοιογενής ως προς το ημίτονο και το συνημίτονο αν όλοι οι όροι της ως προς το ημίτονο και το συνημίτονο έχουν την ίδια ισχύ της ίδιας γωνίας. Για να λύσετε μια ομοιογενή εξίσωση, προχωρήστε ως εξής:
α) να μεταφέρει όλα τα μέλη του στην αριστερή πλευρά·
β) βγάλτε όλους τους κοινούς παράγοντες εκτός παρένθεσης.
γ) εξισώστε όλους τους παράγοντες και τις αγκύλες με 0.
δ) μια ομοιογενής εξίσωση μικρότερου βαθμού λαμβάνεται σε αγκύλες, με τη σειρά της χωρίζεται σε ημίτονο ή συνημίτονο στον υψηλότερο βαθμό.
ε) να λύσετε την εξίσωση που προκύπτει για το tg.
Λύστε την εξίσωση 3sin 2 x + 4 sin x cos x + 5 cos 2 x = 2
Ας χρησιμοποιήσουμε τον τύπο sin 2 x + cos 2 x = 1 και ας απαλλαγούμε από τα ανοιχτά δύο στα δεξιά:
3sin 2 x + 4 sin x cos x + 5 cos x = 2sin 2 x + 2cos 2 x
sin 2 x + 4 sin x cos x + 3 cos 2 x = 0
Διαιρέστε με το cos x:
tg 2 x + 4 tg x + 3 = 0
Αντικαταστήστε το tg x με y και λάβετε μια τετραγωνική εξίσωση:
y 2 + 4y +3 = 0, των οποίων οι ρίζες y 1 = 1, y 2 = 3
Από εδώ βρίσκουμε δύο λύσεις στην αρχική εξίσωση:
x 2 = αρκτάν 3 + k
Λύστε την εξίσωση 3sin x - 5cos x = 7
Προχωρώντας στο x / 2:
6sin (x / 2) * cos (x / 2) - 5cos 2 (x / 2) + 5sin 2 (x / 2) = 7sin 2 (x / 2) + 7cos 2 (x / 2)
Μετακινήστε τα πάντα προς τα αριστερά:
2sin 2 (x / 2) - 6sin (x / 2) * cos (x / 2) + 12cos 2 (x / 2) = 0
Διαιρέστε με συντελεστή (x / 2):
tg 2 (x / 2) - 3tg (x / 2) + 6 = 0
Για εξέταση, παίρνουμε μια εξίσωση της μορφής: a sin x + b cos x = c,
όπου a, b, c είναι κάποιοι αυθαίρετοι συντελεστές και το x είναι άγνωστο.
Χωρίζουμε και τις δύο πλευρές της εξίσωσης σε:
Τώρα οι συντελεστές της εξίσωσης, σύμφωνα με τους τριγωνομετρικούς τύπους, έχουν τις ιδιότητες sin και cos, δηλαδή: το μέτρο τους δεν είναι μεγαλύτερο από 1 και το άθροισμα των τετραγώνων = 1. Ας τους συμβολίσουμε ως cos και sin, αντίστοιχα, όπου είναι το η λεγόμενη βοηθητική γωνία. Τότε η εξίσωση θα πάρει τη μορφή:
cos * sin x + sin * cos x = С
ή αμαρτία (x +) = C
Η λύση σε αυτή την απλούστερη τριγωνομετρική εξίσωση θα είναι
x = (-1) k * arcsin С - + k, όπου
Σημειώστε ότι το cos και το sin χρησιμοποιούνται εναλλακτικά.
Λύστε την εξίσωση sin 3x - cos 3x = 1
Σε αυτή την εξίσωση, οι συντελεστές είναι:
a =, b = -1, οπότε διαιρούμε και τις δύο πλευρές με = 2
Το μάθημα βίντεο "Get an A" περιλαμβάνει όλα τα απαραίτητα θέματα για να περάσετε με επιτυχία την εξέταση στα μαθηματικά σε 60-65 βαθμούς. Πλήρως όλες οι εργασίες 1-13 του Προφίλ Ενιαίας Κρατικής Εξέτασης στα Μαθηματικά. Κατάλληλο και για επιτυχία στη Βασική εξέταση στα μαθηματικά. Αν θέλετε να περάσετε τις εξετάσεις για 90-100 μόρια, πρέπει να λύσετε το μέρος 1 σε 30 λεπτά και χωρίς λάθη!
Μαθήματα προετοιμασίας για τις εξετάσεις για τις τάξεις 10-11, καθώς και για καθηγητές. Όλα όσα χρειάζεστε για να λύσετε το μέρος 1 της εξέτασης στα μαθηματικά (12 πρώτα προβλήματα) και το πρόβλημα 13 (τριγωνομετρία). Και αυτά είναι περισσότερα από 70 μόρια στις εξετάσεις, και ούτε ένας φοιτητής εκατό βαθμών ούτε ένας φοιτητής ανθρωπιστικών σπουδών μπορεί να τα κάνει χωρίς αυτά.
Όλη η θεωρία που χρειάζεστε. Γρήγορες λύσεις, παγίδες και μυστικά της εξέτασης. Όλες οι σχετικές εργασίες του μέρους 1 από την Τράπεζα εργασιών του FIPI έχουν αποσυναρμολογηθεί. Το μάθημα πληροί πλήρως τις απαιτήσεις της εξέτασης-2018.
Το μάθημα περιέχει 5 μεγάλα θέματα, 2,5 ώρες το καθένα. Κάθε θέμα δίνεται από την αρχή, απλό και ξεκάθαρο.
Εκατοντάδες εργασίες ΧΡΗΣΗΣ. Προβλήματα λέξεων και θεωρία πιθανοτήτων. Απλοί και εύκολοι στην απομνημόνευση αλγόριθμοι για την επίλυση προβλημάτων. Γεωμετρία. Θεωρία, υλικό αναφοράς, ανάλυση όλων των τύπων εργασιών USE. Στερεομετρία. Δύσκολες λύσεις, χρήσιμα cheat sheets, ανάπτυξη χωρικής φαντασίας. Τριγωνομετρία από το μηδέν στο πρόβλημα 13. Κατανόηση αντί να στριμώχνω. Οπτική εξήγηση σύνθετων εννοιών. Αλγεβρα. Ρίζες, μοίρες και λογάριθμοι, συνάρτηση και παράγωγος. Η βάση για την επίλυση σύνθετων προβλημάτων του 2ου μέρους της εξέτασης.
Προστασία της ιδιωτικής ζωής σας είναι σημαντική για εμάς. Για το λόγο αυτό, έχουμε αναπτύξει μια Πολιτική Απορρήτου που περιγράφει τον τρόπο με τον οποίο χρησιμοποιούμε και αποθηκεύουμε τις πληροφορίες σας. Διαβάστε την πολιτική απορρήτου μας και ενημερώστε μας εάν έχετε ερωτήσεις.
Συλλογή και χρήση προσωπικών πληροφοριών
Οι προσωπικές πληροφορίες αναφέρονται σε δεδομένα που μπορούν να χρησιμοποιηθούν για την ταυτοποίηση ενός συγκεκριμένου ατόμου ή για επικοινωνία μαζί του.
Ενδέχεται να σας ζητηθεί να δώσετε τα προσωπικά σας στοιχεία ανά πάσα στιγμή όταν επικοινωνήσετε μαζί μας.
Ακολουθούν ορισμένα παραδείγματα των τύπων προσωπικών πληροφοριών που ενδέχεται να συλλέγουμε και πώς μπορούμε να χρησιμοποιήσουμε αυτές τις πληροφορίες.
Ποιες προσωπικές πληροφορίες συλλέγουμε:
- Όταν αφήνετε ένα αίτημα στον ιστότοπο, ενδέχεται να συλλέξουμε διάφορες πληροφορίες, όπως το όνομά σας, τον αριθμό τηλεφώνου, τη διεύθυνση email σας κ.λπ.
Πώς χρησιμοποιούμε τα προσωπικά σας στοιχεία:
- Τα προσωπικά στοιχεία που συλλέγουμε μας επιτρέπουν να επικοινωνήσουμε μαζί σας και να αναφέρουμε μοναδικές προσφορές, προσφορές και άλλες εκδηλώσεις και επερχόμενες εκδηλώσεις.
- Από καιρό σε καιρό, ενδέχεται να χρησιμοποιήσουμε τα προσωπικά σας στοιχεία για να στείλουμε σημαντικές ειδοποιήσεις και μηνύματα.
- Ενδέχεται επίσης να χρησιμοποιήσουμε προσωπικές πληροφορίες για εσωτερικούς σκοπούς, όπως διεξαγωγή ελέγχων, ανάλυση δεδομένων και διάφορες έρευνες, προκειμένου να βελτιώσουμε τις υπηρεσίες που παρέχουμε και να σας παρέχουμε συστάσεις σχετικά με τις υπηρεσίες μας.
- Εάν συμμετέχετε σε κλήρωση, διαγωνισμό ή παρόμοια διαφημιστική εκδήλωση, ενδέχεται να χρησιμοποιήσουμε τις πληροφορίες που παρέχετε για τη διαχείριση τέτοιων προγραμμάτων.
Αποκάλυψη πληροφοριών σε τρίτους
Δεν αποκαλύπτουμε πληροφορίες που λαμβάνουμε από εσάς σε τρίτους.
Εξαιρέσεις:
- Εάν είναι απαραίτητο - σύμφωνα με το νόμο, δικαστική απόφαση, σε δικαστικές διαδικασίες και/ή βάσει δημόσιων αιτημάτων ή αιτημάτων από κυβερνητικές αρχές στην επικράτεια της Ρωσικής Ομοσπονδίας - να αποκαλυφθούν τα προσωπικά σας στοιχεία. Ενδέχεται επίσης να αποκαλύψουμε πληροφορίες σχετικά με εσάς εάν κρίνουμε ότι μια τέτοια αποκάλυψη είναι απαραίτητη ή κατάλληλη για λόγους ασφάλειας, επιβολής του νόμου ή άλλους κοινωνικά σημαντικούς λόγους.
- Σε περίπτωση αναδιοργάνωσης, συγχώνευσης ή πώλησης, ενδέχεται να μεταφέρουμε τις προσωπικές πληροφορίες που συλλέγουμε σε κατάλληλο τρίτο μέρος - τον νόμιμο διάδοχο.
Προστασία προσωπικών πληροφοριών
Λαμβάνουμε προφυλάξεις - συμπεριλαμβανομένων διοικητικών, τεχνικών και φυσικών - για την προστασία των προσωπικών σας δεδομένων από απώλεια, κλοπή και κατάχρηση, καθώς και από μη εξουσιοδοτημένη πρόσβαση, αποκάλυψη, τροποποίηση και καταστροφή.
Σεβασμός του απορρήτου σας σε εταιρικό επίπεδο
Προκειμένου να διασφαλίσουμε ότι τα προσωπικά σας στοιχεία είναι ασφαλή, φέρουμε τους κανόνες εμπιστευτικότητας και ασφάλειας στους υπαλλήλους μας και παρακολουθούμε αυστηρά την εφαρμογή των μέτρων εμπιστευτικότητας.
Επίλυση των απλούστερων τριγωνομετρικών εξισώσεων.
Η λύση των τριγωνομετρικών εξισώσεων οποιουδήποτε επιπέδου πολυπλοκότητας καταλήγει τελικά στην επίλυση των απλούστερων τριγωνομετρικών εξισώσεων. Και σε αυτό, ο τριγωνομετρικός κύκλος αποδεικνύεται και πάλι ο καλύτερος βοηθός.
Ας θυμηθούμε τους ορισμούς του συνημιτόνου και του ημιτόνου.
Το συνημίτονο μιας γωνίας είναι η τετμημένη (δηλαδή η συντεταγμένη κατά μήκος του άξονα) ενός σημείου του μοναδιαίου κύκλου που αντιστοιχεί σε μια περιστροφή κατά μια δεδομένη γωνία.
Το ημίτονο μιας γωνίας είναι η τεταγμένη (δηλαδή η συντεταγμένη κατά μήκος του άξονα) ενός σημείου στον μοναδιαίο κύκλο που αντιστοιχεί σε μια περιστροφή κατά μια δεδομένη γωνία.
Η θετική φορά κίνησης στον τριγωνομετρικό κύκλο είναι η αριστερόστροφη κίνηση. Μια περιστροφή 0 μοιρών (ή 0 ακτίνων) αντιστοιχεί σε ένα σημείο με συντεταγμένες (1; 0)
Θα χρησιμοποιήσουμε αυτούς τους ορισμούς για να λύσουμε τις απλούστερες τριγωνομετρικές εξισώσεις.
1. Ας λύσουμε την εξίσωση
Αυτή η εξίσωση ικανοποιείται από όλες αυτές τις τιμές της γωνίας περιστροφής, που αντιστοιχούν στα σημεία του κύκλου, η τεταγμένη του οποίου είναι ίση με.
Ας σημειώσουμε το σημείο με την τεταγμένη στον άξονα της τεταγμένης:

Ας σχεδιάσουμε μια οριζόντια γραμμή παράλληλη στον άξονα της τετμημένης μέχρι να τέμνεται με τον κύκλο. Παίρνουμε δύο σημεία που βρίσκονται σε έναν κύκλο και έχουν μια τεταγμένη. Αυτά τα σημεία αντιστοιχούν στις γωνίες περιστροφής κατά και ακτίνια:

Αν, αφήνοντας το σημείο που αντιστοιχεί στη γωνία περιστροφής κατά ακτίνια, γυρίσουμε έναν πλήρη κύκλο, τότε θα φτάσουμε στο σημείο που αντιστοιχεί στη γωνία περιστροφής κατά ακτίνια και έχει την ίδια τεταγμένη. Δηλαδή, αυτή η γωνία περιστροφής ικανοποιεί και την εξίσωσή μας. Μπορούμε να κάνουμε όσες «αδρανείς» περιστροφές θέλουμε, επιστρέφοντας στο ίδιο σημείο και όλες αυτές οι τιμές των γωνιών θα ικανοποιήσουν την εξίσωσή μας. Ο αριθμός των "αδρανών" περιστροφών θα υποδηλωθεί με το γράμμα (ή). Εφόσον μπορούμε να κάνουμε αυτές τις περιστροφές και προς θετικές και αρνητικές κατευθύνσεις, (ή) μπορούμε να πάρουμε οποιεσδήποτε ακέραιες τιμές.
Δηλαδή, η πρώτη σειρά λύσεων στην αρχική εξίσωση έχει τη μορφή:
![]() ,, είναι το σύνολο των ακεραίων (1)
,, είναι το σύνολο των ακεραίων (1)
Ομοίως, η δεύτερη σειρά λύσεων είναι:
![]() , όπου , . (2)
, όπου , . (2)
Όπως ίσως μαντέψατε, αυτή η σειρά λύσεων βασίζεται στο σημείο του κύκλου που αντιστοιχεί στη γωνία περιστροφής κατά.
Αυτές οι δύο σειρές λύσεων μπορούν να συνδυαστούν σε μία καταχώρηση:
Αν πάρουμε αυτό το αρχείο (δηλαδή, ζυγό), τότε παίρνουμε την πρώτη σειρά λύσεων.
Αν πάρουμε αυτήν την εγγραφή (δηλαδή την περιττή), τότε παίρνουμε τη δεύτερη σειρά λύσεων.
2. Τώρα ας λύσουμε την εξίσωση
Επειδή η τετμημένη του σημείου του μοναδιαίου κύκλου λαμβάνεται με περιστροφή κατά γωνία, σημειώστε το σημείο με την τετμημένη στον άξονα:

Σχεδιάστε μια κάθετη γραμμή παράλληλη προς τον άξονα μέχρι να τέμνεται με τον κύκλο. Παίρνουμε δύο πόντους ξαπλωμένοι σε κύκλο και έχοντας μια τετμημένη. Αυτά τα σημεία αντιστοιχούν στις γωνίες περιστροφής κατά και ακτίνια. Θυμηθείτε ότι όταν κινούμαστε δεξιόστροφα, έχουμε αρνητική γωνία περιστροφής:

Ας γράψουμε δύο σειρές λύσεων:
![]() ,
,
![]() ,
,
(Φτάνουμε στο επιθυμητό σημείο, περνώντας από τον κύριο πλήρη κύκλο, δηλαδή.
Ας συνδυάσουμε αυτές τις δύο σειρές σε μια καταχώρηση:
![]()
3. Λύστε την εξίσωση
Η εφαπτομένη διέρχεται από το σημείο με συντεταγμένες (1,0) του μοναδιαίου κύκλου παράλληλη προς τον άξονα OY
Σημειώνουμε ένα σημείο πάνω του με τεταγμένη ίση με 1 (ψάχνουμε την εφαπτομένη της οποίας οι γωνίες είναι 1):

Ας συνδέσουμε αυτό το σημείο με την αρχή των συντεταγμένων με μια ευθεία γραμμή και ας σημειώσουμε τα σημεία τομής της ευθείας με τον μοναδιαίο κύκλο. Τα σημεία τομής της ευθείας γραμμής και του κύκλου αντιστοιχούν στις γωνίες περιστροφής επί και:

Δεδομένου ότι τα σημεία που αντιστοιχούν στις γωνίες περιστροφής που ικανοποιούν την εξίσωσή μας βρίσκονται σε απόσταση ακτίνων μεταξύ τους, μπορούμε να γράψουμε τη λύση με αυτόν τον τρόπο:
4. Λύστε την εξίσωση
Η ευθεία των συνεφαπτομένων διέρχεται από το σημείο με τις συντεταγμένες του μοναδιαίου κύκλου παράλληλες προς τον άξονα.
Ας σημειώσουμε στη γραμμή των συνεφαπτομένων ένα σημείο με τετμημένη -1:

Ας συνδέσουμε αυτό το σημείο με την αρχή των συντεταγμένων μιας ευθείας γραμμής και ας το συνεχίσουμε μέχρι την τομή με τον κύκλο. Αυτή η ευθεία θα τέμνει τον κύκλο στα σημεία που αντιστοιχούν στις γωνίες περιστροφής κατά και ακτίνια:

Επειδή αυτά τα σημεία βρίσκονται σε απόσταση ίση μεταξύ τους, μπορούμε να γράψουμε τη γενική λύση αυτής της εξίσωσης ως εξής:
![]()
Στα παραδείγματα που δίνονται, απεικονίζοντας τη λύση των απλούστερων τριγωνομετρικών εξισώσεων, χρησιμοποιήθηκαν πινακικές τιμές τριγωνομετρικών συναρτήσεων.
Ωστόσο, εάν δεν υπάρχει μια τιμή πίνακα στη δεξιά πλευρά της εξίσωσης, τότε αντικαθιστούμε την τιμή στη γενική λύση της εξίσωσης:




ΕΙΔΙΚΕΣ ΛΥΣΕΙΣ:
Σημειώστε στον κύκλο τα σημεία των οποίων η τεταγμένη είναι ίση με 0:

Ας σημειώσουμε στον κύκλο ένα μόνο σημείο, η τεταγμένη του οποίου είναι ίση με 1:

Ας σημειώσουμε στον κύκλο ένα μόνο σημείο του οποίου η τεταγμένη είναι -1:

Δεδομένου ότι συνηθίζεται να υποδεικνύουμε τις τιμές που είναι πλησιέστερα στο μηδέν, γράφουμε τη λύση ως εξής:
Σημειώστε στον κύκλο τα σημεία των οποίων η τετμημένη είναι ίση με 0:

5.
Ας σημειώσουμε στον κύκλο το μοναδικό σημείο του οποίου η τετμημένη είναι ίση με 1:

Ας σημειώσουμε στον κύκλο το μοναδικό σημείο του οποίου η τετμημένη είναι -1:

Και λίγο πιο σύνθετα παραδείγματα:
1.
Το ημίτονο είναι ένα εάν το επιχείρημα είναι
Το όρισμα του ημιτονοειδούς μας είναι ίσο, οπότε παίρνουμε:
Διαιρέστε και τις δύο πλευρές της ισότητας με το 3:
Απάντηση:
2.
Το συνημίτονο είναι μηδέν αν το όρισμα του συνημιτόνου είναι
Το όρισμα του συνημίτονου μας είναι ίσο, οπότε παίρνουμε:
Ας εκφράσουμε, για αυτό κινούμαστε πρώτα προς τα δεξιά με το αντίθετο πρόσημο:
Ας απλοποιήσουμε τη δεξιά πλευρά:
Διαιρέστε και τα δύο μέρη με -2:
Σημειώστε ότι το πρόσημο δεν αλλάζει μπροστά από τον όρο, αφού το k μπορεί να πάρει οποιεσδήποτε ακέραιες τιμές.
Απάντηση:
Και τέλος, παρακολουθήστε το εκπαιδευτικό βίντεο "Επιλογή ριζών σε τριγωνομετρική εξίσωση με χρήση τριγωνομετρικού κύκλου"
Αυτό ολοκληρώνει τη συζήτηση για την επίλυση των απλούστερων τριγωνομετρικών εξισώσεων. Την επόμενη φορά θα μιλήσουμε για το πώς θα λύσουμε.