Περιορισμένη αριθμομηχανή τετράγωνου σχήματος. Ηλεκτρονική αριθμομηχανή. Υπολογίστε το οριστικό ολοκλήρωμα (εμβαδόν καμπύλου τραπεζοειδούς)

18.10.2019

Διαβάστε επίσης

Χαρακτηριστικά της Masha Mironova από το "The Captain's Daughter

Μια σύντομη επισκόπηση της δημιουργικότητας Α

Η εικόνα και τα χαρακτηριστικά της Olga Ilyinskaya με βάση το μυθιστόρημα Oblomov (Goncharov I

Χαρακτηριστικά της Μαρίας Μιρόνοβα από την "Η κόρη του καπετάνιου" Πούσκιν Α

Σύνθεση «Υπήρχε διαφορετικός δρόμος για την Κατερίνα»: θα μπορούσε να είχε ενεργήσει διαφορετικά;

Αυτό το άρθρο θα σας δείξει πώς να βρείτε την περιοχή ενός σχήματος που οριοθετείται από γραμμές χρησιμοποιώντας ολοκληρωμένους υπολογισμούς. Για πρώτη φορά, συναντάμε τη διατύπωση ενός τέτοιου προβλήματος στο λύκειο, όταν μόλις έχει περάσει η μελέτη ορισμένων ολοκληρωμάτων και είναι καιρός να ξεκινήσει μια γεωμετρική ερμηνεία της γνώσης που αποκτήθηκε στην πράξη.

Έτσι, τι απαιτείται για την επιτυχή επίλυση του προβλήματος της εύρεσης της περιοχής ενός σχήματος χρησιμοποιώντας ολοκληρώματα:

Ικανότητα να κατασκευάζει σωστά σχέδια.
Ικανότητα επίλυσης ορισμένου ολοκληρώματος χρησιμοποιώντας τον γνωστό τύπο Newton-Leibniz.
Η ικανότητα να "δούμε" μια πιο συμφέρουσα λύση - δηλαδή, για να καταλάβετε πώς σε αυτήν ή εκείνη την περίπτωση θα είναι πιο βολικό να πραγματοποιηθεί η ενσωμάτωση; Κατά μήκος του άξονα x (OX) ή του άξονα y (OY);
Λοιπόν, πού χωρίς σωστούς υπολογισμούς;) Αυτό περιλαμβάνει την κατανόηση του τρόπου επίλυσης αυτού του άλλου τύπου ολοκληρωμάτων και τους σωστούς αριθμητικούς υπολογισμούς.

Αλγόριθμος για την επίλυση του προβλήματος του υπολογισμού του εμβαδού ενός σχήματος που οριοθετείται από γραμμές:

1. Χτίζουμε ένα σχέδιο. Συνιστάται να το κάνετε αυτό σε ένα κομμάτι χαρτί σε ένα κλουβί, με μεγάλη κλίμακα. Υπογράφουμε το όνομα αυτής της συνάρτησης με ένα μολύβι πάνω από κάθε γράφημα. Η υπογραφή των γραφημάτων γίνεται αποκλειστικά για τη διευκόλυνση περαιτέρω υπολογισμών. Έχοντας λάβει το γράφημα του επιθυμητού σχήματος, στις περισσότερες περιπτώσεις θα είναι αμέσως ορατό ποια όρια ολοκλήρωσης θα χρησιμοποιηθούν. Έτσι, λύνουμε το πρόβλημα γραφικά. Ωστόσο, συμβαίνει ότι οι τιμές των ορίων είναι κλασματικές ή παράλογες. Επομένως, μπορείτε να κάνετε πρόσθετους υπολογισμούς, μεταβείτε στο δεύτερο βήμα.

2. Αν τα όρια ολοκλήρωσης δεν τίθενται ρητά, τότε βρίσκουμε τα σημεία τομής των γραφημάτων μεταξύ τους και βλέπουμε αν η γραφική μας λύση συμπίπτει με την αναλυτική.

3. Στη συνέχεια, πρέπει να αναλύσετε το σχέδιο. Ανάλογα με το πώς βρίσκονται τα γραφήματα συναρτήσεων, υπάρχουν διαφορετικές προσεγγίσεις για την εύρεση του εμβαδού ενός σχήματος. Ας εξετάσουμε διαφορετικά παραδείγματα εύρεσης του εμβαδού ενός σχήματος χρησιμοποιώντας ολοκληρώματα.

3.1. Η πιο κλασική και απλή εκδοχή του προβλήματος είναι όταν πρέπει να βρείτε την περιοχή ενός κυρτού τραπεζοειδούς. Τι είναι ένα καμπύλο τραπεζοειδές; Είναι ένα επίπεδο σχήμα που οριοθετείται από τον άξονα x. (y = 0), ευθεία x = a, x = bκαι οποιαδήποτε καμπύλη συνεχής από έναπριν σι... Επιπλέον, ο αριθμός αυτός είναι μη αρνητικός και βρίσκεται όχι κάτω από τον άξονα της τετμημένης. Σε αυτή την περίπτωση, το εμβαδόν ενός καμπυλόγραμμου τραπεζοειδούς είναι αριθμητικά ίσο με ένα ορισμένο ολοκλήρωμα που υπολογίζεται από τον τύπο Newton-Leibniz:

Παράδειγμα 1 y = x2 - 3x + 3, x = 1, x = 3, y = 0.

Ποιες είναι οι γραμμές που οριοθετούν το σχήμα; Έχουμε παραβολή y = x2 - 3x + 3που βρίσκεται πάνω από τον άξονα OH, είναι μη αρνητικό, γιατί όλα τα σημεία αυτής της παραβολής είναι θετικά. Περαιτέρω, οι ευθείες γραμμές x = 1και x = 3που τρέχουν παράλληλα με τον άξονα OU, είναι οι οριογραμμές του σχήματος αριστερά και δεξιά. Καλά y = 0, είναι ο άξονας x, που περιορίζει το σχήμα από κάτω. Το σχήμα που προκύπτει είναι σκιασμένο όπως φαίνεται στην εικόνα στα αριστερά. Σε αυτή την περίπτωση, μπορείτε να ξεκινήσετε αμέσως την επίλυση του προβλήματος. Έχουμε μπροστά μας ένα απλό παράδειγμα καμπυλόγραμμου τραπεζοειδούς, το οποίο λύνουμε περαιτέρω χρησιμοποιώντας τον τύπο Newton-Leibniz.

3.2. Στην προηγούμενη παράγραφο 3.1, αναλύσαμε την περίπτωση που το καμπύλο τραπεζοειδές βρίσκεται πάνω από τον άξονα x. Τώρα εξετάστε την περίπτωση όταν οι συνθήκες του προβλήματος είναι οι ίδιες, εκτός από το ότι η συνάρτηση βρίσκεται κάτω από τον άξονα x. Ένα μείον προστίθεται στον τυπικό τύπο Newton-Leibniz. Θα εξετάσουμε περαιτέρω πώς να λύσουμε ένα παρόμοιο πρόβλημα.

Παράδειγμα 2 ... Υπολογίστε το εμβαδόν ενός σχήματος που οριοθετείται από γραμμές y = x2 + 6x + 2, x = -4, x = -1, y = 0.

Σε αυτό το παράδειγμα, έχουμε μια παραβολή y = x2 + 6x + 2που πηγάζει κάτω από τον άξονα OH, ευθεία x = -4, x = -1, y = 0... Εδώ y = 0δεσμεύει το επιθυμητό σχήμα από πάνω. Απευθείας x = -4και x = -1αυτά είναι τα όρια εντός των οποίων θα υπολογιστεί ένα καθορισμένο ολοκλήρωμα. Η αρχή της επίλυσης του προβλήματος της εύρεσης της περιοχής ενός σχήματος συμπίπτει σχεδόν πλήρως με το παράδειγμα 1. Η μόνη διαφορά είναι ότι η δεδομένη συνάρτηση δεν είναι θετική και εξακολουθεί να είναι συνεχής στο διάστημα [-4; -1] ... Τι δεν σημαίνει θετικό; Όπως μπορείτε να δείτε από το σχήμα, το σχήμα, το οποίο βρίσκεται εντός του καθορισμένου x, έχει αποκλειστικά «αρνητικές» συντεταγμένες, κάτι που πρέπει να δούμε και να θυμόμαστε όταν λύνουμε το πρόβλημα. Αναζητούμε την περιοχή του σχήματος χρησιμοποιώντας τον τύπο Newton-Leibniz, μόνο με το σύμβολο μείον στην αρχή.

Το άρθρο είναι ημιτελές.

Περνάμε τώρα στην εξέταση των εφαρμογών του ολοκληρωτικού λογισμού. Σε αυτό το μάθημα θα αναλύσουμε μια τυπική και πιο συνηθισμένη εργασία. υπολογισμός του εμβαδού ενός επίπεδου σχήματος χρησιμοποιώντας ένα καθορισμένο ολοκλήρωμα... Τέλος, όλοι όσοι αναζητούν νόημα στα ανώτερα μαθηματικά - μακάρι να το βρουν. Ποτέ δεν ξέρεις. Θα πρέπει να φέρουμε την προαστιακή περιοχή πιο κοντά στη ζωή με στοιχειώδεις συναρτήσεις και να βρούμε την περιοχή της χρησιμοποιώντας ένα καθορισμένο ολοκλήρωμα.

Για να κατακτήσετε με επιτυχία το υλικό, πρέπει:

1) Κατανοήστε το αόριστο ολοκλήρωμα τουλάχιστον στο μεσαίο επίπεδο. Έτσι, τα ανδρείκελα θα πρέπει πρώτα να εξοικειωθούν με το μάθημα Δεν.

2) Να είναι σε θέση να εφαρμόσει τον τύπο Newton-Leibniz και να υπολογίσει ένα οριστικό ολοκλήρωμα. Μπορείτε να δημιουργήσετε ζεστές φιλίες με συγκεκριμένα ολοκληρώματα στη σελίδα Ορισμένο ολοκλήρωμα. Παραδείγματα λύσεων. Η εργασία "υπολογισμός περιοχής χρησιμοποιώντας ένα καθορισμένο ολοκλήρωμα" περιλαμβάνει πάντα την κατασκευή ενός σχεδίου, επομένως, οι γνώσεις και οι δεξιότητές σας στη σχεδίαση σχεδίων θα είναι επίσης ένα επείγον ζήτημα. Τουλάχιστον, πρέπει να είστε σε θέση να δημιουργήσετε μια ευθεία γραμμή, μια παραβολή και μια υπερβολή.

Ας ξεκινήσουμε με ένα καμπύλο τραπεζοειδές. Ένα καμπυλόγραμμο τραπέζιο είναι ένα επίπεδο σχήμα που οριοθετείται από τη γραφική παράσταση κάποιας συνάρτησης y = φά(Χ), ο άξονας ΒΟΔΙκαι γραμμές Χ = ένα; Χ = σι.

Το εμβαδόν ενός καμπύλου τραπεζοειδούς είναι αριθμητικά ίσο με το οριστικό ολοκλήρωμα

Οποιοδήποτε οριστικό ολοκλήρωμα (που υπάρχει) έχει πολύ καλή γεωμετρική σημασία. Στο μάθημα Ορισμένο ολοκλήρωμα. Παραδείγματα λύσεωνείπαμε ότι ορισμένο ολοκλήρωμα είναι ένας αριθμός. Και τώρα ήρθε η ώρα να αναφέρουμε ένα άλλο χρήσιμο γεγονός. Από την άποψη της γεωμετρίας, το οριστικό ολοκλήρωμα είναι η ΠΕΡΙΟΧΗ... Αυτό είναι, ένα ορισμένο ολοκλήρωμα (αν υπάρχει) αντιστοιχεί γεωμετρικά στο εμβαδόν κάποιου σχήματος... Θεωρήστε το οριστικό ολοκλήρωμα

Ολοκληρωτέου

ορίζει μια καμπύλη στο επίπεδο (μπορεί να σχεδιαστεί εάν είναι επιθυμητό) και το ίδιο το καθορισμένο ολοκλήρωμα είναι αριθμητικά ίσο με την περιοχή του αντίστοιχου καμπυλόγραμμου τραπεζοειδούς.

Παράδειγμα 1

, , , .

Αυτή είναι μια τυπική διατύπωση της ανάθεσης. Το πιο σημαντικό σημείο της λύσης είναι η κατασκευή του σχεδίου... Επιπλέον, το σχέδιο πρέπει να κατασκευαστεί ΣΩΣΤΑ.

Κατά την κατασκευή ενός σχεδίου, προτείνω την ακόλουθη σειρά: αρχικάείναι καλύτερο να δημιουργηθούν όλες οι γραμμές (αν υπάρχουν) και μόνο μετά- παραβολές, υπερβολές, γραφικές παραστάσεις άλλων συναρτήσεων. Η τεχνική της κατασκευής σημείο προς σημείο βρίσκεται στο υλικό αναφοράς. Γραφήματα και ιδιότητες στοιχειωδών συναρτήσεων... Εκεί μπορείτε επίσης να βρείτε πολύ χρήσιμο υλικό σε σχέση με το μάθημά μας - πώς να φτιάξετε γρήγορα μια παραβολή.

Σε αυτό το πρόβλημα, η λύση μπορεί να μοιάζει με αυτό.

Ας ολοκληρώσουμε το σχέδιο (σημειώστε ότι η εξίσωση y= 0 καθορίζει τον άξονα ΒΟΔΙ):

Δεν θα εκκολάψουμε το καμπυλόγραμμο τραπεζοειδές, εδώ είναι προφανές για ποια περιοχή μιλάμε. Η λύση συνεχίζεται ως εξής:

Στο τμήμα [-2; 1] γράφημα συνάρτησης y = Χ 2 + 2 βρίσκεται πάνω από τον άξοναΒΟΔΙ, επομένως:

Απάντηση: .

Ποιος δυσκολεύεται να υπολογίσει ένα οριστικό ολοκλήρωμα και να εφαρμόσει τον τύπο Newton-Leibniz

ανατρέξτε στη διάλεξη Ορισμένο ολοκλήρωμα. Παραδείγματα λύσεων... Αφού ολοκληρωθεί η εργασία, είναι πάντα χρήσιμο να εξετάζετε το σχέδιο και να υπολογίζετε εάν η απάντηση είναι πραγματική. Σε αυτή την περίπτωση, "με το μάτι" μετράμε τον αριθμό των κελιών στο σχέδιο - καλά, θα πληκτρολογηθούν περίπου 9, φαίνεται η αλήθεια. Είναι ξεκάθαρο ότι αν λάβαμε, ας πούμε, την απάντηση: 20 τετραγωνικές μονάδες, τότε, προφανώς, κάπου έχει γίνει ένα λάθος - το εν λόγω σχήμα προφανώς δεν χωράει 20 κελιά, το πολύ δέκα. Εάν η απάντηση είναι αρνητική, τότε η εργασία λύθηκε επίσης εσφαλμένα.

Παράδειγμα 2

Υπολογίστε το εμβαδόν ενός σχήματος που οριοθετείται από γραμμές xy = 4, Χ = 2, Χ= 4 και άξονας ΒΟΔΙ.

Αυτό είναι ένα παράδειγμα για μια λύση "φτιάξ' το μόνος σου". Ολοκληρωμένη λύση και απάντηση στο τέλος του σεμιναρίου.

Τι να κάνετε εάν βρίσκεται το καμπύλο τραπεζοειδές κάτω από τον άξοναΒΟΔΙ?

Παράδειγμα 3

Υπολογίστε το εμβαδόν ενός σχήματος που οριοθετείται από γραμμές y = e - x, Χ= 1 και άξονες συντεταγμένων.

Λύση: Ας εκτελέσουμε το σχέδιο:

Αν το καμπύλο τραπεζοειδές βρίσκεται πλήρως κάτω από τον άξονα ΒΟΔΙ , τότε το εμβαδόν του μπορεί να βρεθεί με τον τύπο:

Σε αυτήν την περίπτωση:

Προσοχή! Οι δύο τύποι εργασιών δεν πρέπει να συγχέονται:

1) Εάν σας ζητηθεί να λύσετε μόνο ένα οριστικό ολοκλήρωμα χωρίς γεωμετρική σημασία, τότε μπορεί να είναι αρνητικό.

2) Αν σας ζητηθεί να βρείτε το εμβαδόν ενός σχήματος χρησιμοποιώντας ένα καθορισμένο ολοκλήρωμα, τότε το εμβαδόν είναι πάντα θετικό! Αυτός είναι ο λόγος για τον οποίο εμφανίζεται ένα μείον στον τύπο που μόλις εξετάστηκε.

Στην πράξη, τις περισσότερες φορές το σχήμα βρίσκεται τόσο στο άνω όσο και στο κάτω ημιεπίπεδο και επομένως, από τα απλούστερα σχολικά προβλήματα, προχωράμε σε πιο ουσιαστικά παραδείγματα.

Παράδειγμα 4

Βρείτε το εμβαδόν μιας επίπεδης φιγούρας που οριοθετείται από γραμμές y = 2Χ – Χ 2 , y = -Χ.

Λύση: Πρώτα πρέπει να ολοκληρώσετε το σχέδιο. Όταν κατασκευάζουμε ένα σχέδιο σε προβλήματα στην περιοχή, μας ενδιαφέρουν περισσότερο τα σημεία τομής των γραμμών. Βρείτε τα σημεία τομής της παραβολής y = 2Χ – Χ 2 και ευθεία y = -Χ... Αυτό μπορεί να γίνει με δύο τρόπους. Ο πρώτος τρόπος είναι αναλυτικός. Λύνουμε την εξίσωση:

Ως εκ τούτου, το κατώτερο όριο ολοκλήρωσης ένα= 0, το ανώτερο όριο ολοκλήρωσης σι= 3. Συχνά είναι πιο επικερδές και πιο γρήγορο να κατασκευάζονται οι γραμμές σημείο προς σημείο, ενώ τα όρια της ολοκλήρωσης γίνονται ξεκάθαρα σαν «από μόνα τους». Ωστόσο, η αναλυτική μέθοδος εύρεσης των ορίων πρέπει να χρησιμοποιείται μερικές φορές εάν, για παράδειγμα, το γράφημα είναι αρκετά μεγάλο ή η ακριβής κατασκευή δεν αποκάλυψε τα όρια της ολοκλήρωσης (μπορεί να είναι κλασματικά ή παράλογα). Επιστρέφουμε στο πρόβλημά μας: είναι πιο λογικό να κατασκευάσουμε πρώτα μια ευθεία γραμμή και μόνο μετά μια παραβολή. Ας εκτελέσουμε το σχέδιο:

Ας επαναλάβουμε ότι στην περίπτωση μιας σημειακής κατασκευής, τα όρια ολοκλήρωσης ανακαλύπτονται τις περισσότερες φορές «αυτόματα».

Και τώρα ο τύπος εργασίας:

Εάν στο τμήμα [ ένα; σι] κάποια συνεχής λειτουργία φά(Χ) μεγαλύτερο ή ίσοκάποια συνεχής λειτουργία σολ(Χ), τότε η περιοχή του αντίστοιχου σχήματος μπορεί να βρεθεί με τον τύπο:

Εδώ δεν χρειάζεται πλέον να σκέφτεστε πού βρίσκεται το σχήμα - πάνω από τον άξονα ή κάτω από τον άξονα, αλλά είναι σημαντικό ποιο πρόγραμμα είναι ΠΑΝΩ(σε σχέση με άλλο γράφημα), και ποιο είναι ΠΑΡΑΚΑΤΩ.

Στο υπό εξέταση παράδειγμα, είναι προφανές ότι στο τμήμα η παραβολή βρίσκεται πάνω από την ευθεία γραμμή, και επομένως από το 2 Χ – Χ 2 πρέπει να αφαιρεθεί - Χ.

Η ολοκλήρωση της λύσης μπορεί να μοιάζει με αυτό:

Η περιζήτητη φιγούρα οριοθετείται από μια παραβολή y = 2Χ – Χ 2 επάνω και ευθεία y = -Χαπό κάτω.

Στο τμήμα 2 Χ – Χ 2 ≥ -Χ... Σύμφωνα με τον αντίστοιχο τύπο:

Απάντηση: .

Στην πραγματικότητα, ο σχολικός τύπος για το εμβαδόν ενός καμπυλόγραμμου τραπεζοειδούς στο κάτω ημιεπίπεδο (βλ. παράδειγμα Νο. 3) είναι μια ειδική περίπτωση του τύπου

Από τον άξονα ΒΟΔΙδίνεται από την εξίσωση y= 0, και το γράφημα της συνάρτησης σολ(Χ) βρίσκεται κάτω από τον άξονα ΒΟΔΙ, τότε

Και τώρα μερικά παραδείγματα για μια ανεξάρτητη λύση

Παράδειγμα 5

Παράδειγμα 6

Βρείτε το εμβαδόν ενός σχήματος που οριοθετείται από γραμμές

Κατά την επίλυση προβλημάτων για τον υπολογισμό του εμβαδού με χρήση ορισμένου ολοκληρώματος, μερικές φορές συμβαίνει ένα αστείο περιστατικό. Το σχέδιο έγινε σωστά, οι υπολογισμοί είναι σωστοί, αλλά, κατά λάθος, ... βρέθηκε η περιοχή της λάθος φιγούρας.

Παράδειγμα 7

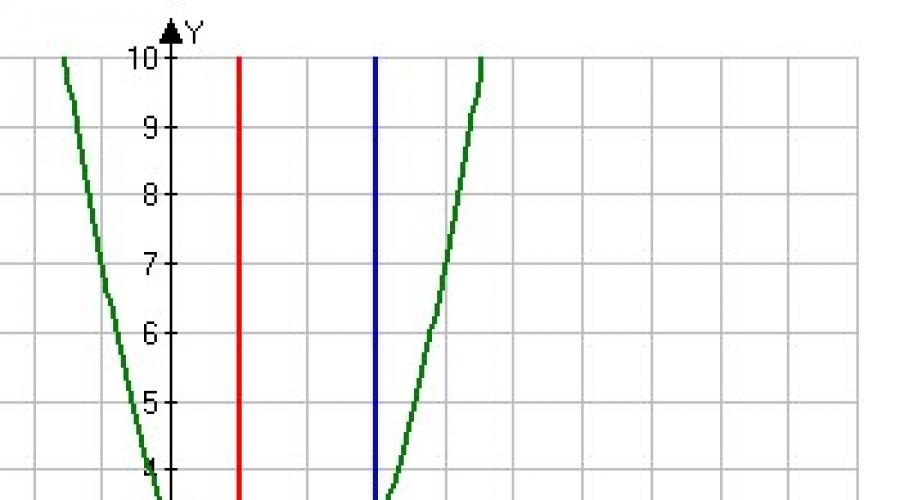
Αρχικά, ας εκτελέσουμε το σχέδιο:

Η φιγούρα της οποίας η περιοχή πρέπει να βρούμε είναι σκιασμένη με μπλε(δείτε προσεκτικά την κατάσταση - από τι περιορίζεται το σχήμα!). Αλλά στην πράξη, λόγω της απροσεξίας, συχνά αποφασίζουν ότι είναι απαραίτητο να βρουν την περιοχή της φιγούρας, η οποία είναι σκιασμένη με πράσινο!

Αυτό το παράδειγμα είναι επίσης χρήσιμο στο ότι υπολογίζει το εμβαδόν ενός σχήματος χρησιμοποιώντας δύο καθορισμένα ολοκληρώματα. Πραγματικά:

1) Στο τμήμα [-1; 1] πάνω από τον άξονα ΒΟΔΙτο γράφημα είναι ευθύ y = Χ+1;

2) Σε τμήμα πάνω από τον άξονα ΒΟΔΙβρίσκεται το γράφημα της υπερβολής y = (2/Χ).

Είναι προφανές ότι οι περιοχές μπορούν (και πρέπει) να προστεθούν, επομένως:

Απάντηση:

Παράδειγμα 8

Υπολογίστε το εμβαδόν ενός σχήματος που οριοθετείται από γραμμές

Ας παραστήσουμε τις εξισώσεις με τη μορφή «σχολείο».

και εκτελέστε ένα σχέδιο σημείο προς σημείο:

Από το σχέδιο φαίνεται ότι το ανώτερο όριο μας είναι "καλό": σι = 1.

Ποιο είναι όμως το κατώτερο όριο;! Είναι σαφές ότι αυτός δεν είναι ακέραιος, αλλά ποιος;

Μπορεί, ένα= (- 1/3); Αλλά πού είναι η εγγύηση ότι το σχέδιο γίνεται με τέλεια ακρίβεια, μπορεί κάλλιστα να αποδειχθεί ότι ένα= (- 1/4). Τι θα γινόταν αν σχεδιάζαμε καθόλου σωστά το γράφημα;

Σε τέτοιες περιπτώσεις, πρέπει να αφιερώσετε επιπλέον χρόνο και να βελτιώσετε αναλυτικά τα όρια της ολοκλήρωσης.

Βρείτε τα σημεία τομής των γραφημάτων

Για να γίνει αυτό, λύνουμε την εξίσωση:

Ως εκ τούτου, ένα=(-1/3).

Η περαιτέρω λύση είναι ασήμαντη. Το κύριο πράγμα είναι να μην μπερδεύεστε σε αντικαταστάσεις και ζώδια. Οι υπολογισμοί εδώ δεν είναι οι πιο εύκολοι. Στο τμήμα

, ,

σύμφωνα με τον αντίστοιχο τύπο:

Απάντηση:

Στο τέλος του μαθήματος, θα εξετάσουμε δύο ακόμη δύσκολες εργασίες.

Παράδειγμα 9

Υπολογίστε το εμβαδόν ενός σχήματος που οριοθετείται από γραμμές

Λύση: Σχεδιάστε αυτό το σχήμα στο σχέδιο.

Για την κατασκευή σημείο προς σημείο του σχεδίου, πρέπει να γνωρίζετε την εμφάνιση του ημιτονοειδούς. Γενικά, είναι χρήσιμο να γνωρίζουμε τα γραφήματα όλων των στοιχειωδών συναρτήσεων, καθώς και ορισμένες τιμές του ημιτόνου. Μπορούν να βρεθούν στον πίνακα τιμών τριγωνομετρικές συναρτήσεις... Σε ορισμένες περιπτώσεις (για παράδειγμα, σε αυτήν), επιτρέπεται η κατασκευή ενός σχηματικού σχεδίου, στο οποίο τα γραφήματα και τα όρια ολοκλήρωσης θα πρέπει να εμφανίζονται σωστά καταρχήν.

Δεν υπάρχουν προβλήματα με τα όρια ενσωμάτωσης, προκύπτουν άμεσα από την προϋπόθεση:

- Το "x" αλλάζει από μηδέν σε "pi". Παίρνουμε μια περαιτέρω απόφαση:

Σε ένα τμήμα, η γραφική παράσταση της συνάρτησης y= αμαρτία 3 Χπου βρίσκεται πάνω από τον άξονα ΒΟΔΙ, επομένως:

(1) Πώς τα ημίτονο και τα συνημίτονα ενσωματώνονται σε περιττούς βαθμούς, μπορείτε να δείτε στο μάθημα Ολοκληρώματα τριγωνομετρικών συναρτήσεων... Τσιμπάμε τον ένα κόλπο.

(2) Χρησιμοποιούμε τη βασική τριγωνομετρική ταυτότητα στη φόρμα

(3) Αλλάξτε τη μεταβλητή t= κοσ Χ, τότε: βρίσκεται πάνω από τον άξονα, επομένως:

Σημείωση:σημειώστε πώς λαμβάνεται το ολοκλήρωμα της εφαπτομένης στον κύβο, εδώ χρησιμοποιείται μια συνέπεια της κύριας τριγωνομετρικής ταυτότητας

Στην προηγούμενη ενότητα που αφιερώθηκε στην ανάλυση της γεωμετρικής σημασίας ενός ορισμένου ολοκληρώματος, λάβαμε έναν αριθμό τύπων για τον υπολογισμό του εμβαδού ενός καμπυλόγραμμου τραπεζοειδούς:

Yandex.RTB R-A-339285-1

S (G) = ∫ a b f (x) d x για μια συνεχή και μη αρνητική συνάρτηση y = f (x) στο τμήμα [a; σι],

S (G) = - ∫ a b f (x) d x για μια συνεχή και μη θετική συνάρτηση y = f (x) στο τμήμα [a; σι].

Αυτοί οι τύποι είναι εφαρμόσιμοι για την επίλυση σχετικά απλών προβλημάτων. Στην πραγματικότητα, συχνά πρέπει να δουλέψουμε με πιο σύνθετα σχήματα. Από αυτή την άποψη, θα αφιερώσουμε αυτήν την ενότητα στην ανάλυση αλγορίθμων για τον υπολογισμό της περιοχής των ψηφίων, τα οποία περιορίζονται από συναρτήσεις σε ρητή μορφή, δηλ. ως y = f (x) ή x = g (y).

Θεώρημα

Έστω οι συναρτήσεις y = f 1 (x) και y = f 2 (x) καθορισμένες και συνεχείς στο τμήμα [a; b], και f 1 (x) ≤ f 2 (x) για οποιαδήποτε τιμή του x από [a; σι]. Τότε ο τύπος για τον υπολογισμό του εμβαδού του σχήματος G που οριοθετείται από τις ευθείες x = a, x = b, y = f 1 (x) και y = f 2 (x) θα έχει τη μορφή S (G) = ∫ abf 2 (x) - f 1 (x) dx.

Ένας παρόμοιος τύπος θα ισχύει για την περιοχή του σχήματος που οριοθετείται από τις ευθείες y = c, y = d, x = g 1 (y) και x = g 2 (y): S (G) = ∫ cd (g 2 (y) - g 1 (y) dy.

Απόδειξη

Ας εξετάσουμε τρεις περιπτώσεις για τις οποίες θα ισχύει ο τύπος.

Στην πρώτη περίπτωση, λαμβάνοντας υπόψη την ιδιότητα της προσθετικότητας της περιοχής, το άθροισμα των εμβαδών του αρχικού σχήματος G και του καμπυλόγραμμου τραπεζοειδούς G 1 είναι ίσο με το εμβαδόν του σχήματος G 2. Σημαίνει ότι

Επομένως, S (G) = S (G 2) - S (G 1) = ∫ abf 2 (x) dx - ∫ abf 1 (x) dx = ∫ ab (f 2 (x) - f 1 (x)) dx.

Μπορούμε να κάνουμε την τελευταία μετάβαση χρησιμοποιώντας την τρίτη ιδιότητα του ορισμένου ολοκληρώματος.

Στη δεύτερη περίπτωση ισχύει η ακόλουθη ισότητα: S (G) = S (G 2) + S (G 1) = ∫ abf 2 (x) dx + - ∫ abf 1 (x) dx = ∫ ab (f 2 ( x) - f 1 (x)) dx

Η γραφική απεικόνιση θα μοιάζει με αυτό:

Αν και οι δύο συναρτήσεις είναι μη θετικές, παίρνουμε: S (G) = S (G 2) - S (G 1) = - ∫ abf 2 (x) dx - - ∫ abf 1 (x) dx = ∫ ab (f 2 (x) - f 1 (x)) dx. Η γραφική απεικόνιση θα μοιάζει με αυτό:

Ας στραφούμε στην εξέταση της γενικής περίπτωσης όταν y = f 1 (x) και y = f 2 (x) τέμνουν τον άξονα O x.

Τα σημεία τομής θα συμβολίζονται ως x i, i = 1, 2,. ... ... , n - 1. Αυτά τα σημεία χωρίζουν το τμήμα [a; b] σε n μέρη x i - 1; x i, i = 1, 2,. ... ... , n, όπου α = x 0< x 1 < x 2 < . . . < x n - 1 < x n = b . Фигуру G можно представить объединением фигур G i , i = 1 , 2 , . . . , n . Очевидно, что на своем интервале G i попадает под один из трех рассмотренных ранее случаев, поэтому их площади находятся как S (G i) = ∫ x i - 1 x i (f 2 (x) - f 1 (x)) d x , i = 1 , 2 , . . . , n

Ως εκ τούτου,

S (G) = ∑ i = 1 n S (G i) = ∑ i = 1 n ∫ xixif 2 (x) - f 1 (x)) dx = = ∫ x 0 xn (f 2 (x) - f ( x)) dx = ∫ abf 2 (x) - f 1 (x) dx

Μπορούμε να κάνουμε την τελευταία μετάβαση χρησιμοποιώντας την πέμπτη ιδιότητα του ορισμένου ολοκληρώματος.

Ας δείξουμε τη γενική περίπτωση στο γράφημα.

Ο τύπος S (G) = ∫ a b f 2 (x) - f 1 (x) d x μπορεί να θεωρηθεί αποδεδειγμένος.

Και τώρα ας προχωρήσουμε σε μια ανάλυση παραδειγμάτων υπολογισμού της περιοχής των ψηφίων που οριοθετούνται από τις γραμμές y = f (x) και x = g (y).

Θα αρχίσουμε να εξετάζουμε οποιοδήποτε από τα παραδείγματα δημιουργώντας ένα γράφημα. Η εικόνα θα μας επιτρέψει να αναπαραστήσουμε πολύπλοκα σχήματα ως συνδυασμούς απλούστερων σχημάτων. Εάν η σχεδίαση γραφημάτων και σχημάτων σε αυτά σας δημιουργεί δυσκολίες, μπορείτε να μελετήσετε την ενότητα για τις βασικές ατομικές συναρτήσεις, τον γεωμετρικό μετασχηματισμό των γραφημάτων συναρτήσεων και τη γραφική παράσταση κατά την εξερεύνηση μιας συνάρτησης.

Παράδειγμα 1

Είναι απαραίτητο να προσδιοριστεί η περιοχή του σχήματος, η οποία οριοθετείται από την παραβολή y = - x 2 + 6 x - 5 και τις ευθείες γραμμές y = - 1 3 x - 1 2, x = 1, x = 4.

Λύση

Ας σχεδιάσουμε τις γραμμές στο γράφημα σε ένα καρτεσιανό σύστημα συντεταγμένων.

Στο τμήμα [1; 4] η γραφική παράσταση της παραβολής y = - x 2 + 6 x - 5 βρίσκεται πάνω από την ευθεία y = - 1 3 x - 1 2. Από αυτή την άποψη, για να λάβουμε μια απάντηση, χρησιμοποιούμε τον τύπο που λήφθηκε νωρίτερα, καθώς και τη μέθοδο για τον υπολογισμό ενός ορισμένου ολοκληρώματος σύμφωνα με τον τύπο Newton-Leibniz:

S (G) = ∫ 1 4 - x 2 + 6 x - 5 - - 1 3 x - 1 2 dx = = ∫ 1 4 - x 2 + 19 3 x - 9 2 dx = - 1 3 x 3 + 19 6 x 2 - 9 2 x 1 4 = = - 1 3 4 3 + 19 6 4 2 - 9 2 4 - - 1 3 1 3 + 19 6 1 2 - 9 2 1 = = - 64 3 + 152 3 - 18 + 1 3 - 19 6 + 9 2 = 13

Απάντηση: S (G) = 13

Ας δούμε ένα πιο σύνθετο παράδειγμα.

Παράδειγμα 2

Είναι απαραίτητο να υπολογίσετε την περιοχή του σχήματος, η οποία οριοθετείται από τις γραμμές y = x + 2, y = x, x = 7.

Λύση

Σε αυτή την περίπτωση, έχουμε μόνο μία ευθεία παράλληλη προς τον άξονα της τετμημένης. Αυτό είναι x = 7. Αυτό απαιτεί να βρούμε μόνοι μας το δεύτερο όριο ολοκλήρωσης.

Ας φτιάξουμε ένα γράφημα και ας σχεδιάσουμε πάνω του τις γραμμές που δίνονται στη δήλωση προβλήματος.

Έχοντας το γράφημα μπροστά στα μάτια μας, μπορούμε εύκολα να προσδιορίσουμε ότι το κατώτερο όριο ολοκλήρωσης θα είναι η τετμημένη του σημείου τομής της γραφικής παράστασης της ευθείας y = x και της ημιπαραβολής y = x + 2. Για να βρούμε την τετμημένη, χρησιμοποιούμε τις ισότητες:

y = x + 2 О Д З: x ≥ - 2 x 2 = x + 2 2 x 2 - x - 2 = 0 D = (- 1) 2 - 4 · 1 · (- 2) = 9 x 1 = 1 + 9 2 = 2 ∈ О Д З x 2 = 1 - 9 2 = - 1 ∉ О Д З

Αποδεικνύεται ότι η τετμημένη του σημείου τομής είναι x = 2.

Εφιστούμε την προσοχή σας στο γεγονός ότι στο γενικό παράδειγμα του σχεδίου, οι ευθείες y = x + 2, y = x τέμνονται στο σημείο (2; 2), επομένως τέτοιοι λεπτομερείς υπολογισμοί μπορεί να φαίνονται περιττοί. Έχουμε δώσει μια τόσο λεπτομερή λύση εδώ μόνο επειδή σε πιο περίπλοκες περιπτώσεις η λύση μπορεί να μην είναι τόσο προφανής. Αυτό σημαίνει ότι οι συντεταγμένες της τομής των γραμμών υπολογίζονται πάντα καλύτερα αναλυτικά.

Στο διάστημα [2; 7] η γραφική παράσταση της συνάρτησης y = x βρίσκεται πάνω από τη γραφική παράσταση της συνάρτησης y = x + 2. Ας εφαρμόσουμε τον τύπο για τον υπολογισμό του εμβαδού:

S (G) = ∫ 2 7 (x - x + 2) dx = x 2 2 - 2 3 (x + 2) 3 2 2 7 = = 7 2 2 - 2 3 (7 + 2) 3 2 - 2 2 2 - 2 3 2 + 2 3 2 = = 49 2 - 18 - 2 + 16 3 = 59 6

Απάντηση: S (G) = 59 6

Παράδειγμα 3

Είναι απαραίτητο να υπολογίσετε την περιοχή του σχήματος, η οποία περιορίζεται από τα γραφήματα των συναρτήσεων y = 1 x και y = - x 2 + 4 x - 2.

Λύση

Ας τραβήξουμε γραμμές στο γράφημα.

Ας ορίσουμε τα όρια της ολοκλήρωσης. Για να γίνει αυτό, προσδιορίζουμε τις συντεταγμένες των σημείων τομής των γραμμών εξισώνοντας τις παραστάσεις 1 x και - x 2 + 4 x - 2. Με την προϋπόθεση ότι το x δεν είναι μηδέν, η ισότητα 1 x = - x 2 + 4 x - 2 γίνεται ισοδύναμη με την εξίσωση του τρίτου βαθμού - x 3 + 4 x 2 - 2 x - 1 = 0 με ακέραιους συντελεστές. Μπορείτε να ανανεώσετε τη μνήμη σας για τον αλγόριθμο για την επίλυση τέτοιων εξισώσεων ανατρέχοντας στην ενότητα "Επίλυση κυβικών εξισώσεων".

Η ρίζα αυτής της εξίσωσης είναι x = 1: - 1 3 + 4 1 2 - 2 1 - 1 = 0.

Διαιρώντας την παράσταση - x 3 + 4 x 2 - 2 x - 1 με το διώνυμο x - 1, παίρνουμε: - x 3 + 4 x 2 - 2 x - 1 ⇔ - (x - 1) (x 2 - 3 x - 1) = 0

Μπορούμε να βρούμε τις υπόλοιπες ρίζες από την εξίσωση x 2 - 3 x - 1 = 0:

x 2 - 3 x - 1 = 0 D = (- 3) 2 - 4 · 1 · (- 1) = 13 x 1 = 3 + 13 2 ≈ 3. 3; x 2 = 3 - 13 2 ≈ - 0. 3

Βρήκαμε το διάστημα x ∈ 1; 3 + 13 2, στο οποίο το σχήμα G περικλείεται πάνω από τη μπλε και κάτω από την κόκκινη γραμμή. Αυτό μας βοηθά να προσδιορίσουμε την περιοχή του σχήματος:

S (G) = ∫ 1 3 + 13 2 - x 2 + 4 x - 2 - 1 xdx = - x 3 3 + 2 x 2 - 2 x - ln x 1 3 + 13 2 = = - 3 + 13 2 3 3 + 2 3 + 13 2 2 - 2 3 + 13 2 - ln 3 + 13 2 - - - 1 3 3 + 2 1 2 - 2 1 - ln 1 = 7 + 13 3 - ln 3 + 13 2

Απάντηση: S (G) = 7 + 13 3 - ln 3 + 13 2

Παράδειγμα 4

Είναι απαραίτητο να υπολογιστεί η περιοχή του σχήματος, η οποία περιορίζεται από τις καμπύλες y = x 3, y = - log 2 x + 1 και τον άξονα της τετμημένης.

Λύση

Ας βάλουμε όλες τις γραμμές στο γράφημα. Μπορούμε να πάρουμε τη γραφική παράσταση της συνάρτησης y = - log 2 x + 1 από τη γραφική παράσταση y = log 2 x, αν την τοποθετήσουμε συμμετρικά γύρω από τον άξονα της τετμημένης και την σηκώσουμε κατά μία μονάδα. Η εξίσωση του άξονα της τετμημένης είναι y = 0.

Ας σημειώσουμε τα σημεία τομής των ευθειών.

Όπως φαίνεται από το σχήμα, οι γραφικές παραστάσεις των συναρτήσεων y = x 3 και y = 0 τέμνονται στο σημείο (0; 0). Αυτό συμβαίνει επειδή x = 0 είναι η μόνη πραγματική ρίζα της εξίσωσης x 3 = 0.

x = 2 είναι η μόνη ρίζα της εξίσωσης - log 2 x + 1 = 0, επομένως οι γραφικές παραστάσεις των συναρτήσεων y = - log 2 x + 1 και y = 0 τέμνονται στο σημείο (2; 0).

x = 1 είναι η μόνη ρίζα της εξίσωσης x 3 = - log 2 x + 1. Από αυτή την άποψη, οι γραφικές παραστάσεις των συναρτήσεων y = x 3 και y = - log 2 x + 1 τέμνονται στο σημείο (1; 1). Η τελευταία πρόταση μπορεί να μην είναι προφανής, αλλά η εξίσωση x 3 = - log 2 x + 1 δεν μπορεί να έχει περισσότερες από μία ρίζες, καθώς η συνάρτηση y = x 3 είναι αυστηρά αύξουσα και η συνάρτηση y = - log 2 x + 1 είναι αυστηρά φθίνουσα.

Η περαιτέρω λύση προϋποθέτει πολλές επιλογές.

Αριθμός επιλογής 1

Μπορούμε να αναπαραστήσουμε το σχήμα G ως το άθροισμα δύο καμπυλόγραμμων τραπεζοειδών που βρίσκονται πάνω από τον άξονα της τετμημένης, το πρώτο από τα οποία βρίσκεται κάτω από τη μέση γραμμή στο τμήμα x ∈ 0. 1, και το δεύτερο είναι κάτω από την κόκκινη γραμμή στο τμήμα x ∈ 1. 2. Αυτό σημαίνει ότι η περιοχή θα είναι S (G) = ∫ 0 1 x 3 d x + ∫ 1 2 (- log 2 x + 1) d x.

Επιλογή αριθμός 2

Το σχήμα G μπορεί να αναπαρασταθεί ως η διαφορά δύο σχημάτων, το πρώτο από τα οποία βρίσκεται πάνω από τον άξονα της τετμημένης και κάτω από την μπλε γραμμή στο τμήμα x ∈ 0. 2, και το δεύτερο βρίσκεται ανάμεσα στις κόκκινες και μπλε γραμμές στο τμήμα x ∈ 1. 2. Αυτό μας επιτρέπει να βρούμε την περιοχή ως εξής:

S (G) = ∫ 0 2 x 3 d x - ∫ 1 2 x 3 - (- log 2 x + 1) d x

Σε αυτήν την περίπτωση, για να βρείτε το εμβαδόν, θα πρέπει να χρησιμοποιήσετε έναν τύπο της μορφής S (G) = ∫ c d (g 2 (y) - g 1 (y)) d y. Στην πραγματικότητα, οι γραμμές που δέσμευαν το σχήμα μπορούν να αναπαρασταθούν ως συναρτήσεις του ορίσματος y.

Λύστε τις εξισώσεις y = x 3 και - log 2 x + 1 για το x:

y = x 3 ⇒ x = y 3 y = - log 2 x + 1 ⇒ log 2 x = 1 - y ⇒ x = 2 1 - y

Παίρνουμε την απαιτούμενη περιοχή:

S (G) = ∫ 0 1 (2 1 - y - y 3) dy = - 2 1 - y ln 2 - y 4 4 0 1 = = - 2 1 - 1 ln 2 - 1 4 4 - - 2 1 - 0 ln 2 - 0 4 4 = - 1 ln 2 - 1 4 + 2 ln 2 = 1 ln 2 - 1 4

Απάντηση: S (G) = 1 ln 2 - 1 4

Παράδειγμα 5

Είναι απαραίτητο να υπολογίσετε το εμβαδόν του σχήματος, το οποίο οριοθετείται από τις γραμμές y = x, y = 2 3 x - 3, y = - 1 2 x + 4.

Λύση

Με την κόκκινη γραμμή, σχεδιάστε στο γράφημα τη γραμμή που καθορίζεται από τη συνάρτηση y = x. Σχεδιάστε με μπλε τη γραμμή y = - 1 2 x + 4 και με μαύρο τη γραμμή y = 2 3 x - 3.

Ας σημειώσουμε τα σημεία τομής.

Να βρείτε τα σημεία τομής των γραφημάτων των συναρτήσεων y = x και y = - 1 2 x + 4:

x = - 1 2 x + 4 О Д З: x ≥ 0 x = - 1 2 x + 4 2 ⇒ x = 1 4 x 2 - 4 x + 16 ⇔ x 2 - 20 x + 64 = 0 D = (- 20) 2 - 4 1 64 = 144 x 1 = 20 + 144 2 = 16; x 2 = 20 - 144 2 = 4 Έλεγχος: x 1 = 16 = 4, - 1 2 x 1 + 4 = - 1 2 16 + 4 = - 4 ⇒ x 1 = 16 δεν έχω λύση x 2 = 4 = 2, - 1 2 x 2 + 4 = - 1 2 4 + 4 = 2 ⇒ x 2 = 4 I e n t e r t e s ⇒ (4; 2) σημείο τομής i y = x και y = - 1 2 x + 4

Να βρείτε το σημείο τομής των γραφημάτων των συναρτήσεων y = x και y = 2 3 x - 3:

x = 2 3 x - 3 О Д З: x ≥ 0 x = 2 3 x - 3 2 ⇔ x = 4 9 x 2 - 4 x + 9 ⇔ 4 x 2 - 45 x + 81 = 0 D = (- 45 ) 2 - 4 4 81 = 729 x 1 = 45 + 729 8 = 9, x 2 45 - 729 8 = 9 4 Έλεγχος: x 1 = 9 = 3, 2 3 x 1 - 3 = 2 3 9 - 3 = 3 ⇒ x 1 = 9 Έχω μια λύση ⇒ (9; 3) τομή σημείου y = x και y = 2 3 x - 3 x 2 = 9 4 = 3 2, 2 3 x 1 - 3 = 2 3 9 4 - 3 = - 3 2 ⇒ x 2 = 9 4 δεν έχει λύση

Βρείτε την τομή των ευθειών y = - 1 2 x + 4 και y = 2 3 x - 3:

1 2 x + 4 = 2 3 x - 3 ⇔ - 3 x + 24 = 4 x - 18 ⇔ 7 x = 42 ⇔ x = 6 - 1 2 6 + 4 = 2 3 6 - 3 = 1 ⇒ (6 ; 1 ) το σημείο τομής y = - 1 2 x + 4 και y = 2 3 x - 3

Μέθοδος αριθμός 1

Ας φανταστούμε το εμβαδόν του απαιτούμενου σχήματος ως το άθροισμα των εμβαδών των μεμονωμένων σχημάτων.

Τότε το εμβαδόν του σχήματος είναι ίσο με:

S (G) = ∫ 4 6 x - - 1 2 x + 4 dx + ∫ 6 9 x - 2 3 x - 3 dx = = 2 3 x 3 2 + x 2 4 - 4 x 4 6 + 2 3 x 3 2 - x 2 3 + 3 x 6 9 = = 2 3 6 3 2 + 6 2 4 - 4 6 - 2 3 4 3 2 + 4 2 4 - 4 4 + + 2 3 9 3 2 - 9 2 3 + 3 9 - 2 3 6 3 2 - 6 2 3 + 3 6 = = - 25 3 + 4 6 + - 4 6 + 12 = 11 3

Μέθοδος αριθμός 2

Το εμβαδόν του αρχικού σχήματος μπορεί να θεωρηθεί ως το άθροισμα των άλλων δύο σχημάτων.

Στη συνέχεια θα λύσουμε την εξίσωση της γραμμής ως προς το x και μόνο μετά από αυτό θα εφαρμόσουμε τον τύπο για τον υπολογισμό της περιοχής του σχήματος.

y = x ⇒ x = y 2 κόκκινη γραμμή y = 2 3 x - 3 ⇒ x = 3 2 y + 9 2 μαύρη γραμμή y = - 1 2 x + 4 ⇒ x = - 2 y + 8

Έτσι, το εμβαδόν ισούται με:

S (G) = ∫ 1 2 3 2 y + 9 2 - - 2 y + 8 dy + ∫ 2 3 3 2 y + 9 2 - y 2 dy = = ∫ 1 2 7 2 y - 7 2 dy + ∫ 2 3 3 2 y + 9 2 - y 2 dy = = 7 4 y 2 - 7 4 y 1 2 + - y 3 3 + 3 y 2 4 + 9 2 y 2 3 = 7 4 2 2 - 7 4 2 - 7 4 1 2 - 7 4 1 + + - 3 3 3 + 3 3 2 4 + 9 2 3 - - 2 3 3 + 3 2 2 4 + 9 2 2 = = 7 4 + 23 12 = 11 3

Όπως μπορείτε να δείτε, οι τιμές είναι οι ίδιες.

Απάντηση: S (G) = 11 3

Αποτελέσματα

Για να βρούμε το εμβαδόν ενός σχήματος, το οποίο περιορίζεται από τις δεδομένες γραμμές, πρέπει να χτίσουμε γραμμές σε ένα επίπεδο, να βρούμε τα σημεία τομής τους, να εφαρμόσουμε τον τύπο για να βρούμε την περιοχή. Σε αυτήν την ενότητα, εξετάσαμε τις πιο συνηθισμένες επιλογές εργασιών.

Εάν παρατηρήσετε κάποιο σφάλμα στο κείμενο, επιλέξτε το και πατήστε Ctrl + Enter

Ικανότητα να κατασκευάζει σωστά σχέδια.
Ικανότητα επίλυσης ορισμένου ολοκληρώματος χρησιμοποιώντας τον γνωστό τύπο Newton-Leibniz.
Η ικανότητα να "δούμε" μια πιο συμφέρουσα λύση - δηλαδή, για να καταλάβετε πώς σε αυτήν ή εκείνη την περίπτωση θα είναι πιο βολικό να πραγματοποιηθεί η ενσωμάτωση; Κατά μήκος του άξονα x (OX) ή του άξονα y (OY);
Λοιπόν, πού χωρίς σωστούς υπολογισμούς;) Αυτό περιλαμβάνει την κατανόηση του τρόπου επίλυσης αυτού του άλλου τύπου ολοκληρωμάτων και τους σωστούς αριθμητικούς υπολογισμούς.

Παράδειγμα 1 y = x2 - 3x + 3, x = 1, x = 3, y = 0.

Παράδειγμα 2 ... Υπολογίστε το εμβαδόν ενός σχήματος που οριοθετείται από γραμμές y = x2 + 6x + 2, x = -4, x = -1, y = 0.

Το άρθρο είναι ημιτελές.

Στην πραγματικότητα, για να βρει κανείς το εμβαδόν ενός σχήματος, δεν χρειάζεται τόση γνώση του αόριστου και ορισμένου ολοκληρώματος. Η εργασία "υπολογισμός περιοχής χρησιμοποιώντας ένα καθορισμένο ολοκλήρωμα" περιλαμβάνει πάντα την κατασκευή ενός σχεδίου, επομένως, οι γνώσεις και οι δεξιότητές σας στο σχέδιο θα είναι ένα πολύ πιο πιεστικό ζήτημα. Από αυτή την άποψη, είναι χρήσιμο να ανανεώνεται η μνήμη των γραφημάτων των βασικών στοιχειωδών συναρτήσεων και, τουλάχιστον, να μπορούμε να κατασκευάσουμε μια ευθεία γραμμή και μια υπερβολή.

Ένα καμπυλόγραμμο τραπέζιο είναι ένα επίπεδο σχήμα που οριοθετείται από έναν άξονα, ευθείες γραμμές και ένα γράφημα μιας συνεχούς συνάρτησης σε ένα τμήμα που δεν αλλάζει πρόσημο σε αυτό το διάστημα. Αφήστε αυτό το σχήμα να βρίσκεται όχι λιγότεροάξονας τετμημένης:

Τότε το εμβαδόν ενός καμπύλου τραπεζοειδούς είναι αριθμητικά ίσο με το οριστικό ολοκλήρωμα... Οποιοδήποτε οριστικό ολοκλήρωμα (που υπάρχει) έχει πολύ καλή γεωμετρική σημασία.

Από την άποψη της γεωμετρίας, το οριστικό ολοκλήρωμα είναι η ΠΕΡΙΟΧΗ.

Αυτό είναι,ένα καθορισμένο ολοκλήρωμα (αν υπάρχει) αντιστοιχεί γεωμετρικά στο εμβαδόν κάποιου σχήματος. Για παράδειγμα, θεωρήστε ένα ορισμένο ολοκλήρωμα. Το ολοκλήρωμα θέτει μια καμπύλη στο επίπεδο που βρίσκεται πάνω από τον άξονα (όσοι επιθυμούν μπορούν να κάνουν ένα σχέδιο) και το ίδιο το καθορισμένο ολοκλήρωμα είναι αριθμητικά ίσο με το εμβαδόν του αντίστοιχου καμπυλόγραμμου τραπεζοειδούς.

Παράδειγμα 1

Αυτή είναι μια τυπική διατύπωση της ανάθεσης. Το πρώτο και σημαντικότερο σημείο της λύσης είναι η κατασκευή του σχεδίου... Επιπλέον, το σχέδιο πρέπει να κατασκευαστεί ΣΩΣΤΑ.

Σε αυτό το πρόβλημα, η λύση μπορεί να μοιάζει με αυτό.
Ας σχεδιάσουμε ένα σχέδιο (σημειώστε ότι η εξίσωση ορίζει τον άξονα):

Στο τμήμα, βρίσκεται το γράφημα της συνάρτησης πάνω από τον άξονα, επομένως:

Απάντηση:

Αφού ολοκληρωθεί η εργασία, είναι πάντα χρήσιμο να εξετάζετε το σχέδιο και να υπολογίζετε εάν η απάντηση είναι πραγματική. Σε αυτή την περίπτωση, "με το μάτι" μετράμε τον αριθμό των κελιών στο σχέδιο - καλά, θα πληκτρολογηθούν περίπου 9, φαίνεται η αλήθεια. Είναι απολύτως σαφές ότι αν λάβαμε, ας πούμε, την απάντηση: 20 τετραγωνικές μονάδες, τότε, προφανώς, κάπου έχει γίνει ένα λάθος - ο αριθμός που εξετάζουμε προφανώς δεν χωράει 20 κελιά, το πολύ δέκα. Εάν η απάντηση είναι αρνητική, τότε η εργασία λύθηκε επίσης εσφαλμένα.

Παράδειγμα 3

Υπολογίστε το εμβαδόν ενός σχήματος που οριοθετείται από γραμμές και άξονες συντεταγμένων.

Λύση: Ας εκτελέσουμε το σχέδιο:

Αν το καμπύλο τραπεζοειδές βρίσκεται κάτω από τον άξονα(ή τουλάχιστον όχι υψηλότεραδεδομένου άξονα), τότε η περιοχή του μπορεί να βρεθεί με τον τύπο:

Σε αυτήν την περίπτωση:

Προσοχή! Οι δύο τύποι εργασιών δεν πρέπει να συγχέονται:

Παράδειγμα 4

Βρείτε το εμβαδόν μιας επίπεδης φιγούρας που οριοθετείται από γραμμές,.

Λύση: Πρώτα πρέπει να ολοκληρώσετε το σχέδιο. Γενικά, όταν κατασκευάζουμε ένα σχέδιο σε προβλήματα σε μια περιοχή, μας ενδιαφέρουν περισσότερο τα σημεία τομής των γραμμών. Βρείτε τα σημεία τομής της παραβολής και της ευθείας. Αυτό μπορεί να γίνει με δύο τρόπους. Ο πρώτος τρόπος είναι αναλυτικός. Λύνουμε την εξίσωση:

Ως εκ τούτου, το κατώτερο όριο ολοκλήρωσης, το ανώτερο όριο ολοκλήρωσης.

Είναι καλύτερα να μην χρησιμοποιήσετε αυτήν τη μέθοδο, αν είναι δυνατόν..

Είναι πολύ πιο επικερδές και πιο γρήγορο να κατασκευάζονται οι γραμμές σημείο προς σημείο, ενώ τα όρια της ολοκλήρωσης γίνονται ξεκάθαρα, λες, «από μόνα τους». Ωστόσο, η αναλυτική μέθοδος εύρεσης των ορίων πρέπει να χρησιμοποιείται μερικές φορές εάν, για παράδειγμα, το γράφημα είναι αρκετά μεγάλο ή η ακριβής κατασκευή δεν αποκάλυψε τα όρια της ολοκλήρωσης (μπορεί να είναι κλασματικά ή παράλογα). Και θα εξετάσουμε επίσης ένα τέτοιο παράδειγμα.

Επιστρέφουμε στο πρόβλημά μας: είναι πιο λογικό να κατασκευάσουμε πρώτα μια ευθεία γραμμή και μόνο μετά μια παραβολή. Ας εκτελέσουμε το σχέδιο:

Και τώρα η φόρμουλα εργασίας: Εάν σε ένα τμήμα κάποια συνεχής συνάρτηση μεγαλύτερο ή ίσοκάποιας συνεχούς συνάρτησης, τότε η περιοχή του σχήματος, που οριοθετείται από τα γραφήματα αυτών των συναρτήσεων και τις ευθείες γραμμές, μπορεί να βρεθεί με τον τύπο:

Εδώ δεν χρειάζεται πλέον να σκέφτεστε πού βρίσκεται η φιγούρα - πάνω από τον άξονα ή κάτω από τον άξονα και, χοντρικά, είναι σημαντικό ποιο πρόγραμμα είναι ΠΑΝΩ(σε σχέση με άλλο γράφημα), και ποιο είναι ΠΑΡΑΚΑΤΩ.

Στο υπό εξέταση παράδειγμα, είναι προφανές ότι στο τμήμα η παραβολή βρίσκεται πάνω από την ευθεία γραμμή και επομένως είναι απαραίτητο να αφαιρεθεί από

Η ολοκλήρωση της λύσης μπορεί να μοιάζει με αυτό:

Το απαιτούμενο σχήμα οριοθετείται από μια παραβολή στο πάνω μέρος και μια ευθεία στο κάτω μέρος.
Στο τμήμα, σύμφωνα με τον αντίστοιχο τύπο:

Απάντηση:

Παράδειγμα 4

Υπολογίστε το εμβαδόν του σχήματος που οριοθετείται από τις γραμμές,,,.

Λύση: Αρχικά, ας εκτελέσουμε το σχέδιο:

Η φιγούρα της οποίας η περιοχή πρέπει να βρούμε είναι σκιασμένη με μπλε(δείτε προσεκτικά την κατάσταση - από τι περιορίζεται το σχήμα!). Αλλά στην πράξη, λόγω απροσεξίας, εμφανίζεται συχνά ένα "πρόβλημα" ότι πρέπει να βρείτε την περιοχή της φιγούρας, η οποία είναι σκιασμένη με πράσινο!

Αυτό το παράδειγμα είναι επίσης χρήσιμο στο ότι υπολογίζει το εμβαδόν ενός σχήματος χρησιμοποιώντας δύο καθορισμένα ολοκληρώματα.

Πραγματικά:

1) Ένα γραμμικό γράφημα βρίσκεται στο τμήμα πάνω από τον άξονα.

2) Το γράφημα της υπερβολής βρίσκεται στο τμήμα πάνω από τον άξονα.

Είναι προφανές ότι οι περιοχές μπορούν (και πρέπει) να προστεθούν, επομένως: