Tanjant denklemi forma sahiptir. Fonksiyon grafiğine teğet denklemi - Bilgi Hipermarketi

İş türü: 7

Koşul

y=3x+2 doğrusu, y=-12x^2+bx-10 fonksiyonunun grafiğine teğettir. Temas noktasının apsisi sıfırdan küçük olduğu için b öğesini bulun.

Karar

x_0 y=-12x^2+bx-10 fonksiyonunun grafiğinde bu grafiğe teğetin geçtiği noktanın apsisi olsun.

x_0 noktasındaki türevin değeri teğetin eğimine eşittir, yani y"(x_0)=-24x_0+b=3. Öte yandan, teğet noktası hem fonksiyonun grafiğine hem de tanjant, yani -12x_0^2+bx_0-10= 3x_0 + 2. Bir denklem sistemi elde ederiz \begin(durumlar) -24x_0+b=3,\\-12x_0^2+bx_0-10=3x_0+2. \end(durumlar)

Bu sistemi çözerek x_0^2=1 elde ederiz, bu da x_0=-1 veya x_0=1 anlamına gelir. Apsis durumuna göre, temas noktaları sıfırdan küçüktür, bu nedenle x_0=-1, sonra b=3+24x_0=-21.

Cevap

İş türü: 7
Konu: Türevin geometrik anlamı. fonksiyon grafiğine teğet

Koşul

y=-3x+4 doğrusu, y=-x^2+5x-7 fonksiyonunun grafiğinin teğetine paraleldir. Temas noktasının apsisini bulun.

Karar

x_0 rastgele bir noktasında y=-x^2+5x-7 fonksiyonunun grafiğine doğrunun eğimi y"(x_0)'dır. Ama y"=-2x+5, yani y"(x_0)=- 2x_0+5.Y=-3x+4 koşulunda belirtilen doğrunun açısal katsayısı -3'tür.Paralel doğruların eğim katsayıları aynıdır.Dolayısıyla öyle bir x_0 değeri buluyoruz ki =-2x_0 +5=-3.

Şunu elde ederiz: x_0 = 4.

Cevap

Kaynak: "Matematik. Sınav-2017 için hazırlık. profil seviyesi. Ed. F. F. Lysenko, S. Yu. Kulabukhova.

İş türü: 7
Konu: Türevin geometrik anlamı. fonksiyon grafiğine teğet

Koşul

Karar

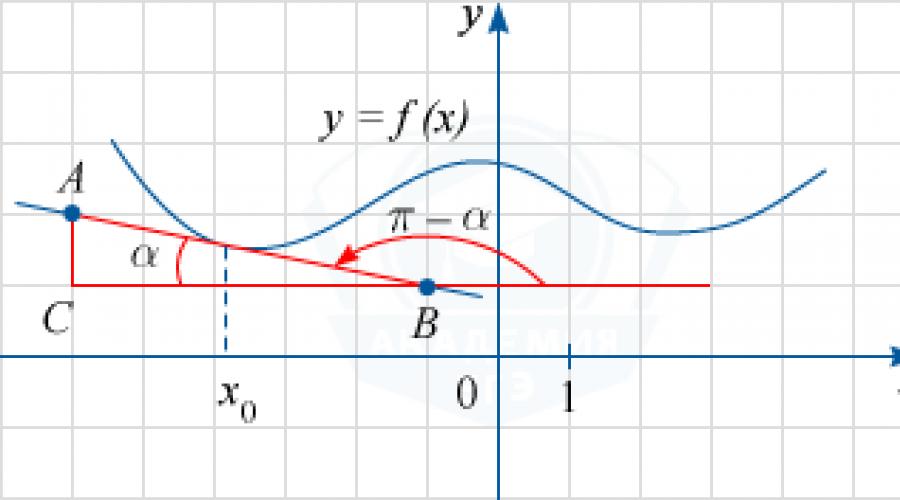
Şekilden, teğetin A(-6; 2) ve B(-1; 1) noktalarından geçtiğini belirledik. C(-6; 1) ile x=-6 ve y=1 doğrularının kesişme noktasını ve \alpha ile ABC açısını belirtin (şekilde dar olduğu görülebilir). Daha sonra AB çizgisi, Ox ekseninin pozitif yönü ile geniş bir \pi -\alfa açısı oluşturur.

Bildiğiniz gibi, tg(\pi -\alpha), f(x) fonksiyonunun x_0 noktasındaki türevinin değeri olacaktır. dikkat, ki tg \alpha =\frac(AC)(CB)=\frac(2-1)(-1-(-6))=\frac15. Buradan, indirgeme formülleriyle şunları elde ederiz: tg(\pi -\alpha) =-tg \alpha =-\frac15=-0.2.

Cevap

Kaynak: "Matematik. Sınav-2017 için hazırlık. profil seviyesi. Ed. F. F. Lysenko, S. Yu. Kulabukhova.

İş türü: 7
Konu: Türevin geometrik anlamı. fonksiyon grafiğine teğet

Koşul

y=-2x-4 doğrusu, y=16x^2+bx+12 fonksiyonunun grafiğine teğettir. Temas noktasının apsisi sıfırdan büyük olduğu için b öğesini bulun.

Karar

x_0, y=16x^2+bx+12 fonksiyonunun grafiğindeki noktanın apsisi olsun.

bu grafiğe teğettir.

x_0 noktasındaki türevin değeri teğetin eğimine eşittir, yani y "(x_0)=32x_0+b=-2. Öte yandan, teğet noktası hem fonksiyonun grafiğine hem de tanjant, yani 16x_0^2+bx_0+12=- 2x_0-4 Bir denklem sistemi elde ederiz \begin(durumlar) 32x_0+b=-2,\\16x_0^2+bx_0+12=-2x_0-4. \end(durumlar)

Sistemi çözerek x_0^2=1 elde ederiz, bu da x_0=-1 veya x_0=1 anlamına gelir. Apsis durumuna göre, temas noktaları sıfırdan büyüktür, bu nedenle x_0=1, sonra b=-2-32x_0=-34.

Cevap

Kaynak: "Matematik. Sınav-2017 için hazırlık. profil seviyesi. Ed. F. F. Lysenko, S. Yu. Kulabukhova.

İş türü: 7
Konu: Türevin geometrik anlamı. fonksiyon grafiğine teğet

Koşul

Şekil, (-2; 8) aralığında tanımlanan y=f(x) fonksiyonunun bir grafiğini göstermektedir. Fonksiyonun grafiğinin teğetinin y=6 doğrusuna paralel olduğu noktaların sayısını belirleyin.

Karar

y=6 doğrusu Öküz eksenine paraleldir. Bu nedenle, fonksiyon grafiğine teğetin Ox eksenine paralel olduğu noktalar buluyoruz. Bu çizelgede bu noktalar uç noktalardır (maksimum veya minimum noktalar). Gördüğünüz gibi 4 ekstremum noktası var.

Cevap

Kaynak: "Matematik. Sınav-2017 için hazırlık. profil seviyesi. Ed. F. F. Lysenko, S. Yu. Kulabukhova.

İş türü: 7
Konu: Türevin geometrik anlamı. fonksiyon grafiğine teğet

Koşul

y=4x-6 doğrusu, y=x^2-4x+9 fonksiyonunun grafiğinin teğetine paraleldir. Temas noktasının apsisini bulun.

Karar

İsteğe bağlı bir noktada x_0 y \u003d x ^ 2-4x + 9 fonksiyonunun grafiğine teğetin eğimi y "(x_0)'dır. Ancak y" \u003d 2x-4, yani y "(x_0) \ u003d 2x_0-4 Koşulda belirtilen y \u003d 4x-7 tanjantının eğimi 4'e eşittir. : x_0 \u003d 4.

Cevap

Kaynak: "Matematik. Sınav-2017 için hazırlık. profil seviyesi. Ed. F. F. Lysenko, S. Yu. Kulabukhova.

İş türü: 7
Konu: Türevin geometrik anlamı. fonksiyon grafiğine teğet

Koşul

Şekil, y=f(x) fonksiyonunun grafiğini ve ona apsis x_0 olan noktada teğetini göstermektedir. f(x) fonksiyonunun x_0 noktasındaki türevinin değerini bulun.

Karar

Şekilden, teğetin A(1; 1) ve B(5; 4) noktalarından geçtiğini belirledik. C(5; 1) ile x=5 ve y=1 doğrularının kesişme noktasını ve \alpha ile BAC açısını belirtin (şekilde keskin olduğu görülebilir). Daha sonra AB çizgisi, Ox ekseninin pozitif yönü ile bir \alfa açısı oluşturur.

"Bir fonksiyonun grafiğine teğet denklemi" video eğitimi, konuya hakim olmak için eğitim materyallerini gösterir. Video dersi sırasında, belirli bir noktada bir fonksiyonun grafiğine teğet denklemi kavramının oluşturulması için gerekli teorik materyal sunulur, böyle bir teğet bulma algoritması sunulur, kullanarak problem çözme örnekleri çalışılan teorik materyal açıklanmıştır.

Video eğitimi, malzemenin görünürlüğünü artıran yöntemler kullanır. Görünüme çizimler, diyagramlar eklenir, önemli sesli yorumlar verilir, animasyon, renkle vurgulama ve diğer araçlar uygulanır.

Video dersi, dersin konusunun sunumu ve bazı y=f(x) fonksiyonunun M(a;f(a) noktasındaki grafiğine teğet görüntüsü ile başlar). Grafiğe belirli bir noktada çizilen teğetin eğiminin, verilen bir noktada f΄(a) fonksiyonunun türevine eşit olduğu bilinmektedir. Cebir dersinden de, y=kx+m doğrusunun denklemi bilinmektedir. Bir noktada teğet denklemi bulma probleminin çözümü, k, m katsayılarını bulmaya indirgeyen şematik olarak sunulmuştur. Fonksiyonun grafiğine ait noktanın koordinatlarını bilerek, koordinatların değerini f(a)=ka+m tanjantının denkleminde yerine koyarak m'yi bulabiliriz. Buradan m=f(a)-ka'yı buluruz. Böylece, belirli bir noktadaki türevin değerini ve noktanın koordinatlarını bilerek, teğet denklemini bu şekilde y=f(a)+f΄(a)(x-a) gösterebiliriz.

Aşağıdaki şemayı izleyerek bir teğet denklemi hazırlama örneğidir. Bir fonksiyon verildiğinde y=x 2 , x=-2. a=-2 kabul ederek, bu noktada fonksiyonun değerini f(a)= f(-2)=(-2) 2 =4 buluyoruz. f΄(х)=2х fonksiyonunun türevini belirliyoruz. Bu noktada türev f΄(a)= f΄(-2)=2 (-2)=-4'e eşittir. Denklemi derlemek için, tüm katsayılar a=-2, f(a)=4, f΄(a)=-4 bulunur, dolayısıyla teğet denklemi y=4+(-4)(x+2). Denklemi basitleştirerek, y \u003d -4-4x elde ederiz.

Aşağıdaki örnekte, y=tgx fonksiyonunun grafiğine orijindeki teğetin denkleminin formüle edilmesi önerilmektedir. Bu noktada a=0, f(0)=0, f΄(х)=1/cos 2 x, f΄(0)=1. Yani teğet denklemi y=x gibi görünüyor.

Bir genelleme olarak, bir noktada fonksiyon grafiğine teğet denkleminin derlenmesi süreci, 4 adımdan oluşan bir algoritma olarak resmileştirilir:

• Temas noktasının apsisi için bir atama yapılmıştır;
• f(a) hesaplanır;
• F΄(х) belirlenir ve f΄(a) hesaplanır. Bulunan değerler a, f(a), f΄(a) teğet denklemi y=f(a)+f΄(a)(x-a) formülüne ikame edilir.

Örnek 1, x \u003d 1 noktasında y \u003d 1 / x fonksiyonunun grafiğine teğet denkleminin derlenmesini ele alır. Problemi çözmek için bir algoritma kullanıyoruz. Bu fonksiyon için a=1 noktasında, f(a)=-1 fonksiyonunun değeri. f΄(х)=1/х 2 fonksiyonunun türevi. a=1 noktasında, türev f΄(a)= f΄(1)=1. Elde edilen veriler kullanılarak, y \u003d -1 + (x-1) veya y \u003d x-2 tanjantının denklemi derlenir.

Örnek 2'de, y \u003d x 3 +3x 2 -2x-2 fonksiyonunun grafiğine teğetin denklemini bulmanız gerekir. Ana koşul, teğetin paralelliği ve y \u003d -2x + 1 düz çizgisidir. İlk önce, y \u003d -2x + 1 düz çizgisinin eğimine eşit teğetin eğimini buluyoruz. Bu düz çizgi için f΄(a)=-2 olduğundan, istenen tanjant için k=-2 olur. (x 3 + 3x 2 -2x-2) ΄ \u003d 3x 2 + 6x-2 fonksiyonunun türevini buluyoruz. f΄(a)=-2 olduğunu bilerek, 3а 2 +6а-2=-2 noktasının koordinatlarını buluruz. Denklemi çözerek 1 \u003d 0 ve 2 \u003d -2 elde ederiz. Bulunan koordinatları kullanarak, iyi bilinen bir algoritma kullanarak teğet denklemi bulabilirsiniz. Fonksiyonun değerini f(a 1)=-2, f(a 2)=-18 noktalarında buluyoruz. f΄(а 1)= f΄(а 2)=-2 noktasındaki türevin değeri. Bulunan değerleri teğet denklemde değiştirerek, ilk nokta için a 1 \u003d 0 y \u003d -2x-2 ve ikinci nokta için a 2 \u003d -2 teğet denklemi y \u003d -2x- elde ederiz. 22.

Örnek 3, y=√x fonksiyonunun grafiğinin (0;3) noktasında çizimi için teğet denkleminin formülasyonunu açıklar. Karar bilinen algoritmaya göre verilir. Temas noktası, a>0 olmak üzere x=a koordinatlarına sahiptir. Fonksiyonun f(a)=√x noktasındaki değeri. f΄(х)=1/2√х fonksiyonunun türevi, bu nedenle, verilen f΄(а)=1/1/2√а noktasında. Elde edilen tüm değerleri teğet denklemde değiştirerek, y \u003d √a + (x-a) / 2√a elde ederiz. Denklemi dönüştürerek y=x/2√a+√a/2 elde ederiz. Teğetin (0; 3) noktasından geçtiğini bilerek, a'nın değerini buluruz. 3=√a/2'den a'yı bulun. Dolayısıyla √a=6, a=36. Tanjant y \u003d x / 12 + 3 denklemini buluyoruz. Şekil, incelenen fonksiyonun grafiğini ve inşa edilen istenen tanjantı göstermektedir.

Öğrencilere yaklaşık Δy=≈f΄(x)Δx ve f(x+Δx)-f(x)≈f΄(x)Δx eşitlikleri hatırlatılır. x=a, x+Δx=x, Δx=x-a alarak, f(x)- f(a)≈f΄(a)(x-a) elde ederiz, dolayısıyla f(x)≈f(a)+ f΄( a)(x-a).

Örnek 4'te 2.003 6 ifadesinin yaklaşık değerini bulmak gerekiyor. f (x) \u003d x 6 fonksiyonunun değerini x \u003d 2.003 noktasında bulmak gerektiğinden, f (x) \u003d x 6, a \u003d 2 alarak iyi bilinen formülü kullanabiliriz. , f (a) \u003d f (2) \u003d 64, f ΄(x)=6х 5 . f΄(2)=192 noktasındaki türev. Bu nedenle, 2.003 6 ≈65-192 0.003. İfadeyi hesapladıktan sonra 2.003 6 ≈64.576 elde ederiz.

"Bir fonksiyonun grafiğine teğetin denklemi" video dersinin okuldaki geleneksel matematik dersinde kullanılması önerilir. Bir uzaktan eğitim öğretmeni için video materyali konuyu daha net bir şekilde açıklamaya yardımcı olacaktır. Konuyla ilgili anlayışlarını derinleştirmek için gerekirse video öğrenciler tarafından öz değerlendirme için önerilebilir.

METİN YORUMLAMASI:

M (a; f (a)) noktasının (a koordinatlarına sahip em ve a'dan eff) y \u003d f (x) fonksiyonunun grafiğine ait olduğunu ve bu noktada bir teğet çizilebileceğini biliyoruz. fonksiyonun grafiği, eksen apsisine dik değil, daha sonra teğetin eğimi f "(a) (a'dan ef vuruşu).

Bir y = f(x) fonksiyonu ve bir M (a; f(a)) noktası verilsin ve f´(a)'nın var olduğu da biliniyor. Verilen bir noktada verilen bir fonksiyonun grafiğine teğet denklemini oluşturalım. Bu denklem, y eksenine paralel olmayan herhangi bir düz çizginin denklemi gibi, y = kx + m (y eşittir ka x artı em) formuna sahiptir, bu nedenle görev katsayıların değerlerini bulmaktır. k ve m (ka ve em)

Eğim k \u003d f "(a). M değerini hesaplamak için, istenen düz çizginin M (a; f (a)) noktasından geçtiği gerçeğini kullanırız. Bunun anlamı, koordinatlarını değiştirirsek düz çizginin denklemindeki M noktasında, doğru eşitliği elde ederiz: f(a) = ka+m, buradan m = f(a) - ka olduğunu buluruz.

Ki ve m katsayılarının bulunan değerlerini düz bir çizginin denkleminde değiştirmeye devam ediyor:

y = kx+(f(a)-ka);

y = f(a)+k(x-a);

y= f(a)+ f"(a) (x- a). ( Y, bir artı ef vuruşundan gelen eff'e eşittir, a çarpı x eksi a).

x=a noktasında y = f(x) fonksiyonunun grafiğine teğet denklemini elde ettik.

Diyelim ki, y \u003d x 2 ve x \u003d -2 (yani a \u003d -2), o zaman f (a) \u003d f (-2) \u003d (-2) 2 \u003d 4; f´(x) \u003d 2x, yani f "(a) \u003d f´(-2) \u003d 2 (-2) \u003d -4. (o zaman a'dan eff dörde, x'ten eff prime iki x'e eşittir, bu da a eşittir eksi dörtten gelen ef vuruş anlamına gelir)

Denklemde bulunan a \u003d -2, f (a) \u003d 4, f "(a) \u003d -4 değerlerini değiştirerek, şunu elde ederiz: y \u003d 4 + (-4) (x + 2) , yani y \u003d -4x -4.

(y eşittir eksi dört x eksi dört)

Orijinde y \u003d tgx (y tanjant x'e eşittir) fonksiyonunun grafiğine teğetin denklemini oluşturalım. Şunlara sahibiz: a = 0, f(0) = tg0=0;

f"(x)= , yani f"(0) = l. Bulunan a=0, f(a)=0, f´(a) = 1 değerlerini denklemde yerine koyarsak: y=x elde ederiz.

Algoritmayı kullanarak fonksiyonun x noktasındaki grafiğine teğet denklemini bulma adımlarımızı genelleştiriyoruz.

GRAFİK y \u003d f (x)'e teğet FONKSİYON DENKLEMİNİ OLUŞTURMA ALGORİTMASI:

1) Temas noktasının apsisini a harfi ile belirtin.

2) f(a)'yı hesaplayın.

3) f'(x)'i bulun ve f'(a)'yı hesaplayın.

4) Bulunan a, f(a), f´(a) sayılarını formülde yerine yaz y= f(a)+ f"(a) (x- a).

Örnek 1. Teğetin denklemini y \u003d - fonksiyonunun grafiğine yazın

nokta x = 1.

Karar. Bu örnekte bunu göz önünde bulundurarak algoritmayı kullanalım.

2) f(a)=f(1)=-=-1

3) f'(x)=; f´(a)= f´(1)= =1.

4) Bulunan üç sayıyı formülde değiştirin: a \u003d 1, f (a) \u003d -1, f "(a) \u003d 1. Şunu elde ederiz: y \u003d -1 + (x-1), y \u003d x-2.

Cevap: y = x-2.

Örnek 2. Verilen bir fonksiyon y = x 3 +3x 2 -2x-2. Teğetin denklemini y \u003d f (x) fonksiyonunun grafiğine, y \u003d -2x +1 düz çizgisine paralel olarak yazın.

Tanjant denklemini derlemek için algoritmayı kullanarak, bu örnekte f(x) = olduğunu dikkate alıyoruz. x 3 +3x 2 -2x-2, ancak temas noktasının apsisi burada belirtilmemiştir.

Şöyle konuşmaya başlayalım. İstenen teğet, y \u003d -2x + 1 düz çizgisine paralel olmalıdır. Ve paralel doğruların eğimleri eşittir. Bu nedenle, teğetin eğimi, verilen doğrunun eğimine eşittir: k cas. = -2. Hok cas. = f "(a). Böylece, a'nın değerini f ´ (a) \u003d -2 denkleminden bulabiliriz.

fonksiyonun türevini bulalım y=f(x):

f"(x) \u003d (x 3 + 3x 2 -2x-2)´ \u003d 3x 2 + 6x-2;f"(a) \u003d 3a 2 + 6a-2.

F "(a) \u003d -2 denkleminden, yani. 3а 2 +6а-2\u003d -2 1 \u003d 0, 2 \u003d -2 buluyoruz. Bu, sorunun koşulunu karşılayan iki teğet olduğu anlamına gelir: biri apsis 0 olan noktada, diğeri apsis -2 olan noktada.

Artık algoritmaya göre hareket edebilirsiniz.

1) 1 \u003d 0 ve 2 \u003d -2.

2) f(a 1) = 0 3 +3 0 2 -2∙0-2=-2; f(a2)= (-2) 3 +3 (-2) 2 -2 (-2)-2=6;

3) f "(a 1) = f" (a 2) = -2.

4) Formülde a 1 = 0, f (a 1) = -2, f "(a 1) = -2 değerlerini değiştirerek, şunu elde ederiz:

y=-2-2(x-0), y=-2x-2.

2 \u003d -2, f (a 2) \u003d 6, f "(a 2) \u003d -2 değerlerini formüle koyarak, şunu elde ederiz:

y=6-2(x+2), y=-2x+2.

Cevap: y=-2x-2, y=-2x+2.

Örnek 3. Noktadan (0; 3) y \u003d fonksiyonunun grafiğine bir teğet çizin. Karar. Bu örnekte f(x) = olduğu göz önüne alındığında, tanjant denklemini derlemek için algoritmayı kullanalım. Burada, Örnek 2'de olduğu gibi, temas noktasının apsisinin açıkça belirtilmediğine dikkat edin. Yine de algoritmaya göre hareket ediyoruz.

1) x = a temas noktasının apsisi olsun; a > 0 olduğu açıktır.

3) f´(x)=()´=; f'(a) =.

4) a, f(a) = , f "(a) = değerlerini formülde yerine koymak

y \u003d f (a) + f "(a) (x-a), şunu elde ederiz:

Duruma göre, teğet (0; 3) noktasından geçer. Denklemde x = 0, y = 3 değerlerini değiştirerek şunu elde ederiz: 3 = , ve sonra =6, a =36.

Gördüğünüz gibi, bu örnekte, algoritmanın sadece dördüncü adımında temas noktasının apsisini bulmayı başardık. a =36 değerini denklemde yerine koyarsak, şunu elde ederiz: y=+3

Şek. Şekil 1, dikkate alınan örneğin geometrik bir resmini sunar: y \u003d fonksiyonunun bir grafiği çizilir, y \u003d +3 düz bir çizgi çizilir.

Cevap: y = +3.

x noktasında türevi olan y = f(x) fonksiyonu için yaklaşık eşitliğin doğru olduğunu biliyoruz: Δyf´(x)Δx

veya daha ayrıntılı olarak, f(x+Δx)-f(x) f´(x) Δx (x'ten ef artı delta x eksi x'ten ef yaklaşık olarak x'ten delta x'e ef üssüne eşittir).

Daha fazla akıl yürütme kolaylığı için notasyonu değiştiriyoruz:

x yerine yazacağız a,

x + Δx yerine x yazacağız

Δx yerine x-a yazacağız.

Daha sonra yukarıda yazılan yaklaşık eşitlik şu şekli alacaktır:

f(x)-f(a)f´(a)(x-a)

f(x)f(a)+f´(a)(x-a). (x'ten gelen ef, x ve a arasındaki farkla çarpılan bir artı ef vuruşundan gelen eff'e yaklaşık olarak eşittir).

Örnek 4. 2.003 6 sayısal ifadesinin yaklaşık değerini bulun.

Karar. x \u003d 2.003 noktasında y \u003d x 6 fonksiyonunun değerini bulmaktan bahsediyoruz. Bu örnekte f(x)=x 6 , a = 2,f(a) = f(2) = 2 olduğunu düşünerek f(x)f(a)+f´(a)(x-a) formülünü kullanalım. 6 =64; x \u003d 2.003, f "(x) \u003d 6x 5 ve dolayısıyla f" (a) \u003d f "(2) \u003d 6 2 5 \u003d 192.

Sonuç olarak şunları elde ederiz:

2.003 6 64+192 0.003, yani. 2.003 6 = 64.576.

Bir hesap makinesi kullanırsak, şunu elde ederiz:

2,003 6 = 64,5781643...

Gördüğünüz gibi, yaklaşıklık doğruluğu oldukça kabul edilebilir.

Aşağıdaki şekli göz önünde bulundurun:

a noktasında türevlenebilen bir y = f(x) fonksiyonunu gösterir. (a; f(a)) koordinatlarıyla işaretlenmiş M noktası. Grafiğin rasgele bir noktası olan P(a + ∆x; f(a + ∆x)) üzerinden, bir kesen MP çizilir.

Şimdi P noktası grafik boyunca M noktasına kaydırılırsa, MP düz çizgisi M noktasının etrafında dönecektir. Bu durumda, ∆x sıfır olma eğiliminde olacaktır. Buradan, bir fonksiyonun grafiğine teğet tanımını formüle edebiliriz.

fonksiyon grafiğine teğet

Fonksiyonun grafiğine teğet, argümanın artışı sıfıra yaklaştığında sekantın limit konumudur. x0 noktasında f fonksiyonunun türevinin varlığının, grafiğin bu noktasında olduğu anlamına geldiği anlaşılmalıdır. teğet ona.

Bu durumda, tanjantın eğimi, bu fonksiyonun f'(x0) noktasındaki türevine eşit olacaktır. Bu türevin geometrik anlamıdır. f fonksiyonunun x0 noktasındaki türevlenebilir grafiğinin teğeti, (x0;f(x0)) noktasından geçen ve eğimi f'(x0) olan bir düz çizgidir.

teğet denklemi

Bir f fonksiyonunun A(x0; f(x0)) noktasındaki grafiğine teğet denklemini bulmaya çalışalım. Eğimi k olan düz bir çizginin denklemi aşağıdaki forma sahiptir:

Eğimimiz türevine eşit olduğundan f'(x0), denklem aşağıdaki formu alacaktır: y = f'(x0)*x + b.

Şimdi b'nin değerini hesaplayalım. Bunu yapmak için, fonksiyonun A noktasından geçtiği gerçeğini kullanırız.

f(x0) = f'(x0)*x0 + b, buradan b'yi ifade edip b = f(x0) - f'(x0)*x0 elde ederiz.

Ortaya çıkan değeri teğet denklemine koyarız:

y = f'(x0)*x + b = f'(x0)*x + f(x0) - f'(x0)*x0 = f(x0) + f'(x0)*(x - x0).

y = f(x0) + f'(x0)*(x - x0).

Aşağıdaki örneği düşünün: x \u003d 2 noktasında f (x) \u003d x 3 - 2 * x 2 + 1 fonksiyonunun grafiğine teğet denklemini bulun.

2. f(x0) = f(2) = 2 2 - 2*2 2 + 1 = 1.

3. f'(x) = 3*x 2 - 4*x.

4. f'(x0) = f'(2) = 3*2 2 - 4*2 = 4.

5. Elde edilen değerleri tanjant formülünde değiştirin, şunu elde ederiz: y = 1 + 4*(x - 2). Parantezleri açıp benzer terimleri getirerek şunu elde ederiz: y = 4*x - 7.

Cevap: y = 4*x - 7.

Teğet denklemi derlemek için genel şema y = f(x) fonksiyonunun grafiğine:

1. x0 belirleyin.

2. f(x0)'ı hesaplayın.

3. f'(x)'i hesaplayın

Teğet eğrinin bir noktasından geçen ve bu noktada birinci mertebeye kadar onunla çakışan düz bir çizgidir (Şekil 1).

Diğer tanım: bu, Δ noktasında kesenin son konumudur x→0.

Açıklama: Eğriyi iki noktada kesen bir doğru alın: ANCAK ve b(resmi görmek). Bu bir sekant. Eğriyle tek bir ortak noktası olana kadar saat yönünde döndüreceğiz. Böylece bir teğet elde ederiz.

Bir teğetin katı tanımı:

fonksiyon grafiğine teğet f bir noktada türevlenebilir xhakkında, noktasından geçen bir çizgidir ( xhakkında; f(xhakkında)) ve bir eğime sahip olmak f′( xhakkında).

Eğimin düz bir çizgisi var y=kx +b. katsayı k ve bir eğim faktörü bu düz çizgi.

Açısal katsayı, bu düz çizginin x ekseni ile oluşturduğu dar açının tanjantına eşittir:

Burada α açısı doğru arasındaki açıdır. y=kx +b ve x ekseninin pozitif (yani saat yönünün tersine) yönü. denir eğim açısı düz(Şekil 1 ve 2).

Eğim açısı düz ise y=kx +b akut, o zaman eğim pozitif bir sayıdır. Grafik artar (Şekil 1).

Eğim açısı düz ise y=kx +b geniş, o zaman eğim negatif bir sayıdır. Grafik azalıyor (Şekil 2).

Doğru, x eksenine paralel ise, doğrunun eğimi sıfırdır. Bu durumda doğrunun eğimi de sıfırdır (çünkü sıfırın tanjantı sıfırdır). Düz çizgi denklemi y = b gibi görünecektir (Şekil 3).

Bir doğrunun eğim açısı 90º (π/2) ise, yani x eksenine dik ise, o zaman düz çizgi eşitlikle verilir. x=c, nerede c- bazı gerçek sayılar (Şekil 4).

Fonksiyonun grafiğine teğetin denklemiy = f(x) noktada xhakkında:

Örnek : Fonksiyonun grafiğine teğetin denklemini bulalım f(x) = x 3 – 2x 2+1 apsisli noktada 2.

Karar .

Algoritmayı takip ediyoruz.

1) Dokunma noktası xhakkında eşittir 2. Hesapla f(xhakkında):

f(xhakkında) = f(2) = 2 3 – 2 ∙ 2 2 + 1 = 8 – 8 + 1 = 1

2) Bul f′( x). Bunu yapmak için önceki bölümde özetlenen farklılaşma formüllerini kullanıyoruz. Bu formüllere göre, X 2 = 2X, a X 3 = 3X 2. Anlamına geliyor:

f′( x) = 3X 2 – 2 ∙ 2X = 3X 2 – 4X.

Şimdi, elde edilen değeri kullanarak f′( x), hesaplamak f′( xhakkında):

f′( xhakkında) = f′(2) = 3 ∙ 2 2 – 4 ∙ 2 = 12 – 8 = 4.

3) Yani, gerekli tüm verilere sahibiz: xhakkında = 2, f(xhakkında) = 1, f ′( xhakkında) = 4. Bu sayıları tanjant denkleminde yerine koyarız ve nihai çözümü buluruz:

y= f(xhakkında) + f′( xhakkında) (x – x o) \u003d 1 + 4 ∙ (x - 2) \u003d 1 + 4x - 8 \u003d -7 + 4x \u003d 4x - 7.

Cevap: y \u003d 4x - 7.

örnek 1 Verilen bir fonksiyon f(x) = 3x 2 + 4x– 5. Teğetin denklemini fonksiyonun grafiğine yazalım. f(x) grafiğin apsisli noktasında x 0 = 1.

Karar. fonksiyon türevi f(x) herhangi bir x için var R . Bulalım:

= (3x 2 + 4x– 5)′ = 6 x + 4.

Sonra f(x 0) = f(1) = 2; (x 0) = = 10. Teğet denklemi şu şekildedir:

y = (x 0) (x – x 0) + f(x 0),

y = 10(x – 1) + 2,

y = 10x – 8.

Cevap. y = 10x – 8.

Örnek 2 Verilen bir fonksiyon f(x) = x 3 – 3x 2 + 2x+ 5. Teğetin denklemini fonksiyonun grafiğine yazalım f(x), çizgiye paralel y = 2x – 11.

Karar. fonksiyon türevi f(x) herhangi bir x için var R . Bulalım:

= (x 3 – 3x 2 + 2x+ 5)′ = 3 x 2 – 6x + 2.

Fonksiyonun grafiğine teğet olduğundan f(x) apsisli noktada x 0 çizgiye paralel y = 2x– 11, o zaman eğimi 2, yani ( x 0) = 2. Bu apsisi 3 koşulundan bulun x– 6x 0 + 2 = 2. Bu eşitlik sadece x 0 = 0 ve x 0 = 2. Her iki durumda da f(x 0) = 5, sonra düz çizgi y = 2x + b fonksiyonun grafiğine (0; 5) veya (2; 5) noktasında dokunur.

İlk durumda sayısal eşitlik doğrudur 5 = 2×0 + b, nerede b= 5 ve ikinci durumda sayısal eşitlik doğrudur 5 = 2 × 2 + b, nerede b = 1.

Yani iki teğet var y = 2x+ 5 ve y = 2x+ 1 fonksiyonun grafiğine f(x) çizgiye paralel y = 2x – 11.

Cevap. y = 2x + 5, y = 2x + 1.

Örnek 3 Verilen bir fonksiyon f(x) = x 2 – 6x+ 7. Teğetin denklemini fonksiyonun grafiğine yazalım f(x) noktadan geçen A (2; –5).

Karar. Gibi f(2) –5, sonra nokta A fonksiyonun grafiğine ait değil f(x). İzin vermek x 0 - temas noktasının apsisi.

fonksiyon türevi f(x) herhangi bir x için var R . Bulalım:

= (x 2 – 6x+ 1)′ = 2 x – 6.

Sonra f(x 0) = x– 6x 0 + 7; (x 0) = 2x 0 - 6. Teğet denklemi şu şekildedir:

y = (2x 0 – 6)(x – x 0) + x– 6x+ 7,

y = (2x 0 – 6)x– x+ 7.

noktadan beri A tanjanta aitse, sayısal eşitlik doğrudur

–5 = (2x 0 – 6)×2– x+ 7,

nerede x 0 = 0 veya x 0 = 4. Bu, noktadan A fonksiyonun grafiğine iki teğet çizmek mümkündür f(x).

Eğer bir x 0 = 0, o zaman tanjant denklemi şu şekildedir: y = –6x+ 7. Eğer x 0 = 4, o zaman tanjant denklemi şu şekildedir: y = 2x – 9.

Cevap. y = –6x + 7, y = 2x – 9.

Örnek 4 Verilen fonksiyonlar f(x) = x 2 – 2x+ 2 ve g(x) = –x 2 - 3. Bu fonksiyonların grafiklerine ortak teğetin denklemini yazalım.

Karar.İzin vermek x 1 - fonksiyonun grafiği ile istenen çizginin temas noktasının apsisi f(x), a x 2 - fonksiyonun grafiği ile aynı çizginin temas noktasının apsisi g(x).

fonksiyon türevi f(x) herhangi bir x için var R . Bulalım:

= (x 2 – 2x+ 2)′ = 2 x – 2.

Sonra f(x 1) = x– 2x 1 + 2; (x 1) = 2x 1 - 2. Teğet denklemi şu şekildedir:

y = (2x 1 – 2)(x – x 1) + x– 2x 1 + 2,

y = (2x 1 – 2)x – x+ 2. (1)

fonksiyonun türevini bulalım g(x):

= (–x 2 – 3)′ = –2 x.