İçin herhangi bir rastgele olayın oluşumu olasılığının tahminleri, ilgilenilen olayların olasılığını, diğer olayların nasıl geliştiğinden farklayıp fark etmeyeceğini belirlemek için çok önemlidir.

Klasik bir şema durumunda, tüm sonuçlar eşit derecede olsa bile, bireyin bireyin olasılığının değerlerini zaten bize bağımsız olarak değerlendirebiliriz. Etkinlik, çeşitli ilköğretim sonuçlarının karmaşık bir seti olsa bile yapabiliriz. Ve eğer birkaç rasgele olay aynı anda veya sırayla oluşursa? Bu, ilgilendiğiniz olayların olasılığını nasıl etkiler?

Birkaç kez bir oyun kemiği atarsam ve "altı" düşmek istiyorum ve her zaman şanslı değilim, bahsi artırmanın gerekli olduğu anlamına gelir, çünkü olasılıkların teorisine göre, ben Bir şans almak için mi? Alalar, olasılık teorisi, böyle bir şeyi onaylamaz. Ne kemikler ne de kart ne de bozuk para ezberlenmeyi bilmiyorum Bize en son ne kadar gösterdiklerini. Tamamen umursamıyorlar, ilk defa ya da bugün onuncu seferde kaderimi yaşadım. Atışı her tekrar ettiğimde, sadece bir şey biliyorum: Bu sefer "altı" olasılığı tekrar altıncaya eşittir. Tabii ki, bu, ihtiyacınız olan sayının asla düşmeyeceği anlamına gelmez. Bu, yalnızca ilk atıştan sonra ve başka bir atma - bağımsız olaylardan sonra kaybımın olduğu anlamına gelir.

A ve B olayları denir bağımsızBirinin uygulanması, başka bir etkinliğin olasılığını etkilemezse. Örneğin, hedefi yenilgi olasılıkları, iki silahın ilk önce hedefin başka bir araca çarpıp gelmediğine bağlı değildir, bu nedenle "ilk silah hedefi vurdu" ve "İkinci araç hedefine" vurguladı.

Eğer iki olay A ve bağımsız olarak ve her birinin olasılığı biliniyorsa, eşzamanlı oluşum ve olayların A ve (belirlenmiş ab) olaylarının olasılığı, aşağıdaki teorem kullanılarak hesaplanabilir.

Bağımsız olaylar için olasılık çarpma teoremi

P (ab) \u003d P (a) * p (b) - Olasılık eşzamanlı İki başlangıcı bağımsız Etkinlikler eşit İşbu olayların olasılıkları.

Misal.Hedefe birinci ve ikinci araçların çekiminde girme olasılıkları sırasıyla eşittir: p 1 \u003d 0.7; p 2 \u003d 0.8. Her iki silahla aynı anda bir voleybola girme olasılığını bulun.

Karar:etkinlikleri zaten gördüğümüz gibi A (ilk silah hit) ve (ikinci araç çarpması) bağımsızdır, yani. P (AV) \u003d P (a) * p (c) \u003d p 1 * p 2 \u003d 0.56.

Kaynak olayların bağımsız olmadığı tahminemelerimize ne olur? Önceki örneği hafifçe değiştirelim.

Misal.Yarışmalarda iki ok hedefi vurur ve bunlardan biri bir etiket çekerse, rakip, gergin olmaya başlar ve sonuçları bozulur. Bu günlük durumu matematiksel bir göreve nasıl dönüştürür ve çözmek için anahat yolları? Bir şekilde, iki senaryoyu, iki farklı görevi derlemek için olayların geliştirilmesi için iki seçeneği bir şekilde bölmek için gerekli olması sezgiseldir. İlk durumda, eğer rakip kaçırılırsa, senaryo gergin atlet için uygun olacak ve doğruluğu daha yüksek olacaktır. İkinci durumda, rakip bir şekilde şansını görüyorsa, ikinci atlet için hedefe vurma olasılığı azalır.

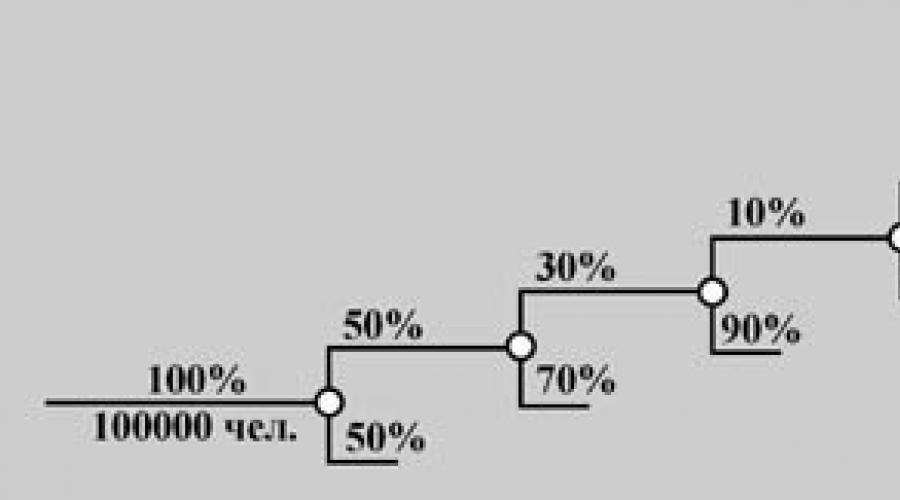
Olası senaryoların ayrılması için (genellikle hipotezler olarak adlandırılırlar), genellikle "Olasılık Ağacı" şemasını kullanırız. Bu şema, muhtemelen uğraşmak zorunda kaldığınız kararlar ağacının anlamında benzerdir. Her şube ayrı bir olay geliştirme senaryosu, yalnızca şimdi sözde kendi değeri var şartlı Olasılık (Q1, Q2, Q 1 -1, Q2 -1).

Bu şema ardışık rastgele olayları analiz etmek için çok uygundur.

Başka bir önemli soruyu bulmak için kalır: ilk olasılık değerleri nereden geliyor? Gerçek durumlar ? Sonuçta, olasılık teorisi aynı madeni paralarla çalışıyor ve kemikler çalıyor mu? Genellikle bu tahminler istatistiklerden alınır ve istatistiksel bilgi olmadığında, kendi araştırmamızı gerçekleştiriyoruz. Ve genellikle veri toplamasından başlamak için gerekli değildir, ancak sorudan, hangi bilgileri ihtiyacımız olmalıyız.

Misal.Şehirde, yüz bin kişinin nüfusuyla değerlendirmemiz gerektiğini varsayalım, örneğin boyalı saçların bakımı için bir balsam için, örneğin, bir balsya için, örneğin, yeni bir ürün için piyasa hacmi. "Olasılık Ağacının" planını düşünün. Aynı zamanda, her bir "dal" üzerindeki olasılık değeri yaklaşık olarak değerlendirmemiz gerekiyor. Öyleyse, pazar kapasitemiz tahminlerimiz:

1) Kadınların tüm sakinlerinden% 50,

2) Tüm kadınların sadece% 30 boya saçı sık sık,

3) onların sadece% 10'u boyalı saçlar için balsamın tadını çıkarın,

4) Bunlardan sadece% 10'u yeni bir ürün denemek için cesaret alabilir,

5) Bunların% 70'i genellikle bizden her şeyi alır, ancak rakiplerimizden.

Karar:Çarpma olasılıkları kanununa göre, ilgilenilen olayların ABD'ye ait olasılığını belirleriz A \u003d (Şehrin bir sakini bu yeni Balsam satın alıyor) \u003d 0.00045.

Şehrin sakinlerinin sayısının bu değerinin bu değerini çarpın. Sonuç olarak, sadece 45 potansiyel alıcımız var ve bu fonun bir balonunun birkaç ay boyunca yeterli olduğunu düşünürsek, ticaret çok meşgul değil.

Bununla birlikte, tahminlerimizden faydalar var.

İlk olarak, farklı iş fikirlerinin tahminlerini karşılaştırabiliriz, şemalarda farklı "gelişme" olacaklar ve elbette olasılık değerleri de farklı olacaktır.

İkincisi, zaten konuştuğumuz gibi, rastgele bir değer, bir şeye bağlı olmadığı için rastgele olarak adlandırılmadığından, rastgele bir değer değildir. Sadece o doğru Değer önceden bilinmiyor. Ortalama alıcı sayısının artırılabileceğini biliyoruz (örneğin, yeni bir ürünün reklamcılığının yardımıyla). Bu nedenle, olasılıkların dağılımının özellikle de etkileyebileceğimiz faktörler üzerindeki "gelişmeye" odaklanmak mantıklıdır.

Müşteri davranışı çalışmasının bir başka nicel örneğini düşünün.

Misal.Gün boyunca, gıda pazarı ortalama 10.000 kişiyi ziyaret eder. Piyasa ziyaretçisinin süt ürünlerinin pavyonuna girme olasılığı 1/2. Bu pavyonda, günde 500 kg'lık çeşitli ürünlerin satılmasıyla ilgili ortalama olarak bilinmektedir.

Pavyonda ortalama alımın sadece 100 g ağırlığında olduğunu iddia etmek mümkün müdür?

Tartışma.Tabii ki, imkansız. Pavyona giren herkes, sonuç olarak, bir şey orada bir şey satın aldı.

Diyagramda gösterildiği gibi, satın alımın ortalama ağırlığının sorusunu cevaplamak için, sorunun cevabını bulmalıyız, pavyona gelen bir kişinin orada bir şey alacağının olasılığı nedir. Eğer bertarafımızda böyle bir veri yoksa, onlara ihtiyacımız var, bir süre pavyonun ziyaretçilerini izledikten sonra onları kendiniz almak zorunda kalacaksınız. Diyelim ki gözlemlerimizin yalnızca köşk ziyaretçilerinin beşteğinin bir şey satın aldığını gösterdiğini varsayalım.

Bu tahminler bizim tarafımızdan elde edilmez, görev basitleşir. Pazara gelen 10.000 kişiden 5000, Süt ürünlerinin pavyonuna girecek, alışveriş sadece 1000 olacaktır. Ortalama alım ağırlığı 500 gramdır. Neyin gerçekleştiğini tam bir fotoğraf oluşturmak için, şartlı "Baterler" mantığı, "Batters" mantığı, aklımızın her aşamasında olduğu kadar "spesifik" bir durumla çalışmamız gerektiğini belirtmek ilginçtir. olasılıklar.

Kendi kendine test görevleri

1. Her biri diğerlerinden bağımsız olarak çalışan N serisi bağlı elementlerden oluşan bir elektrik devresi olduğunu varsayalım.

P olasılığı, her bir elemanın sırasına göre bilinir. Zincirin tüm alanının çalışmasının olasılığını belirleyin (A etkinliği).

2. Öğrenci 25 sınav sorusundan 20 tanesini biliyor. Öğrencinin onun tarafından sunulan üç soruyu bilme ihtimalini bulun.

3. Üretim, her birinin, bir sonraki ay içindeki başarısızlık olasılıklarının sırasıyla P 1, P2, P3 ve P 4'e eşit olduğu, her birinin çalıştığı dört adımdan oluşur. Bir ayda ekipman arızası nedeniyle tek bir üretim durağı olmayacak olasılığını bulun.

Gerçekten ya da hayal gücümüzde meydana gelen olaylar 3 gruba ayrılabilir. Bunlar kesinlikle gerçekleşecek olan güvenilir olaylar, imkansız olaylar ve rastgele olaylar. Olasılıklar teorisi rastgele olaylar tarafından incelenmiştir, yani. Oluşabilecek veya olmayacak olaylar. Bu makale, Matematik EE'nin 4 görevinde (profil seviyesi) olabilecek olasılık teorisi üzerine formül olma olasılığı ve problemleri çözme örneklerinin kısa bir biçiminde bulunacaktır.

Neden olasılık teorisine ihtiyacınız var?

Tarihsel olarak, bu sorunları inceleme ihtiyacı 17. yüzyılda kumarın geliştirilmesi ve profesyonelleşmesiyle ve bir kumarhanenin görünümüyle bağlantılı olarak ortaya çıkmıştır. Çalışma ve araştırmasını gerektiren gerçek bir fenomendi.

Bir kart oyunu, kemikler, rulet, sınırlı sayıda eşit olaydan herhangi biri meydana gelebildiğinde durumlar yarattı. Bir veya başka bir olayın oluşumu olasılığını sayısal değerlendirme yapmaya ihtiyaç vardı.

20. yüzyılda, bu görünüşte anlamlı bilimin, mikrometrede meydana gelen temel süreçlerin bilgisinde önemli bir rol oynadığı ortaya çıktı. Modern bir olasılık teorisi oluşturuldu.

Olasılık teorisinin temel kavramları

Olasılık teorisini incelemek amacıyla olaylar ve olasılıklarıdır. Etkinlik karmaşıksa, olasılıkları bulmak kolay olan basit bileşenlere ayrılabilir.

A ve B olaylarının toplamı, bir etkinliğin bir etkinliğinin veya bir etkinliğin ya da aynı zamanda A ve Olayların bir etkinliğinin veya etkinliğin bulunduğu gerçeğinden oluşur.

A ve B olaylarının çalışması, A etkinliğinin ve etkinliğin gerçekleştiği düşünülerek bir olay olarak adlandırılır.

A ve B olayları aynı anda gerçekleşemezlerse, A ve B'nin acımasızlığına görülür.

ETKİNLİK OLACAKTIR Eğer olamazsa imkansızdır. Bu olay sembolle belirtilir.

Olay A, kesinlikle gerçekleşecekse güvenilir denir. Bu olay sembolle belirtilir.

Her olayın P (a) numarasına göre yapmasına izin verin. Bu P (A) Numarası, aşağıdaki koşullar bu uyumlulukla karşılanırsa, A etkinliği olasılığı olarak adlandırılır.

Önemli özel bir durum, aynı derecede sağlam temel sonuçlar olduğu durumdur ve keyfi sonuçlar Olaylar A etkinliği tarafından oluşturulur. Bu durumda, olasılık formül tarafından girilebilir. Bu şekilde uygulanan olasılık, klasik bir olasılık denir. Bu durumda, 1-4 özelliklerinin yapıldığı kanıtlanabilir.

Matematikte sınavda bulunan olasılıklar teorisi konusundaki görevler temel olarak klasik olasılıkla ilişkilidir. Bu görevler çok basit olabilir. Özellikle basit, gösteri seçeneklerinde olasılık teorisindeki görevlerdir. Olumlu sonuçların sayısını hesaplamak kolaydır, doğrudan koşulda tüm sonuçların sayısını yazdırılır.

Cevap, formül tarafından elde edilir.

Matematik kelimesinden bir görevin olasılığını belirlemek için bir örnek

Masanın üzerinde 20 pies yalan - 5 lahana, elma ile 7 ve pirinç ile 8. Marina bir ezme yapmak istiyor. Pilavla bir ezme yapmanın olasılığı nedir?

Karar.

Toplam Eşit İlköğretim Sonuçları 20'de, yani Marina 20 turttan herhangi birini alabilir. Ancak, Marina'nın pirinçle bir pidrite alacağı olasılığını takdir etmemiz gerekiyor, yani bir kukla olan bir kukla olan bir kukla. Bu, olumlu sonuçların sayısına sahip olduğumuz anlamına gelir (pirinçli pies seçimleri) 8. Olasılık, Olasılık formülle belirlenir:

Bağımsız, zıt ve keyfi olaylar

Ancak, açık bankada görevler daha karmaşık görevlerle tanışmaya başladı. Bu nedenle, okuyucuya ve olasılık teorisinde incelenen diğer konulara dikkat edin.

Olaylar A ve B, her birinin olasılığı başka bir olayın meydana gelip olasılığı bağlı değilse bağımsız olarak adlandırılır.

B, etkinliğin olmadığıdır, yani. Etkinlik B, A etkinliğinin tam tersidir. Karşı olayın olasılığı, doğrudan bir olay olasılığının bir eksi birine eşittir, yani. .

Olasılıkların eklenmesi ve çoğaltılması teoremleri, formüller

Keyfi etkinlikler için A ve bu olayların miktarının olasılığı olasılığı, ortak olaylarının olasılığı olmadan olasılıklarının toplamına eşittir, yani. .

Bağımsız olaylar için A ve bu olayların çalışmalarının olasılığına göre, olasılıklarının ürününe eşittir, yani. bu durumda .

Son 2 ifade, olasılıkların eklenmesi ve çoğaltılması teoremleri denir.

Her zaman çıkış sayısını saymamak çok basittir. Bazı durumlarda, kombinatörüm formüllerini kullanmak gerekir. Bu durumda, en önemlisi, belirli koşulları sağlayan olay sayısının sayılmasıdır. Bazen bu tür sayma bağımsız görevler olabilir.

6 ücretsiz yerde 6 öğrenci oturabilir miyim? İlk öğrenci 6 sandalyenin herhangi birini alacak. Bu seçeneklerin her biri ikinci öğrenciye gerçekleşmenin 5 yoluna karşılık gelir. Üçüncü öğrenci için, dördüncü - 3, beşinci - 2 için 4 ücretsiz yer var, altıncı kalan tek yeri alacak. Tüm seçeneklerin sayısını bulmak için, 6'nın sembolüyle belirtilen bir ürün bulmanız gerekir! Ve "altı faktorum" okuyun.

Genel olarak, bu sorunun cevabı, bizim olgumuzdaki P öğelerinden izinlerin sayısı için formüle verir.

Şimdi öğrencilerimizle birlikte başka bir olgu düşünün. 6 ücretsiz yerle 2 öğrenci oturabilir miyim? İlk öğrenci 6 sandalyenin herhangi birini alacak. Bu seçeneklerin her biri ikinci öğrenciye gerçekleşmenin 5 yoluna karşılık gelir. Tüm seçeneklerin sayısını bulmak için bir iş bulmanız gerekir.

Genel olarak, bu sorunun cevabı, K öğelerinden N öğelerinden gelen konaklama sayısı için formüle verir.

Bizim durumumuzda.

Ve bu seriden son durum. 6'dan üç öğrenciyi kaç yönden seçebilirsin? İlk öğrenci, ikinci yöntemlerde 6 - 5 üçüncü yöntemlerde - dördü. Ancak bu seçenekler arasında, öğrencilerin bir ve aynı zirvesinde 6 kez bulunur. Tüm seçeneklerin numarasını bulmak için değeri hesaplamanız gerekir :. Genel olarak, bu sorunun cevabı, elemanların elemanları tarafından kombinasyonların sayısı için formüle verir:

Bizim durumumuzda.

Matematik kelimesinden problemlerin çözme problemlerinin olasılık tanımına örnekler

Görev 1. ED koleksiyonundan. Yashchenko.

30 börek bir tabakta: 3 etli, 18, lahana ile 18 ve kiraz ile 9. Rastgele sasha bir ezmeyi seçer. Kirazla olacağının olasılığını bulun.

.

Cevap: 0.3.

Görev 2. ED koleksiyonundan. Yashchenko.

Ortalama 20 arızalı 1000 ampulün her bir partisinde. Rastgele ampulün partiden gelen ampulün iyi olacağını öğrenin.

Çözüm: 1000-20 \u003d 980 iyi ışık sayısı. O zaman partiden getirilen ampulün getirilmesi olasılığı iyi olacak:

Cevap: 0.98.

Matematik öğrencilerinde test edilmesinin, 9'dan fazla görevin 9'dan fazla görevi 0,67'ye eşit bir şekilde çözüleceğinin olasılığı. U olabileceği, 8'den fazla görevi doğru bir şekilde çözecek, 0.73'e eşit. U olabileceği olasılığını bulun. Tam olarak 9 görevi doğru şekilde çözecek.

Sayısal bir doğrudan hayal edersek ve 8 ve 9 numaralı noktalara dikkat çekersek, "W. Tam olarak 9 görev "durumunda" W. 8'den fazla görevi çözmek doğrudur, "ancak" W. Koşuluna uygulanmaz. Kesinlikle 9'dan fazla görevi çözecek. "

Ancak, "U. Kesinlikle 9'dan fazla görevi çözecek "U. U. Kesinlikle 8'den fazla görevi çözecek. " Böylece, olayları belirtirsek: "W. Tam olarak 9 görevi çözmek için doğrudur "- A," W. 8'den fazla görevi doğru şekilde çözecek "- B üzerinden" W. Kesinlikle 9'dan fazla görevi çözecektir "C arasındadır. Çözüm şöyle görünecektir:

Cevap: 0.06.

Geometri sınavında, öğrenci bir soruyu sınav sorunları listesinden cevaplar. Bunun "Trigonometri" konusu hakkında bir soru olmadığı olasılığı 0,2'dir. Bu sorunun "dış açılar" konusundaki bu sorunun 0,15'tir. Aynı anda bu iki konuya atıfta bulunan sorular, hayır. Öğrencinin sınavının bu iki konudan biriyle ilgili bir soru olacağının olasılığını bulun.

Olaylarımızın ne verildiğini düşünelim. İki eksik olumsuz verilir. Yani, sorunun "trigonometri" konusuna veya "dış açılar" konusuna atıfta bulunacaktır. Olasılık teoremi tarafından, eksik olayların olasılığı, her olayın olasılıklarının toplamına eşittir, bu olayların olasılıklarının toplamını bulmalıyız:

Cevap: 0.35.

Oda üç lambalı bir fenerle aydınlatılmıştır. Yıl boyunca bir lamba kırma olasılığı 0,29'dur. Yıl boyunca en az bir lamba başarısız olmanın olasılığını bulun.

Olası olayları düşünün. Her biri diğer ampullerden bağımsız olarak üstesinden gelebilen veya boşaltabilecek üç ampul var. Bunlar bağımsız olaylardır.

Sonra bu tür olaylar için seçenekleri belirtiriz. İşaretini kabul ediyoruz: - Işık yanıkları, ampul yandı. Ve hemen, bir etkinliğin olasılığını hesaplıyoruz. Örneğin, "ampul yanmış", "ampul yanığı", "ampul yanıkları", "ampul yanıkları", "ampul yanıkları" olan bir olayın olasılığı: "ampul" olasılığının olasılığı, bir olasılık olarak hesaplanır. "Ampul" olayının karşısındaki olay, yani :.

SADECE 7. Olayların olasılığı olumlu olduğumuzu unutmayın. Bu tür olayların olasılığı, olayların her birinin olasılıklarının toplamına eşittir :.

Cevap: 0,975608.

Aşağıdaki resimde başka bir görevi arayabilirsiniz:

Böylece, formüller olasılığının teorisinin ve EGE sürümünde buluşabileceğiniz sorunları çözme örneklerinin karşılanabileceğini anlıyoruz.

Olasılık nedir?

Bu terim ile karşı karşıya, ilk kez, ne olduğunu anlamadım. Bu nedenle, mevcut açıklamaya çalışacağım.

Olasılık, ihtiyacınız olan olayın olacağı bir ihtimaldir.

Örneğin, bir arkadaşınıza gitmeye, girişi ve hatta yaşadığı zemini hatırlamaya karar verdiniz. Ancak dairenin oda ve konumu unuttu. Ve merdiven üzerinde duruyorsun ve önünüzde seçim yapabileceğiniz kapılar.

İlk kapıyı ararsanız, hangi ihtimalin şansı (olasılık) nedir, arkadaşınızı açar mısınız? Toplam daireler ve arkadaşlar sadece onlardan biri için yaşıyor. Eşit bir şansla herhangi bir kapıyı seçebiliriz.

Ama bu şansı nedir?

Kapılar, istediğiniz kapı. İlk kapıyı arayarak tahmin olasılığı :. Yani, üçten bir kez tam olarak tahmin ediyorsunuz.

Times'i arayarak öğrenmek istiyoruz, kapıyı ne sıklıkla tahmin edeceğiz? Tüm seçenekleri düşünelim:

1. B'yi denirdin. 1y. bir kapı
2. B'yi denirdin. 2y bir kapı
3. B'yi denirdin. 3y. bir kapı

Şimdi bir arkadaşının olabileceği tüm seçenekleri göz önünde bulundurun:

fakat. Başına 1i Kapı
b. Başına 2y Kapı
içinde. Başına 3i Kapı

Tüm seçenekleri bir tablo biçiminde karşılaştırıyoruz. Checkmark, seçtiğiniz seçeneklerin bir arkadaşın konumu ile eşleşmemesi durumunda çakıştığında seçenekleri gösterir.

Her şeyi görebileceğiniz gibi muhtemelen Seçenekleri Bir arkadaşın yeri ve seçiminiz, hangi kapıyı arayacak.

FAKAT toplam olumlu sonuçlar . Yani, sanırım, bir kez kapıyı çağıran, yani. .

Bu olasılık - olumlu bir sonucu (seçtiğiniz bir arkadaşınızın konumu ile çakıştığında) olası olayların sayısına oranıdır.

Tanım bir formüldür. O olasılık, P'yi belirtmek için yapılır:

Bu formül çok uygun değildir, bu yüzden olumlu sonuçların sayısını kabul edeceğiz ve bunun için toplam çıktının sayısıdır.

Olasılık yüzde olarak kaydedilebilir, bunun için sonuçlanan sonucu çarpmanız gerekir:

Muhtemelen, "sonuçlar" kelimesi size koştu. Matematik çeşitli eylemleri aradığından (böyle bir eylemimiz var - bu bir çağrı zil sesidir) deneyler, daha sonra bu deneylerin sonucu bir sonuç olarak adlandırılacak olan gelenekseldir.

Eh, sonuçlar elverişli ve elverişsiz.

Örneğimize geri dönelim. Diyelim ki kapılardan birini aradık, ama yabancı bir adam bize açıldı. Tahmin etmedik. Kalan kapılardan birini ararsanız, arkadaşımızı açacağız olasılığı nedir?

Bunun bir hata olduğunu düşünüyorsan. Başa çıkalım.

İki kapağımız kaldı. Böylece olası adımlarımız var:

1) Arama 1-uu bir kapı
2) Ara 2-uu bir kapı

Arkadaşım, bunların hepsinde, bunlardan birinin arkasında doğru bir şekilde (çünkü aradığımız biri için değildi):

a) arkadaşı 1 inci Kapı
plaj 2-O. Kapı

Yine bir masa çizelim:

Gördüğünüz gibi, elverişli olan seçenekler var. Yani, olasılık eşittir.

Neden olmasın?

Düşündüğümüz durum - bağımlı olayların bir örneği. İlk olay kapıdaki ilk çağrıdır, ikinci olay ikinci kapı zilidir.

Ve bağımlı onlar çağrılır, çünkü aşağıdaki işlemleri etkiliyorlar. Ne de olsa, ilk aramadan sonra, kapıda bir arkadaş açtık, o zaman diğer ikisinden birinde olduğu olasılığı ne olurdu? Sağ, .

Ancak bağımlı olaylar varsa, o zaman olmalı bağımsız? Doğru, var.

Ders kitabı örneği, madalyonun atılmasıdır.

1. Para birimi atmak. Kartalın düşmesi olasılığı nedir, örneğin? Bu doğrudur -, çünkü hepsinin seçenekleri (kartal veya acele, madalyonun kenarındaki olasılığını ihmal edeceğiz), ancak bizi sadece düzenleriz.
2. Ama acele düştü. Tamam, tekrar at. Bir kartalın düşmesi olasılığı nedir? Hiçbir şey değişmedi, her şey aynı. Kaç tane seçenek? İki. Ve bize kaç tane uygun? Bir.

Ve üst üste binlerce kez bir acele çıkacak. Bir kartal serpinti olasılığı her şey yolunda olacaktır. Seçenekler her zaman ve uygundur -.

Bağımlı olayları kolayca bağımsız olarak ayırt edebilir:

1. Deney bir kez yapılırsa (bir jeton attıktan sonra, kapıda 1 zaman araması, vb.), Ardından olaylar her zaman bağımsızdır.
2. Deney birkaç kez gerçekleştirilirse (bozuk para bir kez atılırsa, kapı birkaç kez denir), ardından ilk olay her zaman bağımsızdır. Ve sonra, eğer olumlu ya da tüm sonuçların sayısı değişiyorsa, olaylar bağımlıdır ve değilse, bağımsız.

Olasılığını belirlemek için biraz ısırılalım.

Örnek 1.

Madeni para iki kez atılır. Kartalın üst üste iki kez düşmesi olasılığı nedir?

Karar:

Tüm olası seçenekleri düşünün:

1. Kartal orel
2. Kartal acele
3. Acele etmek
4. Rusk-Ruska.

Tüm seçeneği görebileceğiniz gibi. Bunlardan sadece memnun kalıyoruz. Bu olasılık:

Durumun olasılığını basitçe bulması istenirse, cevap bir ondalık kesir biçiminde verilmelidir. Cevabın yüzde olarak verilmesi gerektiği belirtildi, o zaman çoğalırdık.

Cevap:

Örnek 2.

Bir kutu şeker, tüm şeker aynı sargıya paketlenir. Bununla birlikte, şekerden - fındık ile, brendi ile, kiraz ile, karamelli ve Nugoy ile.

Olasılık nedir, bir şekerleme, fındık ile şeker almak. Cevap yüzde olarak ver.

Karar:

Kaç tane olası sonuç? .

Yani, bir şeker alarak, mevcut kutusundan biri olacak.

Ve kaç elverişli sonuç?

Çünkü kutuda sadece fındık ile şekerler.

Cevap:

Örnek 3.

Bir kutu top. Beyaz, - siyah.

1. Beyaz topu çekmenin olasılığı nedir?
2. Kutuya siyah toplar ekledik. Beyaz topu şimdi çekmenin olasılığı nedir?

Karar:

a) Tüm topların kutusunda. Onlara beyaz.

Olasılık:

b) Şimdi kutudaki toplar oldu. Ve beyaz kadar kaldı -.

Cevap:

Tam olasılık

Tüm olası olayların olasılığı () 'e eşittir.

Kırmızı ve yeşil topların çekmecesinde olduğunu varsayalım. Kırmızı bir top çekmenin olasılığı nedir? Yeşil Top? Kırmızı veya yeşil top?

Olasılık kırmızı bir topu çekin

Yeşil Top:

Kırmızı veya yeşil top:

Gördüğünüz gibi, olası tüm olayların toplamı (). Bu anı anlamak, birçok görevi çözmenize yardımcı olacaktır.

Örnek 4.

Kutuda işaretçiler yatıyor: Yeşil, kırmızı, mavi, sarı, siyah.

Kırmızı keçeli bir kalemle çekmeme olasılığı nedir?

Karar:

Numarayı düşünelim elverişli sonuçlar.

Kırmızı keçeli kalem değil, yeşil, mavi, sarı veya siyah demektir.

Etkinliğin gerçekleşmeyeceği olasılığı, olayın meydana geleceği olasılığı eksi eşittir.

Bağımsız olayların çarpma olasılıklarının kuralı

Zaten bildiğiniz bağımsız olaylar nelerdir.

Ve iki (veya daha fazla) bağımsız etkinliğin üst üste geleceği olasılığını bulmanız gerekiyorsa?

Diyelim ki madeni para zamanını atmanın olasılığını bilmek istiyoruz, kartalları iki kez göreceğiz?

Biz zaten düşündük.

Ve eğer bir para harcıyorsan? Kartalları üst üste görme olasılığı nedir?

Toplam seçenek:

1. Kartal
2. Kartal
3. Kartal
4. Kartal
5. Kartal
6. Acele
7. Kartal acele
8. Rusk-rush

Nasıl olduğunu bilmiyorum, ama yanılıyordum, bu listeyi oluşturuyordum. Vaov! Ve sadece seçenek (önce) bize uygundur.

5 atış için, kendinizin olası sonuçların bir listesini yapabilirsiniz. Fakat matematik senin gibi çok çalışkan değil.

Bu nedenle, önce fark ettiler ve daha sonra bir olay olasılığının her seferinde belirli bir bağımsız olay dizisinin olasılığının azaldığını kanıtlamıştır.

Diğer bir deyişle,

Tüm aynı, kötü niyetli, madeni paraların örneğini düşünün.

Testte bir kartalın olasılığı var mı? . Şimdi bir kez para atıyoruz.

Ardışık bir kartalın olasılığı nedir?

Bu kural, yalnızca aynı olayın ardında birkaç kez gerçekleşeceği ihtimalini bulmamız istenmiyor.

Nehir kartalının sırasını bulmak istiyorsak, bir üst üste kafatası da yapacağız.

Düşme acele olasılığı -, kartal -.

Nehir-Eagle-River-River'in sekansını düşme olasılığı:

Kendinizi kontrol edebilir, tabloya ulaşabilirsiniz.

Eksik olayların olasılıklarının eklenmesi kuralı.

Bu yüzden dur! Yeni tanım.

Başa çıkalım. Yıpranmış madalyonumuzu alın ve zaman atın.
Muhtemel Seçenekler:

1. Kartal
2. Kartal
3. Kartal
4. Kartal
5. Kartal
6. Acele
7. Kartal acele
8. Rusk-rush

Yani tamamlanmamış olaylar, bu belirli, belirtilen bir olay dizisidir. - Bunlar eksik etkinliklerdir.

İki (veya daha fazla) eksik olayın olasılığını belirlemek istiyorsak, bu olayların olasılığını katlıyoruz.

Bir kartal veya acelenin fallosunun iki bağımsız olay olduğunu anlamak gerekir.

Sıra olasılığının nasıl olduğunu belirlemek istiyorsak) (veya başka bir), o zaman olasılıkların çoğalması kuralını kullanıyoruz.
Bir kartalın ilk atışında düşme olasılığı nedir ve ikinci ve üçüncü aceleyle mi?

Ancak, örneğin kartalın tam zamanında düştüğünde, birkaç dizden çıkmanın olasılığını bilmek istiyorsak, yani. Seçenekler ve bu dizilerin olasılığını katlamalıyız.

Toplam seçenek, bize uygundur.

Her dizinin görünümünün olasılığını oluşturarak aynısını alabiliriz:

Böylece, bazı, eksik, olayların olasılığını belirlemek istediğimizde olasılığı katlıyoruz.

Çarpıldığında karıştırılmamasına ve ne zaman katlanmamasına yardımcı olan mükemmel bir kural var:

Madeni para süresini attığımızda, örneğin kartal zamanlarını görme ihtimalini öğrenmek istiyoruz.
Ne olacak?

Düşmeli:
(Kartal ve acele ve acele) veya (acele ve kartal ve acele) veya (acele ve acele ve kartal).
Böylece ortaya çıktı:

Birkaç örneğe bakalım.

Örnek 5.

Kutuda kalemlerle yatıyor. Kırmızı, yeşil, turuncu ve sarı ve siyah. Kırmızı veya yeşil kalemleri çekmenin olasılığı nedir?

Karar:

Örnek 6.

Oyun kemiği iki kez atılır, 8 puanın miktarına düşme olasılığı nedir?

Karar.

Gözlük nasıl alabiliriz?

(ler) veya (ve) veya (ve) veya (ve) veya (ve).

Bir (herhangi bir) yüz düşme olasılığı.

Olasılığını düşünüyoruz:

Egzersiz yapmak.

Artık onları eklediğinizde ve ne zaman çoğalacağınızı düşünmeniz gerektiğinde sizin için netleşti. Değil mi? Biraz pratik yapalım.

Görevler:

Kartlar, tepe, solucanlar, 13 treph ve 13 tef. Her takımın asına.

1. Treph'leri üst üste çekmenin olasılığı nedir (güvertede geri koyduğumuz ilk noktalı kart ve karıştırdığımız ilk noktalı kart)?
2. Siyah bir harita (tepe noktaları veya trahçeler) çekmenin olasılığı nedir?
3. Bir resmi (Warta, Lady, King veya Ace) çekmenin olasılığı nedir?
4. İki resmi üst üste çekmenin olasılığı nedir (ilk noktalı kartı güverteden çıkarırız)?
5. Olasılık, iki kart alma, bir kombinasyon toplama - (para birimi, bayan veya kral) ve kartların çekileceği dizinin ACE'si önemli değil, önemli değil.

Yanıtlar:

Tüm görevleri kendiniz çözebilirseniz, o zaman büyük birsiniz! Şimdi sınavda olasılık teorisi üzerindeki zorluklar fındık gibi tıklayacaksınız!

Olasılık teorisi. Ortalama seviye

Bir örnek düşünün. Diyelim ki bir oyun kemiği atıyoruz. Bu ne tür bir kemik, biliyorsun? Buna kenarlarda sayılarla bir küp denir. Kaç tane yüz, çok sayıda sayı: Ne kadar? Önce.

Yani, kemiği atıyoruz ve düştü ya da düşmek istiyoruz. Ve düşüyor.

Olasılık teorisinde, ne olduğunu söylüyorlar elverişli olay (müreffeh ile karıştırmayın).

Düştüyse, etkinlik de elverişli olacaktır. Toplam sadece iki elverişli olay olabilir.

Ve ne kadar olumsuz? Olası olaylardan bu yana, olumsuz olayların olumsuz olduğu anlamına gelir (bu düşerse veya).

Tanım:

Olasılık, olumlu olayların sayısının olası tüm olayların sayısına oranı olarak adlandırılır.. Yani, olasılık olası tüm olayların oranın hangi oranının olumlu olduğunu gösteriyor.

Latin bir mektubun olasılığını belirtir (görünüşte, İngilizce kelime olasılığından oluşan olasılıktır).

Yüzde ihtimalini ölçmek gelenekseldir (konuya bakınız). Bunun için olasılık değeri çarpılmalıdır. Bir örnek olarak, bir oyun kemiği, olasılığı.

Ve yüzde :.

Örnekler (kendinizi çözmek):

1. Bir jeton atarken, kartal düşerken olasılık nedir? Ve acelenin ne kadar düşeceği?
2. Bir oyun kemiği atarken olasılığı nedir? Ve garip olanı olan?
3. Sıradan, mavi ve kırmızı kalem kutularında. Rastgele tyant bir kalem. Basitçe çekmenin olasılığı nedir?

ÇÖZÜMLER:

1. Kaç tane seçenek? Kartal ve acele - sadece iki. Ve kaç tanesi elverişlidir? Sadece bir tane - kartal. Dolayısıyla olasılık

   Bir şapka ile aynı :.

2. Toplam seçenek: (Küpün kaç tarafı, çok farklı seçenekler). Onlardan elverişli: (bunlar hepsi bile sayılar :).
   Olasılık. Garip, doğal olarak, aynı.
3. Toplam: . Uygun: Olasılık:

Tam olasılık

Yeşil kutudaki tüm kalemler. Kırmızı bir kalem çekmenin olasılığı nedir? Hiç şans yok: olasılığı (sonuçta olumlu olaylar -).

Böyle bir olay imkansız denir.

Ve yeşil bir kalem çekmenin olasılığı nedir? Olumlu olaylar, her şeyin olayları ile tamamen aynıdır (tüm olaylar uygundur). Olasılık olasılığının eşit olduğu anlamına gelir.

Böyle bir olay güvenilir denir.

Yeşil ve kırmızı kalemler kutusunda ise, yeşil veya kırmızıyı çekmenin olasılığı nedir? Bir kez daha. Böyle bir şeyi not edin: Yeşil çekme olasılığı eşittir ve kırmızıdır.

Özetle, bu olasılıklar tam olarak eşittir. Yani, tüm olası olayların olasılıklarının toplamı eşittir.

Misal:

Bir kalem kutusunda, aralarında mavi, kırmızı, yeşil, basit, sarı ve diğerleri turuncu. Yeşil çekmeme olasılığı nedir?

Karar:

Tüm olasılıkların miktarında verildiğini unutmayın. Ve yeşil çekme olasılığı eşittir. Bu olasılığının yeşilin yeşilini eşitlemez.

Bu tekniği hatırlayın:etkinliğin olayın meydana geleceği olasılığına eşit olabileceği olasılığı olamaz.

Bağımsız olaylar ve çarpma kuralı

Para birimi atıyorsun ve iki kere kartalın düştüğünü istiyorsun. Bunun olasılığı nedir?

Tüm olası seçenekleri çalıştıralım ve kaç tane olduğunu belirleyelim:

Eagle-Eagle, River-Eagle, Eagle Nehri, Rushka-nehir. Başka?

Toplam seçenek. Sadece bir şey bizim için uygundur: Kartal Orel. Toplam olasılık eşittir.

Tamam. Ve şimdi bir para birimi atıyoruz. Sakin ol. Olmuş? (Cevap).

Bir sonraki atışın eklenmesiyle, olasılığı azaltıldığını görebilirsiniz. Genel kural denir Çarpma Kuralı:

Bağımsız olayların olasılıkları değişkendir.

Bağımsız olaylar nelerdir? Her şey mantıklıdır: Bunlar birbirlerine bağlı olmayanlardır. Örneğin, birkaç kez para attığımızda, sonucu tüm önceki atışlara bağlı olmayan yeni bir atış üretilir. Aynı başarıyla aynı anda iki farklı para atabiliriz.

Daha fazla örnek:

1. Oyun kemiği iki kez atılır. İki kere de düşme olasılığı nedir?
2. Madeni para fırlatılır. Kartalın ilk kez düşmesi olasılığı nedir ve sonra acelenin iki katı?
3. Oyuncu iki kemik atar. Üzerindeki sayıların miktarının eşit olacağı olasılığı nedir?

Yanıtlar:

1. Olaylar bağımsızdır, çarpma kuralının çalıştığı anlamına gelir :.
2. Kartalın olasılığı eşittir. Acele olasılığı da. Alternatif:
3. 12 Yalnızca iki yol düşerse çalışabilir:.

Eksik olaylar ve ekleme kuralı

İstifsizlik, tam bir olasılık olana kadar birbirini tamamlayan olaylar denir. Adından aynı anda olamayacakları açıktır. Örneğin, bir para atarsanız, bir kartal veya acele düşebilir.

Misal.

Bir kalem kutusunda, aralarında mavi, kırmızı, yeşil, basit, sarı ve diğerleri turuncu. Yeşil veya kırmızıyı çekmenin olasılığı nedir?

Karar.

Yeşil kalemi çekmenin olasılığı eşittir. Kırmızı -.

Toplamda olumlu olaylar: yeşil + kırmızı. Bu, olasılığının yeşil veya kırmızıyı çıkardığı anlamına gelir.

Aynı olasılık bu formda gösterilebilir :.

Bu ilave kuralıdır:eksik olayların olasılıkları katlanır.

Karışık tip görevler

Misal.

Madeni para iki kez atılır. Atışların sonucunun farklı olabileceği olasılığı nedir?

Karar.

İlk kartalın düştüğü, ikincisi ise acele edilmesi ve tam tersi olması gerektiği anlaşılmaktadır. İki çift bağımsız olay var olduğu ortaya çıktı ve bu çiftler birbirleriyle anlaşılmaz. Nereden karıştırılırsa, nereden katlanacağınız, ancak nereye katlanacağınız önemli değil.

Bu gibi durumlar için basit bir kural var. Sendikaların "ve" veya "veya" olaylarını birbirine bağlayarak neler olacağını açıklamaya çalışın. Örneğin, bu durumda:

Düşmeli (Kartal ve Rush) veya (Rushka ve Kartal).

İttifakın olduğu yerlerde "ve", çarpma ve "veya" nerede olursa olsun, ilavesi:

Kendin dene:

1. İki atma sikkesi ile aynı tarafın da aynı tarafın düşmesi olasılığı nedir?
2. Oyun kemiği iki kez atılır. Noktaların düşmesi olasılığı nedir?

ÇÖZÜMLER:

Başka bir örnek:

Para birimi atmak. Kartalın en az bir kere düşmesi olasılığı nedir?

Karar:

Olasılık teorisi. Ana şey hakkında kısaca

Olasılık, olumlu olayların sayısının olası tüm olayların sayısına oranıdır.

Bağımsız olaylar

Diğerinin başlangıcının olasılığının oluşmasında iki olay bağımsızdır.

Tam olasılık

Tüm olası olayların olasılığı () 'e eşittir.

Etkinliğin gerçekleşmeyeceği olasılığı, olayın meydana geleceği olasılığı eksi eşittir.

Bağımsız olayların çarpma olasılıklarının kuralı

Belirli bir bağımsız olay dizisinin olasılığı, her olayın olasılıklarının ürününe eşittir.

Geçersiz olaylar

Eksik, deney sonucu aynı anda olamayan olaylardır. Bir dizi eksik olaylar eksiksiz bir olay grubu oluşturur.

Eksik olayların olasılıkları katlanır.

İttifaklar "ve" ya da "yerine," yerine "ve" "ve" yerine "ya da" yerine "ya da" yerine "ve" yerine neler yapılacağını açıklamak.

Konu bitti. Bu satırları okursanız, o zaman çok havalısınız.

Çünkü insanların sadece% 5'i kendi başlarına bir şey ustalaşabiliyorlar. Ve eğer sonuna kadar okursanız, bu% 5'e girdiniz!

Şimdi en önemli şey.

Bu konudaki teoriyi çözdünüz. Ve ben tekrar ediyorum, ... sadece süper! Akranların mutlak çoğunluğundan daha iyisin.

Sorun şu ki, bunun yeterli olmayabilir ...

Ne için?

Kullanımın başarılı geçmesi için, bütçe üzerindeki enstitüye kabul ve en önemlisi yaşam için.

Sana bir şey ikna etmeyeceğim, sadece bir şey söyleyeceğim ...

İyi bir eğitim alan insanlar, alamayanlardan çok daha fazlasını kazanırlar. Bunlar istatistiklerdir.

Ama bu ana şey değil.

Asıl şey, daha mutlu olmalarıdır (bu araştırmalar var). Belki de onların lehine daha fazla fırsat var ve hayat daha parlak olur? Bilmiyorum...

Ama kendimi düşünün ...

Sınavdaki diğerlerinden daha iyi olduğundan emin olmak ve nihayetinde olmak için neye ihtiyacınız var?

Bu konudaki görevleri çözerek bir elinizi doldurun.

Teoriyi sınavda sormayacaksın.

İhtiyacın olacak bir süre için görevleri çözün.

Ve eğer onları çözmediyseniz (çok!), Kesinlikle aptalca bir yanılıyordun ya da sadece zamanınız yok.

Sporda gibiydi - Kazanmak için birçok kez tekrarlamanız gerekir.

Bir koleksiyon ne istediğinizi bulun, Çözümlerle zorunlu, detaylı analiz Ve karar ver, karar ver!

Görevlerimizi (mutlaka değil) kullanabilirsiniz ve elbette, onları tavsiye ederiz.

Elini görevlerimizin yardımıyla doldurmak için, şimdi okuduğunuz Ders Kitabı YouCever için hayatı uzatmanıza yardımcı olmalısınız.

Nasıl? İki seçenek var:

1. Bu makaledeki tüm gizli görevlere açık erişim - 299 RUB.
2. Ders Kitabının 99 makalesindeki tüm Gizli Görevlere Açık Erişim - 499 RUB.

Evet, ders kitabımızda 99 makalemiz var ve tüm görevler için erişim ve tüm Gizli metinler hemen açılabilir.

Sitenin tüm varlığı için tüm gizli görevlere erişim sağlanır.

Sonuç olarak...

Görevlerimiz beğenmediyse, başkalarını bulurlar. Sadece teoriyi durdurmayın.

"Anlıyorum" ve "karar verebilirim" tamamen farklı becerilerdir. İkisine ihtiyacınız var.

Görevi bul ve karar ver!

Bölüm 1. Rastgele olaylar (50 saat)

Yarı zamanlı öğrenme öğrencileri için tematik disiplin planı

Eğitim öğrencileri için tematik disiplin planı

2.3. Yapısal ve mantıksal disiplin şeması

Matematik Bölüm 2. Olasılık teorisi ve matematiksel istatistik teorisinin unsurları

Bölüm 1 Rastgele Olaylar

Bölüm 3 Matematiksel istatistiklerin unsurları

Bölüm 2 Rastgele Değerler

2.5. Pratik blok

2.6. Balery Derecelendirme Sistemi

Disiplinin Bilgi Kaynakları

Bibliyografik Liste Ana:

3.2. "Matematik Bölüm 2'dir. Olasılık ve matematiksel istatistik unsurları teorisi "Giriş

Bölüm 1. Rastgele Olaylar

1.1. Rastgele bir olay kavramı

1.1.1. Set teorisinden bilgi

1.1.2. İlköğretim etkinlikleri alanı

1.1.3. Olayların sınıflandırılması

1.1.4. Olayların miktarı ve işi

1.2. Rastgele olayların olasılığı.

1.2.1. Göreceli olay sıklığı, olasılık teorisi aksiyomları. Klasik olasılık tanımı

1.2.2. Olasılıkın geometrik tanımı

Kombinatoryal analiz unsurları aracılığıyla bir olayın olasılığının hesaplanması

1.2.4. Olayların olasılığının özellikleri

1.2.5. Bağımsız olaylar

1.2.6. Cihazın sorunsuz çalıştırma olasılığının hesaplanması

Olayların olasılığını hesaplamak için formüller

1.3.1. Bağımsız Test Sırası (Bernoulli Şeması)

1.3.2. Bir olayın şartlı olasılık

1.3.4. Tam olasılık ve bayların formülü formülü

Bölüm 2. Rastgele Değişkenler

2.1. Rastgele değişkenlerin açıklaması

2.1.1. Belirleme ve rastgele değişken belirleme yöntemleri Olasılık teorisinin temel kavramlarından biri rastgele değişken kavramdır. Bazı rastgele değişken örneklerini göz önünde bulundurun:

Rastgele bir miktar ayarlamak için, dağıtım kanunu belirlemeniz gerekir. Rastgele değişkenler, Yunanca harflerle , ,  ve olası değerleri - endeksleri olan Latin harfleri, Yi, Zi.

2.1.2. Ayrık rastgele değişkenler

XI değerine yol açan tüm temel olayları içeren AI olaylarını göz önünde bulundurun:

PI, AI etkinliğinin olasılığını belirtir:

2.1.3. Sürekli rastgele değişkenler

2.1.4. Dağıtım fonksiyonu ve özellikleri

2.1.5. Olasılık dağılımının yoğunluğu ve özellikleri

2.2. Rastgele değişkenlerin sayısal özellikleri

2.2.1. Rastgele bir değişkenin matematiksel beklentisi

2.2.2. Rastgele değişkenin dağılması

2.2.3. Rastgele değişkenin normal dağılımı

2.2.4. Binom dağılımı

2.2.5. Poisson Dağılımı

BÖLÜM 3. Matematiksel istatistiklerin unsurları

3.1. Ana tanımlar

Çubuk grafiği

3.3. Dağıtım parametrelerinin nokta tahminleri

Temel konseptler

Matematiksel beklenti ve dağılımın nokta değerlendirmeleri

3.4. Aralık tahminleri

Aralık değerlendirme kavramı

Aralık Tahminlerinin İnşaatı

Temel İstatistiksel Dağılımlar

Normal dağılımın matematiksel beklentisinin aralık tahminleri

Normal dağılımın varyansının aralık değerlendirilmesi

Sonuç

Sözlük

4. Laboratuar çalışmaları için metodik talimatlar

Bibliyografik Liste

Laboratuar çalışması 1 Rastgele değişkenlerin açıklaması. Sayısal özellikler

Laboratuar çalışmalarını gerçekleştirme prosedürü

Laboratuar çalışması 2 Ana tanımlar. Örneklemenin sistematizasyonu. Boşluk dağıtım parametreleri. Aralık tahminleri.

Dağıtım şekli hakkında istatistiksel hipotez kavramı

Laboratuar çalışmalarını gerçekleştirme prosedürü

Hücre kodu değeri

5. Test için test iş görevini gerçekleştirmek için metodik talimatlar

Test çalışmasının performansı ve olasılıkları için metodikal kurallar

Rastgele değişkenler

Ortalama ikinci dereceden sapma

Matematiksel istatistiklerin unsurları

6. Disiplin Geliştirme Kontrol Ünitesi

Kurstaki sınav için sorular "Matematik Bölüm 2. Matematiksel istatistiklerin olasılık ve unsurları teorisi "

Tablo B'nin devamı

Tablo B'nin sonu

Düzgün dağıtılmış rastgele sayılar

İçerik

Bölüm 1. Rastgele Olaylar ............................................... ... onsekiz

Bölüm 2. Rastgele değişkenler .. .............................. ... .. 41

BÖLÜM 3. Matematiksel istatistiklerin unsurları ................ 64.

4. Laboratuarın uygulanması için metodik talimatlar

5. Kontrolün yürütülmesi için metodik talimatlar

1. Olayların olasılığını hesaplamak için formüller

1.3.1. Bağımsız Test Sırası (Bernoulli Şeması)

Bazı deneylerin aynı koşullarla tekrar tekrar gerçekleştirilebileceğini varsayalım. Bu deneyimin üretilmesine izin verin n. Bir kez, yani bir dizi gerçekleştirilir. n. Testler.

Tanım. Sıra n. denilen testler karşılıklı olarak bağımsız Bu testle ilgili herhangi bir olay varsa, diğer testlerle ilgili olaylara bağlı değildir.

Biraz olayı varsayalım A. olasılıkla oluşabilir p. Bir test sonucu olarak ya da olasılıkla olmaz s.= 1- p..

Tanım . Sıra n.aşağıdaki koşullar yapıldığında testler Bernoulli şeması oluşturur:

sıra n. Testler karşılıklı olarak bağımsızdır

2) bir olayın olasılığı A. Testten teste göre değişmez ve diğer testlerle sonuçlara bağlı değildir.

Etkinlik A. Testin "başarısını" diyorlar ve zıt olay "başarısızlık". Bir etkinlik düşünün

\u003d (B. n. Testler Rivne oluştu m. "Başarı").

Bu olayın olasılığını hesaplamak için Bernoulli Formülü geçerlidir

p.() =
, m. = 1, 2, …, n. , (1.6)

nerede - Kombinasyon sayısı n. Elementler m. :

=
=
.

Örnek 1.16. Küpler üç kez atıyor. Bulmak:

a) 6 puanın iki kez düşeceği olasılığı;

b) Sıra sayısının iki kereden fazla görünmeyeceği olasılığı.

Karar . "Başarı" testlerinin 6 puan görüntüsü ile yüzün küpüne düştüğü düşünülecektir.

a) toplam test sayısı - n.\u003d 3, "Başarı" sayısı - m. \u003d 2. "Başarı" olasılığı - p.=, Ve "başarısızlık" olasılığı - s.\u003d 1 - \u003d. Ardından, Bernoulli formülüne göre, altı puanın iki katı bir küpün üç kez dökümünün sonucunun düşeceğini, eşit olacaktır.

.

b) tarafından belirtir FAKAT 6 sayısının 6 sayısına sahip yüzün iki katından fazla görünmeyeceği gerçeğinde bulunur. Sonra etkinlik olarak temsil edilebilir Üç tutarsızlık toplamı Etkinlikler A \u003d.
,

nerede İÇİNDE 3 0 - İlgi çizgisi asla göründüğünde bir olay,

İÇİNDE 3 1 - Faiz yüzü bir kez göründüğünde olay,

İÇİNDE 3 2 - Faiz yüzünün iki kez göründüğünde olay.

Bernoulli Formülüne (1.6) göre buluruz

p.(FAKAT) \u003d P (
) = p.(
)=
+
+
=

=
.

1.3.2. Bir olayın şartlı olasılık

Koşullu olasılık, bir olayın diğerinin olasılığı üzerindeki etkisini yansıtmaktadır. Deneyin yapıldığı koşulları değiştirme de etkilenir

İlginç bir etkinliğin ortaya çıkma olasılığı.

Tanım. İzin vermek A. ve B. - Bazı olaylar ve olasılık p.(B.)> 0.

Şartlı olasılık Etkinlikler A. "olay" B. zaten"Bu olayların bir ürünü olasılığının, olasılıkların bulunması gereken olaydan daha erken olan bir olayın olasılığına ilişkin oranı olarak adlandırılır. Koşullu olasılık olarak belirtilir p.(A. B.). Sonra tanımı gereği

p. (A.  B.) =
. (1.7)

Örnek 1.17. İki küp kusuyor. İlköğretim olaylarının alanı, sipariş edilen sayı çiftlerinden oluşur.

(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)

(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)

(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)

(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6).

Örnek 1.16 Etkinliğin olduğu bulundu A. \u003d (ilk küp\u003e 4) ve olaydaki gözlük sayısı C. \u003d (Puan miktarı 8) bağımlıdır. İlişki arasında

.

Bu ilişki aşağıdaki gibi yorumlanabilir. İlk atmanın sonucunun, ilk küpte\u003e 4. nokta sayısının, ikinci küpün dökümünün, etkinliği oluşturan 12 çıkıştan birine yol açabileceğini varsayalım. A.:

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6) .

Aynı zamanda bir olay C. Sadece ikisi (5.3) (6.2) 'ya karşılık gelebilir. Bu durumda, bir olay olasılığı C. eşit olacak
. Böylece, bir olayın oluşumu hakkında bilgi A. bir etkinliğin olasılığını etkiledi C..

Olayların çalışması olasılığı

Çarpma teoremi

Olayların çalışması olasılığıA. 1 A. 2  A. n. Formül belirlendi

p.(A. 1 A. 2  A. n.) \u003d P.(A. 1) P.(A. 2  A. 1)) p.(A. n.  A. 1 A. 2  A. n- 1). (1.8)

İki etkinliğin çalışması için, bunu takip eder.

p.(Ab) \u003d P.(A. B) P.{B.) \u003d P.(B. A.) P.{A.). (1.9)

Örnek 1.18. 25 ürün grubunda 5 ürün arızalı. İki ürün art arda seçilir. Seçilen tüm ürünlerin kusurlu olduğu olasılığını belirleyin.

Karar. Olayları belirtir:

A. 1 \u003d (İlk ürün arızalı),

A. 2 \u003d (İkinci ürün arızalıdır),

A. 3 \u003d (Üçüncü ürün arızalı),

A. \u003d (Tüm ürünler arızalıdır).

Etkinlik FAKAT Üç etkinliğin bir eseri var A. = A. 1 A. 2 A. 3 .

Çarpma teoreminden (1.6) teslim almak

p.(A.) \u003d P ( A. 1 A. 2 A. 3 ) = p.(A. 1) p.(A. 2  A. 1))p.(A. 3  A. 1 A. 2).

Klasik olasılık tanımı bulmanızı sağlar p.(A. 1) Arızalı ürün sayısının toplam ürün sayısına oranıdır:

p.(A. 1)= ;

p.(A. 2) – bu birinin nöbetinden sonra kalan arızalı ürün sayısının, kalan ürünlerin toplam sayısına oranı:

p.(A. 2  A. 1))= ;

p.(A. 3) kalan ürünlerin toplam sayısına, iki arızasının nöbet geçirilmesinden sonra kalan kusurlu ürünlerin sayısının oranı:

p.(A. 3  A. 1 A. 2)=.

Sonra bir etkinliğin olasılığı A. eşit olacak

p.(A.) ==
.

Birçoğu, "olasılık teorisi" kavramı ile karşılaşılan, korkunç, bunun dayanılmaz bir şey olduğunu düşünüyorum, çok karmaşık. Ama her şey gerçekten çok trajik değil. Bugün, belirli örneklerle ilgili sorunları çözmek için temel öğrenme kavramını düşüneceğiz.

Bilim

"Olasılık Teorisi" gibi bir matematiğin böyle bir bölümünü çalıştırıyor? Desenler ve değerleri not eder. Bu soru ilk defa, bilim adamları kumar çalışıldığında on sekizinci yüzyıla ilgi duyuyorlardı. Olasılık teorisinin temel kavramının bir olaydır. Bu, deneyim veya gözlem ile belirtilen herhangi bir gerçektir. Ama deneyim nedir? Bir başka temel olasılık teorisi kavramı. Bu, bu koşulların bu bileşiminin tesadüfen yaratılmadığı anlamına gelir, ancak belirli bir hedefle. Gözlem gelince, burada araştırmacı kendisi deneyime katılmıyor, ancak sadece veri olaylarına tanıklık ediyor, ne olduğunu etkilemiyor.

Etkinlikler

Olasılık teorisinin temel kavramının bir olay olduğunu, ancak sınıflandırmayı düşünmemesini öğrendik. Hepsi aşağıdaki kategorilere ayrılmıştır:

• Dürüst.
• İmkansız.
• Rastgele.

Tecrübesi sırasında gözlenen veya yaratılan olaylardan bağımsız olarak, hepsi bu sınıflandırmaya tabidir. Ayrı olarak tanışmak için her tür tür türünü sunuyoruz.

Güvenilir etkinlik

Bu, gerekli olayların yapıldığı durumdur. Özü daha iyi dinlemek için, bazı örnekler getirmek daha iyidir. Fizik ve kimya ve ekonomi ve daha yüksek matematik bu kanuna tabidir. Olasılık teorisi, güvenilir bir olay olarak böyle önemli bir kavram içerir. Örnekler veriyoruz:

• Çalışıyoruz ve ücretler şeklinde bir ücret alıyoruz.
• Kuyu sınavları geçti, rekabet yapıldı, bunun için bir eğitim kurumuna kabul şeklinde bir ödül alıyoruz.
• Gerekirse bankaya para yatırdık, onları geri alırız.

Bu tür olaylar güvenilirdir. Tüm gerekli koşulları yerine getirirsek, beklenen sonucu kesinlikle alacağız.

İmkansız olaylar

Şimdi olasılık teorisinin unsurlarını düşünüyoruz. Bir sonraki olay türünün açıklamasına gitmeyi öneriyoruz, yani imkansız. Başlamak için, en önemli kuralları tartışacağız - imkansız olayın olasılığı sıfırdır.

Bu formülasyondan, problem çözerken geri çekilmesi imkansızdır. Açıklamak için, bu tür olaylara örnekler veriyoruz:

• Bir sıcaklık artı on (bu imkansız) bir sıcaklıkta donmuş su.
• Hiçbir elektrik üretimi etkilemez (önceki örnekte olduğu gibi de imkansızdır).

Yukarıda açıklanan yukarıda açıklanan bu kategorinin özünü yansıttığı için daha fazla örnek verilmemelidir. İmkansız olay hiçbir koşulda asla olmayacak.

Rastgele olaylar

Olasılık teorisinin unsurlarını incelemek, bu tür olaylara özel dikkat gösterilmelidir. Bu bilimsel çalışmalar budur. Tecrübenin bir sonucu olarak, bir şey olabilir veya olmayabilir. Ek olarak, test sınırsız sayıda sürede gerçekleştirilebilir. Parlak örnekler hizmet edebilir:

• Bir madeni paralar bir deneyimdir veya test, bir kartal düşme bir olaydır.
• Bir topu kör bir şekilde çekerek - bir test, kırmızı bir top yakaladı - bu bir olay vb.

Bu tür örnekler sınırsız bir miktar olabilir, ancak genel olarak özü açık olmalıdır. Olaylardaki bilgiyi özetlemek ve sistematikleştirmek için bir tablo verilir. Olasılık çalışmaları teorisi, yalnızca sunulanların son görüşünü çalıştırır.

isim vermek	tanım
Dürüst	Belirli koşullara uyurken% 100 garanti ile meydana gelen olaylar.	Giriş sınavının iyi bir şekilde teslim edilmesiyle bir eğitim kurumuna kabul edin.
İmkansız	Hiçbir koşulda asla olmayacak olaylar.	Hava sıcaklığında plus otuz derece santigrat kar yağışı var.
Rastgele	Deney / test sırasında oluşabilecek veya olmayacak bir olay.	Bir basketbol topu bir yüzüğe atarken zeka veya özlüyor.

Yasalar

Olasılık teorisi, herhangi bir olayı düşme yeteneğini inceleyen bir bilimdir. Diğerleri gibi, bazı kuralları var. Aşağıdaki olasılık teorisi kanunları mevcuttur:

• Rastgele değişkenlerin dizilerinin yakınsama.
• Büyük sayıların kanunu.

Kompleks olasılığını hesaplarken, sonucu daha kolay ve hızlı bir şekilde elde etmek için basit bir olay kompleksini kullanabilirsiniz. Olasılık teorisinin yasalarının bazı teoremler kullanılarak kolayca kanıtlandığını unutmayın. İlk yasa ile tanışmaya başlamaya başlıyoruz.

Rastgele değişkenlerin yakınsama

Yakınsama türlerinin biraz olduğunu unutmayın:

• Rastgele değişkenlerin dizisi olasılıkla istenmektedir.
• Neredeyse imkansız.
• R ortalama kare yakınsama.
• Dağıtım yakınsama.

Yani, yaz ile, özüne dalmak çok zor. Bu konuyu bulmanıza yardımcı olacak tanımları veriyoruz. İlk bakışta başlamak için. Dizinin denir sık sık olasılık gibiAşağıdaki durum gözleniyorsa: n Sonsuzluğa, sıranın çaba sarf edildiği sayı, daha sıfır ve yaklaşık birine yaklaşır.

Aşağıdaki forma git Neredeyse muhtemelen. Sıranın birleştiği söyleniyor neredeyse muhtemelen N için rasgele bir değişkene, sonsuzluk için çaba sarf etmek ve p, büyüklüğü yaklaşık birine dayanır.

Bir sonraki tür yakınsama rustik. SK-Cavergence kullanırken, vektör rastgele işlemlerin incelenmesi, koordinat rastgele süreçlerinin çalışmasına indirgenir.

Son tip kaldı, hadi kısaca anlayalım ve doğrudan görevleri çözmek için hareket ettirin. Dağılımın yakınsama başka bir adı var - "zayıf", sonra nedenini açıklar. Zayıf yakınsama - Bunlar, limit dağılım fonksiyonunun tüm konum noktalarında dağıtım fonksiyonlarının yakınsılmasıdır.

Sözü yerine getirdiğinizden emin olun: zayıf yakınsama, rastgele değerin olasılıksal alanda tanımlanmadığı tüm gerçeklerden farklıdır. Bu mümkündür, çünkü durum yalnızca dağıtım fonksiyonları kullanılarak oluşturulur.

Büyük sayıların yasası

Bu yasanın kanıtındaki mükemmel asistanlar, aşağıdaki gibi olasılık teorisinin teoremleri olacaktır.

• Chebyshev eşitsizliği.
• Chebyshev teoremi.
• Genelleştirilmiş Chebyshev teoremi.
• Markov teoremi.

Bütün bu teoremleri göz önünde bulundurursak, bu sorun birkaç on kadar çarşaf geciktirebilir. Ayrıca asıl görevimiz var - bu pratikte olasılık teorisinin kullanımıdır. Şu anda size sunuyoruz ve bunu yap. Ancak bundan önce, olasılık teorisinin aksiyomlarını göz önünde bulundurun, problem çözerken ana asistanlar olacaktır.

Aksiyomlar

İlk önce imkansız olay hakkında konuştuklarında tanıştık. Hatırlayalım: İmkansız olayın olasılığı sıfırdır. Örnek Çok parlak ve unutulmaz getirdik: kar, otuz derecenin hava sıcaklığına düştü.

İkinci sesler aşağıdaki gibidir: Birine eşit olasılıkla güvenilir bir olay meydana gelir. Şimdi matematiksel bir dilin yardımıyla nasıl yazacağını gösteriyoruz: p (c) \u003d 1.

Üçüncüsü: Rastgele olay meydana gelebilir, ancak her zaman sıfırdan birine kadar değişebilir. Değeri birine yaklaştırsa, şanslar daha fazladır; Değer sıfıra yaklaşırsa, olasılık çok küçüktür. Bunu matematiksel dilde yazıyoruz: 0<Р(С)<1.

Böyle görünen son, dördüncü aksiyomu göz önünde bulundurun: İki olayın toplamı olasılığı olasılıklarının toplamına eşittir. Matematiksel dilini yazıyoruz: P (A + C) \u003d P (a) + p (b).

Olasılık teorisinin atomları, hatırlanması zor olmayan en basit kurallardır. Zaten alınan bilgiye dayanarak bazı görevleri çözmeye çalışalım.

Piyango bileti

Başlamak için, en basit örneği göz önünde bulundurun - piyango. İyi şanslar için bir piyango bileti aldığınızı hayal edin. En az yirmi ruble kazanacağınız olasılığı nedir? Binlerce bilet, biri beş yüz ruble, on yüz ruble, elli yirmi ruble ve yüz beşte bir ödülü olan dolaşıma dahildir. Olasılık teorisindeki görevler, iyi şanslar fırsatını bulmaya dayanır. Şimdi birlikte, sunulan görevin üstündeki çözümü analiz edeceğiz.

Eğer mektup ise ve beş yüz ruble kazançlarını gösterirsek, düşme olasılığı 0,001'e eşit olacaktır. Nasıl aldık? Sadece numaralarını paylaşmak için "mutlu" bilet sayısını paylaşmanız gerekir (bu durumda: 1/1000).

B, yüz ruble kazancıdır, olasılık 0,01'e eşit olacaktır. Şimdi geçmiş eylemde olduğu gibi aynı prensibi kullandık (10/1000)

C - kazançlar yirmi ruble eşittir. Olasılık buluyoruz, 0.05'e eşittir.

Biletlerin geri kalanı bizimle ilgilenmiyor, çünkü ödül havuzu durumunda belirtilenden daha az. Dördüncü Axiom'u uygulayın: En az yirmi ruble kazanma olasılığı P (a) + p (c) + p (c). P harfi bu etkinliğin kökeni olasılığıyla gösterilir, onları daha önce önceki eylemlerde bulduk. Sadece gerekli verileri katlamak için kalır, cevabında 0.061 alıyoruz. Bu sayıdır ve görevin sorusuna bir cevap olacaktır.

Kağıt destesi

Olasılık teorisindeki görevler daha karmaşıktır, örneğin, aşağıdaki görevi alın. Otuz altı karttan bir güverteden önce. Göreviniz, bir yığını karıştırmadan bir üst üste iki haritayı çıkarmak, birinci ve ikinci kartlar ASES olmalı, takım elbisesi hiçbir şey yok.

Başlamak için, ilk kartın ACE olacağı olasılığını, otuz altı için bu dört bölünmesi için buluyoruz. Onu bir kenara erteledi. İkinci kartı verin, üç otuz beşte olasılıkla ACE olacaktır. İkinci etkinliğin olasılığı, ilk önce hangi haritayı çektiğimizi, merak ediyor, ACE ya da değil. Etkinliğin A etkinliğine bağlı olduğu bundan sonra takip eder.

Bir sonraki eylem, eşzamanlı bir uygulama olasılığını buluruz, yani, bir A ve B'nin katlanması ile. Yani, ilk önce ACE'ye çektik.

Her şey açıklığa kavuşmak için, kişiyi bu tür bir öğeye olay olarak veriyoruz. Olayın olan şey olduğunu varsayarak hesaplanır. Aşağıdaki gibi hesaplanır: P (V / A).

Sorunumuzun çözümüne devam edelim: P (a * c) \u003d P (a) * p (in / a) veya p (a * c) \u003d p (c) * p (a / c). Olasılık eşittir (4/36) * (((3/35) / (4/36). Hesaplayın, yüzlerce kadar yuvarlanır. Biz var: 0.11 * (0.09 / 0.11) \u003d 0.11 * 0, 82 \u003d 0.09. Olasılık Bir arka arkaya iki ası uzattığımız dokuz yüzlerce. Değer çok küçük, bu, olayın olasılığının son derece küçük olduğu için izler.

Unutulmuş numara

Olasılık teorisini inceleyen görevler için birkaç seçenek daha ayırmayı öneriyoruz. Bu makalede zaten gördüğünüz bazılarını çözme örnekleri, aşağıdaki görevi çözmeye çalışın: Çocuk, arkadaşının telefon numarasının son rakamını unuttu, ancak arama çok önemliydi, sonra her şeyi sırayla işe almaya başladı. . Üç kereden fazla arama yapmayacak olasılığını hesaplamamız gerekiyor. Sorun sorunu, olasılık teorisinin kuralları, yasaları ve aksiyomları biliniyorsa, en basittir.

Bir çözüm izlemeden önce, kendinizi çözmeye çalışın. Son rakamın sıfırdan dokuza kadar olabileceğini biliyoruz, yani sadece on değer var. İstenen yazma olasılığı 1/10.

Daha sonra, olayın kökeni için seçenekleri göz önünde bulundurmamız gerekiyor, çocuğun tahmin ettiğini ve derhal gerekli olduğunu varsayalım, böyle bir olayın olasılığı 1/10. İkinci seçenek: fişin ilk zili ve ikinci hedefe. Böyle bir olayın olasılığını hesaplayın: 9/10 1/9 ile çarpın, sonuç olarak 1/10 alıyoruz. Üçüncü seçenek: Birinci ve ikinci arama adreste değildi, sadece üçüncü çocuktan oraya istediğin yer var. Böyle bir olayın olasılığını hesaplayın: 9/10 8/9 ve 1 / 8'de çarpın, sonuç olarak 1/10 alıyoruz. Görevin durumu altındaki diğer seçenekler bizimle ilgilenmiyor, sonuçlar tarafından katlanmış kaldık, sonuç olarak 3/10 var. Cevap: Çocuğun üç kattan fazla olmadığını arayacak olasılığı 0,3'e eşittir.

Sayıları olan kartlar

Sizden önce dokuz kart vardır, her biri bir ila dokuzdan numara yazılan sayılar tekrarlanmaz. Kutuya koyuldu ve iyice karıştırıldı. Bunun olasılığını hesaplamanız gerekir.

• çift \u200b\u200bnumarası düşecek;
• iki basamaklı.

Solüsyona geçmeden önce, m'nin başarılı olguların sayısı olduğunu tartışacağız ve N toplam seçenek sayısıdır. Sayı bile olabileceği olasılığını buluyoruz. Dört sayının bile olduğunu hesaplamak zor değil, bizim m olacak, her şey mümkün olan dokuz seçenek, yani, m \u003d 9. Sonra olasılık 0,44 veya 4/9'dur.

İkinci vakayı düşünüyoruz: Dokuz için seçeneklerin sayısı ve hiç başarılı bir sonuç olamaz, yani M sıfır. Uzun kartın iki basamaklı bir sayı içermesi olasılığı, aynı sıfıra eşittir.