Skarové vektory

Pokračujeme v riešení vektorov. V prvej lekcii Vektory pre žnávky Pozreli sme sa na koncepciu vektora, akcií s vektormi, vektorové súradnice a najjednoduchšie úlohy s vektormi. Ak ste túto stránku prvýkrát zadali prvýkrát z vyhľadávacieho nástroja, odporúčam, aby som čítal vyššie uvedený úvodný článok, pretože je potrebné navigovať pojmy používané podľa mňa, notácia pre mňa, mať základné vedomosti o vektoroch a byť schopný Riešiť základné úlohy. Táto lekcia je logickým pokračovaním témy a na to budem definovať typické úlohy, v ktorých sa používa skalárny produkt vektorov. Toto je veľmi dôležité povolanie.. Snažte sa nechať ujsť príklady, užitočný bonus je pripojený k nim - prax vám pomôže opraviť prešiel materiál a "vyplniť ruku" o riešení spoločných úloh analytickej geometrie.

Pridanie vektorov, Vector Multiplication podľa čísla .... Bolo by naivné myslieť si, že matematika neprišla s ničím iným. Okrem už preskúmaných akcií existuje niekoľko ďalších operácií s vektormi, a to: skarové vektory, vektorové umelecké diela vektorov a zmiešané vektory. Skarový produkt vektorov nás zoznámi zo školy, dve ďalšie diela tradične odkazujú na priebeh vyššej matematiky. Témy sú jednoduché, algoritmus na riešenie mnohých úloh stena a je pochopiteľné. Jediná vec. Informácie sú slušné, takže je nežiaduce sa pokúsiť zvládnuť všetko a okamžite. To platí najmä pre žnávky, verte mi, autor nechce cítiť Chikatilo z matematiky. No, nie z matematiky, samozrejme, príliš \u003d) viac pripravení študenti môžu použiť materiály selektívne, v určitom zmysle, "dostať" chýbajúce znalosti, pre vás budem neškodný graf Dracula \u003d)

Otvoríme sa, konečne, dvere a vášnivo vidíme, čo sa stane, keď sa stretnú dve verzie ....

Definícia skalárneho produktu vektorov.
Vlastnosti skalárneho produktu. Typické úlohy

Koncepcia skalárnej práce

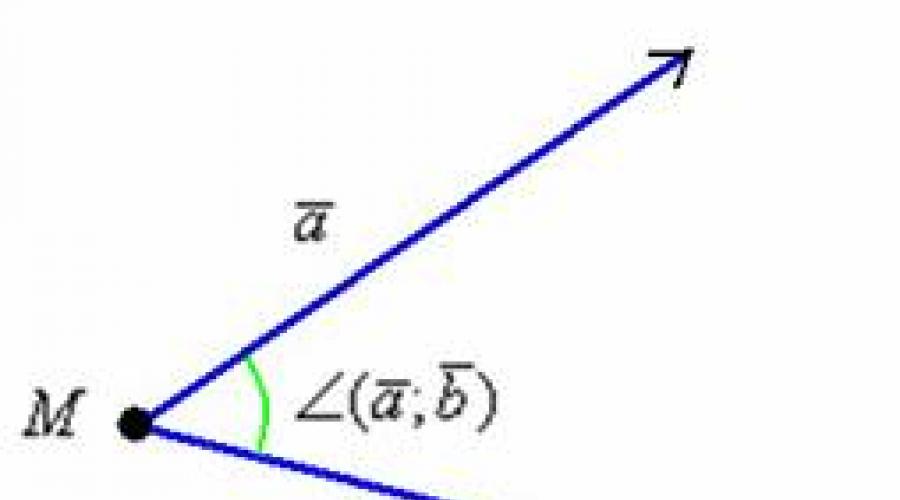
Prvý pro Uhol medzi vektormi. Myslím, že každý je intuitívny, že taký uhol medzi vektormi, ale len v prípade trochu viac. Zvážte voľné nenulové vektory a. Ak tieto vektory odložíte z ľubovoľného bodu, potom sa zobrazí obraz, ktorý mnohí už prezentovali mentálne:

Priznávam, tu som obnovená situácia len na úrovni porozumenia. Ak potrebujete prísnu definíciu uhla medzi vektormi, obráťte sa na učebnicu, pre praktické úlohy, je v zásade za nič. Ďalej budem na miestach, aby som ignoroval nulové vektory v dôsledku ich malého praktického významu. Rezervácia konkrétne pre pokročilých návštevníkov stránok, ktorí ma môžu potupovať v teoretickej neúplnosť niektorých nasledujúcich vyhlásení.

To môže mať hodnoty od 0 do 180 stupňov (od 0 do Radiáni) vrátane. Analyticky sa táto skutočnosť zaznamenáva vo forme dvojitých nerovností: alebo (v radiánoch).

V literatúre sa ikona uhla často preskočí a písať jednoducho.

Definícia: Skalový produkt dvoch vektorov sa nazýva číslo rovnajúce sa produktu týchto vektorov na kosíne rohu medzi nimi:

Toto je teraz dosť prísna definícia.

Zameriavame sa na základné informácie:

Označenie: Skarový výrobok je označený alebo jednoducho.

Výsledkom operácie je číslo: Vektor sa vynásobí vektorom a číslo sa získa. V skutočnosti, ak dĺžky vektorov sú čísla, kosínus uhla - číslo, potom ich práca Tam bude tiež číslo.

Ihneď niekoľko príkladov Warm-up:

Príklad 1.

Rozhodnutie: Používame vzorec . V tomto prípade:

Odpoveď:

Cosine Hodnoty nájdete v trigonometrický stôl. Odporúčam ho vytlačiť - bude potrebné v takmer všetkých častiach veže a bude potrebovať mnohokrát.

Čisto z matematického hľadiska je skalárny produkt bezrozmerne, to znamená, že výsledok je v tomto prípade jednoducho číslo a to je všetko. Z hľadiska úloh fyziky má skarný produkt vždy určitý fyzický význam, to znamená, že je potrebné zadať konkrétnu fyzickú jednotku. Kanonický príklad výpočtu práce sily možno nájsť v akomkoľvek učebni (vzorca presne je skalárnym produktom). Práca sily sa meria v joules, preto bude odpoveď zaznamenaná celkom konkrétne ,.

Príklad 2.

Nájsť, či A uhol medzi vektormi je rovnaký.

Toto je príklad pre nezávislé rozhodnutie, odpoveď na konci hodiny.

Uhol medzi vektormi a hodnotu skalárneho produktu

V príklade 1 bol skalárny produkt pozitívny a v príklade 2 - negatívny. Zistite, čo závisí znak skalárneho produktu. Pozeráme sa na náš vzorec: . Dĺžky nenulových vektorov sú vždy pozitívne: Preto môže znak závisieť len od kosínutej hodnoty.

Poznámka: Pre lepšie pochopenie nižšie uvedených informácií je lepšie preskúmať Cosine harmonogram v metódach Grafov a vlastností funkcie. Pozrite sa, ako sa Cosine na segmente správa.

Ako už bolo uvedené, uhol medzi vektormi sa môže líšiť v rámci A tieto prípady sú možné:

1) ak uhol medzi vektormi akútny: (od 0 do 90 stupňov), potom , I. skarný produkt bude pozitívny zasiahnutýRohom medzi nimi je považovaný za nulu a skalárny produkt bude tiež pozitívny. Vzhľadom k tomu, vzorec je zjednodušený :.

2) ak uhol medzi vektormi hlúpy: (od 90 do 180 stupňov) a zodpovedajúcim spôsobom, skarový produkt Negatívny:. Osobitný prípad: Ak vektory naprPotom sa zvažuje roh medzi nimi odchod: (180 stupňov). Skarový produkt je tiež negatívny, pretože

Spravodlivé a vrátené vyhlásenia:

1) Ak je uhol medzi údajmi vektorov ostrý. Alternatívne sú vektory potiahnuté.

2) Ak je uhol medzi dátovými vektormi hlúpy. Alternatívne sú vektory nasmerované naproti.

Tretí prípad je však osobitný záujem:

3) ak uhol medzi vektormi priamy: (90 stupňov), potom skarový produkt je nula:. Opak je tiež pravda: ak potom. Kompaktné vyhlásenie je formulované takto: Skalový produkt dvoch vektorov je nula, ak a len ak sú tieto vektory ortogonálne. Krátka matematická záznam:

! Poznámka : Opakovanie základy matematickej logikyObojsmerný logický dôsledok ikony je zvyčajne čítať "ak a len potom", "v tom a len v prípade." Ako vidíte, šípky sú zamerané na oboch stranách - "to z toho vyplýva, a späť - z toho vyplýva." Čo, mimochodom, rozdiel od jednostrannej ikony? Ikona schvaľuje len to, žeže "to vyplýva z toho", a nie skutočnosť, že opak má pravdu. Napríklad: Ale nie každá šelma je panther, takže v tomto prípade nie je možné použiť ikonu. Zároveň namiesto ikony môcť Použite jednosmernú ikonu. Napríklad riešenie úlohy sme zistili, že sme dospeli k záveru, že vektory sú ortogonálne: - Takýto záznam bude správny, a ešte relevantnejší ako .

Tretí prípad má veľký praktický význam.pretože vám umožní kontrolovať ortogonálne vektory alebo nie. Túto úlohu vyriešime v druhej časti hodiny.

Vlastnosti skalárneho kusu

Poďme sa vrátiť k situácii, keď dve verzie zasiahnutý. V tomto prípade je uhol medzi nimi nula a vzorec skarného produktu má formulár :. \\ T

A čo sa stane, ak sa vektor vynásobí sami? Je zrejmé, že vektor je potiahnutý sám, takže používame vyššie uvedený zjednodušený vzorec:

Číslo sa volá skalárny námestie A označované ako.

Touto cestou, Vektorové skalárne námestie sa rovná námesti dĺžky tohto vektora:

Z tejto rovnosti môžete získať vzorec pre výpočet dĺžky vektora:

Aj keď sa zdá nepretržité, ale úlohy hodiny budú všetky zmizne. Ak chcete vyriešiť problémy, budeme tiež potrebovať vlastnosti skalárneho kusu.

Pre ľubovoľné vektory a ľubovoľné číslo sú tieto vlastnosti platné:

1) - pohyb alebo komutatívny Zákon skalárnej práce.

2) - distribúcia alebo distribučný Zákon skalárnej práce. Jednoducho, môžete odhaliť konzoly.

3) - priedušné alebo pridružený Zákon skalárnej práce. Konštanta môže byť vyňatá zo skalárneho produktu.

Často, všetky druhy nehnuteľností (ktoré sú stále potrebné!) Vnímané študentmi ako zbytočné odpadky, ktoré je potrebné poslať a hneď po skúške bezpečne zabudnuté. Zdá sa, že tu je dôležité, všetko a tak z prvej triedy vedia, že práca sa nemení z permutácie multiplikátorov :. Musí varovať, vo vyššej matematike s podobným prístupom, je ľahko blokovať palivové drevo. Napríklad, prechodový majetok nie je spravodlivý algebraické matrice. Je to nesprávne vektorové umelecké vektory. Preto v akýchkoľvek vlastnostiach, ktoré sa stretnete v priebehu vyššej matematiky, prinajmenšom je lepšie ponoriť sa pochopiť, čo môžete urobiť, ale prečo je to nemožné.

Príklad 3.

.

Rozhodnutie:Po prvé, objasnenie situácie s vektorom. Čo je to vôbec? Súčet vektorov je úplne definovaný vektor, ktorý je indikovaný. Geometrický výklad činností s vektormi možno nájsť v článku Vektory pre žnávky. Rovnaká petržlen s vektorom je súčet vektorov a.

Takže podľa stavu je potrebné nájsť skalárny produkt. Teoreticky musíte použiť pracovný vzorec Ale problém je, že sme neznáme dĺžkou vektorov a uhlom medzi nimi. Ale v stave vzhľadom na podobné parametre pre vektory, takže pôjdeme rôzne spôsoby:

(1) nahrádzame vyjadrenie vektorov.

(2) Odhaliť konzoly podľa pravidla množenia polynómov, môžete nájsť kúzlo v článku. Komplexné čísla alebo Integráciu frakčnej racionálnej funkcie. Mimochodom sa neopakujem \u003d), aby som na nás odhalil všetky distribučné vlastnosti skalárneho produktu. Máme pravdu.

(3) V prvom a poslednom období sú skalárne štvorce vektorov kompaktné: . V druhom používame preusporiadanie skalárneho produktu :.

(4) Podobné podmienky dávame :.

(5) V prvom termíne používame vzorec skalárneho námestia, ktorý bol spomenutý, nie tak dávno. V poslednom období, teda to isté funguje :. \\ T Druhý termín sa rozširuje podľa štandardného vzorca .

(6) Tieto podmienky nahrádzame a starostlivo vykonávať konečné výpočty.

Odpoveď:

Záporná hodnota skalárneho produktu uvádza, že uhol medzi vektormi je tupý.

Typická úloha je tu príkladom nezávislého riešenia:

Príklad 4.

Nájdite skalárny produkt vektorov a, ak to viete .

Teraz je ďalšia spoločná úloha len novým vektorovým vzorcom. Označenia tu budú trochu zhodné, takže pre jasnosť ho prepisujem iným listom:

Príklad 5.

Nájdite dĺžku vektora, ak .

Rozhodnutie Bude to nasledovné:

(1) Dodávame vyjadrenie vektora.

(2) Použitie dĺžky vzorca:, zatiaľ čo ako vektor "VE", máme celočíselnú výraz.

(3) Používame súhrnný vzorec letného súhrnu. Upozorňujeme, ako to funguje zvedavé tu: "V skutočnosti je to štvorec rozdielu, a v skutočnosti to je." Tí, ktorí si želajú, môžu usporiadať vektory na miestach: - Ukázalo sa, že to isté s presnosťou alkálie.

(4) Ďalej je známe z dvoch predchádzajúcich úloh.

Odpoveď:

Ak hovoríte o dĺžke, nezabudnite zadať rozmer - "jednotky".

Príklad 6.

Nájdite dĺžku vektora, ak .

Toto je príklad pre nezávislé riešenie. Kompletné riešenie a odpoveď na konci hodiny.

Pokračujeme v stlačení užitočných vecí zo skalárneho produktu. Opäť sa pozrieme na náš vzorec . Podľa pravidla pomoci na resetovanie dĺžky vektorov v denominátore ľavej strany:

A časti sa menia miesta:

Aký je význam tohto vzorca? Ak sú známe dĺžky dvoch vektorov a ich skalárneho produktu, potom sa môže vypočítať kosínus uhol medzi dátovými vektormi a následne samotný uhol.

Skarový produkt je číslo? Číslo. Vektor Dĺžka - Čísla? Čísla. Takže frakcia je tiež niektoré číslo. A ak je poznácia kosínus rohu: , Je ľahké nájsť sa sám s použitím reverznej funkcie: .

Príklad 7.

Nájdite uhol medzi vektormi a ak je známe, že.

Rozhodnutie: Používame vzorec:

V konečnej fáze výpočtov sa použil technický príjem - eliminácia iracionality v denominátori. Aby som eliminoval iracionalitu, som damninoval Nizer a menovateľa.

Takže, ak , potom:

Hodnoty inverzných trigonometrických funkcií nájdete trigonometrický stôl. Hoci to sa deje zriedka. V úlohách analytickej geometrie sa zdá, že nejaký nejaký nejaký nejasný medveď sa zdá byť oveľa častejšie a hodnota uhla musí nájsť približne pomocou kalkulačky. V skutočnosti to budeme opakovať takýto obrázok.

Odpoveď:

Nezabudnite uviesť dimenziu - Radiáni a stupne. Osobne sa uistil, že "odstrániť všetky otázky", radšej indikuje, že (ak by podľa podmienok, samozrejme, nie je potrebné prezentovať odpoveď len v radiánoch alebo len v stupňoch).

Teraz sa môžete vyrovnať s komplexnejšou úlohou:

Príklad 7 *

Daniety - dĺžky vektorov a uhol medzi nimi. Nájdite uhol medzi vektormi ,.

Úloha nie je ani tak zložitá ako viacnásobná.
Analyzujeme algoritmus riešenia:

1) Pod podmienkou je potrebné nájsť uhol medzi vektormi, a preto potrebujete použiť vzorec .

2) Nájdite skalárny produkt (pozri príklady číslo 3, 4).

3) Dĺžka vektora a dĺžku vektora nájdeme (pozri príklady číslo 5, 6).

4) Ukončenie rozhodnutia sa zhoduje s príkladom 7 - poznáme číslo, a preto je ľahké nájsť sama o sebe:

Stručné riešenie a odpoveď na konci hodiny.

Druhá časť lekcie je venovaná rovnakému skalárnemu produktu. Súradnice. Bude to ešte jednoduchšie ako v prvej časti.

Skalárny produkt vektorov,
Spýtali sa koordinácie v ortonáli

Odpoveď:

Čo povedať, na riešenie súradníc je oveľa príjemnejší.

Príklad 14.

Nájdite si skalárny produkt vektorov a ak

Toto je príklad pre nezávislé riešenie. Tu môžete použiť asociálnosť operácie, to znamená, že sa nepočítajú, ale okamžite prinášajte tri tri mimo skalárneho produktu a upgrade na to naposledy. Riešenie a odpoveď na konci hodiny.

V závere odseku provokatívny príklad na výpočet dĺžky vektora: \\ t

Príklad 15.

Nájdite vektory dĺžky , Ak

Rozhodnutie:znova sa objavuje metóda predchádzajúcej časti: ale existuje ďalšia cesta:

Nájdite vektor:

A jeho dĺžka v triviálnom vzore :

Skarový produkt tu nie je vôbec.

Nie, ako to nie je pri výpočte dĺžky vektora:
Zastaviť. Neužívajte zrejmý majetok dĺžky vektora? Čo možno povedať o dĺžke vektora? Tento vektor je dlhší vektor 5-krát. Smer je opak, ale nehrajú úlohu, pretože hovoriť o dĺžke. Je zrejmé, že dĺžka vektora sa rovná práci modul Čísla pre dĺžku vektora:
- Znamenie modulu "jesť" možné mínusové číslo.

Touto cestou:

Odpoveď:

Cosine vzorec uhla medzi vektormi, ktoré sú nastavené podľa súradníc

Teraz máme úplné informácie, ktoré majú byť predtým odvodené z Cosine Cosine Formula medzi vektormi prostredníctvom súradníc vektorov:

Cosine Uhol medzi rovinami vektormi a špecifikované v ortonorálnom základe, vyjadruje sa vzorec:
.

Cosine Uhol medzi vesmírnymi vektormi definované v ortonorálnom základe vyjadruje sa vzorec:

Príklad 16.

Uvádzajú sa tri vrcholy trojuholníka. Nájsť (uhol na vrchole).

Rozhodnutie:Podmienkou sa výkres nevyžaduje, ale stále:

Požadovaný uhol je označený zeleným oblúkom. Okamžite zapamätajte si školské označenie rohu: - osobitná pozornosť stredný List je horná časť rohu, ktorý potrebujete. Pre stručnosť bola tiež možné nahrávať jednoducho.

Z výkresu je zrejmé, že uhol trojuholník sa zhoduje s uhlom medzi vektormi a inými slovami: .

Analýza sa výhodne učí vykonávať psychicky.

Nájsť vektorov:

Vypočítame skalárny produkt:

A dĺžka vektorov:

Cosine Corner:

Je to tento postup na vykonanie úlohy, ktorá odporúča žnávky. Pripravenejšie čitatelia môžu zaznamenať výpočty "jedného riadku":

Tu je príklad "zlej" cosine. Získaná hodnota nie je konečná, takže nie je žiadny zvláštny zmysel zbaviť sa iracionátora v denominátoráte.

Nájdite samotný uhol:

Ak sa pozriete na kresbu, výsledok je celkom uvejejúci. Na kontrolu uhla môže byť tiež meraný a transportér. Nepoškodzujte náteru monitora \u003d)

Odpoveď:

V reakcii na to nezabudnite spýtali sa na roh trojuholníka (A nie o uhle medzi vektormi), nezabudnite zadať presnú odpoveď: a približnú hodnotu uhla: nájdené pomocou kalkulačky.

Tí, ktorí si tento proces užili, môžu vypočítať uhly a uistiť sa, že spravodlivosť kanonickej rovnosti

Príklad 17.

Priestor je daný trojuholníkovými súradnicami ich vrcholov. Nájdite uhol medzi stranami a

Toto je príklad pre nezávislé riešenie. Kompletné riešenie a odpoveď na konci hodiny

Malá posledná časť bude venovaná prognózam, v ktorých je skalárny produkt tiež "zapojený":

Vektorová projekcia na vektorov. Projekcia vektora na súradnicové osi.
Cosine Guides Vector

Zvážte vektory a:

Sprogit vektor na vektor, pre to, z začiatku a konca vektora vynechať protpendiculary na vektore (zelené prerušované čiary). Predstavte si, že lúče svetla kolmo spadajú do vektora. Potom bude segment (červená čiara) "tieň" vektora. V tomto prípade je vektorová projekcia na vektore dĺžka segmentu. To znamená, že projekcia je číslo.

Toto číslo je označené nasledovne :, "veľký vektor" označte vektor Ktoré projekcia, "malý vektor substrátu" označte vektor Na ktoré sa predpokladá.

Samotný záznam sa číta takto: "Projekcia vektora" A "na vektore."

Čo sa stane, ak je vektor je "príliš krátky"? Vykonávame priamku obsahujúcu vektor. A vektor "A" sa predpokladá o smere vektora "byť"Jednoducho - na priamke obsahujúcej vektor. To isté sa deje, ak je vektor "A" odložený v tridsiatych kráľovstve - to je stále ľahko znečistené na priamku obsahujúcu by byť vektor.

Ak je roh medzi vektormi akútny (ako na obrázku), potom

Ak vektory ortogonálne, Potom (projekcia je bod, ktorých rozmery sú považované za nulu).

Ak je roh medzi vektormi hlúpy(Na obrázku, mentálne usporiadajte šípku vektora), potom (rovnaká dĺžka, ale zhotovená s mínusovým znakom).

Tieto vektory odložím z jedného bodu:

Je zrejmé, že pri pohybe vektora sa jeho projekcia nezmení

Tam budú úlohy pre nezávislé riešenie, ku ktorému môžete vidieť odpovede.

Ak je v úlohe a dĺžke vektorov, a uhol medzi nimi je prezentovaný "na tanierike s modrou jednotkou", potom stav problému a jeho riešenie vyzerá takto:

Príklad 1.Rozsiahle vektory. Nájdite skalárny produkt vektorov, ak sú ich dĺžky a uhol medzi nimi prezentovaný v nasledujúcom význame:

Iná definícia je tiež definovaná, plne ekvivalentná definícii 1.

Definícia 2.. Skalový produkt vektorov sa nazýva číslo (skalárne), ktoré sa rovná dĺžke dĺžky týchto týchto vektorov na projekcii iného vektora na osi určenom prvým špecifikovaným vektorom. Vzorec podľa definície 2:

Úloha s použitím tohto vzorca sa rieši po ďalšom dôležitom teoretickom bode.

Stanovenie skalárneho produktu vektorov prostredníctvom súradníc

Rovnaké číslo možno získať, ak sú variabilné vektory nastavené ich súradnicami.

Definícia 3. Skarový produkt vektorov je číslo rovnajúce sa súčtu párových diel ich príslušných súradníc.

Na povrchu

Ak sú dva verzie a rovina definované ich dvoma kartéziká obdĺžnikové súradnice

skalový produkt týchto vektorov sa rovná súčtu párových diel ich príslušných súradníc:

.

Príklad 2.Nájdite numerickú veľkosť vektorovej projekcie na osi rovnobežne s vektorom.

Rozhodnutie. Nájdeme skalárny produkt vektorov, skladaním párových diel ich súradníc:

Teraz musíme zodpovedať výslednému skalárnemu produktu vektora dĺžky vektora na vektorovej premietacej osi rovnobežnej s vektorom (podľa vzorca).

Nájdeme dĺžku vektora ako odmocnina od sumy štvorcov svojej súradnice:

.

Zostavujeme rovnicu a vyriešime ho:

Odpoveď. Požadovaná numerická hodnota je mínus 8.

Vo vesmíre

Ak sú dve verzie a priestor definovaný ich troma karteziánmi obdĺžnikových súradníc

,

skarárny produkt týchto vektorov je tiež rovný súčtu párových diel ich príslušných súradníc, iba súradnice sú už tri: \\ t

.

Úlohou nájdenia skalárneho produktu s považovanou metódou - po analýze vlastností skalárneho produktu. Pretože úloha bude musieť určiť, ktorý uhol formulár variabilných vektorov.

Vlastnosti skalárneho produktu vektorov

Algebraické vlastnosti

1. (presunúť majetokZ zmeny miesta variabilných vektorov sa veľkosť ich skalárneho produktu nezmení).

2. (combulator Telefónne číslo Proporte: Skalový produkt vektora vynásobeného niektorými multiplikátormi a ďalší vektor, ktorý sa rovná skalárnemu produktu týchto vektorov, vynásobených rovnakým faktorom).

3. (distribúcia vzhľadom na súčet majetku vektorov: Skalový produkt súčtu dvoch vektorov na treťom vektore sa rovná súčtu skalárnych diel prvého vektora na treťom vektore a druhý vektor na treťom vektore).

4. (skalárna štvorcová vektor viac nula) Ak ide o nonzero vektor, a ak - nulový vektor.

Geometrické vlastnosti

V definíciách záručnej operácie sme sa zaoberali koncepciou uhla medzi dvoma vektormi. Je čas objasniť tento koncept.

Vyššie uvedené číslo zobrazuje dva vektor, ktoré sú uvedené všeobecnému začiatku. A prvá vec, ktorá by venovala pozornosť: existuje dva uhol medzi týmito vektormi - φ 1 a φ 2 . Ktorý z týchto uhlov sa objavuje v definíciách a vlastnostiach skalárneho produktu vektorov? Množstvo uholných uhlov sa rovná 2 π A preto sú kosíny týchto uhlov rovnaké. Definícia skalárneho výrobku obsahuje len kosínus uhol, a nie význam jeho expresie. Ale v nehnuteľnostiach sa uvažuje len jeden uhol. A toto je jeden z dvoch uhlov, ktoré nepresahujú π , to znamená 180 stupňov. Na obrázku je tento uhol indikovaný ako φ 1 .

1. Dvaja volania vektorov ortogonálne a uhol medzi týmito vektormi - priamy (90 stupňov alebo π / 2) ak skarný produkt týchto vektorov je nula :

.

Pravodalizmus vo vektorovej algebre je kolmálnosť dvoch vektorov.

2. Dva no nulové vektor predstavuje ostrý roh (od 0 do 90 stupňov, alebo ktoré je rovnaké - menej π skarný produkt pozitívne .

3. Dva no nulové vektory predstavujú tupý uhol (od 90 do 180 stupňov, alebo že to isté je viac π / 2) Ak a len vtedy, keď skarový produkt Negatívny .

Príklad 3. Vektory sú uvedené v súradniciach:

.

Vypočítajte skalárne diela všetkých párov týchto vektorov. Aký uhol (ostrý, rovný, hlúpy) tvoria tieto páry vektorov?

Rozhodnutie. Výpočet bude pridaním diel príslušných súradníc.

Dostal záporné číslo, takže vektory tvoria hlúpy uhol.

Dostal kladné číslo, takže vektory tvoria ostrý uhol.

Prijaté nula, takže vektory tvoria priamy roh.

Dostal kladné číslo, takže vektory tvoria ostrý uhol.

.

Dostal kladné číslo, takže vektory tvoria ostrý uhol.

Pre seba-test môžete použiť online kalkulačka skalárneho produktu vektorov a kosínom rohov medzi nimi .

Príklad 4. Dĺžky dvoch vektorov a uhol medzi nimi sú uvedené:

.

Určite, s akou hodnotu počtu vektorov a ortogonálnych (kolmých).

Rozhodnutie. Presuňte vektory podľa pravidla množenia polynómov:

Teraz vypočítame každý termín:

.

Urobte rovnicu (rovnosť práce nulovej), predstavujeme podobných členov a riešenie rovnice:

Odpoveď: Máme hodnotu λ \u003d 1,8, v ktorom sú vektory ortogonálne.

Príklad 5.Dokázať, že vektor ortogonálny (kolmý) vektor

Rozhodnutie. Skontrolovať ortogonality, variabilné vektory a ako polynómy, namiesto jeho expresie uvedeného v stave TERK:

.

Na tento účel každý člen (termín) prvých polynómov sa množia každému členovi druhého a získané práce sú zložené:

.

V výsledku výsledok sa frakcia zníži na náklady. Získa sa nasledujúci výsledok:

ZÁVER: V dôsledku násobenia sa ukáže nula, preto ortogonalita (kolmá časť) vektorov.

Vyriešiť úlohu sami, a potom vidieť rozhodnutie

Príklad 6. Dĺžky vektorov sú uvedené a a uhol medzi týmito vektormi je rovnaký π / štyri. Určiť, akú hodnotu μ Vektory a vzájomne kolmé.

Pre seba-test môžete použiť online kalkulačka skalárneho produktu vektorov a kosínom rohov medzi nimi .

Matrix znázornenie skalárneho produktu vektorov a produktu N-dimenzionálnych vektorov

Niekedy je výhra z jasnosti znázornenie dvoch variabilných vektorov vo forme matice. Potom je prvý vektor reprezentovaný ako matricový reťazec a druhá - vo forme matrice stĺpca:

Potom bude skalárny produkt vektorov produkt týchto matríc :

Výsledok je rovnaký ako získaný spôsob, o ktorom sme už uvažovali. Dostali sme jedno jednotné číslo a produkt matrix reťazec na stĺpovej matrici je tiež jedno číslo.

V matici forme je vhodné reprezentovať produkt abstraktných N-dimenzionálnych vektorov. Produktom dvoch štvorrozmerných vektorov bude teda produktom matricového reťazca so štyrmi prvkami na stĺpci matrici tiež so štyrmi prvkami, produktom dvoch päťrozmerných vektorov - produkt matricového reťazca s piatimi prvkami Matica stĺpca aj s piatimi prvkami a tak ďalej.

Príklad 7. Nájsť skalárne diela parných vektorov

,

pomocou reprezentácie matrice.

Rozhodnutia. Prvý pár vektorov. Prvý vektor predstavujeme vo forme reťazec matice a druhý - vo forme stĺpcovej matrice. Nájdeme skalárny produkt týchto vektorov ako produkt matricového reťazca na stĺpci Matrix:

Podobne predstavujeme druhý pár a nájsť:

Ako vidíme, výsledky sa ukázali ako rovnaké dvojice z príkladu 2.

Medzi dvoma vektormi

Výstup kosínutej vzorec rohu medzi dvoma vektormi je veľmi krásna a krátka.

Vyjadrite skalárny produkt vektorov

(1)

v koordinátovom formulári budeme predbežne nájsť skalárny produkt ortu. Skalárny produkt vektora na základe definície:

Čo je zaznamenané vo vyššie uvedenom vzorci: skarový produkt vektora na sebe sa rovná námesti jeho dĺžky. Cosine z nuly sa rovná jednému, takže námestie každého ortu bude rovnať jednému:

Od vektorov

kolmé, potom pár diel Orts bude nula:

Teraz vykonajte násobenie vektorových polynómov:

Nahradíme rovnosť hodnôt zodpovedajúcich skalárnych diel:

Získavame Cosine vzorec rohu medzi dvoma vektormi:

Príklad 8.Uvedené tri body A.(1;1;1), B.(2;2;1), C.(2;1;2).

Nájdite uhol.

Rozhodnutia. Nájdeme súradnice vektorov:

,

.

Podľa Cosine vzorec dostaneme:

Teda.

Pre seba-test môžete použiť online kalkulačka skalárneho produktu vektorov a kosínom rohov medzi nimi .

Príklad 9.Dana Dva vektory

Nájsť množstvo, rozdiel, dĺžku, skalárny produkt a uhol medzi nimi.

2.

I. Skalový produkt sa nakreslí na nulu a len v prípade, že aspoň jeden z vektorov je nula alebo ak sú vektory kolmé. V skutočnosti, ak buď, alebo to.

V prípade, že variabilné vektory nie sú nula, potom kvôli stavu

keď nasleduje:

Vzhľadom k tomu, smer nulového vektora je neistý, nulový vektor môže byť považovaný za kolmého na akýkoľvek vektor. Preto je špecifikovaná vlastnosť skalárneho výrobku môže byť formulovaná v krátkom čase: Skalový produkt sa nakreslí na nulu a len v prípade, keď sú vektory kolmé.

II. Skarový produkt má vlastnosť pohybu:

Táto vlastnosť priamo vyplýva z definície:

pretože rôzne označenia toho istého rohu.

III. Rozvodné právo je mimoriadne dôležité. Jeho použitie je rovnako veľké, ako v obvyklých aritmetike alebo algebre, kde je formulovaný ako: na násobenie sumy, musíte sa vynásobiť každú studňu a zložiť získané diela, t.j.

Je zrejmé, že násobenie multivalovaných čísel v aritmetických alebo polynómoch v algebre je založené na tejto vlastnosti množenia.

Tento zákon má rovnaký významný význam vo vektorovej algebre, pretože na základe toho môžeme požiadať o vektory obvyklé multiplikačné pravidlo polynómov.

Dokážeme, že pre všetky tri vektory A, B, s rovnosťou

Podľa druhej definície skalárneho výrobku, vyjadreného vzorcom, získavame:

Aplikácia NEPOUŽÍVAŤ VLASTNOSTI 2 Projekcie z § 5, nájdeme:

q.E.ED.

IV. Skarový výrobok má presnosť kombinácie v porovnaní s numerickým faktorom; Táto vlastnosť je vyjadrená nasledovne:

t.j. násobiť skalárny produkt vektorov podľa čísla, stačí znásobiť týmto číslom jedným z faktorov.