Kalkulačka Obrázok Square Limited. Online kalkulačka. Zúčtovanie špecifického integrálu (Curvilinear Lispezium Area)

18.10.2019

Tiež

Príbeh Hilgamesh Mýty starovekých taôch o Gilgamesh

História charakteru Mýtus starovekého Grécka Dedala a ICAR číta

Hrdinovia starožitných mýtov znakov gréckej mytológie

Online čítacie knihy mýty klasickej starovekej knihy ôsme

Z tohto článku sa dozviete, ako nájsť oblasť čísel obmedzených riadkami pomocou výpočtov pomocou integrálov. Prvýkrát sa stretávame s takouto úlohou na strednej škole, keď sme práve prešli štúdiom určitých integrálov a je čas začať geometrický výklad poznatkov získaných v praxi.

Takže, čo bude potrebné, aby úspešne vyriešiť problém hľadania oblasti obrázku s pomocou integrálov:

Zručnosti Kompetentne vybudovať výkresy;
Schopnosť vyriešiť špecifickú integrál s pomocou známeho newton-leibnického vzorca;
Schopnosť "vidieť" ziskovejšie riešenie riešenia - t.j. Pochopte, ako v takomto prípade bude vhodnejšie vykonávať integráciu? Pozdĺž osi x (ox) alebo osi hry (OY)?
No, kde bez správnej výpočty?) To zahŕňa pochopenie, ako vyriešiť iný typ integrálov a správne numerické výpočty.

Algoritmus na riešenie úlohy výpočtu oblasti obrázku, obmedzené čiary:

1. Vybudovať výkres. Odporúča sa to urobiť na kus v klietke, s veľkým meradlom. Vyhlásime ceruzku nad každým grafom názov tejto funkcie. Podpis grafov sa vykonáva výlučne pre pohodlie ďalšieho výpočtu. Po prijatí grafu požadovanej hodnoty, vo väčšine prípadov bude vidieť okamžite, na ktoré sa použijú integračné limity. Takto vyriešime úlohu grafickou metódou. Stáva sa však, že hodnoty limitov sú frakčné alebo iracionálne. Preto môžete vykonať ďalšie výpočty, prejdite na krok dva.

2. Ak sú integračné limity jednoznačne špecifikované, nájdeme priesečníkové body grafov medzi sebou a pozeráme sa na to, či sa naše grafické riešenie s analytickým spôsobom zhoduje.

3. Ďalej je potrebné analyzovať výkres. V závislosti od toho, ako sa nachádza grafika funkcií, existujú rôzne prístupy k nájdeniu oblasti obrázku. Zvážte rôzne príklady, aby ste našli oblasť obrázku pomocou integrálov.

3.1. Najklasickejšou a jednoduchá možnosť úlohy je, keď potrebujete nájsť oblasť zakrivenej trapézie. Čo je to curvilinear trapeze? Toto je plochá postava obmedzená na os x (y \u003d 0)priamy x \u003d A, X \u003d B a akúkoľvek krivku kontinuálne v intervale od a. predtým b.. Zároveň je toto číslo negatívne a nie je nižšia ako os Abscissu. V tomto prípade je oblasť zakriveného lichobežníka numericky rovnaká špecifickým integrálom vypočítaným vzorcom Newton Latibender:

Príklad 1. y \u003d x2 - 3x + 3, x \u003d 1, x \u003d 3, y \u003d 0.

Aké riadky sú obmedzené? Máme paraboly y \u003d x2 - 3x + 3ktorý sa nachádza nad osou Ohovárať, je to negatívne, pretože Všetky body tejto paraboly sú pozitívne. Ďalej, priamy x \u003d 1. a x \u003d 3.ktorí bežia rovnobežne s osou Ousú reštriktívne čiary obrázku vľavo a vpravo. Dobre y \u003d 0Je to os x, ktorá obmedzuje obrázok nižšie. Výsledný obrázok je zatienený, ako je možné vidieť z výkresu vľavo. V tomto prípade môžete problém okamžite začať riešiť problém. Máme jednoduchý príklad zakriveného lichobežníka, ktorý je ďalej riešením pomocou Newton-Leibnic vzorec.

3.2. V predchádzajúcom bode 3.1 sa prípad rozkladá, keď je zakrivený lichobežník umiestnený nad osou x. Teraz zvážte prípad, keď sú podmienky úlohy rovnaké, okrem toho, že funkcia beží pod osou x. Štandardný vzorec Newton-Labender sa pridáva mínus. Ako riešiť takúto úlohu ďalej zvážiť.

Príklad 2. . Vypočítajte oblasť tvaru, obmedzené čiary y \u003d x2 + 6x + 2, x \u003d -4, x \u003d -1, y \u003d 0.

V tomto príklade máme parabolu y \u003d x2 + 6x + 2ktorá pochádza z osi Ohováraťrovno x \u003d -4, X \u003d -1, Y \u003d 0. Tu y \u003d 0 Obmedzuje požadovanú hodnotu zhora. Priamy x \u003d -4. a x \u003d -1. Jedná sa o hraniciach, v rámci ktorých sa vypočíta špecifický integrál. Princíp riešenia problému nájsť oblasť obrázku takmer úplne sa zhoduje s príkladom príjmu 1. Jediným rozdielom je, že špecifikovaná funkcia nie je pozitívna a všetko je tiež kontinuálne v intervale [-4; -1] . Čo neznamená pozitívne? Ako možno vidieť z obrázku, postava, ktorá leží v rámci špecifikovanej ICS, má výlučne "negatívne" súradnice, ktoré potrebujeme vidieť a pamätať pri riešení problému. Oblasť obrázku hľadá receptúru Newton Labitsa, len s mínusovým znakom na začiatku.

Článok nie je dokončený.

Prejsť na zváženie integrálnych aplikácií. V tejto lekcii budeme analyzovať typickú a najčastejšiu úlohu. výpočty plochej hodnoty so špecifickým integrálom. Nakoniec ho našiel celý význam významu v najvyššej matematike. Málo. Budeme musieť priniesť oblasť krajiny v živote so základnými funkciami a nájsť svoju oblasť pomocou špecifického integrálu.

Pre úspešný rozvoj materiálu je potrebné:

1) pochopiť neurčitú integrálnu aspoň priemernú úroveň. Teda comeapotes by mali byť oboznámení s lekciou Nie.

2) Byť schopný aplikovať receptúru Newton Labnik a vypočítať špecifický integrál. Zaviesť teplé priateľstvá s určitými integrálmi na stránke Určitý integrálny. Príklady riešení. Úloha "Vypočítajte oblasť s pomocou špecifického integrálu" vždy znamená výstavbu výkresuVaše vedomosti a zručnosti stavebných výkresov preto budú tiež urgentnou otázkou. Minimálne musíte byť schopní postaviť rovnú, parabola a hyperbola.

Začnime s zakriveným trapéziom. Curvilinear Trapezium je plochá postava obmedzená grafom určitej funkcie. y. = f.(x.), os VÔL. a riadky x. = a.; x. = b..

Oblasť zakriveného lichobežníka je numericky rovná špecifickému integrálu

Každý konkrétny integrálny (ktorý existuje) má veľmi dobrý geometrický význam. Na lekcii Určitý integrálny. Príklady riešenípovedali sme, že určitý integrálny je číslo. A teraz je čas uviesť ďalšiu užitočnú skutočnosť. Z hľadiska geometrie je určitá integrálna oblasť. T.j Špecifický integrál (ak existuje) geometricky zodpovedá ploche určitej postavy. Zvážte špecifický integrál

Integrand

určuje krivku na rovine (môže byť ťahaná, ak je to žiaduce), a určitý integrálny sám je numericky rovný ploche zodpovedajúceho zakriveného lichobežníka.

Príklad 1.

, , , .

Ide o typickú formuláciu úloh. Najdôležitejším bodom rozhodnutia je vybudovať výkres. A výkres sa musí vybudovať SPRÁVNY.

Pri budovaní výkresu odporúčam nasledujúci príkaz: najprv Je lepšie postaviť všetky rovné (ak sú) a len neskôr - Paraboly, hyperbola, plány iných funkcií. Technika konštrukcie konštrukcie možno nájsť v referenčnom materiáli. Grafy a vlastnosti základných funkcií. Tam si môžete tiež nájsť veľmi užitočný materiál vo vzťahu k našej lekcii materiálu - ako rýchlo vybudovať parabola.

V tejto úlohe môže toto rozhodnutie vyzerať takto.

Vykonajte výkres (všimnite si, že rovnica y. \u003d 0 Nastavuje os VÔL.):

Strike Curvilinear Trapezia nebude, je to zrejmé, ktorá oblasť je reč. Rozhodnutie pokračuje takto:

Na segmente [-2; 1] Funkčný plán y. = x. 2 + 2 sa nachádza cez osVÔL., Takže:

Odpoveď: .

Kto má problémy s výpočtom určitého integrálu a používanie vzorec Newton-Leibnia

odkazujú na prednášku Určitý integrálny. Príklady riešení. Po dokončení úlohy je vždy užitočné pozrieť sa na kresbu a odhad, skutočný sa ukázal. V tomto prípade, "na oči" počítame počet buniek v kresbe - dobre, približne 9 sa letel, zdá sa, že pravdu. Je celkom jasné, že ak by sme mali, povedzme, odpovedzte: 20 štvorcových jednotiek, je zrejmé, že chyba je vykonaná niekde - na obrázku 20 buniek, to je zjavne namontované, od pevnosti tucet. Ak sa odpoveď ukázala negatívna, úloha sa tiež rozhodne nesprávne.

Príklad 2.

Vypočítajte oblasť tvaru, obmedzené čiary xy. = 4, x. = 2, x. \u003d 4 a os VÔL..

Toto je príklad pre nezávislé riešenie. Kompletné riešenie a odpoveď na konci hodiny.

Čo robiť, ak sa nachádza Curvilinear Trapezia pod osouVÔL.?

Príklad 3.

Vypočítajte oblasť tvaru, obmedzené čiary y. = e - X., x. \u003d 1 a súradnicové osi.

Riešenie: Vykonajte čerpanie:

Ak je zakrivený trapézia plne umiestnené pod osou VÔL. , potom je jeho oblasť nájdená vzorcom:

V tomto prípade:

Pozor! Nezamieňajte dva typy úloh:

1) Ak ste vyzvaní, aby ste vyriešili jednoduchý integrálny bez akéhokoľvek geometrického významu, potom to môže byť záporné.

2) Ak ste vyzvaní, aby ste našli číslo obrázku pomocou špecifického integrálu, potom je oblasť vždy pozitívna! To je dôvod, prečo v práve uvažovaný vzorec sa zobrazí mínus.

V praxi je obraz najčastejšie umiestnený v hornej a dolnej polovice rovine, a preto z najjednoduchších školských grafov prejdite na zmysluplné príklady.

Príklad 4.

Nájdite oblasť plochého tvaru obmedzené čiary y. = 2x. – x. 2 , y. = -x..

Riešenie: Najprv musíte nakresliť výkres. Pri budovaní výkresu v úlohách do oblasti sa najviac zaujímame o priesečníky línií. Nájsť body priesečníka parabola y. = 2x. – x. 2 a priame y. = -x.. To sa dá urobiť dvoma spôsobmi. Prvá metóda je analytická. Riešime rovnicu:

Tak, dolná hranica integrácie a. \u003d 0, Horný integračný limit b. \u003d 3. Často je to často výhodnejšie a rýchlejšie vybudovať riadky toku, zatiaľ čo limity integrácie sa objasňujú ako keby sami ". Avšak, analytický spôsob, ako nájsť limity po tom všetkom, je niekedy potrebné uplatňovať, ak je napríklad harmonogram dostatočne veľký, alebo vyškolená konštrukcia neodhalila integračné limity (môžu byť frakčné alebo ihracionálne). Vrátime sa k našej úlohe: racionálnejšie najprv postaviť priamku a len potom paraboly. Vykonajte výkres:

Opakujte, že v aktuálnej konštrukcii sa najčastejšie zistíte integračné limity.

A teraz pracovný vzorec:

Ak je na segmente [ a.; b.] Niektoré nepretržité funkcie f.(x.) viac alebo rovné Niektoré nepretržité funkcie g.(x.) Potom sa nachádza oblasť zodpovedajúceho čísla podľa vzorca:

Tu, nie je potrebné myslieť, kde je postava umiestnená nad osou alebo pod osou a dôležité Čo je graf vyššie(vzhľadom na iný plán) a čo - nižšie.

V tomto príklade je zrejmé, že na segmente parabola je umiestnený nad rovno, a teda z 2 x. – x. 2 potreba odpočítať x..

Dokončenie riešenia môže vyzerať takto:

Požadovaná hodnota je obmedzená na parabola y. = 2x. – x. 2 hore a rovno y. = -x. dno.

Na segmente 2. x. – x. 2 ≥ -x.. Podľa zodpovedajúceho vzorca:

Odpoveď: .

V skutočnosti, školský vzorec pre oblasť zakrivenej trapézie v dolnej polohe (pozri príklad číslo 3) - špeciálny prípad vzorca

Od osi VÔL. Platné rovnicou y. \u003d 0 a funkčný plán g.(x.) Pod osi VÔL.T.

A teraz niekoľko príkladov nezávislého rozhodnutia

Príklad 5.

Príklad 6.

Nájdite oblasť Obmedzené čiary

V priebehu riešenia úloh na výpočet oblasti so špecifickým integrálom sa niekedy vyskytuje vtipné prípady. Kresba je dokončená správne, výpočty - správne, ale podľa návrstvosti, ... nájdená oblasť nie je číslo.

Príklad 7.

Najprv vykonajte výkres:

Obrázok, ktorej oblasti potrebujeme nájsť, je v poriadku(Pozorne pozrite sa na stav - ako je číslo je obmedzené!). Ale v praxi, podľa nepozornosti, často sa rozhodnú, že musíte nájsť oblasť obrázku, ktorá je tieňovaná zelenou!

Tento príklad je tiež užitočný v tom, že sa považuje za veľkosť dvoch špecifických integrálov. Naozaj:

1) na segmente [-1; 1] cez os VÔL. Nachádza sa program Direct y. = x.+1;

2) Na segmente nad osou VÔL. Nachádza sa graf Hyperbole y. = (2/x.).

Je jasné, že námestie môže (a potrebu) rozkladať, takže:

Odpoveď:

Príklad 8.

Vypočítajte oblasť tvaru, obmedzené čiary

Predstavte si rovnicu v "školskom" forme

a do aktuálneho výkresu:

Z kreslenia je zrejmé, že horná hranica máme "dobré": b. = 1.

Ale čo je dolná hranica?! Je jasné, že to nie je celé číslo, ale čo?

Možno, a.\u003d (- 1/3)? Ale kde je záruka, že kresba je vyrobená s ideálnou presnosťou, môže to byť a.\u003d (- 1/4). A ak by sme vo všeobecnosti nesprávne vybudovali plán?

V takýchto prípadoch musíte stráviť čas navyše a špecifikovať analytické limity integrácie.

Nájdite priesečník grafov

Urobte to, vyriešte rovnicu:

Teda, a.=(-1/3).

Ďalšie riešenie je triviálne. Hlavná vec nie je zmätená v substitúciach a príznakoch. Výpočty nie sú najjednoduchšie. Na rezu

, ,

podľa zodpovedajúceho vzorca:

Odpoveď:

V závere lekcie zvážte dva úlohy sťažujúcejšie.

Príklad 9.

Vypočítajte oblasť tvaru, obmedzené čiary

Riešenie: Zobraziť tento tvar na výkrese.

Pre chatu výkresu je potrebné poznať vzhľad sinusoidov. Všeobecne platí, že je užitočné poznať grafy všetkých základných funkcií, ako aj niektoré hodnoty sínusov. Môžu byť nájdené v tabuľke hodnôt trigonometrické funkcie. V niektorých prípadoch (napríklad v tomto) je možné vytvoriť schematické výkres, na ktorom sa musia v zásade odrážať grafy a limity integrácie.

S hračkami integrácie tu nie sú žiadne problémy, sledujú priamo z podmienky:

- "X" sa líši od nuly na "PI". Vypracujeme ďalšie riešenie:

Na funkcii Cut Graf y. \u003d SIN 3. x. Nachádza sa nad osou VÔL., Takže:

(1) Ako integrovať snínky a kosíny v nepárnych tituloch, môžete sa pozrieť na lekciu Integrály z trigonometrických funkcií. Zapojte jednu sínu.

(2) Používame hlavnú trigonometrickú identitu vo forme

(3) Nahradíme premennú t. \u003d Cos. x., potom: Nachádza sa nad osou, takže:

Poznámka: Venujte pozornosť tomu, ako sa odoberá integrálna z Tangenta na Kube, tu sa tu používa dôsledok hlavnej trigonometrickej identity.

V predchádzajúcej časti venovanej analýze geometrického významu určitého integrálu sme dostali niekoľko vzorcov pre výpočet oblasti zakrivenia Trapezium:

Yandex.rtb R-A-339285-1

S (g) \u003d ∫ A B f (x) d x pre kontinuálne a negatívne funkcie y \u003d f (x) na segmente [A; b]

S (g) \u003d - ∫ a b f (x) d x pre kontinuálnu a ne pozitívnu funkciu Y \u003d F (x) na segmente [A; b].

Tieto vzorce sa uplatňujú na riešenie relatívne jednoduchých úloh. V skutočnosti budeme najčastejšie pracovať s komplexnejšími údajmi. V tomto ohľade sa táto časť venujeme analýze algoritmov na výpočet oblasti obrázkov, ktoré sú obmedzené funkciami explicitne, t.j. Ako y \u003d f (x) alebo x \u003d g (y).

Teorem

Nech sú stanovené funkcie y \u003d f1 (x) a y \u003d f2 (x) a kontinuálne na rozhraní [A; b], s f 1 (x) ≤ f 2 (x) pre akúkoľvek hodnotu X od [A; b]. Potom vzorec pre výpočet plochy obrázku g, ohraničený čiarami X \u003d A, X \u003d B, Y \u003d F1 (X) a Y \u003d F2 (X), bude zobrazený s (g) \u003d ∫ ABF 2 (X) - F 1 (X) DX.

Podobný vzorec sa použije na plochu obrázku, obmedzená čiarami Y \u003d C, Y \u003d D, X \u003d G1 (Y) a X \u003d G2 (Y): S (G) \u003d ∫ CD (G2 (Y) - G1 (Y) DY.

Dôkaz

Budeme analyzovať tri prípady, pre ktoré bude vzorec spravodlivý.

V prvom prípade, vzhľadom na vlastnosť aditívnej plochy, súčet plochy pôvodného obrázku g a zakrivený lichobežník G11 sa rovná ploche obrázku G2. Znamená to, že

Preto S (G) \u003d S (G2) - S (G 1) \u003d ∫ ABF 2 (X) DX - ∫ ABF 1 (X) DX \u003d ∫ AB (F 2 (X) - F 1 (X)) Dx.

Vykonajte posledný prechod, ktorý môžeme používať tretiu vlastnosť konkrétneho integrálu.

V druhom prípade je rovnosť pravdivá: s (g) \u003d s (G2) + S (G 1) \u003d ∫ ABF 2 (X) DX + - ∫ ABF 1 (X) DX \u003d ∫ AB (F2 (X) ) - F 1 (X)) DX

Grafické ilustrácie sa bude pozrieť:

Ak sú obidva funkcie pozitívne, získavame: s (g) \u003d s (g 2) - s (G 1) \u003d - ∫ ABF 2 (X) DX - - ∫ ABF 1 (X) DX \u003d ∫ AB (F 2 (x) - f 1 (x)) dx. Grafické ilustrácie sa bude pozrieť:

Poďme sa obrátiť na zváženie všeobecného prípadu, keď y \u003d f 1 (x) a y \u003d f2 (x) prechádza os x os.

Priesekčné body označujeme ako x i, i \u003d 1, 2 ,. . . , N - 1. Tieto body rozbili segment [A; b] na n časti x I - 1; X I, I \u003d 1, 2 ,. . . , n, kde α \u003d x 0< x 1 < x 2 < . . . < x n - 1 < x n = b . Фигуру G можно представить объединением фигур G i , i = 1 , 2 , . . . , n . Очевидно, что на своем интервале G i попадает под один из трех рассмотренных ранее случаев, поэтому их площади находятся как S (G i) = ∫ x i - 1 x i (f 2 (x) - f 1 (x)) d x , i = 1 , 2 , . . . , n

Teda,

S (g) \u003d σ i \u003d 1 n s (g i) \u003d σ i \u003d 1 n ∫ xixif 2 (x) - f 1 (x)) dx \u003d \u003d ∫ x 0 xn (F 2 (X) - F (X) )) DX \u003d ∫ ABF 2 (X) - F 1 (X) DX

Posledný prechod môžeme implementovať pomocou piateho vlastnosti špecifického integrálu.

V grafe ilustrujeme všeobecný prípad.

Vzorec (g) \u003d ∫ A b f 2 (x) - f 1 (x) d x možno považovať za preukázané.

A teraz prejdeme k analýze príkladov výpočtu oblasti obrázkov, ktoré sú obmedzené na čiary y \u003d f (x) a x \u003d g (y).

Zohľadnenie niektorého z príkladov začneme s výstavbou harmonogramu. Obraz nám umožní reprezentovať komplexné čísla ako kombináciu jednoduchších obrázkov. Ak je výstavba grafov a číslic sťažiť pre nich, môžete preskúmať časť o základných základných funkciách, geometrickej konverzie grafov funkcií, ako aj stavebných grafov počas funkčného výskumu.

Príklad 1.

Je potrebné určiť oblasť obrázku, ktorá je obmedzená na paraboly y \u003d - x 2 + 6 x - 5 a priamky y \u003d - 1 3 x - 1 2, x \u003d 1, x \u003d 4 .

Rozhodnutie

Zobraziť riadky na grafe v systéme karteziánskeho súradnice.

Na segmente [1; 4] Graf parabola y \u003d - x 2 + 6 x - 5 je umiestnený nad rovným y \u003d - 1 3 x - 1 2. V tomto ohľade získate odpoveď, použijeme vzorca skôr, ako aj spôsob výpočtu špecifického integrálu podľa Formule Newton-Leibnitsa:

S (g) \u003d ∫ 1 4 - x 2 + 6 x - 5 - - 1 3 x - 1 2 dx \u003d \u003d ∫ 1 4 - x 2 + 19 3 x - 9 2 DX \u003d - 1 3 x 3 + 19 6 X 2 - 9 2 x 1 4 \u003d \u003d - 1 3 · 4 + 19 6 · 4 2 - 9 2 · 4 - 1 3 · 1 3 + 19 6 · 1 2 - 9 2 · 1 \u003d - 64 3 + 152 3 - 18 + 1 3 - 19 6 + 9 2 \u003d 13

Odpoveď: S (g) \u003d 13

Zvážte zložitejší príklad.

Príklad 2.

Je potrebné vypočítať oblasť obrázku, ktorá je obmedzená na čiary y \u003d x + 2, y \u003d x, x \u003d 7.

Rozhodnutie

V tomto prípade máme len jednu priamku umiestnenú rovnobežne s osou osi. Toto je x \u003d 7. Vyžaduje nás, aby sme našli druhý integračný limit na vlastnú päsť.

Vytvárame harmonogram a prinesieme na to, údaje o stave úloh.

Mať graf pred očami, môžeme ľahko zistiť, že dolná hranica integrácie bude abscisou priesečného bodu plánu y \u003d x a podlahy paraboly y \u003d x + 2. Ak chcete nájsť abscisa, použite rovnosť:

y \u003d X + 2 O d Z: X ≥ - 2 x 2 \u003d X + 2 x 2 - X - 2 \u003d 0 D \u003d (- 1) 2 - 4 · (- 2) \u003d 9 x 1 \u003d 1 + 9 2 \u003d 2 ∈ o dzx 2 \u003d 1 - 9 2 \u003d - 1 ∉ odz

Ukazuje sa, že abscisa z priesečníka je x \u003d 2.

Upozorňujeme na skutočnosť, že vo všeobecnom príklade v kresbe čiary Y \u003d X + 2, Y \u003d X pretína v bode (2; 2), takže takéto podrobné výpočty sa môžu zdať zbytočné. Takéto podrobné rozhodnutie sme viedli len preto, že v zložitejších prípadoch rozhodnutie nemusí byť tak zrejmé. To znamená, že súradnice priesečníka riadkov sú lepšie vždy vypočítať analyticky.

O intervale [2; 7] Graf funkcie Y \u003d X sa nachádza nad grafom funkcie Y \u003d X + 2. Aplikujte vzorec pre výpočet štvorcov:

S (g) \u003d ∫ 2 7 (X - X + 2) DX \u003d X2 2 - 2 3 · (X + 2) 3 2 2 7 \u003d 7 2 2 - 2 3 · (7 + 2) 3 2 - 2 2 2 - 2 3 · 2 + 2 3 2 \u003d 49 2 - 18 - 2 + 16 3 \u003d 59 6

Odpoveď: S (G) \u003d 59 6

Príklad 3.

Je potrebné vypočítať oblasť obrázku, ktorá je obmedzená grafmi funkcií y \u003d 1 x a y \u003d - x 2 + 4 x - 2.

Rozhodnutie

Aplikujte riadky na harmonograme.

Určiť limity integrácie. Aby sme to urobili, definujeme súradnice priesečníckych bodov liniek, vymazanie výrazov 1 x a - x 2 + 4 x - 2. Za predpokladu, že X nie je nula, rovnosť 1 x \u003d x 2 + 4 x - 2 sa stane ekvivalentnou rovnicou tretieho stupňa - x 3 + 4 x 2 - 2 x - 1 \u003d 0 s celočíselnými koeficientmi. Ak chcete obnoviť algoritmus v pamäti riešením takýchto rovníc, môžeme kontaktovať sekciu "riešenie kubických rovníc".

Koreňom tejto rovnice je X \u003d 1: - 1 3 + 4 · 1 2 - 2 · 1 - 1 \u003d 0.

Rozdelenie výrazu - X 3 + 4 x 2 - 2 x - 1 na odraz X - 1, získavame: - x 3 + 4 x 2 - 2 x - 1 ⇔ - (X - 1) (x 2 - 3 x - 1) \u003d 0.

Zostávajúce korene môžeme nájsť z rovnice x 2 - 3 x - 1 \u003d 0:

x 2 - 3 x - 1 \u003d 0 D \u003d (- 3) 2 - 4 · (- 1) \u003d 13 x 1 \u003d 3 + 13 2 ≈ 3. 3; x 2 \u003d 3 - 13 2 ≈ - 0. 3.

Našli sme interval x ∈ 1; 3 + 13 2, na ktorom je obrázok G uzavretý nad modrou a pod červenou čiarou. Pomáha nám určiť oblasť obrázku:

S (g) \u003d ∫ 1 3 + 13 2 - x 2 + 4 x - 2 - 1 xDX \u003d - x 3 + 2 x 2 - 2 x - LN x 1 3 + 13 2 \u003d - 3 + 13 2 3 3 + 2 · 3 + 13 2 2 - 3 + 13 2 - LN3 + 13 2 - - - 1-13 + 2 · 1 2 - 2,1 - LN 1 \u003d 7 + 13 3 - LN 3 + 13 2 .

Odpoveď: S (g) \u003d 7 + 13 3 - LN 3 + 13 2

Príklad 4.

Je potrebné vypočítať oblasť obrázku, ktorá je obmedzená na krivky y \u003d x 3, y \u003d - log 2 x + 1 a os osi.

Rozhodnutie

Budeme aplikovať všetky riadky na harmonograme. Môžeme získať funkciu funkcie y \u003d - log 2 x + 1 z grafu y \u003d log 2 x, ak ho umiestňujeme symetricky vzhľadom na os Abscissu a zvýšite jednu jednotku smerom nahor. Abscissa Axisová rovnica Y \u003d 0.

Označujú priesečníky línií.

Ako je možné vidieť z obrázku, grafy funkcií y \u003d x 3 a y \u003d 0 pretínajú v bode (0; 0). Získa sa, pretože X \u003d 0 je jediný platný koreň rovnice x 3 \u003d 0.

x \u003d 2 je jediný koreň rovnice - log 2 x + 1 \u003d 0, takže grafy funkcií y \u003d - log 2 x + 1 a y \u003d 0 pretínajú v bode (2; 0).

x \u003d 1 je jediný koreň rovnice x 3 \u003d - log 2 x + 1. V tejto súvislosti sa grafy funkcií y \u003d x 3 a y \u003d - log 2 x + 1 pretínajú v bode (1; 1). Posledné vyhlásenie môže byť nejasné, ale rovnica x 3 \u003d - log 2 x + 1 nemôže mať viac ako jeden koreň, pretože funkcia y \u003d x 3 sa striktne zvyšuje, a funkcia y \u003d - log 2 x + 1 sa striktne znižuje .

Ďalšie riešenie zahŕňa niekoľko možností.

Možnosť možnosti 1

Obrázok g si dokážeme predstaviť, ako súčet dvoch krivočiarových lichobežníkov umiestnených nad osou Abscissa, z ktorých prvá je umiestnená pod strednou čiarou na segmente x ∈ 0; 1 a druhá pod červenou čiarou na segmente x ∈ 1; 2. To znamená, že oblasť bude rovná s (g) \u003d ∫ 0 1 x 3 d x + ∫ 1 2 (- log 2 x + 1) d x.

Možnosť voľby 2.

Obrázok g môže byť reprezentovaný ako rozdiel dvoch obrázkov, z ktorých prvý je umiestnený nad osou osi a pod modrou čiarou na segmente x ∈ 0; 2 a druhá medzi červenými a modrými čiarami na segmente x ∈ 1; 2. To nám umožňuje nájsť oblasť takto:

S (g) \u003d ∫ 0 2 x 3 d x - ∫ 1 2 x 3 - (- log 2 x + 1) d x

V tomto prípade, aby ste našli oblasť, bude musieť použiť vzorec formulára S (g) \u003d ∫ c d (G2 (Y) - g 1 (y)) d y. V skutočnosti, riadky, ktoré obmedzujú obrázok, môžu byť reprezentované ako funkcie z argumentu y.

Povolené rovnice y \u003d x 3 a - log 2 x + 1 v porovnaní s X:

y \u003d x 3 ⇒ x \u003d y3 y \u003d - log 2 x + 1 ⇒ log 2 x \u003d 1 - y ⇒ x \u003d 2 1 - y

Dostaneme požadovanú oblasť:

S (g) \u003d ∫ 0 1 (2 1 - y - y3) dy \u003d - 2 1 - y LN 2 - y4 4 0 1 \u003d - 2 1 - 1 LN 2 - 1 4 4 - - 2 1 - 0 LN 2 - 0 4 4 \u003d 1 LN 2 - 1 4 + 2 LN 2 \u003d 1 LN 2 - 1 4

Odpoveď: S (G) \u003d 1 LN 2 - 1 4

Príklad 5.

Je potrebné vypočítať oblasť obrázku, ktorá je obmedzená na čiary y \u003d x, y \u003d 2 3 x - 3, y \u003d - 1 2 x + 4.

Rozhodnutie

S červenou čiarou, použijeme riadok na grafe špecifikovanom funkciou y \u003d x. Modrá s čiarou y \u003d - 1 2 x + 4, v čiernej farbe, označujeme čiaru y \u003d 2 3 x - 3.

Všimnite si body priesečníka.

Nájsť body priesečníka grafov funkcií y \u003d x a y \u003d - 1 2 x + 4:

x \u003d - 1 2 x + 4 Od Z: X ≥ 0 x \u003d - 1 2 x + 4 2 ⇒ x \u003d 1 4 x 2 - 4 x + 16 ⇔ x 2 - 20 x + 64 \u003d 0 d \u003d (- 20) 2 - 4 · 1,64 \u003d 144 x 1 \u003d 20 + 144 2 \u003d 16; X2 \u003d 20 - 144 2 \u003d 4 p RO v E P K A: X 1 \u003d 16 \u003d 4, - 1 2 x 1 + 4 \u003d - 1 2 · 16 + 4 \u003d - 4 ⇒ x 1 \u003d 16 n Som v Li jesť XP a v N a IX 2 \u003d 4 \u003d 2, - 1 2 x 2 + 4 \u003d - 1 2 · 4 + 4 \u003d 2 ⇒ x 2 \u003d 4 Som v l I e \u200b\u200bt s i r e n e m u r a n a n i ⇒ (4; 2) t o h k a n e r e s I y \u003d x a y \u003d - 1 2 x + 4

Nájdeme bod priesečníka grafov funkcií y \u003d x a y \u003d 2 3 x - 3:

x \u003d 2 3 x - 3 OD Z: X ≥ 0 x \u003d 2 3 x - 3 2 ⇔ x \u003d 4 9 x 2 - 4 x + 9 ⇔ 4 x 2 - 45 x + 81 \u003d 0 d \u003d (- 45) 2 - 4 · 4 · 81 \u003d 729 x 1 \u003d 45 + 729 8 \u003d 9, x 2 45 - 729 8 \u003d 9 4 П Р О е Р K A: X 1 \u003d 9 \u003d 3, 2 3 x 1 - 3 \u003d 2 3 · 9 - 3 \u003d 3 ⇒ x 1 \u003d 9 Som v Liemiraneni ⇒ (9; 3) TOH na APERECECECHIY \u003d X a Y \u003d 2 3 x - 3 x 2 \u003d 9 4 \u003d 3 2, 2 3 x 1 - \\ t 3 \u003d 2 3 · 9 4 - 3 \u003d - 3 2 ⇒ x 2 \u003d 9 4 n e i l i e t s i r e n e m u r a v n e n i

Nájdeme bod priesečníka línií y \u003d - 1 2 x + 4 a y \u003d 2 3 x - 3:

1 2 x + 4 \u003d 2 3 x - 3 ⇔ - 3 x + 24 \u003d 4 x - 18 ⇔ 7 x \u003d 42 ⇔ x \u003d 6 - 1 2 · 6 + 4 \u003d 2 3 · 6 - 3 \u003d 1 ⇒ (6) ; 1) t približne HKANERECENIY \u003d - 1 2 x + 4 a Y \u003d 2 3 x - 3

Metóda číslo 1.

Predstavte si oblasť požadovanej hodnoty ako súčet oblastí jednotlivých obrázkov.

Potom sa postava obrázku rovná:

S (g) \u003d ∫ 4 6 x - - 1 2 x + 4 dx + ∫ 6 9 x - 2 3 x - 3 dx \u003d 2 3 x 3 2 + x 2 4 - 4 x 4 6 + 2 3 x 32 - X2 3 + 3 x 6 9 \u003d 2 3 · 6 3 2 + 6 2 4 - 4 · 6 - 2 3 · 4 3 2 + 4 2 4 - 4 · 4 + + 2 3 · 9 3 2 - 9 2 3 + 3 · 9 - 2 3 · 6 3 2 - 6 2 3 + 3 · 6 \u003d - 25 3 + 4 6 + - 4 6 + 12 \u003d 11 3

Metóda číslo 2.

Oblasť pôvodného čísla môže byť reprezentovaná ako súčet dvoch ďalších obrázkov.

Potom vyriešime rovnicu čiary v porovnaní s X a až po tom, čo sme aplikujeme vzorec pre výpočet postavy obrázku.

y \u003d x ⇒ x \u003d y2 až R a s n a i l a i y \u003d 2 3 x - 3 ⇒ x \u003d 3 2 y + 9 2 h e r n i l a i y \u003d - 1 2 x + 4 ⇒ x \u003d - 2 y + 8 s a nil a ni

Táto oblasť je rovnaká:

S (g) \u003d ∫ 1 2 3 2 Y + 9 2 - - 2 y + 8 DY + ∫ 2 3 3 2 Y + 9 2 - Y 2 DY \u003d ∫ 1 2 7 2 Y - 7 2 DY + ∫ 2 3 3 2 Y + 9 2 - Y2 DY \u003d 7 4 Y2 - 7 4 Y12 + - Y3 3 + 3 Y2 4 + 9 2 Y2 3 \u003d 7 4 · 2 2 - 7 4 · 2 - 7 4 · 1 2 - 7 4 · 1 + + - 3 3 3 + 3 · 3 2 4 + 9 2 · 3 - - 2 3 + 3 · 2 2 4 + 9 2 · 2 \u003d 7 4 + 23 12 \u003d 11 3

Ako vidíte, hodnoty sa zhodujú.

Odpoveď: S (G) \u003d 11 3

Výsledok

Ak chcete nájsť oblasť obrázku, ktorá je obmedzená na zadané riadky, musíme vybudovať čiary v lietadle, nájsť body ich križovatky, aplikovať vzorec pre nájdenie oblasti. V tejto časti sme považovali za najčastejšie možnosti úloh.

Ak všimnete chybu v texte, vyberte ho a stlačte kláves CTRL + ENTER

Takže, čo bude potrebné, aby úspešne vyriešiť problém hľadania oblasti obrázku s pomocou integrálov:

Zručnosti Kompetentne vybudovať výkresy;
Schopnosť vyriešiť špecifickú integrál s pomocou známeho newton-leibnického vzorca;
Schopnosť "vidieť" ziskovejšie riešenie riešenia - t.j. Pochopte, ako v takomto prípade bude vhodnejšie vykonávať integráciu? Pozdĺž osi x (ox) alebo osi hry (OY)?
No, kde bez správnej výpočty?) To zahŕňa pochopenie, ako vyriešiť iný typ integrálov a správne numerické výpočty.

Algoritmus na riešenie úlohy výpočtu oblasti obrázku, obmedzené čiary:

2. Ak sú integračné limity jednoznačne špecifikované, nájdeme priesečníkové body grafov medzi sebou a pozeráme sa na to, či sa naše grafické riešenie s analytickým spôsobom zhoduje.

Príklad 1. y \u003d x2 - 3x + 3, x \u003d 1, x \u003d 3, y \u003d 0.

Príklad 2. . Vypočítajte oblasť tvaru, obmedzené čiary y \u003d x2 + 6x + 2, x \u003d -4, x \u003d -1, y \u003d 0.

Článok nie je dokončený.

V skutočnosti, aby sa našla oblasť obrázku, neexistuje žiadna znalosť neistého a definovaného integrálu. Úloha "Vypočítajte oblasť s pomocou špecifického integrálu" vždy znamená výstavbu výkresuPreto oveľa relevantnejšou otázkou bude vaše vedomosti a zručnosti stavebných výkresov. V tejto súvislosti je užitočné obnoviť v pamäti grafiky základných elementárnych funkcií a aspoň by ste mohli stavať rovno a hyperbola.

Curvilinear Lispesion sa nazýva plochá postava, ktorá je obmedzená na os, rovnú a kontinuálny plán na segmente funkcie, ktorá nezmení označenie v tomto intervale. Nech je toto číslo umiestnené nie menej Abscissa Axis:

Potom oblasť zakriveného lichobežníka je numericky rovná špecifickému integrálu. Každý konkrétny integrálny (ktorý existuje) má veľmi dobrý geometrický význam.

Z hľadiska geometrie je určitá integrálna oblasť.

T.j Špecifický integrál (ak existuje) geometricky zodpovedá ploche určitého tvaru. Zvážte napríklad špecifický integrál. Funkcia integrandu nastaví krivku na rovine, ktorá sa nachádza nad osou (ktoré priania môžu nakresliť výkres) a špecifický integrálny sám je numericky rovný ploche zodpovedajúceho zakriveného lichobežníka.

Príklad 1.

Ide o typickú formuláciu úloh. Prvý a najdôležitejší bod rozhodnutia - budovanie výkresu. A výkres sa musí vybudovať SPRÁVNY.

Pri budovaní výkresu odporúčam nasledujúci príkaz: najprv Je lepšie postaviť všetky rovné (ak sú) a len neskôr - Paraboly, hyperbola, plány iných funkcií. Funkčné grafy sú výhodnejšie vybudovať lektvar.

V tejto úlohe môže toto rozhodnutie vyzerať takto.
Vykonajte výkres (všimnite si, že rovnica nastaví os):

V zozname segmentov sa nachádza funkcia cez os, Takže:

Odpoveď:

Po dokončení úlohy je vždy užitočné pozrieť sa na kresbu a odhad, skutočný sa ukázal. V tomto prípade, "na oči" počítame počet buniek v kresbe - dobre, približne 9 sa letel, zdá sa, že pravdu. Je celkom jasné, že ak by sme mali, povedzme, odpovedzte: 20 štvorcových jednotiek, je zrejmé, že chyba je vykonaná niekde - na obrázku 20 buniek, to je zjavne namontované, od pevnosti tucet. Ak sa odpoveď ukázala negatívna, úloha sa tiež rozhodne nesprávne.

Príklad 3.

Vypočítajte oblasť tvaru, obmedzených línií a súradnicových osí.

Rozhodnutie: Vykonajte výkres:

Ak sa nachádza Curvilinear Trapezia pod osou(alebo nakoniec nie vyššia Táto os), potom jeho plocha možno nájsť podľa vzorca:

V tomto prípade:

Pozor! Nezamieňajte dva typy úloh:

1) Ak ste vyzvaní, aby ste vyriešili jednoduchý integrálny bez akéhokoľvek geometrického významu, potom to môže byť záporné.

2) Ak ste vyzvaní, aby ste našli číslo obrázku pomocou špecifického integrálu, potom je oblasť vždy pozitívna! To je dôvod, prečo v práve uvažovaný vzorec sa zobrazí mínus.

V praxi je obraz najčastejšie umiestnený v hornej a dolnej polovice rovine, a preto z najjednoduchších školských grafov prejdite na zmysluplné príklady.

Príklad 4.

Nájdite oblasť plochého postavy, obmedzené čiary ,.

RozhodnutieNajprv musíte nakresliť výkres. Všeobecne povedané, pri budovaní výkresu v úlohách do oblasti sa najviac zaujímame o priesečníky línií. Nájdite body priesečníka parabola a priame. To sa dá urobiť dvoma spôsobmi. Prvá metóda je analytická. Riešime rovnicu:

Takže nižšia integračná hranica, horná hranica integrácie.

Týmto spôsobom je lepšie, ak je to možné, nepoužívajte.

Je oveľa výhodnejšie a rýchlejšie vybudovať riadky linky, zatiaľ čo limity integrácie sú objasnené ako keby sami ". Avšak, analytický spôsob, ako nájsť limity po tom všetkom, je niekedy potrebné uplatňovať, ak je napríklad harmonogram dostatočne veľký, alebo vyškolená konštrukcia neodhalila integračné limity (môžu byť frakčné alebo ihracionálne). A taký príklad, zvážime tiež.

Vrátime sa k našej úlohe: racionálnejšie najprv postaviť priamku a len potom paraboly. Vykonajte výkres:

A teraz pracovný vzorec: Ak na segmente určitú nepretržitú funkciu viac alebo rovné Niektoré nepretržité funkcie, oblasť obrázku, obmedzená grafmi týchto funkcií a priamych, možno nájsť podľa vzorca:

Tu už nie je potrebné myslieť, kde je postava umiestnená - nad osou alebo pod osou, a zhruba, dôležité Čo je graf vyššie(vzhľadom na iný plán) a čo - nižšie.

V tomto príklade je zrejmé, že na segmente parabola je umiestnený nad rovno, a preto je potrebné odpočítať

Dokončenie riešenia môže vyzerať takto:

Požadovaná hodnota je obmedzená na parabola zhora a priame dno.
Na segmente podľa príslušného vzorca:

Odpoveď:

Príklad 4.

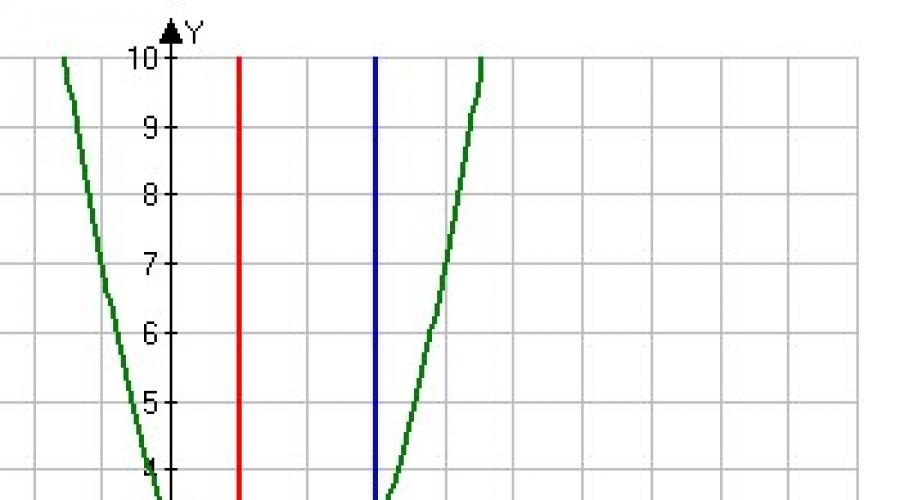
Vypočítajte oblasť tvaru, obmedzené čiary ,,,,

Rozhodnutie: Najprv si výkres:

Obrázok, ktorej oblasti potrebujeme nájsť, je v poriadku (Pozorne pozrite sa na stav - ako je číslo je obmedzené!). Ale v praxi, "Glitch" často vzniká vo všímavosti, ktoré potrebujete nájsť oblasť obrázku, ktorá je tieňovaná zelenou!

Tento príklad je stále užitočný a skutočnosť, že v nej je plocha obrázku zvážiť s použitím dvoch špecifických integrálov.

Naozaj:

1) Rovný program sa nachádza na segmente cez os;

2) Na segmente nad osi je graf hyperbolov.

Je jasné, že námestie môže (a potrebu) rozkladať, takže: