Zadanie B7 - Transformacja wyrażeń logarytmicznych i orientacyjnych. Wyrażenia logarytmiczne

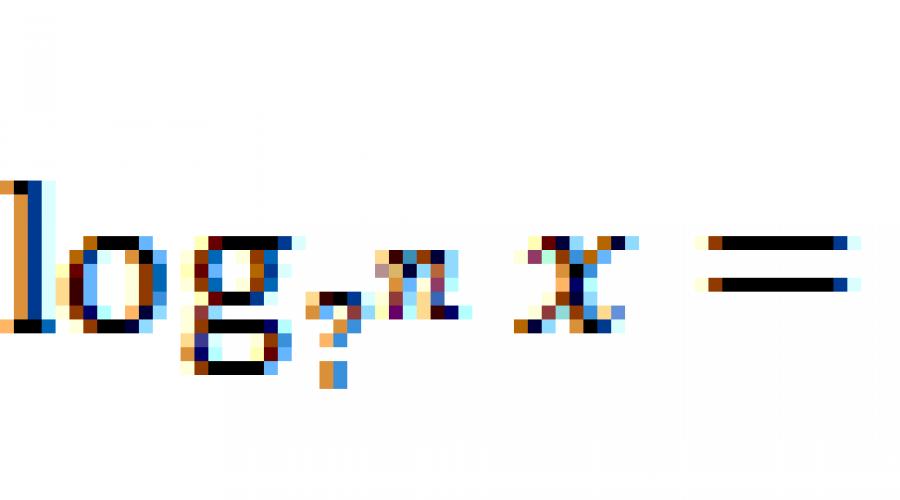
Rodzaj lekcji: Lekcja uogólnienia i systematyzacji wiedzy

Cele:

• aby uaktować wiedzę uczniów o logarytmach i ich nieruchomościach w ramach ogólnego powtórzenia i przygotowania do użycia;
• promowanie rozwoju aktywności umysłowej studentów, umiejętności stosowania wiedzy teoretycznej podczas wykonywania ćwiczeń;
• promowanie rozwoju właściwości osobistych studentów, umiejętności samokontroli i samooceny ich działalności; Kształcić ciężką pracę, pacjent, trwałość, niezależność.

Ekwipunek:komputer, projektor, prezentacja (Załącznik 1), Karty z pracą domową (można dołączyć plik z zadaniem w elektronicznym dzienniku).

Podczas zajęć

I. Moment organizacyjny. Powitanie, nastrój do lekcji.

II. Dyskusja zadanie domowe.

III. Tematy wiadomości i cele lekcji. Motywacja.(Slide 1) Prezentacja.

Nadal uogólniamy powtórzenie kursu matematycznego w ramach przygotowań do egzaminu. A dziś w lekcji porozmawiamy o logarytmach i ich właściwościach.

Zadania do obliczenia logarytmów i transformacji wyrażeń logarytmicznych są koniecznie obecne w materiałach kontrolnych i pomiarowych zarówno poziomów podstawowych, jak i profili. Dlatego celem naszej lekcji jest przywrócenie pomysłów na znaczenie koncepcji "logarytmu" i zaktualizować umiejętności, aby przekształcić wyrażenia logarytmiczne. Zapisz temat lekcji w notebookach.

IV. Aktualizacja wiedzy.

1. / Oral /Zacznij od, pamiętaj, co nazywa się logarytmem. (Slide 2)

(Logarytm dodatniej liczby b dla podstawy A (gdzie A\u003e 0, AH? 1) nazywa się wskaźnikiem stopnia, w którym numer A należy podjąć, aby uzyskać numer B)

Log a b \u003d n<-> A n \u003d b, (a\u003e 0 i 1, b\u003e 0)

Tak, "logarytm" jest "wskaźnikiem stopnia"!

(Slajd 3), a następnie n \u003d b może być przepisany jako \u003d B to główna tożsamość logarytmiczna.

Jeśli podstawa jest \u003d 10, logarytm nazywany jest dziesiętnym i oznaczonym LGB.

Jeśli A \u003d E, logarytm nazywa się naturalnym i oznaczają LNB.

2. / Napisany / (Slajd 4)Wypełnij pomiżenia, aby uzyskać wierną równość:

LOG? x + dziennik A? \u003d Dziennik? (? y)

Dziennik A? - Log? Y \u003d dziennik? (X /?)

Zarejestruj się x? \u003d Plog? (?)

Czek:

jeden; jeden; a, y, x; x, a, a, y; p, a, x.

Są to właściwości logarytmów. A także grupa nieruchomości: (Slide 5)

Czek:

a, 1, n, x; n, x, p, a; x, b, a, y; A, X, B; A, 1, B.

V. Praca doustna

(Slide 6) №1. Oblicz:

a b c d); mi).

Odpowiedzi : a) 4; b) - 2; o 2; d) 7; e) 27.

(Slide 7) №2. Znajdź X:

ale) ; b) (odpowiedzi: a) 1/4; b) 9).

Numer 3. Czy rozważa taki logarytm:

ale) ; b); w) ? (Nie)

Vi. Niezależna praca w grupach, silni uczniowie - konsultanci. (Slide 8)

# 1. Oblicz: .

Nr 2. Uprość:

# 3. Znajdź wartość wyrażenia, jeśli

№ 4. Uprość wyrażenie:

№ 5. Oblicz:

№ 6. Oblicz:

№ 7. Oblicz:

Nr 8. Oblicz:

Po wykonaniu - sprawdzanie i dyskusja na temat zebranego rozwiązania lub za pomocą dokumentów - kamery.

Vii. Rozwiązanie zadania zwiększonej złożoności(Silny student na pokładzie, reszta - w notebookach) (Slajd 9)

Znajdź wartość wyrażenia:

Viii. Zadanie domowe (na karty) zróżnicowane.(Slajd 10)

№1. Oblicz:

Wymieniona równość w konwersji wyrażeń z logarytmami są używane zarówno po prawej stronie, jak iw prawo.

Warto zauważyć, że zapamiętanie efektów z właściwości jest opcjonalne: Podczas przeprowadzania transformacji można wykonać z głównymi właściwościami logarytmów i innych faktów (na przykład, w tym z B≥0), z których odpowiednie Konsekwencje przepływają. "Efekt uboczny" tego podejścia jest manifestujący, że decyzja będzie nieco dłuższa. Na przykład, aby zrobić bez dochodzenia, który jest wyrażony przez wzór I repelly tylko z głównych właściwości logarytmów, będziesz musiał przeprowadzić łańcuch transformacji następującego typu: .

To samo można powiedzieć o ostatniej nieruchomości z powyższej listy, co odpowiada formule Ponieważ wynika również z głównych właściwości logarytmów. Najważniejszą rzeczą do zrozumienia, że \u200b\u200bzawsze istnieje możliwość pozytywnej liczby z logarytmem w wskaźniku, aby zmienić fundament stopnia i numer pod znakiem logarytm. Ze względu na sprawiedliwość, zauważamy, że przykłady, które oznaczają realizację transformacji takiego rodzaju, są rzadkie w praktyce. Dajemy kilka przykładów poniżej tekstu.

Transformacja wyrażeń numerycznych z logarytmami

Właściwości logarytmów pamiętały, teraz nadszedł czas, aby nauczyć się stosować ich w praktyce, aby przekształcić wyrażenia. Naturalnie zaczynają się od transformacji wyrażeń numerycznych, a nie wyrażenia z zmiennymi, ponieważ są one wygodniejsze i łatwiejsze do poznania podstaw. Zrobimy więc i zacząć od bardzo prostych przykładów, aby dowiedzieć się, jak wybrać żądaną własność logarytmu, ale będziemy stopniowo komplikować przykłady, aż do momentu, gdy trzeba użyć kilku nieruchomości z rzędu, aby uzyskać wynik końcowy.

Wybór pożądanych właściwości logarytmów

Właściwości logarytmów nie są tak małe, a jasne jest, że musisz być w stanie wybrać z nich odpowiedni, co w tym konkretnym przypadku doprowadzi do pożądanego wyniku. Zwykle trudno jest to zrobić, porównując typ transformowanego logarytmu lub ekspresji z widokami lewej i prawej części formuł wyrażających właściwości logarytmów. Jeśli lewa lub prawa strona jednego z formuł pokrywa się z danym logarytmem lub wyrażeniem, najprawdopodobniej jest to ta właściwość, która musi być stosowana podczas konwersji. Poniższe przykłady są wyraźnie zademonstrowane.

Zacznijmy od przykładów konwersji wyrażeń przy użyciu definicji logarytmu, który odpowiada formule a dziennik A B \u003d B, A\u003e 0, A ≠ 1, B\u003e \u200b\u200b0.

Przykład.

Oblicz, jeśli to możliwe: a) 5 LOG 5 4, B) 10 LG (1 + 2 · π), b) , D) 2 dziennik 2 (-7), e).

Decyzja.

W przykładzie, pod literą a), struktura dziennika A B jest wyraźnie widoczna, gdzie A \u003d 5, B \u003d 4. Liczby te spełniają warunki A\u003e 0, A ≠ 1, B\u003e \u200b\u200b0, dzięki czemu można użyć równości dziennika a b \u003d b. Mamy 5 dziennika 5 4 \u003d 4.

b) tutaj A \u003d 10, B \u003d 1 + 2 · π, warunki A\u003e 0, A ≠ 1, B\u003e \u200b\u200b0. W tym przypadku istnieje równość 10 LG (1 + 2 · π) \u003d 1 + 2 μl.

c) A w tym przykładzie mamy do czynienia z stopniem dziennika A B, gdzie i B \u003d LN15. Więc .

Pomimo przynależności do tego samego typu dziennika A B (tutaj A \u003d 2, B \u003d -7), wyrażenie pod literą d) nie można przekształcić za pomocą wzoru A dziennik A B \u003d B. Powodem jest to, że nie ma sensu, ponieważ zawiera numer ujemny pod znakiem logarytmu. Co więcej, liczba b \u003d -7 nie spełnia warunku B\u003e 0, co nie pozwala uciekać się do formuły A dziennik A B \u003d B, ponieważ wymaga spełnienia warunków A\u003e 0, A ≠ 1, B \u003e 0. Niemożliwe jest, aby porozmawiać o obliczeniu wartości 2 dziennika 2 (-7). W tym przypadku nagrywanie 2 dziennik 2 (-7) \u003d -7 będzie błędem.

Podobnie, w przykładzie pod literą d), nie można wprowadzić rozwiązania Ponieważ początkowa ekspresja nie ma sensu.

Odpowiedź:

a) 5 LOG 5 4 \u003d 4, B) 10 LG (1 + 2 · π) \u003d 1 + 2 · π, c) , d), e) wyrażenia nie ma sensu.

Często przydatne jest do konwersji, w której liczba dodatnia jest prezentowana w postaci stopnia dowolnej pozytywnej i innej liczby z logarytmem w wskaźniku. Opiera się na tej samej definicji logarytmu dziennika A B \u003d B, A\u003e 0, A ≠ 1, B\u003e \u200b\u200b0, ale formuła jest stosowana do prawej strony, która jest w formularzu B \u003d a b. Na przykład, 3 \u003d e ln3 lub 5 \u003d 5 dziennika 5 5.

Przejdź do aplikacji właściwości logarytmów do konwersji wyrażeń.

Przykład.

Znajdź wartość wyrażenia: a) dziennik -2 1, b) log 1 1, C) Dziennik 0 1, D) Dziennik 7 1, E) LN1, E) LG1, G) Dziennik 3,75, S) Dziennik 5 π 7 1.

Decyzja.

W przykładach pod literami A), b) i c) wyrażenia log -2 1, dziennik 1 1, dziennik 0 1, co nie ma sensu, ponieważ u podstawy logarytmu nie powinno być liczbą ujemną, Zero lub jednostka, ponieważ określiliśmy logarytm tylko dla pozytywnych i różnych od jednostki podstawowej. Dlatego w przykładach A) - C) nie może istnieć żadne pytanie o znalezienie wartości ekspresyjnej.

We wszystkich innych zadaniach jest oczywisty, że istnieją dodatnie i różne liczby z jednostki 7, E, 10, 3,75 i 5 μl 7, i pod objawami logarytmów wszędzie są jednostki. I znamy właściwość jednostki logarytm: dziennik A 1 \u003d 0 dla dowolnego A\u003e 0, A ≠ 1. Zatem wartości wyrażeń b) - e) są równe zero.

Odpowiedź:

a), b), c) wyrażenia nie ma sensu, d) log 7 1 \u003d 0, D) LN1 \u003d 0, E) LG1 \u003d 0, G) Dziennik 3,75 1 \u003d 0, H) Dziennik 5 · E 7 1 \u003d 0.

Przykład.

Oblicz: a), b) lne, c) lg10, d) lOG 5 · π 3 -2 (5 μl 3 -2), e) log -3 (-3), e) log 1 1.

Decyzja.

Oczywiste jest, że musimy skorzystać z właściwości logarytmu podstawy, co odpowiada formule dziennika A \u003d 1 na A\u003e 0, a ≠ 1. Rzeczywiście, w zadaniach pod wszystkimi literami, numer pod znakiem logarytmu pokrywa się ze swoją podstawą. W ten sposób chcę natychmiast powiedzieć, że znaczenie każdej z określonych wyrażeń wynosi 1. Jednak nie trzeba się spieszyć z wnioskami: w zadaniach pod literami A) - d) wartości wyrażeń są naprawdę równe jednemu, aw zadaniach d) i e) początkowe wyrażenia nie tworzą Poczucie, dlatego nie można powiedzieć, że wartości tych wyrażeń są 1.

Odpowiedź:

a), b) lne \u003d 1, c) lg10 \u003d 1, d) lOG 5 · π 3 -2 (5 μl 3 -2) \u003d 1, D), e) wyrażenia nie ma sensu.

Przykład.

Znajdź wartość: a) dziennik 3 3 11, b) , c), d) log -10 (-10) 6.

Decyzja.

Oczywiście pod objawami logarytmów istnieją jakieś stopnie fundacji. Na tej podstawie rozumiemy, że jest to przydatne dla nas tutaj stopień fundamentu: Log A P \u003d P, gdzie A\u003e 0, A ≠ 1 i P jest dowolny ważny numer. Biorąc pod uwagę, mamy następujące wyniki: a) dziennik 3 3 11 \u003d 11, b) , w) . Czy można nagrywać podobną równość dla przykładu pod literą d) rodzaju dziennika -10 (-10) 6 \u003d 6? Nie, jest to niemożliwe, ponieważ log -10 (-10) 6 nie ma sensu.

Odpowiedź:

a) dziennik 3 3 11 \u003d 11, b) , w) , D) Wyrażenie nie ma sensu.

Przykład.

Wyobraź sobie wyrażenie w formie sumy lub różnicy logarytmów na tej samej podstawie: a) , b), c) lg ((- 5) · (-12)).

Decyzja.

a) Pod znakiem logarytm jest praca i znamy właściwość logarytmu pracy kłody A (X · Y) \u003d Log AX + Log AY, A\u003e 0, A ≠ 1, X\u003e 0, Y\u003e 0. W naszym przypadku liczba u podstawy logarytmu i numer w pracy jest pozytywna, czyli spełnienie warunków wybranej nieruchomości, więc możemy spokojnie nałożyć: .

b) Tutaj używamy właściwości logarytmu prywatnego, gdzie A\u003e 0, A ≠ 1, X\u003e 0, Y\u003e 0. W naszym przypadku podstawa logarytmu jest pozytywną numerem E, numerator i mianownik Π są dodatnie, co oznacza, że \u200b\u200bwarunki nieruchomości są satysfakcjonujące, więc mamy prawo do korzystania z wybranej formuły: .

c) Najpierw zauważamy, że wyrażenie LG ((- 5) · (-12)) ma sens. Ale w tym samym czasie, dla niego nie mamy prawa zastosowania formuły logarytmowej pracy dziennika A (X · Y) \u003d Log AX + Log AY, A\u003e 0, A ≠ 1, X\u003e 0, Y\u003e 0, ponieważ liczby -5 i -12 - negatywne i nie spełniają warunków x\u003e 0, y\u003e 0. Oznacza to, że nie można przeprowadzić takiej konwersji: lG ((- 5) · (-12)) \u003d LG (-5) + LG (-12). I co robić? W takich przypadkach początkowa ekspresja wymaga wstępnej transformacji, która pozwala uciec od liczb ujemnych. Porozmawiamy o takich przypadkach transformacji wyrażeń z negatywnymi liczbami pod znakiem logarytm szczegółowo w jednym z następujących przykładów, które są zrozumiałe, a bez wyjaśnienia: lG ((- 5) · (-12)) \u003d LG (5 · 12) \u003d LG5 + LG12.

Odpowiedź:

ale) b) , C) LG ((- 5) · (-12)) \u003d LG5 + LG12.

Przykład.

Uprość wyrażenie: a) dziennik 3 0,25 + dziennik 3 16 + dziennik 3 0,5, b).

Decyzja.

Tutaj pomożemy wszystkim te same właściwości logarytmu pracy i logarytmu prywatnego, którego używaliśmy w poprzednich przykładach, tylko teraz zastosujemy je do prawej do lewej. Oznacza to, że ilość logarytmów przekształca się w logarytm pracy, a różnica między logarytmami - w logarytmie prywatnego. Mieć
ale) dziennik 3 0,25 + dziennik 3 16 + dziennik 3 0.5 \u003d dziennik 3 (0,25 · 16 · 0,5) \u003d dziennik 3 2.
b) .

Odpowiedź:

ale) dziennik 3 0,25 + dziennik 3 16 + dziennik 3 0.5 \u003d dziennik 3 2b) .

Przykład.

Pozbądź się zasięgu pod znakiem logarytmu: a) log 0,7 5 11, b) , C) Dziennik 3 (-5) 6.

Decyzja.

Łatwo jest zobaczyć, że mamy do czynienia z wyrażeniami dziennika A b p. Odpowiednia właściwość logarytmu ma rodzaj dziennika A B P \u003d P · Log A B, gdzie A\u003e 0, A ≠ 1, B\u003e \u200b\u200b0, P jest dowolny prawidłowy numer. Oznacza to, że podczas wykonywania warunków A\u003e 0, A ≠ 1, B\u003e \u200b\u200b0 z logarytmu stopnia dziennika A B P, możemy przenieść się do produktu P · Log A B. Przeprowadzimy tę konwersję z określonymi wyrażeniami.

a) W tym przypadku A \u003d 0,7, B \u200b\u200b\u003d 5 i p \u003d 11. Tak dziennik 0.7 5 11 \u003d 11 · Log 0,7 5.

b) Tutaj wykonywane są warunki A\u003e 0, A ≠ 1, B\u003e \u200b\u200b0. w związku z tym

c) Dziennik ekspresji 3 (-5) 6 ma tę samą strukturę dziennika A B P, A \u003d 3, B \u003d -5, p \u003d 6. Ale dla B, warunek B\u003e 0 nie jest zadowolony, co uniemożliwia użycie dziennika A B P \u003d P · Log A B. Więc nie można poradzić sobie z zadaniem? Jest to możliwe, ale wymagane jest wstępnie konwertujące wyrażenie, porozmawiamy szczegółowo poniżej w punkcie nagłówka. Decyzja będzie: lOG 3 (-5) 6 \u003d dziennik 3 5 6 \u003d 6 · dziennik 3 5.

Odpowiedź:

a) log 0,7 5 11 \u003d 11 · dziennik 0,7 5,
b)
c) log 3 (-5) 6 \u003d 6 · dziennik 3 5.

Dość często formuła logarytmu stopnia podczas transformacji jest konieczna do zastosowania w prawo do lewej jak p · Log A B \u003d Log A B P (wymaga to wydajności tych samych warunków dla A, B i P). Na przykład 3 · LN5 \u003d LN5 3 i LG2 · Log 2 3 \u003d Log 2 3 LG2.

Przykład.

a) Oblicz wartość dziennika 2 5, jeśli wiadomo, że LG2≈0,3010 i LG5≈0,6990. b) Przedstaw frakcję w postaci logarytmu na podstawie 3.

Decyzja.

a) Wzór przejścia do nowej podstawy logarytmu pozwala na reprezentowanie tego logarytmu w postaci stosunku logarytmów dziesiętnych, których wartości są nam znane :. Pozostaje tylko w celu przeprowadzenia obliczeń, mamy .

b) Tutaj wystarczy skorzystać z przejścia do nowej podstawy i zastosować go do prawej strony, czyli w formie . Otrzymać .

Odpowiedź:

a) dziennik 2 5≈2,3223, b) .

Na tym etapie jesteśmy wystarczająco skrupulatnie uważany za konwersję najbardziej prostych wyrażeń przy użyciu głównych właściwości logarytmów i definicji logarytmu. W takich przykładach musieliśmy zastosować jakiś własność i nic więcej. Teraz z spokojnym sumieniem można przenieść się do przykładów, której transformacja wymaga użycia kilku właściwości logarytmów i innych dodatkowych transformacji. Pójdziemy do następnego akapitu. Ale przed tym, krótko, krótko skupimy się na przykładach konsekwencji głównych właściwości logarytmów.

Przykład.

a) Pozbądź się korzenia pod znakiem logarytmu. b) Konwertuj frakcję w logarytmie na bazie 5. c) Często z stopni pod znakiem logarytmu iw jego fundamencie. d) Oblicz wartość wyrażenia . e) Wymień ekspresję stopnia z podstawą 3.

Decyzja.

a) Jeśli pamiętasz o konsekwencji właściwości logarytmu Możesz natychmiast odpowiedzieć: .

b) Używamy formuły Prawo do wyszliśmy .

c) W tym przypadku wynik prowadzi formułę . Otrzymać .

d) I tutaj wystarczy zastosować konsekwencję, że formuła jest odpowiedzialna . Więc .

e) logarytm nieruchomości Pozwala nam osiągnąć pożądany wynik: .

Odpowiedź:

ale) . b) . w) . re) . mi) .

Sekwencyjne używanie kilku właściwości

Prawdziwe zadania związane z transformacją wyrażeń przy użyciu właściwości logarytmów są zazwyczaj bardziej skomplikowane przez tych, których angażujemy w poprzednim akapicie. W nich, z reguły wynik nie jest jednym krokiem, a rozwiązanie jest już w stałym zastosowaniu jednej nieruchomości po drugiej, wraz z dodatkowymi transformacjami tożsamości, takich jak ujawnienie nawiasów, przynosząc podobne warunki, zmniejszenie frakcji itp . Zbrojmy się bliżej takich przykładów. Nie ma tego nic trudnego, główną rzeczą jest działanie starannie i konsekwentnie, obserwując procedurę wykonania działań.

Przykład.

Oblicz wartość wyrażenia (Dziennik 3 15-dziennik 3 5) · 7 dziennika 7 5.

Decyzja.

Różnica logarytmów w nawiasach dla właściwości logarytmu prywatnego można zastąpić dziennikiem logarytmem 3 (15: 5) i dalej obliczają jego dziennik wartości 3 (15: 5) \u003d dziennik 3 3 \u003d 1. A wartość wyrażenia 7 LOG 7 5 z definicji logarytmu jest równa 5. Zastępuj te wyniki w oryginalnym wyrażeniu, otrzymujemy (dziennik 3 15-dziennik 3 5) · 7 Log 7 5 \u003d 1 · 5 \u003d 5.

Daj nam rozwiązanie bez wyjaśnienia:
(Dziennik 3 15-dziennik 3 5) · 7 dziennika 7 5 \u003d dziennik 3 (15: 5) · 5 \u003d
\u003d dziennik 3 3 · 5 \u003d 1 · 5 \u003d 5.

Odpowiedź:

(dziennik 3 15-dziennik 3 5) · 7 dziennika 7 5 \u003d 5.

Przykład.

Jaka jest wartość dziennika wyrażenia numerycznego 3 dziennika 2 2 3 -1?

Decyzja.

Najpierw przekształcamy logarytm, który znajduje się pod znakiem logarytmu, zgodnie z formułą logarytmową: dziennik 2 2 3 \u003d 3. Zatem dziennik 3 dziennik 2 2 3 \u003d dziennik 3 3 i dalszy dziennik 3 3 \u003d 1. Więc dziennik 3 dziennik 2 2 3 -1 \u003d 1-1 \u003d 0.

Odpowiedź:

lOG 3 LOG 2 2 3 -1 \u003d 0.

Przykład.

Uprościć wyrażenie.

Decyzja.

Formuła przejściowa do nowej podstawy logarytmu umożliwia relację logarytmów do jednej podstawy do reprezentowania jako dziennika 3 5. W takim przypadku początkowe wyrażenie przyjmie formę. Z definicji logarytmu 3 dziennika 3 5 \u003d 5, to jest I wartość uzyskanego wyrażenia, ze względu na tę samą definicję logarytmu, jest dwa.

Oto krótka wersja rozwiązania, które zwykle podano: .

Odpowiedź:

.

Aby uzyskać płynne przejście do następujących informacji o pozycji, spójrzmy na wyrażenia 5 2 + LOG 5 3 i LG0.01. Ich struktura nie nadaje się do żadnej z właściwości logarytmów. Więc co się stanie, nie można ich przekształcić za pomocą właściwości logarytmów? Jest to możliwe, jeśli można przeprowadzić wstępne transformacje, które przygotowują te wyrażenia do stosowania właściwości logarytmów. Więc 5 2 + LOG 5 3 \u003d 5 2 · 5 LOG 5 3 \u003d 25 · 3 \u003d 75, i LG0.01 \u003d LG10 -2 \u003d -2. Wtedy szczegółowo zrozumiemy, jak takie szkolenie wyrażeń jest przeprowadzane.

Przygotowanie wyrażeń do zastosowania właściwości logarytmów

Logarytmy w składzie transformowanego wyrażenia bardzo często różnią się od lewej i prawej części formuł odpowiadających właściwości logarytmów. Ale nie mniej niż transformacja tych wyrażeń oznacza wykorzystanie właściwości logarytmów: użycie ich wymaga wstępnego przygotowania. Przygotowanie to prowadzi pewne identyczne transformacje wiodące logarytmy do formularza, wygodne w stosowaniu właściwości.

W przypadku uczciwości zauważamy, że prawie wszelkie transformacje wyrażeń może działać jako przemiany wstępne, od banalnego siłownika takich warunków do stosowania wzorów trygonometrycznych. Jest to zrozumiałe, ponieważ transformowane wyrażenia mogą zawierać dowolne obiekty matematyczne: wsporniki, moduły, frakcje, korzenie, stopnie itp. W ten sposób musisz być gotowy do wykonania jakiegokolwiek potrzebnej konwersji na dalsze możliwość korzystania z właściwości logarytmów.

Natychmiast powiedzmy, że w tym momencie nie ustawiamy sobie zadania, aby sklasyfikować i demontować wszystkie wyobrażalne przemiany wstępne, które dodatkowo stosuje właściwości logarytmów lub definicji logarytmu. Tutaj znajdziemy tylko na czterech z nich, które są najbardziej charakterystyczne i najczęściej występują w praktyce.

A teraz szczegółowo o każdym z nich, po czym jako część naszego tematu pozostanie tylko do radzenia sobie z transformacją wyrażeń ze zmiennymi pod objawami logarytmów.

Wybór stopni pod znakiem logarytmu iw jego fundamencie

Zacznijmy natychmiast od tego przykładu. Pozwól nam być logarytmem. Oczywiście w tej formie jego struktura nie musi używać właściwości logarytmów. Czy w jakiś sposób możesz przekonwertować ten wyrażenie, aby go uprościć, a nawet lepiej obliczyć swoją wartość? Aby odpowiedzieć na to pytanie, spójrzmy starannie w liczbie 81 i 1/9 w kontekście naszego przykładu. Łatwo jest powiedzieć, że numery te pozwalają na reprezentację stopnia numer 3, 81 \u003d 3 4 i 1/9 \u003d 3 -2. W tym przypadku początkowe logarytm przedstawiono w formie i możliwości zastosowania formuły . Więc, .

Analiza demontażowego przykładu tworzy następującą myśl: Jeśli to możliwe, możesz spróbować podkreślić stopień pod znakiem logarytmu iw fundamencie, aby zastosować własność logarytmu lub jego konsekwencji. Pozostaje tylko dowiedzieć się, jak przeznaczyć te stopnie. Podajmy kilka zaleceń w tej sprawie.

Czasami jest to raczej oczywiste, że liczba pod znakiem logarytmu i / lub w jej fundamencie jest niektóre z całego stopnia, jak w powyższym przykładzie. Praktycznie nieustannie muszą poradzić sobie z wykrywaniem TWO, które były dobrze przemyślane: 4 \u003d 2 2, 8 \u003d 2, 16 \u003d 2 4, 32 \u003d 2 5, 64 \u003d 2 6, 128 \u003d 2 7, 256 \u003d 2 8 , 512 \u003d 2 9, 1024 \u003d 2 10. Można to powiedzieć o stopniu potrójnego: 9 \u003d 3 2, 27 \u003d 3 3, 81 \u003d 3 4, 243 \u003d 3 5, ... Ogólnie, nie boli, jeśli będzie to przed naszymi oczami tabela stopni liczb naturalnych w kilkunasie. Nie jest to również trudne do pracy z stopniami całkowitymi dziesięciu, sto tysięcy itp.

Przykład.

Oblicz wartość lub uprościć wyrażenie: a) LOG 6 216, B), C) LOG 0,000001 0,001.

Decyzja.

a) Jest oczywiste, że 216 \u003d 6 3, dlatego dziennik 6 216 \u003d dziennik 6 6 3 \u003d 3.

b) Tabela stopni liczb naturalnych pozwala przedstawić numery 343 i 1/243 w postaci stopni 7 3 i 3 -4, odpowiednio. Dlatego możliwe jest przestrzeganie następującej transformacji danego logarytmu:

c) jako 0,000001 \u003d 10 -6 i 0,001 \u003d 10 -3, a następnie lOG 0,000001 0,001 \u003d LOG 10 -6 10 -3 \u003d (- 3) / (- 6) \u003d 1/2.

Odpowiedź:

a) log 6 216 \u003d 3, b) , C) LOG 0,000001 0,001 \u003d 1/2.

W bardziej złożonych przypadkach, aby podkreślić stopnie liczb muszą uciekać się do.

Przykład.

Konwertuj wyrażenie do prostszego typu dziennika 3 648 · dziennik 2 3.

Decyzja.

Zobaczmy, co jest rozkładem wielu 648 na proste czynniki:

To znaczy 648 \u003d 2 3 · 3 4. W ten sposób, dziennik 3 648 · dziennik 2 3 \u003d dziennik 3 (2 3 · 3 4) · dziennik 2 3.

Teraz logarytm prac przekształca się w ilości logarytmów, po czym stosuje się właściwości logarytmu stopnia:
lOG 3 (2 3 · 3 4) · Log 2 3 \u003d (dziennik 3 2 3 + dziennik 3 3 4) · dziennik 2 3 \u003d
\u003d (3 · dziennik 3 2 + 4) · dziennik 2 3.

Ze względu na dochodzenie z własności logarytmu, do którego odpowiedzialna jest formuła Produkt Log32 · Log23 to praca, a wiadomo, że jest jedną. Biorąc pod uwagę, otrzymujemy 3 · Log 3 2 · Log 2 3 + 4 · Log 2 3 \u003d 3 · 1 + 4 · Log 2 3 \u003d 3 + 4 · Log 2 3.

Odpowiedź:

dziennik 3 648 · dziennik 2 3 \u003d 3 + 4 · dziennik 2 3.

Dość często wyrażenia pod znakiem logarytmowym iw jej fundamencie są robocze lub stosunki korzeni i / lub stopni niektórych liczb, na przykład. Takie wyrażenia mogą być reprezentowane jako stopień. W tym celu przejście z korzeni do stopni i stosowane. Te konwersje pozwalają podświetlić stopnie pod znakiem logarytm i jego podstawy, po czym stosujesz właściwości logarytmów.

Przykład.

Oblicz: a) , b).

Decyzja.

a) Wyrażenie u podstawy logarytmu jest produktem stopni o tych samych podstawach, zgodnie z odpowiednią własnością stopni, mamy 5 2 · 5 -0,5 · 5 -1 \u003d 5 2-0,5-1 \u003d 5 0,5.

Teraz przekształcamy frakcję pod znakiem logarytmu: obracamy się z korzenia do stopnia, po czym użyjemy właściwości stopni z tymi samymi podstawami: .

Pozostaje zastąpienie wyników uzyskanych w początkowej ekspresji, użyj formuły i zakończ transformacje:

b) Od 729 \u003d 3 6, 1/9 \u003d 3 -2, a następnie początkowe wyrażenie można przepisać w formularzu.

Następnie zastosuj właściwość korzenia z stopnia, przeprowadzamy przejście od korzenia do stopnia i użyć właściwości stosunku stopnia, aby przekonwertować logarytm do stopnia: .

Biorąc pod uwagę ostatni wynik, mamy .

Odpowiedź:

ale) , b).

Oczywiste jest, że ogólnie, w celu uzyskania stopni pod znakiem logarytmu, a w fundamencie mogą być wymagane różne transformacje różnych wyrażeń. Dajemy kilka przykładów.

Przykład.

Jaka jest wartość wyrażenia: a) b) .

Decyzja.

Dlatego zauważamy, że określona ekspresja ma formę dziennika A B P, gdzie A \u003d 2, B \u003d X + 1 i P \u003d 4. Numeryczne wyrażenia takiego rodzaju byliśmy konwertowane przez właściwość logarytmu w zakresie dziennika ABP \u003d P · Zaloguj AB, a zatem, z danym wyrażeniem, chcę zrobić to samo, a z dziennika 2 (x + 1) 4 Idź do 4 · Log 2 (x + 1). A teraz obliczmy wartość początkowej ekspresji, a wyrażenie uzyskane po transformacji, na przykład, z X \u003d -2. Mieć dziennik 2 (-2 + 1) 4 \u003d dziennik 2 1 \u003d 0, i 4 · Log 2 (-2 + 1) \u003d 4 · Log 2 (-1) - Nie oznacza wyrażenia. Powoduje to naturalne pytanie: "Co zrobiliśmy źle"?

I powód jest następujący: Wykonaliśmy dziennik transformacji 2 (x + 1) 4 \u003d 4 · dziennik 2 (x + 1), na podstawie formuły dziennika ABP \u003d P · Log AB, ale mamy prawo zastosować to Formuła tylko w przypadku warunku A\u003e 0, A ≠ 1, B\u003e \u200b\u200b0, P - dowolny prawidłowy numer. Oznacza to, że konwersja wykonana przez nas ma miejsce, jeśli x + 1\u003e 0, który jest taki sam x\u003e -1 (dla A i P - warunki są wykonane). Jednak w naszym przypadku zmienna OTZ X do wyrażenia początkowej składa się nie tylko z interwału X\u003e -1, ale także z okresu x<−1 . Но для x<−1 мы не имели права осуществлять преобразование по выбранной формуле.

Potrzeba wzięcia pod uwagę ...

Będziemy nadal demontować transformację dziennika 2 (x + 1) 4 wybranych wyrażeń przez nas, a teraz zobaczmy, co dzieje się z OTZ podczas przenoszenia do wyrażenia 4 · Log 2 (x + 1). W poprzednim akapicie znaleźliśmy nawet ekspresję źródła - jest to zestaw (-∞, -1) ∪ (-1, + ∞). Teraz znajdziemy obszar dopuszczalnych wartości zmiennej X dla wyrażenia 4 · Log 2 (x + 1). Jest określony przez warunek X + 1\u003e 0, który odpowiada zestawowi (-1, + ∞). Oczywiście podczas przemieszczania się z dziennika 2 (x + 1) 4 do 4 · dziennik 2 (x + 1), obszar prawidłowych wartości występuje. I zgodziliśmy się uniknąć transformacji prowadzących do zwężenia OTZ, ponieważ może to prowadzić do różnych negatywnych konsekwencji.

Warto zauważyć tutaj, że przydatne jest kontrolowanie OTZ na każdym etapie transformacji i zapobiec zwężeniu. A jeśli nagle, na pewnym etapie transformacji, pojawił się zwężenie OST, warto szukać bardzo ostrożnie, a to, czy ta transformacja jest dopuszczalna i czy mamy prawo go wykonywać.

Na przykład, powiedzmy, że w praktyce zazwyczaj konieczne jest współpracę z wyrażeniami, których zmienne OTZ są takie, że podczas przeprowadzania transformacji użyj właściwości logarytmów bez ograniczeń w formularzu już nam znanych, a obie od lewej do w prawo i prawo do lewej. Szybko się do tego przyzwyczaisz, a ty zaczynasz wykonywać transformacje mechanicznie, bez myślenia i czy można je prowadzić. W takich chwilach, jak rozładowany, slipper bardziej złożone przykłady, w których niedokładne zastosowanie właściwości logarytmów prowadzi do błędów. Więc musisz zawsze być na czeku i podążaj, że nie ma zwężania OTZ.

Nie boli osobno wybrać główne transformacje na podstawie właściwości logarytmów, które należy przeprowadzić bardzo ostrożnie, co może prowadzić do zwężenia OTZ, aw wyniku - do błędów:

Niektóre transformacje wyrażeń zgodnie z właściwościami logarytmów mogą prowadzić do odwrotnej - rozszerzanie OTZ. Na przykład przejście od 4 · dziennik 2 (x + 1), aby zalogować 2 (X + 1) 4 rozszerza nieparzyste z zestawu (-1, + ∞) do (-∞, -1) ∪ (-1, + ∞). Takie przemiany występują, jeśli pozostają w czasie ODZD dla początkowej ekspresji. Dlatego jedyna wspomniana konwersja 4 · dziennik 2 (x + 1) \u003d dziennik 2 (x + 1) 4 odbywa się na zmiennej OTZ X dla oryginalnego wyrażenia 4 · Log 2 (x + 1), czyli, z X + 1\u003e 0, który jest taki sam (-1, + ∞).

Teraz, że omówiliśmy niuanse, dla których musisz zwrócić uwagę na przynoszenie wyrażeń z zmiennymi z wykorzystaniem właściwości logarytmów, pozostaje dowiedzieć się, jak prawidłowo należy przeprowadzić te przemiany.

X + 2\u003e 0. Czy działa w naszym przypadku? Aby odpowiedzieć na to pytanie, spójrz na zmienną OTZ x. Jest określony przez system nierówności który jest równoważny warunkom X + 2\u003e 0 (w razie potrzeby, zobacz artykuł rozwiązywanie systemów nierówności). W ten sposób możemy spokojnie stosować właściwość logarytmu.

Mieć
3 · LG (X + 2) 7-LG (X + 2) -5 · LG (x + 2) 4 \u003d
\u003d 3 · 7 · LG (X + 2) -Lg (X + 2) -5 · 4 · LG (x + 2) \u003d
\u003d 21 · LG (X + 2) -Lg (x + 2) -20 · LG (X + 2) \u003d
\u003d (21-1-20) · LG (x + 2) \u003d 0.

Możesz działać i w przeciwnym razie korzyść OTZ pozwala na przykład, na przykład:

Odpowiedź:

3 · LG (X + 2) 7-LG (X + 2) -5 · LG (x + 2) 4 \u003d 0.

A co robić, gdy warunki towarzyszącego właściwości logarytmów nie są zadowoleni? Zajmymy się z tym na przykładach.

Załóżmy od nas, aby uprościć ekspresję LG (X + 2) 4 -Lg (x + 2) 2. Transformacja tego wyrażenia, w przeciwieństwie do wyrażenia z poprzedniego przykładu, nie zezwala na dziennik stopnia logarytmu. Dlaczego? OTZ zmienna X w tym przypadku jest kombinacją dwóch szczelin X\u003e -2 i X<−2 . При x>-2 Możemy spokojnie zastosować nieruchomość logarytm i działać jako demontowane powyżej: lG (X + 2) 4-LG (X + 2) 2 \u003d 4 · LG (X + 2) -2 · LG (x + 2) \u003d 2 · LG (x + 2). Ale OTZ zawiera kolejny okres x + 2<0 , для которого последнее преобразование будет некорректно. Что же делать при x+2<0 ? В подобных случаях на помощь приходит . Определение модуля позволяет выражение x+2 при x+2<0 представить как −|x+2| . Тогда при x+2<0 от lg(x+2) 4 −lg(x+2) 2 переходим к lG (- | X + 2 |) 4 -LG (- | X + 2 |) 2 I dalej właściwościami stopnia do LG | X + 2 | 4 -Lg | x + 2 | 2. Uzyskane wyrażenie może być konwertowane przez właściwość logarytmu, ponieważ | x + 2 |\u003e 0 dla dowolnych wartości zmiennej. Mieć lG | X + 2 | 4 -Lg | x + 2 | 2 \u003d 4 · LG | X + 2 | -2 · LG | X + 2 | \u003d 2 · LG | X + 2 |. Teraz możesz uwolnić się od modułu, gdy wykonał swoją pracę. Ponieważ prowadzimy konwersję na x + 2<0 , то 2·lg|x+2|=2·lg(−(x+2)) . Итак, можно считать, что мы справились с поставленной задачей. Ответ: . Полученный результат можно записать компактно с использованием модуля как .

Rozważ inny przykład, aby praca z modułami stała się znajoma. Niech pomyślaliśmy z wyrażenia Idź do sumy i różnicy między logarytmami liniowych odbijania X-1, X-2 i X-3. Najpierw znajdziemy ...

W przedziale (3, + ∞) wartości wyrażeń X-1, X-2 i X-3 są dodatni, więc spokojnie stosujemy właściwości logarytmu sum i różnic:

W przedziale (1, 2) wartości ekspresji X-1 są dodatnie, a wartości wyrażeń X-2 i X-3 są ujemne. Dlatego w rozważanym przedziale prezentujemy X-2 i X-3 za pomocą modułu jako - | X-2 | i - | X-3 | odpowiednio. W którym

Teraz możesz zastosować właściwości logarytmu pracy i prywatnego, ponieważ jest w przedziale (1, 2) wartości wyrażeń X-1, | X-2 | i | X-3 | - Pozytywny.

Mieć

Wyniki można łączyć:

Ogólnie rzecz biorąc, podobne argumenty umożliwiają formuły logarytm na podstawie logarytmu, relacji i stopni w celu uzyskania trzech praktycznie przydatnych wyników, które są dość wygodne w użyciu:

• Logarytm działa z dwóch arbitralnych wyrażeń X i Y typu dziennika A (X · Y) można wymienić za pomocą sumowalnego logarytmy dziennika A | X | + Log A | Y | , A\u003e 0, A ≠ 1.
• Logarytm Prywatny dziennik A (X: Y) można wymienić różnicą między logarytmami dziennikiem | x | -log a | y | , A\u003e 0, A ≠ 1, X i Y - arbitralne wyrażenia.
• Z logarytmu niektórych wyrażeń B w równym stopniu p dziennika A B P Formularz możesz przejść do wyrażenia p · dziennik a | b | , gdzie A\u003e 0, A ≠ 1, P jest liczbą parzystą i B - arbitralną ekspresję.

Podobne wyniki podano na przykład, w instrukcji, aby rozwiązać orientacyjne i logarytmiczne równania w gromadzeniu problemów w matematyce dla wnioskodawców do uniwersytetów pod redaktorami M. I. Scarkavi.

Przykład.

Uprość wyrażenie .

Decyzja.

Dobrze byłoby zastosować właściwości logarytmu, kwot i różnic. Ale czy możemy to tutaj zrobić? Aby odpowiedzieć na to pytanie, musimy znać OTZ.

Definiujemy to:

Jest to raczej oczywiste, że wyrażenia X + 4, X-2 i (X + 4) 13 na wartościach dopuszczalnych wartości zmiennej X mogą podjąć zarówno wartości dodatnie, jak i ujemne. Dlatego będziemy musieli działać przez moduły.

Właściwości modułu umożliwiają przepisanie tak, jak dlatego

Nic nie uniemożliwia również posiadłości tytułu logarytmu, a następnie przynieś podobne warunki:

Druga sekwencja przekształceń prowadzi do tego samego wyniku:

A ponieważ wyrażenie X-2 może przyjmować zarówno wartości pozytywne, jak i ujemne, wtedy przy składaniu równomiernego stopnia 14

Zadania, których rozwiązanie leży transformacja wyrażeń logarytmicznych, dość często spotykaj się na egzaminie.

Aby skutecznie radzić sobie z nimi w minimalnym czasie z wyjątkiem głównych tożsamości logarytmicznej, musisz znać i poprawnie używać niektórych formuł.

Jest to: dziennik A B \u003d B, gdzie a, B\u003e 0 i ≠ 1 (wynika bezpośrednio z definicji logarytmu).

dziennik A B \u003d Log z b / Logowaniem z A lub Log A B \u003d 1 / Log B a
gdzie A, B, C\u003e 0; A, C ≠ 1.

dziennik A M B N \u003d (M / N) Log | A | | b |.
gdzie a, b\u003e 0, a ≠ 1, m, n є r, n ≠ 0.

i zaloguj się z benu b \u003d b
gdzie A, B, C\u003e 0 i A, B, S ≠ 1

Aby pokazać uczciwość czwartej równości, progrologować lewicę i prawą stronę A. Dostajemy dziennik A (i dziennik z b) \u003d dziennik A (b dziennik za pomocą A) lub zaloguj się z b \u003d dziennik z a · dziennik A B; Dziennik z b \u003d dziennik za pomocą · (dziennik z b / bel z a); Dziennik z b \u003d dziennik z b.

Udowodniliśmy równość logarytmów, co oznacza równe wyrażenia pod logarytmami. Udowodniono formułę 4.

Przykład 1.

Oblicz 81 dziennika 27 5 LOG 5 4.

Decyzja.

81 = 3 4 , 27 = 3 3 .

dziennik 27 5 \u003d 1/3 dziennika 3 5, dziennik 5 4 \u003d dziennik 3 4 / dziennik 3 5. W konsekwencji,

dziennik 27 5 · Log 5 4 \u003d 1/3 dziennika 3 5 · (Log 3 4 / Log 3 5) \u003d 1/3 dziennika 3 4.

Następnie 81 LOG 27 5 LOG 5 4 \u003d (3 4) 1/3 LOG 3 4 \u003d (3 LOG 3 4) 4/3 \u003d (4) 4/3 \u003d 4 3 √4.

Możesz niezależnie wykonać następujące zadanie.

Oblicz (8 dziennika 2 3 + 3 1 / Log 2 3) - Log 0,2 5.

Jako końcówka 0,2 \u003d 1/5 \u003d 5 -1; Log 0,2 5 \u003d -1.

Odpowiedź: 5.

Przykład 2.

Oblicz (√11) log. √3 9- Log 121 81.

Decyzja.

Wykonaj wymianę wyrażeń: 9 \u003d 3 2, √3 \u003d 3 1/2, dziennik √3 9 \u003d 4,

121 \u003d 11 2, 81 \u003d 3 4, dziennik 121 81 \u003d 2 log 11 3 (zastosowano formułę 3).

Następnie (√11) Log √3 9- Log 121 81 \u003d (11 1/2) 4-2 LOG 11 3 \u003d (11) 2- LOG 11 3 \u003d 11 2 / (11) LOG 11 3 \u003d 11 2 / ( 11 LOG 11 3) \u003d 121/3.

Przykład 3.

Oblicz dziennik 2 24 / Log 96 2- Log 2 192 / Log 12 2.

Decyzja.

Logarytmy zawarte w przykładzie, wymień logarytmy z podstawą 2.

log 96 2 \u003d 1 / Log 2 96 \u003d 1 / Log 2 (2 5 · 3) \u003d 1 / (log 2 2 5 + dziennik 2 3) \u003d 1 / (5 + dziennik 2 3);

dziennik 2 192 \u003d dziennik 2 (2 6 · 3) \u003d (dziennik 2 2 6 + dziennik 2 3) \u003d (6 + dziennik 2 3);

dziennik 2 24 \u003d dziennik 2 (2 3 · 3) \u003d (dziennik 2 2 3 + dziennik 2 3) \u003d (3 + dziennik 2 3);

lOG 12 2 \u003d 1 / LOG 2 12 \u003d 1 / LOG 2 (2 2 · 3) \u003d 1 / (dziennik 2 2 2 + dziennik 2 3) \u003d 1 / (2 + dziennik 2 3).

Następnie zaloguj 2 24 / Log 96 2 - Log 2 192 / Log 12 2 \u003d (3 + Log 2 3) / (1 / (5 + dziennik 2 3)) - ((6 + dziennik 2 3) / (1 / ( 2 + dziennik 2 3)) \u003d

\u003d (3 + dziennik 2 3) · (5 + dziennik 2 3) - (6 + dziennik 2 3) (2 + dziennik 2 3).

Po ujawnianiu nawiasów i przynosząc podobne warunki, otrzymujemy numer 3. (z uproszczeniem wyrażenia, dziennik 2 3 może wyznaczyć przez N i uprość wyrażenie

(3 + N) · (5 + N) - (6 + N) (2 + N)).

Odpowiedź: 3.

Możesz samodzielnie wykonywać następujące zadanie:

Oblicz (dziennik 3 4 + dziennik 4 3 + 2) · dziennik 3 16 · dziennik 2 144 3.

Tutaj konieczne jest przejście do logarytmów na podstawie 3 i rozkładu na prostych mnożnikach dużych liczb.

Odpowiedź: 1/2.

Przykład 4.

Trzy liczby A \u003d 1 / (log 3 0,5), B \u003d 1 / (log 0,5 3), C \u003d dziennik 0,5 12 - Log 0,5 3. Umieść je w kolejności rosnącej.

Decyzja.

Przekształcamy liczby A \u003d 1 / (log 3 0.5) \u003d dziennik 0,5 3; C \u003d dziennik 0,5 12 - log 0,5 3 \u003d Log 0,5 12/3 \u003d Log 0,5 4 \u003d -2.

Porównać je

log 0,5 3\u003e Log 0,5 4 \u003d -2 i Log 0,5 3< -1 = log 0,5 2, так как функция у = log 0,5 х – убывающая.

Lub 2.< log 0,5 3 < -1. Тогда -1 < 1/(log 0,5 3) < -1/2.

Odpowiedź. W konsekwencji procedura wprowadzania numerów: C; ALE; W.

Przykład 5.

Ile liczb całkowitych znajduje się w przedziale (dziennik 3 1/16; log 2 6 48).

Decyzja.

Definiujemy między tym, jakie stopnie liczby 3 jest numer 1/16. Dostajemy 1/27.< 1 / 16 < 1 / 9 .

Ponieważ funkcja Y \u003d dziennik 3 x wzrasta, a następnie log 3 (1/2 27)< log 3 (1 / 16) < log 3 (1 / 9); -3 < log 3 (1 / 16) < -2.

lOG 6 48 \u003d LOG 6 (36 · 4/3) \u003d dziennik 6 36 + dziennik 6 (4/3) \u003d 2 + dziennik 6 (4/3). Porównaj dziennik 6 (4/3) i 1/5. A dla tego porównaj liczby 4/3 i 6 1/5. Wzniesiony obie liczby za 5 stopni. Otrzymujemy (4/3) 5 \u003d 1024/243 \u003d 4 52/243< 6. Следовательно,

lOG 6 (4/3)< 1 / 5 . 2 < log 6 48 < 2 1 / 5 . Числа, входящие в двойное неравенство, положительные. Их можно возводить в квадрат. Знаки неравенства при этом не изменятся. Тогда 4 < log 6 2 48 < 4 21 / 25.

W związku z tym interwał (LOG 3 1/16; LOG 6 48) obejmuje interwał [-2; 4] i liczby całkowite są na nim umieszczane; -jeden; 0; jeden; 2; 3; cztery.

Odpowiedź: 7 liczb całkowitych.

Przykład 6.

Oblicz 3 LGGG 2 / LG 3 - LG20.

Decyzja.

3 LG LG 2 / LG3 \u003d (3 1 / LG3) LG LG 2 \u003d (3 lo g 3 10) LG LG 2 \u003d 10 LG LG 2 \u003d LG2.

Następnie 3 LGLG2 / LG3 - LG 20 \u003d LG 2 - LG 20 \u003d LG 0,1 \u003d -1.

Odpowiedź 1.

Przykład 7.

Wiadomo, że dziennik 2 (√3 + 1) + dziennik 2 (√6 - 2) \u003d A. Znajdź dziennik 2 (√3 -1) + dziennik 2 (√6 + 2).

Decyzja.

Liczby (√3 + 1) i (√3 - 1); (√6 - 2) i (√6 + 2) - koniugat.

Przeprowadzimy następującą transformację wyrażeń

√3 - 1 \u003d (√3 - 1) · (√3 + 1)) / (√3 + 1) \u003d 2 / (√3 + 1);

√6 + 2 \u003d (√6 + 2) · (√6 - 2)) / (√6 - 2) \u003d 2 / (√6 - 2).

Następnie zaloguj 2 (√3 - 1) + dziennik 2 (√6 + 2) \u003d dziennik 2 (2 / (√3 + 1)) + dziennik 2 (2 / (√6 - 2)) \u003d

LOG 2 2 - LOG 2 (√3 + 1) + LOG 2 2 - LOG 2 (√6 - 2) \u003d 1 - LOG 2 (√3 + 1) + 1 - LOG 2 (√6 - 2) \u003d

2 - Log 2 (√3 + 1) - Log 2 (√6 - 2) \u003d 2 - A.

Odpowiedź: 2 - A.

Przykład 8..

Uprość i znajdź przybliżoną wartość ekspresji (dziennik 3 2 · dziennik 4 3 · dziennik 5 4 · dziennik 6 5 · ... · Log 10 9.

Decyzja.

Wszystkie logarytmy dajemy całkowitej bazie 10.

(log 3 2 · dziennik 4 3 · Log 5 4 · Log 6 5 · ... · Log 10 9 \u003d (LG 2 / LG3) · (LG 3 / LG 4) · (LG 4 / LG 5) · ( LG 5 / LG 6) · ... · (LG 8 / LG 9) · LG 9 \u003d LG 2 ≈ 0,3010. (Przybliżona wartość LG 2 można znaleźć za pomocą tabeli, linii logarytmicznej lub kalkulatora).

Odpowiedź: 0,3010.

Przykład 9..

Oblicz dziennik A 2 B 3 √ (A 11 B -3), jeśli log √ A B3 \u003d 1. (W tym przykładzie i 2 B3 jest podstawą logarytm).

Decyzja.

Jeśli dziennik √ A B3 \u003d 1, a następnie 3 / (0,5 dziennika A B \u003d 1. i zaloguj A B \u003d 1/6.

Następnie zaloguj A 2 B 3√ (A 11 B -3) \u003d 1/2 dziennika A 2 B3 (A 11 B -3) \u003d dziennik A (A 11 B -3) / (2Log A (A 2 B3) ) \u003d (Log Aa 11 + Log AB -3) / (2 (Log A AA 2 + Log AB 3)) \u003d (11 - 3log AB) / (2 (2 + 3log AB)), biorąc pod uwagę, że ten dziennik A B \u003d 1/6 otrzymuje się (11 - 3 · 1/6) / (2 (2 + 3 · 1/6)) \u003d 10,5 / 5 \u003d 2.1.

Odpowiedź: 2.1.

Możesz samodzielnie wykonywać następujące zadanie:

Oblicz dziennik √3 6 √2.1, jeśli dziennik 0.7 27 \u003d a.

Odpowiedź: (3 + a) / (3a).

Przykład 10.

Oblicz 6.5 4 / Log 3 169 · 3 1 / Log 4 13 + Log125.

Decyzja.

6.5 4 / Log 3 169 · 3 1 / Log 4 13 + Log 125 \u003d (13/2) 4/2 Log 3 13 · 3 2 / Log 2 13 + 2log 5 5 3 \u003d (13/2) 2 dziennik 13 3 · 3 2 Dziennik 13 2 + 6 \u003d (13 LOG 13 3/2 LOG 13 3) 2 · (3 LOG 13 2) 2 + 6 \u003d (3/2 LOG 13 3) 2 · (3 dziennik 13 2) 2 + 6 \u003d (3 2 / (2 dziennik 13 3) 2) · (2 \u200b\u200bdziennik 13 3) 2 + 6.

(2 dziennik 13 3 \u003d 3 dziennik 13 2 (Formula 4))

Uzyskujemy 9 + 6 \u003d 15.

Odpowiedź: 15.

Mieć pytania? Nie wiem, jak znaleźć wartość wyrażenia logarytmicznego?
Aby uzyskać pomoc na opiekun - zarejestruj się.
Pierwsza lekcja jest bezpłatna!

wymagana jest witryna, z pełnym lub częściowym kopiowaniem materiału odniesienia do oryginalnego źródła.

Wyrażenia logarytmiczne, rozwiązywanie przykładów. W tym artykule rozważymy zadania związane z rozwiązaniem logarytmów. Zadania podnosi kwestię znalezienia wartości ekspresyjnej. Należy zauważyć, że koncepcja logarytmu jest używana w wielu zadaniach i zrozumieć, że jego znaczenie jest niezwykle ważne. Jeśli chodzi o użycie, logarytm jest używany w rozwiązywaniu równań, w zadaniach zastosowanych, również w zadaniach związanych z badaniem funkcji.

Dajemy przykłady rozumieć poczucie logarytmu:

Podstawowa tożsamość logarytmiczna:

Właściwości logarytmów, które muszą być zawsze zapamiętane:

* Logarytm pracy jest równy sumie logarytmów czynników.

* * *

* Prywatny logarytm (frakcja) jest równa różnicy w logarytmach czynników.

* * *

* Logarytm jest równy produktowi stopnia w logarytmie jego podstawy.

* * *

* Przejście do nowej bazy

* * *

Więcej właściwości:

* * *

Obliczanie logarytmów jest ściśle związane z wykorzystaniem właściwości wskaźników stopnia.

Wymień niektóre z nich:

Istotą tej właściwości jest to, że podczas przesyłania licznika do mianownika i przeciwnie, znak wskaźnika zmienia się na odwrót. Na przykład:

Konsekwencją tej nieruchomości:

* * *

Przy stopniu wznoszenie stopnia, fundacja pozostaje taka sama, a wskaźniki są zmienne.

* * *

Jak widziałeś bardzo prostą koncepcję logarytm. Najważniejsze jest to, że potrzebna jest dobra praktyka, co daje pewne umiejętności. Oczywiście wiedza o wzorach musi. Jeśli umiejętność w konwersji logarytmów elementarnych nie zostanie utworzona, a następnie podczas rozwiązywania prostych zadań można łatwo zezwolić na błąd.

Ćwicz, zdecyduj najpierw najprostsze przykłady z kursu matematyki, a następnie przejdź do bardziej złożonego. W przyszłości na pewno pokazam, jak "straszne" logarytmy są rozwiązywane, nie będzie takimi na egzaminie, ale są interesujące, nie przegap!

To wszystko! Sukces dla ciebie!

Z poważaniem, Alexander Krutitsky

P.S: Będę wdzięczny, jeśli opowiesz o miejscu w sieciach społecznościowych.

Logarits, jak dowolne numery, można złożyć, odliczać i konwertować. Ale ponieważ logarytmy nie są dość zwykłe liczby, istnieją własne zasady, które są nazywane właściwości podstawowe.

Zasady te muszą koniecznie wiedzieć - bez żadnych poważnych zadań logarytmicznych bez nich rozwiązuje. Ponadto są trochę trochę - wszystko można się nauczyć w jeden dzień. Więc postępuj.

Dodawanie i odejmowanie logarytmów

Rozważ dwa logarytm z tymi samymi bazami: dziennik zA. x. i dziennik. zA. y.. Następnie mogą być złożone i potrącone, oraz:

1. log. zA. x. + Dziennik. zA. y. \u003d Dziennik. zA. (x. · y.);
2. log. zA. x. - dziennik. zA. y. \u003d Dziennik. zA. (x. : y.).

Tak więc ilość logarytmów jest równa logarytmowi pracy, a różnica jest logarytmem prywatnym. Uwaga: kluczowy punkt jest tutaj te same podstawy. Jeśli fundamenty są różne, zasady te nie działają!

Formuły te pomogą obliczyć wyrażenie logarytmiczne, nawet gdy pojedyncze części nie są brane pod uwagę (patrz lekcja "Co to jest logarytm"). Spójrz na przykłady - i upewnij się:

LOG 6 4 + LOG 6 9.

Ponieważ podstawy w logarytmach są takie same, używamy sumy suma:
lOG 6 4 + LOG 6 9 \u003d LOG 6 (4 · 9) \u003d dziennik 6 36 \u003d 2.

Zadanie. Znajdź wartość wyrażenia: dziennik 2 48 - Log 2 3.

Fundacje są takie same, używając formuły różnicy:
lOG 2 48 - LOG 2 3 \u003d LOG 2 (48: 3) \u003d dziennik 2 16 \u003d 4.

Zadanie. Znajdź wartość wyrażenia: dziennik 3 135 - dziennik 3 5.

Znowu fundacje są takie same, więc mamy:
lOG 3 135 - LOG 3 5 \u003d LOG 3 (135: 5) \u003d dziennik 3 27 \u003d 3.

Jak widać, początkowe wyrażenia składają się z "złych" logarytmów, które nie są oddzielnie rozpatrywane oddzielnie. Ale po transformacji otrzymuje się dość normalne liczby. W tym fakcie zbudowana jest wiele prac testowych. Ale jaka jest kontrola - takie wyrażenia są pełne (czasami - prawie niezmienione) są oferowane na egzaminie.

Stopień wykonawczy z logarytmu

Teraz trochę komplikuje zadanie. Co jeśli na bazie lub argument logarytm kosztuje dyplom? Następnie wskaźnik tego stopnia można wyjąć z znaku logarytmu zgodnie z następującymi zasadami:

Łatwo jest zobaczyć, że ostatnia reguła podąża za dwoma pierwszym. Ale lepiej go pamiętać, w niektórych przypadkach znacznie zmniejszy ilość obliczeń.

Oczywiście wszystkie te zasady mają sens, jeśli zgodność z logarytmem OTZ: zA. > 0, zA. ≠ 1, x. \u003e 0. a także: Naucz się stosować wszystkie formuły nie tylko od lewej do prawej, ale wręcz przeciwnie, tj. Możesz wykonać liczby skierowane do logarytmu, do samego logarytmu. Który jest najczęściej wymagany.

Zadanie. Znajdź wartość wyrażenia: dziennik 7 49 6.

Pozbądź się stopnia w argumencie na pierwszym wzorze:
log 7 49 6 \u003d 6 · Log 7 49 \u003d 6 · 2 \u003d 12

Zadanie. Znajdź wartość wyrażenia:

[Podpis na rysunek]

Należy pamiętać, że w mianowniku znajduje się logarytm, podstawa i argument, z których są dokładne stopnie: 16 \u003d 2 4; 49 \u003d 7 2. Mamy:

[Podpis na rysunek]

Myślę, że najnowszy przykład wymaga wyjaśnienia. Gdzie zniknęły logarytmy? Do ostatniej chwili pracujemy tylko z mianownikiem. Przedstawili podstawę i argument logarytm w formie stopni i przeprowadzili wskaźniki - otrzymały "trzypiętrowy" frakcję.

Teraz spójrzmy na podstawową frakcję. Numer w liczniku i mianowniku jest tym samym numerem: dziennik 2 7. Ponieważ log 2 7 ≠ 0, możemy zmniejszyć frakcję - 2/4 pozostanie w mianowniku. Zgodnie z zasadami arytmetyki, czwarta może być przeniesiona do licznika, który został wykonany. Rezultatem była odpowiedź: 2.

Przejście do nowej bazy

Mówiąc o zasadach do dodawania i odejmowania logarytmów, szczególnie podkreślam, że działają tylko z tych samych baz. A co, jeśli fundacje są różne? Co jeśli nie są dokładne stopnie tego samego numeru?

Formuły do \u200b\u200bprzejścia na nową bazę przychodzą na ratunek. Sformułujemy je w formie twierdzenia:

Niech Logaritm Log. zA. x.. Następnie dla dowolnej liczby dO. taka dO. \u003e 0 I. dO. ≠ 1, prawdziwa równość:

[Podpis na rysunek]

W szczególności, jeśli umieścisz dO. = x.Dostaniemy:

[Podpis na rysunek]

Od drugiej formuły wynika, że \u200b\u200bbaza i argument logarytmu można zmienić w miejscach, ale jednocześnie wyrażenie "włącza się", tj. Logarytm okazuje się być w mianowniku.

Formuły te są rzadkie w konwencjonalnych wyrażeniach numerycznych. Ocena, jak wygodne są, możliwe jest tylko podczas rozwiązywania równań logarytmicznych i nierówności.

Istnieją jednak zadania, które są ogólnie rozwiązane w dowolnym miejscu jako przejście do nowej podstawy. Rozważ kilka takich:

Zadanie. Znajdź wartość wyrażenia: dziennik 5 16 · dziennik 2 25.

Zauważ, że argumenty obu logarytmów są dokładnymi stopniami. Podsumowuję: dziennik 5 16 \u003d dziennik 5 2 4 \u003d 4log 5 2; Dziennik 2 25 \u003d dziennik 2 5 2 \u003d 2log 2 5;

A teraz "odwróć" drugi logarytm:

[Podpis na rysunek]

Ponieważ praca nie zmienia się od przegrupowania mnożników, spokojnie zmieniamy cztery i dwa, a następnie posortowane z logarytmami.

Zadanie. Znajdź wartość wyrażenia: dziennik 9 100 · LG3.

Podstawa i argument pierwszego logarytmu - dokładne stopnie. Piszemy go i pozbywamy się wskaźników:

[Podpis na rysunek]

Teraz pozbyć się logarytmu dziesiętnego, obracając się do nowej bazy:

[Podpis na rysunek]

Podstawowa tożsamość logarytmiczna

Często rozwiązanie jest wymagane do przesłania numeru jako logarytm dla określonej bazy. W tym przypadku formuły pomogą nam:

W pierwszym przypadku n. Staje się wskaźnikiem zakresu w argumencie. Numer n. Może być absolutnie każdy, ponieważ jest to tylko wartość logarytm.

Druga formuła jest w rzeczywistości parafrazowana definicja. Nazywa się: główną tożsamością logarytmiczną.

W rzeczywistości, co się stanie, jeśli numer b. budować w takim stopniu, że liczba b. w tym zakresie podaje numer zA.? Poprawnie: to najbardziej zA.. Ostrożnie przeczytaj ponownie ten akapit - wiele "powiesić" na nim.

Podobnie jak wzory przejściowe do nowej bazy, główna tożsamość logarytmiczna jest czasami jedynym możliwym rozwiązaniem.

Zadanie. Znajdź wartość wyrażenia:

[Podpis na rysunek]

Należy pamiętać, że log 25 64 \u003d dziennik 5 8 - Wystarczyło kwadratowi od podstawy i argumentu logarytmu. Biorąc pod uwagę zasady mnożenia stopni o tej samej podstawie, otrzymujemy:

[Podpis na rysunek]

Jeśli ktoś nie jest świadomy, to było prawdziwe zadanie EGE :)

Jednostka logarytmiczna i logarytmiczne zero

Podsumowując, dam dwie tożsamości, że trudno jest wymienić właściwości - jest to konsekwencja definicji logarytmu. Są stale odkryte w zadaniach i, co jest zaskakujące, tworzą problemy nawet dla "zaawansowanych" studentów.

1. log. zA. zA. \u003d 1 jest jednostką logarytmiczną. Nagrywaj raz i na zawsze: logarytm na dowolnej podstawie zA. Z bardzo podstawy jest równy.
2. log. zA. 1 \u003d 0 to logarytmiczne zero. Baza zA. Może w jakiś sposób, ale jeśli argument jest jednostką - logarytm jest zero! Dlatego zA. 0 \u003d 1 jest bezpośrednią konsekwencją definicji.

To wszystkie właściwości. Pamiętaj, aby ćwiczyć je zastosować w praktyce! Pobierz łóżeczko na początku lekcji, wydrukuj go - i rozwiąż zadania.