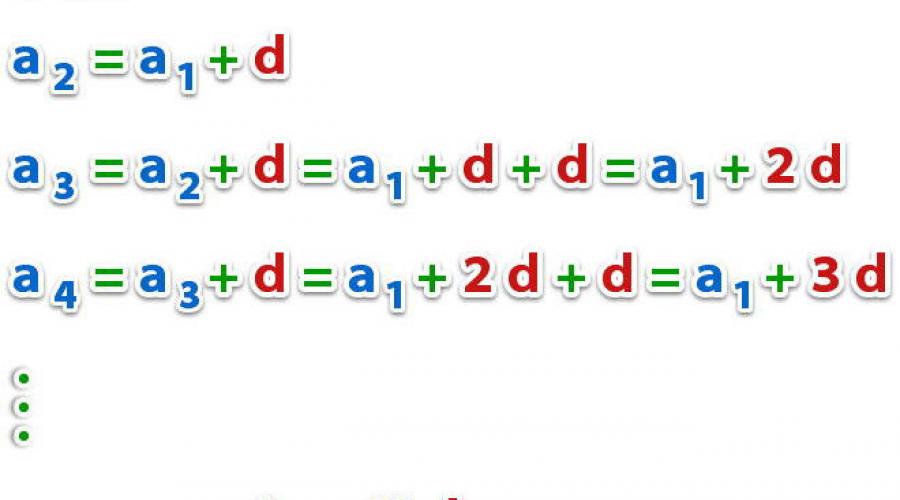
Lub arytmetyka to rodzaj uporządkowanego ciągu liczbowego, którego właściwości są badane na szkolnym kursie algebry. W tym artykule szczegółowo omówiono pytanie, jak znaleźć sumę progresji arytmetycznej.

Czym jest ten postęp?

Zanim przejdziemy do rozważania pytania (jak znaleźć sumę ciągu arytmetycznego), warto zrozumieć, o czym będzie mowa.

Każdy ciąg liczb rzeczywistych uzyskany przez dodanie (odjęcie) pewnej wartości od każdej poprzedniej liczby nazywa się postępem algebraicznym (arytmetycznym). Definicja ta, przetłumaczona na język matematyki, przyjmuje postać:

Tutaj i jest liczbą porządkową elementu wiersza a i. Dzięki temu, znając tylko jedno ziarno, możesz z łatwością odtworzyć całą serię. Parametr d we wzorze nazywa się różnicą progresji.

Można łatwo wykazać, że dla rozpatrywanego szeregu liczb obowiązuje następująca równość:

a n = a 1 + d * (n - 1).

To znaczy, aby znaleźć wartość n-tego elementu w kolejności, dodaj różnicę d do pierwszego elementu a 1 n-1 razy.

Jaka jest suma ciągu arytmetycznego: wzór

Przed podaniem wzoru na wskazaną kwotę warto zastanowić się nad prostym przypadkiem szczególnym. Biorąc pod uwagę progresję liczb naturalnych od 1 do 10, musisz znaleźć ich sumę. Ponieważ w progresji jest niewielu członków (10), możliwe jest rozwiązanie problemu bezpośrednio, czyli zsumowanie wszystkich elementów w kolejności.

S 10 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55.

Warto zastanowić się nad jedną interesującą rzeczą: skoro każdy wyraz różni się od następnego o taką samą wartość d = 1, to sumowanie parami pierwszego z dziesiątym, drugiego z dziewiątym i tak dalej da ten sam wynik. Naprawdę:

11 = 1+10 = 2+9 = 3+8 = 4+7 = 5+6.

Jak widać, tych sum jest tylko 5, czyli dokładnie dwa razy mniej niż liczba elementów w serii. Następnie mnożąc liczbę sum (5) przez wynik każdej sumy (11), dojdziesz do wyniku otrzymanego w pierwszym przykładzie.

Jeśli uogólnimy to rozumowanie, możemy napisać następujące wyrażenie:

S n = n * (a 1 + a n) / 2.

Wyrażenie to pokazuje, że wcale nie jest konieczne sumowanie wszystkich elementów w rzędzie, wystarczy znać wartość pierwszego a 1 i ostatniego a n oraz całkowitą liczbę terminów n.

Uważa się, że Gauss po raz pierwszy pomyślał o tej równości, gdy szukał rozwiązania problemu postawionego przez nauczyciela w szkole: zsumuj pierwsze 100 liczb całkowitych.

Suma elementów od m do n: wzór

Wzór podany w poprzednim akapicie daje odpowiedź na pytanie, jak znaleźć sumę ciągu arytmetycznego (pierwsze elementy), ale często w zadaniach konieczne jest zsumowanie szeregu liczb w środku ciągu. Jak to zrobić?

Najłatwiej odpowiedzieć na to pytanie, rozpatrując następujący przykład: niech będzie konieczne znalezienie sumy wyrazów od m-tego do n-tego. Aby rozwiązać problem, dany odcinek od m do n progresji należy przedstawić w postaci nowego szeregu liczbowego. W tej reprezentacji m-ty wyraz a m będzie pierwszym, a n będzie n- (m-1). W tym przypadku, stosując standardową formułę sumy, otrzymujesz następujące wyrażenie:

S m n = (n - m + 1) * (am + za n) / 2.

Przykład użycia formuł

Wiedząc, jak obliczyć sumę postępu arytmetycznego, warto rozważyć prosty przykład użycia podanych wzorów.

Poniżej znajduje się ciąg liczbowy, powinieneś znaleźć sumę jego członków, zaczynając od 5 i kończąc na 12:

Podane liczby wskazują, że różnica d jest równa 3. Używając wyrażenia dla n-tego elementu, można znaleźć wartości 5. i 12. terminu progresji. Wyszło na to, że:

a 5 = a 1 + d * 4 = -4 + 3 * 4 = 8;

a 12 = a 1 + d * 11 = -4 + 3 * 11 = 29.

Znając wartości liczb na końcach rozważanego postępu algebraicznego, a także wiedząc, które liczby w rzędzie zajmują, możesz użyć wzoru na sumę uzyskaną w poprzednim akapicie. Okaże się:

S 5 12 = (12 - 5 + 1) * (8 + 29) / 2 = 148.

Warto zauważyć, że tę wartość można uzyskać inaczej: najpierw znajdź sumę pierwszych 12 elementów za pomocą standardowego wzoru, następnie oblicz sumę pierwszych 4 elementów za pomocą tego samego wzoru, a następnie odejmij drugi od pierwszej sumy.

Podczas nauki algebry w szkole ogólnokształcącej (klasa 9) jednym z ważnych tematów jest nauka o ciągach liczbowych, które obejmują progresje – geometryczne i arytmetyczne. W tym artykule rozważymy postęp arytmetyczny i przykłady z rozwiązaniami.

Co to jest postęp arytmetyczny?

Aby to zrozumieć, konieczne jest podanie definicji rozważanego postępu, a także podanie podstawowych formuł, które będą dalej wykorzystywane przy rozwiązywaniu problemów.

Wiadomo, że w pewnym postępie algebraicznym pierwszy człon jest równy 6, a siódmy człon równy 18. Trzeba znaleźć różnicę i przywrócić ten ciąg do siódmego członu.

Użyjmy wzoru do wyznaczenia nieznanego wyrazu: a n = (n - 1) * d + a 1. Zastępujemy w nim znane dane z warunku, czyli liczby a 1 i a 7, mamy: 18 = 6 + 6 * d. Z tego wyrażenia możesz łatwo obliczyć różnicę: d = (18 - 6) / 6 = 2. W ten sposób odpowiedzieliśmy na pierwszą część problemu.

Aby odtworzyć sekwencję do 7 wyrazów, powinieneś użyć definicji progresji algebraicznej, czyli a 2 = a 1 + d, a 3 = a 2 + d, i tak dalej. W rezultacie przywracamy całą sekwencję: a 1 = 6, a 2 = 6 + 2 = 8, a 3 = 8 + 2 = 10, a 4 = 10 + 2 = 12, a 5 = 12 + 2 = 14 , a 6 = 14 + 2 = 16, a 7 = 18.

Przykład #3: robienie progresji

Jeszcze bardziej skomplikujmy stan problemu. Teraz trzeba odpowiedzieć na pytanie, jak znaleźć postęp arytmetyczny. Możesz podać następujący przykład: dane dwie liczby, na przykład - 4 i 5. Konieczne jest wykonanie progresji algebraicznej, aby trzy kolejne wyrazy zmieściły się między nimi.

Przed przystąpieniem do rozwiązywania tego problemu konieczne jest zrozumienie, jakie miejsce zajmą dane liczby w przyszłej progresji. Ponieważ będą między nimi jeszcze trzy wyrazy, a 1 = -4 i 5 = 5. Po ustaleniu tego przechodzimy do problemu, który jest podobny do poprzedniego. Ponownie dla n-tego wyrazu używamy wzoru, otrzymujemy: a 5 = a 1 + 4 * d. Skąd: d = (a 5 - a 1) / 4 = (5 - (-4)) / 4 = 2,25. Tutaj nie otrzymaliśmy całkowitej wartości różnicy, ale jest to liczba wymierna, więc wzory na postęp algebraiczny pozostają takie same.

Teraz dodaj znalezioną różnicę do 1 i przywróć brakujące elementy progresji. Otrzymujemy: a 1 = - 4, a 2 = - 4 + 2,25 = - 1,75, a 3 = -1,75 + 2,25 = 0,5, a 4 = 0,5 + 2,25 = 2,75, a 5 = 2,75 + 2,25 = 5, co było zbieżne ze stanem problemu.

Przykład nr 4: pierwszy termin progresji

Podajmy dalej przykłady postępu arytmetycznego z rozwiązaniem. We wszystkich poprzednich problemach znana była pierwsza liczba progresji algebraicznej. Rozważmy teraz problem innego typu: niech podane zostaną dwie liczby, gdzie a 15 = 50 i a 43 = 37. Trzeba znaleźć liczbę, od której zaczyna się ten ciąg.

Stosowane do tej pory formuły zakładają znajomość 1 i d. Nic nie wiadomo o tych liczbach w opisie problemu. Niemniej jednak wypisujemy wyrażenia dla każdego członka, o którym są informacje: a 15 = a 1 + 14 * d i a 43 = a 1 + 42 * d. Otrzymano dwa równania, w których 2 nieznane wielkości (a 1 i d). Oznacza to, że problem sprowadza się do rozwiązania układu równań liniowych.

Najłatwiejszym sposobem rozwiązania tego systemu jest wyrażenie 1 w każdym równaniu, a następnie porównanie otrzymanych wyrażeń. Pierwsze równanie: a 1 = a 15 - 14 * d = 50 - 14 * d; drugie równanie: a 1 = a 43 - 42 * d = 37 - 42 * d. Porównując te wyrażenia, otrzymujemy: 50 - 14 * d = 37 - 42 * d, skąd różnica d = (37 - 50) / (42 - 14) = - 0,464 (podano tylko 3 miejsca po przecinku).

Znając d, możesz użyć dowolnego z dwóch powyższych wyrażeń dla 1. Na przykład pierwszy: a 1 = 50 - 14 * d = 50 - 14 * (-0,464) = 56,496.

Jeśli masz wątpliwości co do wyniku, możesz to sprawdzić, na przykład określić 43 termin progresji, który jest określony w warunku. Otrzymujemy: a 43 = a 1 + 42 * d = 56,496 + 42 * (- 0,464) = 37,008. Mały błąd wynika z faktu, że w obliczeniach zastosowano zaokrąglanie do tysięcznych.

Przykład nr 5: kwota

Spójrzmy teraz na kilka przykładów z rozwiązaniami sumy postępu arytmetycznego.

Niech będzie podany ciąg liczbowy postaci: 1, 2, 3, 4, ...,. Jak obliczyć sumę tych 100 liczb?

Dzięki rozwojowi technologii komputerowej możliwe jest rozwiązanie tego problemu, czyli sekwencyjne sumowanie wszystkich liczb, co komputer zrobi, gdy tylko osoba naciśnie klawisz Enter. Problem można jednak rozwiązać w umyśle, jeśli zwrócimy uwagę, że przedstawiony ciąg liczb jest ciągiem algebraicznym, a jego różnica wynosi 1. Stosując wzór na sumę, otrzymujemy: S n = n * (a 1 + an) / 2 = 100 * (1 + 100) / 2 = 5050.

Ciekawostką jest, że problem ten nazywa się „gaussowskim”, ponieważ na początku XVIII wieku słynny Niemiec, choć miał zaledwie 10 lat, był w stanie rozwiązać go w głowie w kilka sekund. Chłopiec nie znał wzoru na sumę ciągu algebraicznego, ale zauważył, że jeśli dodasz parami liczby na krawędziach ciągu, zawsze otrzymasz jeden wynik, czyli 1 + 100 = 2 + 99 = 3 + 98 = ..., a ponieważ z tych kwot będzie dokładnie 50 (100/2), to aby otrzymać poprawną odpowiedź wystarczy pomnożyć 50 przez 101.

Przykład nr 6: suma członków od n do m

Inny typowy przykład sumy postępu arytmetycznego jest następujący: mając ciąg liczb: 3, 7, 11, 15, ..., musisz znaleźć, jaka będzie suma jego członków od 8 do 14.

Problem rozwiązuje się na dwa sposoby. Pierwsza z nich polega na znalezieniu nieznanych terminów od 8 do 14, a następnie ich sekwencyjnym sumowaniu. Ponieważ terminów jest niewiele, ta metoda nie jest wystarczająco pracochłonna. Proponuje się jednak rozwiązanie tego problemu drugą metodą, która jest bardziej uniwersalna.

Chodzi o to, aby otrzymać wzór na sumę postępu algebraicznego między wyrazami m i n, gdzie n>m są liczbami całkowitymi. Napiszmy dwa wyrażenia na sumę dla obu przypadków:

1. S m = m * (m + a 1) / 2.
2. S n = n * (a n + a 1) / 2.

Ponieważ n>m jest oczywiste, że suma 2 zawiera pierwszą. Ostatni wniosek oznacza, że ​​jeśli weźmiemy różnicę między tymi sumami i dodamy do niej wyraz a m (w przypadku odebrania różnicy odejmuje się ją od sumy S n), to otrzymujemy niezbędną odpowiedź na problem. Mamy: S mn = S n - S m + am = n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am = a 1 * (n - m) / 2 + an * n / 2 + am * (1- m / 2). W tym wyrażeniu konieczne jest zastąpienie wzorów za n i m. Następnie otrzymujemy: S mn = a 1 * (n - m) / 2 + n * (a 1 + (n - 1) * d) / 2 + (a 1 + (m - 1) * d) * (1 - m / 2) = a 1 * (n - m + 1) + d * n * (n - 1) / 2 + d * (3 * m - m 2 - 2) / 2.

Otrzymany wzór jest nieco kłopotliwy, niemniej jednak suma S mn zależy tylko od n, m, a 1 i d. W naszym przypadku a 1 = 3, d = 4, n = 14, m = 8. Podstawiając te liczby, otrzymujemy: S mn = 301.

Jak widać z podanych rozwiązań, wszystkie problemy opierają się na znajomości wyrażenia dla n-tego członu i wzoru na sumę zbioru pierwszych członów. Przed przystąpieniem do rozwiązania któregokolwiek z tych problemów zaleca się uważne przeczytanie stanu, jasne zrozumienie, co należy znaleźć, a dopiero potem przejście do rozwiązania.

Kolejną wskazówką jest dążenie do prostoty, to znaczy, jeśli możesz odpowiedzieć na pytanie bez użycia skomplikowanych obliczeń matematycznych, musisz to zrobić, ponieważ w tym przypadku prawdopodobieństwo popełnienia błędu jest mniejsze. Na przykład w przykładzie ciągu arytmetycznego z rozwiązaniem nr 6 można zatrzymać się na wzorze S mn = n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am i przerwać ogólny problem na osobne podzadania (w tym przypadku najpierw znajdź członków an i am).

Jeśli istnieją wątpliwości co do uzyskanego wyniku, zaleca się jego sprawdzenie, tak jak to zrobiono w niektórych podanych przykładach. Odkryliśmy, jak znaleźć postęp arytmetyczny. Jeśli się zorientujesz, to nie jest takie trudne.

Zanim zaczniemy decydować problemy z postępem arytmetycznym, zastanów się, czym jest ciąg liczb, ponieważ postęp arytmetyczny jest szczególnym przypadkiem ciągu liczb.

Ciąg liczbowy to zbiór liczbowy, którego każdy element ma swój własny numer porządkowy... Elementy tego zbioru nazywane są członkami ciągu. Numer porządkowy elementu sekwencji jest oznaczony indeksem:

Pierwszy element sekwencji;

Piąty element sekwencji;

- „n-ty” element ciągu, tj. pozycja "w kolejce" rz.

Istnieje związek między wartością elementu sekwencji a jego liczbą porządkową. Dlatego możemy myśleć o sekwencji jako funkcji, której argumentem jest liczba porządkowa elementu sekwencji. Innymi słowy, możemy powiedzieć, że ciąg jest funkcją argumentu naturalnego:

Sekwencję można ustawić na trzy sposoby:

1 . Sekwencję można ustawić za pomocą tabeli. W tym przypadku po prostu ustawiamy wartość każdego członka sekwencji.

Na przykład Ktoś postanowił zająć się zarządzaniem czasem osobistym i na początek obliczyć, ile czasu spędza na VKontakte w ciągu tygodnia. Zapisując czas w tabeli, otrzyma sekwencję składającą się z siedmiu elementów:

Pierwszy wiersz tabeli zawiera numer dnia tygodnia, drugi czas w minutach. Widzimy, że w poniedziałek Ktoś spędził 125 minut na VKontakte, czyli w czwartek - 248 minut, a w piątek tylko 15.

2 . Sekwencję można określić za pomocą formuły n-tego terminu.

W tym przypadku zależność wartości elementu ciągu od jego liczby wyraża się bezpośrednio w postaci formuły.

Na przykład, jeśli, to

Aby znaleźć wartość elementu ciągu o podanej liczbie, podstawiamy numer elementu do wzoru n-tego wyrazu.

Robimy to samo, jeśli musimy znaleźć wartość funkcji, jeśli wartość argumentu jest znana. Zamiast tego podstawiamy wartość argumentu do równania funkcji:

Jeśli na przykład , następnie

Jeszcze raz zauważam, że w sekwencji, w przeciwieństwie do dowolnej funkcji numerycznej, argumentem może być tylko liczba naturalna.

3 ... Sekwencję można określić za pomocą formuły, która wyraża zależność wartości elementu sekwencji numerowanego od wartości poprzednich elementów. W tym przypadku nie wystarczy znać tylko numer elementu sekwencji, aby znaleźć jego wartość. Musimy określić pierwszego członka lub kilka pierwszych członków sekwencji.

Rozważmy na przykład sekwencję ,

Możemy znaleźć wartości członków ciągu kolejno zaczynając od trzeciego:

Oznacza to, że za każdym razem, aby znaleźć wartość n-tego elementu ciągu, wracamy do dwóch poprzednich. Ten sposób sekwencjonowania nazywa się nawracający, od łacińskiego słowa powtarzać- Wróć.

Teraz możemy zdefiniować postęp arytmetyczny. Postęp arytmetyczny to prosty szczególny przypadek ciągu liczb.

Postęp arytmetyczny jest ciągiem liczbowym, którego każdy człon, począwszy od drugiego, jest równy poprzedniemu, dodanemu do tej samej liczby.

Numer nazywa się różnica postępu arytmetycznego... Różnica w postępie arytmetycznym może być dodatnia, ujemna lub zerowa.

Jeśli tytuł = "(! LANG: d> 0">, то каждый член арифметической прогрессии больше предыдущего, и прогрессия является !} wzrastający.

Na przykład 2; 5; osiem; jedenaście;...

Jeśli, to każdy element progresji arytmetycznej jest mniejszy niż poprzedni, a progresja jest malejący.

Na przykład 2; -1; -4; -7;...

Jeśli, to wszyscy członkowie progresji mają tę samą liczbę, a progresja to stacjonarny.

Na przykład 2; 2; 2; 2; ...

Główna własność postępu arytmetycznego:

Spójrzmy na zdjęcie.

Widzimy to

, i w tym samym czasie

Dodając te dwie równości, otrzymujemy:

.

Podziel obie strony równości przez 2:

Tak więc każdy element ciągu arytmetycznego, począwszy od drugiego, jest równy średniej arytmetycznej dwóch sąsiednich:

Co więcej, ponieważ

, i w tym samym czasie

, następnie

, i dlatego

Każdy element ciągu arytmetycznego zaczynający się od tytułu = "(! LANG: k> l">, равен среднему арифметическому двух равноотстоящих. !}

Formuła członka.

Widzimy, że dla członków postępu arytmetycznego zachodzą następujące relacje:

i w końcu

Mamy formuła n-tego terminu.

WAŻNY! Każdy element postępu arytmetycznego może być wyrażony w kategoriach i. Znając pierwszy termin i różnicę postępu arytmetycznego, możesz znaleźć dowolnego z jego członków.

Suma n członków postępu arytmetycznego.

W dowolnym ciągu arytmetycznym sumy elementów równoodległych od ekstremów są sobie równe:

Rozważ postęp arytmetyczny z n wyrazami. Niech suma n członków tej progresji będzie.

Uporządkujmy elementy progresji najpierw w kolejności rosnącej liczb, a następnie w kolejności malejącej:

Dodajmy parami:

Suma w każdym nawiasie jest równa, liczba par to n.

Otrzymujemy:

Więc, sumę n wyrazów ciągu arytmetycznego można znaleźć za pomocą wzorów:

Rozważać rozwiązywanie problemów dla progresji arytmetycznej.

1 . Sekwencja jest określona wzorem n-tego terminu: . Udowodnij, że ten ciąg jest postępem arytmetycznym.

Udowodnijmy, że różnica między dwoma sąsiednimi członkami ciągu jest równa tej samej liczbie.

Odkryliśmy, że różnica między dwoma sąsiadującymi elementami sekwencji nie zależy od ich liczby i jest stała. Dlatego z definicji sekwencja ta jest postępem arytmetycznym.

2 . Dostajesz postęp arytmetyczny -31; -27;...

a) Znajdź 31 członków progresji.

b) Określ, czy liczba 41 jest uwzględniona w tej progresji.

a) Widzimy to;

Napiszmy wzór na n-ty termin dla naszej progresji.

Ogólnie

W naszym przypadku , dlatego

Otrzymujemy:

b) Załóżmy, że 41 jest członkiem sekwencji. Znajdźmy jego numer. Aby to zrobić, rozwiązujemy równanie:

Otrzymaliśmy wartość naturalną n, więc tak, liczba 41 jest elementem progresji. Gdyby znaleziona wartość n nie była liczbą naturalną, odpowiedzielibyśmy, że liczba 41 NIE należy do progresji.

3 ... a) Pomiędzy cyframi 2 i 8 wstaw 4 liczby tak, aby razem z podanymi liczbami tworzyły ciąg arytmetyczny.

b) Znajdź sumę członków powstałej progresji.

a) Wstaw cztery cyfry między cyframi 2 i 8:

Otrzymaliśmy postęp arytmetyczny z 6 członkami.

Znajdźmy różnicę w tym postępie. W tym celu użyjemy wzoru dla n-tego terminu:

Teraz łatwo jest znaleźć wartości liczb:

3,2; 4,4; 5,6; 6,8

b)

Odpowiedź: a) tak; b) 30

4. Ciężarówka przewozi partię tłucznia o wadze 240 ton, codziennie zwiększając stawkę transportu o tę samą liczbę ton. Wiadomo, że w ciągu pierwszego dnia przewieziono 2 tony tłucznia. Określ, ile ton gruzu przewieziono dwunastego dnia, jeśli wszystkie prace zostały wykonane w 15 dni.

W zależności od stanu problemu ilość gruzu przewożonego ciężarówką zwiększa się każdego dnia o tę samą liczbę. Dlatego mamy do czynienia z postępem arytmetycznym.

Sformułujmy ten problem w kategoriach postępu arytmetycznego.

Pierwszego dnia przewieziono 2 tony tłucznia: a_1 = 2.

Wszystkie prace zostały zakończone w 15 dni:.

Ciężarówka przewozi partię tłucznia o wadze 240 ton:

Musimy znaleźć.

Najpierw znajdź różnicę w progresji. Użyjmy wzoru na sumę n członów progresji.

W naszym przypadku:

Tak, tak: postęp arytmetyczny nie jest dla Ciebie zabawką :)

No cóż, przyjaciele, jeśli czytacie ten tekst, to wewnętrzny dowód na czapkę mówi mi, że jeszcze nie wiecie, co to jest postęp arytmetyczny, ale naprawdę (nie, w ten sposób: SOOOOO!) chcecie wiedzieć. Dlatego nie będę Was męczył długimi wstępami i od razu przejdę do sedna.

Zacznijmy od kilku przykładów. Rozważ kilka zestawów liczb:

• 1; 2; 3; 4; ...
• 15; 20; 25; 30; ...
• $ \ sqrt (2); \ 2 \ sqrt (2); \ 3 \ sqrt (2); ... $

Co mają ze sobą wspólnego wszystkie te zestawy? Na pierwszy rzut oka nic. Ale tak naprawdę jest coś. Mianowicie: każdy kolejny element różni się od poprzedniego o ten sam numer.

Sędzia dla siebie. Pierwszy zestaw to po prostu kolejne liczby, każda następna więcej niż poprzednia. W drugim przypadku różnica między sąsiednimi liczbami jest już równa pięciu, ale ta różnica jest nadal stała. W trzecim przypadku korzenie w ogóle. Natomiast $ 2 \ sqrt (2) = \ sqrt (2) + \ sqrt (2) $, a $ 3 \ sqrt (2) = 2 \ sqrt (2) + \ sqrt (2) $, czyli i w tym przypadku każdy kolejny element po prostu rośnie o $ \ sqrt (2) $ (i nie bój się, że ta liczba jest nieracjonalna).

Tak więc: wszystkie takie sekwencje nazywane są postępami arytmetycznymi. Podajmy ścisłą definicję:

Definicja. Ciąg liczb, w którym każda następna różni się od poprzedniej o dokładnie taką samą wartość, nazywa się postępem arytmetycznym. Sama kwota, o jaką różnią się liczby, nazywana jest różnicą progresji i jest najczęściej oznaczana literą $ d $.

Oznaczenie: $ \ left (((a) _ (n)) \ right) $ - sama progresja, $ d $ - jej różnica.

I tylko kilka ważnych uwag. Po pierwsze, tylko uporządkowany ciąg liczb: można je czytać ściśle w kolejności, w jakiej zostały napisane - i nic więcej. Nie można zmieniać ani zamieniać numerów.

Po drugie, sama sekwencja może być skończona lub nieskończona. Na przykład zbiór (1; 2; 3) jest oczywiście skończonym ciągiem arytmetycznym. Ale jeśli napiszesz coś w duchu (1; 2; 3; 4; ...) - to już jest niekończący się postęp. Wielokropek po czwórce niejako wskazuje, że nadal dzieje się sporo liczb. Nieskończenie dużo np. :)

Chciałbym również zauważyć, że progresje rosną i maleją. Widzieliśmy już rosnące - ten sam zestaw (1; 2; 3; 4; ...). A oto przykłady malejących progresji:

• 49; 41; 33; 25; 17; ...
• 17,5; 12; 6,5; 1; −4,5; −10; ...
• $ \ sqrt (5); \ \ sqrt (5) -1; \ \ sqrt (5) -2; \ \ sqrt (5) -3; ... $

Dobra, dobra: ten ostatni przykład może wydawać się zbyt skomplikowany. Ale resztę, myślę, że rozumiesz. Dlatego wprowadzimy nowe definicje:

Definicja. Postęp arytmetyczny nazywa się:

1. wzrasta, jeśli każdy następny element jest większy niż poprzedni;
2. maleje, jeśli wręcz przeciwnie, każdy kolejny element jest mniejszy niż poprzedni.

Ponadto istnieją tak zwane sekwencje „stacjonarne” – składają się z tej samej powtarzającej się liczby. Na przykład (3; 3; 3; ...).

Pozostaje tylko jedno pytanie: jak odróżnić progresję rosnącą od malejącej? Na szczęście wszystko zależy od znaku liczby $ d $, czyli progresja różnicy:

1. Jeśli $ d \ gt 0 $, to progresja rośnie;
2. Jeśli $ d \ lt 0 $, to progresja oczywiście maleje;
3. Wreszcie jest przypadek $ d = 0 $ - w tym przypadku cała progresja sprowadza się do stacjonarnego ciągu identycznych liczb: (1; 1; 1; 1; ...) itd.

Spróbujmy obliczyć różnicę $ d $ dla trzech malejących progresji podanych powyżej. Aby to zrobić, wystarczy wziąć dowolne dwa sąsiednie elementy (na przykład pierwszy i drugi) i odjąć liczbę po lewej stronie od liczby po prawej. Będzie to wyglądać tak:

• 41−49=−8;
• 12−17,5=−5,5;
• $ \ sqrt (5) -1- \ sqrt (5) = - 1 $.

Jak widać, we wszystkich trzech przypadkach różnica rzeczywiście okazała się ujemna. A teraz, gdy mniej więcej ustaliliśmy definicje, nadszedł czas, aby dowiedzieć się, jak opisane są progresje i jakie są ich właściwości.

Członkowie progresji i formuła rekurencyjna

Ponieważ elementów naszych sekwencji nie można zamieniać miejscami, można je ponumerować:

\ [\ lewo (((a) _ (n)) \ prawo) = \ lewo \ (((a) _ (1)), \ ((a) _ (2)), ((a) _ (3 )), ... \ Prawidłowy \) \]

Poszczególne elementy tego zestawu nazywane są członkami progresji. Są one oznaczone liczbą: pierwszy termin, drugi termin itd.

Ponadto, jak już wiemy, sąsiadujące elementy progresji są powiązane wzorem:

\ [((a) _ (n)) - ((a) _ (n-1)) = d \ Strzałka w prawo ((a) _ (n)) = ((a) _ (n-1)) + d \]

Krótko mówiąc, aby znaleźć n $-ty termin w progresji, musisz znać n-1 $-ty termin i różnicę w $ d $. Taka formuła nazywa się rekurencyjna, ponieważ za jej pomocą można znaleźć dowolną liczbę, znając tylko poprzednią (a właściwie wszystkie poprzednie). Jest to bardzo niewygodne, więc istnieje bardziej skomplikowany wzór, który redukuje wszelkie obliczenia do pierwszego terminu i różnicy:

\ [((a) _ (n)) = ((a) _ (1)) + \ lewo (n-1 \ prawo) d \]

Z pewnością spotkałeś się już z tą formułą. Uwielbiają je podawać w różnego rodzaju podręcznikach i reszebnikach. A w każdym sensownym podręczniku matematyki jest jedną z pierwszych.

Proponuję jednak trochę poćwiczyć.

Problem numer 1. Wypisz pierwsze trzy wyrazy ciągu arytmetycznego $ \ left (((a) _ (n)) \ right) $, jeśli $ ((a) _ (1)) = 8, d = -5 $.

Rozwiązanie. Znamy więc pierwszy wyraz $ ((a) _ (1)) = 8 $ i różnicę progresji $ d = -5 $. Użyjmy podanej formuły i zastąpmy $ n = 1 $, $ n = 2 $ i $ n = 3 $:

\ [\ początek (wyrównaj) & ((a) _ (n)) = ((a) _ (1)) + \ lewo (n-1 \ prawo) d; \\ & ((a) _ (1)) = ((a) _ (1)) + \ lewo (1-1 \ prawo) d = ((a) _ (1)) = 8; \\ & ((a) _ (2)) = ((a) _ (1)) + \ lewy (2-1 \ prawy) d = ((a) _ (1)) + d = 8-5 = 3; \\ & ((a) _ (3)) = ((a) _ (1)) + \ lewo (3-1 \ prawo) d = ((a) _ (1)) + 2d = 8-10 = -2. \\ \ koniec (wyrównaj) \]

Odpowiedź: (8; 3; -2)

To wszystko! Uwaga: nasza progresja maleje.

Oczywiście $ n = 1 $ nie mogło zostać zastąpione - pierwszy wyraz jest nam już znany. Jednak zastępując jedną, zadbaliśmy o to, aby nasza formuła działała nawet przez pierwszy semestr. W innych przypadkach wszystko sprowadzało się do banalnej arytmetyki.

Problem numer 2. Zapisz pierwsze trzy wyrazy ciągu arytmetycznego, jeśli jego siódmy wyraz to -40, a siedemnasty wyraz to -50.

Rozwiązanie. Zapiszmy stan problemu w zwykły sposób:

\ [((a) _ (7)) = - 40; \ quad ((a) _ (17)) = - 50. \]

\ [\ lewo \ (\ początek (wyrównaj) & ((a) _ (7)) = ((a) _ (1)) + 6d \\ & ((a) _ (17)) = ((a) _ (1)) + 16d \\ \ koniec (wyrównaj) \ prawo. \]

\ [\ lewo \ (\ początek (wyrównaj) & ((a) _ (1)) + 6d = -40 \\ & ((a) _ (1)) + 16d = -50 \\ \ koniec (wyrównaj) \ Prawidłowy. \]

Umieszczam znak systemu, ponieważ te wymagania muszą być spełnione jednocześnie. A teraz zauważ, że jeśli odejmiemy pierwsze od drugiego równania (mamy do tego prawo, ponieważ mamy system), otrzymamy to:

\ [\ początek (wyrównaj) & ((a) _ (1)) + 16d- \ lewo (((a) _ (1)) + 6d \ prawo) = - 50- \ lewo (-40 \ prawo); \\ & ((a) _ (1)) + 16d - ((a) _ (1)) - 6d = -50 + 40; \\ & 10d = -10; \\ & d = -1. \\ \ koniec (wyrównaj) \]

Tak łatwo znaleźliśmy różnicę w progresji! Pozostaje podstawić znalezioną liczbę do dowolnego równania systemu. Na przykład w pierwszym:

\ [\ początek (matryca) ((a) _ (1)) + 6d = -40; \ quad d = -1 \\ \ Downarrow \\ ((a) _ (1)) - 6 = -40; \\ ((a) _ (1)) = - 40 + 6 = -34. \\ \ koniec (matryca) \]

Teraz, znając pierwszy wyraz i różnicę, pozostaje znaleźć drugi i trzeci wyraz:

\ [\ początek (wyrównaj) & ((a) _ (2)) = ((a) _ (1)) + d = -34-1 = -35; \\ & ((a) _ (3)) = ((a) _ (1)) + 2d = -34-2 = -36. \\ \ koniec (wyrównaj) \]

Gotowy! Problem został rozwiązany.

Odpowiedź: (-34; -35; -36)

Zwróć uwagę na ciekawą właściwość progresji, którą odkryliśmy: jeśli weźmiemy wyrazy $ n $ th i $ m $ th i odejmiemy je od siebie, otrzymamy różnicę progresji pomnożoną przez liczbę $ n-m $:

\ [((a) _ (n)) - ((a) _ (m)) = d \ cdot \ lewo (n-m \ prawo) \]

Prosta, ale bardzo przydatna właściwość, którą zdecydowanie powinieneś znać - z jej pomocą możesz znacznie przyspieszyć rozwiązywanie wielu problemów w progresjach. Oto doskonały przykład:

Problem numer 3. Piąty wyraz progresji arytmetycznej to 8,4, a dziesiąty to 14,4. Znajdź piętnasty semestr tego postępu.

Rozwiązanie. Ponieważ $ ((a) _ (5)) = 8,4 $, $ ((a) _ (10)) = 14,4 $, a musisz znaleźć $ ((a) _ (15)) $, wtedy zauważamy następujące :

\ [\ początek (wyrównaj) & ((a) _ (15)) - ((a) _ (10)) = 5d; \\ & ((a) _ (10)) - ((a) _ (5)) = 5d. \\ \ koniec (wyrównaj) \]

Ale przez warunek $ ((a) _ (10)) - ((a) _ (5)) = 14,4-8,4 = 6 $, zatem 5d = 6 $, skąd mamy:

\ [\ początek (wyrównaj) & ((a) _ (15)) - 14,4 = 6; \\ & ((a) _ (15)) = 6 + 14,4 = 20,4. \\ \ koniec (wyrównaj) \]

Odpowiedź: 20,4

To wszystko! Nie musieliśmy układać układów równań i obliczać pierwszego członu i różnicy - wszystko zostało rozwiązane w zaledwie kilku linijkach.

Rozważmy teraz inny rodzaj zadań - znalezienie negatywnych i pozytywnych członków progresji. Nie jest tajemnicą, że jeśli progresja wzrasta, podczas gdy jej pierwszy termin jest ujemny, to prędzej czy później pojawią się w nim dodatnie. I przeciwnie: członkowie progresji malejącej prędzej czy później staną się negatywni.

Jednocześnie nie zawsze jest możliwe obmacywanie tej chwili „z przodu”, sekwencyjnie przechodząc przez elementy. Często problemy są projektowane w taki sposób, że bez znajomości wzorów obliczenia zajęłyby kilka arkuszy - po prostu zasypialiśmy, gdy znaleźliśmy odpowiedź. Dlatego postaramy się rozwiązać te problemy w szybszy sposób.

Problem numer 4. Ile wyrazów ujemnych znajduje się w postępie arytmetycznym -38,5; -35.8; ...?

Rozwiązanie. Tak więc $ ((a) _ (1)) = - 38,5 $, $ ((a) _ (2)) = - 35,8 $, skąd od razu znajdujemy różnicę:

Zauważ, że różnica jest dodatnia, więc progresja wzrasta. Pierwszy wyraz jest ujemny, więc w pewnym momencie naprawdę natkniemy się na liczby dodatnie. Pytanie tylko, kiedy to się stanie.

Spróbujmy dowiedzieć się: jak długo (tj. do jakiej liczby naturalnej $ n $) zachowana jest negatywność terminów:

\ [\ begin (align) & ((a) _ (n)) \ lt 0 \ Rightarrow ((a) _ (1)) + \ left (n-1 \ right) d \ lt 0; \\ & -38.5+ \ lewo (n-1 \ prawo) \ cdot 2.7 \ lt 0; \ quad \ lewo | \ cdot 10 \ prawo. \\ & -385 + 27 \ cdot \ lewo (n-1 \ prawo) \ lt 0; \\ & -385 + 27n-27 \ lt 0; \\ & 27n \ lt 412; \\ & n \ lt 15 \ frac (7) (27) \ Strzałka w prawo ((n) _ (\ max)) = 15. \\ \ koniec (wyrównaj) \]

Ostatnia linijka wymaga wyjaśnienia. Wiemy więc, że $ n \ lt 15 \ frac (7) (27) $. Z drugiej strony zadowolimy się tylko całkowitymi wartościami liczby (dodatkowo: $ n \ in \ mathbb (N) $), więc największa dozwolona liczba to dokładnie $ n = 15 $, a w żadnym wypadku ma 16 lat.

Numer problemu 5. W postępie arytmetycznym $ (() _ (5)) = - 150, (() _ (6)) = - 147 $. Znajdź numer pierwszego pozytywnego wyrazu tego progresji.

Byłby to dokładnie ten sam problem co poprzedni, ale nie znamy $ ((a) _ (1)) $. Ale sąsiednie wyrazy są znane: $ ((a) _ (5)) $ i $ ((a) _ (6)) $, więc łatwo możemy znaleźć różnicę progresji:

Dodatkowo postaramy się wyrazić piąty wyraz w terminach pierwszego i różnicę według standardowej formuły:

\ [\ początek (wyrównaj) & ((a) _ (n)) = ((a) _ (1)) + \ lewo (n-1 \ prawo) \ cdot d; \\ & ((a) _ (5)) = ((a) _ (1)) + 4d; \\ & -150 = ((a) _ (1)) + 4 \ cdot 3; \\ & ((a) _ (1)) = - 150-12 = -162. \\ \ koniec (wyrównaj) \]

Teraz postępujemy analogicznie do poprzedniego zadania. Dowiadujemy się, w którym momencie naszej sekwencji będą liczby dodatnie:

\ [\ begin (align) & ((a) _ (n)) = - 162+ \ left (n-1 \ right) \ cdot 3 \ gt 0; \\ & -162 + 3n-3 \ gt 0; \\ & 3n \ gt 165; \\ & n \ gt 55 \ Strzałka w prawo ((n) _ (\ min)) = 56. \\ \ koniec (wyrównaj) \]

Najmniejsze całkowite rozwiązanie tej nierówności to 56.

Uwaga: w ostatnim zadaniu wszystko zostało zredukowane do ścisłej nierówności, więc opcja $ n = 55 $ nam nie odpowiada.

Teraz, gdy nauczyliśmy się rozwiązywać proste problemy, przejdźmy do bardziej złożonych. Ale najpierw przestudiujmy kolejną bardzo przydatną właściwość progresji arytmetycznych, która zaoszczędzi nam wiele czasu i nierównych komórek w przyszłości :)

Średnia arytmetyczna i równe wcięcia

Rozważmy kilka kolejnych elementów rosnącego ciągu arytmetycznego $ \ left (((a) _ (n)) \ right) $. Spróbujmy zaznaczyć je na osi liczbowej:

Elementy postępu arytmetycznego na osi liczbowej

W szczególności zwróciłem uwagę na arbitralne terminy $ ((a) _ (n-3), ..., ((a) _ (n + 3)) $, a nie żadne $ ((a) _ (1)) , \ ( (a) _ (2)), \ ((a) _ (3)) $ itd. Ponieważ reguła, o której teraz opowiem, działa tak samo dla dowolnych „segmentów”.

A zasada jest bardzo prosta. Zapamiętajmy formułę rekurencji i zapiszmy ją dla wszystkich zaznaczonych członków:

\ [\ początek (wyrównaj) & ((a) _ (n-2)) = ((a) _ (n-3)) + d; \\ & ((a) _ (n-1)) = ((a) _ (n-2)) + d; \\ & ((a) _ (n)) = ((a) _ (n-1) + d; \\ & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n + 1)) + d; \\ \ koniec (wyrównaj) \]

Jednak te równości można przepisać inaczej:

\ [\ początek (wyrównaj) & ((a) _ (n-1)) = ((a) _ (n)) - d; \\ & ((a) _ (n-2)) = ((a) _ (n)) - 2d; \\ & ((a) _ (n-3)) = ((a) _ (n)) - 3d; \\ & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n)) + 2d; \\ & ((a) _ (n + 3)) = ((a) _ (n)) + 3d; \\ \ koniec (wyrównaj) \]

No i co z tego? Oraz fakt, że wyrazy $ ((a) _ (n-1) $ i $ ((a) _ (n + 1)) $ leżą w tej samej odległości od $ ((a) _ (n)) $ . A ta odległość jest równa $ d $. To samo można powiedzieć o członkach $ ((a) _ (n-2)) $ i $ ((a) _ (n + 2)) $ - również są usuwane z $ ((a) _ (n) ) $ taka sama odległość równa 2d $. Możesz kontynuować w nieskończoność, ale znaczenie dobrze obrazuje obraz.

Członkowie progresji leżą w tej samej odległości od centrum

Co to dla nas oznacza? Oznacza to, że możesz znaleźć $ ((a) _ (n)) $, jeśli znane są sąsiednie liczby:

\ [((a) _ (n)) = \ frac (((a) _ (n-1)) + ((a) _ (n + 1))) (2) \]

Wymyśliliśmy doskonałe stwierdzenie: każdy element ciągu arytmetycznego jest równy średniej arytmetycznej sąsiednich wyrazów! Co więcej: możemy odejść od naszych $ ((a) _ (n)) $ w lewo i w prawo nie o jeden krok, ale o krok $ k $ - a i tak formuła będzie poprawna:

\ [((a) _ (n)) = \ frac (((a) _ (n-k)) + ((a) _ (n + k))) (2) \]

Te. możemy łatwo znaleźć jakieś $ ((a) _ (150)) $, jeśli znamy $ ((a) _ (100)) $ i $ ((a) _ (200)) $, ponieważ $ ((a) _ (150)) = \ frac (((a) _ (100)) + ((a) _ (200))) (2) $. Na pierwszy rzut oka może się wydawać, że ten fakt nie daje nam nic pożytecznego. Jednak w praktyce wiele problemów jest specjalnie „wyostrzanych” do użycia średniej arytmetycznej. Spójrz:

Numer problemu 6. Znajdź wszystkie wartości $ x $, dla których liczby $ -6 ((x) ^ (2)) $, $ x + 1 $ i $ 14 + 4 ((x) ^ (2)) $ są kolejnymi członkami postępu arytmetycznego (w kolejności).

Rozwiązanie. Ponieważ wskazane liczby należą do progresji, spełniony jest dla nich warunek średniej arytmetycznej: element centralny $ x + 1 $ można wyrazić w postaci elementów sąsiadujących:

\ [\ begin (wyrównaj) & x + 1 = \ frac (-6 ((x) ^ (2)) + 14 + 4 ((x) ^ (2))) (2); \\ & x + 1 = \ frac (14-2 ((x) ^ (2))) (2); \\ & x + 1 = 7 - ((x) ^ (2)); \\ & ((x) ^ (2)) + x-6 = 0. \\ \ koniec (wyrównaj) \]

Rezultatem jest klasyczne równanie kwadratowe. Jego pierwiastki: $ x = 2 $ i $ x = -3 $ - to są odpowiedzi.

Odpowiedź: -3; 2.

Problem numer 7. Znajdź wartości $$, dla których liczby $ -1; 4-3; (() ^ (2)) + 1 $ tworzą postęp arytmetyczny (w pokazanej kolejności).

Rozwiązanie. Ponownie wyrażamy środkowy wyraz w kategoriach średniej arytmetycznej sąsiednich wyrazów:

\ [\ begin (align) & 4x-3 = \ frac (x-1 + ((x) ^ (2)) + 1) (2); \\ & 4x-3 = \ frac (((x) ^ (2)) + x) (2); \ quad \ left | \ cdot 2 \ po prawej .; \\ & 8x-6 = ((x) ^ (2)) + x; \\ & ((x) ^ (2)) - 7x + 6 = 0. \\ \ koniec (wyrównaj) \]

Znowu równanie kwadratowe. I znowu mamy dwa pierwiastki: $x = 6 $ i $x = 1 $.

Odpowiedź 1; 6.

Jeśli w trakcie rozwiązywania problemu uzyskasz kilka brutalnych liczb lub nie jesteś całkowicie pewien poprawności znalezionych odpowiedzi, istnieje wspaniała technika, która pozwala sprawdzić: czy rozwiązaliśmy problem poprawnie?

Np. w zadaniu nr 6 otrzymaliśmy odpowiedzi -3 i 2. Jak sprawdzić poprawność tych odpowiedzi? Po prostu podłączmy je do stanu początkowego i zobaczmy, co się stanie. Przypomnę, że mamy trzy liczby ($ -6 (() ^ (2)) $, $ + 1 $ i 14 $ + 4 (() ^ (2)) $), które muszą tworzyć ciąg arytmetyczny. Zastąp $ x = -3 $:

\ [\ begin (align) & x = -3 \ Rightarrow \\ & -6 ((x) ^ (2)) = - 54; \\ & x + 1 = -2; \\ & 14 + 4 ((x) ^ (2)) = 50. \ koniec (wyrównaj) \]

Otrzymane numery -54; -2; 50, które różnią się o 52, to niewątpliwie postęp arytmetyczny. To samo dzieje się dla $ x = 2 $:

\ [\ begin (align) & x = 2 \ Rightarrow \\ & -6 ((x) ^ (2)) = - 24; \\ & x + 1 = 3; \\ & 14 + 4 ((x) ^ (2)) = 30. \ koniec (wyrównaj) \]

Znowu progresja, ale z różnicą 27. W ten sposób problem został rozwiązany poprawnie. Zainteresowani mogą sami sprawdzić drugi problem, ale od razu powiem: tam też wszystko jest w porządku.

Generalnie przy rozwiązywaniu ostatnich problemów natknęliśmy się na jeszcze jeden ciekawy fakt, o którym również należy pamiętać:

Jeśli trzy liczby są takie, że druga jest średnią arytmetyczną pierwszej i ostatniej, to te liczby tworzą ciąg arytmetyczny.

W przyszłości zrozumienie tego stwierdzenia pozwoli nam dosłownie „skonstruować” niezbędne progresje w oparciu o stan problemu. Zanim jednak przejdziemy do takiej „konstrukcji”, należy zwrócić uwagę na jeszcze jeden fakt, który bezpośrednio wynika z tego, co już zostało rozważone.

Grupowanie i suma elementów

Wróćmy ponownie do osi liczbowej. Zwróćmy uwagę na kilku członków progresji, między którymi być może. jest wielu innych członków:

Linia liczbowa ma zaznaczonych 6 elementów

Spróbujmy wyrazić „lewy ogon” w postaci $ ((a) _ (n)) $ i $ d $, a „prawy ogon” w postaci $ ((a) _ (k)) $ i $ d $ . To jest bardzo proste:

\ [\ początek (wyrównaj) & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n)) + 2d; \\ & ((a) _ (k-1)) = ((a) _ (k)) - d; \\ & ((a) _ (k-2)) = ((a) _ (k)) - 2d. \\ \ koniec (wyrównaj) \]

Teraz zauważ, że następujące sumy są równe:

\ [\ początek (wyrównaj) & ((a) _ (n)) + ((a) _ (k)) = S; \\ & ((a) _ (n + 1)) + ((a) _ (k-1)) = ((a) _ (n)) + d + ((a) _ (k)) - d = S; \\ & ((a) _ (n + 2)) + ((a) _ (k-2)) = ((a) _ (n)) + 2d + ((a) _ (k)) - 2d = S. \ koniec (wyrównaj) \]

Mówiąc najprościej, jeśli weźmiemy za początek dwa elementy progresji, które w sumie są równe pewnej liczbie $S $, a następnie zaczniemy chodzić od tych elementów w przeciwnych kierunkach (do siebie lub odwrotnie, aby się oddalić) , następnie sumy elementów, na które się natkniemy, również będą równe$S $. Najwyraźniej można to przedstawić graficznie:

Równe wcięcie daje równe kwoty

Zrozumienie tego faktu pozwoli nam rozwiązywać problemy o fundamentalnie wyższym poziomie złożoności niż te, które rozważaliśmy powyżej. Na przykład takie:

Problem numer 8. Wyznacz różnicę ciągu arytmetycznego, w którym pierwszy składnik wynosi 66, a iloczyn drugiego i dwunastego składnika jest najmniejszy z możliwych.

Rozwiązanie. Zapiszmy wszystko, co wiemy:

\ [\ początek (wyrównaj) & ((a) _ (1)) = 66; \\ i d =? \\ & ((a) _ (2)) \ cdot ((a) _ (12)) = \ min. \ koniec (wyrównaj) \]

Nie znamy więc różnicy progresji $d $. Właściwie całe rozwiązanie zostanie zbudowane wokół różnicy, ponieważ iloczyn $ ((a) _ (2)) \ cdot ((a) _ (12)) $ można przepisać w następujący sposób:

\ [\ początek (wyrównaj) & ((a) _ (2)) = ((a) _ (1)) + d = 66 + d; \\ & ((a) _ (12)) = ((a) _ (1)) + 11d = 66 + 11d; \\ & ((a) _ (2)) \ cdot ((a) _ (12)) = \ lewo (66 + d \ prawo) \ cdot \ lewo (66 + 11d \ prawo) = \\ & = 11 \ cdot \ lewy (d + 66 \ prawy) \ cdot \ lewy (d + 6 \ prawy). \ koniec (wyrównaj) \]

Dla tych w zbiorniku: z drugiego nawiasu wyjąłem wspólny dzielnik 11. Poszukiwany iloczyn jest więc funkcją kwadratową względem zmiennej $ d $. Rozważmy zatem funkcję $ f \ left (d \ right) = 11 \ left (d + 66 \ right) \ left (d + 6 \ right) $ - jej wykres będzie parabolą z rozgałęzieniami do góry, ponieważ jeśli rozszerzymy nawiasy, otrzymamy:

\ [\ begin (align) & f \ left (d \ right) = 11 \ left (((d) ^ (2)) + 66d + 6d + 66 \ cdot 6 \ right) = \\ & = 11 (( d) ^ (2)) + 11 \ cdot 72d + 11 \ cdot 66 \ cdot 6 \ koniec (wyrównaj) \]

Jak widać, współczynnik przy wyrazie wiodącym wynosi 11 - jest to liczba dodatnia, więc tak naprawdę mamy do czynienia z parabolą z rozgałęzieniami do góry:

wykres funkcji kwadratowej - parabola

Uwaga: ta parabola przyjmuje swoją minimalną wartość w wierzchołku z odciętą $ ((d) _ (0)) $. Oczywiście tę odciętą możemy obliczyć według standardowego schematu (jest też formuła $ ((d) _ (0)) = (- b) / (2a) \; $), ale byłoby to znacznie rozsądniejsze aby zauważyć, że żądany wierzchołek leży na osi symetrii paraboli, więc punkt $ ((d) _ (0)) $ jest w równej odległości od pierwiastków równania $ f \ left (d \ right) = 0 $:

\ [\ początek (wyrównaj) & f \ lewo (d \ prawo) = 0; \\ & 11 \ cdot \ lewy (d + 66 \ prawy) \ cdot \ lewy (d + 6 \ prawy) = 0; \\ & ((d) _ (1)) = - 66; \ quad ((d) _ (2)) = - 6. \\ \ koniec (wyrównaj) \]

Dlatego nie spieszyłem się z otwieraniem nawiasów: w pierwotnej formie korzenie były bardzo, bardzo łatwe do znalezienia. Zatem odcięta jest równa średniej arytmetycznej liczb -66 i -6:

\ [((d) _ (0)) = \ frac (-66-6) (2) = - 36 \]

Co daje nam odkryta liczba? Dzięki niej wymagany iloczyn przyjmuje najmniejszą wartość (swoją drogą nie policzyliśmy $ ((y) _ (\ min)) $ - nie potrzebujemy tego). Jednocześnie liczba ta jest różnicą między pierwotną progresją, tj. znaleźliśmy odpowiedź :)

Odpowiedź: −36

Problem numer 9. Wstaw trzy liczby między liczby $ - \ frac (1) (2) $ i $ - \ frac (1) (6) $ tak, aby razem z podanymi liczbami tworzyły ciąg arytmetyczny.

Rozwiązanie. Zasadniczo musimy stworzyć sekwencję pięciu liczb, przy czym pierwsza i ostatnia liczba są już znane. Oznaczmy brakujące liczby przez zmienne $ x $, $ y $ i $ z $:

\ [\ lewo (((a) _ (n)) \ prawo) = \ lewo \ (- \ frac (1) (2); x; y; z; - \ frac (1) (6) \ prawo \ ) \]

Zauważ, że liczba $ y $ jest "środkiem" naszego ciągu - jest równoodległa zarówno od liczb $ x $ i $ z $, jak i od liczb $ - \ frac (1) (2) $ i $ - \ frac (1) ( 6) $. A jeśli w tej chwili nie możemy otrzymać $y $ z liczb $x$ i $z $, to sytuacja jest inna z końcami progresji. Zapamiętywanie średniej arytmetycznej:

Teraz, znając $ y $, znajdziemy pozostałe liczby. Zauważ, że $ x $ leży między liczbami $ - \ frac (1) (2) $ i właśnie znalezioną wartością $ y = - \ frac (1) (3) $. Dlatego

Rozumując podobnie, znajdujemy pozostałą liczbę:

Gotowy! Znaleźliśmy wszystkie trzy numery. Zapiszmy je w odpowiedzi w kolejności, w jakiej powinny być wstawione między oryginalne liczby.

Odpowiedź: $ - \ frac (5) (12); \ - \ frac (1) (3); \ - \ frac (1) (4) $

Problem numer 10. Wstaw kilka liczb między liczby 2 i 42, które razem z tymi liczbami tworzą ciąg arytmetyczny, jeśli wiesz, że suma pierwszej, drugiej i ostatniej z wprowadzonych liczb wynosi 56.

Rozwiązanie. Jeszcze trudniejsze zadanie, które jednak rozwiązuje się według tego samego schematu, co poprzednie - poprzez średnią arytmetyczną. Problem polega na tym, że nie wiemy dokładnie, ile liczb wstawić. Dlatego dla jednoznaczności załóżmy, że po wstawieniu wszystkiego będzie dokładnie $ n $ liczb, a pierwsza z nich to 2, a ostatnia to 42. W tym przypadku pożądany ciąg arytmetyczny można przedstawić jako:

\ [\ lewo (((a) _ (n)) \ prawo) = \ lewo \ (2; ((a) _ (2)); ((a) _ (3)); ...; (( a) _ (n-1)); 42 \ prawy \) \]

\ [((a) _ (2)) + ((a) _ (3)) + ((a) _ (n-1)) = 56 \]

Zauważ jednak, że liczby $ ((a) _ (2)) $ i $ ((a) _ (n-1)) $ są otrzymywane z liczb 2 i 42 na krawędziach o jeden krok do siebie, czyli ... do środka sekwencji. To znaczy że

\ [((a) _ (2)) + ((a) _ (n-1)) = 2 + 42 = 44 \]

Ale wtedy wyrażenie napisane powyżej można przepisać w następujący sposób:

\ [\ początek (wyrównaj) & ((a) _ (2)) + ((a) _ (3)) + ((a) _ (n-1)) = 56; \\ & \ lewo (((a) _ (2)) + ((a) _ (n-1)) \ prawo) + ((a) _ (3)) = 56; \\ & 44 + ((a) _ (3)) = 56; \\ & ((a) _ (3)) = 56-44 = 12. \\ \ koniec (wyrównaj) \]

Znając $ ((a) _ (3)) $ i $ ((a) _ (1)) $, możemy łatwo znaleźć różnicę progresji:

\ [\ początek (wyrównaj) & ((a) _ (3)) - ((a) _ (1)) = 12 - 2 = 10; \\ & ((a) _ (3)) - ((a) _ (1)) = \ lewo (3-1 \ prawo) \ cdot d = 2d; \\ & 2d = 10 \ Strzałka w prawo d = 5. \\ \ koniec (wyrównaj) \]

Pozostaje tylko znaleźć resztę członków:

\ [\ początek (wyrównaj) & ((a) _ (1)) = 2; \\ & ((a) _ (2)) = 2 + 5 = 7; \\ & ((a) _ (3)) = 12; \\ & ((a) _ (4)) = 2 + 3 \ cdot 5 = 17; \\ & ((a) _ (5)) = 2 + 4 \ cdot 5 = 22; \\ & ((a) _ (6)) = 2 + 5 \ cdot 5 = 27; \\ & ((a) _ (7)) = 2 + 6 \ cdot 5 = 32; \\ & ((a) _ (8)) = 2 + 7 \ cdot 5 = 37; \\ & ((a) _ (9)) = 2 + 8 \ cdot 5 = 42; \\ \ koniec (wyrównaj) \]

Tak więc już w 9 kroku dojdziemy do lewego końca ciągu - liczby 42. W sumie trzeba było wstawić tylko 7 liczb: 7; 12; 17; 22; 27; 32; 37.

Odpowiedź: 7; 12; 17; 22; 27; 32; 37

Problemy tekstowe z progresją

Podsumowując, chciałbym rozważyć kilka stosunkowo prostych zadań. Cóż, jakie to proste: dla większości uczniów, którzy uczą się matematyki w szkole i nie czytali tego, co jest napisane powyżej, te zadania mogą wydawać się puszką. Niemniej jednak to właśnie takie problemy pojawiają się w OGE i USE w matematyce, dlatego polecam zapoznać się z nimi.

Numer problemu 11. Brygada wyprodukowała w styczniu 62 części, aw każdym kolejnym miesiącu produkowała o 14 części więcej niż w poprzednim. Ile części wykonał zespół w listopadzie?

Rozwiązanie. Oczywiście liczba części, rozplanowanych według miesiąca, będzie oznaczać rosnący postęp arytmetyczny. Ponadto:

\ [\ początek (wyrównaj) & ((a) _ (1)) = 62; \ quad d = 14; \\ & ((a) _ (n)) = 62+ \ lewo (n-1 \ prawo) \ cdot 14. \\ \ end (wyrównaj) \]

Listopad jest 11 miesiącem roku, więc musimy znaleźć $ ((a) _ (11)) $:

\ [((a) _ (11)) = 62 + 10 \ cdot 14 = 202 \]

W konsekwencji w listopadzie wyprodukowanych zostanie 202 części.

Numer problemu 12. W styczniu introligatornia oprawiła 216 książek, a co miesiąc oprawiała o 4 książki więcej niż poprzednia. Ile książek oprawiły warsztaty w grudniu?

Rozwiązanie. Wszystkie takie same:

$ \ początek (wyrównaj) & ((a) _ (1)) = 216; \ quad d = 4; \\ & ((a) _ (n)) = 216+ \ lewo (n-1 \ prawo) \ cdot 4. \\ \ end (wyrównaj) $

Grudzień jest ostatnim, 12-tym miesiącem roku, więc szukamy $ ((a) _ (12)) $:

\ [((a) _ (12)) = 216 + 11 \ cdot 4 = 260 \]

Oto odpowiedź - 260 książek zostanie oprawionych w grudniu.

Cóż, jeśli doczytałeś tak daleko, spieszę ci pogratulować: pomyślnie przeszedłeś „kurs dla młodych wojowników” w progresjach arytmetycznych. Możesz spokojnie przejść do następnej lekcji, gdzie przestudiujemy wzór na sumę progresji, a także ważne i bardzo przydatne konsekwencje z niej.

Pierwszy poziom

Postęp arytmetyczny. Szczegółowa teoria z przykładami (2019)

Sekwencja liczbowa

Więc usiądźmy i zacznijmy pisać jakieś liczby. Na przykład:
Możesz pisać dowolne liczby i może być ich tyle, ile chcesz (w naszym przypadku ich). Bez względu na to, ile liczb napiszemy, zawsze możemy powiedzieć, która jest pierwsza, a która druga i tak dalej do ostatniej, czyli możemy je ponumerować. Oto przykład sekwencji liczb:

Sekwencja liczbowa
Na przykład dla naszej sekwencji:

Przypisany numer jest specyficzny tylko dla jednego numeru w sekwencji. Innymi słowy, w sekwencji nie ma trzech sekund. Druga liczba (podobnie jak -ta liczba) to zawsze jeden.
Liczba z numerem nazywana jest czwartym elementem ciągu.

Zwykle nazywamy cały ciąg literą (na przykład), a każdy element tej sekwencji jest tą samą literą z indeksem równym numerowi tego elementu:.

W naszym przypadku:

Załóżmy, że mamy ciąg liczb, w którym różnica między sąsiednimi liczbami jest taka sama i równa.
Na przykład:

itp.
Ta sekwencja liczb nazywana jest postępem arytmetycznym.
Termin „postęp” został wprowadzony przez rzymskiego autora Boecjusza w VI wieku i był rozumiany w szerszym znaczeniu jako nieskończony ciąg liczb. Nazwa „arytmetyka” została przeniesiona z teorii proporcji ciągłych, którą zajmowali się starożytni Grecy.

Jest to ciąg liczbowy, którego każdy człon jest równy poprzedniemu, dodany do tej samej liczby. Liczba ta nazywana jest różnicą postępu arytmetycznego i jest oznaczona przez.

Spróbuj określić, które ciągi liczb są ciągiem arytmetycznym, a które nie:

a)
b)
C)
D)

Zrozumiany? Porównajmy nasze odpowiedzi:
jest postęp arytmetyczny - b, c.
Nie jest postęp arytmetyczny - a, d.

Wróćmy do podanej progresji () i spróbujmy znaleźć wartość jej składowej. istnieje dwa sposób, aby to znaleźć.

1. Metoda

Do poprzedniej wartości możemy dodawać numer progresji, aż dojdziemy do trzeciego terminu progresji. Dobrze, że nie mamy wiele do podsumowania - tylko trzy wartości:

Tak więc th element opisanego ciągu arytmetycznego jest równy.

2. Metoda

Co by było, gdybyśmy musieli znaleźć wartość trzeciego terminu w progresji? Sumowanie zajęłoby nam więcej niż godzinę i nie jest faktem, że nie pomylilibyśmy się przy dodawaniu liczb.
Oczywiście matematycy wymyślili sposób, w którym nie trzeba dodawać różnicy postępu arytmetycznego do poprzedniej wartości. Przyjrzyj się uważnie rysunkowi, który narysowałeś ... Z pewnością zauważyłeś już pewien wzór, a mianowicie:

Na przykład zobaczmy, jak dodaje się wartość th elementu tego ciągu arytmetycznego:


Innymi słowy:

Spróbuj sam znaleźć w ten sposób wartość członka danego ciągu arytmetycznego.

Obliczony? Porównaj swoje notatki z odpowiedzią:

Zwróć uwagę, że otrzymałeś dokładnie taką samą liczbę jak w poprzedniej metodzie, gdy kolejno dodawaliśmy składowe progresji arytmetycznej do poprzedniej wartości.
Spróbujmy "odpersonalizować" tę formułę - sprowadzimy ją do ogólnej postaci i uzyskamy:

Równanie progresji arytmetycznej.

Progresje arytmetyczne rosną, a czasem maleją.

Rosnąco- progresje, w których każda kolejna wartość członków jest większa od poprzedniej.
Na przykład:

Malejące- progresje, w których każda kolejna wartość członków jest mniejsza od poprzedniej.
Na przykład:

Wyprowadzona formuła jest używana do obliczania terminów zarówno rosnących, jak i malejących postępu arytmetycznego.
Sprawdźmy to w praktyce.
Dostajemy ciąg arytmetyczny składający się z następujących liczb: Sprawdźmy, jaka będzie th liczba tego ciągu arytmetycznego, jeśli użyjemy naszego wzoru do obliczenia:

Od tego czasu:

W ten sposób upewniliśmy się, że formuła działa zarówno w malejącym, jak i rosnącym postępie arytmetycznym.
Spróbuj samodzielnie znaleźć th i th wyraz tego ciągu arytmetycznego.

Porównajmy otrzymane wyniki:

Właściwość progresji arytmetycznej

Skomplikujmy zadanie - wyprowadzimy własność progresji arytmetycznej.
Załóżmy, że otrzymaliśmy następujący warunek:
- postęp arytmetyczny, znajdź wartość.
Spokojnie, mówisz i zaczynasz liczyć zgodnie ze znaną już formułą:

Niech więc:

Dokładnie tak. Okazuje się, że najpierw znajdujemy, a następnie dodajemy do pierwszej liczby i otrzymujemy to, czego szukamy. Jeśli progresja jest reprezentowana przez małe wartości, to nie ma w tym nic skomplikowanego, ale czy dane są liczby w warunku? Przyznaj, jest szansa na pomyłkę w obliczeniach.
Zastanów się teraz, czy można rozwiązać ten problem jednym działaniem przy użyciu dowolnej formuły? Oczywiście tak i to właśnie ją teraz postaramy się wycofać.

Oznaczmy wymagany termin progresji arytmetycznej, ponieważ znamy wzór na jego znalezienie - jest to ten sam wzór, który wyprowadziliśmy na początku:
, następnie:

• poprzedni członek progresji to:
• kolejnym członkiem progresji jest:

Podsumujmy dotychczasowych i kolejnych członków progresji:

Okazuje się, że suma poprzednich i kolejnych członków progresji jest podwojoną wartością członka progresji znajdującego się między nimi. Innymi słowy, aby znaleźć wartość członka progresji ze znanymi poprzednimi i kolejnymi wartościami, konieczne jest ich zsumowanie i podzielenie przez.

Zgadza się, mamy ten sam numer. Naprawmy materiał. Sam oblicz wartość progresji, bo to wcale nie jest trudne.

Bardzo dobrze! O progresji wiesz prawie wszystko! Pozostaje tylko jedna formuła do nauczenia się, którą według legendy bez trudu wywnioskował sobie jeden z największych matematyków wszechczasów, „król matematyków” – Karl Gauss…

Kiedy Karl Gauss miał 9 lat, nauczyciel zajmujący się sprawdzaniem pracy uczniów w innych klasach zadał na lekcji następujący problem: „Oblicz sumę wszystkich liczb naturalnych od do (według innych źródeł do) włącznie”. Wyobraź sobie zdziwienie nauczyciela, gdy jeden z jego uczniów (był nim Karl Gauss) w ciągu minuty udzielił poprawnej odpowiedzi na zadanie, podczas gdy większość kolegów z klasy śmiałka, po długich obliczeniach, otrzymała błędny wynik…

Młody Karl Gauss zauważył pewien wzór, który można łatwo zauważyć.
Powiedzmy, że mamy ciąg arytmetyczny składający się z -tych elementów: Musimy znaleźć sumę danych elementów ciągu arytmetycznego. Oczywiście możemy ręcznie zsumować wszystkie wartości, ale co jeśli w zadaniu trzeba znaleźć sumę jego członków, czego szukał Gauss?

Narysujmy daną progresję. Przyjrzyj się dokładnie podświetlonym liczbom i spróbuj wykonać na nich różne operacje matematyczne.


Próbowałeś tego? Co zauważyłeś? Dobrze! Ich sumy są równe

Teraz powiedz mi, ile takich par jest w danej progresji? Oczywiście dokładnie połowa wszystkich liczb.
Bazując na fakcie, że suma dwóch elementów postępu arytmetycznego jest równa i podobnych równych par, otrzymujemy, że suma całkowita wynosi:
.
Zatem wzór na sumę pierwszych wyrazów dowolnego ciągu arytmetycznego będzie następujący:

W niektórych problemach nie znamy terminu, ale znamy różnicę w progresji. Spróbuj zastąpić sumę we wzorze formułą czwartego terminu.
Co zrobiłeś?

Bardzo dobrze! Wróćmy teraz do problemu, który został postawiony Karlowi Gaussowi: oblicz sam, jaka jest suma liczb rozpoczynających się od -tego i suma liczb zaczynających się od -tego.

Ile dostałeś?
Gauss stwierdził, że suma członków jest równa, a suma członków. Czy tak zdecydowałeś?

W rzeczywistości wzór na sumę członków postępu arytmetycznego został udowodniony przez starożytnego greckiego naukowca Diofantusa w III wieku i przez cały ten czas dowcipni ludzie używali właściwości postępu arytmetycznego z mocą i głównym.
Na przykład wyobraź sobie starożytny Egipt i najbardziej ambitny plac budowy tamtych czasów - budowę piramidy ... Rysunek pokazuje jedną stronę.

Gdzie tu jest progresja, mówisz? Przyjrzyj się uważnie i znajdź wzór w liczbie bloków piasku w każdym rzędzie ściany piramidy.


Czy to nie postęp arytmetyczny? Oblicz, ile bloków potrzeba do zbudowania jednej ściany, jeśli klocki zostaną umieszczone w podstawie. Mam nadzieję, że nie będziesz liczyć przesuwając palcem po monitorze, pamiętasz ostatnią formułę i wszystko, co powiedzieliśmy o progresji arytmetycznej?

W tym przypadku progresja wygląda tak:.
Różnica postępu arytmetycznego.
Liczba członków postępu arytmetycznego.
Podstawmy nasze dane do ostatnich formuł (liczmy bloki na 2 sposoby).

Metoda 1.

Metoda 2.

A teraz możesz obliczyć na monitorze: porównaj uzyskane wartości z liczbą bloków znajdujących się w naszej piramidzie. Czy to się połączyło? Dobra robota, opanowałeś sumę warunków progresji arytmetycznej.
Oczywiście nie można zbudować piramidy z klocków u podstawy, ale z? Spróbuj obliczyć, ile cegieł z piasku potrzeba do zbudowania ściany w tym stanie.
Czy udało Ci się?
Prawidłowa odpowiedź to bloki:

Ćwiczyć

Zadania:

1. Masza nabiera formy do lata. Każdego dnia zwiększa liczbę przysiadów o. Ile razy Masza zrobi przysiady w ciągu tygodni, jeśli na pierwszym treningu zrobiła przysiady.
2. Jaka jest suma wszystkich liczb nieparzystych zawartych w.
3. Podczas przechowywania kłód drwale układają je w taki sposób, aby każda górna warstwa zawierała o jedną kłodę mniej niż poprzednia. Ile bali znajduje się w jednym murze, jeśli bale służą jako podstawa muru.

Odpowiedzi:

1. Zdefiniujmy parametry progresji arytmetycznej. W tym przypadku
   (tygodnie = dni).

   Odpowiedź: Po dwóch tygodniach Masza powinna kucać raz dziennie.

2. Pierwsza liczba nieparzysta, ostatnia liczba.
   Różnica postępu arytmetycznego.
   Liczba liczb nieparzystych w wynosi połowę, jednak fakt ten sprawdzimy za pomocą wzoru na znalezienie -tego wyrazu ciągu arytmetycznego:

   Liczby zawierają liczby nieparzyste.
   Podstaw dostępne dane do wzoru:

   Odpowiedź: Suma wszystkich liczb nieparzystych zawartych w jest równa.

3. Pamiętajmy o problemie piramidy. W naszym przypadku a, ponieważ każda górna warstwa jest zmniejszona o jeden dziennik, to znaczy tylko o kilka warstw.
   Zamieńmy dane do wzoru:

   Odpowiedź: W murze są kłody.

Podsumujmy

1. - ciąg liczb, w którym różnica między sąsiednimi liczbami jest taka sama i równa. Może rosnąć i maleć.
2. Znajdowanie formuły-ty element ciągu arytmetycznego zapisywany jest wzorem -, gdzie jest liczbą liczb w ciągu.
3. Własność członków postępu arytmetycznego- - gdzie to liczba liczb w progresji.
4. Suma członków progresji arytmetycznej można znaleźć na dwa sposoby:
   
   , gdzie jest liczbą wartości.

PROGRES ARYTMETYCZNY. ŚREDNI POZIOM

Sekwencja liczbowa

Usiądźmy i zacznijmy pisać liczby. Na przykład:

Możesz pisać dowolne liczby i może być ich tyle, ile chcesz. Ale zawsze możesz powiedzieć, który z nich jest pierwszy, a który drugi i tak dalej, czyli możemy je ponumerować. To jest przykład sekwencji liczb.

Sekwencja liczbowa to zbiór liczb, z których każdej można przypisać unikalny numer.

Innymi słowy, każda liczba może być powiązana z pewną liczbą naturalną i jedyną. I nie przypiszemy tego numeru żadnemu innemu numerowi z tego zestawu.

Liczba z numerem nazywana jest czwartym elementem ciągu.

Zwykle nazywamy cały ciąg literą (na przykład), a każdy element tej sekwencji jest tą samą literą z indeksem równym numerowi tego elementu:.

Jest to bardzo wygodne, jeśli trzeci wyraz ciągu może być określony jakimś wzorem. Na przykład formuła

ustawia sekwencję:

A formuła to następująca sekwencja:

Na przykład postęp arytmetyczny to ciąg (pierwszy wyraz jest tutaj równy, a różnica). Lub (, różnica).

Formuła N-tego terminu

Powtarzamy formułę, w której aby znaleźć th członka, musisz znać poprzedni lub kilka poprzednich:

Aby znaleźć na przykład trzeci termin progresji za pomocą takiego wzoru, będziemy musieli obliczyć poprzednie dziewięć. Na przykład niech. Następnie:

Jaka jest teraz formuła?

W każdym wierszu dodajemy do, pomnożone przez pewną liczbę. Po co? Bardzo proste: jest to numer obecnego członka minus:

O wiele wygodniej teraz, prawda? Sprawdzamy:

Zdecyduj sam:

W ciągu arytmetycznym znajdź wzór na n-ty wyraz i znajdź setny wyraz.

Rozwiązanie:

Pierwszy termin jest równy. Jaka jest różnica? A oto co:

(ponieważ nazywa się to różnicą, która jest równa różnicy kolejnych członków progresji).

Więc formuła to:

Wtedy setny termin to:

Jaka jest suma wszystkich liczb naturalnych od do?

Według legendy wielki matematyk Karl Gauss, będąc 9-letnim chłopcem, obliczył tę kwotę w kilka minut. Zauważył, że suma pierwszej i ostatniej liczby jest równa, suma drugiej i przedostatniej jest taka sama, suma trzeciej i trzeciej od końca jest taka sama i tak dalej. Ile będzie takich par? Zgadza się, dokładnie połowa liczby wszystkich liczb. Więc,

Ogólny wzór na sumę pierwszych członków dowolnego ciągu arytmetycznego byłby następujący:

Przykład:
Znajdź sumę wszystkich dwucyfrowych wielokrotności.

Rozwiązanie:

Pierwsza taka liczba to. Każdy następny uzyskuje się przez dodanie do poprzedniej liczby. W ten sposób liczby, które nas interesują, tworzą postęp arytmetyczny z pierwszym wyrazem i różnicą.

Formuła dla tego progresji jest równa:

Ilu członków jest w progresji, jeśli wszyscy muszą być dwucyfrowymi?

Bardzo łatwe: .

Ostatni termin w progresji będzie równy. Następnie suma:

Odpowiedź: .

Teraz zdecyduj sam:

1. Zawodnik codziennie biega więcej m niż dzień wcześniej. Ile kilometrów przebiegnie w ciągu tygodni, jeśli przebiegnie km m pierwszego dnia?
2. Rowerzysta pokonuje codziennie więcej kilometrów niż poprzedni. Pierwszego dnia przejechał km. Ile dni potrzebuje na pokonanie kilometra? Ile kilometrów przejedzie ostatniego dnia podróży?
3. Cena lodówki w sklepie spada co roku o tę samą kwotę. Określ, o ile cena lodówki spadała co roku, jeśli wystawiona na sprzedaż za ruble, sześć lat później została sprzedana za ruble.

Odpowiedzi:

1. Najważniejszą rzeczą jest tutaj rozpoznanie ciągu arytmetycznego i określenie jego parametrów. W tym przypadku (tygodnie = dni). Musisz określić sumę pierwszych członków tej progresji:
   .
   Odpowiedź:
2. Podano tutaj: trzeba znaleźć.
   Oczywiście musisz użyć tego samego wzoru na sumę, co w poprzednim zadaniu:
   .
   Zastąp wartości:

   Korzeń oczywiście nie pasuje, więc odpowiedź brzmi.
   Obliczmy odległość przebytą w ciągu ostatniego dnia, korzystając ze wzoru na th term:
   (km).
   Odpowiedź:

3. Dany:. Odnaleźć: .
   Łatwiej się nie da:
   (pocierać).
   Odpowiedź:

PROGRES ARYTMETYCZNY. KRÓTKO O GŁÓWNYM

Jest to ciąg liczb, w którym różnica między sąsiednimi liczbami jest taka sama i równa.

Postęp arytmetyczny może być rosnący () i malejący ().

Na przykład:

Wzór na znalezienie n-tego wyrazu progresji arytmetycznej

zapisany wzorem, gdzie jest liczbą liczb w progresji.

Własność członków postępu arytmetycznego

Pozwala na łatwe odnalezienie członka progresji, jeśli jego sąsiednie członki są znane - gdzie jest liczba numerów w progresji.

Suma członków progresji arytmetycznej

Kwotę można znaleźć na dwa sposoby:

Gdzie jest liczba wartości.

Gdzie jest liczba wartości.

Cóż, temat się skończył. Jeśli czytasz te linijki, to jesteś bardzo fajny.

Ponieważ tylko 5% ludzi jest w stanie opanować coś samodzielnie. A jeśli doczytasz do końca, to jesteś w tych 5%!

Teraz najważniejsza rzecz.

Wymyśliłeś teorię na ten temat. I znowu to jest… po prostu super! Już jesteś lepszy niż większość twoich rówieśników.

Problem w tym, że to może nie wystarczyć...

Po co?

O pomyślne zdanie egzaminu, o przyjęcie do instytutu z ograniczonym budżetem i, CO NAJWAŻNIEJSZE, na całe życie.

Do niczego Cię nie przekonam, powiem tylko jedno...

Osoby, które otrzymały dobre wykształcenie, zarabiają znacznie więcej niż ci, którzy go nie otrzymali. To są statystyki.

Ale to też nie jest najważniejsze.

Najważniejsze, że są BARDZIEJ SZCZĘŚLIWI (są takie badania). Może dlatego, że jest dla nich o wiele więcej możliwości i życie staje się jaśniejsze? Nie wiem...

Ale pomyśl za siebie ...

Czego trzeba, aby być na pewno lepszym od innych na egzaminie i być ostatecznie… bardziej szczęśliwym?

POZNAJ ROZWIĄZYWANIE PROBLEMÓW W TYM TEMACIE.

Na egzaminie nie zostaniesz poproszony o teorię.

Będziesz potrzebować rozwiązuj zadania na chwilę.

A jeśli ich nie rozwiązałeś (DUŻO!), na pewno pójdziesz gdzieś głupio pomylony lub po prostu nie zdążysz.

To jak w sporcie – trzeba to powtarzać w kółko, żeby na pewno wygrać.

Znajdź kolekcję tam, gdzie chcesz, koniecznie z rozwiązaniami, szczegółową analizą i zdecyduj, zdecyduj, zdecyduj!

Możesz skorzystać z naszych zadań (opcjonalnie) i oczywiście je polecamy.

Aby wypełnić swoją rękę naszymi zadaniami, musisz pomóc przedłużyć żywotność podręcznika YouClever, który właśnie czytasz.

Jak? Istnieją dwie opcje:

1. Udostępnij wszystkie ukryte zadania w tym artykule - 299 r
2. Odblokuj dostęp do wszystkich ukrytych zadań we wszystkich 99 artykułach samouczka — 999 rubli

Tak, w naszym podręczniku mamy 99 takich artykułów, a dostęp do wszystkich zadań i wszystkich ukrytych w nich tekstów można otworzyć od razu.

W drugim przypadku Damy ci symulator "6000 problemów z rozwiązaniami i odpowiedziami, dla każdego tematu, dla wszystkich poziomów złożoności." Na pewno wystarczy, aby poradzić sobie z rozwiązywaniem problemów na dowolny temat.

W rzeczywistości jest to znacznie więcej niż tylko symulator – cały program szkoleniowy. W razie potrzeby możesz go również użyć ZA DARMO.

Dostęp do wszystkich tekstów i programów jest zapewniony przez cały okres istnienia serwisu.

Podsumowując...

Jeśli nie lubisz naszych zadań, znajdź inne. Po prostu nie rozwodzij się nad teorią.

„Zrozumiałem” i „Jestem w stanie rozwiązać” to zupełnie inne umiejętności. Potrzebujesz obu.

Znajdź problemy i rozwiąż!