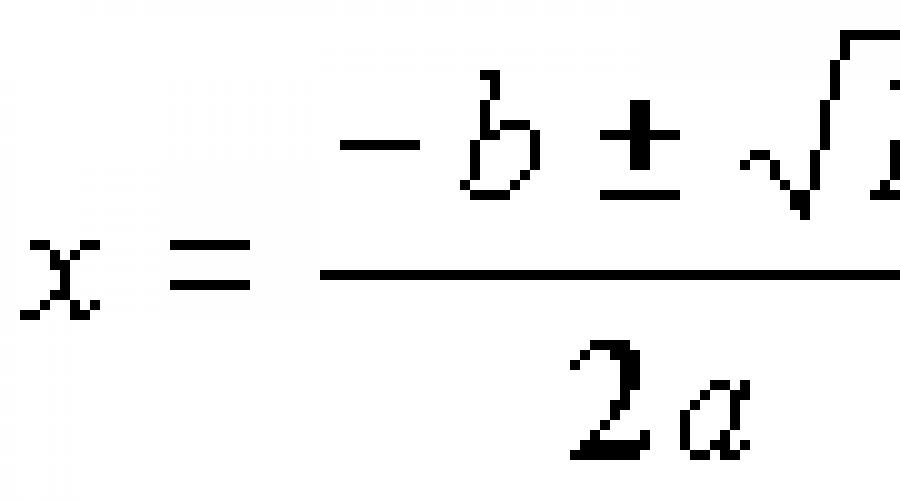
Składane równania są badane w klasie 8, więc nie ma tu nic trudnego. Możliwość ich rozwiązania jest absolutnie konieczna.

Równanie kwadratowe jest równaniem AX 2 + BX + C \u003d 0, gdzie współczynniki A, B i C są dowolnymi liczbami i ≠ 0.

Przed studiowaniem konkretnych metod decyzyjnych zauważamy, że wszystkie równania kwadratowe można podzielić na trzy klasy:

1. Nie masz korzeni;
2. Mieć dokładnie jeden root;
3. Mieć dwa różne korzenie.

Jest to ważna różnica między równaniami kwadratowymi z liniowej, gdzie korzeń zawsze istnieje i jest wyjątkowy. Jak ustalić, ile korzeni ma równanie? Dla tego jest cudowna rzecz - dyskryminujący.

Dyskryminujący

Pozwól równaniu kwadratowym AX 2 + BX + C \u003d 0. Następnie dyskryminujący jest tylko liczba D \u003d B 2 - 4AC.

Ta formuła musi być znana przez serce. Gdzie bierze - teraz nie ma znaczenia. Inne jest ważne: Znak dyskryminacyjny można określić, ile korzeni ma równanie kwadratowe. Mianowicie:

1. IF D.< 0, корней нет;
2. Jeśli d \u003d 0, istnieje dokładnie jeden root;
3. Jeśli D\u003e 0, będą dwa korzenie.

Uwaga: dyskryminujący wskazuje liczbę korzeni, a nie w ogóle na ich znakach, jak z jakiegoś powodu wielu rozważa. Spójrz na przykłady - i zrozumiesz wszystko:

Zadanie. Ile korzeni jest równania kwadratowe:

1. x 2 - 8x + 12 \u003d 0;
2. 5x 2 + 3x + 7 \u003d 0;
3. x 2 - 6x + 9 \u003d 0.

Odnosimy współczynniki dla pierwszego równania i znajdź dyskryminujący:
a \u003d 1, B \u003d -8, C \u003d 12;
D \u003d (-8) 2 - 4 · 1 · 12 \u003d 64 - 48 \u003d 16

Tak więc dyskryminujący jest dodatni, więc równanie ma dwa różne korzenie. Podobnie demontuj drugie równanie:
a \u003d 5; b \u003d 3; C \u003d 7;
D \u003d 3 2 - 4 · 5 · 7 \u003d 9 - 140 \u003d -131.

Dyskryminacyjny jest negatywny, bez korzeni. Ostatnie równanie pozostaje:
a \u003d 1; b \u003d -6; C \u003d 9;
D \u003d (-6) 2 - 4 · 1 · 9 \u003d 36 - 36 \u003d 0.

Dyskryminujący jest zero - korzeń będzie jeden.

Należy pamiętać, że dla każdego równania współczynniki zostały rozładowane. Tak, to długi czas, tak, jest żmudny - ale nie pomywasz współczynników i nie pozwalają na głupie błędy. Wybierz się: szybkość lub jakość.

Przy okazji, jeśli "wypełnisz rękę", po pewnym czasie, nie trzeba już pisać wszystkich współczynników. Takie operacje będą wykonywane w twojej głowie. Większość ludzi zaczyna to robić gdzieś po 50-70 rozwiązanych równań - ogólnie, nie tak bardzo.

Równanie kwadratu Korzenie

Obracamy się teraz, w rzeczywistości decyzji. Jeśli dyskryminujący D\u003e 0, korzenie można znaleźć przez wzory:

Podstawowa formuła korzeni równania kwadratowego

Gdy D \u003d 0 można użyć dowolnego z tych formuł - będzie to ta sama liczba, która będzie odpowiedzią. Wreszcie, jeśli d< 0, корней нет — ничего считать не надо.

1. x 2 - 2x - 3 \u003d 0;
2. 15 - 2x - x 2 \u003d 0;
3. x 2 + 12x + 36 \u003d 0.

Pierwsze równanie:
x 2 - 2x - 3 \u003d 0 ⇒ A \u003d 1; b \u003d -2; C \u003d -3;
D \u003d (-2) 2 - 4 · 1 · (-3) \u003d 16.

D\u003e 0 ⇒ Równanie ma dwa korzenie. Znajdź je:

Drugie równanie:
15 - 2x - x 2 \u003d 0 ⇒ A \u003d -1; b \u003d -2; C \u003d 15;
D \u003d (-2) 2 - 4 · (-1) · 15 \u003d 64.

D\u003e 0 ⇒ Równanie ponownie ma dwa korzenie. Znajdujemy je.

[Rozpocznij (wyrównanie) i ((x) _ (1)) \u003d frac (2+ sqrt (64)) (2 CDOT Left (-1 Po prawej) \u003d - 5; & (x) _ (2)) \u003d frac (2- sqrt (64)) (2 CDOT Left (-1 Po prawej)) \u003d 3. Koniec (wyrównuj)]

Wreszcie trzecia równanie:
x 2 + 12x + 36 \u003d 0 ⇒ A \u003d 1; b \u003d 12; C \u003d 36;
D \u003d 12 2 - 4 · 1 · 36 \u003d 0.

D \u003d 0 ⇒ Równanie ma jeden root. Możesz użyć dowolnej formuły. Na przykład pierwszy:

Jak widać z przykładów, wszystko jest bardzo proste. Jeśli znasz formułę i będziesz w stanie wziąć pod uwagę, nie będzie problemów. Najczęściej występują błędy podczas podstawienia we wzorze współczynników ujemnych. Tutaj ponownie, opisano powyżej, pomoże: spojrzeć na formułę dosłownie, pomaluj każdy krok - i wkrótce pozbyć się błędów.

Niekompletne równania kwadratowe.

Zdarza się, że równanie kwadratowe jest nieco różni się od tego, co podano w definicji. Na przykład:

1. x 2 + 9x \u003d 0;
2. x 2 - 16 \u003d 0.

Łatwo jest zobaczyć, że na tych równań nie ma żadnego z terminów. Takie równania kwadratowe są jeszcze łatwiejsze niż standard: nawet nie muszą rozważyć dyskryminujący. Wprowadzamy nową koncepcję:

AX 2 + BX + C \u003d 0 równania nazywane jest niepełne równanie kwadratowe, jeśli b \u003d 0 lub c \u003d 0, tj. Współczynnik ze zmienną x lub wolnym elementem jest zero.

Oczywiście możliwe jest całkowicie trudny przypadek, gdy oba te współczynniki są zero: b \u003d c \u003d 0. W tym przypadku równanie bierze formę AX 2 \u003d 0. Oczywiście, takie równanie ma jeden root: x \u003d 0 .

Rozważ pozostałe przypadki. Niech B \u003d 0 będzie 0, a następnie otrzymujemy niepełne równanie kwadratowe AX 2 + C \u003d 0. Konwertujemy to trochę:

Ponieważ korzenie kwadratowego arytmetycznego istnieje tylko z liczby nie ujemnej, ta ostatnia równość ma sens wyłącznie w (-c / a) ≥ 0. Wniosek:

1. Jeśli w niepełnym równaniu kwadratowym AX 2 + C \u003d 0, nierówności (-C / A) przeprowadza się ≥ 0, będą dwa korzenie. Formuła podana powyżej;
2. Jeśli (-c / a)< 0, корней нет.

Jak widać, dyskryminujący nie potrzebował - w niekompletnych równaniach kwadratowych nie ma kompleksowych obliczeń. W rzeczywistości nawet nie jest konieczne zapamiętanie nierówności (-c / a) ≥ 0. wystarczy wyrazić wartość x 2 i zobaczyć, co stoi po drugiej stronie znaku równości. Jeśli jest pozytywny numer - korzenie będą dwa. Jeśli negatywne - korzenie w ogóle nie będą.

Teraz zrozumiemy wraz z równaniami AX 2 + BX \u003d 0, w którym wolny element ma zero. Wszystko jest tutaj proste: korzenie zawsze będą dwa. Wystarczy rozkładać wielomian do mnożników:

Mnożnik do wspornika

Praca wynosi zero, gdy przynajmniej jeden z mnożników wynosi zero. Stąd są korzenie. Podsumowując, przeanalizujemy kilka takich równań:

Zadanie. Równania kwadratowe kwadratowe:

1. x 2 - 7x \u003d 0;
2. 5x 2 + 30 \u003d 0;
3. 4x 2 - 9 \u003d 0.

x 2 - 7x \u003d 0 ⇒ x · (x - 7) \u003d 0 ⇒ x 1 \u003d 0; x 2 \u003d - (- 7) / 1 \u003d 7.

5x 2 + 30 \u003d 0 ⇒ 5x 2 \u003d -30 ⇒ x 2 \u003d -6. Bez korzeni, ponieważ Kwadrat nie może być równy liczbie ujemnej.

4x 2 - 9 \u003d 0 ⇒ 4x 2 \u003d 9 ⇒ x 2 \u003d 9/4 ⇒ x 1 \u003d 3/2 \u003d 1,5; x 2 \u003d -1.5.

Wyświetl równanie

Wyrażenie RE. \u003d B. 2 - 4 AC. Połączenie dyskryminujący równanie kwadratowe. Jeśli RE. \u003d 0, równanie ma jeden ważny root; IF D. \u003e 0, równanie ma dwa ważny root.
W przypadku, gdy RE. = 0 Czasami mówią, że równanie kwadratowe ma dwa identyczne korzenie.
Za pomocą oznaczenia RE. \u003d B. 2 - 4 AC. , możesz przepisać formułę (2) jako

Jeśli B. \u003d 2 K. Wzór (2) ma formularz:

gdzie K. \u003d B. / 2 .
Ostatnia formuła jest szczególnie wygodna w przypadkach B. / 2 - Integer, tj. współczynnik B. - Liczba parzysta.
Przykład 1: Rozwiązuj równanie 2 X. 2 - 5 X. + 2 = 0 . Tutaj a \u003d 2, B \u003d -5, C \u003d 2. Mieć RE. \u003d B. 2 - 4 AC. = (-5) 2- 4*2*2 = 9 . Tak jak RE. > 0 , równanie ma dwa korzenie. Znajdź je według formuły (2)

więc X. 1 \u003d (5 + 3) / 4 \u003d 2, x 2 =(5 - 3) / 4 = 1 / 2 ,
to znaczy X. 1 = 2 i X. 2 = 1 / 2 - korzenie określonego równania.
Przykład 2: Rozwiązuj równanie 2 X. 2 - 3 x. + 5 = 0 . Tutaj a \u003d 2, B \u003d -3, C \u003d 5. Znajdujemy dyskryminujący RE. \u003d B. 2 - 4 AC. = (-3) 2- 4*2*5 = -31 . Tak jak RE. 0 Równanie nie ma ważnych korzeni.

Niekompletne równania kwadratowe. Jeśli w równaniu kwadratowym TOPÓR. 2 + BX. + C. =0 Drugi współczynnik B. lub darmowy Dick. DO. równa zero, a następnie wywoływane jest równanie kwadratowe niekompletny. Niekompletne równania są izolowane, ponieważ aby znaleźć swoje korzenie, możliwe jest, aby nie używać formuły głównej równania kwadratowego - łatwiej jest rozwiązać równanie przez metodę rozkładu lewej części czynników.
Przykład 1: Rozwiązuj równanie 2 X. 2 - 5 X. = 0 .
Mieć X. (2 x. - 5) = 0 . Tak samo X. = 0 zarówno 2 X. - 5 = 0 , tj X. = 2.5 . Więc równanie ma dwa korzenie: 0 i 2.5
Przykład 2: Rozwiązuj równanie 3 X. 2 - 27 = 0 .
Mieć 3 X. 2 = 27 . W konsekwencji korzenie tego równania - 3 i -3 .

Twierdzenie Vieta. Jeśli zmniejszone równanie kwadratowe X. 2 + px. + Q. =0 ma ważne korzenie, a następnie ich ilość jest równa - P. i praca jest równa P. , tj

x 1 + x 2 \u003d -p,
x 1 x 2 \u003d q

(Suma korzeni danego równania kwadratowego jest równa drugiego współczynnika podjętych za pomocą przeciwnego znaku, a produkt korzeni jest równy wolnym członkowi).

Z tym programem matematycznym możesz rozwiązać równanie kwadratowe.

Program nie tylko daje zadanie odpowiedzi, ale także wyświetla proces rozwiązania na dwa sposoby:
- za pomocą dyskryminacji
- Korzystanie z twierdzenia Vieta (jeśli to możliwe).

Ponadto odpowiedź jest dokładna, nie przybliżona.
Na przykład, dla równania (81x ^ 2-16x-1 \u003d 0 \\), odpowiedź jest wyprowadzana w tym formularzu:

$$ x_1 \u003d frac (8+ sqrt (145)) (81), quad x_2 \u003d frac (8-1 sqrt (145)) (81) $$, a nie w tym: \\ (x_1 \u003d 0,247 ; quad x_2 \u003d -0.05)

Program ten może być przydatny dla studentów szkół średnich szkół edukacyjnych ogólnych przy przygotowywaniu się do testów i egzaminów, podczas sprawdzania wiedzy przed egzaminem, rodzice do monitorowania rozwiązania wielu problemów w matematyce i algebry. A może jesteś zbyt drogi, aby zatrudnić nauczyciela lub kupić nowe podręczniki? Albo po prostu chcesz odrabiać lekcje w matematyce lub algebry? W tym przypadku można również skorzystać z naszych programów o szczegółowym rozwiązaniu.

W ten sposób możesz przeprowadzić własne szkolenie i / lub szkolenia swoich młodszych braci lub siostry, podczas gdy poziom wykształcenia w dziedzinie rozwiązanych zadań wzrasta.

Jeśli nie znasz zasady wprowadzania kwadratowej wielomianu, zalecamy z nimi zapoznanie się z nimi.

Kwadratowe zasady wprowadzania wielomianów

Jako zmienna może być dowolną literą łacińską.
Na przykład: (x, y, z, a, b, c, o, p, q) itp.

Liczby mogą wejść do całości lub frakcji.
Ponadto numery ułamkowe można podawać nie tylko w postaci dziesiętnej, ale także w postaci zwykłej frakcji.

Zasady wprowadzenia ułamków dziesiętnych.
W frakcjach dziesiętnych frakcyjna część całości może być oddzielona jako punkt i przecinek.
Na przykład możesz wprowadzić frakcje dziesiętne takie jak: 2.5x - 3.5x ^ 2

Zasady wprowadzania zwykłych frakcji.
Tylko liczba całkowita może działać jako numerator, mianownik i całą część frakcji.

Mianownik nie może być negatywny.

Przy wejściu do frakcji numerycznej cyfracyjny oddzielony od mianownika do znaku rozszczepienia: /
Cała część jest oddzielona od znaku ampersa Fraraty &
Wejście: 3 i 1/3 - 5 i 6 / 5Z + 1 / 7Z ^ 2
Wynik: (3 frac (1) (3) - 5 frac (6) (5) z + frac (1) (7) z ^ 2

Przy wejściu do wyrażenia możesz użyć wsporników. W tym przypadku, podczas rozwiązywania równania kwadratowego, wprowadzone wyrażenie jest najpierw uproszczone.
Na przykład: 1/2 (Y - 1) (y + 1) - (5Y-10 i 1/2)

=0

Zdecydować

Stwierdzono, że niektóre skrypty wymagane do rozwiązania tego zadania nie są ładowane, a program może nie działać.
Możesz mieć Adblock dołączony.
W takim przypadku odłącz go i zaktualizuj stronę.

Masz wykonanie javascript w przeglądarce.
Aby wyświetlić rozwiązanie, musisz włączyć JavaScript.
Oto instrukcje, jak włączyć JavaScript w przeglądarce.

Dlatego Jeśli chcąc rozwiązać zadanie, jest bardzo dużo, twoja prośba jest w kolejce.
Po kilku sekundach rozwiązanie pojawi się poniżej.
Proszę czekać SEC ...

Jeśli ty zauważyłem błąd w rozwiązywaniuMożesz napisać o tym w formularzu sprzężenia zwrotnego.
Nie zapomnij określ, jakie zadanie Decydujesz i co wpisz w polu.

Nasze gry, puzzle, emulatory:

Trochę teorii.

Równanie kwadratowe i jego korzenie. Niekompletne równania kwadratowe.

Każde z równań
(- x ^ 2 + 6x + 1,4 \u003d 0, QUAD 8X ^ 2-7x \u003d 0, QUAD X ^ 2- FRAC (4) (9) \u003d 0
Ma wygląd
(AX ^ 2 + BX + C \u003d 0,)
gdzie X jest zmienna, A, B i C - numery.
W pierwszym równaniu A \u003d -1, B \u003d 6 i C \u003d 1,4, w drugim A \u003d 8, B \u003d -7 i C \u003d 0, w trzecim A \u003d 1, B \u003d 0 i C \u003d 4/9. Takie równania są nazywane równania kwadratowe..

Definicja.
Równanie kwadratowe Równanie modelu AX 2 + BX + C \u003d 0, gdzie X jest zmienna, A, B i C są pewnymi liczbami i (a nec 0 \\).

Numery A, B i C są współczynnikami równania kwadratowego. Numer A nazywany jest pierwszym współczynnikiem, liczba B oznacza drugi współczynnik i numer C - bezpłatny członek.

W każdym z równaniach AX 2 + BX + C \u003d 0, gdzie (NEQ 0), największy stopień zmiennej X - kwadrat. Stąd nazwa: równanie kwadratowe.

Należy zauważyć, że równanie kwadratowe nazywane jest również równaniem drugiego stopnia, ponieważ jego lewa część ma wielomian drugiego stopnia.

Równanie kwadratowe, w którym współczynnik w X 2 wynosi 1, zwany biorąc pod uwagę równanie kwadratowe. Na przykład, podane równania kwadratowe są równaniami
(x ^ 2-11x + 30 \u003d 0, quad x ^ 2-6x \u003d 0, quad x ^ 2-8 \u003d 0)

Jeśli w równaniu kwadratowym AX 2 + BX + C \u003d 0, co najmniej jeden z współczynników B lub C wynosi zero, a następnie wywołane jest równanie niekompletne równanie kwadratowe. Tak więc równania -2x 2 + 7 \u003d 0, 3x 2 -10x \u003d 0, -4x 2 \u003d 0 to niekompletne równania kwadratowe. W pierwszym z nich B \u003d 0, w drugim C \u003d 0, w trzeciej B \u003d 0 i C \u003d 0.

Niekompletne równania kwadratowe to trzy gatunki:
1) AX 2 + C \u003d 0, gdzie (c nec 0);
2) AX 2 + BX \u003d 0, gdzie (b NEQ 0);
3) AX 2 \u003d 0.

Rozważ roztwór równań każdego z tych gatunków.

Aby rozwiązać niepełne równanie kwadratowego AX 2 + C \u003d 0, z (C 0), jest przenoszony do jego wolnego członka do prawej strony i wykonaj obie części równania na a:
(x ^ 2 \u003d - frac (c) (a) słupek X_ (1,2) \u003d pm sqrt (- frac (c) (a)))

Ponieważ (C NEQ 0), a następnie (- frac (c) (a) nec 0

Jeśli (- frac (c) (a)\u003e 0), równanie ma dwa korzenie.

Jeśli (- frac (c) (a), aby rozwiązać niekompletne równanie kwadratowe AX 2 + BX \u003d 0, z (b NEQ 0 \\), odrzucają lewą część do mnożników i uzyskać równanie
(X (AX + B) \u003d 0 w prawej stronie lewej (rozpocznij (tablica) (L) x \u003d 0 ax + b \u003d 0 end (tablica) prawy .! w lewo (rozpocznij (Tablica) (L) x \u003d 0 x \u003d - frac (b) (a) end (tablica) prawy.

Tak więc, niepełne równanie kwadratowe AX 2 + BX \u003d 0 z (b NEQ 0 \\ (zawsze ma dwa korzenie.

Niekompletne równanie kwadratowe AX 2 \u003d 0 jest równoważne równania X 2 \u003d 0, a zatem ma jedyny root 0.

Formuła główna równania kwadratu

Rozważ teraz, jak równania kwadratowe rozwiązują, w których oba współczynniki z nieznanym i wolnym członkiem różnią się od zera.

Równanie kwadratu spalnia w ogóle iw rezultacie otrzymujemy formułę główną. Następnie ten formuła może być używana podczas rozwiązywania dowolnego równania kwadratowego.

Resive Square Równolece AX 2 + BX + C \u003d 0

Oddzielając obie części na a, otrzymujemy równowartość przedstawionego równania kwadratu
(x ^ 2 + frac (b) (a) x + frac (c) (a) \u003d 0

Przekształcimy to równanie, podkreślając kwadrat z odbity:
(x ^ 2 + 2x CDOT FRAC (B) (2A) + Left (frac (b) (2a) Po prawej stronie) ^ 2- Left (frac (b) (2a) prawy) ^ 2 + frac (c) (a) \u003d 0 wnęka

(x ^ 2 + 2x CDOT FRAC (B) (2a) + Left (Frac (b) (2a) Po prawej stronie) ^ 2 \u003d Left (Frac (b) (2a) Prawo) ^ 2 - FRAC (C) (a) Urynrow) (w lewo (x + frac (b) (2a) prawy) ^ 2 \u003d frac (b ^ 2) (4a ^ 2) - frac (c) (a) słupek Left (x + frac (b) (2a) prawy) ^ 2 \u003d frac (b ^ 2-4AC) (4a ^ 2) (x + \\ Frac (b) (2a) \u003d pm sqrt (frac (b ^ 2-4Ac) (4a ^ 2)) słupkowy x \u003d - frac (b) (2a) + frac (pm sqrt ( b ^ 2 -4AC)) (2a) wnęka (x \u003d frac (-b-pm sqrt (b ^ 2-4AC)) (2a)

Wyrażenie z przewodnikiem jest nazywane dyskryminujący równanie kwadratu. AX 2 + BX + C \u003d 0 ("Dyskryminacyjny" w łacinie jest wyraźny). Jest oznaczony literą D, tj.
(D \u003d b ^ 2-4AC)

Teraz, stosując oznaczenie dyskryminacyjnego, przepisuj formułę korzeni równania kwadratowego:
(X_ (1,2) \u003d frac (-b pm sqrt (d)) (2a)), gdzie (d \u003d b ^ 2-4AC)

To oczywiste, że:
1) Jeśli D\u003e 0 równanie kwadratowe ma dwa korzenie.
2) Jeśli d \u003d 0, równanie kwadratowe ma jeden root (x \u003d - frac (b) (2a)).
3) Jeśli d jest zatem, w zależności od wartości dyskryminującej, równanie kwadratowe może mieć dwa korzenie (z D\u003e 0), jeden root (o d \u003d 0) lub nie ma korzeni (z D, podczas rozwiązywania równania kwadratowej Ta formuła wskazana jest stosowanie w następujący sposób:
1) Oblicz dyskryminujący i porównaj go za pomocą zera;
2) Jeśli dyskryminacyjny jest dodatni lub równy zero, a następnie użyj formuły głównej, jeśli dyskryminacyjny jest ujemny, a następnie zapisz korzenie.

Twierdzenie Vieta.

AX AX 2 -7x + 10 \u003d 0 ma korzenie 2 i 5. Ilość korzeni wynosi 7, a produkt wynosi 10. Widzimy, że ilość korzeni jest równa drugiego współczynniku podjętego odwrotnym Znak, a produkt korzeni jest równy bezpłatnym członkowi. Taka nieruchomość ma jakiekolwiek równanie kwadratowe o korzeniu.

Suma korzeni przedstawionego równania kwadratu jest równa drugiego współczynniku podjętego przeciwległym znakiem, a produkt korzeni jest równy wolnym członkowi.

Te. Twierdzenie Vieta twierdzi, że korzenie X 1 i X 2 danego równania kwadratowego X 2 + PX + Q \u003d 0 mają nieruchomość:
(Po lewej (rozpocznij (tablica) (L) X_1 + X_2 \u003d -P x_1 CDOT X_2 \u003d q end (tablica) prawy.

Mam nadzieję, że studiowanie tego artykułu, nauczysz się znaleźć korzenie kompletnego równania kwadratowego.

Z pomocy dyskryminacyjnej, tylko kompletne równania kwadratowe są rozwiązane, w celu rozwiązania równań kwadratowych, inne metody, które znajdują się w artykule "Decyzja o niekompletnych równaniach kwadratowych".

Jakie równania kwadratowe są nazywane pełnymi? to równania formy AH2 + B X + C \u003d 0gdzie współczynniki A, B i nie są równe zero. Aby rozwiązać pełne równanie kwadratowe, konieczne jest obliczenie dyskryminacyjnego D.

D \u003d B 2 - 4AS.

W zależności od rodzaju ważności jest dyskryminujący, napiszemy odpowiedź.

Jeśli dyskryminujący jest numerem (D< 0),то корней нет.

Jeśli dyskryminujący jest zero, x \u003d (-b) / 2a. Kiedy dyskryminujący jest liczbą dodatnią (D\u003e 0),

następnie x 1 \u003d (-b - √d) / 2a i x 2 \u003d (-b + √d) / 2a.

Na przykład. Rozwiązuj równanie x 2. - 4x + 4 \u003d 0.

D \u003d 4 2 - 4 · 4 \u003d 0

x \u003d (- (-4)) / 2 \u003d 2

Odpowiedź: 2.

Rozwiązuj równanie 2. x 2. + x + 3 \u003d 0.

D \u003d 1 2 - 4 · 2 · 3 \u003d - 23

Odpowiedź: Brak korzeni.

Rozwiązuj równanie 2. x 2. + 5x - 7 \u003d 0.

D \u003d 5 2 - 4 · 2 · (-7) \u003d 81

x 1 \u003d (-5 - √81) / (2 · 2) \u003d (-5 - 9) / 4 \u003d - 3.5

x 2 \u003d (-5 + √81) / (2 · 2) \u003d (-5 + 9) / 4 \u003d 1

Odpowiedź: - 3.5; jeden.

Wyobraźmy sobie więc rozwiązanie kompletnych równania kwadratowych przez schemat na rysunku1.

Zgodnie z tymi formułami można rozwiązać dowolne kompletne równanie kwadratowe. Musisz tylko starannie monitorować równanie zostało zarejestrowane przez wielomian typu standardowego.

ale x 2. + BX + C, W przeciwnym razie możesz popełnić błąd. Na przykład, w rekordzie równania x + 3 + 2x 2 \u003d 0, jest on błędnie rozwiązany

a \u003d 1, B \u003d 3 i C \u003d 2. Następnie

D \u003d 3 2 - 4 · 1 · 2 \u003d 1, a następnie równanie ma dwa korzenie. I jest to nieprawidłowe. (Patrz roztwór przykładu 2 powyżej).

Dlatego też, jeśli równanie nie jest napisane, a nie do wielomianu standardowego gatunku, na początku pełne równanie kwadratowe powinny być rejestrowane przez wielomian standardowych gatunków (w pierwszej kolejności powinno być nieakceptowane z największym wskaźnikiem, czyli ale x 2. Potem z mniejszym – bX.a potem Darmowy Dick z.

Podczas rozwiązywania danego równania kwadratowego i równania kwadratowe z równomiernym współczynnikiem, z drugim terminem można użyć innych formuł. Zapoznajmy się z tymi formułami. Jeśli w kompletnym równaniu kwadratowym w drugim okresie współczynnik będzie nawet (B \u003d 2K), a następnie równanie zgodnie z wzorami na rysunku 2 można rozwiązać.

Równanie z pełnym kwadratowym jest nazywany powyżej, jeśli współczynnik jest x 2. równy jeden, a równanie weźmie formę x 2 + px + q \u003d 0. Taki równanie można podawać w celu rozwiązania lub uzyskiwanej przez podzielenie wszystkich współczynników do równania współczynnika alestojący x 2. .

Rysunek 3 przedstawia schemat rozwiązywania powyższego kwadratu
równania. Rozważmy na przykładzie stosowanie wzorów rozpatrywanych w niniejszym artykule.

Przykład. Rozwiązuj równanie

3x 2. + 6x - 6 \u003d 0.

Zdecydujmy to równanie za pomocą formuł pokazanych na schemacie Figury 1.

D \u003d 6 2 - 4 · 3 · (- 6) \u003d 36 + 72 \u003d 108

√d \u003d √108 \u003d √ (36 · 3) \u003d 6√3

x 1 \u003d (-6 - 6√3) / (2 · 3) \u003d (6 (-1- √ (3))) / 6 \u003d -1 - √3

x 2 \u003d (-6 + 6√3) / (2 · 3) \u003d (6 (-1+ √ (3))) / 6 \u003d -1 + √3

Odpowiedź: -1 - √3; -1 + √3.

Można go zauważyć, że współczynnik X w tym równaniu jest liczbą równomierną, czyli, B \u003d 6 lub B \u003d 2K, z którego k \u003d 3. Następnie staramy się rozwiązać równanie zgodnie z wzorami pokazanymi na diagramie D 1 \u003d 3 2 - 3 · (- 6) \u003d 9 + 18 \u003d 27

√ (D 1) \u003d √27 \u003d √ (9 · 3) \u003d 3√3

x 1 \u003d (-3 - 3√3) / 3 \u003d (3 (-1 - √ (3))) / 3 \u003d - 1 - √3

x 2 \u003d (-3 + 3√3) / 3 \u003d (3 (-1 + √ (3))) / 3 \u003d - 1 + √3

Odpowiedź: -1 - √3; -1 + √3.. Zauważyłem, że wszystkie współczynniki w tym równaniu kwadratowym są podzielone na 3, a wykonując podział, uzyskujemy zmniejszone równanie kwadratowe X 2 + 2x - 2 \u003d 0 poprzez rozwiązanie tego równania przy użyciu wzorów dla określonego kwadratu
równania Rysunek 3.

D2 \u003d 2 2 - 4 · (- 2) \u003d 4 + 8 \u003d 12

√ (D2) \u003d √12 \u003d √ (4 · 3) \u003d 2√3

x 1 \u003d (-2 - 2√3) / 2 \u003d (2 (-1 - √ (3))) / 2 \u003d - 1 - √3

x 2 \u003d (-2 + 2√3) / 2 \u003d (2 (-1+ √ (3))) / 2 \u003d - 1 + √3

Odpowiedź: -1 - √3; -1 + √3.

Jak widzimy, podczas rozwiązywania tego równania na różnych formułach otrzymaliśmy tę samą odpowiedź. Dlatego dobrze jest świadomy formuł pokazanych w schemacie Figura 1, zawsze możesz rozwiązać dowolne kompletne równanie kwadratowe.

wymagana jest witryna, z pełnym lub częściowym kopiowaniem materiału odniesienia do oryginalnego źródła.

W kontynuacji tematu "Decyzja równań" materiał tego artykułu wprowadzi Państwu równania kwadratowe.

Rozważ wszystko szczegółowo: esencję i rekord równania kwadratowego, ustanawiają załąskie warunki, przeanalizujemy schemat rozwiązania niekompletnych i kompletnych równań, zapoznanie się z formułą korzeni i dyskryminacyjnej, ustanawiają powiązania między korzeniami i współczynnikami, I oczywiście dajemy wizualne rozwiązanie praktycznych przykładów.

Yandex.rtb r-a-339285-1

Równanie kwadratowe, jego typy

Definicja 1.

Równanie kwadratowe - To jest równanie zapisane jako A · x 2 + B · x + c \u003d 0gdzie X. - zmienna, a, b i DO. - Niektóre liczby, podczas gdy zA.brak zera.

Często równania kwadratowe nazywane są również nazwą równania drugiego stopnia, ponieważ w istocie równanie kwadratowe jest równaniem algebraicznym drugiego stopnia.

Dajemy przykład zilustrowania danej definicji: 9 · x 2 + 16 · x + 2 \u003d 0; 7, 5 · x 2 + 3, 1 · x + 0, 11 \u003d 0 itd. - Są to równania kwadratowe.

Definicja 2.

Liczby A, B i DO. - Są to współczynniki równania kwadratu A · x 2 + B · x + c \u003d 0, z współczynnikiem ZA. Nazywa się to pierwszym lub starszym lub współczynnikiem w X 2, B - drugi współczynnik lub współczynnik X., ale DO. Zadzwoń do bezpłatnego członka.

Na przykład w równaniu kwadratowym 6 · x 2 - 2 · x - 11 \u003d 0 Współczynnik starszy wynosi 6, drugi współczynnik jest − 2 i bezpłatny członek jest równy − 11 . Zwróć uwagę na fakt, że gdy współczynniki B.i / lub C są negatywne, używana jest krótka forma nagrywania widoku. 6 · x 2 - 2 · x - 11 \u003d 0, ale nie 6 · x 2 + (- 2) · x + (- 11) \u003d 0.

Wyjaśniamy również ten aspekt: \u200b\u200bjeśli współczynniki ZA. i / lub. B. równy 1 lub − 1 , a potem wyraźny udział w nagraniu równania kwadratu, nie mogą być podejmowane, co wyjaśnia cechy zapisu tych współczynników numerycznych. Na przykład w równaniu kwadratowym Y 2 - y + 7 \u003d 0 Współczynnik starszy wynosi 1, a drugi współczynnik jest − 1 .

Określone i niezamężne równania kwadratowe

Według wartości pierwszego współczynnika równania kwadratowe są podzielone na powyższe i nieodpłatne.

Definicja 3.

Zmniejszone równanie kwadratowe - Jest to równanie kwadratowe, w którym starszy współczynnik jest równy 1. W przypadku innych wartości starszego współczynnika równanie kwadratowe nie jest nieprawidłowe.

Dajemy przykłady: równania kwadratowe x 2 - 4 · x + 3 \u003d 0, x 2 - x - 4 5 \u003d 0 są przedstawione w każdym z których jest starszy współczynnik 1.

9 · x 2 - x - 2 \u003d 0 - integralne równanie kwadratowe, gdzie pierwszy współczynnik różni się od 1 .

Każde rozpoznawane równanie kwadratowe jest możliwe do przekształcenia na daną równanie, jeśli jest on podzielony z obu części do pierwszego współczynnika (równoważna transformacja). Przekształcony równanie będzie miały takie same korzenie jak określone inteligentne równanie lub nie mieć korzeni w ogóle.

Rozważanie konkretnego przykładu pozwoli nam wyraźnie pokazać przejście ze zintegrowanego równania kwadratu do danego.

Przykład 1.

Równanie jest ustawione 6 · x 2 + 18 · x - 7 \u003d 0 . Konieczne jest przekształcenie początkowego równania w powyższym formularzu.

Decyzja

Schemat określonego powyżej jest oddzielony przez obie części początkowego równania na temat współczynnika wyższego szczebla 6. Potem dostajemy: (6 · x 2 + 18 · x - 7): 3 \u003d 0: 3I to jest takie samo jak: (6 · x 2): 3 + (18 · x): 3 - 7: 3 \u003d 0 I dalej: (6: 6) · x 2 + (18: 6) · x - 7: 6 \u003d 0. Stąd: x 2 + 3 · x - 1 1 6 \u003d 0. W ten sposób rozważa się równanie.

Odpowiedź: x 2 + 3 · x - 1 1 6 \u003d 0.

Pełne i niekompletne równania kwadratowe

Zwróć się do definicji równania kwadratu. W nim wyjaśniliśmy to A ≠ 0.. Taki stan jest niezbędny do równania A · x 2 + B · x + c \u003d 0 To było dokładnie kwadrat, ponieważ a \u003d 0. Jest zasadniczo przekształcany na równanie liniowe b · x + c \u003d 0.

W przypadku, gdy współczynniki B. i DO.równa zero (co jest możliwe, zarówno indywidualnie, jak i razem), równanie kwadratowe jest nazywane niekompletnym.

Definicja 4.

Niekompletne równanie kwadratowe - Takie równanie kwadratowe A · x 2 + B · x + c \u003d 0,gdzie przynajmniej jeden z współczynników B.i DO.(lub oba) to zero.

Pełna równanie kwadratowe. - równanie kwadratowe, w którym wszystkie współczynniki numeryczne nie są zerowe.

Poznaliśmy się, dlaczego rodzaje równania kwadratowych są podane dokładnie nazwy.

Dla b \u003d 0 równania kwadratowego ma formularz A · x 2 + 0 · x + c \u003d 0że to samo A · x 2 + C \u003d 0. Dla C \u003d 0. Równanie kwadratowe jest rejestrowane jako A · x 2 + B · x + 0 \u003d 0To jest równoważne A · x 2 + B · x \u003d 0. Dla B \u003d 0. i C \u003d 0. Równanie weźmie pogląd A · x 2 \u003d 0. Równania, które otrzymaliśmy, różni się od równania z pełnym równaniem kwadratowym, ponieważ ich lewe części nie znajdują się z komponentu z zmiennej X, albo wolnego członka ani obu jednocześnie. Właściwie ten fakt został zapytany o nazwę takiego rodzaju równań - niekompletne.

Na przykład, x 2 + 3 · x + 4 \u003d 0 i - 7 · x 2 - 2 · x + 1, 3 \u003d 0 są kompletnymi równaniami kwadratowymi; x 2 \u003d 0, - 5 · x 2 \u003d 0; 11 · x 2 + 2 \u003d 0, - x 2 - 6 · x \u003d 0 - Niekompletne równania kwadratowe.

Decyzja o niekompletnych równań kwadratowych

Powyższa definicja umożliwia odróżnienie następujących rodzajów niepełnych równań kwadratowych:

• A · x 2 \u003d 0, to równanie odpowiada współczynnikom B \u003d 0. i c \u003d 0;
• a · x 2 + C \u003d 0 dla b \u003d 0;
• a · x 2 + B · x \u003d 0 w C \u003d 0.

Rozważ decyzję każdego rodzaju niepełnego równania kwadratu.

Roztwór równania A · x 2 \u003d 0

Jak wspomniano powyżej, równanie odpowiada współczynnikom B. i DO.równy zero. Równanie A · x 2 \u003d 0 Możliwe jest przekształcenie równania do równoważnego x 2 \u003d 0które otrzymujemy, dzielymy obie części równania źródła dla liczby ZA.nie równy zero. Oczywisty fakt, że korzeń równania x 2 \u003d 0 To jest zero, ponieważ 0 2 = 0 . Inne korzenie, to równanie nie ma, co wyjaśniono przez właściwości stopnia: dla dowolnej liczby p,nie równa zero, wiernej nierówności P 2\u003e 0Co następuje, kiedy P ≠ 0. równość P 2 \u003d 0nigdy nie zostanie osiągnięty.

Definicja 5.

Zatem dla niepełnego równania kwadratowego A · x 2 \u003d 0 jest jedyny root x \u003d 0..

Przykład 2.

Na przykład rozwiązanie niekompletne równanie kwadratowe - 3 · x 2 \u003d 0. Jest równoznaczne z równaniem x 2 \u003d 0, jego jedyny korzeń jest x \u003d 0.Następnie początkowe równanie ma jedyny root - zero.

Krótko podjęto decyzję:

- 3 · x 2 \u003d 0, x 2 \u003d 0, x \u003d 0.

Roztwór równania A · x 2 + C \u003d 0

Na kolejce - roztwór niekompletnych równań kwadratowych, gdzie b \u003d 0, C ≠ 0, to znaczy równania formularza A · x 2 + C \u003d 0. Przekształcamy to równanie przeprowadzony termin z jednej części równania do innego, zmieniając znak na odwrót i dzielenie obu części równania do numeru, a nie równa zero:

• transfer DO. W prawej części, która daje równanie A · x 2 \u003d - C;
• podzielmy obie części równania ZA., Dostaję do końca x \u003d - C a.

Nasze transformacje są odpowiednio równoważne, otrzymujące równanie jest również równoważne źródło, a ten fakt umożliwia zakończenie korzeni równania. Z jakiego znaczenia ZA. i DO.wartość wyrażenia zależy - C A: może mieć znak minus (powiedzmy, jeśli A \u003d 1. i C \u003d 2., potem - c a \u003d - 2 1 \u003d - 2) lub znak plus (na przykład, jeśli A \u003d - 2 i C \u003d 6.Następnie - C A \u003d - 6 - 2 \u003d 3); To nie jest zero, ponieważ C ≠ 0.. W sytuacjach, kiedy będziemy mieszkać bardziej szczegółowo w sytuacjach< 0 и - c a > 0 .

W przypadku, gdy - c a< 0 , уравнение x 2 = - c a не будет иметь корней. Утверждая это, мы опираемся на то, что квадратом любого числа является число неотрицательное. Из сказанного следует, что при - c a < 0 ни для какого числа P. Równość P 2 \u003d - C Nie może być prawdziwa.

W przeciwnym razie, gdy - C A\u003e 0: Przypomnijmy pierwiastek kwadratowy i będzie oczywiste, że równanie X 2 \u003d - C A będzie numerem - C A, od - C A 2 \u003d - C a. Nie trudno zrozumieć, że liczba jest - C A jest również źródłem równania X 2 \u003d - C A: Rzeczywiście, - - C A 2 \u003d - C a.

Inne równanie korzeni nie będą miały. Możemy go wykazać za pomocą paskudnej metody. Aby rozpocząć, ustaw oznaczenia znalezione powyżej korzeni x 1. i - x 1.. Sugeruję, że równanie X 2 \u003d - C A jest również rootem x 2.który różni się od korzeni x 1. i - x 1.. Wiemy, że zamiast tego zastępuje do równania X. Jego korzenie przemieniamy równanie w sprawiedliwą równość numeryczną.

Dla x 1. i - x 1. Piszemy: x 1 2 \u003d - C a i dla x 2. - x 2 2 \u003d - c a. Opierając się na właściwościach równości numerycznej, wypełnić jedną równą równość innego, co nam da: x 1 2 - x 2 2 \u003d 0. Użyj właściwości działań z numerami, aby przepisać najnowszą równość jako (x 1 - x 2) · (x 1 + x 2) \u003d 0. Wiadomo, że praca dwóch liczb wynosi następnie zero, jeśli przynajmniej jedna z liczb wynosi zero. Z tego, że to wynika x 1 - x 2 \u003d 0 i / lub. x 1 + x 2 \u003d 0to samo x 2 \u003d x 1 i / lub. x 2 \u003d - x 1. Była oczywista sprzeczność, ponieważ na początku uzgodniono, że korzeń równania x 2. różni się od x 1. i - x 1.. Udowodniliśmy, że równanie nie ma innych korzeni, z wyjątkiem X \u003d - C A i X \u003d - - C.

Podsumowujemy wszystkie rozumowanie powyżej.

Definicja 6.

Niekompletne równanie kwadratowe. A · x 2 + C \u003d 0 odpowiednik równania X 2 \u003d - C A, który:

• nie będzie miało korzenie, gdy - c a< 0 ;
• będą dwa korzenie X \u003d - C A i X \u003d - - C A za pomocą - C\u003e 0.

Dajemy przykłady rozwiązywania równań A · x 2 + C \u003d 0.

Przykład 3.

Określono równanie kwadratowe 9 · x 2 + 7 \u003d 0.Konieczne jest znalezienie jego decyzji.

Decyzja

Przenosimy darmowy członek do prawej części równania, a następnie równanie weźmie formę 9 · x 2 \u003d - 7.
Dzielimy obie części uzyskanych równania 9 , cofnij się do x 2 \u003d - 7 9. W prawej części widzimy numer z znakiem minus, co oznacza: określone równanie nie ma korzeni. Następnie oryginalne niepełne równanie kwadratowe 9 · x 2 + 7 \u003d 0 Nie będzie miał korzeni.

Odpowiedź: równanie 9 · x 2 + 7 \u003d 0nie ma korzeni.

Przykład 4.

Konieczne jest rozwiązanie równania - x 2 + 36 \u003d 0.

Decyzja

Ruszamy 36 na prawą stronę: - x 2 \u003d - 36.
Rozdzieliśmy obie części − 1 , otrzymać x 2 \u003d 36. W prawej części - dodatni numer, stąd możemy to stwierdzić x \u003d 36 lub X \u003d - 36.
Wyjmij korzeń i zapisz wynik końcowy: niepełne równanie kwadratowe - x 2 + 36 \u003d 0 Ma dwa korzenie x \u003d 6. lub x \u003d - 6.

Odpowiedź: x \u003d 6. lub x \u003d - 6.

Roztwór równania A · x 2 + B · x \u003d 0

Będziemy badać trzeci rodzaj niepełnych równania kwadratowych C \u003d 0.. Znaleźć decyzję niekompletnej równania kwadratowego A · x 2 + B · x \u003d 0, Używamy metody rozkładu na mnożnikach. Rozprzestrzenianie się na mnożnikach wielomianu, który znajduje się w lewej części równania, dzięki czemu ogólny mnożnik do wsporników X.. Ten krok będzie miał okazję przekształcić oryginalne niepełne równanie kwadratowe do równoważnika x · (A · x + b) \u003d 0. A to równanie z kolei jest równoważne całości równań x \u003d 0. i A · x + b \u003d 0. Równanie A · x + b \u003d 0 Liniowy i jego korzeń: x \u003d - b a.

Definicja 7.

Tak więc niekompletne równanie kwadratowe A · x 2 + B · x \u003d 0 będzie miał dwa korzenie x \u003d 0. i x \u003d - b a.

Zapnij materiał na przykład.

Przykład 5.

Konieczne jest znalezienie roztworu równania 2 3 · x 2 - 2 2 7 · x \u003d 0.

Decyzja

Prowadzić X. W przypadku wsporników i uzyskaj równanie X · 2 3 · x - 2 2 7 \u003d 0. Równanie to jest równoważne równaniom x \u003d 0. i 2 3 · x - 2 2 7 \u003d 0. Teraz konieczne jest rozwiązanie powstałego równania liniowego: 2 3 · x \u003d 2 2 7, x \u003d 2 2 7 2 3.

Krótko rozwiązywanie równania do pisania w ten sposób:

2 3 · x 2 - 2 2 7 · x \u003d 0 x · 2 3 · x - 2 2 7 \u003d 0

x \u003d 0 lub 2 3 · x - 2 2 \u003d 0

x \u003d 0 lub x \u003d 3 3 7

Odpowiedź: x \u003d 0, x \u003d 3 3 7.

Dyskryminujący, korzenie formuły równania kwadratowego

Aby znaleźć roztwór równań kwadratowych, istnieje formuła do korzeni:

Definicja 8.

x \u003d - B ± D 2 · A gdzie D \u003d b 2 - 4 · · c - Tak zwany dyskryminujący równania kwadratowego.

Nagrywanie X \u003d - B ± D2 · A W istocie oznacza, że \u200b\u200bX 1 \u003d - B + D2 · A, X 2 \u003d - B - D2 · a.

Przydatne będzie zrozumienie, w jaki sposób uzyskano określoną formułę i jak go zastosować.

Wyjście korzeni równania kwadratu

Bądźmy kwestionowani, aby rozwiązać równanie kwadratowe A · x 2 + B · x + c \u003d 0. Wykonaj wiele równoważnych transformacji:

• podziały obie części równania dla liczby zA.Inne niż zero, uzyskujemy zmniejszone równanie kwadratowe: X 2 + B A · x + C a \u003d 0;
• wyróżniamy pełny kwadrat po lewej stronie otrzymanej równania:
  x 2 + ba · x + ca \u003d x 2 + 2 · b2 · A · x + B2 · A 2 - B 2 · A 2 + Ca \u003d X + B2 · A 2 - B 2 · A 2 + Ca .
  Po tym równanie przyjmie formę: X + B2 · A 2 - B2 · A 2 + C A \u003d 0;
• teraz możliwe jest dokonanie transferu dwóch ostatnich terminów do prawej strony, zmieniając znak do przeciwnego, po czym otrzymujemy: X + B2 · A 2 \u003d B 2 · A 2 - C A;
• wreszcie przekształcamy wyrażenie nagrane po prawej stronie ostatniej równości:
  B2 · A 2 - C A \u003d B 2 4 · A 2 - C A \u003d B 2 4 · A 2 - 4 · A · C4 · A 2 \u003d B 2 - 4 · A · C4 · A 2.

W ten sposób przyszliśmy do równania X + B2 · A 2 \u003d B 2 - 4 · A · C4 · A 2, równoważne równanie źródła A · x 2 + B · x + c \u003d 0.

Zrozumieliśmy rozwiązanie takich równań w poprzednich akapitach (decyzja o niekompletnych równań kwadratowych). Doświadczenie uzyskane umożliwia stwierdzenie dotyczące korzeni równania X + B2 · A 2 \u003d B 2 - 4 · A · C4 · A 2:

• w B 2 - 4 · A · C4 · A 2< 0 уравнение не имеет действительных решений;
• dla b2 - 4 · A · C4 · A 2 \u003d 0, równanie ma formę X + B2 · A 2 \u003d 0, a następnie X + B2 · A \u003d 0.

Stąd jedyny root x \u003d - b 2 · a jest oczywisty;

• dla B2 - 4 · A · C4 · A 2\u003e 0, będzie prawidłowy: X + B2 · A \u003d B 2 - 4 · A · C4 · A 2 lub X \u003d B 2 · A - B 2 - 4 · A · C4 · A 2, który jest taki sam jak X + - B2 · A \u003d B 2 - 4 · A · C4 · A 2 lub X \u003d - B 2 · A - B 2 - 4 · A · C 4 · A 2, tj. Równanie ma dwa korzenie.

Możliwe jest stwierdzenie, że obecność lub brak korzeni równania X + B2 · A 2 \u003d B2 - 4 · A · C4 · A 2 (a stąd początkowe równanie) zależy od znaku ekspresji B 2 - 4 · A · C4 · A 2, nagrany po prawej stronie. A znak tego wyrażenia jest ustawiony przez numer licznika (mianownik 4 · A 2 zawsze będzie pozytywny), czyli znak wyrazu B 2 - 4 · A · C. To wyrażenie B 2 - 4 · A · C Nazwa jest dyskryminującym kwadratowej ewakuacji i jest zdefiniowana jako jego oznaczenie litery D. Tutaj możesz nagrać istotę dyskryminacyjnej - według jego wartości, a znak stwierdza się, czy równanie kwadratowe będzie miało ważne korzenie, a jeśli tak jest, jaka jest liczba korzeni - jeden lub dwa.

Wracając do równania X + B2 · A 2 \u003d B 2 - 4 · A · C4 · A 2. Przepisz ją za pomocą oznaczenia dyskryminacyjnego: X + B2 · A 2 \u003d D 4 · A 2.

Ponownie sformułujemy konkluzje:

Definicja 9.

• dla RE.< 0 Równanie nie ma ważnych korzeni;
• dla D \u003d 0. Równanie ma jedyny root X \u003d - B2 · A;
• dla D\u003e 0. Równanie ma dwa korzenie: X \u003d - B2 · A + D4 · A 2 lub X \u003d - B 2 · A - D 4 · A 2. Te korzenie oparte na właściwościach rodników można napisać w postaci: X \u003d - B 2 · A + D2 · A lub - B 2 · a - D2 · a. A kiedy ujawniamy moduły i dają frakcje wspólnym mianownikom, otrzymujemy: x \u003d - B + D2 · A, X \u003d - B - D 2 · a.

Zatem wynikiem naszego rozumowania było usunięcie formuły korzeni równania kwadratu:

x \u003d - B + D2 · A, X \u003d - B - D2 · A, dyskryminujący RE. Obliczony według formuły D \u003d b 2 - 4 · · c.

Te formuły umożliwiają, że dyskryminowane jest większe, aby określić zarówno ważne korzenie. Gdy dyskryminujący jest zero, użycie obu formuł da ten sam root jako jedyny roztwór równania kwadratowego. W przypadku, gdy dyskryminacyjny jest ujemny, próbując użyć formuły root równania kwadratowego, będziemy stawić czoła koniecznością usunięcia korzenia kwadratowego z liczby ujemnej, co doprowadzi nas poza rzeczywiste liczby. Z negatywnym dyskryminującym równanie kwadratowe nie będą ważne korzenie, ale para kompleksowo koniugatowych korzeni, określonych przez te same wzory korzeniowe uzyskane przez nas są możliwe.

Algorytm do rozwiązywania równań kwadratowych na formułach głównych

Możliwe jest rozwiązanie równania kwadratowego, natychmiast jazda na rowerze formuły korzeni, ale zasadniczo, jeśli to konieczne, znajdź złożone korzenie.

W głównej masie przypadków zazwyczaj oznacza, że \u200b\u200bposzukiwanie niekompleksowych, ale ważnych korzeni równania kwadratowego. Następnie optymalnie przed użyciem formuł korzeni równania kwadratowego, najpierw określ dyskryminujący i upewnij się, że nie jest ujemny (w przeciwnym razie stwierdzamy, że równanie nie ma prawidłowych korzeni), a następnie przejdź do obliczenia wartości korzenie.

Argumenty powyżej zapewniają możliwość sformułowania algorytmu do rozwiązania równania kwadratowego.

Definicja 10.

Aby rozwiązać równanie kwadratowe A · x 2 + B · x + c \u003d 0, Czy to jest to konieczne:

• według formuły D \u003d b 2 - 4 · · c znajdź wartość dyskryminacyjnego;
• z D.< 0 сделать вывод об отсутствии у квадратного уравнения действительных корней;
• w D \u003d 0 znajdź jedyny korzeń równania zgodnie z wzorem X \u003d - B2 · A;
• dla d\u003e 0 określ dwa ważne korzenie równania kwadratowego zgodnie z wzorem X \u003d - B ± D2 · a.

Należy pamiętać, że gdy dyskryminujący jest zero, można użyć wzoru x \u003d - b ± D2 · A, daje ten sam wynik, co wzorze X \u003d - B 2 · a.

Rozważmy przykłady.

Przykłady rozwiązań równań kwadratowych

Przedstawiamy rozwiązanie przykładów w różnych wartościach dyskryminacji.

Przykład 6.

Konieczne jest znalezienie korzeni równania x 2 + 2 · x - 6 \u003d 0.

Decyzja

Piszemy współczynniki liczb równania kwadratu: A \u003d 1, B \u003d 2 i C \u003d - 6. Następnie działamy na algorytmie, tj. Przejdziemy do obliczenia dyskryminacji, dla których zastąpimy współczynniki A, B i DO. W wzorze dyskryminacyjnego: D \u003d B2 - 4 · A · C \u003d 2 2 - 4 · 1 · (- 6) \u003d 4 + 24 \u003d 28.

Uzyskaliśmy D\u003e 0, a oznacza to, że początkowe równanie będzie miało dwa ważne korzenie.
Aby je znaleźć, używamy formuły głównej X \u003d - B ± D2 · A i, zastępując odpowiednie wartości, otrzymujemy: x \u003d - 2 ± 28 2 · 1. Upraszczamy wynikowy wyraz, dzięki czemu mnożnik znaku głównego, a następnie cięcie frakcji:

x \u003d - 2 ± 2 · 7 2

x \u003d - 2 + 2 · 7 2 lub x \u003d - 2 - 2 · 7 2

x \u003d - 1 + 7 lub X \u003d - 1 - 7

Odpowiedź: X \u003d - 1 + 7, x \u003d - 1 - 7.

Przykład 7.

Konieczne jest rozwiązanie równania kwadratowego - 4 · x 2 + 28 · x - 49 \u003d 0.

Decyzja

Określ dyskryminujący: D \u003d 28 2 - 4 · (- 4) · (- 49) \u003d 784 - 784 \u003d 0. Dzięki tej wartości dyskryminacyjnej początkowe równanie będzie miało tylko jeden korzeń określony przez wzorze X \u003d - B 2 · a.

x \u003d - 28 2 · (- 4) x \u003d 3, 5

Odpowiedź: x \u003d 3, 5.

Przykład 8.

Konieczne jest rozwiązanie równania 5 · Y2 + 6 · Y + 2 \u003d 0

Decyzja

Współczynniki numeryczne tego równania będą: A \u003d 5, B \u003d 6 i C \u003d 2. Używamy tych wartości, aby znaleźć dyskryminujący: D \u003d B 2 - 4 · A · C \u003d 6 2 - 4 · 5 · 2 \u003d 36 - 40 \u003d - 4. Obliczony dyskryminacyjny jest ujemny, a zatem początkowe równanie kwadratowe nie ma prawidłowych korzeni.

W przypadku, gdy zadanie ma określić złożone korzenie, stosować formułę główną, wykonując działania z numerami złożonymi:

x \u003d - 6 ± - 4 2 · 5,

x \u003d - 6 + 2 · I 10 lub X \u003d - 6 - 2 · I 10,

x \u003d - 3 5 + 1 5 · I lub X \u003d - 3 5 - 1 5 · I.

Odpowiedź: Nie ma ważnych korzeni; Kompleksowe korzenie są następujące: - 3 5 + 1 5 · I, - 3 5 - 1 5 · I.

W programie szkolnym nadal nie ma wymogu poszukać złożonych korzeni, więc jeśli podczas roztworu dyskryminujący jest zdefiniowany jako ujemny, odpowiedź jest natychmiast rejestrowana, że \u200b\u200bnie ma prawidłowych korzeni.

Formula korzeni na nawet drugie współczynniki

Wzór korzeni X \u003d - B ± D2 · A (D \u003d B 2 - 4 · A · C) umożliwia uzyskanie innej formuły, bardziej kompaktowej, co pozwala znaleźć roztwory równań kwadratowych z równomiernym współczynnikiem w X (lub z współczynnikiem typu 2 · N, na przykład, 2 · 3 lub 14 · LN 5 \u003d 2 · 7 · LN 5). Pokazujemy, jak wyświetlana jest formuła.

Bądźmy zadaniem znalezienia roztworu równania kwadratowego A · x 2 + 2 · N · x + C \u003d 0. Działamy na algorytmie: Określ dyskryminujący D \u003d (2 · N) 2 - 4 · A · C \u003d 4 · N2 - 4 · A · C \u003d 4 · (N2 - A · C), a następnie użyj formuła główna:

x \u003d - 2 · N ± D2 · A, X \u003d - 2 · N ± 4 · N2 - A · C2 · A, X \u003d - 2 · N ± 2 N 2 - A · C2 · A, X \u003d - N ± N 2 - A · CA.

Niech wyrażenie N2 - A · C będzie wskazywany jako D 1 (czasami D "). Następnie formuła korzeni równania kwadratowego rozważanego z drugim współczynnikiem 2 · N przyniesie formularz:

x \u003d - N ± D 1 A, gdzie D 1 \u003d N2 - A · C.

Łatwo jest widzieć, że D \u003d 4 · D 1, lub D 1 \u003d D 4. Innymi słowy, D 1 jest jedną czwartą dyskryminacyjną. Jest oczywiste, że znak D 1 jest taki sam jak znak D, co oznacza, że \u200b\u200bznak D1 może również służyć jako wskaźnik obecności lub braku korzeni równania kwadratowego.

Definicja 11.

Zatem, aby znaleźć roztwór równania kwadratowego z drugim współczynnikiem 2 · N, konieczne jest:

• znajdź D 1 \u003d N2 - A · C;
• z d 1.< 0 сделать вывод, что действительных корней нет;
• dla D1 \u003d 0, określ tylko źródło równania zgodnie z wzorem X \u003d - N a;
• dla D1\u003e 0, określ dwa poprawne korzenie według wzoru X \u003d - N ± D 1 a.

Przykład 9.

Konieczne jest rozwiązanie równania kwadratowego 5 · x 2 - 6 · x - 32 \u003d 0.

Decyzja

Drugi współczynnik określonego równania może być reprezentowany jako 2 · (- 3). Następnie przepisuj określone równanie kwadratowe jako 5 · x 2 + 2 · (- 3) · x - 32 \u003d 0, gdzie A \u003d 5, N \u003d - 3 i C \u003d - 32.

Obliczamy czwartą część dyskryminacyjnego: D 1 \u003d N2 - A · C \u003d (- 3) 2 - 5 · (- 32) \u003d 9 + 160 \u003d 169. Wartość uzyskana pozytywnie oznacza to, że równanie ma dwa ważne korzenie. Definiujemy je zgodnie z odpowiednią formułą główną:

x \u003d - N ± D1 A, X \u003d - - 3 ± 169 5, X \u003d 3 ± 13 5,

x \u003d 3 + 13 5 lub X \u003d 3 - 13 5

x \u003d 3 1 5 lub x \u003d - 2

Można by wprowadzić obliczenia i zwykłą formułę korzeni równania kwadratu, ale w tym przypadku rozwiązanie byłoby bardziej kłopotliwe.

Odpowiedź: x \u003d 3 1 5 lub x \u003d - 2.

Uproszczenie gatunków równań kwadratowych

Czasami możliwe jest zoptymalizowanie rodzaju równania źródła, co uprości proces obliczania korzeni.

Na przykład równanie kwadratowe 12 · x 2 - 4 · x - 7 \u003d 0 jest wyraźnie bardziej wygodniejsze do rozwiązywania niż 1200 · x 2 - 400 · x - 700 \u003d 0.

Częczniejsze uproszczenie gatunków równania kwadratu jest wykonywane przez mnożenie lub podział obu części do rodzaju numeru. Na przykład pokazaliśmy uproszczony zapis równania 1200 · x 2 - 400 · x - 700 \u003d 0, otrzymany przez podzielenie obu części do 100.

Taka konwersja jest możliwa, gdy współczynniki równania kwadratowego nie są wzajemnie prostymi numerami. Następnie zazwyczaj dzielą obie części równania do największego wspólnego dzielnika wartości bezwzględnych jego współczynników.

Jako przykład użyj równania kwadratowego 12 · x 2 - 42 · x + 48 \u003d 0. Definiujemy węzeł wartości bezwzględnych jego współczynników: węzły (12, 42, 48) \u003d węzeł (węzeł (12, 42), 48) \u003d węzeł (6, 48) \u003d 6. Będziemy podzielić dwie części oryginalnego równania kwadratowego do 6 i otrzymujemy równoważne równanie kwadratowe 2 · x 2 - 7 · x + 8 \u003d 0.

Mnożenie obu części równania kwadratowego zazwyczaj pozbywa się współczynników frakcyjnych. Jednocześnie pomnożone przez najmniejszego ogólnego wielokrotnego mianownika współczynników. Na przykład, jeśli każda część równania kwadratowego wynosi 1 6 · x 2 + 2 3 · x - 3 \u003d 0 pomnóż od NOC (6, 3, 1) \u003d 6, to zostanie zapisane w prostszej formie X 2 + 4 · x - 18 \u003d 0.

Wreszcie zauważamy, że prawie zawsze pozbywa się minusa w pierwszym współczynniku równania kwadratowego, zmieniając znaki każdego członka równania, który jest osiągnięty przez pomnożenie (lub podziały) obu częściach 1. Na przykład, z równania kwadratowego - 2 · x 2 - 3 · x + 7 \u003d 0, można przejść do jego uproszczonej wersji 2 · x 2 + 3 · x - 7 \u003d 0.

Komunikacja między korzeniami a współczynnikami

Wzór korzeni równań kwadratowych X \u003d - B ± D 2 · Znany nam już wyraża korzenie równania przez współczynniki numeryczne. Opierając się na tej formule, mamy możliwość ustalenia innych zależności między korzeniami i współczynnikami.

Najbardziej znany i stosowany jest formuły twierdzenia Vieta:

x 1 + x 2 \u003d - b a i x 2 \u003d c a.

W szczególności, na zmniejszone równanie kwadratowe, ilość korzeni jest drugim współczynnikiem z przeciwnym znakiem, a produkt korzeni jest bezpłatny. Na przykład, zgodnie z gatunkiem równania kwadratowego 3 · x 2 - 7 · x + 22 \u003d 0, możliwe jest natychmiastowe określenie, że suma jego korzeni wynosi 7 3, a produkt korzeni wynosi 22 3.

Możesz również znaleźć wiele innych linków między korzeniami i współczynnikami równania kwadratowego. Na przykład suma kwadratów korzeni równania kwadratowego może być wyrażona przez współczynniki:

x 1 2 + x 2 2 \u003d (x 1 + x 2) 2 - 2 · x 1 · x 2 \u003d - Ba 2 - 2 · CA \u003d B 2 A 2 - 2 · CA \u003d B 2 - 2 · A · CA 2.

Jeśli zauważysz błąd w tekście, wybierz go i naciśnij Ctrl + Enter