Klasyczne prawdopodobieństwo. Prawdopodobieństwo zdarzenia losowego
Dla szacunki prawdopodobieństwa wystąpienia wszelkich przypadkowych wydarzeń są bardzo ważne dla predymentowania reprezentowania, czy prawdopodobieństwo, że dla nas zainteresowania różni się od tego, jak rozwijają się inne wydarzenia.
W przypadku klasycznego schematu, gdy wszystkie wyniki są równie równie nawet, możemy już ocenić wartości prawdopodobieństwa indywidualności dla nas niezależnie. Możemy to zrobić, nawet jeśli wydarzenie jest złożonym zestawem kilku podstawowych wyników. A jeśli kilka przypadkowych zdarzeń występuje jednocześnie lub sekwencyjnie? W jaki sposób wpływa to na prawdopodobieństwo nam zainteresowania?
Jeśli kilkakrotnie rzucę kości gry i chcę wypadnąć "sześć" i nie mam szczęścia przez cały czas, oznacza to, że konieczne jest zwiększenie zakładu, ponieważ zgodnie z teorią prawdopodobieństw, ja materie mam szczęście? Niestety, teoria prawdopodobieństwa nie zatwierdzi niczego takiego. Ani kości, ani karta ani moneta nie wiem, jak zapamiętać Co pokazali nam ostatni raz. Nie przejmują się całkowicie, po raz pierwszy lub w dziesiątym czasie dzisiaj doświadczam mojego przeznaczenia. Za każdym razem, gdy powtarzam rzut, znam tylko jedną rzecz: tym razem prawdopodobieństwo "sześciu" jest ponownie równa jednej szóstej. Oczywiście nie oznacza to, że numer, którego potrzebujesz, nigdy się nie wypadnie. Oznacza to tylko fakt, że moja strata po pierwszym rzucie i po każdym innym wyrzuceniu - niezależne wydarzenia.
Wydarzenia A i B są nazywane niezależnyJeśli realizacja jednego z nich nie wpływa na prawdopodobieństwo innego wydarzenia. Na przykład prawdopodobieństwa pokonania docelowego pierwszego z dwóch pistoletów nie zależy od tego, czy cel uderzył inny narzędzie, więc zdarzenia "Pierwsza pistolet uderzył w cel" i "Drugie narzędzie uderzyło w cel" niezależny.
Jeśli dwa zdarzenia A i niezależne, i prawdopodobieństwo, że każdy z nich jest znany, prawdopodobieństwo jednoczesnego wystąpienia i zdarzeń A, a zdarzenia w (wyznaczone AB) można obliczyć za pomocą następującego twierdzenia.
Prawdopodobieństwo twierdzenia mnożenia dla niezależnych zdarzeń
P (ab) \u003d p (a) * p (b) - Prawdopodobieństwo jednoczesny Początek dwóch niezależny Wydarzenia równe pracaprawdopodobieństwa tych wydarzeń.Przykład.Prawdopodobieństwa wprowadzenia celu w fotografowaniu pierwszego i drugiego narzędzia są odpowiednio równe: P 1 \u003d 0,7; P 2 \u003d 0,8. Znajdź prawdopodobieństwo dotarcia do jednej siatki z obu broni w tym samym czasie.
Decyzja:jak już widzieliśmy wydarzenia A (pierwsze uderzenie broni) iw (drugi hit narzędziowy) jest niezależny, tj. P (av) \u003d p (a) * p (c) \u003d p 1 * p2 \u003d 0,56.
Co dzieje się z naszymi szacunków, jeśli wydarzenia źródłowe nie są niezależne? Zmieńmy nieznacznie poprzedniego przykładu.
Przykład.Dwie strzały w konkursach strzelają do celów, a jeśli jeden z nich strzela etykietę, przeciwnik zaczyna być zdenerwowany, a jego wyniki pogarszają się. Jak przekształcić tę codzienną sytuację w zadanie matematyczne i konspektu, aby go rozwiązać? Jest intuicyjny, że konieczne jest jakoś podzielić dwie opcje rozwoju zdarzeń, aby skompilować dwa scenariusze, dwa różne zadania. W pierwszym przypadku, jeśli przeciwnik przegapił, skrypt będzie korzystny dla nerwowego zawodnika, a jego dokładność będzie wyższa. W drugim przypadku, jeśli przeciwnik zdekolnik zdał sobie sprawę na jego szansę, prawdopodobieństwo uderzenia celu dla drugiego zawodnika jest zmniejszony.
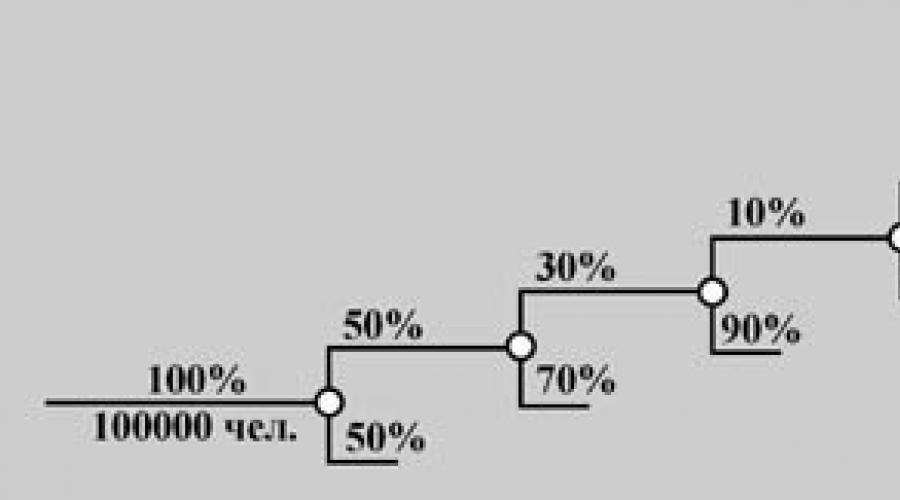
W celu oddzielenia możliwych scenariuszy (często nazywane są hipotezami), często użyjemy schematu "Drzewo prawdopodobieństwa". Ten schemat jest podobny do drzewa decyzji, z którymi prawdopodobnie musiałeś sobie poradzić. Każda gałąź jest oddzielnym scenariuszem rozwoju wydarzenia, tylko teraz ma swoją własną wartość tzw warunkowy Prawdopodobieństwo (Q 1, Q 2, Q 1 -1, Q 2 -1).
Ten schemat jest bardzo wygodny do analizy kolejnych zdarzeń losowych.
Pozostaje dowiedzieć się innego ważnego pytania: skąd pochodzą początkowe wartości prawdopodobieństwa Prawdziwe sytuacje ? W końcu teoria prawdopodobieństwa pracuje z tymi samymi monetami i grającymi kościami? Zwykle te szacunki pochodzą ze statystyk, a gdy nie ma informacji statystycznych, przeprowadzamy własne badania. I często nie jest konieczne uruchomienie go od zbierania danych, ale z pytania, jakie informacje potrzebne.
Przykład.Przypuśćmy, że musimy ocenić w mieście z populacją sto tysięcy mieszkańców objętości rynku dla nowego produktu, który nie jest przedmiotem, na przykład dla balsamu do opieki nad malowanymi włosami. Rozważmy schemat "drzewa prawdopodobieństwa". Jednocześnie wartość prawdopodobieństwa na każdej "oddziału" musimy w przybliżeniu ocenić. Tak więc nasza zdolność rynkowa szacuje:
1) od wszystkich mieszkańców miasta kobiet 50%,
2) wszystkich kobiet często 30% włosów malarskich,
3) z nich tylko 10% cieszy się balsamem do malowanych włosów,
4) z nich tylko 10% może zyskać odwagę, aby wypróbować nowy produkt,
5) z nich 70% zazwyczaj kupuje wszystko od nas, ale od naszych konkurentów.

Decyzja:Zgodnie z prawem wieloznacznego prawdopodobieństwa określamy prawdopodobieństwo wydarzeń interesujących dla nas \u003d (mieszkaniec miasta kupuje ten nowy balsam) \u003d 0,00045.
Pomnóż tę wartość prawdopodobieństwa dla liczby mieszkańców miasta. W rezultacie mamy tylko 45 potencjalnych nabywców, a jeśli uważamy, że jedna bańka tego funduszu wystarczy na kilka miesięcy, handel nie jest zbyt zajęty.
Niemniej jednak istnieją korzyści z naszych szacunków.
Po pierwsze, możemy porównać prognozy różnych pomysłów biznesowych, w schematach będą miały inny "rozwój", a oczywiście wartości prawdopodobieństwa będą również inne.
Po drugie, jak już mówiliśmy, losowa wartość nie jest dlatego, że nazywa się losowo, że nie zależy od niczego. Tylko ona dokładny Wartość nie jest znana z góry. Wiemy, że średnia liczba kupujących może zostać zwiększona (na przykład za pomocą reklamy nowego produktu). Więc ma sens, skupić się na tych "rozwoju", gdzie dystrybucja prawdopodobieństw nie pasuje do nas szczególnie na czynnikach, które jesteśmy w stanie wpływać.
Rozważ kolejny ilościowy przykład badania zachowań klientów.
Przykład.W ciągu dnia rynku żywności odwiedza średnio 10 000 osób. Prawdopodobieństwo, że użytkownik rynku wchodzi w pawilon produktów mlecznych, wynosi 1/2. Wiadomo, że w tym pawilonie średnie na sprzedaż dziennie 500 kg różnych produktów.
Czy można argumentować, że średni zakup w pawilonie waży tylko 100 g?
Dyskusja.Oczywiście jest to niemożliwe. Jasne jest, że nie wszyscy, którzy poszli do pawilonu, w rezultacie coś tam kupił.

Jak pokazano na diagramie, aby odpowiedzieć na pytanie średniej wagi zakupu, musimy znaleźć odpowiedź na pytanie, jakie jest prawdopodobieństwo, że osoba, która przyszła do pawilonu kupi coś tam. Jeśli nie ma takich danych do naszej dyspozycji, i potrzebujemy ich, będziesz musiał je zdobyć, po oglądaniu odwiedzających pawilonu przez jakiś czas. Przypuśćmy, że nasze obserwacje pokazały, że tylko piąty odwiedzających pawilonu kupuje coś.
Gdy tylko te szacunki zostaną uzyskane przez nas zadanie staje się proste. 10 000 osób, które przychodzą na rynek, 5000 wejdzie do pawilonu produktów mlecznych, zakupy będzie tylko 1000. Średnia waga zakupu wynosi 500 gramów. Warto zauważyć, że w celu zbudowania pełnego obrazu tego, co się dzieje, logika warunkowego "baterów" powinna być ustalona na każdym etapie naszego rozumowania, jak również gdybyśmy pracowani z "konkretną" sytuacją, a nie z prawdopodobieństwa.
Zadania do autotestu
1. Załóżmy, że znajduje się obwód elektryczny składający się z serii podłączonych elementów, z których każdy działa niezależnie od reszty.

Prawdopodobieństwo p jest znane w kolejności każdego elementu. Określ prawdopodobieństwo działania całego obszaru łańcucha (zdarzenie A).
2. Student zna 20 na 25 pytań egzaminacyjnych. Znajdź prawdopodobieństwo, że student zna przez niego trzy pytania.
3. Produkcja składa się z czterech kolejnych kroków, na każdym z których działa sprzęt, dla których prawdopodobieństwa awarii w ciągu najbliższego miesiąca są równe odpowiednio P 1, P2, P 3 i P 4. Znajdź prawdopodobieństwo, że w ciągu miesiąca nie będzie jednego przystanku produkcji z powodu awarii sprzętu.
Wydarzenia, które występują naprawdę lub w naszej wyobraźni można podzielić na 3 grupy. Są to niezawodne wydarzenia, które na pewno wystąpią, imprezy niemożliwe i zdarzenia losowe. Teoria prawdopodobieństw jest badana przez przypadkowe wydarzenia, tj. Zdarzenia, które mogą wystąpić lub się nie zdarzają. W tym artykule przedstawi w krótkim formie teorii prawdopodobieństwa formuł i przykładów rozwiązywania problemów na teorii prawdopodobieństwa, które będą w 4 zadaniach matematyki EE (poziom profilu).
Dlaczego potrzebujesz teorii prawdopodobieństwa
Historycznie, potrzeba zbadania tych problemów powstały w XVII wieku w związku z rozwojem i profesjonalizacją hazardu i pojawienie się kasyna. To było prawdziwe zjawisko, które wymagało jego badań i badań.
Gra kart, kości, ruletka stworzyła sytuacje, gdy może wystąpić dowolna z skończonej liczby równych zdarzeń. Była potrzeba podania oceny numerycznej możliwość wystąpienia jednego lub innego wydarzenia.
W XX wieku okazało się, że ta pozornie fryvolous naukę odgrywa ważną rolę w wiedzy o podstawowych procesach występujących w mikrometrze. Utworzono nowoczesną teorię prawdopodobieństwa.
Podstawowe koncepcje teorii prawdopodobieństwa
Przedmiotem studiowania teorii prawdopodobieństwa jest zdarzenia i ich prawdopodobieństwa. Jeśli zdarzenie jest skomplikowane, można go podzielić na proste elementy, których prawdopodobieństwa są łatwe do znalezienia.
Suma wydarzeń A i B nazywana jest wydarzeniem C, która polega na tym, że istnieje zdarzenie A, albo zdarzenie lub wydarzenia A iw tego samego czasie.
Praca wydarzeń A i B nazywana jest wydarzeniem z uwzględnieniem, że zdarzenie A i wydarzenie wystąpiło.
Wydarzenia A i B nazywane są niedocenianiem, jeśli nie mogą wystąpić jednocześnie.
Wydarzenie A nazywa się niemożliwe, jeśli nie może się wydarzyć. To zdarzenie jest oznaczone symbolem.
Wydarzenie A jest nazywany niezawodnym, jeśli na pewno nastąpi. To zdarzenie jest oznaczone symbolem.
Niech każdy wydarzenie zostanie umieszczony zgodnie z numerem p (a). Ta liczba p (A) nazywana jest prawdopodobieństwem zdarzenia A, jeśli spełnione są następujące warunki z tą zgodnością.
Ważnym konkretnym przypadku jest sytuacją, w której występuje równie solidne wyniki podstawowe, a arbitralne wyniki są formowane przez zdarzenia A. W tym przypadku prawdopodobieństwo można wprowadzić za pomocą formuły. Prawdopodobieństwo nałożone w ten sposób nazywa się klasycznym prawdopodobieństwem. Można udowodnić, że w tym przypadku wykonane są właściwości 1-4.
Zadania na temat teorii prawdopodobieństw znajdujących się na egzaminie w matematyce są związane głównie z klasycznym prawdopodobieństwem. Takie zadania mogą być bardzo proste. Szczególnie proste są zadania teorii prawdopodobieństwa w opcjach demonstracyjnych. Łatwo jest obliczyć liczbę korzystnych wyników, bezpośrednio w stanie jest zapisywana liczba wszystkich wyników.

Odpowiedź jest uzyskiwana przez formułę.
Przykład zadania ze słowa matematyki w celu określenia prawdopodobieństwa
Na stole znajduje się 20 placówek - 5 z kapustą, 7 z jabłkami i 8 z ryżem. Marina chce wziąć pasztet. Jakie jest prawdopodobieństwo, że zajmie pasztet z ryżem?
Decyzja.
W sumie równe podstawowe wyniki 20, to jest Marina może wziąć dowolną z 20 ciasta. Ale musimy docenić prawdopodobieństwo, że Marina weźmie pidrit z ryżem, czyli, gdzie jest wybór marionetki z ryżem. Oznacza to, że mamy liczbę korzystnych wyników (wybory ciasta z ryżem) tylko 8. Następnie prawdopodobieństwo zostanie określone przez wzór:
![]()
Niezależne, przeciwne i dowolne wydarzenia
Jednak w otwartym banku zadania zaczęły spełniać bardziej złożone zadania. Dlatego zwracaj uwagę na czytelnika i inne kwestie badane w teorii prawdopodobieństw.
Wydarzenia A i B są nazywane niezależnymi, jeśli prawdopodobieństwo każdego z nich nie zależy od tego, czy wystąpiło inne zdarzenie.
Wydarzenie b jest to, że wydarzenie się nie dzieje, tj. Wydarzenie B jest odwrotnie do zdarzenia A. Prawdopodobieństwo odwrotnego wydarzenia jest równe jednemu minus prawdopodobieństwem wydarzenia bezpośredniego, tj. .
Twierdzenia dodatku i mnożenia prawdopodobieństw, formuł
Dla arbitralnych wydarzeń A i prawdopodobieństwo ilości tych wydarzeń równych sumie ich prawdopodobieństwa bez prawdopodobieństwa ich wspólnego wydarzenia, tj. .
W przypadku niezależnych wydarzeń, a w prawdopodobieństwie pracy tych wydarzeń jest równa produktowi ich prawdopodobieństw, tj. w tym przypadku .
Ostatnie 2 oświadczenia nazywane są twierdzeniami dodawania i mnożenia prawdopodobieństw.
Nie zawsze licząc liczbę wyników jest tak proste. W niektórych przypadkach konieczne jest użycie formuł kombinatorycznych. W tym przypadku najważniejsze jest liczenie liczby zdarzeń, które spełniają pewne warunki. Czasami ten rodzaj liczenia może stać się niezależnymi zadaniami.
Ile sposobów mogę usiąść 6 studentów na 6 darmowych miejsc? Pierwszy uczeń przyjmie dowolne z 6 miejsc. Każda z tych opcji odpowiada 5 sposobowi odbywania się do drugiego ucznia. Dla trzeciego ucznia znajdują się 4 darmowe miejsca, na czwarte - 3, dla piątego - 2, szósta będzie miała jedyne pozostałe miejsce. Aby znaleźć liczbę wszystkich opcji, musisz znaleźć produkt wskazany przez symbol 6! I czytaj "sześć faktoryj".
Ogólnie rzecz biorąc, odpowiedź na to pytanie podaje formułą liczby permutacji z przedmiotów p w naszym przypadku.
Rozważ teraz kolejną sprawę z naszymi uczniami. Ile sposobów mogę usiąść 2 studentów na 6 darmowych miejsc? Pierwszy uczeń przyjmie dowolne z 6 miejsc. Każda z tych opcji odpowiada 5 sposobowi odbywania się do drugiego ucznia. Aby znaleźć liczbę wszystkich opcji, musisz znaleźć pracę.
Ogólnie rzecz biorąc, odpowiedź na to pytanie podaje formułą liczby zakwaterowania z n elementów k elementów
W naszym przypadku .
I ostatni przypadek z tej serii. Ile sposobów możesz wybrać trzech uczniów z 6? Pierwszy student można wybrać 6 w drugiej metodzie - 5 w trzecich metodach - cztery. Ale wśród tych opcji jeden i ten sam początek uczniów znajduje się 6 razy. Aby znaleźć liczbę wszystkich opcji, musisz obliczyć wartość :. Ogólnie rzecz biorąc, odpowiedź na to pytanie podaje formułę liczby kombinacji z elementów według elementów:
W naszym przypadku .
Przykłady rozwiązywania problemów ze słowa matematyki do definicji prawdopodobieństwa
Zadanie 1. Z kolekcji ed. Yashchenko.
Na talerzu 30 placówek: 3 z mięsem, 18 z kapustą i 9 z wiśnią. Sasha losowo wybiera jeden pasztet. Znajdź prawdopodobieństwo, że będzie z wiśnią.
![]() .
.
Odpowiedź: 0,3.
Zadanie 2. Z kolekcji ed. Yashchenko.
W każdej partii 1000 żarówek średnio 20 wadliwych. Znajdź prawdopodobieństwo, że losowo żarówka z imprezy będzie dobra.
Rozwiązanie: liczba dobrych świateł 1000-20 \u003d 980. Potem prawdopodobieństwo, że przyniosła żarówka z partii będzie dobra:
![]()
Odpowiedź: 0,98.
Prawdopodobieństwo, że w ramach testowania w matematyce ucznia U jest, ponad 9 zadań rozwiąże ponad 9 zadań, równych 0,67. Prawdopodobieństwo, że U. poprawnie rozwiązuje więcej niż 8 zadań, równych 0,73. Znajdź prawdopodobieństwo, że U. poprawnie rozwiązuje dokładnie 9 zadań.
Jeśli wyobrażamy sobie numeryczne bezpośrednie i zapoznaj się z punktami 8 i 9, zobaczymy, że warunek "W. Będzie poprawnie rozwiązać dokładnie 9 zadań "w stanie" W. Jest poprawny, aby rozwiązać więcej niż 8 zadań ", ale nie ma zastosowania do stanu" W. Z pewnością rozwiązuje więcej niż 9 zadań. "
Jednak warunek "U. Z pewnością rozwiązuje więcej niż 9 zadań "jest zawarty w" U. Z pewnością rozwiązuje więcej niż 8 zadań. " Tak więc, jeśli oznaczamy wydarzenia: "W. Jest poprawny, aby rozwiązać dokładnie 9 zadań "- przez A" W. Prawidłowo rozwiązuje więcej niż 8 zadań "- przez b" W. Z pewnością rozwiązuje więcej niż 9 zadań "przez C. Rozwiązanie będzie wyglądać tak:
Odpowiedź: 0,06.
Na egzaminie geometrii uczeń odpowiada na jedno pytanie z listy zagadnień egzaminacyjnych. Prawdopodobieństwo, że jest to pytanie na temat "trygonometria" wynosi 0,2. Prawdopodobieństwo, że to pytanie na temat "Zewnętrzne kąty" wynosi 0,15. Pytania, które jednocześnie odnoszą się do tych dwóch tematów, nie. Znajdź prawdopodobieństwo, że egzamin ucznia otrzyma pytanie na jednym z tych dwóch tematów.
Pomyślmy o tym, jakie są nasze wydarzenia. Dostarczamy dwa niepełne wydarzenia. Oznacza to, że pytanie będzie odnosić się do tematu "trygonometria" lub do tematu "Kątowniki zewnętrzne". Według twierdzenia prawdopodobieństwa prawdopodobieństwo niekompletnych zdarzeń jest równe sumie prawdopodobieństwa każdego zdarzenia, musimy znaleźć sumę prawdopodobieństw tych wydarzeń, czyli:
Odpowiedź: 0,35.
Pokój jest oświetlony latarnią z trzema lampami. Prawdopodobieństwo jednej łamania lampy w ciągu roku wynosi 0,29. Znajdź prawdopodobieństwo, że w ciągu roku przynajmniej jedna lampa nie powiedzie się.
Rozważmy możliwe wydarzenia. Mamy trzy żarówki, z których każdy może pokonać lub rozładować niezależnie od każdej innej żarówki. Są to niezależne wydarzenia.
Następnie określamy opcje takich zdarzeń. Przyjmujemy oznaczenie: - lekkie oparzenia, spalona żarówka. I natychmiast obliczymy prawdopodobieństwo wydarzenia. Na przykład prawdopodobieństwo zdarzenia, w którym występują trzy niezależne zdarzenia "zapłonęła żarówka", "oparzenia żarówki", "oparzenia żarówki": gdzie prawdopodobieństwo zdarzenia "żarówka" jest obliczana jako prawdopodobieństwo Wydarzenie naprzeciwko zdarzenia "żarówka", a mianowicie :.
Należy pamiętać, że mamy korzystne niekompletne zdarzenia tylko 7. Prawdopodobieństwo takich zdarzeń jest równe sumie prawdopodobieństwa każdego z zdarzeń :.
Odpowiedź: 0,975608.
Możesz szukać innego zadania na poniższym rysunku:

W ten sposób rozumiemy, że teoria prawdopodobieństwa formuł i przykładów rozwiązywania problemów, które można spotkać w wersji EGE, można spełnić.
Jakie jest prawdopodobieństwo?
W obliczu tego terminu po raz pierwszy nie zrozumiałbym, co to jest. Dlatego postaram się wyjaśnić dostępne.
Prawdopodobieństwo jest szansą, że wydarzenie, jakie będzie się wydarzyć.
Na przykład, zdecydowałeś się udać do znajomego, zapamiętaj wejście, a nawet podłogę, na której żyje. Ale pokój i lokalizacja apartamentu zapomniały. I stoisz na schodach, a przed tobą drzwi do wyboru.
Jaka jest szansa (prawdopodobieństwo), co jeśli zadzwonisz do pierwszych drzwi, czy otworzysz przyjaciela? Całkowite apartamenty i przyjaciel mieszka tylko dla jednego z nich. Z równą szansą możemy wybrać dowolne drzwi.
Ale jaka jest ta szansa?
Drzwi, drzwi, które chcesz. Prawdopodobieństwo zgadywania dzwoniąc do pierwszych drzwi :. Oznacza to, że raz od trzech jesteś dokładnie odgadnąć.
Chcemy się dowiedzieć, jak często odgadniemy drzwi? Rozważmy wszystkie opcje:
- Nazwałeś B. 1Y. drzwi
- Nazwałeś B. 2y. drzwi
- Nazwałeś B. 3Y. drzwi
Teraz rozważ wszystkie opcje, w których może być przyjaciel:
ale. Za 1i. Drzwi
b. Za 2y. Drzwi
w. Za 3i. Drzwi
Porównujemy wszystkie opcje w formie stołu. Checkmark wskazuje opcje, gdy wybór zbiega się z lokalizacją znajomego, krzyż - gdy nie pasuje.
Jak widać wszystko możliwie Opcje Lokalizacja znajomego i wyboru, które drzwi do dzwonienia.
ALE korzystne wynagrodzenia . Oznacza to, że odgadniesz, dzwoniąc do drzwi raz, tj. .
Jest to prawdopodobieństwo - stosunek korzystnego wyniku (gdy twój wybór zbiegł się z lokalizacją znajomego) do liczby możliwych wydarzeń.
Definicja jest formułą. Prawdopodobieństwo określa się do oznaczenia p, więc:
Ta formuła nie jest zbyt wygodna, więc zaakceptujemy liczbę korzystnych wyników, a dla jest całkowitą liczbą wyników.
Prawdopodobieństwo można zarejestrować jako procent, ponieważ musisz pomnożyć wynikowy wynik:
Prawdopodobnie słowo "wyniki" rzuciło się do ciebie. Ponieważ matematyka nazywają różne działania (mamy taką akcję - jest to eksperymenty wywoławcze), wówczas wynik takich eksperymentów jest zwyczajowy, aby nazwać wynikiem.
Cóż, wyniki są korzystne i niekorzystne.
Wróćmy do naszego przykładu. Załóżmy, że nazywaliśmy jedną z drzwi, ale nieznany człowiek otworzył nam. Nie zgadliśmy. Jakie jest prawdopodobieństwo, że jeśli zadzwonisz do jednego z pozostałych drzwi, otworzymy nasz przyjaciel?
Jeśli myślałeś, że jest to błąd. Zajmijmy się.
Mamy dwa drzwi. W ten sposób mamy możliwe kroki:
1) Call. 1-UU. drzwi
2) Zadzwoń 2-UU. drzwi
Przyjaciel, z tym wszystkim, dokładnie za jednym z nich (ponieważ dla tego, w którym zadzwoniliśmy, nie było):
a) przyjaciel 1st. Drzwi
b) każdy 2-o. Drzwi
Narysujmy ponownie stół:

Jak widać, istnieją opcje, których są korzystne. Oznacza to, że prawdopodobieństwo jest równe.
Dlaczego nie?
Sytuacja rozpatrywana - przykład zdarzeń zależnych. Pierwsze wydarzenie jest pierwszym połączeniem na drzwiach, drugim wydarzeniem jest drugi dzwonek do drzwi.
I zależne są one nazywane, ponieważ wpływają na następujące działania. W końcu, jeśli po pierwszym połączeniu otworzyliśmy przyjaciela w drzwiach, a to, co byłoby prawdopodobieństwem, że jest w jednym z pozostałych dwóch? Dobrze, .
Ale jeśli są zdarzenia zależne, musi być niezależny? Prawda, są.
Przykład podręcznika jest rzucanie monetą.
- Rzuć czas monetą. Jakie jest prawdopodobieństwo, że na przykład orzeł? To prawda -, ponieważ opcje wszystkich (albo Orzeł, czy pośpiech, zaniedbujemy prawdopodobieństwo monety na krawędzi), ale tylko organizuje nas.
- Ale wypad spadł. Dobra, rzuć ponownie. Jakie jest prawdopodobieństwo upadku orła? Nic się nie zmieniło, wszystko jest takie samo. Ile opcji? Dwa. I ile nam odpowiada? Jeden.
I niech tysiąc razy w rzędzie wypadnie pośpiech. Prawdopodobieństwo opadu Eagle będzie również. Opcje są zawsze i korzystne -.
Łatwo odróżnić zdarzenia zależne od niezależnego:
- Jeśli eksperyment zostanie przeprowadzony raz (po rzuceniu monet, 1 wezwanie do drzwi itp.), Wówczas zdarzenia są zawsze niezależne.
- Jeśli eksperyment jest przeprowadzany kilka razy (moneta jest rzucana raz, drzwi są wywoływane kilka razy), a następnie pierwsze zdarzenie jest zawsze niezależne. A potem, jeśli liczba korzystnych lub liczba wszystkich wyników zmienia się, zdarzenia są zależne, a jeśli nie, niezależne.
Weźmy trochę ugryzionych, aby określić prawdopodobieństwo.
Przykład 1.
Moneta jest wyrzucana dwukrotnie. Jakie jest prawdopodobieństwo, że orzeł spada dwa razy z rzędu?
Decyzja:
Rozważ wszystkie możliwe opcje:
- Eagle-Orel.
- Eagle-Rush.
- Rush-Orel.
- Rusk-ruska.
Jak widać całą opcję. Z nich jesteśmy zadowoleni wyłącznie. To jest prawdopodobieństwo:
Jeśli warunek zostanie poproszony o znalezienie prawdopodobieństwa, odpowiedź musi zostać podana w formie ułamka dziesiętnego. Gdyby wskazano, że odpowiedź powinna być podana jako procent, pomnożylibyśmy.
Odpowiedź:
Przykład 2.
W pudełku cukierków wszystkie cukierki są pakowane w ten sam folia. Jednak z Candy - z orzechami, z brandy, z wiśnią, z karmelem i nugoyem.
Jakie jest prawdopodobieństwo, biorąc jedno cukierki, zdobyć cukierki z orzechami. Odpowiedź podaj w procentach.
Decyzja:
Ile możliwych wyników? .
To znaczy, biorąc jedno cukierki, będzie to jeden z istniejących pudełek.
I ile korzystnych wyników?
Ponieważ w pudełku tylko cukierki z orzechami.
Odpowiedź:
Przykład 3.
W pudełku piłek. Biały z nich, - czarny.
- Jakie jest prawdopodobieństwo ciągnięcia białej piłki?
- Dodaliśmy czarne kulki do pudełka. Jakie jest prawdopodobieństwo ciągnięcia białej piłki?
Decyzja:
a) w pudełku całych kulek. Biały z nich.
Prawdopodobieństwo jest:
b) Teraz kulki w pudełku stały się. I biały pozostał tyle -.
Odpowiedź:
Pełne prawdopodobieństwo
| Prawdopodobieństwo wszystkich możliwych zdarzeń jest równe (). |
Załóżmy, że w szufladzie czerwonych i zielonych kul. Jakie jest prawdopodobieństwo ciągnięcia czerwonej piłki? Zielona piłka? Czerwona lub zielona piłka?
Prawdopodobieństwo wyciągnij czerwoną piłkę
Zielona piłka:
Czerwona lub zielona piłka:
Jak widać, suma wszystkich możliwych zdarzeń jest równa (). Zrozumienie tego momentu pomoże Ci rozwiązać wiele zadań.
Przykład 4.
W pudełku leży markery: zielony, czerwony, niebieski, żółty, czarny.
Jakie jest prawdopodobieństwo ciągnięcia nie czerwonego pióra z filcu?
Decyzja:
Rozważmy liczbę korzystne wyniki.
Nie czerwony długopis z filcu, oznacza zielony, niebieski, żółty lub czarny.
| Prawdopodobieństwo, że wydarzenie nie wystąpi, jest równe minus prawdopodobieństwa, że \u200b\u200bwydarzenie wystąpi. |
Zasada mnożenia prawdopodobieństwa niezależnych wydarzeń
Jakie są już niezależne wydarzenia.
A jeśli musisz znaleźć prawdopodobieństwo, że dwa (lub więcej) niezależne wydarzenia będą miały miejsce z rzędu?
Przypuśćmy, że chcemy wiedzieć, jakie prawdopodobieństwo, że rzucając czas monetą, zobaczymy Eagle Dwa razy?
Już myśleliśmy.
A jeśli rzutujesz czas monety? Jakie jest prawdopodobieństwo widzenia orła z rzędu?
Całkowite opcje:
- Orzeł
- Orzeł
- Orzeł
- Orzeł
- Orzeł
- Wysypka
- Eagle Rush.
- Rusk-Rush.
Nie wiem, jak się masz, ale pomyliłem się, wykonując tę \u200b\u200blistę. Łał! I tylko opcja (pierwsza) pasuje do nas.
W przypadku 5 rzutów możesz wykonać listę możliwych wyników. Ale matematyka nie jest tak pracowita jak ty.
Dlatego najpierw zauważyli, a następnie udowodniono, że prawdopodobieństwo pewnej sekwencji niezależnych zdarzeń jest zmniejszona za każdym razem w prawdopodobieństwie jednego zdarzenia.
Innymi słowy,
Rozważmy na przykładzie tego samego, źle znanego, monet.
Prawdopodobieństwo orła w teście? . Teraz rzucamy czas monetą.
Jakie jest prawdopodobieństwo kolejnego orła?
Ta reguła działa nie tylko wtedy, gdy zostaniemy poproszeni o znalezienie prawdopodobieństwa, że \u200b\u200bto samo wydarzenie wystąpi kilka razy z rzędu.
Gdybyśmy chcieli znaleźć sekwencję rzeki-orła, gdy czaszka z rzędu również zrobilibyśmy.
Prawdopodobieństwo upadku -, orła -.
Prawdopodobieństwo wypadania przez sekwencję rzeki-orła-rzeki:
Możesz się sprawdzić, dotarł do stołu.
Zasada dodania prawdopodobieństw niepełnych zdarzeń.
Więc przestań! Nowa definicja.
Zajmijmy się. Weź naszą noszącą monetę i rzuć czas.
Możliwe opcje:
- Orzeł
- Orzeł
- Orzeł
- Orzeł
- Orzeł
- Wysypka
- Eagle Rush.
- Rusk-Rush.
Tak niekompletne zdarzenia, jest to pewna, określona sekwencja zdarzeń. - Są to niepełne wydarzenia.
Jeśli chcemy określić, jakie masz prawdopodobieństwo dwóch (lub więcej) niepełnych zdarzeń, składamy prawdopodobieństwo tych wydarzeń.
Konieczne jest zrozumienie, że opadanie orła lub pośpiechu jest dwa niezależne wydarzenia.
Jeśli chcemy określić, jakie jest prawdopodobieństwo sekwencji) (lub jakikolwiek inny), wówczas korzystamy z reguły rozmnażania prawdopodobieństw.
Jakie jest prawdopodobieństwo upadku w pierwszym rzucie orła, a w drugim i trzecim pośpiechu?
Ale jeśli chcemy wiedzieć, jakie jest prawdopodobieństwo wypadania jednej z kilku sekwencji, na przykład, gdy Eagle pada dokładnie czasy, tj. Opcje i musimy złożyć prawdopodobieństwo tych sekwencji.
Łączne opcje, pasuje do nas.
Możemy uzyskać taki sam, tworząc prawdopodobieństwo wyglądu każdej sekwencji:
W ten sposób składamy prawdopodobieństwo, że chcemy określić prawdopodobieństwo niektórych, niekompletnych, sekwencji wydarzeń.
Jest doskonała reguła, która pomaga nie zostać zdezorientowana po pomnożeniu, a kiedy składać:
Wróćmy na przykład, gdy rzuciliśmy czas monety i chcemy dowiedzieć się prawdopodobieństwu widzenia czasów Eagle.
Co się stanie?
Musi upaść:
(Orzeł i pośpiech i pośpiech) lub (pośpiech i orzeł i pośpiech) lub (pośpiech i pośpiech i orzeł).
Okazuje się:
Spójrzmy na kilka przykładów.
Przykład 5.
W pudełku leży z ołówkami. Czerwony, zielony, pomarańczowy i żółty i czarny. Jakie jest prawdopodobieństwo ciągnięcia czerwonych lub zielonych ołówków?
Decyzja:
Przykład 6.
Biała kość jest wyrzucana dwukrotnie, jakie jest prawdopodobieństwo, że 8 punktów spada w wysokości?
Decyzja.
Jak możemy dostać okulary?
(i) lub (oraz) lub (oraz) lub (oraz) lub (oraz).
Prawdopodobieństwo spadającej (dowolnej) twarzy.
Rozważamy prawdopodobieństwo:
Trening.
Myślę, że teraz stało się jasne, gdy trzeba rozważyć prawdopodobieństwa, gdy je dodasz, a kiedy pomnóż. Czyż nie? Praktykujmy trochę.
Zadania:
Weź pokład kartowy, w których kart, szczyt, robaki, 13 trefów i 13 tamburines. Od do asa każdego garnituru.
- Jakie jest prawdopodobieństwo ciągnięcia strypów z rzędu (pierwsza przerywana karta odłożyliśmy do pokładu i mieszać)?
- Jakie jest prawdopodobieństwo wyciągania czarnej mapy (szczyty lub trefie)?
- Jakie jest prawdopodobieństwo wyciągania zdjęcia (Warty, pani, króla lub Ace)?
- Jakie jest prawdopodobieństwo ciągnięcia dwóch zdjęć z rzędu (usuwamy pierwszą kartkę z pokładu)?
- Jakie jest prawdopodobieństwo, biorąc dwie karty, zbieraj kombinację - (waluta, pani lub król) i asa sekwencji, w której karty zostaną wyciągane, nie ma znaczenia.
Odpowiedzi:
Jeśli sam możesz rozwiązać wszystkie zadania, jesteś wielkim! Teraz wyzwania na temat teorii prawdopodobieństwa w egzaminie, klikniesz jak orzechy!
Teoria prawdopodobieństwa. ŚREDNI POZIOM
Rozważ przykład. Przypuśćmy, że rzucamy kością bawiącą się. Jakiego rodzaju kości wiesz? Nazywa się to sześcianem z numerami na krawędziach. Ile twarzy, tak wiele liczb: od tego, ile? Przed.
Więc rzucamy kość i chcemy upadł lub. I odpada.
W teorii prawdopodobieństwa mówią, co się stało korzystne wydarzenie (Nie myl się z zamożnymi).
Jeśli upadł, wydarzenie byłoby również korzystne. Suma może być tylko dwa korzystne wydarzenia.
I ile niekorzystny? Od możliwych wydarzeń oznacza to, że zdarzenia niekorzystne są (to jest, jeśli spada lub).
Definicja:
Prawdopodobieństwo nazywane jest stosunkiem liczby korzystnych zdarzeń do liczby wszystkich możliwych zdarzeń.. Oznacza to, że prawdopodobieństwo pokazuje, że odsetek wszystkich możliwych wydarzeń spada na korzystne.
Oznacz prawdopodobieństwo listu łacińskiego (najwyraźniej, z prawdopodobieństwa angielskiego słowa jest prawdopodobieństwo).
Jest zwyczajowy, aby zmierzyć prawdopodobieństwo procent (zob. Temat). W tym celu należy pomnożyć wartość prawdopodobieństwa. W przykładzie z kością grą, prawdopodobieństwo.
I w procentach :.
Przykłady (rozwiązywanie się):
- Jakie jest prawdopodobieństwo, że rzucanie monety spada orzeł? I jak prawdopodobne wypadnięcie pośpiechu?
- Jakie jest prawdopodobieństwo, że rzucanie kości gry spadnie nawet numer? A co jest dziwne?
- W pudełku zwykłych, niebieskich i czerwonych ołówków. W losowej tyant ołówek. Jakie jest prawdopodobieństwo ciągnięcia prostego?
Rozwiązania:
- Ile opcji? Orzeł i pośpiech - tylko dwa. A ile z nich jest korzystne? Tylko jeden - orzeł. Stąd prawdopodobieństwo
Z kapeluszem, to samo :.
- Całkowite opcje: (Ile boków kostki, tak wiele różnych opcji). Korzystne z nich: (to są nawet liczby nawet :).
Prawdopodobieństwo. Z dziwnymi, naturalnie, taki sam. - Razem :. Korzystny:. Prawdopodobieństwo:.
Pełne prawdopodobieństwo
Wszystkie ołówki w zielonym pudełku. Jakie jest prawdopodobieństwo ciągnięcia czerwonego ołówka? Nie ma szans: prawdopodobieństwo (przecież, korzystne wydarzenia -).
Takie wydarzenie nazywa się niemożliwe.
A jaki jest prawdopodobieństwo wyciągania zielonego ołówka? Korzystne wydarzenia są dokładnie takie same jak wydarzenia wszystkiego (wszystkie wydarzenia są korzystne). Oznacza to, że prawdopodobieństwo jest równe lub.
Taki wydarzenie nazywa się niezawodnym.
Jeśli w pudełku zielonych i czerwonych ołówków, jakie jest prawdopodobieństwo ciągnięcia zieleni lub czerwonego? Jeszcze raz. Zauważ coś takiego: prawdopodobieństwo ciągnięcia zieleni jest równe i czerwone -.
Podsumowując, te prawdopodobieństwa są równe dokładnie. To znaczy, suma prawdopodobieństw wszystkich możliwych zdarzeń jest równa lub.
Przykład:
W pudełku ołówkowym, wśród nich niebieski, czerwony, zielony, prosty, żółty, a reszta są pomarańczowe. Jakie jest prawdopodobieństwo ciągnięcia zieleni?
Decyzja:
Pamiętaj, że wszystkie prawdopodobieństwa są podane w wysokości. I prawdopodobieństwo ciągnięcia zieleni jest równe. Oznacza to, że prawdopodobieństwo nie wyciąga zielonej równej.
Pamiętaj o tej technice:prawdopodobieństwo, że wydarzenie nie wystąpi równe minus prawdopodobieństwa, że \u200b\u200bwydarzenie nastąpi.
Niezależne wydarzenia i reguła mnożenia
Rzucasz czas monety i chcesz oboje razy spadł orzeł. Jakie jest prawdopodobieństwo tego?
Uruchommy wszystkie możliwe opcje i określmy, ile z nich:
Eagle-Eagle, River-Eagle, Eagle-River, Rushka-River. Co jeszcze?
Całkowita opcja. Tylko jedna rzecz jest dla nas odpowiednia: Orła Orel. Całkowite prawdopodobieństwo jest równe.
W porządku. A teraz rzucamy czas monetą. Uspokój się. Stało się? (odpowiedź).
Możesz zobaczyć, że z dodatkiem każdego następnego rzutu, prawdopodobieństwo zmniejsza się. Ogólna zasada jest nazywana zasada mnożenia:
Prawdopodobieństwa niezależnych zdarzeń są zmienne.
Jakie są niezależne wydarzenia? Wszystko jest logiczne: to są te, które nie zależą od siebie. Na przykład, gdy wyrzucamy monetę kilka razy, wytwarzany jest nowy rzut, którego wynikiem nie zależy od wszystkich poprzednich rzutów. Z tym samym sukcesem możemy rzucić dwie różne monety w tym samym czasie.
Więcej przykładów:
- Kość gra jest dwukrotnie rzucana. Jakie jest prawdopodobieństwo, że oboje wypadły?
- Moneta jest rzucana. Jakie jest prawdopodobieństwo, że orzeł spada po raz pierwszy, a następnie dwa razy więcej?
- Gracz rzuca dwie kości. Jakie jest prawdopodobieństwo, że ilość liczb na nich będzie równa?
Odpowiedzi:
- Wydarzenia są niezależne, oznacza to, że działa regułę mnożenia :.
- Prawdopodobieństwo orła jest równe. Prawdopodobieństwo pośpiechu jest również. Alternatywny:
- 12 może działać tylko wtedy, gdy spadnie dwukrotne :.
Niekompletne zdarzenia i zasada dodawania
Inamiczność nazywana są zdarzenia, które się uzupełniają, aż do pełnego prawdopodobieństwa. Z nazwiska nie może się wydarzyć jednocześnie. Na przykład, jeśli rzutujesz monetę, może spojrzeć na orzeł lub pośpiech.
Przykład.
W pudełku ołówkowym, wśród nich niebieski, czerwony, zielony, prosty, żółty, a reszta są pomarańczowe. Jakie jest prawdopodobieństwo ciągnięcia zieleni lub czerwieni?
Decyzja .
Prawdopodobieństwo ciągnięcia zielonego ołówka jest równe. Czerwony -.
W sumie korzystne wydarzenia: zielony + czerwony. Oznacza to, że wyciąganie prawdopodobieństwa na zielono lub czerwono jest równe.
To samo prawdopodobieństwo może być reprezentowane w tym formularzu :.
Jest to zasada dodawania:prawdopodobieństwa niekompletnych zdarzeń są złożone.
Zadania typu mieszanego
Przykład.
Moneta jest wyrzucana dwukrotnie. Jakie jest prawdopodobieństwo, że wynik rzutów będzie inny?
Decyzja .
Rozumie się, że jeśli pierwszy orzeł spadł, drugi powinien być pośpiech i odwrotnie. Okazuje się, że istnieją dwie pary niezależnych wydarzeń, a te pary są niezrozumiałe ze sobą. Bez względu na to, jak się mylić, gdzie mnożyć, ale gdzie się składać.
Istnieje prostą zasadę dla takich sytuacji. Spróbuj opisać, co powinno się wydarzyć, łącząc zdarzenia związków "i" lub "lub". Na przykład w tym przypadku:
Musi spaść (orzeł i pośpiech) lub (Rushka i Eagle).
Gdzie jest sojusz "i", będzie mnożenie, a gdzie "lub" - dodatek:
Spróbuj sam:
- Jakie jest prawdopodobieństwo z dwoma monetami rzucającymi oba razy ta sama strona spada?
- Kość gra jest dwukrotnie rzucona. Jakie jest prawdopodobieństwo wypadania punktów?
Rozwiązania:
Inny przykład:
Rzuć czas monetą. Jakie jest prawdopodobieństwo, że orzeł spada przynajmniej raz?
Decyzja:
Teoria prawdopodobieństwa. Krótko o głównej rzeczy
Prawdopodobieństwo jest stosunkiem liczby korzystnych zdarzeń do liczby wszystkich możliwych zdarzeń.
Niezależne wydarzenia.
Dwa zdarzenia są niezależne, jeśli w przypadku wystąpienia jednego prawdopodobieństwa drugiego nie zmieni się.
Pełne prawdopodobieństwo
Prawdopodobieństwo wszystkich możliwych zdarzeń jest równe ().
Prawdopodobieństwo, że wydarzenie nie wystąpi, jest równe minus prawdopodobieństwa, że \u200b\u200bwydarzenie wystąpi.
Zasada mnożenia prawdopodobieństwa niezależnych wydarzeń
Prawdopodobieństwo pewnej sekwencji niezależnych wydarzeń jest równa produktowi prawdopodobieństwu każdego zdarzenia.
Nieprawidłowe wydarzenia.
Niekompletne jest zdarzenia, które nie mogą się wydarzyć jednocześnie w wyniku eksperymentu. Liczba niepełnych zdarzeń tworzą pełną grupę zdarzeń.
Prawdopodobieństwa niekompletnych zdarzeń są złożone.
Opisując, co powinno się wydarzyć za pomocą sojuszy "i" lub "lub", zamiast "i" umieść znak mnożenia, a zamiast "lub" - dodatek.
Cóż, temat jest zakończony. Jeśli przeczytasz te linie, jesteś bardzo fajny.
Ponieważ tylko 5% ludzi jest w stanie opanować coś samodzielnego. A jeśli przeczytasz do końca, wszedłeś do tych 5%!
Teraz najważniejsza rzecz.
Wykorzystałeś teorię na tym temacie. I powtarzam, to ... To tylko super! Jesteś lepszy niż bezwzględna większość swoich rówieśników.
Problem polega na tym, że może to nie wystarczyć ...
Po co?
W przypadku pomyślnego przekazywania stosowania, dopuszczenia do Instytutu na temat budżetu i, co najważniejsze, na całe życie.
Nie przekonam cię niczego, powiem tylko jedno ...
Ludzie, którzy otrzymali dobrą edukację zarobić znacznie więcej niż tych, którzy go nie otrzymali. Są to statystyki.
Ale to nie jest główna rzecz.
Najważniejsze jest to, że są szczęśliwsi (są takie badania). Być może dlatego, że istnieje znacznie więcej możliwości na korzyść, a życie staje się jaśniejsze? Nie wiem...
Ale pomyśl sam ...
Co musisz być lepszy niż inni na egzaminie i bądź ostatecznie ... szczęśliwszy?
Wypełnij rękę, rozwiązywanie zadań na tym temacie.
Nie zapytasz teorii na egzamin.
Będziesz potrzebować rozwiąż zadania na chwilę.
A jeśli nie rozwiązałeś ich (dużo!), Zdecydowanie bądź głupio błędny lub po prostu nie masz czasu.
To jak w sporcie - musisz powtórzyć wiele razy, aby na pewno wygrać.
Znajdź, gdzie chcesz kolekcję, obowiązkowe z rozwiązaniami, szczegółową analizą I zdecyduj, zdecyduj, zdecyduj!
Możesz używać naszych zadań (koniecznie), a oczywiście polecamy je.
Aby wypełnić rękę z pomocą naszych zadań, musisz pomóc w rozszerzeniu życia do podręcznika Youcever, który czytasz teraz.
W jaki sposób? Istnieją dwie opcje:
- Otwórz dostęp do wszystkich ukrytych zadań w tym artykule - 299 RUB.
- Otwórz dostęp do wszystkich ukrytych zadań we wszystkich 99 artykułach podręcznika - 499 RUB.
Tak, mamy 99 takich artykułów w naszym podręczniku i dostęp do wszystkich zadań, a wszystkie ukryte teksty można natychmiast otwarte.
Dostęp do wszystkich ukrytych zadań jest zapewnione dla całego istnienia witryny.
Podsumowując ...
Jeśli nasze zadania nie lubią, znajdź innych. Po prostu nie zatrzymuj się na teorii.
"Rozumiem" i "Mogę zdecydować" to zupełnie inne umiejętności. Potrzebujesz obu.
Znajdź zadanie i zdecyduj!
Formuły do \u200b\u200bobliczania prawdopodobieństwa zdarzeń
1.3.1. Niezależna sekwencja testowa (Schemat Bernoulli)
Przypuśćmy, że niektóre eksperyment można wykonać wielokrotnie w tych samych warunkach. Niech to doświadczenie zostało wyprodukowane n. Raz, tj. Sekwencja odbywa się z n. Testy.
Definicja. Sekwencja n. testy zwane wzajemnie niezależny Jeśli jakiekolwiek zdarzenie związane z tym testem nie zależy od żadnych zdarzeń związanych z innymi testami.
Przypuśćmy jakiś wydarzenie ZA. może wystąpić z prawdopodobieństwem p. W wyniku jednego testu lub nie wydarzy się z prawdopodobieństwem p.= 1- p..
Definicja . Sekwencja jest n.testy tworzy schemat Bernoulliego, jeśli wykonane są następujące warunki:
sekwencja n. Testy są wzajemnie niezależne
2) Prawdopodobieństwo zdarzenia ZA. Nie różni się od testów do testu i nie zależy od wyniku w innych testach.
Zdarzenie ZA. Nazywają "sukcesem" testu, a odwrotnie wydarzenie jest "porażką". Rozważmy wydarzenie
 \u003d (B. n. Testy wystąpiły Rivne. m. "Sukces").
\u003d (B. n. Testy wystąpiły Rivne. m. "Sukces").
Aby obliczyć prawdopodobieństwo tego wydarzenia, formuła Bernoulli jest ważna
p.( )
=
)
=
 , m.
= 1, 2, …, n.
, (1.6)
, m.
= 1, 2, …, n.
, (1.6)
gdzie  - liczba kombinacji z n. Elementy in. m.
:
- liczba kombinacji z n. Elementy in. m.
:
 =
=
 =
= .
.
Przykład 1.16. Kostki rzucają trzy razy. Znaleźć:
a) Prawdopodobieństwo, że 6 punktów spadnie dwa razy;
b) prawdopodobieństwo, że liczba szóstek nie pojawi się więcej niż dwa razy.
Decyzja . Testy "sukcesu" zostaną uznane za spadek na sześcianę twarzy z obrazem 6 punktów.
a) Całkowita liczba testów - n.\u003d 3, liczba "sukcesów" - m.
\u003d 2. Prawdopodobieństwo "sukcesu" - p.= ,
I prawdopodobieństwo "porażki" - p.\u003d 1 - \u003d. Następnie, zgodnie z formułą Bernoulliego, prawdopodobieństwo, że spadnie w wyniku trzech czasów odlewania sześcianu, będzie równa
,
I prawdopodobieństwo "porażki" - p.\u003d 1 - \u003d. Następnie, zgodnie z formułą Bernoulliego, prawdopodobieństwo, że spadnie w wyniku trzech czasów odlewania sześcianu, będzie równa
 .
.
b) oznaczać ALE Wydarzenie, które leży w fakcie, że twarz z liczbą punktów 6 pojawi się nie więcej niż dwa razy. Wtedy wydarzenie może być reprezentowane jako suma trzech niespójności Wydarzenia A \u003d.
 ,
,
gdzie W 3 0 - wydarzenie, gdy nie pojawia się linia zainteresowań,
W 3 1 - Wydarzenie, gdy strona zainteresowania pojawi się raz,
W 3 2 - Wydarzenie, gdy oblicze zainteresowania pojawi się dwa razy.
Według Formuły Bernoulli (1.6) znajdziemy
p.(ALE)
\u003d P ( )
=
p.(
)
=
p.( )=
)=
 +
+ +
+ =
=
=
 .
.
1.3.2. Warunkowe prawdopodobieństwo zdarzenia
Warunkowe prawdopodobieństwo odzwierciedla wpływ jednego wydarzenia na prawdopodobieństwo innego. Zmiana warunków, w których przeprowadzany jest również eksperyment
prawdopodobieństwo pojawienia się ciekawego wydarzenia.
Definicja. Zostawiać ZA. i B. - Niektóre wydarzenia i prawdopodobieństwo p.(B.)> 0.
Warunkowe prawdopodobieństwo Wydarzenia ZA. pod warunkiem, że "wydarzenie B. jużzdarzyło się "zwanym stosunkiem prawdopodobieństwa produktu tych wydarzeń do prawdopodobieństwa wydarzenia, które wydarzyło się wcześniej niż wydarzenie, którego prawdopodobieństwo należy znaleźć. Warunkowe prawdopodobieństwo jest wskazane jako p.(ZA. B.). Następnie z definicji
p.
(ZA.
B.)
=
 .
(1.7)
.
(1.7)
Przykład 1.17. Dwa kostki rzucają się. Przestrzeń wydarzeń podstawowych składa się z zamówionych par liczb
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6).
Przykład 1.16 Stwierdzono, że wydarzenie ZA. \u003d (liczba okularów na pierwszej kostce\u003e 4) i wydarzenie DO. \u003d (Ilość punktów wynosi 8) zależna. Wśród związków
 .
.
Ten związek można interpretować w następujący sposób. Załóżmy, że wynik pierwszego rzucania jest znany, że liczba punktów na pierwszej kostce\u003e 4. Wynika z tego, że odlewanie drugiego kostki może prowadzić do jednego z 12 wyników stanowiących wydarzenie ZA.:
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6) .
Jednocześnie wydarzenie DO. Tylko dwa z nich mogą odpowiadać (5.3) (6.2). W takim przypadku prawdopodobieństwo wydarzenia DO.
będzie równy  . W ten sposób informacje o występowaniu wydarzenia ZA. wpłynęło na prawdopodobieństwo wydarzenia DO..
. W ten sposób informacje o występowaniu wydarzenia ZA. wpłynęło na prawdopodobieństwo wydarzenia DO..
Prawdopodobieństwo pracy wydarzeń
Twierdzenie mnożenia
Prawdopodobieństwo pracy wydarzeńZA. 1 ZA. 2 ZA. n. Formuła jest określona
p.(ZA. 1 ZA. 2 ZA. n.) \u003d P.(ZA. 1) P.(ZA. 2 ZA. 1)) p.(ZA. n. ZA. 1 ZA. 2 ZA. n- 1). (1.8)
Do pracy dwóch wydarzeń, wynika z tego
p.(Ab) \u003d P.(ZA. B) P.{B.) \u003d P.(B. ZA.) P.{ZA.). (1.9)
Przykład 1.18. W partii 25 produktów 5 produktów uszkodzony. Dwa produkty są kolejno wybrane. Określ prawdopodobieństwo, że wszystkie wybrane produkty są uszkodzone.
Decyzja. Oznacz wydarzenia:
ZA. 1 \u003d (pierwszy uszkodzony produkt),
ZA. 2 \u003d (drugi produkt jest uszkodzony),
ZA. 3 \u003d (trzeci produkt uszkodzony),
ZA. \u003d (Wszystkie produkty są uszkodzone).
Zdarzenie ALE istnieje praca trzech wydarzeń ZA. = ZA. 1 ZA. 2 ZA. 3 .
Z mnożenia twierdzenia (1,6) otrzymać
p.(ZA.) \u003d P ( ZA. 1 ZA. 2 ZA. 3 ) = p.(ZA. 1) p.(ZA. 2 ZA. 1))p.(ZA. 3 ZA. 1 ZA. 2).
Klasyczna definicja prawdopodobieństwa umożliwia znalezienie p.(ZA. 1) jest stosunkiem liczby wadliwych produktów do całkowitej liczby produktów:
p.(ZA. 1)=
 ;
;
p.(ZA. 2) – to jest stosunek liczby wadliwych produktów pozostałych po zajęciu jednego, do całkowitej liczby pozostałych produktów:
p.(ZA. 2
ZA. 1))=
 ;
;
p.(ZA. 3) jest stosunek liczby wadliwych produktów pozostałych po zajęciu dwóch uszkodzonych, do całkowitej liczby pozostałych produktów:
p.(ZA. 3
ZA. 1 ZA. 2)= .
.
Potem prawdopodobieństwo wydarzenia ZA. będzie równy
p.(ZA.)
=

 =
= .
.
Wiele, napotkanych z koncepcją "Teorii prawdopodobieństwa", są przestraszone, myśląc, że jest to coś nieznośnego, bardzo skomplikowanego. Ale wszystko nie jest tak samo tragiczne. Dziś rozważymy podstawową koncepcję uczenia się, aby rozwiązać problemy z konkretnymi przykładami.
Nauka
Jakie badania taką sekcję matematyki jak "teoria prawdopodobieństwa"? To zauważa wzorce i wartości. Po raz pierwszy to pytanie naukowcy byli zainteresowani XVIII wieku, kiedy badano hazard. Podstawową koncepcją teorii prawdopodobieństwa jest wydarzeniem. Jest to jakiś fakt, który jest określany przez doświadczenie lub obserwację. Ale jakie to doświadczenie? Inna podstawowa koncepcja teorii prawdopodobieństwa. Oznacza to, że ta skład okoliczności nie jest tworzona przez przypadek, ale z pewnym celem. Jeśli chodzi o obserwację, tutaj sam badacz nie uczestniczy w doświadczeniu, ale po prostu świadek zdarzenia danych, nie wpływa na to, co się dzieje.
Wydarzenia
Dowiedzieliśmy się, że podstawowa koncepcja teorii prawdopodobieństwa jest wydarzeniem, ale nie uważana za klasyfikację. Wszystkie są podzielone na następujące kategorie:
- Niezawodny.
- Niemożliwy.
- Losowy.
Niezależnie od tego, jakie wydarzenia obserwowane lub tworzą podczas doświadczenia, wszystkie z nich podlegają tej klasyfikacji. Oferujemy każdy rodzaj gatunków, aby zapoznać się oddzielnie.
Niezawodne wydarzenie

Jest to okoliczność, do której wykonany jest niezbędny zestaw zdarzeń. Aby lepiej zagłębić się w istotę, lepiej jest przynieść kilka przykładów. Fizyka i chemia oraz ekonomia i wyższa matematyka podlegają tym prawem. Teoria prawdopodobieństwa obejmuje tak ważną koncepcję jako niezawodne wydarzenie. Dajemy przykłady:
- Pracujemy i otrzymujemy wynagrodzenie w formie wynagrodzenia.
- Przekazano dobrze egzaminy, konkurencja odbyła się, otrzymujemy nagrodę za to w formie wstępu do instytucji edukacyjnej.
- W razie potrzeby zainwestowaliśmy pieniądze w banku, możemy je odzyskać.
Takie zdarzenia są niezawodne. Jeśli spełniliśmy wszystkie niezbędne warunki, na pewno uzyskamy oczekiwany wynik.
Niemożliwe wydarzenia
Teraz uważamy, że elementy teorii prawdopodobieństwa. Proponujemy przejść do wyjaśnienia następnego rodzaju wydarzenia, a mianowicie to niemożliwe. Zacznijmy, omówimy najważniejszą zasadę - prawdopodobieństwo wydarzenia niemożliwego wynosi zero.
Z tego formulacji niemożliwe jest odstawienie podczas rozwiązywania problemów. Aby wyjaśnić, podajemy przykłady takich wydarzeń:
- Woda zamrożona w temperaturze plus dziesięć (jest to niemożliwe).
- Żadna energia elektryczna nie wpływa na produkcję (jest również niemożliwe, jak w poprzednim przykładzie).
Nie należy podawać więcej przykładów, ponieważ powyższe opisane powyżej odzwierciedla istotę tej kategorii. Niemożliwe wydarzenie nigdy się nie wydarzy w żadnych okolicznościach.
Wydarzenia losowe

Studiowanie elementów teorii prawdopodobieństwa należy zwrócić szczególną uwagę na tego typu zdarzenia. To są te studia naukowe. W wyniku doświadczenia coś może się zdarzyć, czy nie. Ponadto test może być przeprowadzony nieograniczoną liczbę razy. Jasne przykłady mogą służyć:
- Obsada monet jest doświadczeniem lub testem, upadek orła jest wydarzeniem.
- Wyciągając piłkę ślepo - test, czerwona piłka złapana - to wydarzenie i tak dalej.
Takie przykłady mogą być nieograniczoną ilością, ale w ogóle istota musi być jasna. Podsumować i systematyzować wiedzę zdobyte na zdarzeniach, podano tabelę. Teoria prawdopodobieństwa studiuje tylko ostatni pogląd na wszystkich prezentowanych.
nazwa | definicja | |
Niezawodny | Zdarzenia występujące z gwarancją 100% przy przestrzeganiu pewnych warunków. | Wstęp do instytucji edukacyjnej z dobrym poddaniem egzaminu wejściowego. |
Niemożliwy | Wydarzenia, które nigdy się nie przydają w żadnych okolicznościach. | Jest śnieg w temperaturze powietrza plus trzydzieści stopni Celsjusza. |
Losowy | Zdarzenie, które może wystąpić lub nie podczas eksperymentu / testu. | Inteligencja lub chybienia przy rzucaniu piłki do koszykówki w pierścień. |
Prawa
Teoria prawdopodobieństwa jest nauka, która studiuje zdolność do wypadania jakiegokolwiek zdarzenia. Podobnie jak inne, ma pewne zasady. Istnieją następujące prawa teorii prawdopodobieństwa:
- Konwergencja sekwencji zmiennych losowych.
- Prawo dużych liczb.
Przy obliczaniu możliwości kompleksu można użyć kompleksu prostych zdarzeń, aby uzyskać łatwiej i szybko uzyskać wynik. Zauważ, że prawa teorii prawdopodobieństwa są łatwo udowodnione za pomocą niektórych twierdzeń. Oferujemy zacząć zapoznać się z pierwszym prawem.
Konwergencja zmiennych losowych

Zauważ, że gatunki konwergencji są nieco:
- Sekwencja zmiennych losowych jest pożądana przez prawdopodobieństwo.
- Prawie niemożliwe.
- R Konwergencja na średnia kwadratowa.
- Konwergencja dystrybucyjna.
Więc z latem bardzo trudno jest zagłębić się w istotę. Dajemy definicje, które pomogą zrozumieć ten temat. Zacząć od pierwszego widoku. Sekwencja nazywa się często jak prawdopodobieństwoJeśli obserwuje się następujący stan: N ma tendencję do nieskończoności, numer, do którego sekwencja dąży, więcej zero i jest przybliżona do jednego.
Przejdź do następującego formularza Prawie prawdopodobnie. Mówi się, że sekwencja zbiega się prawie prawdopodobnie Do zmiennej losowej dla N, dążenie do nieskończoności i p, dążąc do wielkości przybliżone do jednego.
Następny typ to konwergencja jest rustykalna. W przypadku korzystania z konwergencji SK badania wektorowych losowych procesów jest zredukowane do badania ich współrzędnych procesów losowych.
Ostatni typ pozostał, zrozummy krótko i przemieszczać się bezpośrednio do rozwiązania zadań. Konwergencja dystrybucji ma inną nazwę - "słabe", a następnie wyjaśnij dlaczego. Słaba konwergencja - Są to konwergencja funkcji dystrybucji we wszystkich punktach lokalizacji funkcji dystrybucji limitu.
Pamiętaj, aby spełnić obietnicę: słaba konwergencja różni się od całego faktu, że wartość losowa nie jest zdefiniowana na przestrzeni probabilistycznej. Jest to możliwe, ponieważ stan jest utworzony wyłącznie za pomocą funkcji dystrybucji.
Prawo dużych liczb
Doskonali asystenci w dowodzie tego prawa będą twierdzeniami teorii prawdopodobieństwa, takie jak:
- Nierówność chebyseva.
- Twierdzenie Chebyseva.
- Uogólnione twierdzenie ChebSheva.
- Twierdzenie Markova.
Jeśli weźmiemy pod uwagę wszystkie te teorety, ten problem może opóźnić kilka dziesiątek arkuszy. Mamy również główne zadanie - jest to wykorzystanie teorii prawdopodobieństwa w praktyce. Oferujemy Ci teraz i rób to. Ale przedtem rozważ aksjomaty teorii prawdopodobieństwa, będą one głównymi asystentami podczas rozwiązywania problemów.
Axioms.

Od pierwszego spotkaliśmy już się, gdy rozmawiali o wydarzeniu niemożliwym. Pamiętajmy: Prawdopodobieństwo imprezy niemożliwej wynosi zero. Przykład Przynieśliliśmy bardzo jasne i niezapomniane: śnieg spadł w temperaturze powietrza trzydziestu stopni Celsjusza.
Drugie dźwięki w następujący sposób: Niezawodne zdarzenie występuje z prawdopodobieństwem równym jednym. Teraz pokazujemy, jak napisać go za pomocą języka matematycznego: p (c) \u003d 1.
Po trzecie: zdarzenie losowe może wystąpić lub nie, ale możliwość zawsze różni się od zera do jednego. Im bliżej wartość do jednego, szanse są bardziej; Jeśli wartość zbliża się zero, prawdopodobieństwo jest bardzo małe. Piszemy to w języku matematycznym: 0<Р(С)<1.
Rozważ ostatni, czwarty aksjomat, który brzmi taki: prawdopodobieństwo sumy dwóch zdarzeń jest równe sumie ich prawdopodobieństwa. Zapiszymy język matematyczny: p (a + c) \u003d p (a) + p (b).
Asomy teorii prawdopodobieństwa są najprostszymi zasadami, które nie będą trudne do zapamiętania. Spróbujmy rozwiązać kilka zadań, opierając się na wiedzy już otrzymanej.
Kupon

Zacznij, rozważmy najprostszy przykład - loteria. Wyobraź sobie, że kupiłeś jeden bilet loterii na szczęście. Jakie jest prawdopodobieństwo, że wygrasz co najmniej dwadzieścia rubli? Tysiąc biletów jest zaangażowanych w obieg, z których jeden ma nagrodę w pięciuset rubli, dziesięciu stu rubli, pięćdziesięciu dwudziestu rubli i sto pięciu. Zadania na teorii prawdopodobieństwa opierają się na znalezieniu możliwości powodzenia. Teraz razem przeanalizujemy rozwiązanie powyżej przedstawionego zadania.
Jeśli jesteśmy listem i oznaczamy wygrane pięciuset rubli, prawdopodobieństwo wypadania będzie równe 0,001. Jak to zrobiliśmy? Wystarczy podzielić się liczbą biletów "Happy", aby podzielić się ich numerem (w tym przypadku: 1/1000).
B to wygrane stu rubli, prawdopodobieństwo będzie równe 0,01. Teraz działaliśmy na tę samą zasadę, co w przeszłości działanie (10/1000)
C - Wygrane są równe dwadzieścia rubli. Znajdujemy prawdopodobieństwo, wynosi 0,05.
Reszta biletów nie jest nas zainteresowana, ponieważ ich pula nagród jest mniejsza niż określona w stanie. Nałóż czwarty aksjomat: Prawdopodobieństwo wygranej co najmniej dwadzieścia rubli jest p (a) + p (c) + p (c). Litera P jest oznaczona prawdopodobieństwem pochodzenia tego wydarzenia, znaleźliśmy je już w poprzednich działaniach. Pozostaje tylko złożyć niezbędne dane, otrzymujemy 0,061 w odpowiedzi. Jest to numer i będzie odpowiedzią na kwestię zadania.
Talia kart
Zadania dotyczące teorii prawdopodobieństwa są bardziej złożone, na przykład, wykonaj następujące zadanie. Przed wystąpieniem z trzydziestu sześciu kart. Twoim zadaniem jest wyciągnięcie dwóch map w rzędzie bez mieszania stosu, pierwsze i drugie karty muszą być asy, garnitur nie ma nic.
Na początek, znajdziemy prawdopodobieństwo, że pierwsza karta będzie ACE, dla tego czterech dzielą się przez trzydzieści sześć. Odłożył go na bok. Daj drugą kartę, będzie ass z prawdopodobieństwem trzech trzydziestu piątej. Prawdopodobieństwo drugiego zdarzenia zależy od mapy, którą przyciągnęliśmy pierwsze, zastanawiamy się, to był ACE, czy nie. Wynika z tego, że wydarzenie zależy od wydarzenia A.
Kolejna akcja, którą znajdziemy prawdopodobieństwo jednoczesnego wdrożenia, czyli z złożonym a i B. Ich praca jest następująca: Prawdopodobieństwo jednego zdarzenia pomnożone na warunkowe prawdopodobieństwo drugiego, co obliczymy, zakładając, że pierwsze wydarzenie się wydarzyło Oznacza to, że przyciągnęliśmy pierwszy do Ace.
Aby stać się jasne, podajemy oznaczenie takim elementem jako wydarzenia. Jest obliczany, zakładając, że wydarzenie jest tym, co się stało. Jest obliczany w następujący sposób: P (V / A).
Kontynuujmy rozwiązanie naszego problemu: P (A * C) \u003d P (A) * P (w / a) lub p (A * C) \u003d P (C) * P (A / C). Prawdopodobieństwo równa się (4/36) * ((3/35) / (4/36). Oblicz, zaokrąglony do setnych. Mamy: 0,11 * (0,09 / 0,11) \u003d 0,11 * 0, 82 \u003d 0,09. Prawdopodobieństwo Że przedłużymy dwa asy z rzędu, wynosi dziewięć setnych. Wartość jest bardzo mała, wynika z tego, że prawdopodobieństwo wydarzenia jest niezwykle małe.
Zapomniana liczba
Proponujemy demontować kilku więcej opcji do zadań, które badają teorię prawdopodobieństwa. Przykłady rozwiązywania niektórych z nich już widziałeś w tym artykule, spróbuj rozwiązać następujące zadanie: Chłopiec zapomniał ostatniej cyfry numeru telefonu jego przyjaciela, ale ponieważ wezwanie było bardzo ważne, potem zaczął rekrutować wszystko z kolei . Musimy obliczyć prawdopodobieństwo, że zadzwoni go nie więcej niż trzy razy. Problemem problemu jest najprostszy, jeżeli zasady, prawa i aksjomaty teorii prawdopodobieństwa są znane.
Przed oglądaniem rozwiązania spróbuj rozwiązać siebie. Wiemy, że ostatnia cyfra może być od zera do dziewięciu, czyli, istnieją tylko dziesięć wartości. Prawdopodobieństwo wpisywania pożądanego wynosi 1/10.
Następnie musimy rozważyć opcje pochodzenia wydarzenia, przypuszczać, że chłopiec zgaduje i natychmiast zyskał niezbędny, prawdopodobieństwo takiego wydarzenia wynosi 1/10. Druga opcja: pierwszy dzwon poślizgu, a drugi do celu. Oblicz prawdopodobieństwo takiego wydarzenia: 9/10 pomnóż przez 1/9, w rezultacie otrzymujemy również 1/10. Trzecia opcja: Pierwsze i drugie połączenie nie były na adres, tylko od trzeciego chłopca dotarł tam, gdzie chciał. Oblicz prawdopodobieństwo takiego zdarzenia: 9/10 pomnożyć na 8/9 i 1/8, otrzymujemy 1/10 w rezultacie. Inne opcje pod warunkiem zadania nie są zainteresowane USA, pozostaliśmy złożone przez wyniki, w rezultacie mamy 3/10. Odpowiedź: prawdopodobieństwo, że chłopiec zadzwoni nie więcej niż trzy razy równa się 0,3.
Karty z numerami

Istnieją dziewięć kart przed tobą, z których każdy jest napisany numer od jednego do dziewięciu, liczby nie są powtarzane. Zostały umieszczone w pudełku i dokładnie wymieszane. Musisz obliczyć prawdopodobieństwo
- nawiązuje się na parze;
- dwucyfrowa.
Przed przejściem na rozwiązanie omówimy, że m jest liczbą udanych przypadków, a n jest całkowitą liczbą opcji. Znajdujemy prawdopodobieństwo, że numer będzie nawet. Nie trudno jest obliczyć, że nawet cztery liczby, będzie to nasz m, wszystko jest możliwe dziewięć opcji, czyli M \u003d 9. Następnie prawdopodobieństwo wynosi 0,44 lub 4/9.
Rozważamy drugą sprawę: liczba opcji dla dziewięciu, a w ogóle nie może w ogóle nie było pomyślnych wyników, to jest zero. Prawdopodobieństwo, że wydłużona karta będzie zawierać dwucyfrowy numer, to samo równa się zero.