Bendra funkcijos tyrimo internete schema. Pilnas funkcijų tyrimas ir braižymas

Šiandien kviečiame kartu su mumis ištirti ir nubraižyti funkciją. Atidžiai išstudijavę šį straipsnį, jums nereikės ilgai prakaituoti, kad atliktumėte tokią užduotį. Išnagrinėti ir nubrėžti funkciją nėra lengva, darbas yra didelis, reikalaujantis maksimalaus atidumo ir skaičiavimų tikslumo. Kad būtų lengviau suvokti medžiagą, žingsnis po žingsnio išnagrinėsime tą pačią funkciją, paaiškinsime visus savo veiksmus ir skaičiavimus. Sveiki atvykę į nuostabų ir jaudinantį matematikos pasaulį! Pirmyn!

Domenas

Norėdami ištirti ir nubrėžti funkciją, turite žinoti keletą apibrėžimų. Funkcija yra viena iš pagrindinių (pagrindinių) matematikos sąvokų. Jis atspindi ryšį tarp kelių kintamųjų (dviejų, trijų ar daugiau) su pokyčiais. Funkcija taip pat parodo aibių priklausomybę.

Įsivaizduokite, kad turime du kintamuosius, kurie turi tam tikrą variacijų diapazoną. Taigi, y yra x funkcija, su sąlyga, kad kiekviena antrojo kintamojo reikšmė atitinka vieną antrojo reikšmę. Šiuo atveju kintamasis y yra priklausomas ir vadinamas funkcija. Įprasta sakyti, kad kintamieji x ir y yra in. Kad ši priklausomybė būtų aiškesnė, nubraižytas funkcijos grafikas. Kas yra funkcijų grafikas? Tai koordinačių plokštumos taškų rinkinys, kur kiekviena x reikšmė atitinka vieną y reikšmę. Grafikai gali būti įvairūs – tiesi linija, hiperbolė, parabolė, sinusoidė ir pan.

Neįmanoma nubrėžti funkcijų grafiko be tyrimų. Šiandien išmoksime atlikti tyrimus ir nubraižyti funkcijų grafiką. Tyrimo metu labai svarbu užsirašyti. Tai labai palengvins užduotį. Patogiausias tyrimo planas:

1. Domenas.
2. Tęstinumas.
3. Lyginis arba nelyginis paritetas.
4. Periodiškumas.
5. Asimptotės.
6. Nuliai.
7. Ženklų pastovumas.
8. Didėja ir mažėja.
9. Kraštutinumai.
10. Išgaubtumas ir įdubimas.

Pradėkime nuo pirmojo punkto. Raskime apibrėžimo sritį, tai yra, kokiais intervalais egzistuoja mūsų funkcija: y = 1/3 (x ^ 3-14x ^ 2 + 49x-36). Mūsų atveju funkcija egzistuoja bet kurioms x reikšmėms, tai yra, domenas yra lygus R. Ją galima parašyti taip xÎR.

Tęstinumas

Dabar mes ištirsime pertraukos funkciją. Matematikoje terminas „tęstinumas“ atsirado dėl judėjimo dėsnių tyrimo. Kas yra begalinis? Erdvė, laikas, kai kurios priklausomybės (pavyzdys yra kintamųjų S ir t priklausomybė judėjimo uždaviniuose), šildomo objekto temperatūra (vanduo, keptuvė, termometras ir kt.), ištisinė linija (tai yra ta, kuri galima nupiešti nenuplėšiant nuo lapo pieštuko).

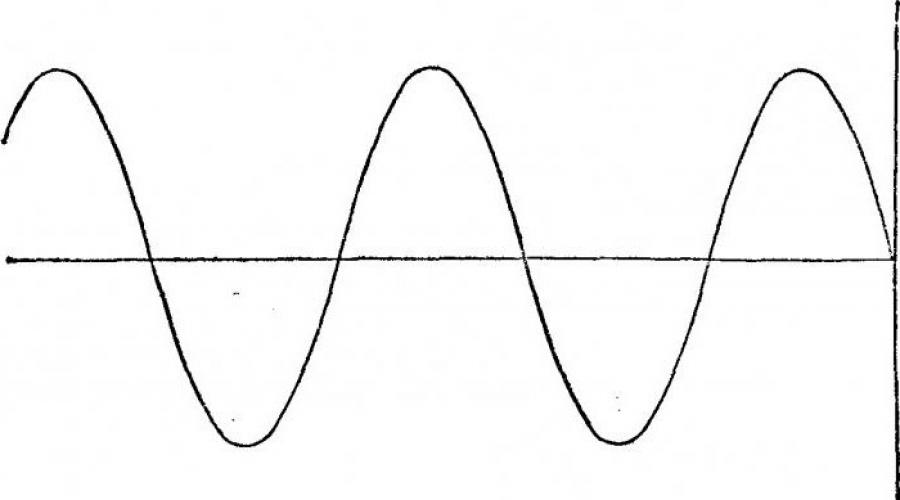
Diagrama laikoma ištisine, jei ji tam tikru momentu nenutrūksta. Vienas ryškiausių tokio grafiko pavyzdžių yra sinusinė banga, kurią galite pamatyti šios dalies paveikslėlyje. Funkcija yra ištisinė tam tikru momentu x0, jei tenkinamos kelios sąlygos:

• šiame taške apibrėžiama funkcija;
• dešinės ir kairės ribos taške yra lygios;
• riba lygi funkcijos reikšmei taške x0.

Jei neįvykdoma bent viena sąlyga, sakoma, kad funkcija neveikia. O taškai, kuriuose funkcija nepertraukiama, paprastai vadinami nenutrūkstamais taškais. Funkcijos, kuri „nutrūks“, kai rodoma grafiškai, pavyzdys yra: y = (x + 4) / (x-3). Be to, y neegzistuoja taške x = 3 (nes neįmanoma padalyti iš nulio).

Nagrinėjamoje funkcijoje (y = 1/3 (x ^ 3-14x ^ 2 + 49x-36)) viskas pasirodė paprasta, nes grafikas bus tęstinis.

Lyginis, nelyginis

Dabar patikrinkite pariteto funkciją. Pirma, šiek tiek teorijos. Lyginė funkcija yra ta, kuri tenkina sąlygą f (-x) = f (x) bet kuriai kintamojo x reikšmei (iš reikšmių diapazono). Pavyzdžiai:

• modulis x (grafas atrodo kaip daw, pirmojo ir antrojo grafiko ketvirčių pusiausvyra);
• x kvadratas (parabolė);
• kosinusas x (kosinusas).

Atkreipkite dėmesį, kad visi šie brėžiniai yra simetriški, žiūrint ordinatės (ty y) atžvilgiu.

Kas tada vadinama nelygine funkcija? Tai yra tos funkcijos, kurios tenkina sąlygą: f (-x) = - f (x) bet kuriai kintamojo x reikšmei. Pavyzdžiai:

• hiperbolė;
• kubinė parabolė;
• sinusoidinė;
• tangentoidą ir pan.

Atkreipkite dėmesį, kad šios funkcijos yra simetriškos taško (0: 0), tai yra, pradžios atžvilgiu. Remiantis tuo, kas buvo pasakyta šioje straipsnio dalyje, lyginė ir nelyginė funkcijos turi turėti savybę: x priklauso apibrėžimų aibei, o -x taip pat.

Panagrinėkime pariteto funkciją. Matome, kad jis neatitinka nė vieno aprašymo. Todėl mūsų funkcija nėra nei lyginė, nei nelyginė.

Asimptotės

Pradėkime nuo apibrėžimo. Asimptotė yra kreivė, kuri yra kuo arčiau grafiko, tai yra, atstumas nuo taško linkęs į nulį. Iš viso yra trys asimptotų tipai:

• vertikaliai, tai yra lygiagrečiai y ašiai;
• horizontaliai, tai yra lygiagrečiai x ašiai;
• linkęs.

Kalbant apie pirmąjį tipą, kai kuriuose taškuose reikia ieškoti tiesių duomenų:

• pertrauka;
• apibrėžimo srities galai.

Mūsų atveju funkcija yra ištisinė, o domenas lygus R. Todėl vertikalių asimptočių nėra.

Funkcijos grafikas turi horizontalią asimptotę, kuri atitinka tokį reikalavimą: jei x linkęs į begalybę arba minus begalybę, o riba lygi tam tikram skaičiui (pavyzdžiui, a). Šiuo atveju y = a – tai horizontalioji asimptotė. Funkcijoje, kurią mes tiriame, nėra horizontalių asimptočių.

Įstrižinė asimptotė egzistuoja tik tuo atveju, jei tenkinamos dvi sąlygos:

• lim (f (x)) / x = k;
• lim f (x) -kx = b.

Tada jį galima rasti pagal formulę: y = kx + b. Vėlgi, mūsų atveju nėra įstrižų asimptotų.

Funkcijos nuliai

Kitas žingsnis yra išnagrinėti funkcijos grafiką nuliais. Taip pat labai svarbu pažymėti, kad užduotis, susijusi su funkcijos nulių radimu, atsiranda ne tik tiriant ir braižant funkcijos grafiką, bet ir kaip savarankiška užduotis bei kaip būdas spręsti nelygybes. Gali reikėti surasti funkcijos nulius grafike arba naudoti matematinį žymėjimą.

Šių reikšmių radimas padės tiksliau nubraižyti funkciją. Paprastais žodžiais tariant, funkcijos nulis yra kintamojo x reikšmė, kai y = 0. Jei grafike ieškote funkcijos nulių, tuomet turėtumėte atkreipti dėmesį į taškus, kuriuose grafikas kerta abscisių ašį.

Norėdami rasti funkcijos nulius, turite išspręsti šią lygtį: y = 1/3 (x ^ 3-14x ^ 2 + 49x-36) = 0. Atlikę reikiamus skaičiavimus, gauname tokį atsakymą:

Pastovumas

Kitas funkcijos (grafiko) tyrimo ir konstravimo etapas – pastovumo intervalų paieška. Tai reiškia, kad turime nustatyti, kokiais intervalais funkcija įgauna teigiamą reikšmę, o kokiais – neigiamą. Tai padaryti padės funkcijos nuliai, rasti ankstesniame skyriuje. Taigi, turime nutiesti tiesią liniją (atskirai nuo grafiko) ir teisinga tvarka paskirstyti joje funkcijos nulius nuo mažiausio iki didžiausio. Dabar reikia nustatyti, kuris iš gautų intervalų turi „+“ ženklą, o kuris „-“.

Mūsų atveju funkcija įgauna teigiamą reikšmę intervalais:

• nuo 1 iki 4;
• nuo 9 iki begalybės.

Neigiama reikšmė:

• nuo minus begalybės iki 1;
• nuo 4 iki 9.

Tai lengva apibrėžti. Įveskite bet kurį skaičių iš intervalo į funkciją ir pažiūrėkite, koks yra atsakymo ženklas (minusas ar pliusas).

Didina ir mažina funkcijas

Norėdami ištirti ir sukurti funkciją, turime išsiaiškinti, kur grafikas padidės (kils į viršų išilgai Oy), o kur kris (nulips išilgai ordinatės).

Funkcija didėja tik tuo atveju, jei didesnė kintamojo x reikšmė atitinka didesnę y reikšmę. Tai reiškia, kad x2 yra didesnis nei x1, o f (x2) yra didesnis nei f (x1). Ir mes stebime visiškai priešingą reiškinį mažėjančioje funkcijoje (kuo daugiau x, tuo mažiau y). Norėdami nustatyti didėjimo ir mažėjimo intervalus, turite rasti:

• apimtis (jau turime);
• išvestinė (mūsų atveju: 1/3 (3x ^ 2-28x + 49);
• Išspręskite lygtį 1/3 (3x ^ 2-28x + 49) = 0.

Atlikę skaičiavimus gauname rezultatą:

Gauname: funkcija didėja intervalais nuo minus begalybės iki 7/3 ir nuo 7 iki begalybės, o mažėja intervale nuo 7/3 iki 7.

Kraštutinumai

Ištirta funkcija y = 1/3 (x ^ 3-14x ^ 2 + 49x-36) yra ištisinė ir egzistuoja bet kurioms kintamojo x reikšmėms. Ekstremalumo taškas rodo šios funkcijos maksimumą ir minimumą. Mūsų atveju jų nėra, o tai labai supaprastina statybos užduotį. Kitu atveju jie taip pat randami naudojant funkcijos išvestinę. Radę nepamirškite juos pažymėti diagramoje.

Išgaubtumas ir įdubimas

Toliau tiriame funkciją y (x). Dabar turime patikrinti, ar jis yra išgaubtas ir įgaubtas. Šių sąvokų apibrėžimai gana sunkiai suvokiami, geriau viską analizuoti su pavyzdžiais. Bandymui: funkcija yra išgaubta, jei ji yra nemažėjanti funkcija. Sutikite, tai nesuprantama!

Turime rasti antros eilės funkcijos išvestinę. Gauname: y = 1/3 (6x-28). Dabar nustatykime dešinę pusę į nulį ir išspręskime lygtį. Atsakymas: x = 14/3. Mes radome vingio tašką, tai yra vietą, kur grafikas keičiasi iš išgaubto į įgaubtą arba atvirkščiai. Intervale nuo minus begalybės iki 14/3 funkcija yra išgaubta, o nuo 14/3 iki plius begalybės – įgaubta. Taip pat labai svarbu atkreipti dėmesį, kad grafiko posūkio taškas būtų lygus ir minkštas, neturėtų būti aštrių kampų.

Papildomų taškų apibrėžimas

Mūsų užduotis yra ištirti ir nubrėžti funkciją. Tyrimą baigėme, dabar bus nesunku nubraižyti funkciją. Norėdami tiksliau ir detaliau atkurti kreivę arba tiesę koordinačių plokštumoje, galite rasti keletą pagalbinių taškų. Juos apskaičiuoti gana paprasta. Pavyzdžiui, imame x = 3, išsprendžiame gautą lygtį ir randame y = 4. Arba x = 5 ir y = -5 ir pan. Galite paimti tiek papildomų taškų, kiek jums reikia sukurti. Jų randama bent 3-5.

Grafiko braižymas

Mums reikėjo ištirti funkciją (x ^ 3-14x ^ 2 + 49x-36) * 1/3 = y. Koordinačių plokštumoje buvo atlikti visi reikalingi užrašai atliekant skaičiavimus. Belieka sukurti grafiką, tai yra sujungti visus taškus vieną su kitu. Taškų sujungimas turi vykti sklandžiai ir tvarkingai, tai įgūdžių reikalas – truputis praktikos ir jūsų grafikas bus tobulas.

Instrukcijos

Raskite funkcijos apimtį. Pavyzdžiui, funkcija sin (x) apibrėžiama per visą intervalą nuo -∞ iki + ∞, o funkcija 1 / x apibrėžiama nuo -∞ iki + ∞, išskyrus tašką x = 0.

Apibrėžkite tęstinumo sritis ir lūžio taškus. Paprastai funkcija yra ištisinė toje pačioje srityje, kurioje ji yra apibrėžta. Norėdami aptikti nenutrūkstamumą, apskaičiuokite argumentui artėjant prie atskirų apibrėžimo srities taškų. Pavyzdžiui, funkcija 1 / x linkusi į begalybę, kai x → 0 +, ir į minus begalybę, kai x → 0-. Tai reiškia, kad taške x = 0 jis turi antrojo tipo nenutrūkstamumą.
Jei ribos pertrūkio taške yra baigtinės, bet ne lygios, tai yra pirmosios rūšies netolydumas. Jei jie lygūs, tada funkcija laikoma tęstine, nors izoliuotame taške ji nėra apibrėžta.

Raskite vertikalius asimptotus, jei tokių yra. Čia jums padės ankstesnio žingsnio skaičiavimai, nes vertikali asimptotė beveik visada yra antrosios rūšies nepertraukiamumo taške. Tačiau kartais iš apibrėžimo srities išskiriami ne atskiri taškai, o ištisi taškų intervalai, o tada vertikalios asimptotės gali būti šių intervalų pakraščiuose.

Patikrinkite, ar funkcija turi specialių savybių: pariteto, nelyginio pariteto ir periodiškumo.
Funkcija bus net jei bet kuriam x srityje f (x) = f (-x). Pavyzdžiui, cos (x) ir x ^ 2 yra lyginės funkcijos.

Periodiškumas yra savybė, kuri sako, kad yra tam tikras skaičius T, vadinamas periodu, kuris bet kuriam x f (x) = f (x + T). Pavyzdžiui, visos pagrindinės trigonometrinės funkcijos (sinusas, kosinusas, liestinė) yra periodinės.

Raskite taškus. Norėdami tai padaryti, apskaičiuokite pateiktos funkcijos išvestinę ir suraskite tas x reikšmes, kuriose ji išnyksta. Pavyzdžiui, funkcija f (x) = x ^ 3 + 9x ^ 2 -15 turi išvestinę g (x) = 3x ^ 2 + 18x, kuri išnyksta, kai x = 0 ir x = -6.

Norėdami nustatyti, kurie ekstremumo taškai yra maksimumai, o kurie - minimumai, atsekkite išvestinės ženklo pokytį rastuose nuliuose. g (x) pakeičia ženklą iš pliuso taške x = -6, o taške x = 0 atgal iš minuso į pliusą. Vadinasi, funkcija f (x) turi minimumą pirmame taške, o antrajame.

Taigi, jūs radote monotoniškumo sritis: f (x) monotoniškai didėja intervale -∞; -6, monotoniškai mažėja -6; 0 ir vėl didėja 0; + ∞.

Raskite antrą išvestinę. Jo šaknys parodys, kur tam tikros funkcijos grafikas bus išgaubtas, o kur – įgaubtas. Pavyzdžiui, antroji funkcijos f (x) išvestinė bus h (x) = 6x + 18. Ji išnyksta ties x = -3, ženklą pakeičiant iš minuso į pliusą. Todėl grafikas f (x) prieš šį tašką bus išgaubtas, po jo – įgaubtas, o pats šis taškas bus vingio taškas.

Funkcija gali turėti ir kitų asimptotų, be vertikalių, bet tik tuo atveju, jei ji įtraukta į jos apibrėžimo sritį. Norėdami juos rasti, apskaičiuokite f (x) ribą kaip x → ∞ arba x → -∞. Jei jis baigtinis, tada jūs radote horizontalią asimptotę.

Įstrižinė asimptotė yra kx + b formos tiesi linija. Norėdami rasti k, apskaičiuokite f (x) / x ribą kaip x → ∞. Norėdami rasti b - ribą (f (x) - kx) tam pačiam x → ∞.

Nubraižykite funkciją ant apskaičiuotų duomenų. Pažymėkite asimptotus, jei tokių yra. Pažymėkite kraštutinius taškus ir juose funkcijos reikšmes. Norėdami didesnio grafiko tikslumo, apskaičiuokite funkcijos reikšmes dar keliuose tarpiniuose taškuose. Tyrimas baigtas.

Atskaitos taškai nagrinėjant funkcijas ir jų grafikų konstravimą yra būdingi taškai – nenutrūkstamumo, ekstremumo, vingio, susikirtimo su koordinačių ašimis taškai. Diferencialinio skaičiavimo pagalba galima nustatyti būdingus funkcijų kitimo požymius: didėjimą ir mažėjimą, maksimumus ir minimumus, grafiko išgaubimo ir įgaubimo kryptį, asimptotų buvimą.

Funkcijos grafiko eskizą galima (ir reikia) nubraižyti suradus asimptotes ir ekstremumo taškus, o tyrimo metu patogu pildyti funkcijos tyrimo sukimosi lentelę.

Paprastai naudojama tokia funkcijų tyrimo schema.

1.Raskite funkcijos sritį, tęstinumo intervalus ir lūžio taškus.

2.Ištirkite lygumo ar nelygumo funkciją (grafiko ašinę arba centrinę simetriją.

3.Raskite asimptotes (vertikalias, horizontalias arba įstrižas).

4.Raskite ir ištirkite funkcijos didėjimo ir mažėjimo intervalus, jos ekstremumo taškus.

5.Raskite kreivės išgaubimo ir įgaubimo intervalus, jos vingio taškus.

6.Raskite kreivės susikirtimo taškus su koordinačių ašimis, jei jos yra.

7.Paruoškite apibendrintą tyrimo lentelę.

8.Sukurkite grafiką, atsižvelgdami į funkcijos tyrimą, atliktą aukščiau nurodytuose taškuose.

Pavyzdys. Naršyti funkciją

ir sudaryti jo grafiką.

7. Sudarykime funkcijos tyrimo suvestinę lentelę, kurioje įvesime visus charakteringus taškus ir intervalus tarp jų. Atsižvelgdami į funkcijos paritetą, gauname tokią lentelę:

Norint visiškai ištirti funkciją ir sudaryti jos grafiką, rekomenduojama naudoti šią schemą:

1) rasti funkcijos sritį;

2) rasti funkcijos ir vertikalių asimptočių (jei jos yra) nenutrūkstamo taškus;

3) ištirti funkcijos elgseną begalybėje, rasti horizontalias ir įstrižas asimptotes;

4) ištirti lygumo (keistingumo) ir periodiškumo (trigonometrinių funkcijų) funkciją;

5) rasti funkcijos monotoniškumo ekstremumus ir intervalus;

6) nustato išgaubimo intervalus ir vingio taškus;

7) jei įmanoma, suraskite susikirtimo taškus su koordinačių ašimis ir keletą papildomų taškų, kurie patikslina grafiką.

Funkcijos tyrimas atliekamas kartu su jos grafiko konstravimu.

9 pavyzdys Ištirkite funkciją ir nubraižykite grafiką.

1. Apibrėžimo sritis:;

2. Funkcija nutrūksta taškuose
,
;

Panagrinėkime vertikalių asimptotų buvimo funkciją.

;
,
─ vertikali asimptotė.

;
,
─ vertikali asimptotė.

3. Ištirkime įstrižųjų ir horizontalių asimptočių buvimo funkciją.

Tiesiai
─ įstrižinė asimptotė, jei
,
.

,
.

Tiesiai
─ horizontali asimptotė.

4. Funkcija lygi, nes
... Funkcijos paritetas rodo grafiko simetriją apie ordinačių ašį.

5. Raskime funkcijos monotoniškumo ir ekstremalių intervalus.

Raskime kritinius taškus, t.y. taškai, kuriuose išvestinė yra 0 arba neegzistuoja:
;
... Turime tris taškus
;

... Šie taškai padalija visą galiojančią ašį į keturias erdves. Apibrėžkime ženklus ant kiekvieno iš jų.

Intervaluose (-∞; -1) ir (-1; 0) funkcija didėja, intervaluose (0; 1) ir (1; + ∞) ─ mažėja. Kertant tašką
išvestinė keičia ženklą iš pliuso į minusą, todėl šiuo metu funkcija turi maksimumą
.

6. Raskite išgaubimo intervalus, vingio taškus.

Raskite taškus, kuriuose yra 0 arba neegzistuoja.

neturi galiojančių šaknų.
,
,

Taškai
ir
realiąją ašį padalinkite į tris intervalus. Apibrėžkime ženklą kiekvienu intervalu.

Taigi, kreivė intervalais
ir
išgaubtas žemyn, intervale (-1; 1) išgaubtas į viršų; vingio taškų nėra, nes funkcija taškuose
ir
nepatikslinta.

7. Raskite susikirtimo su ašimis taškus.

Su ašimi
funkcijos grafikas kertasi taške (0; -1), ir su ašimi
grafikas nesutampa, nes šios funkcijos skaitiklis neturi realių šaknų.

Pateiktos funkcijos grafikas parodytas 1 pav.

1 pav. ─ Funkcijų grafikas

Išvestinės finansinės priemonės sampratos taikymas ekonomikoje. Funkcijos elastingumas

Ekonominiams procesams tirti ir kitoms taikomoms problemoms spręsti dažnai vartojama funkcijos elastingumo sąvoka.

Apibrėžimas. Funkcijos elastingumas
vadinama funkcijos santykinio prieaugio santykio riba iki santykinio kintamojo prieaugio adresu
,. (Vii)

Funkcijos elastingumas parodo apytikslį funkcijos pokyčio procentą
kai keičiamas nepriklausomas kintamasis 1 %.

Funkcijos elastingumas taikomas analizuojant paklausą ir vartojimą. Jei paklausos elastingumas (absoliučia verte)
, tada paklausa laikoma elastinga, jei
─ neutralus, jei
─ neelastingas kainos (arba pajamų) atžvilgiu.

10 pavyzdys Apskaičiuokite funkcijos elastingumą
ir suraskite tamprumo indekso reikšmę = 3.

Sprendimas: pagal (VII) formulę funkcijos elastingumas:

Tada tegul x = 3
Tai reiškia, kad jei aiškinamasis kintamasis padidėja 1%, tai priklausomo kintamojo reikšmė padidėja 1,42%.

11 pavyzdys Tegul paklausa veikia dėl kainos turi formą
, kur ─ pastovus koeficientas. Raskite paklausos funkcijos tamprumo rodiklio reikšmę, kai kaina x = 3 den. vienetų

Sprendimas: apskaičiuokite paklausos funkcijos elastingumą pagal (VII) formulę

Darant prielaidą
piniginių vienetų, gauname
... Tai reiškia, kad už kainą
piniginių vienetų 1% kainos padidėjimas sukels 6% paklausos sumažėjimą, t.y. paklausa yra elastinga.

Norint visiškai ištirti funkciją ir sudaryti jos grafiką, rekomenduojama naudoti šią schemą:
A) rasti apibrėžimo sritį, lūžio taškus; ištirti funkcijos elgseną netoli nutrūkimo taškų (šiuose taškuose suraskite funkcijos ribas kairėje ir dešinėje). Nurodykite vertikalias asimptotes.
B) nustatyti funkcijos lygumą arba nelygumą ir padaryti išvadą apie simetrijos buvimą. Jei, tai funkcija lygi, simetriška OY ašiai; kai funkcija nelyginė, simetriška kilmei; o jei – bendrosios formos funkcija.
C) rasti funkcijos susikirtimo taškus su koordinačių ašimis OY ir OX (jei įmanoma), nustatyti funkcijos pastovaus ženklo intervalus. Funkcijos pastovaus ženklo intervalų ribos nustatomos taškais, kuriuose funkcija lygi nuliui (funkcijos nuliai) arba neegzistuoja, ir šios funkcijos srities ribos. Intervaluose, kur funkcijos grafikas yra virš OX ašies, o kur - žemiau šios ašies.
D) rasti pirmąją funkcijos išvestinę, nustatyti jos nulius ir pastovumo intervalus. Intervaluose, kur funkcija didėja, o kur mažėja. Padarykite išvadą apie ekstremalių buvimą (taškus, kuriuose egzistuoja funkcija ir išvestinė ir per kuriuos pereinant pasikeičia ženklas. Jei keičia ženklą iš pliuso į minusą, tai šioje vietoje funkcija turi maksimumą, o jei iš minuso į pliusą , tada mažiausiai). Raskite funkcijos reikšmes ekstremaliuose taškuose.
E) raskite antrąją išvestinę, jos nulius ir pastovumo intervalus. Intervalais kur< 0 график функции выпуклый, а где – вогнутый. Сделать заключение о наличии точек перегиба и найти значения функции в этих точках.
E) rasti pasvirusius (horizontalius) asimptotus, kurių lygtys turi formą ; kur
.
At funkcijos grafikas turės dvi įstrižas asimptotes, o kiekviena x reikšmė at ir gali atitikti dvi b reikšmes.
G) suraskite papildomų taškų, kad patikslintumėte tvarkaraštį (jei reikia) ir sukurkite grafiką.

1 pavyzdys Išnagrinėkite funkciją ir nubraižykite ją. Sprendimas: A) apibrėžimo apimtis; funkcija yra tęstinė apibrėžimo srityje; - lūžio taškas, nes ; ... Tada yra vertikali asimptotė.
B)
tie. y (x) yra bendroji funkcija.
C) Raskite grafiko susikirtimo taškus su OY ašimi: nustatome x = 0; tada y (0) = - 1, t.y. funkcijos grafikas kerta ašį taške (0; -1). Funkcijos nuliai (grafiko susikirtimo taškai su OX ašimi): nustatome y = 0; tada
.
Kvadratinės lygties diskriminantas yra mažesnis už nulį, todėl nulių nėra. Tada pastovumo intervalų riba yra taškas x = 1, kur funkcija neegzistuoja.
Funkcijos ženklas kiekviename intervale nustatomas pagal konkrečių reikšmių metodą:

Iš diagramos matyti, kad intervale funkcijos grafikas yra po OX ašimi, o intervale - virš OX ašies.
D) Išsiaiškinkite, ar yra kritinių taškų.
.
Kritiniai taškai (kur neegzistuoja) randami iš lygybių ir.

Gauname: x1 = 1, x2 = 0, x3 = 2. Sukurkime pagalbinę lentelę

1 lentelė

(Pirmoje eilutėje yra kritiniai taškai ir intervalai, į kuriuos šie taškai yra padalinti pagal OX ašį; antroje eilutėje nurodomos išvestinės reikšmės kritiniuose taškuose ir ženklai ant intervalų. Ženklus nustato dalinių reikšmių metodas. Trečioje eilutėje nurodomos funkcijos y (x) reikšmės kritiniuose taškuose ir rodoma funkcijos elgsena - didėjanti arba mažėjanti atitinkamais skaitinės ašies intervalais.
E) Raskite funkcijos išgaubimo ir įgaubimo intervalus.
; sudaryti lentelę, kaip nurodyta D dalyje); tik antroje eilutėje užrašome ženklus, o trečioje nurodome išgaubimo tipą. Nes ; tada yra tik vienas kritinis taškas x = 1.
2 lentelė

Taškas x = 1 yra vingio taškas.
E) Raskite pasvirusias ir horizontalias asimptotes

Tada y = x yra įstrižinė asimptotė.
G) Naudodami gautus duomenis sudarome funkcijos grafiką

1). Funkcijos apibrėžimo sritis.
Akivaizdu, kad ši funkcija yra apibrėžta visoje skaičių eilutėje, išskyrus taškus „“ ir „“, nes šiuose taškuose vardiklis yra lygus nuliui, todėl funkcija neegzistuoja, o tiesės ir yra vertikalios asimptotės.

2). Funkcijos elgesys, kai argumentas linkęs į begalybę, nenutrūkstamų taškų buvimas ir įstrižų asimptotų buvimo patikrinimas.
Pirmiausia patikrinkime, kaip funkcija elgiasi artėjant prie begalybės į kairę ir į dešinę.

Taigi už, funkcija linkusi į 1, t.y. - horizontalioji asimptota.
Netoli nutrūkimo taškų funkcijos elgsena apibrėžiama taip:


Tie. artėjant prie nutrūkimo taškų kairėje, funkcija be galo mažėja, o dešinėje – be galo didėja.
Įstrižos asimptotės buvimas nustatomas atsižvelgiant į lygybę:

Įstrižų asimptotų nėra.

3). Sankirtos taškai su koordinačių ašimis.
Čia reikia atsižvelgti į dvi situacijas: rasti susikirtimo tašką su Ox ašimi ir su Oy ašimi. Susikirtimo su Ox ašimi ženklas yra funkcijos nulinė reikšmė, t.y. būtina išspręsti lygtį:

Ši lygtis neturi šaknų, todėl šios funkcijos grafikas neturi susikirtimo taškų su Ox ašimi.
Susikirtimo su Oy ašimi ženklas yra x = 0. Šiuo atveju
,
tie. - funkcijos grafiko susikirtimo taškas su ašimi Oy.

4).Ekstremalių taškų ir didėjimo bei mažėjimo intervalų nustatymas.
Norėdami ištirti šią problemą, apibrėžiame pirmąjį išvestinį variantą:
.
Pirmosios išvestinės reikšmę prilyginkime nuliui.
.
Trupmena lygi nuliui, kai jos skaitiklis lygus nuliui, t.y. ...
Apibrėžkime funkcijos didėjimo ir mažėjimo intervalus.

Taigi funkcija turi vieną ekstremumo tašką ir neegzistuoja dviejuose taškuose.
Taigi funkcija didėja intervalais ir mažėja intervalais ir.

5). Posūkio taškai ir išgaubimo bei įgaubimo sritys.
Ši funkcijos elgsenos charakteristika nustatoma naudojant antrąją išvestinę. Pirmiausia nustatykime, ar yra vingio taškų. Antroji funkcijos išvestinė yra

At ir funkcija yra įgaubta;

už ir funkcija yra išgaubta.

6). Funkcijos braižymas.
Naudodami rastas reikšmes taškuose, sudarome scheminį funkcijos grafiką:

Sprendimas
Pateikta funkcija yra bendroji neperiodinė funkcija. Jo grafikas eina per kilmę, nes.
Pateiktos funkcijos sritis yra visos kintamojo reikšmės, išskyrus ir, kai trupmenos vardiklis išnyksta.
Vadinasi, taškai ir yra funkcijos nepertraukiamumo taškai.
Nes ,

Nes ,
, tada taškas yra antrojo tipo lūžio taškas.
Tiesios linijos ir yra vertikalios funkcijos grafiko asimptotės.
Įstrižųjų asimptotų lygtys, kur .
At ,
.
Taigi už ir funkcijos grafikas turi vieną asimptotę.
Raskime funkcijos didėjimo ir mažėjimo intervalus ir ekstremumo taškus.
.
Pirmoji funkcijos at ir todėl at ir išvestinė, funkcija didėja.
Kada, taigi, kada, funkcija sumažėja.
neegzistuoja,.
, todėl už funkcijos grafikas yra įgaubtas.
At , todėl už funkcijos grafikas yra išgaubtas.

Pravažiuojant taškus,, keičia ženklą. Kai funkcija neapibrėžta, todėl funkcijos grafikas turi vieną vingio tašką.
Nubraižykime funkciją.