Как находится длина средней линии. Трапеция, средняя линия трапеции, треугольник

Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.

Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.

Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля - до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.

1 Дополнительное построение, ведущее к теореме о средней линии треугольника, трапеции и свойствам подобия треугольников.

И она равна половине гипотенузы .
Следствие 1.
Следствие 2.

2 Все прямоугольные треугольники с одинаковым острым углом - подобны. Взгляд на тригонометрические функции.

3 Пример дополнительного построения - высота, опущенная на гипотенузу. Вывод теоремы Пифагора на основе подобия треугольников.

Отсюда видно, что

1 Все прямоугольные треугольники с одинаковым острым углом - подобны. Взгляд на тригонометрические функции.

Треугольники со сторонами штрихованными и с не штрихованными подобны по равенству двух углов. Поэтому откуда

Это значит, что указанные отношения зависят лишь от острого угла прямоугольного треугольника и по сути определяют его. Это одно из оснований появления тригонометрических функций:

Часто запись тригонометрических функций угла в подобных прямоугольных треугольниках наглядней записи соотношений подобия!

2 Пример дополнительного построения - высота, опущенная на гипотенузу. Вывод теоремы Пифагора на основе подобия треугольников.

Опустим на гипотенузу AB высоту CH. Имеем три подобных треугольника ABC, AHC и CHB. Запишем выражения для тригонометрических функций:

Отсюда видно, что . Складывая, получаем теорему Пифагора, поскольку :

Другое доказательство теоремы Пифагора см.в комментарии к задаче 4.
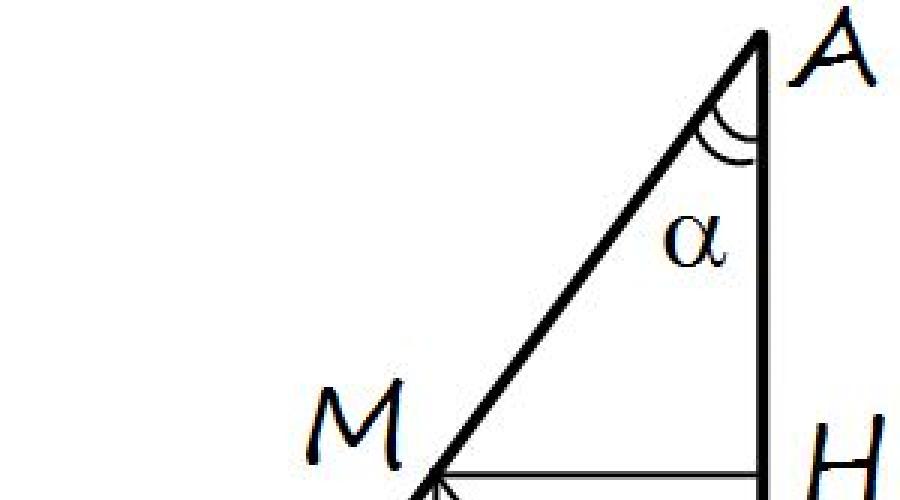
3 Важный пример дополнительного построения – построение угла, равного одному из углов треугольника.

Проводим из вершины прямого угла отрезок прямой, составляющий с катетом CA угол, равный углу CAB заданного прямоугольного треугольника ABC. В результате получим равнобедренный треугольник ACM с углами при основании . Но другой треугольник, получающийся при таком построении, также будет равнобедренным, поскольку каждый его угол при основании равен (по свойству углов прямоугольного треугольника и по построению - из прямого угла «вычли» угол ). В силу того, что треугольники BMC и AMC равнобедренные с общей стороной MC имеем равенство MB=MA=MC, т.е. MC – медиана, проведенная к гипотенузе прямоугольного треугольника , и она равна половине гипотенузы .
Следствие 1. Середина гипотенузы является центром окружности, описанной вокруг этого треугольника, поскольку получилось, что середина гипотенузы равноудалена от вершин прямоугольного треугольника.
Следствие 2. Средняя линия прямоугольного треугольника, соединяющая середину гипотенузы и середину катета, параллельна противоположному катету и равна его половине.

Опустим в равнобедренных треугольниках BMC и AMC высоты MH и MG на основания. Поскольку в равнобедренном треугольнике, высота, опущенная на основание, является также и медианой (и биссектрисой), то MH и MG –линии прямоугольного треугольника, соединяющие середину гипотенузы с серединами катетов. По построению они оказываются параллельными противоположным катетам и равные их половинам, поскольку треугольники равны MHC и MGC равны (причем MHCG – прямоугольник). Этот результат является основанием для доказательства теоремы о средней линии произвольного треугольника и, далее, средней линии трапеции и свойства пропорциональности отрезков, отсекаемых параллельными прямыми на двух пересекающих их прямых.

Задачи
Использование свойств подобия -1
Использование основных свойств - 2
Использование дополнительного построения 3-4

1 2 3 4

Высота, опущенная из вершины прямого угла прямоугольного треугольника равна корню квадратном из длин отрезков, на которые она делит гипотенузу.

Решение представляется очевидным, если знать вывод теоремы Пифагора из подобия треугольников:

\(\mathrm{tg}\beta=\frac{h}{c_1}=\frac{c_2}{h}\),
откуда \(h^2=c_1c_2\).

Найти геометрическое место точек (ГМТ) пересечения медиан всевозможных прямоугольных треугольников, гипотенуза АВ которых зафиксирована.

Точка пересечения медиан любого треугольника отсекает от медианы одну треть, считая от точки ее пересечения с соответствующей стороной. В прямоугольном треугольнике медиана, проведенная из прямого угла, равна половине гипотенузы. Поэтому искомое ГМТ есть окружность радиуса, равной 1/6 от длины гипотенузы, с центром в середине этой (фиксированной) гипотенузы.

Порой темы, которые объясняют в школе, могут быть не всегда понятны с первого раза. Особенно это касается такого предмета, как математика. Но все становится намного сложнее, когда эта наука начинает подразделяться на две части: алгебру и геометрию.

Каждый ученик может обладать способностью к одному из двух направлений, но особенно в начальных классах важно понять базу и алгебры, и геометрии. В геометрии одной из главных тем принято считать раздел о треугольниках.

Как находить среднюю линию треугольника? Давайте разбираться.

Основные понятия

Для начала чтобы разобраться, как находить среднюю линию треугольника, важно понимать, что же это.

Для проведения средней линии нет ограничений: треугольник может быть любым (равнобедренным, равносторонним, прямоугольным). И все свойства, которые относятся к средней линии, будут действовать.

Средняя линия треугольника является отрезком, соединяющим середины 2-х его сторон. Следовательно, любой треугольник может иметь 3 таких линии.

Свойства

Чтобы знать, как находить среднюю линию треугольника, обозначим ее свойства, которые необходимо запомнить, иначе без них будет невозможным решение задач с необходимостью обозначить длину средней линии, поскольку все полученные данные необходимо обосновать и аргументировать теоремами, аксиомами или свойствами.

Таким образом, чтобы ответить на вопрос: «Как найти среднюю линию треугольника АВС?», достаточно знать одну из сторон треугольника.

Приведем пример

Взгляните на рисунок. На нем представлен треугольник ABC со средней линией DE. Обратим внимание, что она параллельна основанию AC в треугольнике. Следовательно, каким бы ни было значение AC, средняя линия DE будет в два раза меньше. К примеру, AC=20, значит DE=10 и т. д.

Вот такими несложными способами можно понять, как находить среднюю линию треугольника. Запомните ее основные свойства и определение, и тогда у вас никогда не возникнет проблем с нахождением ее значения.

Как найти середину треугольника: задачка по геометрии. Основные элементарные задачи по Евклидовой геометрии пришли к нам из античности. В них заключается сама первичная сущность и необходимые базовые знания о восприятии человеком пространственных форм. Одной из таких задач является проблема нахождения середины треугольника. Сегодня эта задачка рассматривается как учебный прием развития интеллектуальных способностей школьников. В древнем же мире, знание того, как найти середину треугольника, применялось и на практике: в землеустройстве, при изготовлении разнообразных механизмов и т.д. В чем же состоит сущность этого геометрического ребуса?

Что такое медиана? Перед решением задачи необходимо ознакомиться с простейшей геометрической терминологией, касающейся треугольников. Прежде всего, у каждого треугольника есть три вершины, три стороны и три угла, от чего и происходит название данной геометрической фигуры. Важно знать, как называются линии, соединяющие вершины с противоположными сторонами: высота, биссектриса и медиана.

Высота − линия перпендикулярная стороне, противоположной вершине, из которой она проводится; биссектриса − делит угол пополам; медиана же делит противоположную исходящей вершине сторону пополам. Для решения этой задачи нужно знать, как найти координаты середины отрезка, ведь именно точка пересечения медиан треугольника и является его серединой.

Находим середины сторон треугольника. Нахождение середины отрезка тоже является классической геометрической задачей, для решения которой понадобится циркуль и линейка без делений. Ставим иглу циркуля в точку окончания отрезка и чертим полукруг, больший половины отрезка в середине последнего. Проделываем то же самое с другой стороны отрезка. Полученные полуокружности обязательно пересекутся в двух точках, ведь их радиусы больше половины исходного отрезка.

Соединяем две точки пересечения окружности прямой линией при помощи линейки. Эта линия пересекает исходный отрезок точно в его середине. Теперь, зная то, как найти середину отрезка, проделываем это с каждой стороной треугольника. После нахождения всех середин сторон треугольника всё готово для построения его собственной середины.

Строим середину треугольника. Соединив прямыми линиями вершины треугольника с серединами противоположных им сторон, получаем три медианы. Может кого-то это и удивит, но одним из законов гармонии этой геометрической фигуры является то, что все три медианы всегда пересекаются в одной точке. Именно эта точка и будет искомой серединой треугольника, которую не так трудно найти, если знать;как построить середину отрезка.

Интересно и то, что точка пересечения медиан представляет собой не только геометрическую, но и "физическую" середину треугольника. То есть, если, к примеру, вырезать треугольник из фанеры, найти его середину и поместить эту точку на кончик иглы, то в идеале такая фигура будет балансировать и не упадет. Элементарная геометрия несет в себе множество подобных захватывающих "тайн", знание которых помогает постигать гармонию окружающего мира и природу более сложных вещей.

\[{\Large{\text{Подобие треугольников}}}\]

Определения

Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого
(стороны называются сходственными, если они лежат напротив равных углов).

Коэффициент подобия (подобных) треугольников – это число, равное отношению сходственных сторон этих треугольников.

Определение

Периметр треугольника – это сумма длин всех его сторон.

Теорема

Отношение периметров двух подобных треугольников равно коэффициенту подобия.

Доказательство

Рассмотрим треугольники \(ABC\) и \(A_1B_1C_1\) со сторонами \(a,b,c\) и \(a_1, b_1, c_1\) соответственно (см. рисунок выше).

Тогда \(P_{ABC}=a+b+c=ka_1+kb_1+kc_1=k(a_1+b_1+c_1)=k\cdot P_{A_1B_1C_1}\)

Теорема

Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Доказательство

Пусть треугольники \(ABC\) и \(A_1B_1C_1\) подобны, причём \(\dfrac{AB}{A_1B_1} = \dfrac{AC}{A_1C_1} = \dfrac{BC}{B_1C_1} = k\) . Обозначим буквами \(S\) и \(S_1\) площади этих треугольников соответственно.

Так как \(\angle A = \angle A_1\) , то \(\dfrac{S}{S_1} = \dfrac{AB\cdot AC}{A_1B_1\cdot A_1C_1}\) (по теореме об отношении площадей треугольников, имеющих по равному углу).

Так как \(\dfrac{AB}{A_1B_1} = \dfrac{AC}{A_1C_1} = k\) , то \(\dfrac{S}{S_1} = \dfrac{AB}{A_1B_1}\cdot\dfrac{AC}{A_1C_1} = k\cdot k = k^2\) , что и требовалось доказать.

\[{\Large{\text{Признаки подобия треугольников}}}\]

Теорема (первый признак подобия треугольников)

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Доказательство

Пусть \(ABC\) и \(A_1B_1C_1\) – треугольники такие, что \(\angle A = \angle A_1\) , \(\angle B = \angle B_1\) . Тогда по теореме о сумме углов треугольника \(\angle C = 180^\circ - \angle A - \angle B = 180^\circ - \angle A_1 - \angle B_1 = \angle C_1\) , то есть углы треугольника \(ABC\) соответственно равны углам треугольника \(A_1B_1C_1\) .

Так как \(\angle A = \angle A_1\) и \(\angle B = \angle B_1\) , то \(\dfrac{S_{ABC}}{S_{A_1B_1C_1}} = \dfrac{AB\cdot AC}{A_1B_1\cdot A_1C_1}\) и \(\dfrac{S_{ABC}}{S_{A_1B_1C_1}} = \dfrac{AB\cdot BC}{A_1B_1\cdot B_1C_1}\) .

Из этих равенств следует, что \(\dfrac{AC}{A_1C_1} = \dfrac{BC}{B_1C_1}\) .

Аналогично доказывается, что \(\dfrac{AC}{A_1C_1} = \dfrac{AB}{A_1B_1}\) (используя равенства \(\angle B = \angle B_1\) , \(\angle C = \angle C_1\) ).

В итоге, стороны треугольника \(ABC\) пропорциональны сходственным сторонам треугольника \(A_1B_1C_1\) , что и требовалось доказать.

Теорема (второй признак подобия треугольников)

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

Доказательство

Рассмотрим два треугольника \(ABC\) и \(A"B"C"\) , таких что \(\dfrac{AB}{A"B"}=\dfrac{AC}{A"C"}\) , \(\angle BAC = \angle A"\) . Докажем, что треугольники \(ABC\) и \(A"B"C"\) – подобны. Учитывая первый признак подобия треугольников, достаточно показать, что \(\angle B = \angle B"\) .

Рассмотрим треугольник \(ABC""\) , у которого \(\angle 1 = \angle A"\) , \(\angle 2 = \angle B"\) . Треугольники \(ABC""\) и \(A"B"C"\) подобны по первому признаку подобия треугольников, тогда \(\dfrac{AB}{A"B"} = \dfrac{AC""}{A"C"}\) .

С другой стороны, по условию \(\dfrac{AB}{A"B"} = \dfrac{AC}{A"C"}\) . Из последних двух равенств следует, что \(AC = AC""\) .

Треугольники \(ABC\) и \(ABC""\) равны по двум сторонам и углу между ними, следовательно, \(\angle B = \angle 2 = \angle B"\) .

Теорема (третий признак подобия треугольников)

Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Доказательство

Пусть стороны треугольников \(ABC\) и \(A"B"C"\) пропорциональны: \(\dfrac{AB}{A"B"} = \dfrac{AC}{A"C"} = \dfrac{BC}{B"C"}\) . Докажем, что треугольники \(ABC\) и \(A"B"C"\) подобны.

Для этого, учитывая второй признак подобия треугольников, достаточно доказать, что \(\angle BAC = \angle A"\) .

Рассмотрим треугольник \(ABC""\) , у которого \(\angle 1 = \angle A"\) , \(\angle 2 = \angle B"\) .

Треугольники \(ABC""\) и \(A"B"C"\) подобны по первому признаку подобия треугольников, следовательно, \(\dfrac{AB}{A"B"} = \dfrac{BC""}{B"C"} = \dfrac{C""A}{C"A"}\) .

Из последней цепочки равенств и условия \(\dfrac{AB}{A"B"} = \dfrac{AC}{A"C"} = \dfrac{BC}{B"C"}\) вытекает, что \(BC = BC""\) , \(CA = C""A\) .

Треугольники \(ABC\) и \(ABC""\) равны по трем сторонам, следовательно, \(\angle BAC = \angle 1 = \angle A"\) .

\[{\Large{\text{Теорема Фалеса}}}\]

Теорема

Если на одной из сторон угла отметить равные между собой отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на второй стороне также равные между собой отрезки.

Доказательство

Докажем сначала лемму: Если в \(\triangle OBB_1\) через середину \(A\) стороны \(OB\) проведена прямая \(a\parallel BB_1\) , то она пересечет сторону \(OB_1\) также в середине.

Через точку \(B_1\) проведем \(l\parallel OB\) . Пусть \(l\cap a=K\) . Тогда \(ABB_1K\) - параллелограмм, следовательно, \(B_1K=AB=OA\) и \(\angle A_1KB_1=\angle ABB_1=\angle OAA_1\) ; \(\angle AA_1O=\angle KA_1B_1\) как вертикальные. Значит, по второму признаку \(\triangle OAA_1=\triangle B_1KA_1 \Rightarrow OA_1=A_1B_1\) . Лемма доказана.

Перейдем к доказательству теоремы. Пусть \(OA=AB=BC\) , \(a\parallel b\parallel c\) и нужно доказать, что \(OA_1=A_1B_1=B_1C_1\) .

Таким образом, по данной лемме \(OA_1=A_1B_1\) . Докажем, что \(A_1B_1=B_1C_1\) . Проведем через точку \(B_1\) прямую \(d\parallel OC\) , причем пусть \(d\cap a=D_1, d\cap c=D_2\) . Тогда \(ABB_1D_1, BCD_2B_1\) - параллелограммы, следовательно, \(D_1B_1=AB=BC=B_1D_2\) . Таким образом, \(\angle A_1B_1D_1=\angle C_1B_1D_2\) как вертикальные, \(\angle A_1D_1B_1=\angle C_1D_2B_1\) как накрест лежащие, и, значит, по второму признаку \(\triangle A_1B_1D_1=\triangle C_1B_1D_2 \Rightarrow A_1B_1=B_1C_1\) .

Теорема Фалеса

Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.

Доказательство

Пусть параллельные прямые \(p\parallel q\parallel r\parallel s\) разбили одну из прямых на отрезки \(a, b, c, d\) . Тогда вторую прямую эти прямые должны разбить на отрезки \(ka, kb, kc, kd\) соответственно, где \(k\) – некоторое число, тот самый коэффициент пропорциональности отрезков.

Проведем через точку \(A_1\) прямую \(p\parallel OD\) (\(ABB_2A_1\) - параллелограмм, следовательно, \(AB=A_1B_2\) ). Тогда \(\triangle OAA_1 \sim \triangle A_1B_1B_2\) по двум углам. Следовательно, \(\dfrac{OA}{A_1B_2}=\dfrac{OA_1}{A_1B_1} \Rightarrow A_1B_1=kb\) .

Аналогично проведем через \(B_1\) прямую \(q\parallel OD \Rightarrow \triangle OBB_1\sim \triangle B_1C_1C_2 \Rightarrow B_1C_1=kc\) и т.д.

\[{\Large{\text{Средняя линия треугольника}}}\]

Определение

Средняя линия треугольника – это отрезок, соединяющий середины любых двух сторон треугольника.

Теорема

Средняя линия треугольника параллельна третьей стороне и равна ее половине.

Доказательство

1) Параллельность средней линию основанию следует из доказанной выше леммы .

2) Докажем, что \(MN=\dfrac12 AC\) .

Через точку \(N\) проведем прямую параллельно \(AB\) . Пусть эта прямая пересекла сторону \(AC\) в точке \(K\) . Тогда \(AMNK\) - параллелограмм (\(AM\parallel NK, MN\parallel AK\) по предыдущему пункту). Значит, \(MN=AK\) .

Т.к. \(NK\parallel AB\) и \(N\) – середина \(BC\) , то по теореме Фалеса \(K\) – середина \(AC\) . Следовательно, \(MN=AK=KC=\dfrac12 AC\) .

Следствие

Средняя линия треугольника отсекает от него треугольник, подобный данному с коэффициентом \(\frac12\) .