Compito B7 - Trasformazione di espressioni logaritmiche e indicative. Espressioni logaritmiche
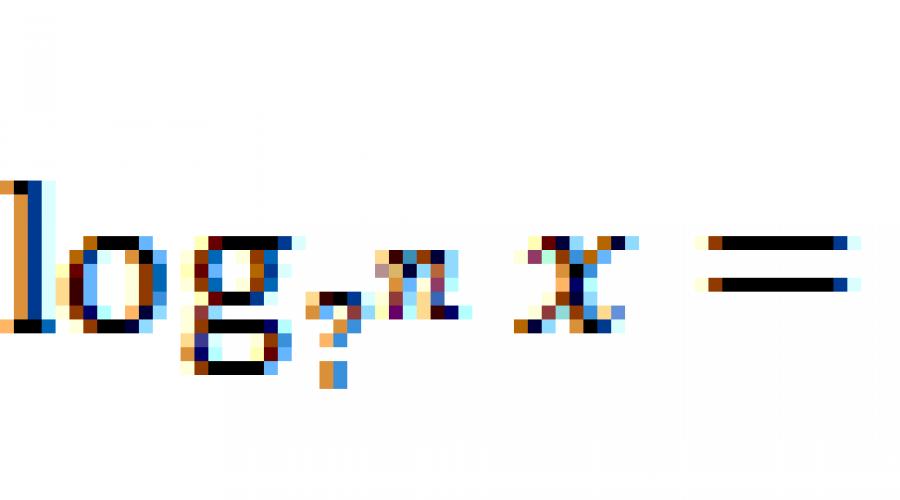
Tipo di lezione: Lezione della generalizzazione e sistematizzazione della conoscenza
Obiettivi:
- per attualizzare la conoscenza degli studenti sui logaritmi e le loro proprietà nel quadro di una ripetizione e preparazione generalizzanti per l'uso;
- promuovere lo sviluppo dell'attività mentale degli studenti, le competenze di applicare la conoscenza teorica durante l'esecuzione di esercizi;
- promuovere lo sviluppo di qualità personali di studenti, capacità di autocontrollo e autovalutazione delle loro attività; Educare il duro lavoro, il paziente, la persistenza, l'indipendenza.
Attrezzatura:computer, proiettore, presentazione (Allegato 1), Carte con i compiti a casa (è possibile allegare un file con un'attività in un diario elettronico).
Durante le classi
I. Momento organizzativo. Saluto, umore alla lezione.
II. Discussione compiti a casa.
III. Temi e obiettivi del messaggio della lezione. Motivazione.(Diapositiva 1) presentazione.
Continuiamo a generalizzare la ripetizione del corso di matematica in preparazione per l'esame. E oggi nella lezione parleremo di logaritmi e delle loro proprietà.
Le attività per il calcolo dei logaritmi e la trasformazione delle espressioni logaritmiche sono necessariamente presenti nei materiali di controllo e di misurazione dei livelli di base e del profilo. Pertanto, lo scopo della nostra lezione è ripristinare le idee sul significato del concetto di "logaritmo" e di aggiornare le competenze per trasformare le espressioni logaritmiche. Scrivi il soggetto della lezione nei notebook.
IV. Attualizzazione della conoscenza.
1. / orale /Per cominciare, ricorda cosa si chiama logaritmo. (Diapositiva 2)
(Il logaritmo del numero positivo B per la base A (dove A\u003e 0, ah? 1) è chiamato un indicatore del grado in cui il numero A deve essere preso per ottenere il numero B)
Log a b \u003d n<-> A N \u003d B, (A\u003e 0 e 1, B\u003e \u200b\u200b0)
Quindi, "logaritmo" è il "indicatore del grado"!
(Diapositiva 3) quindi a n \u003d b può essere riscritto come \u003d B è l'identità logaritmica principale.
Se la base è \u003d 10, allora il logaritmo è chiamato decimale e denotato LGB.
Se A \u003d E, allora il logaritmo è chiamato naturale e denota lnb.
2. / scritto / (Diapositiva 4)Compila i salti per ottenere uguaglianza fedele:
Registrare? x + log a? \u003d Log? (? y)
Log a? - Log? Y \u003d log? (X /?)
Registra una X? \u003d PLog? (?)
![]()
Dai un'occhiata:
uno; uno; A, y, x; x, a, a, y; P, A, X.
Queste sono le proprietà dei logaritmi. E anche un gruppo di proprietà: (Diapositiva 5)
![]()
![]()
![]()
Dai un'occhiata:
a, 1, n, x; n, x, p, a; x, b, a, y; A, X, B; A, 1, B.
V. Lavoro orale
(Diapositiva 6) №1. Calcolare:
a B C D); e).
Risposte : a) 4; B) - 2; alle 2; d) 7; e) 27.
(Diapositiva 7) №2. Trova x:
ma) ; b) (risposte: a) 1/4; b) 9).
Numero 3. Ha senso considerare un tale logaritmo:
ma) ; b); nel) ? (Non)
Vi. Lavoro indipendente in gruppi, forti discepoli - Consulenti. (Diapositiva 8)
# 1. Calcola: ![]() .
.
No. 2. Semplifica:
# 3. Trova il valore dell'espressione se
№ 4. Semplifica l'espressione: ![]()
№ 5. Calcola:
№ 6. Calcola:№ 7. Calcola:
No. 8. Calcola:
Dopo l'esecuzione - controllo e discussione sulla soluzione raccolta o utilizzando il documento - telecamere.
VII. Soluzione del compito di maggiore complessità(Un forte studente sul tabellone, il resto - nei taccuini) (Diapositiva 9)
Trova il valore dell'espressione:
VIII. I compiti a casa (su carte) differenziati.(Diapositiva 10)
№1. Calcolare: ![]()
L'uguaglianza elencata nelle espressioni di conversione con logaritmi viene utilizzata sia a destra sinistra che a sinistra a destra.
Vale la pena notare che per memorizzare gli effetti dalle proprietà è facoltativo: quando si effettuano trasformazioni, è possibile fare con le principali proprietà dei logaritmi e altri fatti (ad esempio, in quello con B≥0), di cui il corrispondente Flusso delle conseguenze. L'effetto "lato" di questo approccio viene manifestato solo dal fatto che la decisione sarà leggermente più lunga. Ad esempio, fare a meno delle indagini, che è espresso dalla formula  E respinge solo dalle principali proprietà dei logaritmi, dovrai effettuare una catena di trasformazioni del tipo seguente:
E respinge solo dalle principali proprietà dei logaritmi, dovrai effettuare una catena di trasformazioni del tipo seguente:  .
.
Lo stesso si può dire sull'ultima proprietà dal suddetto elenco, che corrisponde alla formula  Dal momento che segue anche dalle principali proprietà dei logaritmi. La cosa principale per capire che c'è sempre la possibilità di un numero positivo con un logaritmo nell'indicatore per modificare il fondamento del grado e il numero sotto il segno logaritmo. Per motivi di giustizia, notiamo che esempi che implicano l'attuazione delle trasformazioni di un tale tipo sono rare nella pratica. Diamo alcuni esempi al di sotto del testo.
Dal momento che segue anche dalle principali proprietà dei logaritmi. La cosa principale per capire che c'è sempre la possibilità di un numero positivo con un logaritmo nell'indicatore per modificare il fondamento del grado e il numero sotto il segno logaritmo. Per motivi di giustizia, notiamo che esempi che implicano l'attuazione delle trasformazioni di un tale tipo sono rare nella pratica. Diamo alcuni esempi al di sotto del testo.
Trasformazione di espressioni numeriche con logaritmi
Le proprietà dei logaritmi ricordavano, ora è il momento di imparare ad applicarli in pratica per convertire le espressioni. Inizia naturalmente con la trasformazione di espressioni numeriche e non espressioni con variabili, poiché sono più convenienti e più facili da conoscere le basi. Quindi lo faremo, e iniziamo con esempi molto semplici per imparare a scegliere la proprietà desiderata del logaritmo, ma gradualmente complicheremo esempi, fino al momento in cui è necessario utilizzare diverse proprietà in fila per ottenere il risultato finale.
Selezione delle proprietà desiderate dei logaritmi
Le proprietà dei logaritmi non sono così poco, ed è chiaro che è necessario essere in grado di scegliere da loro il appropriato, che in questo caso particolare porterà al risultato desiderato. Di solito è difficile farlo, confrontando il tipo di logaritmo o espressione trasformata con le viste delle parti sinistra e destra delle formule che esprimono le proprietà dei logaritmi. Se il lato sinistro o destro di una delle formule coincide con un determinato logaritmo o espressione, quindi molto probabilmente è questa proprietà che deve essere applicata durante la conversione. I seguenti esempi sono chiaramente dimostrati.
Iniziamo con esempi di espressioni di conversione utilizzando la definizione di un logaritmo che corrisponde alla formula a registro A B \u003d B, A\u003e 0, A ≠ 1, B\u003e \u200b\u200b0.
Esempio.
Calcola se possibile: a) 5 log 5 4, b) 10 lg (1 + 2 · π), B) ![]() , d) 2 log 2 (-7), e).
, d) 2 log 2 (-7), e).
Decisione.
Nell'esempio, sotto la lettera A), la struttura A Log A B è chiaramente visibile, dove A \u003d 5, B \u003d 4. Questi numeri soddisfano le condizioni A\u003e 0, A ≠ 1, B\u003e \u200b\u200b0, quindi è possibile utilizzare l'uguaglianza un registro A B \u003d b. Abbiamo 5 log 5 4 \u003d 4.
b) qui a \u003d 10, b \u003d 1 + 2 · π, condizioni A\u003e 0, A ≠ 1, B\u003e \u200b\u200b0 sono fatti. In questo caso, c'è un'uguaglianza di 10 LG (1 + 2 · π) \u003d 1 + 2 · π.
c) E in questo esempio abbiamo a che fare con un grado di tipo A Log A B, dove e B \u003d LN15. Così ![]() .
.
Nonostante l'appartenenza allo stesso tipo di un registro A B (qui A \u003d 2, B \u003d -7), l'espressione sotto la lettera d) non può essere convertita dalla formula a registro A B \u003d B. La ragione è che non ha senso, in quanto contiene un numero negativo sotto il segno del logaritmo. Inoltre, il numero B \u003d -7 non soddisfa la condizione B\u003e 0, che non consente di ricorrere alla formula un registro A B \u003d B, poiché richiede l'adempimento delle condizioni A\u003e 0, A ≠ 1, B \u003e 0. Quindi, è impossibile parlare del calcolo del valore di 2 log 2 (-7). In questo caso, registrare 2 log 2 (-7) \u003d -7 sarà un errore.
Allo stesso modo, nell'esempio sotto la lettera D), la soluzione non può essere portata ![]() Dal momento che l'espressione iniziale non ha senso.
Dal momento che l'espressione iniziale non ha senso.
Risposta:
a) 5 log 5 4 \u003d 4, b) 10 lg (1 + 2 · π) \u003d 1 + 2 · π, c) ![]() , d), e) le espressioni non hanno senso.
, d), e) le espressioni non hanno senso.
Spesso è utile per la conversione in cui è presentato un numero positivo sotto forma di un grado di qualsiasi numero positivo e diverso con un logaritmo nell'indicatore. Si basa sulla stessa definizione di logaritmo un registro A B \u003d B, A\u003e 0, A ≠ 1, B\u003e \u200b\u200b0, ma la formula viene applicata a destra sinistra, cioè nel modulo B \u003d un registro A B. Ad esempio, 3 \u003d E LN3 o 5 \u003d 5 log 5 5.
Vai all'applicazione delle proprietà dei logaritmi per convertire le espressioni.
Esempio.
Trova il valore dell'espressione: a) log -2 1, b) log 1 1, c) log 0 1, d) log 7 1, e) ln1, e) lg1, g) log 3,75, s) log 5 · π 7 1.
Decisione.
Negli esempi sotto le lettere a), b) e c) le espressioni di log -2 1, log 1 1, registro 0 1, che non ha senso, perché alla base del logaritmo non dovrebbe essere un numero negativo, zero o unità, perché abbiamo determinato logaritmo solo per positivo e diverso dall'unità base. Pertanto, negli esempi A) - c) non può esserci alcuna questione di trovare il valore dell'espressione.
In tutti gli altri compiti, è ovvio che ci sono numeri positivi e diversi dall'unità 7, E, 10, 3.75 e 5 · π 7, rispettivamente, e sotto i segni dei logaritmi ovunque ci sono unità. E conosciamo la proprietà dell'unità logaritmo: log a 1 \u003d 0 per qualsiasi A\u003e 0, A ≠ 1. Pertanto, i valori delle espressioni B) - E) sono uguali a zero.
Risposta:
a), b), c) espressioni non rendono senso, d) log 7 1 \u003d 0, d) ln1 \u003d 0, e) lg1 \u003d 0, g) log 3,75 1 \u003d 0, h) log 5 · e 7 1 \u003d 0.
Esempio.
Calcola: a), b) lne, c) LG10, D) log 5 · π 3 -2 (5 · π 3 -2), e) log -3 (-3), e) log 1 1.
Decisione.
È chiaro che dobbiamo sfruttare la proprietà del logaritmo della base, che corrisponde al registro della formula A A \u003d 1 a A\u003e 0, a ≠ 1. Infatti, nei compiti sotto tutte le lettere, il numero sotto il segno del logaritmo coincide con la sua base. Pertanto, voglio dire immediatamente che il significato di ciascuna delle espressioni specificate è 1. Tuttavia, non è necessario sbrigarsi con le conclusioni: nei compiti sotto le lettere A) - D) I valori delle espressioni sono veramente uguali a uno, e nei compiti d) ed e) le espressioni iniziali non fanno Senso, quindi non si può dire che i valori di queste espressioni siano 1.
Risposta:
a), b) lne \u003d 1, c) lg10 \u003d 1, d) log 5 · π 3 -2 (5 · π 3 -2) \u003d 1, D), e) le espressioni non hanno senso.
Esempio.
Trova un valore: a) log 3 3 11, b)  , c), d) log -10 (-10) 6.
, c), d) log -10 (-10) 6.
Decisione.
Ovviamente, sotto i segni dei logaritmi ci sono alcuni gradi di fondazione. Sulla base di questo, comprendiamo che ci è utile qui il grado della Fondazione: registro A A P \u003d P, dove A\u003e 0, A ≠ 1 e P è un numero valido. Dato questo, abbiamo i seguenti risultati: a) log 3 3 11 \u003d 11, b)  , nel)
, nel) ![]() . È possibile registrare uguaglianza simile per l'esempio sotto la lettera d) del tipo di registro -10 (-10) 6 \u003d 6? No, è impossibile, dal momento che l'espressione log -10 (-10) 6 non ha senso.
. È possibile registrare uguaglianza simile per l'esempio sotto la lettera d) del tipo di registro -10 (-10) 6 \u003d 6? No, è impossibile, dal momento che l'espressione log -10 (-10) 6 non ha senso.
Risposta:
a) log 3 3 11 \u003d 11, b)  , nel)
, nel) ![]() , d) L'espressione non ha senso.
, d) L'espressione non ha senso.
Esempio.
Immagina un'espressione sotto forma di somma o la differenza di logaritmi sulla stessa base: a)  , b), c) LG ((- 5) · (-12)).
, b), c) LG ((- 5) · (-12)).
Decisione.
a) Sotto il segno del logaritmo è un lavoro, e conosciamo la proprietà logaritmo del lavoro di registro A (x · y) \u003d registro AX + Log Ay, A\u003e 0, A ≠ 1, X\u003e 0, Y\u003e 0. Nel nostro caso, il numero alla base del logaritmo e il numero nel lavoro è positivo, cioè soddisfare le condizioni della proprietà selezionata, quindi possiamo applicarlo tranquillamente: ![]() .
.
b) Qui utilizziamo la proprietà del logaritmo del privato, dove A\u003e 0, a ≠ 1, x\u003e 0, y\u003e 0. Nel nostro caso, la base del logaritmo è un numero positivo e, il numeratore e il denominatore π sono positivi, il che significa che le condizioni della proprietà sono soddisfacenti, quindi abbiamo il diritto di utilizzare la formula scelta:  .
.
c) Innanzitutto, notiamo che l'espressione LG ((- 5) · (-12)) ha senso. Ma allo stesso tempo, per lui, non abbiamo il diritto di applicare la formula logaritmo del lavoro di registro A (x · y) \u003d registro AX + Log Ay, A\u003e 0, A ≠ 1, X\u003e 0, Y\u003e 0, dal momento che i numeri -5 e -12 - negativi e non soddisfano le condizioni x\u003e 0, y\u003e 0. Cioè, è impossibile condurre una tale conversione: lG ((- 5) · (-12)) \u003d LG (-5) + lg (-12). E cosa fare? In tali casi, l'espressione iniziale ha bisogno di una trasformazione preliminare che ti consente di allontanarsi dai numeri negativi. Parleremo di tali casi di trasformazione di espressioni con numeri negativi sotto il segno del logaritmo in dettaglio in uno dei seguenti esempi, che è comprensibile, e senza spiegazione: lG ((- 5) · (-12)) \u003d LG (5 · 12) \u003d LG5 + LG12.
Risposta:
ma) ![]() b)
b)  , c) LG ((- 5) · (-12)) \u003d LG5 + LG12.
, c) LG ((- 5) · (-12)) \u003d LG5 + LG12.
Esempio.
Semplificare l'espressione: a) log 3 0,25 + log 3 16 + log 3 0,5, b).
Decisione.
Qui aiuteremo tutte le stesse proprietà del logaritmo del lavoro e del logaritmo del privato, che abbiamo usato negli esempi precedenti, solo ora li applicheremo a destra a sinistra. Cioè, la quantità di logaritmi si sta trasformando nel logaritmo del lavoro e la differenza tra logaritmi - nel logaritmo di privati. Avere
ma) log 3 0,25 + log 3 16 + log 3 0.5 \u003d log 3 (0,25 · 16 · 0.5) \u003d log 3 2.
b)  .
.
Risposta:
ma) log 3 0,25 + log 3 16 + log 3 0.5 \u003d log 3 2b)  .
.
Esempio.
Sbarazzarsi della misura sotto il segno del logaritmo: a) log 0.7 5 11, b)  , c) log 3 (-5) 6.
, c) log 3 (-5) 6.
Decisione.
È facile vedere che stiamo occupando di espressioni del registro A B p. La proprietà corrispondente del logaritmo ha il tipo di registro A B P \u003d P · Log A B, dove A\u003e 0, A ≠ 1, B\u003e \u200b\u200b0, P è qualsiasi numero valido. Cioè, quando si esegue condizioni A\u003e 0, A ≠ 1, B\u003e \u200b\u200b0 Dal logaritmo del grado di log A B P, possiamo passare al prodotto P · Log A B. Condurremo questa conversione con espressioni specificate.
a) In questo caso, a \u003d 0,7, B \u200b\u200b\u003d 5 e P \u003d 11. Quindi Log 0.7 5 11 \u003d 11 · Log 0.7 5.
b) qui, condizioni A\u003e 0, A ≠ 1, B\u003e \u200b\u200b0 sono eseguiti. perciò 
c) Il registro di espressione 3 (-5) 6 ha la stessa struttura registro A B P, A \u003d 3, B \u003d -5, P \u003d 6. Ma per B, la condizione B\u003e 0 non è soddisfatta, il che rende impossibile utilizzare il registro A B P \u003d P · Log A B. Quindi, è impossibile far fronte al compito? È possibile, ma è richiesta un'espressione pre-conversione, parleremo in dettaglio qui sotto nel punto di intestazione. La decisione sarà: log 3 (-5) 6 \u003d log 3 5 6 \u003d 6 · log 3 5.
Risposta:
a) log 0.7 5 11 \u003d 11 · log 0.7 5,
b) 
c) log 3 (-5) 6 \u003d 6 · log 3 5.
Abbastanza spesso, la formula logaritmo del grado durante la trasformazione è necessaria per applicare direttamente a sinistra come P · Log A B \u003d Log A B P (ciò richiede le prestazioni delle stesse condizioni per A, B e P). Ad esempio, 3 · LN5 \u003d LN5 3 e LG2 · Log 2 3 \u003d log 2 3 LG2.
Esempio.
a) Calcola il valore del registro 2 5, se è noto che LG2≈0,3010 e LG5≈0.6990. b) presentare una frazione sotto forma di un logaritmo basato su 3.
Decisione.
a) La formula per la transizione a una nuova base del logaritmo consente a questo logaritmo di rappresentare sotto forma di un rapporto di logaritmi decimali, i cui valori ci sono noti :. Rimane solo per svolgere calcoli, abbiamo  .
.
b) Qui è sufficiente sfruttare la transizione a una nuova base e applicarla a destra sinistra, cioè sotto forma di  . Ricevere
. Ricevere  .
.
Risposta:
a) log 2 5≈2,3223, b)  .
.
In questa fase, abbiamo sufficientemente considerato scrupolosamente la conversione delle espressioni più semplici utilizzando le principali proprietà dei logaritmi e la definizione di logaritmo. In questi esempi, abbiamo dovuto applicare una specie di proprietà e niente di più. Ora con una coscienza calma, puoi passare agli esempi, la cui trasformazione richiede l'uso di diverse proprietà dei logaritmi e altre trasformazioni aggiuntive. Andremo nel prossimo paragrafo. Ma prima, in breve, si concentreremo brevemente sugli esempi delle conseguenze delle principali proprietà dei logaritmi.
Esempio.
a) Sbarazzarsi della radice sotto il segno del logaritmo. b) Converti frazione nel logaritmo sulla base 5. c) frequentemente dai gradi sotto il segno logaritmo e nella sua fondazione. d) calcola il valore dell'espressione  . e) Sostituire l'espressione del grado con la base 3.
. e) Sostituire l'espressione del grado con la base 3.
Decisione.
a) Se ricordi della conseguenza della proprietà del logaritmo ![]() Puoi rispondere immediatamente:
Puoi rispondere immediatamente: ![]() .
.
b) Usiamo la formula  diritto a sinistra abbiamo
diritto a sinistra abbiamo  .
.
c) In questo caso, il risultato conduce la formula  . Ricevere
. Ricevere  .
.
d) Ed qui è sufficiente applicare una conseguenza che la formula è responsabile  . Così
. Così  .
.
e) Proprietà logaritmo  Ci consente di raggiungere il risultato desiderato:
Ci consente di raggiungere il risultato desiderato: ![]() .
.
Risposta:
ma) ![]() . b)
. b)  . nel)
. nel)  . d)
. d)  . e)
. e) ![]() .
.
Uso sequenziale di diverse proprietà
I compiti reali per la trasformazione delle espressioni che utilizzano le proprietà dei logaritmi sono solitamente più complicati da coloro che ci siamo impegnati nel paragrafo precedente. In essi, di regola, il risultato non è un passo, e la soluzione è già nell'applicazione coerente di una proprietà dopo l'altra, insieme a ulteriori trasformazioni dell'identità, come la divulgazione di parentesi, portando termini simili, riduzione delle frazioni, ecc. . Quindi facciamo più vicino a tali esempi. Non c'è nulla di difficile in questo, la cosa principale è agire ordinatamente e costantemente, osservando la procedura per l'esecuzione di azioni.
Esempio.
Calcolare il valore dell'espressione (Log 3 15-log 3 5) · 7 log 7 5.
Decisione.
La differenza di logaritmi tra parentesi per la proprietà del logaritmo di un privato può essere sostituito con logaritmo log 3 (15: 5), e calcolare ulteriormente il suo registro di valore 3 (15: 5) \u003d log 3 3 \u003d 1. E il valore dell'espressione 7 log 7 5 per definizione di logaritmo è uguale a 5. Sostituire questi risultati nell'espressione originale, otteniamo (log 3 15-log 3 5) · 7 log 7 5 \u003d 1 · 5 \u003d 5.
Diamo una soluzione senza spiegazione:
(Log 3 15-log 3 5) · 7 log 7 5 \u003d log 3 (15: 5) · 5 \u003d
\u003d log 3 3 · 5 \u003d 1 · 5 \u003d 5.
Risposta:
(log 3 15-log 3 5) · 7 log 7 5 \u003d 5.
Esempio.
Qual è il valore del registro di espressioni numeriche 3 log 2 2 3 -1?
Decisione.
Per prima cosa trasformiamo il logaritmo, che si trova sotto il segno del logaritmo, secondo la formula logaritmo: log 2 2 3 \u003d 3. Pertanto, log 3 log 2 2 3 \u003d log 3 3 e ulteriore log 3 3 \u003d 1. Quindi log 3 log 2 2 3 -1 \u003d 1-1 \u003d 0.
Risposta:
log 3 log 2 2 3 -1 \u003d 0.
Esempio.
Semplifica l'espressione.
Decisione.
La formula di transizione alla nuova base del logaritmo consente alla relazione di logaritmi a una base da rappresentare come registro 3 5. In questo caso, l'espressione iniziale prenderà la forma. Per definizione di logaritmo 3 log 3 5 \u003d 5, cioè ![]() , E il valore dell'espressione ottenuto, a causa della stessa definizione del logaritmo, è due.
, E il valore dell'espressione ottenuto, a causa della stessa definizione del logaritmo, è due.
Ecco una breve versione della soluzione di solito indicata:  .
.
Risposta:
 .
.
Per una transizione fluida alle seguenti informazioni dell'oggetto, diamo un'occhiata alle espressioni 5 2 + log 5 3 e LG0.01. La loro struttura non è adatta a nessuna delle proprietà dei logaritmi. Quindi cosa succede, non possono essere convertiti usando le proprietà dei logaritmi? È possibile se è possibile condurre trasformazioni preliminari che preparano queste espressioni all'applicazione delle proprietà dei logaritmi. Così 5 2 + log 5 3 \u003d 5 2 · 5 log 5 3 \u003d 25 · 3 \u003d 75,  e LG0.01 \u003d LG10 -2 \u003d -2. Quindi comprenderemo in dettaglio come viene effettuata tale formazione delle espressioni.
e LG0.01 \u003d LG10 -2 \u003d -2. Quindi comprenderemo in dettaglio come viene effettuata tale formazione delle espressioni.
Preparazione delle espressioni all'applicazione delle proprietà dei logaritmi
Logaritmi nella composizione della composizione dell'espressione trasformata molto spesso differiscono dalle parti sinistra e destra delle formule corrispondenti alle proprietà dei logaritmi. Ma non meno spesso la trasformazione di queste espressioni implica l'uso delle proprietà dei logaritmi: utilizzarli richiede solo una preparazione preliminare. E questa preparazione è nello svolgimento di determinate trasformazioni identiche leader di logaritmi al modulo, conveniente per applicare proprietà.
Per l'equità, notiamo che quasi tutte le trasformazioni di espressioni possono agire come trasformazioni preliminari, dall'attuatore banale di tali termini all'uso delle formule trigonometriche. Questo è comprensibile, poiché le espressioni trasformate possono contenere oggetti matematici: parentesi, moduli, frazioni, radici, gradi, ecc. Pertanto, è necessario essere pronti per eseguire qualsiasi necessaria conversione per poter utilizzare ulteriormente le proprietà dei logaritmi.
Immediatamente, diciamo che in questo punto non ci fermiamo il compito per classificare e smontare tutte le trasformazioni preliminari immaginabili, che applicano ulteriormente le proprietà dei logaritmi o la definizione di logaritmo. Qui ci soffermeremo solo su quattro, che sono più caratteristici e più spesso trovati nella pratica.
E ora in dettaglio su ciascuno di loro, dopo di che, come parte del nostro argomento, rimarrà solo per affrontare la trasformazione delle espressioni con variabili sotto i segni dei logaritmi.
Selezione di gradi sotto il segno del logaritmo e nella sua fondazione
Iniziamo immediatamente dall'esempio. Sia noi logaritmo. Ovviamente, in questa forma, la sua struttura non deve usare le proprietà dei logaritmi. È possibile in qualche modo convertire questa espressione per semplificarlo, e persino meglio calcolare il suo valore? Per rispondere a questa domanda, guardiamo attentamente nei numeri 81 e 1/9 nel contesto del nostro esempio. È facile da notare qui che questi numeri consentono la rappresentazione del grado di numero 3, in effetti, 81 \u003d 3 4 e 1/9 \u003d 3 -2. In questo caso, il logaritmo iniziale viene presentato nella forma e la possibilità di applicare la formula  . Così,
. Così,  .
.
Un'analisi dell'esempio smontato crea il seguente pensiero: se possibile, è possibile provare a evidenziare la laurea sotto il segno del logaritmo e nella sua fondazione per applicare la proprietà del logaritmo o della sua conseguenza. Rimane solo per scoprire come allocare questi gradi. Diamo alcune raccomandazioni su questo problema.
A volte è piuttosto ovvio che il numero sotto il segno del logaritmo e / o nella sua fondazione è parte dell'intero livello come nell'esempio sopra. Praticamente costantemente dover affrontare i rivelati di due, che erano ben pensati: 4 \u003d 2 2, 8 \u003d 2 3, 16 \u003d 2 4, 32 \u003d 2 5, 64 \u003d 2 6, 128 \u003d 2 7, 256 \u003d 2 8 , 512 \u003d 2 9, 1024 \u003d 2 10. Questo si può dire del grado di triplo: 9 \u003d 3 2, 27 \u003d 3 3, 81 \u003d 3 4, 243 \u003d 3 5, ... In generale, non fa male se sarà davanti ai nostri occhi tabella di gradi di numeri naturali all'interno di una dozzina. Inoltre, non è difficile lavorare con gradi interi di dieci, cento, migliaia, ecc.
Esempio.
Calcola il valore o semplificare l'espressione: a) log 6 216, b), c) log 0.000001 0,001.
Decisione.
a) È ovvio che 216 \u003d 6 3, quindi log 6 216 \u003d log 6 6 3 \u003d 3.
b) La tabella di gradi di numeri naturali consente di presentare numeri 343 e 1/243 sotto forma di gradi 7 3 e 3 -4, rispettivamente. Pertanto, è possibile seguire la seguente trasformazione di un determinato logaritmo: 
c) come 0,000001 \u003d 10 -6 e 0,001 \u003d 10 -3, quindi log 0.000001 0.001 \u003d log 10 -6 10 -3 \u003d (- 3) / (- 6) \u003d 1/2.
Risposta:
a) log 6 216 \u003d 3, b) ![]() , c) log 0.000001 0.001 \u003d 1/2.
, c) log 0.000001 0.001 \u003d 1/2.
In casi più complessi, per evidenziare i gradi dei numeri devono ricorrere a.
Esempio.
Converti l'espressione in un tipo più semplice di log 3 648 · log 2 3.
Decisione.
Vediamo cosa è una decomposizione di un numero di 648 per semplici fattori:
Cioè, 648 \u003d 2 3 · 3 4. In questo modo, log 3 648 · log 2 3 \u003d log 3 (2 3 · 3 4) · log 2 3.
Ora il logaritmo delle opere si sta trasformando nella quantità di logaritmi, dopo di che le proprietà del logaritmo del grado sono applicabili:
log 3 (2 3 · 3 4) · log 2 3 \u003d (log 3 2 3 + log 3 3 4) · log 2 3 \u003d
\u003d (3 · log 3 2 + 4) · log 2 3.
A causa dell'indagine dalla proprietà del logaritmo a cui la formula è responsabile  Il prodotto log32 · log23 è un lavoro, ed è noto per essere uno. Considerandolo, otteniamo 3 · log 3 2 · log 2 3 + 4 · log 2 3 \u003d 3 · 1 + 4 · log 2 3 \u003d 3 + 4 · log 2 3.
Il prodotto log32 · log23 è un lavoro, ed è noto per essere uno. Considerandolo, otteniamo 3 · log 3 2 · log 2 3 + 4 · log 2 3 \u003d 3 · 1 + 4 · log 2 3 \u003d 3 + 4 · log 2 3.
Risposta:
log 3 648 · log 2 3 \u003d 3 + 4 · log 2 3.
Abbastanza spesso, le espressioni sotto il segno del logaritmo e nella sua fondazione sono opere o rapporti di radici e / o gradi di alcuni numeri, ad esempio,. Tali espressioni possono essere rappresentate come una laurea. Per questo, la transizione dalle radici ai gradi e applicata. Queste conversioni consentono di evidenziare i gradi sotto il segno logaritmo e nella sua base, dopodiché si applica le proprietà dei logaritmi.
Esempio.
Calcola: a)  , b).
, b).
Decisione.
a) L'espressione alla base del logaritmo è il prodotto di gradi con le stesse basi, secondo la proprietà appropriata dei gradi, abbiamo 5 2 · 5 -0,5 · 5 -1 \u003d 5 2-0.5-1 \u003d 5 0.5.
Ora trasformiamo la frazione sotto il segno del Logaritmo: giriamo dalla radice nel grado, dopo di che useremo la proprietà dei gradi con gli stessi motivi:  .
.
Resta per sostituire i risultati ottenuti nell'espressione iniziale, utilizzare la formula  e finitura trasformazioni:
e finitura trasformazioni: 
b) Dal 729 \u003d 3 6, a 1/9 \u003d 3 -2, quindi l'espressione iniziale può essere riscritta nel modulo.
Quindi, applica la proprietà della radice dal grado, svolgiamo la transizione dalla radice al grado e utilizza la proprietà del grado di laurea per convertire il logaritmo nel grado:  .
.
Considerando l'ultimo risultato, abbiamo  .
.
Risposta:
ma)  , b).
, b).
È chiaro che in generale, per ottenere gradi sotto il segno del logaritmo e, nella sua fondazione, potrebbero essere necessarie varie trasformazioni di varie espressioni. Diamo un paio di esempi.
Esempio.
Qual è il valore dell'espressione: a)  b)
b) ![]() .
.
Decisione.
Pertanto, notiamo che l'espressione specificata ha la forma di registro A B P, dove A \u003d 2, B \u003d X + 1 e P \u003d 4. Espressioni numeriche di tali tipi che siamo stati convertiti dalla proprietà del logaritmo dell'estensione del registro ABP \u003d P · Log AB, quindi, con una determinata espressione, voglio fare lo stesso di, e dal registro 2 (x + 1) 4 Vai a 4 · log 2 (x + 1). E ora calcoliamo il valore dell'espressione iniziale e l'espressione ottenuta dopo la trasformazione, ad esempio, con X \u003d -2. Avere il registro 2 (-2 + 1) 4 \u003d log 2 1 \u003d 0, e 4 · log 2 (-2 + 1) \u003d 4 · log 2 (-1) - Non significato espressione. Ciò provoca una domanda naturale: "Che cosa abbiamo fatto"?
E il motivo è il seguente: abbiamo eseguito il registro di trasformazione 2 (x + 1) 4 \u003d 4 · log 2 (x + 1), in base al registro della formula ABP \u003d P · Log AB, ma abbiamo il diritto di applicarlo Formula solo quando condiziona A\u003e 0, A ≠ 1, B\u003e \u200b\u200b0, P - Qualsiasi numero valido. Cioè, la conversione fatta da noi ha luogo se x + 1\u003e 0, che è la stessa X\u003e -1 (per A e P - le condizioni sono fatte). Tuttavia, nel nostro caso, la variabile OTZ X per l'espressione iniziale consiste non solo dall'intervallo X\u003e -1, ma anche dal periodo x<−1 . Но для x<−1 мы не имели права осуществлять преобразование по выбранной формуле.
La necessità di prendere in considerazione ...
Continueremo a smontare la trasformazione del registro 2 (x + 1) 4 espressioni selezionate da noi, e ora vediamo cosa succede con OTZ quando si sposta in espressione 4 · log 2 (x + 1). Nel paragrafo precedente, abbiamo trovato anche l'espressione sorgente: questo è un set (-∞, -1) ∪ (-1, + ∞). Ora troviamo l'area dei valori ammissibili della variabile X per l'espressione 4 · log 2 (x + 1). È determinato dalla condizione x + 1\u003e 0, che corrisponde al set (-1, + ∞). Ovviamente, quando si sposta dal registro 2 (x + 1) da 4 a 4 · log 2 (x + 1), si verifica l'area dei valori validi. E abbiamo accettato di evitare trasformazioni che portano al restringimento di OTZ, in quanto ciò può portare a varie conseguenze negative.
Vale la pena notare qui per te stesso che è utile controllare l'OTZ ad ogni passo della trasformazione e prevenire il suo restringimento. E se improvvisamente, in qualche fase della trasformazione, c'era un restringimento di OST, allora vale la pena guardare con molta attenzione, e se questa trasformazione è consentita e se abbiamo il diritto di svolgarlo.
Ad esempio, diciamo che in pratica, di solito è necessario lavorare con espressioni, le cui variabili OTZ sono tali che, quando si effettuano trasformazioni, utilizzare le proprietà dei logaritmi senza restrizioni nel modulo già noto a noi, e sia da sinistra giusto e diritto a sinistra. Ti abitui rapidamente e inizi a svolgere le trasformazioni meccanicamente, senza pensare, e se fosse possibile condurli. E in tali momenti, come scaricato, slipper esempi più complessi in cui l'uso inaccessibile delle proprietà dei logaritmi porta agli errori. Quindi è necessario essere sempre su un assegno e segui che non c'è un restringimento di OTZ.
Non ha ferito separatamente selezionare le principali trasformazioni in base alle proprietà dei logaritmi che devono essere eseguiti con molta attenzione, il che può portare a un restringimento di OTZ e di conseguenza - agli errori:
Alcune trasformazioni di espressioni in base alle proprietà dei logaritmi possono portare all'inverse espansione di OTZ. Ad esempio, la transizione da 4 · log 2 (x + 1) al registro 2 (X + 1) 4 espande dispari dal set (-1, + ∞) a (-∞, -1) ∪ (-1, + ∞). Tali trasformazioni si verificano se rimangono all'interno dell'ODZD per l'espressione iniziale. Quindi l'unica conversione menzionata 4 · log 2 (x + 1) \u003d log 2 (x + 1) 4 avviene sulla variabile OTZ x per l'espressione originale 4 · log 2 (x + 1), cioè con x + + 1\u003e 0, che è lo stesso (-1, + ∞).
Ora che abbiamo discusso le sfumature per le quali è necessario prestare attenzione a convertire le espressioni con le variabili utilizzando le proprietà dei logaritmi, resta per capire come correttamente queste trasformazioni devono essere eseguite.
X + 2\u003e 0. Funziona nel nostro caso? Per rispondere a questa domanda, dai un'occhiata alla variabile OTZ X. È determinato dal sistema di disuguaglianza  che è equivalente alla condizione x + 2\u003e 0 (se necessario, vedere l'articolo risolvere sistemi di disuguaglianza). Pertanto, possiamo applicare tranquillamente la proprietà logaritmo.
che è equivalente alla condizione x + 2\u003e 0 (se necessario, vedere l'articolo risolvere sistemi di disuguaglianza). Pertanto, possiamo applicare tranquillamente la proprietà logaritmo.
Avere
3 · LG (X + 2) 7 -LG (X + 2) -5 · LG (X + 2) 4 \u003d
\u003d 3 · 7 · LG (x + 2) -Lg (x + 2) -5 · 4 · LG (x + 2) \u003d
\u003d 21 · LG (X + 2) -LG (X + 2) -20 · LG (X + 2) \u003d
\u003d (21-1-20) · LG (X + 2) \u003d 0.
Puoi agire e in caso contrario, il beneficio di Otz lo consente di fare, ad esempio: 
Risposta:
3 · LG (X + 2) 7 -LG (X + 2) -5 · LG (X + 2) 4 \u003d 0.
E cosa fare quando le condizioni per le proprietà di accompagnamento dei logaritmi non sono soddisfatte? Ci occuperemo sugli esempi.
Supponiamo da noi per semplificare l'espressione LG (X + 2) 4 -LG (X + 2) 2. La trasformazione di questa espressione, in contrasto con l'espressione dall'esempio precedente, non consente il log del grado logaritmo. Perché? La variabile OTZ X in questo caso è una combinazione di due lacune x\u003e -2 e x<−2 . При x>-2 Possiamo applicare tranquillamente la proprietà logaritmo e agire come smontato sopra: lG (X + 2) 4 -LG (X + 2) 2 \u003d 4 · LG (X + 2) -2 · LG (X + 2) \u003d 2 · LG (X + 2). Ma Otz contiene un altro periodo di X + 2<0 , для которого последнее преобразование будет некорректно. Что же делать при x+2<0 ? В подобных случаях на помощь приходит . Определение модуля позволяет выражение x+2 при x+2<0 представить как −|x+2| . Тогда при x+2<0 от lg(x+2) 4 −lg(x+2) 2 переходим к lG (- | X + 2 |) 4 -LG (- X + 2 |) 2 E ulteriormente con la forza delle proprietà della laurea a LG | X + 2 | 4 -LG | X + 2 | 2. L'espressione risultante può essere convertita dalla proprietà logaritmo, dal momento che | X + 2 |\u003e 0 per qualsiasi valori della variabile. Avere lG | X + 2 | 4 -LG | X + 2 | 2 \u003d 4 · LG | X + 2 | -2 · LG | X + 2 | \u003d 2 · LG | X + 2 |. Ora puoi liberarti dal modulo, mentre ha fatto il suo lavoro. Dal momento che stiamo conducendo la conversione a x + 2<0 , то 2·lg|x+2|=2·lg(−(x+2)) . Итак, можно считать, что мы справились с поставленной задачей. Ответ: . Полученный результат можно записать компактно с использованием модуля как .
Considera un altro esempio in modo che il lavoro con i moduli sia diventato familiare. Lascia che abbiamo concepito dall'espressione  Vai alla somma e alla differenza tra i logaritmi dei rimbalzi lineari X-1, X-2 e X-3. Per prima cosa troviamo ...
Vai alla somma e alla differenza tra i logaritmi dei rimbalzi lineari X-1, X-2 e X-3. Per prima cosa troviamo ... 
All'intervallo (3, + ∞) I valori delle espressioni X-1, X-2 e X-3 sono positivi, quindi applichiamo tranquillamente le proprietà del logaritmo di somme e differenze: 
E sull'intervallo (1, 2), i valori dell'espressione X-1 sono positivi e i valori delle espressioni X-2 e X-3 sono negativi. Pertanto, nell'intervallo in esame, presentiamo X-2 e X-3 utilizzando il modulo AS - X-2 | e - | X-3 | rispettivamente. In cui 
Ora è possibile applicare le proprietà del logaritmo del lavoro e del privato, in quanto è sull'intervallo (1, 2) i valori delle espressioni X-1, | X-2 | e | X-3 | - Positivo.
Avere 
I risultati possono essere combinati:
In generale, argomenti simili consentono alle formule logaritmi sulla base dei logaritmi, relazioni e gradi per ottenere tre risultati praticamente utili, che sono abbastanza convenienti da usare:
- Le opere di logaritmo di due espressioni arbitrarie X e Y del tipo di registro A (x · y) possono essere sostituite con il logaritmi SMAFICE LOGARITHMS A | X | + LOG A | Y | , A\u003e 0, A ≠ 1.
- Logaritmo Private Log A (x: y) può essere sostituito con la differenza tra logaritmi log A | x | -log a | y | , A\u003e 0, A ≠ 1, X e Y - espressioni arbitrarie.
- Dal logaritmo di un'espressione B in un grado uniforme P del registro A B P Form è possibile andare all'espressione P · Log A | B | , dove A\u003e 0, A ≠ 1, P è un numero pari e B - un'espressione arbitraria.
Vengono forniti risultati simili, ad esempio, nelle istruzioni per risolvere equazioni indicative e logaritmiche nella raccolta di problemi in matematica per i candidati alle università sotto i redattori di M. I. Scanavi.
Esempio.
Semplifica l'espressione  .
.
Decisione.
Sarebbe bello applicare le proprietà dei logaritmi, importi e differenze. Ma possiamo farlo qui? Per rispondere a questa domanda, dobbiamo conoscere Otz.
Lo definiamo: 
È piuttosto ovvio che le espressioni x + 4, X-2 e (X + 4) 13 sui valori dei valori consentiti della variabile X possono richiedere sia valori positivi e negativi. Pertanto, dovremo agire attraverso i moduli. 
Le proprietà del modulo consentono di riscrivere come, quindi 
Anche nulla impedisce alla proprietà del grado logaritmo, quindi portare termini simili a: 
L'altra sequenza di trasformazioni porta allo stesso risultato: 
e poiché l'espressione X-2 può prendere valori positivi e negativi, quindi quando si invia un tasso di laurea uniforme di 14
Compiti la cui soluzione è in trasformazione di espressioni logaritmiche, abbastanza spesso si incontrano sull'esame.
Per affrontare con successo con loro al momento minima eccetto le principali identità logaritmiche, è necessario conoscere e utilizzare correttamente alcune formule.
Questo è: un registro A B \u003d B, dove A, B\u003e 0 e ≠ 1 (segue direttamente dalla definizione del logaritmo).
log A B \u003d Log con B / Log con A o Registra A B \u003d 1 / Log B A
dove a, b, c\u003e 0; A, c ≠ 1.
log a m b n \u003d (m / n) log | A | | B |
dove a, b\u003e 0, a ≠ 1, m, n є r, n ≠ 0.
e log con b \u003d b log con a
dove a, b, c\u003e 0 e a, b, s ≠ 1
Per mostrare l'equità della quarta uguaglianza, prologa la sinistra e il lato destro dell'a. Riceviamo il registro A (e log con b) \u003d registro A (registro B con A) o registro con B \u003d log con A · log A B; log con b \u003d log con A · (log con b / log con a); Log con B \u003d log con b.
Abbiamo comprovato l'uguaglianza di logaritmi, il che significa uguale alle espressioni sotto logaritmi. La formula 4 è dimostrata.
Esempio 1.
Calcola 81 Log 27 5 Log 5 4.
Decisione.
81 = 3 4 , 27 = 3 3 .
log 27 5 \u003d 1/3 log 3 5, log 5 4 \u003d log 3 4 / log 3 5. Di conseguenza,
log 27 5 · Log 5 4 \u003d 1/3 log 3 5 · (log 3 4 / log 3 5) \u003d 1/3 log 3 4.
Quindi 81 log 27 5 log 5 4 \u003d (3 4) 1/3 log 3 4 \u003d (3 log 3 4) 4/3 \u003d (4) 4/3 \u003d 4 3 √4.
È possibile eseguire in modo indipendente il seguente compito.
Calcola (8 log 2 3 + 3 1 / log 2 3) - Log 0.2 5.
Come punta 0.2 \u003d 1/5 \u003d 5 -1; Log 0,2 5 \u003d -1.
Risposta: 5.
ESEMPIO 2.
Calcola (√11) log. √3 9- log 121 81.
Decisione.
Eseguire la sostituzione delle espressioni: 9 \u003d 3 2, √3 \u003d 3 1/2, log √3 9 \u003d 4,
121 \u003d 11 2, 81 \u003d 3 4, log 121 81 \u003d 2 Log 11 3 (è stato utilizzato Formula 3).
Quindi (√11) log √3 9- log 121 81 \u003d (11 1/2) 4-2 log 11 3 \u003d (11) 2- log 11 3 \u003d 11 2 / (11) log 11 3 \u003d 11 2 / ( 11 Log 11 3) \u003d 121/3.
ESEMPIO 3.
Calcola il log 2 24 / log 96 2- log 2 192 / log 12 2.
Decisione.
Logaritmi contenuti nell'esempio, sostituire i logaritmi con una base 2.
log 96 2 \u003d 1 / log 2 96 \u003d 1 / log 2 (2 5 · 3) \u003d 1 / (log 2 2 5 + log 2 3) \u003d 1 / (5 + log 2 3);
log 2 192 \u003d log 2 (2 6 · 3) \u003d (log 2 2 6 + log 2 3) \u003d (6 + log 2 3);
log 2 24 \u003d log 2 (2 3 · 3) \u003d (log 2 2 3 + log 2 3) \u003d (3 + log 2 3);
log 12 2 \u003d 1 / log 2 12 \u003d 1 / log 2 (2 2 · 3) \u003d 1 / (log 2 2 2 + log 2 3) \u003d 1 / (2 + log 2 3).
Quindi log 2 24 / log 96 2 - log 2 192 / log 12 2 \u003d (3 + log 2 3) / (1 / (5 + log 2 3)) - ((6 + log 2 3) / (1 / ( 2 + log 2 3)) \u003d
\u003d (3 + log 2 3) · (5 + log 2 3) - (6 + log 2 3) (2 + log 2 3).
Dopo aver rivelato parentesi e portando termini simili, otteniamo il numero 3. (con una semplificazione dell'espressione, il registro 2 3 può designare tramite n e semplificare l'espressione
(3 + N) · (5 + N) - (6 + N) (2 + N)).
Risposta: 3.
È possibile eseguire in modo indipendente il seguente compito:
Calcolo (log 3 4 + log 4 3 + 2) · log 3 16 · log 2 144 3.
Qui è necessario effettuare una transizione ai logaritmi basati su 3 e decomposizione su semplici moltiplicatori di grandi numeri.
Risposta: 1/2.
ESEMPIO 4.
Tre numeri A \u003d 1 / (log 3 0.5), B \u003d 1 / (log 0.5 3), c \u003d log 0.5 12 - log 0.5 3. Mettili in ordine crescente.
Decisione.
Trasformiamo i numeri A \u003d 1 / (log 3 0.5) \u003d log 0.5 3; C \u003d log 0.5 12 - log 0.5 3 \u003d log 0.5 12/3 \u003d log 0.5 4 \u003d -2.
Confrontali
log 0.5 3\u003e log 0.5 4 \u003d -2 e log 0.5 3< -1 = log 0,5 2, так как функция у = log 0,5 х – убывающая.
O 2.< log 0,5 3 < -1. Тогда -1 < 1/(log 0,5 3) < -1/2.
Risposta. Di conseguenza, la procedura per il posizionamento dei numeri: C; MA; NEL.
ESEMPIO 5.
Quanti numeri interi si trovano sull'intervallo (log 3 1/16; log 2 6 48).
Decisione.
Definiamo tra quali gradi del numero 3 è il numero 1/16. Otteniamo 1/27.< 1 / 16 < 1 / 9 .
Dal momento che la funzione y \u003d log 3 x è in aumento, quindi log 3 (1/2 27)< log 3 (1 / 16) < log 3 (1 / 9); -3 < log 3 (1 / 16) < -2.
log 6 48 \u003d log 6 (36 · 4/3) \u003d log 6 36 + log 6 (4/3) \u003d 2 + log 6 (4/3). Confronta il log 6 (4/3) e 1/5. E per questo, confronta i numeri 4/3 e 6 1/5. Eretto entrambi i numeri in 5 gradi. Otteniamo (4/3) 5 \u003d 1024/243 \u003d 4 52/243< 6. Следовательно,
log 6 (4/3)< 1 / 5 . 2 < log 6 48 < 2 1 / 5 . Числа, входящие в двойное неравенство, положительные. Их можно возводить в квадрат. Знаки неравенства при этом не изменятся. Тогда 4 < log 6 2 48 < 4 21 / 25.
Di conseguenza, l'intervallo (log 3 1/16; log 6 48 48) include l'intervallo [-2; 4] e gli interi sono posizionati su di esso; -uno; 0; uno; 2; 3; quattro.
Risposta: 7 interi interi.
ESEMPIO 6.
Calcola 3 LGLG 2 / LG 3 - LG20.
Decisione.
3 LG LG 2 / LG 3 \u003d (3 1 / LG3) LG LG 2 \u003d (3 LO G 3 10) LG LG 2 \u003d 10 LG LG 2 \u003d LG2.
Quindi 3 LGLG2 / LG3 - LG 20 \u003d LG 2 - LG 20 \u003d LG 0.1 \u003d -1.
Risposta 1.
Esempio 7.
È noto che il registro 2 (√3 + 1) + log 2 (√6 - 2) \u003d A. Trova registro 2 (√3 -1) + log 2 (√6 + 2).
Decisione.
Numeri (√3 + 1) e (√3 - 1); (√6 - 2) e (√6 + 2) - Coniugate.
Condurremo la seguente trasformazione delle espressioni
√3 - 1 \u003d (√3 - 1) · (√3 + 1)) / (√3 + 1) \u003d 2 / (√3 + 1);
√6 + 2 \u003d (√6 + 2) · (√6 - 2)) / (√6 - 2) \u003d 2 / (√6 - 2).
Quindi log 2 (√3 - 1) + log 2 (√6 + 2) \u003d log 2 (2 / (√3 + 1)) + log 2 (2 / (√6 - 2)) \u003d
Log 2 2 - log 2 (√3 + 1) + log 2 2 - log 2 (√6 - 2) \u003d 1 - log 2 (√3 + 1) + 1 - log 2 (√6 - 2) \u003d
2 - log 2 (√3 + 1) - log 2 (√6 - 2) \u003d 2 - A.
Risposta: 2 - A.
ESEMPIO 8..
Semplificare e trovare il valore approssimativo dell'espressione (log 3 2 · log 4 3 · log 5 4 · log 6 5 · ... · log 10 9.
Decisione.
Tutti i logaritmi che diamo alla base totale 10.
(log 3 2 · log 4 3 · log 5 4 · log 6 5 · ... · log 10 9 \u003d (LG 2 / LG 3) · (LG 3 / LG 4) · (LG 4 / LG 5) · ( LG 5 / LG 6) · ... · (LG 8 / LG 9) · LG 9 \u003d LG 2 ≈ 0.3010. (Il valore Approssimativo LG 2 può essere trovato utilizzando una tabella, una linea logaritmica o una calcolatrice).
Risposta: 0,3010.
Esempio 9..
Calcola il registro A 2 B 3 √ (A 11 B -3) se il registro √ A B 3 \u003d 1. (In questo esempio, e 2 B 3 è la base del logaritmo).
Decisione.
Se registro √ A B 3 \u003d 1, quindi 3 / (0.5 Registro A B \u003d 1. E registrare A B \u003d 1/6.
Quindi registrare A 2 B 3√ (A 11 B -3) \u003d 1/2 Log A 2 B 3 (A 11 B -3) \u003d Log A (A 11 B -3) / (2log A (A 2 B 3) ) \u003d (registro AA 11 + Log AB -3) / (2 (registro A AA 2 + Log AB 3)) \u003d (11 - 3Log AB) / (2 (2 + 3LOG AB)) Considerando che il registro A B \u003d Si ottiene 1/6 (11 - 3 · 1/6) / (2 (2 + 3 · 1/6)) \u003d 10.5 / 5 \u003d 2.1.
Risposta: 2.1.
È possibile eseguire in modo indipendente il seguente compito:
Calcola il registro √3 6 √2.1 se log 0,7 27 \u003d a.
Risposta: (3 + A) / (3a).
Esempio 10.
Calcola 6.5 4 / Log 3 169 · 3 1 / log 4 13 + log125.
Decisione.
6.5 4 / log 3 169 · 3 1 / log 4 13 + log 125 \u003d (13/2) 4/2 log 3 13 · 3 2 / log 2 13 + 2log 5 5 3 \u003d (13/2) 2 log 13 3 · 3 2 Log 13 2 + 6 \u003d (13 log 13 3/2 log 13 3) 2 · (3 log 13 2) 2 + 6 \u003d (3/2 log 13 3) 2 · (3 log 13 2) 2 + 6 \u003d (3 2 / (2 log 13 3) 2) · (2 \u200b\u200blog 13 3) 2 + 6.
(2 log 13 3 \u003d 3 log 13 2 (Formula 4))
Otteniamo 9 + 6 \u003d 15.
Risposta: 15.
Avere domande? Non so come trovare il valore dell'espressione logaritmica?
Per ottenere un aiuto del tutor - registrati.
La prima lezione è gratuita!
il sito, con la copia completa o parziale del riferimento del materiale è richiesto.
Espressioni logaritmiche, esempi di risoluzione. In questo articolo, considereremo i compiti associati alla soluzione dei logaritmi. I compiti sollevano la questione della ricerca del valore dell'espressione. Va notato che il concetto di logaritmo è usato in molti compiti e capire il suo significato è estremamente importante. Per quanto riguarda l'uso, il logaritmo viene utilizzato per risolvere le equazioni, in attività applicate, anche nei compiti associati allo studio delle funzioni.
Diamo esempi per capire il senso del logaritmo:


Identità logaritmica di base:

Le proprietà dei logaritmi che devono sempre essere ricordati:

* Il logaritmo del lavoro è uguale alla somma dei logaritmi dei fattori.
* * *

* Logaritmo privato (frazione) è uguale alla differenza nei logaritmi dei fattori.
* * *
![]()
* Il logaritmo è uguale al prodotto della laurea nel logaritmo della sua base.
* * *

* Transizione a una nuova base
* * *
Altre proprietà:

* * *
Il calcolo dei logaritmi è strettamente correlato all'uso delle proprietà degli indicatori di laurea.
Elenca alcuni di loro:
L'essenza di questa proprietà è che quando si trasferisce il numeratore al denominatore, e al contrario, il segno dell'indicatore cambia al contrario. Per esempio:

Conseguenza di questa proprietà:
* * *
![]()
Quando si emette una laurea in misura, la fondazione rimane la stessa e gli indicatori sono variabili.
* * *
Come hai visto il concetto stesso di logaritmo semplice. La cosa principale è che è necessaria una buona pratica, che dà una certa abilità. Naturalmente, la conoscenza delle formule deve. Se l'abilità nella conversione dei logaritmi elementari non è formata, quindi durante la risoluzione di attività semplici, è possibile consentire facilmente un errore.
Pratica, decidere prima gli esempi più semplici del corso della matematica, poi vai a più complesso. In futuro, mostrerò sicuramente come i logaritmi "terribili" siano risolti, non ci saranno tali sull'esame, ma sono di interesse, da non perdere!
È tutto! Successo a te!
Sinceramente, Alexander Krutitsky
P.S: Sarò grato se racconti del sito sui social network.
Logaritmi, come qualsiasi numero, può essere piegato, dedurre e convertire. Ma dal momento che i logaritmi non sono numeri abbastanza ordinari, ci sono le sue regole che vengono chiamate proprietà di base.
Queste regole devono necessariamente sapere - nessuna attività logaritmica seria è risolta senza di loro. Inoltre, sono piuttosto un po '- tutto può essere appreso in un giorno. Quindi, procedi.
Aggiunta e sottrazione di logaritmi
Considera due logaritmi con le stesse basi: log uN. x. e log. uN. y.. Quindi possono essere piegati e detratti e:
- log. uN. x. + Log. uN. y. \u003d Log. uN. (x. · y.);
- log. uN. x. - log. uN. y. \u003d Log. uN. (x. : y.).
Quindi, la quantità di logaritmi è uguale al logaritmo del lavoro e la differenza è il logaritmo di privato. Nota: il punto chiave qui è stesso terreno. Se le fondamenta sono diverse, queste regole non funzionano!
Queste formule aiuteranno a calcolare l'espressione logaritmica anche quando le singole parti non sono considerate (vedere la lezione "Cos'è il logaritmo"). Dai un'occhiata agli esempi - e assicurati:
Log 6 4 + log 6 9.
Poiché le basi nei logaritmi sono le stesse, usiamo la somma della somma:
log 6 4 + log 6 9 \u003d log 6 (4 · 9) \u003d log 6 36 \u003d 2.
Un compito. Trova il valore dell'espressione: log 2 48 - log 2 3.
Le fondamenta sono le stesse, usando la formula di differenza:
log 2 48 - log 2 3 \u003d log 2 (48: 3) \u003d log 2 16 \u003d 4.
Un compito. Trova il valore dell'espressione: log 3 135 - log 3 5.
Di nuovo le fondamenta sono le stesse, quindi abbiamo:
log 3 135 - Log 3 5 \u003d Log 3 (135: 5) \u003d log 3 27 \u003d 3.
Come puoi vedere, le espressioni iniziali sono costituite da logaritmi "cattivi", che non sono considerati separatamente separatamente. Ma dopo la trasformazione, sono ottenuti numeri abbastanza normali. In questo fatto, sono costruiti molti lavori di prova. Ma qual è il controllo - tali espressioni sono piene (a volte - quasi invariate) sono offerte sull'esame.
Laurea dirigente dal logaritmo
Ora un po 'complica il compito. Cosa succede se alla base o argomento del logaritmo costa una laurea? Quindi l'indicatore di questa misura può essere portato fuori dal segno logaritmo secondo le seguenti regole:
È facile vedere che l'ultima regola segue i loro primi due. Ma è meglio ricordarlo, in alcuni casi ridurrà significativamente la quantità di calcoli.
Naturalmente, tutte queste regole hanno senso se la conformità con il Logaritmo OTZ: uN. > 0, uN. ≠ 1, x. \u003e 0. E anche: impara ad applicare tutte le formule non solo da sinistra a destra, ma al contrario, cioè. Puoi fare numeri di fronte al logaritmo, al logaritmo stesso. Questo è il più spesso richiesto.
Un compito. Trova il valore dell'espressione: log 7 49 6.
Sbarazzati della misura nell'argomento nella prima formula:
log 7 49 6 \u003d 6 · log 7 49 \u003d 6 · 2 \u003d 12
Un compito. Trova il valore dell'espressione:
[Firma per ferire]
Si noti che nel denominatore c'è un logaritmo, la base e l'argomento dei quali sono gradi accurati: 16 \u003d 2 4; 49 \u003d 7 2. Abbiamo:
 [Firma per ferire]
[Firma per ferire] Penso che l'ultimo esempio richieda la spiegazione. Dove sono scomparsi i logaritmi? Fino all'ultimo momento, lavoriamo solo con il denominatore. Hanno presentato la base e l'argomento di un logaritmo lì sotto forma di gradi e condotti gli indicatori - ha ricevuto una frazione "a tre piani".
Ora guardiamo la frazione di base. Il numero nel numeratore e il denominatore è lo stesso numero: log 2 7. Dal momento che il registro 2 7 ≠ 0, possiamo ridurre la frazione - 2/4 rimarranno nel denominatore. Secondo le regole dell'aritmetica, i quattro possono essere trasferiti al numeratore, che è stato fatto. Il risultato è stata la risposta: 2.
Transizione a una nuova base
Parlando delle regole per l'aggiunta e la sottrazione dei logaritmi, ho sottolineato specificamente che funzionano solo con le stesse basi. E se le fondamenta sono diverse? Cosa succede se non sono gradi accurati dello stesso numero?
Le formule per la transizione a una nuova base arrivano in soccorso. Lo formulamo sotto forma di teorema:
Lascia che LOGARITHM LOG. uN. x.. Quindi per qualsiasi numero c. That c. \u003e 0 I. c. ≠ 1, vero uguaglianza:
[Firma per ferire]
In particolare, se metti c. = x.Otterremo:
[Firma per ferire]
Dalla seconda formula ne consegue che la base e l'argomento del logaritmo possono essere modificati in luoghi, ma allo stesso tempo l'espressione "gira", cioè. LOGARITHM risulta essere nel denominatore.
Queste formule sono rare nelle espressioni numeriche convenzionali. Valutare quanto sono convenienti, è possibile solo quando si risolvono equazioni e disuguaglianze logaritmiche.
Tuttavia, ci sono compiti che generalmente non sono risolti da nessuna parte come una transizione a una nuova base. Considera un paio di tali:
Un compito. Trova il valore dell'espressione: log 5 16 · log 2 25.
Si noti che gli argomenti di entrambi i logaritmi sono gradi accurati. Riassumendo: log 5 16 \u003d log 5 2 4 \u003d 4log 5 2; Log 2 25 \u003d log 2 5 2 \u003d 2log 2 5;
E ora "inverte" il secondo logaritmo:
[Firma per ferire]Dal momento che il lavoro non cambia dal riarrangiamento dei moltiplicatori, cambiamo caldamente i quattro e due, quindi risolti con logaritmi.
Un compito. Trova il valore dell'espressione: log 9 100 · LG 3.
La base e l'argomento del primo logaritmo - gradi accurati. Lo scriviamo e lo scriviamo degli indicatori:
[Firma per ferire]Ora sbarazzarsi del logaritmo decimale, girando alla nuova base:
[Firma per ferire]Identità logaritmica di base.
Spesso, la soluzione è necessaria per inviare un numero come logaritmo per una base specificata. In questo caso, le formule ci aiuteranno:
Nel primo caso n. Diventa un indicatore della misura nell'argomento. Numero n. Può essere assolutamente chiunque, perché è solo un valore logaritmo.
La seconda formula è in realtà una definizione parafrassata. Si chiama: l'identità logaritmica principale.
In effetti, cosa succederà se il numero b. costruire in modo tale grado che il numero b. In questa misura dà il numero uN.? Correttamente: questo è il più uN.. Leggere attentamente questo paragrafo - molti "hang" su di esso.
Come le formule di transizione a una nuova base, la principale identità logaritmica è a volte l'unica soluzione possibile.
Un compito. Trova il valore dell'espressione:
[Firma per ferire]
Si noti che il log 25 64 \u003d log 5 8 - ha appena fatto un quadrato dalla base e dall'argomento del logaritmo. Date le regole per la moltiplicazione dei gradi con la stessa base, otteniamo:
[Firma per ferire]Se qualcuno non è consapevole, è stato un vero compito di EGE :)
Unità logaritmica e logaritmica zero
In conclusione, darò due identità che è difficile nominare le proprietà - piuttosto, questa è la conseguenza della definizione di logaritmo. Sono costantemente trovati nei compiti e, che è sorprendente, crea problemi anche per studenti "avanzati".
- log. uN. uN. \u003d 1 è un'unità logaritmica. Registra una volta e per sempre: logaritmo su base uN. Dalla base stessa è uguale a uno.
- log. uN. 1 \u003d 0 è un zero logaritmico. Base uN. Forse in qualche modo, ma se l'argomento è un'unità - logaritmo è zero! Perché uN. 0 \u003d 1 è una conseguenza diretta della definizione.
Questa è tutte le proprietà. Assicurati di praticare applicarli in pratica! Scarica la culla all'inizio della lezione, stampalo - e risolvi le attività.