Vettori di prodotto scalare

Continuiamo a gestire i vettori. Nella prima lezione Vettori per teiere Abbiamo esaminato il concetto di vettore, azioni con vettori, coordinate vettoriali e compiti più semplici con i vettori. Se hai inserito questa pagina per la prima volta dal motore di ricerca, consiglio vivamente di leggere il suddetto articolo di introduzione, poiché è necessario navigare i termini usati da me, notazione da parte mia, per avere conoscenze di base sui vettori e essere in grado per risolvere compiti elementari. Questa lezione è una continuazione logica dell'argomento, e su di esso definirò compiti tipici in cui viene utilizzato il prodotto scalare dei vettori. Questa è un'occupazione molto importante.. Cerca di non perdere gli esempi, un utile bonus è collegato a loro: la pratica ti aiuterà a riparare il materiale superato e "riempire la mano" sulla risoluzione dei compiti comuni della geometria analitica.

Aggiunta di vettori, moltiplicazione vettoriale per numero .... Sarebbe ingenuo pensare che la matematica non abbia avuto nient'altro. Oltre alle azioni già riviste, ci sono una serie di altre operazioni con i vettori, vale a dire: vettori di prodotto scalare, vettori di opere d'arte vettoriale. e vettori misti. Il prodotto scalare dei vettori ci è familiare da scuola, altre due opere si riferiscono tradizionalmente al corso della matematica superiore. I temi sono semplici, l'algoritmo per risolvere molti compiti di stemather ed è comprensibile. L'unica cosa. Le informazioni sono decenti, quindi è indesiderabile provare a padroneggiare tutto e immediatamente. Questo è particolarmente vero per le teiere, credimi, l'autore non vuole sentire Chikatilo dalla matematica. Bene, non dalla matematica, naturalmente, anche \u003d) studenti più preparati possono usare i materiali selettivamente, in un certo senso, "ottenere" la conoscenza mancante, per te sarò un grafico innocuo dracula \u003d)

Apriremo, infine, la porta e vedremo appassionatamente cosa succede quando due versioni si incontrano ....

Definizione di un prodotto scalare di vettori.
Proprietà di un prodotto scalare. Compiti tipici

Il concetto di un lavoro scalare

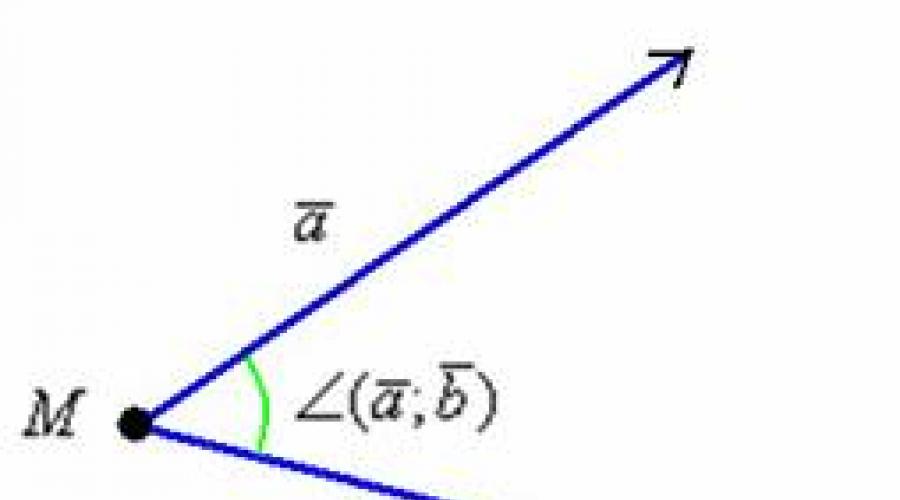
Primo Pro. Angolo tra i vettori.. Penso che tutti siano intuitivi che un tale angolo tra i vettori, ma nel caso un po 'di più. Considerare i vettori di non zero gratuiti e. Se posticipati questi vettori da un punto arbitrario, quindi risulta l'immagine che molti hanno già presentato mentalmente:

Confesso, qui ho obrandato la situazione solo a livello di comprensione. Se hai bisogno di una definizione rigorosa dell'angolo tra i vettori, si prega di contattare il libro di testo, per i compiti pratici, è in linea di principio per niente. Inoltre, in seguito, sarò in luoghi per ignorare zero vettori a causa del loro piccolo significato pratico. La prenotazione effettuata specificamente per i visitatori del sito avanzati che possono rimproverarmi in incompletezza teorica di alcune dichiarazioni successive.

Può prendere valori da 0 a 180 gradi (da 0 a radianti) inclusivi. Analiticamente questo fatto è registrato sotto forma di doppie disuguaglianze: o (in radianti).

In letteratura, l'icona dell'angolo spesso salta e scrivi semplicemente.

Definizione: Il prodotto scalare di due vettori è chiamato il numero pari al prodotto di questi vettori sul coseno dell'angolo tra loro:

Questa è ora una definizione piuttosto rigorosa.

Ci concentriamo sulle informazioni essenziali:

Designazione: Il prodotto scalare è indicato o semplicemente.

Il risultato dell'operazione è un numero: Il vettore è moltiplicato per il vettore e il numero è ottenuto. Infatti, se le lunghezze dei vettori sono i numeri, il coseno dell'angolo - il numero, quindi il loro lavoro Ci sarà anche anche un numero.

Immediatamente un paio di esempi di riscaldamento:

Esempio 1.

Decisione: Usiamo la formula . In questo caso:

Risposta:

I valori dei cosine possono essere trovati in tabella trigonometrica. Raccomando di stamparlo - sarà necessario in quasi tutte le sezioni della torre e avranno bisogno di molte volte.

Puramente da un punto di vista matematico il prodotto scalare è dimensionale, cioè il risultato, in questo caso, è semplicemente il numero e questo è tutto. Dal punto di vista dei compiti dei compiti della fisica, il prodotto scalare ha sempre un certo significato fisico, cioè dopo il risultato, è necessario specificare una particolare unità fisica. L'esempio canonico di calcolare il lavoro della forza può essere trovato in qualsiasi libro di testo (la formula è esattamente un prodotto scalare). Il lavoro di forza è misurato in joule, quindi, la risposta verrà registrata abbastanza specificatamente, ad esempio.

ESEMPIO 2.

Trovare se e l'angolo tra i vettori è uguale.

Questo è un esempio per una decisione indipendente, la risposta alla fine della lezione.

L'angolo tra i vettori e il valore del prodotto scalare

Nell'esempio 1, il prodotto scalare è stato positivo, ed in esempio 2 - negativo. Scopri cosa dipende il segno di un prodotto scalare. Guardiamo la nostra formula: . Le lunghezze dei vettori generico sono sempre positive: pertanto il segno può dipendere solo dal valore del coseno.

Nota: Per una migliore comprensione delle informazioni di seguito, è meglio esplorare il programma del coseno nei metodi Grafici e proprietà della funzione. Guarda come si comporta il coseno sul segmento.

Come già notato, l'angolo tra i vettori può variare all'interno E i seguenti casi sono possibili:

1) IF. angolo tra i vettori acuto: (da 0 a 90 gradi), quindi , IO. il prodotto scalare sarà positivo sondadoL'angolo tra di loro è considerato zero, e il prodotto scalare sarà anche positivo. Poiché, la formula è semplificata :.

2) IF. angolo tra i vettori stupido: (da 90 a 180 gradi) e corrispondentemente, prodotto scalare negativo:. Custodia speciale: se vettori diretto di fronteQuindi l'angolo tra di loro è considerato partito: (180 gradi). Il prodotto scalare è anche negativo perché

Dichiarazioni giuste e di ritorno:

1) Se, l'angolo tra i dati dei vettori è tagliente. In alternativa, i vettori sono rivestiti.

2) Se, l'angolo tra i vettori di dati è stupido. In alternativa, i vettori sono diretti opposti.

Ma il terzo caso è di particolare interesse:

3) IF. angolo tra i vettori dritto: (90 gradi), quindi il prodotto scalare è zero:. Anche il contrario è vero: se, allora. La dichiarazione compatta è formulata come segue: Il prodotto scalare di due vettori è zero se e solo se questi vettori sono ortogonali. Breve registrazione matematica:

! Nota : Ripetere nozioni di base della logica matematica: Un'icona di conseguenza logica a due vie viene solitamente letto "Se e solo allora", "in quello e solo nel caso." Come puoi vedere, le frecce sono dirette su entrambi i lati - "Questo segue da questo, e indietro, da quello, segue." Cosa, a proposito, la differenza dall'icona successiva unilaterale? Icona approva solo quelloche "questo segue questo", e non il fatto che il contrario sia giusto. Ad esempio: ma non tutte le bestia è una pantera, quindi in questo caso è impossibile usare l'icona. Allo stesso tempo, invece di icona può Utilizzare l'icona a unidirezionale. Ad esempio, risolvendo il compito, abbiamo scoperto che abbiamo concluso che i vettori sono ortogonali: - tale record sarà corretto e anche più pertinente di .

Il terzo caso ha un grande significato pratico.Perché ti permette di controllare, vettori ortogonali o meno. Risolviamo questo compito nella seconda sezione della lezione.

Proprietà di un pezzo scalare

Torniamo alla situazione quando due versioni sondado. In questo caso, l'angolo tra di loro è zero, e la formula del prodotto scalare prende il modulo :.

E cosa succederà se il vettore è moltiplicato per te stesso? È chiaro che il vettore è rivestito con se stesso, quindi usiamo la formula semplificata sopra:

Il numero è chiamato square Square. Vettore e indicato come.

In questo modo, La piazza scalare vettoriale è uguale al quadrato della lunghezza di questo vettoriale:

Da questa uguaglianza, è possibile ottenere una formula per calcolare la lunghezza del vettore:

Mentre sembra ininterrotto, ma i compiti della lezione spariranno tutti in posizione. Per risolvere i problemi, avremo anche bisogno proprietà di un pezzo scalare.

Per i vettori arbitrari e qualsiasi numero, le seguenti proprietà sono valide:

1) - movimento o commutativo La legge del lavoro scalare.

2) - Distribuzione o distribuzione La legge del lavoro scalare. Semplicemente, puoi rivelare parentesi.

3) - traspirante o associativo La legge del lavoro scalare. La costante può essere presa fuori dal prodotto scalare.

Spesso, tutti i tipi di proprietà (che sono ancora necessari!) Percepiti dagli studenti come spazzatura non necessaria, che deve essere inviata solo e subito dopo che l'esame è tranquillamente dimenticato. Sembrerebbe che ci sia importante qui, tutto e così dalla prima classe sa che il lavoro non cambia dalla permuta dei moltiplicatori :. Deve avvertire, in matematica più elevata con un approccio simile è facile bloccare la legna da ardere. Quindi, ad esempio, la proprietà di transizione non è giusta per matrici algebriche. È sbagliato per vettori di arte vettoriale. Pertanto, in qualsiasi proprietà che incontrerai nel corso della matematica più alta, almeno, è meglio approfondire cosa puoi fare, ma perché è impossibile.

ESEMPIO 3.

.

Decisione:Innanzitutto, chiarire la situazione con il vettore. A cosa è affatto? La somma dei vettori è un vettore completamente definito, che è indicato attraverso. L'interpretazione geometrica delle azioni con i vettori può essere trovata nell'articolo Vettori per teiere. Lo stesso prezzemolo con un vettore è la somma dei vettori e.

Quindi, per condizione, è necessario trovare un prodotto scalare. In teoria, è necessario applicare la formula di lavoro Ma il problema è che siamo sconosciuti dalla lunghezza dei vettori e dall'angolo tra loro. Ma in condizione date parametri simili per i vettori, quindi andremo diversi modi:

(1) Sostituiamo l'espressione dei vettori.

(2) Rivelare parentesi in base alla regola della moltiplicazione dei polinomi, è possibile trovare un incantesimo nell'articolo. Numeri complessi o Integrando una funzione razionale frazionata. Non ripeterò \u003d) A proposito, per rivelare le staffe per noi tutte le proprietà di distribuzione del prodotto scalare. Abbiamo ragione.

(3) Nel primo e ultimo periodo, i quadrati scalari dei vettori sono compatti: . Nel secondo, usiamo il riarrangiamento del prodotto scalare :.

(4) Diamo termini simili :.

(5) Nel primo mandato, usiamo la formula di una piazza scalare, che è stata menzionata non molto tempo fa. Nell'ultimo termine, di conseguenza, la stessa cosa funziona :. Il secondo termine si sta espandendo secondo la formula standard .

(6) Sosteniamo queste condizioni e eseguire attentamente i calcoli finali.

Risposta:

Il valore negativo del prodotto scalare afferma il fatto che l'angolo tra i vettori è smussato.

Compito tipico, ecco un esempio per una soluzione indipendente:

ESEMPIO 4.

Trova un prodotto scalare di vettori e, se lo sai .

Ora un altro compito comune è solo una nuova formula di lunghezza vettoriale. Le designazioni qui saranno un po 'coincidenti, quindi per chiarezza lo riscriverò con un'altra lettera:

ESEMPIO 5.

Trova la lunghezza del vettore se .

Decisione Sarà il seguente:

(1) Forniamo l'espressione del vettore.

(2) Usando la formula della lunghezza:, mentre come il vettore "VE", abbiamo un'espressione intera.

(3) Usiamo la formula di riepilogo sommario estivo. Si prega di notare come funziona curiosi qui: "In effetti, questo è un quadrato della differenza, e, infatti, è." Coloro che desiderano possono riorganizzare i vettori nei luoghi: - si è scoperto lo stesso con l'accuratezza dell'alcalis.

(4) Ulteriore è già familiare dai due compiti precedenti.

Risposta:

Se stai parlando della lunghezza, non dimenticare di specificare la dimensione - "unità".

ESEMPIO 6.

Trova la lunghezza del vettore se .

Questo è un esempio per una soluzione indipendente. Soluzione completa e risposta alla fine della lezione.

Continuiamo a spremere le cose utili dal prodotto scalare. Ancora diamo un'occhiata alla nostra formula . Secondo la regola di proporzione per resettare la lunghezza dei vettori nel denominatore del lato sinistro:

E le parti cambieranno luoghi:

Qual è il significato di questa formula? Se le lunghezze di due vettori e il loro prodotto scalare sono noti, allora il coseno dell'angolo tra i vettori di dati può essere calcolato e, di conseguenza, l'angolo stesso.

Il prodotto scalare è un numero? Numero. Lunghezza vettoriale - numeri? Numeri. Quindi, la frazione è anche un certo numero. E se il coseno dell'angolo è noto: , è facile trovare un angolo stesso utilizzando la funzione inversa: .

Esempio 7.

Trova l'angolo tra i vettori e, se è noto.

Decisione: Usiamo la formula:

Nella fase finale dei calcoli, è stato utilizzato il ricevimento tecnico - l'eliminazione dell'irrazionalità nel denominatore. Al fine di eliminare l'irrazionalità, ho dominato il nizer e il denominatore.

Quindi se , poi:

I valori delle funzioni trigonometriche inverse possono essere trovati da tabella trigonometrica. Anche se accade raramente. Nei compiti della geometria analitica, qualche tipo di orso vago sembra apparire molto più spesso, e il valore dell'angolo deve trovare approssimativamente utilizzando la calcolatrice. In realtà, ripeteremo ancora una foto del genere.

Risposta:

Ancora una volta, non dimenticare di indicare la dimensione - Radiani e gradi. Personalmente, sarò sicuro di "rimuovere tutte le domande", preferisco indicare sia che (se, per condizione, ovviamente, non è necessario presentare la risposta solo in radianti o solo in gradi).

Ora puoi far fronte a un compito più complesso:

Esempio 7 *

Danies - le lunghezze dei vettori e l'angolo tra di loro. Trova l'angolo tra i vettori ,.

Il compito non è nemmeno così complicato come multiplo.
Analizzeremo l'algoritmo della soluzione:

1) Sotto la condizione è necessario trovare l'angolo tra i vettori e, quindi è necessario utilizzare la formula .

2) Trova un prodotto scalare (vedere Esempi numero 3, 4).

3) Troviamo la lunghezza del vettore e la lunghezza del vettore (vedi esempi numero 5, 6).

4) La fine della decisione coincide con l'esempio numero 7 - conosciamo il numero, e quindi è facile trovare un angolo stesso:

Una breve soluzione e risposta alla fine della lezione.

La seconda sezione della lezione è dedicata allo stesso prodotto scalare. Coordinate. Sarà ancora più facile che nella prima parte.

Prodotto scalare dei vettori,
ha chiesto le coordinate nella base ortonormale

Risposta:

Cosa dire, per affrontare le coordinate è molto più piacevole.

Esempio 14.

Trova un prodotto scalare di vettori e se

Questo è un esempio per una soluzione indipendente. Qui è possibile utilizzare l'associatività dell'operazione, cioè non contare, ma portare immediatamente i primi tre al di fuori del prodotto scalare e aggiornando l'ultima volta. Soluzione e risposta alla fine della lezione.

Nella conclusione del paragrafo provocatorio esempio sul calcolo della lunghezza del vettore:

ESEMPIO 15.

Trova la lunghezza vettori. , se un

Decisione:il metodo della sezione precedente viene visualizzato di nuovo: ma c'è un'altra strada:

Trova un vettore:

E la sua lunghezza nella formula banale :

Il prodotto scalare non è affatto qui.

Non così com'è, quando si calcola la lunghezza del vettore:
Fermare. Non approfittare della proprietà ovvia della lunghezza vettoriale? Cosa si può dire della lunghezza del vettore? Questo vettore è più lungo il vettore 5 volte. La direzione è il contrario, ma non svolge un ruolo, perché parla di lunghezza. Ovviamente, la lunghezza del vettore è uguale al lavoro modulo Numeri per la lunghezza del vettore:
- Il segno del modulo "mangia" un possibile numero negativo.

In questo modo:

Risposta:

La formula del coseno dell'angolo tra i vettori che sono stabiliti dalle coordinate

Ora abbiamo informazioni complete per essere precedentemente derivate dalla formula Coseno Coseno tra i vettori attraverso le coordinate dei vettori:

Angolo del coseno tra i vettori aerei e specificato nella base ortonormale, la formula è espressa:
.

Angolo del coseno tra i vettori spaziali definito nella base ortonormale la formula è espressa:

ESEMPIO 16.

Sono dati tre vertici del triangolo. Trova (angolazione in alto).

Decisione:Per condizione, il disegno non è richiesto, ma ancora:

L'angolo desiderato è contrassegnato da un arco verde. Ricorda immediatamente la designazione scolastica dell'angolo: - Attenzione particolare a mezzo La lettera è la cima dell'angolo di cui hai bisogno. Per Brevity, è stato anche possibile registrare semplicemente.

È chiaro dal disegno che l'angolo del triangolo coincide con l'angolo tra i vettori e, in altre parole: .

L'analisi è preferibilmente imparando a svolgere mentalmente.

Trova i vettori:

Calcoliamo il prodotto scalare:

E la lunghezza dei vettori:

Angolo Cosine:

È questa procedura per eseguire il compito che raccomanda le teiere. I lettori più preparati possono registrare i calcoli della "One Line":

Ecco un esempio di un valore coseno "cattivo". Il valore ottenuto non è definitivo, quindi non vi è alcun senso particolare per sbarazzarsi della irrazionalità nel denominatore.

Trova l'angolo stesso:

Se guardi il disegno, il risultato è abbastanza credibile. Per controllare l'angolo può anche essere misurato e il trasportatore. Non danneggiare il rivestimento del monitor \u003d)

Risposta:

In risposta, non dimenticarlo chiesto sull'angolo del triangolo (e non sull'angolo tra i vettori), non dimenticare di specificare la risposta esatta: e il valore approssimativo dell'angolo: trovato usando la calcolatrice.

Coloro che hanno apprezzato il processo possono calcolare gli angoli e assicurarsi che la giustizia dell'uguaglianza canonica

Esempio 17.

Lo spazio è dato dalle coordinate del triangolo dei loro vertici. Trova l'angolo tra le parti e

Questo è un esempio per una soluzione indipendente. Soluzione completa e risposta alla fine della lezione

La piccola sezione finale sarà dedicata alle proiezioni in cui il prodotto scalare è anche "coinvolto":

Proiezione vettoriale sul vettore. Proiezione di vettore su assi di coordinate.
Vettore delle guide del coseno.

Considera i vettori e:

Vettore sprogit sul vettore, per questo, fuori dall'inizio e dalla fine del vettore ometti perpendicolare Sul vettore (linee tratteggiate verdi). Immagina che i raggi della luce cadano perpendicolarmente nel vettore. Quindi il segmento (linea rossa) sarà una "ombra" del vettore. In questo caso, la proiezione vettoriale sul vettore è la lunghezza del segmento. Cioè, la proiezione è un numero.

Questo numero è indicato come segue:, "vettore grande" indicare il vettore Quale` proiezione, "un piccolo vettore del substrato" indica il vettore SUL che è proiettato.

Il record stesso viene letto come questo: "La proiezione del vettore" A "sul vettore è il vettore."

Cosa succede se il vettore sia "troppo corto"? Eseguiamo una linea retta contenente il vettore. E il vettore "A" sarà già proiettato sulla direzione del vettore "Be"Semplicemente - su una linea retta contenente il vettore di essere. Lo stesso accade se il vettore "A" è posticipato nel trentesimo del regno - è ancora facilmente dissottabile a una linea retta contenente il vettore.

Se angolo tra i vettori acuto (come nella figura), quindi

Se vettori. ortogonale, quindi (la proiezione è un punto, le cui dimensioni sono considerate zero).

Se angolo tra i vettori stupido(Nella figura, riorganizza mentalmente la freccia del vettore), quindi (la stessa lunghezza, ma presa con un segno meno).

Poghererò questi vettori da un punto:

Ovviamente, quando si sposta il vettore, la sua proiezione non cambia

Ci saranno compiti per una soluzione indipendente a cui puoi vedere le risposte.

Se nel compito e nella lunghezza dei vettori, e l'angolo tra di loro è presentato "su un piattino con un azionamento blu", quindi la condizione del problema e la sua soluzione assomiglia a questo:

Esempio 1.Vasti vettori. Trova un prodotto scalare di vettori se le loro lunghezze e angoli tra di loro sono presentate nel seguente significato:

Un'altra definizione è anche definita, completamente equivalente alla definizione 1.

DEFINIZIONE 2.. Il prodotto scalare dei vettori è chiamato numero (scalare), pari alla lunghezza della lunghezza di questi questi vettori sulla proiezione di un altro vettore sull'asse determinato dal primo dei vettori specificati. Formula in base alla definizione 2:

Il compito con l'uso di questa formula è risolto dopo il prossimo punto teorico importante.

Determinazione di un prodotto scalare di vettori attraverso le coordinate

Lo stesso numero può essere ottenuto se i vettori variabili sono impostati dalle loro coordinate.

Definizione 3. Il prodotto scalare dei vettori è un numero pari alla somma delle opere a coppie delle loro rispettive coordinate.

Sulla superficie

Se due versioni e sul piano sono definite dai loro due coordinate rettangolari cartesiane.

il prodotto scalare di questi vettori è uguale alla somma delle opere a coppie delle rispettive coordinate:

.

ESEMPIO 2.Trova la grandezza numerica della proiezione vettoriale sull'asse parallelo al vettore.

Decisione. Troviamo un prodotto scalare dei vettori, piegando le opere a coppie delle loro coordinate:

Ora dobbiamo equiparare il prodotto scalare risultante del vettore della lunghezza vettoriale sulla proiezione vettoriale sull'asse parallelo al vettore (in conformità con la formula).

Troviamo la lunghezza del vettore come una radice quadrata dalla somma dei quadrati della sua coordinata:

.

Compileiamo l'equazione e lo risolviamo:

Risposta. Il valore numerico desiderato è meno 8.

Nello spazio

Se due versioni e lo spazio sono definiti dalle loro tre coordinate rettangolari cartesiane

,

il prodotto scalare di questi vettori è anche uguale alla somma delle opere di accoppiamento delle rispettive coordinate, solo le coordinate sono già tre:

.

Il compito di trovare un prodotto scalare con il metodo considerato - dopo aver analizzato le proprietà del prodotto scalare. Poiché l'attività dovrà determinare quali vettori variabili di forma angolare.

Proprietà del prodotto scalare dei vettori

Proprietà algebriche

1. (spostare la proprietà: Dal cambiamento in luoghi di vettori variabili, la grandezza del loro prodotto scalare non cambia).

2. (combulator Numero di telefono Proport: Il prodotto scalare del vettore moltiplicato da alcuni moltiplicatore e un altro vettore, uguale al prodotto scalare di questi vettori, moltiplicato per lo stesso fattore).

3. (distribuzione relativa alla somma della proprietà dei vettori: Il prodotto scalare della somma di due vettori sul terzo vettore è uguale alla somma delle opere scalari del primo vettore sul terzo vettore e il secondo vettore sul terzo vettore).

4. (vettore quadrato scalare più zero), Se è un vettore diverso da zero, e, se - vettore zero.

Proprietà geometriche

Nelle definizioni dell'operazione in linea, abbiamo già riguardato il concetto di angolo tra due vettori. È tempo di chiarire questo concetto.

La figura sopra mostra due vettore, che sono mostrati all'inizio generale. E la prima cosa per prestare attenzione a: ci sono due angoli tra questi vettori - φ 1 e φ 2 . Quale di questi angoli appare nelle definizioni e nelle proprietà del prodotto scalare dei vettori? La quantità degli angoli considerati è uguale a 2 π E pertanto, i cosini di questi angoli sono uguali. La definizione del prodotto scalare include solo il coseno dell'angolo, e non il significato della sua espressione. Ma solo un angolo è considerato nelle proprietà. E questo è uno dei due angoli che non supera π , cioè, 180 gradi. Nella foto, questo angolo è indicato come φ 1 .

1. Due vettori chiamati ortogonale e l'angolo tra questi vettori - Direct (90 gradi o π / 2) se il prodotto scalare di questi vettori è zero :

.

L'ortodismismo in algebra vettoriale è la perpendicolarità di due vettori.

2. Due vettore non zero costituiscono angolo acuto (da 0 a 90 gradi, o, che è lo stesso - meno π prodotto scalare positivo .

3. Due vettori non zero costituiscono angolo ottuso (da 90 a 180 gradi, o che la stessa cosa è di più π / 2) se e solo quando loro prodotto scalare negativo .

ESEMPIO 3. I vettori sono forniti nelle coordinate:

.

Calcola lavori scalari di tutte le coppie di questi vettori. Quale angolo (acuto, dritto, stupido) forma queste coppie di vettori?

Decisione. Il calcolo sarà l'aggiunta delle opere delle coordinate pertinenti.

Ricevuto un numero negativo, quindi i vettori formano uno stupido angolo.

Ricevuto un numero positivo, quindi i vettori formano un angolo acuto.

Ricevuto zero, quindi i vettori formano un angolo retto.

Ricevuto un numero positivo, quindi i vettori formano un angolo acuto.

.

Ricevuto un numero positivo, quindi i vettori formano un angolo acuto.

Per auto-test puoi usare calcolatrice online Scalare prodotto di vettori e angoli dei coseno tra di loro .

ESEMPIO 4. Vengono fornite le lunghezze dei due vettori e l'angolo tra loro:

.

Determinare, con quale valore del numero di vettori e ortogonali (perpendicolare).

Decisione. Sposta i vettori secondo la regola della moltiplicazione dei polinomi:

Ora calcoliamo ogni termine:

.

Fai un'equazione (uguaglianza del lavoro di zero), presentiamo membri simili e risolvendo l'equazione:

Risposta: Abbiamo un valore λ \u003d 1.8, in cui i vettori sono ortogonali.

ESEMPIO 5.Dimostra quel vettore Vettore ortogonale (perpendicolare)

Decisione. Per controllare l'ortogonalità, i vettori variabili e come polinomiani, sostituire invece della sua espressione fornita nella condizione del terk:

.

Per fare ciò, ciascun membro (il termine) dei primi polinomi si moltiplicano a ciascun membro del secondo e le opere ottenute sono piegate:

.

Nel risultato risultante, la frazione è ridotta a spese. Si ottiene il seguente risultato:

Conclusione: come risultato della moltiplicazione, zero, quindi, l'ortogonalità (perpendicolarità) dei vettori è dimostrato.

Risolvi il compito da soli, e poi vedi la decisione

ESEMPIO 6. Le lunghezze dei vettori sono fornite e, e l'angolo tra questi vettori è uguale π /quattro . Determinare con quale valore μ Vettori e reciprocamente perpendicolari.

Per auto-test puoi usare calcolatrice online Scalare prodotto di vettori e angoli dei coseno tra di loro .

Rappresentazione della matrice del prodotto scalare dei vettori e del prodotto dei vettori n-dimensionali

A volte una vincita per chiarezza è la rappresentazione di due vettori variabili sotto forma di matrici. Quindi il primo vettore è rappresentato come una stringa di matrice e il secondo - nella forma di una matrice di colonna:

Quindi il prodotto scalare dei vettori sarà il prodotto di queste matrici :

Il risultato è lo stesso del metodo ottenuto, che abbiamo già considerato. Abbiamo ricevuto un numero singolo e il prodotto della stringa di matrice sulla matrice della colonna è anche un singolo numero.

In forma di matrice è conveniente rappresentare il prodotto dei vettori n-dimensionali astratti. Pertanto, il prodotto di due vettori quadridimensionali sarà il prodotto della stringa di matrice con quattro elementi sulla matrice della colonna anche con quattro elementi, il prodotto di due vettori tridimensionali - il prodotto della stringa di matrice con cinque elementi sul Matrice della colonna anche con cinque elementi e così via.

Esempio 7. Trova lavori scalari di vettori a vapore

,

usando una rappresentazione a matrice.

Decisione. Prima coppia di vettori. Presentiamo il primo vettore sotto forma di una stringa di matrice e il secondo - nella forma di una matrice di colonna. Troviamo un prodotto scalare di questi vettori come prodotto di una stringa di matrice su una matrice di colonna:

Allo stesso modo, presentiamo la seconda coppia e troviamo:

Come possiamo vedere, i risultati sono aumentati rispetto alle stesse coppie dall'esempio 2.

Angolo tra due vettori

L'uscita della formula del coseno dell'angolo tra due vettori è molto bella e breve.

Per esprimere un prodotto scalare di vettori

(1)

in forma di coordinata, troveremo preliminamente il prodotto scalare di Ort. Il prodotto scalare del vettore su se stesso per definizione:

Ciò che viene registrato nella formula sopra significa: il prodotto scalare del vettore su se stesso è uguale al quadrato della sua lunghezza. Il coseno di zero è uguale a uno, quindi il quadrato di ogni orto sarà uguale a uno:

Dal momento che vettori

parly perpendicolare, quindi coppia lavori di orti sarà zero:

Ora eseguire moltiplicazione dei polinomi vettoriali:

Sosteniamo l'uguaglianza dei valori delle corrispondenti opere scalari di orteggi:

Otteniamo la formula del coseno dell'angolo tra due vettori:

ESEMPIO 8.Sono dati tre punti UN.(1;1;1), B.(2;2;1), C.(2;1;2).

Trova un angolo.

Decisione. Troviamo le coordinate dei vettori:

,

.

Secondo la formula del coseno, otteniamo:

Quindi ,.

Per auto-test puoi usare calcolatrice online Scalare prodotto di vettori e angoli dei coseno tra di loro .

Esempio 9.Dana due vettori.

Trova quantità, differenza, lunghezza, prodotto scalare e angolo tra loro.

2. Resturm

I. Il prodotto scalare è attratto da zero in quello e solo nel caso in cui almeno uno dei vettori è pari a zero o se i vettori sono perpendicolari. In effetti, se neanche, o quello.

Indietro, se i vettori variabili non sono zero, quindi a causa della condizione

quando segue:

Poiché la direzione del vettore zero è incerta, il vettore zero può essere considerato perpendicolare a qualsiasi vettore. Pertanto, la proprietà specificata del prodotto scalare può essere formulata in breve: il prodotto scalare viene disegnato a zero in quello e solo il caso quando i vettori sono perpendicolari.

II. Il prodotto scalare ha una proprietà di movimento:

Questa proprietà segue direttamente dalla definizione:

perché le varie designazioni dello stesso angolo.

III. La legge distributiva è estremamente importante. Il suo uso è grande come nella consueta aritmetica o algebra, dove è formulata come: per moltiplicare la quantità, è necessario moltiplicare ogni pozzo e piegato i lavori ottenuti, I.e ..

Ovviamente, la moltiplicazione dei numeri multilenali in aritmetici o polinomi in Algebra si basa su questa proprietà di moltiplicazione.

Questa legge ha la stessa importante importanza nell'algebra vettoriale, poiché sulla base di esso possiamo applicare ai vettori della consueta regola di moltiplicazione dei polinomi.

Proviamo che per eventuali tre vettori A, B, con l'uguaglianza

Secondo la seconda definizione del prodotto scalare, espresso dalla formula, otteniamo:

Applicando ora Proprietà di 2 proiezioni dal § 5, troviamo:

q.e.d.

IV. Il prodotto scalare ha la precisione della combinazione relativa al fattore numerico; Questa proprietà è espressa come segue:

i.e. Per moltiplicare il prodotto scalare dei vettori da parte del numero, è sufficiente moltiplicare da questo numero uno dei fattori.