Probabilità classica. Probabilità di un evento casuale
Leggi anche
Per le stime della probabilità di un evento di qualsiasi evento casuale sono molto importanti per rappresentare predefinitivamente se la probabilità degli eventi di interesse per noi differisca da come si stanno sviluppando altri eventi.
Nel caso di uno schema classico, quando tutti i risultati sono ugualmente anche, possiamo già valutare i valori della probabilità di un individuo di interesse per noi indipendentemente. Possiamo farlo anche se l'evento è un insieme complesso di diversi risultati elementari. E se diversi eventi casuali si verificano simultaneamente o sequenzialmente? In che modo questo influisce sulla probabilità degli eventi di interesse per noi?
Se lancio un osso suonare diverse volte, e voglio cadere "sei", e non sono fortunato tutto il tempo, significa che è necessario aumentare la scommessa, perché, secondo la teoria delle probabilità, io 'm in procinto di prendere una fortuna? Ahimè, la teoria della probabilità non approva nulla del genere. Né ossa né carta né moneta non so come memorizzare Cosa hanno dimostrato per noi l'ultima volta. Non si preoccupano completamente, per la prima volta o alla decima volta oggi vivo il mio destino. Ogni volta che ripeto il lancio, conosco solo una cosa: questa volta la probabilità del "sei" è di nuovo uguale a un sesto. Certo, questo non significa che il numero di cui hai bisogno non cadrà mai. Ciò significa solo il fatto che la mia perdita dopo il primo tiro e dopo ogni altro tiro - eventi indipendenti.
Eventi A e B sono chiamati indipendenteSe l'implementazione di uno di esse non influisce sulla probabilità di un altro evento. Ad esempio, le probabilità di sconfiggere il bersaglio prima di due pistole non dipendono dal fatto che il bersaglio ha colpito un altro strumento, così gli eventi "la prima pistola ha colpito l'obiettivo" e "il secondo strumento ha colpito l'obiettivo" indipendente.
Se due eventi A e in indipendenti, e la probabilità di ciascuno di essi è noto, la probabilità di occorrenza simultanea ed eventi A, ed eventi in (AB designato) possono essere calcolati utilizzando il seguente teorema.
Teorema di moltiplicazione della probabilità per eventi indipendenti
P (AB) \u003d P (A) * P (B) - Probabilità simultaneo L'inizio di due indipendente Eventi uguali lavoroprobabilità di questi eventi.Esempio.Le probabilità di entrare nel target nella ripresa del primo e del secondo attrezzo sono rispettivamente uguali: p 1 \u003d 0,7; P 2 \u003d 0.8. Trova la probabilità di entrare in un bollente con entrambe le pistole allo stesso tempo.
Decisione:come abbiamo già visto eventi A (il primo colpo della pistola) e in (il secondo colpo dell'utensile) è indipendente, cioè. P (AV) \u003d P (A) * P (c) \u003d P 1 * P 2 \u003d 0,56.
Cosa succede alle nostre stime se gli eventi di origine non sono indipendenti? Cambiamo leggermente l'esempio precedente.
Esempio.Due frecce alle competizioni sparano agli obiettivi, e se uno di loro spara un'etichetta, l'avversario inizia ad essere nervoso e i suoi risultati si deteriorano. Come trasformare questa situazione quotidiana in un compito matematico e contorno modi per risolverlo? È intuitivo che sia necessario in qualche modo dividere le due opzioni per lo sviluppo di eventi, per compilare due scenari, due compiti diversi. Nel primo caso, se l'avversario ha perso, la sceneggiatura sarà favorevole per l'atleta nervoso e la sua accuratezza sarà più alta. Nel secondo caso, se l'avversario ha decensinato la sua possibilità, la probabilità di colpire il bersaglio per il secondo atleta è ridotto.
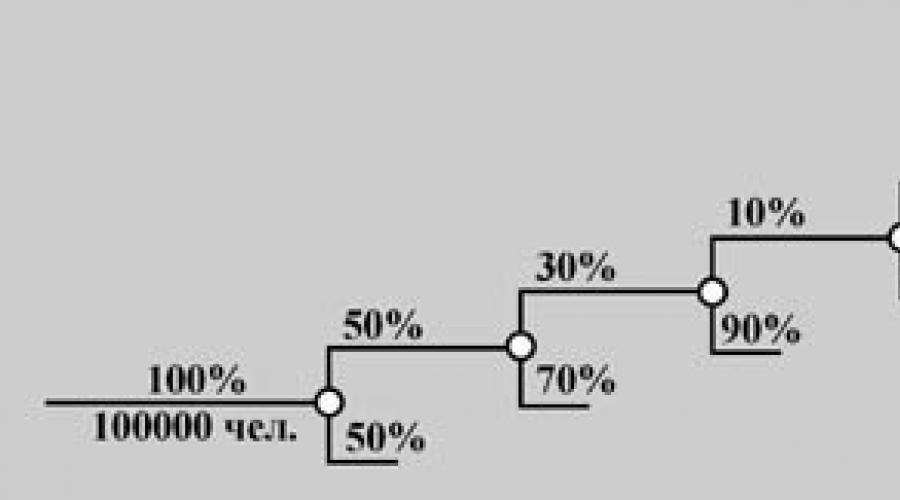
Per la separazione di possibili scenari (sono spesso chiamati ipotesi), useremo spesso lo schema "albero di probabilità". Questo schema è simile nel significato per l'albero delle decisioni con cui probabilmente hai già dovuto affrontare. Ogni ramo è uno scenario di sviluppo di eventi separato, solo ora ha il suo valore del cosiddetto condizionale Probabilità (Q 1, Q 2, Q 1 -1, Q 2 -1).
Questo schema è molto conveniente per analizzare gli eventi casuali consecutivi.
Rimane per scoprire un'altra domanda importante: da dove vengono i valori di probabilità iniziali provengono da Situazioni reali ? Dopo tutto, la teoria della probabilità funziona con le stesse monete e giocando le ossa? Di solito queste stime sono prese dalle statistiche, e quando non ci sono informazioni statistiche, svolgiamo la nostra ricerca. E spesso non è necessario avviarlo dalla raccolta dei dati, ma dalla domanda, quali informazioni dovremmo avere bisogno.
Esempio.Supponiamo che dobbiamo valutare in città con una popolazione di centomila residenti il \u200b\u200bvolume di mercato per un nuovo prodotto, che non è l'argomento, ad esempio, per un balsamo per la cura dei capelli verniciati. Considera lo schema del "albero di probabilità". Allo stesso tempo, il valore di probabilità su ciascun "ramo" dobbiamo valutare approssimativamente. Quindi, la nostra capacità di mercato stima:
1) Da tutti i residenti della città delle donne del 50%,
2) di tutte le donne solo il 30% dipinga i capelli spesso,
3) di loro solo il 10% godono di balsamo per capelli verniciati,
4) Di questi, solo il 10% può ottenere il coraggio di provare un nuovo prodotto,
5) Di questi, il 70% di solito compra tutto da noi, ma dai nostri concorrenti.

Decisione:Secondo la legge di moltiplicare le probabilità, determiniamo la probabilità degli eventi di interesse per noi A \u003d (un residente della città acquista questo nuovo balsamo) \u003d 0,00045.
Moltiplicare questo valore della probabilità per il numero di residenti della città. Di conseguenza, abbiamo solo 45 potenziali acquirenti, e se consideriamo che una bolla di questo fondo sia sufficiente per diversi mesi, il commercio non è troppo occupato.
Ciononostante, ci sono benefici delle nostre stime.
Innanzitutto, possiamo confrontare le previsioni di diverse idee di business, nei regimi avranno un "sviluppo" diverso e, naturalmente, i valori di probabilità saranno anche diversi.
In secondo luogo, come abbiamo già parlato, un valore casuale non è perché è chiamato casuale che non dipenda da nulla. Solo lei accurato Il valore non è noto in anticipo. Sappiamo che il numero medio di acquirenti può essere aumentato (ad esempio, con l'aiuto della pubblicità di un nuovo prodotto). Quindi ha senso concentrarsi su quegli "Sviluppo", dove la distribuzione delle probabilità non si adatta in particolare a noi, sui fattori che siamo in grado di influenzare.
Considera un altro esempio quantitativo dello studio del comportamento del cliente.
Esempio.Durante il giorno, il mercato alimentare visita una media di 10.000 persone. La probabilità che il visitatore del mercato arrivi nel padiglione dei prodotti lattiero-caseari è 1/2. È noto che in questo padiglione in media in vendita al giorno 500 kg di vari prodotti.
È possibile sostenere che l'acquisto medio nel padiglione pesa solo 100 g?
Discussione.Certo, è impossibile. È chiaro che non tutti quelli che sono andati nel padiglione, di conseguenza, qualcosa ha comprato qualcosa lì.

Come mostrato nel diagramma per rispondere alla questione del peso medio dell'acquisto, dobbiamo trovare la risposta alla domanda, qual è la probabilità che una persona che venne al padiglione comprerà qualcosa. Se non ci sono tali dati a nostra disposizione, e ne abbiamo bisogno, dovrai prenderli da solo, dopo aver visto i visitatori del padiglione per qualche tempo. Supponiamo che le nostre osservazioni abbiano dimostrato che solo il quinto dei visitatori del padiglione compra qualcosa.
Non appena queste stime sono ottenute da noi, il compito diventa semplice. Delle 10.000 persone che vengono al mercato, 5000 entreranno nel padiglione dei lattiero-caseari, lo shopping sarà solo 1000. Il peso medio di acquisto è di 500 grammi. È interessante notare che per costruire un quadro completo di ciò che sta accadendo, la logica dei "baters" condizionali dovrebbe essere determinata in ogni fase del nostro ragionamento e se lavoriamo con una situazione "specifica" e non con probabilità.
Attività per auto-test
1. Supponiamo che vi sia un circuito elettrico composto da n serie di elementi collegati, ciascuno dei quali funziona indipendentemente dal resto.

La probabilità P è nota nell'ordine di ciascun elemento. Determina la probabilità del funzionamento dell'intera area della catena (evento A).
2. Lo studente conosce 20 domande di esame su 25. Trova la probabilità che lo studente conosca le tre domande offerte da lui.
3. La produzione è composta da quattro passaggi consecutivi, su ciascuna delle quali funziona l'attrezzatura, per il quale le probabilità di guasto entro il prossimo mese sono uguali al rispettivamente P 1, P 2, P 3 e P 4. Trova la probabilità che in un mese non ci sarà una singola sosta di produzione a causa del malfunzionamento delle attrezzature.
Gli eventi che si verificano in realtà o nella nostra immaginazione possono essere suddivisi in 3 gruppi. Questi sono eventi affidabili che si verificheranno sicuramente, gli eventi impossibili e gli eventi casuali. La teoria delle probabilità è studiata da eventi casuali, cioè. Eventi che possono verificarsi o non accadono. Questo articolo presenterà in una breve forma della teoria della probabilità di formule ed esempi di risoluzione dei problemi sulla teoria della probabilità che sarà in 4 compiti della Matematica EE (livello del profilo).
Perché hai bisogno della teoria della probabilità
Storicamente, la necessità di studiare questi problemi sorti nel 17 ° secolo in relazione allo sviluppo e alla professionalizzazione del gioco d'azzardo e dall'aspetto di un casinò. Era un vero fenomeno che ha richiesto il suo studio e la sua ricerca.
Un gioco di carte, ossa, roulette creato situazioni quando si potrebbe verificarsi una qualsiasi del numero finito di eventi uguali. C'era bisogno di fornire valutazioni numeriche la possibilità di un verificarsi di uno o di un altro evento.
Nel 20 ° secolo si è rivelato che questa scienza apparentemente frivola svolge un ruolo importante nella conoscenza dei processi fondamentali che si verificano nel micrometro. È stata creata una moderna teoria della probabilità.
I concetti di base della teoria della probabilità
L'obiettivo di studiare la teoria della probabilità è eventi e le loro probabilità. Se l'evento è complicato, può essere diviso in componenti semplici le cui probabilità sono facili da trovare.
La somma degli eventi A e B è chiamata evento c, che consiste nel fatto che c'è un evento A, o un evento o eventi A e nello stesso tempo.
Il lavoro degli eventi A e B è chiamato un evento con una considerazione che l'evento a e l'evento si è verificato.
Gli eventi A e B sono chiamati inconcetti se non possono verificarsi simultaneamente.
L'evento A è chiamato impossibile se non può accadere. Questo evento è indicato dal simbolo.
L'evento A è chiamato affidabile se si verificherà sicuramente. Questo evento è indicato dal simbolo.
Lascia che ogni evento sia messo in base al numero P (A). Questo numero P (A) è chiamato probabilità di evento A, se le seguenti condizioni sono soddisfatte con questa conformità.
Un caso particolare importante è la situazione in cui vi sono egualmente risultati elementari elementari e gli esiti arbitrari sono formati da eventi A. In questo caso, la probabilità può essere inserita dalla formula. La probabilità imposta in questo modo è chiamata probabilità classica. Si può dimostrare che in questo caso vengono effettuate le proprietà 1-4.
I compiti sulla teoria delle probabilità che si trovano sull'esame in matematica sono principalmente associati alla probabilità classica. Tali compiti possono essere molto semplici. Particolarmente semplici sono compiti sulla teoria della probabilità nelle opzioni di dimostrazione. È facile calcolare il numero di esiti favorevoli, direttamente nella condizione è scritto il numero di tutti i risultati.

La risposta è ottenuta dalla formula.
Un esempio di un compito dalla Parola di Matematica per determinare la probabilità
Sul tavolo bugia 20 torte - 5 con cavolo, 7 con mele e 8 con riso. Marina vuole prendere un patè. Qual è la probabilità che ci vorrà un patè con il riso?
Decisione.
In totali eguali risultati elementari 20, cioè, Marina può prendere una qualsiasi dei 20 torte. Ma dobbiamo apprezzare la probabilità che Marina prenderà un pidrite con riso, cioè, dove una è la scelta di un burattino con riso. Significa che abbiamo il numero di esiti favorevoli (elezioni di torte con riso) solo 8. Quindi la probabilità sarà determinata dalla formula:
![]()
Eventi indipendenti, opposti e arbitrari
Tuttavia, nella banca aperta, i compiti hanno iniziato a soddisfare compiti più complessi. Pertanto, presta attenzione al lettore e ad altri problemi studiati nella teoria delle probabilità.
Gli eventi A e B sono chiamati indipendenti se la probabilità di ciascuno di essi non dipende dal fatto che sia avvenuto un altro evento.
Evento B è che l'evento non sta accadendo, cioè. Evento B è il contrario dell'evento A. La probabilità dell'evento opposto è uguale a un meno la probabilità di un evento diretto, cioè. .
Teoremi di aggiunta e moltiplicazione delle probabilità, formule
Per gli eventi arbitrari A e la probabilità dell'importo di questi eventi pari alla somma della loro probabilità senza la probabilità del loro evento congiunto, cioè. .
Per eventi indipendenti, A e per la probabilità del lavoro di questi eventi è uguale al prodotto delle loro probabilità, cioè. in questo caso .
Le ultime 2 affermazioni sono chiamate teoremi di aggiunta e moltiplicazione delle probabilità.
Non sempre il conteggio del numero di risultati è così semplice. In alcuni casi, è necessario utilizzare le formule di Combinatorias. In questo caso, il più importante è il conteggio del numero di eventi che soddisfano determinate condizioni. A volte questo tipo di conteggio può diventare compiti indipendenti.
Quanti modi posso sedere 6 studenti su 6 posti gratuiti? Il primo studente prenderà uno dei 6 posti. Ciascuna di queste opzioni corrisponde a 5 modi per avvenire al secondo studente. Per il terzo studente ci sono 4 posti liberi, per il quarto - 3, per il quinto - 2, il sesto prenderà l'unico posto rimanente. Per trovare il numero di tutte le opzioni, è necessario trovare un prodotto che è indicato dal simbolo di 6! E leggere "sei fattoriali".
In generale, la risposta a questa domanda dà la formula per il numero di permutazioni dagli oggetti P nel nostro caso.
Considera ora un altro caso con i nostri studenti. Quanti modi posso sedere 2 studenti su 6 posti gratuiti? Il primo studente prenderà uno dei 6 posti. Ciascuna di queste opzioni corrisponde a 5 modi per avvenire al secondo studente. Per trovare il numero di tutte le opzioni, è necessario trovare un lavoro.
In generale, la risposta a questa domanda dà la formula per il numero di alloggi da n Elements di K Elements
Nel nostro caso .
E l'ultimo caso da questa serie. Quanti modi puoi scegliere tre studenti da 6? Il primo studente può essere scelto 6 nei secondi metodi - 5 nei terzi metodi - quattro. Ma tra queste opzioni, uno e lo stesso superiore degli studenti si trovano 6 volte. Per trovare il numero di tutte le opzioni, è necessario calcolare il valore :. In generale, la risposta a questa domanda fornisce la formula per il numero di combinazioni da elementi per elementi:
Nel nostro caso .
Esempi di risolvere i problemi dalla parola matematica alla definizione di probabilità
Compito 1. Dalla collezione ed. Yashchenko.
Su un piatto di 30 torte: 3 con carne, 18 con cavolo e 9 con ciliegia. Sasha a caso sceglie un patè. Trova la probabilità che sarà con la ciliegia.
![]() .
.
Risposta: 0.3.
Compito 2. Dalla collezione ed. Yashchenko.
In ogni lotto di 1000 lampadine in media 20 difettosi. Trova la probabilità che a caso la lampadina dalla festa sarà buona.
Soluzione: numero di buone luci 1000-20 \u003d 980. Quindi la probabilità che la lampadina portato dalla festa sarà buona:
![]()
Risposta: 0.98.
La probabilità che sotto test in studente di matematica u è, più di 9 compiti risolveranno più di 9 compiti, pari a 0,67. La probabilità che tu. Risolverà correttamente più di 8 compiti, pari a 0,73. Trova la probabilità che tu. Risolverà correttamente 9 compiti.
Se immaginiamo un numero numerico e nota punti 8 e 9, vedremo che la condizione "W. Sarà risolto correttamente esattamente 9 compiti "nella condizione" W. È corretto risolvere più di 8 compiti ", ma non si applica alla condizione" W. Sicuramente risolverà più di 9 compiti. "
Tuttavia, la condizione "U. Risolverà sicuramente più di 9 compiti "è contenuto nel" U. Sicuramente risolverà più di 8 compiti. " Quindi, se indichiamo gli eventi: "W. È corretto risolvere esattamente 9 compiti "- attraverso A" W. Risolverà correttamente più di 8 compiti "- attraverso B," W. Sicuramente risolverà più di 9 compiti "attraverso C. La soluzione sarà simile a questa:
Risposta: 0,06.
Nell'esame geometry, lo scolaro risponde a una domanda dall'elenco dei problemi di esame. La probabilità che questa sia una domanda sull'argomento "trigonometria" è 0,2. La probabilità che questa domanda sull'argomento "angoli esterni" sia 0,15. Domande che si riferiscono simultaneamente a questi due argomenti, n. Trova la probabilità che l'esame dello studente avrà una domanda su uno di questi due argomenti.
Pensiamo a ciò che vengono dati i nostri eventi. Abbiamo dato due eventi incompleti. Cioè, la domanda si riferirà all'argomento "trigonometria" o all'argomento "angoli esterni". Con il teorema della probabilità, la probabilità di eventi incompleti è pari alla somma delle probabilità di ciascun evento, dobbiamo trovare la somma delle probabilità di questi eventi, cioè:
Risposta: 0,35.
La stanza è illuminata con una lanterna con tre lampade. La probabilità di rottura della lampada durante l'anno è 0,29. Trova la probabilità che durante l'anno almeno una lampada fallirà.
Considera possibili eventi. Abbiamo tre lampadine, ognuna delle quali può superare o scaricare indipendentemente da qualsiasi altra lampadina. Questi sono eventi indipendenti.
Quindi specifichiamo le opzioni per tali eventi. Accettiamo la designazione: - La luce brucia, la lampadina bruciata. E immediatamente, calcoliamo la probabilità di un evento. Ad esempio, la probabilità di un evento in cui ci sono tre eventi indipendenti "Lampadina bruciata", "Burn Burns Burns", "Burn Burbs Burns": dove la probabilità della "Light Light Bulb" è calcolata come probabilità di un Evento opposto alla "lampadina" dell'evento, vale a dire :.
Si noti che abbiamo eventi incompleti favorevoli di soli 7. La probabilità di tali eventi è pari alla somma delle probabilità di ciascuno degli eventi :.
Risposta: 0,975608.
Puoi cercare un altro compito nella foto qui sotto:

Pertanto, comprendiamo che la teoria della probabilità di formule ed esempi di risoluzione dei problemi che è possibile soddisfare nella versione EGE può essere soddisfatta.
Cos'è la probabilità?
Di fronte a questo termine per la prima volta, non capirei cosa sia. Pertanto, proverò a spiegare disponibili.
La probabilità è la possibilità che l'evento di cui hai bisogno accada.
Ad esempio, hai deciso di andare ad un amico, ricorda l'ingresso e persino il pavimento su cui vive. Ma la stanza e la posizione dell'appartamento dimenticato. E stai in piedi sulla scala, e di fronte a te porte da scegliere.
Qual è la possibilità (probabilità) di cosa succede se chiami la prima porta, aprirai il tuo amico? Gli appartamenti totali e l'amico vivono solo per uno di loro. Con una pari caso, possiamo scegliere qualsiasi porta.
Ma cos'è questa occasione?
Porte, la porta che vuoi. La probabilità di indovinare chiamando la prima porta :. Cioè, una volta dalle tre sei con precisione.
Vogliamo scoprire i tempi chiamando, quanto spesso indovremo la porta? Consideriamo tutte le opzioni:
- Hai chiamato B. 1y. una porta
- Hai chiamato B. 2Y. una porta
- Hai chiamato B. 3Y. una porta
Ora considera tutte le opzioni in cui un amico può essere:
ma. Per 1I. Porta
b. Per 2Y. Porta
nel. Per 3I. Porta
Confrontiamo tutte le opzioni sotto forma di un tavolo. Il segno di spunta indica le opzioni quando la tua scelta coincide con la posizione di un amico, la croce - quando non corrisponde.
Come puoi vedere tutto possibilmente Opzioni La posizione di un amico e la tua scelta, quale porta chiamare.
MA risultati favorevoli Totale. . Cioè, dal momento che indovini, chiamando la porta una volta, cioè. .
Questa è probabilità - il rapporto tra un risultato favorevole (quando la tua scelta ha coinciso con la posizione di un amico) al numero di eventi possibili.
La definizione è una formula. La probabilità è fatta per denotare P, quindi:
Questa formula non è molto comoda, quindi accetteremo il numero di esiti favorevoli e per è il numero totale di risultati.
La probabilità può essere registrata come percentuale, per questo è necessario moltiplicare il risultato risultante su:
Probabilmente, la parola "esito" si precipitò a te. Dal momento che la matematica chiamano varie azioni (abbiamo una tale azione - questo è un esperimento di chiamata), quindi il risultato di tali esperimenti è consuetudine essere definiti un risultato.
Bene, i risultati sono favorevoli e sfavorevoli.
Torniamo al nostro esempio. Supponi di aver chiamato una delle porte, ma un uomo sconosciuto ci ha aperto. Non abbiamo indovinato. Qual è la probabilità che se chiami una delle porte rimanenti, apriremo il nostro amico?
Se pensavi che questo sia un errore. Affrontiamo.
Abbiamo due porte rimaste. Quindi, abbiamo passi possibili:
1) Chiama 1-uu. una porta
2) Chiama in 2-uu. una porta
Amico, con tutto questo, è accuratamente dietro uno di loro (perché per quello in cui abbiamo chiamato, non lo era):
a) amico per 1 ° Porta
b) ciascuno 2-o. Porta
Disegniamo di nuovo un tavolo:

Come puoi vedere, ci sono opzioni, di cui sono favorevoli. Cioè, la probabilità è uguale.
Perchè no?
La situazione che abbiamo considerato - un esempio di eventi dipendenti. Il primo evento è la prima chiamata sulla porta, il secondo evento è il secondo campanello.
E dipendente sono chiamati perché influenzano le seguenti azioni. Dopotutto, se dopo la prima chiamata, abbiamo aperto un amico nella porta, allora quale sarebbe la probabilità che sia in uno degli altri due? Giusto, .
Ma se ci sono eventi dipendenti, allora ci deve essere indipendente? Vero, ci sono.
L'esempio del libro di testo è il lancio della moneta.
- Getta un tempo di moneta. Qual è la probabilità che l'aquila cada, per esempio? Esatto, perché le opzioni di tutti (o l'aquila, o la corsa, trascineremo la probabilità della moneta sul bordo), ma ci organizzerà solo.
- Ma la corsa è caduta. Ok, togli di nuovo. Qual è la probabilità di cadere aquila? Nulla è cambiato, tutto è lo stesso. Quante opzioni? Due. E quanti ci si adattano? Uno.
E lascia che mille volte di fila cadranno una fretta. Anche la probabilità di un Aquila Fallout sarà tutto. Le opzioni sono sempre e favorevoli -.
Distinguere facilmente gli eventi dipendenti da indipendenti:
- Se l'esperimento viene eseguito una volta (una volta lanciate una moneta, 1 volta chiamata sulla porta, ecc.), Allora gli eventi sono sempre indipendenti.
- Se l'esperimento viene effettuato più volte (la moneta viene lanciata una volta, la porta è chiamata più volte), il primo evento è sempre indipendente. E poi, se il numero di favorevole o il numero di tutti i risultati sta cambiando, gli eventi dipendono e se non, indipendenti.
Prendiamo un po 'morso per determinare la probabilità.
Esempio 1.
La moneta viene lanciata due volte. Qual è la probabilità che l'aquila cada due volte di fila?
Decisione:
Considera tutte le opzioni possibili:
- Eagle-Orel.
- Eagle-Rush.
- Rush-Orel.
- Rusk-Ruska.
Come puoi vedere l'intera opzione. Di questi, siamo soddisfatti solo. Questa è probabilità:
Se viene richiesta la condizione di trovare semplicemente la probabilità, la risposta deve essere data sotto forma di una frazione decimale. Se fosse indicato che la risposta dovrebbe essere data in percentuale, quindi ci moltiplicheremmo.
Risposta:
ESEMPIO 2.
In una scatola di caramelle, tutte le caramelle sono imballate nello stesso involucro. Tuttavia, da caramelle - con dadi, con brandy, con ciliegia, con caramello e con nosudoy.
Qual è la probabilità, prendendo una caramella, prendi caramelle con noci. Risposta da percentuale.
Decisione:
Quanti possibili esiti? .
Cioè, prendendo una caramella, sarà una delle caselle esistenti.
E quanti risultati favorevoli?
Perché nella scatola solo caramelle con noci.
Risposta:
ESEMPIO 3.
In una scatola di palle. Bianco di loro, - nero.
- Qual è la probabilità di tirare la palla bianca?
- Abbiamo aggiunto palle nere alla scatola. Qual è la probabilità di tirare la palla bianca ora?
Decisione:
a) nella confezione di tutte le palle. Bianco di loro.
La probabilità è:
b) Ora le palle nella scatola sono diventate. E il bianco è rimasto tanto -.
Risposta:
Piena probabilità
| La probabilità di tutti gli eventi possibili è uguale a (). |
Supponiamo nel cassetto di palle rosse e verdi. Qual è la probabilità di tirare una palla rossa? Palla verde? Palla rossa o verde?
Probabilità Tirare fuori una palla rossa
Palla verde:
Palla rossa o verde:
Come puoi vedere, la somma di tutti gli eventi possibili è uguale a (). Capire questo momento ti aiuterà a risolvere molti compiti.
ESEMPIO 4.
Nella casella giace indicatori: verde, rosso, blu, giallo, nero.
Qual è la probabilità di tirare non una penna in feltro rossa?
Decisione:
Consideriamo il numero risultati favorevoli.
Non una penna in feltro rossa, significa verde, blu, giallo o nero.
| La probabilità che l'evento non si verificherà è uguale a meno la probabilità che l'evento avverrà. |
La regola di moltiplicare le probabilità di eventi indipendenti
Quali sono gli eventi indipendenti che già conosci.
E se hai bisogno di trovare la probabilità che due (o più) eventi indipendenti si verifichino in fila?
Supponiamo che vogliamo sapere quale probabilità che lanciasse il tempo della moneta, vedremo l'Aquila due volte?
Abbiamo già pensato.
E se lanci un tempo di moneta? Qual è la probabilità di vedere l'aquila di fila?
Opzioni totali:
- Aquila
- Aquila
- Aquila
- Aquila
- Aquila
- Rustica
- Eagle Rush.
- Rusk-Rush.
Non so come sei, ma mi sono sbagliato, inventando questa lista. Wow! E solo l'opzione (prima) ci si adatta.
Per 5 tiri, puoi effettuare un elenco di possibili risultati da solo. Ma la matematica non è così laboriosa come te.
Pertanto, hanno notato per la prima volta, e ha dimostrato che la probabilità di una certa sequenza di eventi indipendenti viene ridotta ogni volta sulla probabilità di un evento.
In altre parole,
Considera l'esempio di tutti gli stessi, malfatti, monete.
La probabilità di un'aquila nel test? . Ora buttiamo un tempo di moneta.
Qual è la probabilità di un'aquila consecutiva?
Questa regola funziona non solo se ci viene chiesto di trovare la probabilità che lo stesso evento avverrà più volte di seguito.
Se volessimo trovare la sequenza del fiume-Aquila, quando teschio di fila, faremmo anche.
La probabilità di cadere Rush -, aquila -.
La probabilità di cadere la sequenza del fiume-Eagle-River-River:
Puoi controllarti, raggiungendo il tavolo.
La regola di aggiunta di probabilità di eventi incompleti.
Quindi fermati! Nuova definizione.
Affrontiamo. Prendi la nostra moneta usurata e lancia it tempi.
Possibili opzioni:
- Aquila
- Aquila
- Aquila
- Aquila
- Aquila
- Rustica
- Eagle Rush.
- Rusk-Rush.
Quindi eventi incompleti, questa è una determinata sequenza di eventi specificata. - Questi sono eventi incompleti.
Se vogliamo determinare quale probabilità di due (o più) eventi incompleti, pieghiamo la probabilità di questi eventi.
È necessario capire che il fallout di un'aquila o di un'aquilone è due eventi indipendenti.
Se vogliamo determinare quale è la probabilità di sequenza) (o qualsiasi altro), quindi usiamo la regola della moltiplicazione delle probabilità.
Qual è la probabilità di cadere al primo tiro di un'aquila, e durante la seconda e la terza corsa?
Ma se vogliamo sapere qual è la probabilità di cadere una delle diverse sequenze, ad esempio quando l'aquila cade esattamente volte, cioè. Opzioni e, dobbiamo piegare le probabilità di queste sequenze.
Opzioni totali, si adatta a noi.
Possiamo ottenere lo stesso creando la probabilità dell'aspetto di ogni sequenza:
Pertanto, pieghiamo la probabilità quando vogliamo determinare la probabilità di alcuni, incompleti, sequenze di eventi.
C'è una regola eccellente che non aiuta a confondarsi quando si è moltiplicato, e quando piegare:
Ritorniamo ad esempio quando abbiamo gettato il tempo della moneta e vogliamo scoprire la probabilità di vedere i tempi d'aquila.
Cosa succederà?
Deve cadere:
(Aquila e fretta e affrettatura) o (fretta e aquila e fretta) o (fretta e fretta e aquila).
Quindi si scopre:
Diamo un'occhiata a pochi esempi.
ESEMPIO 5.
Nella scatola giace con le matite. Rosso, verde, arancione e giallo e nero. Qual è la probabilità di tirare le matite rosse o verdi?
Decisione:
ESEMPIO 6.
L'osso da gioco viene lanciato due volte, qual è la probabilità che 8 punti rientrano nell'importo?
Decisione.
Come possiamo ottenere occhiali?
(s) o (e) o (e) o (e) o (e) o (e) o (e).
La probabilità di cadere un (qualsiasi) faccia.
Consideriamo la probabilità:
Allenarsi.
Penso che ora è diventato chiaro a te quando è necessario considerare le probabilità quando li aggiungi e quando si moltiplicano. Non è vero? Pratichiamo un po '.
Compiti:
Prendi un mazzo di carte in quali carte, picco, worm, 13 Treph e 13 Tambourines. Dall'asso di ogni abito.
- Qual è la probabilità di tirare in fila Trephs in fila (la prima carta punteggiata che ritorniamo al ponte e mescolando)?
- Qual è la probabilità di tirare fuori una mappa nera (picchi o trephies)?
- Qual è la probabilità di tirare fuori una foto (Warta, Lady, King o ACE)?
- Qual è la probabilità di tirare due immagini di fila (rimuoviamo la prima carta punteggiata dal mazzo)?
- Qual è la probabilità, prendendo due carte, raccogli una combinazione - (valuta, signora o re) e Asso della sequenza in cui verranno estratte le carte, non importa.
Risposte:
Se riesci a risolvere tutti i compiti da solo, allora ne sei un grande! Ora le sfide sulla teoria della probabilità nell'esame, cliccherai come dadi!
Teoria della probabilità. LIVELLO MEDIO
Considera un esempio. Supponiamo di lanciare un osso da gioco. Che tipo di osso è questo, lo sai? Questo è chiamato cubo con numeri sui bordi. Quanti volti, tanti numeri: da quanto? Prima.
Quindi, buttiamo l'osso e vogliamo cadere o. E cade.
Nella teoria della probabilità, dicono cosa è successo evento favorevole (Non confondere con prospero).
Se è caduto, l'evento sarebbe anche favorevole. Totale Ci possono essere solo due eventi favorevoli.
E quanto sfavorevole? Dal momento che i possibili eventi, significa che gli eventi sfavorevoli sono (questo è se cade o).
Definizione:
La probabilità è chiamata il rapporto tra il numero di eventi favorevoli al numero di tutti gli eventi possibili.. Cioè, la probabilità mostra quale proporzione di tutti gli eventi possibili cade a favore.
Dentare la probabilità di una lettera latina (apparentemente, dalla probabilità della parola inglese è probabilità).
È consuetudine misurare la probabilità in percentuale (vedere l'argomento,). Per questo, il valore di probabilità deve essere moltiplicato per. In un esempio con un osso che gioca, la probabilità.
E in percentuale:.
Esempi (risolvere te stesso):
- Qual è la probabilità quando lanci una moneta cade l'aquila? E quanto probabilmente la corsa cadrà?
- Qual è la probabilità quando si getta un osso che gioca cadrà un numero pari? E con ciò che è strano?
- Nella confezione di matite ordinarie, blu e rosse. A casuale Tyant una matita. Qual è la probabilità di tirare semplice?
Soluzioni:
- Quante opzioni? Eagle e Rush - solo due. E quanti di loro sono favorevoli? Solo una - aquila. Quindi probabilità
Con un cappello, lo stesso :.
- Opzioni totali: (quanti lati del cubo, tante opzioni diverse). Favorabile di loro: (questi sono tutti anche numeri :).
Probabilità. Con strano, naturalmente, lo stesso. - Totale: . Favorevole:. Probabilità:.
Piena probabilità
Tutte le matite nella scatola verde. Qual è la probabilità di tirare una matita rossa? Non c'è possibilità: la probabilità (dopotutto, eventi favorevoli -).
Un tale evento è chiamato impossibile.
E qual è la probabilità di tirare fuori una matita verde? Gli eventi favorevoli sono esattamente gli stessi degli eventi di tutto (tutti gli eventi sono favorevoli). Significa che la probabilità è uguale a o.
Tale evento è chiamato affidabile.
Se nella confezione di matite verdi e rosse, qual è la probabilità di tirare verde o rosso? Ancora una volta. Nota una cosa del genere: la probabilità di tirare il verde è uguale e rosso -.
In sintesi, queste probabilità sono uguali a esattamente. I.e, la somma delle probabilità di tutti gli eventi possibili è uguale a o.
Esempio:
In una scatola di matita, tra cui blu, rosso, verde, semplice, giallo e il resto è arancione. Qual è la probabilità di non tirare verde?
Decisione:
Ricorda che tutte le probabilità sono fornite nella quantità. E la probabilità di tirare il verde è uguale. Significa che la probabilità non tira fuori il verde uguale.
Ricorda questa tecnica:la probabilità che l'evento non si verificherà uguale a meno la probabilità che l'evento avverrà.
Eventi indipendenti e regola di moltiplicazione
Getti un tempo di moneta e vuoi entrambe le volte l'aquila cadde. Qual è la probabilità di questo?
Facciamo tutte le opzioni possibili e determiniamo quanti di essi:
Eagle-Eagle, River-Eagle, Eagle-River, Rushka-River. Cos'altro?
Opzione totale. Solo una cosa è adatta per noi: Aquila Orel. La probabilità totale è uguale.
Va bene. E ora buttiamo un tempo di moneta. Calmati. È accaduto? (risposta).
Potevi vedere che con l'aggiunta di ogni prossimo lancio, la probabilità è ridotta. La regola generale è chiamata regola di moltiplicazione:
Le probabilità di eventi indipendenti sono variabili.
Quali sono gli eventi indipendenti? Tutto è logico: questi sono quelli che non dipendono l'uno dall'altro. Ad esempio, quando buttiamo una moneta diverse volte, viene prodotto un nuovo tiro, il cui risultato non dipende da tutti i precedenti lanci. Con lo stesso successo, possiamo lanciare due monete diverse allo stesso tempo.
Altri esempi:
- L'osso che gioca viene lanciato due volte. Qual è la probabilità che entrambe le volte cade?
- La moneta viene lanciata i tempi. Qual è la probabilità che l'aquila cada per la prima volta, e poi il doppio della corsa?
- Il giocatore getta due ossa. Qual è la probabilità che la quantità di numeri su di loro sarà uguale?
Risposte:
- Gli eventi sono indipendenti, significa che la regola di moltiplicazione funziona :.
- La probabilità dell'Aquila è uguale. Anche la probabilità di Rush è. Alternato:
- 12 può funzionare solo se cadono due modi :.
Eventi incompleti e regola di aggiunta
L'invito è chiamata eventi che si completano a vicenda fino a una completa probabilità. È chiaro dal nome che non possono accadere contemporaneamente. Ad esempio, se lanci una moneta, potrebbe cadere un aquila o una fretta.
Esempio.
In una scatola di matita, tra cui blu, rosso, verde, semplice, giallo e il resto è arancione. Qual è la probabilità di tirare verde o rosso?
Decisione.
La probabilità di tirare la matita verde è uguale. Rosso -.
Eventi favorevoli in totale: verde + rosso. Significa che la probabilità che tira fuori il verde o il rosso è uguale.
La stessa probabilità può essere rappresentata in questo modulo :.
Questa è la regola di aggiunta:le probabilità di eventi incompleti sono piegati.
Attività di tipo misto
Esempio.
La moneta viene lanciata due volte. Qual è la probabilità che il risultato dei tiri sarà diverso?
Decisione.
Resta inteso che se la prima aquila è caduta, il secondo dovrebbe essere una corsa, e viceversa. Si scopre che ci sono due paia di eventi indipendenti, e queste coppie sono incomprensibili tra loro. Non importa come essere confuso da dove si moltiplica, ma dove piegare.
C'è una semplice regola per tali situazioni. Prova a descrivere cosa dovrebbe accadere collegando gli eventi dei sindacati "e" o "o". Ad esempio, in questo caso:
Deve cadere (Aquila e Rush) o (Rushka e Aquila).
Dove c'è un'alleanza "e", ci sarà moltiplicazione e dove "o" - aggiunta:
Provate voi stessi:
- Qual è la probabilità con due monete da lancio entrambe le volte la stessa parte cade?
- L'osso che gioca viene lanciato due volte. Qual è la probabilità che i punti cadono?
Soluzioni:
Un altro esempio:
Getta un tempo di moneta. Qual è la probabilità che l'aquila cada almeno una volta?
Decisione:
Teoria della probabilità. Brevemente sulla cosa principale
La probabilità è il rapporto tra il numero di eventi favorevoli al numero di tutti gli eventi possibili.
Eventi indipendenti
Due eventi sono indipendenti se al verificarsi di una probabilità dell'inizio dell'altro non cambiano.
Piena probabilità
La probabilità di tutti gli eventi possibili è uguale a ().
La probabilità che l'evento non si verificherà è uguale a meno la probabilità che l'evento avverrà.
La regola di moltiplicare le probabilità di eventi indipendenti
La probabilità di una certa sequenza di eventi indipendenti è uguale al prodotto delle probabilità di ciascun evento.
Eventi non validi
Gli incompleti sono gli eventi che non possono accadere contemporaneamente come risultato dell'esperimento. Un numero di eventi incompleti formano un gruppo completo di eventi.
Le probabilità di eventi incompleti sono piegati.
Descrivendo cosa dovrebbe accadere utilizzando alleanze "e" o "o", invece di "e" mettere il segno di moltiplicazione, e invece di "o" - aggiunta.
Bene, l'argomento è finito. Se leggi queste righe, allora sei molto bello.
Perché solo il 5% delle persone è in grado di padroneggiare qualcosa da solo. E se leggi fino alla fine, allora sei entrato in questi 5%!
Ora la cosa più importante.
Hai capito la teoria su questo argomento. E, ripeto, è ... è solo super! Sei migliore della maggioranza assoluta dei tuoi pari.
Il problema è che questo potrebbe non essere abbastanza ...
Per quello?
Per il successo del passaggio dell'uso, per l'ammissione all'istituto sul bilancio e, soprattutto, per la vita.
Non ti convincerò qualsiasi cosa, dirò solo una cosa ...
Le persone che hanno ricevuto una buona educazione guadagnano molto più di quelle che non lo hanno ricevuto. Queste sono statistiche.
Ma non è la cosa principale.
La cosa principale è che sono più felici (ci sono tali ricerche). Forse perché ci sono molte più opportunità a favore di loro e la vita diventa più luminosa? Non lo so...
Ma, penso a me stesso ...
Quello che devi essere sicuro di essere migliore di altri sull'esame e in definitiva ... Happily?
Compila una mano risolvendo le attività su questo argomento.
Non chiederai alla teoria sull'esame.
Avrai bisogno risolvi compiti per un po '.
E se non li hai risolti (molto!), Sicuramente sei un follemente sbagliato o semplicemente non hai tempo.
È come nello sport - devi ripetere molte volte per vincere di sicuro.
Trova dove vuoi una collezione, obbligatorio con soluzioni, analisi dettagliate E decidere, decidere, decidere!
Puoi usare i nostri compiti (non necessariamente) e, naturalmente, lo consigliamo.
Per riempire la mano con l'aiuto dei nostri compiti, è necessario aiutare a estendere la vita a teccever del libro di testo, che stai leggendo ora.
Come? Ci sono due opzioni:
- Aprire l'accesso a tutti i compiti nascosti in questo articolo - 299 strofina.
- Aprire l'accesso a tutti i compiti nascosti in tutti i 99 articoli del libro di testo - 499 strofina.
Sì, abbiamo 99 articoli del nostro libro di testo e accesso per tutte le attività e tutti i testi nascosti possono essere aperti immediatamente.
L'accesso a tutti i compiti nascosti è fornito per l'intera esistenza del sito.
In conclusione...
Se i nostri compiti non amano, trova gli altri. Basta non fermarsi sulla teoria.
"Capisco" e "Posso decidere" è abilità completamente diverse. Hai bisogno di entrambi.
Trova il compito e decidi!
Formule per il calcolo della probabilità di eventi
1.3.1. Sequenza di prova indipendente (schema Bernoulli)
Supponiamo che alcuni esperimenti possano essere eseguiti ripetutamente con le stesse condizioni. Lascia che questa esperienza venga prodotta n. Una volta, cioè, una sequenza è effettuata da n. Test.
Definizione. Sequenza n. test chiamati reciprocamente indipendente Se qualsiasi evento associato a questo test non dipende da eventi relativi ad altri test.
Supponi qualche evento UN. può verificarsi con probabilità p. Come risultato di un test o non accadere con probabilità q.= 1- p..
Definizione . La sequenza è n.test moduli schema Bernoulli se vengono eseguite le seguenti condizioni:
sequenza n. I test sono reciprocamente indipendenti
2) La probabilità di un evento UN. Non varia da verificare il test e non dipende dal risultato in altri test.
Evento UN. Chiamano il "successo" del test e l'evento opposto è "fallimento". Considera un evento
 \u003d (B. n. I test si sono verificati Rivne. m. "Successo").
\u003d (B. n. I test si sono verificati Rivne. m. "Successo").
Per calcolare la probabilità di questo evento, Bernoulli Formula è valida
p.( )
=
)
=
 , m.
= 1, 2, …, n.
, (1.6)
, m.
= 1, 2, …, n.
, (1.6)
dove  - il numero di combinazioni da n. ELEMENTI IN. m.
:
- il numero di combinazioni da n. ELEMENTI IN. m.
:
 =
=
 =
= .
.
Esempio 1.16. Cubi tirano tre volte. Trovare:
a) la probabilità che 6 punti cadranno due volte;
b) la probabilità che il numero di sei non appaia più di due volte.
Decisione . I test "Successo" saranno considerati per cadere sul cubo del viso con l'immagine di 6 punti.
a) il numero totale di test - n.\u003d 3, il numero di "successo" - m.
\u003d 2. La probabilità di "successo" - p.= ,
E la probabilità di "fallimento" - q.\u003d 1 - \u003d. Quindi, secondo la formula di Bernoulli, la probabilità che il risultato di un casting tre volte di un cubo due volte il lato di sei punti cadrà, sarà uguale a
,
E la probabilità di "fallimento" - q.\u003d 1 - \u003d. Quindi, secondo la formula di Bernoulli, la probabilità che il risultato di un casting tre volte di un cubo due volte il lato di sei punti cadrà, sarà uguale a
 .
.
b) Dentare da MA L'evento che risiede nel fatto che il volto con il numero di punti 6 non apparirà più di due volte. Quindi l'evento può essere rappresentato come la somma di tre incongruenze eventi A \u003d.
 ,
,
dove NEL 3 0 - Un evento quando la linea di interesse non appare mai,
NEL 3 1 - Evento quando il volto di interesse apparirà una volta,
NEL 3 2 - Evento quando il volto di interesse apparirà due volte.
Secondo Bernoulli Formula (1.6) che troviamo
p.(MA)
\u003d P ( )
=
p.(
)
=
p.( )=
)=
 +
+ +
+ =
=
=
 .
.
1.3.2. Probabilità condizionale di un evento
La probabilità condizionale riflette l'impatto di un evento sulla probabilità di un altro. Modifica delle condizioni in cui viene effettuato l'esperimento anche colpisce
la probabilità dell'aspetto di un evento interessante.
Definizione. Lascia che sia. UN. e B. - alcuni eventi e probabilità p.(B.)> 0.
Probabilità condizionale eventi UN. a condizione che "evento B. giàÈ successo "chiamato il rapporto tra la probabilità di un prodotto di questi eventi alla probabilità di un evento che è accaduto prima dell'evento la cui probabilità deve essere trovata. La probabilità condizionale è indicata come p.(UN. B.). Poi per definizione.
p.
(UN.
B.)
=
 .
(1.7)
.
(1.7)
Esempio 1.17. Due cubi si vomitano. Lo spazio degli eventi elementari è composto da coppie di numeri ordinati
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6).
ESEMPIO 1.16 È stato trovato che l'evento UN. \u003d (numero di occhiali sul primo cubo\u003e 4) ed evento C. \u003d (La quantità di punti è 8) dipendente. Tra la relazione
 .
.
Questa relazione può essere interpretata come segue. Supponiamo che il risultato del primo lancio sia noto che il numero di punti sul primo cubo\u003e 4. Ne consegue che il casting del secondo cubo può portare a uno dei 12 risultati che costituiscono l'evento UN.:
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6) .
Allo stesso tempo un evento C. Solo due di loro possono corrispondere a (5.3) (6.2). In questo caso, la probabilità di un evento C.
sarà uguale  . Quindi, informazioni sulla presenza di un evento UN. influenzato la probabilità di un evento C..
. Quindi, informazioni sulla presenza di un evento UN. influenzato la probabilità di un evento C..
La probabilità del lavoro degli eventi
Teorema di moltiplicazione
La probabilità del lavoro degli eventiUN. 1 UN. 2 UN. n. La formula è determinata
p.(UN. 1 UN. 2 UN. n.) \u003d P.(UN. 1) P.(UN. 2 UN. 1)) p.(UN. n. UN. 1 UN. 2 UN. n- 1). (1.8)
Per il lavoro di due eventi, ne consegue questo
p.(Ab.) \u003d P.(UN. B) P.{B.) \u003d P.(B. UN.) P.{UN.). (1.9)
Esempio 1.18. In un lotto di 25 prodotti 5 prodotti difettosi. Due prodotti sono selezionati successivamente. Determina la probabilità che tutti i prodotti selezionati siano difettosi.
Decisione. Dennare gli eventi:
UN. 1 \u003d (primo prodotto difettoso),
UN. 2 \u003d (il secondo prodotto è difettoso),
UN. 3 \u003d (terzo prodotto difettoso),
UN. \u003d (Tutti i prodotti sono difettosi).
Evento MA c'è un lavoro di tre eventi UN. = UN. 1 UN. 2 UN. 3 .
Dal teorema di moltiplicazione (1.6) ricevere
p.(UN.) \u003d P ( UN. 1 UN. 2 UN. 3 ) = p.(UN. 1) p.(UN. 2 UN. 1))p.(UN. 3 UN. 1 UN. 2).
La definizione classica probabilità consente di trovare p.(UN. 1) è il rapporto tra il numero di prodotti difettosi al numero totale di prodotti:
p.(UN. 1)=
 ;
;
p.(UN. 2) – questo è il rapporto tra il numero di prodotti difettosi rimanenti dopo il sequestro di uno, al numero totale dei prodotti rimanenti:
p.(UN. 2
UN. 1))=
 ;
;
p.(UN. 3) IS. il rapporto tra il numero di prodotti difettosi rimanenti dopo il sequestro di due difetti, al numero totale dei prodotti rimanenti:
p.(UN. 3
UN. 1 UN. 2)= .
.
Quindi la probabilità di un evento UN. sarà uguale
p.(UN.)
=

 =
= .
.
Molti, incontrati con il concetto di "teoria della probabilità", sono spaventati, pensando che questo sia qualcosa di insopportabile, molto complicato. Ma tutto non è davvero così tragico. Oggi considereremo il concetto di base di imparare a risolvere i problemi su specifici esempi.
La scienza
Cosa studia una tale sezione di matematica come "teoria della probabilità"? Nota modelli e valori. Per la prima volta questa domanda, gli scienziati erano interessati al diciottesimo secolo, quando è stato studiato il gioco d'azzardo. Il concetto di base della teoria della probabilità è un evento. Questo è tutto ciò che è indicato dall'esperienza o dall'osservazione. Ma qual è l'esperienza? Un altro concetto di base della teoria della probabilità. Significa che questa composizione delle circostanze non è creata per caso, ma con un certo obiettivo. Per quanto riguarda l'osservazione, qui il ricercatore stesso non partecipa all'esperienza, ma semplicemente testimonianza di eventi di dati, non influisce su ciò che sta accadendo.
Eventi
Abbiamo saputo che il concetto di base della teoria della probabilità è un evento, ma non considerato la classificazione. Tutti sono divisi nelle seguenti categorie:
- Affidabile.
- Impossibile.
- Casuale.
Indipendentemente da quali eventi che sono osservati o creati durante l'esperienza, tutti sono soggetti a questa classificazione. Offriamo ogni tipo di specie per familiarizzare separatamente.
Evento affidabile

Questa è la circostanza a cui è necessario il set di eventi necessari. Per migliorare l'essenza, è meglio portare alcuni esempi. La fisica e la chimica e l'economia e la matematica superiore sono soggette a questa legge. La teoria della probabilità include un concetto così importante come un evento affidabile. Diamo esempi:
- Lavoriamo e otteniamo una remunerazione sotto forma di salari.
- Passò bene agli esami, si è tenuta la competizione, riceviamo una ricompensa per questo sotto forma di ammissione a un'istituzione educativa.
- Abbiamo investito denaro in banca, se necessario, li richiamiamo.
Tali eventi sono affidabili. Se abbiamo soddisfatto tutte le condizioni necessarie, allora otterremo sicuramente il risultato atteso.
Eventi impossibili
Ora consideriamo gli elementi della teoria della probabilità. Proponiamo di andare alla spiegazione del prossimo tipo di evento, vale a dire è impossibile. Per cominciare, discuteremo la regola più importante - la probabilità dell'evento impossibile è zero.
Da questa formulazione, è impossibile ritirarsi durante la risoluzione dei problemi. Per spiegare, forniamo esempi di tali eventi:
- Acqua congelata a una temperatura più dieci (è impossibile).
- Nessuna elettricità non influisce sulla produzione (è anche impossibile, come nell'esempio precedente).
Non dovrebbero essere forniti più esempi, poiché i precedenti sopra descritti riflettono l'essenza di questa categoria. L'evento impossibile non accadrà mai in nessuna circostanza.
Eventi casuali

Studiare elementi della teoria della probabilità, è necessario prestare particolare attenzione a questo tipo di eventi. Sono loro che questo scienza studia. Come risultato dell'esperienza, qualcosa può accadere o meno. Inoltre, il test può essere effettuato un numero illimitato di volte. Gli esempi luminosi possono servire:
- Un cast di monete è un'esperienza, o prova, un'aquila che cade è un evento.
- Tirando una palla ciecamente - un test, una palla rossa catturata - questo è un evento e così via.
Tali esempi possono essere una quantità illimitata, ma, in generale, l'essenza deve essere chiara. Per riassumere e sistematizzare le conoscenze acquisite su eventi, viene data una tabella. La teoria della probabilità studia solo l'ultima visione di tutti presentati.
nome | definizione | |
Affidabile | Eventi che si verificano con una garanzia del 100% al rispetto di determinate condizioni. | Ammissione a un'istituzione educativa con una buona resa dell'esame di ammissione. |
Impossibile | Eventi che non accadranno mai in nessuna circostanza. | C'è neve a temperatura dell'aria più trenta gradi Celsius. |
Casuale | Un evento che può verificarsi o meno durante l'esperimento / test. | Intelligenza o manca quando lanci una palla da basket in un anello. |
Legislazione
La teoria della probabilità è una scienza che studia la capacità di cadere qualsiasi evento. Come gli altri, ha alcune regole. Esistono le seguenti leggi della teoria della probabilità:
- Convergenza delle sequenze di variabili casuali.
- La legge di grandi numeri.
Quando si calcola la possibilità di complessi, è possibile utilizzare un complesso di eventi semplici per ottenere il risultato più facile e rapido. Si noti che le leggi della teoria della probabilità sono facilmente dimostrate utilizzando alcuni teoremi. Offriamo di iniziare a conoscere la prima legge.
Convergenza di variabili casuali

Nota che le specie di convergenza sono in qualche modo:
- La sequenza di variabili casuali è desiderata dalla probabilità.
- Quasi impossibile.
- R convergenza quadrata media.
- Convergenza di distribuzione.
Quindi, con l'estate, è molto difficile da approfondire l'essenza. Diamo le definizioni che contribuiranno a capire questo argomento. Per iniziare con la prima vista. La sequenza è chiamata frequentemente come la probabilitàSe viene osservata la seguente condizione: n tende all'infinito, il numero a cui la sequenza è lo sforzo, più zero ed è approssimativo a uno.
Vai alla seguente forma Quasi probabilmente. Si dice che la sequenza converge quasi probabilmente A una variabile casuale per N, lo sforzo per l'infinito, e p, lo sforzo della grandezza approssimativa a uno.
Il tipo successivo è la convergenza è rustica. Quando si utilizza SK-Convergence, lo studio dei processi casuali di vettore è ridotto allo studio dei loro processi casuali di coordinate.
L'ultimo tipo è rimasto, capiamo brevemente e si muoverà direttamente per risolvere i compiti. La convergenza della distribuzione ha un altro nome - "debole", quindi spiegare perché. Convergenza debole - Questi sono la convergenza delle funzioni di distribuzione in tutti i punti della posizione della funzione di distribuzione limite.
Assicurati di soddisfare la promessa: la convergenza debole differisce da tutto il fatto che il valore casuale non è definito sullo spazio probabilistico. Questo è possibile perché la condizione è formata esclusivamente utilizzando le funzioni di distribuzione.
La legge di grandi numeri
Eccellenti assistenti nella prova di questa legge saranno i teoremi della teoria della probabilità, come ad esempio:
- Disuguaglianza di Chebyshev.
- Teorema di Chebyshev.
- Teorema di Chebyshev generalizzato.
- Il teorema di Markov.
Se consideriamo tutti questi teoremi, questo problema può ritardare diverse decine di fogli. Abbiamo anche il compito principale - questo è l'uso della teoria della probabilità in pratica. Ti offriamo adesso e lo facciamo. Ma prima di questo, considera gli assiomi della teoria della probabilità, saranno gli assistenti principali durante la risoluzione dei problemi.
Assiomi

Dal primo posto ci siamo già incontrati quando hanno parlato dell'evento impossibile. Ricordiamo: la probabilità dell'evento impossibile è zero. Esempio Abbiamo portato molto luminoso e memorabile: la neve cadde alla temperatura dell'aria di trenta gradi Celsius.
Il secondo suono come segue: un evento affidabile si verifica con una probabilità uguale a uno. Ora mostriamo come scriverlo con l'aiuto di un linguaggio matematico: P (c) \u003d 1.
Terzo: può verificarsi o meno evento casuale, ma la capacità di variava sempre da zero a uno. Più il valore più vicino a uno, le probabilità sono più; Se il valore si avvicina allo zero, la probabilità è molto piccola. Lo scriviamo in lingua matematica: 0<Р(С)<1.
Considera l'ultimo, quarto Axiom, che suona come questo: la probabilità della somma di due eventi è uguale alla somma della loro probabilità. Scriviamo il linguaggio matematico: P (A + C) \u003d P (A) + P (B).
Gli asoms della teoria della probabilità sono le regole più semplici che non saranno difficili da ricordare. Proviamo a risolvere alcuni compiti, facendo affidamento sulla conoscenza già ricevuta.
Biglietto della lotteria

Per cominciare, considera l'esempio più semplice - lotteria. Immagina di aver comprato un biglietto della lotteria per fortuna. Qual è la probabilità che vincerai almeno venti rubli? Alle migliaia di biglietti sono coinvolti in circolazione, uno dei quali ha un premio in cinquecento rubli, diecentocento rubli, cinquanta-venti rubli e un centinaio di rubli. I compiti sulla teoria della probabilità si basano sulla ricerca dell'opportunità di buona fortuna. Ora insieme analizzeremo la soluzione sopra i compiti presentati.
Se siamo la lettera e denota le vincite di cinquecento rubli, la probabilità di cadere sarà uguale a 0,001. Come abbiamo capito? Hai solo bisogno di condividere il numero di biglietti "Happy" per condividere il loro numero (in questo caso: 1/1000).
B è una vincita di cento rubli, la probabilità sarà uguale a 0,01. Ora abbiamo agito sullo stesso principio come nell'azione passata (10/1000)
C - Le vincite sono uguali a venti rubli. Troviamo la probabilità, equivale a 0,05.
Il resto dei biglietti non è interessato a noi, dal momento che il loro premio è inferiore a quello specificato nella condizione. Applicare il quarto assioma: la probabilità di vincere almeno venti rubli è P (A) + P (c) + P (c). La lettera P è indicata dalla probabilità dell'origine di questo evento, li abbiamo già trovati nelle azioni precedenti. Rimane solo per piegare i dati necessari, otteniamo 0,061 nella risposta. Questo è il numero e sarà una risposta alla questione dell'attività.
Mazzo di carte
I compiti sulla teoria della probabilità sono più complessi, ad esempio, prendere il seguente compito. Prima di te un mazzo da trentasei carte. Il tuo compito è quello di estrarre due mappe di fila senza agitare una pila, la prima e la seconda carta devono essere assi, la tuta non ha nulla.
Per cominciare, troviamo la probabilità che la prima carta sarà ACE, per questo quattro dividi per trentasei. Posticipato da parte. Dare la seconda carta, sarà Asso con la probabilità di tre trenta quinte. La probabilità del secondo evento dipende da quale mappa abbiamo tirato il primo, ci chiediamo, era asso o no. Ne consegue che l'evento dipende dall'evento A.
La prossima azione che troviamo la probabilità di implementazione simultanea, cioè con una piegatura A e B. Il loro lavoro è il seguente: la probabilità di un evento si moltiplicano sulla probabilità condizionale di un altro, che calcoliamo, supponendo che il primo evento sia successo , cioè, abbiamo tirato il primo all'Asso.
Per diventare tutto chiaro, diamo la designazione a tale elemento come eventi. È calcolato, supponendo che l'evento sia ciò che è successo. È calcolato come segue: P (V / A).
Continuiamo la soluzione del nostro problema: P (A * c) \u003d P (A) * P (IN / A) o P (A * C) \u003d P (C) * P (A / C). La probabilità è uguale (4/36) * ((3/35) / (4/36). Calcola, arrotondato ai centesimi. Abbiamo: 0.11 * (0,09 / 0,11) \u003d 0.11 * 0, 82 \u003d 0,09. La probabilità Che estendiamo due assi di fila sono nove centesimi. Il valore è molto piccolo, ne consegue che la probabilità dell'evento è estremamente piccola.
Numero dimenticato
Proponiamo di smontare diverse opzioni per i compiti che studiano la teoria della probabilità. Esempi di risolvere alcuni di essi che hai già visto in questo articolo, prova a risolvere il seguente compito: il ragazzo ha dimenticato l'ultima cifra del numero di telefono del suo amico, ma dal momento che la chiamata è stata molto importante, poi cominciò a reclutare tutto a sua volta . Dobbiamo calcolare la probabilità che non chiamerà non più di tre volte. Il problema del problema è il più semplice, se sono noti le regole, le leggi e gli assiomi della teoria della probabilità.
Prima di guardare una soluzione, prova a risolverti. Sappiamo che l'ultima cifra può essere da zero a nove, cioè, ci sono solo dieci valori. La probabilità di digitare il desiderato è 1/10.
Successivamente, dobbiamo considerare le opzioni per l'origine dell'evento, supponiamo che il ragazzo indovina e abbia immediatamente guadagnato il necessario, la probabilità di un tale evento è 1/10. La seconda opzione: la prima campana della ricevuta e il secondo al bersaglio. Calcola la probabilità di un tale evento: 9/10 moltiplicati di 1/9, di conseguenza otteniamo anche 1/10. La terza opzione: la prima e la seconda chiamata non erano all'indirizzo, solo dal terzo ragazzo è arrivato lì dove voleva. Calcola la probabilità di un tale evento: 9/10 moltiplicare su 8/9 e 1/8, otteniamo 1/10 di conseguenza. Altre opzioni sotto la condizione del compito non sono interessate a noi, siamo rimasti piegati dai risultati, di conseguenza abbiamo 3/10. Risposta: la probabilità che il ragazzo non chiamerà non più di tre volte equivale a 0,3.
Carte con numeri

Ci sono nove carte prima di te, ognuna delle quali è scritta il numero da uno a nove, i numeri non vengono ripetuti. Sono stati messi nella scatola e mescolavano accuratamente. Devi calcolare la probabilità che
- il numero pari cadrà;
- a due cifre.
Prima di passare alla soluzione, discuteremo che M è il numero di casi di successo e n è il numero totale di opzioni. Troviamo la probabilità che il numero sia anche. Non è difficile calcolare che anche quattro numeri, sarà il nostro m, tutto è possibile nove opzioni, cioè, m \u003d 9. Quindi la probabilità è 0,44 o 4/9.
Consideriamo il secondo caso: il numero di opzioni per Nove, e non ci possono avere esito positivo, cioè, M è zero. La probabilità che la carta allungata conterrà un numero a due cifre, lo stesso equivale allo zero.