Calcolatrice di forma quadrata limitata. Calcolatrice online Calcola l'integrale definito (area di un trapezio curvo)

18.10.2019

L'immagine e le caratteristiche di Olga Ilyinskaya basata sul romanzo Oblomov (Goncharov I

Caratteristiche di Maria Mironova da "La figlia del capitano" Pushkin A

Composizione "C'era un percorso diverso per Katerina": avrebbe potuto agire diversamente?

Questo articolo ti mostrerà come trovare l'area di una forma delimitata da linee usando calcoli integrali. Per la prima volta ci imbattiamo nella formulazione di un tale problema al liceo, quando lo studio degli integrali definiti è appena terminato ed è tempo di iniziare un'interpretazione geometrica delle conoscenze acquisite nella pratica.

Quindi, cosa è necessario per risolvere con successo il problema di trovare l'area di una figura usando gli integrali:

Capacità di costruire disegni con competenza;
Capacità di risolvere un integrale definito utilizzando la nota formula di Newton-Leibniz;
La capacità di "vedere" una soluzione più vantaggiosa, ovvero per capire come in questo o quel caso sarà più conveniente effettuare l'integrazione? Lungo l'asse x (OX) o lungo l'asse y (OY)?
Bene, dove senza calcoli corretti?) Questo include capire come risolvere quell'altro tipo di integrali e correggere i calcoli numerici.

Algoritmo per risolvere il problema del calcolo dell'area di una figura delimitata da linee:

1. Costruiamo un disegno. Si consiglia di farlo su un pezzo di carta in una gabbia, su larga scala. Firmiamo il nome di questa funzione con una matita sopra ogni grafico. La firma dei grafici viene eseguita esclusivamente per comodità di ulteriori calcoli. Ricevuto il grafico della figura desiderata, nella maggior parte dei casi sarà immediatamente visibile quali limiti di integrazione verranno utilizzati. Quindi, risolviamo il problema graficamente. Tuttavia, accade che i valori dei limiti siano frazionari o irrazionali. Pertanto, è possibile effettuare ulteriori calcoli, andare al passaggio due.

2. Se i limiti di integrazione non sono impostati in modo esplicito, allora troviamo i punti di intersezione dei grafici tra loro e vediamo se la nostra soluzione grafica coincide con quella analitica.

3. Successivamente, è necessario analizzare il disegno. A seconda di come si trovano i grafici delle funzioni, esistono diversi approcci per trovare l'area di una figura. Consideriamo diversi esempi di trovare l'area di una figura usando gli integrali.

3.1. La versione più classica e semplice del problema è quando è necessario trovare l'area di un trapezio curvo. Cos'è un trapezio curvo? È una figura piatta delimitata dall'asse x. (y = 0), dritto x = a, x = b e qualsiasi curva continua da un prima B... Inoltre, questa cifra non è negativa e si trova non al di sotto dell'asse delle ascisse. In questo caso, l'area di un trapezio curvilineo è numericamente uguale a un integrale definito calcolato dalla formula di Newton-Leibniz:

Esempio 1 y = x2 - 3x + 3, x = 1, x = 3, y = 0.

Quali sono le linee che delimitano la figura? Abbiamo una parabola y = x2 - 3x + 3 che si trova sopra l'asse OH, è non negativo, perché tutti i punti di questa parabola sono positivi. Inoltre, le linee rette x = 1 e x = 3 che corrono paralleli all'asse OU, sono le linee di delimitazione della forma a sinistra e a destra. Bene y = 0, è l'asse x, che limita la figura dal basso. La forma risultante è ombreggiata come mostrato nell'immagine a sinistra. In questo caso, puoi iniziare immediatamente a risolvere il problema. Abbiamo davanti a noi un semplice esempio di trapezio curvilineo, che risolviamo ulteriormente utilizzando la formula di Newton-Leibniz.

3.2. Nel precedente paragrafo 3.1, abbiamo analizzato il caso in cui il trapezio curvo si trova sopra l'asse x. Consideriamo ora il caso in cui le condizioni del problema sono le stesse, tranne per il fatto che la funzione si trova sotto l'asse x. Un meno viene aggiunto alla formula standard di Newton-Leibniz. Considereremo ulteriormente come risolvere un problema simile.

Esempio 2 ... Calcola l'area di una forma delimitata da linee y = x2 + 6x + 2, x = -4, x = -1, y = 0.

In questo esempio, abbiamo una parabola y = x2 + 6x + 2 che nasce da sotto l'asse OH, dritto x = -4, x = -1, y = 0... Qui y = 0 delimita la forma desiderata dall'alto. Diretto x = -4 e x = -1 questi sono i limiti entro i quali verrà calcolato un integrale definito. Il principio di risolvere il problema di trovare l'area di una figura coincide quasi completamente con l'esempio numero 1. L'unica differenza è che la funzione data non è positiva ed è ancora continua sull'intervallo [-4; -1] ... Cosa non significa positivo? Come puoi vedere dalla figura, la figura, che è all'interno della x data, ha coordinate esclusivamente "negative", che è ciò che dobbiamo vedere e ricordare quando risolviamo il problema. Cerchiamo l'area della figura usando la formula di Newton-Leibniz, solo con un segno meno all'inizio.

L'articolo è incompleto.

Passiamo alla considerazione delle applicazioni del calcolo integrale. In questa lezione analizzeremo un compito tipico e più comune. calcolare l'area di una figura piana usando un integrale definito... Infine, tutti coloro che cercano un significato nella matematica superiore, possano trovarlo. Non si sa mai. Dovremo avvicinare alla vita l'area suburbana con funzioni elementari e trovare la sua area utilizzando un integrale definito.

Per padroneggiare con successo il materiale, devi:

1) Comprendere l'integrale indefinito almeno al livello medio. Pertanto, i manichini dovrebbero prima familiarizzare con la lezione Non.

2) Saper applicare la formula di Newton-Leibniz e calcolare un integrale definito. Puoi costruire amicizie calorose con integrali definiti sulla pagina Integrale definito. Esempi di soluzioni. Il compito "calcolare l'area utilizzando un integrale definito" comporta sempre la costruzione di un disegno, quindi, anche le tue conoscenze e abilità nel disegnare disegni saranno un problema urgente. Come minimo, devi essere in grado di costruire una linea retta, una parabola e un'iperbole.

Iniziamo con un trapezio curvo. Un trapezio curvo è una figura piatta delimitata dal grafico di una funzione sì = F(X), l'asse BUE e linee X = un; X = B.

L'area di un trapezio curvo è numericamente uguale all'integrale definito

Qualsiasi integrale definito (che esiste) ha un ottimo significato geometrico. Alla lezione Integrale definito. Esempi di soluzioni abbiamo detto che un integrale definito è un numero. E ora è il momento di affermare un altro fatto utile. Dal punto di vista della geometria, l'integrale definito è l'AREA... Questo è, un integrale definito (se esiste) corrisponde geometricamente all'area di qualche figura... Considera l'integrale definito

Integrando

definisce una curva sul piano (può essere disegnata se lo si desidera) e l'integrale definito stesso è numericamente uguale all'area del corrispondente trapezio curvilineo.

Esempio 1

, , , .

Questa è una tipica formulazione del compito. Il punto più importante della soluzione è la costruzione del disegno... Inoltre, il disegno deve essere costruito GIUSTO.

Quando si costruisce un disegno, consiglio il seguente ordine: All'inizioè meglio costruire tutte le linee (se ce ne sono) e solo dopo- parabole, iperboli, grafici di altre funzioni. La tecnica di costruzione punto per punto può essere trovata nel materiale di riferimento. Grafici e proprietà delle funzioni elementari... Lì puoi anche trovare materiale molto utile in relazione alla nostra lezione: come costruire rapidamente una parabola.

In questo problema, la soluzione potrebbe essere simile a questa.

Completiamo il disegno (notare che l'equazione sì= 0 specifica l'asse BUE):

Non schiuderemo il trapezio curvilineo, qui è ovvio di quale area stiamo parlando. La soluzione continua così:

Sul segmento [-2; 1] grafico della funzione sì = X 2 + 2 situati sopra l'asseBUE, perciò:

Risposta: .

Chi ha difficoltà a calcolare un integrale definito e ad applicare la formula di Newton-Leibniz

fare riferimento alla lezione Integrale definito. Esempi di soluzioni... Dopo che l'attività è stata completata, è sempre utile guardare il progetto e stimare se la risposta è reale. In questo caso, "a occhio" contiamo il numero di celle nel disegno - beh, ne verranno digitati circa 9, sembra la verità. È abbastanza chiaro che se otteniamo, diciamo, la risposta: 20 unità quadrate, allora, ovviamente, è stato commesso un errore da qualche parte - la cifra in questione ovviamente non si adatta a 20 celle, al massimo dieci. Se la risposta è negativa, anche l'attività è stata risolta in modo errato.

Esempio 2

Calcola l'area di una forma delimitata da linee xy = 4, X = 2, X= 4 e asse BUE.

Questo è un esempio di soluzione fai-da-te. Soluzione completa e risposta alla fine del tutorial.

Cosa fare se si trova il trapezio curvo sotto l'asseBUE?

Esempio 3

Calcola l'area di una forma delimitata da linee sì = e - x, X= 1 e assi coordinati.

Soluzione: eseguiamo il disegno:

Se il trapezio curvo completamente posizionato sotto l'asse BUE , quindi la sua area può essere trovata dalla formula:

In questo caso:

Attenzione! I due tipi di compiti non devono essere confusi:

1) Se ti viene chiesto di risolvere solo un integrale definito senza alcun significato geometrico, allora può essere negativo.

2) Se ti viene chiesto di trovare l'area di una figura usando un integrale definito, l'area è sempre positiva! Ecco perché nella formula appena considerata compare un meno.

In pratica, molto spesso la figura si trova sia nel semipiano superiore che in quello inferiore e quindi, dai problemi scolastici più semplici, si passa ad esempi più significativi.

Esempio 4

Trova l'area di una figura piatta delimitata da linee sì = 2X – X 2 , sì = -X.

Soluzione: per prima cosa è necessario completare il disegno. Quando costruiamo un disegno in problemi sull'area, siamo più interessati ai punti di intersezione delle linee. Trova i punti di intersezione della parabola sì = 2X – X 2 e dritto sì = -X... Questo può essere fatto in due modi. Il primo modo è analitico. Risolviamo l'equazione:

Quindi, il limite inferiore di integrazione un= 0, il limite superiore di integrazione B= 3. Spesso è più vantaggioso e veloce costruire le linee punto per punto, mentre i limiti dell'integrazione diventano chiari come “da soli”. Tuttavia, il metodo analitico per trovare i limiti deve ancora essere utilizzato a volte se, ad esempio, il grafico è sufficientemente grande o la costruzione precisa non ha rivelato i limiti di integrazione (possono essere frazionari o irrazionali). Torniamo al nostro problema: è più razionale costruire prima una retta e solo dopo una parabola. Eseguiamo il disegno:

Ripetiamo che nel caso di una costruzione puntuale, i limiti dell'integrazione si scoprono il più delle volte “automaticamente”.

E ora la formula di lavoro:

Se sul segmento [ un; B] qualche funzione continua F(X) Maggiore o uguale qualche funzione continua G(X), quindi l'area della figura corrispondente può essere trovata dalla formula:

Qui non è più necessario pensare dove si trova la figura - sopra o sotto l'asse, ma è importante quale programma è SOPRA(relativo ad un altro grafico), e quale è SOTTO.

Nell'esempio in esame è ovvio che sul segmento la parabola si trova al di sopra della retta, e quindi da 2 X – X 2 deve essere sottratto - X.

Il completamento della soluzione potrebbe essere simile a questo:

La figura ricercata è delimitata da una parabola sì = 2X – X 2 in alto e dritto sì = -X da sotto.

Sul segmento 2 X – X 2 ≥ -X... Secondo la formula corrispondente:

Risposta: .

In effetti, la formula scolastica per l'area di un trapezio curvilineo nel semipiano inferiore (vedi esempio n. 3) è un caso speciale della formula

Poiché l'asse BUE dato dall'equazione sì= 0, e il grafico della funzione G(X) si trova sotto l'asse BUE, poi

E ora un paio di esempi per una soluzione indipendente

Esempio 5

Esempio 6

Trova l'area di una forma delimitata da linee

Nel corso della risoluzione dei problemi per il calcolo dell'area utilizzando un integrale definito, a volte accade un incidente divertente. Il disegno è fatto correttamente, i calcoli sono corretti, ma, inavvertitamente, ... è stata trovata l'area della figura sbagliata.

Esempio 7

Per prima cosa eseguiamo il disegno:

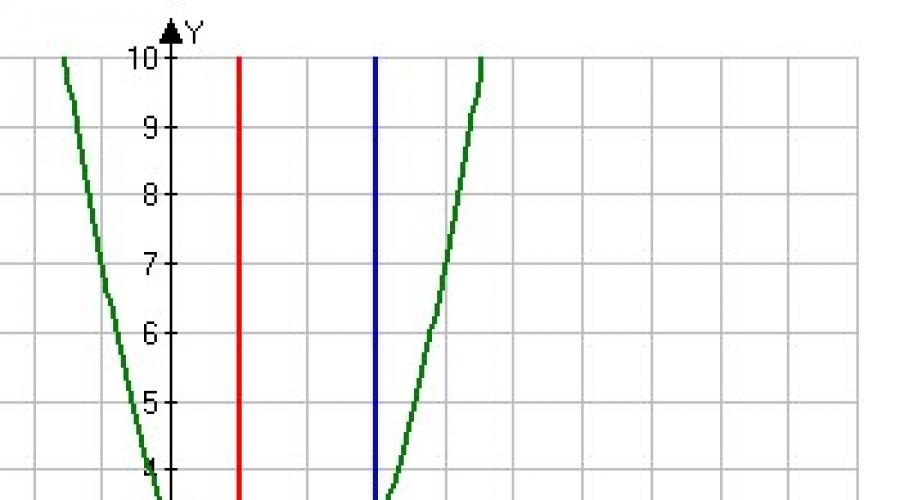
La figura di cui dobbiamo trovare l'area è ombreggiata in blu(osserva attentamente la condizione: da cosa è limitata la cifra!). Ma in pratica, per disattenzione, spesso decidono che è necessario trovare l'area della figura, che è ombreggiata in verde!

Questo esempio è utile anche in quanto calcola l'area di una figura utilizzando due integrali definiti. Veramente:

1) Sul segmento [-1; 1] sopra l'asse BUE il grafico è dritto sì = X+1;

2) Su un segmento sopra l'asse BUE si trova il grafico dell'iperbole sì = (2/X).

È abbastanza ovvio che le aree possono (e dovrebbero) essere aggiunte, quindi:

Risposta:

Esempio 8

Calcola l'area di una forma delimitata da linee

Rappresentiamo le equazioni nella forma "scuola"

ed eseguire un disegno punto per punto:

Dal disegno si può vedere che il nostro limite superiore è "buono": B = 1.

Ma qual è il limite inferiore?! È chiaro che questo non è un numero intero, ma quale?

Forse, un= (-1/3)? Ma dov'è la garanzia che il disegno sia realizzato con perfetta accuratezza, potrebbe anche risultare che un= (- 1/4). E se tracciassimo il grafico in modo errato?

In tali casi, è necessario dedicare ulteriore tempo e affinare analiticamente i limiti dell'integrazione.

Trova i punti di intersezione dei grafici

Per fare ciò, risolviamo l'equazione:

Quindi, un=(-1/3).

L'ulteriore soluzione è banale. La cosa principale è non confondersi con sostituzioni e segni. I calcoli qui non sono dei più facili. Sul segmento

, ,

secondo la formula corrispondente:

Risposta:

Alla fine della lezione, prenderemo in considerazione due compiti più difficili.

Esempio 9

Calcola l'area di una forma delimitata da linee

Soluzione: Disegna questa figura nel disegno.

Per la costruzione punto per punto del disegno, è necessario conoscere l'aspetto della sinusoide. In generale, è utile conoscere i grafici di tutte le funzioni elementari, nonché alcuni valori del seno. Si trovano nella tabella dei valori funzioni trigonometriche... In un certo numero di casi (ad esempio, in questo), è consentito costruire un disegno schematico, sul quale i grafici e i limiti di integrazione dovrebbero essere visualizzati correttamente in linea di principio.

Non ci sono problemi con i limiti di integrazione, seguono direttamente dalla condizione:

- "x" cambia da zero a "pi". Prendiamo un'ulteriore decisione:

Su un segmento, il grafico della funzione sì= peccato 3 X situato sopra l'asse BUE, perciò:

(1) Come si integrano seno e coseno in gradi dispari, puoi vedere nella lezione Integrali di funzioni trigonometriche... Pizzichiamo un seno.

(2) Usiamo l'identità trigonometrica di base nella forma

(3) Cambia la variabile T= cos X, quindi: si trova sopra l'asse, quindi:

Nota: si noti come si prende l'integrale della tangente nel cubo, qui si usa una conseguenza dell'identità trigonometrica principale

Nella sezione precedente dedicata all'analisi del significato geometrico di un integrale definito, abbiamo ottenuto una serie di formule per calcolare l'area di un trapezio curvilineo:

Yandex.RTB R-A-339285-1

S (G) = ∫ a b f (x) d x per una funzione continua e non negativa y = f (x) sul segmento [a; B],

S (G) = - a b f (x) d x per una funzione continua e non positiva y = f (x) sul segmento [a; B].

Queste formule sono applicabili per risolvere problemi relativamente semplici. Spesso, infatti, dobbiamo lavorare con forme più complesse. A questo proposito, dedicheremo questa sezione all'analisi degli algoritmi per il calcolo dell'area delle figure, che sono limitati da funzioni in forma esplicita, ad es. come y = f (x) o x = g (y).

Teorema

Siano definite e continue le funzioni y = f 1 (x) e y = f 2 (x) sul segmento [a; b], e f 1 (x) ≤ f 2 (x) per qualsiasi valore di x da [a; B]. Quindi la formula per calcolare l'area della figura G delimitata dalle linee x = a, x = b, y = f 1 (x) e y = f 2 (x) avrà la forma S (G) = ∫ abf 2 (x) - f 1 (x) dx.

Una formula simile sarà applicabile per l'area della figura delimitata dalle linee y = c, y = d, x = g 1 (y) e x = g 2 (y): S (G) = ∫ cd ( g 2 (y) - g 1 (y) dy.

Prova

Consideriamo tre casi per i quali la formula sarà valida.

Nel primo caso, tenendo conto della proprietà dell'additività dell'area, la somma delle aree della figura originale G e del trapezio curvilineo G 1 è uguale all'area della figura G 2. Significa che

Pertanto, S (G) = S (G 2) - S (G 1) = ∫ abf 2 (x) dx - ∫ abf 1 (x) dx = ∫ ab (f 2 (x) - f 1 (x)) dx.

Possiamo fare l'ultima transizione usando la terza proprietà dell'integrale definito.

Nel secondo caso vale la seguente uguaglianza: S (G) = S (G 2) + S (G 1) = ∫ abf 2 (x) dx + - ∫ abf 1 (x) dx = ∫ ab (f 2 ( x) - f 1 (x)) dx

L'illustrazione grafica sarà simile a:

Se entrambe le funzioni sono non positive, si ottiene: S (G) = S (G 2) - S (G 1) = - ∫ abf 2 (x) dx - - ∫ abf 1 (x) dx = ∫ ab (f 2 (x) - f 1 (x)) dx. L'illustrazione grafica sarà simile a:

Passiamo alla considerazione del caso generale in cui y = f 1 (x) ey = f 2 (x) intersecano l'asse O x.

I punti di intersezione saranno indicati come x i, i = 1, 2,. ... ... , n-1. Questi punti dividono il segmento [a; b] in n parti x i - 1; x io, io = 1, 2,. ... ... , n, dove α = x 0< x 1 < x 2 < . . . < x n - 1 < x n = b . Фигуру G можно представить объединением фигур G i , i = 1 , 2 , . . . , n . Очевидно, что на своем интервале G i попадает под один из трех рассмотренных ранее случаев, поэтому их площади находятся как S (G i) = ∫ x i - 1 x i (f 2 (x) - f 1 (x)) d x , i = 1 , 2 , . . . , n

Quindi,

S (G) = ∑ i = 1 n S (G i) = ∑ i = 1 n ∫ xixif 2 (x) - f 1 (x)) dx = = ∫ x 0 xn (f 2 (x) - f ( x)) dx = ∫ abf 2 (x) - f 1 (x) dx

Possiamo fare l'ultima transizione usando la quinta proprietà dell'integrale definito.

Illustriamo il caso generale sul grafico.

La formula S (G) = ∫ a b f 2 (x) - f 1 (x) d x può considerarsi dimostrata.

E ora passiamo all'analisi di esempi di calcolo dell'area delle figure delimitate dalle linee y = f (x) e x = g (y).

Inizieremo a considerare uno qualsiasi degli esempi costruendo un grafico. L'immagine ci permetterà di rappresentare forme complesse come combinazioni di forme più semplici. Se tracciare grafici e forme su di essi ti crea difficoltà, puoi studiare la sezione sulle funzioni atomiche di base, sulla trasformazione geometrica dei grafici delle funzioni e sul tracciare mentre esplori una funzione.

Esempio 1

È necessario determinare l'area della figura, che è delimitata dalla parabola y = - x 2 + 6 x - 5 e dalle linee rette y = - 1 3 x - 1 2, x = 1, x = 4.

Soluzione

Tracciamo le linee sul grafico in un sistema di coordinate cartesiane.

Sul segmento [1; 4] il grafico della parabola y = - x 2 + 6 x - 5 si trova sopra la retta y = - 1 3 x - 1 2. A questo proposito, per ottenere una risposta, utilizziamo la formula ottenuta in precedenza, nonché il metodo per calcolare un integrale definito secondo la formula di Newton-Leibniz:

S (G) = 1 4 - x 2 + 6 x - 5 - - 1 3 x - 1 2 dx = = ∫ 1 4 - x 2 + 19 3 x - 9 2 dx = - 1 3 x 3 + 19 6 x 2 - 9 2 x 1 4 = = - 1 3 4 3 + 19 6 4 2 - 9 2 4 - - 1 3 1 3 + 19 6 1 2 - 9 2 1 = = - 64 3 + 152 3 - 18 + 1 3 - 19 6 + 9 2 = 13

Risposta: S (G) = 13

Vediamo un esempio più complesso.

Esempio 2

È necessario calcolare l'area della figura, che è delimitata dalle linee y = x + 2, y = x, x = 7.

Soluzione

In questo caso abbiamo una sola retta parallela all'asse delle ascisse. Questo è x = 7. Questo ci richiede di trovare da soli il secondo limite di integrazione.

Costruiamo un grafico e disegniamo su di esso le linee fornite nella dichiarazione del problema.

Avendo il grafico davanti ai nostri occhi, possiamo facilmente determinare che il limite inferiore di integrazione sarà l'ascissa del punto di intersezione del grafico della retta y = x e della semiparabola y = x + 2. Per trovare l'ascissa, usiamo le uguaglianze:

y = x + 2 О Д З: x ≥ - 2 x 2 = x + 2 2 x 2 - x - 2 = 0 D = (- 1) 2 - 4 · 1 · (- 2) = 9 x 1 = 1 + 9 2 = 2 ∈ О Д З x 2 = 1 - 9 2 = - 1 ∉ О Д З

Si scopre che l'ascissa del punto di intersezione è x = 2.

Attiriamo la vostra attenzione sul fatto che nell'esempio generale nel disegno, le linee y = x + 2, y = x si intersecano nel punto (2; 2), quindi tali calcoli dettagliati possono sembrare ridondanti. Abbiamo fornito una soluzione così dettagliata qui solo perché in casi più complessi la soluzione potrebbe non essere così ovvia. Ciò significa che le coordinate dell'intersezione delle linee sono sempre meglio calcolate analiticamente.

Nell'intervallo [2; 7] il grafico della funzione y = x si trova sopra il grafico della funzione y = x + 2. Applichiamo la formula per il calcolo dell'area:

S (G) = ∫ 2 7 (x - x + 2) dx = x 2 2 - 2 3 (x + 2) 3 2 2 7 = = 7 2 2 - 2 3 (7 + 2) 3 2 - 2 2 2 - 2 3 2 + 2 3 2 = = 49 2 - 18 - 2 + 16 3 = 59 6

Risposta: S (G) = 59 6

Esempio 3

È necessario calcolare l'area della figura, che è limitata dai grafici delle funzioni y = 1 x e y = - x 2 + 4 x - 2.

Soluzione

Tracciamo linee sul grafico.

Definiamo i limiti dell'integrazione. Per fare ciò, determiniamo le coordinate dei punti di intersezione delle linee eguagliando le espressioni 1 x e - x 2 + 4 x - 2. Posto che x non è zero, l'uguaglianza 1 x = - x 2 + 4 x - 2 diventa equivalente all'equazione di terzo grado - x 3 + 4 x 2 - 2 x - 1 = 0 a coefficienti interi. Puoi aggiornare la tua memoria dell'algoritmo per risolvere tali equazioni facendo riferimento alla sezione "Risoluzione di equazioni cubiche".

La radice di questa equazione è x = 1: - 1 3 + 4 · 1 2 - 2 · 1 - 1 = 0.

Dividendo l'espressione - x 3 + 4 x 2 - 2 x - 1 per il binomio x - 1, si ottiene: - x 3 + 4 x 2 - 2 x - 1 ⇔ - (x - 1) (x 2 - 3 x - 1) = 0

Possiamo trovare le radici rimanenti dall'equazione x 2 - 3 x - 1 = 0:

x 2 - 3 x - 1 = 0 D = (- 3) 2 - 4 · 1 · (- 1) = 13 x 1 = 3 + 13 2 ≈ 3. 3; x 2 = 3 - 13 2 - 0. 3

Abbiamo trovato l'intervallo x ∈ 1; 3 + 13 2, in cui la figura G è racchiusa sopra la linea blu e sotto la linea rossa. Questo ci aiuta a determinare l'area della forma:

S (G) = ∫ 1 3 + 13 2 - x 2 + 4 x - 2 - 1 xdx = - x 3 3 + 2 x 2 - 2 x - ln x 1 3 + 13 2 = = - 3 + 13 2 3 3 + 2 3 + 13 2 2 - 2 3 + 13 2 - ln 3 + 13 2 - - - 1 3 3 + 2 1 2 - 2 1 - ln 1 = 7 + 13 3 - ln 3 + 13 2

Risposta: S (G) = 7 + 13 3 - ln 3 + 13 2

Esempio 4

È necessario calcolare l'area della figura, che è limitata dalle curve y = x 3, y = - log 2 x + 1 e dall'asse delle ascisse.

Soluzione

Tracciamo tutte le linee sul grafico. Possiamo ottenere il grafico della funzione y = - log 2 x + 1 dal grafico y = log 2 x, se lo disponiamo simmetricamente rispetto all'asse delle ascisse e lo solleviamo di una unità. L'equazione dell'asse delle ascisse è y = 0.

Segnaliamo i punti di intersezione delle linee.

Come si vede dalla figura, i grafici delle funzioni y = x 3 e y = 0 si intersecano nel punto (0; 0). Questo perché x = 0 è l'unica vera radice dell'equazione x 3 = 0.

x = 2 è l'unica radice dell'equazione - log 2 x + 1 = 0, quindi i grafici delle funzioni y = - log 2 x + 1 ey = 0 si intersecano nel punto (2; 0).

x = 1 è l'unica radice dell'equazione x 3 = - log 2 x + 1. A tal proposito, i grafici delle funzioni y = x 3 e y = - log 2 x + 1 si intersecano nel punto (1; 1). L'ultima affermazione potrebbe non essere ovvia, ma l'equazione x 3 = - log 2 x + 1 non può avere più di una radice, poiché la funzione y = x 3 è strettamente crescente e la funzione y = - log 2 x + 1 è rigorosamente decrescente.

Un'ulteriore soluzione presuppone diverse opzioni.

Opzione numero 1

Possiamo rappresentare la figura G come la somma di due trapezi curvilinei posti sopra l'asse delle ascisse, il primo dei quali si trova sotto la mezzeria sul segmento x 0; 1, e il secondo è sotto la linea rossa sul segmento x ∈ 1; 2. Ciò significa che l'area sarà S (G) = ∫ 0 1 x 3 d x + ∫ 1 2 (- log 2 x + 1) d x.

Opzione numero 2

La figura G può essere rappresentata come la differenza di due cifre, la prima delle quali si trova sopra l'asse delle ascisse e sotto la linea blu sul segmento x 0; 2, e il secondo è tra le linee rossa e blu sul segmento x ∈ 1; 2. Questo ci permette di trovare l'area come segue:

S (G) = ∫ 0 2 x 3 d x - ∫ 1 2 x 3 - (- log 2 x + 1) d x

In questo caso, per trovare l'area, dovrai usare una formula della forma S (G) = ∫ c d (g 2 (y) - g 1 (y)) d y. Infatti, le linee che delimitano la forma possono essere rappresentate come funzioni dell'argomento y.

Risolvi le equazioni y = x 3 e - log 2 x + 1 per x:

y = x 3 ⇒ x = y 3 y = - log 2 x + 1 ⇒ log 2 x = 1 - y ⇒ x = 2 1 - y

Otteniamo l'area richiesta:

S (G) = ∫ 0 1 (2 1 - y - y 3) dy = - 2 1 - y ln 2 - y 4 4 0 1 = = - 2 1 - 1 ln 2 - 1 4 4 - - 2 1 - 0 ln 2 - 0 4 4 = - 1 ln 2 - 1 4 + 2 ln 2 = 1 ln 2 - 1 4

Risposta: S (G) = 1 ln 2 - 1 4

Esempio 5

È necessario calcolare l'area della figura, che è delimitata dalle linee y = x, y = 2 3 x - 3, y = - 1 2 x + 4.

Soluzione

Con la linea rossa, disegna sul grafico la linea specificata dalla funzione y = x. Disegna la linea y = - 1 2 x + 4 in blu e disegna la linea y = 2 3 x - 3 in nero.

Segnaliamo i punti di intersezione.

Trova i punti di intersezione dei grafici delle funzioni y = x e y = - 1 2 x + 4:

x = - 1 2 x + 4 О Д З: x ≥ 0 x = - 1 2 x + 4 2 ⇒ x = 1 4 x 2 - 4 x + 16 ⇔ x 2 - 20 x + 64 = 0 D = (- 20) 2 - 4 1 64 = 144 x 1 = 20 + 144 2 = 16; x 2 = 20 - 144 2 = 4 Verifica: x 1 = 16 = 4, - 1 2 x 1 + 4 = - 1 2 16 + 4 = - 4 ⇒ x 1 = 16 non ho una soluzione x 2 = 4 = 2, - 1 2 x 2 + 4 = - 1 2 4 + 4 = 2 ⇒ x 2 = 4 i e n t e r s ⇒ (4; 2) punto di intersezione i y = x e y = - 1 2 x + 4

Trova il punto di intersezione dei grafici delle funzioni y = x e y = 2 3 x - 3:

x = 2 3 x - 3 О Д З: x ≥ 0 x = 2 3 x - 3 2 ⇔ x = 4 9 x 2 - 4 x + 9 ⇔ 4 x 2 - 45 x + 81 = 0 D = (- 45 ) 2 - 4 4 81 = 729 x 1 = 45 + 729 8 = 9, x 2 45 - 729 8 = 9 4 Verifica: x 1 = 9 = 3, 2 3 x 1 - 3 = 2 3 9 - 3 = 3 ⇒ x 1 = 9 ho una soluzione ⇒ (9; 3) punto di intersezione y = x e y = 2 3 x - 3 x 2 = 9 4 = 3 2, 2 3 x 1 - 3 = 2 3 9 4 - 3 = - 3 2 ⇒ x 2 = 9 4 non ha soluzione

Trova l'intersezione delle linee y = - 1 2 x + 4 e y = 2 3 x - 3:

1 2 x + 4 = 2 3 x - 3 - 3 x + 24 = 4 x - 18 ⇔ 7 x = 42 ⇔ x = 6 - 1 2 6 + 4 = 2 3 6 - 3 = 1 ⇒ (6 ; 1 ) il punto di intersezione y = - 1 2 x + 4 e y = 2 3 x - 3

Metodo numero 1

Immaginiamo l'area della figura richiesta come la somma delle aree delle singole figure.

Quindi l'area della figura è uguale a:

S (G) = ∫ 4 6 x - - 1 2 x + 4 dx + ∫ 6 9 x - 2 3 x - 3 dx = = 2 3 x 3 2 + x 2 4 - 4 x 4 6 + 2 3 x 3 2 - x 2 3 + 3 x 6 9 = = 2 3 6 3 2 + 6 2 4 - 4 6 - 2 3 4 3 2 + 4 2 4 - 4 4 + + 2 3 9 3 2 - 9 2 3 + 3 9 - 2 3 6 3 2 - 6 2 3 + 3 6 = = - 25 3 + 4 6 + - 4 6 + 12 = 11 3

Metodo numero 2

L'area della forma originale può essere pensata come la somma delle altre due forme.

Quindi risolveremo l'equazione della linea rispetto a x e solo dopo applicheremo la formula per calcolare l'area della figura.

y = x ⇒ x = y 2 linea rossa y = 2 3 x - 3 ⇒ x = 3 2 y + 9 2 linea nera y = - 1 2 x + 4 ⇒ x = - 2 y + 8

L'area è quindi pari a:

S (G) = ∫ 1 2 3 2 y + 9 2 - - 2 y + 8 dy + ∫ 2 3 3 2 y + 9 2 - y 2 dy = = ∫ 1 2 7 2 y - 7 2 dy + ∫ 2 3 3 2 y + 9 2 - y 2 dy = = 7 4 y 2 - 7 4 y 1 2 + - y 3 3 + 3 y 2 4 + 9 2 y 2 3 = 7 4 2 2 - 7 4 2 - 7 4 1 2 - 7 4 1 + + - 3 3 3 + 3 3 2 4 + 9 2 3 - - 2 3 3 + 3 2 2 4 + 9 2 2 = = 7 4 + 23 12 = 11 3

Come puoi vedere, i valori sono gli stessi.

Risposta: S (G) = 11 3

risultati

Per trovare l'area di una figura, che è delimitata dalle linee specificate, dobbiamo costruire linee su un piano, trovare i loro punti di intersezione, applicare la formula per trovare l'area. In questa sezione, abbiamo esaminato le opzioni di attività più comuni.

Se noti un errore nel testo, selezionalo e premi Ctrl + Invio

Quindi, cosa è necessario per risolvere con successo il problema di trovare l'area di una figura usando gli integrali:

Capacità di costruire disegni con competenza;
Capacità di risolvere un integrale definito utilizzando la nota formula di Newton-Leibniz;
La capacità di "vedere" una soluzione più vantaggiosa, ovvero per capire come in questo o quel caso sarà più conveniente effettuare l'integrazione? Lungo l'asse x (OX) o lungo l'asse y (OY)?
Bene, dove senza calcoli corretti?) Questo include capire come risolvere quell'altro tipo di integrali e correggere i calcoli numerici.

Algoritmo per risolvere il problema del calcolo dell'area di una figura delimitata da linee:

Esempio 1 y = x2 - 3x + 3, x = 1, x = 3, y = 0.

Esempio 2 ... Calcola l'area di una forma delimitata da linee y = x2 + 6x + 2, x = -4, x = -1, y = 0.

L'articolo è incompleto.

Infatti, per trovare l'area di una figura, non è necessaria tanta conoscenza dell'integrale indefinito e definito. Il compito "calcolare l'area utilizzando un integrale definito" comporta sempre la costruzione di un disegno, quindi, le tue conoscenze e abilità di disegno saranno una domanda molto più pertinente. A questo proposito è utile rinfrescare la memoria dei grafici delle funzioni elementari di base, e, almeno, saper costruire una retta e un'iperbole.

Un trapezio curvilineo è una figura piatta delimitata da un asse, linee rette e un grafico di una funzione continua su un segmento che non cambia segno su questo intervallo. Sia localizzata questa figura non meno asse delle ascisse:

Quindi l'area di un trapezio curvilineo è numericamente uguale all'integrale definito... Qualsiasi integrale definito (che esiste) ha un ottimo significato geometrico.

Dal punto di vista della geometria, l'integrale definito è l'AREA.

Questo è, un integrale definito (se esiste) corrisponde geometricamente all'area di qualche figura. Consideriamo ad esempio un integrale definito. L'integrando imposta una curva sul piano che si trova sopra l'asse (chi lo desidera può fare un disegno), e l'integrale definito stesso è numericamente uguale all'area del corrispondente trapezio curvilineo.

Esempio 1

Questa è una tipica formulazione del compito. Il primo e più importante punto della soluzione è la costruzione del disegno... Inoltre, il disegno deve essere costruito GIUSTO.

In questo problema, la soluzione potrebbe essere simile a questa.
Disegniamo un disegno (nota che l'equazione definisce l'asse):

Sul segmento si trova il grafico della funzione sopra l'asse, perciò:

Risposta:

Dopo che l'attività è stata completata, è sempre utile guardare il progetto e stimare se la risposta è reale. In questo caso, "a occhio" contiamo il numero di celle nel disegno - beh, ne verranno digitati circa 9, sembra la verità. È abbastanza chiaro che se otteniamo, diciamo, la risposta: 20 unità quadrate, allora, ovviamente, è stato commesso un errore da qualche parte - la cifra in questione ovviamente non si adatta a 20 celle, al massimo dieci. Se la risposta è negativa, anche l'attività è stata risolta in modo errato.

Esempio 3

Calcola l'area della forma delimitata da linee e assi coordinati.

Soluzione: Eseguiamo il disegno:

Se si trova il trapezio curvo sotto l'asse(o quantomeno non più alto dato asse), allora la sua area può essere trovata dalla formula:

In questo caso:

Attenzione! I due tipi di compiti non devono essere confusi:

1) Se ti viene chiesto di risolvere solo un integrale definito senza alcun significato geometrico, allora può essere negativo.

2) Se ti viene chiesto di trovare l'area di una figura usando un integrale definito, l'area è sempre positiva! Ecco perché nella formula appena considerata compare un meno.

In pratica, molto spesso la figura si trova sia nel semipiano superiore che in quello inferiore e quindi, dai problemi scolastici più semplici, si passa ad esempi più significativi.

Esempio 4

Trova l'area di una figura piatta delimitata da linee.

Soluzione: Per prima cosa devi completare il disegno. In generale, quando si costruisce un disegno in problemi su un'area, siamo più interessati ai punti di intersezione delle linee. Trova i punti di intersezione della parabola e della retta. Questo può essere fatto in due modi. Il primo modo è analitico. Risolviamo l'equazione:

Quindi, il limite inferiore dell'integrazione, il limite superiore dell'integrazione.

È meglio non usare questo metodo, se possibile..

È molto più vantaggioso e veloce costruire le linee punto per punto, mentre i limiti dell'integrazione diventano chiari, per così dire, "da soli". Tuttavia, il metodo analitico per trovare i limiti deve ancora essere utilizzato a volte se, ad esempio, il grafico è sufficientemente grande o la costruzione precisa non ha rivelato i limiti di integrazione (possono essere frazionari o irrazionali). E considereremo anche un esempio del genere.

Torniamo al nostro problema: è più razionale costruire prima una retta e solo dopo una parabola. Eseguiamo il disegno:

E ora la formula di lavoro: Se su un segmento qualche funzione continua Maggiore o uguale di qualche funzione continua, quindi l'area della figura, delimitata dai grafici di queste funzioni e rette, può essere trovata dalla formula:

Qui non è più necessario pensare a dove si trova la figura: sopra o sotto l'asse e, grosso modo, è importante quale programma è SOPRA(relativo ad un altro grafico), e quale è SOTTO.

Nell'esempio in esame è ovvio che sul segmento la parabola si trova al di sopra della retta, e quindi è necessario sottrarre da

Il completamento della soluzione potrebbe essere simile a questo:

La figura richiesta è delimitata da una parabola in alto e una retta in basso.
Sul segmento, secondo la formula corrispondente:

Risposta:

Esempio 4

Calcola l'area della figura delimitata dalle linee,,,.

Soluzione: Per prima cosa eseguiamo il disegno:

La figura di cui dobbiamo trovare l'area è ombreggiata in blu(osserva attentamente la condizione: da cosa è limitata la cifra!). Ma in pratica, a causa della disattenzione, spesso si verifica un "glitch", che è necessario trovare l'area della figura, che è ombreggiata in verde!

Questo esempio è utile anche in quanto calcola l'area di una figura utilizzando due integrali definiti.

Veramente:

1) Un grafico a linee si trova sul segmento sopra l'asse;

2) Il grafico dell'iperbole si trova sul segmento sopra l'asse.

È abbastanza ovvio che le aree possono (e dovrebbero) essere aggiunte, quindi:

Calcolatrice di forma quadrata limitata. Calcolatrice online Calcola l'integrale definito (area di un trapezio curvo)

Leggi anche

risultati