Klasična vjerojatnost. Vjerojatnost slučajnog događaja
Za procjene vjerojatnosti o nastavku bilo kojeg slučajnog događaja vrlo su važne za predujam da predstavljaju li vjerojatnost da se događaji od interesa za nas razlikuje od načina razvoja drugih događaja.
U slučaju klasične sheme, kada su svi ishodi jednako čak i, možemo već ocijeniti vrijednosti vjerojatnosti pojedinca od interesa za nas samostalno. Možemo to učiniti čak i ako je događaj složen skup nekoliko elementarnih ishoda. I ako se pojavi nekoliko slučajnih događaja istovremeno ili uzastopno? Kako to utječe na vjerojatnost zanimljivih događaja za nas?
Ako nekoliko puta bacim kost, i želim ispasti "šest", a ja nisam sretan cijelo vrijeme, to znači da je potrebno povećati okladu, jer, prema teoriji vjerojatnosti, ja - U dao ću sreću? Nažalost, teorija vjerojatnosti ne odobrava ništa slično. Ni kosti niti karticu niti novčić ne znam kako zapamtiti Ono što su nam pokazali posljednji put. Oni se ne brinu u potpunosti, po prvi put ili u desetom trenutku danas doživljavam svoju sudbinu. Svaki put kad ponovim bacanje, znam samo jednu stvar: ovaj put je vjerojatnost "šest" opet jednaka jednom šestom. Naravno, to ne znači da broj koji trebate nikada neće ispasti. To znači samo činjenicu da je moj gubitak nakon prvog bacanja i nakon bilo koje druge događaje nezavisne.
Događaji a i B se nazivaju neovisanAko provedba jednog od njih ne utječe na vjerojatnost drugog događaja. Na primjer, vjerojatnosti poraza cilja prvi od dva pištolja ne ovise o tome je li cilj udario još jedan alat, tako da su događaji "prvi pištolj pogodio cilj" i "drugi alat pogodio je cilj" neovisan.
Ako su dva događaja a i neovisna, a vjerojatnost svakog od njih je poznata, vjerojatnost istovremene pojave i događanja a i događaji u (imenovani ab) mogu se izračunati pomoću sljedećeg teorema.
Vjerojatnost množenja teorema za neovisne događaje
P (ab) \u003d p (a) * p (b) - Vjerojatnost istodobna Na početku dva neovisan Događaji jednaki raditivjerojatnosti ovih događaja.Primjer.Vjerojatnosti unosa cilja u snimanju prvog i drugog alata su jednake: p 1 \u003d 0,7; p 2 \u003d 0.8. Pronađite vjerojatnost da uđete u jedan odlet s oba pištolja u isto vrijeme.
Odluka:kao što smo već vidjeli događaje A (prvi pištolj) iu (drugi pogodak za alat) je neovisan, tj. P (Av) \u003d p (a) * p (c) \u003d p 1 * p 2 \u003d 0.56.
Što se događa s našim procjenama ako izvorni događaji nisu neovisni? Ponovno promijenimo prethodni primjer.
Primjer.Dvije strelice na natjecanjima pucaju ciljeve, a ako jedan od njih puca na etiku, protivnik počinje biti nervozan, a rezultati se pogoršavaju. Kako pretvoriti ovu svakodnevnu situaciju u matematički zadatak i nacrt načina rješavanja? Intuitivno je da je potrebno nekako podijeliti dvije mogućnosti za razvoj događaja, sastaviti dva scenarija, dva različita zadatka. U prvom slučaju, ako je protivnik propustio, skripta će biti povoljna za živčani sportaš i njegova točnost će biti veća. U drugom slučaju, ako je protivnik pristojno shvatio njegovu šansu, je smanjena vjerojatnost udaranja cilja za drugi sportaš.
Za odvajanje mogućih scenarija (često se nazivaju hipoteze), često ćemo koristiti shemu "stabla vjerojatnosti". Ova shema je slična značenjem stablu odluka s kojima ste se vjerojatno već morali nositi. Svaka grana je odvojeni scenarij razvoja događaja, samo sada ima svoju vrijednost tzv. uvjetno Vjerojatnost (Q1, Q 2, Q 1 -1, Q 2 -1).
Ova shema je vrlo pogodna za analizu uzastopnih slučajnih događaja.
Ostaje da saznate još jedno važno pitanje: gdje su početne vrijednosti vjerojatnosti dolaze Stvarne situacije ? Uostalom, teorija vjerojatnosti radi s istim kovanicama i igranje kostiju? Obično se ove procjene uzimaju iz statistike, a kada ne postoje statističke informacije, provodimo vlastita istraživanja. I često nije potrebno pokrenuti od prikupljanja podataka, ali iz pitanja, koje informacije trebamo trebati.
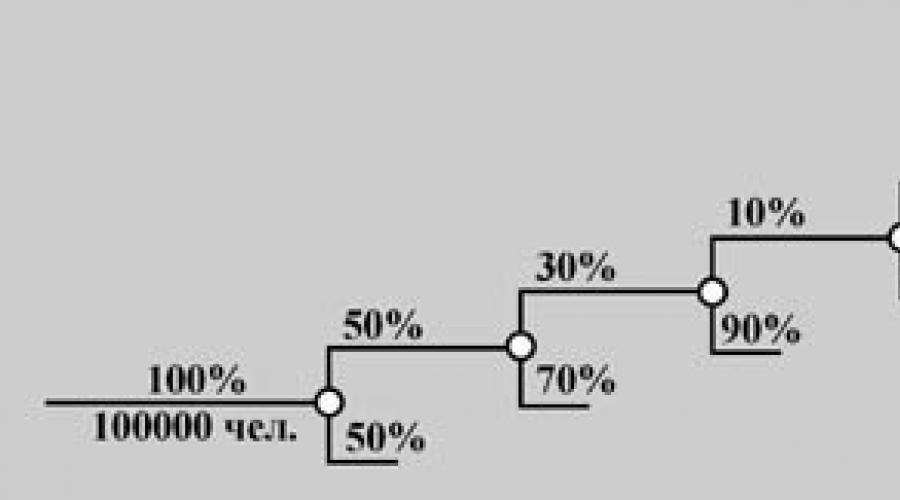
Primjer.Pretpostavimo da trebamo procijeniti u gradu s populacijom od stotinu tisuća stanovnika tržišta za novi proizvod, koji nije predmet, na primjer, za balzam za njegu oslikane kose. Razmotrite shemu "stabla vjerojatnosti". U isto vrijeme, vrijednost vjerojatnosti na svakoj "grani" trebamo približno procijeniti. Dakle, naš tržišni kapacitet procjenjuje:
1) od svih stanovnika Grada žena 50%,
2) svih ženasto 30% boje kose često,
3) od njih samo 10% uživaju balzam za obojenu kosu,
4) Od ovih, samo 10% može dobiti hrabrost da isprobate novi proizvod,
5) Od ovih 70% obično kupuje sve od nas, ali iz naših konkurenata.

Odluka:Prema zakonu umnožavanja vjerojatnosti, određujemo vjerojatnost zanimljivih događaja za nas a \u003d (rezident grada kupuje ovaj novi balzam) \u003d 0.00045.
Pomnožite tu vrijednost vjerojatnosti za broj stanovnika grada. Kao rezultat toga, imamo samo 45 potencijalnih kupaca, a ako uzmemo u obzir da je jedan mjehurić ovog fonda dovoljno nekoliko mjeseci, trgovina nije previše zauzeta.
Ipak, postoje koristi od naših procjena.
Prvo, možemo usporediti predviđanja različitih poslovnih ideja, u shemama će imati različite "razvoja", i, naravno, vrijednosti vjerojatnosti također će biti različite.
Drugo, kao što smo već izgovorili, slučajna vrijednost nije zato što se zove slučajno da ne ovisi o bilo čemu. Samo ona točan Vrijednost nije unaprijed poznata. Znamo da se prosječan broj kupaca može povećati (na primjer, uz pomoć oglašavanja novog proizvoda). Dakle, ima smisla usredotočiti se na one "razvoj", gdje nam raspodjela vjerojatnosti ne odgovara osobi posebno, na čimbenicima koje možemo utjecati.
Razmotrite još jedan kvantitativni primjer proučavanja ponašanja kupaca.
Primjer.Tijekom dana tržište hrane posjećuje prosječno 10.000 ljudi. Vjerojatnost da posjetitelj tržišta dolazi u paviljon mliječnih proizvoda je 1/2. Poznato je da je u ovom paviljonu u prosjeku za prodaju po danu 500 kg različitih proizvoda.
Je li moguće tvrditi da prosječna kupnja u paviljonu teži samo 100 g?
Rasprava.Naravno, to je nemoguće. Jasno je da nisu svi koji su otišli u paviljon, kao rezultat toga, nešto tamo kupilo nešto.

Kao što je prikazano na dijagramu da odgovori na pitanje prosječne težine kupnje, moramo pronaći odgovor na pitanje, što je vjerojatnost da će osoba koja je došla do paviljona kupiti nešto tamo. Ako na raspolaganju nema takvih podataka, a mi ih trebamo, morat ćete ih dobiti sami, nakon gledanja posjetitelja paviljona neko vrijeme. Pretpostavimo da su naša zapažanja pokazala da samo petina posjetitelja paviljona kupuje nešto.
Čim se ove procjene dobiju, zadatak postaje jednostavan. Od 10.000 ljudi koji dolaze na tržište, 5000 će ući u paviljon mliječnih proizvoda, shopping će biti samo 1000. Prosječna težina kupnje je 500 grama. Zanimljivo je napomenuti da bi se izgradila potpuna slika o tome što se događa, logika uvjetnih "baterija" treba odrediti u svakoj fazi našeg razmišljanja, kao i ako smo radili s "specifičnom" situacijom, a ne vjerojatnosti.
Zadaci za samopouzdanje
1. Pretpostavimo da postoji električni krug koji se sastoji od N niza povezanih elemenata, od kojih svaki radi neovisno od ostalih.

Vjerojatnost P je poznata u redu svakog elementa. Odredite vjerojatnost rada cijelog područja lanca (događaj a).
2. Učenik zna 20 od 25 ispitnih pitanja. Pronađite vjerojatnost da učenik zna tri pitanja koju mu nudi.
3. Proizvodnja se sastoji od četiri uzastopna koraka, na svakom od kojih oprema radi, za koje su vjerojatnosti neuspjeha u sljedećem mjesecu jednake odnosno p 1, p 2, p 3 i p 4. Pronađite vjerojatnost da u mjesecu neće biti niti jedan zaustavljanje proizvodnje zbog kvara opreme.
Događaji koji se jako događaju ili u našoj mašti mogu podijeliti u 3 skupine. To su pouzdani događaji koji će se definitivno dogoditi, nemoguće događaje i slučajne događaje. Teorija vjerojatnosti proučava se slučajnim događajima, tj. Događaji koji se mogu dogoditi ili se ne događaju. Ovaj članak će biti prisutan u kratkom obliku teorije vjerojatnosti formula i primjera rješavanja problema na teoriji vjerojatnosti koja će biti u 4 zadatke matematike EE (razina profila).
Zašto trebate teoriju vjerojatnosti
Povijesno gledano, potreba za proučavanjem tih problema nastala je u 17. stoljeću u vezi s razvojem i profesionalizacijom kockanja i izgledom kasina. Bio je to pravi fenomen koji je zahtijevao njegovo istraživanje i istraživanje.
Igra karata, kosti, rulet stvorio je situacije kada se može dogoditi bilo koji od konačnog broja jednakih događaja. Postojala je numerička procjena mogućnost pojave jednog ili drugog događaja.
U 20. stoljeću ispostavilo se da ova naizgled neozbiljna znanost igra važnu ulogu u znanju o temeljnim procesima koji se pojavljuju u mikrometru. Stvorena je moderna teorija vjerojatnosti.
Osnovne pojmove teorije vjerojatnosti
Cilj proučavanja teorije vjerojatnosti je događaji i njihove vjerojatnosti. Ako je događaj kompliciran, može se podijeliti na jednostavne komponente čije su vjerojatnosti lako pronaći.
Zbroj događaja A i B naziva se događaj C, koji se sastoji u činjenici da postoji ili događaj a ili događaj u ili događajima a u isto vrijeme.
Rad događaja A i B naziva se događaj uz razmatranje da se dogodio događaj a i događaj.
Događaji A i B se naziva neosjetljivim ako se ne mogu pojaviti istovremeno.
Događaj A se zove nemoguće ako se ne može dogoditi. Ovaj događaj je označen simbolom.
Događaj A naziva se pouzdano ako će se to dogoditi. Ovaj događaj je označen simbolom.
Neka svaki događaj bude u skladu s brojem p (a). Ovaj broj p (a) naziva se vjerojatnost događaja a, ako su sljedeći uvjeti ispunjeni s ovom sukladnost.
Važan određeni slučaj je situacija kada postoje jednako zvučni elementarni ishodi, a proizvoljni ishodi formiraju se događajima A. U ovom slučaju, vjerojatnost se može unijeti formulom. Vjerojatnost nametnuta na ovaj način naziva se klasična vjerojatnost. Može se dokazati da su u ovom slučaju napravljeni svojstva 1-4.
Zadaci o teoriji vjerojatnosti koje se nalaze na ispitu matematike uglavnom su povezane s klasičnom vjerojatnošću. Takvi zadaci mogu biti vrlo jednostavni. Posebno su jednostavni zadaci na teoriji vjerojatnosti u demonstracijskim mogućnostima. Lako je izračunati broj povoljnih ishoda, izravno u stanju napisan je broj svih ishoda.

Odgovor se dobiva formulom.
Primjer zadatka iz riječi matematike za određivanje vjerojatnosti
Na stolu leži 20 pite - 5 s kupusom, 7 s jabukama i 8 s rižom. Marina želi uzeti pašte. Koja je vjerojatnost da će uzeti paštetu s rižom?
Odluka.
U ukupnim jednakim elementarnim ishodima 20, to jest, marina može potrajati bilo koju od 20 pite. Ali moramo cijeniti vjerojatnost da će Marina uzeti pidriti s rižom, to jest, gdje je jedan izbor lutke s rižom. To znači da imamo broj povoljnih ishoda (izbori pite s rižom) samo 8. Tada će se vjerojatnost odrediti formulom:
![]()
Nezavisni, suprotni i proizvoljni događaji
Međutim, u otvorenoj banci, zadaci su počeli ispunjavati složenije zadatke. Stoga obratite pozornost na čitatelja i druga pitanja proučena u teoriji vjerojatnosti.
Događaji A i B se nazivaju neovisnim ako vjerojatnost svakog od njih ne ovisi o tome je li došlo do drugog događaja.
Događaj b je da se događaj ne događa, tj. Događaj B je suprotno od događaja A. Vjerojatnost suprotnog događaja jednaka je jednom minusu vjerojatnost izravnog događaja, tj. ,
Teoremi dodavanja i množenja vjerojatnosti, formula
Za proizvoljne događaje A i vjerojatnost iznosa tih događaja jednaki sumu njihove vjerojatnosti bez vjerojatnosti njihovog zajedničkog događaja, tj. ,
Za neovisne događaje, a i po vjerojatnosti rada ovih događaja jednaka je proizvodu svojih vjerojatnosti, tj. u ovom slučaju .
Posljednja 2 izjava nazivaju se teoremi dodavanja i množenja vjerojatnosti.
Ne uvijek računajući broj ishoda je tako jednostavan. U nekim slučajevima potrebno je koristiti kombinatorske formule. U ovom slučaju, najvažnije je brojanje broja događaja koji zadovoljavaju određene uvjete. Ponekad ta vrsta brojanja može postati neovisna zadaća.
Koliko načina mogu sjediti 6 studenata na 6 slobodnih mjesta? Prvi student će uzeti bilo koji od 6 mjesta. Svaka od ovih opcija odgovara 5 načina da se dogodi drugi student. Za treći student nalaze se 4 slobodna mjesta, za četvrti - 3, za peti - 2, šesti će uzeti samo preostalo mjesto. Da biste pronašli broj svih opcija, morate pronaći proizvod koji je označen simbolom od 6! I pročitajte "šest faktorija".
Općenito, odgovor na ovo pitanje daje formulu za broj permutacija od P stavki u našem slučaju.
Razmotrite sada još jedan slučaj s našim učenicima. Koliko načina mogu sjediti 2 studenta na 6 slobodnih mjesta? Prvi student će uzeti bilo koji od 6 mjesta. Svaka od ovih opcija odgovara 5 načina da se dogodi drugi student. Da biste pronašli broj svih opcija, morate pronaći posao.
Općenito, odgovor na ovo pitanje daje formulu za broj smještaja od N elemenata K elemenata
U našem slučaju.
I posljednji slučaj iz ove serije. Koliko načina možete odabrati tri studenta od 6? Prvi student može se odabrati 6 u drugim metodama - 5 u trećim metodama - četiri. No, među tim opcijama, jedan i isti vrh studenata nalaze se 6 puta. Da biste pronašli broj svih opcija, potrebno je izračunati vrijednost :. Općenito, odgovor na ovo pitanje daje formulu za broj kombinacija od elemenata po elementima:
U našem slučaju.
Primjeri rješavanja problema iz riječi matematike na definiciju vjerojatnosti
Zadatak 1. iz prikupljanja. Yashchenko.
Na tanjuru od 30 pite: 3 s mesom, 18 s kupusom i 9 s trešnjicom. Sasha nasumce bira jednu paštenju. Pronađite vjerojatnost da će biti s trešnja.
![]() .
.
Odgovor: 0,3.
Zadatak 2. iz prikupljanja. Yashchenko.
U svakoj seriji od 1000 žarulja u prosjeku 20 neispravnih. Pronađite vjerojatnost da će slučajno žarulja iz zabave biti dobra.
Rješenje: Broj dobrih svjetala 1000-20 \u003d 980. Tada će vjerojatnost da će donesena žarulja od stranke biti dobra:
![]()
Odgovor: 0,98.
Vjerojatnost koja pod testiranjem učenika matematike u je, više od 9 zadataka riješit će više od 9 zadataka, jednako 0,67. Vjerojatnost da će U. će ispravno riješiti više od 8 zadataka, jednako 0,73. Pronađite vjerojatnost da će U. će ispravno riješiti točno 9 zadataka.
Ako zamislimo brojčano izravno i bilježimo točke 8 i 9, vidjet ćemo da je stanje "W. To će biti ispravno riješiti točno 9 zadataka "u stanju" W. Točno je riješiti više od 8 zadataka, "ali se ne odnosi na stanje" W. Zasigurno će riješiti više od 9 zadataka. "
Međutim, stanje "U. Sigurno će se riješiti više od 9 zadataka "sadržano je u" U. Sigurno će riješiti više od 8 zadataka. " Dakle, ako označavamo događaje: "W. Točno je riješiti točno 9 zadataka "- kroz" W. Ispravno će riješiti više od 8 zadataka "- kroz B", W. Sigurno će riješiti više od 9 zadataka "kroz C. rješenje će izgledati ovako:
Odgovor: 0,06.
Na ispitu geometrije, školarac odgovara na jedno pitanje s popisa ispitnih pitanja. Vjerojatnost da je ovo pitanje na temu "trigonometrija" je 0,2. Vjerojatnost da je ovo pitanje o temi "vanjskim kutovima" je 0,15. Pitanja koja istovremeno odnose na ove dvije teme, br. Pronađite vjerojatnost da će studentski ispit dobiti pitanje na jednoj od tih dviju tema.
Razmislimo o tome što se naši događaji daju. Dobili smo dva nepotpuna događanja. To je, ili će se pitanje odnositi na temu "trigonometrija" ili na temu "vanjskim kutovima". Teoremom vjerojatnosti, vjerojatnost nepotpunih događaja jednaka je zbroju vjerojatnosti svakog događaja, moramo pronaći zbroj vjerojatnosti tih događaja, odnosno:
Odgovor: 0,35.
Soba je osvijetljena fenjerom s tri svjetiljke. Vjerojatnost razbijanja jedne svjetiljke tijekom godine je 0,29. Pronađite vjerojatnost da će tijekom godine barem jedna lampa propasti.
Razmotrite moguće događaje. Imamo tri žarulje, od kojih svaki može prevladati ili istovariti neovisno o bilo kojoj drugoj žaruljici. To su neovisni događaji.
Zatim navodemo opcije za takve događaje. Prihvaćamo oznaku: - Svjetlo gori, zapaljena žarulja. I odmah, izračunavamo vjerojatnost događaja. Na primjer, vjerojatnost događaja u kojem postoje tri neovisna događanja "svijetlo žarulja", "svjetlo žarulja opeklina", "svjetlo žarulja opeklina": gdje se vjerojatnost događanja "žarulja" izračunava kao vjerojatnost događaj nasuprot događaj "svjetlo žarulja", naime :.
Imajte na umu da imamo povoljne nepotpune događaje od samo 7. Vjerojatnost takvih događaja jednaka je zbroju vjerojatnosti svakog događaja :.
Odgovor: 0,975608.
Možete tražiti drugi zadatak na slici ispod:

Dakle, razumijemo da se teorija vjerojatnosti formula i primjera rješavanja problema s kojima se možete zadovoljiti u verziji EGE.
Što je vjerojatnost?
Suočeni s ovim izrazom po prvi put, ne bih razumio što je to. Stoga ću pokušati objasniti dostupno.
Vjerojatnost je prilika da će se događaj koji trebate dogoditi.
Na primjer, odlučili ste otići prijatelju, sjetiti se ulaza, pa čak i pod na kojem živi. Ali soba i lokacija apartmana zaboravili su. I stojite na stubištu, i ispred vas odaberete.
Koja je prilika (vjerojatnost) onoga što ako nazovete prva vrata, hoćete li otvoriti svog prijatelja? Ukupni apartmani i prijatelj živi samo za jedan od njih. Uz jednaku šansu, možemo odabrati sva vrata.
Ali što je ta prilika?
Vrata, vrata koju želite. Vjerojatnost pogoditi pozivom na prva vrata :. To jest, jednom od tri ste precizno pogodite.
Želimo saznati pozivanjem vremena, koliko često ćemo pogoditi vrata? Razmotrimo sve opcije:
- Nazvali ste B. 1y. vrata
- Nazvali ste B. 2 godine vrata
- Nazvali ste B. 3y. vrata
Sada razmotrite sve opcije u kojima prijatelj može biti:
ali. Po 1i Vrata
b. Po 2 godine Vrata
u. Po 3e Vrata
Usporedimo sve opcije u obliku tablice. Popis oznaka označava opcije kada se vaš izbor podudara s lokacijom prijatelja, križ - kada se ne podudara.
Kao što možete vidjeti sve možda Opcije Mjesto prijatelja i po vašem izboru, koja se nazove.
ALI povoljni ishodi Ukupno . To jest, jer pogađate, nazovite vrata jednom, tj. ,
To je vjerojatnost - omjer povoljnog ishoda (kada se vaš izbor podudarao s lokacijom prijatelja) na broj mogućih događaja.
Definicija je formula. Vjerojatnost je napravljena za označavanje p, pa:
Ova formula nije vrlo pogodna, pa ćemo prihvatiti broj povoljnih ishoda, a za je ukupan broj ishoda.
Vjerojatnost se može zabilježiti kao postotak, za to morate umnožiti rezultirajući rezultat na:
Vjerojatno, riječ "ishodi" požurio vas je. Budući da matematika naziva razne akcije (imamo takvu akciju - to je pokusi zvona zvona), onda je rezultat takvih eksperimenata uobičajeno da se zove ishod.
Pa, ishodi su povoljni i nepovoljni.
Vratimo se na naš primjer. Pretpostavimo da smo nazvali jedno od vrata, ali nam je nepoznato čovjek otvorio. Nismo pogodili. Koja je vjerojatnost da ako nazovete jednu od preostalih vrata, otvorit ćemo naš prijatelj?
Ako ste mislili da je to pogreška. Radimo se s.
Imamo dva vrata. Dakle, imamo moguće korake:
1) poziv 1-uu vrata
2) Nazovite 2-uu vrata
Prijatelj, sa svem to, točno je iza jednog od njih (jer za onaj u kojem smo nazvali, to nije):
a) prijatelj za 1. Vrata
b) svaki 2-o. Vrata
Ponovo ćemo nacrtati stol:

Kao što možete vidjeti, postoje opcije, od kojih su povoljne. To jest, vjerojatnost je jednaka.
Zašto ne?
Situaciju koju smo razmotrili - primjer ovisnih događaja. Prvi događaj je prvi poziv na vrata, drugi događaj je druga zvona.
I ovisni da su pozvani jer utječu na sljedeće akcije. Uostalom, ako nakon prvog poziva otvorili smo prijatelja na vratima, što bi onda bila vjerojatnost da je on u jednoj od ostalih dva? Pravo,.
Ali ako postoje ovisni događaji, onda mora postojati neovisan? Istina, postoji.
Primjer udžbenika je bacanje novčića.
- Jednom baciti novčić. Koja je vjerojatnost da Eagle pada, na primjer? Tako je -, jer opcije svih (bilo orao ili žurbe, mi ćemo zanemariti vjerojatnost novčića na rubu), ali nas organiziramo samo.
- Ali žurba je ispala. U redu, ponovno bacite. Koja je vjerojatnost pada orla? Ništa se nije promijenilo, sve je isto. Koliko opcija? Dva. I koliko nam odgovara? Jedan.
I neka tisuću puta zaredom ispasti u žurbi. Vjerojatnost eagle Fallout će biti sve dobro. Opcije su uvijek i povoljne -.
Razlikovati ovisne događaje od neovisnih:
- Ako se eksperiment provodi jednom (nakon što bacaju novčić, 1 vrijeme poziva na vrata, itd.), Tada su događaji uvijek neovisni.
- Ako se eksperiment provodi nekoliko puta (novac je jednom odbačen, vrata se nazivaju nekoliko puta), a zatim je prvi događaj uvijek neovisan. A onda, ako se broj povoljnog ili broja svih ishoda mijenja, događaji ovise, a ako ne, neovisni.
Uzmimo malo ugriza da odredimo vjerojatnost.
Primjer 1.
Kovanica je bačena dva puta. Koja je vjerojatnost da Eagle padne dva puta u nizu?
Odluka:
Razmotrite sve moguće opcije:
- Orao-orel
- Orao
- Rush-orel
- Rusk-Ruska.
Kao što možete vidjeti cijelu opciju. Od njih smo zadovoljni samo. To je vjerojatnost:
Ako se uvjet traži da jednostavno pronađe vjerojatnost, odgovor se mora dati u obliku decimalne frakcije. Ako je naznačeno da se odgovor treba dati kao postotak, onda bismo se pomnožili.
Odgovor:
Primjer 2.
U kutiji slatkiša, svi slatkiši su pakirani u istom omotu. Međutim, od slatkiša - s maticama, s rakijom, s trešnja, s karamelom i s Nugoyjem.
Koja je vjerojatnost, uzimajući jedan bombon, dobiti slatkiš s orasima. Odgovor dati u postocima.
Odluka:
Koliko mogućih ishoda? ,
To jest, uzimajući jedan slatkiša, to će biti jedan od postojećih kutija.
I koliko povoljnih ishoda?
Jer u kutiji samo slatkiši s orasima.
Odgovor:
Primjer 3.
U kutiji lopti. Bijela od njih, - crna.
- Koja je vjerojatnost povlačenja bijele lopte?
- Dodali smo crne lopte u kutiju. Što je sada vjerojatnost povlačenja bijele lopte?
Odluka:
a) u kutiji cijele loptice. Bijela od njih.
Vjerojatnost je:
b) Sada su kugle u kutiji postale. I bijela je ostala koliko -.
Odgovor:
Puna vjerojatnost
| Vjerojatnost svih mogućih događaja jednaka je (). |
Pretpostavimo u ladici crvenih i zelenih kuglica. Koja je vjerojatnost povlačenja crvene lopte? Zelena lopta? Crvena ili zelena lopta?
Vjerojatnost Izvucite crvenu kuglu
Zelena lopta:
Crvena ili zelena lopta:
Kao što možete vidjeti, zbroj svih mogućih događaja jednaka je (). Razumijevanje ovog trenutka pomoći će vam da riješite mnoge zadatke.
Primjer 4.
U kutiji se nalazi markeri: zelena, crvena, plava, žuta, crna.
Koja je vjerojatnost povlačenja olovke crvenog filca?
Odluka:
Razmotrimo broj povoljni ishodi.
Nije crvena olovka za lice, to znači zeleno, plavo, žuto ili crno.
| Vjerojatnost da se događaj neće dogoditi je jednak minus vjerojatnosti da će se događaj dogoditi. |
Pravilo množenja vjerojatnosti neovisnih događaja
Što su neovisni događaji koje već znate.
A ako trebate pronaći vjerojatnost da će se dva (ili više) neovisnih događaja pojaviti u nizu?
Pretpostavimo da želimo znati što je vjerojatnost da će baciti vrijeme novčića, dvaput ćemo vidjeti orlov?
Već smo mislili.
A ako bacite vrijeme novčića? Koja je vjerojatnost da ćete vidjeti orla u nizu?
Ukupne opcije:
- Orao
- Orao
- Orao
- Orao
- Orao
- Žuriti
- Orao
- Rusk-Rush
Ne znam kako si, ali bio sam u zabludi, čineći ovaj popis. Wow! I samo nam opcija (prvo) odgovara.
Za 5 bacanja, možete sami napraviti popis mogućih ishoda. Ali matematika nisu tako vrijedne poput vas.
Stoga su prvi put primijetili, a zatim su dokazali da se vjerojatnost određenog slijeda neovisnih događaja smanjuje svaki put na vjerojatnost jednog događaja.
Drugim riječima,
Razmislite o primjeru svih istih, zlostavljanih, kovanica.
Vjerojatnost orao u testu? , Sada bacimo vrijeme novčića.
Koja je vjerojatnost uzastopnog orla?
Ovo pravilo funkcionira ne samo ako se traži da pronađemo vjerojatnost da će se isti događaj pojaviti nekoliko puta zaredom.
Ako želimo pronaći slijed rijeke-orao, kada lubanje zaredom, također bismo to učinili.
Vjerojatnost padanja - Eagle -.
Vjerojatnost padanja slijeda rijeke rijeke - rijeke:
Možete se provjeriti, doći do tablice.
Pravilo dodavanja vjerojatnosti nepotpunih događaja.
Zaustavite se! Nova definicija.
Radimo se s. Uzmi naš istrošeni novčić i bacite ga vrijeme.
Moguće opcije:
- Orao
- Orao
- Orao
- Orao
- Orao
- Žuriti
- Orao
- Rusk-Rush
Tako nepotpuni događaji, to je određeni, određeni slijed događaja. - To su nepotpuni događaji.
Ako želimo utvrditi što je vjerojatnost dva (ili više) nepotpunih događaja, preklapamo vjerojatnost ovih događaja.
Potrebno je shvatiti da je posljedice orla ili žurbe dva neovisna događaja.
Ako želimo utvrditi kakva je vjerojatnost sekvence) (ili bilo koje druge), tada koristimo pravilo umnožavanja vjerojatnosti.
Koja je vjerojatnost pada na prvo bacanje orla, a tijekom druge i treće žurbe?
Ali ako želimo znati što je vjerojatnost da će ispaliti jednu od nekoliko sekvenci, na primjer, kada Eagle padne točno vrijeme, tj. Mogućnosti i, moramo preklopiti vjerojatnost ovih sekvenci.
Ukupne opcije, odgovara nam.
Isto možemo dobiti stvaranjem vjerojatnosti izgleda svakog slijeda:
Dakle, mi presavimo vjerojatnost kada želimo odrediti vjerojatnost nekih, nepotpunih, sekvenci događaja.
Postoji izvrsno pravilo koje ne pomaže da se ne zbuni kada se pomnože i kada se može preklopiti:
Povratak na primjer kad smo bacili novac, i želimo saznati vjerojatnost da ćete vidjeti vrijeme orao.
Što ce se dogoditi?
Mora pasti:
(Orao i žurba i žurba) ili (žurba i orao i žurba) ili (žurba i žurba i orao).
Ispada:
Pogledajmo nekoliko primjera.
Primjer 5.
U kutiji leži s olovkom. Crvena, zelena, narančasta i žuta i crna. Koja je vjerojatnost povlačenja crvenih ili zelenih olovaka?
Odluka:
Primjer 6.
Igranje kosti je dvaput bačena, kakva je vjerojatnost da 8 bodova pada u iznosu?
Odluka.
Kako možemo dobiti naočale?
(s) ili (i) ili (i) ili (i) ili (i).
Vjerojatnost pada jednog (bilo kojeg) lica.
Mi smatramo vjerojatnost:
Vježbati.
Mislim da je sada postalo jasno kada trebate razmotriti vjerojatnosti kada ih dodate i kada se pomnožite. Nije li? Vježbajmo malo.
Zadaci:
Uzmite kartonsku palubu u koje karte, vrhunac, crvi, 13 trepha i 13 tambrourina. Od asa svakog odijela.
- Koja je vjerojatnost povlačenja trepsa u nizu (prva točkasta kartica koju smo vratili na palubu i mix)?
- Koja je vjerojatnost povlačenja crne karte (vrhovi ili trephije)?
- Koja je vjerojatnost povlačenja slike (warta, dama, kralj ili asa)?
- Koja je vjerojatnost povlačenja dvije slike u nizu (uklanjamo prvu isprekidanu karticu s palube)?
- Koja je vjerojatnost, uzimajući dvije karte, prikupljaju kombinaciju - (valuta, dama ili kralj) i as sekvenca u kojem će se izvući kartice, nije važno.
Odgovori:
Ako možete sami riješiti sve zadatke, onda ste veliki! Sada izazovi o teoriji vjerojatnosti na ispitu ćete kliknuti poput oraha!
Teorija vjerojatnosti. Prosječna razina
Razmotrite primjer. Pretpostavimo da bacimo kost za igru. Kakvu je to kosti, znaš? To se zove kocka s brojevima na rubovima. Koliko lica, toliko brojeva: od koliko? Prije.
Dakle, bacimo kost i želimo padati ili. I ispada.
U teoriji vjerojatnosti, kažu što se dogodilo povoljan događaj (nemojte brkati s prosperitetom).
Ako je pao, događaj bi također bio povoljan. Ukupno može biti samo dva povoljna događanja.
I koliko nepovoljno? Od mogućih događaja, to znači da su događaji nepovoljni (to je ako ispada ili).
Definicija:
Vjerojatnost se naziva omjer broja povoljnih događaja na broj svih mogućih događaja., To jest, vjerojatnost pokazuje koji udio svih mogućih događaja pada na povoljnosti.
Označite vjerojatnost latinskog pisma (očito, iz engleske riječi vjerojatnost je vjerojatnost).
Uobičajeno je mjeriti vjerojatnost u postocima (vidi temu). Za to se vrijednost vjerojatnosti mora pomnožiti. U primjeru s igrajući kost, vjerojatnost.
I u postocima:.
Primjeri (rješavanje sebe):
- Što je vjerojatnost kada bacanje novčića pada orao? I koliko je vjerojatno da će žurba ispasti?
- Koja je vjerojatnost kada bacanje igranja kosti će pasti i broj? A s onim što je čudno?
- U kutiji običnih, plavih i crvenih olovaka. Na slučajnoj olovci. Koja je vjerojatnost povlačenja jednostavna?
Rješenja:
- Koliko opcija? Eagle i Rush - samo dva. I koliko ih je povoljno? Samo jedan - orao. Stoga vjerojatnost
Uz šešir, isti :.
- Ukupne opcije: (koliko strane kocke, toliko različitih opcija). Povoljni od njih: (To su svi čak i brojevi :).
Vjerojatnost. S neparnim, prirodnim, istim. - Ukupno :. Povoljni :. Vjerojatnost:.
Puna vjerojatnost
Sve olovke u zelenoj kutiji. Koja je vjerojatnost povlačenja crvene olovke? Nema šanse: vjerojatnost (nakon svega, povoljne događaje -).
Takav događaj se zove nemoguć.
I što je vjerojatnost povlačenja zelene olovke? Povoljni događaji su potpuno isti kao i događaji svega (svi događaji su povoljni). To znači da je vjerojatnost jednaka ili.
Takav se događaj naziva pouzdan.
Ako je u kutiji zelenih i crvenih olovaka, koja je vjerojatnost povlačenja zelene ili crvene? Ipak. Napomena Takva stvar: Vjerojatnost povlačenja zelene je jednaka i crvena -.
Ukratko, te vjerojatnosti su jednake upravo to. I.e, zbroj vjerojatnosti svih mogućih događaja jednaka je ili.
Primjer:
U kutiji olovke, među njima plava, crvena, zelena, jednostavna, žuta, a ostalo su narančaste. Koja je vjerojatnost da ne povlačite zelenu?
Odluka:
Zapamtite da su sve vjerojatnosti dane u iznosu. I vjerojatnost povlačenja zelene je jednaka. To znači da vjerojatnost ne izvlači zelenu jednaku.
Zapamtite ovu tehniku:vjerojatnost da se događaj neće dogoditi jednak minus vjerojatnost da će se događaj dogoditi.
Samostalni događaji i pravilo množenja
Baciš vrijeme novčića i želiš da su oba puta orao. Koja je vjerojatnost toga?
Pokrenimo sve moguće opcije i odredite koliko njih:
Eagle-Eagle, riječni orlo, orao-rijeka, Rushka-rijeka. Što drugo?
Ukupna opcija. Samo je jedna stvar pogodna za nas: Eagle Orel. Ukupna vjerojatnost je jednaka.
U redu. A sada bacimo vrijeme novčića. Smiri se. Se dogodilo? (odgovor).
Možete to vidjeti s dodatkom svakog sljedećeg bacanja, vjerojatnost je smanjena. Opće se pravilo naziva pravilo umnožavanja:
Vjerojatnosti neovisnih događaja su varijabilne.
Što su neovisni događaji? Sve je logično: to su oni koji ne ovise jedni o drugima. Na primjer, kada nekoliko puta bacimo novčić, proizvedeno je novo bacanje, od kojih se rezultat ne ovisi o svim prethodnim bacanju. Uz isti uspjeh, možemo baciti dva različita kovanica u isto vrijeme.
Više primjera:
- Igranje kosti je dvaput bačena. Koja je vjerojatnost da oboje ispada?
- Kovanica je bačena vremena. Koja je vjerojatnost da Eagle po prvi put padne, a zatim dvaput požurite?
- Igrač baca dvije kosti. Koja je vjerojatnost da će količina brojeva na njima biti jednaka?
Odgovori:
- Događaji su neovisni, to znači da pravilo umnožavanja funkcionira :.
- Vjerojatnost orla je jednaka. Vjerojatnost žurbe je također. Alternativni:
- 12 može raditi samo ako pada dva puta :.
Nepotpune događaje i pravilo dodavanja
Insobity se nazivaju događajima koji se međusobno nadopunjuju do potpune vjerojatnosti. Iz imena je jasno da se ne mogu istovremeno dogoditi. Na primjer, ako bacite novčić, može ispasti ili orao ili žurbu.
Primjer.
U kutiji olovke, među njima plava, crvena, zelena, jednostavna, žuta, a ostalo su narančaste. Koja je vjerojatnost povlačenja zelene ili crvene?
Odluka.
Vjerojatnost povlačenja zelene olovke jednaka je. Crvena -.
Povoljni događaji ukupno: zelena + crvena. To znači da je vjerojatnost izvađenja zelene ili crvene jednake.
Ista se vjerojatnost može predstavljati u ovom obliku :.
Ovo je pravilo dodavanja:vjerojatnosti nepotpunih događaja su presavijeni.
Zadaci mješovitih vrsta
Primjer.
Kovanica je bačena dva puta. Koja je vjerojatnost da će rezultat bacanja biti drugačiji?
Odluka.
Podrazumijeva se da ako je prvi orao, drugi bi trebao biti žurba i obrnuto. Ispada da postoje dva para neovisnih događaja, a ovi parovi su nerazumljivi jedni s drugima. Bez obzira kako se zbuniti gdje se pomnožiti, ali gdje se preklopiti.
Postoji jednostavno pravilo za takve situacije. Pokušajte opisati što bi se trebalo dogoditi povezivanjem događaja sindikata "i" ili "ili". Na primjer, u ovom slučaju:
Mora pasti (orao i žuriti) ili (Rushka i Eagle).
Gdje postoji savez "i", bit će množenje i gdje je "ili" - dodatak:
Pokušajte sami:
- Što je vjerojatnost s dva novčića u bacanju i istoj strani pada?
- Igranje kosti je dvaput bačena. Koja je vjerojatnost da će točke ispadati?
Rješenja:
Još jedan primjer:
Baciti vrijeme novčića. Koja je vjerojatnost da orao barem jednom spada?
Odluka:
Teorija vjerojatnosti. Ukratko o glavnoj stvari
Vjerojatnost je omjer broja povoljnih događaja na broj svih mogućih događaja.
Nezavisni događaji
Dva događanja su neovisna ako se na pojavu jedne vjerojatnosti početka drugog ne mijenja.
Puna vjerojatnost
Vjerojatnost svih mogućih događaja jednaka je ().
Vjerojatnost da se događaj neće dogoditi je jednak minus vjerojatnosti da će se događaj dogoditi.
Pravilo množenja vjerojatnosti neovisnih događaja
Vjerojatnost određenog slijeda neovisnih događaja jednaka je proizvodu vjerojatnosti svakog događaja.
Nevažeći događaji
Nepotpuni su događaji koji se ne mogu dogoditi istovremeno kao rezultat eksperimenta. Brojni nepotpuni događaji čine potpunu skupinu događaja.
Vjerojatnosti nepotpunih događaja su presavijeni.
Opisujući što bi se trebalo dogoditi pomoću saveza "i" ili "ili", umjesto "i" staviti znak umnožavanja i umjesto "ili" - dodavanje.
Pa, tema je završena. Ako čitate ove linije, onda ste vrlo cool.
Jer samo 5% ljudi može svladati nešto sami. A ako čitate na kraju, onda ste ušli u ovih 5%!
Sada najvažnija stvar.
Shvatili ste teoriju o ovoj temi. I ponavljam, to ... to je samo super! Ti si bolji od apsolutne većine svojih vršnjaka.
Problem je u tome što to možda nije dovoljno ...
Za što?
Za uspješno donošenje uporabe, za upis u Institut o proračunu i, što je najvažnije, za život.
Neću vas ništa uvjeriti, samo ću reći jednu stvar ...
Ljudi koji su dobili dobro obrazovanje zarađuju mnogo više od onih koji ga nisu primili. To su statistika.
Ali to nije glavna stvar.
Glavna stvar je da su sretniji (postoje takva istraživanja). Možda zato što ima mnogo više mogućnosti u korist od njih i život postaje svjetliji? Ne znam...
Ali, razmislite o sebi ...
Što trebate biti sigurni da budete bolji od drugih na ispitu i biti u konačnici ... sretniji?
Napunite ruku rješavanjem zadataka na ovoj temi.
Nećete pitati teoriju na ispitu.
Trebat će vam rješavanje zadataka neko vrijeme.
A ako ih niste riješili (puno!), Definitivno budite glupo pogrešni ili jednostavno nemate vremena.
To je kao u sportu - morate ponoviti mnogo puta kako biste bili sigurni.
Naći gdje želite zbirku, obvezno s rješenjima, detaljna analiza I odlučiti, odlučiti, odlučiti!
Možete koristiti naše zadatke (ne nužno) i mi, naravno, preporučujemo ih.
Da biste ispunili ruku uz pomoć naših zadataka, morate pomoći produžiti život u udžbenik youcever, koji sada čitate.
Kako? Postoje dvije opcije:
- Otvoreni pristup svim skrivenim zadacima u ovom članku - 299 Utrljajte.
- Otvoreni pristup svim skrivenim zadacima u svih 99 članaka udžbenika - 499 trlja.
Da, imamo 99 takvih članaka u našem udžbeniku i pristup za sve zadatke i svi skriveni tekstovi mogu se odmah otvoriti.
Pristup svim skrivenim zadacima pruža se za cijelo postojanje stranice.
U zaključku...
Ako naši zadaci ne vole, pronađite druge. Samo nemojte prestati na teoriji.
"Razumijem" i "mogu odlučiti" potpuno različite vještine. Trebate oboje.
Pronađite zadatak i odlučite!
Formule za izračunavanje vjerojatnosti događaja
1.3.1. Nezavisni slijed testa (Bernoulli shema)
Pretpostavimo da se neki eksperimenti mogu više puta provoditi s istim uvjetima. Neka se ovo iskustvo proizvode n. Jednom, tj., Sekvenca se provodi iz n. Testovi.
Definicija. Slijed n. testovi nazvani međusobno neovisni Ako bilo koji događaj povezan s ovim testom ne ovisi o svim događajima koji se odnose na druge testove.
Pretpostavimo neki događaj A. može se pojaviti s vjerojatnošću p. Kao rezultat jednog testa ili se ne dogodi s vjerojatnošću p:= 1- p..
Definicija . Sekvenca je n.testovi formiraju Bernoulli shemu ako se izvrši sljedeći uvjeti:
slijed n. Testovi su međusobno neovisni
2) vjerojatnost događaja A. Ne razlikuje se od testiranja na test i ne ovisi o rezultatu u drugim testovima.
Događaj A. Oni nazivaju "uspjeh" testa, a suprotan događaj je "neuspjeh". Razmotrite događaj
 \u003d (B. n. Testovi su se pojavili Rivne m. "Uspjeh").
\u003d (B. n. Testovi su se pojavili Rivne m. "Uspjeh").
Da biste izračunali vjerojatnost ovog događaja, Bernoulli Formula vrijedi
p.( )
=
)
=
 , m.
= 1, 2, …, n.
, (1.6)
, m.
= 1, 2, …, n.
, (1.6)
gdje  - broj kombinacija od n. Elementi u m.
:
- broj kombinacija od n. Elementi u m.
:
 =
=
 =
= .
.
Primjer 1.16. Kocke bacaju tri puta. Pronaći:
a) vjerojatnost da će 6 bodova pasti dva puta;
b) vjerojatnost da se broj od šest neće pojaviti više od dva puta.
Odluka . "Uspjeh" testovi će se smatrati padom na kocku lica sa slikom od 6 bodova.
a) ukupan broj testova - n.\u003d 3, broj "uspjeha" - m.
\u003d 2. Vjerojatnost "uspjeha" - p.= ,
I vjerojatnost "neuspjeha" - p:\u003d 1 - \u003d. Zatim, prema Bernoulli formuli, vjerojatnost da će rezultat trostrukog lijevanja kocke dvostruko više od šest bodova će biti jednaka
,
I vjerojatnost "neuspjeha" - p:\u003d 1 - \u003d. Zatim, prema Bernoulli formuli, vjerojatnost da će rezultat trostrukog lijevanja kocke dvostruko više od šest bodova će biti jednaka
 .
.
b) označiti ALI Događaj koji leži u činjenici da će se lice s brojem točaka 6 pojaviti ne više od dva puta. Tada se događaj može zastupati kao zbroj tri nedosljednosti događaji A \u003d.
 ,
,
gdje U 3 0 - događaj kada se ne pojavi liniju interesa,
U 3 1 - događaj kada će se lice od interesa pojaviti jednom,
U 3 2 - događaj kada će se lice od interesa pojaviti dvaput.
Prema Bernoulli formuli (1.6) nalazimo
p.(ALI)
\u003d P ( )
=
p.(
)
=
p.( )=
)=
 +
+ +
+ =
=
=
 .
.
1.3.2. Uvjetna vjerojatnost događaja
Uvjetna vjerojatnost odražava utjecaj jednog događaja na vjerojatnost drugog. Promjena uvjeta u kojima se provodi eksperiment također utječe na
vjerojatnost pojave zanimljivog događaja.
Definicija. Neka biti A. i B. - Neki događaji i vjerojatnost p.(B.)> 0.
Uvjetna vjerojatnost događaji A. pod uvjetom da je "događaj B. većto se dogodilo "nazvao je omjer vjerojatnosti ovih događaja na vjerojatnost događaja koji se dogodio ranije od događaja čija je vjerojatnost potrebna. Uvjetna vjerojatnost je označena kao p.(A. B.). Zatim po definiciji
p.
(A.
B.)
=
 .
(1.7)
.
(1.7)
Primjer 1.17. Dvije kocke bacaju. Prostor osnovnih događaja sastoji se od naručenih parova brojeva
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6).
Primjer 1.16 Utvrđeno je da je događaj A. \u003d (broj naočala na prvoj kocki\u003e 4) i događaj C. \u003d (Količina točaka je 8) ovisna. Među odnosima
 .
.
Taj se odnos može tumačiti kako slijedi. Pretpostavimo da je rezultat prvog bacanja poznat da je broj točaka na prvoj kocki\u003e 4. slijedi da lijevanje druge kocke može dovesti do jednog od 12 ishoda koji čine događaj A.:
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6) .
U isto vrijeme događaj C. Samo dva od njih mogu odgovarati (5.3) (6.2). U ovom slučaju, vjerojatnost događaja C.
biti jednak  , Dakle, informacije o pojavi događaja A. utjecali na vjerojatnost događaja C..
, Dakle, informacije o pojavi događaja A. utjecali na vjerojatnost događaja C..
Vjerojatnost rada događaja
Multiplikacija Teorem
Vjerojatnost rada događajaA. 1 A. 2 A. n. Formula se određuje
p.(A. 1 A. 2 A. n.) \u003d P.(A. 1) P.(A. 2 A. 1)) p.(A. n. A. 1 A. 2 A. n- 1). (1.8)
Za rad dvaju događaja, slijedi to
p.(Ab) \u003d P.(A. B) P.{B.) \u003d P.(B. A.) P.{A.). (1.9)
Primjer 1.18. U seriji od 25 proizvoda 5 proizvoda neispravan. Dva proizvoda se odabire sukcesivno. Odredite vjerojatnost da su svi odabrani proizvodi neispravni.
Odluka. Označava događaje:
A. 1 \u003d (prvi proizvod neispravan),
A. 2 \u003d (drugi proizvod je neispravan),
A. 3 \u003d (Neispravan treći proizvod),
A. \u003d (Svi proizvodi su neispravni).
Događaj ALI postoji posao od tri događaja A. = A. 1 A. 2 A. 3 .
Iz teorema množenja (1.6) primati
p.(A.) \u003d P ( A. 1 A. 2 A. 3 ) = p.(A. 1) p.(A. 2 A. 1))p.(A. 3 A. 1 A. 2).
Definicija klasične vjerojatnosti omogućuje vam da pronađete p.(A. 1) je omjer broja neispravnih proizvoda na ukupan broj proizvoda:
p.(A. 1)=
 ;
;
p.(A. 2) – ovo je omjer broja neispravnih proizvoda koji ostaju nakon oduzimanja jednog, na ukupan broj preostalih proizvoda:
p.(A. 2
A. 1))=
 ;
;
p.(A. 3) je omjer broja neispravnih proizvoda koji ostaju nakon oduzimanja dva neispravna, na ukupan broj preostalih proizvoda:
p.(A. 3
A. 1 A. 2)= .
.
Onda vjerojatnost događaja A. biti jednak
p.(A.)
=

 =
= .
.
Mnogi, naišli na koncept "teorije vjerojatnosti", uplašeni su, misleći da je to nešto nepodnošljivo, vrlo komplicirano. Ali sve nije stvarno tako tragično. Danas ćemo razmotriti osnovni koncept učenja rješavanja problema na određenim primjerima.
Znanost
Koje studije takav dio matematike poput "teorije vjerojatnosti"? On bilježi obrasce i vrijednosti. Po prvi put ovo pitanje, znanstvenici su bili zainteresirani za osamnaesto stoljeće, kada je kockanje proučavano. Osnovni koncept teorije vjerojatnosti je događaj. To je svaka činjenica koja je navedena po iskustvu ili promatranju. Ali što je iskustvo? Još jedan osnovni koncept teorije vjerojatnosti. To znači da ovaj sastav okolnosti ne stvara slučajno, već s određenim ciljem. Što se tiče promatranja, ovdje sam istraživač ne sudjeluje u iskustvu, već jednostavno svjedoči o podacima o podacima, on ne utječe na ono što se događa.
Događaji
Saznali smo da je osnovni koncept teorije vjerojatnosti događaj, ali ne smatra se klasifikacijom. Svi su podijeljeni u sljedeće kategorije:
- Pouzdan.
- Nemoguće.
- Slučajno.
Bez obzira na to koje su događaje koji se promatraju ili stvaraju tijekom iskustva, svi su podložni ovoj klasifikaciji. Svaku vrstu vrsta nudimo zasebno upoznavanje.
Pouzdan događaj

To je okolnost na koju se vrši potreban skup događaja. Kako bi se bolje spustila u suštinu, bolje je donijeti neke primjere. Fizika i kemija i ekonomija i veća matematika podliježu ovom zakonu. Teorija vjerojatnosti uključuje tako važan koncept kao pouzdan događaj. Dajemo primjere:
- Radimo i dobivamo naknadu u obliku plaća.
- Prošlo je dobro ispiti, održano je natjecanje, primamo nagradu za to u obliku upisa u obrazovnu ustanovu.
- Ulovili smo novac u banku, ako je potrebno, vraćamo ih.
Takvi događaji su pouzdani. Ako ispunimo sve potrebne uvjete, onda ćemo definitivno dobiti očekivani rezultat.
Nemoguće događaje
Sada smatramo elemente teorije vjerojatnosti. Predlažemo da odemo na objašnjenje sljedeće vrste događaja, naime je nemoguće. Za početak, raspravljat ćemo o najvažnijem pravilu - vjerojatnost nemogućeg događaja je nula.
Iz ove formulacije nemoguće se povlačiti pri rješavanju problema. Da objasnimo, dajemo primjere takvih događaja:
- Voda zamrznuta na temperaturi plus deset (nemoguće je).
- Nijedna struja ne utječe na proizvodnju (također je nemoguće, kao u prethodnom primjeru).
Više primjera ne treba dati, budući da gore opisani gore odražavaju suštinu ove kategorije. Nemogući događaj nikada se neće dogoditi u bilo koje okolnosti.
Slučajni događaji

Proučavanje elemenata teorije vjerojatnosti, posebnu pozornost treba posvetiti ovoj vrsti događaja. To je oni u ovom znanstvenom studiju. Kao rezultat iskustva, nešto se može dogoditi ili ne. Osim toga, test se može provesti neograničen broj puta. Svijetli primjeri mogu poslužiti:
- List kovanica je iskustvo ili test, eagle pada je događaj.
- Povlačenje lopte slijepo - test, crvena lopta uhvaćena - to je događaj i tako dalje.
Takvi primjeri mogu biti neograničena količina, ali općenito, bit mora biti jasna. Sažeti i sistematizirati znanje stečeno na događajima, dan je tablica. Teorija vjerojatnosti proučava samo posljednji pogled na sve prikazane.
ime | definicija | |
Pouzdan | Događaji koji se pojavljuju sa 100% jamstvom pri ispunjavanju određenih uvjeta. | Ulazak u obrazovnu ustanovu s dobrom predajom prijemnog ispita. |
Nemoguće | Događaji koji se nikada neće dogoditi ni pod kojim okolnostima. | Ima snijeg na temperaturi zraka plus trideset stupnjeva Celzija. |
Slučajan | Događaj koji se može pojaviti ili ne tijekom eksperimenta / testa. | Inteligencija ili propusti prilikom bacanja košarku u prsten. |
Zakoni
Teorija vjerojatnosti je znanost koja proučava sposobnost ispadanja bilo kojeg događaja. Kao i drugi, ima neka pravila. Postoje sljedeći zakoni teorije vjerojatnosti:
- Konvergencija sekvenci slučajnih varijabli.
- Zakon velikih brojeva.
Prilikom izračunavanja mogućnosti kompleksa možete koristiti kompleks jednostavnih događaja kako biste olakšali rezultat i brzo. Imajte na umu da se zakoni teorije vjerojatnosti lako dokazuju korištenjem nekih teorema. Nudimo početak upoznavanja s prvim zakonom.
Konvergencija slučajnih varijabli

Imajte na umu da su vrste konvergencije donekle:
- Slijed slučajnih varijabli poželjno je po vjerojatnosti.
- Skoro nemoguće.
- Rven-kvadratna konvergencija.
- Konvergencija distribucije.
Dakle, s ljetom, vrlo je teško ući u bit. Dajemo definicije koje će pomoći da shvati ovu temu. Početi s prvim pogledom. Sekvence se nazivaju Često kao vjerojatnostAko se poštuje sljedeće stanje: n teži beskonačnosti, broj na koji slijed teži, više nule i približno je.
Idite na sljedeći obrazac Gotovo vjerojatno, Kaže se da sekvenca konvergira gotovo vjerojatno Na slučajnu varijablu za n, težnja za beskonačnosti, i p, nastojeći magnitudu približno jednom.
Sljedeći tip je konvergencija je rustikalna, Kada se koristi SK-konvergencija, proučavanje vektora slučajnih procesa se svede na proučavanje njihovih koordinatnih slučajnih procesa.
Posljednji tip je ostao, dobro ćemo razumjeti i da se izravno kreće na rješavanje zadataka. Konvergencija distribucije ima drugo ime - "slab", a zatim objasnite zašto. Slaba konvergencija - To su konvergencija distribucijskih funkcija na svim točkama funkcije distribucije granica.
Budite sigurni da ispunite obećanje: slaba konvergencija razlikuje od svega sve činjenice da slučajna vrijednost nije definirana na probabilističkom prostoru. To je moguće jer se stanje formira isključivo korištenje distribucijskih funkcija.
Zakon o velikom broju
Odlični asistenti u dokazu o ovom zakonu bit će teoremi teorije vjerojatnosti, kao što su:
- Chebyshev nejednakost.
- Chebyshev teorem.
- Generalizirani chebyshev teorem.
- Markovljeva teorem.
Ako razmotrimo sve te teoreme, onda ovo pitanje može odgoditi nekoliko desetaka listova. Imamo i glavni zadatak - to je korištenje teorije vjerojatnosti u praksi. Nudimo vam upravo sada i učinimo to. No, prije toga, razmislite o aksiomima teorije vjerojatnosti, oni će biti glavni asistenti pri rješavanju problema.
Aksioma

Od prvog smo se već susreli kad su razgovarali o nemogućem događaju. Zapamtimo: vjerojatnost nemogućeg događaja je nula. Primjer smo donijeli vrlo svijetle i nezaboravne: Snijeg je pao na temperaturu zraka od trideset stupnjeva Celzija.
Drugi zvukovi na sljedeći način: Pouzdan se događaj događa s vjerojatnošću jednakom jednom. Sada pokazujemo kako to napisati uz pomoć matematičkog jezika: P (c) \u003d 1.
Treće: slučajni događaj može se pojaviti ili ne, ali sposobnost uvijek varira od nule do jednog. Bliže vrijednost na jednu, šanse su više; Ako se vrijednost približava nuli, vjerojatnost je vrlo mala. Pišemo ga u matematičkom jeziku: 0<Р(С)<1.
Razmotrite posljednji, četvrti aksiom, koji zvuči ovako: vjerojatnost suma od dva događaja jednaka je zbroju njihove vjerojatnosti. Pišemo matematički jezik: P (A + C) \u003d P (a) + p (b).
Asemska teorija vjerojatnosti su najjednostavnija pravila koja neće biti teško pamtiti. Pokušajmo riješiti neke zadatke, oslanjajući se na već primljeno znanje.
Listić lutrije

Za početak, razmotrite najjednostavniji primjer - lutrija. Zamislite da ste kupili jednu lutriju ulaznicu za sreću. Koja je vjerojatnost da ćete osvojiti najmanje dvadeset rubalja? Tisuću ulaznica su uključene u optjecaju, od kojih jedna ima nagradu u pet stotina rublja, deset stotina rublja, pedeset i dva rubalja i stotinu pet. Zadaci o teoriji vjerojatnosti temelje se na pronalaženju mogućnosti sreće. Sada ćemo zajedno analizirati rješenje iznad prikazanih zadataka.
Ako smo pismo i označavaju dobitke od pet stotina rubalja, vjerojatnost ispadanja bit će jednaka 0,001. Kako smo ga dobili? Vi samo trebate podijeliti broj "sretnih" ulaznica za dijeljenje njihovog broja (u ovom slučaju: 1/1000).
B je dobit od stotinu rubalja, vjerojatnost će biti jednaka 0,01. Sada smo se ponašali na istom načelu kao iu prošlom djelovanju (10/1000)
C - Winnings su jednak dvadeset rubalja. Nalazimo vjerojatnost, to je jednaka 0,05.
Ostatak ulaznica nas ne zanima, jer je njihov nagradni fond manji nego što je navedeno u stanju. Primijenite četvrti aksiom: vjerojatnost osvajanja najmanje dvadeset rubalja je P (a) + p (c) + p (c). Pismo P je označeno vjerojatnost porijekla ovog događaja, već smo ih pronašli u prethodnim akcijama. Ostaje samo da se preklopite potrebne podatke, dobivamo 0,061 u odgovoru. To je broj i bit će odgovor na pitanje zadatka.
Paluba
Zadaci o teoriji vjerojatnosti su složeniji, na primjer, uzeti sljedeći zadatak. Prije palube od trideset šest karata. Vaš zadatak je da izvucite dvije karte zaredom bez miješanja stog, prve i druge kartice moraju biti aces, odijelo nema ništa.
Za početak, nalazimo vjerojatnost da će prva kartica biti ACE, jer ova četiri dijele za trideset šest. Odgodio ga je na stranu. Dajte drugoj kartici, to će biti as s vjerojatnošću od tri trideset peta. Vjerojatnost drugog događaja ovisi o tome koja je karta povukla prvi, pitamo se, bilo je to as ili ne. Iz toga slijedi da je događaj ovisi o događaju A.
Sljedeće akcije nalazimo vjerojatnost istovremene provedbe, to jest, s sklopivom A i B. Njihov rad je sljedeći: Vjerojatnost jednog događaja pomnoženost na uvjetnu vjerojatnost drugog, koju izračunavamo, pretpostavljamo da se prvi događaj dogodio , to jest, povukli smo prvi do Acea.
Da bi postao sve jasno, mi dajemo oznaku takvom elementu kao događaji. Izračunava se, pretpostavljajući da je događaj ono što se dogodilo. Izračunava se na sljedeći način: p (v / a).
Nastavimo rješenje našeg problema: P (a * C) \u003d p (a) * p (in / a) ili p (a * c) \u003d p (c) * p (A / c). Vjerojatnost jednaka (4/36) * ((3/35) / (4/36). Izračunajte, zaokružene na stotinke. Imamo: 0.11 * (0.09 / 0.11) \u003d 0.11 * 0, 82 \u003d 0.09. Vjerojatnost da produžimo dvije asove u nizu je devet stotina. Vrijednost je vrlo mala, iz toga slijedi da je vjerojatnost događaja iznimno mala.
Zaboravljeni broj
Predlažemo rastavljanje nekoliko opcija za zadatke koji proučava teoriju vjerojatnosti. Primjeri rješavanja nekih od njih već ste vidjeli u ovom članku, pokušajte riješiti sljedeći zadatak: Dječak je zaboravio posljednju znamenku telefonskog broja svog prijatelja, ali budući da je poziv bio vrlo važan, onda je počeo regrutirati sve zauzvrat , Moramo izračunati vjerojatnost da će nazvati ne više od tri puta. Problem problema je najjednostavniji, ako su poznati pravila, zakoni i aksiomi teorije vjerojatnosti.
Prije gledanja rješenja, pokušajte se riješiti. Znamo da posljednja znamenka može biti od nule do devet, to jest, postoji samo deset vrijednosti. Vjerojatnost upisivanja željenog je 1/10.
Zatim moramo razmotriti mogućnosti za podrijetlo događaja, pretpostavimo da je dječak pogodak i odmah stekao nužnu, vjerojatnost takvog događaja je 1/10. Druga opcija: Prvo zvono klizanja, a drugi na metu. Izračunajte vjerojatnost takvog događaja: 9/10 pomnožite s 1/9, kao rezultat također dobivamo i 1/10. Treća opcija: Prvi i drugi poziv nisu bili na adresi, samo iz trećeg dječaka stigao tamo gdje je htio. Izračunajte vjerojatnost takvog događaja: 9/10 množe se 8/9 i 1/8, dobivamo 1/10 kao rezultat. Ostale opcije pod uvjetom zadatka nisu zainteresirane za nas, ostali smo presavijeni rezultatima, kao rezultat koji imamo 3/10. Odgovor: Vjerojatnost da će dječak nazvati ne više od tri puta jednak 0,3.
Kartice s brojevima

Prije vas postoji devet karata, od kojih je svaki napisao broj od jedan do devet, brojevi se ne ponavljaju. Stavili su se u kutiju i temeljito se miješali. Morate izračunati vjerojatnost da
- parni broj će ispasti;
- dvoznamenkasti.
Prije prebacivanja na rješenje raspravljat ćemo da je m broj uspješnih slučajeva, a n je ukupan broj opcija. Nalazimo vjerojatnost da će broj biti čak i. Nije teško izračunati to čak i četiri broja, to će biti naš m, sve je moguće devet opcija, to jest, m \u003d 9. Tada je vjerojatnost 0,44 ili 4/9.
Smatramo drugi slučaj: broj opcija za devet, a uopće ne može biti uspješnih ishoda, to jest, m je nula. Vjerojatnost da će izdužena kartica sadržavati dvoznamenkasti broj, isto je jednako nula.