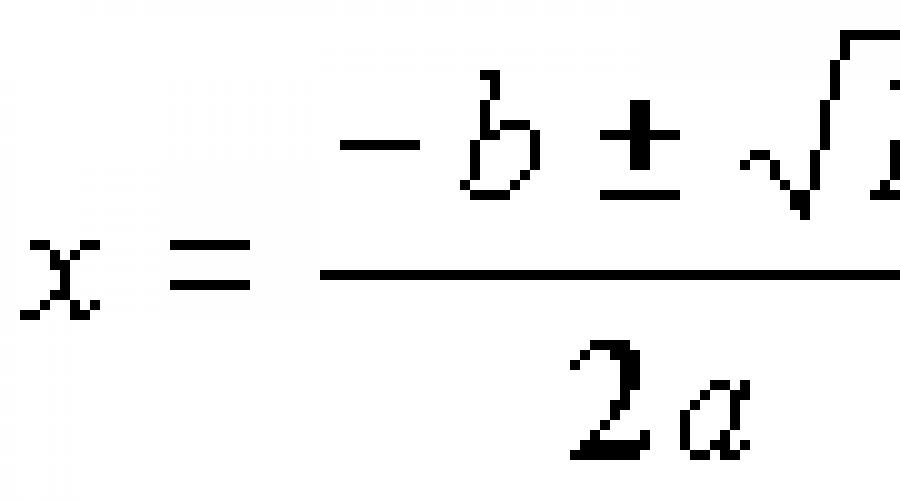
Οι τετραγωνικές εξισώσεις μελετώνται στον βαθμό 8, οπότε δεν υπάρχει τίποτα δύσκολο εδώ. Η δυνατότητα επίλυσης τους είναι απολύτως απαραίτητη.

Η τετραγωνική εξίσωση είναι η εξίσωση του τύπου AX 2 + BX + C \u003d 0, όπου οι συντελεστές Α, Β και C είναι αυθαίρετοι αριθμοί και ένα ≠ 0.

Πριν μελετώσουν συγκεκριμένες μεθόδους λήψης αποφάσεων, σημειώνουμε ότι όλες οι τετραγωνικές εξισώσεις μπορούν να χωριστούν σε τρεις κατηγορίες:

1. Δεν έχουν ρίζες.
2. Έχουν ακριβώς μια ρίζα?
3. Έχουν δύο διαφορετικές ρίζες.

Αυτή είναι μια σημαντική διαφορά μεταξύ των τετραγωνικών εξισώσεων από γραμμική, όπου η ρίζα υπάρχει πάντα και είναι μοναδική. Πώς να καθορίσετε πόσες ρίζες έχουν μια εξίσωση; Για αυτό υπάρχει ένα θαυμάσιο πράγμα - διακριτικός.

Διακριτικός

Αφήστε την τετραγωνική εξίσωση AX 2 + BX + C \u003d 0. Στη συνέχεια, η διακριτική είναι μόνο ο αριθμός D \u003d B 2 - 4ac.

Αυτός ο τύπος πρέπει να είναι γνωστός από την καρδιά. Όπου παίρνει - τώρα δεν έχει σημασία. Άλλο Είναι σημαντικό: Το διακριτικό σήμα μπορεί να καθοριστεί πόσες ρίζες έχει μια τετράγωνη εξίσωση. Και συγκεκριμένα:

1. Αν d< 0, корней нет;
2. Εάν d \u003d 0, υπάρχει ακριβώς μια ρίζα.
3. Εάν d\u003e 0, θα υπάρχουν δύο ρίζες.

Σημείωση: Οι διακριτικές διακρίσεις υποδεικνύουν τον αριθμό των ριζών και καθόλου στις πινακίδες τους, όπως για κάποιο λόγο, πολλοί θεωρούν ότι. Ρίξτε μια ματιά στα παραδείγματα - και θα καταλάβετε τα πάντα:

Μια εργασία. Πόσες ρίζες είναι τετράγωνες εξισώσεις:

1. x 2 - 8x + 12 \u003d 0;
2. 5x 2 + 3x + 7 \u003d 0;
3. x 2 - 6x + 9 \u003d 0.

Αποδέκουμε τους συντελεστές για την πρώτη εξίσωση και να βρούμε τις διακριτικές διακρίσεις:
Α \u003d 1, Β \u003d -8, C \u003d 12;
D \u003d (-8) 2 - 4 · 1 · 12 \u003d 64 - 48 \u003d 16

Έτσι, οι διακριτικές διακρίσεις είναι θετικές, οπότε η εξίσωση έχει δύο διαφορετικές ρίζες. Ομοίως, αποσυναρμολογήστε τη δεύτερη εξίσωση:
a \u003d 5; b \u003d 3; C \u003d 7;
D \u003d 3 2 - 4 · 5 · 7 \u003d 9 - 140 \u003d -131.

Οι διακριτικές διακρίσεις είναι αρνητικές, δεν υπάρχουν ρίζες. Η τελευταία εξίσωση παραμένει:
Α \u003d 1; b \u003d -6; c \u003d 9;
D \u003d (-6) 2 - 4 · 1 · 9 \u003d 36 - 36 \u003d 0.

Οι διακριτικές είναι μηδέν - η ρίζα θα είναι μία.

Παρακαλείστε να σημειώσετε ότι για κάθε εξίσωση οι συντελεστές απορρίφθηκαν. Ναι, είναι πολύ καιρό, ναι, είναι ένα κουραστικό - αλλά δεν θα συγχέετε τους συντελεστές και δεν επιτρέπετε στα ηλίθια λάθη. Επιλέξτε τον εαυτό σας: ταχύτητα ή ποιότητα.

Με την ευκαιρία, αν "γεμίζετε το χέρι", μετά από λίγο, δεν χρειάζεται πλέον να γράψετε όλους τους συντελεστές. Τέτοιες λειτουργίες θα πραγματοποιηθεί στο κεφάλι σας. Οι περισσότεροι άνθρωποι αρχίζουν να το κάνουν κάπου μετά από 50-70 λύσεις εξισώσεις - γενικά, όχι τόσο πολύ.

ROOTS Square Εξίσωση

Τώρα στρίβουμε, στην πραγματικότητα, στην απόφαση. Εάν διακρίσεις d\u003e 0, οι ρίζες μπορούν να βρεθούν από τους τύπους:

Ο βασικός τύπος των ριζών της τετραγωνικής εξίσωσης

Όταν d \u003d 0, μπορείτε να χρησιμοποιήσετε οποιονδήποτε από αυτούς τους τύπους - θα είναι ο ίδιος αριθμός που θα είναι η απάντηση. Τέλος, αν d< 0, корней нет — ничего считать не надо.

1. x 2 - 2x - 3 \u003d 0;
2. 15 - 2x - x 2 \u003d 0;
3. x 2 + 12x + 36 \u003d 0.

Πρώτη εξίσωση:
x 2 - 2x - 3 \u003d 0 ⇒ a \u003d 1; b \u003d -2; c \u003d -3;
D \u003d (-2) 2 - 4 · 1 · (-3) \u003d 16.

Δ\u003e 0 ⇒ Η εξίσωση έχει δύο ρίζες. Βρείτε τους:

Δεύτερη εξίσωση:
15 - 2x - x 2 \u003d 0 ⇒ a \u003d -1; b \u003d -2; C \u003d 15;
D \u003d (-2) 2 - 4 · (-1) · 15 \u003d 64.

Δ\u003e 0 ⇒ Η εξίσωση έχει και πάλι δύο ρίζες. Τα βρίσκουμε

\\ [\\ Ξεκινήστε (Ευθυγράμμιση) & ((x) _ (1)) \u003d \\ Frac (2+ \\ SQRT (64)) (2 \\ CDOT \\ Αριστερά (-1 \\ Δεξιά)) \u003d - 5; \\\\ & ((x) _ (2)) \u003d \\ frac (2- \\ sqrt (64)) (2 \\ cdot \\ αριστερά (-1 \\ δεξιά)) \u003d 3. \\\\ \\ end (ευθυγράμμιση) \\]

Τέλος, η τρίτη εξίσωση:
x 2 + 12x + 36 \u003d 0 ⇒ a \u003d 1; b \u003d 12; C \u003d 36;
D \u003d 12 2 - 4 · 1 · 36 \u003d 0.

D \u003d 0 ⇒ Η εξίσωση έχει μία ρίζα. Μπορείτε να χρησιμοποιήσετε οποιοδήποτε τύπο. Για παράδειγμα, το πρώτο:

Όπως μπορεί να φανεί από παραδείγματα, όλα είναι πολύ απλά. Εάν γνωρίζετε τον τύπο και μπορείτε να λάβετε υπόψη, δεν θα υπάρξουν προβλήματα. Τις περισσότερες φορές, εμφανίζονται σφάλματα κατά τη διάρκεια της υποκατάστασης στον τύπο αρνητικών συντελεστών. Εδώ, πάλι, η ρεσεψιόν που περιγράφεται παραπάνω θα σας βοηθήσει: κοιτάξτε τον τύπο κυριολεκτικά, ζωγραφίστε κάθε βήμα - και πολύ σύντομα να απαλλαγείτε από λάθη.

Ατελείς τετραγωνικές εξισώσεις

Συμβαίνει ότι η τετραγωνική εξίσωση είναι κάπως διαφορετική από αυτό που δίνεται στον ορισμό. Για παράδειγμα:

1. x 2 + 9x \u003d 0;
2. x 2 - 16 \u003d 0.

Είναι εύκολο να το δείτε σε αυτές τις εξισώσεις δεν υπάρχει κανένας από τους όρους. Τέτοιες τετραγωνικές εξισώσεις είναι ακόμη πιο εύκολο από το πρότυπο: δεν χρειάζεται καν να θεωρούν διακρίσεις. Έτσι, εισάγουμε μια νέα ιδέα:

Η εξίσωση AX 2 + BX + C \u003d 0 ονομάζεται ελλιπής τετραγωνική εξίσωση εάν b \u003d 0 ή C \u003d 0, δηλ. Ο συντελεστής με μια μεταβλητή x ή το ελεύθερο στοιχείο είναι μηδέν.

Φυσικά, μια εντελώς δύσκολη περίπτωση είναι δυνατή όταν και οι δύο αυτοί οι συντελεστές είναι μηδέν: b \u003d c \u003d 0. Στην περίπτωση αυτή, η εξίσωση παίρνει το τσεκούρι τύπου 2 \u003d 0. Προφανώς, μια τέτοια εξίσωση έχει μία μόνο ρίζα: x \u003d 0 .

Εξετάστε τις υπόλοιπες περιπτώσεις. Ας b \u003d 0 να είναι 0, τότε λαμβάνουμε μια ελλιπή τετραγωνική εξίσωση του τύπου AX 2 + C \u003d 0. Το μετατρέπουμε λίγο:

Δεδομένου ότι η τετραγωνική τετραγωνική ρίζα υπάρχει μόνο από έναν μη αρνητικό αριθμό, η τελευταία ισότητα έχει νόημα αποκλειστικά στο (-c / a) ≥ 0. Συμπέρασμα:

1. Εάν σε μια ελλιπή τετραγωνική εξίσωση του τύπου AX 2 + C \u003d 0, η ανισότητα (-C / α) εκτελείται ≥ 0, θα υπάρχουν δύο ρίζες. Ο τύπος δίνεται παραπάνω.
2. Αν (-c / a)< 0, корней нет.

Όπως μπορείτε να δείτε, οι διακριτικές διακρίσεις δεν χρειαζόταν - σε ελλιπείς τετραγωνικές εξισώσεις δεν υπάρχουν πολύπλοκοι υπολογιστές. Στην πραγματικότητα, ακόμη και δεν είναι απαραίτητο να θυμόμαστε την ανισότητα (-C / α) ≥ 0. Αρκεί να εκφράσει την τιμή του x 2 και να δούμε τι βρίσκεται στην άλλη πλευρά του σημείου ισότητας. Εάν υπάρχει ένας θετικός αριθμός - οι ρίζες θα είναι δύο. Εάν είναι αρνητική - οι ρίζες δεν θα είναι καθόλου.

Τώρα θα καταλάβουμε με τις εξισώσεις του τύπου AX 2 + BX \u003d 0, στην οποία το ελεύθερο στοιχείο είναι μηδέν. Όλα είναι απλά εδώ: οι ρίζες θα είναι πάντα δύο. Αρκεί να αποσυντεθεί ένα πολυώνυμο σε πολλαπλασιαστές:

Πολλαπλασιαστή για βραχίονα

Το έργο είναι μηδέν, όταν τουλάχιστον ένας από τους πολλαπλασιαστές είναι μηδέν. Από εδώ υπάρχουν ρίζες. Συμπερασματικά, θα αναλύσουμε αρκετές τέτοιες εξισώσεις:

Μια εργασία. Τετράγωνη Τετράγωνη Εξισώσεις:

1. x 2 - 7x \u003d 0;
2. 5x 2 + 30 \u003d 0;
3. 4x 2 - 9 \u003d 0.

x 2 - 7x \u003d 0 ⇒ x · (x - 7) \u003d 0 ⇒ x 1 \u003d 0; x 2 \u003d - (- 7) / 1 \u003d 7.

5x 2 + 30 \u003d 0 ⇒ 5x 2 \u003d -30 ⇒ x 2 \u003d -6. Δεν υπάρχουν ρίζες, επειδή Η πλατεία δεν μπορεί να είναι ίση με αρνητικό αριθμό.

4x 2 - 9 \u003d 0 ⇒ 4x 2 \u003d 9 ⇒ x 2 \u003d 9/4 ⇒ x 1 \u003d 3/2 \u003d 1.5; x 2 \u003d -1,5.

Προβολή εξίσωσης

Εκφραση ΡΕ. \u003d Β. 2 - 4 ac Κλήση Διακριτικός τετράγωνη εξίσωση. Αν ένα ΡΕ. \u003d 0, η εξίσωση έχει μία έγκυρη ρίζα. Αν d \u003e 0, η εξίσωση έχει δύο έγκυρες ρίζες.
Στην περίπτωση πότε ΡΕ. = 0 Μερικές φορές λένε ότι η πλατεία εξίσωση έχει δύο πανομοιότυπες ρίζες.
Χρησιμοποιώντας την ονομασία ΡΕ. \u003d Β. 2 - 4 ac , μπορείτε να ξαναγράψετε τη φόρμουλα (2) ως

Αν ένα ΣΙ. \u003d 2 Κ. Ο τύπος (2) παίρνει τη φόρμα:

Οπου Κ. \u003d Β. / 2 .
Η τελευταία φόρμουλα είναι ιδιαίτερα βολική στις περιπτώσεις όπου ΣΙ. / 2 - Ατέρνες, δηλ. συντελεστής ΣΙ. - Ζυγός αριθμός.
Παράδειγμα 1: Επίλυση εξίσωσης 2 Χ. 2 - 5 x. + 2 = 0 . Εδώ a \u003d 2, b \u003d -5, c \u003d 2. Εχω ΡΕ. \u003d Β. 2 - 4 ac = (-5) 2- 4*2*2 = 9 . Οπως και ΡΕ. > 0 , η εξίσωση έχει δύο ρίζες. Βρείτε τους από τον τύπο (2)

Έτσι Χ. 1 \u003d (5 + 3) / 4 \u003d 2, Χ 2 =(5 - 3) / 4 = 1 / 2 ,
δηλαδή Χ. 1 = 2 και Χ. 2 = 1 / 2 - τις ρίζες της καθορισμένης εξίσωσης.
Παράδειγμα 2: Επίλυση εξίσωσης 2 Χ. 2 - 3 Χ. + 5 = 0 . Εδώ a \u003d 2, b \u003d -3, c \u003d 5. Βρίσκουμε διακριτικές ΡΕ. \u003d Β. 2 - 4 ac = (-3) 2- 4*2*5 = -31 . Οπως και ΡΕ. 0 Η εξίσωση δεν έχει έγκυρες ρίζες.

Ελλιπές τετραγωνικές εξισώσεις. Αν στην τετραγωνική εξίσωση ΤΣΕΚΟΥΡΙ. 2 + BX. + C. =0 Ο δεύτερος συντελεστής ΣΙ. ή Δωρεάν Dick ΝΤΟ. ίσο με το μηδέν, τότε η τετραγωνική εξίσωση καλείται ατελής. Οι ελλιπείς εξισώσεις απομονώνονται επειδή για να βρουν τις ρίζες τους, είναι δυνατόν να μην χρησιμοποιηθούν ο ριζικός τύπος της τετραγωνικής εξίσωσης - είναι ευκολότερο να επιλυθεί η εξίσωση με τη μέθοδο αποσύνθεσης του αριστερού μέρους των παραγόντων.
Παράδειγμα 1: Επίλυση εξίσωσης 2 Χ. 2 - 5 x. = 0 .
Εχω Χ. (2 χ. - 5) = 0 . Έτσι είτε Χ. = 0 είτε 2 Χ. - 5 = 0 , δηλ Χ. = 2.5 . Έτσι η εξίσωση έχει δύο ρίζες: 0 και 2.5
Παράδειγμα 2: Επίλυση εξίσωσης 3 Χ. 2 - 27 = 0 .
Εχω 3 Χ. 2 = 27 . Κατά συνέπεια, οι ρίζες αυτής της εξίσωσης - 3 και -3 .

Θεώρημα Vieta. Εάν η μειωμένη τετραγωνική εξίσωση Χ. 2 + px. + Q. =0 έχει έγκυρες ρίζες, τότε το ποσό τους είναι ίσο - Π. και το έργο είναι ίσο Q. , δηλ

x 1 + x 2 \u003d -p,
x 1 x 2 \u003d q

(Το άθροισμα των ρίζων της δεδομένης τετραγωνικής εξίσωσης ισούται με τον δεύτερο συντελεστή που λαμβάνεται με το αντίθετο σημείο και το προϊόν των ριζών είναι ίσο με ένα ελεύθερο μέλος).

Με αυτό το μαθηματικό πρόγραμμα μπορείτε Επίλυση τετραγωνικής εξίσωσης.

Το πρόγραμμα δεν δίνει μόνο την εργασία απάντησης, αλλά και εμφανίζει τη διαδικασία λύσης με δύο τρόπους:
- με τη βοήθεια των διακρίσεων
- Χρησιμοποιώντας το θεώρημα Vieta (αν είναι δυνατόν).

Επιπλέον, η απάντηση εξέρχεται ακριβής, όχι κατά προσέγγιση.
Για παράδειγμα, για την εξίσωση \\ (81x ^ 2-16x-1 \u003d 0 \\), η απάντηση είναι έξοδος σε αυτή τη μορφή:

$$ x_1 \u003d \\ frac (8+ \\ sqrt (145)) (81), \\ quad x_2 \u003d \\ frac (8-1 \\ sqrt (145)) (81) $$ και όχι σε αυτό: \\ (x_1 \u003d 0.247 · \\ quad x_2 \u003d -0.05 \\)

Το πρόγραμμα αυτό μπορεί να είναι χρήσιμο για τους μαθητές γυμνασίων των σχολών γενικής εκπαίδευσης κατά την προετοιμασία για δοκιμές και εξετάσεις, κατά τον έλεγχο της γνώσης πριν από την εξέταση, οι γονείς παρακολούθησης της λύσης πολλών προβλημάτων στα μαθηματικά και την άλγεβρα. Ή ίσως είστε πολύ ακριβό για να προσλάβετε έναν δάσκαλο ή να αγοράσετε νέα εγχειρίδια; Ή απλά θέλετε να κάνετε την εργασία σας στα μαθηματικά ή την Άλγεβρα όσο το δυνατόν; Σε αυτή την περίπτωση, μπορείτε επίσης να χρησιμοποιήσετε τα προγράμματα μας με μια λεπτομερή λύση.

Έτσι, μπορείτε να πραγματοποιήσετε τη δική σας εκπαίδευση και / ή την εκπαίδευση των νεότερων αδελφών ή των αδελφών σας, ενώ αυξάνεται το επίπεδο εκπαίδευσης στον τομέα των επιδιορθωμένων εργασιών.

Εάν δεν είστε εξοικειωμένοι με τους κανόνες της εισόδου ενός τετραγωνικού πολυωνυμικού, συνιστούμε να εξοικειωθείτε μαζί τους.

Πλατεία Πολυώνιοι κανόνες εισόδου

Καθώς μια μεταβλητή μπορεί να είναι οποιαδήποτε λατινική επιστολή.
Για παράδειγμα: \\ (x, y, z, a, b, c, o, p, q \\), κλπ.

Οι αριθμοί μπορούν να εισέλθουν ολόκληρα ή κλασματικά.
Επιπλέον, οι κλασματικοί αριθμοί μπορούν να χορηγηθούν όχι μόνο με τη μορφή ενός δεκαδικού, αλλά και με τη μορφή ενός συνηθισμένου κλάσματος.

Τους κανόνες για την εισαγωγή δεκαδικών κλασμάτων.
Στα δεκαδικά κλάσματα, το κλασματικό μέρος του συνόλου μπορεί να διαχωριστεί ως σημείο και το κόμμα.
Για παράδειγμα, μπορείτε να εισάγετε δεκαδικά κλάσματα όπως αυτό: 2.5x - 3.5x ^ 2

Κανόνες για την εισαγωγή συνήθων κλάσεων.
Μόνο ένας ακέραιος ακέραιος μπορεί να ενεργεί ως αριθμητής, παρονομαστής και ένα ολόκληρο μέρος του κλάσματος.

Ο παρονομαστής δεν μπορεί να είναι αρνητικός.

Κατά την είσοδο σε ένα αριθμητικό κλάσμα, ο αριθμητής διαχωρίζεται από τον παρονομαστή στο σήμα σχάσης: /
Το όλο μέρος διαχωρίζεται από το Fraraty Ampersand Sign: &
ΕΙΣΑΓΩΓΗ: 3 & 1/3 - 5 & 6 / 5Z + 1 / 7Z ^ 2
Αποτέλεσμα: \\ (3 \\ Frac (1) (3) - 5 \\ Frac (6) (5) Z + \\ Frac (1) (7) Z ^ 2 \\)

Κατά την είσοδο στην έκφραση Μπορείτε να χρησιμοποιήσετε αγκύλες. Σε αυτή την περίπτωση, κατά την επίλυση της τετραγωνικής εξίσωσης, η καταχωρημένη έκφραση απλοποιείται πρώτη.
Για παράδειγμα: 1/2 (Y - 1) (Y + 1) - (5Y-10 & 1/2)

=0

Αποφασίζω

Διαπιστώνεται ότι ορισμένα σενάρια που απαιτούνται για την επίλυση αυτής της εργασίας δεν φορτώνονται και το πρόγραμμα ενδέχεται να μην λειτουργεί.
Μπορεί να έχετε συμπεριληφθεί adblock.
Σε αυτή την περίπτωση, αποσυνδέστε το και ενημερώστε τη σελίδα.

Έχετε εκτέλεση JavaScript στο πρόγραμμα περιήγησής σας.
Για να εμφανιστεί η λύση, πρέπει να ενεργοποιήσετε το JavaScript.
Ακολουθούν οι οδηγίες, πώς να ενεργοποιήσετε το JavaScript στο πρόγραμμα περιήγησής σας.

Επειδή Επιθυμώντας να λύσετε την εργασία είναι πολύ, το αίτημά σας είναι σύμφωνο.
Μετά από λίγα δευτερόλεπτα, η λύση θα εμφανιστεί παρακάτω.
Παρακαλώ περιμένετε sec ...

Αν εσύ παρατήρησε ένα λάθος στην επίλυσηΜπορείτε να γράψετε γι 'αυτό στη φόρμα ανατροφοδότησης.
Μην ξεχάσεις Καθορίστε ποια εργασία Αποφασίζετε και τι Εισάγετε στο πεδίο.

Τα παιχνίδια, τα παζλ, οι εξομοιωτές:

Μια λέξη θεωρία.

Τετράγωνη εξίσωση και τις ρίζες του. Ατελείς τετραγωνικές εξισώσεις

Κάθε μία από τις εξισώσεις
\\ (- x ^ 2 + 6x + 1,4 \u003d 0, \\ Quad 8x ^ 2-7x \u003d 0, \\ Quad X ^ 2- \\ Frac (4) (9) \u003d 0 \\)
Έχει εμφάνιση
\\ (AX ^ 2 + BX + C \u003d 0, \\)
όπου το Χ είναι μεταβλητό, Α, Β και Γ -.
Στην πρώτη εξίσωση Α \u003d -1, Β \u003d 6 και C \u003d 1,4, στο δεύτερο Α \u003d 8, Β \u003d -7 και C \u003d 0, στο τρίτο Α \u003d 1, Β \u003d 0 και C \u003d 4/9. Τέτοιες εξισώσεις καλούνται τετράγωνες εξισώσεις.

Ορισμός.
Τετράγωνη εξίσωση Η εξίσωση του τύπου AX 2 + BX + C \u003d 0, όπου το Χ είναι η μεταβλητή, a, b και c είναι μερικοί αριθμοί και \\ (a \\ neq 0 \\).

Οι αριθμοί Α, Β και C είναι οι συντελεστές της τετραγωνικής εξίσωσης. Ο αριθμός Α ονομάζεται ο πρώτος συντελεστής, ο αριθμός Β είναι ο δεύτερος συντελεστής και ο αριθμός C - ένα ελεύθερο μέλος.

Σε κάθε μία από τις εξισώσεις του τύπου AX 2 + BX + C \u003d 0, όπου \\ (a \\ neq 0 \\), ο μεγαλύτερος βαθμός μεταβλητής X-Square. Ως εκ τούτου το όνομα: τετράγωνη εξίσωση.

Σημειώστε ότι η τετραγωνική εξίσωση ονομάζεται επίσης η εξίσωση του δεύτερου βαθμού, καθώς το αριστερό μέρος του έχει πολυώνυμο δεύτερου βαθμού.

Τετράγωνη εξίσωση στην οποία ο συντελεστής στο x 2 είναι 1, που ονομάζεται Δεδομένης της τετραγωνικής εξίσωσης. Για παράδειγμα, δεδομένης των τετραγωνικών εξισώσεων είναι εξισώσεις
\\ (x ^ 2-11x + 30 \u003d 0, \\ quad x ^ 2-6x \u003d 0, \\ quad x ^ 2-8 \u003d 0 \\)

Εάν στην τετραγωνική εξίσωση AX 2 + BX + C \u003d 0, τουλάχιστον ένας από τους συντελεστές Β ή C είναι μηδέν, τότε μια τέτοια εξίσωση καλείται Ατελής τετραγωνική εξίσωση. Έτσι, οι εξισώσεις -2x 2 + 7 \u003d 0, 3x 2 -10x \u003d 0, -4x2 \u003d 0 είναι ελλιπείς τετραγωνικές εξισώσεις. Στο πρώτο από αυτά b \u003d 0, στο δεύτερο c \u003d 0, στο τρίτο b \u003d 0 και c \u003d 0.

Οι ελλιπείς τετραγωνικές εξισώσεις είναι τρία είδη:
1) AX 2 + C \u003d 0, όπου \\ (c \\ neq 0 \\);
2) AX 2 + BX \u003d 0, όπου \\ (b \\ neq 0 \\);
3) AX 2 \u003d 0.

Εξετάστε τη λύση των εξισώσεων καθενός από αυτά τα είδη.

Για την επίλυση μιας ελλιπούς τετραγωνικής εξίσωσης του τύπου AX 2 + C \u003d 0, με \\ (C \\ NEQ 0 \\), μεταφέρεται στο ελεύθερο μέλος του στη δεξιά πλευρά και κάνει και τα δύο μέρη της εξίσωσης σε:
\\ (x ^ 2 \u003d - \\ frac (c) (α) \\ Δεξιάγραφο x_ (1,2) \u003d \\ pm \\ sqrt (- \\ frac (c) (a)) \\)

Από το \\ (c \\ neq 0 \\), τότε \\ (- \\ frac (c) (a) \\ neq 0 \\)

Εάν \\ (- \\ Frac (C) (A)\u003e 0 \\), η εξίσωση έχει δύο ρίζες.

Εάν \\ (- \\ frac (c) (a), για να λύσετε μια ελλιπή τετραγωνική εξίσωση του τύπου AX 2 + BX \u003d 0, με \\ (b \\ neq 0 \\), μειώνοντας το αριστερό μέρος του σε πολλαπλασιαστές και να πάρει την εξίσωση
\\ (X (ax + b) \u003d 0 \\ Δεξιά \\ Αριστερά \\ (\\ Begin (Array) (L) X \u003d 0 \\\\ AX + B \u003d 0 \\ END (ARTAY) \\ Δεξιά. \\ Δεσφαλμός \\ Αριστερά \\ (\\ Ξεκινήστε (Array) (L) x \u003d 0 \\\\ x \u003d - \\ frac (b) (a) \\ end (array) \\ Δεξιά. \\)

Έτσι, μια ελλιπής τετραγωνική εξίσωση του τύπου AX 2 + BX \u003d 0 με \\ (b \\ neq 0 \\) έχει πάντα δύο ρίζες.

Μια ελλιπής τετραγωνική εξίσωση του τύπου AX2 \u003d 0 ισοδυναμεί με την εξίσωση X 2 \u003d 0 και ως εκ τούτου έχει τη μόνη ρίζα 0.

Τετράγωνη ρίζα εξίσωσης

Σκεφτείτε τώρα πώς οι τετραγωνικές εξισώσεις λύουν στις οποίες και οι δύο συντελεστές με άγνωστο και ελεύθερο μέλος είναι διαφορετικές από το μηδέν.

Spest Square εξίσωση γενικά και ως εκ τούτου λαμβάνουμε τον ριζικό τύπο. Στη συνέχεια, αυτός ο τύπος μπορεί να χρησιμοποιηθεί κατά την επίλυση οποιασδήποτε τετραγωνικής εξίσωσης.

Resister τετράγωνη εξίσωση AX 2 + BX + C \u003d 0

Διαχωρίζοντας και τα δύο μέρη του σε ένα, λαμβάνουμε το ισοδύναμο της παρουσιαζόμενης τετραγωνικής εξίσωσης
\\ (x ^ 2 + \\ frac (b) (a) x + \\ frac (c) (a) \u003d 0 \\)

Μετατρέπουμε αυτή την εξίσωση, επισημαίνοντας την πλατεία του αναπήδησης:
\\ (x ^ 2 + 2x \\ cdot \\ frac (b) (2α) + \\ αριστερά (\\ frac (b) (2α) \\ "δεξιά) ^ 2- αριστερά (\\ frac (b) (2α) ^ ^ 2 + \\ frac (c) (a) \u003d 0 \\ Δεξιάλογα \\)

\\ (x ^ 2 + 2x \\ cdot \\ frac (b) (2a) + \\ αριστερά (\\ frac (b) (2α) \\ "δεξιά) ^ 2 \u003d \\ αριστερά (\\ frac (b) (2α) \\ σωστά) ^ 2 - \\ FRAC (C) (A) \\ Δεξιά \\) \\ (\\ αριστερά (x + \\ frac (b) (2α) \\ σωστά) ^ 2 \u003d \\ frac (b ^ 2) (4a ^ 2) - \\ frac (γ) (α) \\ αφαίρεση \\ αριστερά (x + \\ frac (b) (2α) ~ δεξιά) ^ 2 \u003d \\ frac (b ^ 2-4ac) (4a ^ 2) \\ Δεξιά \\) \\ (x + \\ Frac (b) (2a) \u003d \\ pm \\ sqrt (\\ frac (b ^ 2-4ac) (4a ^ 2)) \\ Δεξιάγραφο x \u003d - \\ frac (b) (2α) + \\ frac (\\ pm \\ sqrt (\\ pm \\ b ^ 2 -4ac)) (2α) \\ Δεξιά \\) \\ (x \u003d \\ frac (-b \\ pm \\ sqrt (b ^ 2-4ac)) (2α) \\)

Η καθοδηγούμενη έκφραση καλείται διακριτική ισοπέδωση Το AX 2 + BX + C \u003d 0 ("διακρίσεις" στα λατινικά είναι ένας διακίνος). Δηλώνεται με το γράμμα D, δηλ.
\\ (D \u003d b ^ 2-4ac \\)

Τώρα, χρησιμοποιώντας την ονομασία των διακριτικών, ξαναγράψουν τον τύπο για τις ρίζες της τετραγωνικής εξίσωσης:
\\ (x_ (1,2) \u003d \\ frac (-b \\ pm \\ sqrt (d)) (2α) \\), όπου \\ (d \u003d b ^ 2-4ac \\)

Είναι προφανές ότι:
1) Εάν d\u003e 0, η τετραγωνική εξίσωση έχει δύο ρίζες.
2) Εάν d \u003d 0, η τετραγωνική εξίσωση έχει μία ρίζα \\ (x \u003d-\\ frac (b) (2α) \\).
3) Εάν το D, ανάλογα με τη διακριτική αξία, η τετραγωνική εξίσωση μπορεί να έχει δύο ρίζες (με D\u003e 0), μία ρίζα (στο D \u003d 0) ή να μην έχουν ρίζες (με D, κατά την επίλυση της τετραγωνικής εξίσωσης για Αυτός ο τύπος, συνιστάται να εφαρμοστεί στον ακόλουθο τρόπο:
1) Υπολογίστε τις διακριτικές και να το συγκρίνετε με το μηδέν.
2) Εάν οι διακριτικές διακρίσεις είναι θετικές ή ίσες με το μηδέν, στη συνέχεια, χρησιμοποιήστε τον τύπο ρίζας, εάν η διακριτική είναι αρνητική, τότε γράψτε τις ρίζες.

Θεώρημα Vieta

Η παρουσιαζόμενη τετράγωνη εξίσωση AX 2 -7x + 10 \u003d 0 έχει ρίζες 2 και 5. Το ποσό των ριζών είναι 7 και το προϊόν είναι 10. Βλέπουμε ότι η ποσότητα των ριζών είναι ίση με το δεύτερο συντελεστή που λαμβάνεται με το αντίθετο σημάδι και το προϊόν των ριζών είναι ίσο με ένα ελεύθερο μέλος. Αυτή η ιδιότητα έχει οποιαδήποτε δεδομένη τετραγωνική εξίσωση που έχει μια ρίζα.

Το άθροισμα των ρίζων της παρουσιαζόμενης τετραγωνικής εξίσωσης είναι ίσο με το δεύτερο συντελεστή που λαμβάνεται με το αντίθετο σημείο και το προϊόν των ριζών είναι ίσο με ένα ελεύθερο μέλος.

Εκείνοι. Το Vieta Theorem υποστηρίζει ότι οι ρίζες του x 1 και x 2 της δεδομένης τετραγωνικής εξίσωσης x 2 + px + q \u003d 0 έχουν ένα ακίνητο:
\\ (\\ Αριστερά \\ (\\ Ξεκινήστε (Array) (L) X_1 + X_2 \u003d -P \\\\\\ / x_1 \\ CDOT X_2 \u003d Q \\ END (ARTAY) \\ RWORE. \\)

Ελπίζω ότι η μελέτη αυτού του άρθρου θα μάθετε να βρείτε τις ρίζες μιας πλήρους τετραγωνικής εξίσωσης.

Με τη βοήθεια διακρίσεων, μόνο οι πλήρεις τετραγωνικές εξισώσεις επιλύονται, για την επίλυση τετραγωνικών εξισώσεων, χρησιμοποιούνται άλλες μέθοδοι που βρίσκετε στο άρθρο "Απόφαση ελλιπών τετραγωνικών εξισώσεων".

Ποιες τετραγωνικές εξισώσεις ονομάζονται γεμάτες; το Εξισώσεις της μορφής ΑΗ 2 + Β x + c \u003d 0όπου οι συντελεστές Α, Β και δεν είναι ίσοι με το μηδέν. Έτσι, για την επίλυση μιας πλήρους τετραγωνικής εξίσωσης, είναι απαραίτητο να υπολογιστεί η διακριτική Δ.

D \u003d B 2 - 4ας.

Ανάλογα με το είδος της σημασίας που είναι διακριτική, θα γράψουμε την απάντηση.

Εάν οι διακριτικές είναι ένας αρνητικός αριθμός (D< 0),то корней нет.

Εάν η διακριτική είναι μηδενική, Χ \u003d (-b) / 2Α. Όταν οι διακριτικές είναι θετικός αριθμός (d\u003e 0),

Τότε x 1 \u003d (-b - √d) / 2a και x 2 \u003d (-B + √ϋ) / 2Α.

Για παράδειγμα. Επίλυση εξίσωσης x 2 - 4x + 4 \u003d 0.

D \u003d 4 2 - 4 · 4 \u003d 0

x \u003d (- (-4)) / 2 \u003d 2

Απάντηση: 2

Επίλυση εξίσωσης 2. x 2 + x + 3 \u003d 0.

D \u003d 1 2 - 4 · 2 · 3 \u003d - 23

Απάντηση: Δεν υπάρχουν ρίζες.

Επίλυση εξίσωσης 2. x 2 + 5x - 7 \u003d 0.

D \u003d 5 2 - 4 · 2 · (-7) \u003d 81

x 1 \u003d (-5 - √81) / (2 · 2) \u003d (-5 - 9) / 4 \u003d - 3.5

x 2 \u003d (-5 + √81) / (2,2) \u003d (-5 + 9) / 4 \u003d 1

Απάντηση: - 3.5; ένας.

Ας φανταστούμε λοιπόν τη λύση των ολοκληρωμένων τετραγωνικών εξισώσεων με το σχήμα στο σχήμα1.

Σύμφωνα με αυτούς τους τύπους, μπορείτε να λύσετε οποιαδήποτε πλήρη τετραγωνική εξίσωση. Πρέπει μόνο να παρακολουθείτε προσεκτικά Η εξίσωση καταγράφηκε με ένα πολυώνυμο ενός τυπικού τύπου.

αλλά x 2 + BX + C, Διαφορετικά, μπορείτε να κάνετε λάθος. Για παράδειγμα, στην καταγραφή της εξίσωσης x + 3 + 2x 2 \u003d 0, μπορεί να λυθεί εσφαλμένα

a \u003d 1, b \u003d 3 και c \u003d 2. Στη συνέχεια

D \u003d 3 2 - 4 · 1 · 2 \u003d 1 και στη συνέχεια η εξίσωση έχει δύο ρίζες. Και αυτό είναι εσφαλμένο. (Δείτε το διάλυμα του Παραδείγματος 2 παραπάνω).

Επομένως, εάν η εξίσωση δεν είναι γραμμένη όχι σε πολυώνυμο ενός τυποποιημένου είδους, αρχικά μια πλήρης τετραγωνική εξίσωση πρέπει να καταγράφεται από ένα πολυώνυμο ενός τυποποιημένου είδους (στην πρώτη θέση θα πρέπει να ξεπεράσει με τον μεγαλύτερο δείκτη, δηλαδή αλλά x 2 Στη συνέχεια, με μικρότερη – bx.και στη συνέχεια δωρεάν πούτσο από.

Κατά την επίλυση μιας δεδομένης τετραγωνικής εξίσωσης και μια τετραγωνική εξίσωση με ομοιόμορφο συντελεστή, με τον δεύτερο όρο, μπορούν να χρησιμοποιηθούν και άλλοι τύποι. Ας εξοικειωθούμε με αυτές τις φόρμουλες. Εάν σε μια πλήρη τετραγωνική εξίσωση στον δεύτερο όρο, ο συντελεστής θα είναι ακόμη και (b \u003d 2k), τότε η εξίσωση σύμφωνα με τους τύπους στο σχήμα 2 μπορεί να λυθεί.

Η πλήρης τετραγωνική εξίσωση ονομάζεται τα παραπάνω, αν ο συντελεστής είναι x 2 ίσο με ένα και η εξίσωση θα λάβει τη φόρμα x 2 + px + q \u003d 0. Μια τέτοια εξίσωση μπορεί να δοθεί στην επίλυση ή επιτυγχάνεται διαιρώντας όλους τους συντελεστές στην εξίσωση του συντελεστή αλλάπαραμένω x 2 .

Το σχήμα 3 δείχνει το σχήμα της επίλυσης του παραπάνω τεμαχίου
εξισώσεις. Σκεφτείτε το παράδειγμα την εφαρμογή των τύπων που εξετάζονται σε αυτό το άρθρο.

Παράδειγμα. Επίλυση εξίσωσης

3x 2 + 6x - 6 \u003d 0.

Ας αποφασίσουμε αυτή την εξίσωση χρησιμοποιώντας τους τύπους που παρουσιάζονται στο σχήμα του σχήματος 1.

D \u003d 6 2 - 4 · 3 · (- 6) \u003d 36 + 72 \u003d 108

√d \u003d √108 \u003d √ (36 · 3) \u003d 6√3

x 1 \u003d (-6 - 6√3) / (2,3) \u003d (6 (-1- √ (3)) / 6 \u003d -1 - √3

x 2 \u003d (-6 + 6√3) / (2,3) \u003d (6 (-1+ √ (3)) / 6 \u003d -1 + √3

Απάντηση: -1 - √3; -1 + √3

Μπορεί να φανεί ότι ο συντελεστής στο Χ σε αυτή την εξίσωση είναι ένας ζυγός αριθμός, δηλαδή, b \u003d 6 ή b \u003d 2k, από όπου k \u003d 3. Στη συνέχεια προσπαθούμε να λύσουμε την εξίσωση σύμφωνα με τους τύπους που εμφανίζεται στο διάγραμμα D στο διάγραμμα D 1 \u003d 3 2 - 3 · (- 6) \u003d 9 + 18 \u003d 27

√ (D 1) \u003d √27 \u003d √ (9 · 3) \u003d 3√3

x 1 \u003d (-3 - 3√3) / 3 \u003d (3 (-1 - √ (3))) / 3 \u003d - 1 - √3

x 2 \u003d (-3 + 3√3) / 3 \u003d (3 (-1 + √ (3))) / 3 \u003d - 1 + √3

Απάντηση: -1 - √3; -1 + √3. Παρατηρήθηκε ότι όλοι οι συντελεστές σε αυτή την τετραγωνική εξίσωση χωρίζονται σε 3 και με την εκτέλεση διαίρεσης, λαμβάνουμε την μειωμένη τετραγωνική εξίσωση x 2 + 2x - 2 \u003d 0 με την επίλυση αυτής της εξίσωσης χρησιμοποιώντας τύπους για το καθορισμένο τετράγωνο για το καθορισμένο τετράγωνο
Εξισώσεις Εικόνα 3.

D 2 \u003d 2 2 - 4 · (- 2) \u003d 4 + 8 \u003d 12

√ (D 2) \u003d √12 \u003d √ (4 · 3) \u003d 2√3

x 1 \u003d (-2 - 2√3) / 2 \u003d (2 (-1 - √ (3))) / 2 \u003d - 1 - √3

x 2 \u003d (-2 + 2√3) / 2 \u003d (2 (-1+ √ (3))) / 2 \u003d - 1 + √3

Απάντηση: -1 - √3; -1 + √3.

Όπως βλέπουμε, κατά την επίλυση αυτής της εξίσωσης σε διάφορους τύπους, λάβαμε την ίδια απάντηση. Επομένως, γνωρίζει καλά τους τύπους που εμφανίζονται στο σχήμα του σχήματος 1, μπορείτε πάντα να λύσετε οποιαδήποτε πλήρη τετραγωνική εξίσωση.

Η θέση, με πλήρη ή μερική αντιγραφή της αναφοράς υλικού στην αρχική πηγή.

Κατά τη συνέχιση του θέματος "Απόφαση εξισώσεων", το υλικό αυτού του άρθρου θα σας παρουσιάσει σε τετραγωνικές εξισώσεις.

Εξετάστε τα πάντα λεπτομερώς: την ουσία και το αρχείο της πλατείας εξίσησης, ορίστε τους συνοδευτικούς όρους, θα αναλύσουμε το σύστημα για τη λύση των ελλιπών και πλήρων εξισώσεων, εξοικειωμένοι με τον τύπο των ριζών και των διακρίσεων, να δημιουργήσουν συνδέσμους μεταξύ ριζών και συντελεστών, Και φυσικά δίνουμε μια οπτική λύση πρακτικών παραδειγμάτων.

Yandex.rtb r-a-339285-1

Τετράγωνη εξίσωση, οι τύποι του

Ορισμός 1.

Τετραγωνική εξίσωση - Αυτή είναι η εξίσωση που καταγράφηκε ως a-x 2 + b · x + c \u003d 0όπου Χ. - μεταβλητή, Α, Β και ΝΤΟ. - μερικοί αριθμοί, ενώ ΕΝΑ.Όχι μηδέν.

Συχνά, οι τετραγωνικές εξισώσεις ονομάζονται επίσης το όνομα των εξισώσεων του δεύτερου βαθμού, καθώς ουσιαστικά η τετραγωνική εξίσωση είναι η αλγεβρική εξίσωση του δεύτερου βαθμού.

Δίνουμε ένα παράδειγμα για να απεικονίσουμε έναν δεδομένο ορισμό: 9 · x 2 + 16 · x + 2 \u003d 0; 7, 5 · x 2 + 3, 1 · x + 0, 11 \u003d 0, κλπ. - Αυτές είναι τετραγωνικές εξισώσεις.

Ορισμός 2.

Αριθμοί Α, Β και ΝΤΟ. - Αυτοί είναι οι συντελεστές της τετραγωνικής εξίσωσης a-x 2 + b · x + c \u003d 0, με τον συντελεστή ΕΝΑ. Ονομάζεται πρώτος ή μεγαλύτερος ή ο συντελεστής στο x 2, b - ο δεύτερος συντελεστής ή ο συντελεστής όταν Χ., αλλά ΝΤΟ. Καλέστε το μέλος δωρεάν.

Για παράδειγμα, σε μια τετραγωνική εξίσωση 6 · x 2 - 2 · x - 11 \u003d 0 Ο ανώτερος συντελεστής είναι 6, ο δεύτερος συντελεστής είναι − 2 και το ελεύθερο μέλος είναι ίσο − 11 . Δώστε προσοχή στο γεγονός ότι όταν οι συντελεστές ΣΙ.και / ή c είναι αρνητικά, τότε χρησιμοποιείται μια σύντομη μορφή μιας εγγραφής προβολής. 6 · x 2 - 2 · x - 11 \u003d 0, αλλά όχι 6 · x 2 + (- 2) · x + (- 11) \u003d 0.

Διευκρινούμε επίσης αυτή την πτυχή: εάν οι συντελεστές ΕΝΑ. και / ή ΣΙ. ίσος 1 ή − 1 Στη συνέχεια, ρητά συμμετοχή στην καταγραφή της τετραγωνικής εξίσωσης, ενδέχεται να μην λαμβάνονται, η οποία εξηγείται από τα χαρακτηριστικά της καταγραφής αυτών των αριθμητικών συντελεστών. Για παράδειγμα, σε μια τετραγωνική εξίσωση Y 2 - y + 7 \u003d 0 Ο ανώτερος συντελεστής είναι 1, και ο δεύτερος συντελεστής είναι − 1 .

Συγκεκριμένες και άγαμες τετραγωνικές εξισώσεις

Με την αξία του πρώτου συντελεστή, οι τετραγωνικές εξισώσεις χωρίζονται στα παραπάνω και απλήρωτα.

Ορισμός 3.

Η μειωμένη τετραγωνική εξίσωση - Αυτή είναι μια τετράγωνη εξίσωση όπου ο παλαιότερος συντελεστής είναι ίσος με 1. Για άλλες τιμές του παλαιότερου συντελεστή, η τετραγωνική εξίσωση δεν είναι άκυρη.

Δίνουμε παραδείγματα: τετραγωνικές εξισώσεις x 2-4 · x + 3 \u003d 0, x 2 - x - 4 5 \u003d 0 παρουσιάζονται σε κάθε μία από τις οποίες ο παλαιότερος συντελεστής είναι 1.

9 · x 2 - x - 2 \u003d 0 - μια ολοκληρωμένη τετραγωνική εξίσωση, όπου ο πρώτος συντελεστής είναι διαφορετικός από 1 .

Οποιαδήποτε ασυνήθιστη εξίσωση είναι δυνατή η μετατροπή σε μια δεδομένη εξίσωση εάν διαιρείται από τα δύο μέρη έως τον πρώτο συντελεστή (ισοδύναμο μετασχηματισμό). Η μετασχηματισμένη εξίσωση θα έχει τις ίδιες ρίζες με την καθορισμένη έξυπνη εξίσωση ή να μην έχει ρίζες καθόλου.

Η εξέταση ενός συγκεκριμένου παραδείγματος θα μας επιτρέψει να αποδείξουμε σαφώς τη μετάβαση από μια ολοκληρωμένη τετραγωνική εξίσωση με το δεδομένο.

Παράδειγμα 1.

Η εξίσωση ορίζεται 6 · x 2 + 18 · x - 7 \u003d 0 . Είναι απαραίτητο να μετατραπεί η αρχική εξίσωση στην παραπάνω φόρμα.

Απόφαση

Το σχέδιο του συγκεκριμένου ανωτέρω διαχωρίζεται και από τα δύο μέρη της αρχικής εξίσωσης στον ανώτερο συντελεστή 6. Στη συνέχεια, έχουμε: (6 · x 2 + 18 · x - 7): 3 \u003d 0: 3Και αυτό είναι το ίδιο με: (6 · x 2): 3 + (18 · x): 3 - 7: 3 \u003d 0 Και επιπλέον: (6: 6) · x 2 + (18: 6) · x - 7: 6 \u003d 0. Από εδώ: x 2 + 3 · x - 1 1 6 \u003d 0. Έτσι, μια εξίσωση θεωρείται ότι καθορίζεται.

Απάντηση: x 2 + 3 · x - 1 1 6 \u003d 0.

Πλήρεις και ελλιπείς τετραγωνικές εξισώσεις

Στρίψτε στον ορισμό της τετραγωνικής εξίσωσης. Σε αυτό το διευκρινίσαμε αυτό Ένα ≠ 0. Μια τέτοια κατάσταση είναι απαραίτητη για την εξίσωση a-x 2 + b · x + c \u003d 0 Ήταν ακριβώς τετράγωνο επειδή a \u003d 0. Είναι ουσιαστικά μετατραπεί σε γραμμική εξίσωση b · x + c \u003d 0.

Στην περίπτωση που οι συντελεστές ΣΙ. και ΝΤΟ.ίση με το μηδέν (το οποίο είναι δυνατό, τόσο μεμονωμένα όσο και από κοινού), η τετραγωνική εξίσωση ονομάζεται ελλιπής.

Ορισμός 4.

Ατελής τετραγωνική εξίσωση - μια τέτοια τετράγωνη εξίσωση a-x 2 + b · x + c \u003d 0,όπου τουλάχιστον ένας από τους συντελεστές ΣΙ.και ΝΤΟ.(ή και τα δύο) είναι μηδέν.

Πλήρης τετραγωνική εξίσωση - μια τετράγωνη εξίσωση στην οποία όλοι οι αριθμητικοί συντελεστές δεν είναι μηδέν.

Αφετιώνουμε γιατί οι τύποι τετραγωνικών εξισώσεων παρέχονται ακριβώς τα ονόματα.

Για b \u003d 0 τετραγωνική εξίσωση παίρνει τη φόρμα A-x 2 + 0 · x + c \u003d 0ότι το ίδιο πράγμα είναι αυτό ένα x 2 + c \u003d 0. Για C \u003d 0. Η τετραγωνική εξίσωση καταγράφεται ως ένα x 2 + b · x + 0 \u003d 0Αυτό είναι ισοδύναμο ένα x 2 + b · x \u003d 0. Για B \u003d 0. και C \u003d 0. Η εξίσωση θα πάρει την άποψη ένα x 2 \u003d 0. Οι εξισώσεις που λάβαμε είναι διαφορετικές από την πλήρη τετραγωνική εξίσωση, δεδομένου ότι τα αριστερά μέρη τους δεν περιλαμβάνονται ούτε ένα συστατικό από τη μεταβλητή Χ ή ένα ελεύθερο μέλος ή ταυτόχρονα. Στην πραγματικότητα, το γεγονός αυτό ζητήθηκε το όνομα ενός τέτοιου είδους εξισώσεων - ελλιπής.

Για παράδειγμα, το Χ 2 + 3 · x + 4 \u003d 0 και - 7 · x 2-2- x + 1, 3 \u003d 0 είναι πλήρεις τετραγωνικές εξισώσεις. x 2 \u003d 0, - 5 · x 2 \u003d 0; 11 · x 2 + 2 \u003d 0, - x 2 - 6 · x \u003d 0 - Ατελείς τετραγωνικές εξισώσεις.

Απόφαση ελλιπών τετραγωνικών εξισώσεων

Ο ανωτέρω ορισμός καθιστά δυνατή τη διάκριση των ακόλουθων τύπων ελλιπών τετραγωνικών εξισώσεων:

• ένα x 2 \u003d 0, αυτή η εξίσωση αντιστοιχεί στους συντελεστές B \u003d 0. και c \u003d 0;
• a-x 2 + c \u003d 0 για b \u003d 0;
• a-x 2 + b · x \u003d 0 στο c \u003d 0.

Εξετάστε την απόφαση κάθε τύπου ελλιπούς τετραγωνικής εξίσωσης.

Λύση της εξίσωσης Α · Χ 2 \u003d 0

Όπως αναφέρθηκε παραπάνω, η εξίσωση αντιστοιχεί στους συντελεστές ΣΙ. και ΝΤΟ.ίσο με το μηδέν. Την εξίσωση ένα x 2 \u003d 0 Είναι δυνατή η μετατροπή της εξίσωσης με την ισοδύναμη με αυτήν x 2 \u003d 0που παίρνουμε, μοιράζοντας και τα δύο μέρη της εξίσωσης πηγής για τον αριθμό ΕΝΑ.δεν είναι ίσο με το μηδέν. Προφανές γεγονός ότι η ρίζα της εξίσωσης x 2 \u003d 0 Αυτό είναι μηδέν επειδή 0 2 = 0 . Άλλες ρίζες, αυτή η εξίσωση δεν έχει, η οποία εξηγείται από τις ιδιότητες του βαθμού: για οποιονδήποτε αριθμό Π,όχι ίση με μηδέν, πιστή ανισότητα P 2\u003e 0Αυτό που ακολουθεί όταν P ≠ 0. ισότητα P 2 \u003d 0δεν θα επιτευχθεί ποτέ.

Ορισμός 5.

Έτσι, για μια ελλιπή τετραγωνική εξίσωση a · x 2 \u003d 0 υπάρχει η μόνη ρίζα x \u003d 0..

Παράδειγμα 2.

Για παράδειγμα, λύουμε μια ελλιπή τετραγωνική εξίσωση - 3 · x 2 \u003d 0. Είναι ισοδύναμο με την εξίσωση x 2 \u003d 0, η μόνη του ρίζα του είναι x \u003d 0., Τότε η αρχική εξίσωση έχει τη μόνη ρίζα - μηδέν.

Εν συντομία, η απόφαση αποφασίζεται:

- 3 · x 2 \u003d 0, x 2 \u003d 0, x \u003d 0.

Λύση της εξίσωσης Α · Χ 2 + C \u003d 0

Στην ουρά - το διάλυμα ελλιπών τετραγωνικών εξισώσεων, όπου b \u003d 0, c ≠ 0, δηλαδή οι εξισώσεις της φόρμας ένα x 2 + c \u003d 0. Μετατρέπουμε αυτή την εξίσωση που διεξήγαμε τον όρο από το ένα μέρος της εξίσωσης με το άλλο, αλλάζοντας το σημάδι στο αντίθετο και διαιρώντας και τα δύο μέρη της εξίσωσης με τον αριθμό, όχι ίση με το μηδέν:

• ΜΕΤΑΦΟΡΑ ΝΤΟ. Στο δεξιό μέρος, το οποίο δίνει την εξίσωση Ένα x 2 \u003d - c;
• Διαιρούμε και τα δύο μέρη της εξίσωσης ΕΝΑ., Παίρνω στο τέλος x \u003d - c a.

Οι μετασχηματιστές μας είναι ισοδύναμες, αντίστοιχα, η προκύπτουσα εξίσωση είναι επίσης ισοδύναμη με την πηγή και το γεγονός αυτό καθιστά δυνατή τη σύναψη των ριζών της εξίσωσης. Από ποιες είναι οι έννοιες ΕΝΑ. και ΝΤΟ.Η αξία της έκφρασης εξαρτάται - C a: Μπορεί να έχει ένα σήμα μείον (ας πούμε αν Α \u003d 1. και C \u003d 2., στη συνέχεια - C a \u003d - 2 1 \u003d - 2) ή ένα σύμβολο συν (για παράδειγμα, εάν A \u003d - 2 και C \u003d 6., τότε - C a \u003d - 6 - 2 \u003d 3). Δεν είναι μηδέν επειδή C ≠ 0.. Ας κατορθώσουμε λεπτομερέστερα σε καταστάσεις όταν - γ< 0 и - c a > 0 .

Στην περίπτωση που - C α< 0 , уравнение x 2 = - c a не будет иметь корней. Утверждая это, мы опираемся на то, что квадратом любого числа является число неотрицательное. Из сказанного следует, что при - c a < 0 ни для какого числа Π. Ισότητα P 2 \u003d - C Α δεν μπορεί να είναι αλήθεια.

Όλα αλλιώς, πότε - C a\u003e 0: ανάκληση της τετραγωνικής ρίζας και θα είναι προφανές ότι η εξίσωση X 2 \u003d - C Α θα είναι ο αριθμός - C Α, δεδομένου ότι - C Α2 \u003d - C Α. Δεν είναι δύσκολο να καταλάβουμε ότι ο αριθμός είναι - C Α είναι επίσης η ρίζα της εξίσωσης Χ 2 \u003d - C Α: πράγματι, - - C Α2 \u003d - C α.

Άλλοι εξίσωση ρίζας δεν θα έχουν. Μπορούμε να το δείξουμε χρησιμοποιώντας τη δυσάρεστη μέθοδο. Αρχικά, ορίστε τις ονομασίες που βρέθηκαν πάνω από τις ρίζες όπως x 1 και - x 1.. Θα προτείνω ότι η εξίσωση X 2 \u003d - C Α είναι επίσης ρίζα x 2που διαφέρει από τις ρίζες x 1 και - x 1.. Γνωρίζουμε ότι, αντικαθιστώντας την εξίσωση αντ 'αυτού Χ. Οι ρίζες του, μετατρέπουμε την εξίσωση σε μια δίκαιη αριθμητική ισότητα.

Για x 1 και - x 1. Γράφουμε: x 1 2 \u003d - C Α, και για x 2 - x 2 2 \u003d - C α. Βασιζόμενοι στις ιδιότητες των αριθμητικών ισοτιμιών, γεμάτο μια σωστή ισότητα από την άλλη, η οποία θα μας δώσει: x 1 2 - x 2 2 \u003d 0. Χρησιμοποιήστε τις ιδιότητες των ενεργειών με αριθμούς για να ξαναγράψετε την τελευταία ισότητα ως (x 1 - x 2) · (x 1 + x 2) \u003d 0. Είναι γνωστό ότι το έργο των δύο αριθμών είναι μηδέν στη συνέχεια και μόνο αν τουλάχιστον ένας από τους αριθμούς είναι μηδέν. Από το δήλωσε ότι το ακολουθεί αυτό x 1 - x 2 \u003d 0 και / ή x 1 + x 2 \u003d 0ότι το ίδιο πράγμα x 2 \u003d x 1 και / ή x 2 \u003d - x 1. Υπήρξε μια προφανής αντίφαση, διότι αρχικά συμφωνήθηκε ότι η ρίζα της εξίσωσης x 2 διαφέρει από x 1 και - x 1.. Έτσι, αποδείξαμε ότι η εξίσωση δεν έχει άλλες ρίζες, εκτός από το x \u003d - C A και x \u003d - - C a.

Συνοψίζουμε όλες τις παραπάνω συλλογιστικές.

Ορισμός 6.

Ατελής τετραγωνική εξίσωση ένα x 2 + c \u003d 0 ισοδύναμο με την εξίσωση X 2 \u003d - C Α, η οποία:

• δεν θα έχει ρίζες όταν - c a< 0 ;
• Θα υπάρχουν δύο ρίζες x \u003d - C A και x \u003d - - C a με - C a\u003e 0.

Δίνουμε παραδείγματα επίλυσης εξισώσεων ένα x 2 + c \u003d 0.

Παράδειγμα 3.

Η τετραγωνική εξίσωση καθορίζεται 9 · x 2 + 7 \u003d 0.Είναι απαραίτητο να βρεθεί η απόφασή του.

Απόφαση

Μεταφέραμε ένα ελεύθερο μέλος στο δεξί μέρος της εξίσωσης, τότε η εξίσωση θα λάβει τη φόρμα 9 · x 2 \u003d - 7.
Διαιρούμε και τα δύο μέρη της αποκτηθέντα εξίσωση 9 , Ελάτε στο x 2 \u003d - 7 9. Στο δεξιό μέρος, βλέπουμε έναν αριθμό με ένα σήμα μείον, πράγμα που σημαίνει: Η καθορισμένη εξίσωση δεν έχει ρίζες. Στη συνέχεια, η αρχική ελλιπής τετραγωνική εξίσωση 9 · x 2 + 7 \u003d 0 Δεν θα έχει ρίζες.

Απάντηση: την εξίσωση 9 · x 2 + 7 \u003d 0Δεν έχει ρίζες.

Παράδειγμα 4.

Είναι απαραίτητο να λύσετε την εξίσωση - x 2 + 36 \u003d 0.

Απόφαση

Μετακινούμε 36 στη δεξιά πλευρά: - x 2 \u003d - 36.
Διαχωρίζουμε και τα δύο μέρη − 1 , πάρτε x 2 \u003d 36. Στο δεξιό μέρος - ένας θετικός αριθμός, από εδώ μπορούμε να συμπεράνουμε αυτό x \u003d 36 ή X \u003d - 36.
Αφαιρέστε τη ρίζα και καταγράψτε το τελικό αποτέλεσμα: μια ελλιπής τετραγωνική εξίσωση - x 2 + 36 \u003d 0 Έχει δύο ρίζες x \u003d 6. ή x \u003d - 6.

Απάντηση: x \u003d 6. ή x \u003d - 6.

Λύση της εξίσωσης Α · Χ 2 + Β · Χ \u003d 0

Θα εξετάσουμε τον τρίτο τύπο ελλιπών τετραγωνικών εξισώσεων όταν C \u003d 0.. Για να βρείτε μια απόφαση μιας ελλιπούς τετραγωνικής εξίσωσης ένα x 2 + b · x \u003d 0, Χρησιμοποιούμε τη μέθοδο αποσύνθεσης σε πολλαπλασιαστές. Εξαπλωθεί σε πολλαπλασιαστές του πολυώνυμου, το οποίο βρίσκεται στο αριστερό μέρος της εξίσωσης, κάνοντας έναν γενικό πολλαπλασιαστή για αγκύλες Χ.. Αυτό το βήμα θα παράσχει την ευκαιρία να μετατρέψει την αρχική ελλιπή τετραγωνική εξίσωση με το ισοδύναμο x · (a · x + b) \u003d 0. Και αυτή η εξίσωση, με τη σειρά τους, ισοδυναμεί με το σύνολο των εξισώσεων x \u003d 0. και Ένα x + b \u003d 0. Την εξίσωση Ένα x + b \u003d 0 Γραμμική και τη ρίζα του: x \u003d - β α.

Ορισμός 7.

Έτσι, μια ελλιπή τετραγωνική εξίσωση ένα x 2 + b · x \u003d 0 θα έχει δύο ρίζες x \u003d 0. και x \u003d - β α.

Στερεώστε το υλικό με ένα παράδειγμα.

Παράδειγμα 5.

Είναι απαραίτητο να βρεθεί η λύση της εξίσωσης 2 3 · x 2 - 2 2 7 · x \u003d 0.

Απόφαση

Ας οδηγήσουμε Χ. Για αγκύλες και να αποκτήσετε εξίσωση x · 2 3 · x - 2 2 7 \u003d 0. Αυτή η εξίσωση είναι ισοδύναμη με τις εξισώσεις x \u003d 0. και 2 3 · x - 2 2 7 \u003d 0. Τώρα είναι απαραίτητο να επιλυθεί η προκύπτουσα γραμμική εξίσωση: 2 3 · Χ \u003d 2 2 7, Χ \u003d 2 2 7 2 3.

Επίλυση της εξίσωσης για να γράψετε με αυτόν τον τρόπο:

2 3 · x 2 - 2 2 7 · x \u003d 0 x · 2 3 · x - 2 2 7 \u003d 0

x \u003d 0 ή 2 3 · x - 2 2 7 \u003d 0

x \u003d 0 ή x \u003d 3 3 7

Απάντηση: x \u003d 0, x \u003d 3 3 7.

Διακρίσεις, ο τύπος ρίζας της τετραγωνικής εξίσωσης

Για να βρείτε μια λύση τετραγωνικών εξισώσεων, υπάρχει ένας τύπος για ρίζες:

Ορισμός 8.

x \u003d - Β ± D 2 · Α όπου D \u003d b 2 - 4 · a · c - τις λεγόμενες διακριτικές διακρίσεις μιας τετραγωνικής εξίσωσης.

Εγγραφή X \u003d - Β ± D2 · Α ουσιαστικά σημαίνει ότι το Χ1 \u003d - Β + D2 · Α, Χ2 \u003d - Β - D2 · α.

Θα είναι χρήσιμο να κατανοήσουμε πώς προέκυψε ο συγκεκριμένος τύπος και πώς να το εφαρμόσει.

Την έξοδο των ριζών της τετραγωνικής εξίσωσης

Ας αμφισβητήσουμε να λύσουμε την τετραγωνική εξίσωση a-x 2 + b · x + c \u003d 0. Εκτελέστε έναν αριθμό ισοδύναμων μετασχηματισμών:

• Διαχωρίζουμε και τα δύο μέρη της εξίσωσης για τον αριθμό ΕΝΑ.Εκτός από το μηδέν, λαμβάνουμε την μειωμένη τετραγωνική εξίσωση: x 2 + Β α · x + c a \u003d 0;
• Επισημάνετε την πλήρη πλατεία στην αριστερή πλευρά της ληφθείσας εξίσωσης:
  x 2 + ba · x + ca \u003d x 2 + 2 · Β 2 · Α · Χ + Β2 · Α 2 - Β 2 · Α2 + Ca \u003d Χ + Β 2 · Α 2 - Β 2 · Α2 + Ca .
  Μετά από αυτό, η εξίσωση θα λάβει τη μορφή: X + B 2 · Α 2 - Β 2 · Α 2 + C Α \u003d 0.
• Τώρα είναι δυνατό να γίνει η μεταφορά των δύο τελευταίων όρων στη δεξιά πλευρά, αλλάζοντας το σημάδι στο αντίθετο, μετά από το οποίο λαμβάνουμε: x + Β 2 · Α2 \u003d Β 2 · Α 2 - C Α.
• Τέλος, μετατρέπουμε την έκφραση που καταγράφηκε στη δεξιά πλευρά της τελευταίας ισότητας:
  Β 2 · Α 2 - C Α \u003d Β24 · Α2 - C Α \u003d Β24 4 · Α2-4 · Α · C4 · Α2 \u003d Β 2-4 · Α · C4 · Α2.

Έτσι, καταλήξαμε στην εξίσωση X + B 2 · A 2 \u003d B 2 - 4 · A · C 4 · A 2, ισοδύναμη εξίσωση πηγής a-x 2 + b · x + c \u003d 0.

Κατανοήσαμε τη λύση τέτοιων εξισώσεων σε προηγούμενες παραγράφους (απόφαση ελλιπών τετραγωνικών εξισώσεων). Η πείρα που αποκτήθηκε καθιστά δυνατή τη σύναψη όσον αφορά τις ρίζες της εξίσωσης X + B 2 · A 2 \u003d B 2 - 4 · A · C 4 · A 2:

• στο B 2 - 4 · A · C 4 · A 2< 0 уравнение не имеет действительных решений;
• Για το Β 2-4 · Α · C4 · Α2 \u003d 0, η εξίσωση έχει τη μορφή Χ + Β 2 · Α2 \u003d 0, κατόπιν Χ + Β 2 · Α \u003d 0.

Ως εκ τούτου, η μόνη ρίζα x \u003d - b 2 · a είναι προφανής?

• Για το Β 2 - 4 · A · C 4 · A 2\u003e 0, θα είναι σωστό: x + Β 2 · Α \u003d Β 2-4 · Α · C 4 · Α2 ή Χ \u003d Β 2 · Α - Β 2 - 4 · Α · C 4 · Α 2, η οποία είναι η ίδια με το Χ + - Β2 · Α \u003d Β 2-4 · Α · C 4 · Α2 ή Χ \u003d - Β 2 · Α - Β 2 - 4 · Α · C 4 · Α 2, δηλ. Η εξίσωση έχει δύο ρίζες.

Είναι δυνατόν να συμπεράνουμε ότι η παρουσία ή η απουσία των ρίζων της εξίσωσης Χ + Β 2 · Α2 \u003d Β 2-4 · Α · C 4 · Α 2 (και επομένως η αρχική εξίσωση) εξαρτάται από το σημάδι της έκφρασης Β 2 - 4 · A · C 4 · A 2, που καταγράφηκε στη δεξιά πλευρά. Και το σημάδι αυτής της έκφρασης ορίζεται από τον αριθμό του αριθμητή, (παρονομαστής 4 · ένα 2 θα είναι πάντα θετική), δηλαδή ένα σημάδι έκφρασης B 2 - 4 · a · c. Αυτή η έκφραση B 2 - 4 · a · c Το όνομα είναι η διακριτική μεταχείριση μιας τετραγωνικής εκκένωσης και ορίζεται ως ο χαρακτηρισμός του γράμματος D. Εδώ μπορείτε να καταγράψετε την ουσία των διακρίσεων - από την αξία του και το σήμα συνάπτεται κατά πόσον η τετραγωνική εξίσωση θα έχει έγκυρες ρίζες και αν είναι, ποιος είναι ο αριθμός των ριζών - ένας ή δύο.

Επιστρέφοντας στην εξίσωση X + B 2 · Α2 \u003d Β 2-4 · Α · C 4 · Α2. Το ξαναγράψω χρησιμοποιώντας τη διακριτική ονομασία: X + B 2 · Α2 \u003d D 4 · Α 2.

Θα διατυπώσουμε ξανά συμπεράσματα:

Ορισμός 9.

• Για ΡΕ.< 0 Η εξίσωση δεν έχει έγκυρες ρίζες.
• Για D \u003d 0. Η εξίσωση έχει τη μόνη ρίζα x \u003d - b 2 · a;
• Για D\u003e 0 Η εξίσωση έχει δύο ρίζες: x \u003d - Β 2 · Α + D4 · Α2 ή Χ \u003d - Β 2 · Α - D 4 · Α2. Αυτές οι ρίζες που βασίζονται στις ιδιότητες των ριζών μπορούν να γραφτούν με τη μορφή: Χ \u003d - Β 2 · Α + D2 · Α ή - Β 2 · Α - D2 · Α. Και όταν αποκαλύπτουμε τις ενότητες και δίνουμε τα κλάσματα στον κοινό παρονομαστή, λαμβάνουμε: x \u003d - B + D 2 · Α, Χ \u003d - Β - D 2 · α.

Έτσι, το αποτέλεσμα της συλλογιστικής μας ήταν η απομάκρυνση του τύπου των ριζών της τετραγωνικής εξίσωσης:

x \u003d - b + d 2 · a, x \u003d - b - d 2 · a, διακριτική ΡΕ. Που υπολογίζεται από τον τύπο D \u003d b 2 - 4 · a · c.

Αυτοί οι τύποι καθιστούν δυνατό όταν οι διακρίσεις είναι μεγαλύτερες για να προσδιοριστούν και οι δύο έγκυρες ρίζες. Όταν οι διακριτικές είναι μηδέν, η χρήση και των δύο τύπων θα δώσει την ίδια ρίζα με το μοναδικό διάλυμα της τετραγωνικής εξίσωσης. Στην περίπτωση που οι διακριτικές διακρίσεις είναι αρνητικές, προσπαθώντας να χρησιμοποιήσετε τη ριζική φόρμουλα της τετραγωνικής εξίσωσης, θα αντιμετωπίσουμε την ανάγκη να αφαιρέσουμε την τετραγωνική ρίζα από τον αρνητικό αριθμό, το οποίο θα μας οδηγήσει πέρα \u200b\u200bαπό τους πραγματικούς αριθμούς. Με μια αρνητική διακριτική, η τετραγωνική εξίσωση δεν θα είναι έγκυρες ρίζες, αλλά είναι δυνατή ένα ζεύγος συνολικών συζευγμένων ριζών, που προσδιορίζεται από τους ίδιους ρίζες τύπους που λαμβάνονται από εμάς.

Αλγόριθμος για την επίλυση τετραγωνικών εξισώσεων σε ρίζες

Είναι δυνατή η επίλυση της τετραγωνικής εξίσωσης, η άμεση ποδηλασία του τύπου των ριζών, αλλά βασικά το κάνει, αν είναι απαραίτητο, βρείτε πολύπλοκες ρίζες.

Στην κύρια μάζα των περιπτώσεων, συνήθως υπονοείται για την αναζήτηση μη σύνθετων, αλλά έγκυρες ρίζες της τετραγωνικής εξίσωσης. Στη συνέχεια, πριν χρησιμοποιήσετε τους τύπους των ριζών της τετραγωνικής εξίσωσης, καθορίστε πρώτα τις διακριτικές και βεβαιωθείτε ότι δεν είναι αρνητικό (διαφορετικά συμπεράνουμε ότι η εξίσωση δεν έχει έγκυρες ρίζες) και στη συνέχεια προχωρήσει στον υπολογισμό της τιμής ρίζα.

Τα παραπάνω επιχειρήματα παρέχουν την ικανότητα διαμόρφωσης ενός αλγορίθμου για την επίλυση μιας τετραγωνικής εξίσωσης.

Ορισμός 10.

Για να λύσετε μια τετράγωνη εξίσωση a-x 2 + b · x + c \u003d 0, είναι απαραίτητο:

• Σύμφωνα με τον τύπο D \u003d b 2 - 4 · a · c να βρουν την αξία των διακριτικών ·
• Με τον Δ.< 0 сделать вывод об отсутствии у квадратного уравнения действительных корней;
• Στο D \u003d 0 βρείτε τη μόνη ρίζα της εξίσωσης σύμφωνα με τον τύπο Χ \u003d - Β 2 · α.
• Για d\u003e 0, καθορίστε τις δύο έγκυρες ρίζες της τετραγωνικής εξίσωσης σύμφωνα με τον τύπο Χ \u003d - Β ± D2 · α.

Σημειώστε ότι όταν οι διακριτικές είναι μηδέν, μπορείτε να χρησιμοποιήσετε τον τύπο Χ \u003d - Β ± D2 · Α, θα δώσει το ίδιο αποτέλεσμα με τον τύπο Χ \u003d - Β 2 · α.

Εξετάστε παραδείγματα.

Παραδείγματα λύσεων τετραγωνικών εξισώσεων

Παρουσιάζουμε τη λύση των παραδειγμάτων σε διαφορετικές τιμές των διακριτικών.

ΠΑΡΑΔΕΙΓΜΑ 6.

Είναι απαραίτητο να βρείτε τις ρίζες της εξίσωσης x 2 + 2 · x - 6 \u003d 0.

Απόφαση

Γράφουμε τους αριθμούς συντελεστών της τετραγωνικής εξίσωσης: a \u003d 1, b \u003d 2 και C \u003d - 6. Στη συνέχεια, ενεργούμε για τον αλγόριθμο, δηλ. Θα προχωρήσουμε στον υπολογισμό των διακριτικών, για τις οποίες θα αντικαταστήσουμε τους συντελεστές Α, Β και ΝΤΟ. Στον τύπο των διακριτικών: D \u003d Β 2 - 4 · Α · C \u003d 2 2-4 · 1 · (- 6) \u003d 4 + 24 \u003d 28.

Έτσι, αποκτήσαμε d\u003e 0, και αυτό σημαίνει ότι η αρχική εξίσωση θα έχει δύο έγκυρες ρίζες.
Για να τα βρείτε, χρησιμοποιούμε τη ρίζα Τύπου Χ \u003d - Β ± D2 · Α και, υποκαθιστώντας τις αντίστοιχες τιμές, λαμβάνουμε: x \u003d - 2 ± 28 2 · 1. Απλοποιούμε την προκύπτουσα έκφραση, κάνοντας έναν πολλαπλασιαστή για το root sign, ακολουθούμενο από την κοπή του κλάσματος:

x \u003d - 2 ± 2 · 7 2

x \u003d - 2 + 2 · 7 2 ή x \u003d - 2-2 · 7 2

x \u003d - 1 + 7 ή x \u003d - 1 - 7

Απάντηση: x \u003d - 1 + 7, x \u003d - 1 - 7.

Παράδειγμα 7.

Είναι απαραίτητο να λύσετε την τετραγωνική εξίσωση - 4 · x 2 + 28 · x - 49 \u003d 0.

Απόφαση

Προσδιορίστε τις διακρίσεις: D \u003d 28 2 - 4 · (- 4) · (- 49) \u003d 784 - 784 \u003d 0. Με αυτή τη διακριτική αξία, η αρχική εξίσωση θα έχει μόνο μία ρίζα που ορίζεται από τον τύπο Χ \u003d - Β 2 · α.

x \u003d - 28 2 · (- 4) x \u003d 3, 5

Απάντηση: x \u003d 3, 5.

Παράδειγμα 8.

Είναι απαραίτητο να λύσετε την εξίσωση 5 · y 2 + 6 · y + 2 \u003d 0

Απόφαση

Οι αριθμητικοί συντελεστές αυτής της εξίσωσης θα είναι: Α \u003d 5, Β \u003d 6 και C \u003d 2. Χρησιμοποιούμε αυτές τις τιμές για να βρούμε μια διακριτική διάκριση: d \u003d B 2 - 4 · a · c \u003d 6 2-4 · 5,2 \u003d 36 - 40 \u003d - 4. Η υπολογιζόμενη διακριτική είναι αρνητική, επομένως, η αρχική τετραγωνική εξίσωση δεν έχει έγκυρες ρίζες.

Στην περίπτωση που η εργασία είναι να καθορίσετε πολύπλοκες ρίζες, εφαρμόστε τον τύπο ρίζας, εκτελώντας δράσεις με πολύπλοους αριθμούς:

x \u003d - 6 ± - 4 2 · 5,

x \u003d - 6 + 2 · i 10 ή x \u003d - 6 - 2 · i 10,

x \u003d - 3 5 + 1 5 · i ή x \u003d - 3 5-1 5 · i.

Απάντηση: Δεν υπάρχουν έγκυρες ρίζες. Οι πολύπλοκες ρίζες έχουν ως εξής: - 3 5 + 1 5 · Ι, - 3 5 - 1 5 · Ι.

Στο σχολικό πρόγραμμα, δεν υπάρχει ακόμη απαίτηση να αναζητήσουμε πολύπλοκες ρίζες, οπότε εάν κατά τη διάρκεια της λύσης, η διάκριση ορίζεται ως αρνητική, η απάντηση καταγράφεται αμέσως ότι δεν υπάρχουν έγκυρες ρίζες.

Ρίζες φόρμουλας για ακόμη και δεύτερους συντελεστές

Ο τύπος των ρίζων Χ \u003d - Β ± D2 · Α (D \u003d B 2-4 · A · C) καθιστά δυνατή την απόκτηση άλλου τύπου, πιο συμπαγής, επιτρέποντας την εξεύρεση λύσεων τετραγωνικών εξισώσεων με ένα ομοιόμορφο συντελεστή στο Χ (ή με συντελεστή τύπου 2 · Ν, για παράδειγμα, 2,3 ή 14 · LN 5 \u003d 2 · 7 · LN 5). Δείχνουμε πώς εμφανίζεται αυτή η φόρμουλα.

Ας είμαστε το καθήκον να βρούμε το διάλυμα της τετραγωνικής εξίσωσης Α · Χ 2 + 2 · Ν · Χ + C \u003d 0. Δρούμε τον αλγόριθμο: Προσδιορίστε τις διακριτικές d \u003d (2 · n) 2-4 · Α · C \u003d 4 · Ν2-4 · Α · C \u003d 4 · (Ν2 - Α · C) και στη συνέχεια χρησιμοποιήστε το Τύπος ρίζας:

x \u003d - 2 · n ± D2 · Α, Χ \u003d - 2 · Ν ± 4 · Ν2- Α · C2 · Α, Χ \u003d-2- Ν ± 2 Ν2 - Α · C2 · Α, Χ \u003d - Ν ± N 2 - A · Ca.

Αφήστε την έκφραση N 2 - A · C να υποδεικνύεται ως D 1 (μερικές φορές d "). Στη συνέχεια ο τύπος των ριζών της τετραγώνης εξίσωσης υπό εξέταση με τον δεύτερο συντελεστή 2 · n θα λάβει τη φόρμα:

x \u003d - Ν ± D 1 Α, όπου D1 \u003d N 2 - A · C.

Είναι εύκολο να το δείτε ότι το d \u003d 4 · d 1, ή D 1 \u003d D4. Με άλλα λόγια, το D 1 είναι ένα τέταρτο των διακριτικών. Είναι προφανές ότι το σημάδι D 1 είναι το ίδιο με το σημείο D, το οποίο σημαίνει ότι το σημάδι D 1 μπορεί επίσης να χρησιμεύσει ως δείκτης της παρουσίας ή της απουσίας των ριζών της τετραγωνικής εξίσωσης.

Ορισμός 11.

Έτσι, για να βρεθεί η λύση της τετραγωνικής εξίσωσης με τον δεύτερο συντελεστή 2 · n, είναι απαραίτητο:

• Βρείτε D 1 \u003d N 2 - A · C;
• Με d 1.< 0 сделать вывод, что действительных корней нет;
• Για d 1 \u003d 0, προσδιορίστε τη μόνη ρίζα της εξίσωσης σύμφωνα με τον τύπο X \u003d - N a;
• Για d 1\u003e 0, καθορίστε τις δύο έγκυρες ρίζες σύμφωνα με τον τύπο Χ \u003d - Ν ± D 1 α.

Παράδειγμα 9.

Είναι απαραίτητο να λύσετε την τετραγωνική εξίσωση 5 · x 2 - 6 · x - 32 \u003d 0.

Απόφαση

Ο δεύτερος συντελεστής της καθορισμένης εξίσωσης μπορεί να αντιπροσωπεύεται ως 2 · (- 3). Στη συνέχεια, ξαναγράψτε την καθορισμένη τετραγωνική εξίσωση ως 5 · x 2 + 2 · (- 3) · x - 32 \u003d 0, όπου a \u003d 5, n \u003d - 3 και c \u003d - 32.

Υπολογίζουμε το τέταρτο μέρος των διακριτικών: D 1 \u003d Ν2 - Α · C \u003d (- 3) 2 - 5 · (- 32) \u003d 9 + 160 \u003d 169. Η τιμή που λαμβάνεται θετικά, αυτό σημαίνει ότι η εξίσωση έχει δύο έγκυρες ρίζες. Τα ορίζουμε σύμφωνα με την αντίστοιχη ρίζα:

x \u003d - Ν ± D 1 Α, Χ \u003d ---3 ± 169 5, Χ \u003d 3 ± 13 5,

x \u003d 3 + 13 5 ή x \u003d 3 - 13 5

x \u003d 3 1 5 ή x \u003d - 2

Θα ήταν δυνατή η πραγματοποίηση υπολογισμών και η συνήθης τύπος των ριζών της τετραγωνικής εξίσωσης, αλλά στην περίπτωση αυτή η λύση θα ήταν πιο δυσκίνητη.

Απάντηση: x \u003d 3 1 5 ή x \u003d - 2.

Απλούστευση των ειδών τετραγωνικών εξισώσεων

Μερικές φορές είναι δυνατή η βελτιστοποίηση του τύπου της εξίσωσης πηγής, η οποία θα απλοποιήσει τη διαδικασία υπολογισμού των ριζών.

Για παράδειγμα, μια τετράγωνη εξίσωση 12 · x 2 - 4 · x - 7 \u003d 0 είναι σαφώς πιο βολικό για την επίλυση από 1200 · x 2-400 · x - 700 \u003d 0.

Πιο συχνά η απλούστευση του είδους της τετραγωνικής εξίσωσης εκτελείται από τον πολλαπλασιασμό ή τη διαίρεση και των δύο τμημάτων του σε ένα είδος αριθμού. Για παράδειγμα, δείξαμε ένα απλοποιημένο αρχείο της εξίσωσης 1200 · x 2 - 400 · x - 700 \u003d 0, που λαμβάνεται διαιρώντας και τα δύο μέρη κατά 100.

Μια τέτοια μετατροπή είναι δυνατή όταν οι συντελεστές της τετραγωνικής εξίσωσης δεν είναι αμοιβαία απλοί αριθμοί. Στη συνέχεια, συνήθως διαιρείται και τα δύο μέρη της εξίσωσης με το μεγαλύτερο κοινό διαιρέτη απόλυτων τιμών των συντελεστών της.

Ως παράδειγμα, χρησιμοποιήστε μια τετραγωνική εξίσωση 12 · x 2 - 42 · x + 48 \u003d 0. Ορίζουμε τον κόμβο των απόλυτων τιμών των συντελεστών του: κόμβους (12, 42, 48) \u003d κόμβος (κόμβος (12, 42), 48) \u003d κόμβος (6, 48) \u003d 6. Θα διαιρέσουμε τα δύο μέρη της αρχικής τετραγωνικής εξίσωσης με 6 και λαμβάνουμε την ισοδύναμη τετράγωνη εξίσωση 2 · x 2 - 7 · x + 8 \u003d 0.

Ο πολλαπλασιασμός και των δύο τμημάτων της τετραγωνικής εξίσωσης είναι συνήθως απαλλαγμένος από κλασματικούς συντελεστές. Ταυτόχρονα πολλαπλασιάζεται ο μικρότερος γενικός πολλαπλός παρονομαστής των συντελεστών της. Για παράδειγμα, εάν κάθε μέρος της τετραγωνικής εξίσωσης είναι 1 6 · x 2 + 2 3 · x - 3 \u003d 0 πολλαπλασιάζεται από το NOC (6, 3, 1) \u003d 6, τότε θα καταγραφεί σε μια απλούστερη μορφή x 2 + 4 · x - 18 \u003d 0.

Τέλος, σημειώνουμε ότι σχεδόν πάντα να απαλλαγούμε από το μείον τον πρώτο συντελεστή της τετραγωνικής εξίσωσης, αλλάζοντας τα σημάδια κάθε μέλους της εξίσωσης, η οποία επιτυγχάνεται με τον πολλαπλασιασμό (ή τα τμήματα) και των δύο τμημάτων του 1. Για παράδειγμα, από μια τετράγωνη εξίσωση - 2 · x 2 - 3 · x + 7 \u003d 0, μπορείτε να μεταβείτε στην απλοποιημένη έκδοση 2 · x 2 + 3 · x - 7 \u003d 0.

Επικοινωνία μεταξύ ριζών και συντελεστών

Ο τύπος των ριζών των τετραγωνικών εξισώσεων X \u003d - Β ± D 2 · Α ήδη γνωστός στους ΗΠΑ εκφράζει τις ρίζες της εξίσωσης μέσω των αριθμητικών συντελεστών του. Βασιζόμενοι σε αυτόν τον τύπο, έχουμε την ευκαιρία να θέσουμε άλλες εξαρτήσεις μεταξύ των ριζών και των συντελεστών.

Το πιο διάσημο και εφαρμόσιμο είναι οι τύποι του θεώρημα Vieta:

x 1 + x 2 \u003d - Β Α και Χ2 \u003d C α.

Συγκεκριμένα, για τη μειωμένη τετραγωνική εξίσωση, η ποσότητα των ριζών είναι ο δεύτερος συντελεστής με το αντίθετο σημείο και το προϊόν των ριζών είναι δωρεάν. Για παράδειγμα, σύμφωνα με τα είδη της τετραγωνικής εξίσωσης 3 · x 2 - 7 · x + 22 \u003d 0, είναι δυνατόν να προσδιοριστεί αμέσως το άθροισμα των ριζών του είναι 7 3 και το προϊόν των ριζών είναι 22 3.

Μπορείτε επίσης να βρείτε έναν αριθμό άλλων συνδέσμων μεταξύ των ριζών και των συντελεστών της τετραγωνικής εξίσωσης. Για παράδειγμα, το άθροισμα των τετραγώνων των ριζών της τετραγωνικής εξίσωσης μπορεί να εκφραστεί μέσω των συντελεστών:

x 1 2 + x 2 2 \u003d (x 1 + x 2) 2 - 2- x 1-x 2 \u003d - Ba2-2- Ca \u003d Β 2 Α2-2 · Ca \u003d Β 2-2 · Α · Ca 2.

Εάν παρατηρήσετε ένα λάθος στο κείμενο, επιλέξτε το και πατήστε Ctrl + Enter