Ποιο είναι το προϊόν του φορέα και αν. Vector έργα τέχνης των φορείων που δίνονται από τις συντεταγμένες
Γωνία μεταξύ φορέων
Προκειμένου να εισαγάγουμε την έννοια ενός διανύσματος ενός διανύσματος δύο διανυσμάτων, πρέπει πρώτα να καταλάβετε την έννοια ως τη γωνία μεταξύ αυτών των φορέων.
Ας δώσουμε δύο διάνυσμα $ \\ overline (α) $ και $ \\ overline (β) $. Πάρτε στο χώρο οποιοδήποτε σημείο $ o $ και δημοσιεύστε τα διανύσματα $ \\ overline (α) \u003d \\ overline (OA) $ και $ \\ overline (β) \u003d \\ overline (OB) $, τότε η γωνία $ aob $ θα είναι Ονομάζεται η γωνία μεταξύ αυτών των φορέων (Σχήμα 1).
Ονομασία: $ ∠ (\\ overline (α), \\ overline (β)) $
Η έννοια του φορέα τέχνης και της φόρμουλας
Ορισμός 1.
Το προϊόν φορέα δύο φορείων ονομάζεται διάνυσμα, κάθετα και στους δύο διανύσματα δεδομένων και το μήκος του θα είναι ίσο με το προϊόν αυτών των φορέων με μια γωνία Sine μεταξύ των φορέων δεδομένων, καθώς και σε αυτόν τον φορέα με δύο αρχικά έχουν έναν αυστηρότερο προσανατολισμό , όπως το σύστημα συντεταγμένων του Cartian.
Ονομασία: $ \\ overline (α) x \\ overline (β) $.
Μαθηματικά, μοιάζει με αυτό:
- $ | \\ Overline (α) x \\ overline (β) | \u003d | overline (α) || \\ overline (β) | Sin\u2061∠ (\\ overline (α), \\ overline (β)) $ |
- $ \\ overline (α) x \\ overline (β) ⊥ \\ overline (α) $, $ \\ overline (α) x \\ overline (β) ⊥ \\ overline (β) $ \\
- $ (\\ Overline (α) x \\ overline (β), \\ overline (α), \\ overline (β)) $ και $ (\\ overline (i), \\ overline (k), \\ overline (k)) $ εξίσου προσανατολισμένο (Εικ. 2)
Προφανώς, το εξωτερικό προϊόν των φορέων θα είναι ίσο με το μηδενικό φορέα σε δύο περιπτώσεις:
- Εάν το μήκος ενός ή και των δύο φορείων είναι μηδέν.
- Εάν η γωνία μεταξύ αυτών των φορέων θα είναι $ 180 \\ circ $ ή $ 0 ^ \\ circ $ (όπως στην περίπτωση αυτή, ο κόλπος είναι μηδέν).
Για να δείτε οπτικά πώς βρίσκεται ο φορέας φορέων, εξετάστε τα ακόλουθα παραδείγματα της λύσης.
Παράδειγμα 1.
Βρείτε το μήκος του φορέα $ \\ overline (δ) $, το οποίο θα είναι το αποτέλεσμα ενός διανυσμάτων διανυσμάτων, με συντεταγμένες $ \\ overline (α) \u003d (0,4,0) $ και $ \\ overline (β) \u003d ( 3.0.0) $.
Απόφαση.
Εικόνες Αυτοί οι φορείς στον κεντρικό χώρο συντεταγμένων Cartesian (Εικ. 3):
Εικόνα 3. Φορείς στον κεντρικό χώρο συντεταγμένων. Συγγραφέας24 - Ανταλλαγή Διαδικτύου Φοιτητών
Βλέπουμε ότι αυτοί οι φορείς βρίσκονται στους άξονες των $ OX $ και $ OY $, αντίστοιχα. Συνεπώς, η γωνία μεταξύ τους θα είναι $ 90 ^ \\ cirg $. Βρείτε τα μήκη αυτών των φορέων:
$ | \\ Overline (α) | \u003d \\ sqrt (0 + 16 + 0) \u003d $ 4
$ | \\ Overline (β) | \u003d \\ sqrt (9 + 0 + 0) \u003d $ 3
Στη συνέχεια, εξ ορισμού 1, λαμβάνουμε την ενότητα $ | \\ overline (Δ) | $
$ | \\ Overline (δ) | \u003d | \\ overline (α) || \\ overline (β) | sin90 ^ \\ cirg \u003d 4 \\ cdot 3 \\ cdot 1 \u003d 12 $
Απάντηση: $ 12 $.
Υπολογισμός της τέχνης διάνυσμα σύμφωνα με τις συντεταγμένες των φορέων
Από τον ορισμό 1 ρέει αμέσως και η μέθοδος εύρεσης ενός προϊόντος φορέα για δύο φορείς. Δεδομένου ότι ο φορέας εκτός από την αξία έχει επίσης μια κατεύθυνση, είναι αδύνατο να το βρείτε μόνο με μια κλιμακωτή τιμή. Αλλά εκτός του, εξακολουθεί να υπάρχει ένας τρόπος να βρεθούν διανύσματα με αυτές τις συντεταγμένες.
Ας μας δώσουμε ένα διάνυσμα $ \\ overline (α) $ και $ \\ overline (β) $, το οποίο θα έχει συντονίσει $ (Α_1, Α_2, Α_3) $ και $ (β_1, β_2, β_3) $, αντίστοιχα. Στη συνέχεια, ο φορέας του φορέα εργασίας (δηλαδή, οι συντεταγμένες του μπορούν να βρεθούν σύμφωνα με τον ακόλουθο τύπο:
$ \\ overline (α) x \\ overline (β) \u003d \\ beach (vmatrix) \\ overline (i) \\ overline (j) & \\ overline (k) \\\\ α_1 α_2 α_3 \\\\ \\ \\ end (vmatrix) $
Διαφορετικά, αποκαλύπτοντας τον καθοριστικό παράγοντα, έχουμε τις ακόλουθες συντεταγμένες
$ \\ overline (α) x \\ overline (β) \u003d (α_2 β_3-α_3 β_2, α -3 β_1-α_1 β_3, α_1 β_2-α_2 β_1) $
Παράδειγμα 2.
Βρείτε φορέα διάνυσμα Προϊόν Collinear Vector $ \\ overline (α) $ και $ \\ overline (β) $ με συντεταγμένες $ (0.3.3) $ και $ (- 1,2,6) $.
Απόφαση.
Χρησιμοποιούμε τον παραπάνω τύπο. Λαμβάνω
$ \\ Overline (α) x \\ overline (β) \u003d \\ beach (vmatrix) \\ overline (i) \\ overline (j) & \\ overline (k) \\\\ 0 & 3 & 3 \\\\ - 1 & 2 & 6 \\ Τέλος (vmatrix) \u003d (18-6) \\ overline (i) - (0 + 3) \\ overline (j) + (0 + 3) \\ overline (k) \u003d 12 \\ overline (j) -3 \\ ) +3 \\ overline (k) \u003d (12, -3.3) $
Απάντηση: $ (12, -3.3) $.
Ιδιότητες του έργου τέχνης διάνυσμα
Για αυθαίρετα αναμειγνύεται τρεις διανύσματα $ \\ overline (α) $, $ \\ overline (β) $ και $ \\ overline (γ) $, καθώς και $ R∈R $, τις ακόλουθες ιδιότητες:
Παράδειγμα 3.
Βρείτε την περιοχή του παραλληλογράφου των οποίων οι κορυφές έχουν συντεταγμένες των $ (3.0.0) $, $ (0,0,0) $, $ (0,8,0) $ και $ (3.8.0) $.
Απόφαση.
Αρχικά, θα δείξουμε αυτό το παραλληλόγραμμο στον χώρο του συντεταγμένου (Εικ. 5):
Εικόνα 5. Δημοσκόπιο στον χώρο του συντεταγμένου. Συγγραφέας24 - Ανταλλαγή Διαδικτύου Φοιτητών
Βλέπουμε ότι οι δύο πλευρές αυτού του παραλληλογράφου κατασκευάζονται χρησιμοποιώντας κολλητικούς φορείς με συντεταγμένες $ \\ overline (α) \u003d (3.0.0) $ και $ \\ overline (β) \u003d (0,8,0) $. Χρησιμοποιώντας το τέταρτο ακίνητο, έχουμε:
$ S \u003d \\ overline (α) x \\ overline (β) | $
Θα βρούμε το διάνυσμα $ \\ overline (α) x \\ overline (β) $:
$ \\ Overline (α) x \\ overline (β) \u003d \\ begin (vmatrix) \\ overline (i) \\ overline (j) & \\ overline (k) \\\\ 3 & 0 \\ end (Vmatrix) \u003d 0 \\ overline (i) -0 \\ overline (j) +24 \\ overline (k) \u003d (0,0,24) $
Ως εκ τούτου
$ S \u003d \\ overline (α) x \\ overline (β) | \u003d \\ sqrt (0 + 0 + 24 ^ 2) \u003d 24 $
Διάνυσμα τέχνη - Πρόκειται για ένα ψευδοκτόμενο, κάθετο επίπεδο, χτισμένο σε δύο απόσυρρες, το οποίο είναι το αποτέλεσμα μιας δυαδικής επιχείρησης "πολλαπλασιασμού φορέα" πάνω από φορείς σε τρισδιάστατο χώρο Ευκλείδους. Το προϊόν φορέα δεν έχει τις ιδιότητες της επιρροής και της συσχετισμικής συνεργασίας (είναι αντι-επιτακτικό) και, σε αντίθεση με το κλιμακωτό προϊόν των φορέων, είναι ένας φορέας. Χρησιμοποιείται ευρέως σε πολλές τεχνικές και φυσικές εφαρμογές. Για παράδειγμα, η στιγμή της ώθησης και η δύναμη Lorentz που καταγράφηκαν μαθηματικά με τη μορφή ενός φορέα εργασίας. Το προϊόν φορέα είναι χρήσιμο για την "μέτρηση" της κάθετης φορείς των φορέων - η μονάδα του προϊόντος φορέα δύο φορέων είναι ίση με το προϊόν των μονάδων τους, εάν είναι κάθετα και μειώνεται στο μηδέν, εάν οι φορείς είναι παράλληλοι ή αντιπαράλληλο .
Μπορείτε να προσδιορίσετε το προϊόν φορέα με διάφορους τρόπους και θεωρητικά, στο χώρο οποιασδήποτε διάστασης n, είναι δυνατόν να υπολογιστεί το προϊόν των φορέων Ν-1, αφού έλαβε το μόνο διάνυσμα κάθετο σε όλους τους. Αλλά εάν η εργασία περιορίζεται σε μη τετριμμένα δυαδικά έργα με αποτελέσματα φορέα, τότε το παραδοσιακό προϊόν φορέα ορίζεται μόνο σε τρισδιάστατους και επτά διαστάσεων χώρους. Το αποτέλεσμα ενός προϊόντος φορέα, όπως το κλιμακωτό, εξαρτάται από τη μετρική του ευκλειιδικού χώρου.
Σε αντίθεση με τον τύπο υπολογισμού σύμφωνα με τις συντεταγμένες φορείων του κλιματιστικού προϊόντος σε ένα τρισδιάστατο ορθογώνιο σύστημα συντεταγμένων, ο τύπος για το προϊόν φορέα εξαρτάται από τον προσανατολισμό του ορθογώνιου συστήματος συντεταγμένων ή, διαφορετικά, της "χειροτονίας" του.
Ορισμός:
Ένα προϊόν φορέα Α στον φορέα Β στο χώρο R 3 ονομάζεται διάνυσμα C, ικανοποιώντας τις ακόλουθες απαιτήσεις:
Το μήκος του φορέα C είναι ίση με το προϊόν των διανυσμάτων Α και Β στην ημιτονοθήκη της γωνίας Φ μεταξύ τους:
| C | \u003d | a || b | SIN φ?
Ο διάνυσμα C είναι ορθογώνιος σε κάθε ένα από τα φορείς Α και Β.
Ο φορέας C κατευθύνεται έτσι ώστε η κορυφή των φορέων ABC να είναι σωστή.
Στην περίπτωση του χώρου R7, απαιτείται η συσχετισμικότητα των τριών φορέων Α, Β, Γ.
Ονομασία:
c \u003d\u003d\u003d a × b

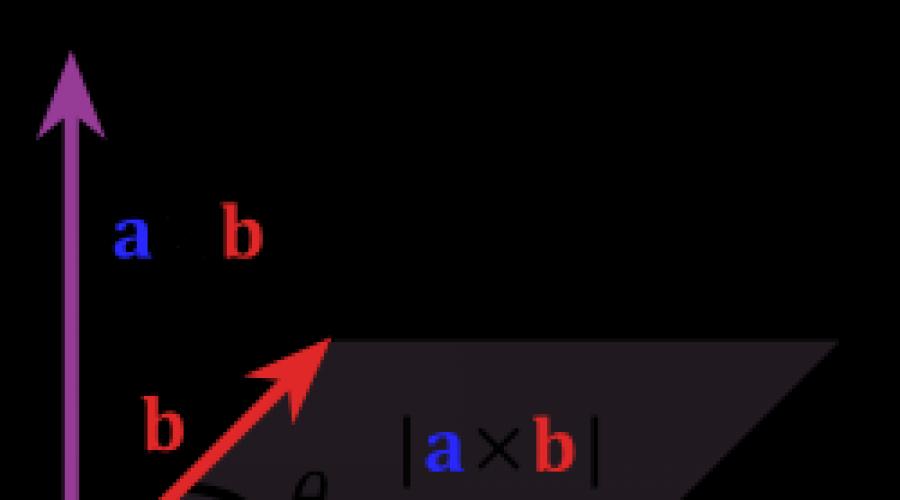
Σύκο. 1. Η περιοχή του παραλληλογράφου είναι ίση με τη μονάδα διανύσματος προϊόντος
Γεωμετρικές ιδιότητες του φορέα εργασίας:
Η απαραίτητη και επαρκής προϋπόθεση για την κολλητικότητα δύο μη μηδενικών φορέων είναι η ισότητα μηδέν της τέχνης φορέα τους.
Μονάδα τέχνης διάνυσμα ισούται με πλατεία ΜΙΚΡΟ. Ένα παραλληλόγραμμο χτισμένο στις εκδόσεις που δόθηκαν στη γενική αρχή των φορέων ΕΝΑ. και ΣΙ. (Βλ. Εικ. 1).
Αν ένα ΜΙ. - Ενιαία διάνυσμα, ορθογώνιοι φορείς ΕΝΑ. και ΣΙ. και επιλέχθηκε έτσι ώστε η τρόικα Α, Β, Ε - δεξιά, και ΜΙΚΡΟ. - την περιοχή του παραλληλόγραμμου που χτίστηκε σε αυτά (που δόθηκε στη γενική εκκίνηση), τότε ο τύπος ισχύει για το προϊόν φορέα:
\u003d S Ε.
Εικ.2. Ο όγκος παραλληλεπίπεδο όταν χρησιμοποιεί το διάνυσμα και το κλιμακωτό προϊόν των φορέων. Οι διακεκομμένες γραμμές δείχνουν τις προβολές του φορέα C σε ένα × Β και διανύσματα A στο B × C, το πρώτο βήμα είναι να βρουν τα scalar έργα.
Αν ένα ΝΤΟ. - Ορισμένοι διάνυσμα, π
- οποιοδήποτε αεροπλάνο που περιέχει αυτόν τον φορέα, ΜΙ. - Ενιαίος διάνυσμα που βρίσκεται στο αεροπλάνο π
και ορθογώνιο k c, G.- Ενιαίο διάνυσμα, ορθογώνιο στο αεροπλάνο π
και κατευθύνθηκε έτσι ώστε η κορυφή των φορέων ΗΚΓ είναι σωστό, τότε για οποιοδήποτε αεροπλάνο π
Διάνυσμα ΕΝΑ. Formula Fair:
\u003d Pr e a | c | g
όπου pr e μια προβολή του φορέα e σε ένα
| C | Vector Module με
Όταν χρησιμοποιείτε φορέα και scalar έργα, μπορείτε να υπολογίσετε τον όγκο των παραλληλεπίπεδων, που χτίστηκε στις εκδόσεις που δόθηκαν στη γενική αρχή των εκδόσεων. Α, Β. και ΝΤΟ.. Ένα τέτοιο προϊόν από τρεις φορείς ονομάζεται μικτό.
V \u003d | A (B × C) |
Το σχήμα δείχνει ότι αυτή η ένταση μπορεί να βρεθεί με δύο τρόπους: το γεωμετρικό αποτέλεσμα διατηρείται ακόμη και κατά την αντικατάσταση του "Scalar" και "Vector" λειτουργεί σε μέρη:
V \u003d a × b c \u003d a b × c
Το μέγεθος του προϊόντος φορέα εξαρτάται από το ημίχρονο της γωνίας μεταξύ των αρχικών φορέων, οπότε το προϊόν φορέα μπορεί να θεωρηθεί ως ένα βαθμό "κάθετα" των φορέων καθώς και ένα κλιμακωτό προϊόν μπορεί να θεωρηθεί ως βαθμός "παραλληλισμού" . Το προϊόν φορέα δύο απλών φορέων είναι 1 (ένα διάνυσμα), εάν οι αρχικοί φορείς είναι κάθετοι και ίσοι με 0 (μηδέν διάνυσμα), εάν οι φορείς είναι παράλληλοι ή αντι-παράλληλοι.
Έκφραση για φορέα εργασίας στις καρτεσιανές συντεταγμένες
Εάν δύο φορείς ΕΝΑ. και ΣΙ. Που ορίζονται από τις ορθογώνιες καρκινικές συντεταγμένες τους και με μεγαλύτερη ακρίβεια - που παρουσιάζονται σε ορθογονική βάση
a \u003d (a x, a y, a z)
b \u003d (b x, b y, b z)
και το σύστημα συντεταγμένων είναι το σωστό, τότε η τέχνη φορέα τους έχει την εμφάνιση
\u003d (Ένα y b z-z b y, ένα z b x-x b z, ένα x b y-a y b x)
Για να απομνημονεύσετε αυτόν τον τύπο:
i \u003d σε ijk a j b k
Οπου Ε IJK.- Σύμβολο Levi-Civita.
Πριν δώσετε την έννοια του φορέα εργασίας, στρίψτε στο ζήτημα του προσανατολισμού ενός παραγγελθέντος τριπλού διανυσμάτων A →, B →, C → σε τρισδιάστατο χώρο.
Θα αναβάλουμε τους φορείς A →, B →, C → από ένα σημείο. Ο προσανατολισμός του τριπλού Α →, Β →, C → είναι δεξιός ή αριστερά, ανάλογα με την κατεύθυνση του φορέα C →. Σε ποια κατεύθυνση η μικρότερη περιστροφή του φορέα Α → ΚΒ → από το άκρο του φορέα C →, ο τύπος τρόικας Α →, Β →, C → προσδιορίζεται.
Εάν η συντομότερη περιστροφή πραγματοποιείται αριστερόστροφα, τότε το τρίκλινο των διανυσμάτων A →, B →, C → που ονομάζεται σωστάΑν δεξιόστροφα - leva.
Στη συνέχεια, πάρτε δύο μη collinear διάνυσμα A → και B →. Στη συνέχεια, θα απενεργοποιήσω από το σημείο ΑΒ → \u003d A → και A C → \u003d B →. Κατασκευάζουμε τον φορέα Α D → \u003d C →, το οποίο είναι ταυτόχρονα κάθετο σε ένα b → και ένα c →. Έτσι, κατά την κατασκευή του ίδιου του φορέα ένα d → \u003d C → μπορούμε να κάνουμε ένα bicon, να τη θέσουμε ή μία κατεύθυνση ή το αντίθετο (βλέπε εικόνα).

Παραγγείλαμε τρεις διανύσματα A →, B →, C → → ίσως, όπως σκέφτηκα δεξιά ή αριστερά, ανάλογα με την κατεύθυνση του φορέα.
Από τα παραπάνω, μπορούμε να εισέλθουμε στον ορισμό ενός φορέα εργασίας. Αυτός ο ορισμός χορηγείται για δύο φορείς που ορίζονται στο ορθογώνιο σύστημα συντεταγμένων τρισδιάστατου χώρου.
Ορισμός 1.
Vector προϊόν δύο διανυσμάτων Α → και Β → Θα καλέσουμε έναν τέτοιο φορέα που καθορίζεται στο ορθογώνιο σύστημα συντεταγμένων τρισδιάστατου χώρου έτσι ώστε:
- Εάν οι φορείς είναι → και Β → Colline, θα είναι μηδέν.
- Θα είναι κάθετη προς τον φορέα Α → και ο φορέας Β → δηλαδή ∠ A → C → \u003d ∠ B → C → \u003d Π 2;
- Το μήκος του καθορίζεται από τον τύπο: C → \u003d A → · b → · SIN ∠ A →, B →?
- Στρατό φορέων Α →, Β →, C → έχει τον ίδιο προσανατολισμό με το καθορισμένο σύστημα συντεταγμένων.
Vector έργα τέχνης των διανυσμάτων A → και B → έχει την ακόλουθη ονομασία: A → × B →.
Συντεταγμένες του φορέα εργασίας
Δεδομένου ότι οποιοσδήποτε φορέας έχει ορισμένες συντεταγμένες στο σύστημα συντεταγμένων, μπορείτε να εισαγάγετε τον δεύτερο ορισμό ενός προϊόντος φορέα, το οποίο θα σας επιτρέψει να βρείτε τις συντεταγμένες του σύμφωνα με τις καθορισμένες συντεταγμένες των φορέων.
Ορισμός 2.
Στο ορθογώνιο σύστημα συντεταγμένων τρισδιάστατου χώρου Προϊόν φορέα δύο διανυσμάτων Α → \u003d (a x; a y; a z) και b → \u003d (b x; b y; b z) Που ονομάζεται διάνυσμα C → \u003d a → × b → \u003d (AY · BZ - AZ · BY) · I → + (AZ · BX - AX · BZ) · J → + (AX · BY - AY · BX) · K → όπου i →, J →, K → είναι οι φορείς συντονισμού.
Το προϊόν διάνυσμα μπορεί να εισαχθεί ως καθοριστικός παράγοντας τετραγωνικής μήτρας τρίτης τάξης, όπου η πρώτη γραμμή είναι ή →, J →, K →, η δεύτερη γραμμή περιέχει τις συντεταγμένες του φορέα Α → και την τρίτη - τις συντεταγμένες του φορέα Β → Σε ένα δεδομένο σύστημα ορθογώνιας συντεταγμένης συντεταγμένης, αυτός ο καθοριστικός παράγοντας της μήτρας μοιάζει με αυτό: C → \u003d a → × b → \u003d i → J → K → axayazbxbybz
Αποκτήστε αυτόν τον καθορισμό για τα στοιχεία της πρώτης γραμμής, λαμβάνουμε την ισότητα της πρώτης γραμμής, λαμβάνουμε την ισότητα: C → \u003d a → × b → \u003d i → j → k → axazbxbybz \u003d ayazbybx · i → → → \u003d \u003d a → × B → \u003d (AY · BZ - AZ · BY) · I → + (AZ · BX - AX · BZ) · J → + (AX · BY - AY · BX) · K →
Ιδιότητες του φορέα εργασίας
Είναι γνωστό ότι το προϊόν φορέα στις συντεταγμένες φαίνεται να είναι ο καθοριστικός παράγοντας της μήτρας C → \u003d a → × b → \u003d i → J → k → a x a y a z b x b y b z, έπειτα στη βάση Ιδιότητες του καθοριστικού παράγοντα της μήτρας Εμφανίζει τα ακόλουθα Ιδιότητες του φορέα εργασίας:
- Αντικατάσταση A → × B → \u003d - B → × a →,
- Κατανομή Α (1) → + Α (2) → × B \u003d Α (1) → × Β → + Α (2) → × Β → ή → × Β (1) → + b (2) → \u003d a → × b (1) → + a → × b (2) →;
- Συνεργασία λ · A → × B → \u003d λ · A → × b → ή → × (λ / b →) \u003d λ · A → × b →, όπου λ είναι αυθαίρετο έγκυρο αριθμό.
Αυτές οι ιδιότητες δεν έχουν δύσκολες αποδείξεις.
Για παράδειγμα, μπορούμε να αποδείξουμε την αντι-κτιριακή ιδιότητα του προϊόντος φορέα.
Απόδειξη της κατά της επιρροής
Εξ ορισμού A → × B → \u003d I → J → K → a x a y a z b x b y b z και b → k → \u003d i → j → k → b x b y b z a x a y a z. Και αν οι δύο γραμμές των πινάκων αναδιάταξη σε θέσεις, η τιμή του καθοριστικού προσδιορισμού της μήτρας θα πρέπει να αλλάζει στο αντίθετο, επομένως, επομένως ένα → × b → \u003d i → J → k → axayazbxbybz \u003d - i → j → k → Bxbybzaxaz \u003d - b → × a → και αποδεικνύει την αντι-επιτόρθωση της εργασίας φορέα.
Vector Art - Παραδείγματα και λύσεις
Στις περισσότερες περιπτώσεις, υπάρχουν τρεις τύποι εργασιών.
Στα καθήκοντα του πρώτου τύπου, το μήκος δύο φορέων και η γωνία μεταξύ τους είναι συνήθως και πρέπει να βρείτε το μήκος του προϊόντος φορέα. Σε αυτή την περίπτωση, χρησιμοποιήστε τον ακόλουθο τύπο C → \u003d A → B → SIN ∠ A →, B →.
Παράδειγμα 1.
Βρείτε το μήκος του φορέα προϊόντος διανυσμάτων Α → και Β →, εάν είναι γνωστό ένα → \u003d 3, B → \u003d 5, ∠ A →, B → \u003d π 4.
Απόφαση
Χρησιμοποιώντας τον ορισμό του μήκους του προϊόντος φορέα διανυσμάτων Α → και Β → i Επίλυση αυτής της εργασίας: a → × b → \u003d a → b → · Sin ∠ a →, b → \u003d 3 · 5 · Sin π 4 \u003d 15 2 2.
Απάντηση: 15 2 2 .
Τα αντικείμενα του δεύτερου τύπου σχετίζονται με τις συντεταγμένες των φορέων, σε αυτά ένα προϊόν φορέα, το μήκος του κ.λπ. Αναζητήθηκε μέσω των γνωστών συντεταγμένων των συγκεκριμένων φορέων A → \u003d (a x; a y; a z) και B → \u003d (b x; b y; b z) .
Για αυτόν τον τύπο εργασίας, μπορείτε να λύσετε πολλές επιλογές εργασιών. Για παράδειγμα, οι συντεταγμένες των φορέων Α → και Β →, αλλά μπορούν να δοθούν οι αποσύνθεντές τους στους φορείς συντεταγμένων της φόρμας. B → \u003d b x · i → + b y · j → + b z · k → και C → \u003d a → × b → \u003d (AY · BZ - AZ · BY) · I → + (AZ · BX - AX · BZ) · J → + (AX · BY-AY · BX) · K → Διανύσματα A → και B → μπορούν να ρυθμιστούν από τις συντεταγμένες των σημείων της έναρξης και του τέλους τους.
Εξετάστε τα ακόλουθα παραδείγματα.
Παράδειγμα 2.
Στο σύστημα ορθογώνιας συντεταγμένης, δίδεται δύο φορείς Α → \u003d (2, 1; - 3), Β → \u003d (0 ,- 1, 1). Βρείτε την τέχνη φορέα τους.
Απόφαση
Στον δεύτερο ορισμό, βρίσκουμε ένα προϊόν φορέα δύο διανυσμάτων στις καθορισμένες συντεταγμένες: A → × B → \u003d (AY · BZ - AZ · BY) · Ι → + (AZ · BX - AX · BZ) · J → + (AX · BY - AY · BX) · K → \u003d \u003d (1,1 - (- 3) · (- 1)) · Ι → + (- 3) · 0-2 · 1) · J → + ( 2 · (- 1) - 1 · 0) · k → \u003d - 2 i → 2 J → - 2 k →.
Εάν καταγράψετε ένα προϊόν φορέα μέσω του καθοριστικού μήτρα, τότε το διάλυμα αυτού του παραδείγματος έχει ως εξής: A → × B → \u003d I → J → K → AbayazbxbyBz \u003d I → J → K → 2 1 - 3 0 - 1 1 \u003d - 2 Ι → - 2 J → - 2 K →.
Απάντηση: A → × B → \u003d - 2 Ι → 2 J → - 2 K →.
Παράδειγμα 3.
Βρείτε το μήκος του διανυσμάτων διανυσμάτων I → - J → και i → + J → + K →, όπου i →, J →, K → - Orthops του ορθογώνιου συστήματος συντεταγμένων καρτεσών.
Απόφαση
Για να ξεκινήσετε, θα βρούμε τις συντεταγμένες του καθορισμένου προϊόντος διάνυσμα I → - J → → → + J → + k → σε αυτό το ορθογώνιο σύστημα συντεταγμένων.
Είναι γνωστό ότι οι διανύσματα I → - J → και I → + J → + K → έχουν συντεταγμένες (1 ,-1, 0) και (1, 1, 1), αντίστοιχα. Βρείτε το μήκος του προϊόντος φορέα χρησιμοποιώντας τον καθοριστικό παράγοντα της μήτρας, τότε έχουμε i → - J → × I → + J → K → 1 - 1 0 1 1 \u003d - i → - J → + 2 k →.
Συνεπώς, το προϊόν διάνυσμα I → J → × I → + J → + k → έχει συντεταγμένες (- 1, - 1, 2) σε ένα δεδομένο σύστημα συντεταγμένων.
Θα βρούμε το μήκος του προϊόντος φορέα σύμφωνα με τον τύπο (βλέπε τμήμα εύρεση του μήκους του φορέα): i → - J → × I → + J → + k → \u003d - 1 2 + - 1 2 + 2 2 \u003d 6.
Απάντηση: I → - J → × I → + J → + k → \u003d 6. .
Παράδειγμα 4.
Σε ένα ορθογώνιο σύστημα συντονισμού, οι συντεταγμένες τριών σημείων Α (1, 0, 1), Β (0, 2, 3), C (1, 4, 2). Βρείτε κάποιο διάνυσμα κάθετο ένα b → και ένα c → ταυτόχρονα.
Απόφαση
Φορητές Α Β → και A C → έχουν τις ακόλουθες συντεταγμένες (- 1, 2, 2) και (0, 4, 1), αντίστοιχα. Έχοντας βρει ένα διανύσιο προϊόν διανυσμάτων Α Β → και A C →, είναι προφανές ότι είναι ένας κάθετος διάνυσμα εξ ορισμού και σε ένα b → και σε ένα C →, δηλαδή, είναι το διάλυμα της εργασίας μας. Το βρίσκουμε ένα b → × a c → \u003d i → j → k → 1 2 2 0 4 1 \u003d - 6 i → + j → - 4 k →.
Απάντηση: - 6 I → + J → - 4 K →. - ένας από τους κάθετους φορείς.
Οι εργασίες τρίτου τύπου επικεντρώνονται στη χρήση των ιδιοτήτων τέχνης φορέα. Μετά τη χρήση του οποίου θα λάβουμε μια λύση σε μια δεδομένη εργασία.
Παράδειγμα 5.
Φορείς Α → και Β → κάθετα και τα μήκη τους είναι ίσα, αντίστοιχα, 3 και 4. Βρείτε το μήκος του προϊόντος φορέα 3 · a → - b → × a → 2 · b → \u003d 3 · a → × a →-2 · b → + - b → × a →-2 · b → \u003d \u003d 3 · A → × A → + 3 · A → × - 2 · B → + - B → × A → + - B → × - 2 · b →.
Απόφαση
Με την ιδιοκτησία της διανομής του προϊόντος φορέα, μπορούμε να γράψουμε 3 · A → B → × A → 2 · B → \u003d 3 · A → × a → - 2 · b → + - b → → - 2 · b → \u003d \u003d 3 · A → × A → + 3 · A → × - 2 · B → + - B → × A → + - B → × - 2 · b →
Από την ιδιοκτησία της συσχετισμότητας, θα πραγματοποιήσουμε αριθμητικούς συντελεστές για το σημάδι των φορέων έργων στην τελευταία έκφραση: 3 · A → × A → + 3 · A → × - 2 · b → + - + - + - B → × - 2 · b → \u003d \u003d 3 · a → × a → + 3 · (- 2) · a → × b → + (- 1) · b → × a → + (- 1) · (- 2 ) · B → × b → \u003d \u003d 3 · A → × a → - 6 · a → × b → - b → × a → + 2 · b → × b →
Vector Works a → × a → και b → × b → ίση με 0, ως → × a → \u003d a → → → · sin 0 \u003d 0 και b → × b → \u003d b → b → \u003d sin 0 \u003d 0, Στη συνέχεια 3 · A → × A → - 6 · A → × B → B → × A → + 2 · B → × B → \u003d - 6 · A → × b → - B → × a →. .
Από την αντι-επιτόρθωση του προϊόντος φορέα, 6 · a → × b → - b → → → \u003d - 6 · a → × b → (- 1) · a → × b → \u003d - 5 · a → × b → . .
Χρησιμοποιώντας τις ιδιότητες της εργασίας φορέα, λαμβάνουμε την ισότητα 3 · ένα → - B → × A →-2 · b → \u003d \u003d - 5 · a → × b →.
Με την κατάσταση, τους φορείς Α → και Β → κάθετα, δηλαδή, η γωνία μεταξύ τους είναι ίση με π 2. Τώρα παραμένει μόνο να υποκαταστήσετε τις τιμές που βρίσκονται στους αντίστοιχους τύπους: 3 · a →-b → × a → - 2 · b → \u003d - 5 · a → × b → \u003d 5 · a → × b → \u003d 5 · A → B → · SIN (A →, B →) \u003d 5 · 3 · 4 · SIN Π 2 \u003d 60.
Απάντηση: 3 · A → - B → × A →-2 · B → \u003d 60.
Το μήκος του διανύσματος γινόμενο των διανυσμάτων στύσης είναι ίσο με Α → × B → \u003d Α → Β · → SIN ∠ A →, Β →. Δεδομένου ότι είναι ήδη γνωστό (από το γήπεδο σχολείο) ότι η περιοχή τριγώνου είναι ίσο με το μισό του έργου του μήκους των δύο πλευρών του πολλαπλασιάζεται με τη γωνία μεταξύ των μερών. Ως εκ τούτου, το μήκος του διανύσματος προϊόντος είναι ίση με την περιοχή του παραλληλογράμμου - ένα διπλό τρίγωνο, δηλαδή το προϊόν των μερών, με τη μορφή των διανυσμάτων Α → Β και →, εν αναμονή της από το ένα σημείο, στη γωνία κόλπων μεταξύ τους αμαρτία ∠ a →, b →.
Αυτή είναι η γεωμετρική έννοια του φορέα προϊόντος.

Η φυσική έννοια του έργου φορέα
Σε μηχανική, ένα από τα τμήματα της φυσικής, χάρη στο φορέα του προϊόντος, μπορείτε να προσδιορίσετε τη στιγμή της δύναμης σε σχέση με το σημείο του χώρου.
Ορισμός 3.
Κάτω από τη στιγμή της ισχύος F → εφαρμόζεται στο σημείο Β, σε σχέση με το σημείο Α μας καταλαβαίνουμε το ακόλουθο προϊόν διάνυσμα Α Β → F →.
Εάν παρατηρήσετε ένα λάθος στο κείμενο, επιλέξτε το και πατήστε Ctrl + Enter
Αγγλικά: Η Wikipedia κάνει τον ιστότοπο πιο ασφαλές. Χρησιμοποιείτε ένα παλιό πρόγραμμα περιήγησης ιστού που δεν θα μπορέσει να συνδεθεί με τη Wikipedia στο μέλλον. Ενημερώστε τη συσκευή σας ή επικοινωνήστε με το διαχειριστή πληροφορικής σας.
中文: 维基 科 正在 使 使 更加 更加 全 全 您 您 正在 使用 旧 的 浏览 浏览 这 这 在 无法 无法 连接 维基 维基 请 请 更 更 您 的 设备 或 联络 您 的 να 管理员 以下 以下 更 更 长 更 更 具 技术性 的 更更(仅英语).
Español: Wikipedia Está Haciendo El Sitio Más Seguro. Usted Está Utilizando Un Navegador Web Viejo Que Sera Δεν Capaz De Conectarse η Wikipedia EN El Futuro. Activeice su distractivo o Επαφή με ένα su admilitydator informático. Más abajo hay una acedización más larga y más técnica en inglés.
ﺎﻠﻋﺮﺒﻳﺓ: ويكيبيديا تسعى لتأمين الموقع أكثر من ذي قبل. أنت تستخدم متصفح وب قديم لن يتمكن من الاتصال بموقع ويكيبيديا في المستقبل. يرجى تحديث جهازك أو الاتصال بغداري تقنية المعلومات الخاص بك. يوجد تحديث فني أطول ومغرق في التقنية باللغة الإنجليزية تاليا.
Français: Wikipédia Va Bientôt Augmenter La Sécurité de Son site. Vous Utilisez Actupellement Un Navigateur Web Ongien, Qui Ne Pourra Plus SE Connection à Wikipédia Lorsque Sera Sera Fait. Merci de Mettre à Gour Bottre Appareil Ou de Contre Vottre Administrateur Informatique à CETTE FIN. DES Πληροφορίες Supplémentaires Plus Techniques et et englais sont disponibles ci-dessous.
日本語: ウィキペディア で は サイト の セキュリティ を 高 め て い い バージョン バージョン ご 古く 今後 今後 今後 ウィキペディア 接続 でき でき なく なる 能 性 更 する する ます デバイス か 管理 管理 者 ご 相談 ください 管理 管理 者 ご 相談 ください ください技術面詳しい詳しい更更情報は以下にで提供しています.
Deutsch: Wikipedia Erhöht πεθαίνουν sicherheit der webseite. Du benutzt einen alten webbrowser, der σε zukunft nicht mehr auf wikipedia zugreifen können wird. Bitte aktualisiere dein gerät oder sprich deinen it-διαχειριστής ένα. Ausführlichere (und technisch detaillierretre) hinweise findest du unten στην αγγλική βλάστηση.
Italiano: Wikipedia sta rendendo il sito più sicuro. STAI USANDO UN BROWSER Web Che Non Sar στο Grado di Connetersi μια Wikipedia στο Futuro. Ανά favore, aggiorna il tuo dissititivo o contatta il tuo amministratore πληροφορικό. Più στο Basso è Disponibile Un Aggiornato PiùtaTagloio E Tecnico στην Inglese.
Magyar: Biztonságosabb lesz μια wikipédia. Ένα Böngésző, Amit Használsz, Nem Lesz Képes Kapcsolódni Jövőben. Használj modernebb szoftrutr velyzd ένα πρόβλημα ένα renszergazdádnak. Alább Olvashatod ένα részletesebb magyarázatatot (Αγκόλλιος).
Svenska: Wikipedia Gör Sidan Mer Säker. Du använder en Äldre webbläsare som inte kommer att kunna läsa wikipedia i framtiden. Uppdatera Din Ενισχύστε το Eller Kontakta DIN IT-Administrateör. Det finns en längre och mer teknisk förklaring på engelska längre ned.
हिन्दी: विकिपीडिया साइट को और अधिक सुरक्षित बना रहा है। आप एक पुराने वेब ब्राउज़र का उपयोग कर रहे हैं जो भविष्य में विकिपीडिया से कनेक्ट नहीं हो पाएगा। कृपया अपना डिवाइस अपडेट करें या अपने आईटी व्यवस्थापक से संपर्क करें। नीचे अंग्रेजी में एक लंबा और अधिक तकनीकी अद्यतन है।
Κατάργηση της υποστήριξης για τις ανασφαλείς εκδόσεις πρωτοκόλλων TLS, ειδικά TLSV1.0 και TLSV1.1, το οποίο το λογισμικό του προγράμματος περιήγησης βασίζεται στη σύνδεση με τους ιστότοπούς μας. Αυτό συνήθως προκαλείται από ξεπερασμένα προγράμματα περιήγησης, ή παλαιότερα smartphones Android. Ή θα μπορούσε να είναι παρεμβολές από το εταιρικό ή το προσωπικό λογισμικό "web security", το οποίο πραγματικά υποβαθμίζει την ασφάλεια σύνδεσης.
Πρέπει να αναβαθμίσετε το πρόγραμμα περιήγησης ιστού ή να διορθώσετε με άλλο τρόπο αυτό το ζήτημα για να αποκτήσετε πρόσβαση στους ιστότοπούς μας. Αυτό το μήνυμα θα παραμείνει μέχρι την 1η Ιανουαρίου 2020. Μετά την ημερομηνία αυτή, το πρόγραμμα περιήγησής σας δεν θα μπορέσει να δημιουργήσει μια σύνδεση με τους διακομιστές μας.
Ορισμός. Ο φορέας του φορέα Α στον φορέα Β ονομάζεται διάνυσμα που χαρακτηρίζεται από το σύμβολο [", b] (ή lxb), έτσι ώστε 1) το μήκος του φορέα [a, b] είναι ίσο με (p, όπου y είναι η γωνία μεταξύ των φορέων Α και Β (Σχήμα31), 2) φορέα [Α, Β) κάθετα σε φορείς Α και Β, δηλ. κάθετη προς το επίπεδο αυτών των φορέων. 3) Ο φορέας [Α, Β] κατευθύνεται έτσι ώστε από το άκρο αυτού του φορέα, η μικρότερη περιστροφή από το Α προς Β είναι ορατό αριστερόστροφα (Εικ. 32). Σύκο. 32 Εικ.31 Με άλλα λόγια, οι φορείς Α, Β και [Α, Β) σχηματίζουν τους σωστούς τρεις φορείς, δηλ. Που βρίσκεται τόσο μεγάλο, δείκτη και μεσαία δάχτυλα του δεξιού χεριού. Εάν διανύσματα Α και Β Colline, υποθέτουμε ότι [Α, Β] \u003d 0. εξ ορισμού, το μήκος του προϊόντος φορέα είναι αριθμητικά ίσο με την περιοχή παραλληλόγραμμου SA (Εικ. 33), που χτίστηκε στους μεταβλητές διανύσματα Α και Β ως Στα πλάγια: 6.1. Ιδιότητες του φορέα εργασίας 1. Το προϊόν φορέα είναι ίσο με το μηδενικό φορέα και μόνο όταν τουλάχιστον ένας από τους μεταβλητές φορείς είναι μηδέν ή όταν αυτοί οι κολλητικοί φορείς (εάν φορείς Α και Β Colline, τότε η γωνία μεταξύ τους είναι είτε 0 είτε η γωνία μεταξύ τους είναι 0 ή η γωνία μεταξύ τους 7g). Είναι εύκολο να φτάσετε από το γεγονός ότι αν μετρήσετε τον φορέα μηδέν με ένα clincons οποιουδήποτε φορέα, η κατάσταση της κολλητότητας των φορέων Α και Β μπορεί να εκφραστεί έτσι 2. Το προϊόν φορέα είναι αντι-επιτακτικό, δηλαδή πάντα. Στην πραγματικότητα, οι φορείς (Α, Β) και έχουν το ίδιο μήκος και κολλ. Οι κατευθύνσεις αυτών των φορέων είναι αντίθετα αντίθετα λόγω του άκρου του φορέα [Α, Β] η μικρότερη περιστροφή από το Α στο Β θα παρατηρηθεί έναντι των δεικτών του ρολογιού και από το τέλος του φορέα [Β, Α] - δεξιόστροφα ( Εικ. 34). 3. Το προϊόν φορέα έχει ιδιότητα διανομής σε σχέση με την προσθήκη. 4. Ο αριθμητικός πολλαπλασιαστήρας L μπορεί να γίνει για το σημάδι του προϊόντος φορέα 6.2. Το προϊόν φορέα των φορέων που καθορίζονται από τις συντεταγμένες αφήστε τους φορείς και επίσης να καθοριστούν από τις συντεταγμένες τους στη βάση. Χρησιμοποιώντας την ιδιότητα διανομής του προϊόντος φορέα, βρίσκουμε ένα προϊόν φορέα φορείων που δίνονται από τις συντεταγμένες. Μικτή εργασία. Αποδυναμίζουμε τα φορέα έργα των ορνιθών συντεταγμένων (Εικ. 35): Συνεπώς, για το προϊόν φορέα των φορέων Α και Β, λαμβάνουμε από τον τύπο (3) τον ακόλουθο τύπο έκφρασης (4) μπορεί να γραφτεί σε ένα συμβολικό, εύκολα αξέχαστο Μορφή, εάν χρησιμοποιείτε τον καθοριστικό παράγοντα της 3ης τάξης: αποσυνθέτηση αυτού του καθοριστικού παράγοντα για τα στοιχεία της 1ης γραμμής, λαμβάνουμε (4). Παραδείγματα. 1. Βρείτε την περιοχή του παραλληλόγραμμου που χτίστηκε στην επιθυμητή περιοχή του φορέα, ώστε να βρούμε \u003d από όπου 2. Βρείτε μια περιοχή τριγώνου (εικ. 36). Είναι σαφές ότι η περιοχή B "D Triangle είναι ίση με το ήμισυ του τετράγωνου παραλληλόγραμμου σχετικά με το AU V. Υπολογισμός του προϊόντος διάνυσμα (A, B | Διανύσματα A \u003d OA και B \u003d OH, παίρνουμε μια παρατήρηση. Το προϊόν διάνυσμα είναι Δεν είναι σύμφωνο, δηλαδή η ισότητα ((α, β), γ) \u003d [Α, Β, Γ)) στη γενική περίπτωση είναι εσφαλμένη. Για παράδειγμα, όταν το A \u003d SS J, έχουμε § 7. Το μικτό προϊόν του Οι διανύσματα τους αφήνουν να έχουν τρεις διανύσματα Α, Β και S. Μετακινήστε τους διανύσματα A και 1\u003e σύντομα. Ως αποτέλεσμα, λαμβάνουμε το διάνυσμα [a, 1\u003e]. Πολλαπλασιάστε το Scalar στον φορέα C: (Kb), γ). Ο αριθμός ([Α, Β], Ε) ονομάζεται μικτό προϊόν φορέων Α, β. με και υποδεικνύεται από το σύμβολο (Α, 1), Ε). 7.1. Γεωμετρική έννοια της μικτής εργασίας αναβολή των φορέων α , Β και από το αφοσιωμένο σημείο O (Εικ. 37). Εάν και τα τέσσερα σημεία OH, Α, Β, Γ βρίσκονται στο ίδιο επίπεδο (οι διανύσματα Α, Β και C καλούνται σε αυτήν την περίπτωση συνθέτουν), τότε ένα μικτό προϊόν ( [Α, Β], γ) \u003d 0. Αυτό προκύπτει από το γεγονός ότι ο φορέας [Α, Β | κάθετος στο επίπεδο στο οποίο οι φορείς Α και 1 υποβλήθηκαν σε κάθε χώρο ", οπότε, ο διάνυσμα με. / αν t Τα σημεία O, Α, Β, C δεν βρίσκονται στο ίδιο επίπεδο οστό (διανύσματα Α, Β και με NonComplaunar), χτίζουμε στις άκρες της ΟΑ, OB και παραλληλεπίπεδου (Εικ. 38 α). Με τον ορισμό του προϊόντος φορέα, έχουμε (A, B) \u003d έτσι με, όπου έτσι είναι μια περιοχή παραλληλόγραμμου OADB και το C είναι ένα μόνο διάνυσμα, κάθετα σε διανύσματα Α και Β και τέτοια που η Τρόικα Α, Β, Γ - Δεξιά , δηλαδή Οι φορείς Α, Β και C βρίσκονται, αντίστοιχα, τόσο μεγάλα, δείκτη και μεσαία δάχτυλα του δεξιού χεριού (Εικ. 38 β). Πολλαπλασιάζοντας και τα δύο μέρη της τελευταίας ισότητας στο δεξιό κλιματισμό στον φορέα C, λαμβάνουμε ότι το προϊόν φορέα των φορέων των καθορισμένων συντεταγμένων. Μικτή εργασία. Ο αριθμός των RGS C είναι ίσος με το ύψος του H που κατασκευάστηκε παραλληλεπίπεδο, που λαμβάνεται με το σήμα "+", εάν η γωνία μεταξύ των φορέων με και με οξεία (τρόικα Α, Β, C - δεξιά) και με το σημάδι "-" , εάν η γωνία είναι ηλίθια (τρόικα Α, Β, С - αριστερά), έτσι ώστε, έτσι να αναμειγνύεται το προϊόν των φορέων Α, Β και ίσο με τον όγκο V παραλληλεπίπεδο, που χτίστηκε σε αυτούς τους φορείς όπως και τα τρόικα Α, Β, C - Δεξιά, και -V, αν η τρόικα Α, Β, S - αριστερά. Με βάση τη γεωμετρική έννοια της μικτής εργασίας, μπορεί να συναχθεί το συμπέρασμα ότι πολλαπλασιάζοντας τους διανύσματα TC A, B και C σε οποιαδήποτε άλλη σειρά, πάντα θα λαμβάνουμε είτε +7 είτε -K. Σημάδι παραγωγής. 38 Η συντήρηση θα εξαρτηθεί μόνο επειδή οι τρίτο σχηματίζουν τους μεταβλητές φορείς - δεξιά ή αριστερά. Εάν οι διανύσματα Α, Β, με τη σωστή τρόικα, τότε ο Τριογλυφικός Β, Γ, Α και ο, Α, Β είναι επίσης σωστός. Την ίδια στιγμή, και τα τρία στρατεύματα Β, και, με. Α, S, Β και S, Β, Α - Αριστερά. Έτσι, (Α, Β, Γ) \u003d (Β, S, Α) \u003d (S, Α, Β) \u003d - (Β, Α, Γ) \u003d - (Α, S, Β) \u003d - (S, Β, αλλά). Η Esherase υπογραμμίζουμε ότι το μικτό προϊόν των φορέων είναι ίσο με το Nuduchoga μόνο όταν οι μεταβλητές διανύσματα Α, Β, με έναν σύντομο: (Α, Β, με έναν σύντομο) 7.2. Μικτή εργασία στις συντεταγμένες Αφήστε τους φορείς Α, Β, να καθορίζονται από τις συντεταγμένες τους με βάση I, J, K: A \u003d (x \\, y \\, z]), b \u003d (x2, y2\u003e z2), c \u003d (x3, uz, 23). Βρίσκουμε την έκφραση για τη μικτή δουλειά τους (Α, Β, Γ). Έχουμε ένα μικτό προϊόν φορείων που δίδονται από τις συντεταγμένες στη βάση Ι, J, K, ίση με τον καθορισμό τρίτης τάξης, οι σειρές των οποίων αποτελούνται ανάλογα από τις συντεταγμένες του πρώτου, το δεύτερο και τρίτο των μεταβλητών φορέων. Απαιτείται και επαρκή προϋπόθεση για τον σύντροφο των φορέων και του Y \\, Z |), B \u003d (H U2. 22), C \u003d (ZHZ, UZ, 23) θα καταγραφεί με τον ακόλουθο τρόπο | z, AG2 Y2 -2 \u003d 0. Ultra παράδειγμα. Ελέγξτε αν οι φορείς είναι "\u003d (7,4,6), Β \u003d (2, 1,1), C \u003d (19, II, 17). Οι υπό εξέταση φορείς θα συνοδεύονται ή μη ανταγωνίζονται ανάλογα με το αν θα είναι μηδέν ή δεν υπάρχει καθοριστικός παράγοντας για να το αποσυντεθεί σύμφωνα με τα στοιχεία της πρώτης συμβολοσειράς, παίρνουμε d \u003d 7-6-4-15 + 6-3 \u003d 0 ^ - Διανύσματα n, b, με έναν σύντομο τρόπο. 7.3. Το προϊόν διπλού διανύσματος διπλά διάνυσμα προϊόν [Α, [Β, C]] είναι ένας φορέας κάθετος στους διανύσματα Α και [Β, Γ]. Επομένως, βρίσκεται στο επίπεδο των φορέων Β και C και μπορεί να αποσυντεθεί σε αυτούς τους φορείς. Μπορεί να αποδειχθεί ότι ο τύπος είναι έγκυρος [Α, [\u003e, S]] \u003d Β (Α, Ε) - με (Α, Κ). Ασκήσεις 1. Τρεις διανύσματα AV \u003d C, F; \u003d O και ca \u003d b χρέρουν ως πλευρές του τριγώνου. Εκφράστε το A, B και με διανύσματα που ταιριάζουν με τους Medians Am, DN, CP Triangle. 2. Ποια προϋπόθεση θα πρέπει να σχετίζεται ο φορέας p και q με τον φορέα p + q διαιρούμενο τη γωνία μεταξύ τους στο μισό; Θεωρείται ότι και οι τρεις φορείς αποδίδονται στη γενική αρχή. 3. Υπολογίστε το μήκος των διαγώνων του παραλληλόγραμμα που κατασκευάζονται στους φορείς Α \u003d 5Ρ + 2q και B \u003d P - 3q, αν είναι γνωστό ότι | p | \u003d 2V / 2, | Q | \u003d 3 h- (p7ci) \u003d f. 4. Ανακάλυψη του ρομβού ως πλευράς Α και Β του ρόμβου, αποδεικνύεται ότι η διαγώνια ρόμβος είναι αμοιβαία κάθετη. 5. Υπολογίστε το κλιμακωτό προϊόν των φορέων Α \u003d 4i + 7J + 3k και B \u003d 31 - 5J + Κ. 6. Βρείτε ένα φορέα μονάδας A0, παράλληλο διάνυσμα Α \u003d (6, 7, -6). 7. Εντοπίστε την προεξοχή του φορέα Α \u003d L + J-KHA Vector B \u003d 21 - J - 3k. 8. Εντοπίστε την συνίνη της γωνίας μεταξύ των φορέων, εάν α (-4,0,4), σε (-1,6,7), C (1,10,9). 9. Βρείτε ένα μόνο φορέα του p °, ταυτόχρονα κάθετο διάνυσμα Α \u003d (3, 6, 8) και άξονα οξώματος. 10. Υπολογίστε το γωνιακό κόλπο μεταξύ των διαγώνων της παραλληλόλουλας, που χτίστηκε φορείς Α \u003d 2i + J-K, B \u003d I-3J + K όπως στις πλευρές. Υπολογίστε το ύψος H παραλληλεπίπεδο, ενσωματωμένο σε φορείς Α \u003d 31 + 2J - 5k, Β \u003d Ι-Ι + 4KNC \u003d Ι-3J + Κ, αν η βάση λαμβάνεται από παραλληλόγραμμο, χτισμένα διανύσματα Α και Ι). Απαντήσεις