Funktsiyani onlayn o'rganishning umumiy sxemasi. To'liq funktsiyani o'rganish va chizish

Bugun biz sizni funktsiyani biz bilan o'rganish va grafigini yaratishga taklif qilamiz. Ushbu maqolani diqqat bilan o'rganib chiqqandan so'ng, bunday vazifani bajarish uchun siz uzoq vaqt terlashingiz shart emas. Funktsiyani o'rganish va chizish oson emas, ish hajmli, maksimal e'tibor va hisob-kitoblarning aniqligini talab qiladi. Materialni idrok etishni osonlashtirish uchun biz bir xil funktsiyani bosqichma-bosqich o'rganamiz, barcha harakatlarimiz va hisob-kitoblarimizni tushuntiramiz. Matematikaning ajoyib va ​​hayajonli olamiga xush kelibsiz! Bor!

Domen

Funktsiyani o'rganish va chizish uchun siz bir nechta ta'riflarni bilishingiz kerak. Funksiya matematikadagi asosiy (asosiy) tushunchalardan biridir. O'zgarishlar bilan bir nechta o'zgaruvchilar (ikki, uch yoki undan ko'p) o'rtasidagi munosabatni aks ettiradi. Funktsiya to'plamlarning bog'liqligini ham ko'rsatadi.

Tasavvur qiling-a, bizda ma'lum diapazonga ega bo'lgan ikkita o'zgaruvchi bor. Demak, ikkinchi o‘zgaruvchining har bir qiymati ikkinchining bir qiymatiga to‘g‘ri kelishi sharti bilan y x ning funksiyasidir. Bunda y o'zgaruvchisi bog'liq bo'lib, u funksiya deyiladi. X va y o'zgaruvchilari ichida ekanligini aytish odatiy holdir. Ushbu bog'liqlikni yanada aniqroq qilish uchun funktsiya grafigi chiziladi. Funksiya grafigi nima? Bu koordinata tekisligidagi nuqtalar to'plami bo'lib, bu erda x ning har bir qiymati y ning bitta qiymatiga to'g'ri keladi. Grafiklar har xil bo'lishi mumkin - to'g'ri chiziq, giperbola, parabola, sinusoid va boshqalar.

Funksiya grafigini tadqiqotsiz tuzish mumkin emas. Bugun biz tadqiqot o'tkazish va funktsiya grafigini tuzishni o'rganamiz. Tadqiqot davomida eslatma qilish juda muhimdir. Bu vazifani ancha osonlashtiradi. Eng qulay tadqiqot rejasi:

1. Domen.
2. Davomiylik.
3. Juft yoki toq paritet.
4. Davriylik.
5. Asimptotalar.
6. Nollar.
7. Belgilarning doimiyligi.
8. O'sish va pasayish.
9. Ekstremallar.
10. Qavariqlik va botiqlik.

Birinchi nuqtadan boshlaylik. Ta'rif sohasini topamiz, ya'ni funksiyamiz qaysi intervallarda mavjud: y = 1/3 (x ^ 3-14x ^ 2 + 49x-36). Bizning holatda funksiya x ning istalgan qiymatlari uchun mavjud, ya'ni soha R ga teng. Uni quyidagicha yozish mumkin xÎR.

Davomiylik

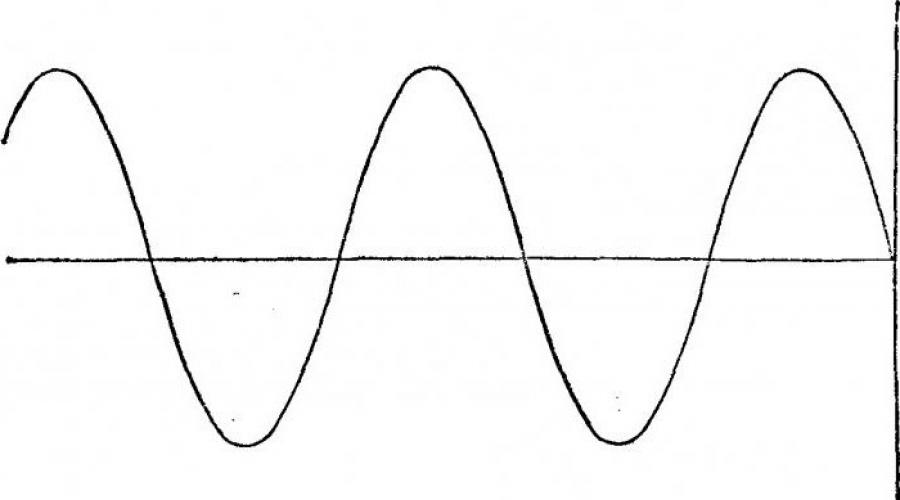
Endi biz tanaffus funksiyasini tekshiramiz. Matematikada "uzluksizlik" atamasi harakat qonunlarini o'rganish natijasida paydo bo'lgan. Cheksiz nima? Fazo, vaqt, ba'zi bog'liqliklar (masalan, S va t o'zgaruvchilarning harakatga bog'liqligi masalalari), qizdirilgan ob'ektning harorati (suv, tovoq, termometr va boshqalar), uzluksiz chiziq (ya'ni bitta uni qalamdan yirtmasdan chizish mumkin).

Agar biror nuqtada buzilmasa, diagramma uzluksiz hisoblanadi. Bunday grafikning eng aniq misollaridan biri sinus to'lqin bo'lib, uni ushbu bo'limdagi rasmda ko'rishingiz mumkin. Agar bir qator shartlar bajarilsa, funktsiya x0 nuqtada uzluksiz bo'ladi:

• bu nuqtada funksiya aniqlanadi;
• nuqtadagi o'ng va chap chegaralar teng;
• limit funksiyaning x0 nuqtadagi qiymatiga teng.

Agar kamida bitta shart bajarilmasa, funksiya buzilgan deyiladi. Va funksiya uzluksiz bo'lgan nuqtalar odatda uzilish nuqtalari deb ataladi. Grafik ko'rinishda "buzilishi" mumkin bo'lgan funksiyaga misol: y = (x + 4) / (x-3). Bundan tashqari, y x = 3 nuqtada mavjud emas (chunki uni nolga bo'lish mumkin emas).

Biz ko'rib chiqayotgan funktsiyada (y = 1/3 (x ^ 3-14x ^ 2 + 49x-36)) hamma narsa oddiy bo'lib chiqdi, chunki grafik uzluksiz bo'ladi.

Juft toq

Endi funksiyani paritet uchun tekshiring. Birinchidan, bir oz nazariya. X o'zgaruvchining istalgan qiymati uchun (qiymatlar oralig'idan) f (-x) = f (x) shartni qanoatlantiradigan funktsiya juft funktsiyadir. Bunga misollar kiradi:

• modul x (grafik shablonga o'xshaydi, grafikning birinchi va ikkinchi choragining bissektrisasi);
• x kvadrat (parabola);
• kosinus x (kosinus).

E'tibor bering, bu chizmalarning barchasi ordinataga (ya'ni y) nisbatan qaralganda simmetrikdir.

Xo'sh, g'alati funktsiya nima deb ataladi? Bu shartni qanoatlantiradigan funksiyalar: f (-x) = - f (x) x o'zgaruvchining istalgan qiymati uchun. Misollar:

• giperbola;
• kubik parabola;
• sinusoid;
• tangentoid va boshqalar.

E'tibor bering, bu funktsiyalar nuqtaga (0: 0), ya'ni koordinataga nisbatan simmetrikdir. Maqolaning ushbu qismida aytilganlarga asoslanib, juft va toq funksiya quyidagi xususiyatga ega bo'lishi kerak: x ta'riflar to'plamiga kiradi va -x ham.

Funktsiyani paritet uchun ko'rib chiqamiz. Ko'ramizki, u tavsiflarning hech biriga to'g'ri kelmaydi. Demak, bizning funksiyamiz na toq, na juft.

Asimptotalar

Keling, ta'rifdan boshlaylik. Asimptot - bu grafikga imkon qadar yaqin bo'lgan egri chiziq, ya'ni nuqtadan masofa nolga intiladi. Umuman olganda, asimptotalarning uchta turi mavjud:

• vertikal, ya'ni y o'qiga parallel;
• gorizontal, ya'ni x o'qiga parallel;
• moyil.

Birinchi turga kelsak, ma'lumotlarning to'g'ri chiziqlarini ba'zi nuqtalarda izlash kerak:

• sindirish;
• ta'rif sohasining oxiri.

Bizning holatlarimizda funksiya uzluksiz, aniqlanish sohasi esa R ga teng. Shuning uchun vertikal asimptotlar mavjud emas.

Funksiya grafigi gorizontal asimptotaga ega bo‘lib, u quyidagi talabga javob beradi: agar x cheksizlik yoki minus cheksizlikka moyil bo‘lsa va chegara ma’lum songa teng bo‘lsa (masalan, a). Bu holda, y = a - bu gorizontal asimptota. Biz tekshirayotgan funktsiyada gorizontal asimptotlar yo'q.

Egri asimptota faqat ikkita shart bajarilgan taqdirdagina mavjud bo'ladi:

• lim (f (x)) / x = k;
• lim f (x) -kx = b.

Keyin uni quyidagi formula bo'yicha topish mumkin: y = kx + b. Shunga qaramay, bizning holatlarimizda hech qanday qiyshiq asimptotlar yo'q.

Funktsiya nollari

Keyingi qadam funksiya grafigini nollarda tekshirishdan iborat. Shuni ham ta'kidlash kerakki, funktsiyaning nollarini topish bilan bog'liq vazifa faqat funktsiya grafigini o'rganish va chizishda emas, balki mustaqil vazifa sifatida va tengsizliklarni yechish usuli sifatida ham amalga oshiriladi. Grafikda funksiyaning nollarini topish yoki matematik belgilardan foydalanish talab qilinishi mumkin.

Ushbu qiymatlarni topish funktsiyani aniqroq rejalashtirishga yordam beradi. Oddiy qilib aytganda, funktsiyaning noli x o'zgaruvchining qiymati bo'lib, bunda y = 0 bo'ladi. Agar siz grafikda funktsiyaning nollarini qidirsangiz, u holda grafikning abscissa o'qini kesib o'tadigan nuqtalariga e'tibor berishingiz kerak.

Funksiyaning nollarini topish uchun quyidagi tenglamani yechish kerak: y = 1/3 (x ^ 3-14x ^ 2 + 49x-36) = 0. Kerakli hisob-kitoblarni amalga oshirgandan so'ng, biz quyidagi javobni olamiz:

Doimiylik

Funksiyani (grafikni) tadqiq qilish va qurishning keyingi bosqichi doimiylik intervallarini topishdan iborat. Bu shuni anglatadiki, biz qaysi oraliqlarda funktsiya musbat qiymatni olishini va qaysi birida - salbiyni aniqlashimiz kerak. Oldingi bo'limda topilgan nol funksiyasi bizga buni amalga oshirishga yordam beradi. Shunday qilib, biz to'g'ri chiziq qurishimiz kerak (grafikdan alohida) va unga funksiyaning nollarini to'g'ri tartibda eng kichikdan kattagacha taqsimlashimiz kerak. Endi siz hosil bo'lgan intervallarning qaysi biri "+" belgisiga ega ekanligini va qaysi "-" ekanligini aniqlashingiz kerak.

Bizning holatda, funktsiya oraliqlarda ijobiy qiymat oladi:

• 1 dan 4 gacha;
• 9 dan cheksizgacha.

Salbiy ma'nosi:

• minus cheksizlikdan 1 gacha;
• 4 dan 9 gacha.

Buni aniqlash oson. Funksiyaga oraliqdan istalgan raqamni kiriting va javob qanday belgi ekanligini ko'ring (minus yoki ortiqcha).

O'sish va kamaytirish funktsiyalari

Funksiyani tekshirish va qurish uchun grafik qayerda ortishi (Oy boʻylab yuqoriga koʻtarilishi) va qayerga tushishi (ordinata boʻylab pastga emaklab borish)ni aniqlashimiz kerak.

Funktsiya faqat x o'zgaruvchining katta qiymati y ning katta qiymatiga to'g'ri kelsagina ortadi. Ya'ni, x2 x1 dan, f (x2) esa f (x1) dan katta. Va biz kamayuvchi funktsiyada butunlay qarama-qarshi hodisani kuzatamiz (qanchalik ko'p bo'lsa, y). O'sish va pasayish oraliqlarini aniqlash uchun siz quyidagilarni topishingiz kerak:

• qamrov (bizda allaqachon mavjud);
• lotin (bizning holimizda: 1/3 (3x ^ 2-28x + 49);
• 1/3 (3x ^ 2-28x + 49) = 0 tenglamani yeching.

Hisob-kitoblardan so'ng biz natijaga erishamiz:

Biz olamiz: funktsiya minus cheksizlikdan 7/3 gacha va 7 dan cheksizgacha bo'lgan oraliqlarda ortadi va 7/3 dan 7 gacha bo'lgan intervalda kamayadi.

Ekstremallar

Tekshirilayotgan funktsiya y = 1/3 (x ^ 3-14x ^ 2 + 49x-36) uzluksiz va x o'zgaruvchining har qanday qiymatlari uchun mavjud. Ekstremum nuqta bu funktsiyaning maksimal va minimalini ko'rsatadi. Bizning holatlarimizda hech kim yo'q, bu qurilish vazifasini sezilarli darajada osonlashtiradi. Aks holda, ular funktsiyaning hosilasi yordamida ham topiladi. Topib olgandan so'ng, ularni jadvalda belgilashni unutmang.

Qavariqlik va botiqlik

Biz y (x) funktsiyasini qo'shimcha tekshirishni davom ettiramiz. Endi biz uni konveks va konkavlik uchun tekshirishimiz kerak. Ushbu tushunchalarning ta'riflarini idrok etish juda qiyin, hamma narsani misollar bilan tahlil qilish yaxshiroqdir. Sinov uchun: agar u kamaymaydigan funksiya bo'lsa, funksiya qavariq bo'ladi. Qabul qiling, bu tushunarsiz!

Ikkinchi tartibli funksiyaning hosilasini topishimiz kerak. Biz olamiz: y = 1/3 (6x-28). Endi o'ng tomonni nolga qo'yamiz va tenglamani yechamiz. Javob: x = 14/3. Biz burilish nuqtasini, ya'ni grafikning qavariqdan botiqlikka yoki aksincha o'zgarishini topdik. Minus cheksizlikdan 14/3 gacha bo'lgan oraliqda funktsiya qavariq, 14/3 dan plyus cheksizlikka qadar esa botiq bo'ladi. Shuni ham ta'kidlash kerakki, grafikdagi burilish nuqtasi silliq va yumshoq bo'lishi kerak, o'tkir burchaklar bo'lmasligi kerak.

Qo'shimcha nuqtalarning ta'rifi

Bizning vazifamiz funktsiyani tekshirish va chizishdir. Biz tadqiqotni tugatdik, endi funktsiyani chizish qiyin bo'lmaydi. Koordinata tekisligida egri chiziq yoki to'g'ri chiziqni aniqroq va batafsil ko'rsatish uchun siz bir nechta yordamchi nuqtalarni topishingiz mumkin. Ularni hisoblash juda oson. Masalan, x = 3 ni olib, hosil bo'lgan tenglamani yechib, y = 4 ni topamiz. Yoki x = 5 va y = -5 va hokazo. Siz qurish uchun qancha qo'shimcha ball olishingiz mumkin. Ulardan kamida 3-5 tasi topiladi.

Grafik chizish

Biz funktsiyani tekshirishimiz kerak edi (x ^ 3-14x ^ 2 + 49x-36) * 1/3 = y. Hisob-kitoblar paytida barcha kerakli eslatmalar koordinata tekisligida amalga oshirildi. Bajarilishi kerak bo'lgan narsa faqat grafik yaratish, ya'ni barcha nuqtalarni bir-biriga bog'lashdir. Nuqtalarni bog'lash silliq va toza bo'lishi kerak, bu mahorat masalasi - ozgina mashq qiling va sizning jadvalingiz mukammal bo'ladi.

Ko'rsatmalar

Funktsiya doirasini toping. Masalan, sin (x) funksiyasi -∞ dan + ∞ gacha bo'lgan butun oraliqda, 1 / x funksiyasi esa -∞ dan + ∞ gacha, x = 0 nuqtasidan tashqari aniqlanadi.

Davomiylik sohalari va uzilish nuqtalarini aniqlang. Odatda funksiya aniqlangan sohada uzluksiz bo‘ladi. Uzluksizliklarni aniqlash uchun argument ta'rif domenidagi ajratilgan nuqtalarga yaqinlashganda hisoblang. Masalan, 1 / x funksiyasi x → 0 + bo'lganda cheksizlikka, x → 0- bo'lganda esa minus cheksizlikka intiladi. Bu x = 0 nuqtada ikkinchi turdagi uzilishga ega ekanligini anglatadi.
Agar uzilish nuqtasidagi chegaralar chekli bo'lsa, lekin teng bo'lmasa, bu birinchi turdagi uzilishdir. Agar ular teng bo'lsa, u holda funksiya uzluksiz hisoblanadi, garchi ajratilgan nuqtada u aniqlanmagan.

Agar mavjud bo'lsa, vertikal asimptotalarni toping. Oldingi bosqichdagi hisob-kitoblar bu erda sizga yordam beradi, chunki vertikal asimptota deyarli har doim ikkinchi turdagi uzilish nuqtasida bo'ladi. Biroq, ba'zan ta'rif sohasidan alohida nuqtalar emas, balki nuqtalarning butun intervallari chiqarib tashlanadi, keyin esa vertikal asimptotlar bu intervallarning chetlarida joylashgan bo'lishi mumkin.

Funktsiyaning maxsus xususiyatlari bor yoki yo'qligini tekshiring: paritet, toq paritet va davriylik.
Agar f (x) = f (-x) domenidagi har qanday x uchun funktsiya hatto bo'ladi. Masalan, cos (x) va x ^ 2 juft funksiyalardir.

Davriylik - bu har qanday x f (x) = f (x + T) uchun davr deb ataladigan ma'lum bir T soni mavjudligini bildiruvchi xususiyatdir. Masalan, barcha asosiy trigonometrik funktsiyalar (sinus, kosinus, tangens) davriydir.

Nuqtalarni toping. Buning uchun berilgan funktsiyaning hosilasini hisoblang va u yo'qolgan joyda x ning qiymatlarini toping. Masalan, f (x) = x ^ 3 + 9x ^ 2 -15 funktsiyasi g (x) = 3x ^ 2 + 18x hosilasiga ega, u x = 0 va x = -6 da yo'qoladi.

Qaysi ekstremum nuqtalari maksimal va qaysilari minimal ekanligini aniqlash uchun topilgan nollarda hosila belgisining o‘zgarishini kuzating. g (x) x = -6 nuqtada plyusdan belgini, x = 0 nuqtada esa minusdan plyusga orqaga o'zgaradi. Binobarin, f (x) funksiya birinchi nuqtada, ikkinchi nuqtada esa minimumga ega.

Shunday qilib, siz monotonlik hududlarini topdingiz: f (x) -∞ oraliqda monoton ravishda ortadi; -6, monoton ravishda -6 ga kamayadi; 0 va yana 0 ga ortadi; + ∞.

Ikkinchi hosilani toping. Uning ildizlari berilgan funksiya grafigi qayerda qavariq va qayerda botiq bo'lishini ko'rsatadi. Masalan, f (x) funktsiyasining ikkinchi hosilasi h (x) = 6x + 18 bo'ladi. U x = -3 da yo'qoladi, ishorani minusdan ortiqchaga o'zgartiradi. Shuning uchun, bu nuqtadan oldingi f (x) grafigi qavariq, undan keyin - botiq bo'ladi va bu nuqtaning o'zi egilish nuqtasi bo'ladi.

Funktsiya vertikaldan tashqari boshqa asimptotalarga ham ega bo'lishi mumkin, lekin faqat uning ta'rif sohasiga kiritilgan bo'lsa. Ularni topish uchun f (x) chegarasini x → ∞ yoki x → -∞ shaklida hisoblang. Agar u cheklangan bo'lsa, siz gorizontal asimptotani topdingiz.

Qiya asimptota kx + b ko'rinishdagi to'g'ri chiziqdir. k ni topish uchun f (x) / x chegarasini x → ∞ shaklida hisoblang. Xuddi shu x → ∞ uchun b - chegarani (f (x) - kx) topish uchun.

Funksiyani hisoblangan ma’lumotlar ustiga chizing. Agar mavjud bo'lsa, asimptotalarni belgilang. Ekstremum nuqtalarni va ulardagi funktsiya qiymatlarini belgilang. Grafikning aniqligi uchun funktsiyaning qiymatlarini yana bir nechta oraliq nuqtalarda hisoblang. Tadqiqot yakunlandi.

Funktsiyalarni o'rganish va ularning grafiklarini qurishda mos yozuvlar nuqtalari xarakterli nuqtalar - uzilish, ekstremum, burilish, koordinata o'qlari bilan kesishish nuqtalari. Differensial hisoblash yordamida funksiyalar o'zgarishining xarakterli belgilarini aniqlash mumkin: o'sish va kamayish, maksimal va minimal, grafikning qavariq va botiqlik yo'nalishi, asimptotalarning mavjudligi.

Funksiya grafigining eskizi asimptota va ekstremum nuqtalarni topgandan keyin chizilishi mumkin (va kerak) va oʻrganish davomida funksiyani oʻrganish uchun pivot jadvalini toʻldirish qulay.

Odatda, quyidagi funktsiyalarni o'rganish sxemasidan foydalaniladi.

1.Funksiyaning aniqlanish sohasi, uzluksizlik intervallari va uzilish nuqtalarini toping.

2.Funksiyani tenglik yoki toqlik (grafaning eksenel yoki markaziy simmetriyasi) uchun o‘rganing.

3.Asimptotlarni toping (vertikal, gorizontal yoki qiya).

4.Funksiyaning ortish va kamayish oraliqlarini, ekstremum nuqtalarini toping va tekshiring.

5.Egri chiziqning qavariqlik va botiqlik oraliqlarini, uning egilish nuqtalarini toping.

6.Egri chiziqning koordinata o'qlari bilan kesishish nuqtalarini toping, agar ular mavjud bo'lsa.

7.Tadqiqotning umumiy jadvalini tayyorlang.

8.Yuqoridagi nuqtalar bo'yicha bajarilgan funktsiyani o'rganishni hisobga olgan holda grafik tuzing.

Misol. Funktsiyani o'rganish

va uning grafigini tuzing.

7. Funksiyani o'rganishning yig'ma jadvalini tuzamiz, bu erda barcha xarakterli nuqtalarni va ular orasidagi intervallarni kiritamiz. Funktsiyaning paritetini hisobga olib, biz quyidagi jadvalni olamiz:

Funktsiyani to'liq o'rganish va uning grafigini tuzish uchun quyidagi sxemadan foydalanish tavsiya etiladi:

1) funksiya sohasini toping;

2) funksiya va vertikal asimptotalarning uzilish nuqtalarini toping (agar ular mavjud bo'lsa);

3) funksiyaning cheksizlikdagi harakatini tekshirish, gorizontal va qiya asimptotalarni topish;

4) funksiyani juftlik (toqlik) va davriylik (trigonometrik funksiyalar uchun) uchun tekshirish;

5) funksiyaning monotonligining ekstremal va intervallarini toping;

6) qavariqlik oraliqlarini va burilish nuqtalarini aniqlash;

7) iloji bo'lsa, koordinata o'qlari bilan kesishgan nuqtalarni va grafikni aniqlaydigan ba'zi qo'shimcha nuqtalarni toping.

Funktsiyani o'rganish uning grafigini qurish bilan bir vaqtda amalga oshiriladi.

9-misol Funktsiyani o'rganing va grafikni chizing.

1. Ta'rif doirasi:;

2. Funksiya nuqtalarda buziladi
,
;

Vertikal asimptotalarning mavjudligi uchun funktsiyani ko'rib chiqamiz.

;
,
─ vertikal asimptota.

;
,
─ vertikal asimptota.

3. Qiyma va gorizontal asimptotalarning mavjudligi funksiyasini tekshiramiz.

Streyt
─ qiya asimptota agar
,
.

,
.

Streyt
─ gorizontal asimptota.

4. Funksiya juft, chunki
... Funksiyaning pariteti ordinata o'qiga nisbatan grafikning simmetriyasini ko'rsatadi.

5. Funksiyaning monotonlik va ekstremallik oraliqlarini toping.

Kritik nuqtalarni topamiz, ya'ni. hosila 0 bo'lgan yoki mavjud bo'lmagan nuqtalar:
;
... Bizda uch ochko bor
;

... Ushbu nuqtalar butun o'qni to'rtta bo'shliqqa ajratadi. Keling, belgilarni aniqlaylik ularning har birida.

(-∞; -1) va (-1; 0) oraliqlarda funksiya ortib boradi, (0; 1) va (1; + ∞) ─ oraliqlarida esa kamayadi. Bir nuqtani kesib o'tishda
hosila belgisi plyusdan minusga o'zgaradi, shuning uchun bu nuqtada funktsiya maksimalga ega
.

6. Qavariq intervallarni, burilish nuqtalarini toping.

Qaysi nuqtalarni toping 0 yoki mavjud emas.

haqiqiy ildizlarga ega emas.
,
,

Ballar
va
haqiqiy o'qni uchta intervalgacha bo'ling. Keling, belgini aniqlaylik har bir intervalda.

Shunday qilib, oraliqlarda egri
va
qavariq pastga, oraliqda (-1; 1) qavariq yuqoriga; nuqtalarda funktsiya beri hech qanday burilish nuqtalari mavjud emas
va
aniqlanmagan.

7. O’qlar bilan kesishish nuqtalarini toping.

Eksa bilan
funktsiya grafigi (0; -1) nuqtada va o'q bilan kesishadi
grafik ustma-ust tushmaydi, chunki bu funksiyaning numeratori haqiqiy ildizlarga ega emas.

Berilgan funksiyaning grafigi 1-rasmda keltirilgan.

1-rasm ─ Funksiya grafigi

Hosila tushunchasining iqtisodiyotda qo‘llanilishi. Funksiyaning elastikligi

Iqtisodiy jarayonlarni o'rganish va boshqa qo'llaniladigan muammolarni hal qilish uchun ko'pincha funktsiyaning elastikligi tushunchasi qo'llaniladi.

Ta'rif. Funksiyaning elastikligi
funktsiyaning nisbiy o'sish nisbati chegarasi deyiladi o'zgaruvchining nisbiy o'sishiga da
,. (Vii)

Funksiyaning egiluvchanligi funksiya o‘zgarishining taxminan foizini ko‘rsatadi
mustaqil o'zgaruvchini o'zgartirganda 1% ga.

Funktsiyaning elastikligi talab va iste'molni tahlil qilishda qo'llaniladi. Agar talabning egiluvchanligi (mutlaq qiymatda)
, agar talab elastik deb hisoblanadi
─ neytral, agar
─ narxga (yoki daromadga) nisbatan noelastik.

10-misol Funksiyaning elastikligini hisoblang
uchun elastiklik indeksining qiymatini toping = 3.

Yechish: funktsiyaning elastikligi formulasi (VII) bo'yicha:

Shunday qilib, x = 3 bo'lsin
Bu shuni anglatadiki, agar tushuntirish o'zgaruvchisi 1% ga oshsa, u holda bog'liq o'zgaruvchining qiymati 1,42% ga oshadi.

11-misol Talab amal qilsin narx haqida shaklga ega
, qayerda ─ doimiy koeffitsient. X = 3 den narxdagi talab funksiyasining elastiklik indeksining qiymatini toping. birliklar

Yechish: (VII) formula bo‘yicha talab funksiyasining elastikligini hisoblang.

Taxmin qilib
pul birliklari, biz olamiz
... Bu shuni anglatadiki, narxda
pul birliklari 1% narx oshishi talabning 6% pasayishiga olib keladi, ya'ni. talab elastik.

Funktsiyani to'liq o'rganish va uning grafigini tuzish uchun quyidagi sxema tavsiya etiladi:
A) aniqlash sohasini, uzilish nuqtalarini toping; uzilish nuqtalari yaqinidagi funksiyaning harakatini o‘rganing (bu nuqtalarda funksiyaning chap va o‘ngdagi chegaralarini toping). Vertikal asimptotalarni belgilang.
B) funksiyaning juft yoki toqligini aniqlang va simmetriya borligi haqida xulosa chiqaring. Agar funktsiya juft bo'lsa, OY o'qiga nisbatan simmetrik bo'lsa; funktsiya toq bo'lsa, koordinataga nisbatan simmetrik; va agar - umumiy shaklning funktsiyasi.
C) funksiyaning OY va OX koordinata o‘qlari bilan kesishish nuqtalarini toping (agar iloji bo‘lsa), funksiyaning doimiy ishorasi intervallarini aniqlang. Funksiyaning doimiy ishorali intervallari chegaralari funksiya nolga teng (funktsiyaning nollari) yoki mavjud boʻlmagan nuqtalar va ushbu funksiya sohasi chegaralari bilan aniqlanadi. Funktsiya grafigi OX o'qi ustida joylashgan oraliqlarda va bu o'qning ostida joylashgan.
D) funksiyaning birinchi hosilasini toping, uning nollarini va doimiylik intervallarini aniqlang. Funktsiya ortib borayotgan va kamaygan oraliqlarda. Ekstrema (funksiya va hosila mavjud bo'lgan nuqtalar va u orqali o'tishda u ishorani o'zgartiradi. Agar u ishorani ortiqcha dan minusga o'zgartirsa, bu nuqtada funktsiya maksimalga, agar minusdan minusga o'zgaradigan bo'lsa) borligi haqida xulosa chiqaring. ortiqcha, keyin minimal). Ekstremum nuqtalarda funksiya qiymatlarini toping.
E) ikkinchi hosilani, uning nollarini va doimiylik oraliqlarini toping. Qaerda intervallarda< 0 график функции выпуклый, а где – вогнутый. Сделать заключение о наличии точек перегиба и найти значения функции в этих точках.
E) tenglamalari ko'rinishga ega bo'lgan qiya (gorizontal) asimptotalarni toping ; qayerda
.
Da funktsiya grafigi ikkita qiya asimptotaga ega bo'ladi va x ning har bir qiymati at va b ning ikkita qiymatiga mos kelishi mumkin.
G) jadvalni aniqlashtirish uchun qo'shimcha nuqtalarni toping (agar kerak bo'lsa) va grafikni tuzing.

1-misol Funktsiyani ko'rib chiqing va grafigini tuzing. Yechish: A) ta’rif doirasi; funksiya aniqlanish sohasida uzluksiz; - sinish nuqtasi, chunki ; ... Keyin vertikal asimptota.
B)
bular. y (x) umumiy funktsiyadir.
C) Grafikning OY o'qi bilan kesishish nuqtalarini toping: x = 0 ni o'rnatamiz; keyin y (0) = - 1, ya'ni. funktsiya grafigi (0; -1) nuqtada o'qni kesib o'tadi. Funktsiyaning nollari (grafikning OX o'qi bilan kesishish nuqtalari): biz y = 0 ni o'rnatamiz; keyin
.
Kvadrat tenglamaning diskriminanti noldan kichik, shuning uchun ham nollar mavjud emas. U holda doimiylik oraliqlarining chegarasi funksiya mavjud bo'lmagan x = 1 nuqtadir.
Funktsiyaning har bir oraliqdagi belgisi ma'lum qiymatlar usuli bilan aniqlanadi:

Diagrammadan ko'rinib turibdiki, intervalda funksiya grafigi OX o'qi ostida, intervalda esa OX o'qi ustida joylashgan.
D) Kritik nuqtalar mavjudligini aniqlang.
.
Kritik nuqtalar (qaerda yoki mavjud emas) tengliklardan topiladi va.

Biz olamiz: x1 = 1, x2 = 0, x3 = 2. Keling, yordamchi jadval tuzamiz

1-jadval

(Birinchi qatorda bu nuqtalar OX o'qi bo'linadigan kritik nuqtalar va intervallar mavjud; ikkinchi qatorda kritik nuqtalardagi lotin qiymatlari va intervallardagi belgilar ko'rsatilgan. Belgilar usul bilan aniqlanadi. uchinchi qator y (x) funktsiyasining kritik nuqtalardagi qiymatlarini ko'rsatadi va funktsiyaning xatti-harakati ko'rsatilgan - raqamli o'qning mos keladigan oraliqlarida ortib borayotgan yoki kamaygan.
E) Funksiyaning qavariqlik va botiqlik oraliqlarini toping.
; D bandidagi kabi jadval tuzing); faqat ikkinchi qatorda biz belgilarni yozamiz, uchinchisida esa qavariq turini ko'rsatamiz. Chunki ; u holda faqat bitta kritik nuqta x = 1 bo'ladi.
jadval 2

X = 1 nuqtasi burilish nuqtasidir.
E) Qiya va gorizontal asimptotalarni toping

U holda y = x qiya asimptotadir.
G) Olingan ma’lumotlardan foydalanib, funksiya grafigini tuzamiz

1). Funktsiyani aniqlash maydoni.
Shubhasiz, bu funktsiya butun son chizig'ida aniqlanadi, chunki "" va "" nuqtalari bundan mustasno bu nuqtalarda maxraj nolga teng va shuning uchun funksiya mavjud emas, to'g'ri chiziqlar esa vertikal asimptotlardir.

2). Argument cheksizlikka moyil bo'lganda funktsiyaning harakati, uzilish nuqtalarining mavjudligi va qiya asimptotalarning mavjudligini tekshirish.
Keling, avvalo cheksizlikka chapga va o'ngga yaqinlashganda funksiya qanday ishlashini tekshirib ko'raylik.

Shunday qilib, uchun, funktsiya 1 ga intiladi, ya'ni. - gorizontal asimptota.
Uzluksizlik nuqtalari yaqinida funktsiyaning harakati quyidagicha aniqlanadi:


Bular. chap tarafdagi uzilish nuqtalariga yaqinlashganda, funksiya cheksiz kamayadi, o'ngda esa cheksiz ortadi.
Egri asimptotaning mavjudligi tenglikni hisobga olgan holda aniqlanadi:

Egri asimptotlar yo'q.

3). Koordinata o'qlari bilan kesishish nuqtalari.
Bu erda ikkita holatni ko'rib chiqish kerak: Ox o'qi bilan va Oy o'qi bilan kesishish nuqtasini toping. Ox o'qi bilan kesishish belgisi funktsiyaning nol qiymati, ya'ni. tenglamani yechish kerak:

Bu tenglamaning ildizlari yo'q, shuning uchun bu funktsiya grafigida Ox o'qi bilan kesishish nuqtalari mavjud emas.
Oy o'qi bilan kesishish belgisi x = 0. Bu holda,
,
bular. - funksiya grafigining Oy o'qi bilan kesishish nuqtasi.

4).Ekstremum nuqtalarni va ortish va pasayish intervallarini aniqlash.
Ushbu muammoni o'rganish uchun biz birinchi hosilani aniqlaymiz:
.
Birinchi hosilaning qiymatini nolga tenglashtiramiz.
.
Kasr, uning numeratori nolga teng bo'lsa, nolga teng, ya'ni. ...
Funksiyaning ortish va kamayish intervallarini aniqlaymiz.

Shunday qilib, funktsiya bitta ekstremum nuqtasiga ega va ikkita nuqtada mavjud emas.
Shunday qilib, funktsiya oraliqlarda ortadi va va intervallarda kamayadi.

5). Burilish nuqtalari va konveks va botiqlik joylari.
Funktsiya harakatining bu xarakteristikasi ikkinchi hosila yordamida aniqlanadi. Avval burilish nuqtalarining mavjudligini aniqlaylik. Funktsiyaning ikkinchi hosilasi

At va funksiya botiq;

uchun va funksiya qavariq.

6). Funksiya grafigini tuzish.
Nuqtalardagi topilgan qiymatlardan foydalanib, biz funktsiyaning sxematik grafigini tuzamiz:

Yechim
Berilgan funksiya umumiy davriy bo'lmagan funksiyadir. Uning grafigi kelib chiqishi orqali o'tadi, chunki.
Berilgan funktsiya sohasi o'zgaruvchining barcha qiymatlari bo'lib, kasrning maxraji yo'qoladi va bundan tashqari.
Demak, va nuqtalar funksiyaning uzilish nuqtalari hisoblanadi.
Chunki ,

Chunki ,
, keyin nuqta ikkinchi turdagi tanaffus nuqtasidir.
To'g'ri chiziqlar va funksiya grafigining vertikal asimptotalari.
Egri asimptotalar tenglamalari, bu erda, .
Da ,
.
Shunday qilib, for va funksiya grafigi bitta asimptotaga ega.
Funksiyaning ortish va kamayish intervallari va ekstremum nuqtalari topilsin.
.
Funktsiyaning birinchi hosilasi at va demak, at va funksiyasi ortadi.
Qachon, demak, qachon, funksiya kamayadi.
uchun mavjud emas,.
, shuning uchun, uchun funksiyaning grafigi botiq.
Da , shuning uchun, uchun funksiyaning grafigi qavariq.

Nuqtalardan o'tayotganda, belgisini o'zgartiradi. Agar funktsiya aniqlanmagan bo'lsa, shuning uchun funktsiya grafigida bitta burilish nuqtasi mavjud.
Keling, funktsiyani chizamiz.