Kare şekil hesap makinesi sınırlı. Çevrimiçi hesap makinesi Belirli integrali hesaplayın (kavisli bir yamuğun alanı)

18.10.2019

Ayrıca okuyun

Bu makale, integral hesaplamaları kullanarak çizgilerle sınırlanmış bir şeklin alanını nasıl bulacağınızı gösterecektir. İlk kez, böyle bir problemin formülasyonu ile lisede, belirli integrallerin çalışılmasının henüz geçtiği ve pratikte kazanılan bilgilerin geometrik bir yorumuna başlamanın zamanı geldiğinde karşılaşıyoruz.

Öyleyse, integralleri kullanarak bir şeklin alanını bulma problemini başarılı bir şekilde çözmek için gerekenler:

Çizimleri yetkin bir şekilde oluşturma yeteneği;
İyi bilinen Newton-Leibniz formülünü kullanarak belirli bir integrali çözebilme;
Daha avantajlı bir çözümü “görme” yeteneği - yani, Bu veya bu durumda entegrasyonu gerçekleştirmenin nasıl daha uygun olacağını anlamak için? x ekseni (OX) veya y ekseni (OY) boyunca mı?
Peki, doğru hesaplamalar olmadan nerede?) Bu, diğer türdeki integrallerin nasıl çözüleceğini ve sayısal hesaplamaları doğru yapmayı içerir.

Çizgilerle sınırlanmış bir şeklin alanını hesaplama problemini çözmek için algoritma:

1. Bir çizim oluşturuyoruz. Bunu, büyük ölçekli bir kafeste bir kağıt parçası üzerinde yapmanız önerilir. Her grafiğin üzerine bu fonksiyonun adını kurşun kalemle imzalıyoruz. Grafiklerin imzası, yalnızca daha sonraki hesaplamaların rahatlığı için yapılır. İstenen şeklin grafiğini aldıktan sonra, çoğu durumda hangi entegrasyon sınırlarının kullanılacağı hemen görülecektir. Böylece problemi grafiksel olarak çözmüş oluyoruz. Bununla birlikte, sınırların değerlerinin kesirli veya irrasyonel olduğu da olur. Bu nedenle ek hesaplamalar yapabilirsiniz, ikinci adıma geçin.

2. İntegrasyon sınırları açıkça belirlenmemişse, grafiklerin birbirleriyle kesişme noktalarını buluruz ve grafik çözümümüzün analitik çözümle örtüşüp örtüşmediğine bakarız.

3. Ardından, çizimi analiz etmeniz gerekir. Fonksiyon grafiklerinin nasıl yerleştirildiğine bağlı olarak, bir şeklin alanını bulmak için farklı yaklaşımlar vardır. İntegral kullanarak bir şeklin alanını bulmanın farklı örneklerini ele alalım.

3.1. Sorunun en klasik ve basit versiyonu, kavisli bir yamuğun alanını bulmanız gerektiği zamandır. Eğri yamuk nedir? Bu, x ekseni ile sınırlandırılmış düz bir şekildir. (y = 0), Düz x = a, x = b ve herhangi bir eğri sürekli aönce B... Ayrıca bu rakam negatif değildir ve apsis ekseninin altında yer almaz. Bu durumda, eğrisel bir yamuğun alanı, Newton-Leibniz formülüyle hesaplanan belirli bir integrale sayısal olarak eşittir:

örnek 1 y = x2 - 3x + 3, x = 1, x = 3, y = 0.

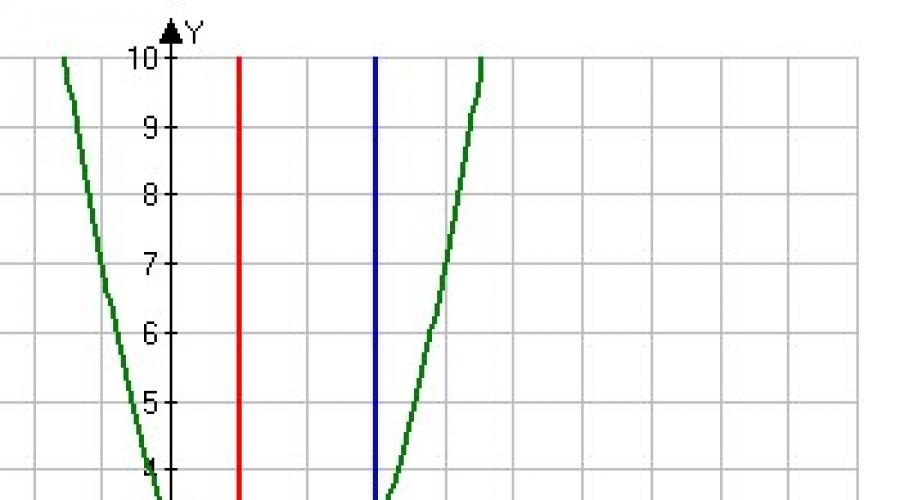
Figürü sınırlayan çizgiler nelerdir? bir parabolümüz var y = x2 - 3x + 3 eksenin üzerinde bulunan AH, negatif değil, çünkü bu parabolün tüm noktaları pozitiftir. Ayrıca, düz çizgiler x = 1 ve x = 3 eksene paralel uzanan kuruluş birimi, şeklin sol ve sağdaki sınırlayıcı çizgileridir. İyi y = 0, şekli aşağıdan sınırlayan x eksenidir. Ortaya çıkan şekil, soldaki resimde görüldüğü gibi gölgelendirilmiştir. Bu durumda, sorunu hemen çözmeye başlayabilirsiniz. Önümüzde Newton-Leibniz formülünü kullanarak çözeceğimiz basit bir eğrisel yamuk örneği var.

3.2. Önceki paragraf 3.1'de, eğri yamuğun x ekseninin üzerinde olduğu durumu analiz ettik. Şimdi, fonksiyonun x ekseninin altında olması dışında, problemin koşullarının aynı olduğu durumu düşünün. Standart Newton-Leibniz formülüne bir eksi eklenir. Benzer bir sorunun nasıl çözüleceğini daha fazla ele alacağız.

Örnek 2 ... Çizgilerle sınırlanmış bir şeklin alanını hesaplayın y = x2 + 6x + 2, x = -4, x = -1, y = 0.

Bu örnekte bir parabolümüz var. y = x2 + 6x + 2 eksenin altından kaynaklanan AH, Düz x = -4, x = -1, y = 0... Buraya y = 0İstenen şekli yukarıdan sınırlar. doğrudan x = -4 ve x = -1 bunlar, belirli bir integralin hesaplanacağı sınırlardır. Bir şeklin alanını bulma problemini çözme ilkesi, 1 numaralı örnekle neredeyse tamamen örtüşmektedir. Tek fark, verilen fonksiyonun pozitif olmaması ve aralıkta hala sürekli olmasıdır. [-4; -1] ... Ne demek olumlu değil? Şekilden de görebileceğiniz gibi, belirtilen x içinde olan şekil, sadece “negatif” koordinatlara sahiptir, bu da problemi çözerken görmemiz ve hatırlamamız gereken şeydir. Şeklin alanını Newton-Leibniz formülünü kullanarak, yalnızca başında eksi işareti ile ararız.

Makale eksik.

Şimdi integral hesabın uygulamalarının değerlendirilmesine dönüyoruz. Bu derste tipik ve en yaygın bir görevi analiz edeceğiz. belirli bir integral kullanarak düz bir şeklin alanını hesaplama... Son olarak, yüksek matematikte anlam arayanlar - bulsunlar. Asla bilemezsin. Banliyö bölgesini temel fonksiyonlarla hayata yakınlaştırmamız ve alanını belirli bir integral kullanarak bulmamız gerekecek.

Malzemede başarılı bir şekilde ustalaşmak için şunları yapmalısınız:

1) Belirsiz integrali en azından orta düzeyde anlar. Bu nedenle, aptallar önce derse aşina olmalıdırlar. Olumsuz.

2) Newton-Leibniz formülünü uygulayabilir ve belirli bir integrali hesaplayabilir. Sayfada belirli integrallerle sımsıcak dostluklar kurabilirsiniz. Kesin integral. Çözüm örnekleri. "Belirli bir integral kullanarak alanı hesaplama" görevi her zaman bir çizim oluşturmayı içerir. bu nedenle, çizim oluşturma konusundaki bilgi ve becerileriniz de acil bir konu olacaktır. En azından düz bir çizgi, bir parabol ve bir hiperbol oluşturabilmeniz gerekir.

Kavisli bir yamuk ile başlayalım. Eğrisel bir yamuk, bazı fonksiyonların grafiğiyle sınırlanan düz bir şekildir. y = F(x), Eksen ÖKÜZ ve çizgiler x = a; x = B.

Eğri bir yamuğun alanı sayısal olarak belirli integrale eşittir

Herhangi bir belirli integralin (var olan) çok iyi bir geometrik anlamı vardır. Derste Kesin integral. Çözüm örnekleri Belirli bir integralin bir sayı olduğunu söylemiştik. Ve şimdi başka bir yararlı gerçeği belirtmenin zamanı geldi. Geometri açısından, belirli integral ALAN'dır.... Yani, belirli bir integral (varsa) geometrik olarak bir şeklin alanına karşılık gelir... Belirli integrali düşünün

İntegrand

düzlemde bir eğri tanımlar (istenirse çizilebilir) ve belirli integralin kendisi sayısal olarak karşılık gelen eğrisel yamuğun alanına eşittir.

örnek 1

, , , .

Bu, ödevin tipik bir formülasyonudur. Çözümün en önemli noktası çizimin yapımıdır.... Ayrıca, çizim inşa edilmelidir SAĞ.

Bir çizim oluştururken aşağıdaki sırayı öneririm: Başta tüm düz çizgileri (varsa) oluşturmak daha iyidir ve yalnızca sonrasında- paraboller, hiperboller, diğer fonksiyonların grafikleri. Nokta nokta yapım tekniği referans malzemede bulunabilir. Temel fonksiyonların grafikleri ve özellikleri... Orada ayrıca dersimizle ilgili çok faydalı materyaller bulabilirsiniz - bir parabolün nasıl hızlı bir şekilde oluşturulacağı.

Bu problemde, çözüm şöyle görünebilir.

Çizimi tamamlayalım (denklemin y= 0 ekseni belirtir ÖKÜZ):

Eğrisel yamuğu taramayacağız, burada hangi alandan bahsettiğimiz açık. Çözüm şöyle devam ediyor:

Segmentte [-2; 1] fonksiyon grafiği y = x 2 + 2 konumlu eksenin üstündeÖKÜZ, Öyleyse:

Cevap: .

Belirli bir integrali hesaplamada ve Newton-Leibniz formülünü uygulamada zorluk çekenler

derse bakın Kesin integral. Çözüm örnekleri... Görev tamamlandıktan sonra, plana bakmak ve cevabın gerçek olup olmadığını tahmin etmek her zaman yararlıdır. Bu durumda, "gözle" çizimdeki hücre sayısını sayıyoruz - peki, yaklaşık 9 yazılacak, gerçek gibi görünüyor. Diyelim ki cevabı aldıysak: 20 birim kare, o zaman, açıkçası, bir yerde bir hata yapıldı - söz konusu rakam açıkça 20 hücreye uymuyor, en fazla on. Cevap olumsuzsa, görev de yanlış çözüldü.

Örnek 2

Çizgilerle sınırlanmış bir şeklin alanını hesaplayın xy = 4, x = 2, x= 4 ve eksen ÖKÜZ.

Bu, kendin yap çözümüne bir örnektir. Çözümü tamamlayın ve öğreticinin sonunda yanıtlayın.

Kavisli yamuk bulunursa ne yapmalı eksenin altındaÖKÜZ?

Örnek 3

Çizgilerle sınırlanmış bir şeklin alanını hesaplayın y = eski, x= 1 ve koordinat eksenleri.

Çözüm: Çizimi uygulayalım:

Eğri yamuk ise tamamen aksın altında bulunur ÖKÜZ , o zaman alanı şu formülle bulunabilir:

Bu durumda:

Dikkat! İki tür görev karıştırılmamalıdır:

1) Herhangi bir geometrik anlamı olmayan belirli bir integrali çözmeniz istenirse, negatif olabilir.

2) Belirli bir integral kullanarak bir şeklin alanını bulmanız istenirse, alan her zaman pozitiftir! Bu nedenle, az önce ele alınan formülde bir eksi belirir.

Uygulamada, çoğu zaman şekil hem üst hem de alt yarı düzlemlerde bulunur ve bu nedenle en basit okul problemlerinden daha anlamlı örneklere geçilir.

Örnek 4

Çizgilerle sınırlanmış düz bir şeklin alanını bulun y = 2x – x 2 , y = -x.

Çözüm: İlk önce çizimi tamamlamanız gerekiyor. Alandaki problemlerde bir çizim oluştururken, en çok çizgilerin kesişme noktalarıyla ilgileniriz. Parabolün kesişme noktalarını bulun y = 2x – x 2 ve düz y = -x... Bu iki şekilde yapılabilir. Birinci yol analitiktir. Denklemi çözüyoruz:

Bu nedenle, integralin alt sınırı a= 0, entegrasyonun üst sınırı B= 3. Entegrasyonun sınırları “kendi kendine” netleşirken, çizgileri nokta nokta oluşturmak genellikle daha karlı ve daha hızlıdır. Bununla birlikte, örneğin grafik yeterince büyükse veya kesin yapı entegrasyonun sınırlarını ortaya çıkarmıyorsa (bunlar kesirli veya irrasyonel olabilir) bazen sınırları bulma analitik yönteminin kullanılması gerekir. Sorunumuza dönüyoruz: önce düz bir çizgi ve ancak o zaman bir parabol oluşturmak daha mantıklı. Çizimi uygulayalım:

Noktasal bir yapı söz konusu olduğunda, integrasyon sınırlarının çoğunlukla “otomatik olarak” bulunduğunu tekrarlayalım.

Ve şimdi çalışma formülü:

Segmentte ise [ a; B] bazı sürekli fonksiyon F(x) büyük veya eşit bazı sürekli fonksiyon G(x), daha sonra karşılık gelen şeklin alanı aşağıdaki formülle bulunabilir:

Burada artık şeklin nerede olduğunu düşünmenize gerek yok - eksenin üstünde veya altında, ancak hangi programın YUKARIDA olduğu önemlidir(başka bir grafiğe göre), ve hangisi AŞAĞIDA.

Söz konusu örnekte, segmentte parabolün düz çizginin üzerinde ve dolayısıyla 2'den itibaren yer aldığı açıktır. x – x 2 çıkarılmalıdır - x.

Çözümün tamamlanması şöyle görünebilir:

Aranan şekil bir parabol ile sınırlandırılmıştır. y = 2x – x 2 üst ve düz y = -x aşağıdan.

2. segmentte x – x 2 ≥ -x... İlgili formüle göre:

Cevap: .

Aslında, alt yarı düzlemde eğrisel bir yamuğun alanı için okul formülü (bkz. örnek No. 3), formülün özel bir halidir.

eksen beri ÖKÜZ denklem tarafından verilen y= 0 ve fonksiyonun grafiği G(x) eksenin altında bulunur ÖKÜZ, sonra

Ve şimdi bağımsız bir çözüm için birkaç örnek

Örnek 5

Örnek 6

Çizgilerle sınırlanmış bir şeklin alanını bulun

Belirli bir integral kullanarak alan hesaplama problemlerini çözerken bazen komik bir olay olur. Çizim doğru yapılmış, hesaplamalar doğru, ancak yanlışlıkla ... yanlış şeklin alanı bulundu.

Örnek 7

İlk önce çizimi uygulayalım:

Alanı bulmamız gereken şekil mavi gölgeli(duruma dikkatlice bakın - rakam ne ile sınırlıdır!). Ancak pratikte, dikkatsizlik yoluyla, genellikle şeklin yeşil gölgeli alanını bulmanın gerekli olduğuna karar verirler!

Bu örnek, iki belirli integral kullanarak bir şeklin alanını hesaplaması açısından da yararlıdır. Yok canım:

1) Segmentte [-1; 1] eksenin üstünde ÖKÜZ grafik düz y = x+1;

2) Eksenin üzerindeki bir segmentte ÖKÜZ hiperbol grafiği bulunur y = (2/x).

Alanların eklenebileceği (ve eklenmesi gerektiği) oldukça açıktır, bu nedenle:

Cevap:

Örnek 8

Çizgilerle sınırlanmış bir şeklin alanını hesaplayın

Denklemleri "okul" formunda gösterelim

ve noktadan noktaya bir çizim yürütün:

Üst sınırımızın "iyi" olduğu çizimden görülebilir: B = 1.

Ama alt sınır nedir?! Bunun bir tamsayı olmadığı açık, ama hangisi?

Belki, a= (- 1/3)? Ancak, çizimin kusursuz bir doğrulukla yapıldığının garantisi nerede, pekala ortaya çıkabilir. a= (- 1/4). Grafiği hiç yanlış çizersek ne olur?

Bu gibi durumlarda ek zaman harcamanız ve entegrasyonun sınırlarını analitik olarak iyileştirmeniz gerekir.

Grafiklerin kesişme noktalarını bulun

Bunu yapmak için denklemi çözüyoruz:

Buradan, a=(-1/3).

Diğer çözüm önemsizdir. Ana şey, ikame ve işaretlerde kafa karıştırmamaktır. Buradaki hesaplamalar en kolay olanlar değil. segmentte

, ,

ilgili formüle göre:

Cevap:

Dersin sonunda, iki zor görevi daha ele alacağız.

Örnek 9

Çizgilerle sınırlanmış bir şeklin alanını hesaplayın

Çözüm: Bu şekli çizime çizin.

Çizimin nokta nokta inşası için sinüzoidin görünümünü bilmeniz gerekir. Genel olarak, sinüsün bazı değerlerinin yanı sıra tüm temel fonksiyonların grafiklerini bilmek yararlıdır. Değer tablosunda bulunabilirler trigonometrik fonksiyonlar... Bazı durumlarda (örneğin, bu durumda), grafiklerin ve entegrasyon sınırlarının prensipte doğru bir şekilde gösterilmesi gereken şematik bir çizim yapılmasına izin verilir.

Entegrasyon sınırlarıyla ilgili herhangi bir sorun yoktur, doğrudan şu koşuldan kaynaklanırlar:

- "x" sıfırdan "pi"ye değişir. Bir karar daha veriyoruz:

Bir segmentte, fonksiyonun grafiği y= günah 3 x eksenin üzerinde bulunur ÖKÜZ, Öyleyse:

(1) Sinüs ve kosinüslerin tek derecelerde nasıl entegre edildiğini derste görebilirsiniz. trigonometrik fonksiyonların integralleri... Bir sinüsü çimdikliyoruz.

(2) Formda temel trigonometrik kimliği kullanıyoruz

(3) Değişkeni değiştirin T= çünkü x, o zaman: eksenin üzerinde bulunur, bu nedenle:

Not: küpteki tanjantın integralinin nasıl alındığına dikkat edin, burada ana trigonometrik kimliğin bir sonucu kullanılır

Belirli bir integralin geometrik anlamının analizine ayrılan önceki bölümde, eğrisel bir yamuğun alanını hesaplamak için bir dizi formül elde ettik:

Yandex.RTB R-A-339285-1

S (G) = ∫ a b f (x) d x sürekli ve negatif olmayan bir fonksiyon için y = f (x) [a; B],

S (G) = - ∫ a b f (x) d x sürekli ve pozitif olmayan bir fonksiyon için y = f (x) [a; B].

Bu formüller nispeten basit problemleri çözmek için geçerlidir. Aslında, genellikle daha karmaşık şekillerle çalışmak zorundayız. Bu bağlamda, bu bölümü açık bir biçimde fonksiyonlarla sınırlandırılan şekillerin alanını hesaplamak için algoritmaların analizine ayıracağız, yani. y = f (x) veya x = g (y) olarak.

teorem

y = f 1 (x) ve y = f 2 (x) fonksiyonları [a; b] ve f 1 (x) ≤ f 2 (x), [a; B]. Daha sonra x = a, x = b, y = f 1 (x) ve y = f 2 (x) çizgileriyle sınırlanan G şeklinin alanını hesaplama formülü S (G) = ∫ şeklinde olacaktır. abf 2 (x) - f 1 (x) dx.

Şeklin y = c, y = d, x = g 1 (y) ve x = g 2 (y) çizgileriyle sınırlanan alanı için benzer bir formül geçerli olacaktır: S (G) = ∫ cd ( g 2 (y) - g 1 (y) dy.

Kanıt

Formülün geçerli olacağı üç durumu ele alalım.

İlk durumda, alan toplama özelliği dikkate alındığında, orijinal şekil G ve eğrisel yamuk G 1'in alanlarının toplamı, şekil G 2'nin alanına eşittir. Demek oluyor

Bu nedenle, S (G) = S (G 2) - S (G 1) = ∫ abf 2 (x) dx - ∫ abf 1 (x) dx = ∫ ab (f 2 (x) - f 1 (x)) dx.

Belirli integralin üçüncü özelliğini kullanarak son geçişi yapabiliriz.

İkinci durumda, aşağıdaki eşitlik geçerlidir: S (G) = S (G 2) + S (G 1) = ∫ abf 2 (x) dx + - ∫ abf 1 (x) dx = ∫ ab (f 2 ( x) - f 1 (x)) dx

Grafik gösterimi şöyle görünecektir:

Her iki fonksiyon da pozitif değilse, şunu elde ederiz: S (G) = S (G 2) - S (G 1) = - ∫ abf 2 (x) dx - - ∫ abf 1 (x) dx = ∫ ab (f) 2 (x) - f 1 (x)) dx. Grafik gösterimi şöyle görünecektir:

y = f 1 (x) ve y = f 2 (x)'in O x ekseniyle kesiştiği genel durumu ele alalım.

Kesişme noktaları x i, i = 1, 2, olarak gösterilecektir. ... ... , n - 1. Bu noktalar [a; b] n parçaya x ben - 1; x ben, ben = 1, 2,. ... ... , n, burada α = x 0< x 1 < x 2 < . . . < x n - 1 < x n = b . Фигуру G можно представить объединением фигур G i , i = 1 , 2 , . . . , n . Очевидно, что на своем интервале G i попадает под один из трех рассмотренных ранее случаев, поэтому их площади находятся как S (G i) = ∫ x i - 1 x i (f 2 (x) - f 1 (x)) d x , i = 1 , 2 , . . . , n

Buradan,

S (G) = ∑ ben = 1 n S (G i) = ∑ ben = 1 n ∫ xixif 2 (x) - f 1 (x)) dx = = ∫ x 0 xn (f 2 (x) - f ( x)) dx = ∫ abf 2 (x) - f 1 (x) dx

Belirli integralin beşinci özelliğini kullanarak son geçişi yapabiliriz.

Genel durumu grafik üzerinde gösterelim.

S (G) = ∫ a b f 2 (x) - f 1 (x) d x formülü kanıtlanmış kabul edilebilir.

Şimdi y = f (x) ve x = g (y) çizgileriyle sınırlanan şekillerin alanını hesaplama örneklerinin analizine geçelim.

Örneklerden herhangi birini bir grafik oluşturarak düşünmeye başlayacağız. Görüntü, karmaşık şekilleri daha basit şekillerden oluşan gruplar halinde temsil etmemize izin verecektir. Eğer üzerlerine grafikler ve şekiller çizmek size zorluk çıkarıyorsa, temel atomik fonksiyonlar, fonksiyonların grafiklerinin geometrik dönüşümü ve bir fonksiyonu keşfederken çizim yapma konularını inceleyebilirsiniz.

örnek 1

Parabol y = - x 2 + 6 x - 5 ve düz çizgiler y = - 1 3 x - 1 2, x = 1, x = 4 ile sınırlanan şeklin alanını belirlemek gerekir.

Çözüm

Grafikteki doğruları Kartezyen koordinat sisteminde çizelim.

Segmentte [1; 4] y = - x 2 + 6 x - 5 parabolünün grafiği y = - 1 3 x - 1 2 düz çizgisinin üzerinde bulunur. Bu bağlamda, bir cevap elde etmek için, Newton-Leibniz formülüne göre belirli bir integrali hesaplama yönteminin yanı sıra daha önce elde edilen formülü kullanıyoruz:

S (G) = ∫ 1 4 - x 2 + 6 x - 5 - - 1 3 x - 1 2 dx = = ∫ 1 4 - x 2 + 19 3 x - 9 2 dx = - 1 3 x 3 + 19 6 x 2 - 9 2 x 1 4 = = - 1 3 4 3 + 19 6 4 2 - 9 2 4 - - 1 3 1 3 + 19 6 1 2 - 9 2 1 = = - 64 3 + 152 3 - 18 + 1 3 - 19 6 + 9 2 = 13

Cevap: S (G) = 13

Daha karmaşık bir örneğe bakalım.

Örnek 2

y = x + 2, y = x, x = 7 çizgileriyle sınırlanan şeklin alanını hesaplamak gerekir.

Çözüm

Bu durumda, apsis eksenine paralel sadece bir düz çizgimiz var. Bu x = 7. Bu, ikinci entegrasyon sınırını kendi başımıza bulmamızı gerektirir.

Bir grafik oluşturalım ve üzerine problem ifadesinde verilen çizgileri çizelim.

Grafiği gözümüzün önünde tutarak, integrasyonun alt sınırının, y = x düz çizgisinin grafiğinin ve y = x + 2 yarı parabolünün grafiğinin kesişme noktasının apsisi olacağını kolayca belirleyebiliriz. Apsisi bulmak için eşitlikleri kullanırız:

y = x + 2 О Д З: x ≥ - 2 x 2 = x + 2 2 x 2 - x - 2 = 0 D = (- 1) 2 - 4 · 1 · (- 2) = 9 x 1 = 1 + 9 2 = 2 О О Д З x 2 = 1 - 9 2 = - 1 ∉ О Д З

Kesişme noktasının apsisinin x = 2 olduğu ortaya çıktı.

Çizimdeki genel örnekte, y = x + 2, y = x doğrularının (2; 2) noktasında kesiştiği gerçeğine dikkatinizi çekiyoruz, bu nedenle bu tür ayrıntılı hesaplamalar gereksiz görünebilir. Burada bu kadar ayrıntılı bir çözüm sağladık çünkü daha karmaşık durumlarda çözüm çok açık olmayabilir. Bu, çizgilerin kesişim koordinatlarının her zaman en iyi analitik olarak hesaplandığı anlamına gelir.

[2 aralığında; 7] y = x fonksiyonunun grafiği, y = x + 2 fonksiyonunun grafiğinin üzerinde bulunur. Alanı hesaplamak için formülü uygulayalım:

S (G) = ∫ 2 7 (x - x + 2) dx = x 2 2 - 2 3 (x + 2) 3 2 2 7 = = 7 2 2 - 2 3 (7 + 2) 3 2 - 2 2 2 - 2 3 2 + 2 3 2 = = 49 2 - 18 - 2 + 16 3 = 59 6

Cevap: S (G) = 59 6

Örnek 3

y = 1 x ve y = - x 2 + 4 x - 2 fonksiyonlarının grafikleri ile sınırlandırılan şeklin alanını hesaplamak gerekir.

Çözüm

Grafiğe çizgiler çizelim.

Entegrasyonun sınırlarını tanımlayalım. Bunu yapmak için, 1 x ve - x 2 + 4 x - 2 ifadelerini eşitleyerek çizgilerin kesişme noktalarının koordinatlarını belirleriz. x'in sıfır olmaması koşuluyla, 1 x = - x 2 + 4 x - 2 eşitliği, üçüncü derece - x 3 + 4 x 2 - 2 x - 1 = 0 denklemine tamsayı katsayılarıyla eşdeğer olur. "Kübik denklemleri çözme" bölümüne bakarak bu tür denklemleri çözmek için algoritma hafızanızı tazeleyebilirsiniz.

Bu denklemin kökü x = 1: - 1 3 + 4 · 1 2 - 2 · 1 - 1 = 0'dır.

- x 3 + 4 x 2 - 2 x - 1 ifadesini x - 1 binomuna bölerek şunu elde ederiz: - x 3 + 4 x 2 - 2 x - 1 ⇔ - (x - 1) (x 2 - 3 x - 1) = 0

Kalan kökleri x 2 - 3 x - 1 = 0 denkleminden bulabiliriz:

x 2 - 3 x - 1 = 0 D = (- 3) 2 - 4 1 (- 1) = 13 x 1 = 3 + 13 2 ≈ 3. 3; x 2 = 3 - 13 2 ≈ - 0. 3

x ∈ 1 aralığını bulduk; 3 + 13 2, burada G rakamı mavinin üstüne ve kırmızı çizginin altına alınır. Bu, şeklin alanını belirlememize yardımcı olur:

S (G) = ∫ 1 3 + 13 2 - x 2 + 4 x - 2 - 1 xdx = - x 3 3 + 2 x 2 - 2 x - ln x 1 3 + 13 2 = = - 3 + 13 2 3 3 + 2 3 + 13 2 2 - 2 3 + 13 2 - ln 3 + 13 2 - - - 1 3 3 + 2 1 2 - 2 1 - ln 1 = 7 + 13 3 - ln 3 + 13 2

Cevap: S (G) = 7 + 13 3 - ln 3 + 13 2

Örnek 4

y = x 3, y = - log 2 x + 1 eğrileri ve apsis ekseni ile sınırlanan şeklin alanını hesaplamak gerekir.

Çözüm

Tüm çizgileri grafiğe koyalım. y = log 2 x + 1 fonksiyonunun grafiğini apsis ekseni etrafında simetrik olarak düzenlersek ve bir birim yukarı kaldırırsak, y = log 2 x grafiğinden alabiliriz. Apsis ekseninin denklemi y = 0'dır.

Doğruların kesişme noktalarını işaretleyelim.

Şekilden de görüleceği gibi, y = x 3 ve y = 0 fonksiyonlarının grafikleri (0; 0) noktasında kesişmektedir. Bunun nedeni, x = 0, x 3 = 0 denkleminin tek gerçek köküdür.

x = 2 denkleminin tek köküdür - log 2 x + 1 = 0, bu nedenle y = - log 2 x + 1 ve y = 0 fonksiyonlarının grafikleri (2; 0) noktasında kesişir.

x = 1, x 3 = - log 2 x + 1 denkleminin tek köküdür. Bu bağlamda, y = x 3 ve y = - log 2 x + 1 fonksiyonlarının grafikleri (1; 1) noktasında kesişir. Son ifade açık olmayabilir, ancak x 3 = - log 2 x + 1 denkleminin birden fazla kökü olamaz, çünkü y = x 3 işlevi kesinlikle artıyor ve y = - log 2 x + 1 işlevi kesin olarak azalmaktadır.

Diğer çözüm, birkaç seçeneği varsayar.

Seçenek numarası 1

G şeklini, ilki x ∈ 0 segmentinde orta çizginin altında bulunan, apsis ekseninin üzerinde bulunan iki eğrisel yamuk toplamı olarak temsil edebiliriz; 1 ve ikincisi x ∈ 1 segmentindeki kırmızı çizginin altındadır; 2. Bu, alanın S (G) = ∫ 0 1 x 3 d x + ∫ 1 2 (- log 2 x + 1) d x olacağı anlamına gelir.

Seçenek numarası 2

G şekli, birincisi apsis ekseninin üzerinde ve x ∈ 0 segmentindeki mavi çizginin altında bulunan iki şeklin farkı olarak temsil edilebilir; 2 ve ikincisi x ∈ 1 segmentindeki kırmızı ve mavi çizgiler arasındadır; 2. Bu, alanı aşağıdaki gibi bulmamızı sağlar:

S (G) = ∫ 0 2 x 3 d x - ∫ 1 2 x 3 - (- log 2 x + 1) d x

Bu durumda, alanı bulmak için S (G) = ∫ c d (g 2 (y) - g 1 (y)) d y biçiminde bir formül kullanmanız gerekecektir. Aslında, şekli sınırlayan çizgiler, y argümanının fonksiyonları olarak gösterilebilir.

y = x 3 denklemlerini çözün ve - x için 2 x + 1'i loglayın:

y = x 3 ⇒ x = y 3 y = - log 2 x + 1 ⇒ log 2 x = 1 - y ⇒ x = 2 1 - y

Gerekli alanı alıyoruz:

S (G) = ∫ 0 1 (2 1 - y - y 3) dy = - 2 1 - y ln 2 - y 4 4 0 1 = = - 2 1 - 1 ln 2 - 1 4 4 - - 2 1 - 0 ln 2 - 0 4 4 = - 1 ln 2 - 1 4 + 2 ln 2 = 1 ln 2 - 1 4

Cevap: S (G) = 1 ln 2 - 1 4

Örnek 5

y = x, y = 2 3 x - 3, y = - 1 2 x + 4 çizgileriyle sınırlanan şeklin alanını hesaplamak gerekir.

Çözüm

Kırmızı çizgi ile y = x fonksiyonu tarafından belirtilen çizgiyi grafik üzerine çizin. y = - 1 2 x + 4 çizgisini mavi çizin ve y = 2 3 x - 3 çizgisini siyah çizin.

Kesişme noktalarını işaretleyelim.

y = x ve y = - 1 2 x + 4 fonksiyonlarının grafiklerinin kesişim noktalarını bulun:

x = - 1 2 x + 4 О Д З: x ≥ 0 x = - 1 2 x + 4 2 ⇒ x = 1 4 x 2 - 4 x + 16 ⇔ x 2 - 20 x + 64 = 0 D = (- 20) 2 - 4 1 64 = 144 x 1 = 20 + 144 2 = 16; x 2 = 20 - 144 2 = 4 Kontrol edin: x 1 = 16 = 4, - 1 2 x 1 + 4 = - 1 2 16 + 4 = - 4 ⇒ x 1 = 16 bir çözümüm yok x 2 = 4 = 2, - 1 2 x 2 + 4 = - 1 2 4 + 4 = 2 ⇒ x 2 = 4 I e t e r t e s ⇒ (4; 2) kesişme noktası i y = x ve y = - 1 2 x + 4

y = x ve y = 2 3 x - 3 fonksiyonlarının grafiklerinin kesişim noktasını bulun:

x = 2 3 x - 3 О Д З: x ≥ 0 x = 2 3 x - 3 2 ⇔ x = 4 9 x 2 - 4 x + 9 ⇔ 4 x 2 - 45 x + 81 = 0 D = (- 45 ) 2 - 4 4 81 = 729 x 1 = 45 + 729 8 = 9, x 2 45 - 729 8 = 9 4 Kontrol edin: x 1 = 9 = 3, 2 3 x 1 - 3 = 2 3 9 - 3 = 3 ⇒ x 1 = 9 Bir çözümüm var ⇒ (9; 3) nokta kesişimi y = x ve y = 2 3 x - 3 x 2 = 9 4 = 3 2, 2 3 x 1 - 3 = 2 3 9 4 - 3 = - 3 2 ⇒ x 2 = 9 4 çözümü yok

y = - 1 2 x + 4 ve y = 2 3 x - 3 doğrularının kesişimini bulun:

1 2 x + 4 = 2 3 x - 3 ⇔ - 3 x + 24 = 4 x - 18 ⇔ 7 x = 42 ⇔ x = 6 - 1 2 6 + 4 = 2 3 6 - 3 = 1 ⇒ (6 ; 1 ) kesişim noktası y = - 1 2 x + 4 ve y = 2 3 x - 3

Yöntem numarası 1

Gerekli şeklin alanını, bireysel şekillerin alanlarının toplamı olarak hayal edelim.

O zaman şeklin alanı şuna eşittir:

S (G) = ∫ 4 6 x - - 1 2 x + 4 dx + ∫ 6 9 x - 2 3 x - 3 dx = = 2 3 x 3 2 + x 2 4 - 4 x 4 6 + 2 3 x 3 2 - x 2 3 + 3 x 6 9 = = 2 3 6 3 2 + 6 2 4 - 4 6 - 2 3 4 3 2 + 4 2 4 - 4 4 + + 2 3 9 3 2 - 9 2 3 + 3 9 - 2 3 6 3 2 - 6 2 3 + 3 6 = = - 25 3 + 4 6 + - 4 6 + 12 = 11 3

Yöntem numarası 2

Orijinal şeklin alanı, diğer iki şeklin toplamı olarak düşünülebilir.

Sonra doğrunun denklemini x'e göre çözeceğiz ve ancak bundan sonra şeklin alanını hesaplamak için formülü uygulayacağız.

y = x ⇒ x = y 2 kırmızı çizgi y = 2 3 x - 3 ⇒ x = 3 2 y + 9 2 siyah çizgi y = - 1 2 x + 4 ⇒ x = - 2 y + 8

Böylece, alan şuna eşittir:

S (G) = ∫ 1 2 3 2 y + 9 2 - - 2 y + 8 dy + ∫ 2 3 3 2 y + 9 2 - y 2 dy = = ∫ 1 2 7 2 y - 7 2 dy + ∫ 2 3 3 2 y + 9 2 - y 2 dy = = 7 4 y 2 - 7 4 y 1 2 + - y 3 3 + 3 y 2 4 + 9 2 y 2 3 = 7 4 2 2 - 7 4 2 - 7 4 1 2 - 7 4 1 + + - 3 3 3 + 3 3 2 4 + 9 2 3 - - 2 3 3 + 3 2 2 4 + 9 2 2 = = 7 4 + 23 12 = 11 3

Gördüğünüz gibi değerler aynı.

Cevap: S (G) = 11 3

sonuçlar

Verilen çizgilerle sınırlı bir şeklin alanını bulmak için, bir düzlemde çizgiler oluşturmamız, kesişme noktalarını bulmamız, alanı bulmak için formülü uygulamamız gerekir. Bu bölümde, en yaygın görev seçeneklerini inceledik.

Metinde bir hata fark ederseniz, lütfen seçin ve Ctrl + Enter tuşlarına basın

Öyleyse, integralleri kullanarak bir şeklin alanını bulma problemini başarılı bir şekilde çözmek için gerekenler:

Çizimleri yetkin bir şekilde oluşturma yeteneği;
İyi bilinen Newton-Leibniz formülünü kullanarak belirli bir integrali çözebilme;
Daha avantajlı bir çözümü “görme” yeteneği - yani, Bu veya bu durumda entegrasyonu gerçekleştirmenin nasıl daha uygun olacağını anlamak için? x ekseni (OX) veya y ekseni (OY) boyunca mı?
Peki, doğru hesaplamalar olmadan nerede?) Bu, diğer türdeki integrallerin nasıl çözüleceğini ve sayısal hesaplamaları doğru yapmayı içerir.

Çizgilerle sınırlanmış bir şeklin alanını hesaplama problemini çözmek için algoritma:

örnek 1 y = x2 - 3x + 3, x = 1, x = 3, y = 0.

Örnek 2 ... Çizgilerle sınırlanmış bir şeklin alanını hesaplayın y = x2 + 6x + 2, x = -4, x = -1, y = 0.

Makale eksik.

Aslında, bir şeklin alanını bulmak için, belirsiz ve belirli integral hakkında çok fazla bilgiye ihtiyaç duymaz. "Belirli bir integral kullanarak alanı hesaplama" görevi her zaman bir çizim oluşturmayı içerir. bu nedenle bilginiz ve çizim becerileriniz çok daha acil bir konu olacaktır. Bu bağlamda, temel temel fonksiyonların grafiklerinin hafızasını yenilemek ve en azından bir düz çizgi ve bir hiperbol oluşturabilmek faydalıdır.

Eğrisel bir yamuk, bir eksen, düz çizgiler ve bu aralıkta işaretini değiştirmeyen bir segment üzerindeki sürekli bir fonksiyonun grafiği ile sınırlanan düz bir şekildir. Bu rakamın bulunmasına izin verin Az değil apsis ekseni:

Sonra eğri bir yamuğun alanı sayısal olarak belirli integrale eşittir... Herhangi bir belirli integralin (var olan) çok iyi bir geometrik anlamı vardır.

Geometri açısından, belirli integral ALAN'dır..

Yani, belirli bir integral (varsa) geometrik olarak bir şeklin alanına karşılık gelir. Örneğin, belirli bir integrali düşünün. İntegrant, eksenin üzerinde bulunan düzlemde bir eğri ayarlar (isteyenler çizim yapabilir) ve belirli integralin kendisi sayısal olarak karşılık gelen eğrisel yamuğun alanına eşittir.

örnek 1

Bu, ödevin tipik bir formülasyonudur. Çözümün ilk ve en önemli noktası çizimin yapımıdır.... Ayrıca, çizim inşa edilmelidir SAĞ.

Bu problemde, çözüm şöyle görünebilir.
Bir çizim çizelim (denklemin ekseni tanımladığını unutmayın):

Segmentte, fonksiyonun grafiği bulunur eksenin üstünde, Öyleyse:

Cevap:

Görev tamamlandıktan sonra, plana bakmak ve cevabın gerçek olup olmadığını tahmin etmek her zaman yararlıdır. Bu durumda, "gözle" çizimdeki hücre sayısını sayıyoruz - peki, yaklaşık 9 yazılacak, gerçek gibi görünüyor. 20 birim kare, o zaman, açıkçası, bir yerde bir hata yapılmış - söz konusu rakam açıkça 20 hücreye uymuyor, en fazla on. Cevap olumsuzsa, görev de yanlış çözüldü.

Örnek 3

Çizgilerle sınırlanmış bir şeklin alanını hesaplayın ve eksenleri koordine edin.

Çözüm: Çizimi uygulayalım:

Kavisli yamuk bulunursa eksenin altında(ya da en azından daha yüksek değil verilen eksen), daha sonra alanı aşağıdaki formülle bulunabilir:

Bu durumda:

Dikkat! İki tür görev karıştırılmamalıdır:

1) Herhangi bir geometrik anlamı olmayan belirli bir integrali çözmeniz istenirse, negatif olabilir.

2) Belirli bir integral kullanarak bir şeklin alanını bulmanız istenirse, alan her zaman pozitiftir! Bu nedenle, az önce ele alınan formülde bir eksi belirir.

Uygulamada, çoğu zaman şekil hem üst hem de alt yarı düzlemlerde bulunur ve bu nedenle en basit okul problemlerinden daha anlamlı örneklere geçilir.

Örnek 4

Çizgilerle sınırlanmış düz bir şeklin alanını bulun.

Çözüm: İlk önce çizimi tamamlamanız gerekiyor. Genel olarak konuşursak, bir alan üzerindeki problemlerde çizim oluştururken, en çok çizgilerin kesişme noktalarıyla ilgileniriz. Parabol ve doğrunun kesişim noktalarını bulun. Bu iki şekilde yapılabilir. Birinci yol analitiktir. Denklemi çözüyoruz:

Dolayısıyla, entegrasyonun alt sınırı, entegrasyonun üst sınırı.

Mümkünse bu yöntemi kullanmamak daha iyidir..

Entegrasyonun sınırları adeta "kendi kendine" netleşirken, çizgileri nokta nokta oluşturmak çok daha karlı ve daha hızlıdır. Bununla birlikte, örneğin grafik yeterince büyükse veya kesin yapı entegrasyonun sınırlarını ortaya çıkarmıyorsa (bunlar kesirli veya irrasyonel olabilir) bazen sınırları bulma analitik yönteminin kullanılması gerekir. Ve biz de böyle bir örnek ele alacağız.

Sorunumuza dönüyoruz: önce düz bir çizgi ve ancak o zaman bir parabol oluşturmak daha mantıklı. Çizimi uygulayalım:

Ve şimdi çalışma formülü: Bir segmentte sürekli bir fonksiyon varsa büyük veya eşit bazı sürekli fonksiyonlardan sonra, bu fonksiyonların ve düz çizgilerin grafikleriyle sınırlanan şeklin alanı aşağıdaki formülle bulunabilir:

Burada artık şeklin nerede olduğunu düşünmenize gerek yok - eksenin üstünde veya eksenin altında ve kabaca konuşursak, hangi programın YUKARIDA olduğu önemlidir(başka bir grafiğe göre), ve hangisi AŞAĞIDA.

İncelenen örnekte, segmentte parabolün düz çizginin üzerinde yer aldığı açıktır ve bu nedenle,

Çözümün tamamlanması şöyle görünebilir:

Gerekli şekil, üstte bir parabol ve altta düz bir çizgi ile sınırlandırılmıştır.
Segmentte, ilgili formüle göre:

Cevap:

Örnek 4

Çizgilerle sınırlanan şeklin alanını hesaplayın,,,.

Çözüm: Önce çizimi yapalım:

Alanı bulmamız gereken şekil mavi gölgeli(duruma dikkatlice bakın - rakam neyle sınırlıdır!). Ancak uygulamada, dikkatsizlik nedeniyle, genellikle yeşil gölgeli şeklin alanını bulmanız gereken bir "aksaklık" ortaya çıkar!

Bu örnek, iki belirli integral kullanarak bir şeklin alanını hesaplaması açısından da yararlıdır.

Yok canım:

1) Eksenin üzerindeki segmentte bir çizgi grafiği bulunur;

2) Hiperbol grafiği, eksenin üzerindeki doğru parçası üzerinde bulunur.

Alanların eklenebileceği (ve eklenmesi gerektiği) oldukça açıktır, bu nedenle: