Równanie styczne ma postać. Równanie stycznej do wykresu funkcji - Hipermarket wiedzy

Typ pracy: 7

Stan: schorzenie

Prosta y = 3x + 2 jest styczna do wykresu funkcji y = -12x ^ 2 + bx-10. Znajdź b, zakładając, że odcięta punktu styku jest mniejsza od zera.

Rozwiązanie

Niech x_0 będzie odciętą punktu na wykresie funkcji y = -12x ^ 2 + bx-10, przez którą przechodzi styczna do tego wykresu.

Wartość pochodnej w punkcie x_0 jest równa nachyleniu stycznej, czyli y "(x_0) = - 24x_0 + b = 3. Z drugiej strony punkt stycznej należy zarówno do wykresu funkcji a tangens, czyli -12x_0 ^ 2 + bx_0-10 = 3x_0 + 2. Otrzymujemy układ równań \ początek (przypadki) -24x_0 + b = 3, \\ - 12x_0 ^ 2 + bx_0-10 = 3x_0 + 2. \ koniec (przypadki)

Rozwiązując ten układ, otrzymujemy x_0 ^ 2 = 1, co oznacza albo x_0 = -1, albo x_0 = 1. Zgodnie z warunkiem odcięta punktu dotykowego jest mniejsza od zera, a więc x_0 = -1, a następnie b = 3 + 24x_0 = -21.

Odpowiedź

Typ pracy: 7
Temat: Geometryczne znaczenie pochodnej. Wykres funkcji tangens

Stan: schorzenie

Prosta y = -3x + 4 jest równoległa do stycznej do wykresu funkcji y = -x ^ 2 + 5x-7. Znajdź odciętą punktu kontaktu.

Rozwiązanie

Nachylenie prostej do wykresu funkcji y = -x ^ 2 + 5x-7 w dowolnym punkcie x_0 jest równe y "(x_0). Ale y" = - 2x + 5, więc y "(x_0 ) = - 2x_0 + 5. Kątowy współczynnik prostej y = -3x + 4 określony w warunku jest równy -3. Linie równoległe mają to samo nachylenie. Dlatego znajdujemy wartość x_0 taką, że = -2x_0 + 5 = -3.

Otrzymujemy: x_0 = 4.

Odpowiedź

Źródło: „Matematyka. Przygotowanie do egzaminu-2017. Poziom profilu ”. Wyd. FF Łysenko, SJ Kulabuchowa.

Typ pracy: 7
Temat: Geometryczne znaczenie pochodnej. Wykres funkcji tangens

Stan: schorzenie

Rozwiązanie

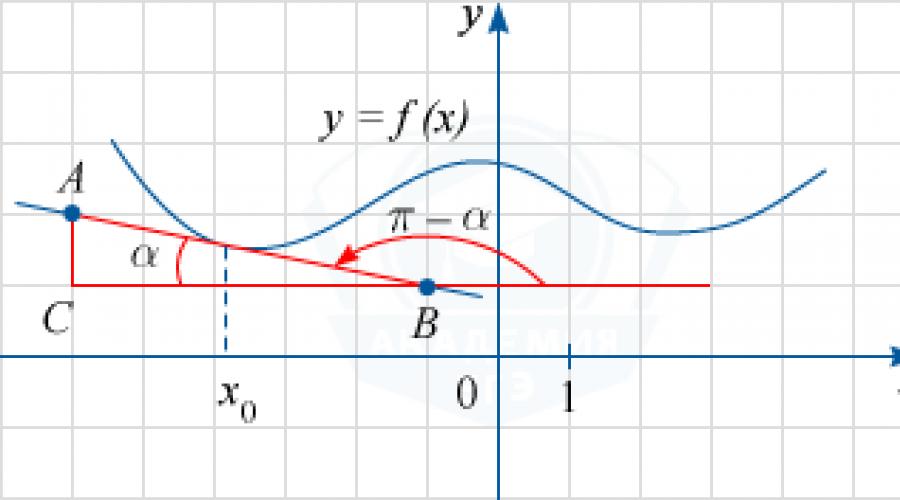
Z rysunku określamy, że styczna przechodzi przez punkty A (-6; 2) i B (-1; 1). Przez C (-6; 1) oznaczamy punkt przecięcia prostych x = -6 i y = 1, a przez \ alpha kąt ABC (na rysunku widać, że jest ostry). Wtedy linia AB tworzy kąt rozwarty \ pi - \ alpha z dodatnim kierunkiem osi Ox.

Jak wiadomo, tg (\ pi - \ alpha) będzie wartością pochodnej funkcji f (x) w punkcie x_0. Zauważ, że tg \ alpha = \ frac (AC) (CB) = \ frac (2-1) (- 1 - (- 6)) = \ frac15. Stąd, korzystając ze wzorów redukcyjnych, otrzymujemy: tg (\ pi - \ alpha) = -tg \ alpha = - \ frac15 = -0,2.

Odpowiedź

Źródło: „Matematyka. Przygotowanie do egzaminu-2017. Poziom profilu ”. Wyd. FF Łysenko, SJ Kulabuchowa.

Typ pracy: 7
Temat: Geometryczne znaczenie pochodnej. Wykres funkcji tangens

Stan: schorzenie

Linia y = -2x-4 jest styczna do wykresu funkcji y = 16x ^ 2 + bx + 12. Znajdź b, zakładając, że odcięta punktu styku jest większa od zera.

Rozwiązanie

Niech x_0 będzie odciętą punktu na wykresie funkcji y = 16x ^ 2 + bx + 12, przez którą

jest styczną do tego wykresu.

Wartość pochodnej w punkcie x_0 jest równa nachyleniu stycznej, czyli y "(x_0) = 32x_0 + b = -2. Z drugiej strony punkt stycznej należy zarówno do wykresu funkcji i tangens, czyli 16x_0 ^ 2 + bx_0 + 12 = - 2x_0-4 Otrzymujemy układ równań \ początek (przypadki) 32x_0 + b = -2, \\ 16x_0 ^ 2 + bx_0 + 12 = -2x_0-4. \ koniec (przypadki)

Rozwiązując system, otrzymujemy x_0 ^ 2 = 1, co oznacza albo x_0 = -1, albo x_0 = 1. Zgodnie z warunkiem odcięta punktu styku jest większa od zera, więc x_0 = 1, a następnie b = -2-32x_0 = -34.

Odpowiedź

Źródło: „Matematyka. Przygotowanie do egzaminu-2017. Poziom profilu ”. Wyd. FF Łysenko, SJ Kulabuchowa.

Typ pracy: 7
Temat: Geometryczne znaczenie pochodnej. Wykres funkcji tangens

Stan: schorzenie

Rysunek przedstawia wykres funkcji y = f (x), zdefiniowanej na przedziale (-2; 8). Określ liczbę punktów, w których styczna do wykresu funkcji jest równoległa do prostej y = 6.

Rozwiązanie

Linia y = 6 jest równoległa do osi Wół. Dlatego znajdujemy punkty, w których styczna do wykresu funkcji jest równoległa do osi Ox. Na tym wykresie takie punkty są punktami ekstremalnymi (punktami maksimum lub minimum). Jak widać, istnieją 4 punkty ekstremum.

Odpowiedź

Źródło: „Matematyka. Przygotowanie do egzaminu-2017. Poziom profilu ”. Wyd. FF Łysenko, SJ Kulabuchowa.

Typ pracy: 7
Temat: Geometryczne znaczenie pochodnej. Wykres funkcji tangens

Stan: schorzenie

Prosta y = 4x-6 jest równoległa do stycznej do wykresu funkcji y = x ^ 2-4x + 9. Znajdź odciętą punktu kontaktu.

Rozwiązanie

Nachylenie stycznej do wykresu funkcji y = x ^ 2-4x + 9 w dowolnym punkcie x_0 jest równe y "(x_0). Ale y" = 2x-4, więc y "(x_0) = 2x_0 -4. Nachylenie stycznej y = 4x-7, określone w warunku, wynosi 4. Proste równoległe mają takie samo nachylenie.W związku z tym znajdujemy wartość x_0 taką, że 2x_0-4 = 4. Otrzymujemy: x_0 = 4 .

Odpowiedź

Źródło: „Matematyka. Przygotowanie do egzaminu-2017. Poziom profilu ”. Wyd. FF Łysenko, SJ Kulabuchowa.

Typ pracy: 7
Temat: Geometryczne znaczenie pochodnej. Wykres funkcji tangens

Stan: schorzenie

Rysunek przedstawia wykres funkcji y = f (x) oraz styczną do niej w punkcie z odciętą x_0. Znajdź wartość pochodnej funkcji f (x) w punkcie x_0.

Rozwiązanie

Z rysunku określamy, że styczna przechodzi przez punkty A (1; 1) i B (5; 4). Przez C (5; 1) oznaczamy punkt przecięcia prostych x = 5 i y = 1, a przez \ alpha kąt BAC (na rysunku widać, że jest ostry). Wtedy prosta AB tworzy kąt \alfa z dodatnim kierunkiem osi Ox.

Lekcja wideo „Równanie stycznej z wykresem funkcji” przedstawia materiał edukacyjny do opanowania tematu. W trakcie lekcji wideo prezentowany jest materiał teoretyczny niezbędny do sformułowania koncepcji równania stycznej do wykresu funkcji w danym punkcie, algorytm znajdowania takiej stycznej, przykłady rozwiązywania problemów z wykorzystaniem badanych opisano materiał teoretyczny.

Samouczek wideo wykorzystuje techniki poprawiające przejrzystość materiału. W prezentacji wstawiane są zdjęcia, diagramy, podawane są ważne komentarze głosowe, stosowana jest animacja, podświetlanie kolorem i inne narzędzia.

Samouczek wideo rozpoczyna się prezentacją tematu lekcji i obrazu stycznej do wykresu jakiejś funkcji y = f (x) w punkcie M (a; f (a)). Wiadomo, że nachylenie linii stycznej narysowanej do wykresu w danym punkcie jest równe pochodnej funkcji f΄ (a) w danym punkcie. Również z przebiegu algebry znane jest równanie prostej y = kx + m. Schematycznie przedstawiono rozwiązanie problemu znalezienia równania stycznej w punkcie, które sprowadza się do znalezienia współczynników k, m. Znając współrzędne punktu należącego do wykresu funkcji, możemy znaleźć m podstawiając wartość współrzędnych do równania stycznego f (a) = ka + m. Z niego znajdujemy m = f (a) -ka. Znając zatem wartość pochodnej w danym punkcie i współrzędne punktu, można przedstawić równanie stycznej w ten sposób y = f (a) + f΄ (a) (x-a).

Poniżej znajduje się przykład sporządzenia równania stycznego zgodnie z diagramem. Funkcja ma y = x 2, x = -2. Przyjmując a = -2, znajdujemy wartość funkcji w tym punkcie f (a) = f (-2) = (- 2) 2 = 4. Wyznacz pochodną funkcji f΄ (x) = 2x. W tym momencie pochodna to f΄ (a) = f΄ (-2) = 2 · (-2) = - 4. Aby skomponować równanie, wszystkie współczynniki są znalezione a = -2, f (a) = 4, f΄ (a) = - 4, stąd równanie stycznej y = 4 + (- 4) (x + 2). Upraszczając równanie, otrzymujemy y = -4-4x.

Poniższy przykład proponuje zapisanie równania stycznej w początku na wykres funkcji y = tgx. W tym momencie a = 0, f (0) = 0, f΄ (x) = 1 / cos 2 x, f΄ (0) = 1. Zatem równanie styczne wygląda tak: y = x.

Uogólniając, proces sporządzania równania stycznej do wykresu funkcji w pewnym momencie jest sformalizowany w postaci algorytmu składającego się z 4 kroków:

• Wprowadzono oznaczenie a odciętej punktu styczności;
• F(a) oblicza się;
• Wyznacza się F(x) i oblicza f΄(a). Znalezione wartości a, f (a), f΄ (a) są podstawiane do wzoru równania stycznego y = f (a) + f΄ (a) (x-a).

Przykład 1 dotyczy sporządzenia równania stycznej do wykresu funkcji y = 1 / x w punkcie x = 1. Aby rozwiązać problem, używamy algorytmu. Dla danej funkcji w punkcie a = 1 wartość funkcji f (a) = - 1. Pochodna funkcji f΄ (x) = 1 / x 2. W punkcie a = 1 pochodna f΄ (a) = f΄ (1) = 1. Z uzyskanych danych sporządza się równanie dla stycznej y = -1 + (x-1) lub y = x-2.

W przykładzie 2 musisz znaleźć równanie stycznej do wykresu funkcji y = x 3 + 3x 2 -2x-2. Głównym warunkiem jest równoległość stycznej i prostej y = -2x + 1. Najpierw znajdujemy nachylenie stycznej równe nachyleniu prostej y = -2x + 1. Ponieważ f΄ (a) = -2 dla danej prostej, to k = -2 dla żądanej stycznej. Znajdź pochodną funkcji (x 3 + 3x 2 -2x-2) ΄ = 3x 2 + 6x-2. Wiedząc, że f΄ (a) = - 2, znajdujemy współrzędne punktu 3a 2 + 6a-2 = -2. Rozwiązując równanie, otrzymujemy 1 = 0 i 2 = -2. Korzystając ze znalezionych współrzędnych, możesz znaleźć równanie styczne za pomocą dobrze znanego algorytmu. Znajdź wartość funkcji w punktach f (a 1) = - 2, f (a 2) = - 18. Wartość pochodnej w punkcie f΄ (a 1) = f΄ (a 2) = - 2. Podstawiając znalezione wartości do równania stycznej, otrzymujemy dla pierwszego punktu a 1 = 0 y = -2x-2, a dla drugiego punktu a 2 = -2 równanie stycznej y = -2x-22.

Przykład 3 opisuje sporządzenie równania prostej stycznej do narysowania jej w punkcie (0; 3) na wykres funkcji y = √x. Rozwiązanie jest wykonane według znanego algorytmu. Punkt styczny ma współrzędne x = a, gdzie a> 0. Wartość funkcji w punkcie f (a) = √x. Pochodna funkcji f΄(x) = 1/2√x, zatem w tym punkcie f΄(a) = 1/2√a. Podstawiając wszystkie otrzymane wartości do równania stycznych, otrzymujemy y = √a + (x-a) / 2√a. Przekształcając równanie, otrzymujemy y = x / 2√a + √a / 2. Wiedząc, że styczna przechodzi przez punkt (0; 3), znajdujemy wartość a. Znajdź a z 3 = √a / 2. Stąd √a = 6, a = 36. Znajdujemy równanie linii stycznej y = x / 12 + 3. Rysunek przedstawia wykres rozważanej funkcji i zbudowaną żądaną linię styczną.

Uczniom przypomina się przybliżone równości Δy = ≈f΄ (x) Δx i f (x + Δx) -f (x) ≈f΄ (x) Δx. Biorąc x = a, x + Δx = x, Δx = x-a, otrzymujemy f (x) - f (a) ≈f΄ (a) (x-a), stąd f (x) ≈f (a) + f΄ ( a) (xa).

W przykładzie 4 konieczne jest znalezienie przybliżonej wartości wyrażenia 2.003 6. Ponieważ konieczne jest znalezienie wartości funkcji f (x) = x 6 w punkcie x = 2,003, możemy skorzystać ze znanego wzoru, przyjmując f (x) = x 6, a = 2, f (a ) = f (2) = 64, f ΄ (x) = 6x 5. Pochodna w punkcie f΄ (2) = 192. Dlatego 2,003 6 ≈65-192 0,003. Obliczając wyrażenie, otrzymujemy 2,003 6 ≈64,576.

Lekcja wideo „Równanie stycznej z wykresem funkcji” jest zalecana do wykorzystania na tradycyjnej lekcji matematyki w szkole. Nauczycielowi e-learningu wideo pomoże lepiej wyjaśnić temat. Nagranie wideo może być polecane do samodzielnej oceny przez uczniów, jeśli to konieczne, aby pogłębić ich zrozumienie tematu.

KOD TEKSTOWY:

Wiemy, że jeśli punkt M (a; f (a)) (em o współrzędnych a i ff z a) należy do wykresu funkcji y = f (x) i jeśli w tym punkcie do wykresu funkcji to jest możliwe narysowanie stycznej, która nie jest prostopadła do osi odciętej, wtedy nachylenie stycznej jest równe f "(a) (eff prim z a).

Załóżmy, że dana jest funkcja y = f (x) i punkt M (a; f (a)), a wiadomo również, że istnieje f´ (a). Skomponujmy równanie stycznej do wykresu danej funkcji w danym punkcie. Równanie to, podobnie jak równanie dowolnej prostej nierównoległej do osi rzędnych, ma postać y = kx + m (gra równa się ka x plus em), więc zadaniem jest znalezienie wartości współczynników k i m. (Ka i em)

Nachylenie k = f "(a). Do obliczenia wartości m używamy faktu, że pożądana linia prosta przechodzi przez punkt M (a; f (a)). Oznacza to, że jeśli podstawimy współrzędne punktu M do równania prostej otrzymujemy poprawną równość : f (a) = ka + m, skąd stwierdzamy, że m = f (a) - ka.

Pozostaje zamienić znalezione wartości współczynników k i m do równania linii prostej:

y = kx + (f(a)-ka);

y = f(a) + k(x-a);

tak= F(a)+ F"(a) (x- a). ( wartość jest równa eff z plus eff uderzeniu z a pomnożone przez x minus a).

Otrzymaliśmy równanie stycznej do wykresu funkcji y = f (x) w punkcie x = a.

Jeśli powiedzmy, y = x 2 i x = -2 (czyli a = -2), to f (a) = f (-2) = (-2) 2 = 4; f´ (x) = 2x, więc f "(a) = f´ (-2) = 2 · (-2) = -4. ef skok z a jest równy minus cztery)

Podstawiając znalezione wartości a = -2, f (a) = 4, f "(a) = -4 do równania, otrzymujemy: y = 4 + (- 4) (x + 2), tj. y = -4x -4.

(y równa się minus cztery x minus cztery)

Skomponujmy równanie stycznej z wykresem funkcji y = tgx (y jest równe stycznej x) w punkcie początkowym. Mamy: a = 0, f (0) = tg0 = 0;

f "(x) =, więc f" (0) = l. Zastępując znalezione wartości a = 0, f (a) = 0, f´ (a) = 1 do równania, otrzymujemy: y = x.

Uogólnijmy nasze kroki w celu znalezienia równania stycznej do wykresu funkcji w punkcie x za pomocą algorytmu.

ALGORYTM DO UKŁADANIA RÓWNANIA TANGENIALNEJ DO FUNKCJI WYKRESU y = f (x):

1) Oznacz odcięty punkt styczności z literą a.

2) Oblicz f (a).

3) Znajdź f´ (x) i oblicz f´ (a).

4) Podstaw znalezione liczby a, f (a), f´ (a) do wzoru tak= F(a)+ F"(a) (x- a).

Przykład 1. Narysuj równanie stycznej do wykresu funkcji y = - in

punkt x = 1.

Rozwiązanie. Użyjemy algorytmu, biorąc pod uwagę, że w tym przykładzie

2) f (a) = f (1) = - = -1

3) f´(x) =; f´ (a) = f´ (1) = = 1.

4) Podstaw znalezione trzy liczby: a = 1, f (a) = -1, f "(a) = 1 we wzorze. Otrzymujemy: y = -1+ (x-1), y = x-2 .

Odpowiedź: y = x-2.

Przykład 2. Dana funkcja y = x 3 + 3x 2 -2x-2... Napisz równanie stycznej do wykresu funkcji y = f (x), równolegle do prostej y = -2x +1.

Korzystając z algorytmu do zbudowania równania stycznego, bierzemy pod uwagę, że w tym przykładzie f (x) = x 3 + 3x 2 -2x-2, ale odcięta punktu stycznego nie jest tutaj wskazana.

Zacznijmy myśleć w ten sposób. Żądana styczna musi być równoległa do prostej y = -2x + 1. A linie równoległe mają równe nachylenia. Oznacza to, że nachylenie stycznej jest równe nachyleniu danej prostej: k cas. = -2. Hok ca. = f "(a). Zatem możemy znaleźć wartość a z równania f ´ (a) = -2.

Znajdź pochodną funkcji y =F(x):

F"(x) = (x 3 + 3x 2 -2x-2) ´ = 3x 2 + 6x-2;F„(a) = 3a 2 + 6a-2.

Z równania f "(a) = -2, tj. 3a 2 + 6a-2= -2 znajdujemy a 1 = 0, a 2 = -2. Zatem istnieją dwie styczne, które spełniają warunek problemu: jedna w punkcie z odciętą 0, druga w punkcie z odciętą -2.

Teraz możesz śledzić algorytm.

1) a 1 = 0 i 2 = -2.

2) f (a 1) = 0 3 + 3 0 2 -2 ∙ 0-2 = -2; f (a 2) = (-2) 3 + 3 (-2) 2 -2 (-2) -2 = 6;

3) f "(a 1) = f" (a 2) = -2.

4) Zastępując wartości a 1 = 0, f (a 1) = -2, f ”(a 1) = -2 we wzorze otrzymujemy:

y = -2-2 (x-0), y = -2x-2.

Zastępując wartości a 2 = -2, f (a 2) = 6, f ”(a 2) = -2 we wzorze otrzymujemy:

y = 6-2 (x + 2), y = -2x + 2.

Odpowiedź: y = -2x-2, y = -2x + 2.

Przykład 3. Z punktu (0; 3) narysuj styczną do wykresu funkcji y =. Rozwiązanie. Wykorzystajmy algorytm do zbudowania równania stycznego, biorąc pod uwagę, że w tym przykładzie f (x) =. Zauważ, że tutaj, tak jak w przykładzie 2, odcięta punktu styczności nie jest wyraźnie wskazana. Niemniej jednak działamy zgodnie z algorytmem.

1) Niech x = a będzie odciętą punktu styczności; jasne jest, że a>0.

3) f´ (x) = () ´ =; f´(a) =.

4) Podstawiając wartości a, f (a) =, f "(a) = do wzoru

y = f (a) + f "(a) (x-a), otrzymujemy:

Z założenia styczna przechodzi przez punkt (0; 3). Podstawiając do równania wartości x = 0, y = 3, otrzymujemy: 3 =, a dalej = 6, a = 36.

Jak widać, w tym przykładzie dopiero w czwartym kroku algorytmu udało nam się znaleźć odciętą punktu styczności. Podstawiając do równania wartość a = 36, otrzymujemy: y = + 3

Na ryc. 1 pokazuje geometryczną ilustrację rozważanego przykładu: wykreślany jest wykres funkcji y =, rysowana jest linia prosta y = +3.

Odpowiedź: y = +3.

Wiemy, że dla funkcji y = f (x), która ma pochodną w punkcie x, obowiązuje przybliżona równość: Δyf´ (x) Δx (delta y jest w przybliżeniu równa eff liczbie pierwszej x pomnożonej przez delta x)

lub, bardziej szczegółowo, f (x + Δx) -f (x) f´ (x) Δx (eff od x plus delta x minus eff od x jest w przybliżeniu równe eff od x do delta x).

Dla wygody dalszego rozumowania zmieniamy notację:

zamiast x napiszemy a,

zamiast x + Δx piszemy x

zamiast Δx napiszemy x-a.

Wtedy przybliżona równość zapisana powyżej przybierze postać:

f (x) -f (a) f´ (a) (x-a)

f (x) f (a) + f' (a) (x-a). (ff z x jest w przybliżeniu równe ff z plus ef prim od a, pomnożonej przez różnicę między x i a).

Przykład 4. Znajdź przybliżoną wartość wyrażenia liczbowego 2.003 6.

Rozwiązanie. Mówimy o znalezieniu wartości funkcji y = x 6 w punkcie x = 2,003. Użyjmy wzoru f (x) f (a) + f´ (a) (xa), biorąc pod uwagę, że w tym przykładzie f (x) = x 6, a = 2, f (a) = f (2) = 2 6 = 64; x = 2,003, f „(x) = 6x 5, a zatem f” (a) = f „(2) = 6 · 2 5 = 192.

W rezultacie otrzymujemy:

2,003 6 64 + 192 0,003, tj. 2,003 6 = 64,576.

Jeśli użyjemy kalkulatora, otrzymamy:

2,003 6 = 64,5781643...

Jak widać, dokładność aproksymacji jest całkiem akceptowalna.

Rozważmy następujący rysunek:

Przedstawia pewną funkcję y = f (x), która jest różniczkowalna w punkcie a. Zaznaczono punkt M współrzędnymi (a; f (a)). Sieczna MR jest rysowana przez dowolny punkt P (a + ∆x; f (a + ∆x)) wykresu.

Jeśli teraz punkt P zostanie przesunięty zgodnie z wykresem do punktu M, to prosta MR obróci się wokół punktu M. W tym przypadku ∆x będzie dążył do zera. Stąd możemy sformułować definicję stycznej do wykresu funkcji.

Wykres funkcji tangens

Styczna do wykresu funkcji to graniczna pozycja siecznej, gdy przyrost argumentu dąży do zera. Należy rozumieć, że istnienie pochodnej funkcji f w punkcie x0 oznacza, że ​​w tym punkcie grafu istnieje tangens do niego.

W tym przypadku nachylenie stycznej będzie równe pochodnej tej funkcji w tym punkcie f '(x0). To jest geometryczne znaczenie pochodnej. Styczna do wykresu funkcji f różniczkowalnej w punkcie x0 jest linią prostą przechodzącą przez punkt (x0; f (x0)) i mającą nachylenie f'(x0).

Równanie styczne

Spróbujmy uzyskać równanie stycznej do wykresu jakiejś funkcji f w punkcie A (x0; f (x0)). Równanie prostej o nachyleniu k wygląda następująco:

Ponieważ nasze nachylenie jest równe pochodnej f '(x0), to równanie przyjmuje postać: y = f '(x0)* x + b.

Teraz obliczmy wartość b. Aby to zrobić, wykorzystujemy fakt, że funkcja przechodzi przez punkt A.

f (x0) = f ’(x0) * x0 + b, stąd wyrażamy b i otrzymujemy b = f (x0) - f’ (x0) * x0.

Podstaw otrzymaną wartość do równania stycznego:

y = f ’(x0) * x + b = f’ (x0) * x + f (x0) - f ’(x0) * x0 = f (x0) + f’ (x0) * (x - x0).

y = f (x0) + f ’(x0) * (x - x0).

Rozważmy następujący przykład: znajdź równanie stycznej do wykresu funkcji f (x) = x 3 - 2 * x 2 + 1 w punkcie x = 2.

2.f (x0) = f (2) = 2 2 - 2 * 2 2 + 1 = 1.

3.f '(x) = 3 * x 2 - 4 * x.

4.f '(x0) = f' (2) = 3 * 2 2 - 4 * 2 = 4.

5. Zastąp otrzymane wartości we wzorze stycznej, otrzymujemy: y = 1 + 4 * (x - 2). Rozwijając nawiasy i podając podobne wyrażenia, otrzymujemy: y = 4 * x - 7.

Odpowiedź: y = 4 * x - 7.

Ogólny schemat sporządzenia równania stycznego do wykresu funkcji y = f (x):

1. Określ x0.

2. Oblicz f (x0).

3. Oblicz f '(x)

Tangens Jest linią prostą przechodzącą przez punkt na krzywej i pokrywającą się z nim w tym punkcie aż do pierwszego rzędu (rys. 1).

Inna definicja: jest to graniczna pozycja siecznej przy Δ x→0.

Wyjaśnienie: Weź linię prostą, która przecina krzywą w dwóch punktach: A oraz b(patrz rysunek). To jest sieczna. Obrócimy go zgodnie z ruchem wskazówek zegara, aż znajdzie tylko jeden wspólny punkt z krzywą. To da nam linię styczną.

Ścisła definicja stycznej:

Wykres funkcji tangens F różniczkowalna w punkcie xO, jest linią prostą przechodzącą przez punkt ( xO; F(xO)) i mając nachylenie F′( xO).

Zbocze ma prostą linię formy y =kx +b... Współczynnik k i jest nachylenie ta prosta linia.

Nachylenie jest równe stycznej kąta ostrego utworzonego przez tę linię prostą do osi odciętej:

Tutaj kąt α jest kątem między linią prostą y =kx +b i dodatni (tj. przeciwny do ruchu wskazówek zegara) kierunek odciętej. Nazywa się to kąt nachylenia linii prostej(rys. 1 i 2).

Jeśli kąt nachylenia jest prosty y =kx +b ostre, wtedy nachylenie jest liczbą dodatnią. Wykres rośnie (rys. 1).

Jeśli kąt nachylenia jest prosty y =kx +b tępy, wtedy nachylenie jest ujemne. Wykres maleje (rys. 2).

Jeżeli linia prosta jest równoległa do osi odciętej, to kąt nachylenia linii prostej wynosi zero. W tym przypadku nachylenie prostej również wynosi zero (ponieważ styczna zera wynosi zero). Równanie linii prostej będzie miało postać y = b (rys. 3).

Jeżeli kąt nachylenia linii prostej wynosi 90º (π / 2), czyli jest prostopadły do ​​osi odciętej, to linia prosta jest równa równości x =C, gdzie C- jakaś liczba rzeczywista (rys. 4).

Równanie stycznej do wykresu funkcjitak = F(x) w punkcie xO:

Przykład: Znajdź równanie stycznej do wykresu funkcji F(x) = x 3 – 2x 2 + 1 w miejscu z odciętą 2.

Rozwiązanie .

Postępujemy zgodnie z algorytmem.

1) Punkt dotykowy xO równa się 2. Oblicz F(xO):

F(xO) = F(2) = 2 3 – 2 ∙ 2 2 + 1 = 8 – 8 + 1 = 1

2) Znajdź F′( x). W tym celu stosujemy formuły różnicowania opisane w poprzedniej sekcji. Zgodnie z tymi formułami x 2 = 2x, a x 3 = 3x 2. Znaczy:

F′( x) = 3x 2 – 2 ∙ 2x = 3x 2 – 4x.

Teraz używając wynikowej wartości F′( x), obliczamy F′( xO):

F′( xO) = F′ (2) = 3 ∙ 2 2 - 4 ∙ 2 = 12 - 8 = 4.

3) Mamy więc wszystkie niezbędne dane: xO = 2, F(xO) = 1, F ′( xO) = 4. Podstaw te liczby do równania stycznego i znajdź ostateczne rozwiązanie:

y = F(xO) + F′( xO) (x - x о) = 1 + 4 ∙ (x - 2) = 1 + 4x - 8 = –7 + 4x = 4x - 7.

Odpowiedź: y = 4x - 7.

Przykład 1. Funkcja jest podana F(x) = 3x 2 + 4x- 5. Napisz równanie stycznej do wykresu funkcji F(x) w punkcie wykresu z odciętą x 0 = 1.

Rozwiązanie. Pochodna funkcji F(x) istnieje dla dowolnego x r ... Znajdźmy to:

= (3x 2 + 4x- 5) ′ = 6 x + 4.

Następnie F(x 0) = F(1) = 2; (x 0) = = 10. Równanie styczne to:

tak = (x 0) (x – x 0) + F(x 0),

tak = 10(x – 1) + 2,

tak = 10x – 8.

Odpowiedź. tak = 10x – 8.

Przykład 2. Funkcja jest podana F(x) = x 3 – 3x 2 + 2x+ 5. Napisz równanie stycznej do wykresu funkcji F(x) równolegle do linii prostej tak = 2x – 11.

Rozwiązanie. Pochodna funkcji F(x) istnieje dla dowolnego x r ... Znajdźmy to:

= (x 3 – 3x 2 + 2x+ 5) ′ = 3 x 2 – 6x + 2.

Od stycznej do wykresu funkcji F(x) w miejscu z odciętą x 0 równolegle do linii prostej tak = 2x- 11, to jego nachylenie wynosi 2, czyli ( x 0) = 2. Znajdźmy tę odciętą z warunku, że 3 x– 6x 0 + 2 = 2. Ta równość obowiązuje tylko dla x 0 = 0 i dla x 0 = 2. Ponieważ w obu przypadkach F(x 0) = 5, to linia prosta tak = 2x + b dotyka wykresu funkcji w punkcie (0; 5) lub w punkcie (2; 5).

W pierwszym przypadku równość liczbowa jest prawdziwa 5 = 2 × 0 + b, gdzie b= 5, a w drugim przypadku równość liczbowa jest prawdziwa 5 = 2 × 2 + b, gdzie b = 1.

Więc są dwie styczne tak = 2x+ 5 i tak = 2x+ 1 do wykresu funkcji F(x) równolegle do linii prostej tak = 2x – 11.

Odpowiedź. tak = 2x + 5, tak = 2x + 1.

Przykład 3. Funkcja jest podana F(x) = x 2 – 6x+ 7. Napisz równanie stycznej do wykresu funkcji F(x) przechodząc przez punkt A (2; –5).

Rozwiązanie. Bo F(2) –5, następnie punkt A nie należy do wykresu funkcji F(x). Pozwalać x 0 - odcięta punktu styczności.

Pochodna funkcji F(x) istnieje dla dowolnego x r ... Znajdźmy to:

= (x 2 – 6x+ 1) ′ = 2 x – 6.

Następnie F(x 0) = x– 6x 0 + 7; (x 0) = 2x 0 - 6. Równanie styczne to:

tak = (2x 0 – 6)(x – x 0) + x– 6x+ 7,

tak = (2x 0 – 6)x– x+ 7.

Od punktu A należy do prostej stycznej, to równość liczbowa

–5 = (2x 0 - 6) × 2– x+ 7,

gdzie x 0 = 0 lub x 0 = 4. Oznacza to, że przez punkt A możesz narysować dwie styczne do wykresu funkcji F(x).

Jeśli x 0 = 0, to równanie styczne ma postać tak = –6x+ 7. Jeśli x 0 = 4, to równanie styczne ma postać tak = 2x – 9.

Odpowiedź. tak = –6x + 7, tak = 2x – 9.

Przykład 4. Podane funkcje F(x) = x 2 – 2x+ 2 i g(x) = –x 2 - 3. Zapiszmy równanie wspólnej stycznej do wykresów tych funkcji.

Rozwiązanie. Pozwalać x 1 - odcięta punktu styczności żądanej linii prostej z wykresem funkcji F(x), a x 2 - odcięta punktu styczności tej samej prostej z wykresem funkcji g(x).

Pochodna funkcji F(x) istnieje dla dowolnego x r ... Znajdźmy to:

= (x 2 – 2x+ 2) ′ = 2 x – 2.

Następnie F(x 1) = x– 2x 1 + 2; (x 1) = 2x 1 - 2. Równanie styczne to:

tak = (2x 1 – 2)(x – x 1) + x– 2x 1 + 2,

tak = (2x 1 – 2)x – x+ 2. (1)

Znajdź pochodną funkcji g(x):

= (–x 2 - 3) ′ = –2 x.