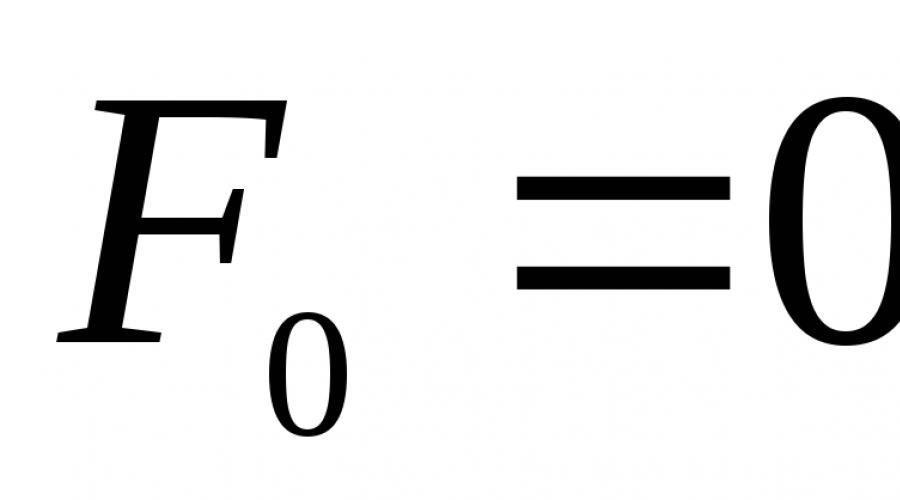
इतालवी गणितज्ञ लियोनार्डो फाइबोनैकी 13 वीं शताब्दी में रहते थे और यूरोप में पहले में से एक अरबी (भारतीय) आंकड़ों का उपयोग करना शुरू कर दिया। वह खरगोशों के कुछ कृत्रिम कार्य के साथ आया, जो खेत पर उगाए जाते हैं, और उनमें से सभी को मादा माना जाता है, नर को अनदेखा कर दिया जाता है। दो महीने तक खेले जाने के बाद खरगोशों को गुणा करना शुरू हो जाता है, और फिर हर महीने खरगोश के साथ जन्म देता है। खरगोश कभी नहीं मरते।

यह निर्धारित करने की आवश्यकता है कि खेत के माध्यम से कितने खरगोश होंगे एन महीनों, यदि केवल एक नवजात खरगोश समय के प्रारंभिक क्षण में था।

जाहिर है, किसान के पहले महीने में एक खरगोश और एक खरगोश - दूसरे महीने में। तीसरे महीने के लिए चौथे - तीन, आदि पर दो खरगोश होंगे। खरगोशों की संख्या को दर्शाता है एन मासिक। इस तरह,
,
,
,
,
, …

आप एक एल्गोरिदम बना सकते हैं जो आपको खोजने की अनुमति देता है किसी के साथ एन.

समस्या की स्थिति के अनुसार, खरगोशों की कुल संख्या
में एनमहीने को तीन घटकों में जोड़ा जाता है:

एक महीने के खरगोश जो मात्रा में प्रजनन करने में सक्षम नहीं हैं

;

इस प्रकार, हमें मिलता है

. (8.1)

फॉर्मूला (8.1) आपको संख्याओं की संख्या की गणना करने की अनुमति देता है: 0, 1, 1, 2, 3, 5, 55, 13, 21, 34, 55, 89, 144, 23, 55, 99, 144, 23, 55 99, 144, 23, 55, 89, 144, 23

इस अनुक्रम में संख्याओं को बुलाया जाता है fibonacci संख्या .

अगर लिया गया
तथा
फॉर्मूला (8.1) का उपयोग करके, आप अन्य सभी फाइबोनैकी संख्याओं को परिभाषित कर सकते हैं। सूत्र (8.1) कहा जाता है आवर्तक सूत्र () पुनरावृत्ति - लैटिन में "वापसी")।

उदाहरण 8.1।मान लीजिए कि एक सीढ़ी है एन कदम। हम एक चरण में एक कदम के साथ, या - दो चरणों में एक कदम में चढ़ाई कर सकते हैं। उठाने के विभिन्न तरीकों के कितने संयोजन हैं?

यदि एक एन \u003d 1, समस्या को हल करने के लिए केवल एक विकल्प है। के लिये एन \u003d 2 2 विकल्प हैं: दो एकल चरण या एक डबल। के लिये एन \u003d 3 3 विकल्प हैं: तीन एकल कदम, या एक एकल और एक डबल, या एक डबल और एक।

निम्नलिखित मामले में एन \u003d 4, हमारे पास 5 संभावनाएं हैं (1 + 1 + 1 + 1, 2 + 1 + 1, 1 + 2 + 1, 1 + 1 + 2, 2 + 2)।

ताकि मनमानी के लिए दिए गए प्रश्न का उत्तर दिया जा सके एन, विकल्पों की संख्या को दर्शाता है और निर्धारित करने की कोशिश करें
प्रसिद्ध के अनुसार तथा
। अगर हम एक ही कदम से शुरू करते हैं, तो हमारे पास है शेष के लिए संयोजन एन कदम। यदि आप एक डबल चरण से शुरू करते हैं, तो हमारे पास है
शेष के लिए संयोजन एन-1 कदम। के लिए विकल्पों की कुल संख्या एन+1 चरण बराबर है

. (8.2)

एक जुड़वा के रूप में परिणामी सूत्र सूत्र (8.1) जैसा दिखता है। फिर भी, यह संयोजनों की संख्या की पहचान करने की अनुमति नहीं देता है fibonacci संख्याओं के साथ । हम देखते हैं, उदाहरण के लिए, वह
, लेकिन अ
। हालांकि, निम्नलिखित निर्भरता है:

.

यह सच है एन \u003d 1, 2, और प्रत्येक के लिए भी मान्य एन। Fibonacci संख्या और संयोजनों की संख्या हालांकि, प्रारंभिक मानों के समान सूत्र द्वारा गणना की जाती है
,
तथा
,
वे उनसे अलग हैं।

उदाहरण 8.2।यह उदाहरण समस्याग्रस्त कोडिंग समस्याओं के लिए व्यावहारिक है। हमें लंबाई के सभी बाइनरी शब्दों की संख्या मिलती है एनएक पंक्ति में कई शून्य नहीं युक्त। के माध्यम से इस संख्या से निरूपित करें । जाहिर है
, और लंबाई 2 के शब्द, हमारी सीमा को संतुष्ट, हैं: 10, 01, 11, यानी।
। रहने दो
- ऐसा शब्द एन प्रतीक। यदि प्रतीक
टी
मनमानी हो सकती है (
) -बस्ट शब्द जिनमें एक पंक्ति में कई शून्य नहीं होते हैं। तो, अंत में इकाई के साथ शब्दों की संख्या बराबर है
.

यदि प्रतीक
, मुझे जरूर
, और पहले
प्रतीक
विचाराधीन सीमाओं के संबंध में मनमानी हो सकती है। इसलिए, वहाँ है
लंबाई शब्द एन अंत में शून्य के साथ। इस प्रकार, हमारे लिए ब्याज के शब्दों की कुल संख्या बराबर है

.

उस पर विचार करना
तथा
संख्याओं का परिणामी अनुक्रम फाइबोनैकी की संख्या है।

उदाहरण 8.3।उदाहरण के लिए 7.6 हमने पाया कि निरंतर वजन के बाइनरी शब्दों की संख्या टी (और लंबाई क।) बराबरी का । अब हमें निरंतर वजन के बाइनरी शब्दों की संख्या मिलती है टीएक पंक्ति में कई शून्य नहीं युक्त।

आप इस तरह का तर्क दे सकते हैं। रहने दो
विचाराधीन शब्दों में शून्य की संख्या। किसी भी शब्द में है
निकटतम शून्य के बीच अंतराल, जिनमें से प्रत्येक में एक या कई इकाइयाँ हैं। यह मान लिया है कि
। अन्यथा, पास के शून्य के बिना एक भी शब्द नहीं है।

यदि आप प्रत्येक अंतर से बिल्कुल एक इकाई को हटाते हैं, तो हमें शब्द लंबाई मिलती है
युक्त शून्य। ऐसा कोई भी शब्द कुछ से संकेतित किया जा सकता है (और इसके अलावा केवल एक) क।-बेंडेड शब्द युक्त ज़ुलोस, जिनमें से कोई भी पास नहीं है। तो, वांछित संख्या लंबाई के सभी शब्दों की संख्या के साथ मेल खाती है
चिकनी शून्य, यानी समान रूप से
.

उदाहरण 8.4।हम साबित करते हैं कि राशि
किसी भी पूरे के लिए Fibonacci संख्या के बराबर । प्रतीक
अर्थ है सबसे छोटा पूर्णांक, अधिक या बराबर । उदाहरण के लिए, अगर
टी
; क्या हो अगर
टी
सील। ("अधिकतम सीमा")। प्रतीक भी होता है
मतलब सबसे बड़ा पूर्णांक छोटा या बराबर । अंग्रेजी में इस ऑपरेशन को कहा जाता है मंज़िल ("मंज़िल")।

यदि एक
टी
। यदि एक
टी
। यदि एक
टी
.

इस प्रकार, मामलों के लिए, राशि वास्तव में Fibonacci संख्याओं के बराबर है। अब हम एक सामान्य मामले के लिए सबूत देते हैं। चूंकि पुनर्निर्मित समीकरण (8.1) का उपयोग करके फाइबोनैकी की संख्या प्राप्त की जा सकती है, समानता की जानी चाहिए:

.

और यह वास्तव में किया जाता है:

यहां हमने पहले प्राप्त फॉर्मूला (4.4) का उपयोग किया:
.

Fibonacci संख्या की राशि

हम पहले की राशि को परिभाषित करते हैं एन Fibonacci संख्या।

0+1+1+2+3+5 = 12,

0+1+1+2+3+5+8 = 20,

0+1+1+2+3+5+8+13 = 33.

यह ध्यान रखना आसान है कि प्रत्येक समीकरण के सही हिस्से को जोड़कर, हमें फिर से फाइबोनैकी की संख्या मिलती है। पहले की राशि निर्धारित करने के लिए सामान्य सूत्र एन Fibonacci संख्याओं का रूप है:

हम गणितीय प्रेरण की विधि का उपयोग करके इसे साबित करते हैं। ऐसा करने के लिए हम लिखते हैं:

यह राशि बराबर होनी चाहिए
.

-1 पर समीकरण के बाएं और दाएं हाथ को कम करने के बाद, हम समीकरण (6.1) प्राप्त करते हैं।

Fibonacci संख्या के लिए फॉर्मूला

प्रमेय 8.1। फाइबोनैकी संख्याओं की गणना सूत्र द्वारा की जा सकती है

.

सबूत। के लिए इस सूत्र के न्याय को सुनिश्चित करें एन \u003d 0, 1, और फिर मनमानी के लिए इस सूत्र की वैधता साबित करें एन प्रेरण द्वारा। Fibonacci के दो निकटतम संख्याओं के दृष्टिकोण की गणना करें:

हम देखते हैं कि इन संख्याओं का अनुपात 1.618 के मूल्य के पास उतार-चढ़ाव करता है (यदि आप कई पहले मूल्यों को अनदेखा करते हैं)। फिबोनाची की यह संपत्ति ज्यामितीय प्रगति की याद ताजा है। संस्था
, (
)। फिर अभिव्यक्ति

बी द्वारा परिवर्तित

जो सादगी के बाद दिखता है

.

हमें एक वर्ग समीकरण प्राप्त हुआ, जिनकी जड़ें बराबर हैं:

अब हम लिख सकते हैं:

(कहा पे सी। एक स्थिर है)। दोनों सदस्य तथा उदाहरण के लिए नंबर फाइबोनैकी न दें
, जबकि
। हालांकि, अंतर
एक पुनरावर्ती समीकरण को संतुष्ट करता है:

के लिये एन\u003d 0 यह अंतर देता है , अर्थात:
। हालाँकि एन\u003d 1 हमारे पास है
। प्राप्त करना
यह स्वीकार करना आवश्यक है:
.

अब हमारे पास दो अनुक्रम हैं: तथा
जो समान दो संख्याओं के साथ शुरू होता है और एक ही पुनरावर्ती सूत्र को संतुष्ट करता है। वे बराबर होना चाहिए:
। प्रमेय साबित हुआ है।

वृद्धि के रूप में एन सदस्य जबकि बहुत बड़ा हो जाता है
, और एक सदस्य की भूमिका अंतर कम हो गया है। इसलिए, बड़े पैमाने पर एन हमें भर्ती किया जा सकता है

.

हम 1/2 को नजरअंदाज करते हैं (चूंकि फाइबोनैकी की संख्या वृद्धि के साथ अनंतता में वृद्धि होती है एन अनन्त तक)।

रवैया
बुला हुआ गोल्डन क्रॉस सेक्शनइसका उपयोग गणित के बाहर किया जाता है (उदाहरण के लिए, मूर्तिकला और वास्तुकला में)। गोल्डन क्रॉस सेक्शन विकर्ण और पक्ष के बीच संबंध है सही पेंटागन (चित्र 8.1)।

अंजीर। 8.1। सही पेंटागन और इसके विकर्ण

गोल्डन सेक्शन के पदनाम के लिए, यह पत्र का उपयोग करने के लिए प्रथागत है
प्रसिद्ध एथेनियन स्केलशन फिडिया के सम्मान में।

साधारण संख्या

सभी प्राकृतिक संख्या, बड़ी इकाइयां, दो वर्गों में विघटित। पहले संख्याओं में संख्याएं शामिल हैं जिनमें बिल्कुल दो प्राकृतिक divisors, एक इकाई और खुद, दूसरे के लिए - अन्य सभी। प्रथम श्रेणी संख्या को बुलाया जाता है सरल, और दूसरा - यौगिक। पहले तीन दसों में सरल संख्या: 2, 3, 5, 7, 11, 13, 17, 1 9, 23, 2 9, ...

प्राइम नंबरों के गुण और सभी प्राकृतिक संख्याओं के साथ उनके संबंध का अध्ययन यूक्लाइड (3 शताब्दी में हमारे युग) द्वारा किया गया था। यदि आप एक पंक्ति में सरल संख्याएं लिखते हैं, तो आप देख सकते हैं कि सापेक्ष घनत्व कम हो जाता है। पहले दस के लिए, वे 4, यानी 40% के लिए खाते हैं, एक सौ 25, यानी 25%, प्रति हजार - 168, यानी। 17% से कम, प्रति मिलियन - 78498, यानी 8% से कम, आदि .. हालांकि, उनकी कुल संख्या अनंत है।

सरल संख्याओं में जोड़े जैसे जोड़ होते हैं, जिसके बीच का अंतर दो के बराबर होता है (तथाकथित साधारण जुड़वाँ) हालांकि, इस तरह के भाप की अंग या अनंतता साबित नहीं हुई है।

यूक्लिड ने यह स्पष्ट माना कि केवल प्राइम नंबरों के गुणा की मदद से, सभी प्राकृतिक संख्याएं प्राप्त की जा सकती हैं, और प्रत्येक प्राकृतिक संख्या प्रमुख संख्याओं के उत्पाद के रूप में एकवचन रूप से (गुणक के लिए प्रक्रिया की सटीकता के साथ) का प्रतिनिधित्व करती है। इस प्रकार, सरल संख्या एक प्राकृतिक पंक्ति का एक गुणात्मक आधार बनाती है।

प्राइम नंबरों के वितरण के अध्ययन ने एक एल्गोरिदम का निर्माण किया जो आपको प्राइम नंबरों की तालिका प्राप्त करने की अनुमति देता है। ऐसा एल्गोरिदम है swelto eratosthen (3 शताब्दी ईसा पूर्व)। इस विधि में निर्दिष्ट अनुक्रम के उन पूर्णांक के चयन (उदाहरण के लिए, ओवरक्लॉकिंग) में शामिल होते हैं
जो कम से कम एक साधारण संख्या को छोटे से साझा करते हैं
.

प्रमेय 8 . 2 . (यूक्लाइड का प्रमेय)। प्राइम नंबरों की संख्या अनंत है.

सबूत। लियोनार्ड यूलर (1707-1783) द्वारा प्रस्तावित विधि को साबित करने की संख्या साबित करने की संख्या साबित करने की संख्या को साबित करने की संख्या को साबित करने की संख्या। यूलर ने सभी सादगी पर काम की समीक्षा की पी:

के लिये
। यह उत्पाद अभिसरण करता है, और यदि यह प्रकट होता है, तो सामान्य कारकों पर प्राकृतिक संख्याओं के अपघटन की विशिष्टता के कारण यह पता चला है कि यह श्रृंखला के योग के बराबर है जहां से यूलर पहचान निम्नानुसार है:

.

कितने समय से
दाएं विचलन (हार्मोनिक श्रृंखला) पर पंक्ति, फिर यूलर की पहचान यूक्लाइड के प्रमेय का पालन करती है।

रूसी गणितज्ञ पीएल। Chebyshev (1821-1894) फॉर्मूला लाया जो सीमाओं को निर्धारित करता है जिसमें प्राइम नंबरों की संख्या समाप्त हुई थी
से अधिक नहीं एक्स।:

,

कहा पे
,
.

राज्य शिक्षा प्रतिष्ठान

"क्रिवान सेंट्रल स्कूल"

Zhabinkovsky जिला

Fibonacci संख्या और गोल्डन अनुभाग

अनुसंधान

काम पूरा हो गया है:

छात्र 10 वर्ग

Sadovnikchik Valery Alekseevna

नेता:

Lavrenyuk Larisa Nikolaevna,

शिक्षक सूचना विज्ञान I.

गणित 1 योग्यता

Fibonacci और प्रकृति

पौधों की संरचना की एक विशेषता विशेषता और उनके विकास सर्पिलिटी है। एक और गोथे, जो न केवल एक महान कवि नहीं थे, बल्कि एक प्रकृतिवादी, सभी जीवों के विशिष्ट संकेतों में से एक के साथ सर्पिलिटी माना जाता है, जीवन के सबसे अंतरंग सार का अभिव्यक्ति। पौधे मूंछें सर्पीकर, सर्पिलों का परीक्षण पेड़ों के टुकड़ों में किया जाता है, सर्पिल सूरजमुखी में स्थित होते हैं, सर्पिल आंदोलनों (राष्ट्र) जड़ों और शूटिंग के विकास के साथ मनाए जाते हैं।

पहली नज़र में, ऐसा लगता है कि पत्तियों की संख्या, फूल बहुत व्यापक सीमा में बदल सकते हैं और कोई मान ले सकते हैं। लेकिन यह निष्कर्ष दिवालिया होने के लिए बाहर निकलता है। अध्ययनों से पता चला है कि पौधों में पौधों की अंगुली मनमानी नहीं है, ऐसे मूल्य हैं जिन्हें अक्सर सामना किया जाता है और मूल्यों को बहुत दुर्लभ होता है।

जंगल में, पेंटगोनल समरूपता के आधार पर आकार व्यापक - स्टारफिश, समुद्री हेजहोग, फूल हैं।

फोटो .13। बटरकप

55 या 89 पंखुड़ियों की कैमोमाइल संख्या में।

फोटो .14। कैमोमाइल

पाइरेथ्रम में 34 पंखुड़ी हैं।

फॉट। पंद्रह। गुलदाउदी का एक प्रकार

चलो पाइन टक्कर देखें। इसकी सतह पर तराजू सख्ती से प्राकृतिक हैं - दो सर्पिलों के साथ जो लगभग समकोण पर छेड़छाड़ करते हैं। पाइन शंकुओं में ऐसी सर्पल की संख्या 8 और 13 या 13 और 21 है।

फोटो .16। शंकु

सूरजमुखी के टोकरी में, बीज दो सर्पिलों में भी स्थित होते हैं, उनकी संख्या आमतौर पर 34/55, 55/89 होती है।

फोटो .17। सूरजमुखी

हम गोले को देखते हैं। यदि आप पहले से "कठोरता की पसलियों" की संख्या का पुनर्मूल्यांकन करते हैं, तो राकुशकु रकोशाई में लिया गया - यह 21 हो गया। दूसरा, तीसरा, पांचवां, दसवें सीवर लें - हर किसी के पास सतह पर 21 किनारों होंगे। यह देखा जा सकता है, मोलस्क न केवल अच्छे इंजीनियरों थे, वे फिबोनास्सी की संख्या "जानते थे"।

फोटो .18। शेल

यहां फिर से हम फाइबोनैकी नंबरों के नियमित संयोजन को देखते हैं: 2/3, 3/5, 5/8, 8/13, 13/21, 21/34, 34/55, 55/89। सीमा में उनका दृष्टिकोण सोने के अनुपात के लिए प्रयास कर रहा है, 0.61803 की एक स्पष्ट संख्या ...

Fibonacci और पशु संख्या

समुद्री सितारों से किरणों की संख्या कई फाइबोनैकी संख्याओं से मेल खाती है या उनके करीब 5.8, 13,21,34,55 के बराबर है।

फोटो .9। एक प्रकार की मछली जिस को पाँच - सात बाहु के सदृश अंग होते है

आधुनिक आर्थ्रोपोड बहुत विविध हैं। लैंगस्टम में पांच फीट जोड़े भी हैं, पूंछ पांच पंखों पर, पेट को पांच खंडों में बांटा गया है, और प्रत्येक पैर में पांच भाग होते हैं।

फॉट। बीस लम्बा

कुछ कीट में, पेट में आठ खंड होते हैं, आठ भागों से युक्त तीन जोड़े होते हैं, और आठ अलग-अलग समग्र अंग मुंह के मुंह को छोड़ देते हैं। हमारे अच्छी तरह से फ्रेंडली मच्छर - पैरों के तीन जोड़े, पेट को आठ खंडों में विभाजित किया जाता है, सिर पर पांच मूंछ - एंटेना। मच्छर लार्वा 12 सेगमेंट पर आकार दिया गया है।

फॉट। 21। मच्छर

गोभी पेट की मक्खी पांच भागों को ढंकती हैं, पैरों के तीन जोड़े होते हैं, और लार्वा को आठ खंडों में बांटा गया है। दो पंखों में से प्रत्येक सूक्ष्म छिद्रों से आठ भागों तक विभाजित है।

कई कीड़ों के कैटरपिलर 13 सेगमेंट के सदस्य हैं, उदाहरण के लिए, हिनवुड, मुकेदा, कोझेनेकी मुरीश में। अधिकांश कीट बीटल में, कैटरपिलर को 13 सेगमेंट में आकार दिया जाता है। बीटल के पैरों की संरचना की बहुत विशेषता। प्रत्येक पैर में कंधे, प्रकोष्ठ और पंजे से उच्चतम जानवरों की तरह तीन भाग होते हैं। बीटल के पतले, ओपनवर्क पंजे पांच भागों के सदस्य हैं।

ओपनवर्क, पारदर्शी, भार रहित ड्रैगनफ्लाई पंख प्रकृति की "इंजीनियरिंग" निपुणता की एक उत्कृष्ट कृति हैं। इस छोटे से उड़ान मांसपेशियों के डिजाइन पर क्या अनुपात आधारित हैं? कई ड्रैगनफ्लियों में शरीर की लंबाई तक पंखों के दायरे का अनुपात 4/3 है। ड्रैगनफली का शरीर दो मुख्य भागों में बांटा गया है: एक विशाल मामला और एक लंबी पतली पूंछ। तीन भागों आवास में प्रतिष्ठित हैं: सिर, छाती, पेट। पेट पांच खंडों से टूट गया है, और पूंछ में आठ भाग होते हैं। आपको अभी भी अपने सदस्यों के साथ तीन हिस्सों में तीन जोड़े पैरों को जोड़ने की जरूरत है।

फॉट। 22। Dragonfly

कई फाइबोनैकी संख्याओं की तैनाती के पूरे हिस्से की सदस्यता के इस अनुक्रम में देखना आसान है। पूंछ की लंबाई, आवास और ड्रैगनफ्लियों की कुल लंबाई को सोने के अनुपात से जुड़ा हुआ है: पूंछ की लंबाई का अनुपात और आवास कुल लंबाई के अनुपात के बराबर पूंछ की लंबाई तक होता है।

यह आश्चर्य की बात नहीं है कि ड्रैगनफ्लाई इतना सही दिखता है, क्योंकि यह स्वर्ण अनुपात के नियमों के अनुसार बनाया गया है।

रणनीति से ढकी रणनीति की पृष्ठभूमि पर कछुए का दृश्य - घटना अद्भुत है। खोल के केंद्र में, बड़े विवाद वाली सींग वाली प्लेटों के साथ एक बड़ा अंडाकार क्षेत्र, और किनारों पर - छोटी प्लेटों की एक सीमा।

फॉट। 23। कछुए

किसी भी कछुए को ले लो - हमारे करीब से एक विशाल समुद्र, सूप कछुए - और आप यह सुनिश्चित करेंगे कि खोल पर चित्र उनके समान है: अंडाकार क्षेत्र पर 13 आसपास की सींग वाली प्लेटें हैं - केंद्र में 5 प्लेटें और 8 - किनारों के साथ, और परिधीय किमिया के बारे में 21 प्लेटों (चिली कछुए में शैल की परिधि पर बिल्कुल 21 प्लेटें)। 5 अंगुलियों की खोपड़ी में पंजे पर, और कशेरुका ध्रुव में 34 कशेरुका शामिल हैं। यह ध्यान रखना आसान है कि सभी निर्दिष्ट मान फाइबोनैकी नंबरों से मेल खाते हैं। नतीजतन, कछुए का विकास, उसके शरीर का गठन, पूरे हिस्से की सदस्यता कई फाइबोनैकी के कानून के तहत की गई थी।

ग्रह पर उच्चतम प्रकार का जानवर स्तनधारियों है। कई पशु प्रजातियों में पसलियों की संख्या तेरह के बराबर या करीब है। पूरी तरह से अलग स्तनधारियों में - व्हेल, ऊंट, हिरण, दौरे - किनारों की संख्या 13 ± 1. कशेरुका की संख्या बहुत अधिक बदलती है, खासकर पूंछ के कारण, जो एक ही प्रकार के जानवर में भी अलग-अलग लंबाई हो सकती है। लेकिन उनमें से कई के पास वर्सन की संख्या समान रूप से या करीब 34 और 55 है। इसलिए, चीन में 55 - विशाल हिरण में 34 कशेरुका।

घरेलू अंगों के कंकाल में तीन समान हड्डी लिंक होते हैं: कंधे (श्रोणि) हड्डियां, अग्रसर की हड्डियां (टिबिया) और पंजा की हड्डियां (पैर) होती हैं। रुकें, बदले में, तीन हड्डी लिंक शामिल हैं।

कई पालतू जानवरों से फाइबोनैकी की संख्या में दांतों की संख्या: एक खरगोश में 14 जोड़े, कुत्ते, सूअर, घोड़े हैं - 21 ± 1 दांतों की जोड़ी। जंगली जानवरों में, दांतों की संख्या अधिक व्यापक रूप से बदलती है: एक छोटा शिकारी 54 के बराबर होता है, हाइना 34 है, डॉल्फ़िन के प्रकारों में से एक 233 तक पहुंचता है। पालतू जानवरों के कंकाल में हड्डियों की कुल संख्या (दांतों को ध्यान में रखते हुए ) 230 के करीब एक ही समूह में, और दूसरी तरफ - 300. यह ध्यान दिया जाना चाहिए कि छोटी सुनवाई की हड्डियों और गैर-स्थायी हड्डियों को कंकाल हड्डियों की संख्या में शामिल नहीं किया गया है। उनके खाते के साथ, कई जानवरों में कंकाल की हड्डियों की कुल संख्या 233 के करीब हो जाएगी, और अन्य 300 से अधिक हो जाएंगे। जैसा कि हम देखते हैं, शरीर की सदस्यता, कंकाल के विकास के साथ, संख्या में एक अलग परिवर्तन की विशेषता है जानवरों के विभिन्न अंगों में हड्डियों की, और ये संख्याएं फाइबोनैकी संख्याओं या उनके बहुत करीब के अनुरूप होती हैं, जो 3, 5, 8, 134, 21, 34, 55, 89, 144, 233 का निर्माण करती हैं। के आकार का अनुपात अधिकांश चिकन अंडे 4: 3 (कुछ 3/2 में), कद्दू के बीज - 3: 2, तरबूज के बीज - 3/2 है। पाइन शंकु की लंबाई उनके व्यास की लंबाई का अनुपात 2: 1 हो गया। बिर्च पत्तियों के आयाम बहुत करीब हैं, और acorns - 5: 2।

ऐसा माना जाता है कि यदि आपको फूल लॉन (घास और फूलों) को दो हिस्सों में विभाजित करने की आवश्यकता है, तो आपको इन बैंड को चौड़ाई में बराबर नहीं बनाना चाहिए, अगर आप उन्हें 5: 8 या 8 के संदर्भ में लेते हैं तो यह अधिक सुंदर होगा: 13, यानी "गोल्डन क्रॉस सेक्शन" नामक अनुपात का लाभ उठाएं।

Fibonacci संख्या और फोटो

फोटोग्राफिक कला के संबंध में, गोल्डन सेक्शन का नियम 9 असमान आयतों पर दो क्षैतिज और दो लंबवत रेखाओं के साथ फ्रेम को विभाजित करता है। संतुलित छवियों को शूट करने के कार्य को सुविधाजनक बनाने के लिए, फोटोग्राफरों ने कार्य को थोड़ा सा सरल बना दिया है और फाइबोनैकी संख्याओं के अनुसार 9 बराबर आयताकारों पर फ्रेम साझा करना शुरू कर दिया है। तो गोल्डन क्रॉस सेक्शन नियम तीसरे के नियम में परिवर्तित हो गया था, जो संरचना बनाने के सिद्धांतों में से एक को संदर्भित करता है।

फॉट। 24। फ्रेम और गोल्डन सेक्शन

आधुनिक डिजिटल कैमरों के दृश्यों में, फोकस पॉइंट पोजीशन 2/8 या गोल्डन क्रॉस सेक्शन के नियम के अनुसार फ्रेम को विभाजित करने वाली काल्पनिक रेखाओं पर स्थित हैं।

फोटो .25। डिजिटल कैमरा और फोकस अंक

Photo.26।

Photo.27। फोटोग्राफी और फोकस अंक

तीसरे का उपयोग सभी साजिश रचनाओं पर लागू होता है: आप परिदृश्य या चित्र, अभी भी जीवन या रिपोर्ट को दूर करते हैं। जबकि आपकी सद्भाव की भावना अधिग्रहित हो गई है और बेहोश हो गई है, तीसरे के धार्मिक शासन का पालन करने से आप चित्र अभिव्यक्तिपूर्ण, सामंजस्यपूर्ण, संतुलित होने की अनुमति देंगे।

Photo.28। फोटोग्राफी और आकाश और पृथ्वी 1 से 2 का दृष्टिकोण।

प्रदर्शन के लिए सबसे सफल उदाहरण परिदृश्य है। रचना का सिद्धांत इस तथ्य में निहित है कि आकाश और सुखाने (या पानी की सतह) के पास 1: 2 का अनुपात होना चाहिए। फ्रेम का एक तिहाई आकाश के नीचे छोड़ा जाना चाहिए, और भूमि के नीचे दो तिहाई या इसके विपरीत।

Photo.29। फूल फोटोग्राफी सर्पिल

Fibonacci और अंतरिक्ष

ग्रह पृथ्वी पर पानी और सुशी का अनुपात 62% और 38% है।

पृथ्वी और चंद्रमा के आयाम सुनहरे अनुपात में हैं।

Fot.30। भूमि और चंद्रमा के आकार

यह आंकड़ा पृथ्वी के सापेक्ष आयामों और पैमाने पर चंद्रमा दिखाता है।

भूमि त्रिज्या खींचो। हम पृथ्वी के केंद्रीय बिंदु से चंद्रमा के केंद्रीय बिंदु तक एक सेगमेंट करते हैं, जिसकी लंबाई बराबर होगी)। त्रिभुज बनाने के लिए दो सेगमेंट डेटा को जोड़ने के लिए एक सेगमेंट बनाएं। हमें एक सुनहरा त्रिकोण मिलता है।

शनि अपने कई मापों में सोने का अनुपात दिखाता है

Photo.31। शनि और उसके छल्ले

हरे रंग की रेखाओं द्वारा दिखाए गए अनुसार, अंगूठियों के व्यास के साथ सोने के अनुपात के संबंध में शनि का व्यास बहुत करीब है। त्रिज्या बी।ब्लू लाइन द्वारा दिखाए गए अनुसार, अंगूठियों का न्यूट्रिन हिस्सा अंगूठियों के बाहरी व्यास के बहुत करीब है।

सूर्य से ग्रहों की दूरी भी सुनहरा अनुपात का पालन करती है।

Photo.32। सूर्य से दूरी ग्रह

रोजमर्रा की जिंदगी में गोल्डन सेक्शन

गोल्डन सेक्शन का उपयोग हर रोज उपभोक्ता वस्तुओं के विपणन और डिजाइन के क्षेत्र में शैली और आकर्षक देने के लिए भी किया जाता है। कई उदाहरण हैं, लेकिन हम केवल कुछ को चित्रित करेंगे।

Photo.33। प्रतीकटोयोटा।

Photo.34। गोल्डन सेक्शन और कपड़े

Photo.34। गोल्डन सेक्शन और मोटर वाहन डिजाइन

Photo.35। प्रतीकसेब

Photo.36। प्रतीकगूगल

व्यावहारिक अनुसंधान

अब हम अभ्यास में प्राप्त ज्ञान लागू करते हैं। हम पहले ग्रेड 8 के छात्रों के बीच माप लेते हैं।

यदि आप सावधानी से टेलीविजन तस्वीर को देखते हैं, तो इसके आयाम 16 से 9 या 16 से 10 होंगे, जो गोल्डन क्रॉस सेक्शन के नजदीक भी है।

में माप और निर्माण का संचालन Coreldraw x4 और रूसी समाचार चैनल फ्रेम 24 का उपयोग करके, आप निम्न का पता लगा सकते हैं:

ए) फ्रेम की चौड़ाई तक लंबाई अनुपात 1.7 है।

बी) फ्रेम में व्यक्ति 3/8 की दूरी पर स्थित फोकस बिंदुओं पर स्थित है।

इसके बाद, हम समाचार पत्र "izvestia" के आधिकारिक माइक्रोब्लॉगिंग, दूसरे शब्दों में, ट्विटर पेज पर जाते हैं। 4: 3Vidim के किनारों के साथ मॉनिटर स्क्रीन के लिए, "कैप" पृष्ठ पृष्ठ की पूरी ऊंचाई से 3/8 है।

सावधानी से सेना के शुल्क को देखकर, आप निम्न पा सकते हैं:

ए) रूसी संघ के रक्षा मंत्री के फोरेज में 1.4 के बराबर 21.73 के 15.52 के निर्दिष्ट हिस्सों का अनुपात है।

बी) सीमा गार्ड आरबी के फोर्ज में 44.42 से 21.33 के निर्दिष्ट हिस्सों के आयाम हैं, जो 2.1 है।

सी) यूएसएसआर के समय को पफिंग में 49.67 से 31.04 के निर्दिष्ट हिस्सों के आयाम हैं, जो 1.6 है।

इस मॉडल के लिए, कपड़े की लंबाई 113.13 मिमी है।

यदि आप "सही" लंबाई के लिए एक पोशाक "खींचते हैं, तो हमें यह तस्वीर मिलती है।

सभी आयामों में कुछ त्रुटि होती है, क्योंकि वे फोटोग्राफी में आयोजित किए गए थे, जो आपको एक प्रवृत्ति को देखने से नहीं रोकता - सब कुछ जो पूरी तरह से एक स्वर्ण क्रॉस सेक्शन में एक डिग्री या दूसरे में होता है।

निष्कर्ष

वन्यजीवन की दुनिया हमारे सामने पूरी तरह से अलग दिखाई देती है - जंगम, अस्थिर और आश्चर्यजनक विविधता। जीवन हमें विविधता और रचनात्मक संयोजन की विशिष्टता का एक शानदार कार्निवल दर्शाता है! निर्जीव प्रकृति की दुनिया मुख्य रूप से समरूपता की दुनिया है, जिनके पास स्थिरता और सौंदर्य है। प्रकृति की दुनिया मुख्य रूप से सद्भाव की दुनिया है जिसमें "गोल्डन सेक्शन" मान्य है।

“गोल्डन क्रॉस सेक्शन सत्य का क्षण प्रतीत होता है, जिसमें निष्पादन के बिना यह संभव नहीं है, सामान्य रूप से, कुछ ऐसा है। जो कुछ भी हमने शोध का एक तत्व लिया है, "गोल्डन क्रॉस सेक्शन" हर जगह होगा; यदि इसका कोई अवलोकन नहीं है, तो यह ऊर्जा, आणविक या सेलुलर स्तरों पर जरूरी है।

वास्तव में, प्रकृति अपने मौलिक पैटर्न के प्रकटीकरण में एकान्त (और इसलिए एक!) बन जाती है। उन्होंने पाया कि "सर्वाधिक सफल" समाधान विभिन्न प्रकार के ऑब्जेक्ट्स पर विभिन्न प्रकार के रूपों पर लागू होते हैं। संगठन की निरंतरता और विवेकीन पदार्थ की ओर बढ़ती है - इसकी कॉर्पस्क्यूलर और लहर प्रकृति, रसायन शास्त्र में प्रवेश करती है, जहां पूर्णांक स्टॉइचियोमेट्री के कानून, निरंतर और परिवर्तनीय संरचना के रासायनिक यौगिकों, देता है। वनस्पतिविद, निरंतरता और विसंगति में फिलोएक्सिस, विवेहीता क्वांटा, विकास क्वांटा, विवेकीन की एकता और स्थानिक अस्थायी संगठन की निरंतरता में उनकी विशिष्ट अभिव्यक्ति मिलती है। और पहले से ही पौधे अंगों के संख्यात्मक संबंधों में, "कई संबंधों का सिद्धांत" प्रकट होता है, जो ए गर्स्की द्वारा पेश किया गया है, रसायन शास्त्र के मुख्य कानून की पूर्ण पुनरावृत्ति है।

बेशक, बयान यह है कि ये सभी घटनाएं फाइबोनैकी अनुक्रमों पर बनाई गई हैं, यह बहुत ज़ोरदार लगती है, लेकिन चेहरे पर प्रवृत्ति। और इसके अलावा, वह इस दुनिया में सबकुछ की तरह, परिपूर्ण से दूर है।

एक सुझाव है कि कई फाइबोनैकी एक अधिक मौलिक और सही सोने के लॉगरिदमिक अनुक्रम को अनुकूलित करने का प्रयास है, जो व्यावहारिक रूप से समान है, बस कहीं से शुरू होता है और कहीं भी नहीं जाता है। प्रकृति को किसी प्रकार के सिद्धांत की आवश्यकता होनी चाहिए, जिससे आप धक्का दे सकते हैं, यह कुछ भी नहीं बना सकता है। फाइबोनैकी अनुक्रम के पहले सदस्यों के संबंध गोल्डन सेक्शन से बहुत दूर हैं। लेकिन जितना आगे हम आगे बढ़ रहे हैं, उतना ही इन विचलन चिकना हो गए हैं। किसी भी पंक्ति को निर्धारित करने के लिए, यह अपने तीन सदस्य को एक साथ आने के लिए पर्याप्त है। लेकिन सोने के अनुक्रम के लिए नहीं, यह इसके लिए पर्याप्त है, यह एक ही समय में ज्यामितीय और अंकगणितीय प्रगति है। आपको लगता है कि यह अन्य सभी अनुक्रमों का आधार प्रतीत होता है।

गोल्डन लॉगरिदमिक अनुक्रम के प्रत्येक सदस्य सोने के अनुपात () की डिग्री है। पंक्ति का एक हिस्सा इस तरह दिखता है:... ; ; ; ; ; ; ; ; ; ; ... यदि हम तीन पात्रों के स्वर्ण अनुपात के मूल्य को गोल करते हैं, तो हमें मिलता है=1,618 , तो पंक्ति इस तरह दिखती है:... 0,090 0,146; 0,236; 0,382; 0,618; 1; 1,618; 2,618; 4,236; 6,854; 11,090 ... प्रत्येक अगले सदस्य को न केवल पिछले पर गुणा करके प्राप्त किया जा सकता है1,618 , लेकिन दो पिछले वाले लोगों के अतिरिक्त भी। इस प्रकार, घातीय वृद्धि दो आसन्न तत्वों को जोड़कर प्रदान की जाती है। यह एक शुरुआत और अंत के बिना एक संख्या है, और यह उस पर है कि यह एक समान फाइबोनैकी अनुक्रम बनने की कोशिश कर रहा है। एक अच्छी तरह से परिभाषित शुरुआत होने के बाद, वह आदर्श के लिए प्रयास करती है, कभी भी नहीं पहुंचती है। यही जीवन है।

फिर भी, सभी देखा और पढ़ने के संबंध में, काफी प्राकृतिक प्रश्न उत्पन्न होते हैं:
ये नंबर कहां से आए? ब्रह्मांड के इस वास्तुकार कौन है, जिन्होंने इसे सही बनाने की कोशिश की? क्या वह हर तरह से था? और यदि हां, तो यह क्यों आया? उत्परिवर्तन? मुक्त चयन? आगे क्या होगा? सर्पिल ट्विस्ट या स्पिन?

एक प्रश्न का उत्तर ढूंढना, आपको अगला मिलेगा। मैं इसे हल करता हूं, आपको दो नए मिलेगा। आप उन्हें समझेंगे, तीन और दिखाई देंगे। निर्णय लेना और उन्हें रखने के लिए, पांच अनसुलझे प्राप्त करें। फिर आठ, फिर तेरह, 21, 34, 55 ...

प्रयुक्त स्रोतों की सूची

Vasyutinsky, एन गोल्डन अनुपात / Vasyutinsky एन, मॉस्को, यंग गार्ड, 1 99 0, - 238 पी। - (यूरेका)।

वोरोबेव, एनएन। Fibonacci संख्या

एक्सेस मोड: । एक्सेस दिनांक: 17. 11. 2015।

एक्सेस मोड: । एक्सेस दिनांक: 16. 11. 2015।

एक्सेस मोड: । एक्सेस दिनांक: 13. 11. 2015।

बी। बिगग्स की सामग्री के अनुसार "हेडर धुंध से बाहर आया"

Fibonacci और व्यापार के बारे में

विषय के लिए एक प्रविष्टि के रूप में, हम थोड़ी देर के लिए तकनीकी विश्लेषण की ओर मुड़ते हैं। यदि हम संक्षेप में बात करते हैं, तो तकनीकी विश्लेषण पिछले ऐतिहासिक डेटा के आधार पर संपत्ति की कीमत के भविष्य के आंदोलन की भविष्यवाणी करने का कार्य रखता है। उनके समर्थकों की सबसे प्रसिद्ध शब्द कीमत पहले से ही सभी आवश्यक जानकारी शामिल है। तकनीकी विश्लेषण के कार्यान्वयन ने विनिमय चश्मा के विकास के साथ शुरुआत की और शायद अब तक पूरी तरह से पूरा नहीं किया गया है, क्योंकि संभावित रूप से असीमित कमाई होती है। Tectalize में सबसे मशहूर तकनीक (शर्तें) समर्थन और प्रतिरोध, जापानी मोमबत्तियों, आंकड़ों के स्तर और दूसरों के आंकड़े हैं।

मेरी राय में स्थिति की विरोधाभासी निम्नलिखित है - वर्णित अधिकांश विधियों को इतनी महान वितरण मिली है कि, उनकी प्रभावशीलता के लिए सबूत आधार की कमी के बावजूद, उन्हें वास्तव में बाजार के व्यवहार को प्रभावित करने का अवसर मिला। इसलिए, मौलिक डेटा का आनंद लेने वाले संदेह भी इन अवधारणाओं को ध्यान में रखना चाहिए क्योंकि वे बहुत बड़ी संख्या में अन्य खिलाड़ियों ("तकनीक") को ध्यान में रखते हैं। तकनीकी विश्लेषण इतिहास पर अच्छी तरह से काम कर सकता है, लेकिन किसी भी अभ्यास में किसी को भी कमाने के लिए संभव बनाना संभव नहीं है - अमीर होना बहुत आसान है, एक बड़ी संस्करण पुस्तक बनाना "तकनीकी विश्लेषण का उपयोग कर एक करोड़पति कैसे बनें" .. ।

इस अर्थ में, फाइबोनैकी का सिद्धांत एक हवेली के लायक है, जो विभिन्न तिथियों के लिए कीमतों की भविष्यवाणी करने के लिए भी उपयोग किया जाता है। उसके अनुयायियों को आमतौर पर "वेवविंग्स" कहा जाता है। यह सटीक रूप से एक हवेली है क्योंकि यह बाजार के साथ एक साथ दिखाई दिया, लेकिन बहुत पहले - साथ ही 800 साल भी। एक और विशेषता यह है कि सिद्धांत लगभग सब कुछ और सबकुछ के विवरण के लिए एक विश्व अवधारणा के रूप में प्रतिबिंबित किया गया था, और बाजार केवल अपने आवेदन के लिए एक विशेष मामला है। सिद्धांत और उसके अस्तित्व की प्रभावशीलता इसे नए समर्थकों और बाजारों के आधार पर बाजारों के व्यवहार के कम से कम विवादास्पद और आम तौर पर स्वीकृत विवरण तैयार करने के नए प्रयासों के साथ प्रदान करती है। लेकिन हां - कुछ सफल बाजार भविष्यवाणियां जो भाग्य के साथ समान हो सकती हैं, सिद्धांत अभी भी उन्नत नहीं है।

फाइबोनैकी सिद्धांत का सार

फिबोनैकी लंबे समय तक रहते थे, खासकर अपने समय के लिए, जीवन जो कई गणितीय कार्यों को हल करने के लिए समर्पित था, उन्हें अपने विशाल श्रम में "खातों की पुस्तक" (13 वीं शताब्दी की शुरुआत) में तैयार किया गया था। वह हमेशा रहस्यवादी संख्याओं में रुचि रखते थे - शायद वह आर्किमिडीज या यूक्लाइड की तुलना में कम जेराह नहीं था। स्क्वायर समीकरणों से जुड़ी चुनौतियों को फाइबोनैकी से पहले आंशिक रूप से हल किया गया था, उदाहरण के लिए, प्रसिद्ध उमर खायम - वैज्ञानिकों और एक कवि द्वारा; हालांकि, फाइबोनैकी ने खरगोशों के पुनरुत्पादन के कार्य को तैयार किया, निष्कर्ष जिनसे उन्होंने उन्हें शताब्दियों में अपनी ओर से खोने की अनुमति नहीं दी।

संक्षेप में, कार्य निम्नानुसार है। जगह में, दीवार से सभी तरफ से फंसे हुए, दो खरगोशों को रखा, और खरगोशों की किसी भी जोड़ी अपने अस्तित्व के दूसरे महीने से शुरू होने वाले हर महीने एक और जोड़े की रोशनी लेती है। समय में खरगोशों का पुनरुत्पादन अनुक्रम द्वारा वर्णित किया जाएगा: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, आदि गणितीय दृष्टिकोण से, अनुक्रम केवल अद्वितीय था, क्योंकि कई उत्कृष्ट गुण हैं:

• लगातार दो संख्याओं का योग निम्नलिखित अनुक्रमों की संख्या है;

• पांचवें से शुरू होने वाले प्रत्येक अनुक्रमों का अनुपात, पिछले एक के लिए, 1.618 है;

• किसी भी संख्या के वर्ग के बीच का अंतर और बाईं ओर दो पदों में संख्या का वर्ग फाइबोनैकी की संख्या होगी;

• संख्याओं के बगल में खड़े वर्गों का योग फाइबोनैकी की संख्या होगी, जो संख्याओं के वर्ग में अधिक ऊंचा होने के बाद दो पदों के माध्यम से खड़ी होती है

इन निष्कर्षों में से, दूसरा सबसे दिलचस्प है, क्योंकि यह संख्या 1.618 का उपयोग करता है, जिसे गोल्डन सेक्शन के नाम से जाना जाता है। यह संख्या प्राचीन यूनानियों के लिए जानी गई थी जो इसे पारफेनन के निर्माण के दौरान उपयोग करते थे (वैसे, चेक्सम सेंट्रल बैंक द्वारा दी गई कुछ आंकड़ों के मुताबिक)। कोई कम दिलचस्प नहीं है और तथ्य यह है कि 1.618 की संख्या सूक्ष्म और मैक्रोस्केल में प्रकृति में पाया जा सकता है - स्नेल खोल पर सर्पिल के मोड़ से ब्रह्मांड आकाशगंगाओं के बड़े सर्पिल तक। प्राचीन मिस्र के लोगों द्वारा बनाई गई गीज़ा में पिरामिड में फाइबोनैकी पंक्ति के कई पैरामीटर भी शामिल थे। आयताकार, जिसमें से एक तरफ 1.618 गुना है, आंखों के लिए सबसे अच्छा लग रहा है - इस अनुपात में लियोनार्डो दा विंची ने अपनी पेंटिंग्स के लिए किया, और एक और अधिक योजना में, वे कभी-कभी खिड़कियां या दरवाजे बनाते समय उपयोग करते थे। यहां तक \u200b\u200bकि एक लहर, लेख की शुरुआत में तस्वीर में, को फाइबोनैकी के सर्पिल के रूप में दर्शाया जा सकता है।

जंगल में, फाइबोनैकी अनुक्रम स्वयं को अक्सर प्रकट नहीं करता है - यह पंजे, दांत, सूरजमुखी, वेब और यहां तक \u200b\u200bकि बैक्टीरिया के प्रजनन में भी पाया जा सकता है। यदि वांछित है, तो अनुक्रम मानव चेहरे और शरीर सहित लगभग हर चीज में पाया जाता है। फिर भी, एक राय है कि कई आरोप जो प्राकृतिक और ऐतिहासिक घटनाओं में फिबोनाकी की संख्याएं गलत हैं - यह एक आम मिथक है, जो अक्सर वांछित परिणाम के तहत गलत है।

वित्तीय बाजारों में Fibonacci संख्या

पहले में से एक, जो वित्तीय बाजार में फाइबोनैकी नंबरों की नियुक्ति में सबसे घनिष्ठ रूप से व्यस्त था, आर। इलियट था। उनके कार्य इस अर्थ में गायब नहीं हुए थे कि फाइबोनैकी सिद्धांत के उपयोग के साथ बाजार विवरण अक्सर "इलियट की तरंगों" के रूप में जाना जाता है। बाजारों के विकास का आधार यहां सुपरकॉकर्स से मानवता के विकास के लिए एक मॉडल था जो तीन कदम आगे और दो पीछे की तरफ था। तथ्य यह है कि मानवता गैर-रैखिक रूप से लगभग सभी के लिए विकसित हो रही है - प्राचीन मिस्र का ज्ञान और डेमोक्रिटस की परमाणु शिक्षण मध्य युग में पूरी तरह से खो गया था, यानी लगभग 2000 साल; 20 वीं शताब्दी ने इस तरह के डरावनी और मानव जीवन की अस्थिरता को जन्म दिया, जो कि यूनानियों के दंडित युद्धों के युग में भी कल्पना करना मुश्किल था। हालांकि, यहां तक \u200b\u200bकि अगर हम सत्य के लिए कदम और उनकी संख्या का सिद्धांत लेते हैं, तो यह प्रत्येक चरण के आकार का अस्पष्ट रहता है, जो इलियट की तरंगों को ईगल और रश के पूर्वानुमानित बल से तुलनीय बनाता है। शुरुआती बिंदु और तरंगों की संख्या की सही गणना और स्पष्ट रूप से सिद्धांत की मुख्य कमजोरी होगी।

फिर भी, सिद्धांत में स्थानीय प्रगति थी। बॉब पोस्टेचर, जिसे इलियट के छात्र माना जा सकता है, सही ढंग से 80 के दशक के शुरुआती बाजार की भविष्यवाणी की, और 1 9 87 - एक कुंडा के रूप में। यह वास्तव में हुआ, जिसके बाद बॉब स्पष्ट रूप से एक प्रतिभा की तरह महसूस किया - कम से कम दूसरों की नजर में, वह वास्तव में एक निवेश गुरु बन गया। इलियट वेव प्रमेय पोस्टर की सदस्यता लें 20,000 तक बढ़ी,हालांकि, 1 99 0 के दशक की शुरुआत में, अमेरिकी बाजार द्वारा भविष्यवाणी की गई "मृत्यु और अंधेरे" के बाद से थोड़ा इंतजार करने का फैसला किया गया। हालांकि, जापानी बाजार के लिए यह काम किया, और सिद्धांत के कई समर्थकों, एक लहर के लिए "देर", एक लहर के लिए, या तो उनकी पूंजी, या उनकी पूंजीगत ग्राहकों को खो दिया। समान रूप से, समान सफलताओं के साथ, सिद्धांत अक्सर विदेशी मुद्रा बाजार में व्यापार के लिए आवेदन करने की कोशिश कर रहा है।

सिद्धांत में विभिन्न व्यापारिक अवधि शामिल हैं - साप्ताहिक से, जो इसे दशकों तक गणना तक, Thekanalysis के लिए मानक रणनीतियों से संबंधित है, यानी मौलिक भविष्यवाणियों के क्षेत्र में बंद हो जाता है। लहरों की संख्या में भिन्नता के कारण यह संभव है। उपरोक्त वर्णित सिद्धांत की कमजोरियों को अपने एडीप्ट को तरंगों की दिवालियापन के बारे में बात नहीं करने की अनुमति नहीं है, बल्कि उनके बीच अपनी गलतियों के बारे में और प्रारंभिक स्थिति की गलत परिभाषा के बारे में है। यह एक भूलभुलैया की तरह दिखता है - भले ही आपके पास एक वफादार कार्ड हो, फिर आप केवल तभी जा सकते हैं जब आप समझते हैं कि आप कहां हैं। अन्यथा, मानचित्र से कोई फायदा नहीं है। इलियट की तरंगों के मामले में, न केवल उनके स्थान की शुद्धता में बल्कि कार्ड की वफादारी में संदेह करने के लिए सभी संकेत हैं।

निष्कर्ष

मानवता के लहर विकास में वास्तविक आधार है - मध्य युग में, मुद्रास्फीति और अपस्फीति की लहरें एक-दूसरे के साथ वैकल्पिक होती हैं, जब युद्ध ने अपेक्षाकृत शांतिपूर्ण शांतिपूर्ण जीवन को बदल दिया। कम से कम संदेह के कुछ मामलों में प्रकृति में फिबोनाची अनुक्रम का अवलोकन भी नहीं होता है। इसलिए, ईश्वर कौन है: एक गणितज्ञ या यादृच्छिक संख्या जनरेटर - को अपना जवाब देने का अधिकार है। निजी तौर पर, मेरी राय ऐसी है कि हालांकि सभी मानव इतिहास और बाजारों को तरंग अवधारणा में दर्शाया जा सकता है, लेकिन प्रत्येक लहर की ऊंचाई और अवधि किसी को भी भविष्यवाणी करने के लिए नहीं दी जाती है।

साथ ही, अमेरिकी बाजार पर 200 वर्षों के अवलोकनों और 100 से अधिक वर्षों को स्पष्ट रूप से यह कहने की अनुमति है कि शेयर बाजार बढ़ रहा है, जो विकास और स्थिरता की विभिन्न अवधि के माध्यम से गुजर रहा है। यह तथ्य शेयर बाजार में लंबी अवधि की कमाई के लिए पर्याप्त है, बिना विवादास्पद सिद्धांतों का सहारा लिया जाएगा और उचित जोखिमों के हिस्से के रूप में इसकी तुलना में अधिक पूंजी पर भरोसा किया जा सकता है।

खानलियेवा दाना

इस पेपर में, हमने अपने आस-पास की वास्तविकता में फाइबोनैकी अनुक्रम की संख्या के अभिव्यक्ति का अध्ययन और विश्लेषण किया। हमें पौधों में सर्पिल की संख्या, किसी भी क्षैतिज विमान में शाखाओं की संख्या और फाइबोनैकी अनुक्रम की संख्या के बीच एक अद्भुत गणितीय संबंध मिला। हमने एक व्यक्ति की संरचना में सख्त गणित भी देखा। मानव डीएनए अणु, जिसमें पूरे मानव विकास कार्यक्रम एन्क्रिप्ट किया गया है, श्वसन प्रणाली, कान संरचना - सब कुछ कुछ संख्यात्मक अनुपात का पालन करता है।

हमें आश्वस्त किया गया था कि प्रकृति के पास गणित द्वारा व्यक्त किए गए कानून हैं।

और गणित तो ज्ञान का एक महत्वपूर्ण उपकरण प्रकृति के रहस्य।

डाउनलोड:

पूर्वावलोकन:

Mbou "Pervomaisk माध्यमिक विद्यालय"

ऑरेनबर्ग क्षेत्र के ओरेनबर्ग जिले

अनुसंधान

"संख्या का रहस्य

Fibonacci "

प्रदर्शन किया: Canaliyeva दाना

ग्रेड 6 छात्र

वैज्ञानिक सलाहकार:

Gazizova Valery Valerievna

उच्चतम श्रेणी के गणित शिक्षक

पी। प्रायोगिक

2012

व्याख्यात्मक नोट ................................................ .............................. ........ 3।

परिचय Fibonacci संख्या का इतिहास। ............................................. ..................... 4।

अध्याय 1. वन्यजीवों में फाइबोनैकी की संख्या ....... ....... …………………………………... पांच।

अध्याय 2. सर्पिल Fibonacci ............................................. .... .......... ............... ..... नौ।

अध्याय 3. किसी व्यक्ति के आविष्कारों में फाइबोनैकी की संख्या ......... ............................ ..... .. 13

अध्याय 4. हमारा शोध ............................................. ........................... .... 16।

अध्याय 5. निष्कर्ष, निष्कर्ष ............................................ .............................. 19।

इंटरनेट की प्रयुक्त साहित्य और वेबसाइटों की सूची ....................................... .. ...... 21।

अध्ययन का उद्देश्य:

मनुष्य, गणितीय अमूर्तता मनुष्य द्वारा बनाई गई, पौधे और पशु दुनिया के आस-पास के व्यक्ति के आविष्कार।

अध्ययन का विषय:

अध्ययन वस्तुओं और घटनाओं का रूप और संरचना।

इस अध्ययन का उद्देश्य:

फाइबोनैकी संख्याओं और जीवित रहने और गैर-जीवित वस्तुओं की संरचना में सुनहरे खंड के कानून के अभिव्यक्ति का अन्वेषण करें

fibonacci संख्याओं का उपयोग करने के उदाहरण खोजें।

कार्य के कार्य:

Fibonacci और सर्पिल Fibonacci की एक पंक्ति बनाने की विधि का वर्णन करें।

गणितीय पैटर्न देखें, मनुष्य की संरचना में, गोल्डन क्रॉस सेक्शन की घटना के दृष्टिकोण से शांति और निर्जीव प्रकृति का संयंत्र करें।

नवीनता अध्ययन:

आसपास की वास्तविकता में फाइबोनैकी संख्याओं का उद्घाटन।

व्यवहारिक महत्व:

अन्य स्कूल वस्तुओं के अध्ययन में अधिग्रहित ज्ञान और अनुसंधान कौशल का उपयोग।

दक्षताएं और योग्यताएं:

प्रयोग और प्रयोग का आचरण।

विशेष साहित्य का उपयोग करना।

एकत्रित सामग्री की समीक्षा करने की क्षमता का अधिग्रहण (रिपोर्ट, प्रस्तुति)

चित्र, आरेख, तस्वीरों के साथ डिजाइन काम।

आपके काम की चर्चा में सक्रिय भागीदारी।

अनुसंधान की विधियां:

अनुभवजन्य (अवलोकन, प्रयोग, माप)।

सैद्धांतिक (ज्ञान का तार्किक स्तर)।

व्याख्यात्मक नोट।

"संख्या दुनिया का प्रबंधन! संख्या देवताओं और प्राणियों पर शासन करने वाली शक्ति है! " - इसलिए उन्होंने अधिक प्राचीन पायथागोरियन कहा। क्या यह आज पायथागोरा की शिक्षाओं का आधार है? स्कूल विज्ञान संख्या में अध्ययन करना, हम यह सुनिश्चित करना चाहते हैं कि वास्तव में, पूरे ब्रह्मांड की घटना कुछ संख्यात्मक संबंधों के अधीन है, गणित और जीवन के बीच इस अदृश्य संबंध को ढूंढें!

क्या यह वास्तव में हर फूल में है

और अणु में और आकाशगंगा में,

संख्यात्मक पैटर्न

यह सख्त "सूखा" गणित?

हम सूचना के एक आधुनिक स्रोत में बदल गए - इंटरनेट पर और फिबोनाची संख्याओं के बारे में पढ़ा, जादुई संख्याओं के बारे में जो एक महान पहेली बनाते हैं। यह पता चला है कि इन नंबरों को मानव हृदय की लय में और संगीत लय में, ड्रैगनफ्लाई और स्टारफिश के पंखों में सूरजमुखी और पाइन शंकुओं में पाया जा सकता है ...

हमारी दुनिया में संख्याओं का यह अनुक्रम इतना आम क्यों है?

हम फाइबोनैकी नंबरों के रहस्यों के बारे में जानना चाहते थे। हमारी गतिविधि का परिणाम और यह शोध कार्य था।

परिकल्पना:

आसपास की वास्तविकता में, सबकुछ गणितीय सटीकता के साथ आश्चर्यजनक रूप से सामंजस्यपूर्ण कानूनों में बनाया गया है।

दुनिया में सबकुछ विचारशील है और हमारी डिजाइनर - प्रकृति की सबसे महत्वपूर्ण गणना की जाती है!

परिचय कई फाइबोनैकी की कहानी।

इतालवी गणितज्ञ मध्य युग लियोनार्डो पिसंस्की द्वारा अद्भुत संख्याएं खोली गईं, जिसे फाइबोनैकी नाम के तहत अधिक प्रसिद्ध किया गया था। पूर्व में यात्रा, उन्होंने अरब गणित की उपलब्धियों से मुलाकात की, उन्हें पश्चिम में स्थानांतरित करने में योगदान दिया। उनके एक कार्यों में, "कंप्यूटिंग बुक" नाम के तहत, उन्होंने यूरोप को हर समय और लोगों की सबसे बड़ी खोजों में से एक प्रस्तुत किया - एक दशमलव संख्या प्रणाली।

एक बार, उन्होंने एक गणितीय कार्य के समाधान पर अपना सिर तोड़ दिया। उन्होंने प्रजनन खरगोशों के अनुक्रम का वर्णन करने वाला एक सूत्र बनाने की कोशिश की।

रैलीिंग एक संख्यात्मक संख्या थी, प्रत्येक बाद की संख्या जिसमें से दो पिछले दो का योग होता है:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, ...

इस अनुक्रम को बनाने वाली संख्या को "फाइबोनैकी संख्या" कहा जाता है, और अनुक्रम स्वयं एक फाइबोनैकी अनुक्रम है।

"तो क्या?" - आप आपको बताएंगे, "क्या हम खुद को ऐसी संख्यात्मक पंक्तियों के साथ आए हैं जो दी गई प्रगति के लिए बड़े होते हैं?" दरअसल, जब कई फाइबोनैकी दिखाई दिए, कोई भी, वह स्वयं सहित, संदेह नहीं था कि वह ब्रह्मांड के सबसे महान रहस्यों में से एक के करीब कैसे पहुंचे!

फाइबोनैकी का नेतृत्व एक समलैंगिक जीवनशैली के नेतृत्व में किया गया था, प्रकृति में बहुत समय बिताया, और जंगल में घूमते हुए, उन्होंने देखा कि ये संख्याएं सचमुच उनका पीछा कर रही थीं। प्रकृति में हर जगह, वह फिर से इन संख्याओं से मुलाकात की। उदाहरण के लिए, पौधों की पंखुड़ियों और पत्तियों ने इस संख्यात्मक श्रृंखला में सख्ती से रखी।

फाइबोनैकी नंबरों में, एक दिलचस्प विशेषता है: पिछले एक के लिए फाइबोनैकी की बाद की संख्या को विभाजित करने से निजी, क्योंकि संख्याएं स्वयं बढ़ती हैं, 1.618 के लिए प्रयास करती हैं। यह मध्य युग में विभाजन की यह निरंतर संख्या है जिसे दिव्य अनुपात कहा जाता था, और अब इसे गोल्ड क्रॉस सेक्शन या गोल्डन अनुपात कहा जाता है।

बीजगणित में, यह संख्या gpeech अक्षर fi (f) द्वारा इंगित की गई है

तो, φ \u003d 1,618

233 / 144 = 1,618

377 / 233 = 1,618

610 / 377 = 1,618

987 / 610 = 1,618

1597 / 987 = 1,618

2584 / 1597 = 1,618

कितनी बार हमने एक चीज़ को दूसरे से विभाजित नहीं किया, उनके साथ नंबर पड़ोसियों, हम हमेशा 1, 618 प्राप्त करते हैं। और यदि हम दूसरी तरफ करते हैं, तो हम एक छोटी संख्या को अधिक विभाजित करते हैं, फिर हमें 0, 618 मिलते हैं , यह 1, 618 के विपरीत संख्या है, जिसे सोने का अनुपात भी कहा जाता है।

Fibonacci एक संख्या केवल एक गणितीय घटना रह सकती है, अगर यह इस तथ्य के लिए नहीं था कि पौधे में और जानवरों की दुनिया में सुनहरे विभाजन में सभी शोधकर्ता, कला का जिक्र नहीं करते हैं, इस श्रृंखला में हमेशा इस श्रृंखला में आया, की अंकगणितीय अभिव्यक्ति के रूप में गोल्डन डिवीजन का कानून।

वैज्ञानिकों ने प्राकृतिक घटनाओं और प्रक्रियाओं के लिए इस संख्यात्मक श्रृंखला के आगे उपयोग का विश्लेषण किया, पाया कि ये संख्याएं शाब्दिक रूप से वन्यजीवन की सभी वस्तुओं, पौधों में, जानवरों और मनुष्यों में निहित हैं।

एक अद्भुत गणितीय खिलौना ब्रह्मांड के निर्माता द्वारा सभी प्राकृतिक वस्तुओं में एम्बेडेड एक अद्वितीय कोड बन गया।

उन उदाहरणों पर विचार करें जहां Fibonacci नंबर रहते हैं और निर्जीव प्रकृति पाए जाते हैं।

वन्यजीवन में Fibonacci संख्या।

यदि आप हमारे आस-पास के पौधों और पेड़ों को देखते हैं, तो यह देखा जा सकता है कि उनमें से प्रत्येक पर कितनी पत्तियां हैं। दूर से, ऐसा लगता है कि पौधों पर शाखाएं और पत्तियां किसी भी क्रम में यादृच्छिक रूप से स्थित हैं। हालांकि, सभी पौधों में यह चमत्कारी रूप से है, गणितीय रूप से सटीक योजना बनाई गई है, जहां से यह शाखाओं और पत्तियों की तरह बढ़ेगा, जो स्टेम या ट्रंक के पास स्थित होगा। उपस्थिति के पहले दिन से, पौधे इन कानूनों के आधार पर वास्तव में अपने विकास में होना चाहिए, यानी कोई शीट नहीं, कोई फूल मौका से प्रकट नहीं होता है। उपस्थिति से पहले भी, पौधे पहले से ही accogrammed है। भविष्य के पेड़ पर कितनी शाखाएं होंगी, जहां शाखाएं बढ़ेगी, प्रत्येक शाखा पर कितनी पत्तियां होंगी, और कैसे, किस क्रम में पत्ते स्थित होंगे। नर्ड्स और गणितज्ञों का संयुक्त कार्य प्रकृति की इन अद्भुत घटनाओं पर प्रकाश डालता है। यह पता चला कि शाखा (फ्योटैक्सिस) पर पत्तियों के स्थान पर, साइकल में पत्तियों के बीच, स्लाइस में पत्तियों के बीच, चक्र में कई फाइबोनैकी प्रकट होते हैं, और इसलिए, गोल्डन सेक्शन का कानून प्रकट होता है.

यदि आप वन्यजीवन में संख्यात्मक पैटर्न खोजने का लक्ष्य निर्दिष्ट करते हैं, तो ध्यान दें कि ये संख्याएं अक्सर विभिन्न सर्पिल रूपों में पाए जाते हैं जो पौधों की दुनिया इतनी समृद्ध होती है। उदाहरण के लिए, पत्तियों की कटिंग सर्पिल के डंठल के समीप होती है, जो बीच में गुजरती हैदो आसन्न पत्तियां: पूर्ण कारोबार - ओस्निक, - ओक, - poplar और नाशपाती, - विलो।

सूरजमुखी के बीज, बैंगनी के इचिनेसिया और कई अन्य पौधे सर्पिल स्थित हैं, और प्रत्येक दिशा के सर्पिल की संख्या - फाइबोनैकी की संख्या।

सूरजमुखी, 21 और 34 सर्पिल। इचिनेसिया, 34 और 55 सर्पिल।

रंगों का एक स्पष्ट, सममित रूप भी सख्त कानून के अधीन है।.

कई रंगों में पंखुड़ियों की संख्या होती है - बिल्कुल फाइबोनैकी रेंज से संख्याएं। उदाहरण के लिए:

आईरिस, 3let। बटरकप, 5 लेप। Zlatocevet, 8 लेप। डेल्फिनियम,

13 लेप।

chicory, 21let। एस्ट्रा, 34 ली। डेज़ी, 55 पी।

कई फाइबोनैकी कई जीवित प्रणालियों के संरचनात्मक संगठन की विशेषता है।

हमने पहले ही कहा है कि फाइबोनैकी की पंक्ति में पड़ोसी नंबरों के संबंधों में संख्या φ \u003d 1.618 है। यह पता चला है कि दोनों व्यक्ति स्वयं केवल एक स्टोरहाउस हैं।

हमारे शरीर के विभिन्न हिस्सों के अनुपात में एक संख्या है, जो सुनहरा खंड के बहुत करीब है। यदि ये अनुपात गोल्डन सेक्शन के सूत्र के साथ मेल खाते हैं, तो किसी व्यक्ति की उपस्थिति या शरीर को पूरी तरह से फोल्ड माना जाता है। मानव शरीर पर सुनहरे उपाय की गणना करने का सिद्धांत एक स्कीमा के रूप में चित्रित किया जा सकता है।

M / m \u003d 1,618

मानव शरीर की संरचना में एक सुनहरे खंड का पहला उदाहरण:

यदि आप पिल्ला के मानव शरीर का केंद्र लेते हैं, और माप की प्रति इकाई एक व्यक्ति और पिल्ला बिंदु के बीच की दूरी, तो मानव ऊंचाई संख्या 1.618 के बराबर होती है।

मानवीय हाथ

यह सिर्फ अपने हथेली को अपने आप को लाने और सावधानीपूर्वक इंडेक्स उंगली को देखने के लिए पर्याप्त है, और आप तुरंत इसे गोल्डन सेक्शन का सूत्र ढूंढते हैं। हमारे हाथ की प्रत्येक उंगली में तीन फालेंज होते हैं।
पूरी उंगली की लंबाई से अनुपात में उंगली के दो पहली फालंचों का योग और गोल्डन सेक्शन की संख्या (अंगूठे को छोड़कर) देता है।

इसके अलावा, मध्य उंगली और छोटी उंगली के बीच का अनुपात भी सुनहरे वर्गों की संख्या के बराबर है।

एक व्यक्ति के पास 2 हाथ होते हैं, प्रत्येक हाथ पर उंगलियों में 3 फालेंज होते हैं (अंगूठे को छोड़कर)। प्रत्येक तरफ 5 अंगुलियां होती हैं, यानी, केवल 10, लेकिन दो दो चरण अंगूठे के अपवाद के साथ केवल 8 अंगुलियों को गोल्डन सेक्शन के सिद्धांत के अनुसार बनाया जाता है। हालांकि ये सभी संख्या 2, 3, 5 और 8 फिबोनासी अनुक्रम की संख्या हैं।

प्रकाश आदमी की संरचना में गोल्डन अनुपात

अमेरिकी भौतिक विज्ञानी बीडी.यूएएसटी और डॉ एएल। फिजिको-रचनात्मक अध्ययनों के दौरान गोल्डबर्गर ने पाया कि मानव फेफड़ों की संरचना में एक गोल्डन क्रॉस सेक्शन भी मौजूद है।

ब्रोंची की विशिष्टता, मानव फेफड़ों के घटक, उनकी विषमता में संलग्न है। ब्रोंची में दो मुख्य श्वसन पथ होते हैं, जिनमें से एक (बाएं) लंबा होता है, और दूसरा (दाएं) छोटा होता है।

यह पाया गया कि यह विषमता ब्रोंची की शाखाओं में सभी छोटे श्वसन पथ में जारी है। इसके अलावा, शॉर्ट और लांग ब्रोंची की लंबाई का अनुपात भी 1: 1.618 के बराबर एक गोल्डन क्रॉस सेक्शन है।

कलाकार, वैज्ञानिक, फैशन डिजाइनर, डिजाइनर गोल्डन सेक्शन के अनुपात के आधार पर अपनी गणना, चित्र या स्केच बनाते हैं। वे गोल्डन सेक्शन के सिद्धांत पर भी बनाए गए मानव शरीर से माप का उपयोग करते हैं। लियोनार्डो दा विंची और ली कॉर्बूसियर अपनी उत्कृष्ट कृतियों को बनाने से पहले सुनहरे अनुपात के कानून के तहत बनाए गए मानव शरीर के मानकों को ले लिया।
मानव शरीर के अनुपात का एक और, अधिक प्रायोजन अनुप्रयोग है। उदाहरण के लिए, मानव शरीर के हिस्सों के टुकड़ों पर इन संबंधों, आपराधिक विश्लेषकों और पुरातत्त्वविदों का उपयोग पूरे की उपस्थिति को बहाल करते हैं।

डीएनए अणु की संरचना में सोने का अनुपात।

जीवित प्राणियों की शारीरिक विशेषताओं के बारे में सभी जानकारी, चाहे वह एक पौधे, एक जानवर या व्यक्ति है, एक डीएनए माइक्रोस्कोपिक अणु में संग्रहीत किया जाता है, जिसकी संरचना में सुनहरा अनुपात का कानून भी होता है। डीएनए अणु में दो लंबवत मुड़दार सर्पिल होते हैं। इनमें से प्रत्येक सर्पिल की लंबाई 34 एंगस्ट्रॉम, चौड़ाई 21 एंगस्ट्रॉम है। (1 एंगस्ट्रॉम - सेंटीमीटर का एक वेलोमिलियन हिस्सा)।

तो 21 और 34 संख्याएं हैं, एक दूसरे के बाद फाइबोनैकी संख्याओं के अनुक्रम में, यानी, डीएनए अणु के लॉगरिदमिक सर्पिल की लंबाई और चौड़ाई का अनुपात गोल्डन सेक्शन 1: 1.618 का सूत्र होता है।

न केवल कताई, बल्कि सभी फ़्लोटिंग, क्रॉलिंग, फ्लाइंग और कूदते फाई की संख्या का पालन करने के लिए भाग्य से बच नहीं गए। हृदय की मांसपेशियों को इसकी मात्रा के 0, 618 तक कम हो जाता है। घोंघा खोल की संरचना फाइबोनैकी के अनुपात से मेल खाती है। और ऐसे उदाहरणों को बहुत कुछ पाया जा सकता है - प्राकृतिक वस्तुओं और प्रक्रियाओं का पता लगाने की इच्छा होगी। दुनिया को फिबोनाची संख्याओं से इतनी अनुमति दी गई है कि कभी-कभी ऐसा लगता है: केवल ब्रह्मांड और समझाया जा सकता है।

सर्पिल Fibonacci।

गणित में कोई अन्य रूप नहीं है जिसमें सर्पिल के समान अद्वितीय गुण होंगे, क्योंकि
सर्पिल की संरचना गोल्डन सेक्शन के नियम पर आधारित है!

सर्पिल के गणितीय निर्माण को समझने के लिए, गोल्डन क्रॉस सेक्शन दोहराएं।

गोल्डन सेक्शन असमान हिस्सों पर सेगमेंट का एक आनुपातिक विभाजन है, जिसमें पूरे सेगमेंट अधिकांश भाग से संबंधित है, क्योंकि उनमें से अधिकतर छोटे से संबंधित हैं, या, दूसरे शब्दों में, छोटे सेगमेंट अधिक से अधिक है हर एक चीज़।

वह (ए + बी) / ए \u003d ए / बी है

इस तरह के पक्षों के साथ आयत को सुनहरा आयताकार कहा जाता है। इसके लंबे पक्ष 1,168: 1 के अनुपात में छोटी पार्टियों के साथ सहसंबंधित होते हैं।
गोल्डन आयताकार में कई असामान्य गुण हैं। स्वर्ण आयताकार वर्ग से काटकर, जिस का पक्ष आयताकार के छोटे पक्ष के बराबर है,

हम फिर से छोटे आकार के एक सुनहरा आयताकार प्राप्त करते हैं।

इस प्रक्रिया को अनंतता जारी रखा जा सकता है। वर्गों को काटने के लिए, हम सभी छोटे और छोटे सोने के आयत प्राप्त करेंगे। इसके अलावा, वे लॉगरिदमिक सर्पिल के साथ स्थित होंगे, जो प्राकृतिक वस्तुओं के गणितीय मॉडल में महत्वपूर्ण है।

उदाहरण के लिए, सूरजमुखी के बीज, अनानास, कैक्टस, गुलाब की पंखुड़ियों की संरचना आदि के स्थान पर एक सर्पिल आकार देखा जा सकता है।

हम सर्पिल की सर्पिल संरचना को आश्चर्यचकित और प्रसन्न कर रहे हैं।

अधिकांश घोंघे जो सिंक होते हैं, खोल एक सर्पिल के रूप में बढ़ता है। हालांकि, इसमें कोई संदेह नहीं है कि इन अनुचित प्राणियों को न केवल हेलिक्स के बारे में कोई विचार नहीं है, लेकिन सर्पिल सिंक बनाने के लिए भी सबसे सरल गणितीय ज्ञान नहीं है।
लेकिन जब ये अनुचित प्राणी सर्पिल खोल के रूप में विकास और अस्तित्व के आदर्श रूप को निर्धारित करने और चुनने में सक्षम थे? क्या ये जीवित प्राणी, जिन्हें विश्व वैज्ञानिक जीवन के आदिम रूपों को बुलाते हैं, गणना करते हैं कि शेल का सर्पिल रूप उनके अस्तित्व के लिए आदर्श है?

कम से कम बेतुका कुछ प्राकृतिक परिस्थितियों के एक यादृच्छिक कोच के साथ जीवन के इस तरह के आदिम रूप की उत्पत्ति की व्याख्या करने की कोशिश कर रहा है। यह काफी स्पष्ट है कि यह परियोजना सृजन के बारे में जागरूक है।

सर्पिल आदमी में हैं। सर्पिल की मदद से, हम सुनते हैं:

साथ ही, किसी व्यक्ति के आंतरिक कान में एक कोचली ("स्नेल") प्राधिकरण है, जो ध्वनि कंपन को प्रेषित करने का कार्य करता है। यह बोनिफॉर्म संरचना तरल से भरी हुई है और सोने के अनुपात वाले घोंघे के रूप में बनाई गई है।

सर्पिल हमारे हथेलियों और उंगलियों पर हैं:

पशु दुनिया में, हम सर्पिल के कई उदाहरण भी पा सकते हैं।

एक सर्पिल, सींग और पशु पूंछ के रूप में विकसित हो रहे हैं, शेरों के पंजे और तोते के क्लैक्स लॉगरिदमिक रूप हैं और धुरी के आकार जैसा दिखते हैं, सर्पिल से संपर्क करने के लिए प्रवण होते हैं।

दिलचस्प बात यह है कि एक तूफान कुंडल, चक्रवात बादल मोड़ और यह अंतरिक्ष से स्पष्ट रूप से देखा जाता है:

सागर और समुद्री तरंगों में, सर्पिल गणितीय रूप से चार्ट पर अंक 1,1,2,3,5,8,13,21,34 और 55 के साथ प्रतिबिंबित किया जा सकता है।

इस तरह के एक "घर" और "गद्य" सर्पिल भी सबकुछ सीखेंगे।

आखिरकार, सर्पिल में पानी बाथरूम से बाहर निकलता है:

हां, और हम आपके साथ सर्पिल में रहते हैं, क्योंकि गैलेक्सी गोल्डन सेक्शन के सूत्र के अनुरूप एक सर्पिल है!

इसलिए, हमने पाया कि यदि आप एक सुनहरा आयताकार लेते हैं और इसे छोटे आयतों में विभाजित करते हैं फाइबोनैकी के सटीक अनुक्रम में, और फिर उनमें से प्रत्येक को इस तरह के अनुपात में बांटा गया है, यह एक ऐसी प्रणाली को बदल देगा जिसे फाइबोनैकी सर्पिल कहा जाता है।

हमने सबसे अप्रत्याशित विषयों और घटनाओं में यह सर्पिल पाया। अब यह स्पष्ट है कि सर्पिल को "जीवन की वक्र" कहा जाता है।
सर्पिल विकास का प्रतीक बन गया, क्योंकि यह सब कुछ ठीक से विकसित करता है।

मानव आविष्कारों में फिबोनासी संख्या।

स्वाभाविक रूप से सिलाई स्वाभाविक रूप से फाइबोनैकी संख्याओं, वैज्ञानिकों और कला के लोगों के अनुक्रम द्वारा व्यक्त कानून उनकी रचनाओं में इस कानून को शामिल करने के लिए अनुकरण करने का प्रयास करता है।

फाई का अनुपात आपको अंतरिक्ष में वास्तुशिल्प संरचनाओं को फिट करने के लिए चित्रकला की उत्कृष्ट कृतियों को बनाने की अनुमति देता है।

न केवल विज्ञान के आंकड़े, बल्कि आर्किटेक्ट्स, डिजाइनर और कलाकार भी रॉकशल नॉटिलस में इस निर्दोष सर्पिल द्वारा आश्चर्यचकित हैं,

सबसे छोटी जगह होने और सबसे छोटी गर्मी की कमी सुनिश्चित करना। अमेरिकी और थाई आर्किटेक्ट्स कम से कम स्थान में अधिकतम रखने के मुद्दे में "कैमरे के साथ नॉटिलस" के उदाहरण से प्रेरित हैं, प्रासंगिक परियोजनाओं के विकास में लगे हुए हैं।

प्राचीन काल से, गोल्डन सेक्शन का अनुपात पूर्णता, सद्भाव और यहां तक \u200b\u200bकि दिव्यता का उच्चतम अनुपात माना जाता है। मूर्तियों में और संगीत में भी सुनहरा रवैया का पता लगाया जा सकता है। एक उदाहरण मोजार्ट के संगीत कार्यों है। यहां तक \u200b\u200bकि हब्रू के स्टॉक कोर्स और वर्णमाला में सोने का रिश्ता होता है।

लेकिन हम एक प्रभावी सौर स्थापना बनाने के एक अद्वितीय उदाहरण पर रहना चाहते हैं। न्यूयॉर्क एडन ड्यूयर के एक अमेरिकी स्कूलबॉय ने पेड़ों के बारे में अपने ज्ञान को एक साथ दिया है और पाया है कि यदि आप गणित को आकर्षित करते हैं तो सौर ऊर्जा संयंत्रों की दक्षता को बढ़ाया जा सकता है। शीतकालीन चलने पर होने के नाते, डुएर ने सोचा, क्यों पेड़ शाखाओं और पत्तियों के "ड्राइंग" हैं। वह जानता था कि पेड़ पर शाखाएं फाइबोनैकी अनुक्रम के अनुसार स्थित हैं, और पत्तियां प्रकाश संश्लेषण की जाती हैं।

किसी बिंदु पर, अद्भुत लड़के ने यह जांचने का फैसला किया कि शाखा शाखाओं को अधिक धूप इकट्ठा करने में मदद नहीं करती है या नहीं। आइडन ने पत्तियों के बजाए छोटे सौर पैनलों के साथ अपने पिछवाड़े में एक अनुभवी स्थापना का निर्माण किया और इसे कार्रवाई में चेक किया। यह पता चला कि सामान्य फ्लैट सौर पैनल की तुलना में, उसका "पेड़" 20% अधिक ऊर्जा होता है और 2.5 घंटे के लिए अधिक प्रभावी ढंग से काम करता है।

एक स्कूलबॉय द्वारा निर्मित एक ड्वेयर सौर पेड़ और ग्राफिक्स का मॉडल।

"और इस तरह की एक स्थापना एक फ्लैट पैनल की तुलना में कम जगह लेती है, सर्दियों में सूर्य की तुलना में 50% अधिक एकत्र करता है, भले ही यह दक्षिण में न देखे, और उस मात्रा में बर्फ यह जमा नहीं होता है। इसके अलावा, फॉर्म में डिजाइन युवा आविष्कारक नोट्स "शहरी परिदृश्य के लिए एक पेड़ अधिक उपयुक्त है।"

ईदाना मान्यता प्राप्त सबसे अच्छे युवा प्राकृतिक वैज्ञानिकों में से एक। प्रतियोगिता "2011 युवा प्रकृतिवादी" ने न्यूयॉर्क प्राकृतिक विज्ञान संग्रहालय का आयोजन किया। ईदान ने अपने आविष्कार के पेटेंट के लिए प्रारंभिक आवेदन दायर किया.

वैज्ञानिक सक्रिय रूप से फाइबोनैकी संख्या और गोल्डन सेक्शन के सिद्धांत को विकसित करना जारी रखते हैं।

यू। Fibonacci संख्याओं का उपयोग matyatsevich हिल्बर्ट की 10 वीं समस्या हल करता है।

फाइबोनैकी और गोल्डन सेक्शन का उपयोग करके कई साइबरनेटिक कार्यों (खोज सिद्धांत, गेम, प्रोग्रामिंग) को हल करने के सुरुचिपूर्ण तरीके उत्पन्न हो रहे हैं।

यहां तक \u200b\u200bकि गणितीय फाइबोनाचची-एसोसिएशन संयुक्त राज्य अमेरिका में भी बनाया गया है, जो 1 9 63 से एक विशेष पत्रिका पैदा करता है।

इसलिए, हम देखते हैं कि फाइबोनैकी संख्याओं के अनुक्रम का दायरा बहुत बहुमुखी है:

प्रकृति में होने वाली घटनाओं को देखते हुए, वैज्ञानिकों ने हड़ताली निष्कर्ष निकाला कि जीवन, क्रांति, दुर्घटना, दिवालियापन, समृद्धि की अवधि, कानून और स्टॉक और विदेशी मुद्रा बाजारों में विकास की तरंगों की अवधि, पारिवारिक जीवन चक्र, आदि में होने वाली घटनाओं का पूरा अनुक्रम पर चक्र, तरंगों के रूप में समयरेखा पर आयोजित किया जाता है। इन चक्रों और तरंगों को फाइबोनैकी की संख्यात्मक संख्या के अनुसार भी वितरित किया जाता है!

इस ज्ञान पर निर्भर करते हुए, एक व्यक्ति भविष्य में विभिन्न घटनाओं की भविष्यवाणी करने और उन्हें प्रबंधित करने के लिए सीखेंगे।

4. हमारा शोध।

हमने अपनी टिप्पणियों को जारी रखा, और संरचना का अध्ययन किया

देवदारू शंकु

येरो

मोसर

पु रूप

और उन्हें आश्वस्त किया गया था कि इनमें पहली नज़र में ऐसी अलग-अलग वस्तुएं, यह अदृश्य रूप से उन लोगों को फिबोनासी अनुक्रमों की सबसे अधिक संख्या प्रस्तुत करती है।

तो, चरण 1।

एक पाइन शंकु लें:

इसे देखने पर विचार करें:

हम फिबोनाची सर्पिल की दो श्रृंखला देखते हैं: एक - दक्षिणावर्त, दूसरा उनके खिलाफ है, उनकी संख्या8 और 13।

चरण दो।

यारो ले लो:

ध्यान से उपजी और रंगों की संरचना पर विचार करें:

ध्यान दें कि प्रत्येक नई यारो शाखा साइनस से बढ़ती है, और नई शाखाएं नई शाखा से बढ़ती हैं। पुरानी और नई शाखाओं को फोल्ड करना, हमें प्रत्येक क्षैतिज विमान में फाइबोनैकी की संख्या मिली।

चरण 3।

और विभिन्न जीवों की रूपरेखा में फिबोनैकी संख्याएं प्रकट होती हैं? प्रसिद्ध मच्छर पर विचार करें:

हम देखते हैं: 3। पैरों के जोड़े, सिर5 मास्टर - एंटेना, पेट में विभाजित है8 खंड।

आउटपुट:

हमारे अध्ययनों में, हमने देखा कि हमारे आस-पास के पौधों, जीवित जीवों, और यहां तक \u200b\u200bकि किसी व्यक्ति की संरचना में भी, फाइबोनैकी के अनुक्रम से संख्याएं हैं, जो उनकी संरचना की सद्भाव को दर्शाती हैं।

पाइन टक्कर, यारो, मच्छर, लोगों को गणितीय सटीकता के साथ व्यवस्थित किया जाता है।

हम प्रश्न के उत्तर की तलाश में थे: फाइबोनैकी को कई फाइबोनैकी वास्तविकता कैसे होती है? लेकिन, इसका जवाब, नए और नए प्रश्न प्राप्त हुए।

ये नंबर कहां से आए? ब्रह्मांड के इस वास्तुकार कौन है, जिन्होंने इसे सही बनाने की कोशिश की? सर्पिल ट्विस्ट या स्पिन?

एक व्यक्ति इस दुनिया को कितना अद्भुत जानता है !!!

एक प्रश्न का उत्तर ढूंढना निम्नलिखित प्राप्त करता है। इसे चमकता है, दो नए हो जाते हैं। उनके साथ टूट गया, तीन और दिखाई देंगे। फैसला किया और उनमें से, पांच अनसुलझे प्राप्त करेंगे। फिर आठ, फिर तेरह, 21, 34, 55 ...

पहचानना?

निष्कर्ष।

सभी वस्तुओं में खुद को निर्माता

एक अद्वितीय कोड रखी,

और एक जो गणित के साथ दोस्त

वह जानता है और समझता है!

हमने आसपास की वास्तविकता में फाइबोनैकी अनुक्रम की संख्या के अभिव्यक्ति का अध्ययन और विश्लेषण किया। हमने यह भी सीखा कि इस संख्यात्मक श्रृंखला के पैटर्न, "गोल्डन" समरूपता के पैटर्न समेत, जीवित जीवों की जीन संरचनाओं में ग्रहों और अंतरिक्ष प्रणालियों में प्राथमिक कणों के ऊर्जा संक्रमण में प्रकट होते हैं।

हमें पौधों में सर्पिल की संख्या, किसी भी क्षैतिज विमान में शाखाओं की संख्या और फाइबोनैकी अनुक्रम में संख्याओं की संख्या के बीच एक अद्भुत गणितीय संबंध मिला। हमने देखा कि विभिन्न जीवों की रूपरेखा भी इस रहस्यमय कानून का पालन करती है। हमने एक व्यक्ति की संरचना में सख्त गणित भी देखा। मानव डीएनए अणु, जिसमें मनुष्य के विकास के लिए संपूर्ण कार्यक्रम, श्वसन प्रणाली, कान की संरचना एन्क्रिप्ट की जाती है, क्या सभी कुछ संख्यात्मक संबंधों का पालन कर रहे हैं।

हमने सीखा कि पाइन शंकु, घोंघा गोले, महासागर तरंगें, पशु सींग, चक्रवात बादल और आकाशगंगाएं - वे सभी लॉगरिदमिक सर्पिल बनाते हैं। यहां तक \u200b\u200bकि मानव उंगली, जो गोल्डन अनुपात में एक-दूसरे के संबंध में तीन फालेंजों से बना है, संपीड़ित होने पर एक सर्पिल आकार लेता है।

समय की अनंत काल और ब्रह्मांड के प्रकाश वर्षों में एक पाइन conine और सर्पिल आकाशगंगा साझा करते हैं, लेकिन संरचना एक ही बनी हुई है: गुणांक1,618 ! शायद यह एक सर्वोपरि कानून है, प्राकृतिक घटनाओं का प्रबंधन।

इस प्रकार, सद्भाव के लिए जिम्मेदार विशेष संख्यात्मक पैटर्न के अस्तित्व के बारे में हमारी परिकल्पना की पुष्टि की जाती है।

दरअसल, दुनिया में सब कुछ हमारे सबसे महत्वपूर्ण डिजाइनर - प्रकृति द्वारा विचारशील और गलत अनुमानित है!

हमें विश्वास था कि प्रकृति के अपने कानून व्यक्त किए गए हैंगणित। और गणित एक बहुत ही महत्वपूर्ण उपकरण है

प्रकृति के रहस्यों के ज्ञान के लिए।

इंटरनेट साहित्य और वेबसाइटों की सूची:

1. Vorobyev एन एन। Fibonacci संख्या। - एम, विज्ञान, 1 9 84।
2. Gick एम। प्रकृति और कला में अनुपात के सौंदर्यशास्त्र। - एम, 1 9 36।

3. Dmitriev ए कैओस, फ्रैक्टल और जानकारी। // विज्ञान और जीवन, संख्या 5, 2001।
4. कस्निट्स्की एस ई। सद्भाव, विरोधाभास // संस्कृति से बुने हुए और

एक जिंदगी। - 1 9 82. - № 10।
5. मलय गार्मोनिया - विरोधाभास // एमएन की पहचान। - 1 9 82. - № 1 9।
6. सोकोलोव ए गोल्डन सेक्शन // के रहस्य युवाओं की तकनीक। - 1 9 78.- № 5।
7. स्वर्ण अनुपात के स्टाकोव ए पी कोड। - एम, 1 9 84।
8. Urmansev यू। ए। समरूपता की प्रकृति और प्रकृति की समरूपता। - एम, 1 9 74।
9. Urmansev यू। ए गोल्डन सेक्शन // प्रकृति। - 1 9 68. - № 11।

10. शेवेलव आईएसएच, मारुटेव मा, शेमेलेव आई.पी. गोल्डन सेक्शन / थ्री

सद्भाव की प्रकृति का दृश्य। - एम।, 1 99 0।

11. सुबनिकोव ए वी।, कोपत्सिक वी। ए। विज्ञान और कला में समरूपता। -म।:

दुनिया भर की दुनिया, सबसे छोटे अदृश्य कणों से शुरू हो रही है, और अंतहीन ब्रह्मांड की दूरस्थ आकाशगंगाओं के साथ समाप्त हो रही है, बहुत सारे अनसुलझा रहस्यों का भुगतान करती है। हालांकि, उनमें से कुछ वैज्ञानिकों के जिज्ञासु दिमाग के कारण रहस्य के घूंघट द्वारा उठाए गए हैं।

ऐसा एक उदाहरण है गोल्डन सेक्शन और फाइबोनैकी नंबर इसकी नींव का आधार। यह पैटर्न गणितीय रूप में मैपिंग कर रहा है और अक्सर मानव पर्यावरण में पाया जाता है, एक बार फिर इस मामले के परिणामस्वरूप उठने की संभावना को छोड़कर।

Fibonacci संख्या और उनके अनुक्रम

Fibonacci संख्याओं का क्रम कई संख्याओं को कॉल करें, जिनमें से प्रत्येक पिछले दो का योग है:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 …

इस अनुक्रम की एक विशेषता संख्यात्मक मान है जो इस श्रृंखला की संख्या को एक दूसरे पर विभाजित करने के कारण प्राप्त की जाती हैं।

फाइबोनैकी नंबरों की संख्या में अपने दिलचस्प पैटर्न हैं:

• कई फाइबोनैकी संख्याओं में, निम्नलिखित में विभाजित प्रत्येक संख्या मूल्य दिखाने के लिए दिखाएगी 0,618 । पंक्ति की शुरुआत से दूर की संख्या, अनुपात अधिक सटीक। उदाहरण के लिए, पंक्ति की शुरुआत में किए गए आंकड़े 5 तथा 8 देखेंगे 0,625 (5/8=0,625 )। यदि आप नंबर लेते हैं 144 तथा 233 फिर वे अनुपात दिखाएंगे 0.618 .
• बदले में, यदि कई फाइबोनैकी नंबरों में संख्या को पिछले एक में विभाजित किया गया है, तो विभाजन का नतीजा तलाश करेगा 1,618 । उदाहरण के लिए, वही आंकड़े ऊपर निर्दिष्ट हैं: 8/5=1,6 तथा 233/144=1,618 .
• एक के माध्यम से एक में विभाजित संख्या मूल्य के दृष्टिकोण को दिखाएगी 0,382 । और पंक्ति की शुरुआत से दूर, संख्याएं ली जाती हैं, संबंध के मूल्य को अधिक सटीक: 5/13=0,385 तथा 144/377=0,382 । रिवर्स ऑर्डर में डिकलिंग नंबर परिणाम देंगे 2,618 : 13/5=2,6 तथा 377/144=2,618 .

उपरोक्त गणना विधियों का उपयोग करके और संख्याओं के बीच अंतराल को बढ़ाने के मूल्यों की अगली श्रृंखला प्रदर्शित की जा सकती है: 4.235, 2.618, 1.618, 0.618, 0.382, 0.236, जिसका व्यापक रूप से विदेशी मुद्रा बाजार में फाइबोनैकी उपकरण में उपयोग किया जाता है।

गोल्डन अनुभाग या दिव्य अनुपात

बहुत स्पष्ट रूप से "गोल्डन सेक्शन" और एक सेगमेंट के साथ फाइबोनैकी समानता की संख्या का प्रतिनिधित्व करता है। यदि खंड एवी को इस तरह के अनुपात में इस तरह के अनुपात में विभाजित किया गया है:

एसी / सूर्य \u003d विमान / एवी, तो यह एक "गोल्डन सेक्शन" होगा

निम्नलिखित लेख भी पढ़ें:

आश्चर्य की बात है कि यह ठीक है यह अनुपात कई फाइबोनैकी संख्याओं में पता लगाया गया है। पंक्ति से कुछ संख्याएं लेना, आप गणना कर सकते हैं कि यह ऐसा है। उदाहरण के लिए, फिबोनासी संख्याओं के इस तरह के अनुक्रम ... 55, 89, 144 ... नंबर 144 एबी का एक पूरा खंड होने दें, जिसे ऊपर वर्णित किया गया था। चूंकि 144 पिछली संख्याओं का योग है, फिर 55 + 8 9 \u003d एसी + सूर्य \u003d 144।

सेगमेंट निर्णय निम्नलिखित परिणाम दिखाएगा:

एसी / सन \u003d 55/89 \u003d 0,618

सूर्य / ab \u003d 89/144 \u003d 0.618

यदि आप एक पूर्णांक के लिए एबी का सेगमेंट लेते हैं, या प्रति यूनिट, तो एसी \u003d 55 इस पूरे से 0.382 होगा, और विमान \u003d 89 0.618 के बराबर होगा।

Fibonacci नंबर कहां हैं

फाइबोनैकी नंबरों का नियमित अनुक्रम ग्रीक और मिस्र के लोगों को लियोनार्डो फिबोनैकी से पहले जानता था। इस नाम ने प्रसिद्ध गणितज्ञ के बाद विद्वानों में इस गणितीय घटना के व्यापक प्रसार को सुनिश्चित करने के बाद इस नाम का अधिग्रहण किया है।

यह ध्यान रखना महत्वपूर्ण है कि फाइबोनैकी की स्वर्ण संख्या सिर्फ विज्ञान नहीं है, बल्कि आसपास की दुनिया का गणितीय मानचित्रण नहीं है। कई प्राकृतिक घटनाएं, पौधे और पशु विश्व प्रतिनिधियों के पास उनके अनुपात में "गोल्डन सेक्शन" होता है। यह सर्पिल शैल कर्ल भी है, और सूरजमुखी के बीज, कैक्टि, अनानास का स्थान भी है।

सर्पिल, "गोल्डन सेक्शन" के नियमों द्वारा अधीनस्थ शाखाओं के अनुपात, एक तूफान, वेब स्पाइडर, कई आकाशगंगाओं के रूप, बुनाई डीएनए अणुओं और कई अन्य घटनाओं के निर्माण के गठन को रेखांकित करते हैं।

छिपकली की पूंछ की लंबाई उसके धड़ के लिए 62 से 38 का अनुपात है। चॉकरी की प्रक्रिया, आप पत्ती का एक टुकड़ा छोड़ने से पहले, उत्सर्जन करता है। पहली शीट जारी होने के बाद, दूसरी उत्सर्जन दूसरी शीट की रिहाई से पहले जारी की जाती है, जो पहले उत्सर्जन की सशर्त रूप से स्वीकार्य इकाई से 0.62 के बराबर होती है। तीसरा emection 0.38 है, और चौथा - 0.24।

एक व्यापारी के लिए, तथ्य यह है कि विदेशी मुद्रा बाजार में कीमत की कीमत अक्सर फाइबोनैकी सोने की संख्या की नियमितताओं के अधीन होती है। इस अनुक्रम के आधार पर, कई औजारों का निर्माण किया गया है कि एक व्यापारी अपने शस्त्रागार में उपयोग कर सकता है

व्यापारियों के उपकरण द्वारा अक्सर उपयोग किया जाता है "" मूल्य आंदोलन के लक्ष्यों के साथ-साथ इसके सुधार के स्तर को दिखाने के लिए उच्च सटीकता के साथ भी हो सकता है।