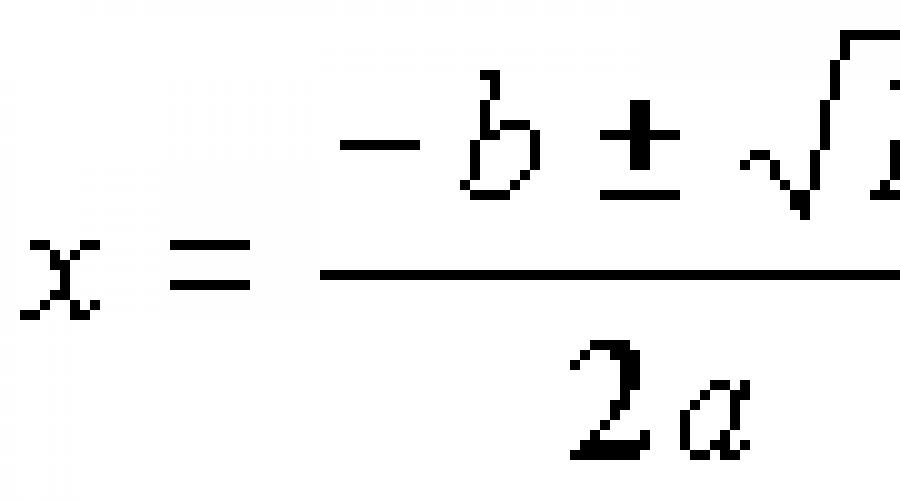
स्क्वायर समीकरणों का अध्ययन ग्रेड 8 में किया जाता है, इसलिए यहां कुछ भी मुश्किल नहीं है। उन्हें हल करने की क्षमता बिल्कुल जरूरी है।

स्क्वायर समीकरण फॉर्म एक्स 2 + बीएक्स + सी \u003d 0 का समीकरण है, जहां गुणांक ए, बी और सी मनमानी संख्याएं हैं, और एक ≠ 0।

विशिष्ट निर्णय विधियों का अध्ययन करने से पहले, हम ध्यान देते हैं कि सभी वर्ग समीकरणों को तीन वर्गों में विभाजित किया जा सकता है:

1. जड़ें नहीं हैं;
2. बिल्कुल एक जड़ है;
3. दो अलग-अलग जड़ें हैं।

यह रैखिक से वर्ग समीकरणों के बीच एक महत्वपूर्ण अंतर है, जहां रूट हमेशा मौजूद है और अद्वितीय है। यह निर्धारित करने के लिए कि कितने जड़ों में समीकरण है? इसके लिए एक अद्भुत बात है - विभेदक.

विभेदक

स्क्वायर समीकरण कुल्हाड़ी 2 + बीएक्स + सी \u003d 0. दें, फिर भेदभाव सिर्फ संख्या डी \u003d बी 2 - 4AC है।

इस सूत्र को दिल से जाना जाना चाहिए। वह कहाँ लेती है - अब इससे कोई फर्क नहीं पड़ता। अन्य यह महत्वपूर्ण है: भेदभावपूर्ण संकेत निर्धारित किया जा सकता है कि कितने जड़ों में एक वर्ग समीकरण है। अर्थात्:

1. अगर डी< 0, корней нет;
2. यदि डी \u003d 0, ठीक एक जड़ है;
3. यदि डी\u003e 0, दो जड़ें होंगी।

कृपया ध्यान दें: भेदभाव जड़ों की संख्या को इंगित करता है, न कि उनके संकेतों पर, कुछ कारणों से, कई विचार करते हैं। उदाहरणों पर एक नज़र डालें - और आप सब कुछ समझेंगे:

एक कार्य। स्क्वायर समीकरण कितनी जड़ें हैं:

1. x 2 - 8x + 12 \u003d 0;
2. 5x 2 + 3x + 7 \u003d 0;
3. x 2 - 6x + 9 \u003d 0।

हम पहले समीकरण के लिए गुणांक को पीछे हटाते हैं और भेदभावपूर्ण पाते हैं:
ए \u003d 1, बी \u003d -8, सी \u003d 12;
डी \u003d (-8) 2 - 4 · 1 · 12 \u003d 64 - 48 \u003d 16

तो, भेदभाव सकारात्मक है, इसलिए समीकरण में दो अलग-अलग जड़ें हैं। इसी प्रकार, दूसरे समीकरण को अलग करें:
ए \u003d 5; b \u003d 3; सी \u003d 7;
डी \u003d 3 2 - 4 · 5 · 7 \u003d 9 - 140 \u003d -131।

भेदभाव नकारात्मक है, कोई जड़ नहीं। अंतिम समीकरण बनी हुई है:
ए \u003d 1; b \u003d -6; सी \u003d 9;
डी \u003d (-6) 2 - 4 · 1 · 9 \u003d 36 - 36 \u003d 0।

भेदभाव शून्य है - जड़ एक होगी।

कृपया ध्यान दें कि प्रत्येक समीकरण के लिए गुणांक निर्वहन किया गया था। हां, यह एक लंबा समय है, हाँ, यह एक थकाऊ है - लेकिन आप गुणांक को भ्रमित नहीं करेंगे और बेवकूफ गलतियों की अनुमति नहीं देंगे। अपने आप को चुनें: गति या गुणवत्ता।

वैसे, यदि आप "हाथ भरें", थोड़ी देर के बाद, सभी गुणांक लिखने की आवश्यकता नहीं है। इस तरह के परिचालन आप अपने सिर में किया जाएगा। अधिकांश लोग 50-70 हल समीकरणों के बाद कहीं ऐसा करना शुरू करते हैं - सामान्य रूप से, इतना नहीं।

रूट्स स्क्वायर समीकरण

अब हम वास्तव में निर्णय के लिए बदल जाते हैं। यदि भेदभावपूर्ण डी\u003e 0, सूत्रों द्वारा जड़ों को पाया जा सकता है:

वर्ग समीकरण की जड़ों का मूल सूत्र

जब डी \u003d 0, आप इनमें से किसी भी सूत्र का उपयोग कर सकते हैं - यह वही संख्या होगी जो उत्तर होगा। अंत में, अगर डी< 0, корней нет — ничего считать не надо.

1. x 2 - 2x - 3 \u003d 0;
2. 15 - 2x - x 2 \u003d 0;
3. x 2 + 12x + 36 \u003d 0।

पहला समीकरण:
x 2 - 2x - 3 \u003d 0 ⇒ A \u003d 1; b \u003d -2; सी \u003d -3;
डी \u003d (-2) 2 - 4 · 1 · (-3) \u003d 16।

डी\u003e 0 ⇒ समीकरण में दो जड़ें हैं। उन्हें लगता है:

दूसरा समीकरण:
15 - 2x - x 2 \u003d 0 ⇒ A \u003d -1; b \u003d -2; सी \u003d 15;
डी \u003d (-2) 2 - 4 · (-1) · 15 \u003d 64।

डी\u003e 0 ⇒ समीकरण फिर से दो जड़ें हैं। हम उन्हें पाते हैं

\\ [\\ _ प्रारंभ (align) & ((x) _ (1)) \u003d \\ frac (2+ \\ sqrt (64)) (2 \\ cdot \\ बाएं (-1 \\ दाएं) \u003d - 5; \\\\ & ((x) _ (2)) \u003d \\ frac (2- \\ sqrt (64)) (2 \\ cdot \\ छोड़ा (-1 \\ दाएं) \u003d 3। \\\\ \\ end (संरेखित) \\]

अंत में, तीसरा समीकरण:
x 2 + 12x + 36 \u003d 0 ⇒ A \u003d 1; b \u003d 12; सी \u003d 36;
डी \u003d 12 2 - 4 · 1 · 36 \u003d 0।

डी \u003d 0 ⇒ समीकरण में एक रूट है। आप किसी भी सूत्र का उपयोग कर सकते हैं। उदाहरण के लिए, पहला:

जैसा कि उदाहरणों से देखा जा सकता है, सबकुछ बहुत आसान है। यदि आप सूत्र को जानते हैं और विचार करने में सक्षम हैं, तो कोई समस्या नहीं होगी। अक्सर, नकारात्मक गुणांक के सूत्र में प्रतिस्थापन के दौरान त्रुटियां होती हैं। यहां, फिर से वर्णित रिसेप्शन मदद करेगा: स्वरूप को सचमुच देखें, हर कदम पेंट करें - और जल्द ही त्रुटियों से छुटकारा पाएं।

अपूर्ण वर्ग समीकरण

ऐसा होता है कि स्क्वायर समीकरण परिभाषा में जो कुछ दिया गया है उससे कुछ अलग है। उदाहरण के लिए:

1. x 2 + 9x \u003d 0;
2. x 2 - 16 \u003d 0।

यह देखना आसान है कि इन समीकरणों में शर्तों में से कोई भी नहीं है। इस तरह के वर्ग समीकरण मानक से भी आसान हैं: उन्हें भेदभाव पर विचार करने की भी आवश्यकता नहीं है। तो, हम एक नई अवधारणा पेश करते हैं:

कुल्हाड़ी 2 + बीएक्स + सी \u003d 0 समीकरण को अपूर्ण वर्ग समीकरण कहा जाता है यदि बी \u003d 0 या सी \u003d 0, यानी एक चर एक्स या मुक्त तत्व के साथ गुणांक शून्य है।

बेशक, एक पूरी तरह से मुश्किल मामला संभव है जब इन दोनों गुणांक शून्य हैं: बी \u003d सी \u003d 0. इस मामले में, समीकरण फॉर्म एक्स 2 \u003d 0. लेता है, जाहिर है, इस तरह के एक समीकरण में एक ही रूट है: x \u003d 0 ।

शेष मामलों पर विचार करें। बी \u003d 0 0 हो, फिर हम फॉर्म एक्स 2 + सी \u003d 0. के अपूर्ण वर्ग समीकरण प्राप्त करते हैं: हम इसे थोड़ा बदलते हैं:

चूंकि अंकगणितीय वर्ग रूट केवल एक गैर-ऋणात्मक संख्या से मौजूद है, इसलिए बाद की समानता विशेष रूप से (-सी / ए) ≥ 0. निष्कर्ष:

1. यदि फॉर्म एक्स 2 + सी \u003d 0 के अपूर्ण वर्ग समीकरण में, असमानता (-सी / ए) का प्रदर्शन ≥ 0 किया जाता है, तो दो जड़ें होंगी। सूत्र ऊपर दिया गया है;
2. यदि (-c / a)< 0, корней нет.

जैसा कि आप देख सकते हैं, भेदभाव की आवश्यकता नहीं थी - अपूर्ण वर्ग समीकरणों में कोई जटिल कंप्यूटिंग नहीं है। वास्तव में, असमानता (-सी / ए) ≥ 0. को याद रखना भी आवश्यक नहीं है। यह x 2 के मूल्य को व्यक्त करने के लिए पर्याप्त है और देखें कि समानता चिह्न के दूसरी तरफ क्या खड़ा है। यदि कोई सकारात्मक संख्या है - जड़ें दो होंगी। यदि नकारात्मक - जड़ें बिल्कुल नहीं होंगी।

अब हम फॉर्म एक्स 2 + बीएक्स \u003d 0 के समीकरणों के साथ समझेंगे, जिसमें मुक्त तत्व शून्य है। सब कुछ यहां सरल है: जड़ें हमेशा दो होंगी। गुणक को बहुपदों को विघटित करने के लिए पर्याप्त है:

ब्रैकेट के लिए गुणक

काम शून्य है, जब कम से कम एक गुणक शून्य शून्य है। यहां से जड़ें हैं। अंत में, हम ऐसे कई समीकरणों का विश्लेषण करेंगे:

एक कार्य। स्क्वायर स्क्वायर समीकरण:

1. x 2 - 7x \u003d 0;
2. 5x 2 + 30 \u003d 0;
3. 4x 2 - 9 \u003d 0।

x 2 - 7x \u003d 0 ⇒ x · (x - 7) \u003d 0 ⇒ x 1 \u003d 0; x 2 \u003d - (- 7) / 1 \u003d 7।

5x 2 + 30 \u003d 0 ⇒ 5x 2 \u003d -30 ⇒ x 2 \u003d -6। कोई जड़ नहीं, क्योंकि वर्ग एक नकारात्मक संख्या के बराबर नहीं हो सकता है।

4x 2 - 9 \u003d 0 ⇒ 4x 2 \u003d 9 ⇒ x 2 \u003d 9/4 ⇒ x 1 \u003d 3/2 \u003d 1.5; x 2 \u003d -1.5।

समीकरण देखें

की अभिव्यक्ति डी \u003d बी। 2 - 4 एसी कॉल विभेदक वर्ग समीकरण। यदि एक डी \u003d 0, समीकरण में एक वैध रूट है; अगर डी \u003e 0, समीकरण में दो वैध जड़ें हैं।
मामले में जब डी = 0 कभी-कभी वे कहते हैं कि वर्ग समीकरण में दो समान रूट हैं।
पदनाम का उपयोग करना डी \u003d बी। 2 - 4 एसी , आप सूत्र (2) को फिर से लिख सकते हैं

यदि एक बी \u003d 2 के। सूत्र (2) फॉर्म लेता है:

कहा पे क। \u003d बी। / 2 .
अंतिम सूत्र विशेष रूप से उन मामलों में सुविधाजनक है जहां बी / 2 - पूर्णांक, यानी गुणक बी - सम संख्या।
उदाहरण 1: समीकरण हल करें 2 एक्स। 2 - 5 एक्स + 2 = 0 । यहाँ ए \u003d 2, बी \u003d -5, सी \u003d 2। है डी \u003d बी। 2 - 4 एसी। = (-5) 2- 4*2*2 = 9 । जैसा डी > 0 , समीकरण में दो जड़ें हैं। फॉर्मूला (2) द्वारा उन्हें खोजें

तोह फिर एक्स। 1 \u003d (5 + 3) / 4 \u003d 2, एक्स 2 =(5 - 3) / 4 = 1 / 2 ,
अर्थात एक्स। 1 = 2 तथा एक्स। 2 = 1 / 2 - निर्दिष्ट समीकरण की जड़ें।
उदाहरण 2: समीकरण हल करें 2 एक्स। 2 - 3 एक्स। + 5 = 0 । यहाँ ए \u003d 2, बी \u003d -3, सी \u003d 5। हम भेदभावपूर्ण पाते हैं डी \u003d बी। 2 - 4 एसी। = (-3) 2- 4*2*5 = -31 । जैसा डी 0 समीकरण में वैध जड़ें नहीं हैं।

अपूर्ण वर्ग समीकरण। यदि वर्ग समीकरण में कुल्हाड़ी। 2 + बीएक्स। + सी। =0 दूसरा गुणांक बी या मुक्त डिक सी। शून्य के बराबर, फिर वर्ग समीकरण कहा जाता है अधूरा। अपूर्ण समीकरण अलग हैं क्योंकि उनकी जड़ों को खोजने के लिए, यह संभव है कि स्क्वायर समीकरण के रूट फॉर्मूला का उपयोग न करें - कारकों के बाएं हिस्से के अपघटन की विधि से समीकरण को हल करना आसान है।
उदाहरण 1: समीकरण हल करें 2 एक्स। 2 - 5 एक्स। = 0 .
है एक्स। (2 एक्स। - 5) = 0 । तो एक्स। = 0 भी 2 एक्स। - 5 = 0 , अर्थात एक्स। = 2.5 । तो समीकरण में दो जड़ें हैं: 0 तथा 2.5
उदाहरण 2: समीकरण हल करें 3 एक्स। 2 - 27 = 0 .
है 3 एक्स। 2 = 27 । नतीजतन, इस समीकरण की जड़ें - 3 तथा -3 .

विएटा प्रमेय। यदि कम वर्ग समीकरण एक्स। 2 + पीएक्स। + प्र। =0 वैध जड़ें हैं, तो उनकी राशि बराबर है - पी , और काम बराबर है प्र , अर्थात

x 1 + x 2 \u003d -p,
x 1 x 2 \u003d q

(दिए गए वर्ग समीकरण की जड़ों का योग विपरीत संकेत के साथ दूसरे गुणांक के बराबर है, और जड़ों का उत्पाद एक मुफ्त सदस्य के बराबर है)।

इस गणितीय कार्यक्रम के साथ आप कर सकते हैं स्क्वायर समीकरण हल करें.

कार्यक्रम न केवल उत्तर कार्य देता है, बल्कि समाधान प्रक्रिया को दो तरीकों से भी प्रदर्शित करता है:
- भेदभाव की मदद से
- वियतनाम प्रमेय का उपयोग (यदि संभव हो)।

इसके अलावा, उत्तर आउटपुट सटीक है, अनुमानित नहीं।
उदाहरण के लिए, समीकरण \\ (81x ^ 2-16x-1 \u003d 0 \\) के लिए, उत्तर इस फॉर्म में आउटपुट है:

$$ x_1 \u003d \\ frac (8+ \\ sqrt (145)) (81), \\ quad x_2 \u003d \\ frac (8-1 \\ sqrt (145)) (81) $$ और इसमें नहीं: \\ (x_1 \u003d 0.247 ; \\ quad x_2 \u003d -0.05 \\)

यह कार्यक्रम परीक्षण और परीक्षाओं की तैयारी करते समय सामान्य शिक्षा स्कूलों के उच्च विद्यालयों के छात्रों के लिए उपयोगी हो सकता है, परीक्षा से पहले ज्ञान की जांच करते समय, माता-पिता गणित और बीजगणित में कई समस्याओं के समाधान की निगरानी के लिए। या शायद आप एक ट्यूटर को किराए पर लेने या नई पाठ्यपुस्तकों को खरीदने के लिए बहुत महंगा हैं? या आप बस गणित या बीजगणित में अपने होमवर्क को यथासंभव बनाना चाहते हैं? इस मामले में, आप हमारे कार्यक्रमों का विस्तृत समाधान भी उपयोग कर सकते हैं।

इस प्रकार, आप अपने छोटे भाइयों या बहनों के अपने प्रशिक्षण और / या प्रशिक्षण का संचालन कर सकते हैं, जबकि हल किए गए कार्यों के क्षेत्र में शिक्षा का स्तर बढ़ता है।

यदि आप एक वर्ग बहुपद में प्रवेश करने के नियमों से परिचित नहीं हैं, तो हम उनके साथ खुद को परिचित करने की सलाह देते हैं।

स्क्वायर बहुपद इनपुट नियम

एक चर के रूप में कोई लैटिन पत्र हो सकता है।
उदाहरण के लिए: \\ (x, y, z, a, b, c, o, p, q \\), आदि

नंबर पूरे या आंशिक में प्रवेश कर सकते हैं।
इसके अलावा, फ्रैक्शनल नंबरों को न केवल दशमलव के रूप में, बल्कि सामान्य अंश के रूप में भी प्रशासित किया जा सकता है।

दशमलव अंशों में प्रवेश करने के नियम।
दशमलव भिन्नताओं में, पूरे के आंशिक हिस्से को एक बिंदु और अल्पविराम के रूप में अलग किया जा सकता है।
उदाहरण के लिए, आप इस तरह दशमलव अंशों को दर्ज कर सकते हैं: 2.5x - 3.5x ^ 2

सामान्य अंशों में प्रवेश करने के नियम।
केवल एक पूर्णांक एक संख्यात्मक, denominator और अंश का एक संपूर्ण हिस्सा के रूप में कार्य कर सकता है।

Denominator नकारात्मक नहीं हो सकता है।

एक संख्यात्मक अंश दर्ज करते समय, संख्यात्मक संख्यात्मक से विखंडक से अलग हो गए: /
पूरा भाग Frarity Ampersand साइन से अलग है: &
इनपुट: 3 और 1/3 - 5 और 6 / 5Z + 1 / 7Z ^ 2
परिणाम: \\ (3 \\ frac (1) (3) - 5 \\ frac (6) (5) z + \\ frac (1) (7) z ^ 2 \\)

अभिव्यक्ति में प्रवेश करते समय आप कोष्ठक का उपयोग कर सकते हैं। इस मामले में, स्क्वायर समीकरण को हल करते समय, दर्ज अभिव्यक्ति को पहले सरलीकृत किया जाता है।
उदाहरण के लिए: 1/2 (वाई - 1) (वाई + 1) - (5Y-10 और 1/2)

=0

तय

यह पाया जाता है कि इस कार्य को हल करने के लिए आवश्यक कुछ स्क्रिप्ट लोड नहीं हुई हैं, और प्रोग्राम काम नहीं कर सकता है।
आपके पास एडब्लॉक शामिल हो सकता है।
इस मामले में, इसे डिस्कनेक्ट करें और पृष्ठ को अपडेट करें।

आपके पास अपने ब्राउज़र में जावास्क्रिप्ट निष्पादन है।
समाधान को प्रकट करने के लिए, आपको जावास्क्रिप्ट को सक्षम करने की आवश्यकता है।
निर्देश दिए गए हैं, अपने ब्राउज़र में जावास्क्रिप्ट को कैसे सक्षम करें।

चूंकि कार्य को हल करने की इच्छा बहुत अधिक है, आपका अनुरोध लाइन में है।
कुछ सेकंड के बाद, समाधान नीचे दिखाई देगा।
कृपया प्रतीक्षा करें एसईसी ...

अगर तुम हल करने में गलती कीआप इसके बारे में प्रतिक्रिया फॉर्म में लिख सकते हैं।
मत भूलो निर्दिष्ट करें कि क्या कार्य है आप तय करते हैं और क्या क्षेत्र में प्रवेश करें.

हमारे खेल, पहेली, अनुकरणकर्ता:

सिद्धांत का एक सा।

स्क्वायर समीकरण और इसकी जड़ें। अपूर्ण वर्ग समीकरण

प्रत्येक समीकरण
\\ (- x ^ 2 + 6x + 1,4 \u003d 0, \\ quad 8x ^ 2-7x \u003d 0, \\ quad x ^ 2- \\ frac (4) (9) \u003d 0 \\)
उपस्थिति है
\\ (कुल्हाड़ी ^ 2 + bx + c \u003d 0, \\)
जहां एक्स परिवर्तनीय, ए, बी और सी - संख्या है।
पहले समीकरण ए \u003d -1, बी \u003d 6 और सी \u003d 1.4 में, दूसरे ए \u003d 8, बी \u003d -7 और सी \u003d 0 में, तीसरे ए \u003d 1, बी \u003d 0 और सी \u003d 4/9 में। ऐसे समीकरणों को बुलाया जाता है वर्ग समीकरण.

परिभाषा।
वर्ग समीकरण फॉर्म एक्स 2 + बीएक्स + सी \u003d 0 के समीकरण, जहां एक्स चर है, ए, बी और सी कुछ संख्याएं हैं, और \\ (a \\ neq 0 \\)।

संख्या ए, बी और सी वर्ग समीकरण के गुणांक हैं। संख्या ए को पहली गुणांक कहा जाता है, संख्या बी दूसरा गुणांक और संख्या सी है - एक नि: शुल्क सदस्य।

फॉर्म एक्स 2 + बीएक्स + सी \u003d 0 के प्रत्येक समीकरण में, जहां \\ (a \\ neq 0 \\), चर एक्स-स्क्वायर की सबसे बड़ी डिग्री। इसलिए नाम: वर्ग समीकरण।

ध्यान दें कि वर्ग समीकरण को दूसरी डिग्री के समीकरण भी कहा जाता है, क्योंकि इसके बाएं हिस्से में दूसरी डिग्री बहुपद है।

स्क्वायर समीकरण जिसमें x 2 पर गुणांक 1 है, जिसे कहा जाता है स्क्वायर समीकरण दिया। उदाहरण के लिए, स्क्वायर समीकरण दिए गए समीकरण हैं
\\ (x ^ 2-11x + 30 \u003d 0, \\ quad x ^ 2-6x \u003d 0, \\ quad x ^ 2-8 \u003d 0 \\)

यदि स्क्वायर समीकरण कुल्हाड़ी 2 + बीएक्स + सी \u003d 0 में, कम से कम एक गुणांक बी या सी शून्य है, तो इस तरह के एक समीकरण कहा जाता है अपूर्ण वर्ग समीकरण। तो, समीकरण -2x 2 + 7 \u003d 0, 3x 2 -10x \u003d 0, -4x 2 \u003d 0 अपूर्ण वर्ग समीकरण हैं। उनमें से पहले बी \u003d 0 में, दूसरे सी \u003d 0 में, तीसरे बी \u003d 0 और सी \u003d 0 में।

अपूर्ण वर्ग समीकरण तीन प्रजाति हैं:
1) कुल्हाड़ी 2 + सी \u003d 0, जहां \\ (c \\ neq 0 \\);
2) एक्स 2 + बीएक्स \u003d 0, जहां \\ (b \\ neq 0 \\);
3) कुल्हाड़ी 2 \u003d 0।

इन प्रजातियों में से प्रत्येक के समीकरणों के समाधान पर विचार करें।

फॉर्म 2 + सी \u003d 0 के अपूर्ण वर्ग समीकरण को हल करने के लिए, \\ (c \\ neq 0 \\) के साथ, इसे अपने मुक्त सदस्य को दाएं हाथ में स्थानांतरित कर दिया जाता है और समीकरण के दोनों हिस्सों को एक पर बनाते हैं:
\\ (x ^ 2 \u003d - \\ frac (c) (a) \\ rethrow x_ (1,2) \u003d \\ pm \\ sqrt (- \\ frac (c) (a)) \\)

चूंकि \\ (c \\ neq 0 \\), फिर \\ (- \\ frac (c) (a) \\ neq 0 \\)

यदि \\ (- \\ frac (c) (a)\u003e 0 \\), समीकरण में दो जड़ें हैं।

यदि \\ (- \\ frac (c) (a), फॉर्म एक्स 2 + बीएक्स \u003d 0 के अपूर्ण वर्ग समीकरण को हल करने के लिए, \\ (b \\ neq 0 \\) के साथ, वे अपने बाएं भाग को मल्टीप्लियर में गिरा देते हैं और समीकरण प्राप्त करते हैं
\\ (एक्स (एक्स + बी) \u003d 0 \\ राइटारो \\ Left \\ (\\ BEGIN (सरणी) (l) x \u003d 0 \\\\ ax + b \u003d 0 \\ end (सरणी) \\ राइट। \\ Riderow \\ Left \\ (\\ BEGIN (सरणी) (l) x \u003d 0 \\\\ x \u003d - \\ frac (b) (a) \\ end (सरणी) \\ अधिकार। \\)

तो, फॉर्म एक्स 2 + बीएक्स \u003d 0 के अपूर्ण वर्ग समीकरण \\ (b \\ neq 0 \\) के साथ हमेशा दो जड़ें होती हैं।

फॉर्म एक्स 2 \u003d 0 के अपूर्ण वर्ग समीकरण समीकरण x 2 \u003d 0 के बराबर है और इसलिए एकमात्र रूट 0 है।

वर्ग समीकरण रूट फॉर्मूला

अभी इस पर विचार करें कि वर्ग समीकरण कैसे हल करते हैं जिसमें अज्ञात और नि: शुल्क सदस्य दोनों गुणांक शून्य से अलग होते हैं।

सामान्य रूप से स्पेंट स्क्वायर समीकरण और नतीजतन हम रूट फॉर्मूला प्राप्त करते हैं। फिर किसी भी वर्ग समीकरण को हल करते समय इस सूत्र का उपयोग किया जा सकता है।

स्क्वायर समीकरण कुल्हाड़ी 2 + बीएक्स + सी \u003d 0

इसके दोनों हिस्सों को एक पर अलग करना, हम प्रस्तुत वर्ग समीकरण के बराबर प्राप्त करते हैं
\\ (x ^ 2 + \\ frac (b) (a) x + \\ frac (c) (a) \u003d 0 \\)

हम इस समीकरण को बदलते हैं, बाउंस के वर्ग को हाइलाइट करते हैं:
\\ (x ^ 2 + 2x \\ cdot \\ frac (b) (2a) + \\ _ बाएं (\\ frac (b) (2a) \\ राइट) ^ 2- \\ बाएं (\\ frac (b) (2a) \\ राइट) ^ ^ 2 + \\ frac (c) (a) \u003d 0 \\ राइटारो \\)

\\ (x ^ 2 + 2x \\ cdot \\ frac (b) (2a) + \\ बाएं (\\ frac (b) (2a) \\ राइट) ^ 2 \u003d \\ bept (\\ frac (b) (2a) \\ राइट) ^ ^ 2 - \\ frac (c) (a) \\ राइटारो \\) \\ (\\ Left (x + \\ frac (b) (2a) \\ अधिकार) ^ 2 \u003d \\ frac (b ^ 2) (4a ^ 2) - \\ frac (c) (a) \\ retharrow \\ Left (x + \\ frac (b) (2a) \\ राइट) ^ 2 \u003d \\ frac (b ^ 2-4ac) (4a ^ 2) \\ राइटारो \\) \\ (x + \\) Frac (b) (2a) \u003d \\ pm \\ sqrt (\\ frac (b ^ 2-4ac) (4a ^ 2)) \\ Retharrow x \u003d - \\ frac (b) (2a) + \\ frac (\\ pm \\ sqrt ( बी ^ 2 -4AC)) (2 ए) \\ राइटारो \\) \\ (x \u003d \\ frac (-b \\ pm \\ sqrt (b ^ 2-4ac)) (2 ए) \\)

निर्देशित अभिव्यक्ति कहा जाता है विवेकपूर्ण वर्ग समीकरण एक्स 2 + बीएक्स + सी \u003d 0 (लैटिन में "भेदभाव" एक विशिष्ट है)। यह पत्र डी, यानी द्वारा दर्शाया गया है
\\ (D \u003d b ^ 2-4ac \\)

अब, भेदभाव के पदनाम का उपयोग करके, वर्ग समीकरण की जड़ों के लिए सूत्र को फिर से लिखें:
\\ (x_ (1,2) \u003d \\ frac (-b \\ pm \\ sqrt (d)) (2a) \\), जहां \\ (d \u003d b ^ 2-4ac \\)

यह स्पष्ट है कि:
1) यदि डी\u003e 0, वर्ग समीकरण में दो जड़ें हैं।
2) यदि डी \u003d 0, वर्ग समीकरण में एक रूट \\ (x \u003d - \\ frac (b) (2a) \\) है।
3) यदि डी इस प्रकार, भेदभावपूर्ण मूल्य के आधार पर, वर्ग समीकरण में दो जड़ें हो सकती हैं (डी\u003e 0 के साथ), एक रूट (डी \u003d 0 पर) या जड़ें नहीं हैं (डी के साथ, वर्ग समीकरण को हल करते समय) यह सूत्र, यह सलाह दी जाती है कि निम्न तरीके से आवेदन करें:
1) भेदभाव की गणना करें और इसे शून्य से तुलना करें;
2) यदि भेदभाव सकारात्मक या शून्य के बराबर है, तो रूट फॉर्मूला का उपयोग करें, यदि भेदभाव नकारात्मक है, तो जड़ों को लिखें।

विएटा प्रमेय

प्रस्तुत वर्ग समीकरण कुल्हाड़ी 2 -7x + 10 \u003d 0 की जड़ों 2 और 5. जड़ों की मात्रा 7 है, और उत्पाद 10 है। हम देखते हैं कि जड़ों की मात्रा विपरीत के साथ दूसरे गुणांक के बराबर है साइन, और जड़ों का उत्पाद एक नि: शुल्क सदस्य के बराबर है। ऐसी संपत्ति में किसी भी स्क्वायर समीकरण में जड़ है।

प्रस्तुत वर्ग समीकरण की जड़ों का योग विपरीत संकेत के साथ किए गए दूसरे गुणांक के बराबर है, और जड़ों का उत्पाद एक नि: शुल्क सदस्य के बराबर है।

वे। विएटा प्रमेय का तर्क है कि दिए गए वर्ग समीकरण x 2 + px + q \u003d 0 के x 1 और x 2 की जड़ें एक संपत्ति है:
\\ (\\ Left \\ (\\ BEGIN (सरणी) (l) x_1 + x_2 \u003d -p \\\\ x_1 \\ cdot x_2 \u003d q \\ end (सरणी) \\ अधिकार। \\)

मुझे उम्मीद है कि इस लेख का अध्ययन करने के लिए, आप एक पूर्ण वर्ग समीकरण की जड़ों को ढूंढना सीखेंगे।

भेदभाव की मदद से, स्क्वायर समीकरणों को हल करने के लिए, केवल पूर्ण वर्ग समीकरण हल किए जाते हैं, "अपूर्ण वर्ग समीकरणों के निर्णय" लेख में जो अन्य विधियां उपयोग की जाती हैं।

किस वर्ग समीकरण को पूर्ण कहा जाता है? यह फॉर्म आह 2 + बी एक्स + सी \u003d 0 के समीकरणजहां गुणांक ए, बी और शून्य के बराबर नहीं हैं। तो, एक पूर्ण वर्ग समीकरण को हल करने के लिए, भेदभाव डी की गणना करना आवश्यक है।

डी \u003d बी 2 - 4AS।

इस पर निर्भर करता है कि किस प्रकार का महत्व भेदभावपूर्ण है, हम जवाब लिखेंगे।

यदि भेदभाव एक नकारात्मक संख्या है (d)< 0),то корней нет.

यदि भेदभाव शून्य है, x \u003d (-b) / 2a। जब भेदभाव एक सकारात्मक संख्या (d\u003e 0) है,

फिर x 1 \u003d (-बी - √ डी) / 2 ए, और x 2 \u003d (-बी + √ डी) / 2 ए।

उदाहरण के लिए। समीकरण हल करें एक्स 2 - 4x + 4 \u003d 0।

डी \u003d 4 2 - 4 · 4 \u003d 0

x \u003d (- (-4)) / 2 \u003d 2

उत्तर: 2

समीकरण 2 को हल करें। एक्स 2 + x + 3 \u003d 0।

डी \u003d 1 2 - 4 · 2 · 3 \u003d - 23

उत्तर: कोई जड़ नहीं.

समीकरण 2 को हल करें। एक्स 2 + 5x - 7 \u003d 0.

डी \u003d 5 2 - 4 · 2 · (-7) \u003d 81

x 1 \u003d (-5 - √81) / (2 · 2) \u003d (-5 - 9) / 4 \u003d - 3.5

x 2 \u003d (-5 + √81) / (2 · 2) \u003d (-5 + 9) / 4 \u003d 1

उत्तर: - 3.5; एक.

तो आइए चित्रा 1 में योजना द्वारा पूर्ण वर्ग समीकरणों के समाधान की कल्पना करें।

इन सूत्रों के अनुसार, आप किसी भी पूर्ण वर्ग समीकरण को हल कर सकते हैं। आपको केवल सावधानीपूर्वक निगरानी करने की आवश्यकता है समीकरण एक मानक प्रकार के बहुपद द्वारा दर्ज किया गया था।

लेकिन अ एक्स 2 + बीएक्स + सी, अन्यथा आप एक त्रुटि कर सकते हैं। उदाहरण के लिए, समीकरण एक्स + 3 + 2 एक्स 2 \u003d 0 के रिकॉर्ड में, यह गलती से हल किया जा सकता है

ए \u003d 1, बी \u003d 3 और सी \u003d 2. फिर

डी \u003d 3 2 - 4 · 1 · 2 \u003d 1 और फिर समीकरण में दो जड़ें हैं। और यह गलत है। (ऊपर उदाहरण 2 का समाधान देखें)।

इसलिए, यदि समीकरण एक मानक प्रजातियों के बहुपद के रूप में नहीं लिखा गया है, तो पहले एक पूर्ण वर्ग समीकरण को एक मानक प्रजातियों के बहुपद द्वारा दर्ज किया जाना चाहिए (पहली जगह में सबसे महान संकेतक के साथ अनलॉक किया जाना चाहिए, जो कि है लेकिन अ एक्स 2 फिर छोटे के साथ – बीएक्स।और फिर मुफ्त डिक से।

किसी दिए गए वर्ग समीकरण को हल करते समय और एक गुणांक के साथ एक वर्ग समीकरण, दूसरी अवधि के साथ, अन्य सूत्रों का उपयोग किया जा सकता है। आइए इन सूत्रों से परिचित हो जाएं। यदि दूसरे कार्यकाल में एक पूर्ण वर्ग समीकरण में, गुणांक भी (बी \u003d 2 के) होगा, तो आंकड़े 2 में सूत्रों के अनुसार समीकरण हल किया जा सकता है।

पूर्ण वर्ग समीकरण को उपरोक्त कहा जाता है, यदि गुणांक है एक्स 2 एक के बराबर और समीकरण फॉर्म ले जाएगा x 2 + px + q \u003d 0। ऐसे समीकरण को हल करने के लिए दिया जा सकता है, या गुणांक समीकरण में सभी गुणांक को विभाजित करके प्राप्त किया जा सकता है लेकिन अके पक्ष में होना एक्स 2 .

चित्रा 3 उपरोक्त वर्ग को हल करने की योजना दिखाता है
समीकरण। इस आलेख में विचार किए गए सूत्रों के आवेदन के उदाहरण पर विचार करें।

उदाहरण। समीकरण हल करें

3एक्स 2 + 6x - 6 \u003d 0।

आइए चित्रा 1 योजना में दिखाए गए सूत्रों का उपयोग करके इस समीकरण का निर्णय लें।

डी \u003d 6 2 - 4 · 3 · (- 6) \u003d 36 + 72 \u003d 108

√d \u003d √108 \u003d √ (36 · 3) \u003d 6√3

x 1 \u003d (-6 - 6√3) / (2 · 3) \u003d (6 (-1- √ (3))) / 6 \u003d -1 - √3

x 2 \u003d (-6 + 6√3) / (2 · 3) \u003d (6 (-1+ √ (3))) / 6 \u003d -1 + √3

उत्तर: -1 - √3; -1 + √3

यह देखा जा सकता है कि इस समीकरण में एक्स पर गुणांक एक भी संख्या है, जो कि बी \u003d 6 या बी \u003d 2k है, जहां से के \u003d 3. से हम आरेख में दिखाए गए सूत्रों के अनुसार समीकरण को हल करने का प्रयास करते हैं 1 \u003d 3 2 - 3 · (- 6) \u003d 9 + 18 \u003d 27

√ (d 1) \u003d √27 \u003d √ (9 · 3) \u003d 3√3

x 1 \u003d (-3 - 3√3) / 3 \u003d (3 (-1 - √ (3))) / 3 \u003d - 1 - √3

x 2 \u003d (-3 + 3√3) / 3 \u003d (3 (-1 + √ (3))) / 3 \u003d - 1 + √3

उत्तर: -1 - √3; -1 + √3। ध्यान दिया कि इस वर्ग समीकरण में सभी गुणांक 3 में विभाजित हैं और विभाजन प्रदर्शन करके, हम निर्दिष्ट वर्ग के लिए सूत्रों का उपयोग करके इस समीकरण को हल करके कम वर्ग समीकरण x 2 + 2x - 2 \u003d 0 प्राप्त करते हैं
समीकरण चित्र 3।

डी 2 \u003d 2 2 - 4 · (- 2) \u003d 4 + 8 \u003d 12

√ (d 2) \u003d √12 \u003d √ (4 · 3) \u003d 2√3

x 1 \u003d (-2 - 2√3) / 2 \u003d (2 (-1 - √ (3))) / 2 \u003d - 1 - √3

x 2 \u003d (-2 + 2√3) / 2 \u003d (2 (-1+ √ (3))) / 2 \u003d - 1 + √3

उत्तर: -1 - √3; -1 + √3।

जैसा कि हम देखते हैं, विभिन्न सूत्रों पर इस समीकरण को हल करते समय, हमें एक ही उत्तर प्राप्त हुआ। इसलिए, यह चित्रा 1 योजना में दिखाए गए सूत्रों के बारे में अच्छी तरह से अवगत है, आप हमेशा किसी भी पूर्ण वर्ग समीकरण को हल कर सकते हैं।

साइट, मूल स्रोत के लिए सामग्री संदर्भ की पूर्ण या आंशिक प्रतिलिपि के साथ आवश्यक है।

"समीकरणों के निर्णय" विषय की निरंतरता में, इस लेख की सामग्री आपको वर्ग समीकरणों के साथ पेश करेगी।

विस्तार से सबकुछ पर विचार करें: वर्ग समीकरण का सार और रिकॉर्ड, साथ में शर्तों को निर्धारित करता है, हम अपूर्ण और पूर्ण समीकरणों के समाधान के लिए योजना का विश्लेषण करेंगे, जड़ों और भेदभाव के सूत्र से परिचित हो जाते हैं, जड़ों और गुणांक के बीच संबंध स्थापित करते हैं, और निश्चित रूप से हम व्यावहारिक उदाहरणों का एक दृश्य समाधान देते हैं।

Yandex.rtb r-a-339285-1

वर्ग समीकरण, इसके प्रकार

परिभाषा 1।

द्विघात समीकरण - यह समीकरण दर्ज किया गया है a · x 2 + b · x + c \u003d 0कहां है एक्स। - चर, ए, बी और सी। - कुछ संख्या, जबकि ए।शून्य नहीं।

अक्सर, वर्ग समीकरणों को द्वितीय डिग्री समीकरणों का नाम भी कहा जाता है, क्योंकि संक्षेप में वर्ग समीकरण दूसरी डिग्री के बीजगणितीय समीकरण है।

हम एक दी गई परिभाषा को चित्रित करने के लिए एक उदाहरण देते हैं: 9 · x 2 + 16 · x + 2 \u003d 0; 7, 5 · x 2 + 3, 1 · x + 0, 11 \u003d 0, आदि - ये वर्ग समीकरण हैं।

परिभाषा 2।

संख्या ए, बी और सी। - ये वर्ग समीकरण के गुणांक हैं a · x 2 + b · x + c \u003d 0, गुणांक के साथ ए। इसे पहले, या पुराने, या x 2, b - दूसरे गुणांक, या गुणांक पर गुणांक कहा जाता है एक्स।, लेकिन अ सी। मुक्त सदस्य को कॉल करें।

उदाहरण के लिए, एक वर्ग समीकरण में 6 · x 2 - 2 · x - 11 \u003d 0 वरिष्ठ गुणांक 6 है, दूसरा गुणांक है − 2 और नि: शुल्क सदस्य बराबर है − 11 । इस तथ्य पर ध्यान दें कि जब गुणांक बीऔर / या सी नकारात्मक हैं, फिर एक दृश्य रिकॉर्डिंग का एक संक्षिप्त रूप उपयोग किया जाता है। 6 · x 2 - 2 · x - 11 \u003d 0, लेकिन नहीं 6 · x 2 + (- 2) · x + (- 11) \u003d 0.

हम इस पहलू को भी स्पष्ट करते हैं: यदि गुणांक ए। और / या बी बराबरी का 1 या − 1 , फिर वर्ग समीकरण की रिकॉर्डिंग में स्पष्ट भागीदारी, उन्हें नहीं लिया जा सकता है, जिसे इन संख्यात्मक गुणांक के रिकॉर्ड की विशेषताओं द्वारा समझाया गया है। उदाहरण के लिए, एक वर्ग समीकरण में Y 2 - y + 7 \u003d 0 वरिष्ठ गुणांक 1 है, और दूसरा गुणांक है − 1 .

निर्दिष्ट और अविवाहित वर्ग समीकरण

पहले गुणांक के मूल्य से, वर्ग समीकरण उपरोक्त और अवैतनिक में विभाजित होते हैं।

परिभाषा 3।

वर्ग समीकरण - यह एक वर्ग समीकरण है जहां पुराने गुणांक 1 के बराबर है। पुराने गुणांक के अन्य मूल्यों के लिए, वर्ग समीकरण गैर-अमान्य है।

हम उदाहरण देते हैं: स्क्वायर समीकरण x 2 - 4 · x + 3 \u003d 0, x 2 - x - 4 5 \u003d 0 उनमें से प्रत्येक में पुराने गुणांक 1 में प्रस्तुत किए जाते हैं।

9 · x 2 - x - 2 \u003d 0 - एक अभिन्न वर्ग समीकरण, जहां पहले गुणांक अलग है 1 .

किसी भी व्यस्त वर्ग समीकरण को किसी दिए गए समीकरण में परिवर्तित करना संभव है यदि इसे दोनों भागों से पहले गुणांक (समतुल्य परिवर्तन) में विभाजित किया गया है। परिवर्तित समीकरण में निर्दिष्ट बुद्धिमान समीकरण के समान जड़ें होंगी या जड़ों को बिल्कुल नहीं होना चाहिए।

एक विशिष्ट उदाहरण पर विचार हमें स्पष्ट रूप से दिए गए एक अभिन्न वर्ग समीकरण से संक्रमण को स्पष्ट रूप से प्रदर्शित करने की अनुमति देगा।

उदाहरण 1।

समीकरण 6 · x 2 + 18 · x - 7 \u003d 0 सेट किया गया है . उपर्युक्त रूप में प्रारंभिक समीकरण को परिवर्तित करना आवश्यक है।

फेसला

निर्दिष्ट उपरोक्त की योजना वरिष्ठ गुणांक 6 पर प्रारंभिक समीकरण के दोनों हिस्सों द्वारा अलग की गई है। फिर हमें मिलता है: (6 · x 2 + 18 · x - 7): 3 \u003d 0: 3और यह वही है: (6 · x 2): 3 + (18 · x): 3 - 7: 3 \u003d 0 और आगे: (6: 6) · x 2 + (18: 6) · x - 7: 6 \u003d 0। यहां से: x 2 + 3 · x - 1 1 6 \u003d 0। इस प्रकार, एक समीकरण को निर्दिष्ट माना जाता है।

उत्तर: x 2 + 3 · x - 1 1 6 \u003d 0।

पूर्ण और अधूरा वर्ग समीकरण

वर्ग समीकरण की परिभाषा को चालू करें। इसमें हमने स्पष्ट किया एक ≠ 0। इस तरह की एक शर्त समीकरण के लिए आवश्यक है a · x 2 + b · x + c \u003d 0 यह बिल्कुल वर्ग था क्योंकि A \u003d 0 यह अनिवार्य रूप से रैखिक समीकरण में परिवर्तित किया जाता है b · x + c \u003d 0.

मामले में जब गुणांक बी तथा सी।शून्य के बराबर (जो व्यक्तिगत रूप से और एक साथ संभव है), वर्ग समीकरण को अपूर्ण कहा जाता है।

परिभाषा 4।

अपूर्ण वर्ग समीकरण - इस तरह के एक वर्ग समीकरण a · x 2 + b · x + c \u003d 0,जहां कम से कम गुणांक बीतथा सी।(या दोनों) शून्य है।

पूर्ण वर्ग समीकरण - एक वर्ग समीकरण जिसमें सभी संख्यात्मक गुणांक शून्य नहीं हैं।

हम इसमें शामिल हैं कि स्क्वायर समीकरणों के प्रकार बिल्कुल नाम क्यों दिए गए हैं।

बी \u003d 0 वर्ग समीकरण के लिए फॉर्म लेता है A · x 2 + 0 · x + c \u003d 0वही बात यह है कि a · x 2 + c \u003d 0। के लिये C \u003d 0। वर्ग समीकरण के रूप में दर्ज किया गया है a · x 2 + b · x + 0 \u003d 0वह समतुल्य है a · x 2 + b · x \u003d 0। के लिये B \u003d 0। तथा C \u003d 0। समीकरण दृश्य ले जाएगा a · x 2 \u003d 0। हमारे द्वारा प्राप्त किए गए समीकरण पूर्ण वर्ग समीकरण से अलग हैं, जिसमें उनके बाएं भागों में या तो एक्स वैरिएबल या एक मुफ्त सदस्य या दोनों में एक घटक शामिल नहीं है। असल में, इस तथ्य से इस तरह के एक प्रकार के समीकरणों का नाम पूछा गया था - अपूर्ण।

उदाहरण के लिए, x 2 + 3 · x + 4 \u003d 0 और - 7 · x 2 - 2 · x + 1, 3 \u003d 0 पूर्ण वर्ग समीकरण हैं; x 2 \u003d 0, - 5 · x 2 \u003d 0; 11 · x 2 + 2 \u003d 0, - x 2 - 6 · x \u003d 0 - अपूर्ण वर्ग समीकरण।

अपूर्ण वर्ग समीकरणों का निर्णय

उपरोक्त परिभाषा निम्नलिखित प्रकार के अपूर्ण वर्ग समीकरणों को अलग करना संभव बनाता है:

• a · x 2 \u003d 0, यह समीकरण गुणांक से मेल खाता है B \u003d 0। और c \u003d 0;
• b \u003d 0 के लिए a · x 2 + c \u003d 0;
• c \u003d 0 पर a · x 2 + b · x \u003d 0।

प्रत्येक प्रकार के अपूर्ण वर्ग समीकरण के निर्णय पर विचार करें।

समीकरण का समाधान a · x 2 \u003d 0

जैसा ऊपर बताया गया है, समीकरण गुणांक से मेल खाता है बी तथा सी।शून्य के बराबर। समीकरण a · x 2 \u003d 0 समीकरण को इसके बराबर परिवर्तित करना संभव है x 2 \u003d 0जो हम प्राप्त करते हैं, संख्या के लिए स्रोत समीकरण के दोनों हिस्सों को साझा करते हैं ए।शून्य के बराबर नहीं। स्पष्ट तथ्य यह है कि समीकरण की जड़ x 2 \u003d 0 यह शून्य है क्योंकि 0 2 = 0 । अन्य जड़ों, इस समीकरण में संख्या नहीं है, जिसे डिग्री के गुणों द्वारा समझाया गया है: किसी भी संख्या के लिए पी,शून्य, वफादार असमानता के बराबर नहीं पी 2\u003e 0क्या इस प्रकार है कि कब पी ≠ 0 समानता पी 2 \u003d 0कभी हासिल नहीं किया जाएगा।

परिभाषा 5।

इस प्रकार, एक अपूर्ण वर्ग समीकरण के लिए a · x 2 \u003d 0 एकमात्र जड़ है x \u003d 0।.

उदाहरण 2।

उदाहरण के लिए, हम एक अपूर्ण वर्ग समीकरण हल करते हैं - 3 · x 2 \u003d 0। यह समीकरण के बराबर है x 2 \u003d 0, उसकी एकमात्र जड़ है x \u003d 0।, फिर प्रारंभिक समीकरण में एकमात्र जड़ है - शून्य।

संक्षेप में निर्णय इसलिए किया गया है:

- 3 · x 2 \u003d 0, x 2 \u003d 0, x \u003d 0।

समीकरण का समाधान a · x 2 + c \u003d 0

कतार पर - अपूर्ण वर्ग समीकरणों का समाधान, जहां बी \u003d 0, सी ≠ 0, वह है, फॉर्म के समीकरण a · x 2 + c \u003d 0। हम इस समीकरण को समीकरण के एक हिस्से से दूसरे हिस्से से दूसरे हिस्से में परिवर्तित करते हैं, संकेत को विपरीत में बदलते हैं और समीकरण के दोनों हिस्सों को संख्या में विभाजित करते हैं, शून्य के बराबर नहीं:

• स्थानांतरण सी। सही भाग में, जो समीकरण देता है A · x 2 \u003d - c;
• हम समीकरण के दोनों भागों को विभाजित करते हैं ए।, मैं अंत x \u003d - c a में मिलता हूं।

हमारे परिवर्तन क्रमशः समकक्ष हैं, परिणामी समीकरण स्रोत के बराबर भी है, और यह तथ्य समीकरण की जड़ों को समाप्त करना संभव बनाता है। अर्थ क्या है ए। तथा सी।अभिव्यक्ति का मूल्य निर्भर करता है - सी ए: इसमें एक शून्य संकेत हो सकता है (मान लें अगर ए \u003d 1। तथा सी \u003d 2।, फिर - सी ए \u003d - 2 1 \u003d - 2) या प्लस साइन (उदाहरण के लिए, यदि ए \u003d - 2 तथा सी \u003d 6।, फिर - सी ए \u003d - 6 - 2 \u003d 3); यह शून्य नहीं है क्योंकि सी ≠ 0।। आइए उन स्थितियों में अधिक विस्तार से रहें - सी ए< 0 и - c a > 0 .

मामले में जब - सी ए< 0 , уравнение x 2 = - c a не будет иметь корней. Утверждая это, мы опираемся на то, что квадратом любого числа является число неотрицательное. Из сказанного следует, что при - c a < 0 ни для какого числа पी समानता पी 2 \u003d - सी ए सत्य नहीं हो सकता है।

अन्यथा, जब - सी ए\u003e 0: वर्ग रूट को याद करें, और यह स्पष्ट होगा कि समीकरण x 2 \u003d - सी ए नंबर - सी ए होगा, क्योंकि सी ए 2 \u003d - सी ए। यह समझना मुश्किल नहीं है कि संख्या है - सी ए समीकरण एक्स 2 \u003d - सी ए: वास्तव में, - सी ए 2 \u003d - सी ए की जड़ भी है।

अन्य जड़ों समीकरण नहीं होगा। हम इसे गंदा विधि का उपयोग करके प्रदर्शित कर सकते हैं। शुरू करने के लिए, जड़ों के ऊपर पाए गए पदों को सेट करें एक्स 1 तथा - एक्स 1।। मैं सुझाव दूंगा कि समीकरण x 2 \u003d - c a भी जड़ है एक्स 2जो जड़ों से अलग है एक्स 1 तथा - एक्स 1।। हम जानते हैं कि इसके बजाय समीकरण में प्रतिस्थापित करना एक्स। इसकी जड़ें, हम समीकरण को निष्पक्ष संख्यात्मक समानता में बदल देते हैं।

के लिये एक्स 1 तथा - एक्स 1। हम लिखते हैं: x 1 2 \u003d - c a, और के लिए एक्स 2 - एक्स 2 2 \u003d - सी ए। संख्यात्मक समानता के गुणों पर निर्भर, एक सही समानता को दूसरे से भरें, जो हमें देगा: x 1 2 - x 2 2 \u003d 0। नवीनतम समानता को फिर से लिखने के लिए संख्याओं के साथ क्रियाओं के गुणों का उपयोग करें (x 1 - x 2) · (x 1 + x 2) \u003d 0। यह ज्ञात है कि दो संख्याओं का कार्य शून्य है और केवल तभी यदि संख्या में से कम संख्या शून्य है। ने कहा कि यह इस प्रकार है x 1 - x 2 \u003d 0 और / या x 1 + x 2 \u003d 0वही बात x 2 \u003d x 1 और / या x 2 \u003d - x 1। एक स्पष्ट विरोधाभास था, क्योंकि पहले यह सहमति हुई कि समीकरण की जड़ एक्स 2 से भिन्न है एक्स 1 तथा - एक्स 1।। इसलिए, हमने साबित किया कि समीकरण में अन्य जड़ें नहीं हैं, एक्स \u003d - सी ए और एक्स \u003d - - सी ए को छोड़कर।

हम उपरोक्त सभी तर्क को सारांशित करते हैं।

परिभाषा 6।

अपूर्ण वर्ग समीकरण a · x 2 + c \u003d 0 समीकरण x 2 \u003d - सी ए के बराबर, जो:

• जड़ों की नहीं होगी जब - सी ए< 0 ;
• दो जड़ें x \u003d - c a और x \u003d - - c a के साथ - c a\u003e 0 होगा।

हम समीकरणों को हल करने के उदाहरण देते हैं a · x 2 + c \u003d 0.

उदाहरण 3।

वर्ग समीकरण निर्दिष्ट है 9 · x 2 + 7 \u003d 0।उसका निर्णय ढूंढना आवश्यक है।

फेसला

हम समीकरण के दाएं हाथ के हिस्से में एक नि: शुल्क सदस्य स्थानांतरित करते हैं, फिर समीकरण फॉर्म ले जाएगा 9 · x 2 \u003d - 7।
हम प्राप्त समीकरण के दोनों भागों को विभाजित करते हैं 9 , x 2 \u003d - 7 9 पर आएं। सही हिस्से में, हम एक शून्य चिह्न के साथ एक संख्या देखते हैं, जिसका अर्थ है: निर्दिष्ट समीकरण में कोई जरूरी नहीं है। फिर मूल अपूर्ण वर्ग समीकरण 9 · x 2 + 7 \u003d 0 जड़ें नहीं होगी।

उत्तर: समीकरण 9 · x 2 + 7 \u003d 0इसकी जड़ें नहीं हैं।

उदाहरण 4।

समीकरण को हल करना आवश्यक है - x 2 + 36 \u003d 0.

फेसला

हम 36 को दाईं ओर ले जाते हैं: - x 2 \u003d - 36.
हम दोनों भागों को विभाजित करते हैं − 1 , प्राप्त x 2 \u003d 36। सही भाग में - एक सकारात्मक संख्या, यहां से हम यह निष्कर्ष निकाल सकते हैं x \u003d 36 या X \u003d - 36।
रूट निकालें और अंतिम परिणाम लिखें: एक अपूर्ण वर्ग समीकरण - x 2 + 36 \u003d 0 इसमें दो जड़ें हैं x \u003d 6। या x \u003d - 6.

उत्तर: x \u003d 6। या x \u003d - 6.

समीकरण का समाधान a · x 2 + b · x \u003d 0

हम तीसरे प्रकार के अपूर्ण वर्ग समीकरणों की जांच करेंगे C \u003d 0।। अपूर्ण वर्ग समीकरण का निर्णय खोजने के लिए a · x 2 + b · x \u003d 0, हम गुणक पर अपघटन की विधि का उपयोग करते हैं। बहुपद के गुणक पर फैला हुआ, जो समीकरण के बाएं हिस्से में है, कोष्ठक के लिए एक सामान्य गुणक बनाकर एक्स।। यह कदम मूल अपूर्ण वर्ग समीकरण को समकक्ष में बदलने का अवसर प्रदान करेगा x · (· x + b) \u003d 0। और यह समीकरण, बदले में, समीकरणों की कुलता के बराबर है x \u003d 0। तथा A · x + b \u003d 0। समीकरण A · x + b \u003d 0 रैखिक, और इसकी जड़: x \u003d - b a.

परिभाषा 7।

इस प्रकार, एक अधूरा वर्ग समीकरण a · x 2 + b · x \u003d 0 दो जड़ें होंगी x \u003d 0। तथा x \u003d - b a.

एक उदाहरण से सामग्री को तेज करें।

उदाहरण 5।

समीकरण 2 3 · x 2 - 2 2 7 · x \u003d 0 के समाधान को ढूंढना आवश्यक है।

फेसला

चलो एक्स। कोष्ठक के लिए और समीकरण x · 2 3 · x - 2 2 7 \u003d 0 प्राप्त करें। यह समीकरण समीकरणों के बराबर है x \u003d 0। और 2 3 · x - 2 2 7 \u003d 0। अब परिणामी रैखिक समीकरण को हल करना आवश्यक है: 2 3 · x \u003d 2 2 7, x \u003d 2 2 7 2 3।

इस तरह से लिखने के लिए समीकरण को संक्षेप में हल करना:

2 3 · x 2 - 2 2 7 · x \u003d 0 x · 2 3 · x - 2 2 7 \u003d 0

x \u003d 0 या 2 3 · x - 2 2 7 \u003d 0

x \u003d 0 या x \u003d 3 3 7

उत्तर: x \u003d 0, x \u003d 3 3 7।

भेदभावपूर्ण, वर्ग समीकरण के जड़ें सूत्र

वर्ग समीकरणों का समाधान खोजने के लिए, जड़ों के लिए एक सूत्र है:

परिभाषा 8।

एक्स \u003d - बी ± डी 2 · ए कहाँ डी \u003d बी 2 - 4 · ए सी - एक वर्ग समीकरण के तथाकथित भेदभाव।

रिकॉर्डिंग एक्स \u003d - बी ± डी 2 · सार में इसका मतलब है कि एक्स 1 \u003d - बी + डी 2 · ए, एक्स 2 \u003d - बी - डी 2 · ए।

यह समझने के लिए उपयोगी होगा कि निर्दिष्ट सूत्र कैसे लिया गया था और इसे कैसे लागू किया जाए।

वर्ग समीकरण की जड़ों का उत्पादन

हमें वर्ग समीकरण को हल करने के लिए चुनौती दीजिए a · x 2 + b · x + c \u003d 0। कई समकक्ष परिवर्तन करें:

• हम संख्या के लिए समीकरण के दोनों भागों को विभाजित करते हैं ए।शून्य के अलावा, हम कम वर्ग समीकरण प्राप्त करते हैं: x 2 + b a · x + c a \u003d 0;
• हम प्राप्त समीकरण के बाईं ओर पूर्ण वर्ग को हाइलाइट करते हैं:
  एक्स 2 + बा · एक्स + सीए \u003d एक्स 2 + 2 · बी 2 · ए · एक्स + बी 2 · ए 2 - बी 2 · ए 2 + सीए \u003d एक्स + बी 2 · ए 2 - बी 2 · ए 2 + सीए ।
  उसके बाद, समीकरण फॉर्म ले जाएगा: एक्स + बी 2 · ए 2 - बी 2 · 2 + सी ए \u003d 0;
• अब पिछले दो पदों को दाईं ओर हाथ में स्थानांतरित करना संभव है, विपरीत रूप से संकेत को बदलना, जिसके बाद हम प्राप्त करते हैं: एक्स + बी 2 · ए 2 \u003d बी 2 · 2 - सी ए;
• अंत में, हम अंतिम समानता के दाईं ओर दर्ज की गई अभिव्यक्ति को बदलते हैं:
  बी 2 · ए 2 - सी ए \u003d बी 2 4 · ए 2 - सी ए \u003d बी 2 4 · ए 2 - 4 · ए · सी 4 · ए 2 \u003d बी 2 - 4 · ए · सी 4 · ए 2।

इस प्रकार, हम समीकरण x + b 2 · 2 \u003d बी 2 - 4 · ए · सी 4 · ए 2, समकक्ष स्रोत समीकरण में आए थे a · x 2 + b · x + c \u003d 0.

हम पिछले पैराग्राफ (अपूर्ण वर्ग समीकरणों के निर्णय) में ऐसे समीकरणों के समाधान को समझ गए। प्राप्त अनुभव समीकरण एक्स + बी 2 · ए 2 \u003d बी 2 - 4 · ए 2 \u003d बी 2 - 4 · ए 2 की जड़ों के बारे में निष्कर्ष निकालना संभव बनाता है:

• बी 2 - 4 · a · c 4 · 2 पर< 0 уравнение не имеет действительных решений;
• बी 2 - 4 · ए सी 4 · ए 2 \u003d 0 के लिए, समीकरण में फॉर्म x + b 2 · 2 \u003d 0 है, फिर x + b 2 · a \u003d 0।

इसलिए एकमात्र रूट x \u003d - b 2 · ए स्पष्ट है;

• बी 2 - 4 · ए सी 4 · ए 2\u003e 0 के लिए, यह सही होगा: एक्स + बी 2 · ए \u003d बी 2 - 4 · ए · सी 4 · ए 2 या एक्स \u003d बी 2 · ए - बी 2 - 4 · ए · सी 4 · ए 2, जो एक्स + - बी 2 · ए \u003d बी 2 - 4 · ए · सी 4 · ए 2 या एक्स \u003d - बी 2 · ए - बी 2 - 4 · ए · सी 4 · ए 2, यानी समीकरण में दो जड़ें हैं।

यह निष्कर्ष निकालना संभव है कि समीकरण X + B 2 · 2 \u003d b 2 - 4 · a · c 4 · 2 (और इसलिए प्रारंभिक समीकरण) की जड़ों की उपस्थिति या अनुपस्थिति अभिव्यक्ति बी के संकेत पर निर्भर करती है 2 - 4 · ए · सी 4 · एक 2, दाईं ओर दर्ज किया गया। और इस अभिव्यक्ति का संकेत संख्याओं की संख्या से निर्धारित है, (denominator) 4 · 2 हमेशा सकारात्मक रहेगा), यानी, अभिव्यक्ति का संकेत बी 2 - 4 · ए · सी। यह अभिव्यक्ति बी 2 - 4 · ए · सी नाम एक वर्ग निकासी का भेदभाव है और इसे पत्र डी के पदनाम के रूप में परिभाषित किया गया है। यहां आप भेदभाव के सार को रिकॉर्ड कर सकते हैं - इसके मूल्य से और संकेत निष्कर्ष निकाला गया है कि वर्ग समीकरण में वैध जड़ें होंगी, और यदि यह है, तो जड़ों की संख्या क्या है - एक या दो।

समीकरण X + B 2 · 2 \u003d b 2 - 4 · A · C 4 · A 2 पर लौट रहा है। मैं इसे भेदभावपूर्ण पदनाम का उपयोग करके फिर से लिखता हूं: एक्स + बी 2 · 2 \u003d डी 4 · ए 2।

हम फिर से निष्कर्ष निकालेंगे:

परिभाषा 9।

• के लिये डी< 0 समीकरण में कोई वैध जड़ें नहीं हैं;
• के लिये डी \u003d 0। समीकरण में एकमात्र रूट x \u003d - b 2 · ए;
• के लिये D\u003e 0 समीकरण में दो जड़ें हैं: x \u003d - बी 2 · ए + डी 4 · ए 2 या एक्स \u003d - बी 2 · ए - डी 4 · ए 2। रेडिकल के गुणों के आधार पर ये जड़ें फॉर्म में लिखी जा सकती हैं: एक्स \u003d - बी 2 · ए + डी 2 · ए या - बी 2 · ए - डी 2 · ए। और जब हम मॉड्यूल प्रकट करते हैं और सामान्य संप्रदाय को अंश देते हैं, तो हम प्राप्त करते हैं: x \u003d - बी + डी 2 · ए, एक्स \u003d - बी - डी 2 · ए।

इस प्रकार, हमारे तर्क का परिणाम वर्ग समीकरण की जड़ों के सूत्र को हटाने का निष्कासन था:

एक्स \u003d - बी + डी 2 · ए, एक्स \u003d - बी - डी 2 · ए, भेदभाव डी सूत्र द्वारा गणना की गई डी \u003d बी 2 - 4 · ए सी.

ये सूत्र इसे संभव बनाते हैं जब दोनों वैध जड़ों को निर्धारित करने के लिए बड़े होते हैं। जब भेदभाव शून्य होता है, तो दोनों सूत्रों का उपयोग समान रूट को वर्ग समीकरण के एकमात्र समाधान के रूप में देगा। इस मामले में जब भेदभाव नकारात्मक होता है, वर्ग समीकरण के रूट फॉर्मूला का उपयोग करने की कोशिश कर रहा है, तो हमें स्क्वायर रूट को नकारात्मक संख्या से हटाने की आवश्यकता का सामना करना पड़ेगा, जो हमें वास्तविक संख्याओं से परे ले जाएगा। एक नकारात्मक भेदभाव के साथ, वर्ग समीकरण वैध जड़ें नहीं होगी, लेकिन हमारे द्वारा प्राप्त एक ही रूट सूत्रों द्वारा निर्धारित की गई जड़ों की एक जोड़ी संभव है।

रूट सूत्रों पर वर्ग समीकरणों को हल करने के लिए एल्गोरिदम

स्क्वायर समीकरण को हल करना संभव है, तुरंत जड़ों के सूत्र को साइकिल चलाना, लेकिन मूल रूप से वे करते हैं, यदि आवश्यक हो, जटिल जड़ों को ढूंढें।

मामलों के मुख्य द्रव्यमान में, आमतौर पर इसे गैर-जटिल, लेकिन वर्ग समीकरण की वैध जड़ों की खोज के लिए निहित किया जाता है। फिर स्क्वायर समीकरण की जड़ों के सूत्रों का उपयोग करने से पहले, पहले भेदभाव को निर्धारित करें और सुनिश्चित करें कि यह नकारात्मक नहीं है (अन्यथा हम निष्कर्ष निकालते हैं कि समीकरण में कोई वैध जड़ें नहीं हैं), और फिर जड़ों के मूल्य की गणना करने के लिए आगे बढ़ें।

ऊपर दिए गए तर्क एक वर्ग समीकरण को हल करने के लिए एक एल्गोरिदम तैयार करने की क्षमता प्रदान करते हैं।

परिभाषा 10।

एक वर्ग समीकरण को हल करने के लिए a · x 2 + b · x + c \u003d 0, यह आवश्यक है:

• सूत्र के अनुसार डी \u003d बी 2 - 4 · ए सी भेदभाव के मूल्य का पता लगाएं;
• d के साथ< 0 сделать вывод об отсутствии у квадратного уравнения действительных корней;
• डी \u003d 0 पर फॉर्मूला एक्स \u003d - बी 2 · ए के अनुसार समीकरण की एकमात्र जड़ पाते हैं;
• डी\u003e 0 के लिए, फॉर्मूला एक्स \u003d - बी ± डी 2 · ए के अनुसार वर्ग समीकरण की दो मान्य जड़ें निर्धारित करें।

ध्यान दें कि जब भेदभाव शून्य होता है, तो आप फॉर्मूला एक्स \u003d - बी ± डी 2 · ए का उपयोग कर सकते हैं, यह एक ही परिणाम देगा क्योंकि फॉर्मूला एक्स \u003d - बी 2 · ए।

उदाहरणों पर विचार करें।

वर्ग समीकरणों के समाधान के उदाहरण

हम भेदभाव के विभिन्न मूल्यों पर उदाहरणों का समाधान प्रस्तुत करते हैं।

उदाहरण 6।

समीकरण की जड़ों को ढूंढना आवश्यक है x 2 + 2 · x - 6 \u003d 0.

फेसला

हम वर्ग समीकरण के नंबर गुणांक लिखते हैं: ए \u003d 1, बी \u003d 2 और सी \u003d - 6। इसके बाद, हम एल्गोरिदम पर कार्य करते हैं, यानी। हम भेदभाव की गणना करने के लिए आगे बढ़ेंगे, जिसके लिए हम गुणांक ए, बी को प्रतिस्थापित करेंगे तथा सी। भेदभाव के सूत्र में: डी \u003d बी 2 - 4 · ए · सी \u003d 2 2 - 4 · 1 · (- 6) \u003d 4 + 24 \u003d 28।

तो, हमने डी\u003e 0 प्राप्त किया, और इसका मतलब है कि प्रारंभिक समीकरण में दो वैध जड़ें होंगी।
उन्हें खोजने के लिए, हम रूट फॉर्मूला एक्स \u003d - बी ± डी 2 · ए और, संबंधित मानों को प्रतिस्थापित करने का उपयोग करते हैं, हम प्राप्त करते हैं: x \u003d - 2 ± 28 2 · 1। हम परिणामी अभिव्यक्ति को सरल बनाते हैं, रूट संकेत के लिए गुणक बनाते हुए, अंश को काटने के बाद:

x \u003d - 2 ± 2 · 7 2

x \u003d - 2 + 2 · 7 2 या x \u003d - 2 - 2 · 7 2

x \u003d - 1 + 7 या x \u003d - 1 - 7

उत्तर: x \u003d - 1 + 7, x \u003d - 1 - 7।

उदाहरण 7।

वर्ग समीकरण को हल करना आवश्यक है - 4 · x 2 + 28 · x - 49 \u003d 0.

फेसला

भेदभाव का निर्धारण करें: डी \u003d 28 2 - 4 · (- 4) · (- 4 9) \u003d 784 - 784 \u003d 0। इस भेदभावपूर्ण मूल्य के साथ, प्रारंभिक समीकरण में फॉर्मूला एक्स \u003d - बी 2 · ए द्वारा परिभाषित केवल एक रूट होगा।

x \u003d - 28 2 · (- 4) x \u003d 3, 5

उत्तर: x \u003d 3, 5.

उदाहरण 8।

समीकरण को हल करना आवश्यक है 5 · y 2 + 6 · y + 2 \u003d 0

फेसला

इस समीकरण के संख्यात्मक गुणांक होंगे: ए \u003d 5, बी \u003d 6 और सी \u003d 2। हम इन मानों का उपयोग एक भेदभाव खोजने के लिए करते हैं: डी \u003d बी 2 - 4 · ए · सी \u003d 6 2 - 4 · 5 · 2 \u003d 36 - 40 \u003d - 4। गणना की गई भेदभाव नकारात्मक है, इस प्रकार, प्रारंभिक वर्ग समीकरण में वैध जड़ें नहीं हैं।

इस मामले में जब कार्य जटिल जड़ों को निर्दिष्ट करना है, तो जटिल सूत्र लागू करना, जटिल संख्याओं के साथ कार्य करना:

x \u003d - 6 ± - 4 2 · 5,

x \u003d - 6 + 2 · i 10 या x \u003d - 6 - 2 · i 10,

x \u003d - 3 5 + 1 5 · I या x \u003d - 3 5 - 1 5 · i।

उत्तर: कोई वैध जड़ें नहीं हैं; कॉम्प्लेक्स रूट्स निम्नानुसार हैं: - 3 5 + 1 5 · I, - 3 5 - 1 5 · I.

स्कूल कार्यक्रम में, जटिल जड़ों को देखने की कोई आवश्यकता नहीं है, इसलिए यदि समाधान के दौरान भेदभाव को नकारात्मक के रूप में परिभाषित किया जाता है, तो उत्तर तुरंत दर्ज किया जाता है कि कोई वैध जड़ें नहीं हैं।

यहां तक \u200b\u200bकि दूसरे गुणांक के लिए फॉर्मूला जड़ें

जड़ों का सूत्र एक्स \u003d - बी ± डी 2 · ए (डी \u003d बी 2 - 4 · ए · सी) एक और सूत्र, अधिक कॉम्पैक्ट प्राप्त करना संभव बनाता है, जो वर्ग समीकरणों के समाधान को एक्स पर एक गुणांक के साथ ढूंढने की इजाजत देता है (या एक प्रकार 2 गुणांक के साथ · एन, उदाहरण के लिए, 2 · 3 या 14 · ln 5 \u003d 2 · 7 · ln 5)। हम दिखाते हैं कि यह सूत्र कैसे प्रदर्शित होता है।

आइए स्क्वायर समीकरण ए · एक्स 2 + 2 · एन एक्स + सी \u003d 0 के समाधान को खोजने का कार्य बनें। हम एल्गोरिदम पर कार्य करते हैं: भेदभाव डी \u003d (2 · एन) 2 - 4 · ए · सी \u003d 4 · एन 2 - 4 · ए · सी \u003d 4 · (एन 2 - ए · सी) निर्धारित करें, और फिर उपयोग करें रूट फॉर्मूला:

एक्स \u003d - 2 · एन ± डी 2 · ए, एक्स \u003d - 2 · एन ± 4 · एन 2 - ए · सी 2 · ए, एक्स \u003d - 2 · एन ± 2 एन 2 - ए · सी 2 · ए, एक्स \u003d - एन ± एन 2 - ए · सीए।

अभिव्यक्ति एन 2 - ए · सी को डी 1 (कभी-कभी डी ") के रूप में इंगित किया जाना चाहिए। फिर दूसरे गुणांक 2 · एन के साथ विचाराधीन स्क्वायर समीकरण की जड़ों का सूत्र फॉर्म ले जाएगा:

एक्स \u003d - एन ± डी 1 ए, जहां डी 1 \u003d एन 2 - ए · सी।

यह देखना आसान है कि डी \u003d 4 · डी 1, या डी 1 \u003d डी 4। दूसरे शब्दों में, डी 1 भेदभाव का एक चौथाई है। यह स्पष्ट है कि साइन डी 1 साइन डी के समान है, जिसका अर्थ है कि साइन डी 1 स्क्वायर समीकरण की जड़ों की उपस्थिति या अनुपस्थिति के संकेतक के रूप में भी कार्य कर सकता है।

परिभाषा 11।

इस प्रकार, दूसरे गुणांक 2 · एन के साथ वर्ग समीकरण के समाधान को खोजने के लिए, यह आवश्यक है:

• डी 1 \u003d एन 2 - ए · सी खोजें;
• डी 1 के साथ।< 0 сделать вывод, что действительных корней нет;
• डी 1 \u003d 0 के लिए, फॉर्मूला एक्स \u003d - एन ए के अनुसार समीकरण की एकमात्र जड़ निर्धारित करें;
• डी 1\u003e 0 के लिए, फॉर्मूला एक्स \u003d - एन ± डी 1 ए के अनुसार दो मान्य जड़ें निर्धारित करें।

उदाहरण 9।

स्क्वायर समीकरण 5 · x 2 - 6 · x - 32 \u003d 0 को हल करना आवश्यक है।

फेसला

निर्दिष्ट समीकरण का दूसरा गुणांक 2 · (3) के रूप में दर्शाया जा सकता है। फिर निर्दिष्ट वर्ग समीकरण को 5 · x 2 + 2 · (- 3) · x - 32 \u003d 0 के रूप में फिर से लिखें, जहां ए \u003d 5, एन \u003d - 3 और सी \u003d - 32।

हम भेदभाव के चौथे हिस्से की गणना करते हैं: डी 1 \u003d एन 2 - ए · सी \u003d (- 3) 2 - 5 · (- 32) \u003d 9 + 160 \u003d 16 9। सकारात्मक रूप से प्राप्त मूल्य, इसका मतलब है कि समीकरण में दो वैध जड़ें हैं। हम संबंधित रूट सूत्र के अनुसार उन्हें परिभाषित करते हैं:

एक्स \u003d - एन ± डी 1 ए, एक्स \u003d - - 3 ± 16 9 5, एक्स \u003d 3 ± 13 5,

x \u003d 3 + 13 5 या x \u003d 3 - 13 5

x \u003d 3 1 5 या x \u003d - 2

गणना करना संभव होगा और वर्ग समीकरण की जड़ों के सामान्य सूत्र से, लेकिन इस मामले में समाधान अधिक बोझिल होगा।

उत्तर: x \u003d 3 1 5 या x \u003d - 2।

वर्ग समीकरणों की प्रजातियों का सरलीकरण

कभी-कभी स्रोत समीकरण के प्रकार को अनुकूलित करना संभव है, जो जड़ों की गणना करने की प्रक्रिया को सरल बना देगा।

उदाहरण के लिए, एक वर्ग समीकरण 12 · x 2 - 4 · x - 7 \u003d 0 1200 · x 2 - 400 · x - 700 \u003d 0 से हल करने के लिए स्पष्ट रूप से अधिक सुविधाजनक है।

अधिक बार स्क्वायर समीकरण की प्रजातियों का सरलीकरण गुणा या उसके दोनों भागों के विभाजन द्वारा एक प्रकार की संख्या में किया जाता है। उदाहरण के लिए, हमने समीकरण 1200 · x 2 - 400 · x - 700 \u003d 0 का एक सरलीकृत रिकॉर्ड दिखाया, दोनों भागों को 100 से विभाजित करके प्राप्त किया गया।

इस तरह का रूपांतरण संभव है जब वर्ग समीकरण के गुणांक पारस्परिक रूप से सरल संख्या नहीं हैं। फिर आमतौर पर समीकरण के दोनों हिस्सों को अपने गुणांक के पूर्ण मूल्यों के सबसे बड़े आम विभाजक के लिए विभाजित कर रहे हैं।

उदाहरण के तौर पर, एक वर्ग समीकरण 12 · x 2 - 42 · x + 48 \u003d 0 का उपयोग करें। हम अपने गुणांक के पूर्ण मूल्यों के नोड को परिभाषित करते हैं: नोड्स (12, 42, 48) \u003d नोड (नोड (12, 42), 48) \u003d नोड (6, 48) \u003d 6। हम मूल वर्ग समीकरण के दो हिस्सों को 6 में विभाजित करेंगे और हम समकक्ष वर्ग समीकरण 2 · x 2 - 7 · x + 8 \u003d 0 प्राप्त करेंगे।

वर्ग समीकरण के दोनों हिस्सों का गुणा आमतौर पर आंशिक गुणांक से छुटकारा मिलता है। साथ ही इसके गुणांक के सबसे छोटे सामान्य एकाधिक संप्रदाय से गुणा किया गया। उदाहरण के लिए, यदि वर्ग समीकरण का प्रत्येक भाग 1 6 · x 2 + 2 3 · x - 3 \u003d 0 एनओसी (6, 3, 1) \u003d 6 से गुणा है, तो यह एक सरल रूप x 2 में दर्ज हो जाएगा + 4 · x - 18 \u003d 0।

अंत में, हम ध्यान देते हैं कि लगभग हमेशा स्क्वायर समीकरण के पहले गुणांक पर ऋण से छुटकारा पाता है, समीकरण के प्रत्येक सदस्य के संकेतों को बदलते हुए, जो 1 के दोनों हिस्सों को गुणा (या विभाजन) द्वारा प्राप्त किया जाता है। उदाहरण के लिए, एक वर्ग समीकरण से - 2 · x 2 - 3 · x + 7 \u003d 0, आप इसके सरलीकृत संस्करण 2 · x 2 + 3 · x - 7 \u003d 0 पर जा सकते हैं।

जड़ों और गुणांक के बीच संचार

स्क्वायर समीकरणों की जड़ों का सूत्र एक्स \u003d - बी ± डी 2 · पहले से ही हमारे लिए ज्ञात रूप से ज्ञात समीकरण की जड़ों को अपने संख्यात्मक गुणांक के माध्यम से व्यक्त करता है। इस सूत्र पर निर्भर करते हुए, हमारे पास जड़ों और गुणांक के बीच अन्य निर्भरताओं को स्थापित करने का अवसर है।

सबसे प्रसिद्ध और लागू वियतनाम प्रमेय के सूत्र हैं:

x 1 + x 2 \u003d - b a और x 2 \u003d c a।

विशेष रूप से, कम वर्ग समीकरण के लिए, जड़ों की मात्रा विपरीत संकेत के साथ दूसरा गुणांक है, और जड़ों का उत्पाद नि: शुल्क है। उदाहरण के लिए, वर्ग समीकरण 3 की प्रजातियों के अनुसार 3 · x 2 - 7 · x + 22 \u003d 0, तुरंत यह निर्धारित करना संभव है कि इसकी जड़ों का योग 7 3 है, और जड़ों का उत्पाद 22 3 है।

आप स्क्वायर समीकरण की जड़ों और गुणांक के बीच कई अन्य लिंक भी पा सकते हैं। उदाहरण के लिए, स्क्वायर समीकरण की जड़ों के वर्गों का योग गुणांक के माध्यम से व्यक्त किया जा सकता है:

x 1 2 + x 2 2 \u003d (x 1 + x 2) 2 - 2 · x 1 · x 2 \u003d - बा 2 - 2 · ca \u003d b 2 a 2 - 2 · ca \u003d b 2 - 2 · · ca 2।

यदि आपको पाठ में कोई गलती दिखाई देती है, तो कृपया इसे चुनें और Ctrl + Enter दबाएं