Цель. Учить детей составлять геометрические фигуры из определенного количества палочек, пользуясь приемом пристроения к одной фигуре, взятой за основу, другой. Материал. Детские развивающие игры, уроки, поделки

20.03.2019

«Я тебя люблю» на разных языках мира Как будет по осетински я тебя люблю

Книга сентября: мемуары Карины Добротворской

Игры на сплочение для детского лагеря Логические игры для лагеря в отряде

1. Пример

Цель. Учить детей составлять геометрические фигуры из определенного количества палочек, пользуясь приемом пристроения к одной фигуре, взятой за основу, другой.

Материал: У детей на столах счетные палочки, доска, мел на данном и следующем занятиях.

Ход работы. 1. Воспитатель предлагает детям отсчитать по 5 палочек, проверить и положить их перед собой. Затем говорит: "Скажите, сколько потребуется палочек, чтобы составить треугольник, каждая сторона которого будет равна одной палочке. Сколько потребуется палочек для составления двух таких треугольников? У вас только 5 палочек, но из них надо составить тоже 2 равных треугольника. Подумайте, как это можно сделать, и составляйте".

После того как большинство детей выполнят задание, воспитатель просит их рассказать, как надо составить 2 равных треугольника из 5 палочек. Обращает внимание ребят на то, что выполнять задание можно по-разному. Способы выполнения надо зарисовать. При объяснении пользоваться выражением "пристроил к одному треугольнику другой снизу" (слева и т.д.), а в объяснении решения задачи пользоваться также выражением "пристроил к одному треугольнику другой, используя лишь 2 палочки".

2. Составить 2 равных квадрата из 7 палочек (воспитатель предварительно уточняет, какую геометрическую фигуру можно составить из 4 палочек). Дает задание: отсчитать 7 палочек и подумать, как из них составить на столе 2 равных квадрата.

После выполнения задания рассматривают разные способы пристроения к одному квадрату другого, воспитатель зарисовывает их на доске.

Вопросы для анализа: "Как составил 2 равных квадрата из 7 палочек? Что сделал сначала, что потом? Из скольких палочек составил 1 квадрат? Из скольких палочек пристроил к нему второй квадрат? Сколько потребовалось палочек для составления 2 равных квадратов?"

2. Пример

Цель. Составлять фигуры путем пристроения. Видеть и показывать при этом новую, полученную в результате составления фигуру; пользоваться выражением: "пристроил к одной фигуре другую", обдумывать практические действия.

^ Ход работы. Воспитатель предлагает детям вспомнить, какие фигуры они составляли, пользуясь приемом пристроения. Сообщает, чем они сегодня будут заниматься - учиться составлять новые, более сложные фигуры. Дает задания:

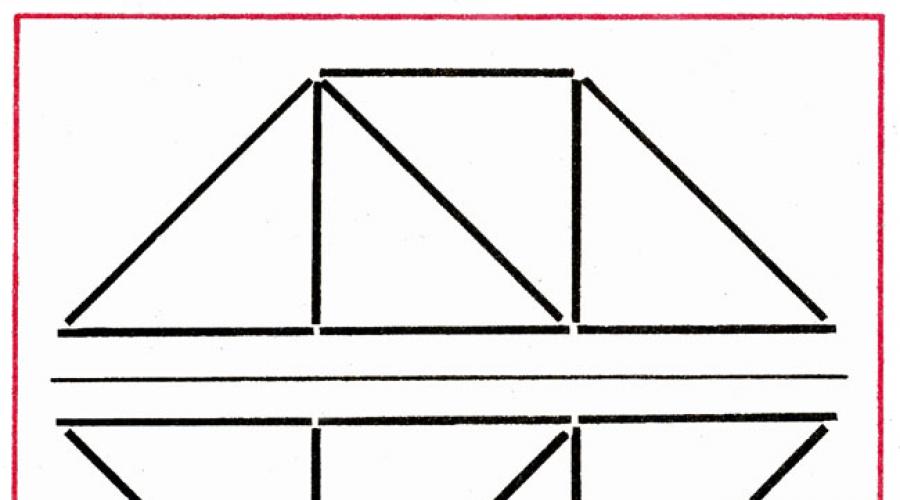
После выполнения задания воспитатель предлагает всем детям составить 3 треугольника в ряд так, чтобы получилась новая фигура - четырехугольник (рис. 2). Этот вариант решения дети зарисовывают мелом на доске. Воспитатель просит показать 3 отдельных треугольника, четырехугольник и треугольник (2 фигуры), четырехугольник.

Рис. 2 Составление фигур из треугольников

2. Из 9 палочек составить 4 равных треугольника. Подумать, как это можно сделать, рассказать, затем выполнять задание.

После этого воспитатель предлагает детям нарисовать мелом на доске составленные фигуры и рассказать о последовательности выполнения задания.

Вопросы для анализа: "Как составил 4 равных треугольника из 9 палочек? Какой из треугольников составил первым? Какие фигуры получились в результате и сколько?"

Воспитатель, уточняя ответы детей, говорит: "Начинать составлять фигуру можно с любого треугольника, а потом к нему пристраивать другие справа или слева, сверху или снизу".

3. Пример

Цель. Упражнять детей в самостоятельных поисках путей составления фигур на основе предварительного обдумывания хода решения.

^ Ход работы. Воспитатель задает детям вопросы: "Из скольких палочек можно составить квадрат, каждая из сторон которого равна одной палочке? 2 квадрата? (из 8 и 7). Как будете составлять 2 квадрата из 7 палочек?"

По мере выполнения воспитатель вызывает нескольких детей зарисовать составленные ими фигуры на доске и рассказать последовательность составления. Предлагает всем детям составить фигуру из 3 равных квадратов, расположенных в ряд, по горизонтали. На доске рисует такую же и говорит: "Посмотрите на доску. Здесь нарисовано, как можно по-разному решать эту задачу. Можно пристраивать к одному квадрату другой, а затем и третий. (Показывает.) А можно составить прямоугольник из 8 палочек, затем разделить его на 3 равных квадрата 2 палочками". (Показывает.) Затем задает вопросы: "Какие фигуры получились и сколько? Сколько прямоугольников получилось? Найдите и покажите их".

2. Из 5 палочек составить квадрат и 2 равных треугольника. Сначала рассказать, а затем составлять.

При выполнении этого задания дети, как правило, допускают ошибку: составляют 2 треугольника усвоенным способом - пристроением, в результате чего получается четырехугольник. Поэтому воспитатель обращает внимание ребят на условие задачи, необходимость составления квадрата, предлагает наводящие вопросы: "Сколько палочек нужно для составления квадрата? Поскольку у вас палочек? Можно ли составить, пристраивая 1 треугольник к другому? Как составить? С какой фигуры надо начинать составлять?" После выполнения задания дети объясняют, как они делали: надо составить квадрат и разделить его 1 палочкой на 2 равных треугольника.

4. Пример

Цель. Упражнять детей в умении высказывать предположительное решение, догадываться.

^ Ход работы. 1. Из 9 палочек составить квадрат и 4 треугольника. Подумать и сказать, как надо составлять. (Несколько детей высказывают предположения.)

Если дети затрудняются, воспитатель советует: "Вспомните, как составляли из 5 палочек квадрат и 2 треугольника. Подумайте и догадайтесь, как можно выполнить задание. Тот, кто первым решит задачу, зарисует полученную фигуру на доске".

После выполнения и зарисовки ответа воспитатель предлагает всем детям составить у себя одинаковые фигуры (рис. 3).

Рис. 3 Составление фигур из треугольников

Вопросы для анализа: "Какие геометрические фигуры получились? Сколько треугольников, квадратов, четырехугольников? Как составляли? Как удобнее, быстрее составлять?"

2. Из 10 палочек составить 2 квадрата - маленький и большой.

3. Из 9 палочек составить 5 треугольников.

При необходимости в ходе выполнения второго и третьего заданий воспитатель дает наводящие вопросы, советы: "Сначала подумайте, затем составьте. Не повторяйте ошибок, ищите новый ход решения. Говорится ли в задаче о размере треугольников? Это задачи на смекалку, надо сообразить, догадаться, как решить задачу".

Итак, в начальный период обучения детей 5 лет решению простых задач на смекалку они самостоятельно, в основном практически действуя с палочками, ищут путь решения. С целью развития у них умения планировать ход мысли следует предлагать детям высказывать предварительные рассуждения или сочетать их с практическими пробами, объяснять способ и путь решения.

Возможно несколько видов решения задач первой группы. Усвоив способ пристроения фигур при условии общности сторон, дети очень легко и быстро дают 2-3 варианта решения. Каждая фигура при этом отличается от прежней пространственным положением. Одновременно дети осваивают способ построения заданных фигур путем деления полученной геометрической фигуры на несколько (четырехугольник или квадрат на 2 треугольника, прямоугольник - на 3 квадрата).

Решение с детьми 5-6 лет более сложных задач на перестроение фигур следует начинать с тех, в которых с целью изменения фигуры надо убрать определенное количество палочек и наиболее простых - на перекладывание палочек.

Процесс поисков детьми решения задач второй и третьей групп гораздо сложнее, нежели первой группы. Для этого нужно запомнить и осмыслить характер преобразования и результат (какие фигуры должны получиться и сколько) и постоянно в ходе поисков решения соотносить его с предполагаемыми или уже осуществленными изменениями. В процессе решения необходим зрительный и мыслительный анализ задачи, умение представить возможные изменения в фигуре.

Таким образом, в процессе решения задач дети должны овладеть такими мыслительными операциями анализа задачи, в результате которых можно представить мысленно различные преобразования, проверить их, затем, отбросив неверные, искать и пробовать новые ходы решения. Обучение должно быть направлено на формирование у детей умения обдумывать ходы мысленно, полностью или частично решать задачу в уме, ограничивать практические пробы.

В какой последовательности надо предлагать детям 5-6 лет задачи на смекалку второй и третьей групп?

В фигуре, состоящей из 5 квадратов, убрать 4 палочки, оставив один прямоугольник (рис. 4).

Рис. 4

В фигуре, состоящей из 6 квадратов, убрать 2 палочки, чтобы осталось 4 равных квадрата (рис. 5).

Рис. 5

Составить домик из 6 палочек, а затем переложить 2 палочки так, чтобы получился флажок (рис. 6).

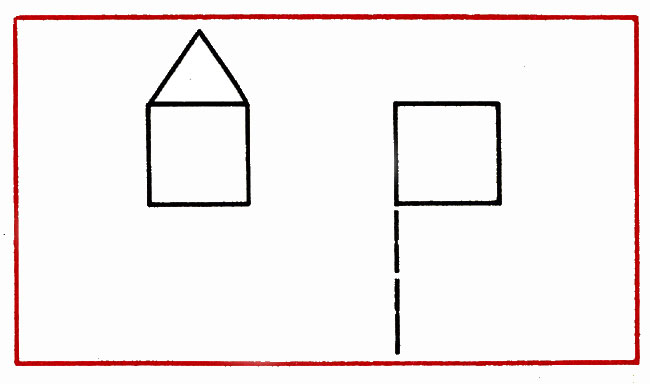
Рис. 6

В данной фигуре переложить 2 палочки, чтобы получилось 3, равных треугольника (рис. 7).

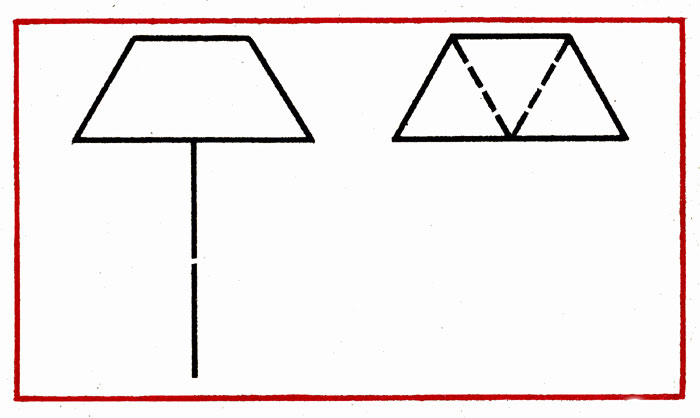
Рис. 7

В фигуре, состоящей из 5 квадратов, убрать 3 палочки, чтобы осталось 3 таких же квадрата (рис. 8).

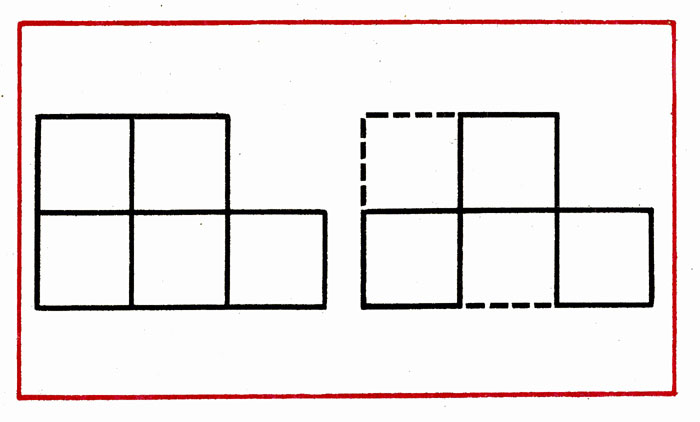
Рис. 8

В фигуре, состоящей из 4 квадратов, убрать 2 палочки, чтобы осталось 2 неравных квадрата (рис. 9).

Рис. 9

В фигуре из 5 квадратов убрать 4 палочки, чтобы осталось 2 неравных квадрата (рис. 10).

Рис. 10

В фигуре из 5 квадратов убрать 4 палочки, чтобы остались 3 квадрата (рис. 11).

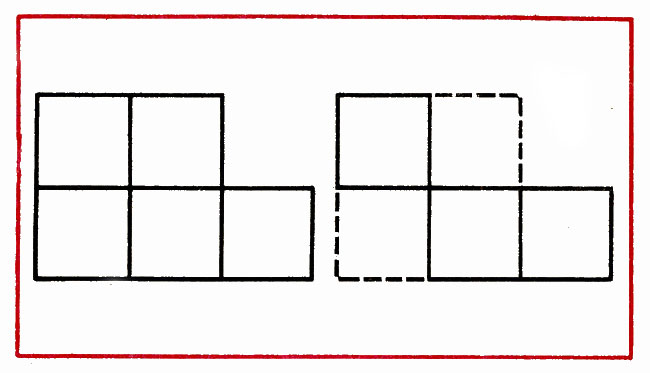
Рис. 11

В фигуре из 4 квадратов переложить 2 палочки так, чтобы получилось 5 квадратов (рис. 12).

Рис. 12

В фигуре из 5 квадратов убрать 4 палочки, чтобы осталось 3 квадрата (рис. 13).

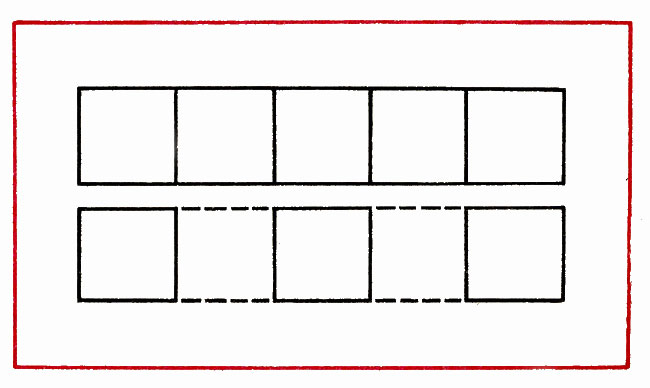
Рис. 13

Для этих и других аналогичных задач на смекалку характерно то, что преобразование, необходимое для решения, ведет к изменению количества квадратов, из которых составлена заданная фигура (задачи 2, 5 и др.), изменению их размера (задачи 6, 7), видоизменению фигур, например преобразование квадратов в прямоугольник в задаче 1.

В ходе занятий с целью руководства поисковой деятельностью детей воспитатель пользуется различными приемами, способствующими воспитанию у них положительного отношения к длительному настойчивому поиску, но в то же время быстроты реакции, отказа от выработанного пути поисков. Интерес детей поддерживается желанием достичь успеха, для чего нужна актив-, ная работа мысли.
^

Преобразование одной фигуры в другую. Изменение количества квадратов в фигуре.

1. Пример

Цель. Упражнять детей в умении решать задачи путем целенаправленных практических проб и обдумывания хода решения.

Материал: счетные палочки у детей, у воспитателя - изображенные графически задачи (на этом и следующих занятиях).

^ Ход работы. 1. Воспитатель показывает детям таблицу с изображенной на ней фигурой, предлагает составить из палочек такую же (рис. 4). Рассматривает ее вместе с детьми, определяет количество квадратов. Затем говорит: "Это задача. Послушайте, что нужно сделать, чтобы решить ее. Надо догадаться, какие 4 палочки убрать, чтобы получился 1 прямоугольник. Сначала подумайте, как это можно сделать, а затем убирайте палочки".

После того как будет решена задача, воспитатель вызывает одного ребенка к доске, тот показывает и рассказывает, как нужно ее решить. Педагог одобряет попытки детей действовать самостоятельно.

2. Дана фигура из 6 квадратов. Надо убрать 2 палочки, чтобы осталось 4 таких же квадрата (рис. 5).

После составления детьми по образцу такой фигуры идет анализ по вопросам: "Сколько квадратов в фигуре? Как расположены? Как считаете, какие из палочек, образующих квадраты, надо убрать, чтобы сразу уменьшилось их количество?"

Дети самостоятельно решают задачу. Воспитатель в случае затруднения помогает им, ориентируя на поиск правильных способов.

2. Пример

Цель. Упражнять детей в умении осуществлять целенаправленные пробы, ограничивать количество практических проб за счет обдумывания хода поисков, догадки.

^ Ход работы. 1. Дана фигура из 5 квадратов. Надо убрать 3 палочки, оставив 3 квадрата (рис. 8). Воспитатель задает вопросы, побуждает детей к решению задачи: "Сколько квадратов в фигуре? Сколько должно остаться? Сколько палочек нужно убрать? Эта задача на смекалку, надо догадаться, какие 3 палочки нужно убрать, чтобы квадратов стало меньше - 3?"

Дети приступают к решению. Воспитатель напоминает о необходимости предварительного обдумывания хода поисков решения. В случае затруднения он напоминает условие задачи, предлагает не повторять пробных действий, которые не приводят к правильному решению.

Один из детей, решивших задачу в числе первых, зарисовывает и объясняет решение у доски.

2. Дана фигура из 4 равных квадратов. Надо убрать 2 палочки, чтобы получилось 2 неравных квадрата (рис. 9).

Вопросы для анализа составленной по образцу фигуры: "Сколько квадратов? Можете ли доказать, что они равны? Подумайте, как решить задачу".

По предложению воспитателя один ребенок объясняет у доски решение задачи.

3. Пример

Цель. Высказывать предположительный ход поиска решения, проверять его путем целенаправленных поисковых действий.

^ Ход занятия. 1. Дана фигура из 5 равных квадратов; надо убрать 4 палочки, чтобы стало 3 равных квадрата (рис. 13).

Воспитатель, обращаясь к детям, говорит: "Рассмотрите фигуру, подумайте, как можно решить задачу, какие из палочек убрать, чтобы изменилась эта фигура. Сначала расскажите, а потом убирайте палочки".

Воспитатель спрашивает некоторых детей (но так, чтобы их рассказы не слышали другие ребята), предлагает всем решить задачу самостоятельно. Дети объясняют решение задачи у доски, с тем, чтобы по ходу рассказа можно было сделать зарисовку фигур.

2. Дана фигура из 4 квадратов: надо переложить 2 палочки, чтобы получилось 5 равных квадратов (рис. 12).

Воспитатель после составления детьми фигуры и анализа задачи говорит детям, чтобы они, прежде чем переложить палочки, подумали, ведет ли это действие к увеличению количества квадратов, рассказали о том, как они думают решать задачу. В ходе проверки решения воспитатель подчеркивает, что решить задачу можно по-разному.

В процессе обучения на занятиях, дети 5-6 лет активно включаются не только в практический поиск решения, но и в умственный. Об этом свидетельствуют их высказывания, рассуждения о путях решения. Так, детям была дана фигура из 5 квадратов; надо убрать 4 палочки, чтобы осталось 3 таких же квадрата (рис. 14). Отвечая на вопрос воспитателя о том, как будут решать задачу, одни отвечают: "Я беру вот эти палочки (а, б и к) и эту (в). Что же тогда получится? (Задумывается.) Нет, не знаю как". Другие рассуждают: "Я думаю, что убрать надо 2 угловые палочки (е, ж) и еще где-то посмотреть надо". "Я догадалась. Посмотрела и догадалась: если эти убрать (показывает на г, д, и, з), то будет 3 квадрата: один, два, три".

Рис. 14

В ходе выполнения заданий дети овладевают умением на основе обдумывания процесса поиска (анализа задачи) предполагать решение, проверять его практически, искать новые пути, обосновывать их.

Для обучения детей самостоятельному анализу задачи, поиску решения, умению догадываться целесообразно использование различных методических приемов , указаний о необходимости поискового подхода к решению задачи: "Сначала подумайте, как бы вы решили задачу, и расскажите об этом. Проверьте свое предположение, переложив палочки или даже не трогая их. Если считаете, что ошиблись, надо придумать, как решить задачу по-другому, а не повторять своих ошибок. Надо внимательно рассмотреть фигуру и догадаться, как решить задачу". Оценка, подтверждение правильности или ошибочности хода: "Эту палочку ты убрал правильно, подумай, как дальше решать задачу" - и другое стимулируют активность ребят, помогают им находить правильное решение.

^ В работе с детьми 7-го года жизни усложняется характер задач на преобразование фигур. Решаются они путем сочетания практических и мысленных проб или только в плане умственного действия - в уме, с обоснованием, выражением в речи хода решения.

Последовательность выполнения детьми 6-7 лет задач на преобразование фигур.

Переложить 1 палочку чтобы домик был перевернут в другую сторону (рис. 15).

Рис. 15

В фигуре, состоящей из 9 квадратов, убрать 4 палочки, чтобы осталось 5 квадратов (рис. 16).

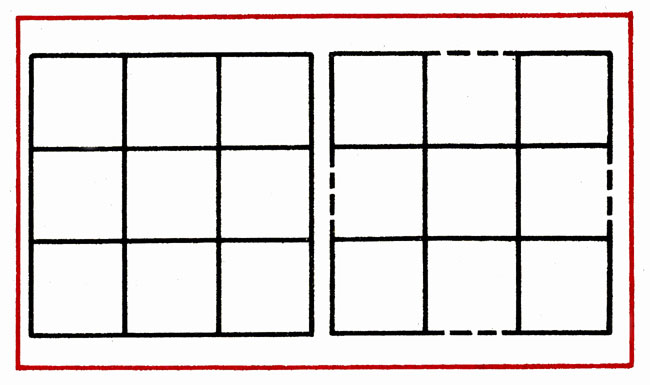
Рис. 16

В фигуре из 6 квадратов убрать 3 палочки, чтобы осталось 4 квадрата (рис. 17).

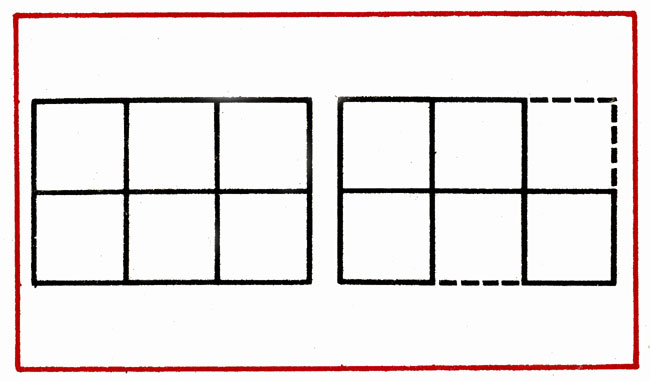
Рис. 17

В фигуре, похожей на ключ, переложить 4 палочки, чтобы получилось 3 квадрата (рис. 18).

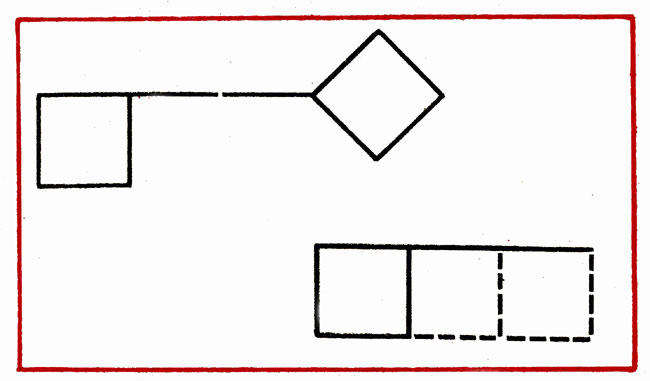
Рис. 18

В фигуре из 6 квадратов убрать 2 палочки так, чтобы осталось 4 равных квадрата (рис. 19).

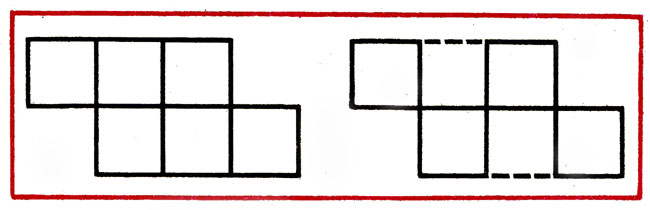
Рис. 19

В фигуре, изображающей стрелу, переложить 4 палочки так, чтобы получилось 4 треугольника (рис. 20).

Рис. 20

В фигуре из 5 квадратов переложить 3 палочки, чтобы стало 4 квадрата (рис. 21).

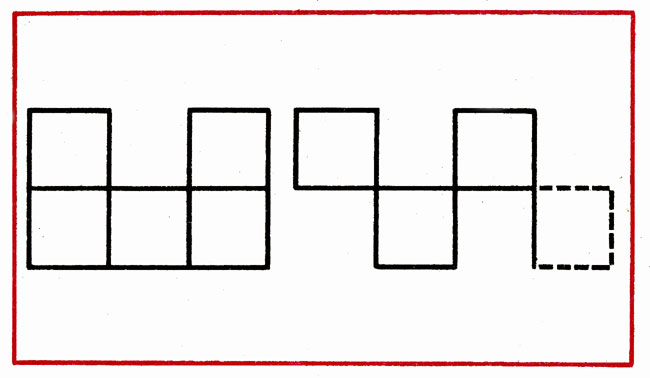
Рис. 21

В фигуре переложить 3 палочки так, чтобы получилось 4 равных треугольника (рис. 22).

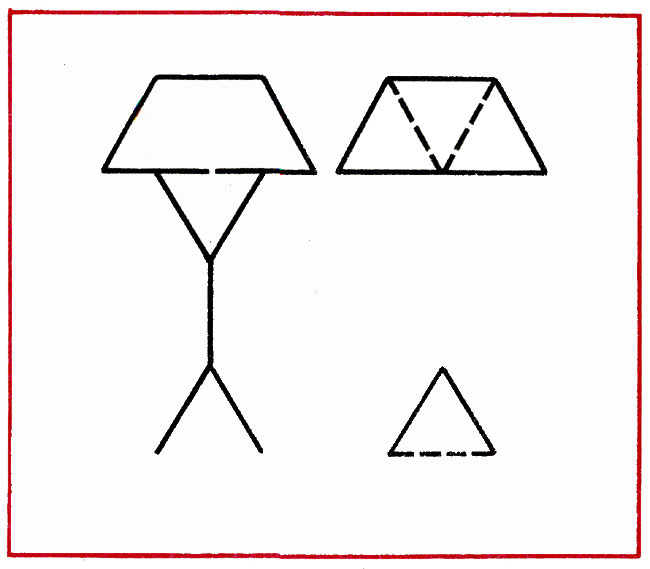
Рис. 22

В фигуре, состоящей из 4 квадратов, переложить 3 палочки так, чтобы получилось 3 таких же квадрата (рис.23).

Рис. 23

Переложить 4 палочки так, чтобы из топора получилось 4 равных треугольника (рис. 24).

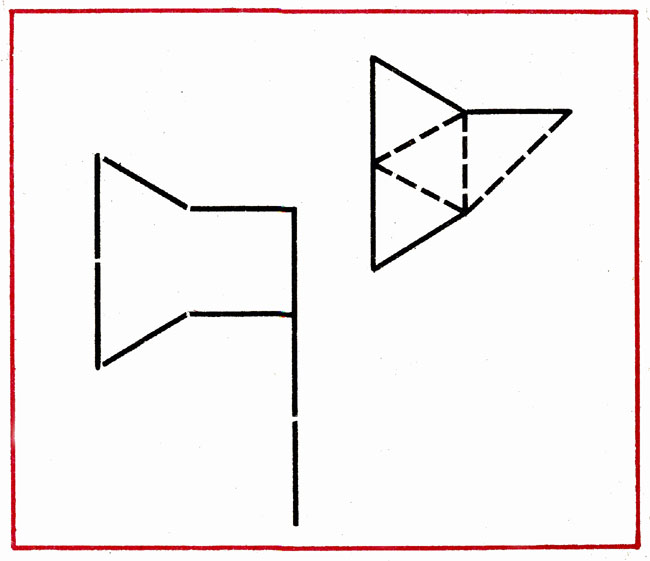
Рис.24

В фигуре, напоминающей фонарь, переложить 4 палочки, чтобы получился четырехугольник, состоящий из 4 равных треугольников (рис. 25).

Рис. 25

Переложить 2 палочки так, чтобы фигура; похожая на корову, смотрела в другую сторону (рис. 26).

Рис. 26

Какое наименьшее количество палочек нужно переложить, чтобы убрать мусор из совочка? (рис. 27.)

Рис. 27

В

подготовительной к школе группе обучение детей решению задач на смекалку способствует дальнейшему развитию их умственной деятельности, способности планировать ход поисков

В главе 12 уже говорилось о полимино и его создателе С. Голомбе. После опубликования статьи о полимино на страницах журнала Scientific American A957) игра стала необыкновенно популярным математическим развлечением. Обнаружились сотни новых задач и причудливых конфигураций полимино. О них и пойдет здесь речь.

Напомним, что фигуры, которыми на шахматной доске можно покрыть пять соседних клеток, образующих связную область, носят название пентамино. Существует двенадцать таких фигур. Если эти фигуры расположить так, как показано на рис. 234, то становится видно, что каждая фигура по форме напоминает какую-нибудь латинскую букву, поэтому для запоминания формы и названия фигур (каждую фигуру мы будем называть какой-нибудь буквой) достаточно знать конец латинского алфавита (Т, U, V, W, X, Y, Z) и слово FiLiPiNo.

Рис. 234

В главе 12 (см. рис. 71) было показано, что из двенадцати элементов пентамино общей площадью в 60 квадратиков можно сложить прямоугольники четырех размеров: 3х20, 4х15, 5х12 и 6х10. Те же 12 фигур можно уложить на шахматной доске размером 8x8, причем квадрат из четырех лишних клеток (площадь доски равна 64 квадратикам) может находиться в любом месте доски.

Любой элемент пентамино можно утроить с помощью каких-нибудь девяти фигур из числа оставшихся (подразумевается, что из этих девяти пентамино будет сложена фигура, подобная выбранной, но в три раза выше и длиннее). Из двенадцати пентамино можно еще построить два прямоугольника 5x6. Последняя задача носит название задачи на суперпозицию, потому что построенные фигуры можно наложить друг на друга. Голомб сообщил мне пять новых задач на суперпозицию, которые впервые публикуются в этой книге. Если читатель до сих пор не понял всей прелести пентамино, ему необходимо вырезать из картона набор элементов пентамино и поломать голову над некоторыми из приведенных ниже задач.

Во всех головоломках элементы пентамино можно класть на плоскость любой стороной.

1. Разбейте двенадцать пентамино на три группы по четыре элемента в каждой. Затем найдите фигуру площадью в 20 квадратиков, которую можно сложить из элементов каждой группы. Одно из возможных решений изображено на рис. 235.

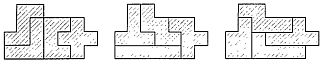
Рис. 235

2. Разбейте двенадцать пентамино на три группы по четыре элемента. Каждую группу разделите пополам и найдите такую фигуру (для каждой группы свою), имеющую площадь в 10 квадратиков, которую можно сложить из обеих пар элементов в отдельности.

Одно из решений показано на рис. 236. Можете ли вы придумать другие решения, чтобы хотя бы в одном из них фигуры не имели отверстий?

Рис. 236

3. Разбейте двенадцать пентамино на три группы по четыре элемента. К каждой группе добавьте мономино (один квадратик) и постройте прямоугольник размером 3x7. Как это сделать, показано на рис. 237.

Рис. 237

Решение единственно с одной лишь оговоркой: в первом прямоугольнике мономино и элемент Y пентамино можно переворачивать, не меняя общей формы и площади составленной из них односвязной фигуры.

Доказать единственность решения можно следующим образом.

Прежде всего заметим, что на рис. 238 элемент X должен обязательно использоваться в паре с элементом U. Ни элемент F, ни элемент W не годятся для того, чтобы завершить построение прямоугольника.

Рис. 238

Если элемент X дополнить элементом U, то в том же самом прямоугольнике 3x7 уже нельзя будет использовать элементы F и W. Следовательно, из трех прямоугольников размером 3 х 7 в одном будут использованы элементы X и U, второй будет содержать элемент W (но не U), а третий - элемент F (но не U). Если теперь перебрать все возможные варианты прямоугольников и сравнить их (это отнимет у вас достаточно много времени), то окажется, что предполагаемое решение (см. рис. 237) единственно.

4. Разбейте двенадцать пентамино на четыре группы по три элемента в каждой. Найдите такой многоугольник площадью в 15 квадратов, который можно сложить из трех элементов каждой группы.

Решение этой головоломки неизвестно; с другой стороны, никто до сих пор не доказал, что задача неразрешима.

5. Найдите на шахматной доске область минимального размера, на которой умещается любой из двенадцати элементов пентамино.

Минимальная площадь такой области равна девяти квадратам, и известно всего две ее формы (рис. 239).

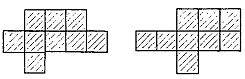
Рис. 239

Каждая фигура рис. 239 удовлетворяет поставленным условиям; для доказательства достаточно заметить, что на ней умещается любой элемент пентамино. Доказательство того, что число квадратов не может быть меньше девяти, проводится следующим образом.

Если бы годилась фигура, содержащая меньше девяти квадратов, то элементами I, X и V можно было бы закрыть не более восьми квадратов. При этом у элементов I и X было бы три общих квадрата. (В противном случае либо потребовалось бы девять квадратов, либо, что было бы излишней роскошью, самая длинная прямая состояла бы из шести квадратов.) Этого можно достичь всего лишь двумя разными способами (рис. 240), но в том и в другом случае нужен еще и девятый квадрат, чтобы уместить элемент U.

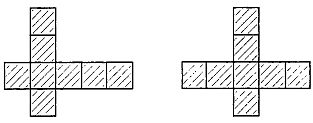
Рис. 240

Таким образом, восьми квадратов не хватает, в то время как из приведенных примеров видно, что девяти квадратов достаточно.

С появлением компьютеров задачи с пентамино начали исследовать на них. В главе 12 уже упоминалось о том, как Дана Скотт с помощью компьютера нашла все способы составления из двенадцати элементов пентамино шахматной доски размером 8х8 с квадратным отверстием в четыре клетки в центре. Было найдено 65 принципиально различных решений (два решения, получающиеся одно из другого поворотом или отражением, считаются одинаковыми). К. Б. Хейселгроув, математик из Манчестерского университета, перечислил с помощью компьютера все возможные варианты прямоугольника размером 6х10, сложенного из двенадцати пентамино. Он нашел 2389 различных решений, не считая тех, которые получаются друг из друга поворотами и отражениями! Кроме того, он проверил программу, составленную Даной Скотт для шахматной доски 8x8.

Из пентамино получаются прекрасные головоломки. На рис. 241,а изображена пирамида из 64 клеток, которую можно сложить из двенадцати элементов пентамино и квадратного тетрамино 2x2.

Необыкновенно сложно собрать из двенадцати пентамино крест, показанный на рис. 241,б. Для фигуры, изображенной на рис. 241,в, решения до сих пор не найдено (никто ее не сложил, но и невозможность построения тоже не доказана). Даже для случая, когда отверстие в форме мономино вырезано в другом месте, решения тоже не найдено. Рис. 241,г представляет собой фигуру, наиболее близкую по форме к предыдущей. По-видимому, также неразрешима головоломка Герберта Тейлора, показанная на рис. 241,д; правда, до сих пор никому не удалось доказать, что решения не существует.

К счастью, не все нерешенные задачи окутаны мраком неизвестности. Так, Т. М. Робинсон доказал, что, например, фигуру, которая изображена на рис. 241, е, нельзя сложить из двенадцати пентамино.

Рис. 241

С краев она ограничена 22 квадратами, а если внимательно изучить элементы пентамино и выписать, сколько квадратов каждого элемента может находиться на краю складываемой фигуры, то в сумме для всех элементов это число окажется равным 21, то есть на единицу меньше, чем надо. Такой способ рассуждений обычно используется в головоломках о складывании зигзагообразных брусочков. (На бумаге или картоне надо нарисовать прямоугольник с пилообразным краем и разрезать его на куски любой формы. Перемешайте куски и попробуйте сложить из них первоначальный прямоугольник.) Обычно различают внутренние и внешние части фигуры и в первую очередь стараются сложить края головоломки.

Полимино, занимающие четыре квадрата шахматной доски, называются тетрамино. В отличие от пентамино из пяти его различных элементов нельзя сложить прямоугольник. Для доказательства раскрасим в шахматном порядке прямоугольники площадью в 20 квадратов - их всего два: 4х5 и 2х10 (рис. 242).

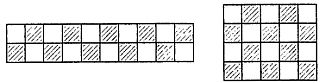
Рис. 242

Четырьмя из пяти элементов тетрамино можно накрыть два черных и два белых квадрата (рис. 243), а пятый, Т-образный элемент, всегда покрывает три квадрата одного цвета и один - другого.

Рис. 243

Поэтому все пять фигур тетрамино вместе занимают область, состоящую из нечетного числа квадратов каждого цвета, а оба прямоугольника, о которых идет речь, содержат по 10 квадратов каждого цвета, то есть состоят из четного числа квадратов.

С другой стороны, если взять несколько разных элементов пентамино, то любой из них вместе с пятью тетрамино образует набор, из которого можно построить квадрат размером 5x5. Два примера таких построений показаны на рис. 244.

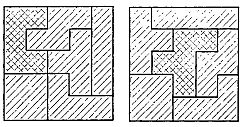
Рис. 244

Возникает интересный вопрос: сколько разных пентамино можно использовать для этой цели?

Аспирант-математик Орегонского университета Р. Джуэтт предложил задачу о домино (полимино из двух квадратов), совершенно непохожую на те задачи, которыми мы занимались до сих пор. Существует ли такой прямоугольник, сложенный из костей домино, в котором нельзя провести ни вертикальную, ни горизонтальную прямую, соединяющую противоположные стороны? В прямоугольнике, изображенном на рис. 245, для примера такая линия проведена между верхним и нижним основаниями. Если представить себе, что вместо домино взяты кирпичи, то существование такой линии («шва») будет свидетельствовать о непрочной кладке.

Рис. 245

Таким образом, задача Джуэтта сводится к вопросу о том, как надо класть прямоугольные кирпичи, чтобы постройка не развалилась.

Соответствующие прямоугольники мы в дальнейшем будем называть «прочными» прямоугольниками. Очень многие, взявшись за эту задачу, вскоре сдаются, уверенные, что она неразрешима; на самом же деле существует бесконечное множество ее решений.

Я предлагаю читателю вооружиться набором домино (более чем достаточно взять обычный комплект из 28 костей) и попытаться определить размеры самого маленького из «прочных» прямоугольников, который можно из них сложить.

С тех пор как эта глава появилась в Scientific American, в изучении полимино и «прочных» прямоугольников произошли большие изменения. В 1965 году вышла книга Голомба «Полимино», в которой проводится тщательное исследование предмета.

Выяснилось, что головоломка Г. Тейлора (рис. 241, д) и зубчатый квадрат (рис. 241, в) неразрешимы; однако ни для той, ни для другой фигуры до сих пор не найдено краткого и изящного доказательства невозможности их построения.

Можно сложить зубчатый квадрат, в котором мономино (отверстие) находится на краю, рядом с углом или в углу. Найдены шестнадцать разных решений последнего типа. Однако пока не известно, может ли мономино отстоять от угла дальше чем на одну клетку.

Пэттон, много лет занимающийся «прочными» прямоугольниками, составленными из домино, прислал мне новые интересные задачи. Каковы, например, минимальные размеры «прочного» прямоугольника, в котором одинаковое число костей домино расположено по вертикали и горизонтали? Может быть, читателю захочется самому найти решение, поэтому я привожу только ответ: размер прямоугольника 5x8.

Складывая из домино «прочные» квадраты, можно придумать массу игр, которые, насколько мне известно, совсем не изучены.

Например, противники кладут по очереди домино на квадратную шахматную доску. Выигрывает тот, кто первым построит вертикальную и горизонтальную линии «потери прочности» или наоборот: тот, кто первым построит такие линии, проигрывает.

Ответы

На рис. 246 и 247 показано, как можно сложить пирамиду и крест.

Рис. 246 Как сложить пирамиду.

Рис. 247 Как выложить крест.

Оба решения не являются единственными.

Для определения того, какой элемент пентамино надо добавить к пяти тетрамино, чтобы из всех шести фигур можно было построить квадрат размером 5x5, годятся все элементы пентамино, кроме элементов I, T, X и V.

Самый маленький «прочный» прямоугольник, который можно сложить из домино, имеет размер 5x6. Два принципиально различных решения изображены на рис. 248.

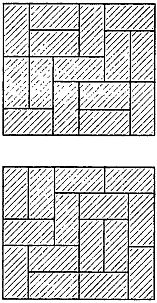
Рис. 248 Ответы к задаче о «прочных» прямоугольниках.

Нетрудно показать, что минимальная ширина «прочного» прямоугольника должна быть больше четырех. (Случаи, когда ширина прямоугольника равна 2, 3 и 4, лучше всего рассматривать по отдельности.) Поскольку квадрат размером 5x5 состоит из нечетного числа квадратов, а площадь области, построенной из домино, всегда четна, то минимальные размеры прямоугольника равны 5x6.

Прямоугольник 5x6 можно увеличить до размеров шахматной доски (8х8), и он все-таки будет «прочным». Пример такого построения изображен на рис. 249.

Рис. 249 Прочный прямоугольник на шахматной доске размером 8x8 клеток.

Как это ни удивительно, но не существует «прочных» прямоугольников размером 6x6. Этот факт имеет замечательное доказательство.

Представьте себе, что прямоугольник 6x6 целиком покрыт домино. Для этого нужно 18 костей домино (половина площади), а чтобы разделить прямоугольник на клетки, понадобится 10 линий (пять вертикальных и пять горизонтальных). Прямоугольник будет «прочным», если прямая из образующих сетку пересекает по крайней мере одно домино.

Приступая к доказательству, прежде всего покажем, что в любом «прочном» прямоугольнике каждая прямая сетки границ пересекает четное число элементов домино. Рассмотрим любую вертикальную прямую сетки. Площадь слева от нее четна (то есть выражается четным числом единичных квадратов): 6, 12, 18, 24 или 30. Те домино, которые целиком находятся слева от этой прямой, должны занимать четную площадь, поскольку каждый элемент домино покрывает два квадрата. Домино, которые разрезаются этой прямой, тоже занимают слева от нее четную площадь, потому что эта площадь равна разности двух четных чисел (всей площади слева от прямой и площади неразрезанных домино, тоже находящихся слева). Но поскольку разрезанное домино занимает всего один квадрат слева от выбранной прямой, то число элементов домино, разрезаемых прямой, должно быть четным. Сетка в квадрате 6x6 состоит из девяти прямых. Чтобы прямоугольник был «прочным», каждая прямая должна пересекать по крайней мере два домино.

Ни одно домино нельзя пересечь более чем одной линией сетки, поэтому сетка разрезает по крайней мере 12 домино. А в квадрате 6x6 всего лишь 18 домино!

Аналогичным образом можно показать, что прямоугольник 6x8 будет «прочным» только в том случае, если каждый отрезок сетки границ пересекает ровно два домино. Такой прямоугольник изображен на рис. 250.

Рис. 250 Прочный прямоугольник 6x8.

В самом общем виде результат можно сформулировать так: из домино можно сложить «прочный» прямоугольник, если его площадь четна, а длина и ширина больше четырех; исключение составляет квадрат 6х6. В действительности, чтобы сложить прямоугольник большего размера, нужно применить к прямоугольникам 5х6 и 6х8 метод увеличения длины или ширины на две единицы.

Проще всего объяснить, как это делается, с помощью рис. 251.

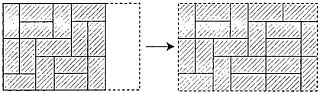
Рис. 251 Общее решение задачи о построении «прочного» прямоугольника.

Для удлинения фигуры в горизонтальном направлении на две единицы надо положить по одному домино рядом с каждым домино, лежащим горизонтально, а все вертикальные домино надо выдвинуть до новых границ, заложив освободившееся место горизонтальными домино.

Может быть, для читателя окажется интересным рассмотреть в качестве кирпичей элементы тримино. В частности, возникает вопрос: каковы наименьшие размеры «прочного» прямоугольника, который можно сложить из двух или большего числа «прямых тримино» (то есть прямоугольников размером 1x3)?

Примечания:

Kraitchik M. Mathematical Recreations. - 1942, p. 184.

Голомб С. Полимино. - М.: Мир, 1975.

Психоаналитический тест 6 квадратов онлайн на блоге психолога счастья. Самая полная и широкая психоаналитическая интерпретация ваших рисунков этого теста. Дорисуйте 6 рисунков и получите психологическую расшифровку теста.

Психоаналитические тесты

Чем Психоаналитический тест 6 квадратов отличается от психологического?

Практически не отличается, поскольку практика психологии — это прямая наследница психоанализа.

На блоге психолога счастья уже собрана приличная коллекция психологических и психоаналитических тестов онлайн.

Психологические тесты онлайн на www.сайт

Сегодня психолога счастья пополнится настоящим тестом, основанным на психоанализе.

Психоанализ, психиатрия, психология или психотерапия?

Рассмотрим кратко развитие психологического тестирования в исторической последовательности развития основополагающих наук.

Психолог, психоаналитик, психотерапевт и психиатр — кого выбрать?

Сперва возникла психиатрия, затем врач-психиатр Зигмунд Фрейд основал психоаналитическую школу психиатрии, потом от психоанализа отпочковалась ветка врачебной психологии — психотерапия, и ветка психологической науки.

Психолог работает с душой человека, он не ставит диагнозы и не назначает препараты, психолог работает в пределах душевной и личностной нормы. Однако он может осуществлять психотерапевтическое воздействие и применять психоаналитические методики в своей работе. — не медицинский психолог.
Психоаналитик-психолог работает методом психоанализ, он анализирует психическое, сновидения, личность клиента.
Психоаналитик-врач может к психоанализу добавить лечебные методики, жесткий гипноз и физио процедуры.
Психотерапевт — это врач, прошедший психологическую или психоаналитическую подготовку.
Психиатр — врач, который работает с душевнобольными людьми и клиентами с различными патологиями и расстройствами личности. Он работает в ненормой.

Сегодня мы познакомимся с психоаналитическим — и проанализируем некоторые черты нашей личности и отношение к некоторым сферам нашей жизни.

Психоаналитический тест 6 квадратов онлайн

Перед Вами на рисунке 6 квадратов, в каждом из которых незаконченный рисунок — причем закончить его можно каким угодно способом.

Прежде чем Вы начнете выполнять инструкцию к этому тесту, давайте договоримся о некоторых аспектах интерпретации.

Низ каждого квадрата — это материальный план, а верх квадрата — это духовный план бытия.
Левая треть квадрата — это прошлое, середина — настоящее и правая треть квадрата — будущее.
Если у Вас на рисунках есть законченные объекты — например животное, какой то знак — поищите в Интернете символическое значение этих объектов.
Назовите каждый рисунок — это даст дополнительную информацию по теме квадрата, даже если рисунок символический — все равно попробуйте дать ему название.
Поскольку основной анализ Вы будете делать самостоятельно — эта информация может Вам дать много нюансов.

Вопросы по анализу теста 6 квадратов можете задавать в комментариях к этой статье.

Инструкция к тесту Психоаналитический тест 6 квадратов:

Инструкция: дорисуйте последовательно (справа налево и сверху вниз — начиная с левого верхнего квадрата с точкой) рисунок в каждом из 6 квадратов.

Рисуйте быстро, не задумываясь и не пытаясь угадать, что должно быть нарисовано и как это будет расшифровано.

В психоаналитических тестах нет заранее готовой интерпретации и оценки тестового материала.

Расшифровка теста 6 квадратов

Краткое значение каждого из 6 квадратов-рисунков, которое призвано лишь натолкнуть Вас на собственный инсайт — открытие о себе.

Квадрат № 1 ЦЕЛИ

Рисунок, который Вы дорисовали в этом квадрате показывает какой характер имеют Ваши цели.

Если через точку в центре Вы провели линию или несколько лини — смотрите в какую сторону направлен рисунок, сколько этих линий-целей.
Когда точка становится центром фигуры, возможно сейчас у вас есть , которой вы следуете. Если точка — глаз какого-либо существа, то вы очень хорошо представляете себе, чего хотите.

Если же вы нарисовали рядом много других точек, значит, у вас много целей и вы не можете выбрать главную.

Квадрат № 2 КОНФОРМИЗМ

Ваш рисунок во втором квадрате говорит о том, насколько вы со стороны других людей или чужих идей.

Если вы нарисовали еще одну волнистую линию или больше, вы зависимы от мнения других.
Если у вас появился самостоятельный объект — кораблик, самолет или еще что-то, — вы склонны к самостоятельному принятию решения.

Сам по себе объект в этом рисунке сообщает насколько вы консервативная или творческая личность.

Квадрат № 3 ДОМ

Рисунок 3 квадрата показывает ваше отношение к семье и к дому.

Маленький квадратик на рисунке показывает и семейные принципы, а все остальное — внешний мир.
Где у вас больше элементов, туда больше направлено ваше внимание.

Если маленький квадрат стал окошком, а остальное пространство — комнатой, значит, семья для вас — все, а остальной мир — лишь фон.

Квадрат № 4 КОММУНИКАБЕЛЬНОСТЬ

Рисунок в 4 квадрате позволяет измерить вашу — умение взаимодействовать и находить общий язык с другими людьми.

Если вы соединила две линии — вы общительный человек. Если линии стали единым целым — рекой или дорогой, значит, общение с людьми лежит в основе вашей жизни.

Если на рисунке появились новые объекты — расшифруйте их символическое значение — это даст более широкое понимание ваших способностей общаться.

Квадрат № 5 МЫШЛЕНИЕ

На этом рисунке мы проверяем: конкретное или абстрактное у вас мышление.

Если вы нарисовали что-то реальное — фрукт, человека, машинку, — у вас . Это значит, что вы дружите с логикой и можете сделать успешную карьеру менеджера или финансиста.
Нарисовали непонятный узор из кружочков, завитушек и точек? Вы мыслите творчески. Вам покорятся и живопись, и театральная сцена!

Опять же все внимание символическим значениям нарисованных объектов и их расположению на квадрате.

Квадрат № 6 ЛЮБОВЬ

На этом рисунке вы поймете свое отношение к взаимодействию с противоположным полом.

Эта картинка трактуется почти как сны. Если вы объединили две линии в нечто высокое — у вас есть запретные мысли. Факел — вам не хватает страсти. Или, к примеру, небоскреб с окошками — вы в стадии выбора партнера. Если это деревья, значит, вам нужна теплота и романтика.

Рисунок в 6 квадрате показывает вашу позицию и или в дружеских.

ВНИМАНИЕ: Отметьте тот квадрат, который вызвал наибольшее затруднение или в котором так и не удалось ничего толкового нарисовать.

Возможно во время рисования в одном из квадратов Вы испытали какое-то чувство: обиду, раздражение, страсть, нежность или что-то еще — напишите в комментариях и скажу как это можно интерпретировать.

Пример расшифровки теста 6 квадратов-рисунков

Давайте коротко пройдемся по расшифровке психоаналитического теста, возможно это немного вам облегчит оценку и анализ ваших собственных рисунков.

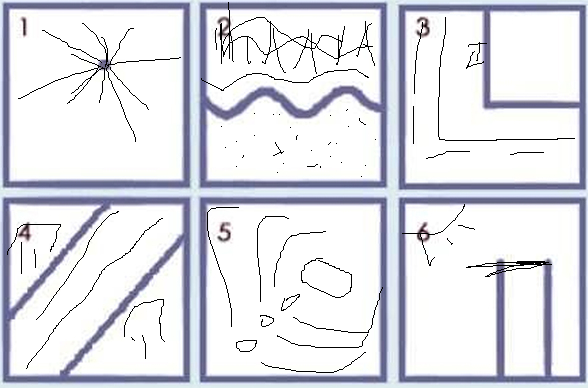
Пример заполненного теста 6 квадратов

Сразу оговорюсь — расшифровка рисунков далеко не полная — поскольку формат онлайн не позволяет развернуться вширь и вглубь.

Квадрат № 1. Много линий пересекает точку в центре — у человека возможно прямо сейчас, в настоящем очень много текущих и проблемных задач, которые сковывают энергетику человека, словно он попал в паутину (рисунок напоминает паука). Хотя, возможно сам человек бы увидел растрескавшуюся землю (пустыню) — тогда мы бы говорили о его одиночестве и опустошенности, или солнце — настроение близко к апатии и усталости. И все это касается достижения целей, исполнения мечт и решения повседневных задач.
Квадрат № 2. Человек скорее зависим, конформен. Причем в духовном плане он испытывает влияние сразу нескольких идей и похоже совсем запутался, а вот почва из под ног у него уходит. Его засасывает в трясину рутинных дел, в которых тоже много несобранности.
Квадрат № 3. Человек только ищет выходы на то, чтобы создать семью, построить собственный дом. Холодность и одиночество. Есть влияние из прошлого, которое мешает ему установить четкие границы, кроме того в отношениях с кандидатом, возможно происходит конфликт двух систем ценностей.

Квадрат № 4. Есть какие то проблемы в общении, попытка увязать свое прошлое и будущее. Причем четкого плана в общении с другими людьми нет — куда кривая выведет. Поведенческий репертуар узок — требуется дальнейшее развитие коммуникативных навыков.
Квадрат № 5. Мышление конкретное, хотя зачатки творческих способностей есть, но они не развиты в полную силу. Опять всплывает тема «паука» — я бы рекомендовал изучить этот символ подробнее.
Считается, что именно паук является символом судьбы человека, а также символом тех, кто лично создает свою судьбу.
Паук - древний символ созидания, творчества и трудолюбия.
А вот с этим материалом хорошо бы — например, к автору блога.
Квадрат № 6. Человеку в прошлом недоставало любви, или скорее наоборот — память о прошлых взаимоотношениях греет. В настоящее время на любовном фронте пусто. То ли вывешен флаг «о помощи», либо человек ждет весеннюю ласточку, которая принесет добрую весть. есть желание в ближайшем будущем соединить свое сердце с другим.

Предложение к тесту 6 квадратов от психолога счастья

С удовольствием отвечу на вопросы и запросы в каждом комментарии к этому тесту.

Если Вы хотите заказать полный анализ этого теста , применительно к вашей нынешней ситуации или проблеме — закажите услугу 3-х месячный абонемент с психологом (со скидкой в 950 рублей) и получите расшифровку теста 6 квадратов бонусом — в подарок к этой услуге* .

* Количество полных анализов теста ограничено, поскольку это отнимает много времени!

Блог психолога счастья — место, где Ваши мечты обретают силу.

Психоаналитический тест 6 квадратов прошли? Поделитесь его результатом в комментариях — очень интересна ваша оценка этого теста.

Психологический тест онлайн от психолога счастья. Введение в соционику. Краткий психологический портрет 16 типов личности. Определите по тесту свой […]

Из всего многообразия головоломок наиболее приемлемы в старшем дошкольном возрасте(5-7 лет) головоломки с палочками (можно использовать спички без серы). Их называют задачами на смекалку геометрического характера, так как в ходе решения, как правило, идет трансфигурация, преобразование одних фигур в другие, а не только изменение их количества. В дошкольном возрасте используются самые простые головоломки. Для организации работы с детьми необходимо иметь наборы обычных счетных палочек для составления из них наглядно представленных задач-головоломок. Кроме этого, потребуются таблицы с графически изображенными на них фигурами, которые подлежат преобразованию. На обратной стороне таблиц указывается, какое преобразование надо проделать и какая фигура должна получиться в результате.

Задачи на смекалку различны по степени сложности, характеру преобразования (трансфигурации). Их нельзя решать каким-либо усвоенным ранее способом. В ходе решения каждой новой задачи ребенок включается в активный поиск пути решения, стремясь при этом к конечной цели, требуемому видоизменению или построению пространственной фигуры.

Для детей 5-7 лет задачи на смекалку можно объединить в 3 группы (по способу перестроения фигур, степени сложности).

Задачи на составление заданной фигуры из определенного количества палочек: составить 2 равных квадрата из 7 палочек, 2 равных треугольника из 5 палочек.

Задачи на изменение фигур, для решения которых надо убрать указанное количество палочек.

Задачи на смекалку, решение которых состоит в перекладывании палочек с целью видоизменения, преобразования заданной фигуры.

В ходе обучения способам решения, задачи на смекалку даются в указанной последовательности, начиная с более простых, с тем чтобы усвоенные детьми умения и навыки готовили ребят к более сложным действиям. Организуя эту работу, воспитатель ставит цель - учить детей приемам самостоятельного поиска решения задач, не предлагая никаких готовых приемов, способов, образцов решения.

К такому самостоятельному поиску решения самых простых задач первой группы дети подготовлены в результате повседневной работы. Для этого достаточно дополнительно поупражнять их в составлении геометрических фигур (квадратов, прямоугольников, треугольников) из счетных палочек.

Составление геометрических фигур

(подготовительные игровые упражнения для детей 5 лет)

Цель. Упражнять детей в составлении геометрических фигур на плоскости стола, анализе и обследовании их зрительно-осязательным способом.

Материал: счетные палочки длиной 5 см (15-20 штук на ребенка), 2 толстые нитки длиной 25-30 см.

Ход работы. Воспитатель предлагает детям назвать известные им геометрические фигуры. После перечисления сообщает цель: "Будем составлять фигуры на столе и рассказывать о них". Дает задания:

1. Составить квадрат и треугольник маленького размера.

Вопросы для анализа: "Сколько палочек потребовалось для составления квадрата? Треугольника? Почему? Покажите стороны, углы, вершины фигур".

2. Составить маленький и большой квадраты.

Вопросы для анализа: "Из скольких палочек составлена каждая сторона большого квадрата? Весь квадрат? Почему левая, правая, верхняя и нижняя стороны квадрата составлены из одного и того же количества палочек?"

Можно дать задание на составление большого и маленького треугольника. Анализ выполнения задания проводится аналогично.

3. Составить прямоугольник, верхняя и нижняя стороны которого будут равны 3 палочкам, а левая и правая -2.

После анализа детям предлагают составить любой четырехугольник и доказать правильность выполнения задания.

4. Составить из ниток последовательно фигуры: круг и овал, большие и маленькие квадраты, треугольники, прямоугольники и четырехугольники. Маленькие фигуры составляются из нитки, сложенной вдвое.

Анализ фигур проводится по схеме: "Сравните и скажите, чем отличаются, чем похожи фигуры. Докажите, что фигура составлена правильно".

Уточнение представлений детей о геометрических фигурах; их элементарных свойствах (количество углов и сторон), упражнение в составлении будут способствовать усвоению детьми способов решения головоломок первой группы. Их предлагают детям в определенной последовательности:

Составить 2 равных треугольника из 5 палочек.

Составить 2 равных квадрата из 7 палочек.

Составить 3 равных треугольника из 7 палочек.

Составить 4 равных треугольника из 9 палочек.

Составить 3 равных квадрата из 10 палочек.

Из 5 палочек составить квадрат и 2 равных треугольника.

Из 9 палочек составить квадрат и 4 треугольника.

Из 10 палочек составить 2 квадрата: большой и маленький (маленький квадрат составляется из 2 палочек внутри большого).

Из 9 палочек составить 5 треугольников (4 маленьких треугольника, полученных в результате при-строения, образуют 1 большой).

Из 9 палочек составить 2 квадрата и 4 равных треугольника (из 7 палочек составляют 2 квадрата и делят на треугольники 2 палочками).

Для того чтобы решить эти задачи, нужно владеть способом при-строения, присоединения одной фигуры к другой. Впервые получив такое задание, дети пытаются составить 2 отдельных треугольника, квадрата. После ряда безуспешных попыток догадываются о необходимости пристроения к одному треугольнику, квадрату другого, для чего достаточно 2, 3 палочек.

По мере накопления детьми опыта в решении подобных задач методом "проб и ошибок" количество неправильных проб, практических действий начинает сокращаться. Исходя из этого, воспитатель, сохраняя занимательность, игровой характер упражнений, направляет ребят на целенаправленные пробы, которым предшествует хотя бы элементарное обдумывание конкретного хода решения. В процессе поиска решения обращает внимание ребят на то, что, прежде чем составлять ответ, надо подумать, как это можно сделать. Достаточно провести 3-4 занятия, в процессе которых дети овладевают способами пристроения к одной фигуре другой так, чтобы одна или несколько сторон оказались общими.

Примеры (для детей 5-6 лет)

Составление фигур из треугольников и квадратов

Цель. Учить детей составлять геометрические фигуры из определенного количества палочек, пользуясь приемом пристроения к одной фигуре, взятой за основу, другой.

Материал: У детей на столах счетные палочки, доска, мел на данном и следующем занятиях.

Ход работы. 1. Воспитатель предлагает детям отсчитать по 5 палочек, проверить и положить их перед собой. Затем говорит: "Скажите, сколько потребуется палочек, чтобы составить треугольник, каждая сторона которого будет равна одной палочке. Сколько потребуется палочек для составления двух таких треугольников? У вас только 5 палочек, но из них надо составить тоже 2 равных треугольника. Подумайте, как это можно сделать, и составляйте".

Цель. Составлять фигуры путем пристроения. Видеть и показывать при этом новую, полученную в результате составления фигуру; пользоваться выражением: "пристроил к одной фигуре другую", обдумывать практические действия.

Ход работы. Воспитатель предлагает детям вспомнить, какие фигуры они составляли, пользуясь приемом пристроения. Сообщает, чем они сегодня будут заниматься - учиться составлять новые, более сложные фигуры. Дает задания:

Рис. 2 Составление фигур из треугольников

Цель. Упражнять детей в самостоятельных поисках путей составления фигур на основе предварительного обдумывания хода решения.

Ход работы. Воспитатель задает детям вопросы: "Из скольких палочек можно составить квадрат, каждая из сторон которого равна одной палочке? 2 квадрата? (из 8 и 7). Как будете составлять 2 квадрата из 7 палочек?"

2. Из 5 палочек составить квадрат и 2 равных треугольника. Сначала рассказать, а затем составлять.

Цель. Упражнять детей в умении высказывать предположительное решение, догадываться.

Ход работы. 1. Из 9 палочек составить квадрат и 4 треугольника. Подумать и сказать, как надо составлять. (Несколько детей высказывают предположения.)

Рис. 3 Составление фигур из треугольников

2. Из 10 палочек составить 2 квадрата - маленький и большой.

3. Из 9 палочек составить 5 треугольников.

В какой последовательности надо предлагать детям 5-6 лет задачи на смекалку второй и третьей групп?

В фигуре, состоящей из 5 квадратов, убрать 4 палочки, оставив один прямоугольник (рис. 4).

В фигуре, состоящей из 6 квадратов, убрать 2 палочки, чтобы осталось 4 равных квадрата (рис. 5).

Составить домик из 6 палочек, а затем переложить 2 палочки так, чтобы получился флажок (рис. 6).

В данной фигуре переложить 2 палочки, чтобы получилось 3, равных треугольника (рис. 7)

В фигуре, состоящей из 5 квадратов, убрать 3 палочки, чтобы осталось 3 таких же квадрата (рис. 8).

В фигуре, состоящей из 4 квадратов, убрать 2 палочки, чтобы осталось 2 неравных квадрата (рис. 9).

В фигуре из 5 квадратов убрать 4 палочки, чтобы осталось 2 неравных квадрата (рис. 10).

В фигуре из 5 квадратов убрать 4 палочки, чтобы остались 3 квадрата (рис. 11).

В фигуре из 4 квадратов переложить 2 палочки так, чтобы получилось 5 квадратов (рис. 12).

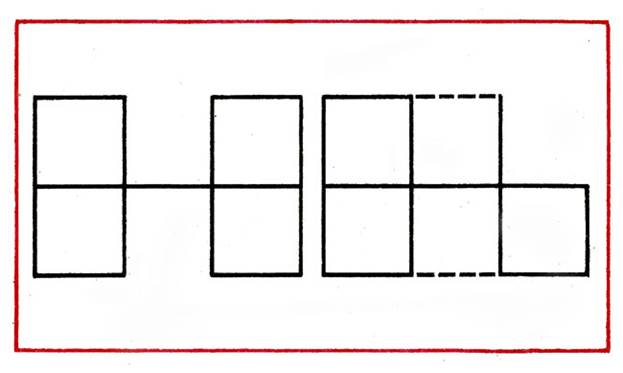
В фигуре из 5 квадратов убрать 4 палочки, чтобы осталось 3 квадрата (рис. 13).

Преобразование одной фигуры в другую. Изменение количества квадратов в фигуре.

Цель. Упражнять детей в умении решать задачи путем целенаправленных практических проб и обдумывания хода решения.

Материал: счетные палочки у детей, у воспитателя - изображенные графически задачи (на этом и следующих занятиях).

Ход работы. 1. Воспитатель показывает детям таблицу с изображенной на ней фигурой, предлагает составить из палочек такую же (рис. 4). Рассматривает ее вместе с детьми, определяет количество квадратов. Затем говорит: "Это задача. Послушайте, что нужно сделать, чтобы решить ее. Надо догадаться, какие 4 палочки убрать, чтобы получился 1 прямоугольник. Сначала подумайте, как это можно сделать, а затем убирайте палочки".

2. Дана фигура из 6 квадратов. Надо убрать 2 палочки, чтобы осталось 4 таких же квадрата (рис. 5).

Цель. Упражнять детей в умении осуществлять целенаправленные пробы, ограничивать количество практических проб за счет обдумывания хода поисков, догадки.

Ход работы. 1. Дана фигура из 5 квадратов. Надо убрать 3 палочки, оставив 3 квадрата (рис. 8). Воспитатель задает вопросы, побуждает детей к решению задачи: "Сколько квадратов в фигуре? Сколько должно остаться? Сколько палочек нужно убрать? Эта задача на смекалку, надо догадаться, какие 3 палочки нужно убрать, чтобы квадратов стало меньше - 3?"

Один из детей, решивших задачу в числе первых, зарисовывает и объясняет решение у доски.

2. Дана фигура из 4 равных квадратов. Надо убрать 2 палочки, чтобы получилось 2 неравных квадрата (рис. 9).

По предложению воспитателя один ребенок объясняет у доски решение задачи.

Цель. Высказывать предположительный ход поиска решения, проверять его путем целенаправленных поисковых действий.

Ход занятия. 1. Дана фигура из 5 равных квадратов; надо убрать 4 палочки, чтобы стало 3 равных квадрата (рис. 13).

2. Дана фигура из 4 квадратов: надо переложить 2 палочки, чтобы получилось 5 равных квадратов (рис. 12).

Для обучения детей самостоятельному анализу задачи, поиску решения, умению догадываться целесообразно использование различных методических приемов, указаний о необходимости поискового подхода к решению задачи: "Сначала подумайте, как бы вы решили задачу, и расскажите об этом. Проверьте свое предположение, переложив палочки или даже не трогая их. Если считаете, что ошиблись, надо придумать, как решить задачу по-другому, а не повторять своих ошибок. Надо внимательно рассмотреть фигуру и догадаться, как решить задачу". Оценка, подтверждение правильности или ошибочности хода: "Эту палочку ты убрал правильно, подумай, как дальше решать задачу" - и другое стимулируют активность ребят, помогают им находить правильное решение.

В работе с детьми 7-го года жизни усложняется характер задач на преобразование фигур. Решаются они путем сочетания практических и мысленных проб или только в плане умственного действия - в уме, с обоснованием, выражением в речи хода решения.

Последовательность выполнения детьми 6-7 лет задач на преобразование фигур.

Переложить 1 палочку чтобы домик был перевернут в другую сторону (рис. 15).

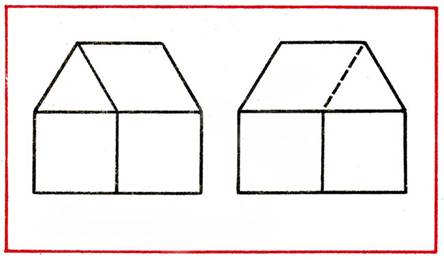
В фигуре, состоящей из 9 квадратов, убрать 4 палочки, чтобы осталось 5 квадратов (рис. 16).

В фигуре из 6 квадратов убрать 3 палочки, чтобы осталось 4 квадрата (рис. 17).

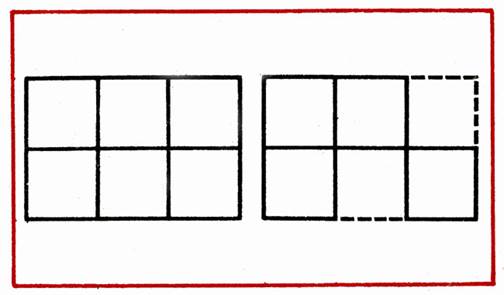
В фигуре, похожей на ключ, переложить 4 палочки, чтобы получилось 3 квадрата (рис. 18).

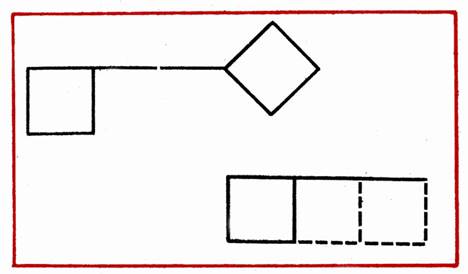
В фигуре из 6 квадратов убрать 2 палочки так, чтобы осталось 4 равных квадрата (рис. 19).

В фигуре, изображающей стрелу, переложить 4 палочки так, чтобы получилось 4 треугольника (рис. 20).

В фигуре из 5 квадратов переложить 3 палочки, чтобы стало 4 квадрата (рис. 21).

Рис. 21 В фигуре переложить 3 палочки так, чтобы получилось 4 равных треугольника

В фигуре, состоящей из 4 квадратов, переложить 3 палочки так, чтобы получилось 3 таких же квадрата (рис.23).

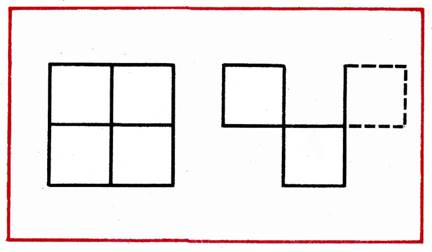
Переложить 4 палочки так, чтобы из топора получилось 4 равных треугольника (рис. 24).

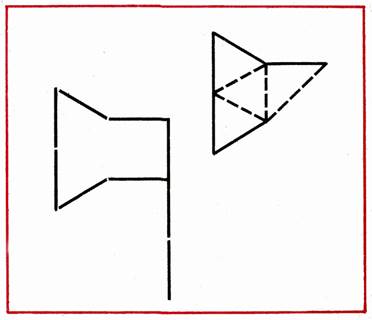
В фигуре, напоминающей фонарь, переложить 4 палочки, чтобы получился четырехугольник, состоящий из 4 равных треугольников (рис. 25).

Переложить 2 палочки так, чтобы фигура; похожая на корову, смотрела в другую сторону (рис. 26).

Какое наименьшее количество палочек нужно переложить, чтобы убрать мусор из совочка? (рис. 27.)

В подготовительной к школе группе обучение детей решению задач на смекалку способствует дальнейшему развитию их умственной деятельности, способности планировать ход поисков.

Примеры (для детей 6-7 лет)

Преобразование фигур

Цель. Упражнять детей в умении осуществлять целенаправленные поисковые действия умственного и практического плана, частичном мысленном решении задачи.

Ход работы. Воспитатель сообщает детям: "Сегодня будем решать новые, более сложные задачи на смекалку. Составьте из палочек вот такую фигуру (показывает) и расскажите, из каких геометрических фигур она состоит".

1. Дана фигура из 6 квадратов. Надо убрать 2 палочки, чтобы осталось 4 квадрата (рис. 19).

Воспитатель помогает детям в нахождении способов решения: "Подумайте, какие палочки надо убрать, чтобы квадратов стало меньше. Не торопитесь перекладывать палочки, сначала подумайте, как надо решать задачу. Убирать палочки можно только в том случае, если уменьшается количество квадратов в фигуре".

Решение задачи проверяется у доски.

2. Дана фигура, похожая на стрелу. Надо переложить 4 палочки, чтобы получилось 4 треугольника (рис. 20).

После анализа и уточнения условия задачи воспитатель спрашивает, кто из детей уже догадался, как решить ее. По заданию воспитателя некоторые дети высказывают предположительное решение так, чтобы не слышали другие. Воспитатель предлагает им проверить догадки практически. Поощряет действия, направленные на мысленное решение задачи, рассуждения, подчеркивает, что эта задача имеет несколько решений, которые зарисовываются на доске.

Цель. Планировать в уме полный или частичный ход решения, представлять изменения, которые произойдут в фигуре в результате преобразования, высказывать предположения.

Ход работы. В фигуре, похожей на лампу, переложить 3 палочки так, чтобы стало 4 равных треугольника (рис. 22).

Вопросы для анализа: "Как вы считаете, какие палочки и куда надо переложить? Что изменится в результате этого?"

Воспитатель предлагает детям высказать свои предположения и решать задачу.

В случае неправильного хода поисков (как показано на рис. 28) воспитатель поясняет, что при решении некоторых головоломок геометрические фигуры (треугольники, квадраты) могут находиться на расстоянии одна от другой.

Цель. Учить детей решать задачи на основе мысленного анализа путем выдвижения Гипотезы (предположения) и проверки ее.

Материал: магнитная доска с составленной на ней из палочек фигурой.

Ход работы. В фигуре фонаря переложить 4 палочки так, чтобы получился четырехугольник, состоящий из 4 равных треугольников (рис. 24).

Воспитатель говорит детям: "Вы решали много задач на составление фигуры из палочек. Эту задачу составлять из палочек не будете. Смотрите на доску, где зарисована эта задача, и попробуйте решить ее". Затем задает вопросы: "Из. скольких палочек составлена фигура фонаря? Сколько палочек нужно переложить, чтобы получилась другая фигура? Какая фигура должна получиться? Рассмотрите этот четырехугольник (показывает верхнюю часть фигуры). Какие здесь фигуры? Как можно составить такую фигуру?"

Далее детям предлагается проверить на магнитной доске ход решения, который они считают верным. Неверные пути дважды практическим способом не проверяются; в таких случаях воспитатель стимулирует поиск нового пути решения.

В подготовительной к школе группе многие дети при условии систематического обучения целенаправленно анализируют задачи на смекалку и обнаруживают простые рациональные способы их решения. Так, в задаче по преобразованию стрелы в 4 равных треугольника (показана на рис. 29) дети осмысленно объясняют возможные преобразования. Например, рассуждают: "Я вот так переложу палочки: эту (а) сюда, эту и эту (б и в) тоже вниз, чтобы получились треугольники, а эту (ж)... сейчас подумаю, куда ее положить... Вниз можно или сюда, и должно получиться 4 треугольника (рис. 29, б)", "Я думаю так решить эту задачу: 3 палочки (з, и, к) положить вот так, сверху, получится 3 треугольника, а эту (ж) - она ведь здесь не нужна - я положу сверху, получатся 4 треугольника, мы так раньше составляли" (рис. 29, в).

В ходе обучения время поиска детьми решения задачи сокращается, меняется характер проб, обдумывание решения начинает занимать все большее место. Поэтому на определенном этапе предложенную задачу дети смогли решить, анализируя ее на основе только графического изображения. Практическое составление и видоизменение фигур служило здесь средством проверки.

В результате регулярно организуемых педагогом занятий, упражнений по решению задач-головоломок дети приобретают способность подходить к каждой нестандартной задаче творчески, с позиции поиска нового пути решения, а не использования уже известного им. Характер поисковых действий при этом постепенно меняется: от практических ("проб и ошибок") - к целенаправленным практическим действиям (с целью намеченного преобразования), и от них - к мысленным пробам через предугадывание пути решения.

От решения задач-головоломок с помощью воспитателя (на основе частичных подсказок, использования наводящих вопросов, подтверждения частичного решения) дети переходят к полностью самостоятельному быстрому решению задач.

Дети 6-7 лет могут сами придумывать элементарные задачи на смекалку (головоломки с палочками). Для этого педагогу необходимо провести с детьми беседу о том, как придумываются такие задачи, что в них задано (какая-либо фигура), какое преобразование требуется осуществить (видоизменить фигуру, уменьшить или увеличить количество квадратов, треугольников, прямоугольников).

Головоломки с палочками, придуманные детьми:

Переложить 6 палочек, чтобы из корабля получился танк (рис. 30, а). (Ренат М., 6 лет 10 мес.)

В фигуре переложить 3 палочки, чтобы получился воздушный змей (рис. 30, б). (Лена М., 7 лет.)

Переложить 5 палочек, чтобы из вазы получился телевизор (рис. 30, в).

Переложить 1 палочку так, чтобы получилось 5 равных квадратов (рис. 30, г).

Переложить 3 палочки так, чтобы получилось 4 равных треугольника (рис. 30, д). (Илья М., 4 года 7 мес.).

Головоломки с палочками

Эти задачи очень просты, в каждой из них требуется произвести преобразование фигур путем перекладывания палочек. Они придуманы детьми по аналогии с теми задачами, что решались ими ранее, но, безусловно, являются показателем более высокого уровня развития пространственного представления, мышления.

Дети способны представить возможные пространственные, качественные изменения не только в ходе решения предложенной им задачи, но и в составляемой ими самостоятельно. Все это свидетельствует о развитии у них смекалки и сообразительности. При этом смекалку следует понимать как способность быстро устанавливать связи между частями задачи, направлять решение на правильный поиск его, исключая при этом ошибочный путь, отбрасывать несущественные элементы задачи.

Только на основе анализа условий задачи, самостоятельных поисков в результате овладения умственными операциями (обобщение, сравнение, анализ и др.) становится возможным проявление смекалки и самостоятельное умозаключение.

По мере овладения детьми приемами решения задач изменяется соотношение действий и рассуждений в ходе их решения. В начале обучения дети с трудом обосновывают свои до конца неосознанные практические действия, поэтому и процесс поиска складывается в основном из одних практических проб. Словесное выражение хода решения отражено в замечаниях: "Эти возьму", "Сюда положу", "Так нужно" и др. Под влиянием упражнений у детей начинают преобладать рассуждения, действия же становятся более целесообразными, сокращается их количество, назначение. Меняется характер и роль рассуждений: от рассуждений в процессе практических действий - к рассуждениям, предваряющим эти действия (выдвижение предположения, гипотезы решения). Кроме того, меняется качество рассуждений, которые сопровождают практические действия. Дети 6-7 лет аргументируют решение, доказывают правильность или ошибочность хода, исходя из данных задачи и цели трансфигурации. Они овладевают умением предполагать решение и проверять его без практических действий, т. е. в процессе умственного действия находить правильное решение задачи.

Задачи-смекалки геометрического характера частично включаются непосредственно в содержание занятий по формированию элементарных математических представлений в старшей и подготовительной к школе группах с целью активизации детской мысли, развития логического мышления, выработки умения догадываться, смекалки и сообразительности, что важно человеку для жизни, трудовой деятельности. При этом следует соблюдать строгую последовательность в усложнении самих задач, требований к организации поиска решения их детьми. - От занятия к занятию уточняется и усложняется анализ задач, характер поисковых действий, уровень проявления самостоятельности мышления и решения, сочетание действий и рассуждений.

“Пентамино” - одна из самых популярных мировых головоломок, пик популярности пришелся на конец 60-х годов. Сама игра подробно описывалась в журнале “Наука и жизнь”. В эту головоломку могут играть и дети и взрослые.

Запатентовал головоломку “Pentomino” Соломон Вольф Голомб , житель Балтимора, математик и инженер, профессор университета Южная Калифорния. Игра состоит из плоских фигур, каждая из которых состоит из пяти одинаковых квадратов, соединённых между собой сторонами, отсюда и название. Существуют еще версия головоломок Тетрамино, состоящие из четырех квадратов, от этой игры и произошел известный Тетрис.

Элементы Пентамино

Игровой набор “Пентамино” состоит из 12 фигурок. Каждая фигура обозначается латинской буквой, форму которой она напоминает. При решении задач и головоломок фигурки можно вертеть и переворачивать, поэтому при изготовлении игры своими руками элементы делайте двухсторонними.

Игры и игрушки на основе Пентамино

Сейчас в интернет магазинах можно найти игры и головоломки, сделанный на основе элементов Пентамино.

Пентамино своими руками

Предлагаем сделать элементы игры из плотного картона или пластика и обклеить цветной бумагой или клеящейся пленкой. Внизу представлен вариант изготовления из картона.

Рисуем каждый элемент на твердом картоне или пластике. Рисовать лучше, каждый элемент по отдельности, не складывая в прямоугольник - так вырезать будет легче.

Вырезаем первую фигуру “U”, перепроверяем размеры. Далее вырезаем все остальные элементы, проверяя чтобы они спокойно входили в элемент “U” своими выпуклыми частями. Подрезаем, если надо лишнее. На фотографии показаны элементы с размером квадратного модуля 2,5 х 2,5 сантиметра.

Обводим готовый картонный элемент на сложенной вдвое цветной бумаге и вырезаем сразу две цветные детали. Лучше цветные детали делать чуть меньше, чем картонные, и приклеиваются лучше, и края не будут отклеиваться от частого использования.

Клеим цветную бумагу с двух сторон к картону.

Находим коробочку для хранения деталей, куда потом будем складывать также схемы и задания к игре. Схемы можно распечатывать на сайте, а можно рисовать и раскрашивать на тетрадном листе в клеточку.

Читайте также

Преобразование одной фигуры в другую. Изменение количества квадратов в фигуре.

Примечания:

Психоаналитические тесты

Психоанализ, психиатрия, психология или психотерапия?

Психоаналитический тест 6 квадратов онлайн

Инструкция к тесту Психоаналитический тест 6 квадратов:

Расшифровка теста 6 квадратов

Квадрат № 1 ЦЕЛИ

Квадрат № 2 КОНФОРМИЗМ

Квадрат № 3 ДОМ

Квадрат № 4 КОММУНИКАБЕЛЬНОСТЬ

Квадрат № 5 МЫШЛЕНИЕ

Квадрат № 6 ЛЮБОВЬ

Пример расшифровки теста 6 квадратов-рисунков

Предложение к тесту 6 квадратов от психолога счастья

Элементы Пентамино

Популярные головоломки

Игры и игрушки на основе Пентамино

Пентамино своими руками